The Impact of Flow Rate Variations on the Power Performance and Efficiency of Proton Exchange Membrane Fuel Cells: A Focus on Anode Flooding Caused by Crossover Effect and Concentration Loss

Abstract

This study investigates the effects of anode and cathode inlet flow rates (ṁ) on the power performance of bipolar plates in a polymer electrolyte membrane fuel cell (PEMFC). The primary objective is to derive optimal flow rate conditions by comparatively analyzing concentration loss in the I−V curve and crossover phenomena at the anode, thereby establishing flow rates that prevent reactant depletion and water flooding. A single-cell computational model was constructed by assembling a commercial bipolar plate with a gas diffusion layer (GDL), catalyst layer (CL), and proton exchange membrane (PEM). The model simulates current density generated by electrochemical oxidation-reduction reactions. Hydrogen and oxygen were supplied at a 1:3 ratio under five proportional flow rate conditions: hydrogen (${\dot{m}}_{H_2}$ = 0.76–3.77 LPM) and oxygen (${\dot{m}}_{O_2}$ = 2.39–11.94 LPM). The Butler–Volmer equation was employed to model voltage drop due to overpotential, while numerical simulations incorporated contact resistivity, surface permeability, and porous media properties. Simulation results demonstrated a 24.40% increase in current density when raising ${\dot{m}}_{H_2}$ from 2.26 to 3.02 LPM and ${\dot{m}}_{O_2}$ from 7.17 to 9.56 LPM. Further increases to ${\dot{m}}_{H_2}$ = 3.77 LPM and ${\dot{m}}_{O_2}$ = 11.94 LPM yielded a 10.20% improvement, indicating that performance enhancements diminish beyond a critical threshold. Conversely, lower flow rates (${\dot{m}}_{H_2}$ = 0.76 and 1.5 LPM, ${\dot{m}}_{O_2}$ = 2.39 and 4.67 LPM) induced hydrogen-depleted regions, triggering crossover phenomena that exacerbated anode contamination and localized flooding.

1. Introduction

A fuel cell is an energy conversion device that directly transforms the chemical energy of a fuel into electricity. Unlike conventional internal combustion engines that use fossil fuels, fuel cells have no moving parts, resulting in no vibration or noise, and their only byproducts are water and heat generated from electrochemical reactions. Owing to these advantages, fuel cells are attracting attention as eco-friendly power systems in construction equipment, portable power systems, and the transportation sector [1].

Fuel cells share several characteristics with batteries. Batteries require recharging or replacement once their stored energy is depleted, and their lifespan is limited due to electrode degradation. In fuel cells, during prolonged operation, repeated moisture–dry cycles cause contraction and expansion of the membrane–electrode assembly (MEA), leading to widespread mechanical damage, such as cracks. This increases the permeability of reactant materials, resulting in enhanced crossover and flooding. Additionally, long-term operation causes degradation of electrode materials, reducing the active surface area of platinum (Pt) at the cathode and increasing maintenance and replacement costs—drawbacks both systems share [2].

On the other hand, as long as fuel and oxygen are continuously supplied, fuel cells can generate electricity continuously, are lighter than batteries, and can be easily configured into large stacks to provide high output. In particular, the ability to refuel instantly using fuel tanks allows for continuous operation, enabling recharging even during operation [3].

Various types of fuel cells have been studied depending on the operating environment and the type of electrolyte responsible for ion conduction. Among them, the polymer electrolyte membrane fuel cell (PEMFC) is most widely used. It converts chemical energy into electrical energy through oxidation-reduction reactions, where hydrogen (H₂) at the anode and oxygen (O₂) at the cathode serve as a fuel and an oxidant, respectively. PEMFCs are characterized by low operating temperatures (<100 °C), rapid response times of less than 4 ms, and a theoretical efficiency of up to 83% [3,4].

As shown in Figure 1a, a typical PEMFC unit cell consists of a bipolar plate (current collector, CC), gas channels (GC) for hydrogen and oxygen supply and water removal, a gas diffusion layer (GDL) for reactant transport through the porous medium, a catalyst layer (CL) where oxidation-reduction reactions occur at the triple-phase boundary (TPB), and a proton exchange membrane (PEM) for cation and electron transport [5,6].

With the expansion of PEMFC applications and market growth, various technical challenges related to fuel cell performance and durability have emerged. In particular, as illustrated in Figure 1b, performance degradation due to concentration loss during reactant transport and oxygen crossover has been identified as a major issue affecting power output and efficiency. Concentration loss occurs when the supply rate of reactants at the anode and cathode cannot keep up with the electrochemical reaction rate, leading to reactant depletion in the activation area and a subsequent decrease in current density and power output. This limitation becomes more pronounced under high-load conditions, significantly impeding fuel cell performance.

Anode crossover refers to the phenomenon where oxygen and water vapor molecules, rather than hydrogen, diffuse from the cathode to the anode through the proton exchange membrane (PEM). In this process, oxygen directly reacts at the electrodes, causing corrosion and degradation of the anode catalyst performance. Alternatively, gaseous and liquid H₂O back-diffuses into the anode flow channel, blocking hydrogen access to the anode catalyst and interfering with oxidation reactions. This not only reduces the long-term durability of fuel cells but also creates an imbalance in power performance [6].

Additionally, flooding due to uneven water distribution within the flow channels and membrane dry-out disrupts stable fuel cell operation, reducing reactant supply rates and inducing concentration loss. Particularly in large-scale commercialization of PEMFCs, higher output and current density are required. If water management is not properly implemented, massive water accumulation and flooding can obstruct reactant diffusion, leading to rapid performance degradation. To address these issues, ongoing research focuses on optimizing the reactant supply, applying gradient porosity structures in gas diffusion layers (GDLs) [7], and developing durable catalysts and membranes [8]. These efforts aim to maximize PEMFC performance and accelerate practical commercialization.

Various studies have been conducted to improve the durability and performance of PEMFCs. He et al. [9] quantitatively analyzed the degradation mechanisms of the PEMFC catalyst layer under dynamic operating conditions, demonstrating that the Pt dissolution rate increases by up to 28% compared to steady-state conditions, carbon corrosion reduces catalyst layer porosity by 15%, and the catalyst layer thickness decreases by 0.7 μm annually under dynamic load conditions. The study emphasized that mechanical stress and chemical reactions under dynamic conditions accelerate catalyst degradation and highlighted the importance of transient condition analysis for durability prediction. However, it did not analyze the effects of flow rate variation under steady-state conditions on catalyst degradation and cathode flooding. Chen et al. [10] experimentally analyzed flooding suppression strategies in PEMFCs under high-load conditions. The experimental results demonstrated that under high current density (≥2.0 A/cm²), increased water production causes GDL pore saturation and flooding, which impedes oxygen diffusion and accelerates concentration loss. While increasing the flow rate improves liquid water removal, exceeding 3.0 LPM induces a reactant concentration imbalance. They experimentally verified that flow rates within the 1.8–2.5 LPM range simultaneously mitigated concentration loss and flooding, emphasizing the necessity of flow rate optimization strategies for PEMFC commercialization. Lee et al. [11] performed numerical analyses on the effects of channel height and width in bipolar plates. The results showed that increasing the channel height reduced the pressure drop and thus decreased the power performance, while increasing the channel width improved the power performance by increasing the contact area with the gas diffusion layer. Cha et al. [12] conducted experiments by lowering the operating temperature from the standard 65 °C for low-temperature fuel cells. The results indicated that as temperature decreased, power performance dropped by 34% due to reduced mass transport and ionic conductivity.

While previous studies have focused on the channel geometry and operating temperature to enhance power performance, there has been a lack of research on how variations in flow rate, which affect concentration loss, oxygen crossover, and water flooding, impact reactant transport and electrochemical reaction characteristics. Therefore, in this study, the effects of the inlet flow rate on the power performance and efficiency of hydrogen fuel cells are analyzed using numerical simulations. Through this analysis, the impact of flow rate changes on concentration loss—a factor contributing to performance degradation—and oxygen crossover leading to water flooding is examined, and the necessity of optimal inlet flow rate conditions for maintaining maximum power and efficiency is proposed.

2. Methods

2.1. Numerical Analysis Model

Figure 2 shows the flow channel regions of the commercial bipolar plate model used in the numerical analysis. Figure 2a depicts the overlapping fluid regions of the fuel (anode) and oxygen (cathode) channels. Oxygen is supplied along the negative X-axis direction, while hydrogen flows in the positive X-axis direction. Figure 2b,c illustrate the anode flow channels for hydrogen and cathode flow channels for oxygen, respectively. Both channels feature identical serpentine parallel flow channel patterns. The reactants are divided into 74 microchannel bundles under 2 mm for the exhaust process. A counter-flow channel design was adopted, where reactants flow in opposite directions, and this configuration was selected as the baseline model for analysis.

Figure 3 presents a single fuel cell model incorporating a membrane–electrode assembly (MEA) into the commercial bipolar plate geometry. Figure 3a shows the full PEMFC model, while Figure 3b displays a cross-sectional view along line AB in Figure 3a. The model consists of nine stacked layers forming a single cell, with the thicknesses of CC and GC based on specifications of commercial bipolar plates. For the MEA, thin membranes risk durability issues and fuel leakage, whereas thick membranes increase resistance and degrade performance. Thus, membrane thickness was selected from prior studies to balance performance and durability, as shown in

Table 1. Geometric parameters of a PEMFC single cell.

Structures		Thickness (μm)
Cathode	Current collector, CC	1000
Cathode	Gas channel, GC	400
Membrane–electrode assembly, MEA		740
Anode	Gas channel, GC	400
Anode	Current collector, CC	1000

[13,14,15,16].

Numerical results were obtained using planes within the model, as shown in Figure 3c. Planes were generated at GDLs of the anode and cathode, 0.2 mm away from GCs, to analyze reactant distribution and flooding phenomena caused by electrochemical reactions. Current density and heat generation results were evaluated at the interface between CL and PEM.

2.2. Governing Equation of PEMFCs

In this study, numerical analysis of the fuel cell was conducted to investigate the power performance of the PEMFC. For this purpose, the fuel cell was assumed to operate under steady-state conditions, with the reactant gases modeled as pure hydrogen and air (ideal gases). Additionally, as shown in Figure 3, nine structural layers were stacked in a sandwich configuration. Due to the complex interactions occurring at the contact interfaces and within the structures, the application of appropriate governing equations with source terms in each region is critical [16].

Figure 4 illustrates the governing equations applied to the source terms within the PEMFC structural components. The color of each region represents the domain of material behavior, while the symbols denote areas where numerical values are calculated based on the governing equations of the source terms. The following sections describe the governing equations and source terms implemented in the above analysis [17].

2.2.1. Laminar Flow Model

First, the flow channels within the fuel cell adopted a microchannel bundle geometry, and due to the low Reynolds number, the laminar flow model was applied as follows:

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla ·\left(\rho \overrightarrow{u}\right)=S_m$$

(1)

$$\nabla ·\left(\overrightarrow{u}\right)=S_m=0$$

(2)

When selecting the laminar flow model, the continuity equation shown in Equation (1) was applied. Here, $S_m$ denotes the mass source term, $\rho$ is density, $t$ is time, ∇ is the vector differential operator, and $\overrightarrow{u}$ is the velocity vector. In fuel cell analysis, if the reaction gases were incompressible, the mass source term was defined, as shown in Equation (2).

2.2.2. Conservation of Momentum Equation

The conservation of momentum equation is defined as shown in Equation (3), where $\epsilon$ is porosity, $\mu$ is the viscosity coefficient, $K_p$ is permeability, and $S_P$ denotes the momentum source term. The momentum source term was applied to GC, GDL, and CL. For porous media, such as the GDL and CL, Darcy’s law was simplified and applied, as shown in Equation (4):

$${\displaystyle \frac{\partial \left(\epsilon \rho \overrightarrow{u}\right)}{\partial t}}+\nabla ·\left(ϵ\rho \overrightarrow{u}\overrightarrow{u}\right)=-ϵ\nabla P+\nabla ·\left(ϵ\mu \nabla \overrightarrow{u}\right)+S_p$$

(3)

$$\mathsf{ϵ}\overrightarrow{u}=-{\displaystyle \frac{k_p}{\mu }}\nabla P$$

(4)

2.2.3. Conservation of Energy Equation

Equation (5) corresponds to the conservation of energy equation, where $T$ denotes absolute temperature, $c_p$ is the specific heat capacity, $k_{eff}$ is the effective thermal conductivity, and $S_T$ represents the energy source term. The energy source term was applied to all regions except GC and was composed of Joule heating, heat from water production, latent heat, and electrical work, as shown in Equation (6):

$${\displaystyle \frac{\partial \left(\epsilon \rho c_{p}T\right)}{\partial t}}+\nabla ·\left(ϵ\rho c_p\overrightarrow{u}T\right)=\nabla ·\left(k^{eff}\nabla T\right)+ S_T$$

(5)

$$S_T=I^2{R}_{ohm}+\beta S_{H_{2}O}{h}_r+r_w{h}_L+\eta R_{a,c}$$

(6)

In the above equation, $I$ denotes the current, $R_{ohm}$ is the ohmic resistance, $\beta$ is the reaction coefficient, $S_{H_{2}O}$ represents the water formation source term, $h_r$ signifies the reaction heat, $r_w$ is the condensation rate, $\eta$ denotes the overpotential, and $R_{a,c}$ corresponds to the reaction rate at the electrodes.

2.2.4. Conservation of Species Equation

Equation (7) corresponds to the equation for water formation and transport. Here, $s$ denotes water saturation, ${\rho }_l$ is the density of liquid water, and ${\mu }_l$ is the viscosity of liquid water. In the catalyst layer (CL), which is a highly resistive porous region, the process was influenced by capillary pressure ($P_c$):

$${\displaystyle \frac{\partial \left(ϵ{\rho }_{l}s\right)}{\partial t}}+\nabla ·\left({\rho }_l{\displaystyle \frac{k_p{s}^3}{{\mu }_l}}{\displaystyle \frac{d{P}_c}{ds}}\nabla s\right)=r_w$$

(7)

Equation (8) represents the conservation of species based on Fick’s law of diffusion. Here, $c_i$ is the concentration of species $\mathrm{i}$, $D_{i,eff}$ is the effective mass diffusion coefficient of species $\mathrm{i}$, and $S_i$ denotes the source term for hydrogen, oxygen, and water, respectively. Equations (9)–(11) define the source terms for hydrogen, oxygen, and water at the anode and cathode, where $\mathrm{F}$ is Faraday’s constant and $j_{a,c}$ denotes the current density at the anode and cathode:

$${\displaystyle \frac{\partial \left(ϵc_i\right)}{\partial t}}+\nabla ·\left(\epsilon \overrightarrow{u}{c}_i\right)=\nabla ·\left(D_{i,eff}\nabla c_i\right)+S_i$$

(8)

$$S_{H_2}=-{\displaystyle \frac{1}{2F{c}_{totla, a}}}{j}_a$$

(9)

$$S_{O_2}=-{\displaystyle \frac{1}{4F{c}_{total,c}}} j_c$$

(10)

$$S_{H_{2}O}={\displaystyle \frac{1}{2F{c}_{total,c}}} j_c$$

(11)

2.2.5. Conservation of Current Equation

Equations (12) and (13) represent the current conservation equations. The electrochemical process of the fuel cell, namely, the oxidation-reduction reaction, occurred at the triple-phase boundary (TPB) within CL on both sides of the membrane. The transport equations for protons (H⁺) and electrons (e⁻) were influenced by the potential difference between CC, which is in the solid phase, and the membrane phase:

$$\nabla ·\left({\sigma }_s\nabla {\varnothing }_s\right)+ j_s=0$$

(12)

$$\nabla ·\left({\sigma }_m\nabla {\varnothing }_m\right)+ j_m=0$$

(13)

Equation (12) describes the process in which electrons (e⁻) move through the electrode and CC. Here, ${\sigma }_s$ is the electrode conductivity, ${\varnothing }_s$ is the electrode potential, and $j_s$ corresponds to the electron source term in the solid phase. Equation (13) represents the transport of protons (H⁺) through the membrane and CL, where ${\sigma }_m$ is the electrolyte conductivity, ${\varnothing }_m$ is the ionic potential, and $j_m$ denotes the ion source term in the membrane phase.

2.3. Overvoltage and Loss Mechanisms in Fuel Cells

In fuel cell systems, the key parameter for evaluating performance is the current density generated by electrochemical reactions. This current density was derived from the Butler–Volmer equation in the anode and cathode regions, as shown in Equations (14) and (15), and describes the relationship between current and potential in electrochemical reactions:

$$j_a=j_a^{ref}{\left({\displaystyle \frac{C_{H_2}}{C_{H_2}^{ref}}}\right)}^{{\gamma }_a}\left[exp\left({\displaystyle \frac{{\alpha }_{a}nF}{RT}}{\eta }_a\right)-exp\left({\displaystyle \frac{-{\alpha }_{a}nF}{RT}}{\eta }_a\right)\right]$$

(14)

$$j_c=j_c^{ref}{\left({\displaystyle \frac{C_{O_2}}{C_{O_2}^{ref}}}\right)}^{{\gamma }_c}\left[exp\left({\displaystyle \frac{{\alpha }_{c}nF}{RT}}{\eta }_c\right)-exp\left({\displaystyle \frac{-{\alpha }_{c}nF}{RT}}{\eta }_c\right)\right]$$

(15)

$${\eta }_a={\varphi }_s-{\varphi }_m-V_{ref}$$

(16)

$${\eta }_c={\varphi }_s-{\varphi }_m-V_{oc} \left(V_{ref}=V_{oc}\right)$$

(17)

In the above equations, $\gamma$ denotes the exponent representing the reaction concentration dependency of the fuel electrode (anode) and oxygen electrode (cathode). Here, $R$ is the gas constant, $\alpha$ is the charge transfer coefficient, and $n$ is the number of electrons involved in the reaction. Equations (16) and (17) calculate the overpotential at the anode and cathode, respectively. $V_{ref}$ corresponds to the reference potential. For the anode, the reference potential was set to ‘0’ since it is grounded. To establish a potential difference, the cathode was assigned the reference potential as the open-circuit voltage ($V_{oc}$), which was calculated via the Nernst potential equation in Equation (18):

$$V_{oc}=\mathrm{E}={\displaystyle \frac{-\mathsf{\Delta }{G}_0}{2F}}+{\displaystyle \frac{RT}{2F}} ln\left({\displaystyle \frac{P_{H_2}\sqrt{P_{O_2}}}{P_{H_{2}O}}}\right)$$

(18)

In the equation, $\mathsf{\Delta }{G}_0$ denotes the Gibbs free energy change of the reaction under standard pressure and temperature conditions, and $P_i$ represents the partial pressure of each reactant species. The Nernst potential refers to the potential generated to counteract the ion concentration gradient across the membrane under electrochemical equilibrium. Typically, under standard conditions ($T_{amb}=25° \mathrm{C}$, $P_{atm}=101.325 \mathrm{k}\mathrm{P}\mathrm{a}$), the theoretical Nernst potential is 1.229 V.

Figure 5 illustrates the irreversible voltage loss process in a PEMFC through the I−V curve, highlighting the contributions of activation loss, ohmic loss, and concentration loss. When the Butler–Volmer equation was applied to numerically simulate the behavior of an actual fuel cell, the voltage decreased from the theoretical maximum voltage, also known as the Nernst potential, due to three mechanisms.

Additionally, through Figure 5, it was confirmed that the governing equations described earlier could construct an I−V curve graph, where voltage decreased as current density increased due to three types of losses, and this exhibited the same trend as the I−V curve experimentally presented by Yuan et al. [18].

Activation loss arose from overcoming the activation energy barrier required to initiate electrochemical reactions at the catalyst layers. Ohmic loss was caused by electrical resistance to proton and electron transport across components, such as the membrane and current collectors. Concentration loss occurred due to the reduced reactant concentration at high current densities, which limited the ability to sustain the reaction under heavy load.

As a result, based on the governing equations derived earlier, the voltage in the PEMFC system, with increasing current density, was expressed as the difference between the theoretical voltage and the losses, as shown in Equation (19):

$$\mathrm{V}=V_{oc}-V_{act}-V_{ohm}-V_{con}$$

(19)

2.4. Boundary Conditions for Numerical Analysis

Fuel cells require a continuous supply of fuel and oxidant to generate power. However, if the inlet flow rate is excessive, issues such as increased power consumption by pumps and auxiliary devices can arise. Conversely, if the inlet flow rate is insufficient, effective delivery and diffusion of reactants are hindered, which can lead to reactant crossover and concentration loss, ultimately limiting the current density. Therefore, in this study, numerical analysis was conducted by selecting the inlet flow rate as a variable that affects both power performance and mass transport.

Table 2. PEMFC model boundary conditions for numerical analysis.

Content		Condition
Numerical analysis program		Ansys fluent
Working fluid		H2, O2, H2O (Vapor)
Operating pressure (kPa)		151.33
Outlet pressure (kPa)		101.33
Inlet temperature (K)		338.15
$\mathrm{Open}-\mathrm{circuit} \mathrm{voltage}, V_{oc}$ (V)		1.1
$\mathrm{Contact} \mathrm{resistivity} (\mathsf{\Omega }/{\mathrm{m}}^2$)		$2\times {10}^{-6}$
$\mathrm{Face} \mathrm{permeability} ({\mathrm{m}}^2$)		$1\times {10}^{-11}$
Relative humidity (%)	Anode	20
	Cathode	60
Porosity in GDL, CL		0.55
Operating cell voltage (V)		1–0.4
Mass flow rate (LPM)	Case	1	2	3	4	5
	Anode	0.76	1.5	2.26	3.02	3.77
	Cathode	2.39	4.67	7.17	9.56	11.94

presents the boundary conditions for the numerical analysis of the PEMFC model. The main operating fluids were set as hydrogen (H₂), oxygen (O₂), and water vapor (H₂O). To facilitate water management through uniform diffusion and exhaust of the operating fluids within the flow channels, the inlet pressure ($P_{inlet}$) was set to 151.325 kPa and the outlet pressure ($P_{outlet}$) to 101.325 kPa. In addition, increasing the operating pressure raised the partial pressure of the reactants, which increased the chemical reaction rate and had the advantage of reducing activation loss. For the operating temperature ($T_{op}$), a value of 338.15 K was applied to both the anode and cathode, considering stability and performance, in order to prevent power loss due to thermal degradation from electrochemical reactions within the PEMFC. To match the experimentally measured open-circuit voltage, a voltage of 1.1 V, which is lower than the Nernst voltage, was used.

To accurately simulate power loss and electrical conductivity within the fuel cell, a contact resistivity of $2\times {10}^{-6} \mathsf{\Omega }/{\mathrm{m}}^2$ was applied at the interface between CC and GDL. Additionally, as shown in Figure 6, a face permeability of $1\times {10}^{-11} {\mathrm{m}}^2$ was assigned to the contact interface between GC and GDL to enable reactants to move perpendicular to the flow channel direction from the anode to the cathode through the porous medium. Notably, in PEMFCs, reactants must be efficiently transported from GC through GDL to CL, where face permeability plays a critical role in regulating the movement of reactants and products. For porous media, such as the GDL and CL, a porosity of 0.55 was assigned, which serves as a key parameter controlling reactant diffusion and water removal. If porosity is not properly adjusted, insufficient reactant supply or water accumulation may occur, leading to electrode flooding phenomena [19].

Additionally, to investigate anode flooding, identified as a key factor in performance degradation in the fuel cell model, the relative humidity (RH) was set to 20% at the anode and 60% at the cathode. This configuration created extreme conditions at the anode, deviating from typical membrane hydration states. For the cathode, 60% RH was selected because it generally exhibits high electrochemical reaction performance and prevents flooding caused by water generated in the porous media or flow channels [20].

To reproduce the actual operating environment of the fuel cell and quantitatively represent the interactions of electrochemical reactions under various voltage conditions, the operating voltage ($V_{cell}$) was incrementally reduced from 1 V to 0.4 V in 0.1 V steps during the analysis. The inlet flow rates were maintained at a hydrogen-to-oxygen ratio of 1:3, based on the manufacturer’s specifications for the bipolar plates. Furthermore, starting from the baseline Case 1, which used hydrogen at 0.76 LPM and oxygen at 2.39 LPM, Cases 2 to 5 were proportionally scaled by factors of 2, 3, 4, and 5, respectively. Detailed flow rate values are provided in Table 2.

2.5. Grid Dependency Tests of PEMFC Model

Prior to conducting numerical analysis, grid dependency verification was performed to analyze the impact of grid geometry and quantity on the simulation results and ensure the reliability and accuracy of the analysis.

The PEMFC model used in this study was constructed based on the actual size and geometry of the bipolar plate and flow channels, which inherently included a highly complex structure. However, applying uniform mesh refinement across all components of the PEMFC system is inefficient and does not guarantee highly reliable results. Therefore, it was determined that mesh generation priorities should be assigned according to the functional roles of components, considering grid sensitivity.

For CC, which is part of the bipolar plate, this region is a solid domain where the primary functions are current and heat conduction, with no fluid flow or electrochemical reactions occurring. Thus, fine mesh refinement was deemed less critical and excluded from high-priority areas. In contrast, GC, GDL, CL, and PEM were identified as critical regions requiring refined mesh due to their roles in reactant diffusion, electron/ion transport, and water management. By focusing mesh refinement on these critical areas, the computational time was minimized while ensuring the reliability of the simulation results [21].

Based on this mesh generation strategy, numerical analysis was conducted under six grid conditions to verify grid dependency. For all grid conditions, the inlet flow rate of Case 5 and the operating voltage of 0.8 V were uniformly applied. The number of mesh elements was configured to increase progressively from G1 to G6, with the mesh geometry specified as a hybrid of hexahedral and tetrahedral structures. The number of meshes used for each case is provided in

Table 3. The number of elements used for grid dependency.

Condition	Elements
G1	17,103,455
G2	20,027,960
G3	29,583,851
G4	45,106,287
G5	71,900,518
G6	135,104,270

.

Figure 7a compares the current density in the fuel cell according to grid size. The current density generated by electrochemical reactions within the PEMFC is a critical indicator reflecting electron transfer characteristics. Analysis results showed that the current density increased by 0.88% from grid condition G1 to G3 but decreased by 0.29% when transitioning to grid condition G4. Subsequently, under grid conditions G5 and G6, the current density stabilized at the same value of 0.52 A/cm². This indicates that when the number of grids increased beyond a certain level, the performance of electron transfer and reactant diffusion converged stably.

Figure 7b shows the temperature in the cathode catalyst layer (CL), where electrochemical reactions are concentrated, as a function of grid size. The temperature within the CL influenced the electrochemical reaction rate, and higher temperatures generally accelerated reaction kinetics. If the temperature is not calculated accurately, the reliability of the reaction model may be compromised. The analysis revealed a 0.04% temperature increase when transitioning from grid condition G1 to G2. However, from grid condition G3 onward, the temperature remained constant. This suggests that, similar to the current density results, increasing the number of grids beyond a certain threshold did not significantly affect the temperature analysis outcomes.

Commonly, after the G4 grid condition exhibited uniform differences, the G5 grid condition was selected for subsequent analysis processes. This decision was based on its ability to provide accurate and reliable results while balancing grid density and computational efficiency. Specifically, the G5 condition showed a 37% increase in grid count compared to G4 but maintained an error rate below 0.04%, whereas the G6 condition required 47% more grids than G5 without improving accuracy. Thus, G5 was deemed optimal in terms of reliability and computational efficiency.

Figure 8 illustrates the grid generated using the G5 condition and its orthogonality, confirming that a refined mesh was formed in the membrane–electrode assembly (MEA) region. The grid exhibited a high average orthogonal quality of 0.8, ensuring numerical stability and precision.

3. Results and Discussions

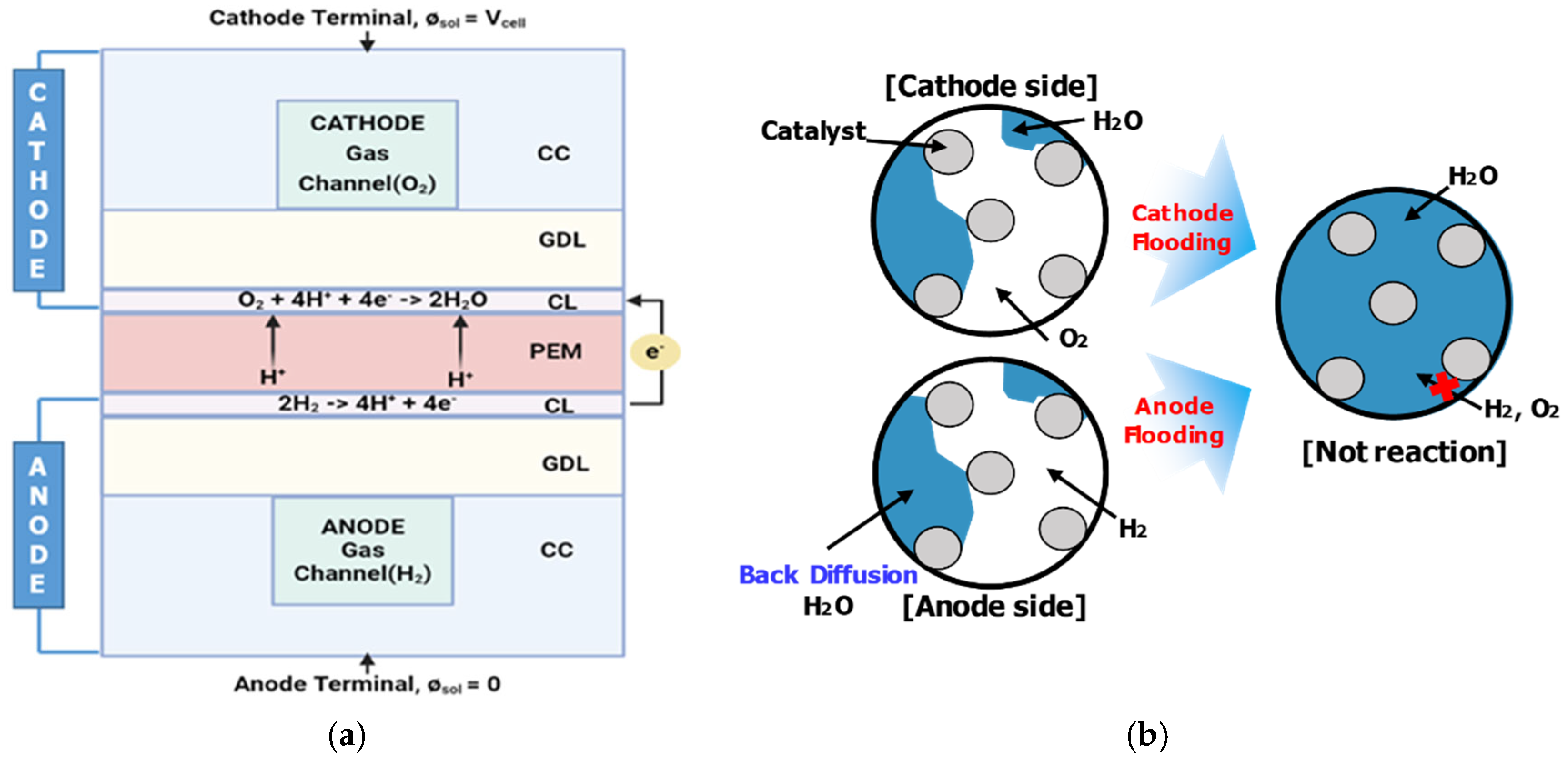
3.1. I−V and I−P Polarization Curves with Concentration Loss

A representative method for evaluating the performance of a PEMFC is to analyze the I−V and I−P polarization curves. The I−V curve reflects the electrochemical reaction rate and internal resistance characteristics of the fuel cell, while the I−P curve is used to determine the operating conditions at which the fuel cell delivers maximum power [22]. Therefore, in this study, the power performance of the fuel cell was analyzed by varying the mass flow rates of hydrogen and oxygen. If the reactant flow rate inside the fuel cell is insufficient, concentration loss increases due to a lack of reactants, whereas excessive flow rates can reduce the overall system efficiency.

Figure 9a presents the numerical analysis results of current density under varying hydrogen and oxygen inlet flow rates. Under all conditions, the current density exhibited a proportional increase with higher flow rates, while the operating voltage decreased. This behavior was attributed to the boundary conditions and governing equations implemented in the study, which accounted for activation loss, ohmic loss, and concentration loss within the PEMFC system.

Figure 9b illustrates the power density as a function of the inlet flow rate. Since power density was influenced by current density, it showed a proportional relationship in the low-current-density region. However, in the high-current-density region, power density peaked and then decreased due to concentration loss.

Additionally,

Table 4. Results of current density and power density with cell voltage in each case.

Condition	Current Density (A/cm2)
Cell Voltage (V)	Case 1	Case 2	Case 3	Case 4	Case 5
1.0	0.03	0.03	0.03	0.03	0.03
0.9	0.14	0.27	0.27	0.27	0.27
0.8	0.22	0.40	0.51	0.51	0.52
0.7	0.25	0.41	0.59	0.72	0.74
0.6	0.28	0.48	0.65	0.83	0.85
0.5	0.30	0.53	0.71	0.88	0.93
0.4	0.30	0.53	0.75	0.93	1.02
Condition	Power Density (W/cm2)
Cell Voltage (V)	Case 1	Case 2	Case 3	Case 4	Case 5
1.0	0.03	0.03	0.03	0.03	0.03
0.9	0.12	0.24	0.24	0.24	0.24
0.8	0.17	0.32	0.42	0.41	0.42
0.7	0.18	0.29	0.42	0.50	0.52
0.6	0.17	0.29	0.39	0.50	0.51
0.5	0.15	0.26	0.35	0.44	0.46
0.4	0.12	0.21	0.30	0.37	0.41

provides the current density and power density values corresponding to the results shown in Figure 9a,b.

For Case 1 with hydrogen 0.76 LPM and oxygen 2.39 LPM, the minimum flow rate was applied, and the maximum current density observed was 0.30 A/cm². In the high-voltage regions of 1.0 V and 0.9 V, voltage reduction due to activation loss was prominent, followed by concentration loss caused by insufficient flow rates. This resulted in a steeper voltage decline compared to the increase in current density, with a faster drop relative to other cases. The maximum power density of 0.18 W/cm² occurred at a cathode terminal operating voltage of 0.7 V. In high-current regions, power density decreased due to an inefficient relationship between rising current density and voltage.

For Case 2 with hydrogen 1.50 LPM and oxygen 4.67 LPM, where flow rates doubled compared to Case 1, the maximum current density increased to 0.53 A/cm². The improved reactant supply mitigated activation and ohmic losses, resulting in a gentler voltage decline. However, insufficient flow rates still induced concentration loss, causing a sharp voltage drop after 0.8 V. The maximum power density reached 0.32 W/cm² at 0.8 V, marking a 77.78% increase over Case 1, attributed to enhanced current density from higher flow rates.

For Case 3 with hydrogen 2.26 LPM and oxygen 7.17 LPM, tripling the flow rates of Case 1, the maximum current density rose to 0.75 A/cm². As flow rates stabilized, voltage drops from activation and ohmic losses slowed. Conversely, concentration loss became more significant, driving voltage decline after 0.8 V. The maximum power density of 0.42 W/cm² at 0.8 V represented a 31.25% improvement over Case 2.

For Case 4 with hydrogen 3.02 LPM and oxygen 9.56 LPM, quadrupling the flow rates of Case 1, the maximum current density reached 0.93 A/cm². Voltage drops from activation/ohmic losses remained gradual, while concentration loss emerged at 0.7 V. Further flow rate increases had minimal impact on voltage improvement. The maximum power density of 0.50 W/cm² at 0.7 V showed a 19.05% increase over Case 3, though power density gains began to diminish.

For Case 5 with hydrogen 3.77 LPM and oxygen 11.94 LPM, five times the flow rates of Case 1, the maximum current density reached 1.02 A/cm², corresponding to the limiting current density under the PEMFC model conditions. The maximum power density of 0.52 W/cm² at 0.7 V showed only a 4.0% increase over Case 4, indicating diminishing returns despite higher flow rates.

In PEMFCs, the phenomenon where the rate of current density increase diminished despite rising flow rates stemmed from the interaction between reactant diffusion and electrochemical reaction kinetics. This was explained within the numerical analysis of the PEMFC model using the convection–diffusion equation, Butler–Volmer equation, and Darcy’s law in porous media. Specifically, under high-flow conditions, increased flow velocity in the convection term and insufficient time for reactants to diffuse or reside within the porous GDL and CL led to reactant expulsion before reaching the catalyst layer. This resulted in concentration loss due to hindered reactant supply in the catalyst layer, causing a slowdown in current density growth. Thus, at low flow rates, flooding caused by crossover blocked reaction channels and pores, impairing performance, while at high flow rates, excessive velocity itself became a performance-limiting factor.

Additionally, it was observed that at a cell voltage of 0.4 V, all flow rate conditions exhibited the maximum current density. This reflects the characteristic where the current load continued to increase even as the voltage decreased. Furthermore, since power density was derived from the relationship between current and voltage, it did not necessarily peak at the same voltage. Therefore, for high-current operation, ensuring sufficient flow supply is essential, and optimizing the flow rate to minimize concentration loss remains critical, even as the cell voltage decreases.

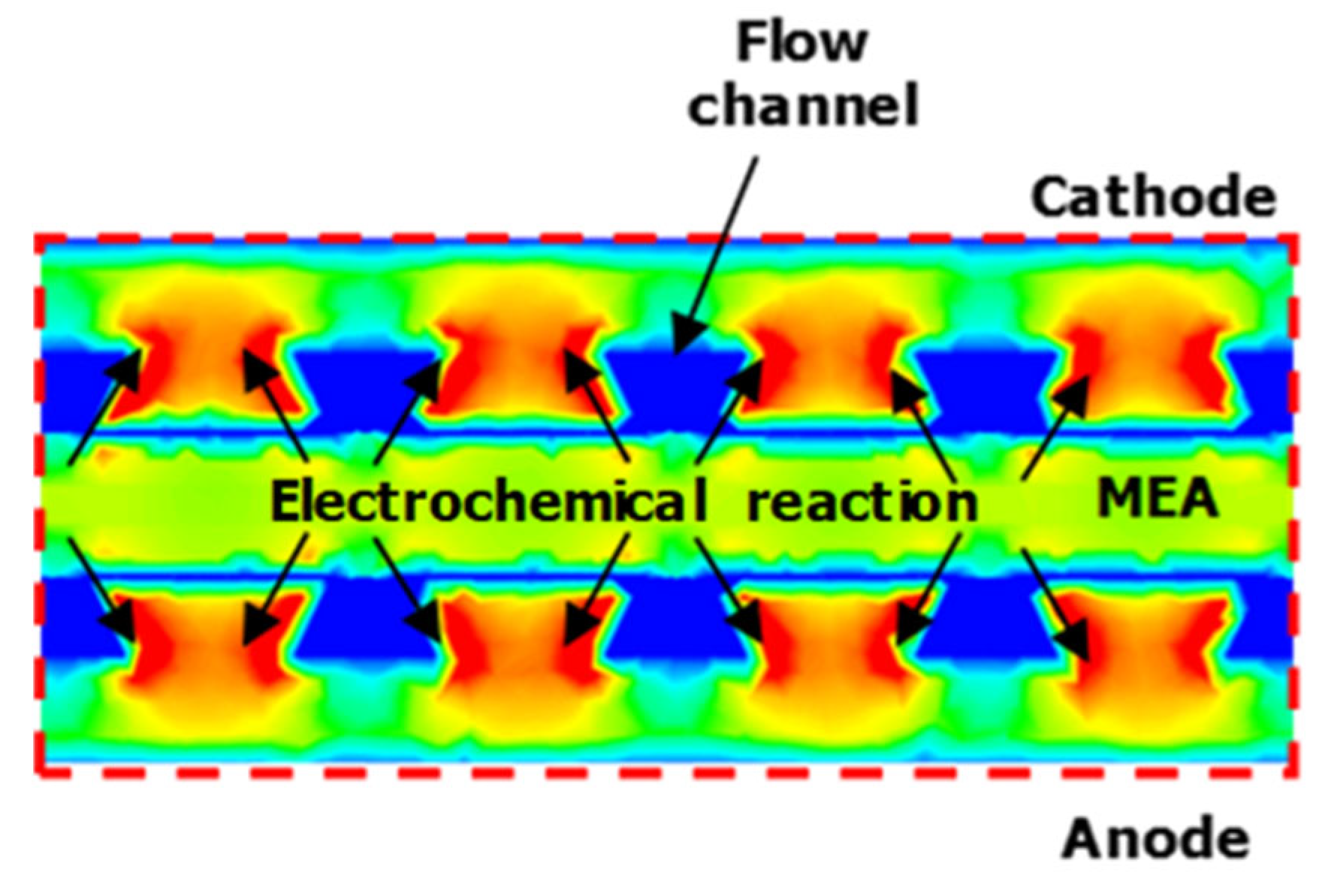
Figure 10 presents the current density distribution generated by electrochemical reactions across the PEM plane and the A-B cross-section of Figure 3a under different operating voltages. In Figure 10a,b, corresponding to Case 1 and 2 conditions, insufficient flow rates prevented uniform diffusion of reactants across the entire area, resulting in unreacted zones and low current density. Additionally, reactant deficiency reduced current density again at 0.5 V and 0.4 V.

In Figure 10c,d, corresponding to Case 3 and 4 conditions, the increased inlet flow rates eliminated reactant deficiency up to 0.8 V compared to previous cases. This reduction in reactant deficiency was due to decreased concentration loss effects.

In Figure 10e, corresponding to Case 5 with the maximum inlet flow rate, unlike Case 4, no reactant deficiency was observed up to an operating voltage of 0.7 V. Additionally, the I−P curve in Figure 9b showed that the maximum power of 0.52 W/cm² occurred at 0.7 V, attributed to the uniform distribution of reactants across the entire flow channel area, generating current density throughout the entire surface.

Figure 11 corresponds to the detailed current density distribution generated by electrochemical reactions under Case 5 conditions. The current was produced by electrochemical reactions at MEA, which consisted of GDL, CL, and PEM. Additionally, it was observed that the generated current circulated between the anode and cathode until the equilibrium potential was maintained. The current then migrated to CC, the conductive components of each electrode, in accordance with electrical conductivity. The non-conductive flow channels solely supplied reactants and exhibited no current density due to the absence of electron movement. This enabled the tracking of electron movement generated by electrochemical reactions.

3.2. Cell Temperature of Each Structure with Mass Flow Rate

In a PEMFC system, temperature variations affect the electrochemical reaction rate and evaporation/condensation phenomena within the flow channels. Additionally, efficient thermal management prevents degradation and extends the fuel cell’s lifespan. Therefore, proper temperature regulation during PEMFC operation plays a critical role in optimizing system performance [23].

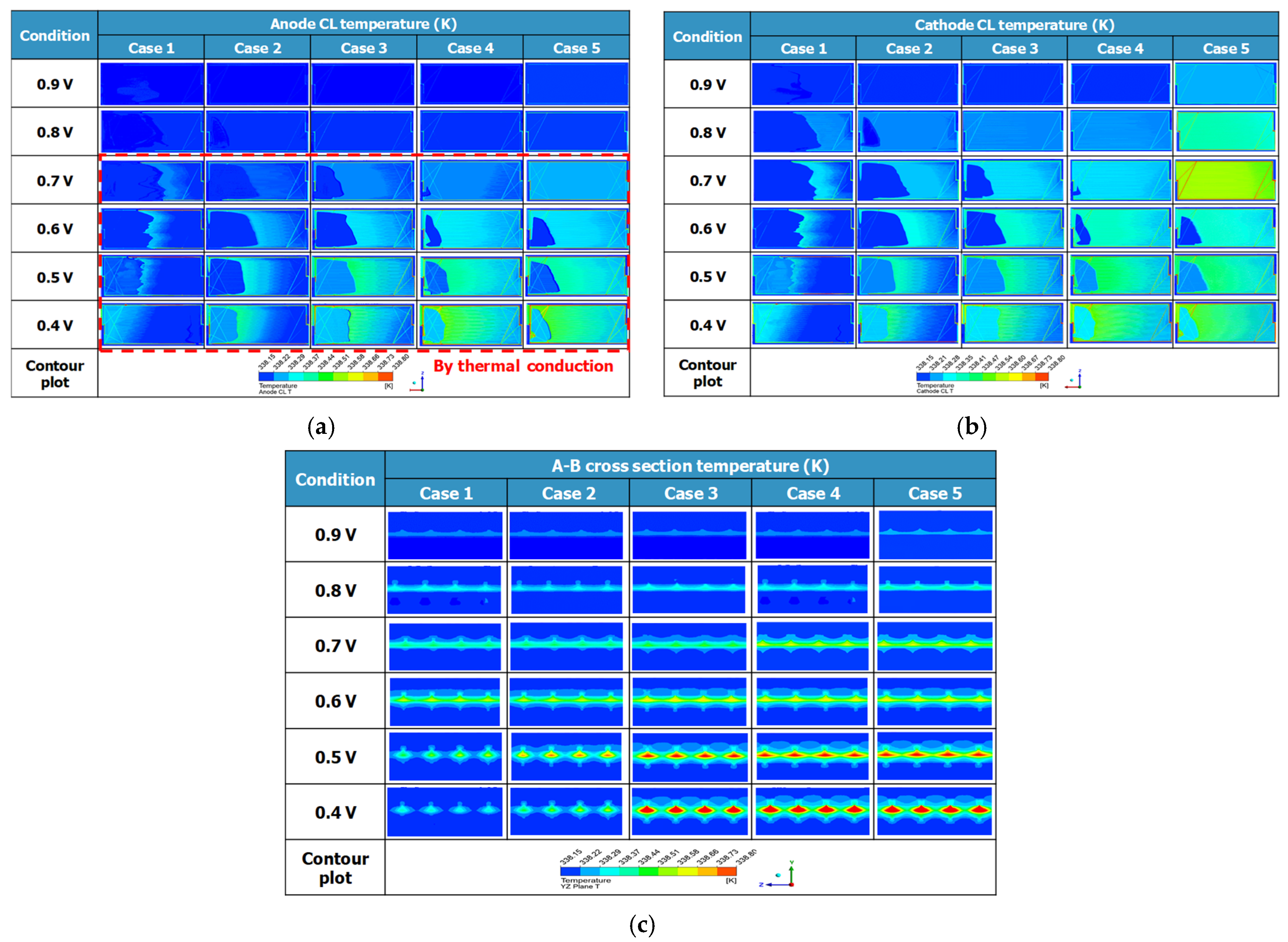
In a PEMFC system, temperature changes occur due to heat generated by electrochemical reactions in the cathode CL, and these temperature differences induce heat conduction through each contacted structural component. Figure 12a illustrates the temperature distribution in the anode CL. The anode CL did not exhibit temperature variation because it separated hydrogen into protons and electrons through oxidation reactions without generating heat. However, as flow rates increased from Case 1 to 5 and the operating voltage decreased from 0.9 V to 0.4 V, temperature variations intensified. This was attributed to heat generated by reduction reactions at the cathode, which conducted through MEA. Additionally, higher current loads and sufficient reactant supply correlated with increased temperature variations.

Figure 12b illustrates the temperature distribution in the cathode CL. In the cathode CL, heat was generated during the reduction reaction, where oxygen, hydrogen ions, and electrons combined to form water. As the operating voltage decreased, the current load increased proportionally with the electrochemical reactions, resulting in elevated temperature variations. This trend was confirmed by the higher temperature distribution, indicating elevated inlet temperatures as the voltage dropped from 0.9 V to 0.4 V. Additionally, increased inlet flow rates promoted chemical reactions, and the improved reactant distribution area led to more uniform heat distribution.

Figure 12c presents the temperature variation distribution across the A-B cross-section under different inlet flow rates and operating voltages. As the operating voltage decreased from 0.9 V to 0.4 V, temperature changes became more pronounced in the PEM and CL due to increased heat generation. Notably, localized temperature rises were observed at the interface adjacent to GC, where reactant diffusion occurred.

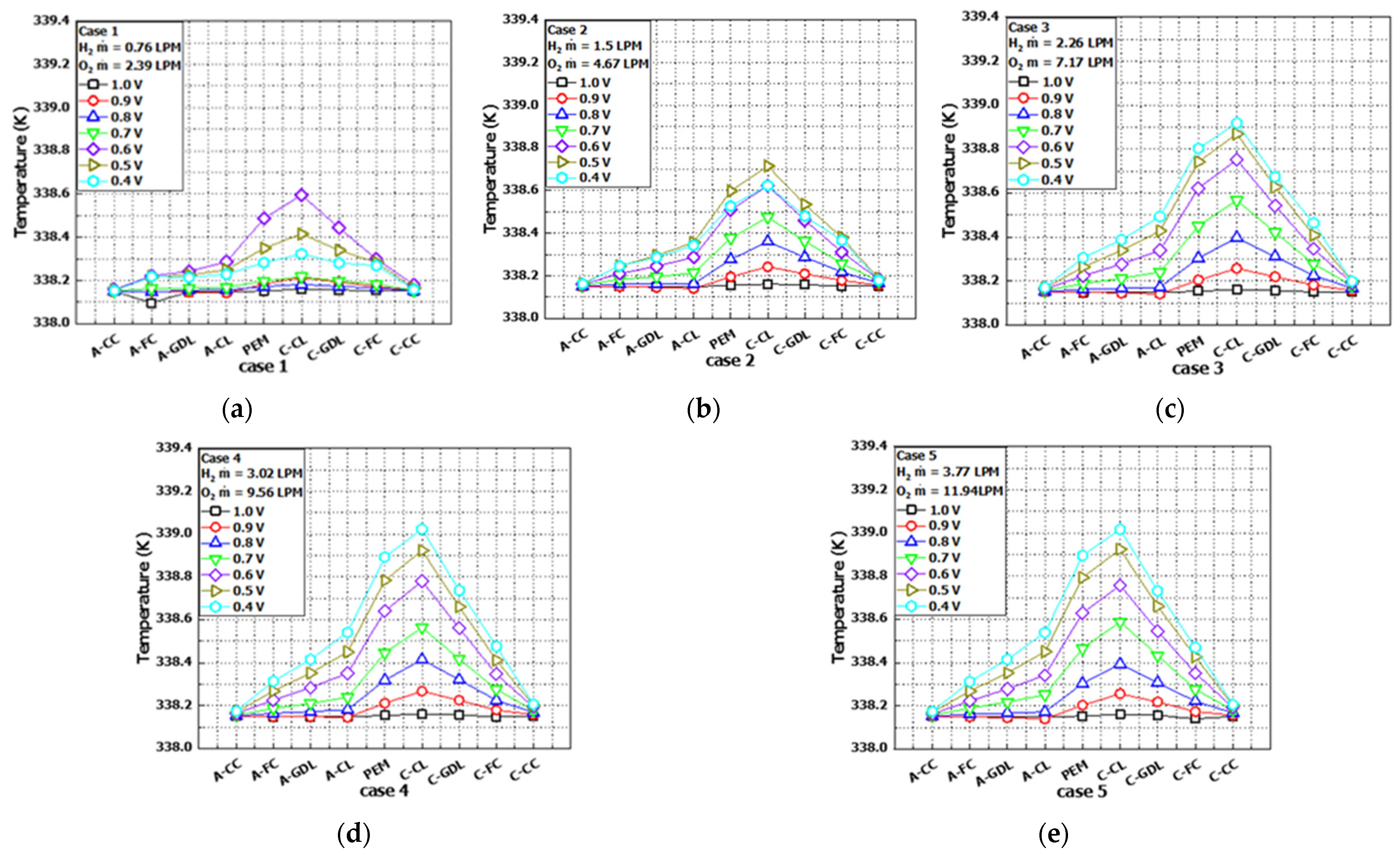
Figure 13 shows the temperature distributions from Figure 12 according to each case condition. In all cases, the region with the highest temperature was the CL of the cathode, and the PEM, which was in contact due to heat conduction, exhibited the next highest temperature. Figure 13a,b corresponds to Case 1 and Case 2, respectively. In Case 1, at an operating voltage of 0.6 V, the maximum temperature increased by 0.13% compared to the inlet temperature, while in Case 2, at an operating voltage of 0.5 V, the maximum temperature increased by 0.16% compared to the inlet temperature. In both cases, due to insufficient reactant flow, a continuous temperature rise up to 0.4 V was not observed. However, Figure 13c–e, which corresponds to Case 3, Case 4, and Case 5, respectively, showed that increasing the inlet flow rate led to the maximum temperature change due to electrochemical reactions up to an operating voltage of 0.4 V.

Notably, Figure 13e presents the results for Case 5, which had the maximum inlet flow rates of hydrogen at 3.77 LPM and oxygen at 11.94 LPM. Compared to the inlet temperature of 338.15 K, Case 5 exhibited a 0.25% temperature rise. However, its maximum temperature remained identical to Case 4 at 339.02 K. This temperature consistency was attributed to unreacted reactants in the increased flow rates acting as a coolant by absorbing heat generated during the exhaust process, thereby stabilizing the cell temperature.

The maximum temperature variation of 1 K observed in the numerical analysis may seem negligible. However, in practical fuel cell systems where hundreds to thousands of cells are arranged in parallel, even minor temperature changes in a single cell can accumulate across multiple cells. This cumulative effect could lead to significant thermal degradation, causing dry-out of the electrolyte membrane, reduced ionic conductivity, and a shortened lifespan of MEA. Additionally, hydrogen exposed to the external environment poses combustion risks. Therefore, temperature control through flow rate regulation is critical to minimize energy consumption in external cooling systems and enhance the stability and durability of fuel cells.

3.3. Reaction Species Distribution and Crossover Effect

In a PEMFC system, oxidation-reduction reactions can produce diverse outcomes depending on the operating conditions. Concentration gradients may result in non-uniform reactant distribution and inefficient water management, potentially leading to flooding. Therefore, to analyze these phenomena, mass fraction distribution diagrams at GC cross-sections of each electrode were presented.

Figure 14a displays the mass fraction distribution of hydrogen, the primary fuel in the PEMFC. From Case 1 to Case 5, the hydrogen flow rate increased. In Case 1, as the voltage decreased from 0.9 V to 0.4 V, the hydrogen flow rate required for the reaction increased, leading to pronounced fuel deficiency. In contrast, Case 2 showed no deficiency at 0.9 V due to higher flow rates, with improved deficiency zones across other voltage conditions. As flow rates further increased in Cases 3, 4, and 5, the hydrogen concentration rose proportionally, and deficiency zones gradually diminished. Ultimately, uniform hydrogen distribution was achieved across the entire reaction flow channel GC. These results suggested that increased flow rates mitigated hydrogen starvation-induced inhomogeneity and enhanced system reaction efficiency.

Figure 14b shows the water vapor mass fraction distribution in the humidified fuel. In the anode, water vapor primarily enhanced ionic conductivity by humidifying PEM and facilitating hydrogen ion transport, rather than participating in oxidation reactions. Consequently, water vapor flow rates increased alongside hydrogen, exhibiting deficiency zones under low-voltage conditions similar to hydrogen. However, in Cases 1, 2, and 3 under specific voltage conditions, water vapor and liquid water were regenerated. This regeneration was attributed to back-diffusion of oxygen and water moving from the cathode to the anode as a result of concentration gradients. According to Wilberforce et al. [24], the primary driving mechanisms for water molecule transport are electro-osmotic drag, in which water is transported from the anode to the cathode due to potential differences between the electrodes, and back-diffusion, where water moves from the cathode to the anode because of concentration gradients. In this study, the irregular and non-steady mixing of hydrogen, oxygen, and water through the membrane during these processes was identified as the crossover effect.

Crossover negatively impacted PEMFC systems. First, when crossover oxygen reacted with hydrogen in the anode CL, electrons generated in the CL did not travel through external circuits, leading to power loss. Second, crossover caused non-uniform distribution in GC of both electrodes, inducing localized chemical reactions that reduced the durability and lifespan of the electrolyte membrane. Therefore, optimizing the inlet flow rate to prevent crossover is essential.

Figure 15a presents the mass fractions of hydrogen and water in the anode GC. As the operating voltage decreased, the mass fraction of hydrogen in the GC declined because the amount of hydrogen consumed in chemical reactions increased. However, from Case 1 to Case 5, the reduction in hydrogen mass fraction was mitigated due to the sufficient hydrogen concentration in the flow channel as the flow rate increased.

According to the water transport mechanisms described earlier, in the sulfonic acid groups (SO₃⁻H⁺) of the Nafion PEM within the PEMFC, protons (H⁺) combined with water to form hydronium ions (H₃O⁺). As hydrogen decreased, this led to a hydration phenomenon where water was also reduced [25,26]. Therefore, hydrogen and water should exhibit identical trends in their mass fraction graphs. However, under low-flow, high-voltage conditions in Figure 15a, discrepancies in the mass fraction trends of hydrogen and water were observed. This was attributed to crossover, where water generated at the cathode underwent back-diffusion due to concentration gradients, causing an increase in the water mass fraction.

To determine whether crossover-induced flooding occurred in the anode, Figure 15b and

Table 5. Evaluation of the crossover index in the anode based on the difference in hydrogen and water mass fractions.

Condition	Crossover Index
Cell Voltage (V)	Case 1	Case 2	Case 3	Case 4	Case 5
1.0	0.10	0.03	0.01	−0.03	0.00
0.9	0.41	1.12	0.09	0.05	0.00
0.8	0.19	0.09	0.06	0.00	0.00
0.7	0.07	0.15	0.00	−0.04	0.00
0.6	0.11	0.05	−0.01	−0.08	−0.10
0.5	0.14	0.05	−0.02	−0.10	−0.12
0.4	0.18	0.04	−0.01	−0.09	−0.12

numerically quantify the crossover phenomenon. Mass fractions can be converted to the same unit by multiplying the molar concentration of each chemical species by the mass flow rate. Thus, the difference between the mass fractions of hydrogen and water was defined as the crossover rate. The crossover rate was set to a baseline of ‘0’. A zero difference between hydrogen and water indicates no flooding caused by crossover, signifying that water was solely utilized for proton transport through the electrolyte membrane.

A crossover index exceeding ‘0’, a positive value, indicates a higher mass fraction of water compared to hydrogen, numerically confirming that water back-diffused from the cathode to the anode. Based on this, Cases 1 and 2 across all voltage conditions, Case 3 at 1.0 V, 0.9 V, and 0.8 V, and Case 4 at 0.9 V were identified as regions where crossover-induced flooding occurred.

Notably, under the 0.9 V condition of Case 1 in Table 5, the current density was 0.14 A/cm², which was lower than that of other conditions, and the crossover index reached its maximum value of 0.41. This result indicates that water back-diffused by crossover caused flooding in the anode GC, which hindered the oxidation reaction of hydrogen in the catalyst layer, leading to a lower current density.

A negative crossover index indicated a higher mass fraction of hydrogen compared to water. This was observed in Cases 3, 4, and 5 within the voltage range of 0.7 V to 0.4 V. Furthermore, as the inlet flow rate increased from Case 3 to Case 5, the crossover index tended to approach ‘0’ or negative values. This trend was interpreted as a result of relatively reduced reactant concentration gradients within the fuel cell due to increased flow rates. Therefore, these findings suggest that increasing the flow rate alone can prevent unnecessary water accumulation and enable efficient water management by balancing hydrogen and oxygen reactions.

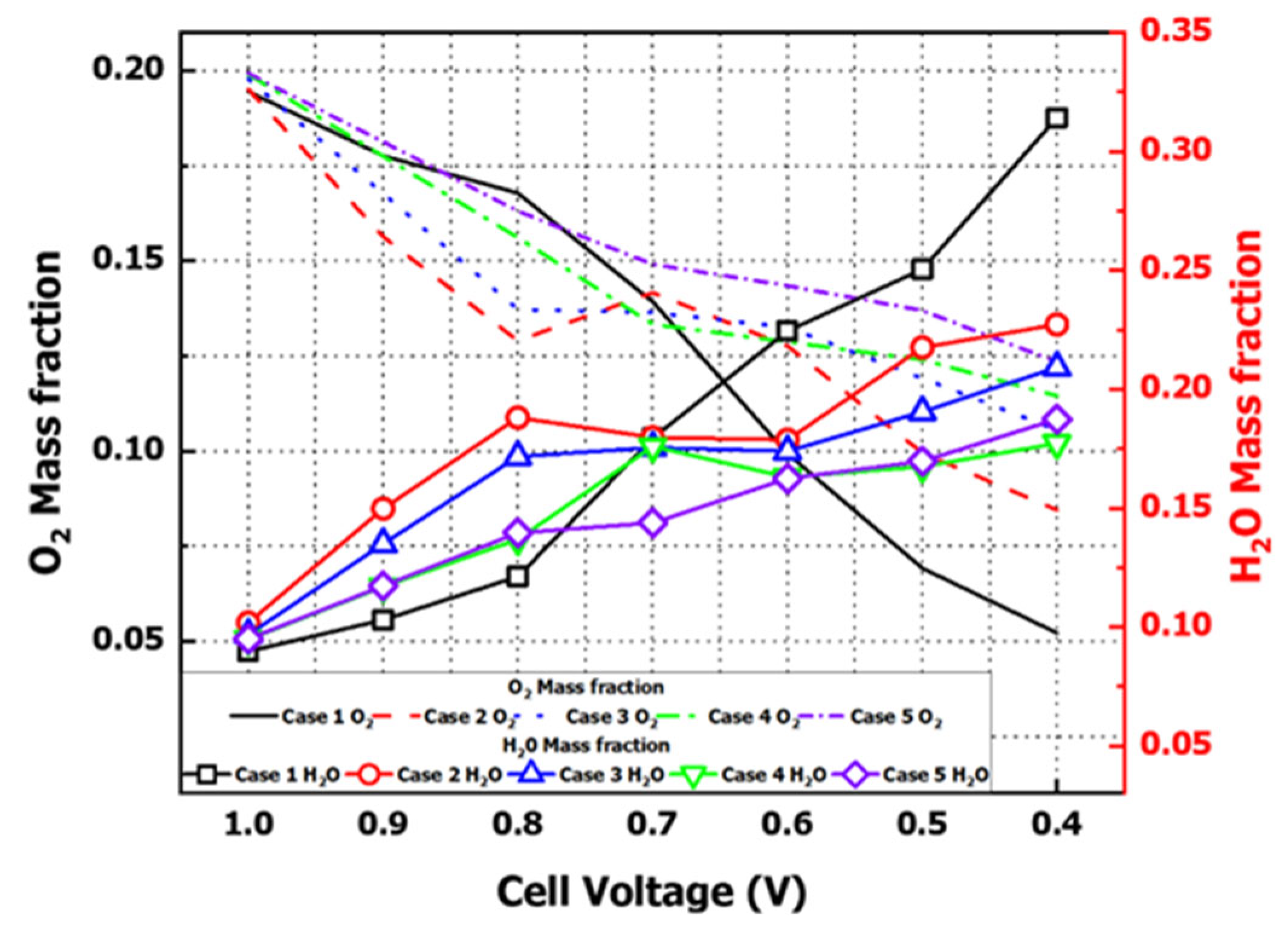
Figure 16a displays the mass fraction distribution of oxygen, the oxidizing agent used in the PEMFC, across the cathode GC cross-section, while Figure 16b illustrates the mass fraction distribution of water produced by reduction reactions and water vapor included for humidification in the same cross-section. As the voltage decreased, oxygen exhibited a decreasing distribution, whereas water increased. This occurred because oxygen was consumed in chemical reactions at the cathode CL, and water was produced through the reaction of hydrogen cations and electrons with oxygen.

Figure 17 numerically illustrates the mass fraction distributions of oxygen and water from Figure 16 as functions of voltage. As previously described, a decrease in oxygen correlated with an increase in water, confirming the inverse relationship. These results demonstrate a trade-off between oxygen and water at the cathode due to reduction reactions.

Contrary to the expectation that oxygen levels would increase proportionally with chemical reactions as flow rates rose, increasing the flow rate from Case 1 to Case 5 resulted in reduced water production at lower voltages. This was attributed to insufficient contact and diffusion times with the electrodes due to higher flow velocity at elevated inlet flow rates. Therefore, Figure 16 and Figure 17 demonstrate that flooding did not occur in the cathode.

3.4. Relationship Between Comprehensive System Efficiency and Mass Flow Rate

The quantitative evaluation of fuel cell performance can be discussed in terms of system efficiency. According to O’Hayre et al. [27], the theoretical maximum efficiency of a typical fuel cell can be defined by Equation (20). Here, $\mathsf{\Delta }G$ represents the Gibbs free energy, defined as the product of the number of electrons involved in the reaction, the Faraday constant, and the Nernst potential. Then, $\mathsf{\Delta }H$ denotes the reaction enthalpy, which is the difference in formation enthalpy between reactants and products, accounting for phase changes. The generated water can be expressed as the higher heating value (HHV) if it exists in liquid form, or the lower heating value (LHV) if in gaseous form. The PEMFC used in this study corresponded to a low-temperature fuel cell operating at 338.15 K, so the HHV was selected as the reference [28]. Consequently, with Gibbs free energy at 237.36 kJ/mol and reaction enthalpy at 285.83 kJ/mol, the theoretical maximum efficiency was determined to be 83%:

$${\eta }_{theoretical}={\displaystyle \frac{\mathsf{\Delta }G}{\mathsf{\Delta }H}}={\displaystyle \frac{-nFE}{\mathsf{\Delta }H}}=83\mathrm{\%}$$

(20)

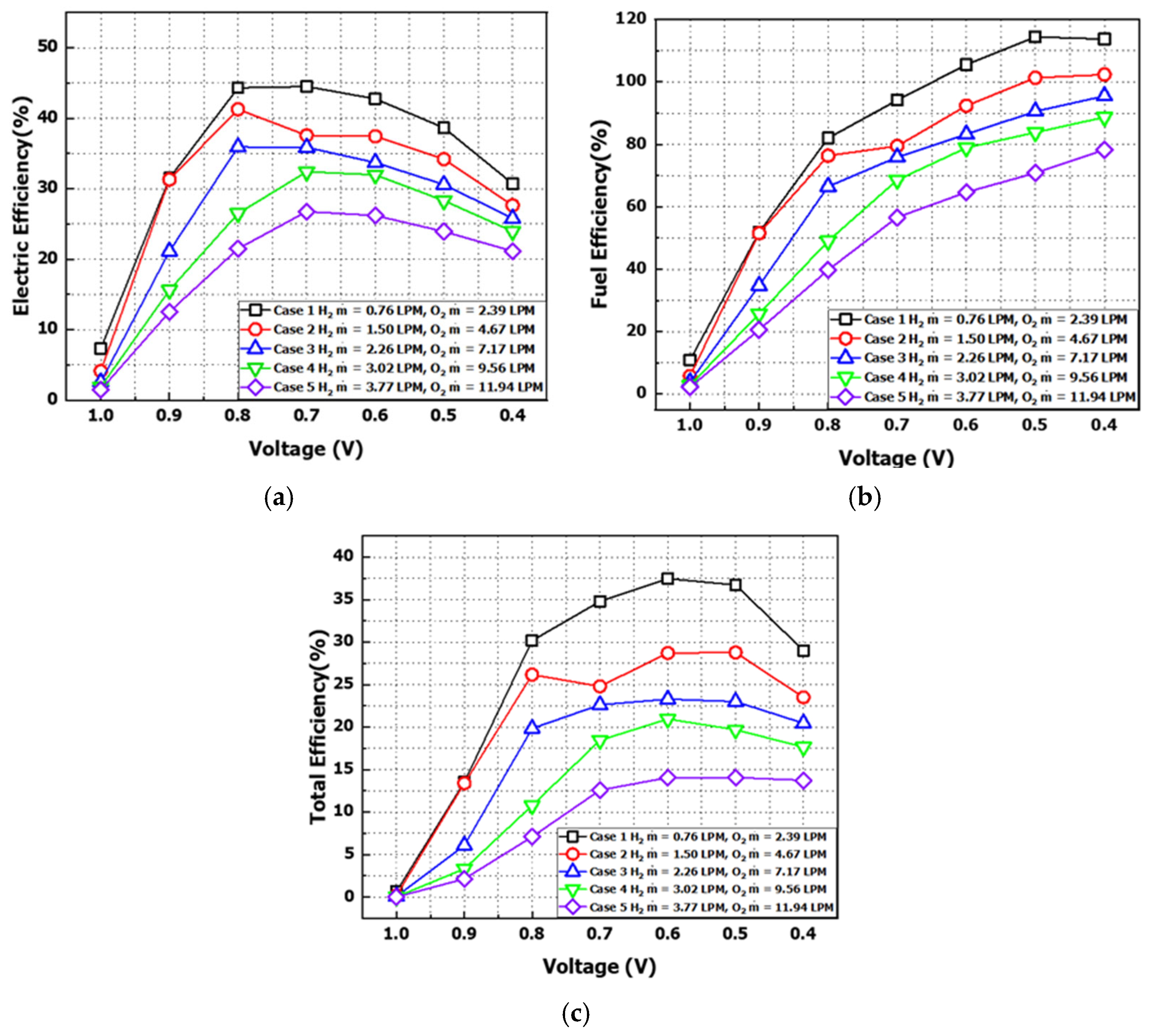
The electrical efficiency of low-temperature fuel cells, such as PEMFCs, was defined as the ratio of the net electrical output to the total energy input from hydrogen fuel to each electrode, as expressed in Equation (21) [29]. Here, $P_{net}$ represents net power, and ${\dot{E}}_{chemical}$, defined as the product of the inlet flow rate and higher heating value (HHV), corresponds to the electrochemical reaction energy. The power efficiency at each cell voltage is presented in Figure 18a. Across all flow rate conditions, maximum efficiency points were observed at 0.7 V and 0.8 V. Case 1 exhibited a maximum power efficiency of 45%, while Case 5 yielded a minimum efficiency of 21%. Additionally, lower flow rates correlated with higher efficiency, attributed to higher power output relative to fuel input. However, efficiency sharply decreased under high current loads at low voltages.

$${\eta }_{power}={\displaystyle \frac{P_{net}}{{\dot{E}}_{chemical}}}={\displaystyle \frac{Vj}{\dot{m}\mathsf{\Delta }H}}$$

(21)

As another efficiency metric for PEMFCs, fuel utilization efficiency was cited as defined in Equation (22). It is defined as the ratio of the flow rate consumed in the reaction to the flow rate supplied at the anode inlet, where 100% efficiency indicates that all hydrogen supplied was consumed in the reaction [26,27,28,29]:

$${\eta }_{fuel}={\displaystyle \frac{j/nF}{{\dot{m}}_{supplied}}}={\displaystyle \frac{{\dot{m}}_{reacted}}{{\dot{m}}_{supplied}}}$$

(22)

Figure 18b illustrates the fuel efficiency by voltage under varying inlet flow rates. As the voltage decreased, the required fuel amount increased, leading to proportional improvements in fuel utilization efficiency. In Cases 1 and 2, efficiency exceeded 100% in certain regions, attributed to the crossover effects described in Figure 15b, where back-diffused water in the anode outlet region increased the total flow rate beyond the inlet supply.

Figure 18c and

Table 6. Total system efficiency of PEMFCs under all conditions.

Condition	Total Efficiency (%)
Cell Voltage (V)	Case 1	Case 2	Case 3	Case 4	Case 5
1.0	0.68	0.20	0.08	0.04	0.03
0.9	13.81	13.54	6.09	3.35	2.16
0.8	30.76	26.45	19.82	10.85	7.15
0.7	35.47	25.07	22.59	18.57	12.68
0.6	38.19	29.03	23.28	21.08	14.18
0.5	37.43	29.09	22.98	19.82	14.19
0.4	29.57	23.76	20.43	17.76	13.85

present the total efficiency of the PEMFC system, illustrating the combined effects of theoretical efficiency, power efficiency, and fuel efficiency using Equation (23):

$${\eta }_{total}={\eta }_{theoretical}\times {\eta }_{power}\times {\eta }_{fuel}$$

(23)

According to the results, all conditions reached maximum efficiency at 0.6 V, after which the overall system efficiency gradually decreased as the supply flow rates of hydrogen and oxygen increased. Case 1, with the lowest inlet flow rate, exhibited the highest system efficiency. This was analyzed to result from higher fuel utilization under low-flow conditions and the absence of unreacted fuel discharge due to insufficient flow rates. However, from Case 1 to Case 3, under specific voltage conditions, increasing current loads led to voltage drops caused by reactant deficiency and crossover-induced flooding. In the I−P curve, this resulted in power outputs lower than required for practical operation, rendering these conditions difficult to utilize despite their high efficiency. Therefore, selecting optimal flow rates to balance efficiency, current, and power is critical in PEMFC system operation.

To analyze the optimal inlet flow rate conditions, Figure 19 presents the total system efficiency alongside the I−V curve. In Cases 1 and 2, efficiency sharply declined beyond the maximum point as voltage decreased and current density increased. This trend was attributed to flooding caused by crossover and dominant concentration losses, rendering these conditions unsuitable for practical operation.

In Case 3, as an intermediate flow rate condition, current density and efficiency increased compared to Cases 1 and 2 due to improved inlet flow rates. However, flooding—a key issue identified in this PEMFC study—occurred, and the maximum current density of 1.02 A/cm² was not achieved. Thus, this condition was deemed insufficient for optimal flow rate selection.

Case 5 exhibited the highest current density but was deemed unsuitable as the optimal flow rate condition due to its lower overall efficiency of 14% compared to Case 4. Additionally, the increase in current diminished progressively despite higher flow rates. This suggests the necessity of optimizing inlet flow rates to prevent unnecessary fuel consumption and achieve a mass flow rate that balances performance enhancement.

For a quantitative comparison of the results in Figure 19,

Table 7. Comparison of increasing rates of hydrogen inlet flow, current, and power density.

Condition	Rate of Increase (%)
	H2 Mass Flow Rate	Max. Current Density	Max. Power Density
Case 1
	(+) 97.36	(+) 76.81	(+) 77.78
Case 2
	(+) 50.67	(+) 39.94	(+) 31.25
Case 3
	(+) 33.63	(+) 24.40	(+) 19.05
Case 4
	(+) 24.83	(+) 10.20	(+) 4.00
Case 5

presents the hydrogen flow rate increase ratio, current density increase ratio, and power density increase ratio across all conditions. Notably, when comparing Cases 3 and 4, a 33.63% increase in the hydrogen inlet flow rate resulted in 24.40% and 19.05% increases in current and power density, respectively. Between Cases 4 and 5, the hydrogen flow rate increased by 24.83%, but current and power density showed only 10.20% and 4.00% increases, indicating diminishing returns in current and power gains despite higher flow rates.

Consequently, Case 4, with hydrogen at 3.02 LPM and oxygen at 9.56 LPM, was identified as the optimal inlet condition for the PEMFC used in this study, as it achieved higher efficiency with less fuel.

4. Conclusions

This study conducted a comparative analysis of flow rate variations in a single cell with a commercial bipolar plate to minimize concentration loss and crossover-induced flooding, which are key factors affecting both the enhancement and degradation of PEMFC performance. Numerical simulations were employed to evaluate how flow rate changes impact power performance, efficiency, and phenomena, such as reactant deficiency and crossover. Based on these findings, optimal operating conditions and hydrogen/oxygen inlet flow rates were proposed:

(1)

As the inlet flow rate increased, current and power density rose, while voltage decreased. In Cases 1 and 2, the maximum current and power densities were low at 0.53 A/cm² and 0.32 W/cm², respectively, due to concentration losses caused by reactant deficiency and flooding. In contrast, Cases 3 and 4 showed improved maximum current and power densities of 0.93 A/cm² and 0.49 W/cm², as increased flow rates mitigated activation and ohmic losses while reducing concentration loss effects. However, under the excessively high flow rate of Case 5, further performance improvements approached limits, with current and power densities plateauing at 1.02 A/cm² and 0.52 W/cm². These results highlighted the importance of selecting optimal inlet flow rates to minimize concentration loss and optimize current/power performance.

(2)

Temperature variations during PEMFC operation were concentrated in the cathode catalyst layer, with the maximum temperature in Cases 4 and 5 reaching 339 K, a 0.25% increase compared to the inlet temperature. Notably, under Case 5 conditions, excessive unreacted flow provided a cooling effect during the exhaust process, suppressing further temperature rise. These findings confirmed that proper control of inlet flow rates is critical for ensuring the thermal stability and extended lifespan of PEMFC systems.

(3)

Mass distribution diagrams and the crossover index were utilized to analyze the impact of inlet flow rate variations on flooding caused by reactant deficiency and crossover. In the anode flow channels of Cases 1, 2, and 3, crossover due to hydrogen deficiency and back-diffusion was identified as the cause of voltage drops. Additionally, in Cases 4 and 5, where the crossover index showed values of ‘0’ or negative, increased flow rates improved reactant distribution uniformity and reduced flooding. In the cathode flow channel, a trade-off relationship between oxygen and generated water was observed, and no water accumulation due to flooding occurred.

(4)

The total efficiency of the PEMFC system was influenced by the combined effects of theoretical efficiency, power efficiency, and fuel efficiency, with efficiency tending to decrease as flow rates increased. When transitioning from Case 3 to Case 4, the current and power density increase rates were significantly higher at 24.40% and 19.05%, respectively, while efficiency remained stable at approximately 20%. However, transitioning from Case 4 to Case 5 resulted in lower increase rates of 10.20% and 4.00% for current and power density, with an efficiency of approximately 14%, highlighting the limitations of excessive flow rate supply in Case 5. Therefore, this study concluded that Case 4 represents the most suitable inlet flow rate condition for the PEMFC system.

In conclusion, this study demonstrated that optimal control of inlet flow rates is essential to maximize the performance and efficiency of PEMFCs. Specifically, the hydrogen flow rate of 3.02 LPM and oxygen flow rate of 9.56 LPM in Case 4 were evaluated as the ideal conditions for the single-cell configuration used in this study, satisfying both power performance and efficiency without inducing flooding.