Abstract
Deep learning-based models have achieved considerable success in partial discharge (PD) fault diagnosis for power systems, enhancing grid asset safety and improving reliability. However, traditional approaches often rely on centralized training, which demands significant resources and fails to account for the impact of noisy operating conditions on Intelligent Electronic Devices (IEDs). In a gas-insulated switchgear (GIS), PD measurement data collected in noisy environments exhibit diverse feature distributions and a wide range of class representations, posing significant challenges for trained models under complex conditions. To address these challenges, we propose a Self-Supervised Asynchronous Federated Learning (SSAFL) approach for PD diagnosis in noisy IED environments. The proposed technique integrates asynchronous federated learning with self-supervised learning, enabling IEDs to learn robust pattern representations while preserving local data privacy and mitigating the effects of resource heterogeneity among IEDs. Experimental results demonstrate that the proposed SSAFL framework achieves overall accuracies of 98% and 95% on the training and testing datasets, respectively. Additionally, for the floating class in IED 1, SSAFL improves the F1-score by 5% compared to Self-Supervised Federated Learning (SSFL). These results indicate that the proposed SSAFL method offers greater adaptability to real-world scenarios. In particular, it effectively addresses the scarcity of labeled data, ensures data privacy, and efficiently utilizes heterogeneous local resources.
1. Introduction
Gas-insulated switchgears (GISs) play a pivotal role in ensuring the reliability of power grid infrastructures. They maintain stable power system operations and significantly influence overall grid reliability [1]. However, a GIS operates under extreme conditions, including high temperatures and pressures, which can lead to insulation degradation. Additionally, manufacturing, transportation, and assembly processes introduce inherent risks, potentially causing latent faults [2].
Various insulation defects in GISs include corona defects, particle defects, void defects, and floating electrode defects. Over time, these defects progressively deteriorate the insulation system, potentially leading to breakdowns [3,4,5,6]. Among these, floating faults are the most frequently observed and are often caused by poor contact, rusted components, or loose bolts in the GIS [7]. Partial discharge (PD) typically results from insulation aging due to voids, cracks, impurities, and deficiencies within insulation materials [8]. The ultra-high-frequency (UHF) method is widely used for identifying PD sources and fault types due to its strong anti-interference capabilities and high sensitivity [9,10].
Over the years, machine learning techniques have been applied to PD classification using UHF signal measurements in time-resolved PD (TRPD) and phase-resolved PD (PRPD) analyses [11,12,13,14,15]. While effective, these approaches rely heavily on expert knowledge, are susceptible to manual errors, exhibit limited feature transferability, and often require lengthy training times [16]. To address these limitations, deep neural networks (DNNs) have demonstrated strong performance in PD pattern recognition [17,18]. For instance, recurrent neural networks (RNNs) with long short-term memory (LSTM) units have been used to classify PDs in gas-insulated systems based on PRPDs [19], and convolutional neural networks (CNNs) have been used to automatically extract discriminative features from UHF signal patterns [20,21]. The combination of CNN and LSTM models have also shown improved classification accuracy [22]. However, the large number of parameters in DNN models can lead to overfitting [23], and they typically require fully labeled datasets for supervised training. The scarcity of labeled PD data degrades classification accuracy [24], and obtaining labeled samples through fault experiments is labor-intensive and time-consuming.
In contrast to earlier centralized approaches [17,18,19,20,21,22], recent studies have begun to address the challenges of limited labeled data and data privacy in PD diagnosis. To mitigate the shortage of labeled samples, semi-supervised learning (SemiSL) and self-supervised learning (SSL) techniques have been applied to PD classification. In SemiSL approaches, to expand the training dataset, a model is initially trained on a labeled dataset and then used to create pseudo-labels for unlabeled data [25,26,27,28,29,30,31]. On the other hand, SSL trains an online network on unlabeled data while using a target network to provide stable supervision, producing a pretrained model that can be fine-tuned with labeled data [32,33,34]. Both approaches reduce the need for extensive manual labeling by exploiting abundant unlabeled data.
To address data privacy concerns, federated learning (FL) enables training models on a distributed system utilizing multiple intelligent electronic devices (IEDs) that only share model parameters for global aggregation [35,36,37,38]. However, conventional FL faces challenges due to varying IED resources, as each training round must wait for the slowest device, thereby significantly prolonging the process, as well as limiting the representation learning of the global model. Asynchronous FL (AFL) overcomes this limitation by aggregating model updates without delay, thereby ensuring the coverage of the global model by using a first-in-first-out scheme to immediately incorporate updates from faster devices and eliminate idle time [39,40,41]. This asynchronous strategy greatly enhances training efficiency in heterogeneous environments while preserving data privacy.
Despite these advancements, most prior studies have addressed these issues in isolation rather than providing a unified solution. Moreover, in distributed learning systems such as FL, heterogeneity in IED resources makes it difficult to achieve an optimal global model. To overcome these limitations, we propose an integrated approach that combines SSL with AFL. This method enables robust representation learning from unlabeled data while maintaining data privacy and the heterogeneous resources on local devices. The proposed method allows efficient model training across IEDs with varying resource capacities and concurrently addresses the key challenges of limited labeled data, privacy concerns, and resource heterogeneity at the same time.
In this study, we propose a Self-Supervised Asynchronous Federated Learning (SSAFL) approach for PD diagnosis using phase-resolved PDs (PRPDs) in GIS systems. The proposed scheme consists of two phases: global communication and local downstream tasks. During the global communication phase, each IED trains its online network using unlabeled data enhanced with data augmentation techniques and updates its target network. The server then asynchronously aggregates the model parameters from different IEDs before distributing the updated parameters back to them. In the downstream task phase, the online model is integrated with a Multi-Layer Perceptron (MLP) to train on labeled data. The process and its results are described as follows:
- SSAFL leverages data augmentation techniques to address the scarcity of labeled data in GIS fault diagnosis while ensuring data privacy and efficiently utilizing heterogeneous IED resources.
- Experimental results demonstrate that SSAFL significantly outperforms supervised learning methods and reduces training time by approximately 30% compared to Self-Supervised Federated Learning (SSFL). This improvement is achieved by minimizing the waiting time between IEDs, thereby accelerating the communication process.
The remainder of this paper is organized as follows: Section 2 describes the experimental data for PRPD-based fault diagnosis in GIS. Section 3 formulates the PD diagnosis problem and introduces SSAFL by integrating self-supervised learning with asynchronous federated learning. Section 4 presents performance evaluations for the proposed models. Finally, Section 5 concludes this study.
2. Experimental Analysis
In this section, we describe the experimental setup and analysis of PRPDs and on-site noise using a UHF sensor in GISs.
2.1. Experiment Setup
Figure 1 illustrates the experimental setup for detecting PD signals in GISs. Figure 1a presents a block diagram of the setup, which includes a high-voltage source, a voltage divider, an artificial PD cell, an external UHF sensor, and a data acquisition system (DAS) [19,42]. The DAS comprises a band-pass filter, a logarithmic amplifier, a peak detector, an analog-to-digital converter (ADC), and a PC. As shown in Figure 1b, the high-voltage test site features a high-voltage source operating at 60 Hz, while a voltage divider scales the applied voltage accordingly.
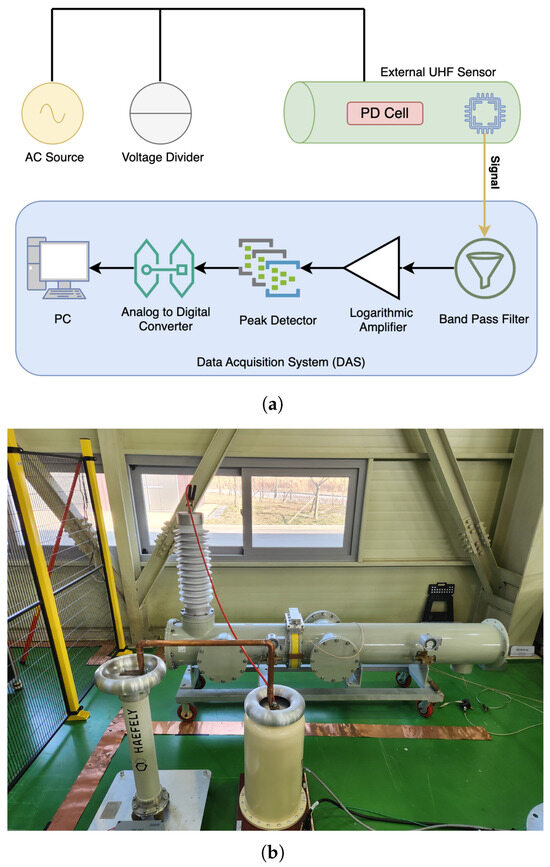
Figure 1.
Experimental system for PRPD analysis: (a) block diagram of experimental setup, (b) high-voltage test site.
In this study, PD signals were measured using a UHF sensor connected to a 45 dB logarithmic amplifier, with a band-pass filter covering the operating bandwidth from 500 MHz to 1.5 GHz. Within the DAS, a peak detector processed the amplified UHF signal and extracted the envelope of the PD pulses by capturing their peak values. The resulting low-frequency envelope signal was then digitized by an ADC at a sampling rate of samples per second, where Hz corresponds to the power system frequency. In the subsequent digital processing stage, the maximum value was selected from each group of eight consecutive samples; consequently, each power cycle yielded samples, which were used to construct the PRPD measurements. The measured PRPD signal for power cycles is defined as follows:
where is the measured signal of the p-th data point and the m-th power cycle.
2.2. PRPD Analysis
Artificial PD cells were used to simulate four types of faults: corona discharges, floating electrodes, void defects, and free particles. Each artificial PD cell was filled with SF6 gas at 0.2 MPa. Corona discharge was simulated by attaching a sharp protrusion at the center of an electrode under an applied test voltage of 11 kV using a needle with a tip radius of m. Floating discharge was induced by an unconnected electrode at a test voltage of 10 kV, where the middle electrode was positioned 1 mm from the grounded electrode and 10 mm from the high-voltage electrode. Void defects were simulated by introducing a small gap between the upper electrode and an epoxy disc with an applied test voltage of 8 kV. Particle discharge was induced by placing a 1 mm metallic sphere on a concave ground electrode, with a test voltage of 10 kV applied.
Figure 2 shows the three-dimensional (3D) PRPD data for the four fault types. Figure 2a shows the corona discharge pulses over two half-cycles. However, the signs of the last half-cycle (rounded at 290°) were clearer than those of the previous half-cycle (nearly 90°). As shown in Figure 2d, the signals measured by the sensor were similar to those of the corona fault. However, the signals of the voids in the two half-cycles were more similar. The floating discharge, which can be observed in Figure 2b, was centralized with high-amplitude pulses presented across phases, with the amplitude of the floating PDs reaching 250, whereas the maximum measurable value for the DAS was 255. As shown in Figure 2c, the signals of the particle fault are concentrated, and the amplitude range is lower than that of the floating fault in Figure 2b.
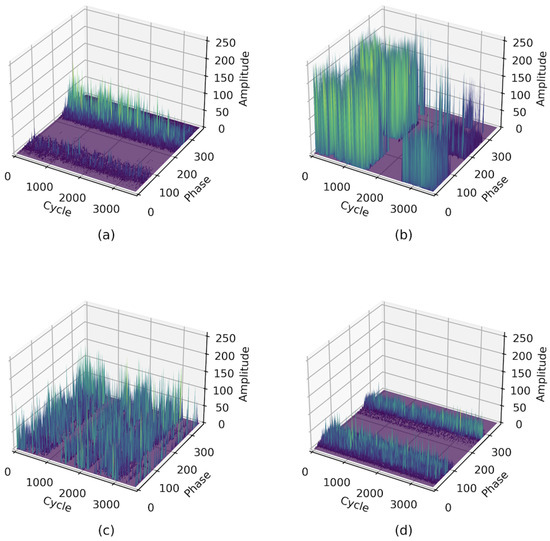
Figure 2.
Sequential phase-resolved PDs (PRPDs) for fault types in GIS: (a) corona, (b) floating, (c) particle, and (d) void.
2.3. Online Noise Analysis
Figure 3 presents on-site noise measurements collected by four different IEDs, where online UHF PD monitoring systems measured online noise in GISs in South Korea. Each online noise source was found to have distribution patterns that depend on its location. Table 1 provides a statistical analysis for online noises using the minimum of the maximum, maximum of the maximum maximum, mean of the mean, and mean of the standard deviations of amplitude. The minimum and maximum values of the peak amplitudes define the overall signal range, while the mean values and standard deviations capture the central tendency and dispersion of the noise levels, respectively.
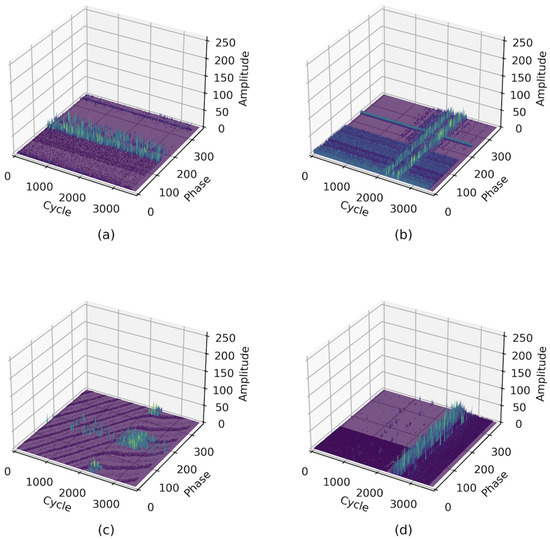
Figure 3.
Noise measurements: (a) IED 1, (b) IED 2, (c) IED 3, and (d) IED 4.

Table 1.
Statistical analysis of noise levels.
For a detailed online noise and PD analysis, Figure 4 illustrates the overlapping distribution among different types of PD signals and noise based on their statistical features: on the x axis and on the y axis. These are defined as and . Floating discharges showed consistently high max values regardless of mean. Void discharges varied widely in max values but produced mean values in the range . Noise signals were generally found where and . Specifically, noise types 1, 2, and 3 appeared around mean PD values of approximately 0.1, 1.0, and 0.2, respectively, while noise type 4 exhibited a scattered distribution with mean values ranging between 0 and 1.
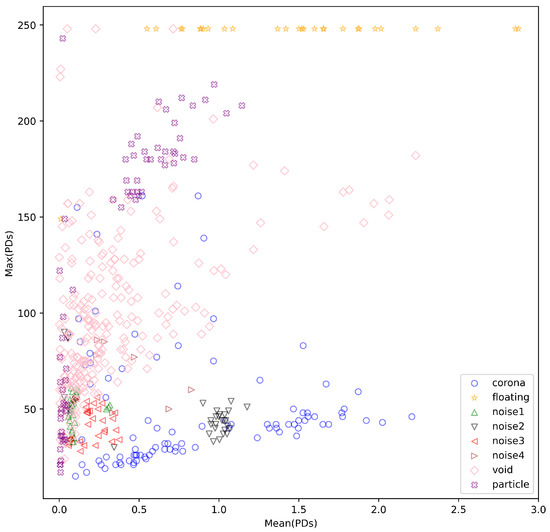
Figure 4.
Distribution of PD types and noises based on mean (PDs) and max (PDs).
3. Proposed Scheme
3.1. Problem Description
Fault diagnosis approaches based on centralized deep learning require large labeled datasets to learn effective feature representations [23]. However, the lack of sufficient labeled data can significantly degrade the accuracy of deep-learning-based fault classification in GISs. Additionally, obtaining labels for unlabeled data is resource-intensive, often requiring substantial time and labor. Moreover, centralized learning raises concerns about data privacy and security risks.
Synchronous Federated Learning (SFL) has been introduced to address these challenges by keeping data localized. However, it incurs high costs due to strict synchronization requirements [40]. Specifically, the server must wait for all IEDs to complete their local training before aggregating their models, leading to inefficiencies. Network unreliability and heterogeneous IED resources further exacerbate slowdowns in SFL.
In this study, we propose a novel approach that simultaneously addresses the scarcity of labeled data, data privacy and security concerns, and the heterogeneity of local resources. This is achieved by integrating self-supervised learning—where an online network and a target network learn from unlabeled data—with asynchronous federated learning [39].
3.2. Proposed of Self-Supervised Asynchronous Federated Learning
Figure 5 shows a flow diagram of the SSAFL. We assume a set of K IEDs (denoted as ), each holding fault data that include labeled and unlabeled samples. Each IED k has a local dataset of samples comprising unlabeled and labeled examples. We denote the unlabeled samples as and the labeled samples as , where is the j-th unlabeled sample at IED k, and is the i-th labeled sample with its label.
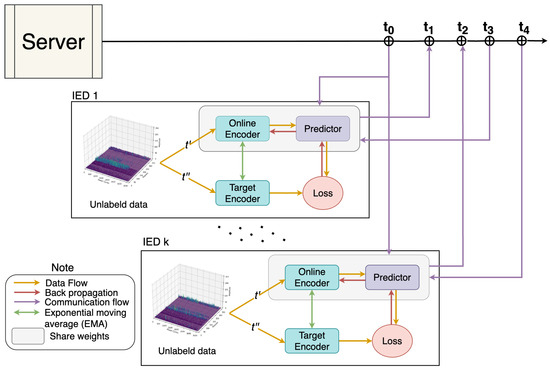
Figure 5.
Global communication process between IEDs and server. At the time , server sends to all IEDs. After that, IEDs optimize using . At the time , IED 1 sends to server. Then, server aggregates with . During that process, at the time , other IEDs k send to server as well. At time , server has completed aggregating and then sends it to IED 1. After that, at the time , server sends the aggregated to IED k after finished the aggregating process.
For clarity, we use the following notations throughout the SSAFL procedure: (online network), (target network), g (global), and ∗ (optimized weights or models). Using these notations, the key steps of the proposed SSAFL process are as follows:
- Step 1—Initialization: The server initializes the global online model with parameters at time t. The model architecture is based on MobileNet-V3 [43], where the pretrained weights are frozen, and the remaining parts are randomly initialized. The server then sends these global model weights to all IEDs.
- Step 2—Local Pretraining: Upon receiving , each IED initializes its local online network and its local target network with parameters and , respectively, based on . The IED then optimizes its local online model and its local target model using its unlabeled data . To facilitate this, each unlabeled sample is transformed via a set of augmentation functions (described in Section III.C.) into a pair of augmented inputs . The online network and the target network process this augmented pair to generate outputs (from the online network) and (from the target network). The online network is then updated by minimizing the loss based on these outputs. Meanwhile, the target network parameters are updated using an exponential moving average (EMA) with a decay rate , producing . At the end of local pretraining, the IED sends to the server, completing the communication round.
- Step 3—Global Communication: After the server receives an updated model from an IED, it integrates this update with the current global model using an aggregation function , producing a new global model . The server immediately sends back to the IED. This asynchronous update process continues for each IED until the global communication phase concludes. Once global aggregation is complete, the server instructs all IEDs to transition to the downstream task phase by broadcasting the final global model .
- Step 4—Local Downstream Tasks: Upon receiving , each IED begins the downstream training phase. The IED combines its received online model with a newly initialized MLP (denoted as ) to create the downstream model . This model is then trained on the IED’s labeled dataset to produce optimized downstream parameters .
The proposed architecture offers a novel approach to fault diagnosis. It harnesses the capability of self-supervised learning to utilize unlabeled samples while simultaneously leveraging federated learning to safeguard data privacy in a distributed training environment. This combination is well suited to distributed fault diagnosis systems. Algorithm 1 presents the overall structure of the proposed method.
| Algorithm 1 Self-Supervised Asynchronous Federated Learning (SSAFL) Algorithm |
| Input: List of IEDs, , Number of communication rounds T, Local Training epochs and pre-train task , Local training epochs at downstream task , Batch-size B, Downstream task learning rate , target decay rate , mixing hyper-parameter . |
| Server Aggregate |
| 1: Initialized |
| 2: for to T do |
| 3: for in K do |
| 4: Pre-training |
| 5: A() |
| 6: end for |
| 7: end for |
| Output: Global model |
| Local Pre-training |
| 1: Initialize: |
| 2: for epoch in do |
| 3: for batch in B do |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: end for |
| 10: end for |
| 11: return: |
| Local Downstream Tasks |
| 1: Initialize: |
| 2: for epoch in do |
| 3: for batch in B do |
| 4: |
| 5: |
| 6: end for |
| 7: end for |
| 8: return |
3.3. Global Communication
Before initiating the global communication phase, the server and IEDs adopt the MobileNet-V3 architecture and freeze all pretrained model parameters. The server then initializes the global model and distributes it to all IEDs. It then waits to receive an updated model from any IED to begin asynchronous aggregation.
On the IED side, each IED applies data augmentation to its unlabeled data to improve representation learning. We employed five augmentation techniques [44,45], which are described as follows:
- Gaussian noise adding: Introduce Gaussian noise with and to the original signal.
- Gaussian noise scaling: Similar to above but with (with the same ) to scale the original signal.
- Random cropping: Zero out a random segment of the signal (segment length is 20% of the original data length).
- Phase shifting: Phase shifting augmentation is implemented by adding a random phase offset to the PD signals, which introduces a phase synchronization error into the augmented data [45]. This process simulates a phase synchronization error between the electrical equipment and the fault diagnosis system.
- Amplitude scaling: Multiply the signal by a random factor in the range of [0.8, 1.2], capping the maximum amplitude at 255 after scaling.
Using these augmented inputs, each IED trains its local network, as described in Step 2. The online network is optimized by minimizing the loss , defined as the mean squared error between the online and target network outputs, as follows:
where and are the outputs of the online and target networks, respectively, for the augmented pair . After updating the online network, the target network parameters are updated via the EMA of the online weights as
where denotes the target decay rate. Once the local training is completed, the IED sends to the server. The server incorporates this update into the global model using an aggregation function as
where denotes the contribution of the IED update. By applying a mixing parameter , the server asynchronously aggregates model updates from the IEDs using a first-in, first-out (FIFO) queue mechanism. This asynchronous aggregation allows the global model to update as soon as each IED sends its result without waiting for all IEDs in every round. Additionally, each IED employs its own hyperparameter settings to maximize local resource utilization. For example, during a global communication round involving two devices (IED 1 and IED 2), the server may receive model parameters from IED 2 while it is still aggregating those from IED 1. Instead of instantly responding to IED 2 with an updated model, the server first completes the aggregation of IED 1’s contribution, then processes that of IED 2, and only then sends the updated global model to IED 2. Importantly, the server’s aggregation time is minimal and negligible compared to the training time required by each IED. Therefore, in terms of device waiting times, the overall process effectively functions in an asynchronous manner.
Although IEDs updates are processed asynchronously as they arrive, the global communication concludes only after a predefined number of communication rounds (e.g., ). At that point, the server signals all IEDs to begin the next phase of the process. These design choices enable the proposed SSAFL to effectively address key challenges, including asynchronous update delays, data heterogeneity among IEDs, and varying IED system constraints.
3.4. Downstream Tasks
During the downstream training phase, each IED optimizes parameters of its downstream model . Model is essentially the final global online model combined with an added MLP at the end. In this phase, IEDs train on their locally labeled data using mini-batches of size B. The downstream task uses a cross-entropy loss defined as
where C is the number of classes, and is the one-hot encoded ground truth label for sample . Additionally, subscript b denotes the index of the b-th batch in the training samples with thin mini-batch B. The model parameters were updated using the Adam optimizer during training.
4. Performance Evaluation
This section presents the experimental results and performance evaluation of the proposed SSAFL using PRPDs in various noisy environments. To ensure the reliability of the assessments, each experiment was repeated five times, and the average results were analyzed to derive the final conclusions.
4.1. Hyperparameter Optimization
Table 2 lists the number of PRPD samples per IED in the GIS covering four types of PRPD faults: corona, floating, particle, and void. Noise signals were recorded on-site using UHF sensors, and each IED’s training data consisted of PRPDs and the IED’s own noise signals. We split the data into training and testing sets at a 90:10 ratio for each fault category. To simulate the limited labeled data, we assumed that only half of the training samples were labeled.

Table 2.
The number of samples in each IED.
Table 3 lists the value ranges considered for each hyperparameter during the tuning process. The optimal hyperparameter configuration identified was , , , , , , and . This configuration yielded the highest overall accuracy for the PD dataset. To ensure robust results, we conducted each experiment five times with different random initializations and averaged the outcomes to confirm the robustness of the proposed model. The experiment approaches are described in the following:

Table 3.
Minimum and maximum bounds of hyperparameter optimization.
- Centralized Supervised Learning [42] (no data privacy, fully labeled data): All IED data are aggregated on a central server without any privacy restrictions. It assumes all data are labeled and does not address scenarios with limited labeled data.
- Centralized Self-supervised Learning [33] (no data privacy): This approach aggregates data on a central server and leverages self-supervised learning to handle limited labels. While it addresses the scarcity of labeled data by utilizing unlabeled data, it disregards data privacy concerns.
- Supervised Federated Learning [46] (fully labeled data, homogeneous IED resources): This federated approach preserves data privacy by keeping data local, but it assumes all local data are labeled and that all IEDs have similar resources. It therefore still suffers from labeled data scarcity and cannot handle heterogeneity in IED resources.
- Supervised Asynchronous Federated Learning [40] (fully labeled data): This approach allows asynchronous updates to manage heterogeneous IED resources. However, it still requires fully labeled data and thus suffers from labeled data scarcity.
- Self-Supervised Federated Learning [47] (homogeneous IED resources): This method addresses data privacy and mitigates labeled data scarcity by using self-supervised learning in a federated setting. However, it assumes homogeneous IED resources and does not resolve issues related to IED heterogeneity.
- Self-Supervised Asynchronous Federated Learning: This approach simultaneously addresses the scarcity of labeled data, preserves data privacy, and accommodates heterogeneous IED resources.
All experiments were conducted using two machines. The first machine was equipped with an AMD Ryzen 2990 WX CPU and three identical NVIDIA GeForce RTX 2080 Ti GPUs. The second machine had an Intel Core i9-10900X CPU and an NVIDIA GeForce RTX 4090 GPU. Both machines performed experiments using PyTorch 2.5.1.
4.2. Experimental Results
Figure 6 illustrates the loss values of SSFL and SSAFL across global communication rounds. Both curves show a decreasing trend, indicating convergence of the global model. In SSFL, each communication round involved all IEDs, with every device uploading its updated model parameters to the server. In contrast, SSAFL allowed only a single IED to send its updated model parameters to the server in each round. Therefore, to monitor global model convergence, we used the loss value of the global model in SSAFL, while in SSFL, we used the mean loss value of the global model across all IEDs.
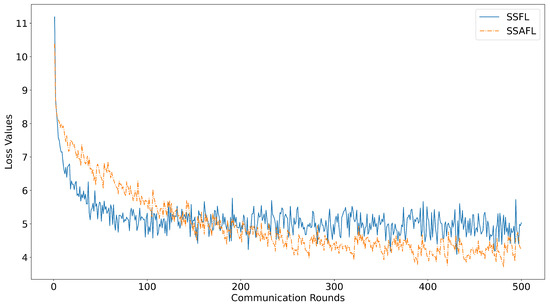
Figure 6.
Test loss of the global model over communication rounds for SSFL and SSAFL: SSFL shows the mean loss across all IEDs, while SSAFL shows the loss value from a single IED.
Table 4 lists the performance outcomes of the different techniques on the training and testing datasets. It evaluates various combinations of training strategies, for example, by comparing centralized training to federated learning (synchronous and asynchronous) and using supervised and self-supervised learning. In the centralized scenario, all IED data (training and testing) were aggregated into a single dataset for model training and evaluation. As shown in Table 4, the proposed SSAFL achieved competitive accuracy and significantly improved training efficiency. Specifically, the proposed SSAFL achieved 98.26% in training accuracy and 95.28% in testing accuracy. In terms of training time, the asynchronous FL strategy drastically reduced the training duration, which was nearly 60% shorter than that of the fully supervised FL case and approximately 29% shorter than that of the self-supervised FL case.

Table 4.
Mean of accuracy for different methods.
Table 5 lists the breakdown performances of the individual IEDs. The proposed SSAFL achieved the highest training accuracy of 98.85% on IED 1, which is slightly higher than the best training accuracy of SSFL (98.84% on IED 3). For testing, the proposed SSAFL achieved 95.71% accuracy on IED 4 compared to SSFL’s highest test accuracy of 94.83% on IED 3. These results indicate that the proposed SSAFL delivers higher accuracy than SSFL on the training and test sets across all IEDs, demonstrating superior overall performance.

Table 5.
Accuracy performance outcomes for IEDs.
Table 6 lists the precision, recall, and F1-score [48] results for each fault class on IED 1 by comparing SSAFL with SSFL. As listed in Table 6, the proposed SSAFL method achieved higher values for these metrics across most fault classes. For floating, the proposed SSAFL achieved 100% precision, whereas SSFL achieved 95% precision. For the noise class, the proposed SSAFL attained 100% recall and F1-score values, outperforming SSFL (which achieved approximat ely 94% recall and 97% F1-score). These improvements highlight the effectiveness of the proposed approach for imbalanced data and multiple fault categories. Additionally, Figure 7 provides a confusion matrix for the classification results of SSFL and SSAFL on IED 1, offering an overview of the performance of each model across fault classes.

Table 6.
Precision, recall, and F1-score comparisons on test dataset with IED 1.
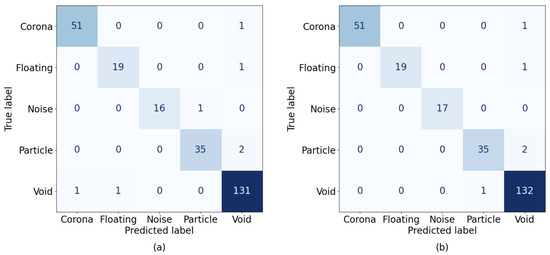
Figure 7.
Confusion matrix for (a) SSFL and (b) the proposed SSAFL, both obtained from experiments conducted on IED 1.
5. Conclusions
This study proposes a novel SSAFL approach for PD fault diagnosis in GISs. This approach integrates asynchronous federated learning and self-supervised representation learning to address key challenges in this domain. By leveraging asynchronous federated learning, SSAFL enhances data privacy and reduces communication costs among IEDs, even in heterogeneous resource environments. Additionally, the self-supervised component enables the model to learn effective feature representations from unlabeled data, thereby reducing dependence on large labeled datasets.
We validated the proposed SSAFL on multiple local IEDs using real on-site noise conditions and PRPD data. The experimental dataset included four fault types—corona, floating electrode, void, and particle—generated using artificial cells. The experimental results demonstrate that SSAFL achieved high accuracy, precision, recall, and F1-score measures in fault classification. Furthermore, the asynchronous approach significantly reduced training time compared to conventional synchronous federated learning. These findings suggest that SSAFL, trained on local IEDs with limited labeled data, is more suitable for real-world applications than traditional centralized or fully supervised techniques.
Author Contributions
Y.-H.K. conceived the presented idea. V.N.H. and H.N.-N. developed the model and performed the computations. Y.-W.Y. and H.-S.C. verified the experimental setup and results. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by grants from the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korean government (MOTIE) (Nos. 20225500000120 and 20221A10100011).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Hyeon-Soo Choi has been employed by the Genad System. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclatures
The following nomenclatures are used in this manuscript:
| ADC | Analog-to-digital converter |
| AFL | Asynchronous federated learning |
| CNNs | Convolution neural networks |
| DAS | Data acquisition system |
| DNNs | Deep neural networks |
| FIFO | First-in, first-out |
| FL | Federated learning |
| GIS | Gas-insulated switchgear |
| IEDs | Intelligent electronic devices |
| LSTM | Long short-term memory |
| MLP | Multi-Layer Perceptron |
| PD | Partial discharge |
| PRPDs | Phase-resolved PDs |
| RNNs | Recurrent neural networks |
| SemiSL | Semi-supervised learning |
| SSAFL | Self-Supervised Asynchronous Federated Learning |
| SSL | Self-supervised learning |
| SSFL | Self-Supervised Federated Learning |
| UHF | Ultra-high-frequency |
References
- Han, X.; Li, J.; Zhang, L.; Pang, P.; Shen, S. A Novel PD Detection Technique for Use in GIS Based on a Combination of UHF and Optical Sensors. IEEE Trans. Instrum. Meas. 2019, 68, 2890–2897. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Chen, H.; Shi, T.; Song, Y.; Han, X.; Li, J. A Novel IEPE AE-Vibration-Temperature-Combined Intelligent Sensor for Defect Detection of Power Equipment. IEEE Trans. Instrum. Meas. 2023, 72, 9506809. [Google Scholar] [CrossRef]
- Song, H.; Zhang, Z.; Tian, J.; Sheng, G.; Jiang, X. Multiscale Fusion Simulation of the Influence of Temperature on the Partial Discharge Signal of GIS Insulation Void Defects. IEEE Trans. Power Deliv. 2022, 37, 1304–1314. [Google Scholar] [CrossRef]
- Xia, C.; Ren, M.; Chen, R.; Yu, J.; Li, C.; Wang, Y.C.K.; Wang, S.; Dong, M. Multispectral optical partial discharge detection, recognition, and assessment. IEEE Trans. Instrum. Meas. 2022, 71, 7002911. [Google Scholar] [CrossRef]
- Lu, B.; Huang, W.; Xiong, J.; Song, L.; Zhang, Z.; Dong, Q. The study on a new method for detecting corona discharge in gas insulated switchgear. IEEE Trans. Instrum. Meas. 2022, 71, 9000208. [Google Scholar] [CrossRef]
- Ren, M.; Dong, M.; Liu, Y.; Miao, J.; Qiu, A. Partial discharges in SF6 gas filled void under standard oscillating lightning and switching impulses in uniform and non-uniform background fields. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 138–148. [Google Scholar] [CrossRef]
- Zeng, F.; Tang, J.; Zhang, X.; Zhou, S.; Pan, C. Typical Internal Defects of Gas-Insulated Switchgear and Partial Discharge Characteristics. In Simulation and Modelling of Electrical Insulation Weaknesses in Electrical Equipment; InTech: Rijeka, Croatia, 2018. [Google Scholar] [CrossRef]
- Tenbohlen, S.; Coenen, S.; Djamali, M.; Müller, A.; Samimi, M.H.; Siegel, M. Diagnostic Measurements for Power Transformers. Energies 2016, 9, 347. [Google Scholar] [CrossRef]
- Shu, Z.; Wang, W.; Yang, C.; Guo, Y.; Ji, J.; Yang, Y.; Shi, T.; Zhao, Z.; Zheng, Y. External partial discharge detection of gas-insulated switchgears using a low-noise and enhanced-sensitivity UHF sensor module. IEEE Trans. Instrum. Meas. 2023, 72, 3518210. [Google Scholar] [CrossRef]
- Gao, W.; Zhao, D.; Ding, D.; Yao, S.; Zhao, Y.; Liu, W. Investigation of frequency characteristics of typical PD and the propagation properties in GIS. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1654–1662. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, F.; Zhang, Y.; Hou, S. Feature Extraction and Classification of Partial Discharge Signal in GIS Based on Hilbert Transform. In Proceedings of the International Conference on Information Control, Electrical Engineering and Rail Transit (ICEERT), Lanzhou, China, 23–25 October 2021; pp. 208–213. [Google Scholar] [CrossRef]
- Li, L.; Tang, J.; Liu, Y. Partial Discharge Recognition in Gas Insulated Switchgear Based on Multi-Information Fusion. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1080–1087. [Google Scholar] [CrossRef]
- Firuzi, K.; Vakilian, M.; Phung, B.T.; Blackburn, T.R. Partial Discharges Pattern Recognition of Transformer Defect Model by LBP & HOG Features. IEEE Trans. Power Deliv. 2019, 34, 542–550. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, S.; Shu, N.; Tang, J.; Li, W. GIS Partial Discharge Pattern Recognition Based on the Chaos Theory. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 783–790. [Google Scholar] [CrossRef]
- Abubakar, A.; Zachariades, C. Phase-resolved partial discharge (PRPD) pattern recognition using image processing template matching. Sensors 2024, 24, 3565. [Google Scholar] [CrossRef]
- Chauhan, N.K.; Singh, K. A Review on Conventional Machine Learning vs. Deep Learning. In Proceedings of the International Conference on Computing, Power and Communication Technologies (GUCON), Greater Noida, India, 28–29 September 2018; pp. 347–352. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, J.; Yang, Z.; Jing, Q.; Qi, Z.; Wang, J.; Geng, Y. A domain adaptive deep transfer learning method for gas-insulated switchgear partial discharge diagnosis. IEEE Trans. Power Deliv. 2021, 37, 2514–2523. [Google Scholar] [CrossRef]
- Tuyet-Doan, V.-N.; Anh, P.-H.; Lee, B.; Kim, Y.-H. Deep ensemble model for unknown partial discharge diagnosis in gas-insulated switchgears using convolutional neural networks. IEEE Access 2021, 9, 80524–80534. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Nguyen, V.H.; Yun, S.J.; Kim, Y.H. Recurrent neural network for partial discharge diagnosis in gas-insulated switchgear. Energies 2018, 11, 1202. [Google Scholar] [CrossRef]
- Do, T.-D.; Tuyet-Doan, V.-N.; Cho, Y.-S.; Sun, J.-H.; Kim, Y.-H. Convolutional-Neural-Network-Based Partial Discharge Diagnosis for Power Transformer Using UHF Sensor. IEEE Access 2020, 8, 207377–207388. [Google Scholar] [CrossRef]
- Chen, C.H.; Chou, C.J. Deep learning and long-duration PRPD analysis to uncover weak partial discharge signals for defect identification. Appl. Sci. 2023, 13, 10570. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, R.; Tian, X.; Yu, Z.; Wang, H.; Elhanashi, A.; Saponara, S. A real-time transformer discharge pattern recognition method based on CNN-LSTM driven by few-shot learning. Electr. Power Syst. Res. 2023, 219, 109241. [Google Scholar] [CrossRef]
- Salman, S.; Liu, X. Overfitting mechanism and avoidance in deep neural networks. arXiv 2019, arXiv:1901.06566. [Google Scholar] [CrossRef]
- Albelwi, S. Survey on self-supervised learning: Auxiliary pretext tasks and contrastive learning methods in imaging. Entropy 2022, 24, 551. [Google Scholar] [CrossRef]
- Lee, D.H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. In Proceedings of the Workshop on Challenges in Representation Learning, 30th International Conference on Machine Learning (ICML 2013), Atlanta, GA, USA, 16–21 June 2013; Volume 3, p. 896. [Google Scholar]
- Sohn, K.; Berthelot, D.; Carlini, N.; Zhang, Z.; Zhang, H.; Raffel, C.A.; Li, C.L. FixMatch: Simplifying semi-supervised learning with consistency and confidence. Adv. Neural Inf. Process. Syst. 2020, 33, 596–608. [Google Scholar] [CrossRef]
- Berthelot, D.; Carlini, N.; Goodfellow, I.; Papernot, N.; Oliver, A.; Raffel, C.A. MixMatch: A holistic approach to semi-supervised learning. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Tai, H.T.; Youn, Y.W.; Choi, H.S.; Kim, Y.H. Semi-supervised learning-based partial discharge diagnosis in gas-insulated switchgear. IEEE Access 2024, 12, 115171–115181. [Google Scholar] [CrossRef]
- Yang, J.; Hu, K.; Zhang, J.; Bao, J. Semi-supervised learning for gas insulated switchgear partial discharge pattern recognition in the case of limited labeled data. Eng. Appl. Artif. Intell. 2024, 137, 109193. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Y.; Zhang, Y.; Liu, Z.; Zhang, M. A semi-supervised approach for partial discharge recognition combining graph convolutional network and virtual adversarial training. Energies 2024, 17, 4574. [Google Scholar] [CrossRef]
- Morette, N.; Heredia, L.C.; Ditchi, T.; Mor, A.R.; Oussar, Y. Partial discharges and noise classification under HVDC using unsupervised and semi-supervised learning. Int. J. Electr. Power Energy Syst. 2020, 121, 106129. [Google Scholar] [CrossRef]
- Grill, J.B.; Strub, F.; Altché, F.; Tallec, C.; Richemond, P.; Buchatskaya, E.; Valko, M. Bootstrap your own latent—a new approach to self-supervised learning. Adv. Neural Inf. Process. Syst. 2020, 33, 21271–21284. [Google Scholar] [CrossRef]
- Davaslioglu, K.; Boztaş, S.; Ertem, M.C.; Sagduyu, Y.E.; Ayanoglu, E. Self-supervised RF signal representation learning for NextG signal classification with deep learning. IEEE Wirel. Commun. Lett. 2022, 12, 65–69. [Google Scholar] [CrossRef]
- Geiping, J.; Garrido, Q.; Fernandez, P.; Bar, A.; Pirsiavash, H.; LeCun, Y.; Goldblum, M. A cookbook of self-supervised learning. arXiv 2023, arXiv:2304.12210. [Google Scholar] [CrossRef]
- Tuyet-Doan, V.N.; Youn, Y.W.; Choi, H.S.; Kim, Y.H. Shared knowledge-based contrastive federated learning for partial discharge diagnosis in gas-insulated switchgear. IEEE Access 2024, 12, 34993–35007. [Google Scholar] [CrossRef]
- Yan, J.; Wang, Y.; Liu, W.; Wang, J.; Geng, Y. Partial discharge diagnosis via a novel federated meta-learning in gas-insulated switchgear. Rev. Sci. Instrum. 2023, 94, 024704. [Google Scholar] [CrossRef] [PubMed]
- Hou, S.; Lu, J.; Zhu, E.; Zhang, H.; Ye, A. A federated learning-based fault detection algorithm for power terminals. Math. Probl. Eng. 2022, 2022, 9031701. [Google Scholar] [CrossRef]
- Wu, C.; Wu, F.; Lyu, L.; Huang, Y.; Xie, X. Communication-efficient federated learning via knowledge distillation. Nat. Commun. 2022, 13, 2032. [Google Scholar] [CrossRef]
- Xie, C.; Koyejo, S.; Gupta, I. Asynchronous federated optimization. arXiv 2019, arXiv:1903.03934. [Google Scholar] [CrossRef]
- Chen, Y.; Ning, Y.; Slawski, M.; Rangwala, H. Asynchronous online federated learning for edge devices with non-IID data. In Proceedings of the 2020 IEEE International Conference on Big Data (Big Data), Atlanta, GA, USA, 10–13 December 2020; pp. 15–24. [Google Scholar]
- Xu, C.; Qu, Y.; Xiang, Y.; Gao, L. Asynchronous federated learning on heterogeneous devices: A survey. Comput. Sci. Rev. 2023, 50, 100595. [Google Scholar] [CrossRef]
- Tuyet-Doan, V.N.; Nguyen, T.T.; Nguyen, M.T.; Lee, J.H.; Kim, Y.H. Self-attention network for partial-discharge diagnosis in gas-insulated switchgear. Energies 2020, 13, 2102. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Adam, H. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Hu, C.; Wu, J.; Sun, C.; Yan, R.; Chen, X. Robust supervised contrastive learning for fault diagnosis under different noises and conditions. In Proceedings of the 2021 International Conference on Sensing, Measurement & Data Analytics in the Era of Artificial Intelligence (ICSMD), Nanjing, China, 21–23 October 2021; pp. 1–6. [Google Scholar]
- Dang, N.Q.; Ho, T.T.; Vo-Nguyen, T.D.; Youn, Y.W.; Choi, H.S.; Kim, Y.H. Supervised contrastive learning for fault diagnosis based on phase-resolved partial discharge in gas-insulated switchgear. Energies 2023, 17, 4. [Google Scholar] [CrossRef]
- McMahan, H.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, FL, USA, 20–22 April 2017; Volume 54, pp. 1273–1282. [Google Scholar] [CrossRef]
- Yan, R.; Qu, L.; Wei, Q.; Huang, S.C.; Shen, L.; Rubin, D.L.; Zhou, Y. Label-efficient self-supervised federated learning for tackling data heterogeneity in medical imaging. IEEE Trans. Med. Imaging 2023, 42, 1932–1943. [Google Scholar] [CrossRef]
- Dalianis, H. Evaluation metrics and evaluation. In Clinical Text Mining; Springer: Cham, Switzerland, 2018; pp. 45–53. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).