Robust Adaptive Fractional-Order PID Controller Design for High-Power DC-DC Dual Active Bridge Converter Enhanced Using Multi-Agent Deep Deterministic Policy Gradient Algorithm for Electric Vehicles

Abstract

The Dual Active Bridge converter (DABC), known for its bidirectional power transfer capability and high efficiency, plays a crucial role in various applications, particularly in electric vehicles (EVs), where it facilitates energy storage, battery charging, and grid integration. The Dual Active Bridge Converter (DABC), when paired with a high-performance CLLC filter, is well-regarded for its ability to transfer power bidirectionally with high efficiency, making it valuable across a range of energy applications. While these features make the DABC highly efficient, they also complicate controller design due to nonlinear behavior, fast switching, and sensitivity to component variations. We have used a Fractional-order PID (FOPID) controller to benefit from the simple structure of classical PID controllers with lower complexity and improved flexibility because of additional filtering gains adopted in this method. However, for a FOPID controller to operate effectively under real-time conditions, its parameters must adapt continuously to changes in the system. To achieve this adaptability, a Multi-Agent Reinforcement Learning (MARL) approach is adopted, where each gain of the controller is tuned individually using the Deep Deterministic Policy Gradient (DDPG) algorithm. This structure enhances the controller’s ability to respond to external disturbances with greater robustness and adaptability. Meanwhile, finding the best initial gains in the RL structure can decrease the overall efficiency and tracking performance of the controller. To overcome this issue, Grey Wolf Optimization (GWO) algorithm is proposed to identify the most suitable initial gains for each agent, providing faster adaptation and consistent performance during the training process. The complete approach is tested using a Hardware-in-the-Loop (HIL) platform, where results confirm accurate voltage control and resilient dynamic behavior under practical conditions. In addition, the controller’s performance was validated under a battery management scenario where the DAB converter interacts with a nonlinear lithium-ion battery. The controller successfully regulated the State of Charge (SOC) through automated charging and discharging transitions, demonstrating its real-time adaptability for BMS-integrated EV systems. Consequently, the proposed MARL-FOPID controller reported better disturbance-rejection performance in different working cases compared to other conventional methods.

1. Introduction

The Dual Active Bridge (DAB) DC-DC converter has been widely applied in various fields such as renewable energy, electric vehicles (EVs), energy storage, due to its excellent flexibility and efficiency. Its support of bidirectional power flow and galvanic isolation, and enabling of high power density all make it particularly suitable for applications that require robust energy exchange–such as EV battery charging, grid-connected storage, and utilization with renewable power sources [1]. The DAB converter ability in wide voltage-range operation adds up to its flexibility, positioning it as part of the important devices in the recent energy systems. These topologies, in employing different types of filters to minimise the level of hazardous harmonics produced due to high switching speeds. Especially the CLLC filter enables soft-switching (including zero-voltage and zero-current-mode) at a wide input range, so that an EMI reduction and power density improvement are obtained. Due to these features, CLLC filters are especially suitable for the DAB systems which require small form factor and low power [2,3,4]. Nevertheless, the control of the DAB converter remains difficult because of its non-linear and fast switching behavior as well as its sensitivity to changes inside the load and at the input. These constraints may compromise performance degradation, the variability of output, and the non-constant system behaviour of a dynamic system. The challenges can best be tackled by a control technology, which is adaptable, robust, providing dependable and constant performance under the various operating conditions [5,6]. The ideal solution should take into consideration the non-linearities of the converter in addition to maintaining a fast transient behaviour, as well as a stable and efficient operation.

During the years, a wide set of advanced control strategies has been developed and implemented for the DABC in order to deal with its intense non-linear behavior and to improve performance under different operating conditions. Sliding Mode Control (SMC) [7,8], Fuzzy Logic Control [9], and Backstepping Control [10,11,12] have been widely acknowledged for their robustness to parameter uncertainties and external disturbances, in addition to guaranteeing fast transient response and accurate tracking for nonlinear systems. On the other hand, Neural Network-based Control, which can learn and adapt to complex nonlinearities through data-driven modeling, has also emerged as a promising approach [13,14]. However, this type of controller generally demands heavy computational resources for training and real-time implementation, which is less suitable for high switching frequency systems like the DAB converter. Although these controllers reveal some favorable aspects, the DAB converter is inherently a time-varying system; hence, adaptive control design based on system dynamics is emphasized. It is well known that the disturbance-rejection performance of an adaptive controller surpasses that of a fixed-gain controller, especially under changing parameters, loads, and external disturbances [15,16,17]. To address the complexity and high computational cost associated with advanced nonlinear control techniques, fractional-order controllers have emerged as a preferred alternative. The Fractional-Order PID (FOPID) controller is particularly well-suited for fine-tuned control in systems involving pressure/flow dynamics, offering enhanced flexibility in shaping control responses [18,19,20,21]. By extending the classical PID framework, FOPID provides superior control precision and better dynamic adaptation over a broader frequency range. Unlike classical controllers, FOPID enables more flexible adjustment of system dynamics, making it efficient for addressing nonlinear and dynamic behaviors. Its functional advantages include higher robustness, enhanced disturbance-rejection capabilities, faster transient response, and improved steady-state performance. Additionally, its relatively simple algorithm makes it convenient for real-time applications [19,20].

Recent studies have demonstrated the usefulness of FOPID control in power systems and power converters [19,22,23,24,25]. For example, the application of FOPID controllers to DC-DC converters has shown substantial improvements in voltage regulation, reduced overshoot, and enhanced dynamic response under load changes. In grid-connected power systems, FOPID-based controllers have also been utilized to regulate inverter dynamics, leading to smoother power delivery and improved system stability in the presence of grid disturbances [21]. These results highlight the practical benefits of FOPID controllers in real-world applications, as they provide an optimal balance between performance and implementation feasibility. Due to their high degree of flexibility and relatively low computational demand, FOPID controllers are increasingly considered viable alternatives for intelligent control in power electronics, particularly in Dual Active Bridge (DAB) converters [25]. One of the critical aspects of a successful FOPID controller is effective gain tuning. The performance and effectiveness of FOPID controllers depend heavily on the proper selection of proportional, integral, and derivative gains, along with the fractional orders of integration and differentiation. While fixed gain values are easier to implement, they often fail to adapt to varying operating conditions, resulting in suboptimal performance, increased steady-state error, and reduced robustness to disturbances or parameter variations. Given that the DAB converter is a nonlinear system with time-varying loads, the use of fixed-gain controllers may not be sufficient to exploit the full potential of the FOPID framework [19,24].

To overcome these shortcomings, recent studies have focused on the optimization and dynamic tuning of FOPID controller gains to achieve better adaptability and efficiency. Recent developments in power electronics control have explored the combination of FOPID controllers with other control techniques to improve dynamic performance and transitional behavior [26,27,28,29]. These hybrid strategies aim to leverage the strengths of multiple control methods to address the complex dynamics of modern systems. One notable advancement is the development of the FOPID-SMC controller. Sliding Mode Control (SMC) is well known for its strong robustness to system uncertainties and external disturbances [30]. With the incorporation of fractional-order elements, the resulting controller benefits from precise tuning of performance indices, which enhances transient response, reduces chattering effects, and minimizes overshoot compared to conventional SMC. However, these advantages come at the cost of increased design complexity and potentially higher processing requirements for implementation. Another hybrid approach is the integration of FOPID with Fuzzy Logic Control. Fuzzy controllers are well suited for nonlinear and uncertain systems that lack an accurate mathematical model [31,32]. When integrated with FOPID, the controller can finely tune system responses with suitable damping values across a broader frequency range than integer-order PID controllers. This combination also helps to smooth control actions and improve the system’s ability to respond to load variations. Nevertheless, the design process is more complex and typically requires extensive optimization to achieve optimal performance. FOPID has also been combined with Neural Network-based Control. Neural networks are capable of learning and adapting to temporal changes within dynamic systems by adjusting internal weights. When integrated with FOPID, the controller gains the ability to adapt its parameters in real-time, resulting in greater flexibility and robustness [33,34]. However, this approach demands significant computational resources, and the need to train neural networks may hinder real-time applicability. These hybrid control strategies demonstrate that it is possible to enhance the dynamic behavior of DAB converters by combining the precision tuning and adaptability of FOPID with the robustness and flexibility of other advanced control designs. Nonetheless, the increased design complexity and computational demands must be carefully managed to ensure practical feasibility, particularly for real-time applications.

Reinforcement Learning (RL) schemes coupled with FOPID controllers provide a potent methodology to further improve the control of complex systems. Reinforcement learning (RL) makes it possible for controllers to learn and cope with time-varying environments by interacting with the system and optimizing control actions according to the feedback, avoiding the shortfall of the fix-gain controller [35,36]. The key benefit of integrating RL with FOPID controllers is that it allows on-line, real-time tuning of the control parameters. This flexibility guarantees that performance is optimized over diverse operating conditions and increases the disturbance rejection and robustness of the system [37]. Furthermore, RL-based control approaches can address nonlinearities, uncertainties and disturbances of power electronic systems without the accurate model being known, which provides a great convenience for the controller design process. Recent works have been made on some successful RL-enhanced FOPID controllers. For example, a model-based RL was employed in FOPID synthesis using probabilistic inference for learning control coordinate to refine PID parameters and tested on robust performance in underactuated mechanical systems [31,38,39]. These developments demonstrate that the RL-embedded FOPID controllers can offer adaptive, high-performance, and robust control solutions for power converters, especially in systems where high precision and reliability are required. Although combining RL with various controllers offers such promising potential, three major issues need to be tackled to further exploit its strengths [40,41]. The first problem is to enhance the adaptability and robustness of the controller in broader disturbance and more different operating conditions. Although RL has the advantage of the ability to adjust, to achieve stable and reliable performance adaptation in diverse scenarios, a reliable and efficient learning model is necessary [42,43]. This is especially important for power converters, whose work is nonlinear and the time-varying. Improving adaptability of the developed RL-FOPID system is necessary to reliably control a system in dynamic and uncertain environment. The second issue concerns the high computational cost and time to obtain the initial gains for the FOPID controller according to the RL [41]. The initialization where the RL agents explore and learn the parameter space is also often computationally expensive and long with a heavy overheat in the sense that if when the devices are real-time this can lead to significant delay. This difficulty becomes even greater when fractional-order parameters are incorporated which further enlarge the searching domain [31]. Finding the appropriate strategy to initialize the RL algorithm is essential, for speeding up the convergence and decreasing the complexity for practicality. The third challenge is to establish a right policy selection for the RL framework that can lead to optimal control dynamics without introducing excessive computational load. Choosing a good policy between exploration and exploitation is vital to achieve the optimal solutions in a time-effective way. A good policy doesn’t only result in better learning efficiency, but also a well convergence of controller to the system dynamics and does not consume excessive amount of compute resources. Solving these three problems is the key to the good performance of the RL-enhanced FOPID controlled in generating robust, adaptive and efficient solutions for advanced PES.

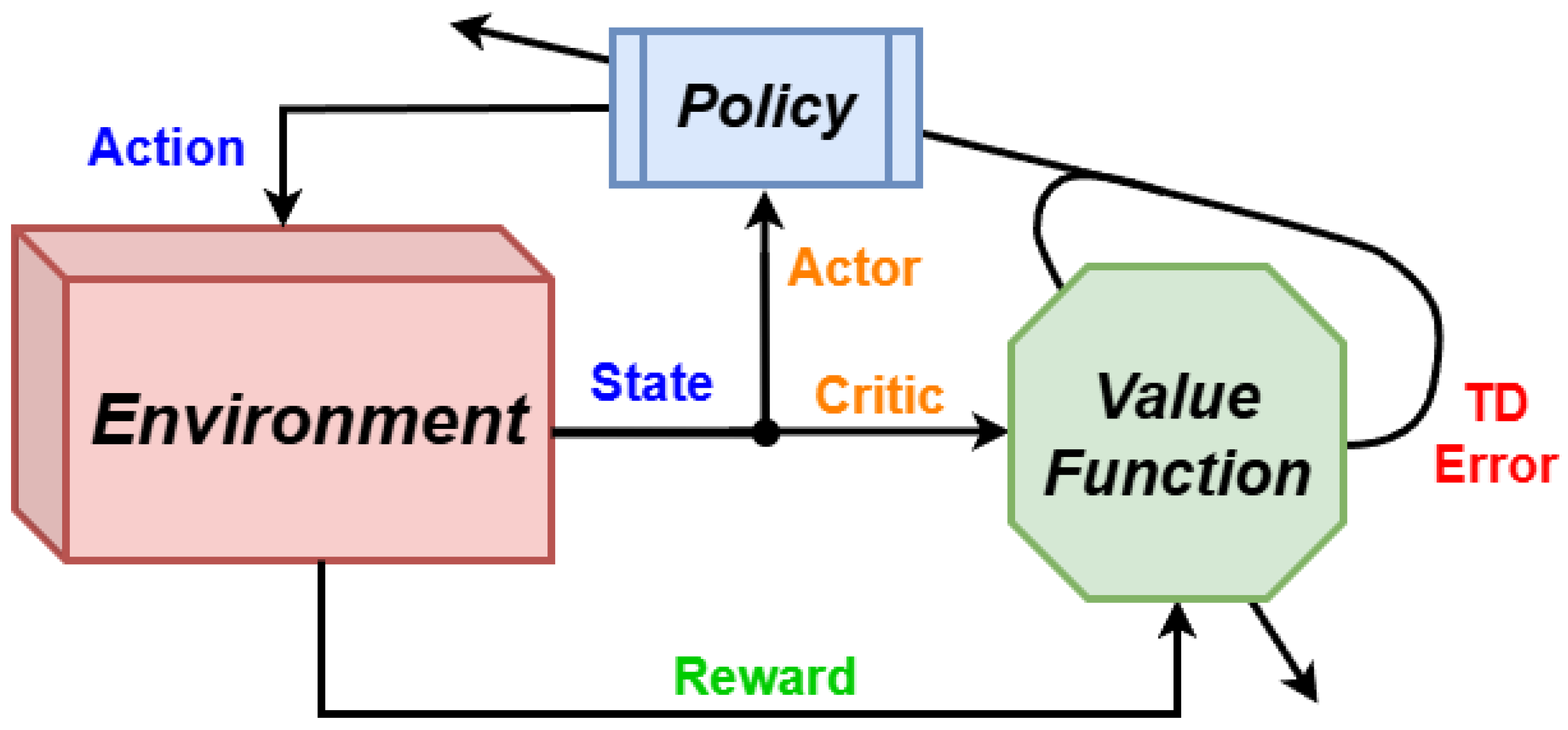
To enhance the adaptivity and robustness of the controller under different types of disturbances and operating points as well as its generalization capability, in this paper, we employ the Deep Deterministic Policy Gradient (DDPG) algorithm [44,45]. Actor-critic is a model-free DDPG: Actor-critic architectures are also suited to finding optimal policies for controller design in continuous-action spaces, where the output can be the control action for power converters [46,47,48]. It is a combination of Q-learning and policy gradient, suitable for learning deterministic policy and capable of dealing with the nonlinear dynamics for converters. Due to the off-policy nature of the algorithm, the ALRAC algorithm can utilize experience replay buffers to increase sample efficiency and stability of training. DDPG has several unique advantages compared to other RL algorithms [49,50]. Similar to the earlier version known as Deterministic Policy Gradient (DPG), DDPG is cast as an analysis to approximated actor (policy) and critic (value function) with deep model, and is another more scalable version when the system is more complex. Also, Deep Q-learning (DQN) has been proved to be very effective for discrete action spaces, but does not work well for continuous control tasks, which are the cases of the power converters that require high-precision control [51,52]. Another popular one Soft Actor-Critic (SAC) concentrates on stochastic policies to encourage exploration and could potentially add more computational overhead than deterministic approach of DDPG [53,54]. Especially, DDPG is a good choice for the DAB application since it can cope with continuous control inputs as well as provide stable policy updates and it is still computationally efficient, which makes it a strong and practical alternative for power electronics control in real-time applications.

To handle simultaneous tuning of multiple gains for the FOPID controller, we used Multi-Agent Reinforcement Learning (MRL) [55,56]. In this setting, each gain is controlled by a separate agent, resulting in decentralized learning and optimization. This structure provides the controller with more flexibility and scalability, since the gain of each agent can be tuned according to the dynamics of the system. The MRL promotes the cooperation styles control and enhances performance in complex environments [56]. For example, in the application of industrial wave energy converters, MRL controllers have exhibited better energy capture performance when comparing to conventional controllers [57]. MRL has been applied in more and more fields, and it has been known to have a distinct advantage compared with individual agent. In power grid control, environments designed only for complex power system operations, such as Power Grid world, have been developed. Such settings enable agents to represent heterogeneous systems and learn to make policies that improve power flow solutions, resulting in better control of grid level variables and operational costs [58,59]. In the same way, MRL seems to be used in frequency regulation with the model of each generator controller as an individual agent. Such a distributed method allows the agents to learn their own control policies, and in turn provides a good frequency stability and system stability [60]. MRL has also been used in load frequency control of multi-area power systems, where cooperative learning behavior among agents have resulted in optimized joint controllers, showing the superiority of control strategies that can greatly enhance the system performance and stability. These uses demonstrate MRL’s advantages in terms of ability to scale, resilience and efficiency, especially in case of collective actions and decentralized decision making. MRL is more versatile and adaptable than the single agent-based methods in the control of complex environment with non-stationary changes. The proposed algorithm can provide high throughput, but the Multi-Agent RL can encounter trouble with determining the best initial gains to ensure the effective operation of the system. This optimization is very sensitive to the initial gain values which may slow the convergence or result in bad solutions if not properly chosen [61,62]. To resolve this problem and improve the performance of the algorithm, we use metaheuristic algorithms for selection of proper initial gains. By offering well-tuned initial points, these algorithms can reduce the amount of nodes and edges that need to be passed at each iteration, leading to faster convergence and, ultimately, better overall performance in complex scenarios.

Recent studies have also explored the use of advanced control strategies and hybrid intelligence in emerging energy systems, emphasizing the integration of machine learning and metaheuristics for real-time optimization [63,64,65,66]. These works highlight the importance of adaptive, data-driven control frameworks that are robust under dynamic and uncertain operating conditions, which aligns with the approach adopted in this study. There have been some researches for metaheuristic algorithms e.g., PSO, GA, ALO to be used to find optimal gain values for given applications [67,68,69]. Nevertheless the gain tuning of such methods is not yet satisfactory in the case of wide disturbances [70,71]. To avoid the time consuming task of discovering optimal initial gains for the RL mechanism, we have used the Grey Wolf Optimization Algorithm (GWO) [72]. GWO is a novel metaheuristic optimization algorithm that mimics the basic rules of the wolves’ population and their prey, and has the advantage of simplicity and being an efficient approach for exploring complex search spaces. Using the GWO to find the initial values of the gains gives a better starting point for the RL agents, which leads to faster convergence of the learning and less computations. This coordination ensures that the controller can better improve its performance. The GWO is a successful metaheuristic algorithm using the mating habits of wolves and has several advantages compared to the other algorithms. One of its major strengths is its capacity of balancing exploration and exploitation, allowing to explore the set of solutions then existing solutions can be further refined for improving their quality [73,74,75,76]. GWO has shown competitive numerical performance on a wide range of problems such as benchmark functions and real-world engineering problems, which have verified its generality and flexibility. Some comparative studies have been made to compare GWO with other metaheuristic techniques as it achieves better performance in special cases and situations, especially in finding an optimal solution effectively, and it will be an effective tool for performing optimization tasks in different fields [77]. However, despite significant advances in the adaptive control algorithms of DAB converters, some fundamental issues are still not resolved. Conventional FOPID controllers, which are more flexible modifications of classical PID controllers, are sometimes designed with static or manually-tunable parameters, resulting in a restricted applicability for dynamic operating environments [78,79,80,81]. The traditional RL-based controllers for power converters are often based on a single-agent framework, which leads to the relatively high complexity of tuning multiple parameters in high space dimension and the slow convergence. Furthermore, the initialization of RL agents is still a major bottleneck, because initialization with bad conditions could result in longer training time or suboptimal control performance. This paper fills these gaps by introducing a GWO-aided MARL framework for real-time applicable, more accurate control-oriented FOPID design in the DAB converters. 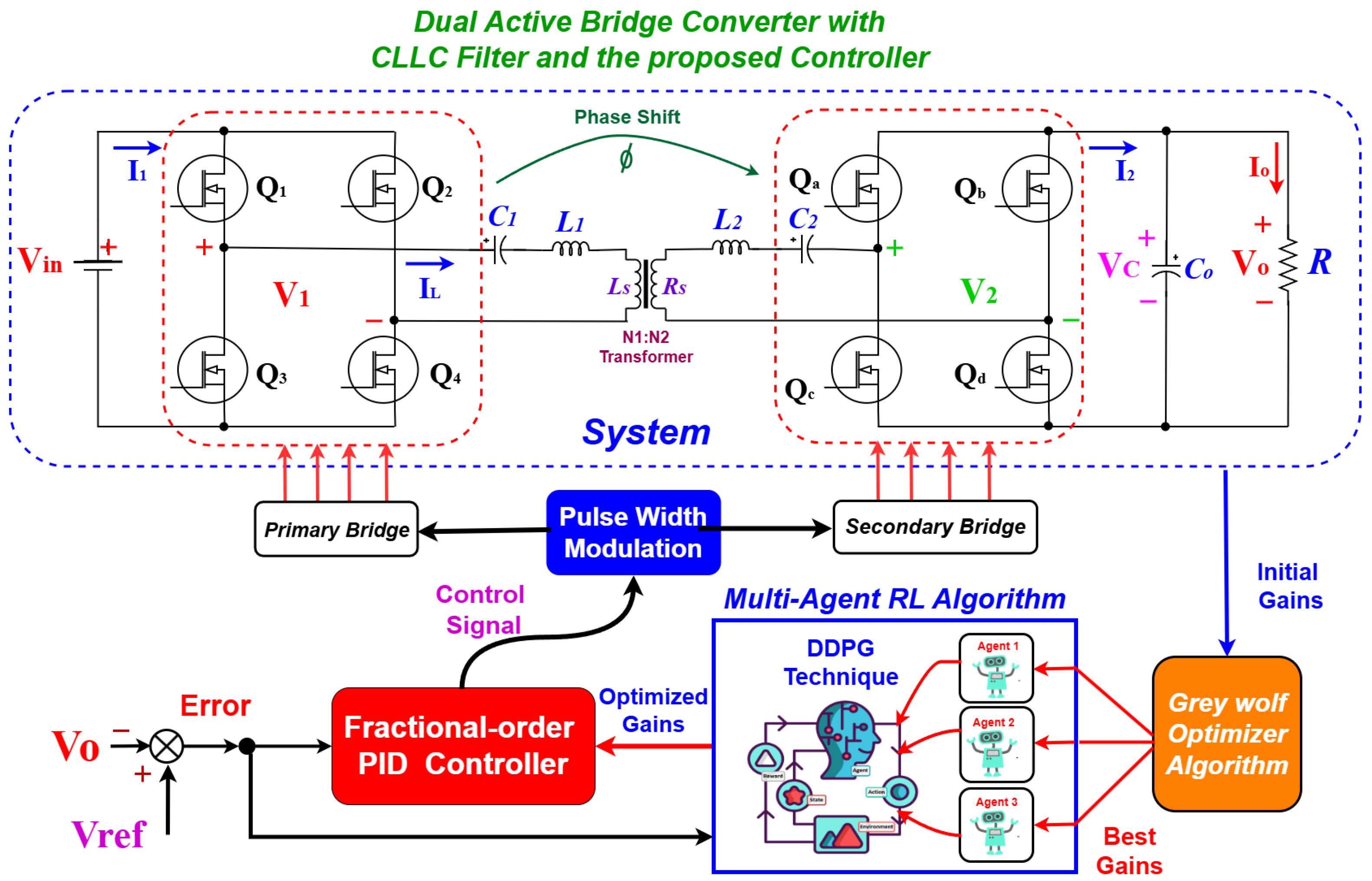Figure 1 is presented in detail to illustrate the system topology using the proposed controller and its operation.

By combining DDPG for policy optimization, MARL for decentralized gain regulation, and SOA for efficient initialization, our approach addresses the key challenges in implementing RL-enhanced FOPID controllers for DAB converters. This comprehensive strategy enhances the controller’s adaptability, reduces computational complexity, and ensures robust performance across a wide range of operating conditions. The main contributions of this work can be summerized as:

• Designed a FOPID controller tailored for DAB converters, leveraging its extended flexibility and superior dynamic performance compared to classical PID controllers.
• Adopted the RL-DDPG algorithm for real-time tuning of FOPID controller gains, ensuring adaptability to varying operating conditions and disturbances. Our work utilizes a Model-free approach by adopting this method, leading to reduced dependency on system modeling and significantly lowering computational burden.
• Implemented a Multi-agent framework for decentralized and dynamic regulation of individual controller gains, improving scalability and robustness.
• To ensure faster convergence and improved learning stability, the Grey Wolf Optimizer (GWO) was employed to initialize the actor’s parameters, providing the best starting gains for the DDPG algorithm.
• Conducted real-time validation of the proposed control strategy using a Hardware-in-Loop (HIL) setup to assess its performance under practical operating conditions. Demonstrated the controller’s effectiveness in achieving precise voltage and current regulation, robust disturbance rejection, and improved transient and steady-state performance.

2. Mathematical Modeling of the System

A popular topology in power electronics for isolation and bi-directional power flow is DAB. The DAB converter’s capacity to deliver high-density power conversion with high accuracy of power flow control is crucial, especially in systems like electric vehicles and renewable energy integrations. By enabling zero voltage switching (ZVS) and reducing switching losses, the application of a CLLC resonant filter with series and parallel resonant components increases the converter’s efficiency. This part derives an averaged state-space model that incorporates the dynamics required to create reliable control strategies for a DAB converter with a CLLC-filter [4].

DAB converter images and figures: The DAB converter, as depicted in the images of Figure 1 and Figure 2, uses a high-frequency transformer and switching cells to create a bidirectional power flow path between two voltage sources. The switching state inverter, which has two bridges (primary and secondary) with four switches each (Q1–Q4 for the primary bridge and Qa–Qd for the secondary bridge), regulates power transfer. DAB converters can be utilized in battery energy storage systems, electric vehicles, and renewable energy applications thanks to the high frequency transformer’s galvanic isolation and voltage conversion capabilities.

While the phase shift between the two bridges regulates the quantity and direction of power delivered, this symmetrical switching action helps to minimize switching stress and guarantees smooth power flow. With this converter, three operational modes can be produced based on the bridges’ switching function. Figure 2 illustrates how the switches operate together. This converter’s switching features allow it to operate in both step-up and step-down modes.

Table 1. List of components.

Components	Definitions	Values
$V_o$	Output voltage	100–500 V
$V_{in}$	Supply voltage	200–350 V
$P_{out}$	Max Output power	20 kW
$L_s,R_s$	Resistor & Inductor of Transformer	5 μH 0.3 Ω
$R_C$	Leakage resistance for Capacitors	0.3 Ω
$R_L$	Leakage resistance for Inductors	0.25 Ω
$L_1$	Primary-side Inductor	$130\mathsf{\mu }\mathrm{H}$
$L_2$	Secondary-side Inductor	$80\mathsf{\mu }\mathrm{H}$
$C_1$	Primary-side Capacitor	$50\mathsf{\mu }\mathrm{H}$
$C_2$	Secondary-side Capacitor	$32\mathsf{\mu }\mathrm{H}$
$C_o$	Output Capacitor	$1.5\mathrm{mF}$
R	Resistor-Load	5 Ω
$\varphi$	Phase Shift (assumed)	0.1

lists the values of the circuit parameters.

2.1. Averaged Modeling of the System

Figure 3 displays the averaged model of the DAB converter with a CLLC filter, which attempts to accurately depict the behavior of the system under CCM conditions. Since this model only represents the average behavior of the converter during a single switching period, it acknowledges the high frequency switching of the converter. Investigating and tracking the voltage output ($V_O$) for the system inputs and disturbances is the aim of this model.

State-Space Formulation

Kirchhoff’s voltage and current laws applied to each component are used to build the averaged state-space model of the DAB converter with a CLLC filter. These states consist of the current flowing through the inductor and the voltages across the capacitors. The system’s states are Inductor Current ($I_L$) and Capacitor Voltages ($V_{C_1},V_{C_o},V_{C_2}$):

$$\mathbf{x}\left(t\right)=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]=\left[\begin{array}{c}{I}_L\\ V_{C_1}\\ V_{C_2}\\ V_o\end{array}\right]$$

(1)

The input to the system is the input voltage $V_{in}$, defined as:

$$\begin{array}{c}\hfill \begin{array}{c}u\left(t\right)=V_{in}\hfill \end{array}\end{array}$$

(2)

The output is the output voltage $V_O$, defined as:

$$\begin{array}{c}\hfill \begin{array}{c}y\left(t\right)=V_{C_o}=V_o\hfill \end{array}\end{array}$$

(3)

Using Kirchhoff’s Voltage Law (KVL) and Kirchhoff’s Current Law (KCL), the dynamic equations governing the states of the system are as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle I_L^{.}=\frac{1}{L_{eq}}\left(V_{in}-V_{C_1}-V_{C_2}-V_o\right)}\hfill \end{array}\end{array}$$

(4)

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle V_{C_1}^{.}=\frac{1}{C_1}{I}_L}\hfill \end{array}\end{array}$$

(5)

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle V_{C_2}^{.}=\frac{1}{C_2}{I}_L}\hfill \end{array}\end{array}$$

(6)

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle V_{C_o}^{.}=\frac{1}{C_o}\left({\displaystyle I_L-\frac{V_{Co}}{R}}\right)}\hfill \end{array}\end{array}$$

(7)

The above dynamic equations can be expressed in state-space form:

$$\begin{array}{c}\hfill \begin{array}{c}\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right),\hfill \\ y\left(t\right)=Cx\left(t\right)+Du\left(t\right)\hfill \end{array}\end{array}$$

(8)

The state-space matrices are given as:

$$A=\left[\begin{array}{cccc}0& {\displaystyle -\frac{1}{L_{eq}}}& {\displaystyle -\frac{1}{L_{eq}}}& {\displaystyle -\frac{1}{L_{eq}}}\\ {\displaystyle \frac{1}{C_1}}& 0& 0& 0\\ {\displaystyle \frac{1}{C_2}}& 0& 0& 0\\ {\displaystyle \frac{1}{C_o}}& 0& 0& {\displaystyle -\frac{1}{R{C}_o}}\end{array}\right];B=\left[\begin{array}{c}{\displaystyle \frac{1}{L_{eq}}}\\ 0\\ 0\\ 0\end{array}\right];C=\left[\begin{array}{cccc}0& 0& 0& 1\end{array}\right]$$

(9)

The values of the components are listed in Table 1.

Parasitic elements were included to the real-time testing environment to guarantee a more accurate depiction of actual system behavior, even if they were left out of the mathematical modeling to make the analysis simpler.

3. Controller Design

Fractional-Order PID Controller

The FOPID technique is an extended version of the conventional PID, enhanced through fractional-order calculus. The primary advantage of this controller is its enhanced flexibility, achieved through the inclusion of two additional fractional parameters [31]. The FOPID controller extends the classical PID by incorporating two fractional powers as $\lambda$ (for integration) and $\mu$ (for differentiation), offering enhanced flexibility in tuning dynamic responses. The FOPID controller transfer function is given by:

$$\begin{array}{c}\hfill \begin{array}{c}\begin{array}{c}{\displaystyle G_{FOPID}\left(s\right)=K_D{s}^{\mu }+K_P+\frac{K_I}{s^{\lambda }}}\hfill \end{array}\hfill \end{array}\end{array}$$

(10)

The relevant controller parameters are represented as $K_D,K_I,K_P$. It is clear that the differ-integral order function contains additional terms $\mu$ and $\lambda$. It is visible that the five effective gains of the controller ( $K_D,\mu ,K_P,\lambda ,K_I$) play crucial role in the performance and efficiency of the work and must be selected as the best-selected ones. To optimize these gains, we have proposed Multli-agent RL algorithm using DDPG method. The details related to this optimization algorithm is described in the following sections.

4. Multi-Agent Reinforcement Learning Framework for FOPID Optimization

4.1. Reinforcement Learning Framework

Reinforcement Learning (RL) is a learning paradigm where agents interact with an environment to maximize a cumulative reward by taking sequential actions based on observed states. In the context of FOPID optimization, RL is employed to fine-tune the controller’s gains ($K_D,K_I,K_P$) for optimal system performance. Instead of treating the optimization as a single-agent problem, we utilize a Multi-Agent Reinforcement Learning (MRL) approach, where three independent agents collaboratively learn to adjust their respective parameters [36].

Unlike conventional single-agent RL frameworks, the proposed multi-agent structure delegates each gain ($K_D,K_I,K_P$) to a dedicated agent. This reduces the complexity of joint action spaces, improves exploration in high-dimensional domains, and accelerates convergence by allowing independent learning paths. As reported in [14] and validated in our experiments, multi-agent systems also enhance scalability for tuning multiple FOPID gains concurrently.

Roles of the Agents

Each agent is responsible of tuning a gain in FOPID controller based on the error generated by the system. These agents are classified as below:

• Agent 1: Responsible for optimizing $K_P$, which controls the proportional response and directly affects the rise time of the system.
• Agent 2: Tunes $K_I$, which eliminates steady-state errors by integrating the error over time.
• Agent 3: Adjusts $K_D$, which anticipates future errors and reduces overshoot by responding to the error’s rate of change.

Each agent interacts with the shared environment representing the dynamic behavior of the FOPID-controlled system. The agents observe the same state, defined as:

$$\begin{array}{c}\hfill \begin{array}{c}{s}_t=\left[\begin{array}{ccc}e\left(t\right),& \dot{e}\left(t\right),& {\int }_0^{t}e\left(\tau \right)d\tau \end{array}\right]\hfill \end{array}\end{array}$$

(11)

where $e\left(t\right)$ is the error between the reference and the output, $\dot{e}\left(t\right)$ is the rate of change of the error, and ${\int }_0^{t}e\left(\tau \right)d\tau$ represents the accumulated error.

The agents select actions $a_t^{\left(i\right)}$, representing adjustments to their respective parameters:

$$\begin{array}{c}\hfill \begin{array}{c}{a}_t^{\left(i\right)}=\Delta K_i,i\in \{P,I,D\}\hfill \end{array}\end{array}$$

(12)

The collective goal of the agents is to minimize a global cost function:

$$\begin{array}{c}\hfill \begin{array}{c}J={\int }_0^T\left(w_1{e}^2\left(t\right)+w_2{\dot{e}}^2\left(t\right)+w_3{u}^2\left(t\right)\right)dt\hfill \end{array}\end{array}$$

(13)

where $w_1,w_2$, and $w_3$ are weights prioritizing tracking accuracy, error smoothness, and control effort, respectively, and $u\left(t\right)$ is the control signal generated by the FOPID controller. Each agent receives a reward derived from the cost function:

$$\begin{array}{c}\hfill \begin{array}{c}{R}_t^{\left(i\right)}=-\left(w_1{e}^2\left(t\right)+w_2{\dot{e}}^2\left(t\right)+w_3{u}^2\left(t\right)\right)-\beta |\Delta K_i|\hfill \end{array}\end{array}$$

(14)

where $\beta$ penalizes large parameter changes, ensuring smooth updates.

By collaboratively minimizing J, the agents adaptively tune the FOPID controller to achieve superior performance in terms of rise time, settling time, and steady-state error. The weights $w_1,w_2$, and $w_3$ in the cost function were selected to balance the trade-offs between minimizing tracking error, ensuring smooth control signals, and reducing oscillations. These weights directly impact the controller’s performance by emphasizing specific objectives. A grid search method was employed to determine the optimal values for the weights. This method involved testing combinations of $w_1,w_2$, and $w_3$ within a predefined range and selecting the combination that provided the best trade-off in terms of response time, stability, and control effort in experimental testing. The final selected values are $w_1=0.5,w_2=0.3$, and $w_3=0.2$, as they yielded the most satisfactory performance in simulated and HIL environments.

4.2. Adoption of Deep Deterministic Policy Gradient (DDPG)

To facilitate learning in the continuous state and action spaces of this problem, we adopt the DDPG algorithm. DDPG is a model-free, off-policy reinforcement learning algorithm that combines the actor-critic architecture with DPG, making it well-suited for continuous control tasks [36].

Looking at Figure 4, we can give a clear clarification of our proposed method. As illustrated in Figure 4, the RL process follows an actor-critic architecture. Each component plays a critical role in optimizing the FOPID controller’s parameters. The reward signal, as shown in Figure 4, flows from the environment to the critic. It reflects the system’s performance, guiding the learning process to minimize tracking error, reduce oscillations, and balance control effort, thereby optimizing the FOPID controller’s behavior.

In the MRL framework, each agent independently applies the DDPG algorithm to optimize its respective parameter ($K_D,K_I,K_P$). The shared environment and collaborative learning dynamics enable the agents to collectively minimize the global cost function J, achieving superior control performance. The use of DDPG ensures stability, scalability, and efficiency in continuous action spaces, making it an ideal choice for this problem.

Table 2. Multi-Agent Reinforcement Learning Framework with DDPG.

Step	Description
1. Input	Initial FOPID controller gains $\{K_P,K_I,K_D,\lambda ,\mu \}$; RL policy parameters $\theta$ and Q-function parameters $\varphi$; Empty replay buffer D; Initial state of the system $s_0$; Target parameters for actor ${\theta }_{\mathrm{target}}$ and critic ${\varphi }_{\mathrm{target}}$ equal to main parameters $\theta ,\varphi$.
2. Initialization	Initialize environment (DAB converter); set reward weights $w_1,w_2,w_3$; define cost function: $J={\int }_0^T(w_1{e}^2\left(t\right)+w_2{\dot{e}}^2\left(t\right)+w_3{u}^2\left(t\right))\mathrm{d}t$.
3. Repeat	At each time step: observe current state $s_t=[e\left(t\right),\dot{e}\left(t\right),{\int }_0^{t}e\left(\tau \right)\mathrm{d}\tau ]$.
4. Action Selection	Select action $a_t=[\Delta K_P,\Delta K_I,\Delta K_D]$ using policy ${\mu }_{\theta }\left(s_t\right)$ with added noise $\mathcal{N}(0,{\sigma }^2)$ for exploration; clip action to feasible range.
5. Apply Action	Apply $a_t$ to system; observe reward $r_t$, next state $s_{t+1}$, and done flag d.
6. Store Transition	Save tuple $(s_t,a_t,r_t,s_{t+1},d)$ to replay buffer D.
7. Reset (if done)	If $s_{t+1}$ is terminal, reset environment.
8. Sample Batch	Sample mini-batch $\mathcal{B}=\left\{(s,a,r,s^{\prime },d)\right\}$ from D.
9. Compute Targets	$y(r,s^{\prime },d)=r+\gamma (1-d)Q_{{\varphi }_{\mathrm{target}}}(s^{\prime },{\mu }_{{\theta }_{\mathrm{target}}}\left(s^{\prime }\right))$.
10. Critic Update	Minimize critic loss: $\mathcal{L}\left(\varphi \right)={\displaystyle \frac{1}{\left|\mathcal{B}\right|}}\sum {(Q_{\varphi }(s,a)-y)}^2$.
11. Actor Update	Apply policy gradient: ${\nabla }_{\theta }J\approx {\displaystyle \frac{1}{\left|\mathcal{B}\right|}}\sum {\nabla }_a{Q}_{\varphi }(s,a){\nabla }_{\theta }{\mu }_{\theta }\left(s\right)$.
12. Target Update	Update target networks: ${\theta }_{\mathrm{target}}\leftarrow \tau \theta +(1-\tau ){\theta }_{\mathrm{target}}$ and similarly for $\varphi$.
13. Loop	Repeat until convergence or max episodes reached.
14. Output	Optimized FOPID gains $\{K_P,K_I,K_D,\lambda ,\mu \}$.

details the training process algorithm, including initialization, state observation, action selection, reward computation, and updates for both actor and critic networks. It emphasizes the adaptive tuning of FOPID controller gains to enhance performance under varying operating conditions.

In addition, to improve the efficiency and convergence of the RL process, the Grey Wolf Optimizer (GWO) algorithm was employed to determine the initial gains of the FOPID controller. GWO is a nature-inspired optimization technique based on the social hierarchy and hunting behavior of grey wolves. It is particularly effective in exploring complex, high-dimensional solution spaces, providing near-optimal solutions to optimization problems.

4.3. Grey Wolf Optimization Algorithm

The GWO algorithm is a nature-inspired metaheuristic, which mimics the social hierarchy and hunting behavior of Grey wolves. The algorithm simulates the hunting process through encircling, attacking, and searching for prey. The wolves’ positions are updated based on the alpha, beta, and delta wolves, which represent the best solutions found so far.

The balance between exploration and exploitation is managed by adaptive coefficients, allowing the algorithm to effectively navigate the search space. GWO is known for its simplicity, ease of implementation, and ability to solve various optimization problems efficiently [72]. The behavior of wolves is illustrated based on the benchmark of Figure 5.

The optimized gains of FOPID controller and reached using GWO algorithm and they have listed in

Table 3. Optimized gains by GWO.

Gains	Values
$K_I$	0.781
$K_D$	0.24
$K_P$	1.008
$\mu$	0.87
$\lambda$	0.905

for better clarification.

A complete flow chart of the proposed controller is depicted in Figure 6 with all details for more clarity.

To validate the effectiveness of GWO in initializing FOPID parameters for the RL agents, we conducted a comparative study against other widely used metaheuristic algorithms including PSO, GA, Artificial Bee Colony (ABC), and Antlion Optimization (ALO). The comparison focused on transient performance, convergence behavior, and robustness.

Table 4. Performance comparison of metaheuristic optimizers for FOPID tuning.

Method	Set. Time (s)	Overshoot (%)	Cost	Convergence	Robust.
GWO	1.80	4.5	0.0038	Fast	High
PSO	2.30	7.0	0.0055	Moderate	Moderate
GA	2.50	8.2	0.0061	Slow	Moderate
ABC	2.40	6.8	0.0058	Moderate	Moderate
ALO	2.15	6.0	0.0049	Moderate	High

summarizes the performance metrics, clearly indicating the superior capabilities of GWO in terms of convergence speed, overshoot reduction, and cost minimization.

Among the metaheuristic algorithms evaluated, GWO demonstrated the fastest convergence, lowest overshoot, and best cost function performance, confirming its effectiveness in providing optimal initial gains for the RL-FOPID controller.

Unlike gain-scheduled or piecewise-linear control strategies, the proposed method does not rely on local linearization of the DAB converter model. The combination of FOPID with agent-based RL technique enables the controller to adapt directly to nonlinear system dynamics across the full operational envelope, without the need for mode switching or segmented design.

4.4. Motivation

The integration of FOPID, MARL, and GWO is structurally motivated to address the nonlinear and time-varying characteristics of DAB converters. The FOPID controller offers enhanced flexibility in shaping the system’s dynamic response, particularly under uncertain and nonlinear operating conditions. However, optimal tuning of its five parameters ($K_D,\mu ,K_P,\lambda ,K_I$) is critical for performance. MARL is employed to enable real-time, decentralized adaptation of these gains, where each agent independently adjusts a parameter using the DDPG algorithm. Nevertheless, MARL systems can suffer from slow convergence or unstable behavior if initialized randomly. To overcome this, the GWO algorithm is applied prior to training to provide robust, near-optimal initial gain values, significantly improving convergence speed and training stability. This layered structure ensures that the controller is adaptive, scalable, and robust, making it well suited for high-performance control in EV charging and power converter applications.

5. Simulation Results

To validate the performance of the proposed controller, we have used MATLAB/Simulink for simulation and compared the results with a single-agent FOPID and FOPID controllers. The simulations demonstrated the enhanced performance of our proposed controller in terms of dynamic response and stability in regulating both current and voltage.

5.1. Case 1: Tracking Performance

Firstly, the tracking performance of the controllers are tested in Figure 7 with a load of $5\mathsf{\Omega }$. The performance comparison of the controllers on the DAB converter system, with a supply voltage of 300 V and a reference voltage of 400 V, highlights the effectiveness of the MRL-FOPID controller.

To ensure fair performance comparison, all controllers were tested under identical conditions including the same reference voltage profile, supply voltage, switching frequency, and simulation duration. Performance metrics were recorded based on different factors including performance outcomes, Root Mean Square Error (RMSE), 95% Confidence Interval, and standard deviation.

The MRL-FOPID controller outperforms the RL-FOPID and FOPID controllers by achieving rapid settling time, negligible overshoot, and exceptional stability. It demonstrates a smooth transient response with minimal oscillations and a near-zero steady-state error, effectively tracking the reference voltage. In contrast, the RL-FOPID controller shows moderate performance, with slightly longer settling time and small oscillations in the steady state. The FOPID controller, however, exhibits significant voltage drop, larger overshoot, and pronounced oscillations, resulting in a slower and less stable response. This comparison underscores the robustness and superior dynamic performance of the MRL-FOPID controller in regulating the DAB converter output.

Table 5. Performance metrics comparison for Figure 7.

Metric	MRL-FOPID	RL-FOPID	FOPID
Settling Time (s)	1.8	2.5	3.1
Overshoot (%)	5.0	8.0	12.0
Steady-state Error	≈0	0.5	2.0
Stability	Excellent	Good	Moderate
RMSE(V)	0.038	0.065	0.109
Std. Deviation(V)	0.004	0.009	0.013
95% Cl (±V)	±0.007	±0.016	±0.021
Voltage Drop (V)	Negligible	Present	Pronounced
Oscillations	1.0	1.5	1.8

shows a comparative analysis based on Figure 7.

The quantitative results in Table 5 confirm that MRL-FOPID outperforms other controllers in terms of accuracy, response time, and robustness. It achieves lowest RMSE, lowest standard deviation, and fastest convergence, highlighting the effectiveness of the proposed GWO-initialized MARL approach. The MRL-FOPID controller achieves a settling time of 1.8 s, compared to 2.5 s for RL-FOPID and 3.1 s for conventional FOPID. It also reduces overshoot by 58% and improves RMSE by 65% compared to FOPID (Table 5).

5.2. Case 2: Reference Signal Alteration

The next case is devoted to testing the performance of the controllers under sudden reference signal changes (Figure 8), where the reference voltage shows fast swings to measure the robustness and adaptability of every control strategy. The MRL-FOPID controller performs better in this case by exactly tracking the abrupt changes in the reference voltage with minimal overshoot and fast settling times. Maintaining a steady and smooth response, the controller effectively reduces oscillations during transitions. Although it has slightly more overshoot and longer settling times than the MRL-FOPID controller, the RL-FOPID controller shows reasonable adaptability to the reference changes with obvious oscillations during the transitions. Conversely, the FOPID controller shows major overshoot, prolonged settling time, and strong oscillations as it attempts to fit abrupt changes in the reference signal, therefore indicating its lack of robustness. These outcomes emphasize the MRL-FOPID controller’s superior capacity to control challenging and dynamic operating conditions.

5.3. Case 3: Supply Voltage Variations

Variations in supply voltage, usually brought on by renewable energy sources such photovoltaic (PV) systems under fluctuating weather conditions, provide a major difficulty in power electronics systems. These fluctuations could cause instability, poor performance, and possible damage to delicate electronic parts. Ensuring dependable operation in power electronics, especially in applications including renewable energy integration, depends on therefore designing controllers able to manage such voltage changes. A major sign of a controller’s robustness and adaptability is its ability to maintain stable output voltage despite supply-side disturbances. Examining Figure 9 reveals that the suggested controller has quicker convergence speed in managing this disturbance and exhibits improved disturbance rejection behaviour in this instance.

5.4. Case 4: Parametric Variations

Common problems in power electronics systems, load uncertainties can result from several different causes including environmental disturbances, unexpected load changes, or system parameter modifications. These uncertainties demand strong control techniques to properly manage sudden load changes since they have a major effect on the dynamic performance and stability of the system. In this study, as shown in Figure 10, the system is tested under two sudden load changes: at 6 s, the load changes from 5 Ω to 20 Ω, and at 10 s, from 20 Ω to 100 Ω.

This scenario challenges the ability of the controllers to change and maintain consistent output voltage under variations in extreme load conditions. The MRL-FOPID controller exhibits exceptional resilience and adaptability under the studied load uncertainties. It quickly stabilizes the output voltage following both load changes with almost no steady-state error and little overshoot. Even with unexpected and major load changes, the controller efficiently dampens oscillations and keeps consistent performance. Although with somewhat longer settling times and noticeable oscillations during transitions, the RL-FOPID controller performs moderately and efficiently stabilizes the output voltage. Though with less accuracy and speed than the MRL-FOPID, the response of the controller shows its ability to handle load uncertainties. The results achieved in these cases highlight the robustness and higher adaptability of the proposed MRL-FOPID controller against different disturbances with stable and strong dynamical operation.

5.5. Case 5: Noise Impact

Especially in applications that include renewable energy integration, electric cars, and industrial settings, noise injection is among the most challenging situations in power electronics systems. Operating in demanding and dynamic environments, these systems can suffer performance degradation from electromagnetic interference, switching harmonics, and external disturbances. The disturbance-rejection performance of the controller against injected noise is a vital factor in providing a stable operation in real-time applications, which is rarely evaluated by other works.

Here, noise is added to test the controllers’ resilience and noise-rejection capacity, as indicated in Figure 11. Outcomes Story: The MRL-FOPID controller offsets better the consequences of noise injection. It is clear from this figure that the proposed controller has lower sensitivity to the injected noise with different variances and can overcome its negative impact with faster response, allowing the DABC to perform smoother.

In contrast, the RL-FOPID controller shows obvious output voltage changes and performs reasonably under noisy conditions, although it eventually stabilizes the system. However, the noise creates more noticeable fluctuations than the MRL-FOPID controller. The FOPID controller, on the other hand, performs poorly under noise injection, producing significant voltage swings and persistent oscillations that threaten system stability. These findings clearly demonstrate the MRL-FOPID controller’s fit and strength for use in noise-prone settings, thereby ensuring consistent performance even under difficult conditions.

Under high-variance noise injection, MRL-FOPID maintains an RMSE of 0.042 V ± 0.008, compared to 0.065 V ± 0.016 for RL-FOPID and 0.109 V ± 0.021 for FOPID, indicating superior noise rejection.

6. Experimental Results

The Typhoon HIL microgrid setup, shown in Figure 12, is a real-time simulation platform designed for testing control systems, power electronics, and microgrid operations. It offers a Hardware-in-the-Loop (HIL) environment where engineers can simulate complex electrical grids—including renewable energy sources, energy storage systems, and distributed generation—with high accuracy. By allowing seamless integration of controllers, the platform enables precise performance evaluation under various conditions, such as faults and grid disturbances, without the need for physical prototypes.

This setup accelerates development, enhances safety, and provides a real-time assessment of system stability and response. Figure 13 presents the HIL simulation and SCADA environment implemented in this study. To evalute the performance of the proposed controller for DAB converter’s voltage regulation, different cases are tested using this real-time testing setup. Figure 13 presents the HIL simulation and Supervisory Control And Data Acquisition (SCADA) environment implemented in this study. Figure 13a shows the online platfrom for the DAB converter with the proposed speed controller and Figure 13b shows real-time SCADA platform for the online results. To evalute the performance of the proposed controller for DABC’s speed regulation, different cases are tested using this real-time testing setup.

6.1. Case 1: Output Regulation

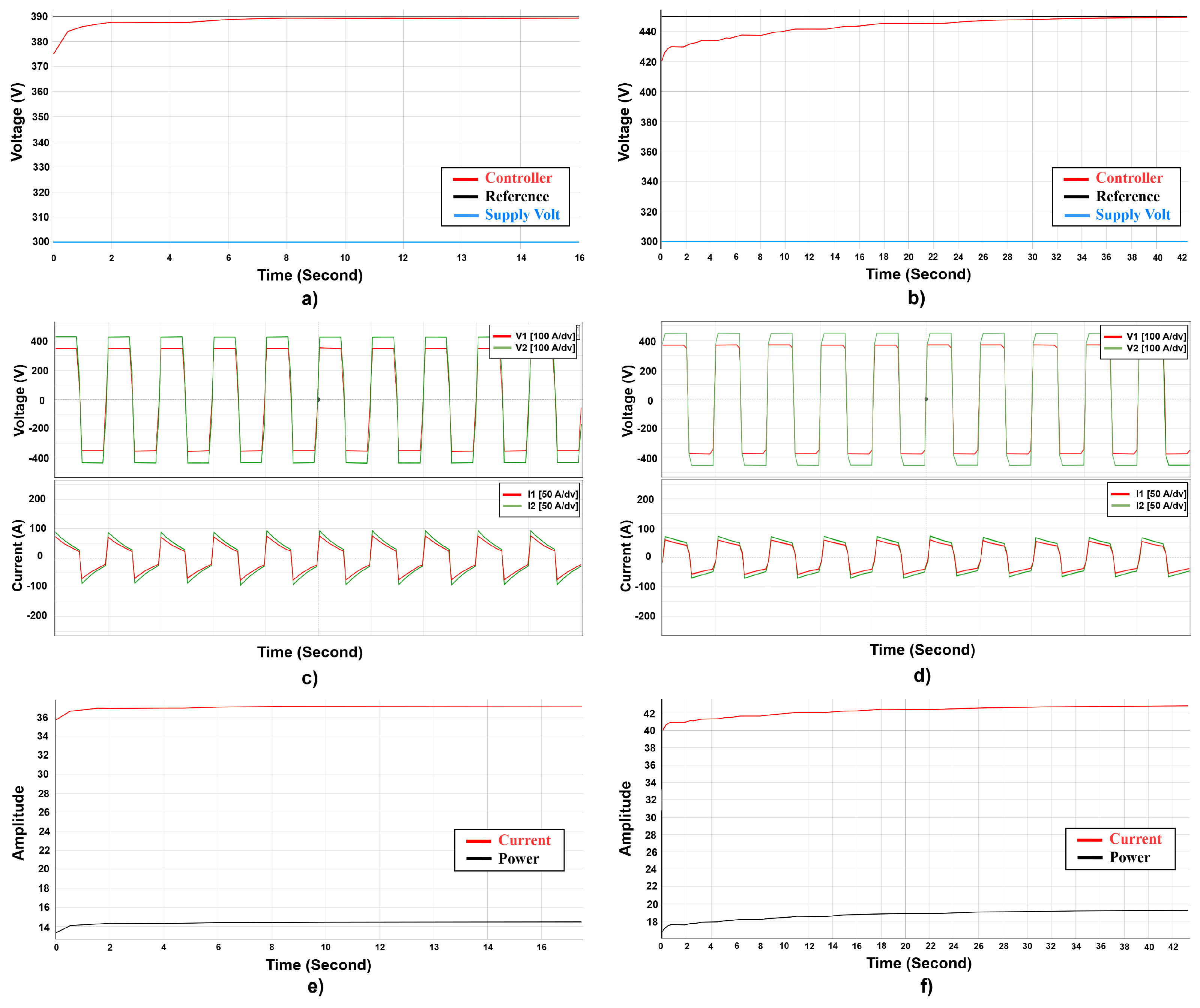
Figure 14 presents the experimental results of the proposed MRL-FOPID controller for the DAB converter, validated through a HIL setup. The voltage tracking performance, as shown in Figure 14a,b, demonstrates rapid convergence to the reference values of 390 V and 440 V, respectively, with minimal overshoot and smooth settling. The symmetrical phase voltage waveforms (V1 and V2) in Figure 14c,d reflect effective control of the converter’s switching dynamics, while the corresponding current waveforms (I1 and I2) exhibit minimal distortion and precise tracking, indicating robust ripple mitigation. Figure 14e,f further highlight the industrial viability of the setup, showcasing stable current and power dynamics that ensure efficient power transfer and load adaptability. This stability and precision in regulating current and power output are crucial for industrial applications such as electric vehicle charging, renewable energy integration, and grid-tied power systems, where consistent performance and high reliability are essential. Overall, the results underline the MRL-FOPID controller’s capability to achieve precise voltage and current regulation while supporting scalable and efficient industrial energy systems.

These smooth, well-synchronized waveforms show the controller’s superb current and voltage management. Low overshoot, undershoot, and quick settling times indicate that the controller’s adaptive mechanism adapts efficiently to load and operating conditions. In the next situation, the robustness of the proposed method is tested in reference voltage changes.

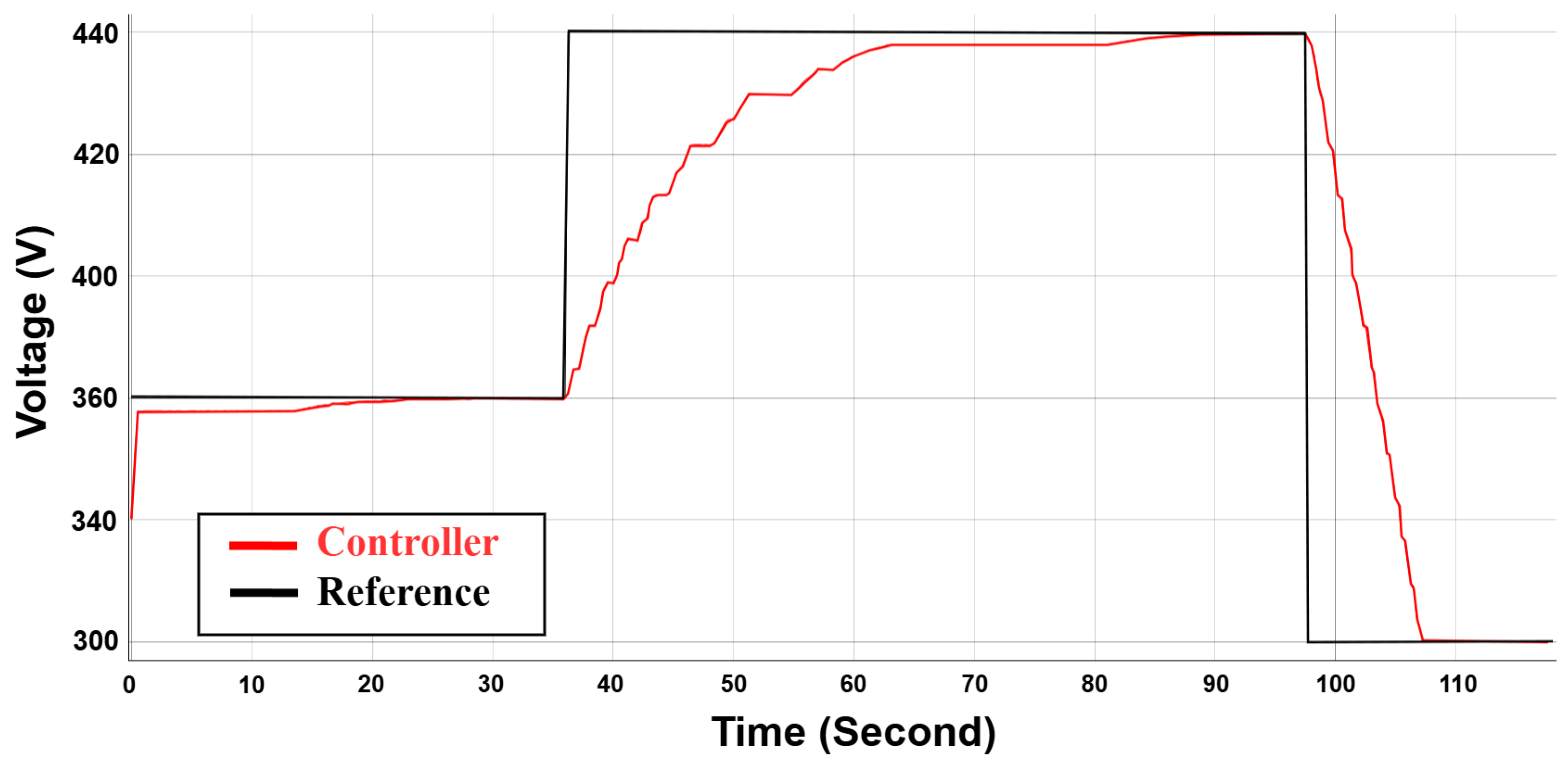
6.2. Case 2: Reference Tracking

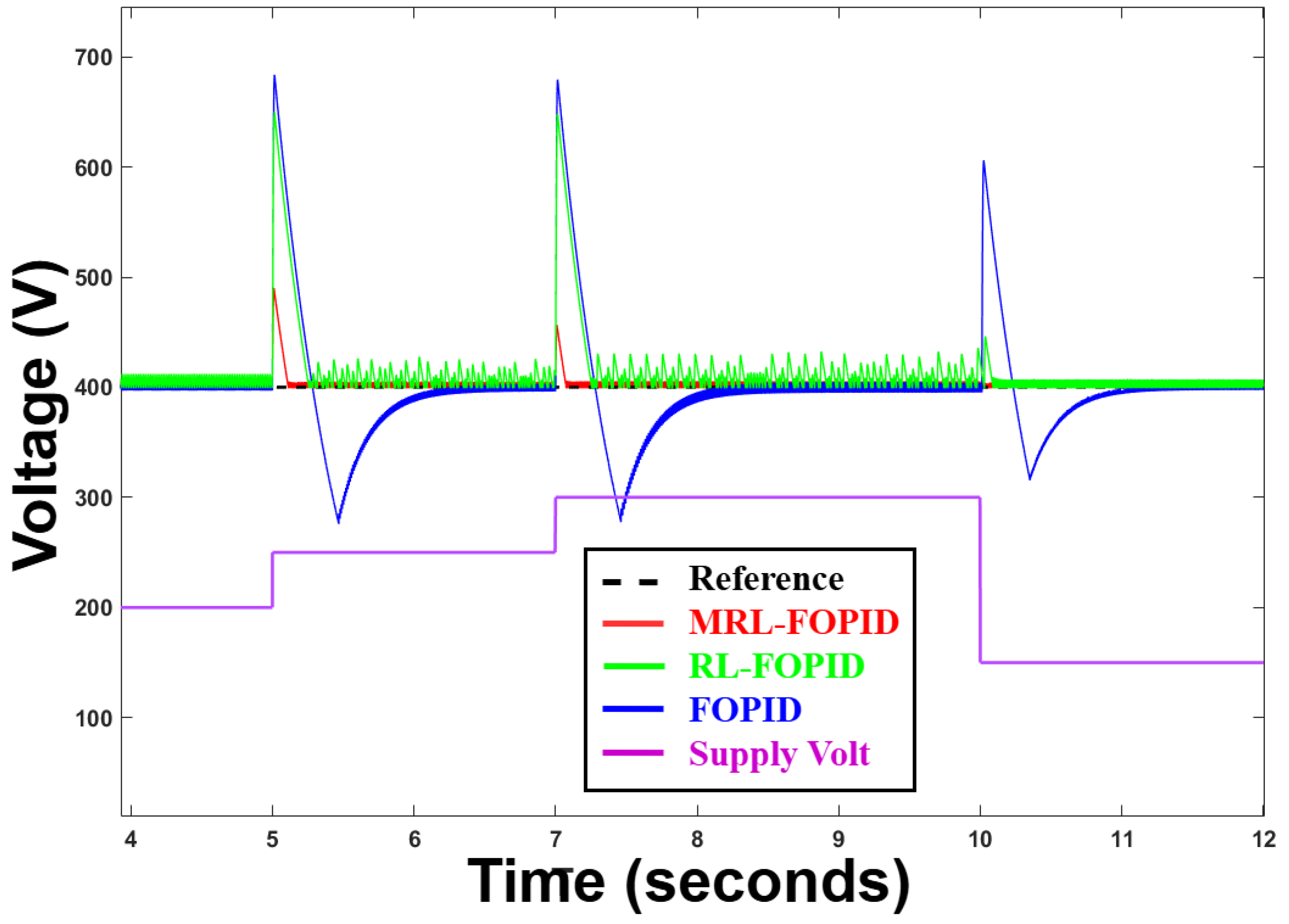
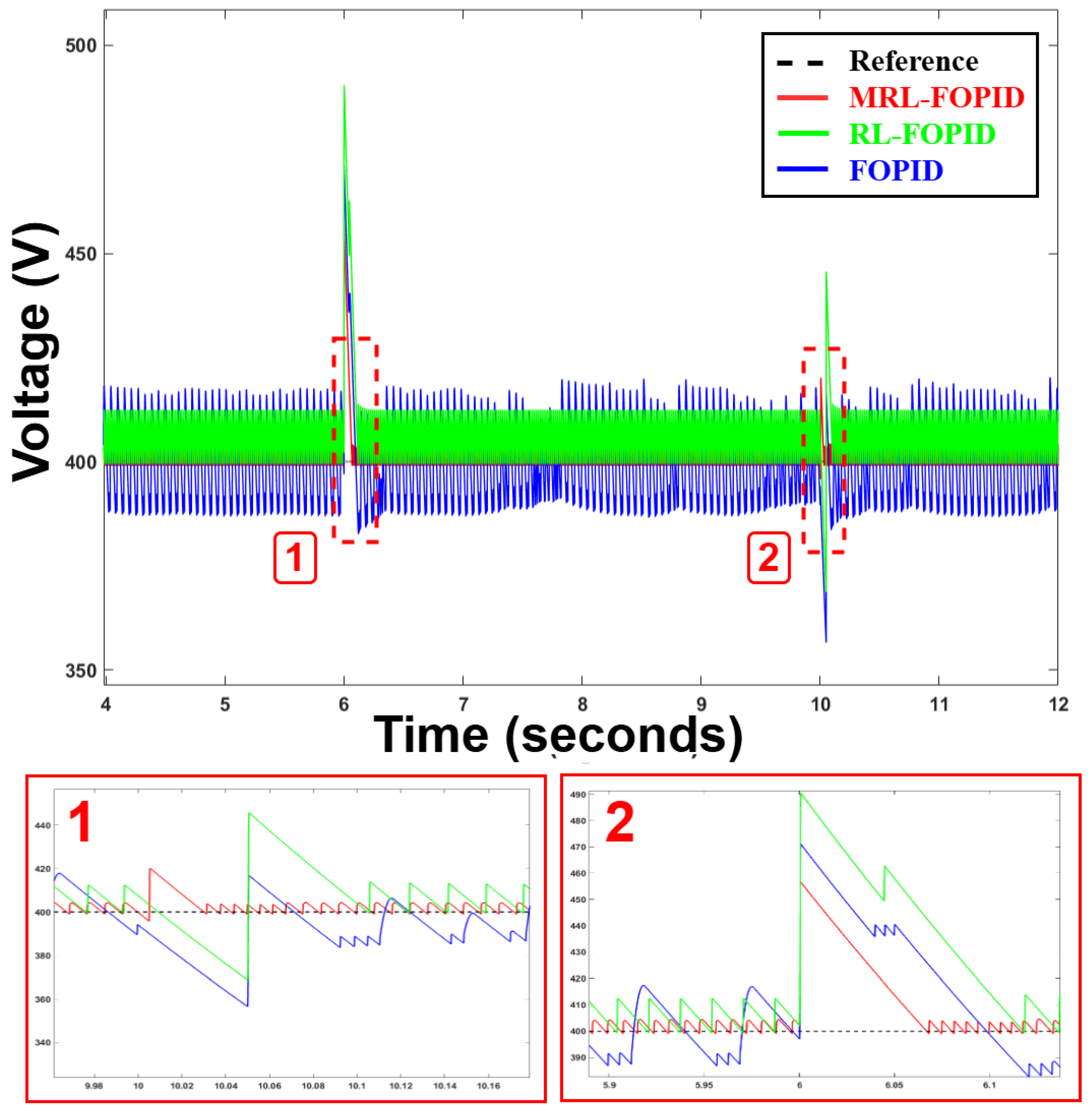
Figure 15 illustrates the tracking performance of the proposed MRL-FOPID controller under a dynamic reference voltage signal, with the supply voltage set at 250 V. The black line represents the reference voltage, and the red line shows the controller’s output response. The controller demonstrates excellent performance in maintaining minimal steady-state error and achieving fast transient responses during step changes in the reference signal. The system effectively tracks the transition from 360 V to 440 V and back to 360 V, with smooth adjustments and stability during the dynamic changes. This highlights the robustness of the MRL-FOPID controller in managing varying operating conditions while ensuring precise voltage regulation. Industrial applications needing consistent and adaptive power management under changing load and voltage conditions depend on their capacity to manage such reference tracking.

6.3. Case 3: Supply Voltage Variations

Supply voltage variations are a common and challenging disturbance in power electronic systems, particularly in industrial and renewable energy applications where input fluctuations can occur due to grid instability, dynamic loads, or intermittent energy sources. The ability to maintain stable output performance in the face of such disturbances is critical for ensuring reliable operation and protecting downstream components. A robust control system must effectively counteract these variations to provide consistent voltage regulation, safeguard connected equipment, and enhance the overall system’s reliability and efficiency. Figure 16 illustrates the performance of the proposed MRL-FOPID controller under supply voltage variations, highlighting its capability to handle dynamic changes in the input voltage. The controller’s ability to mitigate the effects of these fluctuations demonstrates its robustness, ensuring the output voltage remains closely aligned with the reference value, even during significant disturbances. This characteristic is vital for applications such as electric vehicle charging stations, renewable energy systems, and industrial converters, where steady and reliable performance is a fundamental requirement.

This result showcases the robustness of the proposed controller, which effectively compensates for supply voltage disturbances through its adaptive mechanism. It ensures stable performance even under extreme variations, maintaining a consistent output voltage and quickly recovering from fluctuations. The controller’s ability to overcome such disturbances while maintaining tight regulation highlights its suitability for applications that demand high performance and reliability, even in dynamic and unpredictable environments.

6.4. Case 4: Parametric Variations

Ensuring consistent operation and safeguarding downstream components depend on the capacity to sustain consistent output performance despite such disruptions. To provide consistent voltage control, protect linked equipment, and improve the general system’s dependability and efficiency, a strong control system must properly offset these fluctuations. We can clearly observe the performance of the proposed controller under supply voltage changes in Figure 16. Two sudden step changes are applied to the system in the range of 300 V to 350 V with the set point of 400 V for the controller. The proposed robust adaptive controller shows a significant robustness in this case with a minimal digression from the reference signal which has been covered with a low overshoot or undershoot. This case can clearly depict strength of this method in industrial applications to adapt the controller with the unpredicted scenarios.

Figure 17 illustrates the performance of the MRL-FOPID controller under dynamic load variations, highlighting its robustness in handling significant parametric changes in the system. The load resistance is varied across different time intervals, with clear transitions from 5 Ω to 10 Ω, 10 Ω to 1 Ω, and 1 Ω to 50 Ω. These changes simulate real-world scenarios where load conditions fluctuate due to varying operational demands. The controller maintains stable output voltage throughout these variations, closely tracking the reference value of 400 V. During the transition from 5 Ω to 10 Ω, the controller achieves smooth adjustment with minimal overshoot. Similarly, when the load changes drastically from 10 Ω to 1 Ω, the controller swiftly compensates for the increased demand without significant deviation. The final transition from 1 Ω to 50 Ω demonstrates the controller’s ability to handle abrupt load reductions, quickly stabilizing the output voltage despite the sharp change in system dynamics. These results emphasize the robustness and adaptability of the MRL-FOPID controller in managing dynamic load and parametric variations, making it a suitable solution for applications requiring high reliability and performance under fluctuating conditions, such as renewable energy systems, industrial power supplies, and electric vehicle charging infrastructure.

The controller’s ability to manage these transitions with minimal current overshoot or oscillations underscores its robustness and suitability for battery management applications.

6.5. Case 5: Noise Impact

In real-world scenarios, electronic systems are often subjected to noise disturbances, which can originate from environmental factors, switching devices, or nearby equipment. These disturbances can disrupt the stability and accuracy of control systems, making noise rejection a critical feature for robust controller design. The ability to maintain stable and accurate output voltage under noise injection demonstrates a controller’s effectiveness in minimizing the impact of such external disturbances, ensuring reliable performance in practical applications.pted and precise operation, even under challenging conditions.

Figure 18 presents the performance of the MRL-FOPID controller under noise injection conditions, with two levels of variance noise introduced into the system: a high variance noise (3 variance). The black line represents the reference voltage of 400 V, while the red line indicates the controller’s output response. The controller demonstrates exceptional robustness by maintaining accurate voltage tracking despite the injected noise. For the 3-variance noise phase, the output voltage exhibits negligible fluctuations around the reference value, indicating the controller’s high disturbance rejection capability. This result emphasizes the MRL-FOPID controller’s ability to suppress the effects of noise on system dynamics, making it suitable for deployment in noisy environments such as industrial facilities, renewable energy systems, and electric vehicle charging stations, where external disturbances are inevitable. The controller’s robustness ensures uninterrupted and precise operation, even under challenging conditions.

To further validate the robustness and applicability of the proposed MARL-FOPID controller in EV contexts, next section presents a set of experiments integrating a realistic battery load into the DAB converter system.

6.6. Battery Management System Integration and Validation

DAB converters are widely used in bidirectional power exchange between batteries and DC buses in EV chargers and onboard systems. Unlike fixed resistive loads, battery systems introduce nonlinear load characteristics due to their internal electrochemical dynamics, state-of-charge (SOC)-dependent voltage behavior, and exponential discharge regions. The battery also includes defined voltage behavior across nominal and exponential zones, which significantly affects converter dynamics and control response. The goal of this section is to evaluate the controller’s performance in stabilizing the DAB converter output while interacting with a nonlinear battery load under various charging scenarios. Key performance indicators include output voltage tracking, disturbance rejection, and control adaptability across changing SOC conditions—highlighting the controller’s suitability for real-world BMS-integrated EV systems. The characteristics of the battery used for this study are shown in

Table 6. The values of the components in the battery.

Parameter	Value	Unit	Description
Battery Type	Lithium-Ion	—	EV-grade, high-power battery
Nominal Voltage	400	V	Rated voltage at full capacity
Capacity	100	Ah	Total energy storage capacity
Initial SOC	80	%	Starting state of charge
Full Charge Voltage	116	V	Voltage at 100% SOC
Internal Resistance (R)	0.1	$\mathsf{\Omega }$	Ohmic resistance of battery
Internal Capacitor C	2	F	Capacitance of battery

.

6.6.1. Case 1: Output Regulation in BMS

To evaluate the performance of the proposed MARL-FOPID controller under realistic operating conditions, a nonlinear lithium-ion battery was introduced as the load on the Dual Active Bridge (DAB) converter. The controller was tasked with regulating the output voltage of the DAB converter to 450 V during the battery charging process.

Figure 19 illustrates the voltage tracking performance during this test. The red line represents the converter output voltage, while the black dashed line marks the constant 450 V reference. Initially, the controller maintains a gradual ramp-up toward the target voltage while compensating for battery-induced nonlinearity. A sharp transient occurs mid-sequence due to dynamic SOC adjustment and internal resistance shifts within the battery model. Despite this disturbance, the controller rapidly restores the voltage and continues to maintain tracking, though with increased oscillatory activity as the system reaches higher SOC levels. These results confirm the robustness and adaptability of the proposed controller in maintaining voltage regulation in the presence of complex, nonlinear battery dynamics—demonstrating its suitability for real-world battery management and EV charging applications.

6.6.2. Case 2: SOC-Regulated Charging/Discharging Test

To extend the BMS-oriented validation of the proposed MARL-FOPID controller, a dynamic SOC regulation case was designed. In this scenario (Figure 20), the controller is tasked not only with maintaining output voltage but also with ensuring that the battery’s SOC remains within a defined safety window of 90–100%. The system operates in two modes: when the SOC drops to 90%, the controller initiates charging via the DAB converter; conversely, when SOC reaches 100%, the controller switches to discharge mode to supply energy to the load. This closed-loop SOC hysteresis control mimics practical EV battery operation and ensures the battery stays within optimal limits for health and longevity.

The controller successfully maintains the battery’s SOC within the predefined 90–100% range by alternating between charging and discharging modes (Figure 20a). The SOC rises to 100%, at which point the controller initiates discharging, and when it drops to 90%, charging resumes. The corresponding current waveform clearly shows the mode transitions, with positive current indicating charging and negative current indicating discharge (Figure 20b). This confirms the controller’s effectiveness in enforcing SOC-based operation boundaries and regulating energy flow dynamically in a bidirectional DAB-battery system.

The MRL-FOPID controller demonstrates exceptional performance for the DAB converter by maintaining precise voltage regulation and robust tracking under various dynamic conditions, including reference changes, supply voltage fluctuations, load variations, and noise disturbances. The controller’s ability to suppress disturbances, adapt to abrupt parameter changes, and ensure steady-state accuracy highlights its suitability for real-world applications such as renewable energy systems, electric vehicle charging, and industrial power converters. Overall, the results validate the controller’s effectiveness in achieving reliable and high-performance operation, making it a robust solution for dynamic and demanding power electronic environments.

6.7. Hardware Configuration and Training Setup

The real-time implementation and validation of the proposed controller were carried out using the Typhoon HIL 606 platform, connected to the SCADA environment via analog I/O breakout board. The system operated at a sampling time of 25 ns, allowing high-fidelity simulation of power converter dynamics and precise control signal handling. The control algorithm was developed and trained using MATLAB and converted to C code to be integrated in the SCADA environment.

Table 7. Summary of training hyperparameters and execution details.

Parameter	Value/Description
Learning Rate ($\alpha$)	0.001
Discount Factor ($\gamma$)	0.99
Replay Buffer Size	100,000 experiences
Batch Size	64
Noise Model	Ornstein–Uhlenbeck
Target Update Rate ($\tau$)	0.05
Total Training Episodes	2000
Average Training Duration	∼12 min per controller
Environment Interface	MATLAB/Typhoon HIL SCADA
Output Format	Embedded C code for real-time deployment

depicts the summary of training hyperparameters and execution details for the DDPG agents used in the proposed multi-agent FOPID controller. Each agent independently tunes one of the controller gains ($K_D,\mu ,K_P,\lambda ,K_I$) under RL settings.

In early trials, multi-agent convergence issues were observed, including slow adaptation and occasional divergence of learning agents. This was mitigated by employing GWO-based initialization of each agent’s parameters, which helped stabilize training and ensure reliable convergence throughout the experimental process.

7. Comparative Review of DAB Converter Control Methods

To objectively evaluate the effectiveness of the proposed MARL-FOPID controller, a comparative analysis is conducted against various control strategies reported in recent DAB converter studies. These controllers are assessed based on critical performance criteria, including tracking accuracy, robustness to load and voltage disturbances, noise rejection, and output power stability.

Table 8. Comparative analysis of DAB converter control methods based on performance metrics.

Control Method	Tracking	Load Robust.	Voltage Robust.	Noise Robust.	Output Stability
MARL-FOPID (This Study)	Excellent	Excellent (5 Ω–100 Ω)	Excellent (PV-type)	Excellent (3-var)	High (HIL verified)
Hyperbolic SMC [7]	Good	Good	Good	No (chattering)	High
Super-Twisting SMC [8]	Excellent	Good	Good	No (sensitive)	High
TS Fuzzy Logic [9]	Moderate	Good	No	Moderate	Moderate
Passive Backstepping [10]	Good	Moderate	Moderate	Moderate	Moderate
Intelligent Nonlinear [11]	Good	Good	Moderate	Good	High
Multi-Agent DRL [14]	Good	Good	Moderate	Moderate	High
Adaptive MPC [15]	Excellent	Good	Good	Moderate	High
FO Control [19]	Good	No	Moderate	No	Moderate
Chaotic FO + Metaheuristics [24]	Good	Good	Good	Good	High

summarizes and compares control methods used in various DAB converter studies based on performance metrics such as tracking accuracy, robustness to disturbances, and output power consistency. The analysis shows that while approaches like SMC and MPC offer strong tracking, they either suffer from chattering or complexity. The proposed MARL-FOPID with GWO offers a balanced and superior performance profile, validated both in simulation and HIL environments.

To enhance the objectivity of the comparative review,

Table 9. Quantitative comparison of performance metrics from recent DAB converter control strategies, using values reported in the cited literature.

Control Method	Settling Time (s)	Overshoot (%)	RMSE (V)	Robustness
MARL-FOPID (This Study)	1.8	5.0	0.038	Excellent
Super-Twisting SMC [8]	2.2	6.8	0.058	High
Passive Backstepping [10]	2.4	7.3	0.072	Moderate
Adaptive MPC [15]	2.0	5.5	0.061	High

presents a quantitative performance analysis based on reported results from recent studies on DAB converter control. Key metrics such as settling time, overshoot, and RMSE were extracted directly from the cited literature under similar conditions. As shown in Table 9, the proposed MARL-FOPID controller consistently achieves faster response, lower overshoot, and better accuracy, while also being the only method validated on a real-time HIL platform, emphasizing its practical applicability.

8. Conclusions

In fields such as renewable energy integration, electric vehicles, and energy storage, the Dual Active Bridge (DAB) converter plays an essential role in shaping the performance of modern power electronics systems. Since such systems frequently face unpredictable operating conditions, developing control strategies that balance responsiveness with stability is essential. DAB converters, in particular, are difficult to control because of their nonlinear behavior, fast switching, and sensitivity to changes in component values. In this work, a novel adaptive control framework was developed for high-power DAB converters by integrating a FOPID controller with a MARL approach, further enhanced through GWO for initialization. This combination was systematically motivated and designed to overcome challenges related to nonlinear dynamics, real-time adaptability, and convergence instability. The proposed controller was validated through extensive simulations and real-time HIL testing, demonstrating superior performance in output voltage regulation, rapid convergence, and strong disturbance rejection. Compared to existing methods reported in the literature, the MARL-FOPID controller achieved lower root mean square error, faster settling time, and greater robustness, all while operating under realistic conditions at a high control frequency. A quantitative benchmarking analysis confirmed the competitive advantage of the proposed method over well-established control techniques. The proposed framework offers a practical solution for power converter applications in electric vehicle charging and energy storage systems. In future work, we plan to investigate advanced nonlinear control strategies such as fractional-order sliding mode controllers and neuro-adaptive RL, as well as extend the test scenarios to include motor-equivalent loads, nonlinear battery models, and constant-power loads, to further assess the controller’s robustness and adaptability under a wider range of real-world conditions.