An Assistive System for Thermal Power Plant Management

Abstract

The estimation of available active power in coal-fired thermal power plant units involves considerable complexity and remains a critical task for plant operators. To avoid compromising system stability, operators often operate the thermal unit below its full capacity. To address this issue, the aim of this paper is to facilitate the process of estimating the maximum active electrical power by applying an assistive system based on ANFIS (Adaptive Neuro-Fuzzy Inference System), a method that combines the strengths of neural networks and fuzzy logic. Since the generated electric energy is directly linked to the amount of thermal energy produced, the analysis is focused on the boiler combustion process. It has been shown that the key factors in this process are the coal mills and their achievable capacity, as well as the calorific value of coal. Therefore, the proposed assistive system is based on the estimation of the available capacity of each active mill, which is then combined with the estimated calorific value of the coal to determine the achievable active electrical power of the unit. The conducted analysis and experiments confirm the validity of this approach.

1. Introduction

Energy sources represent a fundamental element of socio-economic development. Ensuring energy resources and supply security has become a key factor in the development of human society, as well as in shaping global political and economic relations [1]. Over the past few decades, economic growth in developing countries has contributed to a steady increase in energy consumption, and research suggests that this trend is expected to continue in the near future [2].

Serbia, as a developing country, has been experiencing consistent growth in energy consumption, particularly electricity. According to current projections, this trend is expected to continue until 2030 [3], with electricity consumption projected to increase from the current levels of 38,506 GWh [4]. Based on the 2024 data, the primary producers of electricity are coal-fired thermal power plants, accounting for over $70\%$ of total electricity generation. However, electricity production from coal-based thermal power plants has a negative impact on the environment [5]. Since coal-based power plants are still the primary source of electricity generation in many countries, they represent one of the main contributors to environmental pollution. In recent years, considerable attention has been devoted to the prediction of emissions such as (${\mathrm{CO}}_2$) [6,7] and (${\mathrm{NO}}_{\mathrm{x}}$) [8]. Despite all the advancements, environmental pollution remains an inevitable aspect of electricity production based on this approach. For this reason, developed countries are increasingly striving to transition toward renewable energy sources [9,10,11]. Due to the unreliability of supply from renewable energy sources, this transition poses a significant challenge [12] for developed countries, and especially for developing countries such as Serbia.

The Electric Power Grid of Serbia is in a very unfavorable position. The growing electricity demand contrasts with the limited and slowly improving production capacity, which is further constrained by the poor quality of coal. In this situation, the most effective strategy is to extract the maximum possible output from the available infrastructure.

However, in practice, operating a thermal power plant unit at its maximum achievable capacity remains a significant challenge for operators. The primary reason for this challenge is the uncertainty regarding the unit’s maximum capacity. Consequently, the operator is left to estimate the unit’s capacity independently, based on prior experience and individual judgment. Considering that overloading the unit may lead to an outage, it becomes clear why operators tend to operate it below its achievable capacity.

The aim of this paper is to develop an assistive system for operators that suggests, based on the current state of the thermal power plant unit, the maximum active electrical power the unit can generate under regular operating conditions. This would not only make the operator’s job easier and reduce the impact of human factors but would also enable increased production capacity using the existing infrastructure.

Analysis of the thermal power plant unit operation showed that the coal combustion process has a key influence on the total unit electrical power. In addition to coal characteristics, the combustion process is significantly affected by its preparation. In thermal power plant units rated over $100\mathrm{MW}$, such as unit B1 of the Nikola Tesla power plant in Obrenovac with an installed capacity of $650\mathrm{MW}$, which serves as the case study for the research presented in this paper, the boiler is fired with the aero-mixture, a combination of pulverized coal particles and hot air at the mill outlet, which, as will be shown, is one of the main indicators of mill load. This aero-mixture is entirely formed by eight fan mills, whose uneven operating conditions significantly affect the combustion process and, consequently, the total unit active power. The fan mills have been identified as the main operational constraint in boiler performance. If the achievable coal processing capacity of the mills is exceeded, due to the physical constraints of their working principle, they become overloaded, potentially leading to clogging, gradual deterioration, and ultimately, mill failure with serious operational consequences.

The critical role of mills in thermal power plant operation has been confirmed by numerous studies [13]. Their proper functioning is further highlighted in several research works addressing this topic [14,15,16,17,18]. These studies employ advanced analysis techniques, including vibration and acoustic signal processing, as well as mathematical modeling, to assess mill condition. However, most of them focus on predicting service intervals, which, while valuable, does not provide direct support to operators in assessing the real-time maximum capacity of the mills.

The goal of this paper is to develop an assistive system that estimates the current condition of each of the eight mills, based on their real-time operating parameters, in terms of maximum load, and, accordingly, suggests the maximum achievable active power of the unit at a given moment. The literature contains a large number of studies and results related to mill operation management, including capacity estimation based on coal characteristics, the condition of beater wheels, and air balance [19,20,21,22]. However, all these methods assume a priori knowledge of process parameters or models. The concept introduced in this paper follows the spirit of machine learning, where complete knowledge about the milling process is embedded in the data itself. To the best of our knowledge, this concept is novel. Due to the complexity of exact mathematical modeling, caused by numerous mutual interactions, the proposed solution is based on soft computing approaches, specifically employing fuzzy logic and neural networks through ANFIS (Adaptive Neuro-Fuzzy Inference System) [23,24,25], as further detailed in the following sections.

This paper begins by analyzing and formulating the problem of estimating the achievable capacity of a coal mill and available active power of a thermal power plant unit. Based on the identified challenges, a conceptual framework is developed to address the problem, accompanied by illustrations of the issues the assistive system must overcome. Particular attention is given to the selection of the ANFIS structure, its architecture, and the training process. Subsequently, the overall system structure and operating principle are defined. The ANFIS is then trained using the collected data and evaluated through testing. Finally, conclusions are drawn based on the conducted analysis.

2. Problem Formulation

A fundamental process in electricity generation within a thermal power plant unit is the conversion of fuel energy, coal in this case, into thermal energy through combustion in the boiler. The main objective is to maximize fuel utilization while minimizing the emission of harmful gases. One commonly used method for firing thermal power plant units above $100\mathrm{MW}$, which largely satisfies these requirements, is pulverized coal combustion. The aforementioned component represents a crucial part of boiler combustion and simultaneously offers the greatest potential for further improvements [26,27].

This method is based on combustion using a pulverized coal–air mixture (hereinafter referred to as the aero-mixture), which is a blend of pre-crushed coal powder and hot air from the furnace. A key challenge in this combustion method lies in the processing of raw coal into an aero-mixture. Fan mills play a crucial role in preparing this mixture. Accordingly, the entire combustion process of the unit heavily depends on their operational condition, which inevitably degrades with increased operating time and workload. To better understand the impact of mill condition degradation on electricity production, it is essential to comprehend the entire combustion process and its role within the system.

Combustion begins in the raw coal bunkers, from which coal falls by gravity onto a belt conveyor, known as the feeder of the fan mill. The feeder, using a leveling device, which is a metal limiter that prevents the coal layer on the feeder from exceeding a specified level where it is positioned, forms a uniform coal layer and delivers it to the mill’s inlet channel. At this point, the coal is mixed with hot air, ranging from $650°\mathrm{C}$ to $900°\mathrm{C}$, originating from the top of the furnace, referred to as recirculation line gases, and with primary air at $220°\mathrm{C}$. The flow of the primary air is controlled by regulating the primary air damper, which is a valve at the outlet of the primary air line, whose position directly controls the amount of primary air entering the mill. This mixture of air and coal is transported through pipelines to the center of the fan mill, which consists of a metal casing lined with reinforced metal sheathing. The core of the mill is the beater wheel, a large rotating assembly equipped with blades and additional metal linings. It pulverizes large pieces of coal by striking them against its blades and crushing them against the mill’s inner lining.

The mixing of hot air with coal particles enables the drying of the coal. Simultaneously, the beater wheel acts as a fan, generating the airflow required to transport the pulverized coal to the burners mounted on the walls of the boiler furnace. To prevent the furnace from being fired with inadequately crushed coal, a return line is installed on the mill’s outlet line. Oversized coal particles, due to their weight, are redirected through this line back to the center of the mill for additional grinding, thereby ensuring proper particle size and enabling efficient combustion of coal in the air.

When the fan mill is in good condition, with undamaged metal linings on the beater wheel and mill walls, the process operates without issues. However, problems arise when the metal linings on the beater wheel and the protective linings on the internal walls of the mill become worn or deformed. These damages increase internal clearances within the mill, resulting in poorer coal pulverization and reduced ventilation performance. Consequently, the achievable capacity of the mill is reduced. Numerous studies have analyzed and attempted to improve these deficiencies. However, the issues remain unresolved [28,29,30,31]. By exceeding the achievable capacity of the mill, a situation arises in which more coal is fed into the mill than can be subsequently transported to the burners. Continuous overloading of the mill in this manner may lead to the accumulation of coal deposits inside the mill, significantly increasing the risk of spontaneous ignition. Such conditions can escalate into explosions within the mill, with potentially fatal consequences for overall system safety [32].

In order to prevent unwanted scenarios, it is necessary to operate the mills in accordance with their achievable capacity. A precise calculation of the maximum capacity of the mill would require a complex analysis [33], based on the condition assessment of the beater wheel and the characteristics of the coal being processed. Such an analysis would involve shutting down the mill, performing a visual inspection of the beater wheel, and conducting laboratory testing of the coal, procedures that are not feasible during regular operation.

To ensure that the capacity assessment remains relevant, it is necessary to develop a method for real-time evaluation of the beater wheel condition during operation. For the stated assessment, available parameters include those of the mill and the overall thermal power plant unit. Among these, the temperature of the aero-mixture stands out as a key indicator that reliably reflects the mill’s achievable capacity. The justification lies in the achievable capacity of coal drying. For complete combustion, coal particles must be fully dried and heated to their ignition temperature. In practice, these conditions are met by maintaining the outlet aero-mixture temperature within the range of $170°\mathrm{C}$ to $185°\mathrm{C}$. Accordingly, regulation of the pulverized aero-mixture temperature is performed by adjusting the primary air flow via the primary air damper. However, it has been shown that this regime can be maintained only within a specific coal processing capacity range, as illustrated by the aero-mixture temperature regulation limits diagram in Figure 1.

The diagram shown in Figure 1 presents the mill’s regulation characteristics, developed under the assumptions that the moisture content of coal dust does not vary with capacity, that the aero-mixture temperature remains constant within the operating range, and that the raw coal temperature is constant. It illustrates changes in fluid composition and quantity depending on the transport of pulverized coal downstream of the mill, increased by the mass of coal vapor per unit time. The drying fluid consists of the following: (a) combustion products recirculated from the furnace—recirculated gases, (b) hot air from the air heater—primary air, (c) moisture evaporated from the coal, (d) leakage air drawn from the boiler house, (e) false air drawn from the furnace, and (e) recirculated cold combustion products. As shown, the mill operates within a limited range of allowable capacity, within which effective drying of coal is achieved and the aero-mixture temperature is being regulated, as illustrated on the right side of the diagram. At maximum drying capacity, the flow of primary air (b) is reduced to the technical minimum of the primary air damper, necessary for unobstructed pneumatic transport of coal.

Based on the above analysis, the proposed approach relies on estimating the maximum mill capacity that enables maintaining the outlet aero-mixture temperature within the acceptable range, while ensuring that the primary air damper remains at its technical minimum. Although this requirement may initially appear straightforward, experimental results demonstrate that it is far more complex in practice.

The complexity of the problem arises from the numerous factors that influence mill operation and its achievable capacity in various ways. Key factors include the following: the condition of the beater wheel (most conveniently described by the number of operating hours since the last overhaul), coal properties (such as grindability, granulometry, moisture content, chemical composition, and sand content), temperatures of the incoming fluids to the mill (primary air and aero-mixture), and the uniformity of coal feeding to the mill.

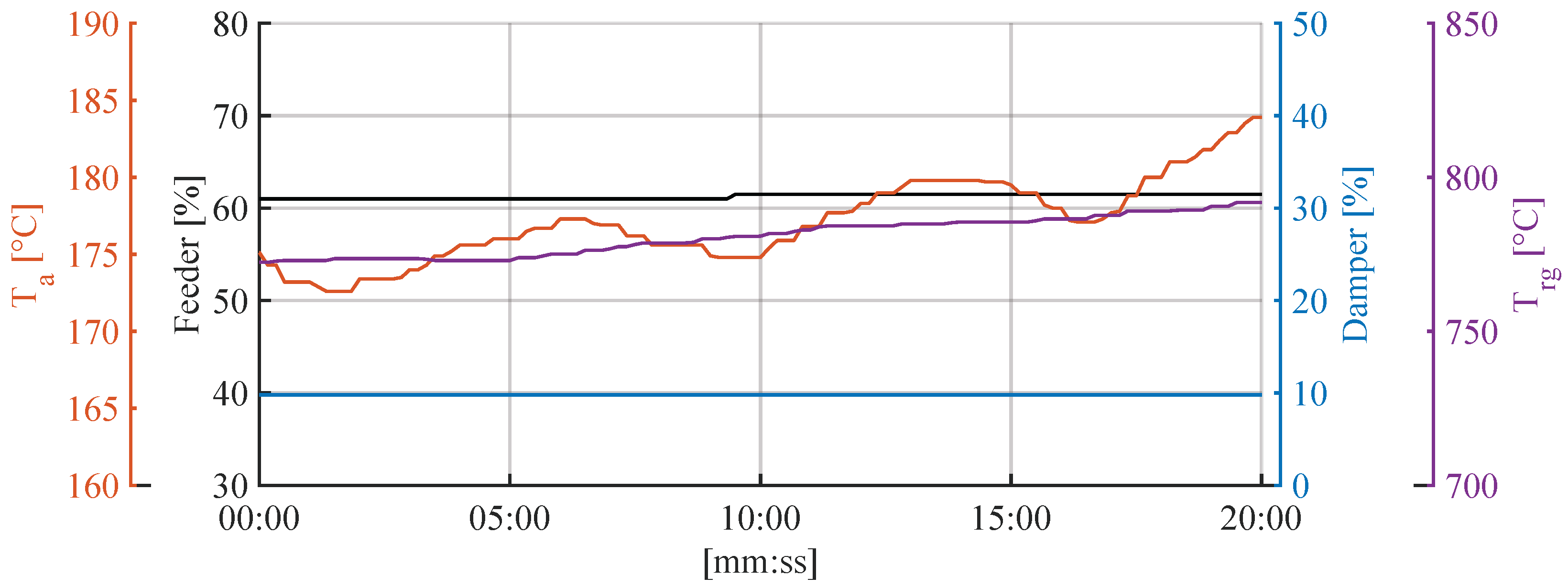
Beater wheel degradation is an inevitable consequence of processing large quantities of coal, as shown in Figure 2. Continuous abrasion of the internal linings limits the operational lifespan of the beater wheel and directly affects mill performance. The extent of this effect is best demonstrated by comparing mill behavior after 300 and 1250 operating hours following beater wheel overhaul.

Although all other mill parameters remain nearly identical in terms of average values, under the same conditions, defined by constant feeder speed and the primary air damper set to its technical minimum, the measured temperature of the aero-mixture differs by more than $5°\mathrm{C}$ with respect to the mean value, indicating a significant impact of beater wheel wear on the overall milling process.

Based on the previously discussed example of beater wheel degradation and its impact on aero-mixture temperature, as shown in Figure 2, it can be concluded that the instantaneous deviation from the average temperature value is variable in both observed cases. The main contributing factors to this behavior are fluctuations in coal properties, primarily grindability and moisture content, as well as irregularities in coal supply from the bunker. Variations in coal accumulation on the feeder lead to changes in the instantaneous coal input to the mill, which further affects process stability.

It has been established that all of these parameters are closely correlated with the beater wheel load, which can be monitored through the current of the beater wheel drive motor. As illustrated in the corresponding diagram shown in Figure 3, fluctuations in the aero-mixture temperature closely follow variations in mill current, confirming a direct link between these parameters and the complexity of the milling process.

The next factor influencing the formation of the aero-mixture is the set of fluids used in its generation, with particular emphasis on the temperature of the recirculation gases, as illustrated in Figure 4.

In contrast to the temperature of the primary air, which can be actively regulated, the temperature of the recirculation gases cannot be directly regulated and varies depending on the current thermodynamic conditions within the furnace.

It has been shown that the temperature of the recirculated gases can fluctuate by more than $200°\mathrm{C}$ during operation, which may significantly affect the coal drying process. This effect is especially evident at the mill’s maximum capacity, when the recirculated gas becomes the dominant component of the aero-mixture. This phenomenon is depicted in Figure 4, where it can be observed that, even under constant mill operating parameters and stable coal supply with minimal oscillations, the temperature of the aero-mixture exhibits an increasing trend, driven by a progressive rise in the temperature of the gas in the recirculation line. These results highlight the significant impact of the recirculated gas on the coal drying process and overall system stability.

In addition to the basic mill parameters and their impact on the aero-mixture temperature, the effects of other measurable parameters related to mill operation were also analyzed, including mill vibrations, primary air temperature, feeder motor current, and numerous others. However, based on the conducted experiments and correlation analysis, it was found that these parameters are not sufficiently reliable for accurate estimation of the aero-mixture temperature.

Based on the previously presented analysis, it can be concluded that the most useful input parameters for the future model are the mill operating time, mill drive motor current, recirculation gas temperature at the mill inlet, and primary air flow. This selection of parameters is crucial because assessing mill capacity is inherently a complex task, with unit operators facing substantial operational challenges. This complexity is further increased by the fact that six to eight mills are typically in operation simultaneously, each with a different maximum capacity, which significantly complicates the estimation of the unit’s active power.

3. Proposed Structure of the Assistive System

In order to support operators in addressing the outlined problem during regular operation, this paper focuses on the development of an assistive system designed to enable more accurate estimation of the maximum achievable capacity of each coal mill, expressed through its corresponding feeder speed. Although feeder speed is a key control parameter, it represents only one of several variables that influence mill performance, as illustrated in Figure 2, Figure 3 and Figure 4. Moreover, direct real-time calculation of this capacity is not feasible due to the complexity of the process and the large number of interdependent influencing factors. 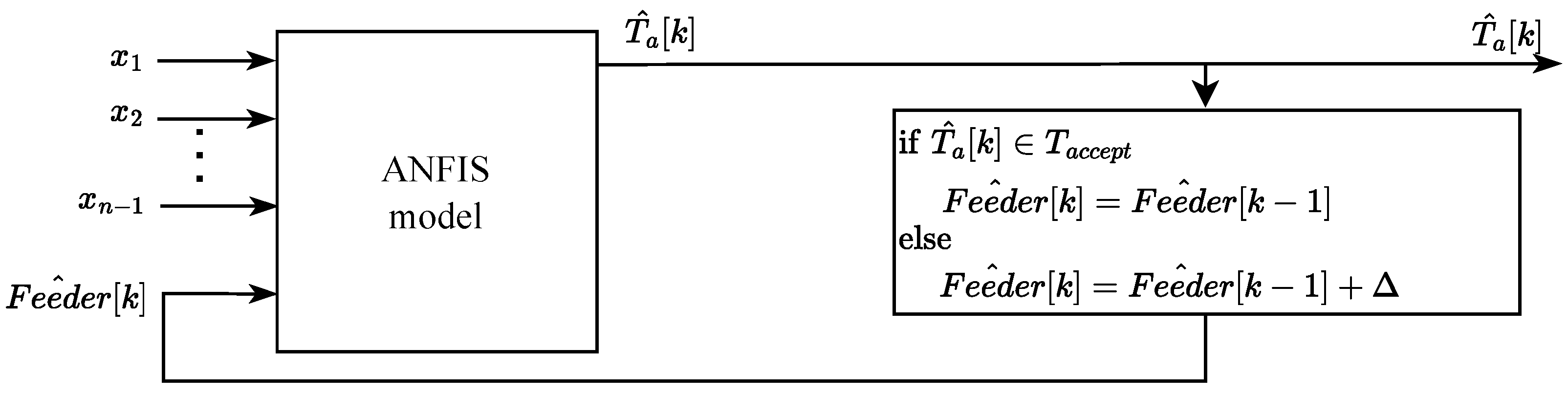To overcome this limitation, the proposed approach is based on estimating the maximum feeder speed by first predicting the aero-mixture temperature, as illustrated in Figure 5. The core of the method lies in a process model that estimates this temperature using all relevant input parameters. Since the primary goal is to determine the maximum allowable feeder speed for each mill, the model is specifically designed to serve that purpose. Based on the current operating parameters, a recursive algorithm is applied to estimate the feeder speed that enables maintaining the desired outlet temperature of the aero-mixture. The functioning of the recursive algorithm is based on the premise that the aero-mixture temperature should not drop below 170 °C over an extended period. To achieve this, the algorithm starts by initializing the feeder speed variable to the current actual feeder speed. Subsequently, the algorithm gradually increases the feeder speed while continuously monitoring the predicted aero-mixture temperature. As the speed increases, the algorithm tracks how the estimated temperature decreases. At a certain point, the estimated temperature will fall below the desired technical minimum, which determines the maximum allowable feeder speed, corresponding to the mill’s maximum capacity. These estimates for each individual mill in operation, combined with the coal’s calorific value, are then used to evaluate the available active electrical power of the thermal power plant unit.

To better understand the operation of the entire assistive system, a schematic diagram of the assistive system workflow is shown in Figure 6, where ANFIS ${\mathrm{Mill}}_{\mathrm{i}}$, $i\in [1,8]$ represents the ANFIS-based system for each individual mill, as depicted in Figure 5.

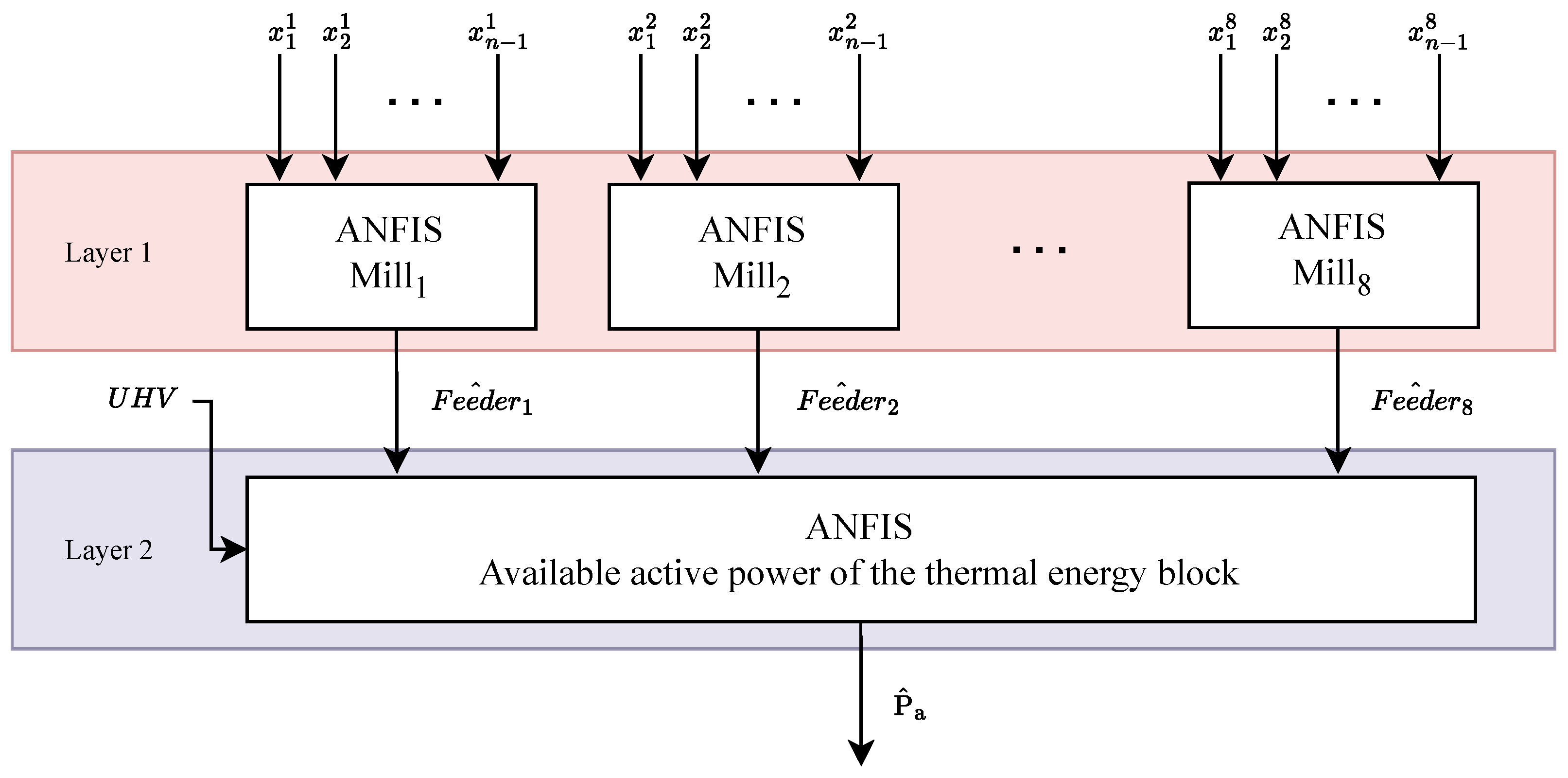
In this way, the assistive system would take into account the current condition of the mill, as well as operating conditions related to coal characteristics and the thermodynamic parameters of the boiler, enabling real-time estimation. Based on the estimated achievable feeder speed for each of the eight operating mills in steady-state conditions, together with the coal’s calorific value, the achievable plant unit capacity in terms of active electrical power could be determined with a high level of reliability. This estimation would enable operators to have real-time insight into the unit’s maximum available active electrical power, taking into account the current operating conditions and coal characteristics. However, defining an appropriate mathematical model represents a significant challenge. As previously stated, the system is multivariable, which significantly complicates the analysis. Establishing strictly defined mathematical relationships between all relevant parameters is extremely difficult to formalize due to the presence of complex non-linear interactions within the system. For this reason, the proposed approach abandons traditional process modeling based on physical relationships and instead explores solutions within the domain of soft computing methods, which are better suited for handling complex and imprecisely defined systems. In an effort to develop a system model that retains an interpretable structure, ANFIS has emerged among numerous contemporary methods as a representative approach that combines the most beneficial features of neural networks and fuzzy inference systems. This approach enables flexible modeling of complex processes, while also allowing the model to be refined and adapted based on expert knowledge acquired through operational experience. The proposed assistive system in no way affects the existing functionalities within boiler regulation, such as fuel distribution, air quantity control, main controller operations, steam pressure and temperature management, and the control of NOx, CO, and ${\mathrm{O}}_2$ concentrations.

ANFIS is a hybrid approach that combines artificial neural networks (ANNs) and fuzzy inference systems (FISs), forming a robust framework for modeling and solving complex real-world problems. The method is grounded in a fuzzy system whose parameters are trained using a learning algorithm inspired by neural network theory, thereby integrating the advantages of both techniques. From the ANN perspective, the ability to learn from data represents a key strength, while the primary advantage of FIS lies in its capacity to construct a base of linguistic rules. Multiple integration strategies exist for combining ANN and FIS, and the choice of method largely depends on the specific application context and the complexity of the problem being addressed [34,35,36]. Since most training techniques are not memory-intensive, these characteristics make the ANFIS model superior compared to alternative approaches, including some types of neural networks, enabling efficient processing and modeling of complex systems under real-world conditions.

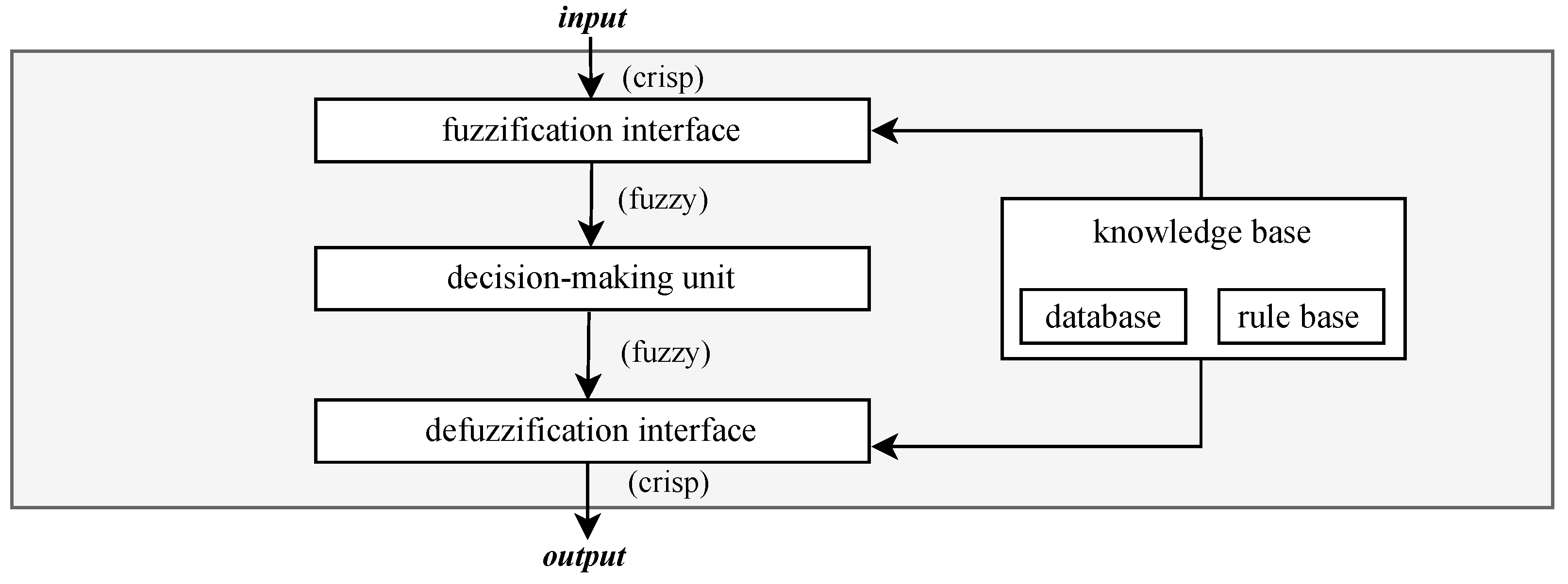
Depending on the specific implementation, the ANFIS architecture may differ in its structure and training method, but the foundation of each such system is a fuzzy inference system. The system is composed of several essential components, as illustrated in Figure 7.

The components shown in Figure 7 jointly constitute the fuzzy inference system and, at the same time, define the structure of the ANFIS architecture. In order to achieve the desired input–output mapping, the parameters defining the system components are learned using appropriate optimization-based training methods. These methods are designed to adjust the internal parameters of the model based on the training dataset and typically rely on well-established optimization techniques [37]. Accordingly, the same ANFIS model structure will be used for estimating the aero-mixture temperature as well as for assessing the available active electrical power of the thermal power plant unit. The essential difference between these two models lies in training the same architectures with different datasets.

To enable the application of the ANFIS structure for estimating the aero-mixture temperature and the active electrical power of the thermal power plant unit, appropriate datasets must be prepared for training the adaptive parameters of the fuzzy inference system.

Experimental data used for training and testing the ANFIS system were collected between June 2024 and March 2025, using measurements from three different mills of the B1 thermal power unit at the Nikola Tesla power plant in Obrenovac. During this period, seven experiments were conducted, with a total duration exceeding 30 h of unit operation. Thanks to this extended time interval, various boiler thermal regimes, seasons, and different phases of mill beater wheel exploitation were covered. Through manual signal inspection, sequences deemed unsuitable for training the ANFIS model were identified and excluded. Among the excluded sequences are situations such as mill failures, conveyor belt breakage at the feeder, mill start-up and shutdown, mill clogging, and similar events.

This approach enabled the formation of a representative set of system steady-states, which will be used for further training of the ANFIS model for aero-mixture temperature estimation.

The experimental investigations encompassed a wide range of loads, including feeder speeds ranging from 40% to 80%, air–coal mixture temperatures between 165 °C and 195 °C, active power of the unit between 410 MW and 650 MW, a recirculation gas temperature between 650 °C and 900 °C, and system operation with primary air damper openness of up to 70%. All experiments were performed on three mills to monitor the wear of the beater wheel and changes in its characteristics during operation. All data were collected with a sampling frequency of 5 s.

The temperature measurements of the pulverized coal–air mixture and the recirculation gases were performed using thermocouple-based sensors, known for their wide temperature range that varies depending on the thermocouple type. In this particular case, the sensors were equipped with a Type K thermocouple, which was based on a nickel-chromium/nickel combination. These sensors come with a calibration certificate at a single point, at a temperature of 1000 °C.

The operating range of the sensors covers temperatures up to 1000 °C. In the temperature range from −40 °C to 375 °C, the permissible error is ±1.5 °C, while for the temperature range from 375 °C to 1000 °C, the permissible error is ±0.004$·\left|t\right|$, where |t| is the absolute value of the actual temperature.

The sensor for measuring the temperature of the pulverized coal–air mixture was positioned at the outlet of the fan mill, while the sensor for measuring the temperature of the recirculation gases was located at the junction of the recirculation gas line with the primary air line.

The first step involves defining the training dataset for the ANFIS model used to estimate the aero-mixture temperature. It should be emphasized at this point that additional analysis has shown that formulating a reliable model requires each mill to have its own model. Although data were collected from three different mills, the dataset used for training was formed exclusively based on data from a single mill, and all presented results related to the ANFIS for aero-mixture temperature estimation pertain exclusively to that mill. This approach is justified by the fact that the same methodology would be applied for other mills, allowing the presented results to be considered representative under the same conditions.

Based on the problem formulation, the following parameters were selected as input variables:

• Operating time since the last overhaul of the beater wheel—an indicator of the expected wear of the mill’s beater wheel linings.
• Mill current—an indicator of the mill load that reflects current coal characteristics and fluctuations in coal feed at the mill inlet.
• Recirculation line gas temperature at the mill inlet—a key factor in the coal drying process, along with primary air.
• Primary air flow at the mill inlet—although the objective is to analyze a regime in which the primary air damper is set to its technical minimum, it has been shown that, due to the physical configuration of the mill, this flow still varies enough to cause aero-mixture temperature changes of several degrees.

A major challenge at this stage, even before further analysis, lies in the dynamics of the process itself. Although there are studies where ANFIS has been applied for dynamic system identification [38,39], its application in this case proves to be unsuitable. The main reason for this is the complexity of the system. As outlined in the problem formulation, the process is clearly multivariable, involving more than four input predictors. When the need to capture system dynamics through several previous measurements is considered, the total number of ANFIS inputs increases significantly. Since the complexity of the model grows exponentially with the number of inputs, training such a system becomes practically infeasible.

Since the primary objective of the model is to estimate the achievable capacity of each mill during operation, tracking system dynamics over time is not of critical importance. Moreover, the model is not expected to react to short-term fluctuations caused by disturbances, but rather to follow the macro-level values under steady-state conditions. Accordingly, the ANFIS model is designed to estimate the steady-state aero-mixture temperature based on the corresponding steady-state values of the input parameters. In this way, the model becomes independent of the system’s dynamic behavior, while the influence of frequent measurement noise and outliers is significantly reduced. The selection of the time window for signal averaging was made based on an analysis of the system’s temporal behavior, which led to the choice of a two-minute interval. This duration represents a compromise between two opposing requirements: on one hand, it must be short enough to capture the current state of the physical processes in the mill; on the other hand, it must be sufficiently long to filter out dynamic effects and external disturbances.

Creating the dataset for ANFIS training related to power estimation is considerably simpler compared to the problem of estimating the aero-mixture temperature. Since the available active electrical power primarily depends on the amount and quality of coal delivered to the boiler, the estimation can be based on the total engagement of all mills in operation and the estimated calorific value of the coal, which is already available. It is reasonable to conclude that increased mill engagement and higher coal quality result in greater active electrical power output. However, quantifying the individual and combined influence of these factors on active electrical power is a non-trivial task. For this reason, ANFIS is again selected as a suitable model structure for addressing the problem. Since the number of inputs for this system includes the feeder speeds of all eight mills in operation, along with the estimated coal calorific value, the complexity of the ANFIS architecture increases significantly. Given the nature of the influence that coal calorific value effects on the active electrical power output of the thermal unit, it was decided that each ANFIS input representing the normalized feeder speed of a given mill should be scaled by the normalized estimated calorific value of the coal:

$$x_i={\widehat{Feeder}}_i·{\displaystyle \frac{CCVE}{CC{V}_{MAX}}},$$

(1)

where $x_i$ denotes the input corresponding to mill i, ${\widehat{Feeder}}_i$ denotes the maximum estimated speed of the i-th feeder, $CCVE$ is the Coal Calorific Value Estimation, and $CC{V}_{MAX}$ is the Coal Calorific Value maximum, 10.000 kJ/kg.

As with the ANFIS model for aero-mixture temperature estimation, the objective here is to model the steady-state behavior of the unit rather than its transient regimes or dynamic effects. In comparison to mill operation, the time constants associated with the active power output of the unit are significantly larger, which indicates the need for data averaging over a longer time window. Based on the observed process dynamics, the appropriate averaging interval was experimentally determined to be 4 min.

In accordance with the defined averaging procedure for the ANFIS for estimating the aero-mixture temperature and the active power of the unit, datasets for training were formed based on data collected during the conducted experiments.

A total of 1245 samples were obtained for training the ANFIS model for aero-mixture temperature estimation, while 2857 samples were formed for training the ANFIS model for active power estimation. From these datasets, 20% of the samples were set aside for testing using chronological selection, while the remaining data was used for training the ANFIS models.

To avoid overfitting of the ANFIS model, the k-fold cross-validation method was used, implemented within the tunefis function of the MATLAB R2023b software package. Experimental results showed that the use of four folds provides optimal results in terms of model accuracy and stability.

The final step before training the ANFIS architecture is to define and configure all essential parameters that influence both the training process and the resulting model performance:

• Definition of input and output variables.
• Selection of the type of fuzzy inference system.
• Specification of the type and number of membership functions for both input and output variables.
• Selection of the defuzzification method.
• Definition of the system training method.

The following configuration is adopted:

• The input and output variables are the same as those previously introduced for aero-mixture temperature estimation and the assessment of the available active electrical power of the thermal power plant unit.
• The Sugeno fuzzy inference system is selected due to its computational efficiency, compatibility with optimization and adaptive techniques, and the fact that it ensures output surface continuity, which makes it suitable for application in complex engineering systems such as ANFIS.
• It is assumed that this choice may significantly influence the quality of the obtained results. Therefore, a comparative analysis is conducted to evaluate the impact of representing each variable with either two or three membership functions, as well as the effect of using Gaussian versus triangular membership functions.
• In general, defuzzification using the default centroid method is sufficiently accurate for most applications and is therefore retained without modification.
• Based on the literature [37], three training techniques will be compared: a hybrid method (denoted as ANFIS(H)), training based on a genetic algorithm (ANFIS(GA)), and training based on particle swarm optimization (ANFIS(PSO)). In the case of the hybrid method proposed by Jang [23], the rule set was adopted in accordance with the grid partition method, which is the most commonly used approach [40]. In contrast, for the genetic algorithm and particle swarm optimization, the rule learning process was treated as a set of optimization parameters. The ability to learn the rule set significantly mitigates the risk of overfitting [41].

4. Results and Discussion

As performance evaluation metrics for the obtained ANFIS models, the following were used: the Root Mean Square Error (RMSE) on the test dataset, the training time required for the fuzzy system, and the total number of generated decision rules.

The results obtained for the ANFIS model designed for aero-mixture temperature estimation are presented in

Table 1. Performance of the ANFIS model for aero-mixture temperature estimation under different training configurations.

		MFs Number = 2				MFs Number = 3
MF Shape	Algorithm	Training RMSE	Test RMSE	Training Time [s]	No. of Rules	Training RMSE	Test RMSE	Training Time [s]	No. of Rules
TRIMF	ANFIS(H)	0.97	15.34	9.12	32	-	DIV *	-	-
	ANFIS(GA)	2.26	2.30	80.86	16	2.01	2.452	2813.53	117
	ANFIS(PSO)	2.75	2.79	51.87	16	2.22	2.31	1056.56	118
GAUSSMF	ANFIS(H)	-	DIV *	-	-	-	DIV *	-	-
	ANFIS(GA)	2.08	2.13	71.39	16	1.87	1.92	1365.73	112
	ANFIS(PSO)	2.35	2.51	47.49	16	2.01	2.09	975.84	114

* The obtained ANFIS diverged, so the RMSE value is not of interest.

.

In the same manner, the ANFIS is applied to estimate the achievable active electrical power of the thermal power plant unit, using the corresponding training dataset, as presented in

Table 2. Results of ANFIS system training for estimation of the achieved active electrical power of the thermal power plant unit under various training settings.

		MFs Number = 2				MFs Number = 3
MF Shape	Algorithm	Training RMSE	Test RMSE	Training Time [s]	No. of Rules	Training RMSE	Test RMSE	Training Time [s]	No. of Rules
TRIMF	ANFIS(H)	-	DIV *	-	-	-	DIV *	-	-
	ANFIS(GA)	6.09	6.72	161.84	32	5.12	5.67	12,066.42	339
	ANFIS(PSO)	5.69	6.22	148.51	32	5.03	5.62	5791.11	344
GAUSSMF	ANFIS(H)	0.51	23.53	7.65	64	0.22	21.68	1707.24	729
	ANFIS(GA)	5.58	5.96	182.49	32	4.95	5.16	11,606.95	332
	ANFIS(PSO)	6.55	6.72	150.25	30	5.91	6.83	3258.52	342

* The obtained ANFIS diverged, so the RMSE value is not of interest.

.

When comparing the obtained results presented in Table 1 and Table 2 for training both ANFIS models, it can be concluded that training based on the hybrid approach does not yield satisfactory results. The main drawback of this method lies in the assumption that all possible rules are present, as shown in the results, which leads to overfitting, particularly when using three membership functions in the input and output layers.

On the other hand, based on the presented data, it can be observed that ANFIS(H), using the hybrid training method, is significantly faster than heuristic approaches, whereas the genetic algorithm (ANFIS(GA)) is the slowest among the analyzed techniques.

The shape of the membership functions also influences performance: genetic algorithm and particle swarm optimization methods perform better with Gaussian membership functions. The results indicate that Gaussian membership functions consistently achieved lower RMSE values compared to Triangular functions, both on the training and testing datasets. This can be attributed to the smoother transition characteristics of Gaussian functions, which are more suitable for capturing the non-linear relationships inherent in the data. Additionally, another advantage of Gaussian membership functions is that they are represented by two parameters, while Triangular functions require three, which results in a reduced number of parameters. The hybrid method, due to inherent limitations, fails to demonstrate a consistent improvement in performance across different types of membership functions.

The presented Table 1 and Table 2 clearly indicate that increasing the number of rules yields improved modeling results, which comes at the cost of increasingly significant memory and computational resources. For instance, in the case of two membership functions per input variable with a total of 16 rules, it is necessary to adjust 118 parameters, while in the case of three membership functions with a total of 112 rules, the number of parameters to be adjusted during training reaches 711. It is evident that as the number of parameters increases, the risk of overfitting becomes more pronounced. Since the primary objective is to obtain a precise estimation of the target parameters, the ANFIS training criterion is based on the lowest Root Mean Square Error (RMSE) achieved on the training and test set. The best RMSE results, as shown in Table 1 and Table 2, indicate that for both ANFIS models, used for estimating the aero-mixture temperature and the unit’s active electrical power, the optimal configuration consists of three Gaussian membership functions per input variable, with training performed using a genetic algorithm.

Although RMSE on the training and test sets served as the key criterion for evaluating the satisfactory performance of the model, a deeper analysis of the designed system requires considering additional indicators. Before proceeding with data analysis, it is essential to thoroughly examine the training process of the optimal ANFIS model.

Due to the significantly higher complexity of the problem of estimating the air–coal mixture temperature compared to estimating the active power of the unit, the focus will be placed on the ANFIS model designed for temperature estimation.

Observing the criterion function shown in Figure 8 through generations and applying the k-fold cross-validation method with four folds, minor jumps are noticed when switching between training and test sets during the k-fold procedure. These jumps represent an encouraging result, as they clearly indicate the quality of the training process without signs of overfitting.

Since the ANFIS model is designed to operate with measured data under demanding conditions, it is expected that measurement noise will inevitably occur during real-world application. To assess the model’s robustness under such conditions, the reduction in estimation quality will be analyzed, expressed through the increase in RMSE due to noise presence at the system inputs.

Due to physical limitations and sensor resolution, noise is inherently present in measurements of recirculated gas temperature, mill current, and primary air flow at the mill inlet. To quantify the noise impact on estimation, the first part of the simulation introduces noise at only one system input, with noise generated by superimposing Gaussian noise of zero mean and a standard deviation of 5% of the estimated mean value of the given signal. In the subsequent part of the simulation, all the mentioned inputs are subjected to the same noise.

The RMSE analysis results, presented in

Table 3. RMSE dependence of the ANFIS model for estimating the aero-mixture temperature, depending on measurement noise.

Simulation	Without Noise *	Noise on ${\mathbf{I}}_{\mathbf{mill}}$	Noise on ${\mathbf{Q}}_{\mathbf{p}}$	Noise on ${\mathbf{T}}_{\mathbf{rg}}$	Noise on All *
RMSE	1.9242	4.1786	3.4392	3.1827	5.4807

* The noise applies only to the inputs ${\mathrm{I}}_{\mathrm{mill}}$, ${\mathrm{Q}}_{\mathrm{p}}$, and ${\mathrm{T}}_{\mathrm{rg}}$.

, clearly show an increase in RMSE in the presence of noise, but the results remain satisfactory, especially considering that the 5% white noise contamination is not a realistic assumption. Further analysis shows that the noised mill current has the greatest impact on system degradation, while the influence of the noised recirculation line temperature is the least pronounced, which is consistent with previous analyses.

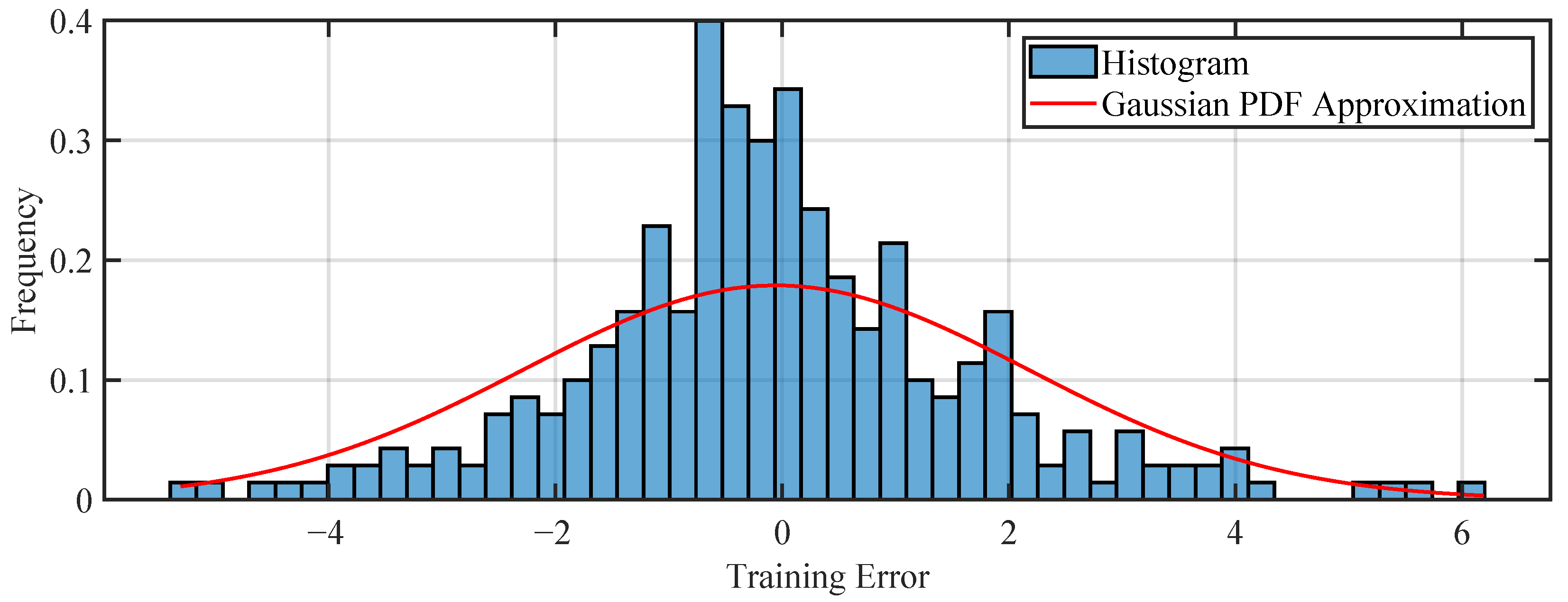
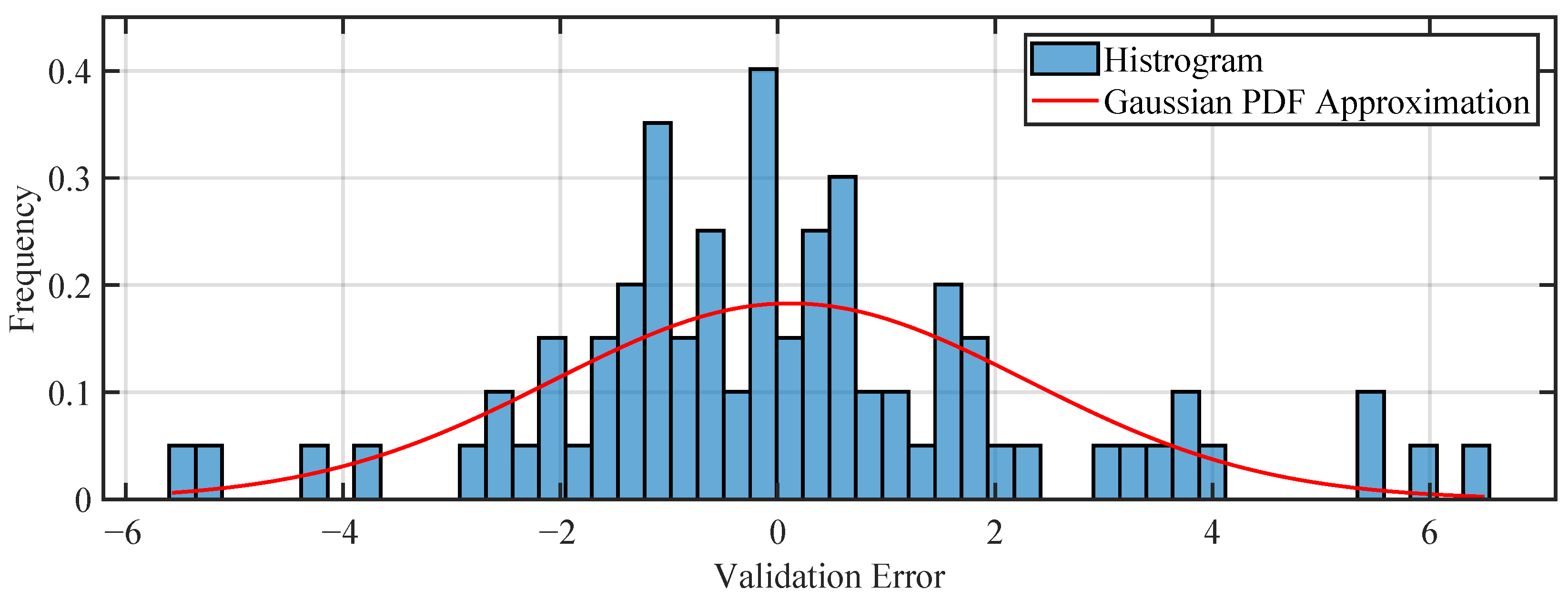
Before proceeding to the analysis of specific cases, we will examine the error histograms for the training and test sets, shown in Figure 9 and Figure 10. At first glance, these histograms indicate that the errors follow a Gaussian distribution, which is a positive result. Additionally, the standard deviation of the error on the training set is approximately 2.186 °C, while on the validation set it is 2.232 °C, which is considered satisfactory given the measurement uncertainties.

An analogous approach can be applied to the ANFIS model for estimating the unit’s active power. However, due to the simplicity of this model and the fact that the obtained results are similar to those previously analyzed, their detailed presentation will not be included in the paper.

To better understand the behavior of the designed and trained ANFISs, it is appropriate to analyze their performance on real operating data. The first model considered is the ANFIS for aero-mixture temperature estimation, as illustrated in Figure 11, Figure 12 and Figure 13.

The first graph in Figure 11 illustrates the system’s behavior in a scenario involving an increase in the temperature of the recirculation gas line, as well as a sudden rise in primary air flow. Since the ANFIS model was trained on data corresponding to the operating regime in which the primary air damper is set to its technical minimum, with minimal flow oscillations, such conditions represent an atypical scenario. Nevertheless, the model successfully predicts the system’s response, clearly indicating that ANFIS has learned the process behavior beyond the standard operating range.

The second graph in Figure 12 illustrates a case of uneven coal supply, which as previously noted, is reflected in fluctuations of the mill current, a key indicator of coal grindability and feed stability. Despite these oscillations, the model’s error in predicting the aero-mixture temperature does not exceed $3°\mathrm{C}$, which is considered more than acceptable for this application.

The third graph in Figure 13, although not demonstrating results as accurate as in the previous cases, illustrates additional capabilities of the ANFIS. It depicts a situation in which the coal’s maximum drying capacity is exceeded, resulting in a sudden and unexpected drop in the temperature of the aero-mixture, despite no change in any of the input parameters. Since the ANFIS model was trained on data corresponding to regular operating conditions, it continues to predict higher temperatures, failing to recognize a deviation not represented in the training set. However, this behavior can be interpreted as a beneficial feature: the discrepancy between the predicted and actual temperature in such cases may serve as an indicator of potential mill clogging, suggesting an additional application of the ANFIS for anomaly detection.

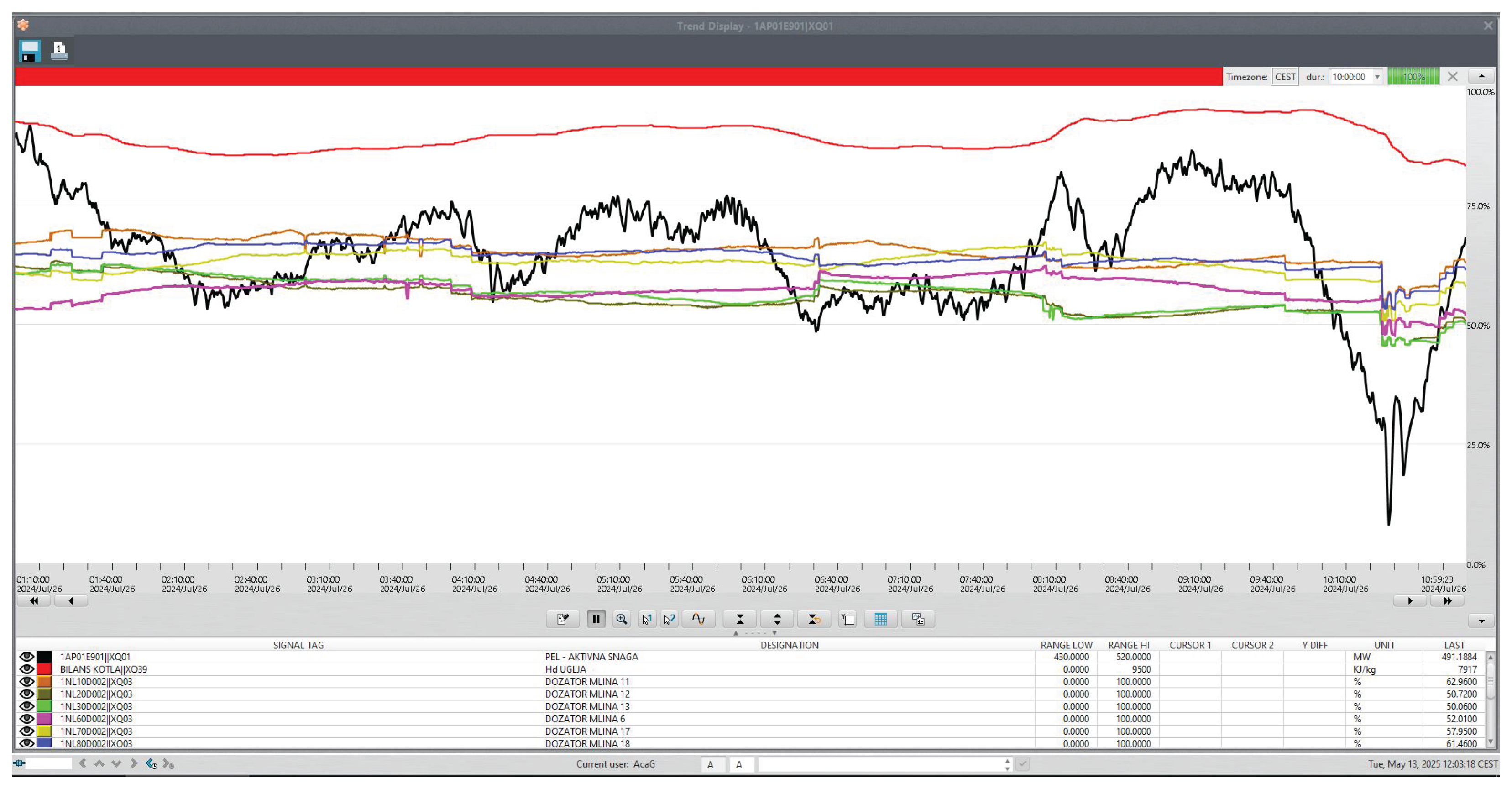
When moving to the analysis of ANFIS results for estimating the active electrical power of the unit, the outcome remains satisfactory. To clearly confirm the obtained results, the real application of the ANFIS for active power estimation was tested over a duration of 10 h, using data collected on 26 July 2024, covering the time interval from 1:00 h to 11:00 h, with a sampling period of 5 s. Figure 14 shows the SCADA monitor for 26 July 2024, covering the same time interval, displaying data on active electrical power, the speeds of all operating mills, and the estimated calorific value of the coal.

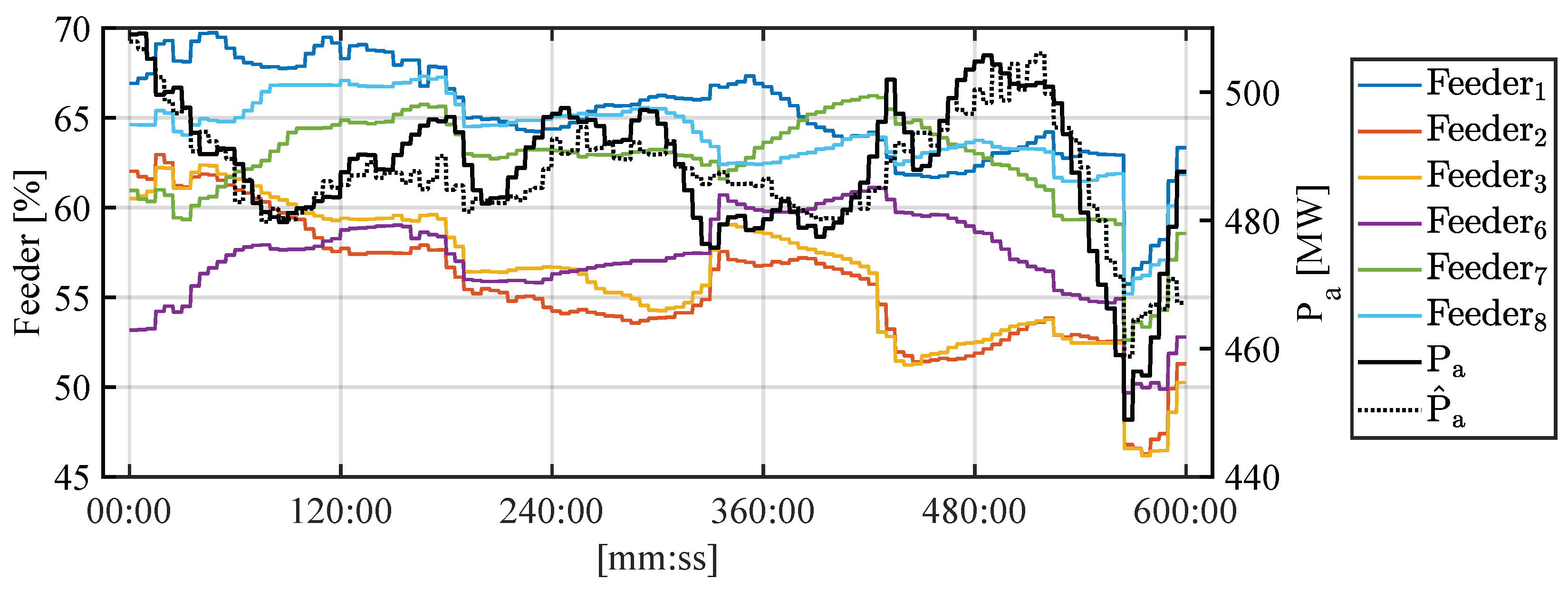
To evaluate the assistive system, we utilized the available data, allowing the model to estimate the achievable active electrical power at the system output. Figure 15 presents both the measured and estimated values of active power, averaged over a 4 min interval.

It can be observed that over a ten-hour period of real unit operation, the estimated active electrical power deviates by no more than 7 MW from the measured value, which can be considered a highly encouraging result given the system’s complexity and the nature of the available data.

5. Conclusions

This paper explored the concept of an assistive system based on the ANFIS architecture, aimed at supporting operators in assessing key parameters related to the achievable capacity of a thermal power plant unit. The primary focus was placed on estimating the available capacity of the mills in operation and the achievable active electrical power of the overall unit. Based on a detailed analysis of the fan mill operating process, key parameters that characterize mill performance have been identified. The parameter that proved to be the most reliable indicator of the available mill capacity is the temperature of the air–coal mixture at the mill outlet. When the mill operates at its maximum capacity, this temperature is no longer regulated by the primary air damper and becomes directly dependent on the coal load applied to the mill. The analysis showed that the unit’s active electrical power depends on the engagement of the operating mills, specifically, on the speed of the feeders supplying coal to the mills, as well as on the calorific value of the coal. Based on this, the system is structured into two layers. In the first layer, the feeder speed corresponding to the maximum mill capacity is determined based on the estimated air–coal mixture temperature. In the second layer, using the estimated maximum feeder speeds from the first layer and the current calorific value of the coal, the ANFIS estimates the achievable active electrical power of the thermal power plant unit. This structure enables a hierarchical approach in which the operation of each mill is first optimized individually and thoroughly, and the resulting outputs are then systematically integrated into the overall capacity estimation of the entire unit. To effectively facilitate the training of the ANFIS architecture, appropriate datasets were constructed to represent the stationary states of the system, with carefully averaged signals designed to eliminate the influence of transient phenomena and dynamic behavior.

Two separate ANFIS architectures were developed, one specifically designed for estimating the air–coal mixture temperature and the other for estimating the unit’s active electrical power, with the optimal number and type of membership functions determined through a series of experimental tests.

Several training methods were compared: the conventional hybrid approach and two heuristic techniques (genetic algorithm and particle swarm optimization), with heuristic methods demonstrating superior performance in terms of both reliability and robustness. The models were evaluated using real data from a thermal power plant, demonstrating high accuracy: the estimation error for the air–coal mixture temperature did not exceed $3°\mathrm{C}$ on the test set, while the error in estimating the unit’s active electrical power remained within $7\mathrm{MW}$ over ten hours of continuous operation.

In addition, it was observed that the ANFIS model can also support failure detection, such as identifying mill clogging events. The results confirm that ANFIS can be effectively applied to model complex, non-linear systems in the power sector, thereby significantly supporting operational decision-making.