Ground Heat Exchangers from Artificial Ground-Freezing Probes for Tunnel Excavations
Abstract
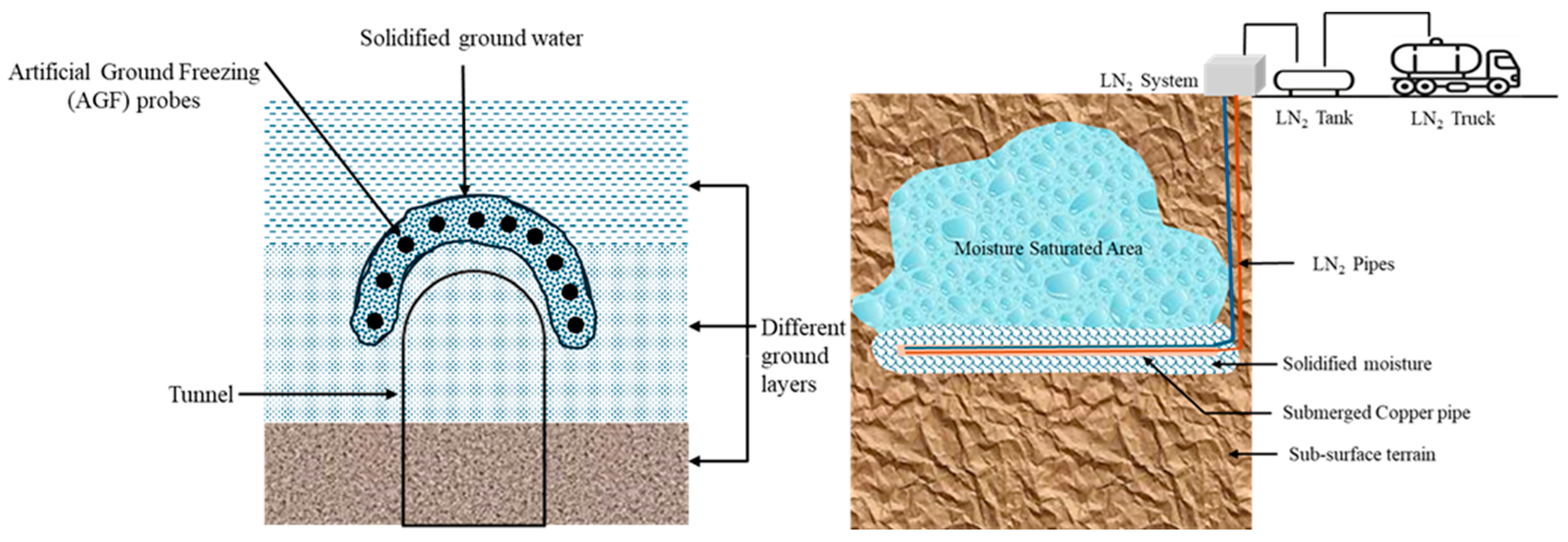
1. Introduction
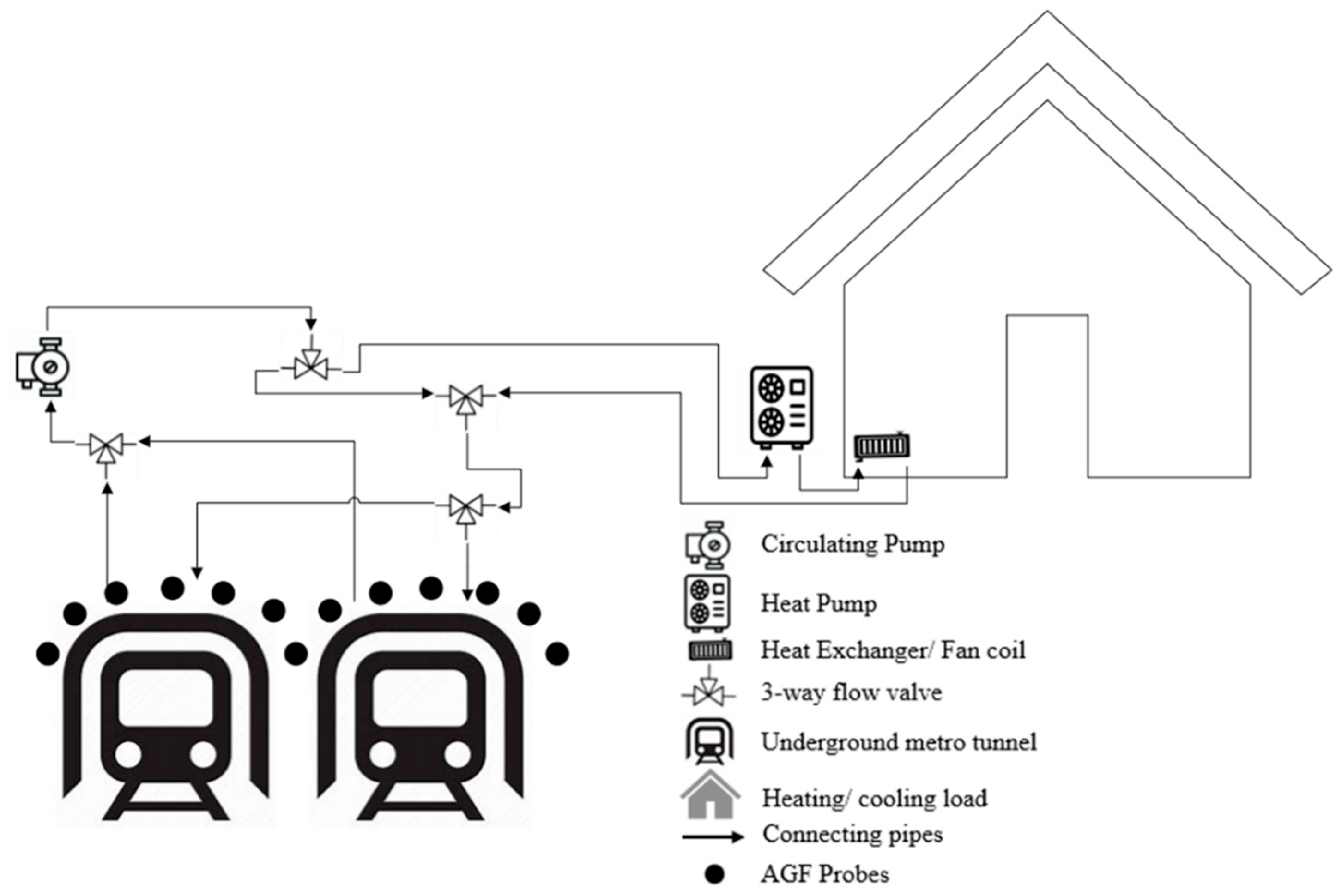
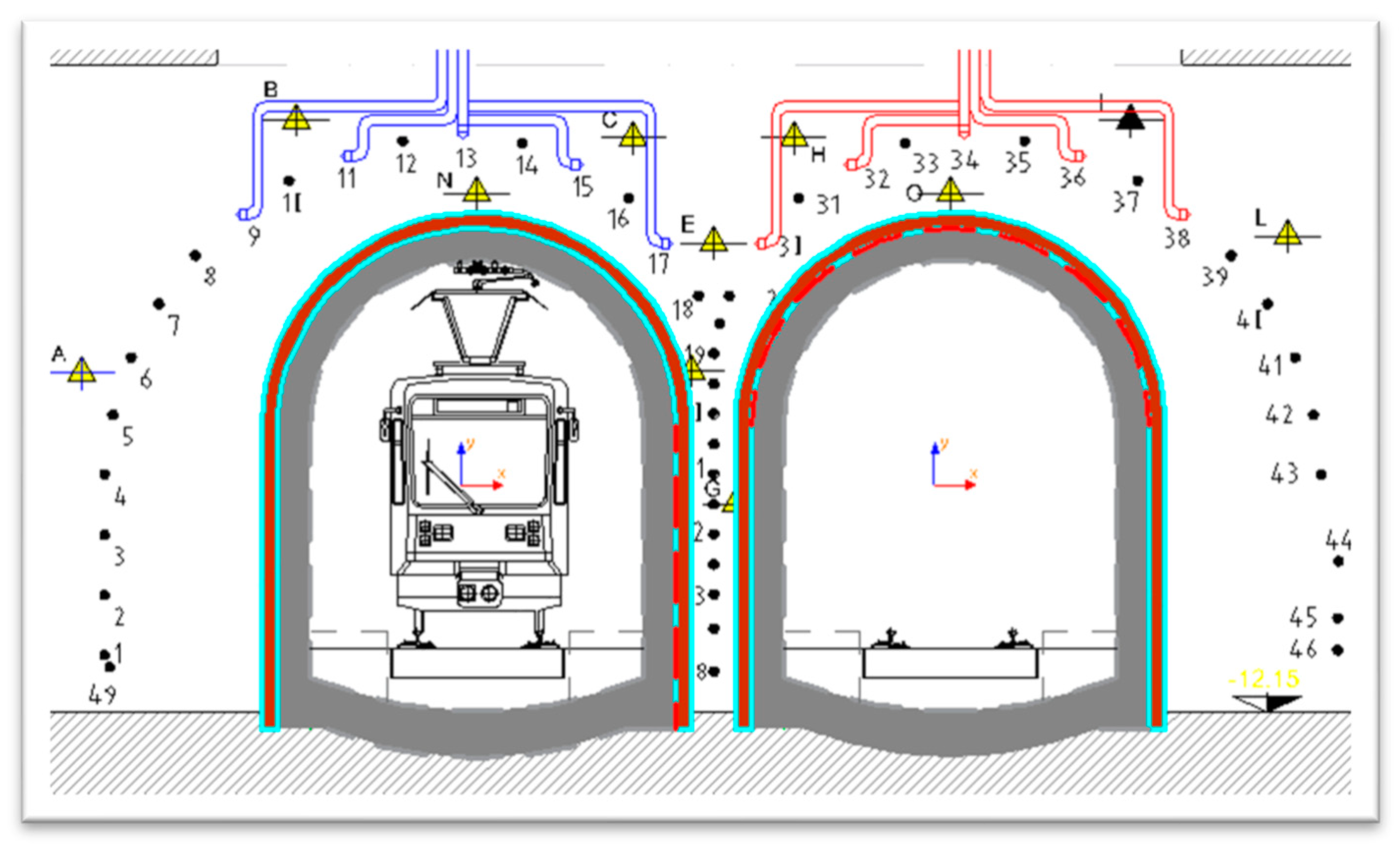
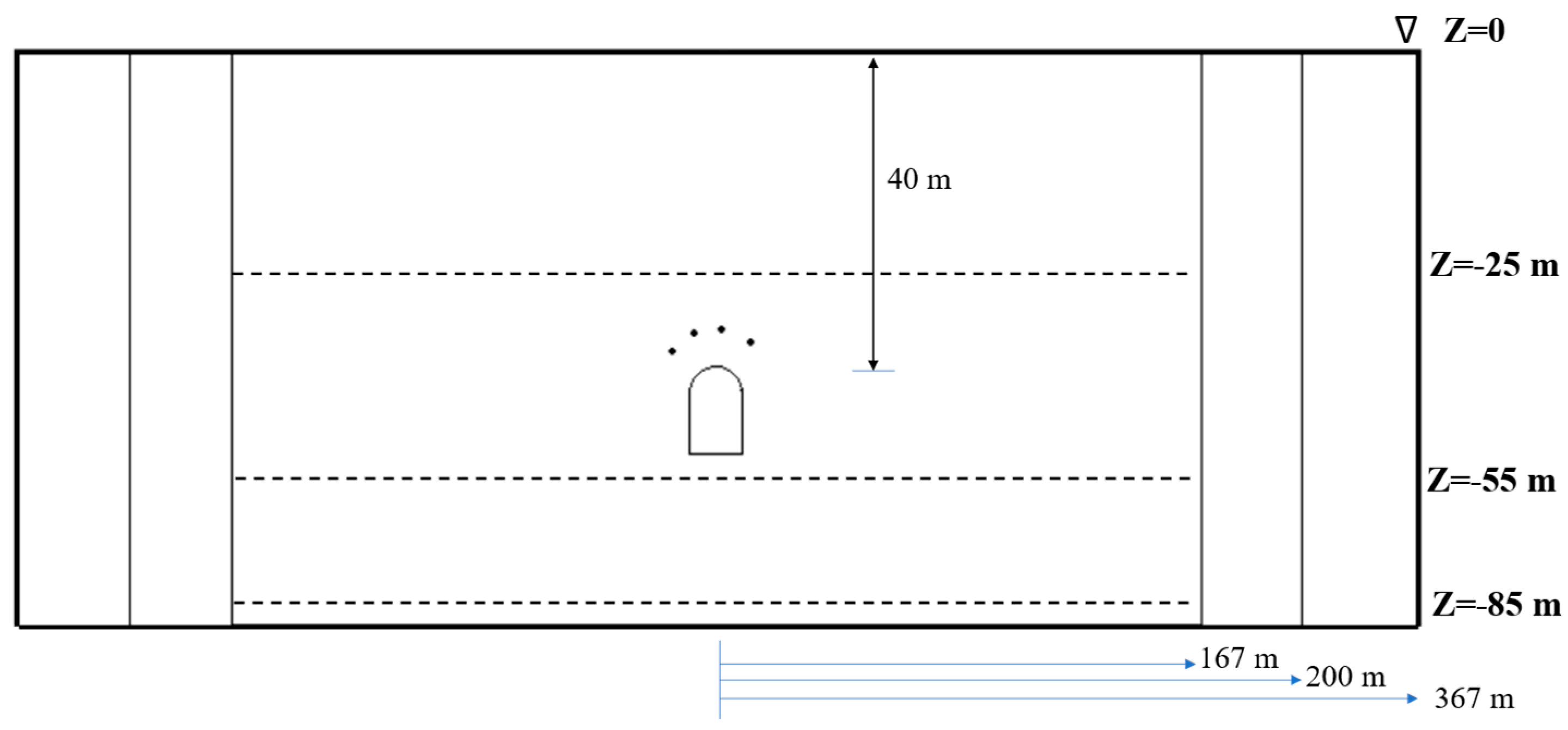
2. Experiment Setup
3. Numerical Model
3.1. Mathematical Model
3.1.1. Heat Transfer Model in Soil Domain
3.1.2. Heat Transfer Model in Pipe
- Water in the pipes behaves as an incompressible fluid;
- Fluid flow in the pipes is assumed to be fully developed and one-dimensional;
- A frictional pressure drop is taken into account during the solution;
- The thermophysical properties of the materials are considered constant;
- The model is solved for a total duration of the experiments, which is five months, by simulating both cooling and heating applications of the tunnel;
- The heat transfer between the air in the tunnel and the surface of the tunnel is neglected.
3.2. Boundary and Initial Conditions
3.2.1. Boundary Conditions
3.2.2. Initial Conditions
3.2.3. Material Properties
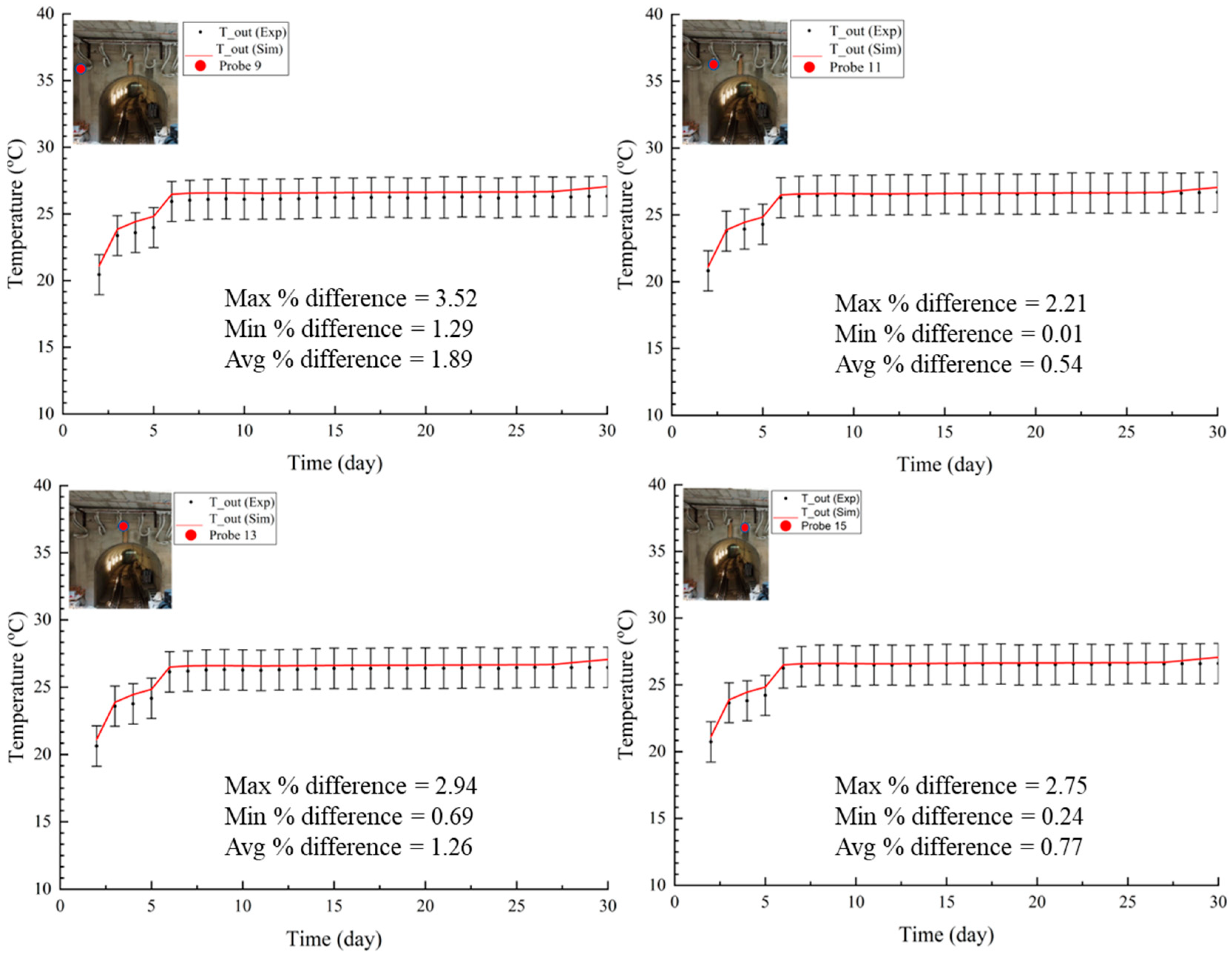
3.3. Mesh Sensitivity Analysis
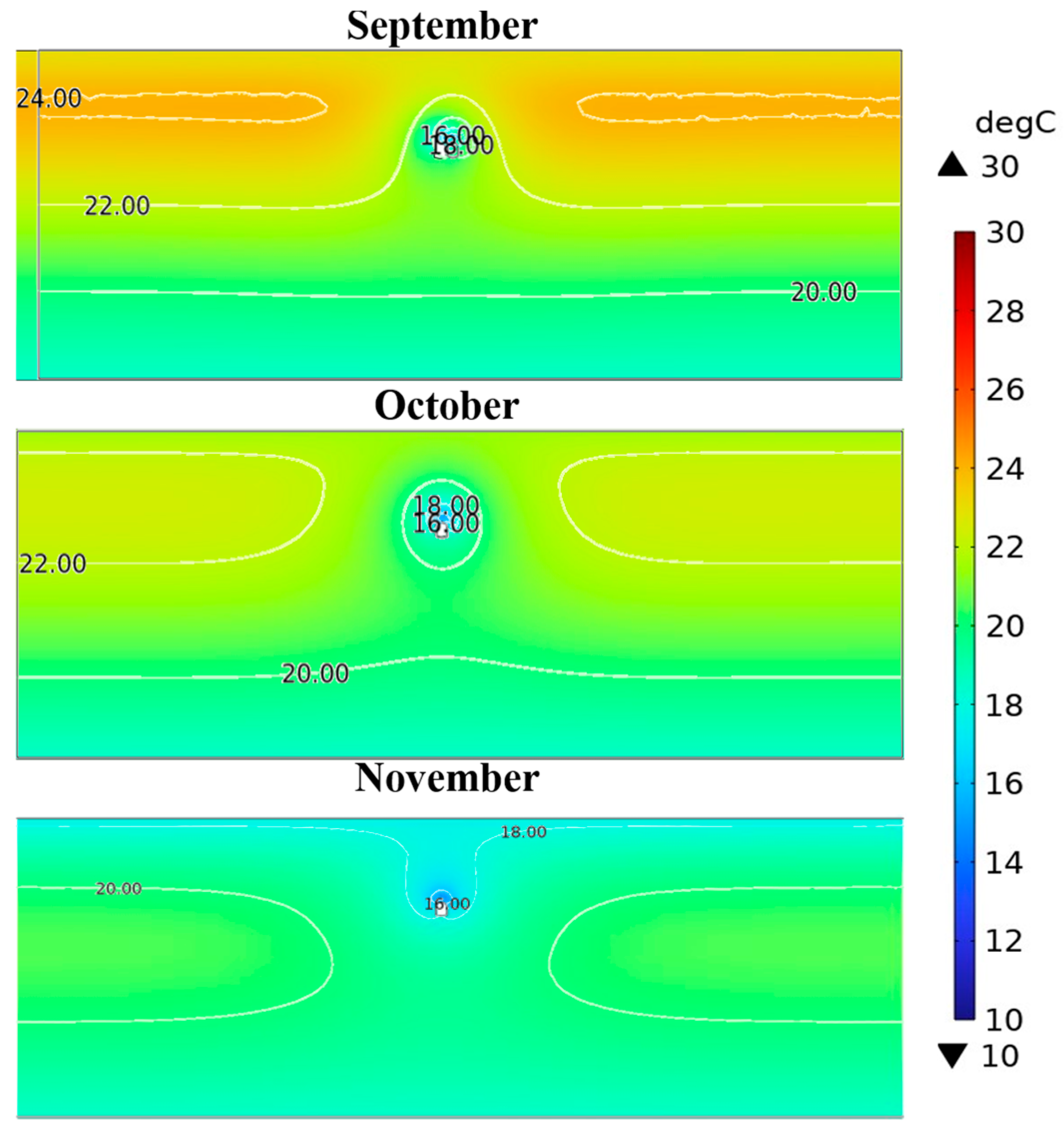
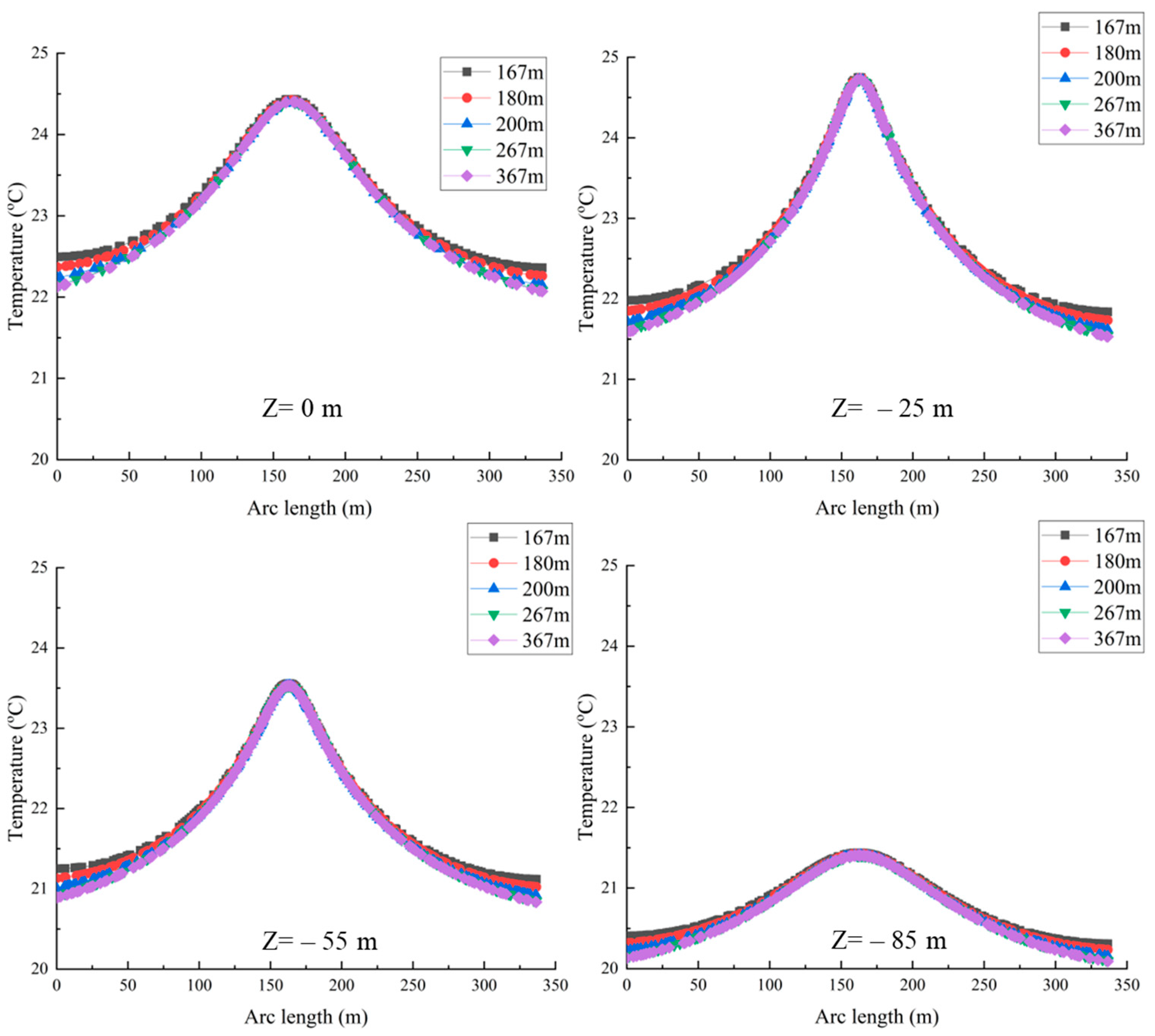
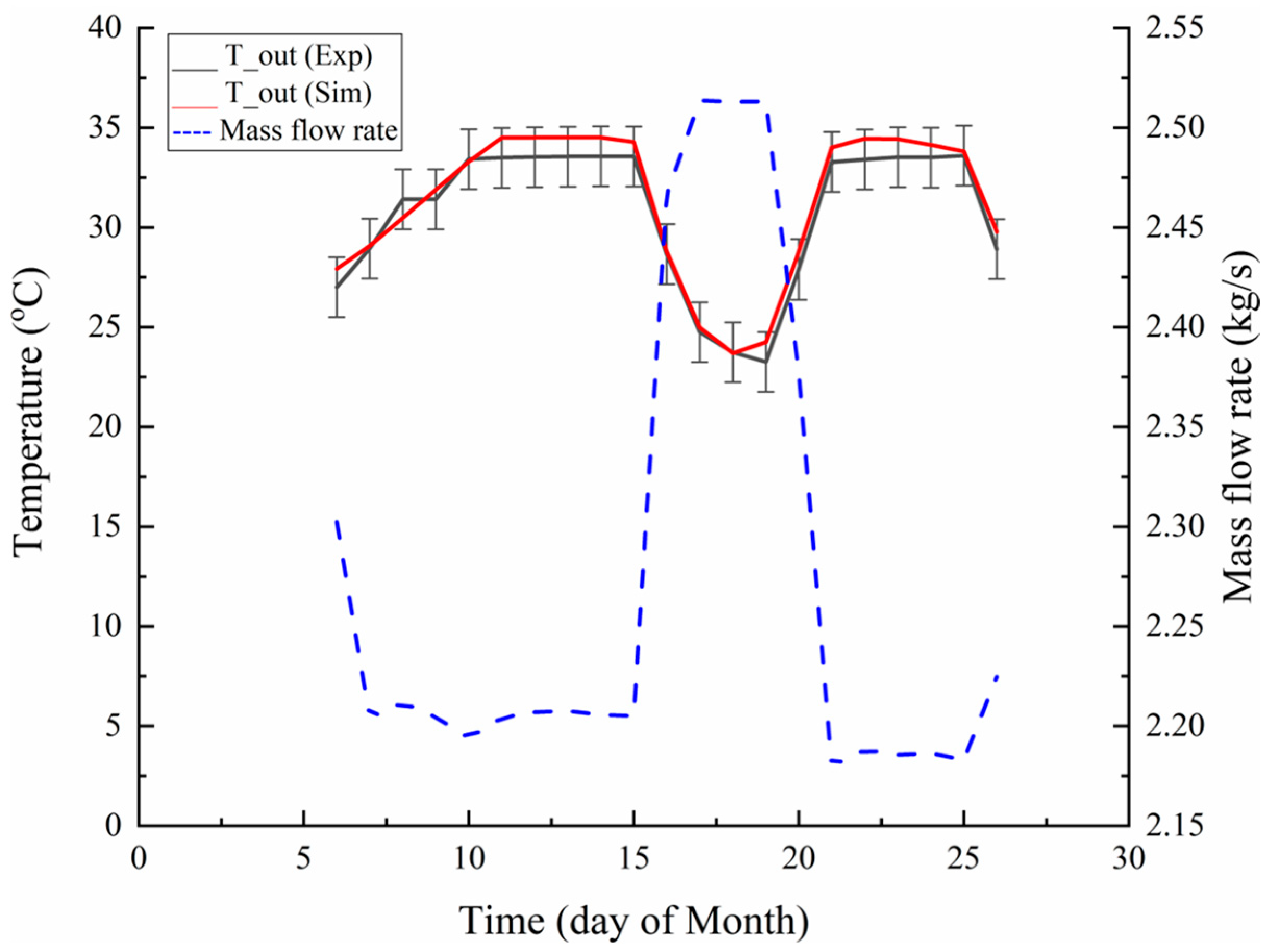
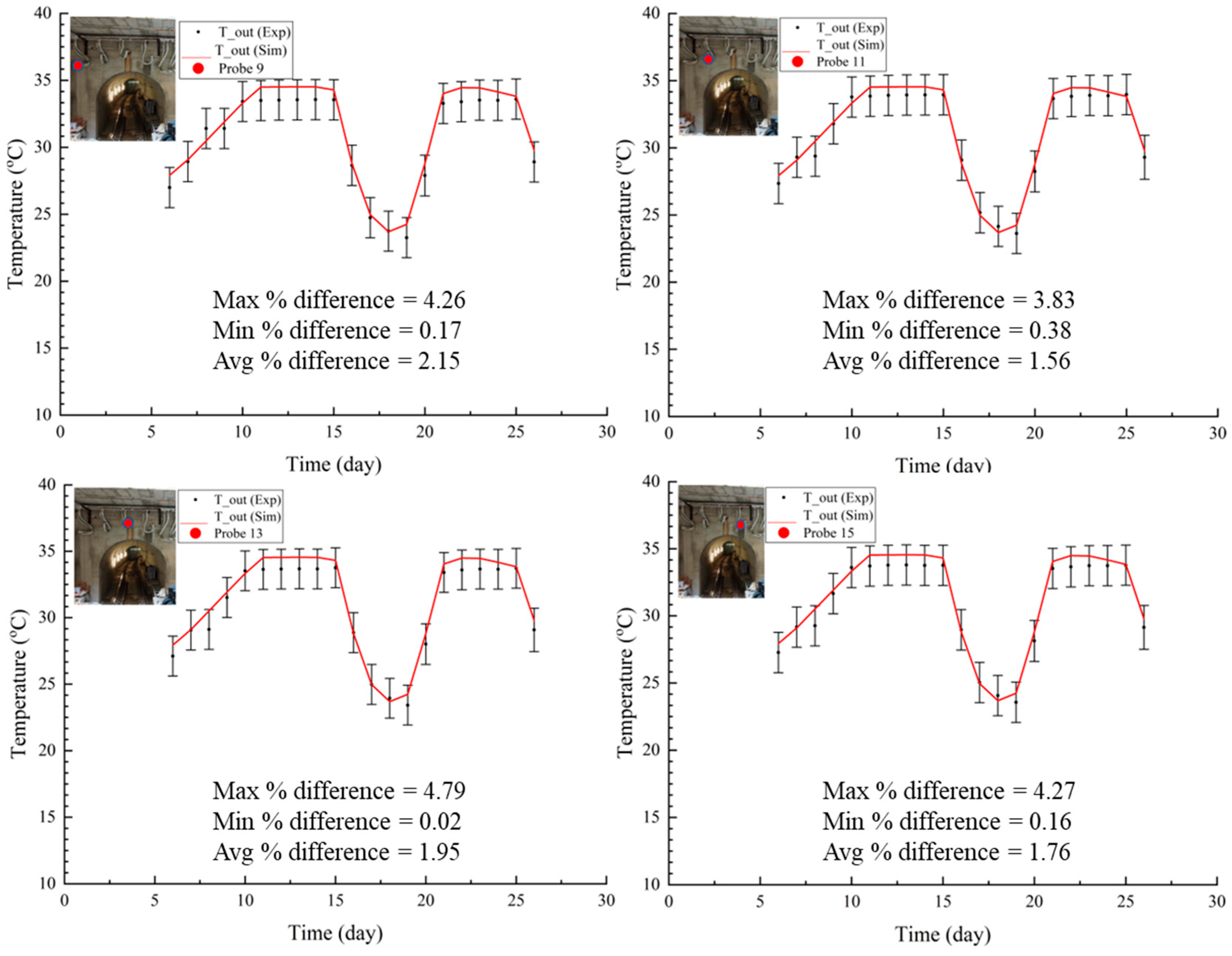
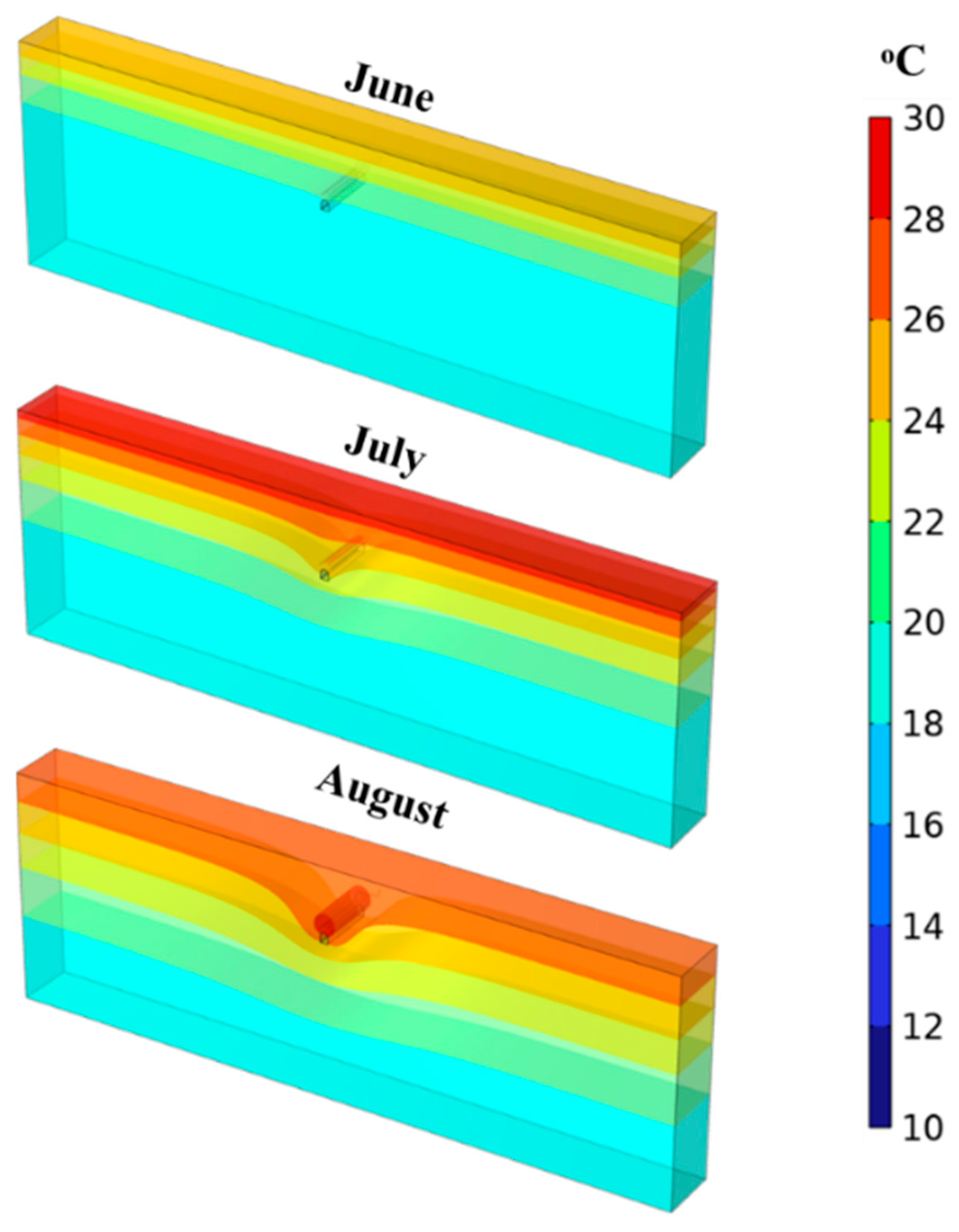
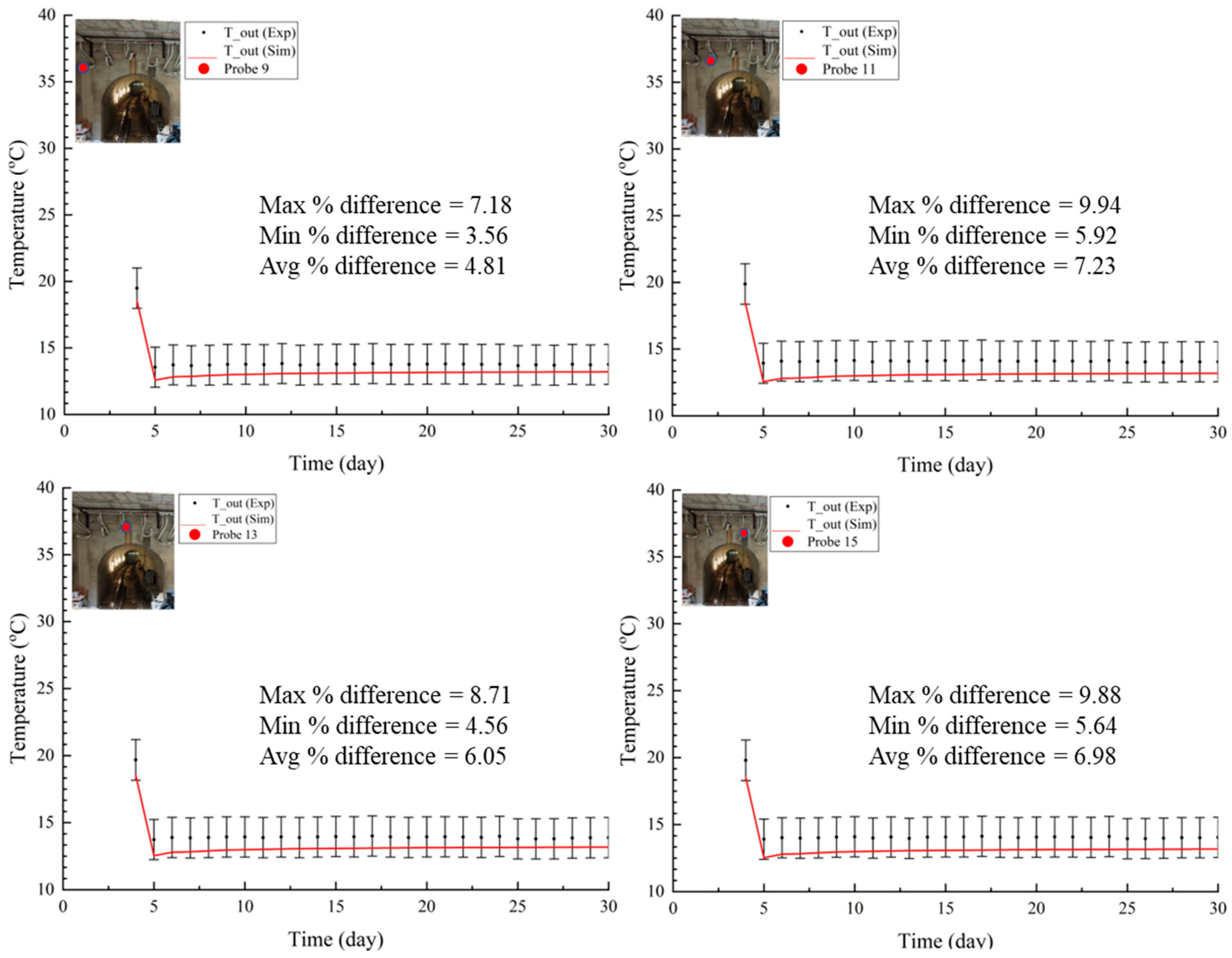
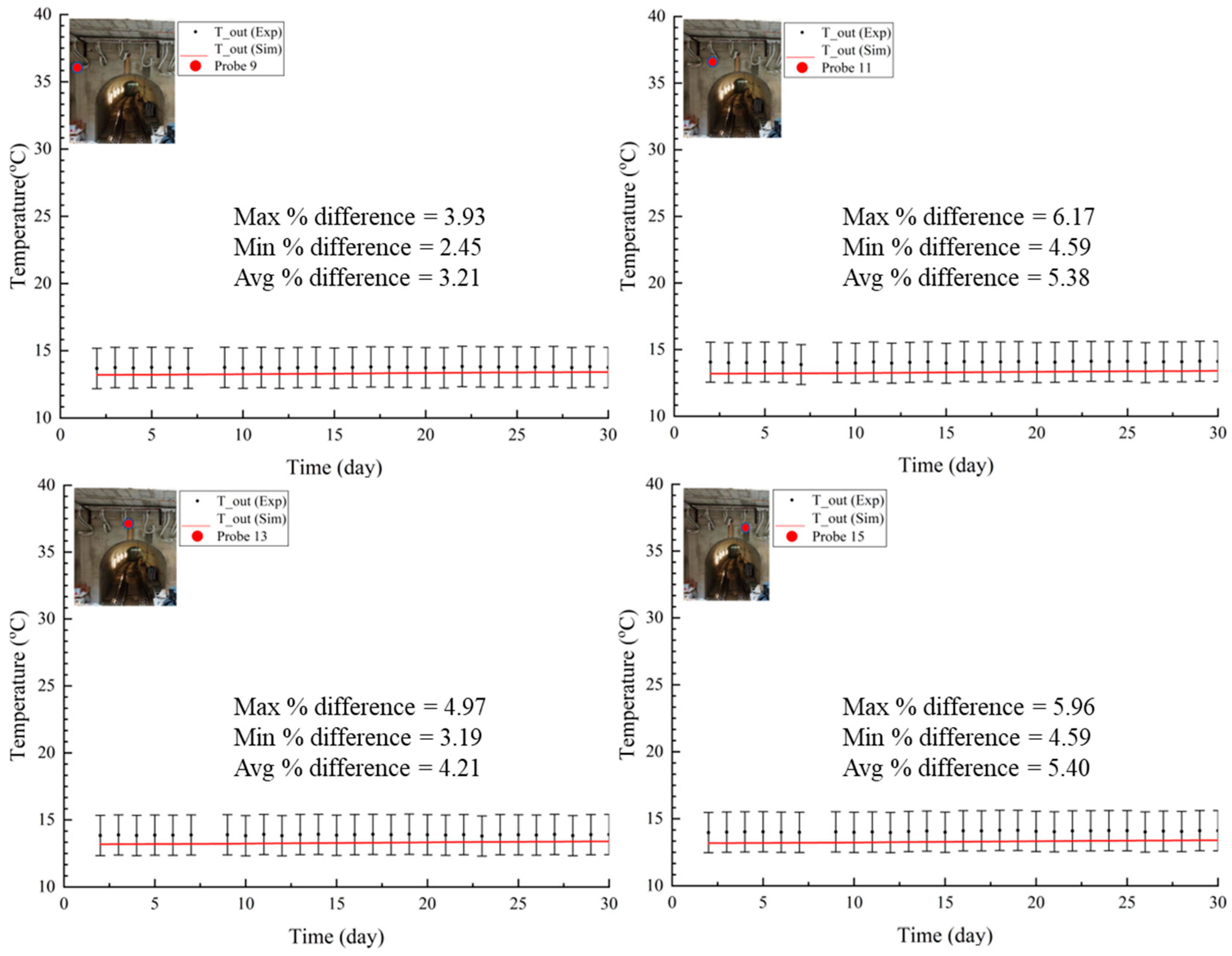
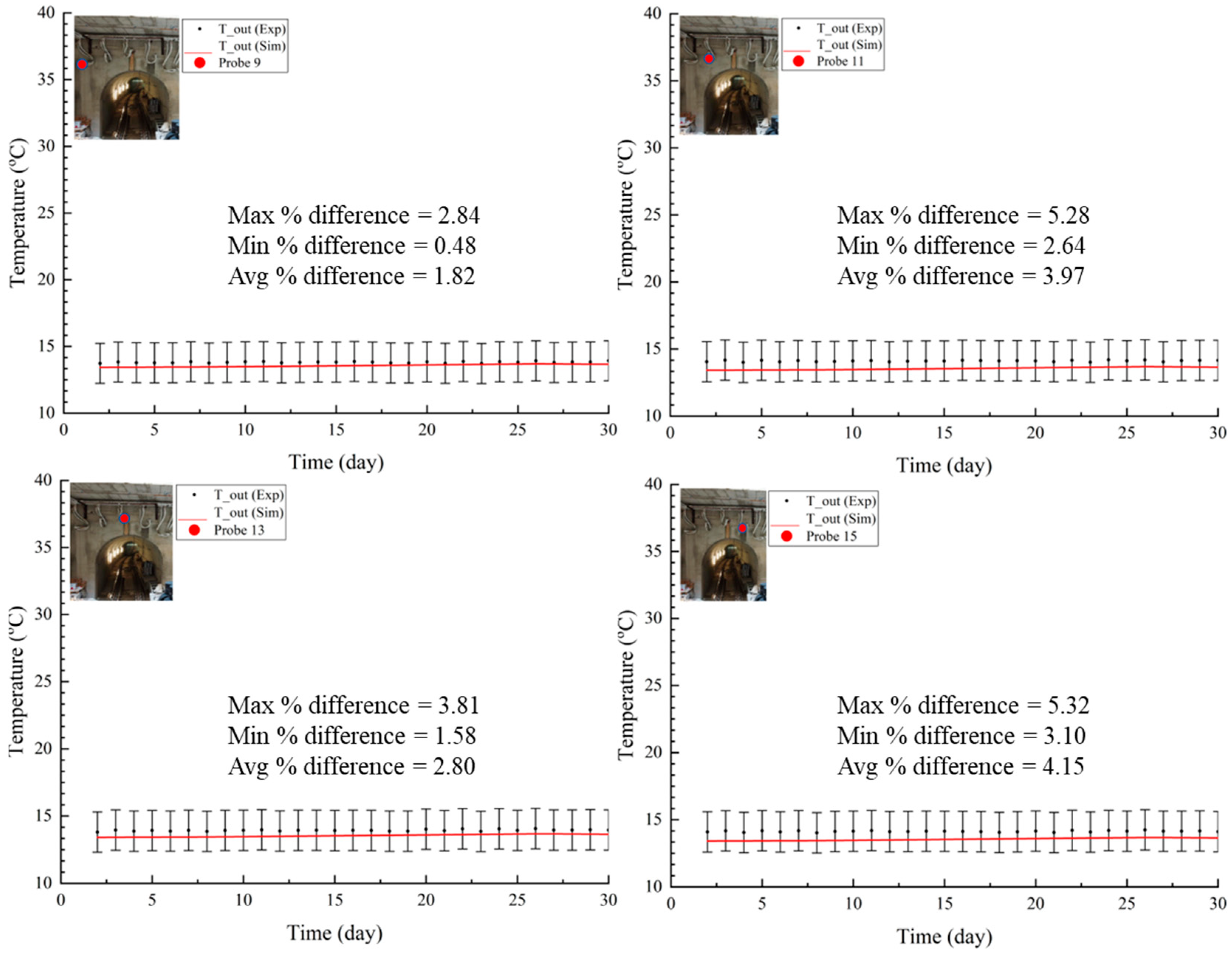
4. Results
4.1. Cooling Mode
4.2. Heating Mode
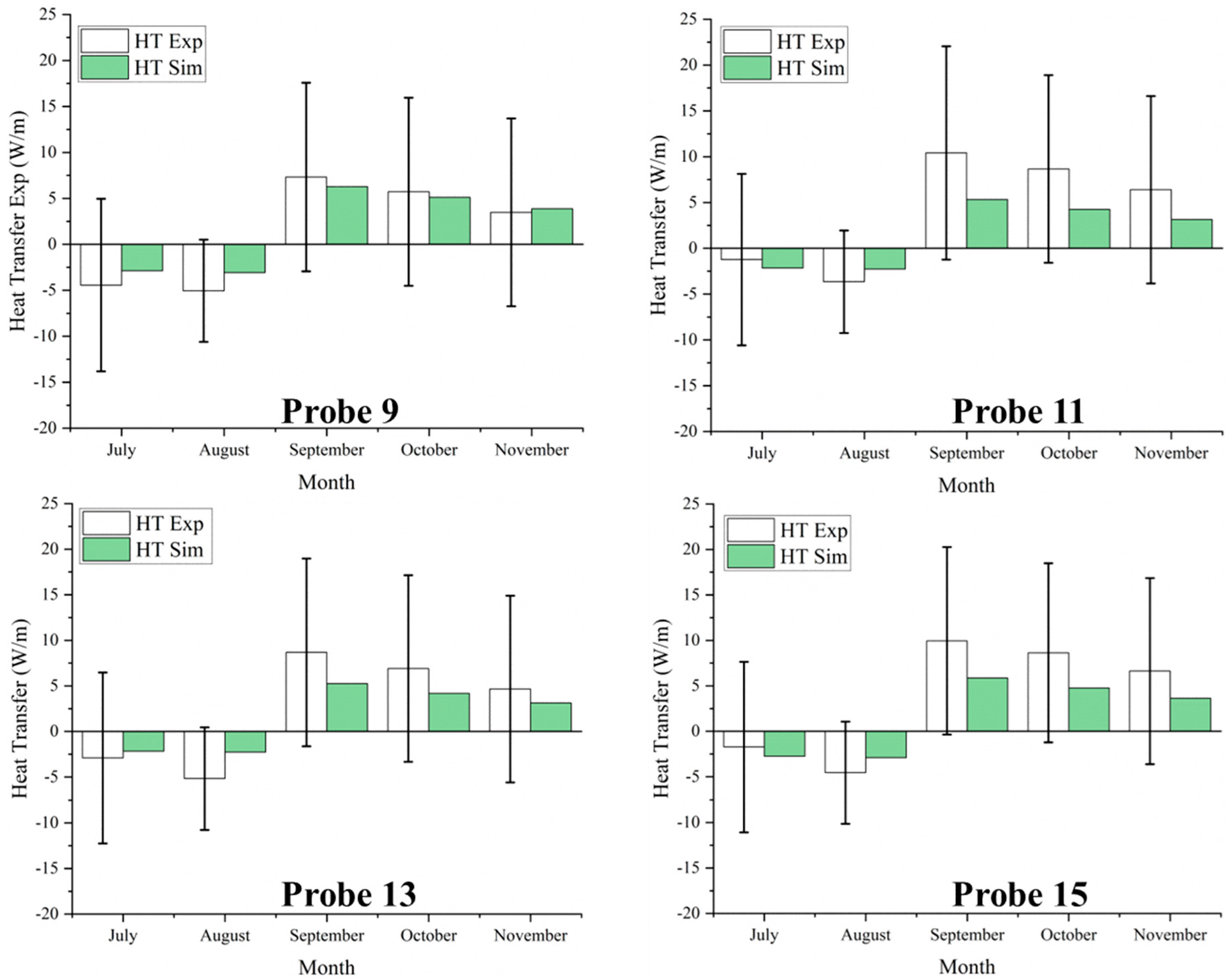
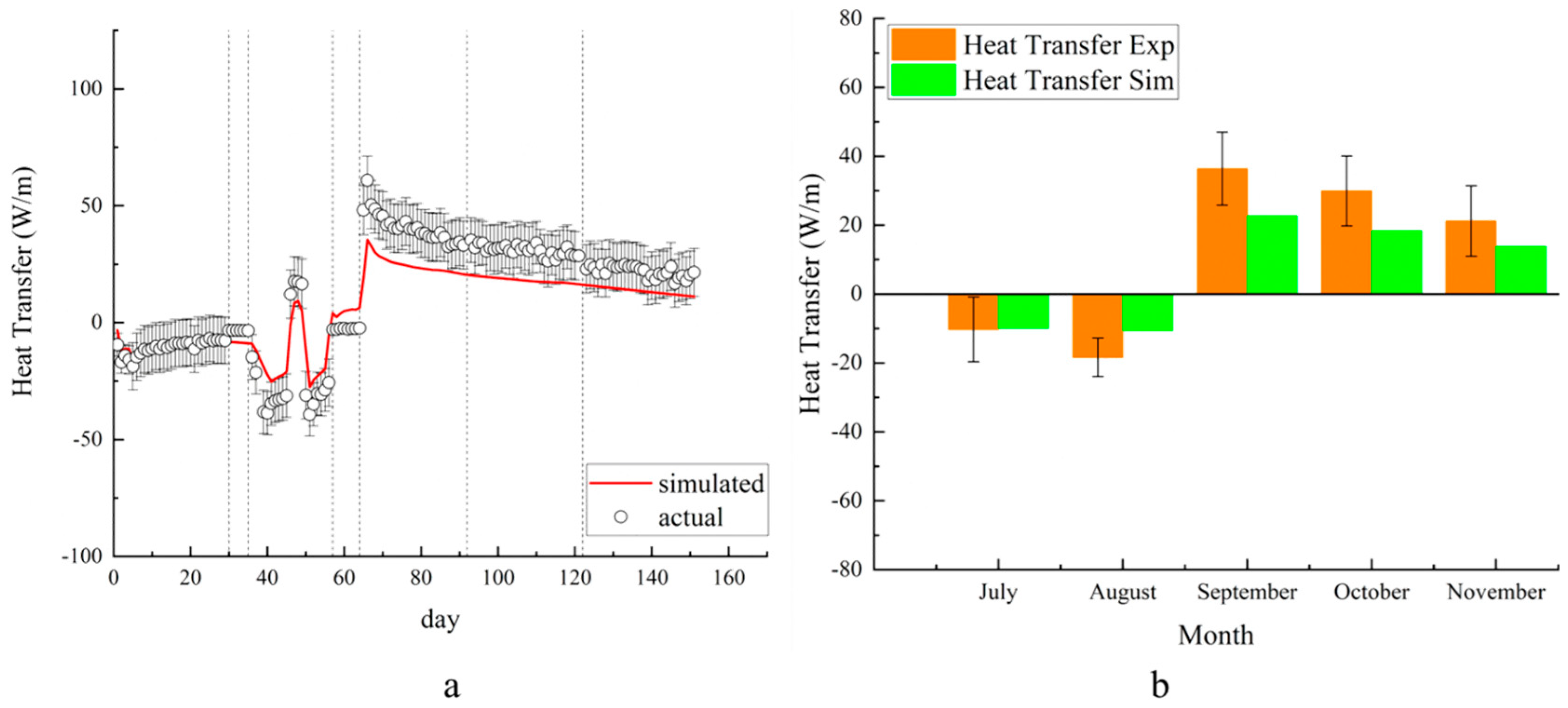
4.3. Heating Transfer
5. Conclusions and Future Work
- The experimental campaign in Piazza Municipio, Napoli, Italy, aimed to convert artificial ground-freezing probes into a ground heat exchanger for ground-coupled heating/cooling systems. This could greatly reduce the installation costs for ground loops for ground-source heat pump systems, which typically represent 50% of the total cost;
- Data collection for the experimental campaign included 151 days, demonstrating tunnel performance for cooling and heating applications from July to November;
- A numerical model was developed and validated with the experimental data. The model simulates operations under similar conditions to understand the impact of heat transfer on the tunnel’s adjacent ground;
- The average values for combined heat transfer per unit length in W/m from all probes are 10.27 W/m and 18.4 W/m during cooling operation for the months of July and August, respectively. During the heating operation, the system obtained the average heat transfer values per unit length of 36.4 W/m, 29.9 W/m, and 21.2 W/m during the months of September, October, and November, respectively. The average cooling and heating energy extracted by the probes during the entire operation is calculated to be 1.3 MWh and 7.06 MWh, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | |
| IEA | International Energy Agency |
| GHG | Greenhouse Gas |
| AGF | Artificial Ground Freezing |
| COP | Coefficient of Performance |
| GSHP | Ground Source Heat Pump |
| EGD | European Green Deal |
| GHE | Ground Heat Exchanger |
| ASHP | Air-Source Heat Pump |
| HTF | Heat Transfer Fluid |
| HDPE | High-Density Polyethylene |
| Miscellaneous | |
| Uncertainty in temperature | |
| Uncertainty in mass flow rate | |
| N | No of terms |
| Solid temperature | |
| Thermal conductivity of solid | |
| Heat transfer with pipe | |
| Density of fluid | |
| Specific heat capacity of fluid | |
| Thermal conductivity of fluid | |
| Tgrnd | Ground temperature |
| Ambient temperature | |
| Standard deviation | |
| Uncertainty in heat transfer rate | |
| Specific heat capacity for solid | |
| Heat transferred between fluid and surroundings | |
| Density of solid | |
| Area of pipe | |
| Fluid temperature | |
| Fluid velocity | |
| Convective heat transfer | |
| θ | Time |
Appendix A
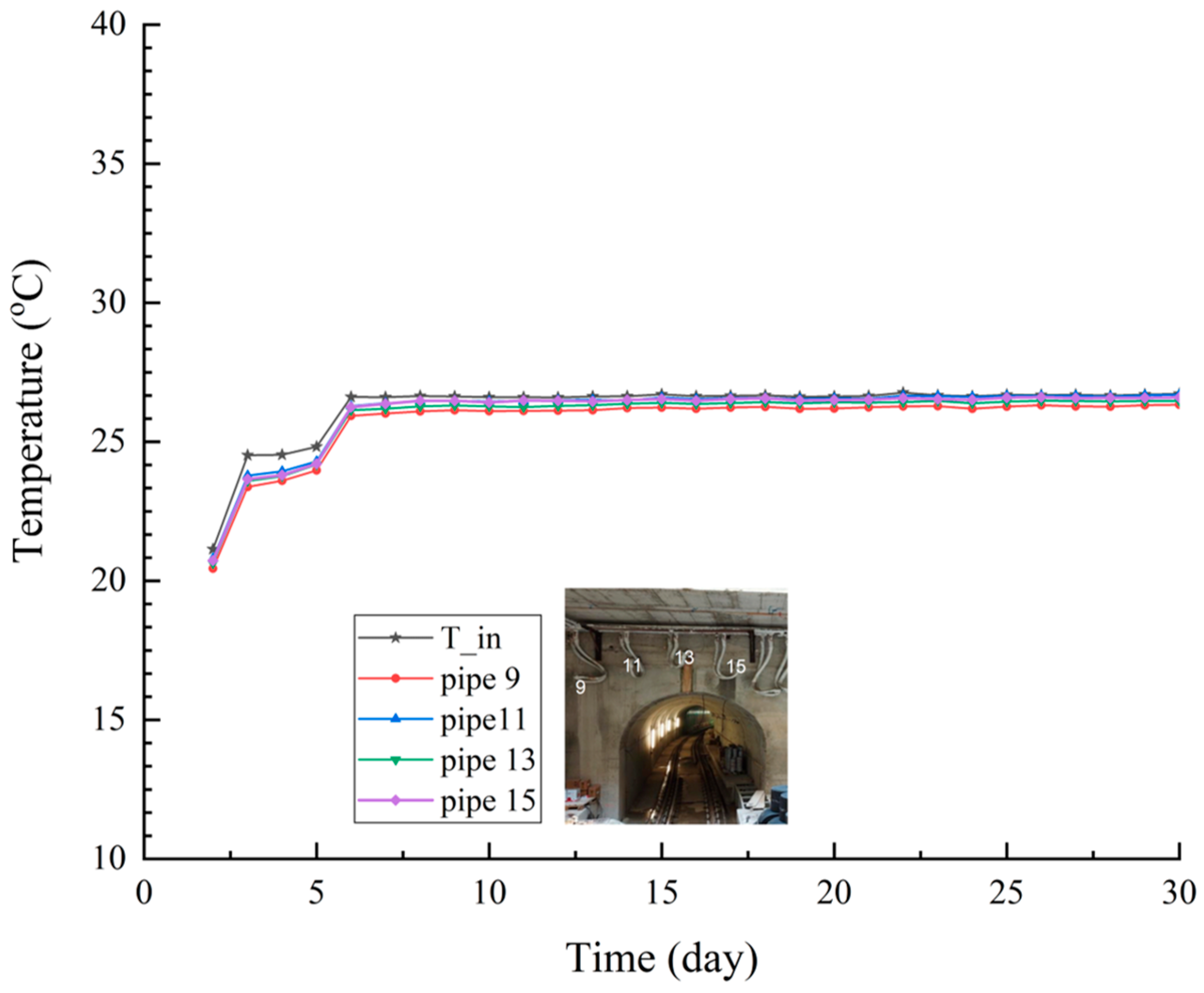
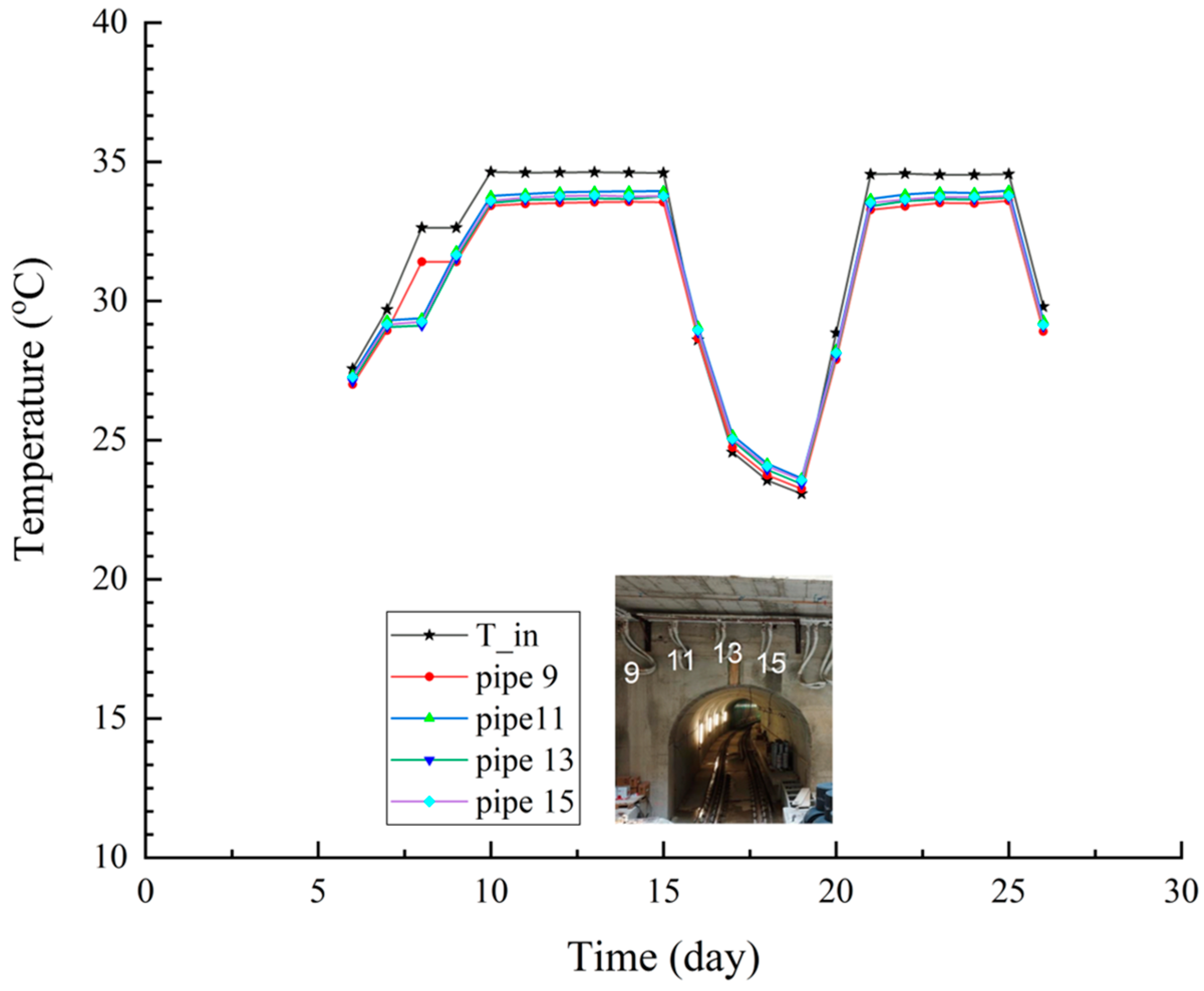
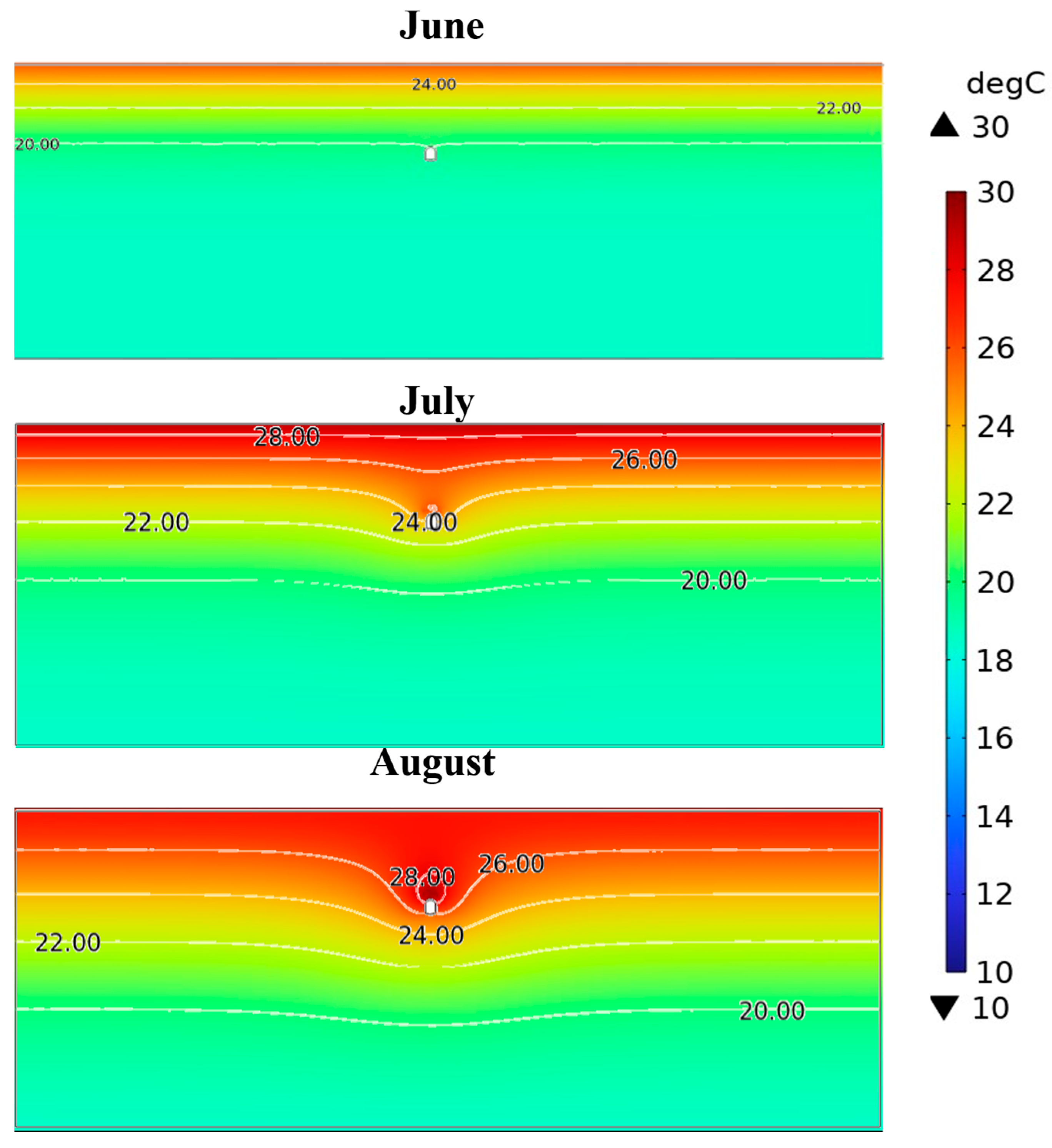
Appendix B

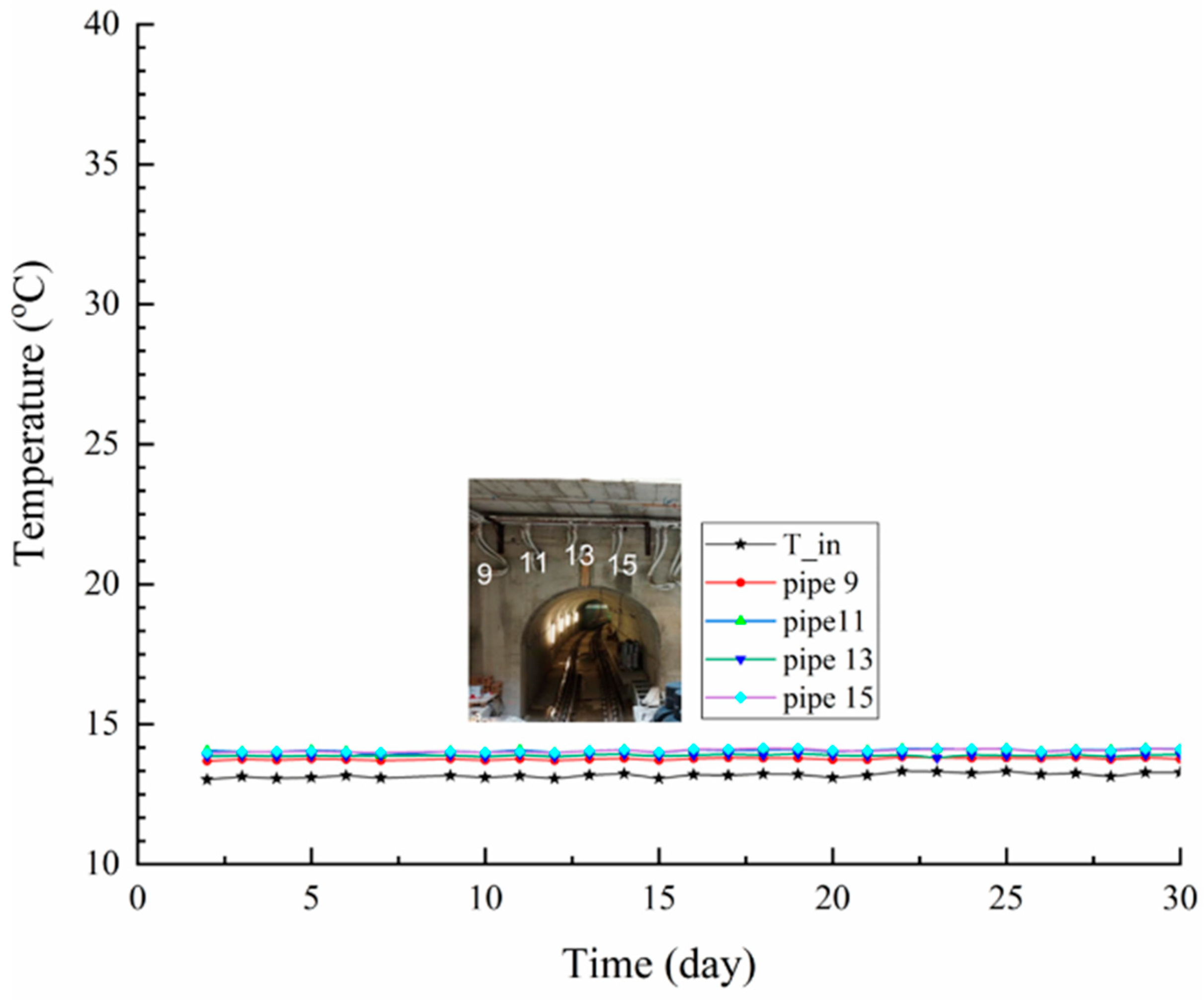

References
- Scarlat, N.; Dallemand, J.F.; Monforti-Ferrario, F.; Banja, M.; Motola, V. Renewable Energy Policy Framework and Bioenergy Contribution in the European Union—An Overview from National Renewable Energy Action Plans and Progress Reports. Renew. Sustain. Energy Rev. 2015, 51, 969–985. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’sullivan, M.; Jones, M.W.; Andrew, R.M.; Gregor, L.; Hauck, J.; Le Quéré, C.; Luijkx, I.T.; Olsen, A.; Peters, G.P.; et al. Global Carbon Budget 2022. Earth Syst. Sci. Data 2022, 14, 4811–4900. [Google Scholar] [CrossRef]
- Luqman, M.; Mahmood, F.; Al-Ansari, T. Supporting Sustainable Global Food Security through a Novel Decentralised Offshore Floating Greenhouse. Energy Convers. Manag. 2023, 277, 116577. [Google Scholar] [CrossRef]
- EUR-Lex. European Parliament Directive of the European Parliament and of the Council as Regards the Promotion of Energy from Renewable Sources. Eur. Comissmion 2021, 0218, 5–24. [Google Scholar]
- IRENA. World Energy Transitions Outlook: 1.5 °C Pathway; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2022; ISBN 9789292604295. [Google Scholar]
- Bhamare, D.K.; Rathod, M.K.; Banerjee, J. Passive Cooling Techniques for Building and Their Applicability in Different Climatic Zones—The State of Art. Energy Build. 2019, 198, 467–490. [Google Scholar] [CrossRef]
- Firfiris, V.K.; Martzopoulou, A.G.; Kotsopoulos, T.A. Passive Cooling Systems in Livestock Buildings towards Energy Saving: A Critical Review. Energy Build. 2019, 202, 109368. [Google Scholar] [CrossRef]
- La Roche, P.; Yeom, D.J.; Ponce, A. Passive Cooling with a Hybrid Green Roof for Extreme Climates. Energy Build. 2020, 224, 110243. [Google Scholar] [CrossRef]
- Alahmer, A.; Ajib, S. Solar Cooling Technologies: State of Art and Perspectives. Energy Convers. Manag. 2020, 214, 112896. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, D.; Tam, V.W.Y.; Tao, Y.; Zhang, G.; Setunge, S.; Shi, L. A Critical Review of Combined Natural Ventilation Techniques in Sustainable Buildings. Renew. Sustain. Energy Rev. 2021, 141, 110795. [Google Scholar] [CrossRef]
- Fraia, S.D.; Shah, M.; Vanoli, L. A Biomass-Based Polygeneration System for a Historical Building: A Techno-Economic and Environmental Analysis. Energy Convers. Manag. 2023, 291, 117336. [Google Scholar] [CrossRef]
- Stryi-Hipp, G. Renewable Heating and Cooling: Technologies and Applications; Woodhead Publishing: Cambridge, UK, 2015; ISBN 9781782422181. [Google Scholar]
- Zhuang, Z.; Li, Y.; Chen, B.; Guo, J. Chinese Kang as a Domestic Heating System in Rural Northern China—A Review. Energy Build. 2009, 41, 111–119. [Google Scholar] [CrossRef]
- Ahmed, F.; Mahmood, M.; Waqas, A.; Ahmad, N.; Ali, M. Thermal Analysis of Macro-Encapsulated Phase Change Material Coupled with Domestic Gas Heater for Building Heating. Sustain. Energy Technol. Assess. 2021, 47, 101533. [Google Scholar] [CrossRef]
- Prakash, J.; Roan, D.; Tauqir, W.; Nazir, H.; Ali, M.; Kannan, A. Off-Grid Solar Thermal Water Heating System Using Phase-Change Materials: Design, Integration and Real Environment Investigation. Appl. Energy 2019, 240, 73–83. [Google Scholar] [CrossRef]
- Ge, T.S.; Wang, R.Z.; Xu, Z.Y.; Pan, Q.W.; Du, S.; Chen, X.M.; Ma, T.; Wu, X.N.; Sun, X.L.; Chen, J.F. Solar Heating and Cooling: Present and Future Development. Renew. Energy 2018, 126, 1126–1140. [Google Scholar] [CrossRef]
- Mosallat, F.; Elmekkawy, T.; Friesen, D.L.; Molinski, T.; Loney, S.; Bibeau, E.L. Modeling, Simulation and Control of Flat Panel Solar Collectors with Thermal Storage for Heating and Cooling Applications. Procedia Comput. Sci. 2013, 19, 686–693. [Google Scholar] [CrossRef][Green Version]
- Carvalho, A.D.; Moura, P.; Vaz, G.C.; De Almeida, A.T. Ground Source Heat Pumps as High Efficient Solutions for Building Space Conditioning and for Integration in Smart Grids. Energy Convers. Manag. 2015, 103, 991–1007. [Google Scholar] [CrossRef]
- Chandrashekar, M. Heat Pumps. In Proceedings of the Selected Lectures from the 1980 International Symposium on Solar Energy Utilization, London, ON, Canada, 10–24 August 1981; pp. 447–468. [Google Scholar] [CrossRef]
- Ratchawang, S.; Chotpantarat, S.; Chokchai, S.; Takashima, I.; Uchida, Y.; Charusiri, P. A Review of Ground Source Heat Pump Application for Space Cooling in Southeast Asia. Energies 2022, 15, 4992. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, G.; Zhang, A.; Jin, Y.; Ru, R.; Tian, M. Frosting Phenomenon and Frost-Free Technology of Outdoor Air Heat Exchanger for an Air-Source Heat Pump System in China: An Analysis and Review. Energies 2018, 11, 2642. [Google Scholar] [CrossRef]
- Lucia, U.; Simonetti, M.; Chiesa, G.; Grisolia, G. Ground-Source Pump System for Heating and Cooling: Review and Thermodynamic Approach. Renew. Sustain. Energy Rev. 2017, 70, 867–874. [Google Scholar] [CrossRef]
- Chesser, M.; Lyons, P.; O’Reilly, P.; Carroll, P. Air Source Heat Pump In-Situ Performance. Energy Build. 2021, 251, 111365. [Google Scholar] [CrossRef]
- Song, C.; Li, Y.; Rajeh, T.; Ma, L.; Zhao, J.; Li, W. Application and Development of Ground Source Heat Pump Technology in China. Prot. Control Mod. Power Syst. 2021, 6, 17. [Google Scholar] [CrossRef]
- Wang, X.; Xia, L.; Bales, C.; Zhang, X.; Copertaro, B.; Pan, S.; Wu, J. A Systematic Review of Recent Air Source Heat Pump (ASHP) Systems Assisted by Solar Thermal, Photovoltaic and Photovoltaic/Thermal Sources. Renew. Energy 2020, 146, 2472–2487. [Google Scholar] [CrossRef]
- Yang, L.W.; Xu, R.J.; Hua, N.; Xia, Y.; Zhou, W.B.; Yang, T.; Belyayev, Y.; Wang, H.S. Review of the Advances in Solar-Assisted Air Source Heat Pumps for the Domestic Sector. Energy Convers. Manag. 2021, 247, 114710. [Google Scholar] [CrossRef]
- ASHRAE (American Society of Heating Refrigerating and Air-Conditioning Engineers). Handbook HVAC Systems and Equipment; American Society of Heating Refrigerating and Air-Conditioning Engineers: Peachtree Corners, GA, USA, 2012; ISBN 9781936504268. [Google Scholar]
- Valancius, R.; Singh, R.M.; Jurelionis, A.; Vaiciunas, J. A Review of Heat Pump Systems and Applications in Cold Climates: Evidence from Lithuania. Energies 2019, 12, 4331. [Google Scholar] [CrossRef]
- Sivasakthivel, T.; Murugesan, K.; Sahoo, P.K. Study of Technical, Economical and Environmental Viability of Ground Source Heat Pump System for Himalayan Cities of India. Renew. Sustain. Energy Rev. 2015, 48, 452–462. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. Ground-Source Heat Pumps: Fundamentals, Experiments and Applications; Joe Hayton: Pateley Bridge, UK, 2015; ISBN 9780128042205. [Google Scholar]
- Lu, Q.; Narsilio, G.A.; Aditya, G.R.; Johnston, I.W. Economic Analysis of Vertical Ground Source Heat Pump Systems in Melbourne. Energy 2017, 125, 107–117. [Google Scholar] [CrossRef]
- Nouri, G.; Noorollahi, Y.; Yousefi, H. Solar Assisted Ground Source Heat Pump Systems—A Review. Appl. Therm. Eng. 2019, 163, 114351. [Google Scholar] [CrossRef]
- Menegazzo, D.; Lombardo, G.; Bobbo, S.; De Carli, M.; Fedele, L. State of the Art, Perspective and Obstacles of Ground-Source Heat Pump Technology in the European Building Sector: A Review. Energies 2022, 15, 2685. [Google Scholar] [CrossRef]
- United Nations. Economic Commission for Europe. Economic and Social: Railway Tunnels in Europe and North America. Repos. Open Sci. Access Portal 2002, 7, 27–28. [Google Scholar]
- Revesz, A.; Chaer, I.; Thompson, J.; Mavroulidou, M.; Gunn, M.; Maidment, G. Ground Source Heat Pumps and Their Interactions with Underground Railway Tunnels in an Urban Environment: A Review. Appl. Therm. Eng. 2016, 93, 147–154. [Google Scholar] [CrossRef]
- Davies, G.; Boot-Handford, N.; Curry, D.; Dennis, W.; Ajileye, A.; Revesz, A.; Maidment, G. Combining Cooling of Underground Railways with Heat Recovery and Reuse. Sustain. Cities Soc. 2019, 45, 543–552. [Google Scholar] [CrossRef]
- Tong, L.; Songtao, H.; Shan, L.; Wang, Y. Study on Heat Transfer Performance of Metro Tunnel Capillary Heat Exchanger. Sustain. Cities Soc. 2019, 45, 683–685. [Google Scholar] [CrossRef]
- Mao, Z.; Hu, S.; Guan, Y.; Ji, Y.; Liu, G.; Tong, Z.; Wang, Y.; Tong, L. Performance Analysis of a Hybrid Subway Source Heat Pump System Using Capillary Heat Exchanger. Appl. Therm. Eng. 2021, 197, 117367. [Google Scholar] [CrossRef]
- Tong, Z.; Guan, Y.; Cao, T.; Ji, Y.; Hu, S.; Liu, G.; Liu, N.; Fan, Y. Onsite Measurement and Performance Analysis of Capillary Heat Pump System Used in Subway Tunnels. Appl. Therm. Eng. 2022, 204, 118008. [Google Scholar] [CrossRef]
- Ji, Y.; Wu, W.; Qi, H.; Wang, W.; Hu, S. Heat Transfer Performance Analysis of Front-End Capillary Heat Exchanger of a Subway Source Heat Pump System. Energy 2022, 246, 123424. [Google Scholar] [CrossRef]
- Ji, Y.; Wu, W.; Hu, S. Long-Term Performance of a Front-End Capillary Heat Exchanger for a Metro Source Heat Pump System. Appl. Energy 2023, 335, 120772. [Google Scholar] [CrossRef]
- Yu, Y.; You, S.; Zhang, H.; Ye, T.; Wang, Y.; Wei, S. A Review on Available Energy Saving Strategies for Heating, Ventilation and Air Conditioning in Underground Metro Stations. Renew. Sustain. Energy Rev. 2021, 141, 110788. [Google Scholar] [CrossRef]
- Ji, Y.; Yin, Z.; Jiao, J.; Ji, C.; Hu, S. Long-Term Operational Characteristics of Subway Source Heat Pump System under Various Tunnel Internal Heat Source Intensities. Renew. Energy 2024, 236, 121445. [Google Scholar] [CrossRef]
- Ji, Y.; Ji, C.; Shen, S.; Zhang, J.; Hu, S. Performance and Optimal Design Parameters of Tunnel Lining CHEs under Typical Design Conditions. Renew. Energy 2025, 238, 121962. [Google Scholar] [CrossRef]
- Ji, Y.; Shen, S.; Wang, X.; Zhang, H.; Qi, H.; Hu, S. Impact of Groundwater Seepage on Thermal Performance of Capillary Heat Exchangers in Subway Tunnel Lining. Renew. Energy 2024, 227, 120551. [Google Scholar] [CrossRef]
- Alzoubi, M.A.; Xu, M.; Hassani, F.P.; Poncet, S.; Sasmito, A.P. Artificial Ground Freezing: A Review of Thermal and Hydraulic Aspects. Tunn. Undergr. Space Technol. 2020, 104, 103534. [Google Scholar] [CrossRef]
- Crippa, C.; Manassero, V. Artificial Ground Freezing at Sophiaspoortunnel (The Netherlands)—Freezing Parameters: Data Acquisition and Processing. In Proceedings of the GeoCongress 2006: Geotechnical Engineering in the Information Technology Age, Reston, VA, USA, 21 February 2006; American Society of Civil Engineers: Reston, VA, USA, 2006; Volume 2006, p. 254. [Google Scholar]
- Colombo, G.; Lunardi, P.; Cavagna, B.; Cassani, G.; Manassero, V. The Artificial Ground Freezing Technique Application for the Naples Underground. In Word Tunnel Congress 2008 on Underground Facilities for Better Environment and Safety; Central Board of Irrigation & Power: New Delhi, India, 2008; pp. 910–921. [Google Scholar]
- Mauro, A.; Normino, G.; Cavuoto, F.; Marotta, P.; Massarotti, N. Modeling Artificial Ground Freezing for Construction of Two Tunnels of a Metro Station in Napoli (Italy). Energies 2020, 13, 1272. [Google Scholar] [CrossRef]
- Meglio, A.D.; Massarotti, N.; Mauro, A.; Trombetta, V. Coupled Geothermal Energy Simulations. J. Phys. Conf. Ser. 2022, 2177, 012004. [Google Scholar] [CrossRef]
- Ahmed, F.; Massarotti, N.; Mauro, A.; Normino, G. A Novel Ground Source Heat Exchanger in an Underground Metro Tunnel. J. Phys. Conf. Ser. 2024, 2685, 012037. [Google Scholar] [CrossRef]
- Lancellotta, G.D.S.; Wernecke, R. Application of Artificial Ground-Freezing to Construct a Passenger Interchange Tunnel for the Subway Line 14 in Paris, France. Environ. Sci. Eng. Geol. 2017, 19, 2461–2467. [Google Scholar]
- Massarotti, N.; Mauro, A.; Normino, G.; Vanoli, L.; Verde, C.; Allocca, V.; Calcaterra, D.; Coda, S.; de Vita, P.; Forzano, C.; et al. Innovative Solutions to Use Ground-Coupled Heat Pumps in Historical Buildings: A Test Case in the City of Napoli, Southern Italy. Energies 2020, 14, 296. [Google Scholar] [CrossRef]
- Parali, L.; Durmaz, F.; Aydin, O. Calibration of a Platinum Resistance Thermometer (Pt-100) and Its Measurement Uncertainty Analysis. Celal Bayar Üniversitesi Fen. Bilim. Derg. 2018, 14, 41–49. [Google Scholar] [CrossRef]
- Portata, M.D.I. RIF100. “Misuratore di Portata”. pp. 1–31. Available online: https://www.riels.it/it/rif100-rif100-misuratore-di-portata-elettromagnetico?srsltid=AfmBOoqmP618CTbO6At-Ji3SdE-KzclGhMitons-8R6OTxhyHJ9WHg3o (accessed on 1 June 2025).
- Janna, W.S. Natural-Convection Systems. In Engineering Heat Transfer; CRC Press: Boca Raton, FL, USA, 2018; pp. 8–47. [Google Scholar]
- Pimentel, E.; Papakonstantinou, S.; Anagnostou, G. Numerical Interpretation of Temperature Distributions from Three Ground Freezing Applications in Urban Tunnelling. Tunn. Undergr. Space Technol. 2012, 28, 57–69. [Google Scholar] [CrossRef]

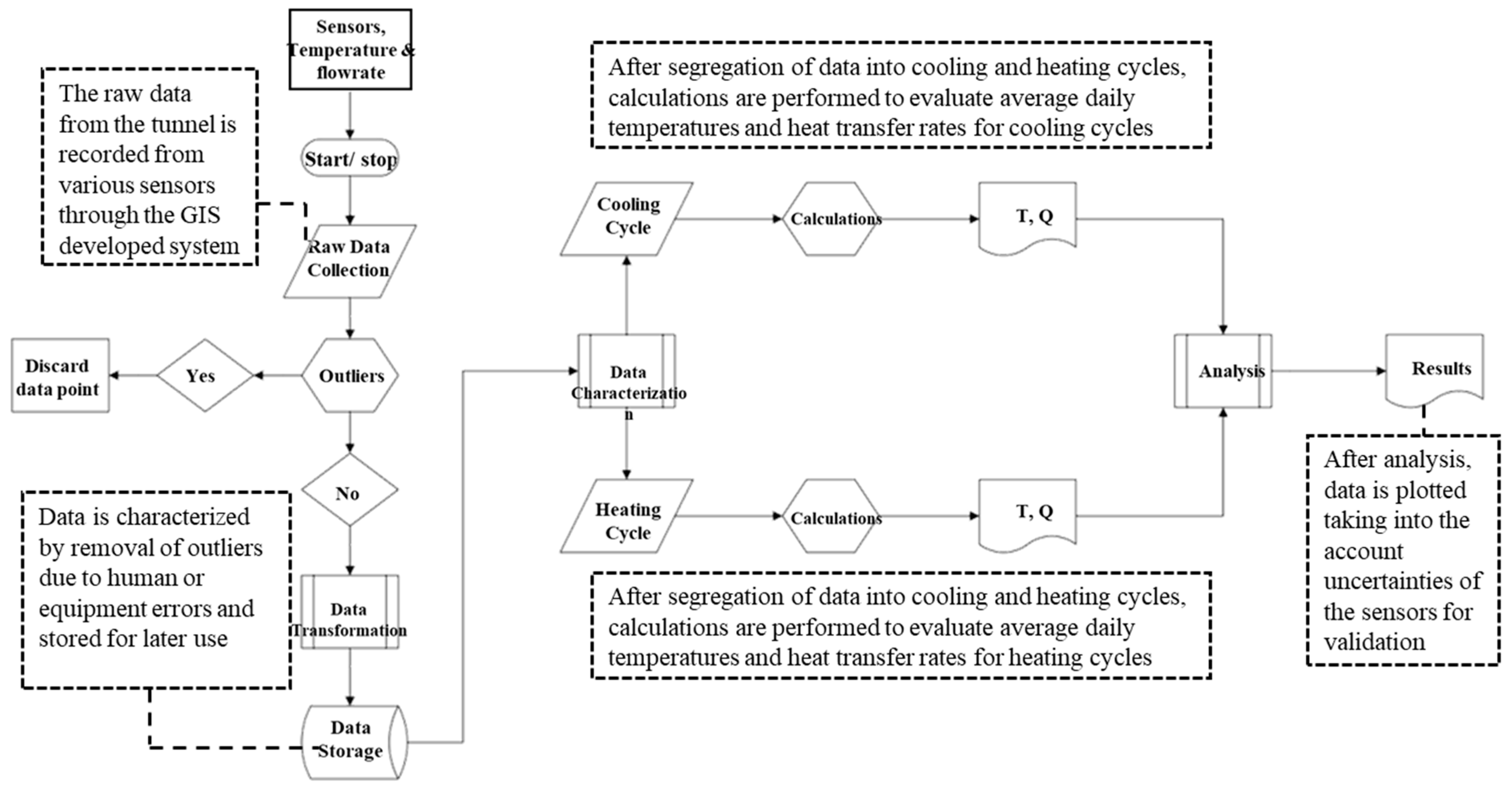

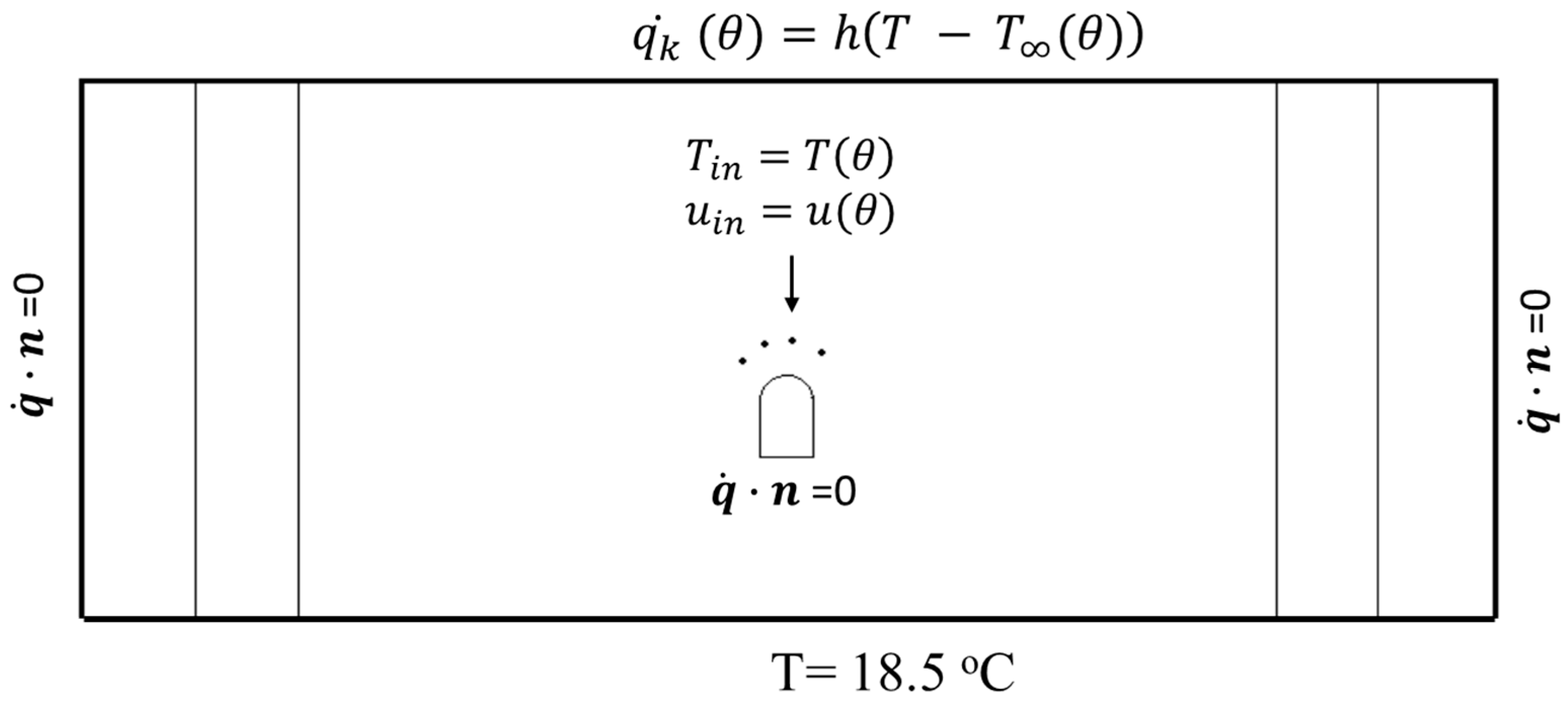
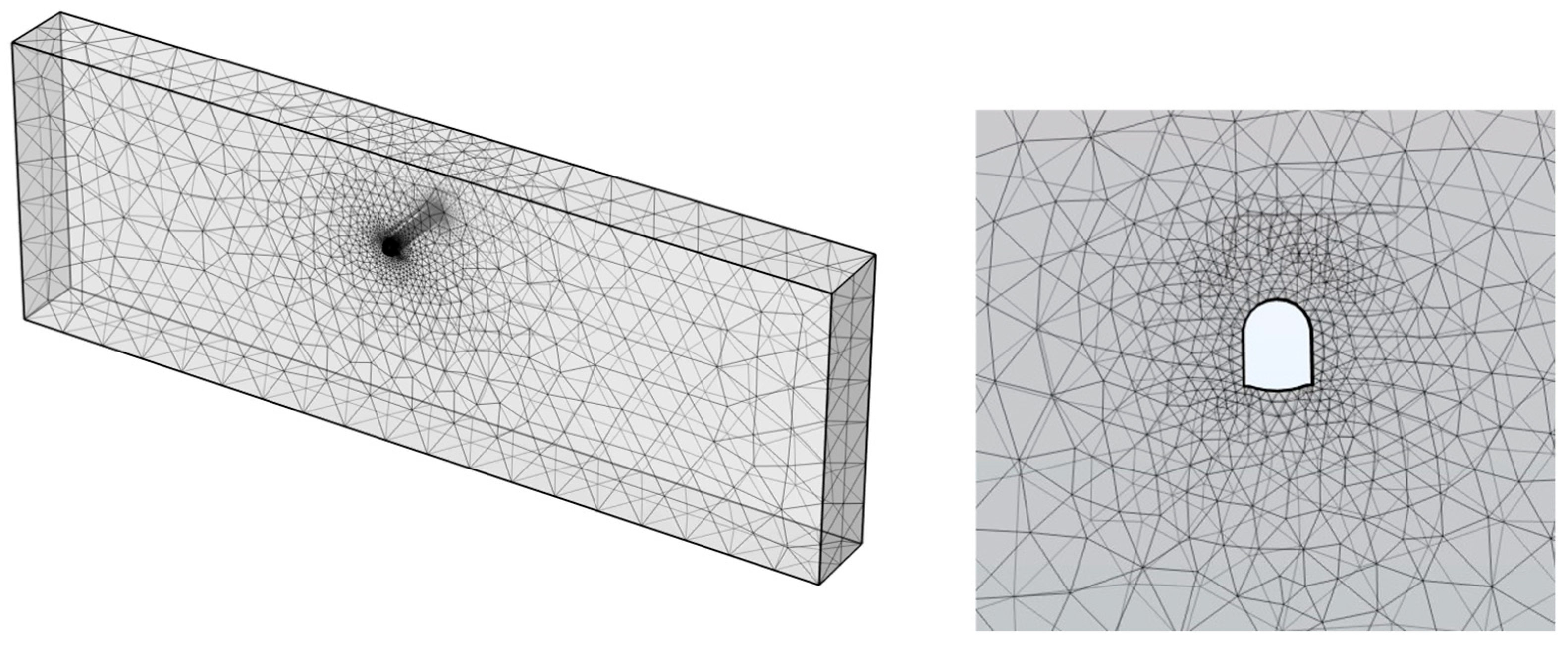

| Factor | GSHP | ASHP | References |
|---|---|---|---|
| Heat Source | Ground is used as source | Ambient air outside the building, even in cold climates | [20,21] |
| Efficiency | More efficient due to stable heat source | The efficiency is less than that of GSHP systems, especially in colder/hotter climates. | [22,23] |
| Installation | Comparatively installation require specialized process of drilling | Typically, easy to install. | [20,24,25,26] |
| Noise | Low almost negligible noise production during operation | Higher noise production during operations | [27,28] |
| Maintenance | The maintenance is lower as compared to ASHP but when required it can be difficult | The maintenance is easy as components are easily accessible | [29,30] |
| Cost | High installation costs required, due to drilling and loop installation but low operating cost | Lower installation costs but higher operating costs | [29,31,32] |
| Material Properties (Pozzolana) | Values |
|---|---|
| Porosity ℇ | 0.51 |
| (kg/m3) | 1172 |
| Thermal conductivity k (W/m/K) | 1.28 |
| Heat capacity Cp (kJ/m3/K) | 3150 |
| Permeability kf (m/s) | 10−6 |
| Mesh Level | No. of Elements | Avg. Domain Temp. (Cooling) (°C) | Avg. Domain Temp. (Heating) (°C) |
|---|---|---|---|
| Coarse | 5109 | 21.455 | 21.763 |
| Medium | 16,067 | 21.927 | 21.788 |
| Fine | 68,331 | 21.807 | 21.938 |
| Extremely Fine | 178,948 | 21.751 | 21.888 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, F.; Massarotti, N.; Mauro, A.; Normino, G. Ground Heat Exchangers from Artificial Ground-Freezing Probes for Tunnel Excavations. Energies 2025, 18, 2965. https://doi.org/10.3390/en18112965
Ahmed F, Massarotti N, Mauro A, Normino G. Ground Heat Exchangers from Artificial Ground-Freezing Probes for Tunnel Excavations. Energies. 2025; 18(11):2965. https://doi.org/10.3390/en18112965
Chicago/Turabian StyleAhmed, Fawad, Nicola Massarotti, Alessandro Mauro, and Gennaro Normino. 2025. "Ground Heat Exchangers from Artificial Ground-Freezing Probes for Tunnel Excavations" Energies 18, no. 11: 2965. https://doi.org/10.3390/en18112965
APA StyleAhmed, F., Massarotti, N., Mauro, A., & Normino, G. (2025). Ground Heat Exchangers from Artificial Ground-Freezing Probes for Tunnel Excavations. Energies, 18(11), 2965. https://doi.org/10.3390/en18112965







