Cooperative Control for Multi-Agent Systems with Deception Attack Based on an Attack Detection Mechanism
Abstract
1. Introduction
2. Preliminaries and Problem Formulation
2.1. Information Transmission Among Agents
2.2. Problem Statement
2.3. Control Objectives
- (a)
- The adaptive cooperative security control is achieved under DA;
- (b)
- All signals are bounded in the closed-loop system.
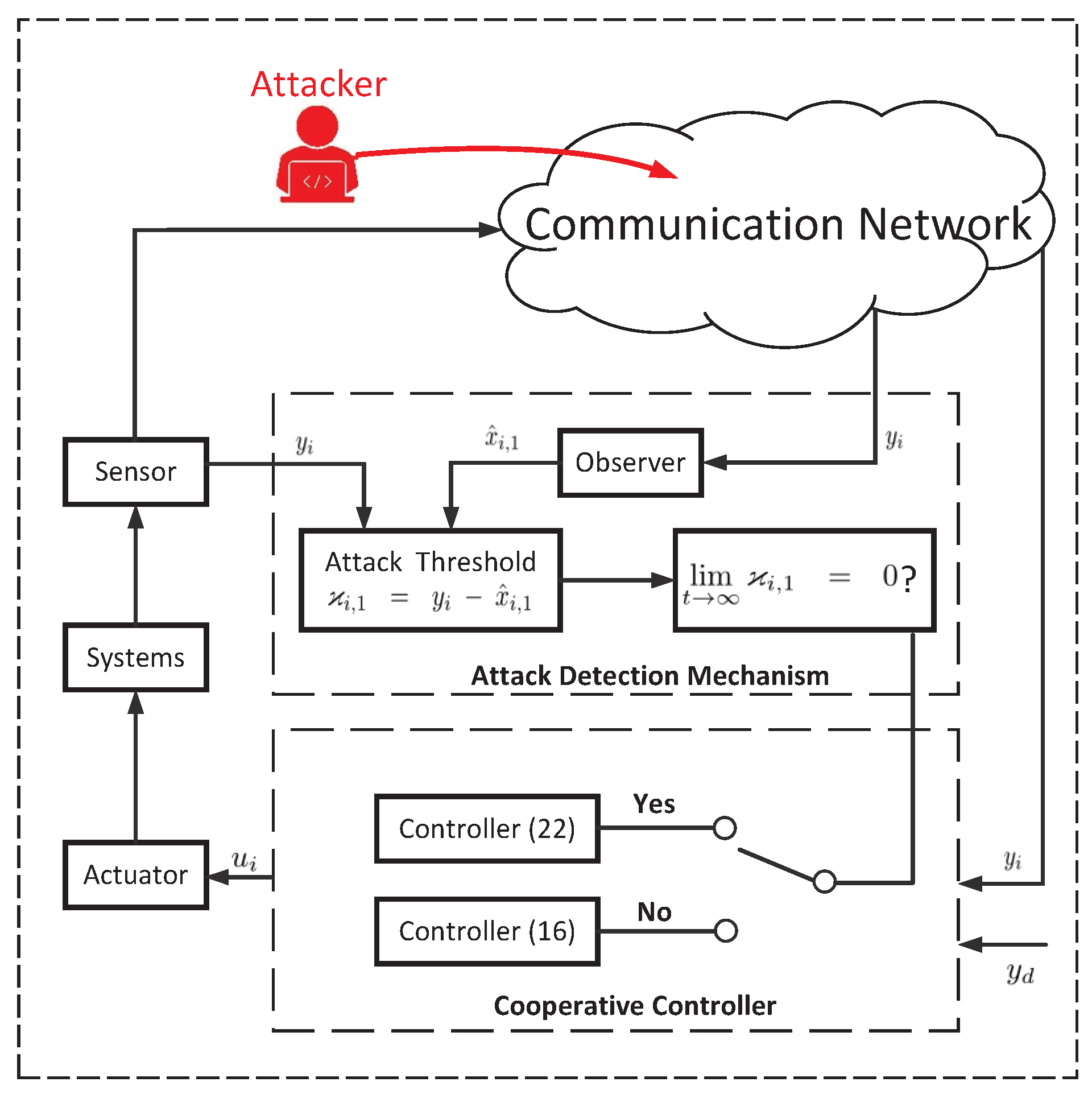
3. Detection Method Design
3.1. Attack Detection Observer Design
3.2. Attack Detection Mechanism
4. Main Results
4.1. Nussbaum Functions Method
4.2. Controller Design and Stability Analysis
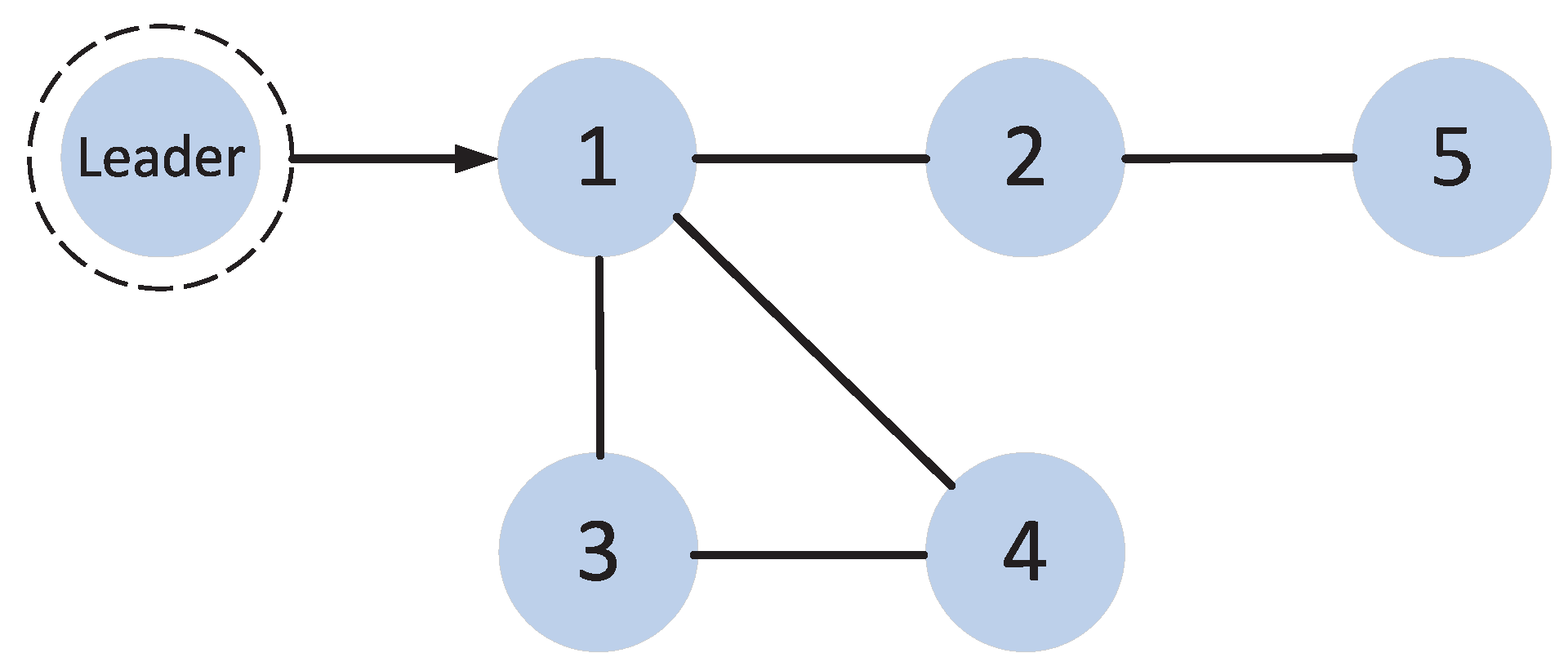
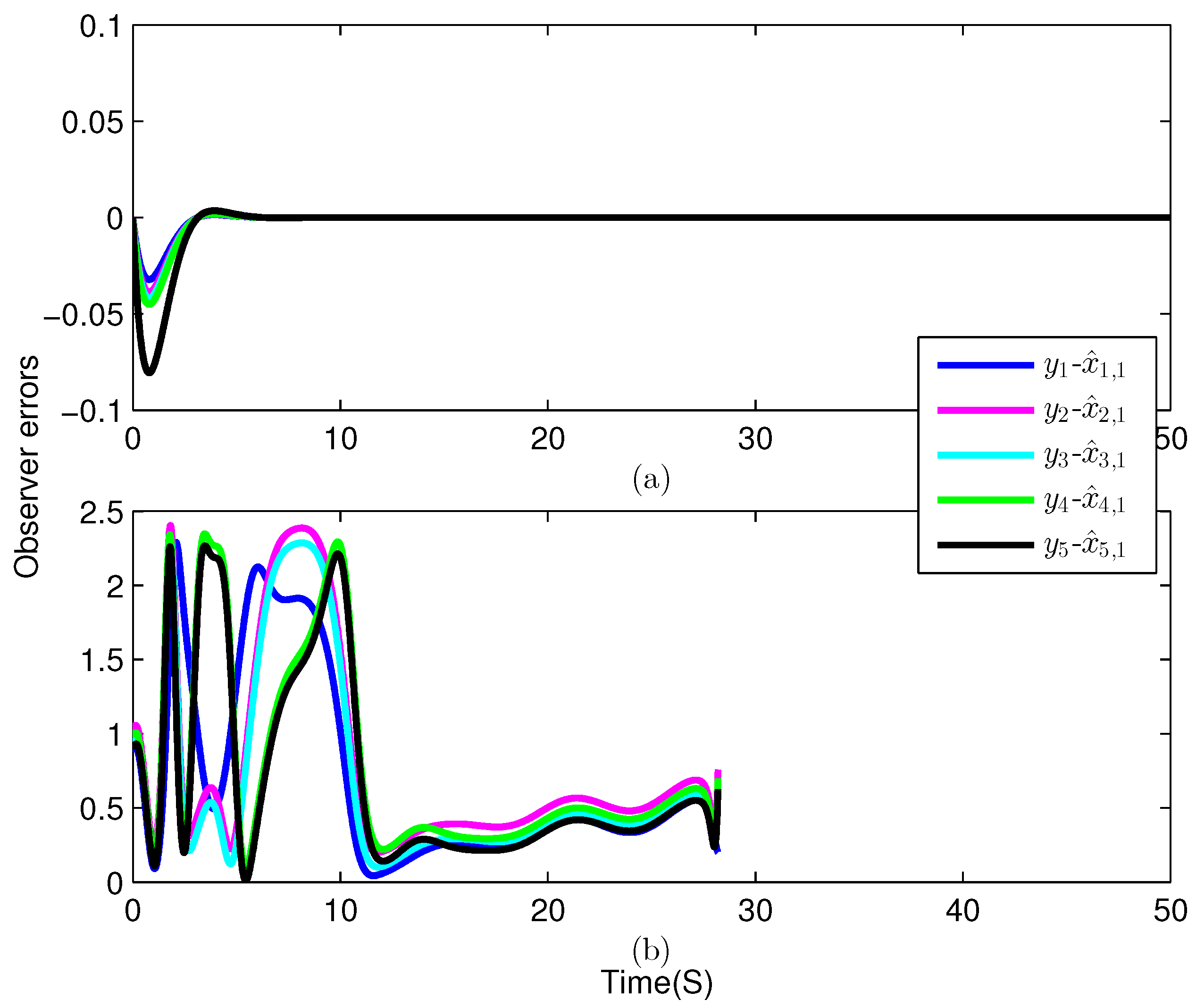
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, F.; Qin, J.; Kang, Y. Multi-agent system based distributed pattern search algorithm for non-convex economic load dispatch in smart grid. IEEE Trans. Power Syst. 2018, 34, 2093–2102. [Google Scholar] [CrossRef]
- Hu, Z.; Su, R.; Wang, R.; Liu, G.; Zhang, K.; Xie, X. Robust distributed load frequency control for multiarea wind energy-dominated microgrids considering phasor measurement unit failures. IEEE Internet Things J. 2024, 11, 23475–23484. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Li, Y.; Gooi, H.B.; Xin, H. Multi-agent based optimal scheduling and trading for multi-microgrids integrated with urban transportation networks. IEEE Trans. Power Syst. 2020, 36, 2197–2210. [Google Scholar] [CrossRef]
- Ogren, P.; Fiorelli, E.; Leonard, N.E. Cooperative control of mobile sensor networks: Adaptive gradient climbing in a distributed environment. IEEE Trans. Autom. Control 2004, 49, 1292–1302. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, K.; Su, R.; Wang, R. Robust cooperative load frequency control for enhancing wind energy integration in multi-area power systems. IEEE Trans. Autom. Sci. Eng. 2025, 22, 1508–1518. [Google Scholar] [CrossRef]
- Liu, G.; Sun, Q.; Su, H.; Wang, M. Adaptive cooperative fault-tolerant control for output-constrained nonlinear multi-agent systems under stochastic fdi attacks. IEEE Trans. Circuits Syst. Regul. 2025, 99, 1–12. [Google Scholar] [CrossRef]
- Liu, G.; Sun, Q.; Su, H.; Hu, Z. Adaptive tracking control for uncertain nonlinear multi-agent systems with partially sensor attack. IEEE Trans. Autom. Sci. Eng. 2025, 22, 6270–6279. [Google Scholar] [CrossRef]
- He, W.; Gao, X.; Zhong, W.; Qian, F. Secure impulsive synchronization control of multi-agent systems under deception attacks. Inf. Sci. 2018, 459, 354–368. [Google Scholar] [CrossRef]
- Hu, Z.; Su, R.; Ling, K.-V.; Guo, Y.; Ma, R. Resilient event-triggered MPC for load frequency regulation with wind turbines under false data injection attacks. IEEE Trans. Autom. Sci. Eng. 2024, 21, 7073–7083. [Google Scholar] [CrossRef]
- Wang, X.; Cao, Y.; Niu, B.; Song, Y. A novel bipartite consensus tracking control for multiagent systems under sensor deception attacks. IEEE Trans. Cybern. 2023, 53, 5984–5993. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, Y.; Zhang, W.; Alsaadi, F.E. Sampled-based consensus for nonlinear multiagent systems with deception attacks: The decoupled method. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 561–573. [Google Scholar] [CrossRef]
- Zhang, D.-W.; Liu, G.-P. Predictive sliding-mode control for networked high-order fully actuated multiagents under random deception attacks. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 484–496. [Google Scholar] [CrossRef]
- Ren, C.-E.; Li, J.; Shi, Z.; Guan, Y.; Chen, C.L.P. Adaptive impulsive consensus of nonlinear multiagent systems with limited bandwidth under uncertain deception attacks. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 4592–4604. [Google Scholar] [CrossRef]
- Aboelwafa, M.M.; Seddik, K.G.; Eldefrawy, M.H.; Gadallah, Y.; Gidlund, M. A machine-learning-based technique for false data injection attacks detection in industrial IoT. IEEE Internet Things J. 2020, 7, 8462–8471. [Google Scholar] [CrossRef]
- Ma, R.; Hu, Z. Deep-Neural-Network-Controlled Safety-Critical Systems with Uncertainty Resilience. IEEE Internet Things J. 2024, 11, 24061–24072. [Google Scholar] [CrossRef]
- Khalaf, M.; Youssef, A.; El-Saadany, E. Joint detection and mitigation of false data injection attacks in agc systems. IEEE Trans. Smart Grid 2018, 10, 4985–4995. [Google Scholar] [CrossRef]
- Lu, A.-Y.; Yang, G.-H. Detection and identification of sparse sensor attacks in cyber physical systems with side information. IEEE Trans. Autom. Control 2022, 9, 5349–5364. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Dörfler, F.; Bullo, F. Attack detection and identification in cyber-physical systems. IEEE Trans. Sutomatic Control 2013, 58, 2715–2729. [Google Scholar] [CrossRef]
- Shoukry, Y.; Nuzzo, P.; Puggelli, A.; Sangiovanni-Vincentelli, A.L.; Seshia, S.A.; Tabuada, P. Secure state estimation for cyber-physical systems under sensor attacks: A satisfiability modulo theory approach. IEEE Trans. Autom. Control 2017, 62, 4917–4932. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H. Secure state estimation against sparse sensor attacks with adaptive switching mechanism. IEEE Trans. Autom. Control 2017, 63, 2596–2603. [Google Scholar] [CrossRef]
- Hespanhol, P.; Porter, M.; Vasudevan, R.; Aswani, A. Sensor switching control under attacks detectable by finite sample dynamic watermarking tests. IEEE Trans. Autom. Control 2020, 66, 4560–4574. [Google Scholar] [CrossRef]
- Ding, D.; Han, Q.-L.; Wang, Z.; Ge, X. Recursive filtering of distributed cyber-physical systems with attack detection. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6466–6476. [Google Scholar] [CrossRef]
- Ma, R.; Hu, Z.; Xu, L.; Wu, L. Distributed Secure Estimation Against Sparse False Data Injection Attacks. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2685–2697. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Luo, W.; Wu, L. Resilient distributed fuzzy load frequency regulation for power systems under cross-layer random denial-of-service attacks. IEEE Trans. Cybern. 2022, 52, 2396–2406. [Google Scholar] [CrossRef]
- Ding, F.; Shan, H.; Han, X.; Jiang, C.; Peng, C.; Liu, J. Security-based resilient triggered output feedback lane keeping control for human–machine cooperative steering intelligent heavy truck under denial-of-service attacks. IEEE Trans. Fuzzy Syst. 2023, 31, 2264–2276. [Google Scholar] [CrossRef]
- Gao, Z.; Song, Y.; Polycarpou, M.M. Adaptive security control using output only for quantized nonlinear systems under irregularly intermittent DoS attacks. IEEE Trans. Cybern. 2024, 54, 6755–6766. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Luo, W.; Wu, L. Intrusion-detector-dependent distributed economic model predictive control for load frequency regulation with PEVs under cyber attacks. IEEE Trans. Circuits Syst. I Regular Pap. 2021, 68, 3857–3868. [Google Scholar] [CrossRef]
- Kazemi, Z.; Safavi, A.A.; Arefi, M.M.; Naseri, F. Finite-time secure dynamic state estimation for cyber–physical systems under unknown inputs and sensor attacks. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 4950–4959. [Google Scholar] [CrossRef]
- Huang, X.; Dong, J. An adaptive secure control scheme for t–s fuzzy systems against simultaneous stealthy sensor and actuator attacks. IEEE Trans. Fuzzy Syst. 2021, 29, 1978–1991. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Wen, G.; Zhai, X.; Peng, Z.; Rahmani, A. Fault-tolerant secure consensus tracking of delayed nonlinear multi-agent systems with deception attacks and uncertain parameters via impulsive control. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 105043. [Google Scholar] [CrossRef]
- Liu, G.; Pan, Y.; Lam, H.-K.; Liang, H. Event-triggered fuzzy adaptive quantized control for nonlinear multi-agent systems in nonaffine pure-feedback form. Fuzzy Sets Syst. 2021, 416, 27–46. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, J.; Wen, C.; Su, X. Distributed control of nonlinear systems with unknown time-varying control coefficients: A novel nussbaum function approach. IEEE Trans. Autom. Control 2023, 68, 4191–4203. [Google Scholar] [CrossRef]
- Shang, Y.; Chen, B.; Lin, C. Consensus tracking control for distributed nonlinear multiagent systems via adaptive neural backstepping approach. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 2436–2444. [Google Scholar] [CrossRef]
- Maaruf, M.; Ahmad, S.; Hamanah, W.; Baraean, A.; Shafiul, A.; Mohammad, A.; Shafiullah, M. Advanced Optimization Methods for Nonlinear Backstepping Controllers for Quadrotor-Slung Load Systems. IEEE Access 2025, 13, 66607–66621. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhang, K.; Hu, Z. Cooperative Control for Multi-Agent Systems with Deception Attack Based on an Attack Detection Mechanism. Energies 2025, 18, 2962. https://doi.org/10.3390/en18112962
Zhang S, Zhang K, Hu Z. Cooperative Control for Multi-Agent Systems with Deception Attack Based on an Attack Detection Mechanism. Energies. 2025; 18(11):2962. https://doi.org/10.3390/en18112962
Chicago/Turabian StyleZhang, Shuhan, Kai Zhang, and Zhijian Hu. 2025. "Cooperative Control for Multi-Agent Systems with Deception Attack Based on an Attack Detection Mechanism" Energies 18, no. 11: 2962. https://doi.org/10.3390/en18112962
APA StyleZhang, S., Zhang, K., & Hu, Z. (2025). Cooperative Control for Multi-Agent Systems with Deception Attack Based on an Attack Detection Mechanism. Energies, 18(11), 2962. https://doi.org/10.3390/en18112962





