Abstract
When large-scale and clustered distributed photovoltaic devices are connected to an active distribution network, the safe and stable operation of the distribution network is seriously threatened, and it is difficult to satisfy the demand for preservation of supply. Multi-agent reinforcement learning provides an idea of zonal balance control, but it is difficult to fully satisfy operation constraints. In this paper, a multi-level control framework based on a local physical model and a multi-agent sequential update algorithm is proposed. The framework generates parameters through an upper-layer reinforcement learning algorithm, which are passed into the objective function of the lower-layer local physical model. The lower-layer local physical model will incorporate safety constraints to determine the power setpoints of the devices; meanwhile, the sequential updating algorithm is integrated into a centralized training–decentralized execution framework, which can increase the efficiency of the sample utilization and promote the monotonic improvement of the strategies. The modified 10 kV IEEE 69-node system is studied as an example, and the results show that the proposed framework can effectively reduce the total operating cost of the active distribution network, while meeting the demand of the system to preserve the supply and ensure the safe and stable operation of the system.
1. Introduction
The increasing shortage of conventional energy sources and the pollution of the environment they cause have contributed to the rapid development of clean energy sources [1]. These energy sources are grid-connected in the form of distributed generation (DG) to realize energy restructuring and environmental protection [2,3,4], such as electric vehicles [5,6,7] and various renewable energy sources. Meanwhile, with the increasing maturity and decreasing cost of PV power generation technology [8], large-scale and clustered distributed photovoltaics (DPV) technology connected to the grid changes the network structure of the system [9], affects the distribution network system’s current distribution, and increases the risk of voltage overruns at power system nodes, which seriously threatens the safe and stable operation of the distribution network, as well as affecting the planning and control of the distribution network [10,11,12].
In response to the above, the concept of an active distribution network (ADN) has been proposed. Compared with traditional distribution networks, an ADN emphasizes that distributed resources in the grid should actively participate in the operation and control of the grid [13,14]. That is to say, in addition to the traditional grid-side equipment, distributed power generation and user-side resources in the grid should also participate in the operation and control of the grid to jointly ensure the supply–demand balance and stable operation of the distribution network system [15]. Ref. [16] pioneers an innovative cyber–physical interdependent restoration scheduling framework that uniquely leverages ad hoc device-to-device communication networks to support post-disaster distribution system recovery, effectively coordinating DERs and scarce emergency repair resources. Ref. [17] develops a widely applicable frequency dynamics-constrained restoration scheduling method for the active distribution system restoration problem dominated by inverter-based DERs, which can enhance the resilience of distribution networks with a high penetration of RESs.
In response to the above problems, traditional regulation methods are mainly carried out in a centralized framework. Based on a powerful central controller that controls the power output of each specific device through a bidirectional communication network, so as to guarantee the balance of supply and demand as well as the safe and stable operation of the distribution grid. Ref. [18] proposes a two-stage robust optimization method for soft open point operation in ADN to maintain the voltage in the desired range and reduce the power loss. Ref. [19] proposes a local voltage control strategy for ADN that converts the original non-convex mixed-integer nonlinear programming (MINLP) model into an efficiently solved mixed-integer linear programming (MILP) model to achieve the stable operation of distribution networks. However, as the scale of heterogeneous distributed energy sources expands and the complexity and volatility of the distribution network increases, centralized algorithms suffer from decreased efficiency and high communication burden, making it difficult to meet the demand for efficient real-time scheduling.
In contrast, distributed frameworks with high reliability, flexibility, and scalability [20,21] are ideal for realizing the secure and guaranteed operation of active distribution networks [22]. Meanwhile, to address the complex dynamic control problem after a large number of distributed PV accesses, deep reinforcement learning (DRL) [23,24,25] has become a research hotspot in the field of distribution grid control in recent years due to its data-driven and autonomous optimization characteristics [26,27,28]. To cope with the centralized control bottleneck of DRL, multi-agent reinforcement learning (MARL) divides the system into many regions managed by multiple agents, each of which makes decisions independently and optimizes collaboratively through communication to achieve distributed control [29,30,31]. Ref. [32] proposes an attention-enhanced multi-agent reinforcement learning method to address the observation perturbation problem of distributed Volt-VAR control by approximating global rewards through a hybrid network based on an attention mechanism. Ref. [33] introduces a soft open point that can be used to regulate the power of the feeder, while dividing the control zone according to the electrical distance, and realizes multi-area soft open point coordinated voltage control based on MARL. Ref. [34] utilizes graph convolutional networks to extract features from graph structure information and distribution network states, and combines with MARL to achieve the safe, stable, and economic operation of the distribution network.
As various heterogeneous resources are connected to the distribution network, the stable operation of the distribution network is not only constrained by its own current balance, but also needs to satisfy the power and capacity constraints of generators, energy storage devices, and distributed photovoltaic and other devices. However, due to the black-box nature of neural networks, this will inevitably lead to the violation of these security constraints during operation [35,36,37]. Nowadays, the methods used to deal with the above problems can be divided into three main categories, as shown in Table 1 below: (1) Penalty function method. The safety constraints are incorporated into the reward function through the Lagrange multiplier method [38,39], which is the most direct but least effective solution, because it cannot completely guarantee the safety of the agents’ actions and will affect the convergence of the strategy. (2) Trust domain method. This converts the security constraints of system operation into a trust domain and restricts the actions of the agents to be generated only within the trust domain [40,41]. This method can ensure the security of the final policy, but it can lead to a policy that is too conservative to be optimal. (3) Security exploration method. This utilizes a priori knowledge from the power system dispatcher to guide the agents to explore in a safe direction and to demonstrate the correct action when the risk in the agents’ action is noticed, thus improving the security of the training process [42,43,44]. However, due to the increasing size of the distribution network, data privacy issues, and the local observability of the environment, it is challenging to obtain correct and sufficient a priori knowledge. Inaccurate knowledge may lead to misdirection of the agents’ actions, which can lead to serious safety issues.

Table 1.
Classification of safety reinforcement learning algorithms.
In this paper, to address the above problem, we propose a local physical model-based control framework, which, unlike the previous MARL algorithm that directly outputs the power of each controllable device through a deep neural network, outputs a set of parameters to form the objective function of the local physical model, and obtains the final output power by solving this optimization model so that it can always satisfy the system operation constraints. In addition, we further propose a hybrid model–data-driven multi-agent algorithm with sequential update to improve the efficiency of sample utilization and the convergence of the policy. A case study of the modified 10 kV IEEE 69-node system demonstrates the feasibility and effectiveness of the proposed framework.
The contributions of this paper are twofold:
- Compared with previous security reinforcement learning algorithms, this paper proposes a multi-agent security reinforcement learning algorithm based on a local physical model, which ensures the security of the policy through strict physical model constraints. The proposed method does not rely on any a priori knowledge and is fully guaranteed to satisfy the security constraints of the system during operation.
- For large-scale and clustered distributed photovoltaic grid connections, we design a training structure based on a centralized training–decentralized execution (CTDE) framework, while incorporating a sequential updating methodology to enhance the effectiveness of the training and to achieve zonal balancing control and efficient power preservation.
The remainder of this article is organized as follows: Section 2 describes the proposed security reinforcement learning algorithm based on local physical models, Section 3 presents a multi-agent sequential update algorithm based on the CTDE framework, Section 4 demonstrates the effectiveness of the method through a case study, and finally Section 5 concludes the full paper.
2. Materials and Methods
2.1. A Secure Scheduling Framework Based on Local Physical Models
In this section, the framework is discussed in depth and the problem formulation and model building process are explained in detail.
2.1.1. Overall Framework and Core Principles
In the previously proposed algorithms, the output power of various distributed resources is usually modeled as the behavior of the agents, i.e., the final device output power will be determined by the output of the DNN. However, it is difficult for the output of DNN to strictly satisfy the physical constraints, and thus these approaches encounter a series of obstacles in distribution network scheduling when considering the physics-based constraints. Therefore, the local physical model-based security scheduling framework proposed in this paper aims to solve the security constraint failure problem of traditional reinforcement learning algorithms in distributed PV high-penetration scenarios.
The specific framework structure is shown in Figure 1. The framework adopts a multi-layer control architecture, in which the upper layer consists of a multi-agent reinforcement learning algorithm and the lower layer consists of a local physical model containing constraints on the safe operation of the device. Aiming to satisfy the demand for supply, etc., each agent in the upper layer receives the local observation value of the environment and outputs a set of parameters, which will be passed to the local physical model in the lower layer to compose its objective function, and finally can be solved to obtain the safety regulation scheme of the equipment, so as to meet the security and supply preservation needs of active distribution networks.
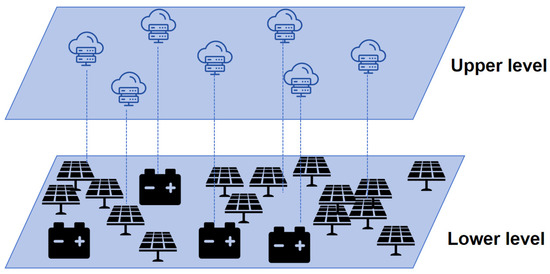
Figure 1.
Multi-level scheduling framework structure.
As shown in Figure 2, the specific data flow of the proposed algorithm is as follows: firstly, the upper-layer DNN accepts historical load, historical tariff, and historical power generation as inputs, and then outputs a set of parameters as a part of the objective function of the lower-layer local physical model, so as to determine the specific output power of the equipment by solving the optimization model; the final operational setpoints must meet the safe operation constraints strictly, so as to ensure the normal operation of the system. The operation setpoints will act in the environment to determine the power setpoints of each distributed resource in the active distribution network to minimize the operation cost of the active distribution network based on the optimal tidal current, which will be used as the reward value. Then, the upper layer of the policy network consisting of DNNs will maximize the cumulative rewards by adjusting its own parameters and finally converge to obtain the optimal policy.
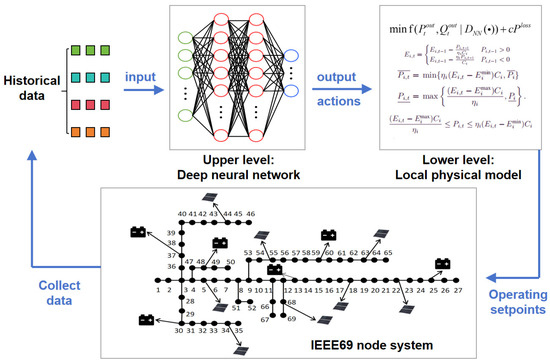
Figure 2.
The data flow of the proposed framework.
2.1.2. Local Optimization Models Based on Physical Models
There are a variety of operational constraints in an active distribution network, the violation of any one of which may lead to equipment damage or even to the collapse of the entire system. It is therefore necessary to ensure that the operational setpoints of each device do not violate its physical-based constraints. However, due to the black-box nature of neural networks, the randomness and unpredictability of their outputs will make it difficult to always satisfy the physical constraints. Therefore, the method proposed in this paper will be able to effectively address this problem as detailed below:
Based on the safe operation constraints of equipment such as energy storage devices, the local optimization model is shown as follows:
subject to:
where denotes the output value of the deep neural network in the upper layer and also the parameters of the objective function of this local optimization model. We use to emphasize that is a function, and what is needed here is the output value of the function. denotes the economic cost coefficient associated with the amount of energy storage losses. and denote the charging and discharging power efficiency coefficients, and denotes the capacity constraint of the energy storage device. Constraint (2) represents the state of charge (SOC) constraints of the energy storage device, constraints (3) to (6) describe the boundaries of the output power of the device, and constraint (7) describes the power loss incurred during the operation of the energy storage device. We modeled the charge and discharge constraints (2) of energy storage devices using the Big M method:
2.1.3. Global ADN Model
The radial DistFlow model [45,46,47] is often used to describe the global ADN operational model as follows:
subject to:
where the objective function (8) of the global ADN model aims to minimize the total operating cost of the active distribution network, where the first summation denotes the cost of active power purchased from the main grid and the second summation denotes the total penalty of system load curtailment. denotes the electricity price at moment . and denote the penalty coefficients for active and reactive load curtailment. denotes the active power purchased from the main grid. and denote the load curtailment of node at moment . Constraints (9) and (10) ensure the balance of active and reactive currents at each moment in the active distribution network. Constraint (11) is used to limit the line capacity. Constraints (12) and (13) indicate that the active and reactive load shedding should not exceed the load demand at that node, respectively, and at the same time should not be less than 0. Constraints (14) and (15) indicate the voltage landings at each node with respect to the line currents, while limiting the node voltage magnitude. Constraints (16) to (20) are boundary constraints and capacity constraints for the distributed PV output power as well as the power purchased from the main grid, respectively.
Based on the operational setpoints of each device obtained after solving the lower-layer local physical model, it can be solved by an existing solver such as the Gurobi solver. The final obtained total operating cost of the active distribution network will be fed back to the upper-layer reinforcement learning algorithm as a reward value.
2.2. A Partition Balancing Control Strategy Based on Sequential Updates
In this section, based on the Proximal Policy Optimization (PPO) algorithm, we further extend it to the multi-agent domain and incorporate the idea of sequential updating as a reinforcement learning algorithm in the upper layer. The detailed structure of the neural network and the training process are as follows.
2.2.1. Dec-POMDP Formulation
Considering that the uncertainty and volatility of the active distribution network is enhanced after the access of clustered and scaled distributed PV technology, such as PV output power, etc., and considering that the Decentralized Partial Observable Markov Decision Process (Dec-POMDP), which can model this uncertainty as local observability, is well suited to deal with this type of problem, the specific modeling process is as follows:
A Dec-POMDP is usually represented by a tuple . Here, is a set of agents, is the state space, and is the products of all agents’ action spaces, known as the joint action space. In this paper, both and are continuous. is a global reward signal shared by all agents. is the state transfer function of the environment, where is the joint action of all agents. is a local observation of the agent . is the discount factor, and is the initial state distribution. At each moment of the decision-making process, each agent receives a local observation , and simultaneously selects an action . These actions form a joint action . These joint actions will be passed on to the localized physical model in the lower level, which ultimately yields the operational setpoints for each device. The operational setpoints lead the system to the next state according to the state transfer function. The environment feeds back a global reward signal . Each agent has a localized action-observation history .
In this paper, we take the historical loadings, the historical electricity prices, the historical PV output power, and the charging state of the energy storage devices as states. Each agent can only access local observations about individual nodes within its own partition:
where denotes the group of nodes accessing the distributed photovoltaic devices and denotes the group of nodes accessing the energy storage device.
Based on the given local observations, each agent outputs the following action:
After the operational setpoints obtained from solving the local physical model at the lower level interact with the environment, the environment will feed back the global reward value, which consists of the total operational cost of the active distribution network, so that each agent will continuously update its own parameters to jointly contribute to the reduction in the system’s operational cost.
2.2.2. Sequential Update Strategy
Next, we describe the sequential update strategy in more detail.
First, we decompose the multi-agent system into multiple groups. Then, let denote a sequentially ordered subset of agents, and let denote its complement. Let be a joint policy, and for any joint observation and joint action , the advantage function can be decomposed as [48]:
For two disjoint subsets of agents, and , the multi-agent advantage function of with respect to is defined as [48]:
Based on Equation (23), the joint advantage function is decomposed into the sum of the local advantage functions of the individual agents, thus making the evaluation of each agent’s contribution to the global performance quantifiable. Based on this, the policy of the current m-th agent can be updated based on the m − 1 agents that have been previously updated. Based on the PPO clipping [49], the agents aim to de-maximize the expected joint return, defined as:
where the parameter is the clipping range. Therefore, the optimal policy of each agent with monotonical improvement is obtained through the idea of sequential updating as follows:
The specific framework is shown in Figure 3. Based on the above sequential updating idea and existing local physical models, we propose a centralized training–decentralized execution (CTDE) multi-level control framework for the safe and efficient regulation of the active distribution network with a large number of distributed photovoltaic (PV) devices accessing it on this basis. For the CTDE framework, it is only necessary to perform centralized training through a global critic network during the training process. Therefore, each agent only needs to transmit its own information to the operations center and does not require communication between agents. During execution, each agent makes decisions based solely on its own local observations, which includes historical data from the operations center, and there is no communication or interaction between agents.
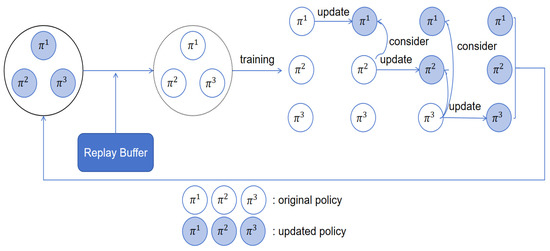
Figure 3.
Sequential update framework. Each agent considers the updated policy information when updating its own policy parameters.
As shown in Figure 4, each agent interacts with the environment to receive local observations from the environment and update its own policy parameters, while the centralized critic is trained using joint observations to ensure global coordination. During execution, each agent independently makes decisions based on local observations and its own policy network to form a joint action that reduces the communication burden and achieves partitioned balanced control.
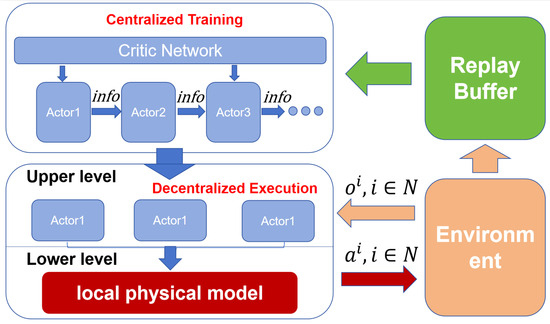
Figure 4.
CTDE framework based on local physical models and sequential updating.
Therefore, the proposed hybrid model-data driven approach is shown in Algorithm 1 and Figure 5. The idea of sequential updating promotes the agent policy update to allow further enhancement on the existing foundation, which can effectively guarantee the monotonic improvement of the policy, while the local physical model can ensure that the operational setpoints of the device can fully satisfy the security constraints, avoiding the uncertainty damage caused by the black-box nature of neural networks.
| Algorithm 1 The Proposed Hybrid Model–Data-Driven Approach with MAPPO |
| 1: Initialize replay buffer , Number of episode , Episode length . 2: do 3:’ do 4: do 5: . 6: end for 7: . 8: Solve the local model and obtain operation set-points. 9: and record them in buffer . 10: end for 11: Sample a mini-batch from . 12: do 13: based on Equations (25) and (26). 14: end for 15: by using MSE: 16: 17: end for |
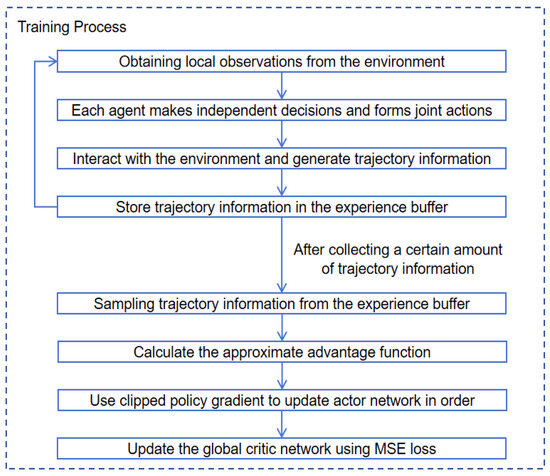
Figure 5.
The flowchart of the model training.
3. Results
In this section, we evaluate the performance of the proposed framework. The details of the corresponding simulation setup are first presented. Then, the secure supply-preserving operation of the active distribution network is realized by the proposed algorithm in an adapted IEEE 69-node system. Finally, we compare the proposed algorithm with the existing MADDPG algorithm and the penalty function-based multi-agent safe reinforcement learning algorithm to illustrate the advantages of the algorithm.
3.1. Simulation Setup
The proposed framework was evaluated in the modified IEEE 69-node system shown in Figure 6, which contains a large number of distributed photovoltaic as well as energy storage devices. The maximum generation capacity of PVs connected to nodes 5, 34, 44, 55, 63, 18, 22, and 68 is 60 KWh, 50 kWh, 60 kWh, 30 kWh, 40 kWh, 50 kWh, 50 kWh, and 50 MWh. The charge and discharge factor and maximum charge and discharge power for all energy storage devices are 0.99 and 20 kW, respectively. The load curve characteristics were obtained from the State Grid Jibei Electric Power Company Limited. Assuming that the direction of power injection into the nodes is positive, the total operating cost is considered as a reward signal and the metrics were used for evaluating the effectiveness of different algorithms. The local physical model and the global active distribution network model were solved by the Gurobi solver. Fully connected networks were chosen for both the global critic network and the policy network, and ReLU was used as the activation function. Each network has two hidden layers with 128 neurons per layer and was trained on Pytorch 2.4.1 in Python 3.8.19. The specific parameters of the algorithm are shown in Table 2 below.
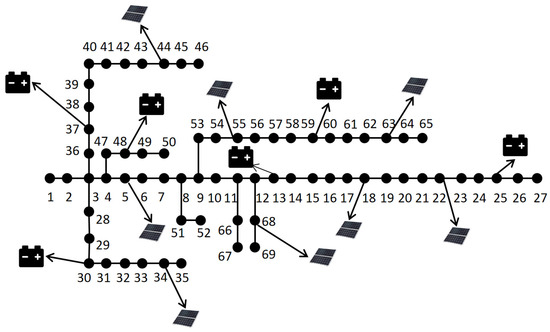
Figure 6.
A distribution network modified from the IEEE 69-node system.

Table 2.
Parameterization of the proposed algorithm.
3.2. Performance Evaluation of the Proposed Algorithm
After applying the proposed framework in the adapted IEEE 69-node system, the final scheduling is shown in Figure 7 below:
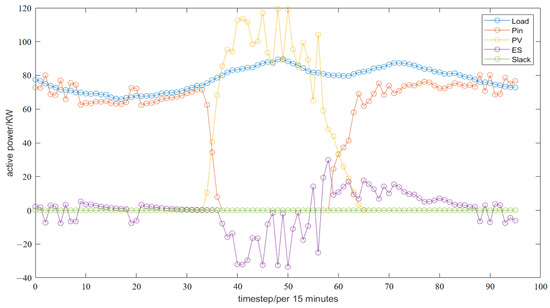
Figure 7.
Scheduling curves for distributed resources over the course of a day. The output of all energy storage devices is aggregated into a single entity, and the same applies to distributed photovoltaic power generation.
In the earlier time period, due to the weak intensity of solar radiation, the PV power generation is almost 0. At the same time, due to the low initial SOC of the storage device, the supply and demand balance at this time mainly relies on the power purchased from the main grid, while with the advancement of time, the PV power generation gradually rises and becomes the main contributor to the supply and demand balance, while the remaining PV power generation in excess of the load demand will be deposited into the storage device, realizing the distributed efficient utilization of PV. As the intensity of solar radiation diminishes and the amount of photovoltaic power generated diminishes, energy storage devices will inject energy into the grid to reduce the pressure on the supply and demand balance. Ultimately, the load curtailment at each node remains zero at each time step, which satisfies the active distribution network’s demand for preservation of supply.
Meanwhile, due to the volatility and uncertainty brought by a large number of distributed PV accesses, it is difficult to always satisfy the safe operation constraints in active distribution networks, and voltage overruns have become a common problem in active distribution networks. By integrating with local physical models, our proposed algorithm can effectively ensure that the safe operation constraints in active distribution networks are not violated at all times. As shown in Figure 8, the per unit value of voltage of each node is always maintained at [0.95, 1.05].
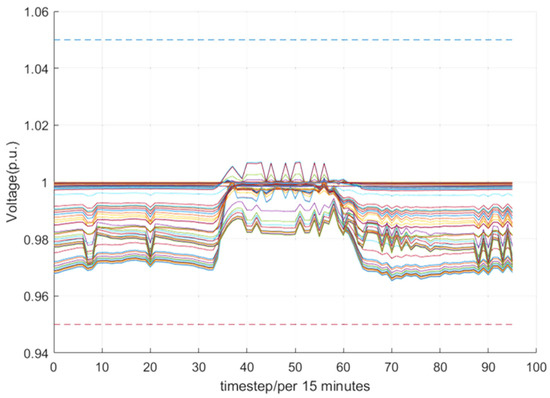
Figure 8.
The per unit value of voltage of each node in the active distribution network at each moment. The colored lines represent the voltage curves of different nodes, while dashed lines indicate the safe voltage boundaries.
3.3. Comparison with Existing Algorithms
The proposed framework is further compared with the MADDPG algorithm, which incorporates a local physical model, and the penalty function method, which incorporates sequential updating. The MADDPG algorithm combines a policy gradient approach with Q-learning, a value function approximation method, to solve complex decision problems by learning a deterministic policy. The penalty function method transforms a constrained optimization problem into an unconstrained problem by adding a penalty term to reflect the degree of violation of the constraints. Figure 9 shows the training process of these two methods, the proposed algorithm, and the optimal benchmarks.
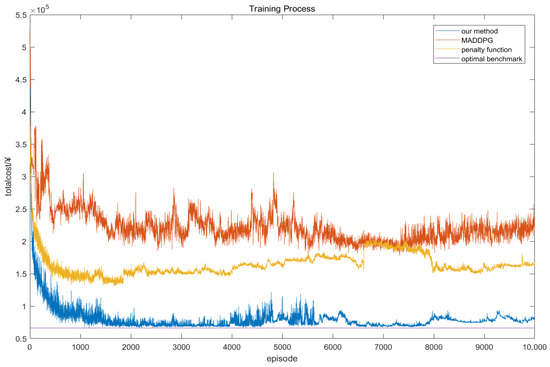
Figure 9.
The comparison of training process between the proposed approach and other benchmarks.
Specifically, we trained each of the three algorithms with 10,000 training cycles and obtained the benchmark values through the model-based optimal benchmarking algorithm. It can be observed that for the proposed algorithms in this paper, the total operating cost of the active distribution network decreases dramatically in the first 100 cycles, indicating that the proposed algorithms are able to learn the system dynamics in a short period of time. In the subsequent training cycles, the decrease in the total operating cost of the system gradually becomes slower until it basically reaches convergence around the 500th cycle. The final total operating cost is CNY 77,241.9062.
Compared with the MADDPG algorithm, the total operating cost of the proposed algorithm decreases faster and can converge to a lower operating cost in earlier cycles; meanwhile, the corresponding curve of the MADDPG algorithm has large fluctuations, while the algorithm proposed in this paper reaches a relatively stable result after a certain number of training cycles, which indicates that the sequential updating framework is able to effectively facilitate the monotonic improvement of the strategies, and at the same time, the convergence of the strategy is guaranteed. The final total operating cost of the MADDPG algorithm is CNY 222,106.1435. The cost of the proposed algorithm is reduced by 65.22% compared to the MADDPG algorithm.
For the penalty function method, the fact that it requires a trade-off between the importance of the distribution network operating costs and the penalty term makes it difficult to balance both. When the strategy wants to reduce the distribution network operating costs more, it will likely lead to the violation of the operating constraints, while when the strategy wants to satisfy the operating constraints, it may also lead to an increase in load curtailment, which will increase the operating costs. The final total operating cost of the penalty function method is CNY 164,154.3329. The cost of the proposed algorithm is reduced by 52.95% compared to the penalty function method.
The result of the optimal benchmark is CNY 66,268.4955. The optimal benchmark is achieved by solving the global ADN model containing energy storage devices and distributed PV directly through Gurobi, without an iterative process or a decentralized framework. The closer our proposed framework is to the optimal benchmark, the better the algorithm performs. The difference between our method and the optimal benchmark is less than 14.20%, which indicates its ability to approximate the optimal solution.
In addition, we use the load shedding of each time step as a metric to judge the fulfillment of the supply preservation demand. The specific results of these three algorithms for the system’s supply preservation demand after 10,000 cycles of training are shown in Figure 10 and Figure 11.
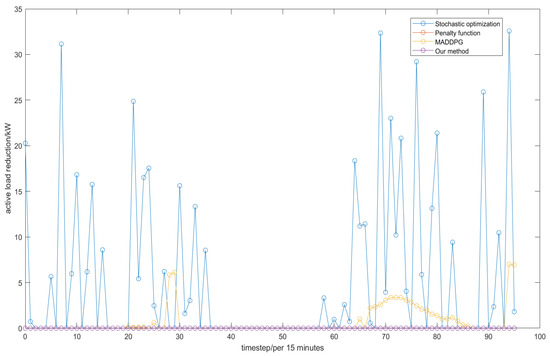
Figure 10.
The comparison of active load shedding between the proposed approach and other benchmarks.
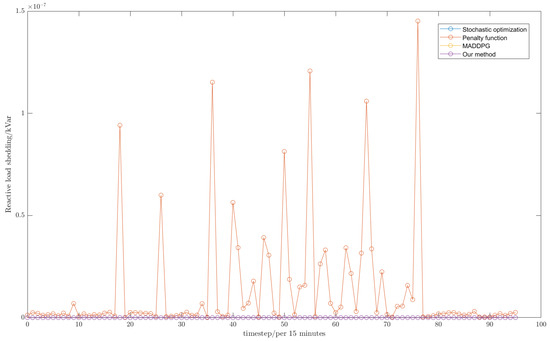
Figure 11.
The comparison of reactive load shedding between the proposed approach and other benchmarks. The blue line and yellow line overlap with the purple line.
From the above figure, it can be seen that only through stochastic optimization will the active load shedding at each time step become very large, reaching a maximum of 32.5727 kW, and making it difficult to meet the demand of the system to maintain the supply. After optimization through the MADDPG algorithm, the final active load curtailment achieves a significant decrease. It remains 0 in most of the time steps and its maximum load shedding is 7.0008 kW. The penalty function method is better than the MADDPG algorithm in terms of active load shedding, but it is worse in terms of reactive load shedding. This is because the circulation of power between nodes leads to a drop in the node voltage, while the penalty function method converts the node voltage constraint into a penalty function, resulting in the upper limit of the power circulation between nodes no longer being affected by the node voltage constraint. Thus, its load curtailment is almost maintained at 0, but it is difficult to fully satisfy the node voltage constraint in the end. Meanwhile, the penalty function method needs to balance the weights between the load curtailment and the penalty function, resulting in its inability to ensure that the active and reactive load curtailment is completely 0 in order to reduce the violation of the voltage constraint. With both active and reactive load shedding, our proposed algorithms are able to make the final result completely 0, which can efficiently satisfy the system’s demand of preserving the supply.
4. Discussion
The large-scale access of distributed photovoltaic technology is reshaping the shape and operation modes of distribution grids, while traditional control strategies have faced difficulty in coping with the volatility and uncertainty challenges it brings. While multi-agent reinforcement learning is well suited for solving high-dimensional nonlinear complex problems and provides new ideas for active distribution network regulation and control, it still has certain problems in security constraint handling, etc., due to the black-box nature of neural networks.
The partitioned balancing control strategy proposed in this paper provides a feasible solution to the above problem through multi-level control, sequential updating approach and local physical model-based security control architecture. Specifically, parameters are generated by an upper-level reinforcement learning algorithm to form the objective function of the lower-level local physical model, which is then combined with safety constraints to solve for the device output power, thus ensuring that the system always satisfies the operational constraints. In addition, incorporating the sequential update algorithm into a centralized training decentralized execution framework facilitates efficient sample utilization and promotes monotonic improvement of the policy. The modified IEEE 69-node system case study verifies that the strategy can effectively reduce the total operating cost of the active distribution network and realize the safe and secure operation of the system.
Subsequently, we will focus on researching the real-time optimization of algorithms to enhance the system’s ability to respond to rapid changes, and at the same time, we will work on attenuating the burden of global communication to further enhance autonomous coordination capability within the sub-district, and to promote the development of the active distribution network towards intelligence and security.
5. Conclusions
By applying the framework proposed in this paper to the modified IEEE 69-node system, we can achieve the economic operation of an ADN while ensuring the safety and feasibility of physical equipment operations such as energy storage. This ultimately keeps the load shedding at 0, meeting the supply guarantee requirements.
At the same time, we conducted a comparative analysis using the existing MADDPG algorithm and penalty function method. Specifically, the final ADN operating cost of the algorithm we propose is CNY 77,241.9062, which is a 65.22% improvement over the MADDPG algorithm’s CNY 222,106.1435 and a 52.95% improvement over the penalty function method’s CNY 164,154.3329. It is only 14.21% lower than the optimal benchmark of CNY 66,268.4955.
In addition, we also studied changes in load shedding. For the framework proposed in this paper, the final ADN load shedding always remains at 0. For the MADDPG algorithm, it remains 0 in most of the time steps and its maximum load shedding is 7.0008 kW. For the penalty function method, it is better than the MADDPG algorithm in terms of active load shedding, but it is worse in terms of reactive load shedding.
Author Contributions
Conceptualization, B.Z. and Y.L.; methodology, W.W.; software, W.Q. and R.Z.; validation, B.Z., Z.J. and T.Q.; formal analysis, B.Z. and W.W.; investigation, Y.L. and Q.H.; resources, W.Q., R.Z. and Z.J.; data curation, B.Z. and Y.L.; writing—original draft preparation, B.Z.; writing—review and editing, Y.L., W.W. and T.Q.; visualization, R.Z. and Z.J.; supervision, Y.L. and T.Q.; project administration, W.Q. and Q.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the science and technology project of State Grid Jibei Electric Power Company Limited, grant number 520101240002.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors Wei Wang, Tao Qian, and Qinran Hu declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. Bingxu Zhai, Yuanzhuo Li, Wei Qiu, Rui Zhang, and Zhilin Jiang are employed by the State Grid Jibei Electric Power Company Limited.
Abbreviations
The following abbreviations are used in this manuscript:
| DG | Distributed generation |
| DPV | Distributed photovoltaics |
| ADN | Active distribution network |
| MINLP | Mixed-integer nonlinear programming |
| MILP | Mixed-integer linear programming |
| DRL | Deep reinforcement learning |
| MARL | Multi-agent reinforcement learning |
| CTDE | Centralized training decentralized execution |
| DNN | Deep neural network |
| SOC | State of charge |
| MADDPG | Multi-agent deep deterministic policy gradient |
| PPO | Proximal policy optimization |
| ReLU | Rectified linear unit |
References
- Ma, Z. Form and Development Trend of Future Distribution System; China Electric Power Research Institute: Beijing, China, 2015. [Google Scholar]
- Lopes, J.A.P.; Hatziargyriou, N.; Mutale, J.; Djapic, P.; Jenkins, N. Integrating distributed generation into electric power systems: A review of drivers, challenges and opportunities. Electr. Power Syst. Res. 2007, 77, 1189–1203. [Google Scholar] [CrossRef]
- Qian, T.; Fang, M.; Hu, Q.; Shao, C.; Zheng, J. V2Sim: An Open-Source Microscopic V2G Simulation Platform in Urban Power and Transportation Network. IEEE Trans. Smart Grid 2025, 1. [Google Scholar] [CrossRef]
- Qian, T.; Liang, Z.; Shao, C.; Guo, Z.; Hu, Q.; Wu, Z. Unsupervised learning for efficiently distributing EVs charging loads and traffic flows in coupled power and transportation systems. Appl. Energy 2025, 377, 124476. [Google Scholar] [CrossRef]
- Liang, Z.; Qian, T.; Korkali, M.; Glatt, R.; Hu, Q. A Vehicle-to-Grid planning framework incorporating electric vehicle user equilibrium and distribution network flexibility enhancement. Appl. Energy 2024, 376, 124231. [Google Scholar] [CrossRef]
- Shang, Y.; Li, D.; Li, Y.; Li, S. Explainable spatiotemporal multi-task learning for electric vehicle charging demand prediction. Appl. Energy 2025, 384, 125460. [Google Scholar] [CrossRef]
- Xie, S.; Wu, Q.; Zhang, M.; Guo, Y. Coordinated Energy Pricing for Multi-Energy Networks Considering Hybrid Hydrogen-Electric Vehicle Mobility. IEEE Trans. Power Syst. 2024, 39, 7304–7317. [Google Scholar] [CrossRef]
- Xin-gang, Z.; Zhen, W. Technology, cost, economic performance of distributed photovoltaic industry in China. Renew. Sustain. Energy Rev. 2019, 110, 53–64. [Google Scholar] [CrossRef]
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galvan, E.; PortilloGuisado, R.C.; Prats, M.A.M.; Leon, J.I.; Moreno-Alfonso, N. Power-Electronic Systems for the Grid Integration of Renewable Energy Sources: A Survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
- Hu, Z.; Su, R.; Veerasamy, V.; Huang, L.; Ma, R. Resilient Frequency Regulation for Microgrids Under Phasor Measurement Unit Faults and Communication Intermittency. IEEE Trans. Ind. Inform. 2025, 21, 1941–1949. [Google Scholar] [CrossRef]
- Braun, M.; Stetz, T.; Bründlinger, R.; Mayr, C.; Ogimoto, K.; Hatta, H.; Kobayashi, H.; Kroposki, B.; Mather, B.; Coddington, M.; et al. Is the distribution grid ready to accept large-scale photovoltaic deployment? State of the art, progress, and future prospects. Prog. Photovolt. Res. Appl. 2012, 20, 681–697. [Google Scholar] [CrossRef]
- Yan, G.; Wang, Q.; Zhang, H.; Wang, L.; Wang, L.; Liao, C. Review on the Evaluation and Improvement Measures of the Carrying Capacity of Distributed Power Supply and Electric Vehicles Connected to the Grid. Energies 2024, 17, 4407. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, Z.; Liu, X.; Yang, L.; Dan, Y.; Zhu, Y.; Ding, Y.; Wang, Q. Bi-level Coordinated Planning of Active Distribution Network Considering Demand Response Resources and Severely Restricted Scenarios. J. Mod. Power Syst. Clean Energy 2021, 9, 1088–1100. [Google Scholar] [CrossRef]
- Huang, S.; Han, D.; Pang, J.Z.F.; Chen, Y. Optimal Real-Time Bidding Strategy for EV Aggregators in Wholesale Electricity Markets. IEEE Trans. Intell. Transp. Syst. 2025, 26, 5538–5551. [Google Scholar] [CrossRef]
- Xie, S.; Wu, Q.; Hatziargyriou, N.D.; Zhang, M.; Zhang, Y.; Xu, Y. Collaborative Pricing in a Power-Transportation Coupled Network: A Variational Inequality Approach. IEEE Trans. Power Syst. 2023, 38, 783–795. [Google Scholar] [CrossRef]
- Wang, C.; Yan, M.; Pang, K.; Wen, F.; Teng, F. Cyber-Physical Interdependent Restoration Scheduling for Active Distribution Network via Ad Hoc Wireless Communication. IEEE Trans. Smart Grid 2023, 14, 3413–3426. [Google Scholar] [CrossRef]
- Wang, C.; Lin, W.; Wang, G.; Shahidehpour, M.; Liang, Z.; Zhang, W.; Chung, C.Y. Frequency-Constrained Optimal Restoration Scheduling in Active Distribution Networks With Dynamic Boundaries for Networked Microgrids. IEEE Trans. Power Syst. 2025, 40, 2061–2077. [Google Scholar] [CrossRef]
- Ji, H.; Wang, C.; Li, P.; Ding, F.; Wu, J. Robust Operation of Soft Open Points in Active Distribution Networks With High Penetration of Photovoltaic Integration. IEEE Trans. Sustain. Energy 2019, 10, 280–289. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.; Li, P.; Wang, C.; Ji, H.; Ge, L.; Song, Y. Local voltage control strategy of active distribution network with PV reactive power optimization. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Li, X.; Hu, C.; Luo, S.; Lu, H.; Piao, Z.; Jing, L. Distributed Hybrid-Triggered Observer-Based Secondary Control of Multi-Bus DC Microgrids Over Directed Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 2467–2480. [Google Scholar] [CrossRef]
- Qi, J.; Ying, A.; Zhang, B.; Zhou, D.; Weng, G. Distributed Frequency Regulation Method for Power Grids Considering the Delayed Response of Virtual Power Plants. Energies 2025, 18, 1361. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Y.; Pang, K.; Shahidehpour, M.; Wang, Q.; Wang, G.; Wen, F. Imposing Fine-Grained Synthetic Frequency Response Rate Constraints for IBR-Rich Distribution System Restoration. IEEE Trans. Power Syst. 2025, 40, 2799–2802. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, G.; Sadeghi, A.; Giannakis, G.B.; Sun, J. Two-Timescale Voltage Control in Distribution Grids Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2020, 11, 2313–2323. [Google Scholar] [CrossRef]
- Chen, X.; Qu, G.; Tang, Y.; Low, S.; Li, N. Reinforcement Learning for Selective Key Applications in Power Systems: Recent Advances and Future Challenges. IEEE Trans. Smart Grid 2022, 13, 2935–2958. [Google Scholar] [CrossRef]
- Qian, T.; Liang, Z.; Shao, C.; Zhang, H.; Hu, Q.; Wu, Z. Offline DRL for Price-Based Demand Response: Learning From Suboptimal Data and Beyond. IEEE Trans. Smart Grid 2024, 15, 4618–4635. [Google Scholar] [CrossRef]
- Qian, T.; Ming, W.; Shao, C.; Hu, Q.; Wang, X.; Wu, J.; Wu, Z. An Edge Intelligence-Based Framework for Online Scheduling of Soft Open Points With Energy Storage. IEEE Trans. Smart Grid 2024, 15, 2934–2945. [Google Scholar] [CrossRef]
- Qian, T.; Liang, Z.; Chen, S.; Hu, Q.; Wu, Z. A Tri-Level Demand Response Framework for EVCS Flexibility Enhancement in Coupled Power and Transportation Networks. IEEE Trans. Smart Grid 2025, 16, 598–611. [Google Scholar] [CrossRef]
- Cao, D.; Zhao, J.; Hu, J.; Pei, Y.; Huang, Q.; Chen, Z.; Hu, W. Physics-Informed Graphical Representation-Enabled Deep Reinforcement Learning for Robust Distribution System Voltage Control. IEEE Trans. Smart Grid 2024, 15, 233–246. [Google Scholar] [CrossRef]
- Jiang, C.; Lin, Z.; Liu, C.; Chen, F.; Shao, Z. MADDPG-Based Active Distribution Network Dynamic Reconfiguration with Renewable Energy. Prot. Control. Mod. Power Syst. 2024, 9, 143–155. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, J. Two-Stage Volt/Var Control in Active Distribution Networks With Multi-Agent Deep Reinforcement Learning Method. IEEE Trans. Smart Grid 2021, 12, 2903–2912. [Google Scholar] [CrossRef]
- Wang, T.; Ma, S.; Tang, Z.; Xiang, T.; Mu, C.; Jin, Y. A Multi-Agent Reinforcement Learning Method for Cooperative Secondary Voltage Control of Microgrids. Energies 2023, 16, 5653. [Google Scholar] [CrossRef]
- Yang, X.; Liu, H.; Wu, W. Attention-Enhanced Multi-Agent Reinforcement Learning Against Observation Perturbations for Distributed Volt-VAR Control. IEEE Trans. Smart Grid 2024, 15, 5761–5772. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, F.; Yan, D.; Qian, G.; Li, J.; Shi, X.; Xu, J.; Wei, M.; Ji, H.; Yu, H. Multi-Agent Deep Reinforcement Learning-Based Distributed Voltage Control of Flexible Distribution Networks with Soft Open Points. Energies 2024, 17, 5244. [Google Scholar] [CrossRef]
- Zhan, H.; Jiang, C.; Lin, Z. A Novel Graph Reinforcement Learning-Based Approach for Dynamic Reconfiguration of Active Distribution Networks with Integrated Renewable Energy. Energies 2024, 17, 6311. [Google Scholar] [CrossRef]
- Zhang, Q.; Dehghanpour, K.; Wang, Z.; Qiu, F.; Zhao, D. Multi-Agent Safe Policy Learning for Power Management of Networked Microgrids. IEEE Trans. Smart Grid 2021, 12, 1048–1062. [Google Scholar] [CrossRef]
- Zhang, J.; Sang, L.; Xu, Y.; Sun, H. Networked Multiagent-Based Safe Reinforcement Learning for Low-Carbon Demand Management in Distribution Networks. IEEE Trans. Sustain. Energy 2024, 15, 1528–1545. [Google Scholar] [CrossRef]
- Li, H.; He, H. Learning to Operate Distribution Networks With Safe Deep Reinforcement Learning. IEEE Trans. Smart Grid 2022, 13, 1860–1872. [Google Scholar] [CrossRef]
- Bhatnagar, S.; Lakshmanan, K. An Online Actor–Critic Algorithm with Function Approximation for Constrained Markov Decision Processes. J. Optim. Theory Appl. 2012, 153, 688–708. [Google Scholar] [CrossRef]
- Hua, D.; Peng, F.; Liu, S.; Lin, Q.; Fan, J.; Li, Q. Coordinated Volt/VAR Control in Distribution Networks Considering Demand Response via Safe Deep Reinforcement Learning. Energies 2025, 18, 333. [Google Scholar] [CrossRef]
- Kim, D.; Oh, S. TRC: Trust Region Conditional Value at Risk for Safe Reinforcement Learning. IEEE Robot. Autom. Lett. 2022, 7, 2621–2628. [Google Scholar] [CrossRef]
- Zhang, Q.; Leng, S.; Ma, X.; Liu, Q.; Wang, X.; Liang, B.; Liu, Y.; Yang, J. CVaR-Constrained Policy Optimization for Safe Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 830–841. [Google Scholar] [CrossRef]
- Chen, P.; Liu, S.; Wang, X.; Kamwa, I. Physics-Shielded Multi-Agent Deep Reinforcement Learning for Safe Active Voltage Control With Photovoltaic/Battery Energy Storage Systems. IEEE Trans. Smart Grid 2023, 14, 2656–2667. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, S.; Wang, L.; Lu, Z.; Wu, C.; Wen, X.; Shou, G. Autonomous Driving via Knowledge-Enhanced Safe Reinforcement Learning. IEEE Trans. Intell. Veh. 2024, 1–14. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, J.; Qiu, J.; Liang, G.; Dong, Z.Y. Cooperative Wind Farm Control With Deep Reinforcement Learning and Knowledge-Assisted Learning. IEEE Trans. Ind. Inform. 2020, 16, 6912–6921. [Google Scholar] [CrossRef]
- Lin, H.; Shen, X.; Guo, Y.; Ding, T.; Sun, H. A linear Distflow model considering line shunts for fast calculation and voltage control of power distribution systems. Appl. Energy 2024, 357, 122467. [Google Scholar] [CrossRef]
- Neumann, F.; Hagenmeyer, V.; Brown, T. Assessments of linear power flow and transmission loss approximations in coordinated capacity expansion problems. Appl. Energy 2022, 314, 118859. [Google Scholar] [CrossRef]
- Song, T.; Han, X.; Zhang, B. Multi-Time-Scale Optimal Scheduling in Active Distribution Network with Voltage Stability Constraints. Energies 2021, 14, 7107. [Google Scholar] [CrossRef]
- Kuba, J.; Feng, X.; Ding, S.; Dong, H.; Wang, J.; Yang, Y. Heterogeneous-Agent Mirror Learning: A Continuum of Solutions to Cooperative MARL. arXiv 2022, arXiv:2208.01682. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Wang, Y.; Bayen, A.M.; Wu, Y. The Surprising Effectiveness of MAPPO in Cooperative, Multi-Agent Games. arXiv 2021, arXiv:2103.01955. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).