Numerical Investigation and Optimization of Transpiration Cooling Plate Structures with Combined Particle Diameter
Abstract
1. Introduction
2. Numerical Modeling and Validation
2.1. Geometric Models and Mathematical Models
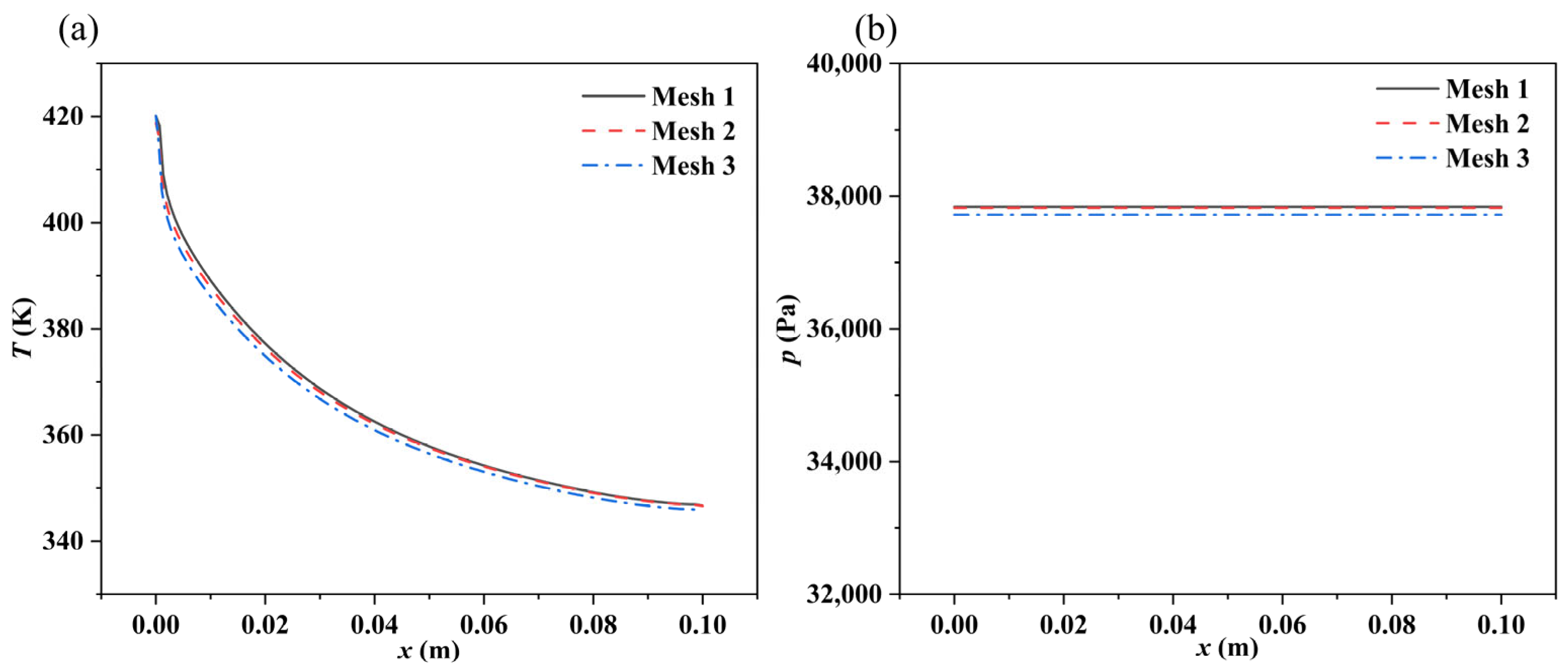
2.2. Mesh Independence Verification
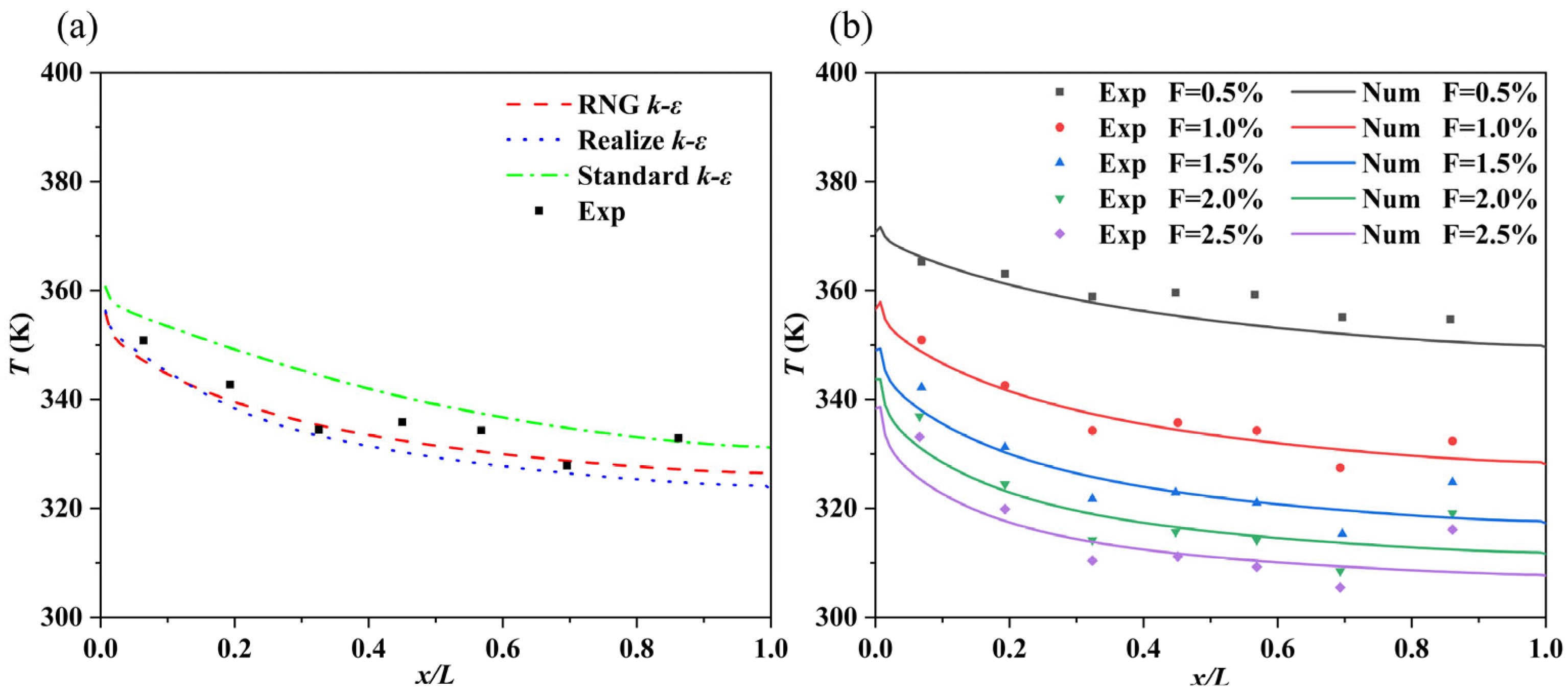
2.3. Numerical Method Validation
3. Analysis of Results and Discussion
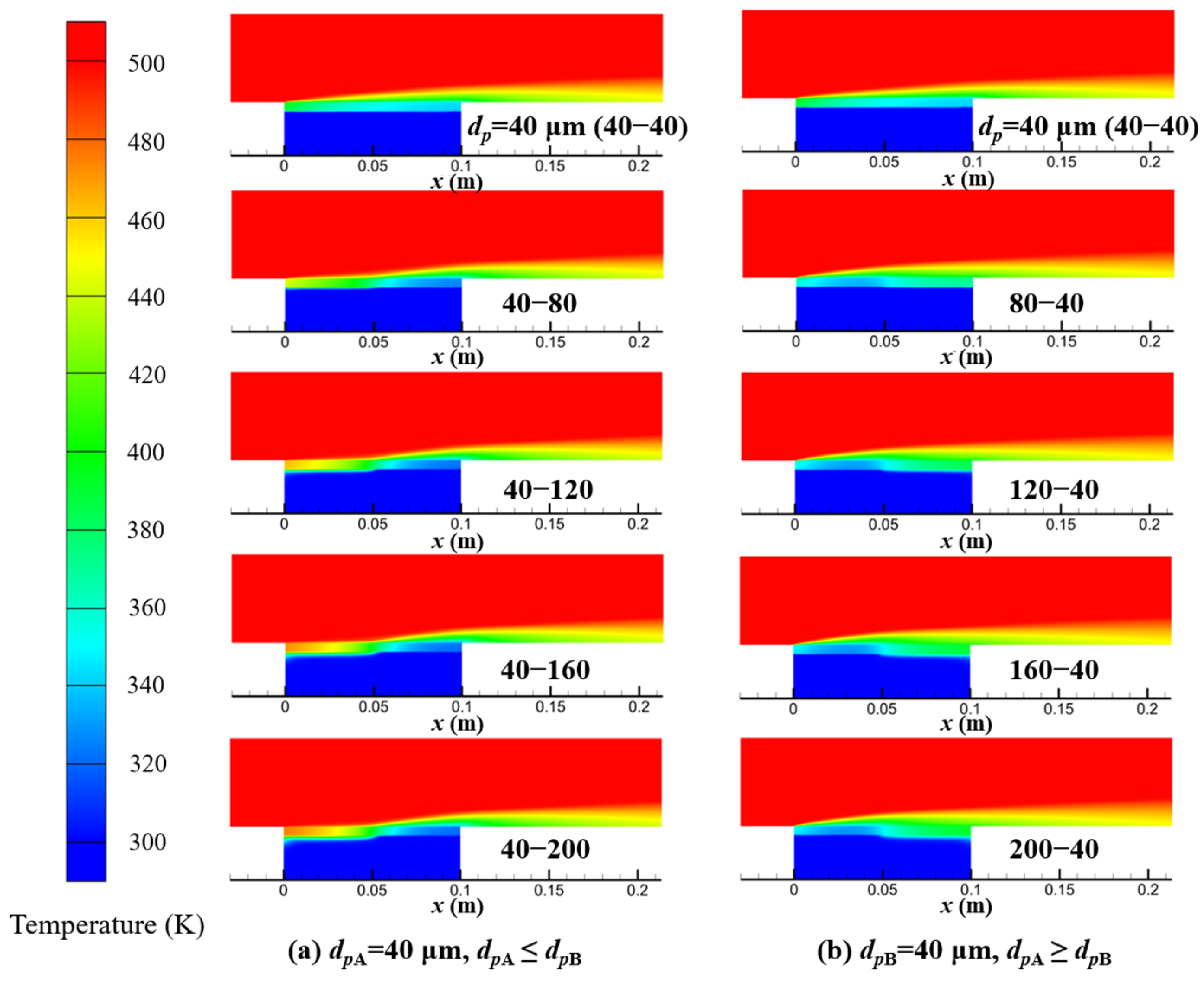
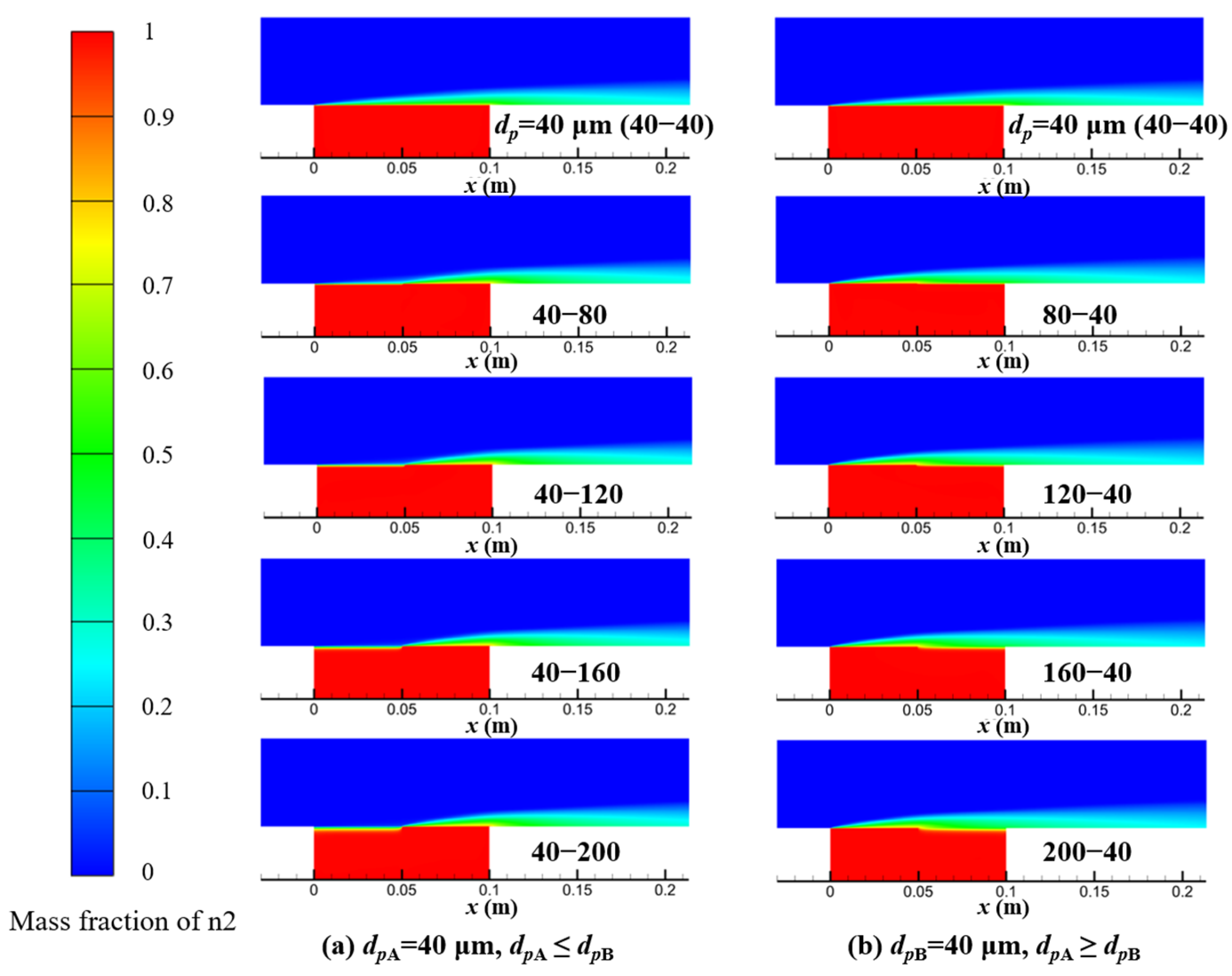
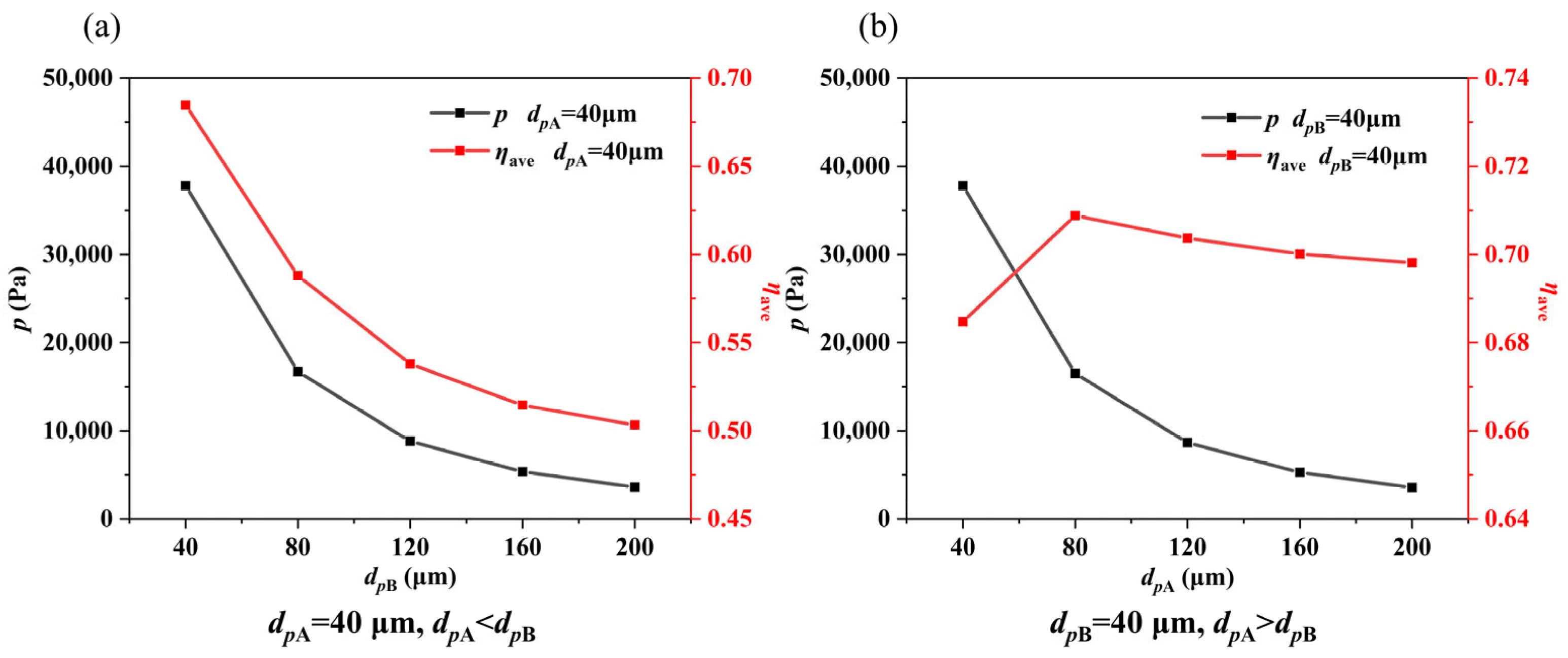
3.1. Cooling Performance of Porous Plate Structure
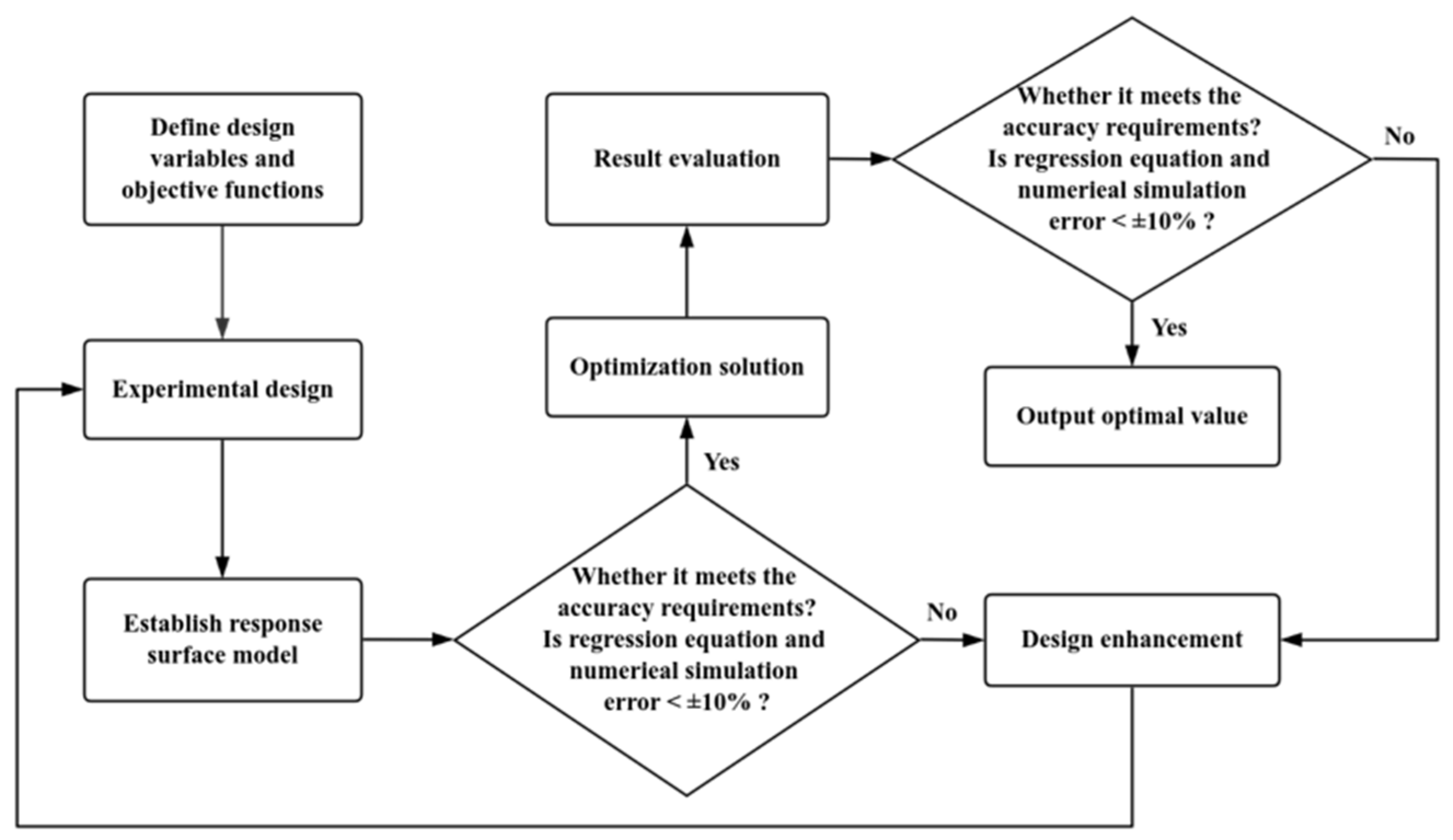
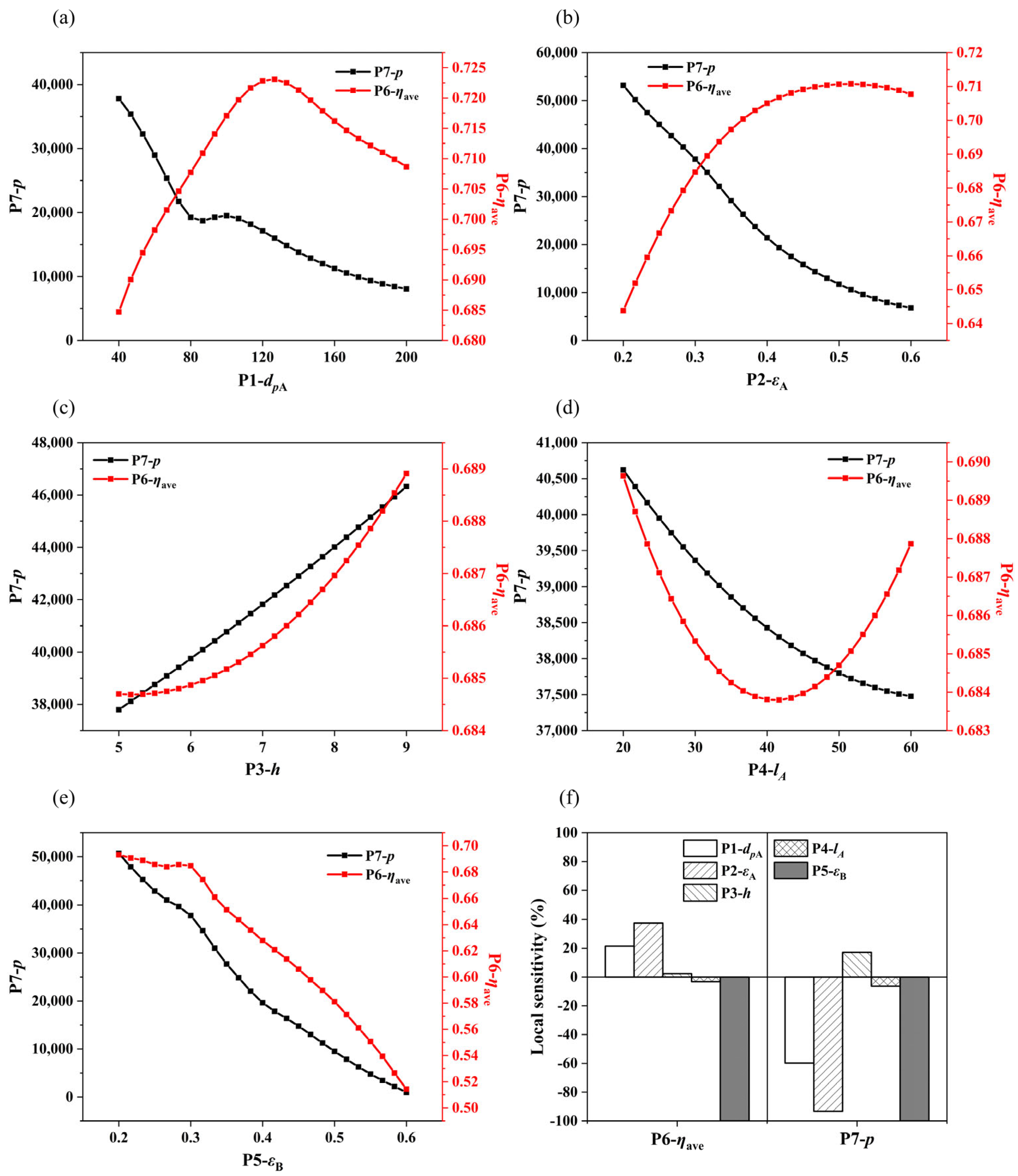
3.2. Response Surface Methodology for Optimal Design
3.2.1. Parameter Setting
3.2.2. Response Surface Model Construction
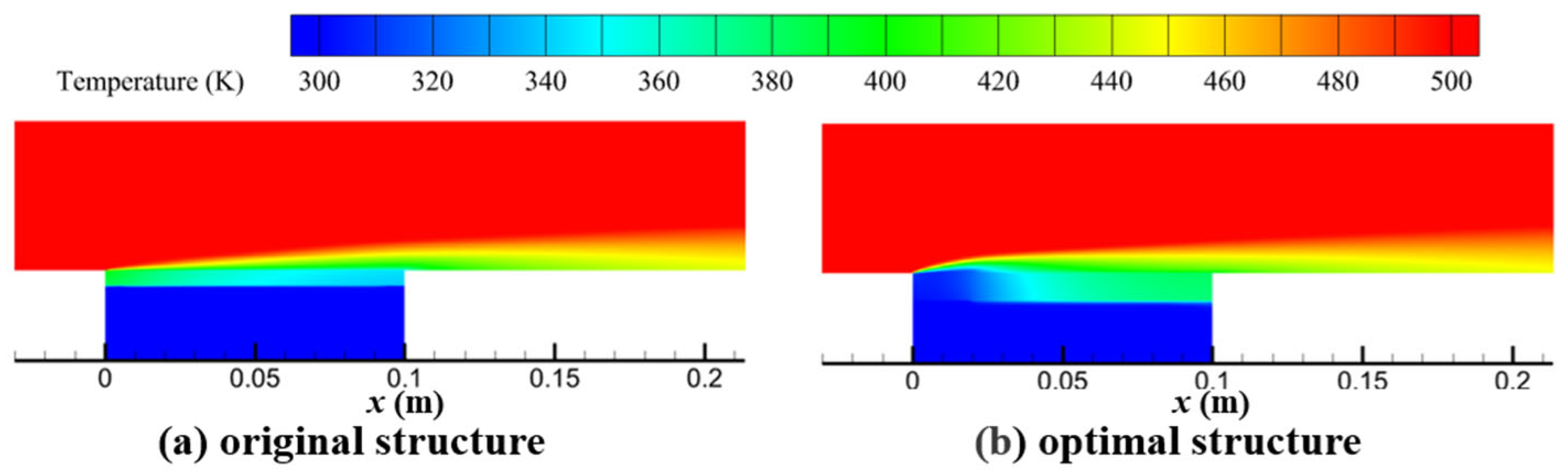
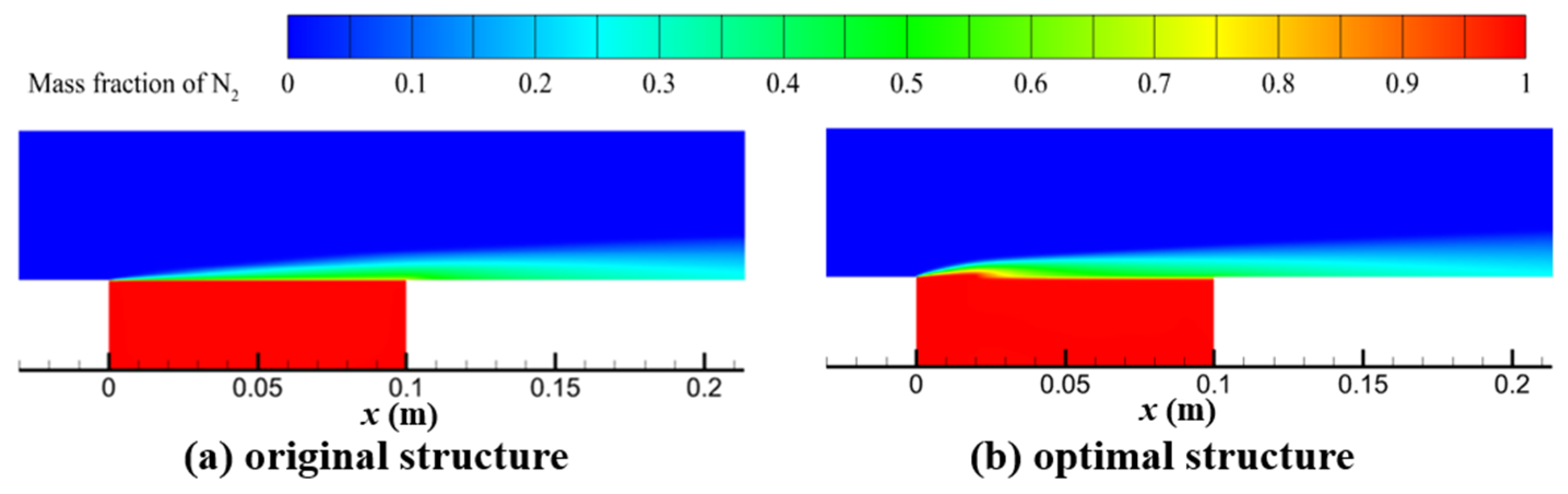
3.3. Analysis of Optimization Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | |||
| Latin symbols | Greek symbols | ||
| C | inertial coefficient | ρ | density, kg/m3 |
| dp | particle diameter, m | ε | porosity |
| E | total energy, J | μ | dynamic viscosity, Pa·s |
| F | coolant injection rate | τ | stress, N |
| h | height of hot end wall, m | η | cooling effectiveness |
| J | mass diffusion flux, kg/(s·m2) | Subscript | |
| k | thermal conductivity, W/(m·K) | ave | average |
| K | permeability of porous media, m2 | c | coolant |
| l | total length of hot end wall, m | eff | effective |
| p | pressure, Pa | f | fluid |
| T | temperature, K | s | solid |
| U | velocity, m/s | w | wall |
| Y | species mass fraction | ∞ | main stream |
References
- Wang, L. Development trend analysis of thermal protection technology for hypersonic vehicles. Aerodyn. Missile J. 2014, 2, 68–75+80. [Google Scholar]
- Wang, L.; Wang, Y. Research progress and trend analysis of thermal protection technology for hypersonic vehicles. Aerosp. Mater. Technol. 2016, 46, 1–6. [Google Scholar]
- Uyanna, O.; Najafi, H. Thermal protection systems for space vehicles: A review on technology development, current challenges and future prospects. Acta Astronaut. 2020, 176, 341–356. [Google Scholar] [CrossRef]
- Langener, T.; von Wolfersdorf, J.; Selzer, M.; Hald, H. Experimental investigations of transpiration cooling applied to C/C material. Int. J. Therm. Sci. 2012, 54, 70–81. [Google Scholar] [CrossRef]
- Liu, Y.-Q.; Xiong, Y.-B.; Jiang, P.-X.; Wang, Y.-P.; Sun, J.-G. Effects of local geometry and boundary condition variations on transpiration cooling. Int. J. Heat Mass Transf. 2013, 62, 362–372. [Google Scholar] [CrossRef]
- Strauss, F.T.; Witte, J.; General, S.; Manfletti, C.; Schlechtriem, S. Experiments on nitrogen and hydrogen transpiration cooling in a model scramjet combustor. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, UH, USA, 9–11 July 2018. [Google Scholar]
- Zhang, B.; Huang, H.; Huang, J.; Chen, J. An experimental investigation on performance of transpiration cooling with liquid water through C/SiC porous ceramic. Appl. Therm. Eng. 2020, 178, 115526. [Google Scholar] [CrossRef]
- Jiang, P.-X.; Huang, G.; Zhu, Y.; Xu, R.; Liao, Z.; Lu, T. Experimental investigation of biomimetic self-pumping and self-adaptive transpiration cooling. Bioinspir. Biomimetics 2017, 12, 056002. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Zhu, Y.; Liao, Z.; Jiang, P.-X. Experimental investigation of self-pumping internal transpiration cooling. Int. J. Heat Mass Transf. 2018, 123, 514–522. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, M.; Zhang, L.; Hu, C.; Tang, D.; Yang, L.; Song, Y. Forced Convection Heat Transfer in Porous Structure: Effect of Morphology on Pressure Drop and Heat Transfer Coefficient. J. Therm. Sci. 2021, 30, 363–393. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, J.; Yang, G. Numerical Simulation of Heat and Momentum Transport at the Coupled Interface between a Rectangular Channel and Porous Media. J. Therm. Sci. 2022, 31, 332–343. [Google Scholar] [CrossRef]
- Liu, Y.-Q.; Jiang, P.-X.; Xiong, Y.-B.; Wang, Y.-P. Experimental and numerical investigation of transpiration cooling for sintered porous flat plates. Appl. Therm. Eng. 2013, 50, 997–1007. [Google Scholar] [CrossRef]
- Huang, Z. Research on the Transpiration Cooling Supersonic and High Temperature Flow. Ph.D. Thesis, Tsinghua University, Beijing, China, 2015. [Google Scholar]
- Meng, L.; Jiang, P.; Jiang, F.; Yu, L.; Ren, Z. Experimental investigation of the heat transfer for transpiration cooling through a sintered porous plate. J. Tsinghua Univ. (Sci. Technol.) 2005, 45, 1537–1539. [Google Scholar]
- Wu, N.; Wang, J.; Dong, W.; Ding, R. An experimental investigation on combined sublimation and transpiration cooling for sintered porous plates. Int. J. Heat Mass Transf. 2018, 116, 685–693. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Ma, J.; Lin, J.; Peng, J.; Qu, D.; Chen, L. An experimental investigation on transpiration cooling under supersonic condition using a nose cone model. Int. J. Therm. Sci. 2014, 84, 207–213. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, L.; Wang, X.; Ma, J.; Lin, J. An experimental investigation on transpiration cooling of wedge shaped nose cone with liquid coolant. Int. J. Heat Mass Transf. 2014, 75, 442–449. [Google Scholar] [CrossRef]
- Jiang, P.-X.; Huang, G.; Zhu, Y.; Liao, Z.; Huang, Z. Experimental investigation of combined transpiration and film cooling for sintered metal porous struts. Int. J. Heat Mass Transf. 2017, 108, 232–243. [Google Scholar] [CrossRef]
- Wu, N.; Wang, J.; He, F.; Chen, L.; Ai, B. Optimization transpiration cooling of nose cone with non-uniform permeability. Int. J. Heat Mass Transf. 2018, 127, 882–891. [Google Scholar] [CrossRef]
- Rong, Y.; Wei, Y.; Zhan, R. Research on thermal protection by opposing jet and transpiration for high speed vehicle. Aerosp. Sci. Technol. 2016, 48, 322–327. [Google Scholar] [CrossRef]
- Shen, L.; Wang, J. Numerical investigation on the optimization of local transpiration cooling effectiveness. Appl. Therm. Eng. 2017, 127, 58–69. [Google Scholar] [CrossRef]
- Dong, W.; Wang, J.; Chen, S.; Ai, B.; Luo, X. Modelling and investigation on heat transfer deterioration during transpiration cooling with liquid coolant phase-change. Appl. Therm. Eng. 2018, 128, 381–392. [Google Scholar] [CrossRef]
- Wang, W.; Tao, G.; Ke, D.; Luo, J.; Cui, J. Transpiration cooling of high pressure turbine vane with optimized porosity distribution. Appl. Therm. Eng. 2022, 223, 119831. [Google Scholar] [CrossRef]
- Liu, T.; Liu, Y.; Ding, R.; Zhu, J.; He, F.; Wang, J. Numerical simulation and structural optimization of transpiration cooling with gradient porous matrix in supersonic condition. Int. J. Therm. Sci. 2024, 198, 108871. [Google Scholar] [CrossRef]
- Xu, J.-C.; Du, S.; Zhou, Y.-P.; Li, Z.-Y. Research on the heat transfer characteristics of through-hole transpiration cooling based on ceramic matrix composites. Appl. Therm. Eng. 2024, 257, 124360. [Google Scholar] [CrossRef]
- Chen, W.; Wang, K.; Wang, Y.; Tu, S.; Liu, Z.; Su, H. Numerical investigation and optimal design of transpiration cooling plate structure for gradient porosity. Int. J. Therm. Sci. 2023, 197, 108755. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Du, S.; Li, D.; Gao, Y. Optimization studies of transpiration cooling using porous medium with gradually-changed structure. Front. Heat Mass Transf. 2020, 15, 1–13. [Google Scholar] [CrossRef]
- He, F.; Wu, N.; Ran, F.; Wang, J. Numerical investigation on the transpiration cooling of three-dimensional hypersonic inlet. Aerosp. Sci. Technol. 2020, 106, 106152. [Google Scholar] [CrossRef]
- Ding, R. Feasibility Study on the Application of Transpiration Cooling on Hypersonic Vehicle. Ph.D. Thesis, University of Science and Technology of China, Anhui, China, 2021. [Google Scholar]
- Liu, Y.; Wang, Y.; Jiang, P. The effects of boundary condition variations on transpiration cooling. J. Eng. Thermophys. 2010, 31, 667–670. [Google Scholar]
- Vafai, K.; Kim, S.J. On the limitations of the brinkman-forchheimer extended darcy equation. Int. J. Heat Fluid Flow 1995, 16, 11–15. [Google Scholar] [CrossRef]
- Wang, J.H.; Wang, H.N. A Discussion of Transpiration Cooling Problems through an Analytical Solution of Local Thermal Nonequilibrium Model. J. Heat Transf. 2006, 128, 1093–1098. [Google Scholar] [CrossRef]
- He, F.; Wang, J.; Xu, L.; Wang, X. Modeling and simulation of transpiration cooling with phase change. Appl. Therm. Eng. 2013, 58, 173–180. [Google Scholar] [CrossRef]
- Liu, Y.-Q.; Jiang, P.-X.; Jin, S.-S.; Sun, J.-G. Transpiration cooling of a nose cone by various foreign gases. Int. J. Heat Mass Transf. 2010, 53, 5364–5372. [Google Scholar] [CrossRef]
- Su, H.; He, F.; Wang, J.; Luo, X.; Ai, B. Numerical investigation on the effects of porous cone parameters on liquid transpiration cooling performance. Int. J. Therm. Sci. 2021, 161, 106743. [Google Scholar] [CrossRef]
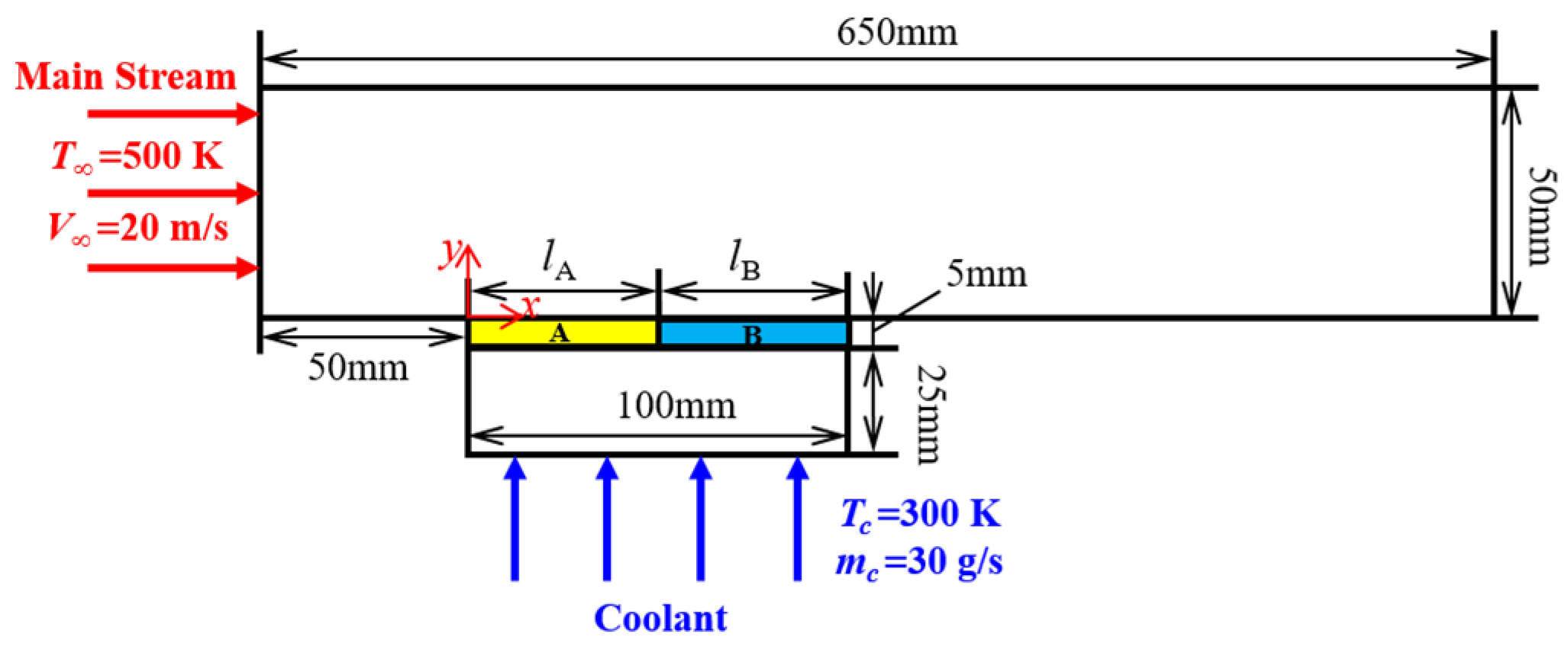
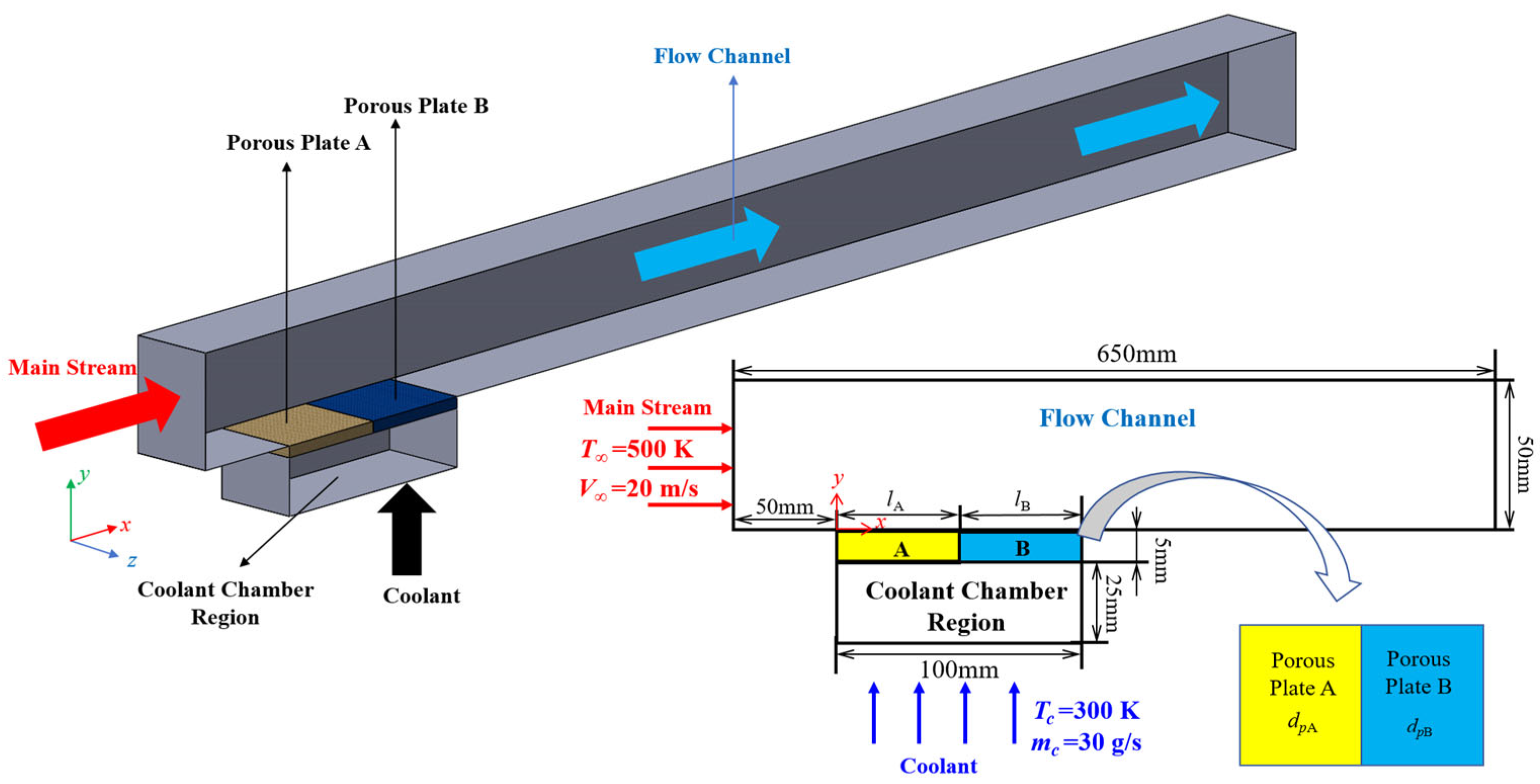





| Boundary Conditions | Value | |
|---|---|---|
| Main Stream (air) | Temperature (T∞) | 500 K |
| Velocity (V∞) | 20 m/s | |
| Coolant (N2) | Temperature (Tc) | 300 K |
| Mass Flow Rate (mc) | 30 g/s | |
| Porous Media (Inconel-600) | Density | 8420 kg/m3 |
| Thermal Conductivity | 20.615 W/(m·K) | |
| Specific Heat | 460 J/(kg·K) | |
| Computational Domain | Governing Equations |
|---|---|
| Main Stream Channel and Cooling Chamber | Continuity equation: |
| Momentum equation: | |
| Energy equation: | |
| Component equation: | |
| Porous Media Region | Continuity equation: |
| Momentum equation: , | |
| Energy equation: |
| Factor | Variable | Initial Value | Lower Limit | Upper Limit |
|---|---|---|---|---|
| dpA/μm | P1 | 40 | 40 | 200 |
| εA | P2 | 0.3 | 0.2 | 0.6 |
| h/mm | P3 | 5 | 5 | 9 |
| lA/mm | P4 | 50 | 20 | 60 |
| εB | P5 | 0.3 | 0.2 | 0.6 |
| Initial Value | Optimal Value | ||
|---|---|---|---|
| P1−dpA/μm | 40 | 163.67 | |
| P2−εA | 0.3 | 0.4671 | |
| P3−h/mm | 5 | 9 | |
| P4−lA/mm | 50 | 20 | |
| P5−εB | 0.3 | 0.4627 | |
| P6−ηave | Predictive value | 0.6738 | 0.7226 |
| Simulated value | 0.6827 | 0.7238 | |
| Error | 1.30% | 0.17% | |
| P7−p/Pa | Predictive value | 39,755 | 3230 |
| Simulated value | 37,824 | 3191 | |
| Error | 5.11% | 1.22% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Liu, Y.; Zhang, X.; Kong, M.; Liu, H. Numerical Investigation and Optimization of Transpiration Cooling Plate Structures with Combined Particle Diameter. Energies 2025, 18, 2950. https://doi.org/10.3390/en18112950
Wang D, Liu Y, Zhang X, Kong M, Liu H. Numerical Investigation and Optimization of Transpiration Cooling Plate Structures with Combined Particle Diameter. Energies. 2025; 18(11):2950. https://doi.org/10.3390/en18112950
Chicago/Turabian StyleWang, Dan, Yaxin Liu, Xiang Zhang, Mingliang Kong, and Hanchao Liu. 2025. "Numerical Investigation and Optimization of Transpiration Cooling Plate Structures with Combined Particle Diameter" Energies 18, no. 11: 2950. https://doi.org/10.3390/en18112950
APA StyleWang, D., Liu, Y., Zhang, X., Kong, M., & Liu, H. (2025). Numerical Investigation and Optimization of Transpiration Cooling Plate Structures with Combined Particle Diameter. Energies, 18(11), 2950. https://doi.org/10.3390/en18112950





