Abstract
To investigate the physical phenomena interactions between airstream and liquid injection or droplets within a complex multi-stage swirl flow field, this study investigated the flow field and spray characteristics in a central stage direct injection combustor with a variety of optical diagnostic techniques, including using time-resolved particle image velocimetry (PIV) to measure the swirl flow field, using time-resolved planar Mie scattering (PMie) to measure the spray pattern, and using a laser particle size analyzer (LPSA) to measure the spray droplet size and its distribution. The results indicate that the lip recirculation zone (LRZ) and the swirl jet zone (SJZ) significantly influence droplet spatial and size distribution characteristics, such as spray penetration, cone angle, and droplet size. Due to the unique characteristics of the dual-stage swirl atomizer, the spray cone angle and penetration do not increase monotonically with the gas Weber number (). For the pilot stage, at a constant , both the spray cone angle and penetration increase with higher fuel injection velocity. At different fuel injection velocities, the spray penetration increases with rising . When the fuel injection velocity is low, the cone angle initially increases and then decreases as grows. The results about the effect of on droplet size distribution further support this conclusion. The Sauter mean diameter (SMD) of the main and pilot stage decreases with increasing relative pressure drop of air until reaching a stable state. The aerodynamic shear of the swirling airstream is sufficient to promote thorough fuel atomization, ensuring that the SMD remains low at the whole operating condition. Therefore, for the dual-stage swirl atomizer investigated in this study, good atomization can be achieved under low operating conditions, which provides a theoretical foundation and data support for the improvement and design of a low-emission, high-performance atomizer.
1. Introduction
In recent years, the International Civil Aviation Organization (ICAO) has introduced progressively stringent nitrogen oxides (NOx) emission standards through its Committee on Aviation Environmental Protection (CAEP). To comply with these evolving airworthiness requirements, the development of low-emission combustion technologies has become a critical priority. Three primary approaches have gained prominence: Rich-burn Quick-quenching Lean-burn (RQL) [1], Lean Premixed Pre-evaporation (LPP) [2], and Lean Direct Injection (LDI) [3]. The RQL combustor, divided into an axial rich zone, a quenching zone, and a lean zone, effectively suppresses thermal NOx formation by maintaining low-temperature and low-oxygen conditions. However, this configuration presents challenges, including oversized combustor dimensions and difficulties in controlling the equivalence ratio across zones [4]. In contrast to conventional designs, the LPP approach mitigates NOx generation through a dual-stage combustion strategy (main and pilot stages) combined with thorough fuel–air premixing prior to ignition. This mechanism effectively reduces peak flame temperatures and eliminates localized hot spots. Nevertheless, LPP systems have inherent limitations: their narrow flame stability margins often lead to combustion anomalies such as thermoacoustic oscillations, flashback, and auto-ignition [5]. Unlike LPP systems, LDI operates via direct fuel injection into the combustion chamber. This method relies on rapid atomization and air–fuel mixing through aerodynamic shear forces before flame stabilization. By bypassing the premixed pre-vaporization phase, LDI inherently eliminates the risks of flashback and auto-ignition while enabling a more compact combustion chamber design. Its NOx suppression mechanism primarily depends on distributed micro-combustion zones that minimize localized high-temperature regions. This spatial combustion control, coupled with reduced fuel residence time in high-temperature environments, significantly curtails thermal NOx formation pathways.
Rolls-Royce (RR) has been at the forefront of extensive research into centrally staged Lean Direct Injection (LDI) and the multiplex direct-injection array architectures. Their research framework systematically explores critical parameters, including fuel staging strategies, emission characteristics, and turbulent flame stabilization mechanisms. Advanced laser-based diagnostics, such as hydroxyl radical (OH*) chemiluminescence spectroscopy, have been utilized to quantify heat release distribution, complemented by high-fidelity flame imaging to resolve spatiotemporal combustion dynamics [6]. Notably, parametric studies have demonstrated that pilot stage vortex intensity plays a crucial role in governing two key operability metrics: ignition reliability and lean blowout (LBO) limits. Although LDI architectures have not yet been incorporated into current Rolls-Royce production engines, full-scale rig testing has demonstrated groundbreaking NOx reductions of more than 35–45% compared to CAEP/6 regulatory baselines under cruise conditions [7]. RR introduced the Lean-Burn combustion chamber in the 1990s. This design achieved enhanced combustion efficiency, reduced emissions, and improved the overall performance of aero engines by optimizing fuel atomization and air–fuel blending processes. Lazik et al. [8] investigated the effects of swirl intensity during the main combustion phase and the inlet flow parameters of the Lean-Burn combustion chamber on exit performance, temperature distribution, and pollutant emissions. The research findings indicate that as the air pressure drop increases, the atomization quality improves, thereby enhancing ignition performance. However, an excessive increase in air pressure drop reduces the residence time of fuel within the recirculation zone, which adversely affects flame stability. When the swirl intensity of the main stage is high, a central recirculation zone forms, causing larger droplets to migrate toward the wall surface while smaller droplets accumulate in the central recirculation zone, leading to degraded ignition performance. Additionally, under conditions of higher swirl intensity, the spray cone angle becomes wider, resulting in a shorter axial flame length and a longer radial flame length. This configuration is unfavorable for ignition but advantageous for flameout. Mosbach et al. [9] investigated the variation laws of fuel distribution and flame structure under high-altitude inflow conditions in a Lean-Burn low-pollution combustion scheme. Antoshkiv et al. [10] demonstrated that an increase in the spray cone angle leads to a more uniform fuel distribution near the nozzle axis, thereby enhancing ignition performance. Read et al. [11] employed planar laser-induced fluorescence (PLIF) to analyze the impact of spray pattern on the high-altitude re-ignition capability of engines. Their findings revealed that greater aerodynamic forces improve fuel atomization, resulting in smaller droplet sizes, which in turn facilitates enhanced engine ignition performance. It is evident that flow field distribution and atomization characteristics play a critical role in combustion processes. Consequently, further research into these aspects is warranted.
In terms of atomization mechanisms, Feng et al. [12] performed a modal decomposition analysis on the non-reactive flow field of the dual-swirl combustion chamber using large eddy simulation, identified coherent structures within the flow field, and extracted energy-based spatial distributions corresponding to all characteristic frequency. Wu et al. [13,14] investigated the breakup process and atomization structure of a jet in a subsonic transverse flow by the pulse schlieren technique and phase Doppler particle analyzer (PDPA). By varying the liquid type, nozzle diameter, liquid–gas momentum ratio (), and other parameters, they analyzed the liquid breakup process and spray structure, determining the position of the liquid breakup point. Measurements were conducted to assess the size, axial velocity, and volume flux of the liquid downstream of the nozzle outlet at different axial positions. The results indicate that higher liquid jet velocities lead to greater penetration, with the jet liquid column trajectory influenced by . Additionally, the resistance coefficient is minimally affected by liquid viscosity. When is low, large droplets are concentrated at the center of the liquid mist, and intense momentum exchange occurs between the liquid column surface waves and the airstream. When is high, the distribution of large droplets shifts upward. The spray droplet sizes are confined to a limited region, indicating a non-uniform spatial mass distribution. The height of the maximum volume flux position represents the region of highest droplet concentration. Lubarsky et al. [15] investigated the outer boundary of the spray trajectory for different nozzle structures at room temperature and high pressure using high-speed imaging technology and employed photoconductive techniques to determine the breakup point of the jet liquid column. Their findings reveal that the breakup point position is significantly influenced by jet velocity and liquid turbulence intensity within the nozzle orifice. Compared to nozzles with fan-shaped chamfering, nozzles without chamfering exhibit faster jet breakup. Within a Weber number () range of 400 to 1600, the jet trajectory remains relatively unchanged, as the breakup mode in this regime is primarily shear-driven. Since droplet penetration depends on the initial jet velocity, penetration in transverse airstream is positively correlated with the square root of the liquid–gas momentum flux ratio within the range of 5 to 100. S. B. Tambe et al. [16] used PIV and Mie scattering techniques to examine cases in which a water jet was injected vertically into a rotating cross-flow from the central axis of a swirler. Axial swirlers with blade installation angles of 30°, 45°, and 60° were used to generate rotating airstream. The results show that at a radial position of R = 15 mm, the velocity in the cross-flow direction reaches its peak. Due to centrifugal forces and a decrease in radial velocity, the radial penetration of the jet continues to increase in the downstream region. As swirl intensity and q increase, the radial penetration of the water jet expands, and the water jet plume continues to develop in the circumferential direction.
Patil et al. [17] employed a novel method to capture laser-induced fluorescence (LIF) images of liquid jet breakup by illuminating the bottom region of a transverse jet with a laser. They precisely measured the penetration, jet width, and diffusion angle of the liquid column. Their findings indicate that when the exceeds 10, the liquid jet expands in the vertical direction upon exiting the nozzle, and as it moves downstream, its width gradually increases—eventually reaching 4 to 7 times the diameter of the jet outlet. They also proposed a sheet fracture mode, which is primarily influenced by the Reynolds number (). Eslamian et al. [18] further examined the relationship between the breakup process of a transverse jet and downstream droplet size under high-temperature and high-pressure conditions. Their results suggest that while jet penetration is predominantly governed by the momentum flux ratio under standard conditions, additional parameters influence penetration and jet trajectory under varying pressures and temperatures. Furthermore, they identified a specific liquid injection velocity at given pressure, temperature, and airstream conditions that maximizes the fuel injection surface area, thereby optimizing atomization quality. Lee et al. [19] demonstrated that as the gas Weber number () increases, the onset of liquid column fragmentation shifts closer to the nozzle outlet. Additionally, higher enhance turbulent vortex energy in the gas, leading to windward-side fragmentation of the liquid column. Patil et al. [20] investigated the effect of jet instability on the temporal and spatial fluctuations of downstream spray characteristics by capturing transient images of two opposing jets breaking simultaneously within an atomizer. Hsiang et al. [21] conducted a systematic study on the influence of key dimensionless parameters—, , and Ohnesorge number ()—on transverse jet atomization, elucidating their primary effects on droplet breakup. They also developed a criterion based on Re and We to determine whether droplet breakup occurs. Gong et al. [22] explored the atomization process of a liquid transverse jet under different swirl numbers (0.49, 0.86, 1.48) and found that higher swirl numbers improve atomization uniformity. Fujiwara et al. [23] studied the breakup process of a single nozzle during the main combustion stage of an actual engine, mapping the nozzle trajectory in this phase. Sikroria et al. [24] applied shadow imaging techniques to compare the breakup process of a transverse jet under conditions of uniform inlet airstream and 15° swirling inlet airstream. Their results indicate that due to the high tangential velocity of swirling airstream, atomized particles are significantly smaller. Song et al. [25] utilized PDPA and Mie scattering techniques to investigate the breakup, penetration, droplet size, and distribution of Jet A-1 aviation kerosene in an air cross-flow. They derived correlations between nozzle diameter and droplet Sauter mean diameter (SMD) ratio, air Weber number, liquid–gas momentum flux ratio, and liquid–gas density ratio. Analysis of jet trajectories revealed that the air Weber number predominantly influences near-field behavior close to the nozzle, while ambient pressure becomes the dominant factor governing jet trajectory in the far-field region. Fang et al. [26] employed multiple laser diagnostic techniques such as PMie, PDPA, and high-speed PIV to obtain information on the spray cone angle, mean droplet diameter (SMD), droplet velocity, and gas flow velocity of multi-swirl airblast atomizer. The research results indicated that the flow field has a significant impact on spray characteristics and the behavior of droplets of different sizes. Small droplets with lower initial momentum tend to be entrained by the recirculation zone, and these droplets have a tendency to coalesce, resulting in an increase in SMD in this region.
Although numerous studies have investigated atomization-related flow fields, spray characteristics, and liquid jet breakup, the atomization process of fuel in real engines typically occurs under non-uniform swirl conditions, in particular, the influence of swirl on droplet breakup, fuel distribution, and particle size remains insufficiently understood. Moreover, most existing studies on jet atomization focus on transverse jets, while limited research has explored atomization along the airstream direction. Additionally, previous studies primarily consider single-swirler and single-nozzle configurations, whereas practical engine applications commonly employ multi-stage nozzles. To address these gaps, this study employs a range of advanced laser diagnostic techniques, including time-resolved particle image velocimetry (PIV), planar Mie scattering (PMie), and laser particle size analyzer (LPSA), to measure key parameters such as air velocity, droplet Sauter mean diameter (SMD), spray cone angle, and spray penetration. The primary objective is to investigate the effects of a dual-stage swirl flow field on the atomization process and to analyze how different aerodynamic parameters influence spray characteristics. The remainder of this paper is structured as follows: Section 2 discusses the fuel and aerodynamic parameters in the dual-swirl airblast atomizer, along with the experimental methods and test equipment employed. Section 3 presents an analysis of the experimental results and theoretical findings, focusing on the interaction between swirl, spray spatial distribution, and droplet size. Finally, Section 4 summarizes the key conclusions derived from this study.
2. Materials and Methods
To study the interaction between swirling air and fuel spray, the atomization test bench and the corresponding test zone are illustrated in Figure 1. The figure shows that the dual-stage swirl atomizer used in this study comprises three main components: the pilot stage atomizer, the dual-stage axial swirler, and the main stage atomizer. Additionally, the test zone and the fields of view for PIV, PMie, and LPSA are also depicted. The axial and radial directions of the cross-section are denoted as Z and R, respectively. For LPSA, the droplet SMD is measured at three axial positions (Z = 10 mm, 30 mm, and 50 mm) downstream of the atomizer.
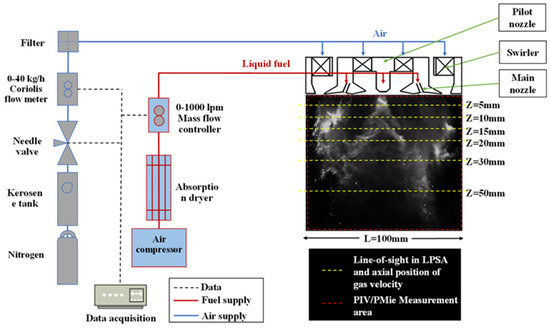
Figure 1.
Scheme of the atomization test rig and the PIV/PMie test zone and LPSA measuring position.
The dry compressed air is transported to the nozzle through a mass flow controller (0–1000 LPM, uncertainty ±2% FS). To calculate the air pressure drop across the swirler, a differential pressure sensor (0–10 psi, uncertainty ±0.05%) is used to measure both the inlet and exhaust pressures of the nozzle under test. In this study, aviation kerosene RP-3 [26] serves as the working liquid. The fuel pressure is controlled by adjusting an electric needle valve, and the fuel mass flow rate is measured using a Coriolis flowmeter (0–40 kg/h, uncertainty ±0.1%). Two pressure sensors (0–600 kPa, uncertainty ±0.1%) are employed to monitor the pressure differential of the test nozzle. A LabVIEW 2018-based program is used to control the opening of the electric needle valve to adjust the pressure differential of the nozzle, and subsequently regulate the fuel mass flow rate (). All instruments were carefully calibrated prior to each test.
As shown in Figure 2, the arrangement of the pilot and main stage axial swirlers is concentric and co-rotating, both equipped with straight blades. The blade angles of the pilot and main stages are 40° and 50°, respectively. The main stage nozzle is a nine-point direct-injection nozzle arranged circumferentially, with the nozzle outlet directed 20° from the axial direction. The pilot stage is a pressure atomization nozzle installed at the center of the swirler. The swirler’s diameter is 87 mm, with a length of 30 mm. The airflow ratio between the main stage and the pilot stage is 4:1, and the effective flow area of the swirler is 562 mm2. All experiments in this study were conducted in an open space. The mass flow rate characteristic of the nozzles is shown in Figure 3.
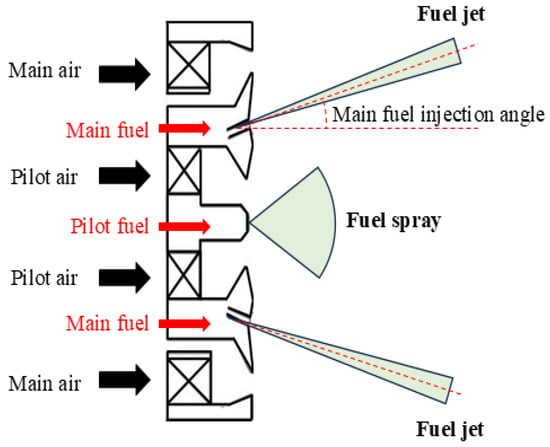
Figure 2.
Central-staged lean direct injection combustor structure diagram.
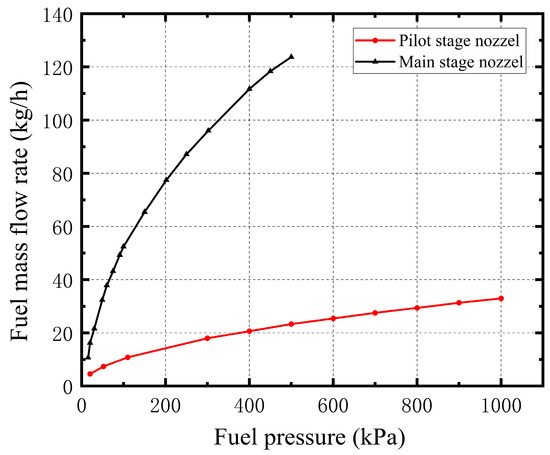
Figure 3.
Mass flow rate characteristic.
In this study, time-resolved PIV, time-resolved PMie, and an LPSA were used to measure the air flow field, spray spatial distribution, and SMD. The PIV system consists primarily of a dual-cavity Nd: YLF laser with a wavelength of 527 nm, a high-speed camera, a synchronous signal generator, and a smoke generator. In the experiment, the Nd: YLF laser operates in double-pulse mode with a frequency set to 2000 Hz and a single pulse energy of 20 mJ. The laser beam forms a sheet light with a thickness of 1 mm using a cylindrical lens optical system. The high-speed camera is synchronized with the Nd: YLF laser by the synchronous signal generator at 2000 Hz. It is equipped with a Nikon lens (focal length of 105 mm, aperture f/2.8), providing a field of view of 42 × 60 mm2 and a resolution of 45.83 pixels/mm. The system uses a smoke generator to atomize smoke oil into tracer particles with a particle size of 2 μm, which are highly dispersive and flowable. For measuring spray spatial distribution, PMie is used based on the principle of plane laser scattering (PLS). The spray droplets are illuminated by the Nd: YLF laser sheet, and the Mie scattering from the spray is captured by a high-speed camera, synchronized with the laser at a frequency of 2000 Hz. The droplet size is measured using LPSA. LPSA utilizes Fraunhofer diffraction to assess the distribution of scattered light. By analyzing the relationship between light energy distribution and droplet size, the droplet size distribution is obtained. The droplet size measurement range of LPSA spans from 0.1 μm to 2080 μm, with a maximum frequency of 10 kHz and a measurement accuracy of ±0.5%.
The dimensionless numbers describing the atomization process in this study are the gas Weber number () and the liquid–gas momentum ratio () [27]:
In the formula, and are gas density and liquid density, respectively, is the diameter of nozzel, is the liquid surface tension coefficient, is the air velocity, and is the outlet velocity of the fuel jet, which can be obtained from formula (3):
In the formula, is the fuel mass flow rate.
The following are the PIV test results for the dual-stage swirl flow field and the PMie test results of the pilot stage spray and main stage spray, with the test conditions shown in Table 1, Table 2 and Table 3. The pictures of PIV and PMie are the time-averaged result of 2000 transient images, and the camera’s acquisition frequency is 2000 Hz.

Table 1.
PIV test conditions.

Table 2.
PMie and droplet size distribution test conditions of pilot stage spray.

Table 3.
PMie and droplet size distribution test conditions of main stage spray.
3. Results
3.1. Flow Fields Distribution
Figure 4 presents the time-averaged flow field vector diagram for different air pressure drops () under normal temperature and pressure conditions. The diagram reveals distinct lip recirculation zones (LRZs) and high-velocity swirl jet zones (SJZs) in the flow field after dual-stage swirl coupling. The primary structure of the flow field exhibits strong resemblance to the large eddy simulation results reported by Feng et al. [12]. As the pressure drop increases, although the LRZ is significantly enhanced, the simultaneous intensification of the SJZ causes the LRZ to become compressed. The convergence position of the dual-stage swirling flow remains relatively stable, indicating a consistent flow field structure. The formation of the LRZ is less influenced by pressure drop variations. Due to the presence of the swirler lip, a low-pressure zone forms in this region, entraining swirling air back into the area and leading to LRZ formation. The SJZ increases significantly with rising pressure drop, demonstrating that SJZ behavior is primarily governed by air pressure drop. Although the overall shape of the flow field remains largely unchanged, the radial velocity distribution exhibits noticeable asymmetry, particularly near the flow field’s center, where velocity fluctuations are more pronounced. However, due to the centrifugal force acting on the airstream after exiting the swirler, the flow extends radially, increasing the swirling jet angle. As this angle expands, the axial flow region enlarges, leading to a rapid decrease in radial velocity.
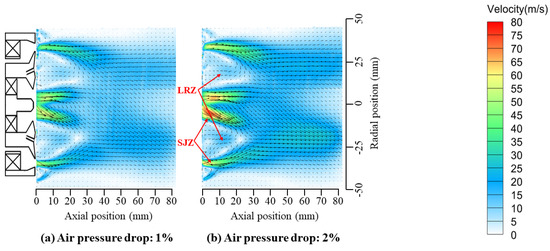
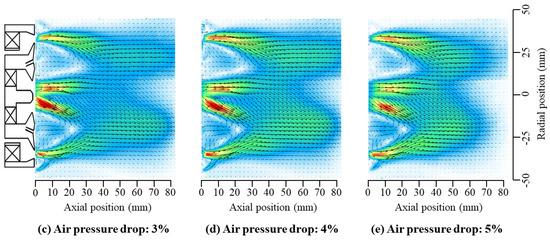
Figure 4.
Air flow field.
As depicted in Figure 5 and Figure 6, the radial distribution of the velocity reveals a tendency for the flow to contract toward the center. This distribution reflects the velocity concentration regions within the flow field, particularly at Z = 5 mm and Z = 10 mm, where the velocity reaches its maximum. This indicates that velocity is primarily concentrated in these areas. In swirling flows, higher velocity generally corresponds to stronger turbulent kinetic energy and improved mixing capability. As the pressure drop increases, the maximum velocity also rises, suggesting that a higher pressure drop enhances the velocity level of the flow field, facilitating atomization, mixing, and combustion. The radial velocity distribution of the flow field exhibits significant fluctuations. At Z = 5 mm, the velocity distribution trend is similar to that at Z = 10 mm, but the overall velocity is higher. From Z = 5 mm to Z = 15 mm, the fluctuation range of the flow velocity increases, with the axial velocity even displaying significant negative values. This indicates the presence of reverse flow in this region, which is associated with the LRZ in the flow field, confirming its non-uniformity. At Z = 15 mm, the fluctuations in flow velocity become more pronounced, with a larger difference between peak and valley values, further enhancing the non-uniformity of the flow. At Z = 30 mm, the fluctuation range of the flow velocity decreases at multiple radial positions, and the swirl jet intensity in the main stage surpasses that of the pilot stage. By Z = 50 mm, the velocity distribution stabilizes, transitioning into a single-peak profile.
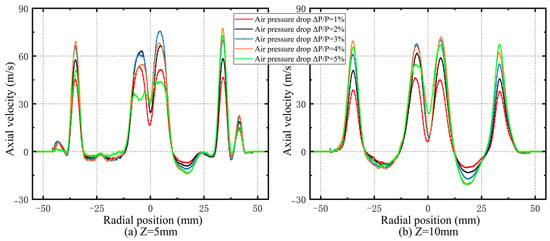
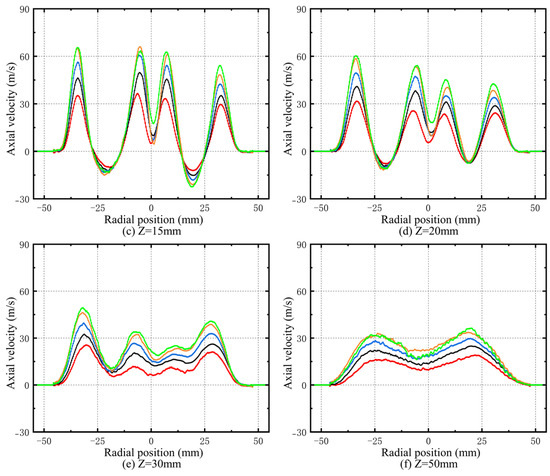
Figure 5.
Radial distributions of axial velocity at various axial position.
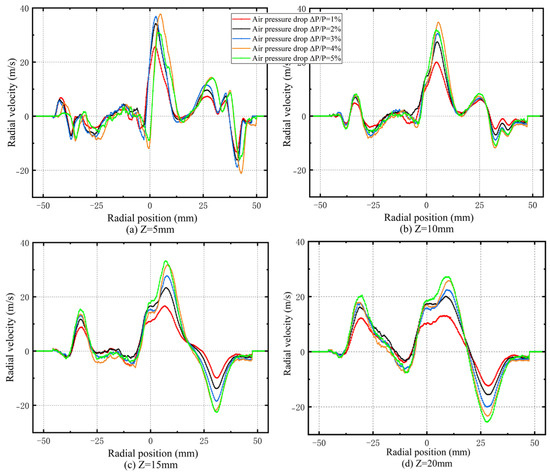
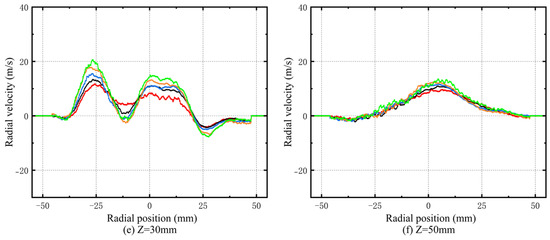
Figure 6.
Radial distributions of radial velocity at various axial position.
3.2. Spray Pattern
3.2.1. Pilot Stage Spray
To quantitatively analyze the spray’s spatial distribution under different operating parameters, two key metrics are defined: spray cone angle and axial penetration. Axial penetration refers to the axial distance from the atomizer outlet to the point containing 95% of the spray’s total integrated liquid intensity, reflecting the interactions among the spray’s axial jet, air swirl jet, and recirculation. The spray cone angle, a critical parameter for quantifying fuel dispersion, differs from that of conventional pressure atomizers, as the spray quality of swirl atomizers primarily rely on aerodynamic shear forces. This interaction with the swirling flow field results in less distinct spray boundaries. To ensure measurement consistency, the cone angle is defined as the radial span encompassing 95% of the total integrated intensity in spray PMie images.
Since the PMie and PIV experiments share the same equipment and the laser illuminates the same position, the flow field vector is superimposed on the PMie image to better analyze the atomization process. From Figure 7, the relationship between spray formation and flow dynamics can be observed. At a , the air velocity is low, the airstream remains relatively stable, the spray diffusion is limited, and the cone angle is small, indicating poor atomization. As the pressure drop increases (2% to 4%), the Mie scattering area expands significantly, suggesting improved atomization and finer spray. This phenomenon is closely related to the enhancement of the swirling jet zone (SJZ) and lip recirculation zone (LRZ) in the flow field. Stronger aerodynamic shear from the swirling jet leads to more thorough spray breakup, while the recirculation zone entrains smaller droplets back upstream, maintaining a suitable droplet size and distribution for more uniform atomization. At a , the Mie scattering area is at its largest and most uniform, indicating optimal atomization, further confirming the influence of flow field characteristics on spray performance. The spray cone angle is closely linked to the fuel injection velocity and flow field characteristics.
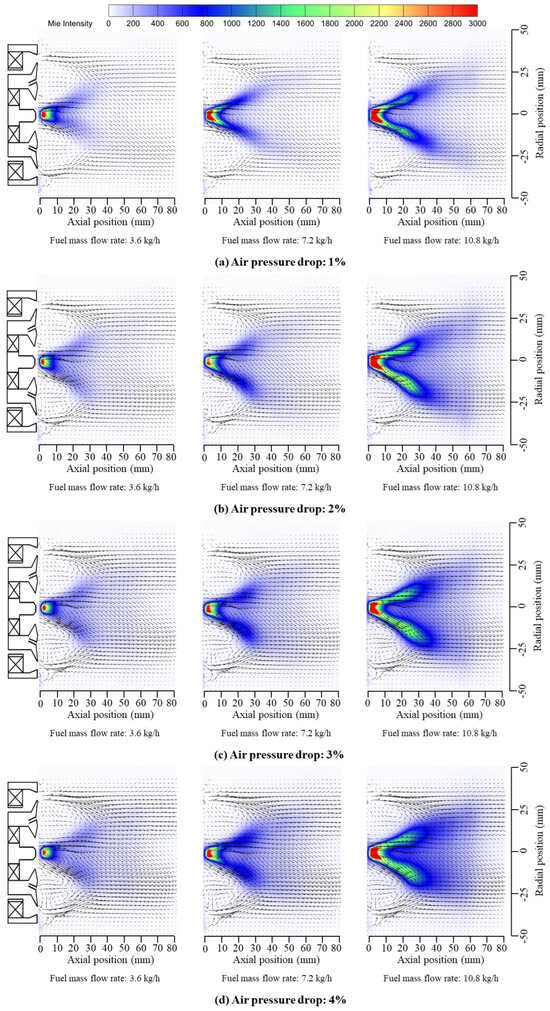
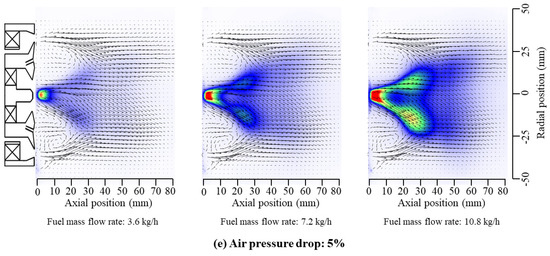
Figure 7.
Overlay of flow field on pilot stage spray.
As shown in Figure 8, spray penetration increases with rising and , as the inertial force on fuel droplet increases with greater axial momentum. Under swirling flow conditions, the droplets more easily overcome surface tension and backflow resistance, allowing them to travel downstream. As fuel injection velocity increases, the spray cone angle expands at the same . For , when increases from 0.76 m/s to 1.62 m/s, the spray cone angle grows from 46.73° to 53.89°; when increases further to 2.43 m/s, the angle increases from 53.89° to 60.13°, though the growth rate declines from 15.3% to 11.6%. At , the increase in the spray cone angle with fuel injection velocity is minimal, whereas at , the spray cone angle continues to expand with fuel injection velocity. For , spray penetration increases monotonically from 30.67 mm to 40.77 mm as rises. However, the spray cone angle initially increases and then decreases with increasing . This behavior stems from the nature of the pilot stage nozzle, which operates based on pressure atomization. Initially, the spray forms due to inertial forces but exhibits poor atomization. As rises, aerodynamic shear breaks larger ligaments or droplets into finer liquid filaments and droplets, enhancing atomization and diffusion, leading to a wider spray cone angle and improved atomization. However, at low fuel mass flow rates, excessive gas shear transfers a significant amount of momentum to the fuel, directing it more axially and suppressing radial dispersion. When , the fuel atomizes into very fine droplets that are more easily entrained by the airstream. The strong central contraction of the flow field further compresses radial dispersion, reducing the cone angle. For , spray penetration increases monotonically from 37.64 mm to 59.23 mm as rises. The spray cone angle first increases, then decreases, and then slightly increases again. When , the trend is similar to that observed at . However, as continues to rise, the relatively large fuel mass flow and broad droplet distribution allow some droplets to maintain a certain spray cone angle, leading to a slight increase in the cone angle. For , spray penetration monotonically increases from 53.89 mm to 64.69 mm with increasing , while the spray cone angle first decreases and then increases. This may be attributed to the high fuel mass flow rate in this condition. The high fuel supply pressure, combined with aerodynamic shear, enhances fuel breakup. At lower , droplets remain dispersed in the airstream, maintaining a larger spray cone angle. However, as increases, stronger aerodynamic forces further break down droplets, making them more susceptible to airstream entrainment. This axial movement slightly reduces the spray cone angle. As increases further, droplet breakup stabilizes, and droplet size remains relatively unchanged. Under strong aerodynamic influence, smaller droplets tend to spread more, causing the spray cone angle to increase again. Spray penetration is closely related to the spray cone angle. Generally, a larger cone angle indicates broader spray dispersion within the airstream, allowing the spray to better interact with the swirling flow. Additionally, higher kinetic energy in the flow field enhances spray penetration capability.
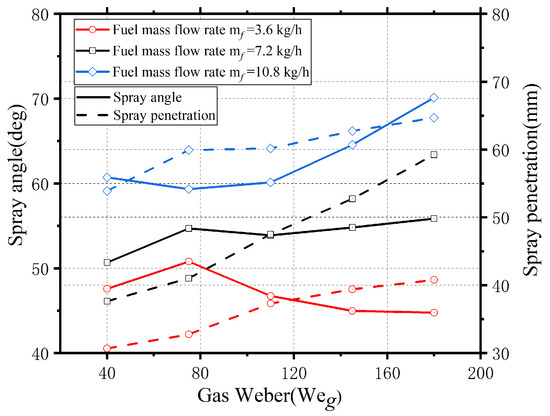
Figure 8.
Effects of gas Weber number on spray cone angle and penetration of the pilot stage.
3.2.2. Main Stage Spray
The spray results, as shown in Figure 9, reveal that when the pressure drop is 1% and the fuel injection velocity is high (), the Mie scattering intensity is large, and the spray pattern closely resembles a jet. This pattern tends to shrink toward the center as it moves downstream, with the atomization effect being suboptimal. This is due to the relatively low swirl intensity, weak aerodynamic shear, and a high mass flow rate of the jet, which results in significant initial axial momentum. As a result, the jet is better able to resist shear by the SJZ and the entrainment of fuel droplets by the LRZ. When the fuel injection velocity is low (), the Mie scattering area increases with the rise in , leading to a more uniform spray distribution. The spray’s axial penetration and cone angle also increase. As shown in Figure 10, with increasing fuel injection velocity, the spray’s axial penetration initially decreases, then increases, while the spray cone angle consistently increases. This behavior can be explained by the fact that at , the aerodynamic shear effect is weak, and the fuel droplet size is large, leading to a stronger spray penetration. However, as increases, the shear effect of the airstream strengthens, reducing the droplet size and accelerating jet breakup, leading to more small droplets. Although the number of small droplets increases, their momentum decreases, making them more susceptible to entrainment by the LRZ and resistance from the radial component of the airstream, which reduces spray penetration. As continues to increase, the shear effect intensifies, significantly improving atomization and reducing droplet size. The presence of many small droplets allows for better energy absorption from the airstream, promoting axial diffusion and mixing, thereby improving spray penetration.
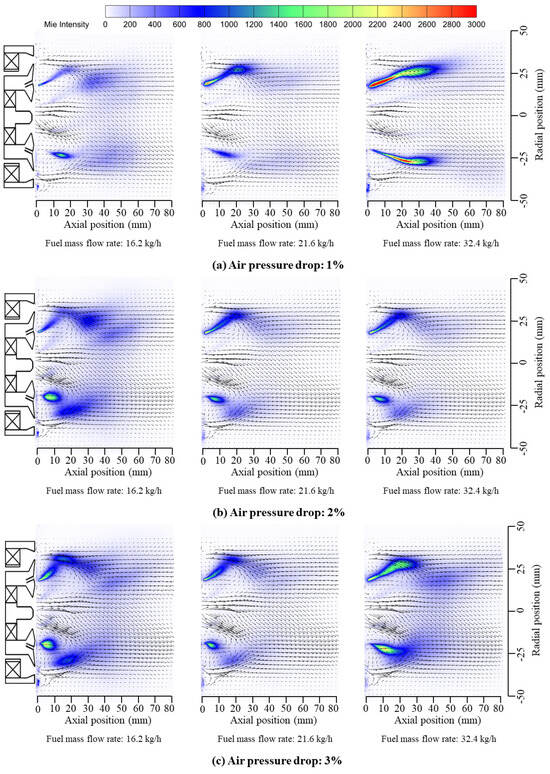
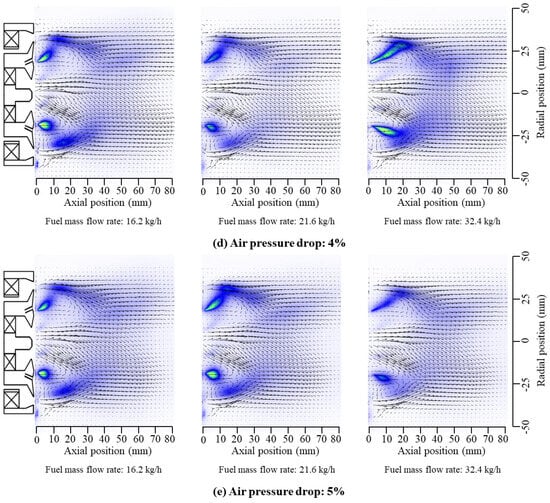
Figure 9.
Overlay of flow field on main stage spray.
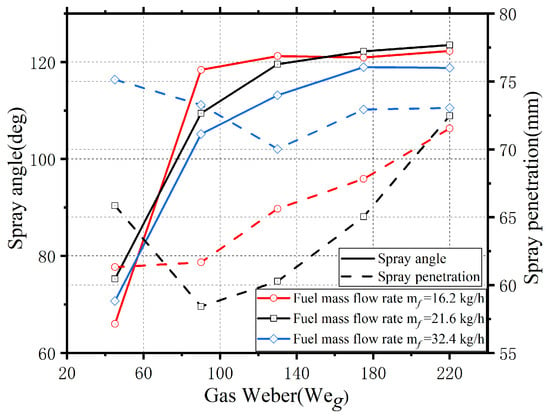
Figure 10.
Effects of gas Weber number on spray cone angle and penetration patterns of main stage.
3.3. Droplet Size Distribution
3.3.1. SMD of Pilot Stage
The following presents the variation in the SMD of the pilot stage spray with respect to the gas Weber number and the downstream position of the swirler. The test conditions are provided in Table 2. The mean SMD presented in this study represents the average of three measurements, with error bars indicating the uncertainty.
It can be observed from Figure 11 and Figure 12 that, at the same axial position, the SMD decreases with an increase in the gas Weber number across different fuel injection velocities, this is similar to the experimental result of Fang et al. [26]. According to the PIV results, at high , the gas velocity near the nozzle outlet increases, resulting in stronger aerodynamic forces. This causes the fuel to experience intense shear and breakup immediately after injection, leading to the formation of smaller droplets. As the pilot stage is a pressure atomization nozzle, it can be seen from Figure 3 that an increase in fuel mass flow rate and fuel pressure enhances the inertial force, improving the primary atomization. When the Weber number is zero, the SMD of the fuel is at its largest, ranging from 400 to 500 μm, as the nozzle relies solely on pressure atomization without pneumatic shear, resulting in poor atomization. As increases, the SMD decreases rapidly. Even at , there is a significant reduction in SMD, highlighting the importance of pneumatic shear in air atomization. For example, when the fuel injection velocity is , the maximum SMD decreases from 469.99 μm to 42.49 μm, a more than tenfold reduction. This also demonstrates that an increase in the spray cone angle does not necessarily indicate worse atomization. Instead, the fuel is more effectively atomized into smaller droplets, which are better controlled by the airstream, resulting in a more concentrated spray. When the fuel injection velocity is , the SMD decreases from 184.73 μm to 60.2 μm, a 67.41% reduction. At , the SMD decreases from 143.91 μm to 82.19 μm, a reduction of 42.89%. When the air pressure is reduced to 3%, or , the shear breakup of the fuel by aerodynamic forces reaches its critical limit. Beyond this point, further increases in the air pressure drop result in minimal changes to the SMD. At low fuel injection velocities (0.76 m/s to 1.62 m/s), the SMD at Z = 10 mm is near its minimum value, indicating that atomization is almost complete. As the spray travels downstream, the SMD increases slightly, likely due to droplet group collisions and aggregation, as well as the entrainment of the swirl reflux. This trend is consistent with the PIV results, which show that as the axial distance increases, the swirling airstream velocity decays, and turbulent kinetic energy decreases, facilitating droplet aggregation.
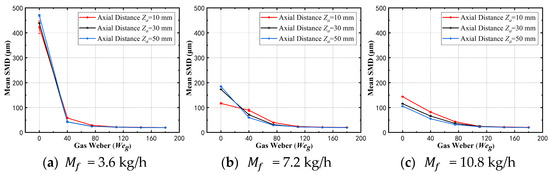
Figure 11.
SMD of pilot stage with gas Weber number at different fuel mass flow rate.
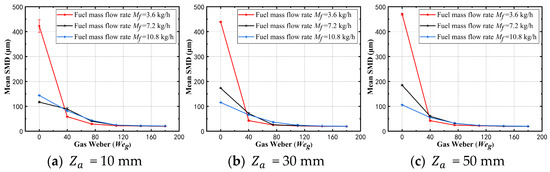
Figure 12.
SMD of pilot stage with gas Weber number at different axial distances.
Figure 13 displays the typical distribution of pilot stage for droplet sizes. These results correspond to cases where SMD are 25.61 μm. This distribution follows the Rosin–Rammler method, and there are two parameters, namely Spread Parameter (N) and span. A higher value of N indicates a narrower particle size distribution range. Additionally, a Span closer to 0 signifies greater uniformity in particle size and improved size consistency. In Figure 13, N is 19.3 and span is 0.19. The uniformity of droplet size in the pilot stage is highly satisfactory.
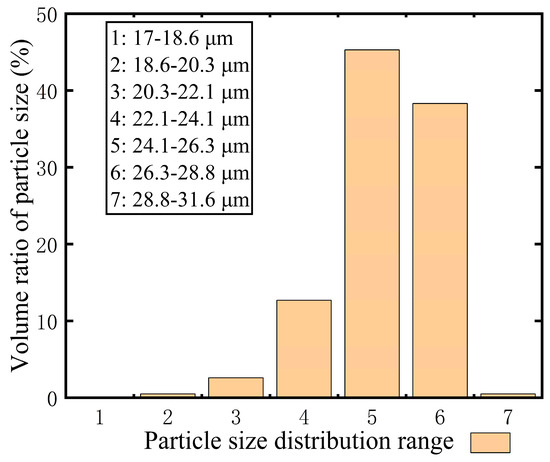
Figure 13.
The typical distribution of droplet sizes (pilot stage).
3.3.2. Main Stage SMD
The following presents the variation in the SMD of the main stage spray with respect to the gas Weber number and the downstream position of the swirler. The test conditions are provided in Table 3.
From Figure 14 and Figure 15, it can be observed that at the same axial position and different fuel injection velocities, the SMD generally decreases with an increase in the . At the same gas Weber number and axial position, as the fuel injection velocity increases, the Liquid–gas momentum ratio also increases, leading to a gradual rise in both the fluctuation amplitude. This occurs because, as the spray quality increases, the Rayleigh-Taylor (RT) instability intensifies during the liquid flow process, causing the formation of larger droplets. Consequently, the jet atomization and mixing effects deteriorate. At the same axial position and fuel injection velocity, the SMD decreases as increases. This is due to the increased aerodynamic shear with higher air pressure drops, which makes it easier for the liquid to break up, thus promoting fuel atomization and reducing the droplet size. When , the SMD for different fuel injection velocities is roughly 120–160 μm, indicating larger droplets. As increases from 175 to 215, with the fuel injection velocity increasing from 4.58 m/s to 6.86 m/s, the SMD remains relatively constant, ranging between 22 and 33 μm. This is because the higher pressure drop and Weber number lead to more thorough atomization, and the spray quality changes less. This also highlights the influence of droplet size on spray penetration: as droplet size decreases, the momentum of the droplet group becomes more dispersed, and the penetration increases. In comparison to the pilot stage spray at a lower , a smaller SMD is obtained more quickly, achieving better atomization almost immediately. In contrast, the atomization process in the main stage requires more time, which also helps explain the variation in cone angle and penetration distance with . At the same fuel injection velocity but different axial distances, the fuel SMD decreases as increases. The largest SMD is observed at Z = 10 mm, where atomization is the least efficient. At fuel injection velocities of 3.43 m/s and 4.58 m/s, the fuel SMD reaches its minimum and stabilizes when is 130 and 175. For a fuel injection velocity of 6.86 m/s, the change in SMD is smaller than at lower velocities. When , the rate of change in SMD decreases. This indicates that under the current conditions, the effect of aerodynamic shear on fuel atomization has reached its critical maximum. Additionally, the spray SMD at different fuel injection velocities and intake conditions is generally larger at Z = 10 mm and smaller at Z = 50 mm.
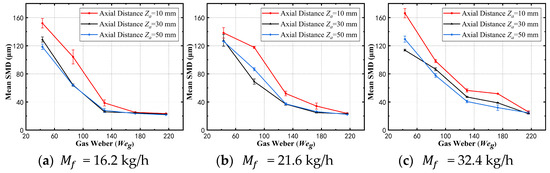
Figure 14.
SMD of main stage with gas Weber number at different fuel mass flow rate.
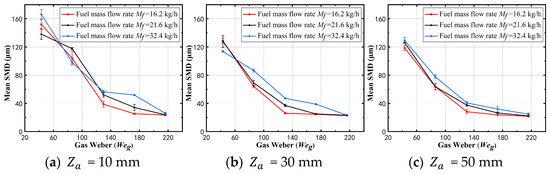
Figure 15.
SMD of main stage with gas Weber number at different axial distances.
Figure 16 displays the typical distribution of the main stage for droplet sizes. These results correspond to cases where SMD is 28.52 μm. In Figure 16, N is 12.1 and span is 0.28. The uniformity of droplet size in the main stage is highly satisfactory.
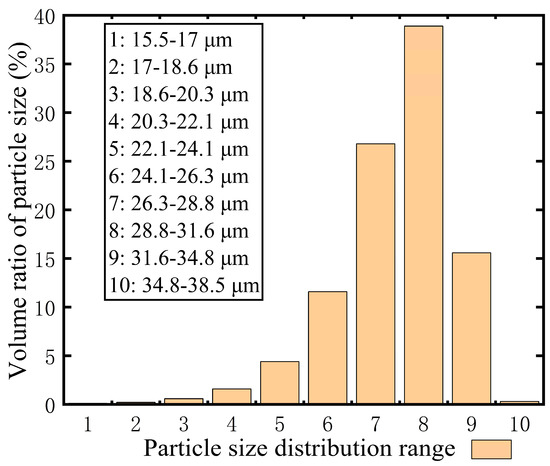
Figure 16.
The typical distribution of droplet sizes (main stage).
4. Conclusions
This paper investigates the interaction between a dual-stage swirl flow field and liquid fuel using experimental methods. Advanced laser diagnostic techniques, including PIV, PMie, and LPSA, were employed to measure key atomization parameters such as airstream velocity, Sauter mean diameter (SMD), spray penetration, and spray cone angle. The study focuses on understanding the influence of the air swirl flow field on the atomization process and spray characteristics. The main findings are as follows:
- (1)
- For dual-stage swirl flow field, the air velocity distribution is non-uniform, particularly in the central upstream region, where velocity variations are more pronounced. The flow field exhibits a tendency to contract toward the center along the axial downstream. The velocity of the flow field is primarily concentrated between axial positions Z = 5 mm and Z = 10 mm, where distinct lip recirculation zones (LRZs) and high-velocity swirling axial jet zones (SJZs) are observed.
- (2)
- The primary dimensionless parameters affecting spray penetration, spray cone angle, and droplet SMD are the liquid–gas momentum ratio () and the gas Weber number (). For the pilot stage spray, when the fuel injection velocity () is low, the spray cone angle does not increase monotonically with rising . Instead, when the gas shear effect on the fuel becomes too strong, the radial dispersion of the spray is suppressed, causing smaller droplets to follow the high velocity airstream. This inward contraction initially increases the spray cone angle before causing it to decrease. The spray penetration increases significantly with increasing . The SMD of the spray is influenced by , , and axial distance. At high pressure drops, the aerodynamic shear of the swirling airstream is sufficient to promote thorough fuel atomization, maintaining the SMD within an optimal range. As increases, when , the SMD stabilizes, indicating that the aerodynamic shear effect of the air swirl on the fuel has reached its maximum.
- (3)
- For the main stage spray, when the is high, the penetration does not increase monotonically with rising . As aerodynamic shear intensifies, the jet breaks into progressively smaller droplets, causing to first increase and then decrease, which in turn results in an initial decrease followed by an increase in spray penetration. The variation trends in the spray characteristics of both the main and pilot stages are further confirmed by SMD measurements. For the main stage spray, greater initial momentum transfers the jet into a broader range, improving atomization. Additionally, the larger the axial position, the smaller its influence on SMD. Consequently, the swirl atomizer examined in this study achieves superior atomization within the lower operational conditions, providing a theoretical foundation and data support for the design of a high-performance swirl atomizer.
Author Contributions
Conceptualization, C.L.; Methodology, W.J., Y.L. and S.W.; Validation, W.J.; Formal analysis, W.J. and Y.M.; Investigation, Z.Q. and F.L.; Resources, J.Y.; Data curation, W.J. and Z.Q.; Writing—original draft, W.J.; Writing—review & editing, Y.L. and C.L.; Supervision, D.M. and K.W.; Project administration, S.W. and G.X.; Funding acquisition, C.L. and G.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science and Technology Major Project (J2019-III-0005-0048) and National Science and Technology Major Project (J2019-III-0002-0045) and supported by the Strategic Priority Research Program of the Chinese Academy of Sciences, Grant No. XDC0142002.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chang, C.T.; Holdeman, J.D. Low Emissions RQL Flametube Combustor Test Results. NTRS; 2001. Available online: https://ntrs.nasa.gov/api/citations/20030062196/downloads/20030062196.pdf (accessed on 1 April 2025).
- Dhanuka, S.K.; Temme, J.E.; Driscoll, J.F.; Mongia, H.C. Vortex-shedding and mixing layer effects on periodic flashback in a lean premixed prevaporized gas turbine combustor. Proc. Combust. Inst. 2009, 32, 2901–2908. [Google Scholar] [CrossRef]
- Tacina, R.; Wey, C.; Laing, P.; Mansour, A. Sector Tests of a Low NOx, Lean-Direct-Injection, Multipoint Integrated Module Combustor Concept. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002; pp. 533–544. [Google Scholar]
- Candel, S. Combustion dynamics and control: Progress and challenges. Proc. Combust. Inst. 2002, 29, 1–28. [Google Scholar] [CrossRef]
- Yang, Z.; Breisacher, K.; Oyediran, A. Combustion-acoustic instability analysis of LPP combustor. II-Longitudinal modes. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000. [Google Scholar]
- Tacina, R.; Mao, C.-P.; Wey, C. Experimental investigation of a multiplex fuel injector module for low emission combustors. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 827. [Google Scholar]
- Liu, Y.; Sun, X.; Sethi, V.; Nalianda, D.; Li, Y.-G.; Wang, L. Review of modern low emissions combustion technologies for aero gas turbine engines. Prog. Aerosp. Sci. 2017, 94, 12–45. [Google Scholar] [CrossRef]
- Lazik, W.; Doerr, T.; Bake, S.; Bank, R.V.D.; Rackwitz, L. Development of Lean-Burn Low-NOx Combustion Technology at Rolls-Royce Deutschland. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; pp. 797–807. [Google Scholar]
- Mosbach, T.; Sadanandan, R.; Meier, W.; Eggels, R. Experimental Analysis of Altitude Relight Under Realistic Conditions Using Laser and High-Speed Video Techniques. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; pp. 523–532. [Google Scholar]
- Antoshkiv, O.; Bake, S.; Berg, H.-P. Spray Phenomena and their Influence on the Ignition Performance of a Modern Aeroengine Combustor. In Proceedings of the 22nd European Conference on Liquid Atomization and Spray Systems, Como Lake, Italy, 8–10 September 2008. [Google Scholar]
- Read, R.W.; Rogerson, J.W.; Hochgreb, S. Planar Laser-Induced Fluorescence Fuel Imaging During Gas-Turbine Relight. J. Propuls. Power 2013, 29, 961–974. [Google Scholar] [CrossRef]
- Feng, X.; Suo, J.; Li, Q.; Zheng, L. Modal Decomposition Study of the Non-Reactive Flow Field in a Dual-Swirl Combustor. Energies 2023, 16, 6182. [Google Scholar] [CrossRef]
- Wu, P.-K.; Kirkendall, K.A.; Fuller, R.P.; Nejad, A.S. Breakup processes of liquid jets in subsonic crossflows. J. Propuls. Power 1997, 13, 64–73. [Google Scholar] [CrossRef]
- Wu, P.-K.; Kirkendall, K.A.; Fuller, R.P.; Nejad, A.S. Spray structures of liquid jets atomized in subsonic crossflows. J. Propuls. Power 1998, 14, 173–182. [Google Scholar] [CrossRef]
- Lubarsky, E.; Shcherbik, D.; Bibik, O.; Gopala, Y.; Bennewitz, J.W.; Zinn, B.T. Fuel jet in cross flow-Experimental study of spray characteristics. In Advanced Fluid Dynamics; IntechOpen: London, UK, 2012; pp. 59–80. [Google Scholar]
- Tambe, S.B.; Jeng, S.-M. A Study of Liquid Jets Injected Transversely into a Swirling Crossflow. In Proceedings of the 21st Annual Conference on Liquid Atomization and Spray Systems, Zhenjiang, China, 23–26 October 2020. [Google Scholar]
- Patil, S.; Sahu, S. Liquid jet core characterization in a model crossflow airblast atomizer. Int. J. Multiph. Flow 2021, 141, 103688. [Google Scholar] [CrossRef]
- Eslamian, M.; Amighi, A.; Ashgriz, N. Atomization of Liquid Jet in High-Pressure and High-Temperature Subsonic Crossflow. AIAA J. 2014, 52, 1374–1385. [Google Scholar] [CrossRef]
- Lee, K.; Aalburg, C.; Diez, F.J.; Faeth, G.M.; Sallam, K.A. Primary Breakup of Turbulent Round Liquid Jets in Uniform Crossflows. AIAA J. 2007, 45, 1907–1916. [Google Scholar] [CrossRef]
- Patil, S.; Sahu, S. Breakup dynamics and near nozzle spray fluctuations in a twin-jet cross-flow airblast atomizer. At. Sprays 2019, 29, 217–250. [Google Scholar] [CrossRef]
- Hsiang, L.P.; Faeth, G.M. Near-limit drop deformation and secondary breakup. Multiph. Flow 1992, 18, 635–652. [Google Scholar] [CrossRef]
- Gong, X.; Choi, K.J.; Cernansky, N.P. Lean Direct Wall Injection Mode Atomization of Liquid Jets in Swirling Flow. J. Propuls. Power 2006, 22, 209–211. [Google Scholar] [CrossRef]
- Fujiwara, H.; Matsuura, K.; Shimodaira, K.; Hayashi, S.; Kobayashi, M.; Oda, T.; Horikawa, A.; Matsuyama, R.; Ogata, H.; Kinoshita, Y. Suppression of NOx Emission of a Lean Staged Combustor for an Aircraft Engine. In Proceedings of the ASME Turbo Expo 2011: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Sikroria, T.; Kushari, A.; Syed, S.; Lovett, J.A. Experimental Investigation of Liquid Jet Breakup in a Cross Flow of a Swirling Air Stream. J. Eng. Gas Turbines Power-Trans. ASME 2014, 136, 061501. [Google Scholar] [CrossRef]
- Song, J.; Cain, C.C.; Lee, J.G. Liquid Jets in Subsonic Air Crossflow at Elevated Pressure. In Proceedings of the ASME Turbo Expo: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Fang, C.; Liu, Y.; Wang, S.; Liu, C.; Liu, F.; Yang, J.; Wang, K.; Mu, Y.; Xu, G.; Zhu, J. Aerodynamic effect on atomization characteristics in a swirl cup airblast fuel injector. Phys. Fluids 2023, 35, 103319. [Google Scholar] [CrossRef]
- Broumand, M.; Birouk, M. Liquid jet in a subsonic gaseous crossflow: Recent progress and remaining challenges. Prog. Energy Combust. Sci. 2016, 57, 1–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).