1. Introduction
In recent years, the collapse of transmission towers due to the combined effects of foundation sliding and wind loads has become an increasingly frequent and critical concern [
1,
2]. Such foundation deformations can manifest as settlement, displacement, or tilting, ultimately leading to significant structural damage or even the total collapse of towers [
3,
4]. A notable example occurred in October 2013, when Typhoon Fitow made landfall in Wenzhou, Zhejiang Province. The severe winds and landslides during this event caused extensive damage to the power infrastructure, resulting in the collapse of multiple transmission towers. These incidents highlight the vulnerability of transmission towers under changing foundation conditions and extreme wind loads.
Transmission towers face a dual threat from changes in foundation conditions (such as settlement, tilting, and horizontal displacement) and extreme wind loads. Uneven foundation settlement and horizontal displacement can lead to changes in the force distribution of the transmission tower, causing deformation, damage, and structural failure [
5,
6]. Furthermore, tower failures directly attributed to extreme wind loads alone are also common and widely documented [
7,
8,
9,
10].
Research on the impact of foundation condition changes on transmission towers has been partially explored by scholars. In terms of experimental analysis, Tian et al. [
5] studied the effects of foundation deformation on transmission towers and analyzed the response behavior of transmission towers under foundation deformation. Tian et al. [
11] also studied the seismic fragility analysis of a transmission tower-line system using shake table tests. Through full-scale tests, Wang [
12] studied the failure mechanism of steel tubular transmission towers and concluded that the pole’s eventual collapse resulted from the buckling instability of the compression members in its legs. White [
13] treated transmission towers as important surface features and studied the behavior of transmission towers in mining areas affected by foundation movements. Tan [
14], Ye [
15], and Dou [
16] et al. conducted proportional simulation experiments to analyze the changes in the bearing capacity of different tower types under surface deformation effects. Rao et al. [
17] experimentally investigated the failure causes of damaged transmission towers and compared the results with relevant regulatory provisions. Shu et al. [
18] performed scaled model tests on transmission towers with foundation displacement, revealing that foundation displacement significantly affects the truss members near the support and pointing out the severe adverse effects of wind loads on transmission tower bearing capacity under foundation sliding conditions [
19].
In terms of simulation analysis, Ahmed et al. [
20] studied the impact of foundation deformation on the safety of transmission towers under bolt slip conditions in steel towers. Yang [
21] conducted finite element simulations to analyze the axial force and its variation trends of components under different scenarios (such as foundation settlement, sliding, and tilting), determining the foundation deformation limits of a transmission tower under various conditions. Then, Yang [
22] also evaluated the stress state and structural reinforcement methods for transmission towers with foundation settlement. Shu [
23,
24,
25] studied the resistance of transmission towers in mining areas to foundation deformation under different conditions and analyzed the impact of foundation deformation on transmission tower safety. Yang et al. [
26] conducted safety analyses of foundation deformation in transmission towers in mining areas under various conditions, revealing the internal force and deformation patterns of critical tower components. Zheng et al. [
27] used finite element simulations to study the maximum stress in transmission towers under different conditions and analyzed the deformation patterns of tower legs caused by tilting and landslides. Wang et al. [
28] analyzed the stress variation patterns of key members based on the foundation deformation studies under different conditions in landslide areas.
These studies indicate that transmission towers are particularly sensitive to foundation tilting, and efforts should be made to minimize the impact of foundation sliding on the structure. However, most existing studies have focused only on the single impact of foundation displacement and have not thoroughly explored the failure process and safety limits of transmission towers under the combined effects of foundation sliding and wind loads.
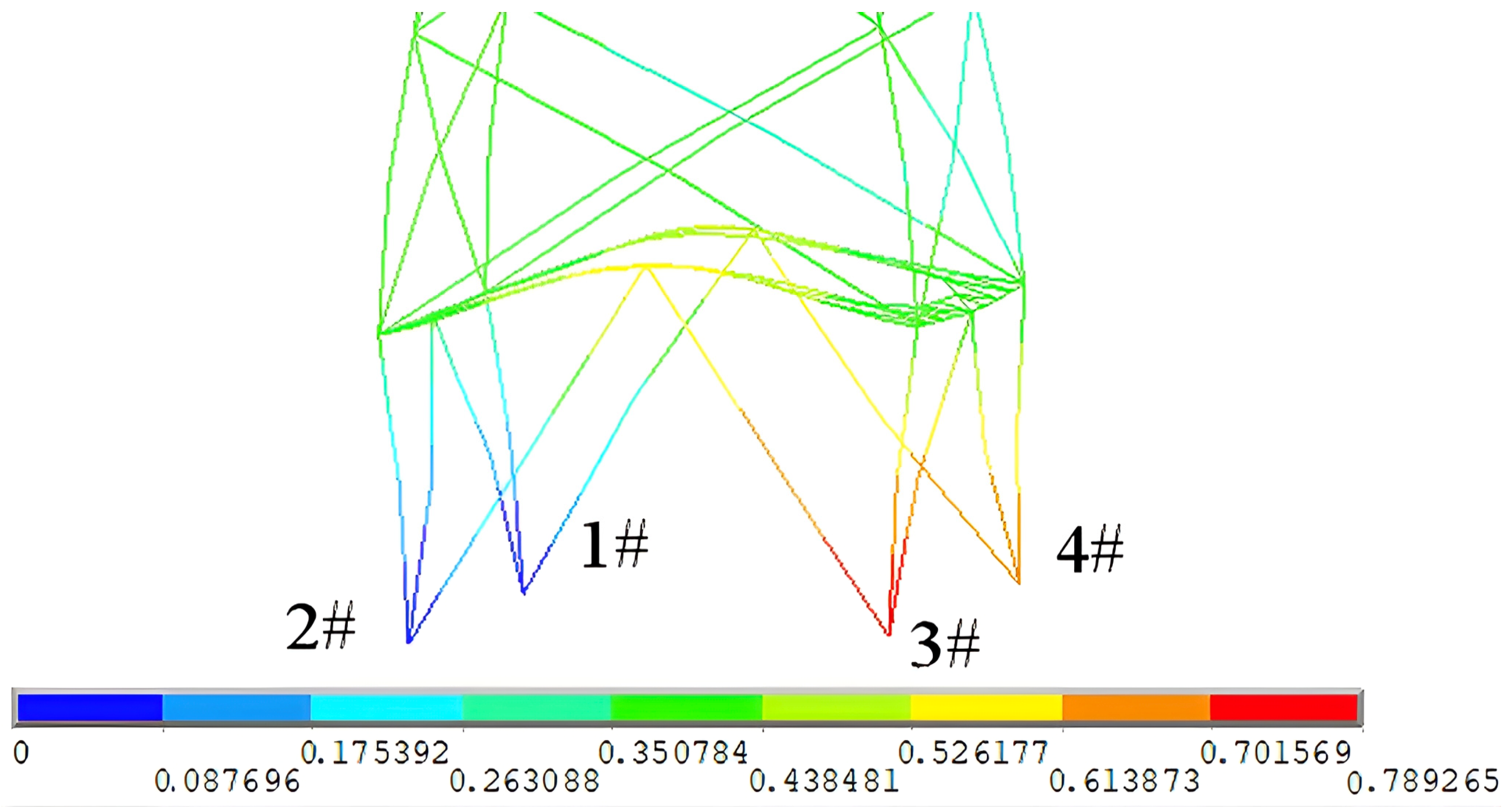
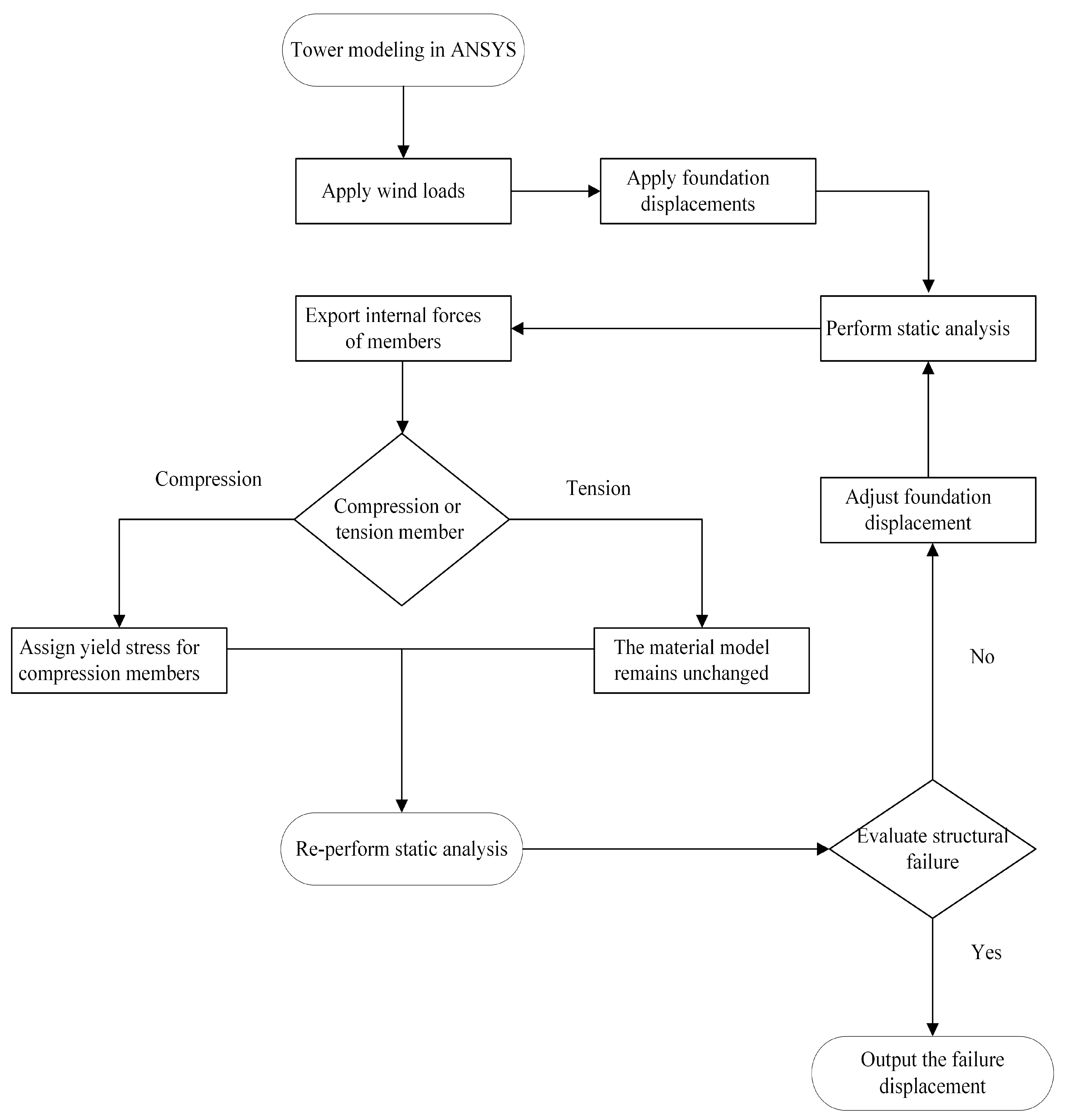
The main work of this study includes the following components: (1) We utilized a real-world transmission tower foundation sliding incident as a case study, in which ANSYS 18.0 finite element software and the allowable stress criterion were employed to conduct a numerical back-analysis of the sliding event. The simulation results were then compared with observed field damage to validate the reliability of the finite element model. (2) We carried out a sensitivity analysis of foundation sliding to compare the critical failure displacements between single-foundation sliding and same-side foundation sliding scenarios. (3) We investigated the combined effects of foundation sliding and wind loads on the structural responses of transmission towers and established a critical displacement threshold for tower failure to serve as a reference for damage assessment and engineering intervention.
5. Discussion
This study investigated the structural responses of a transmission tower under the combined effect of two wind load cases and seven foundation displacement scenarios. A systematic analysis was conducted to assess the influence of foundation sliding on the structural response and member failure paths. Based on the results, the following conclusions are drawn:
- (1)
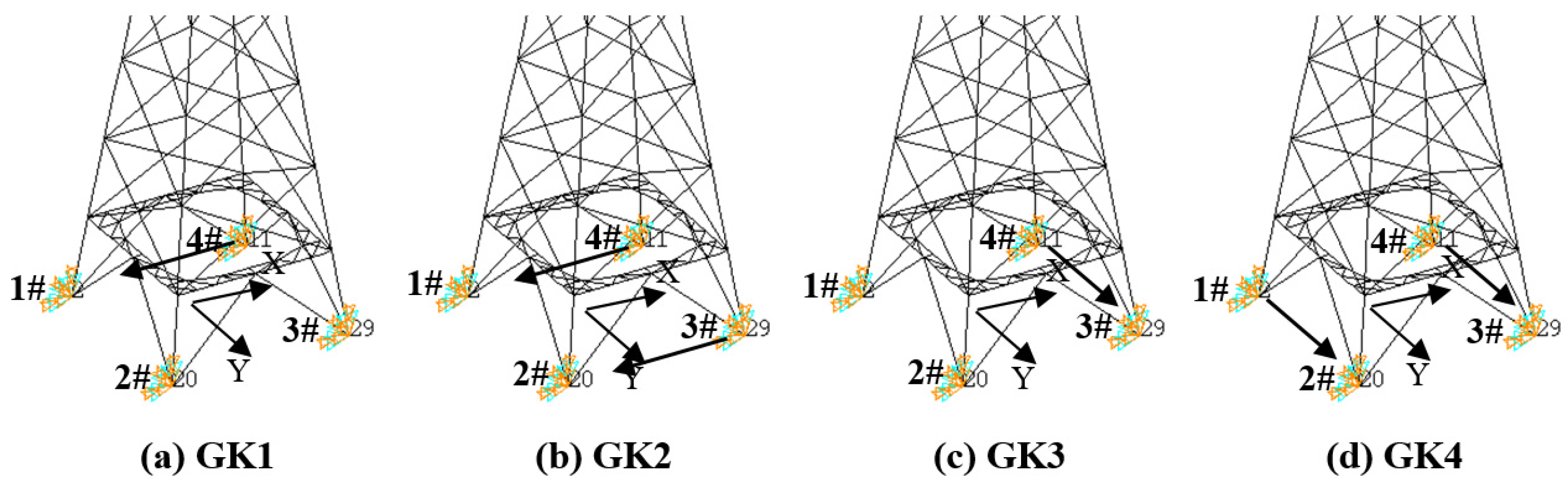
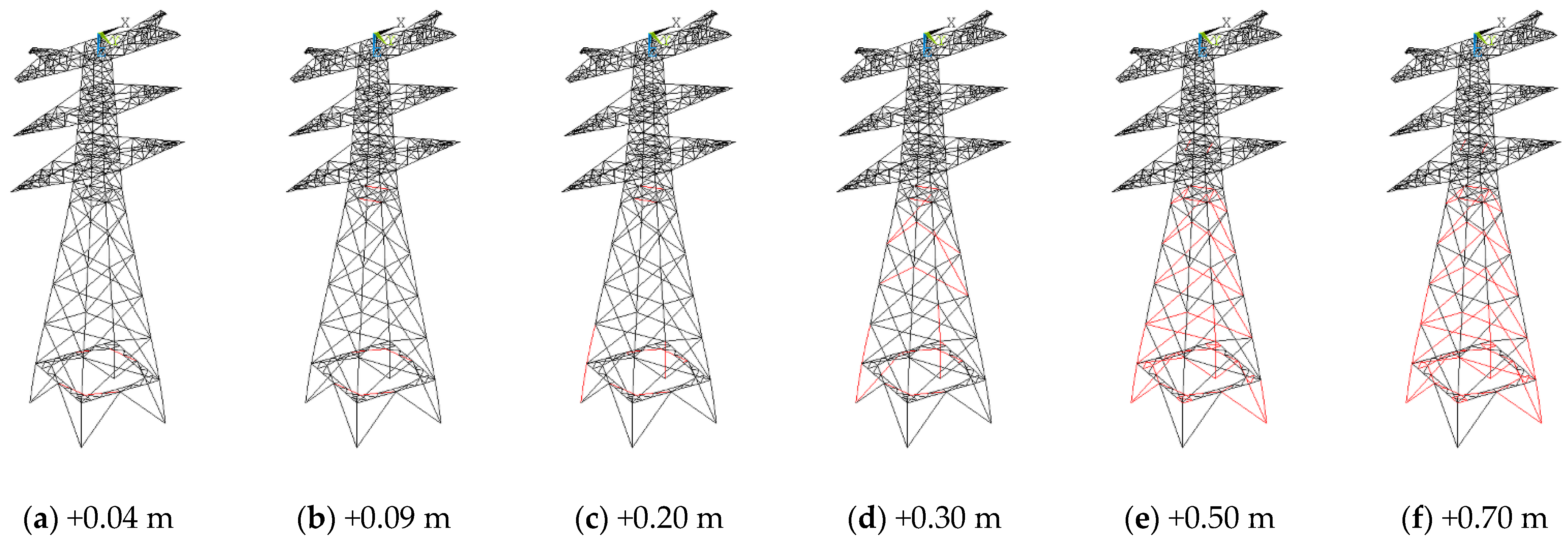
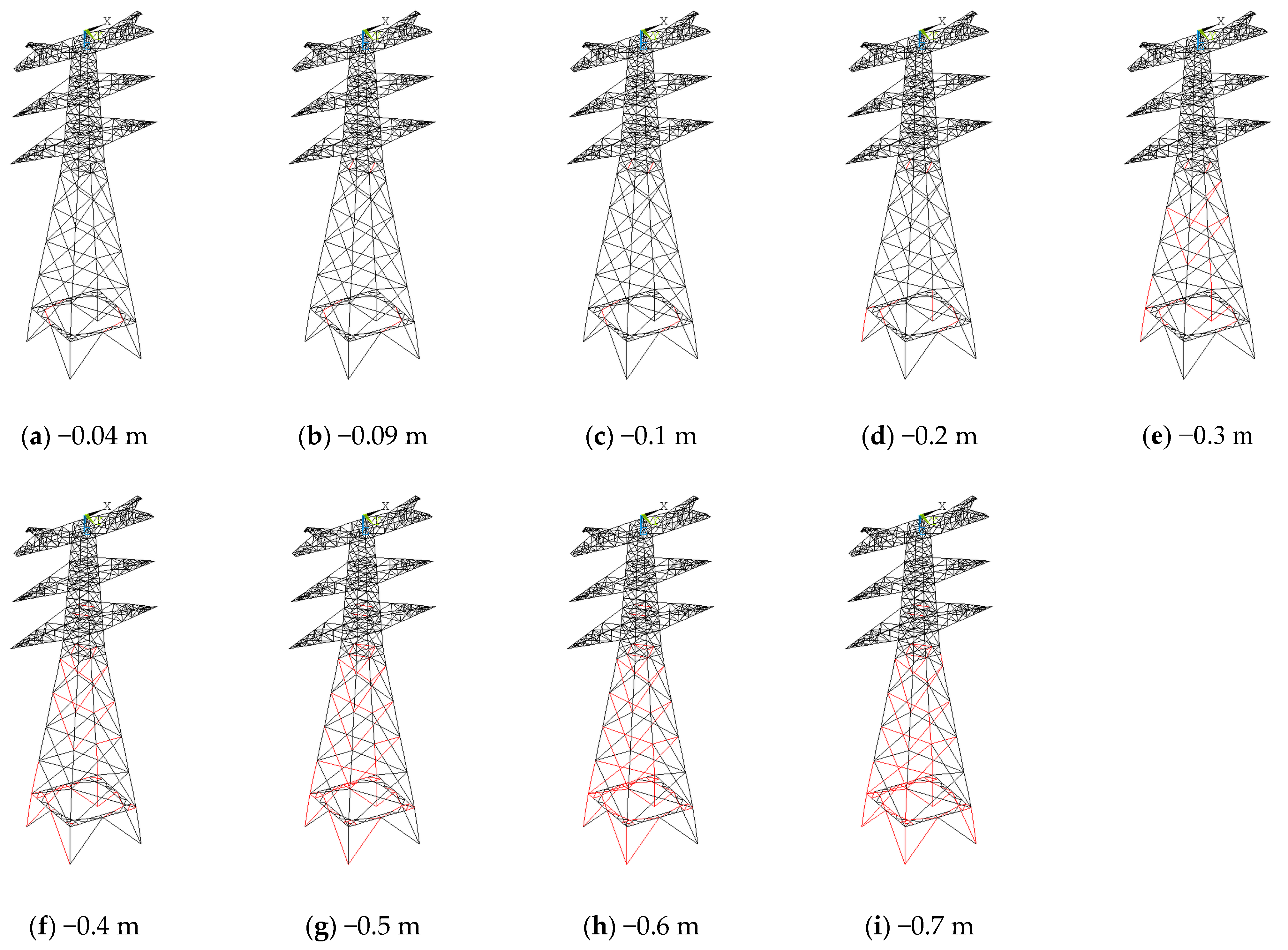
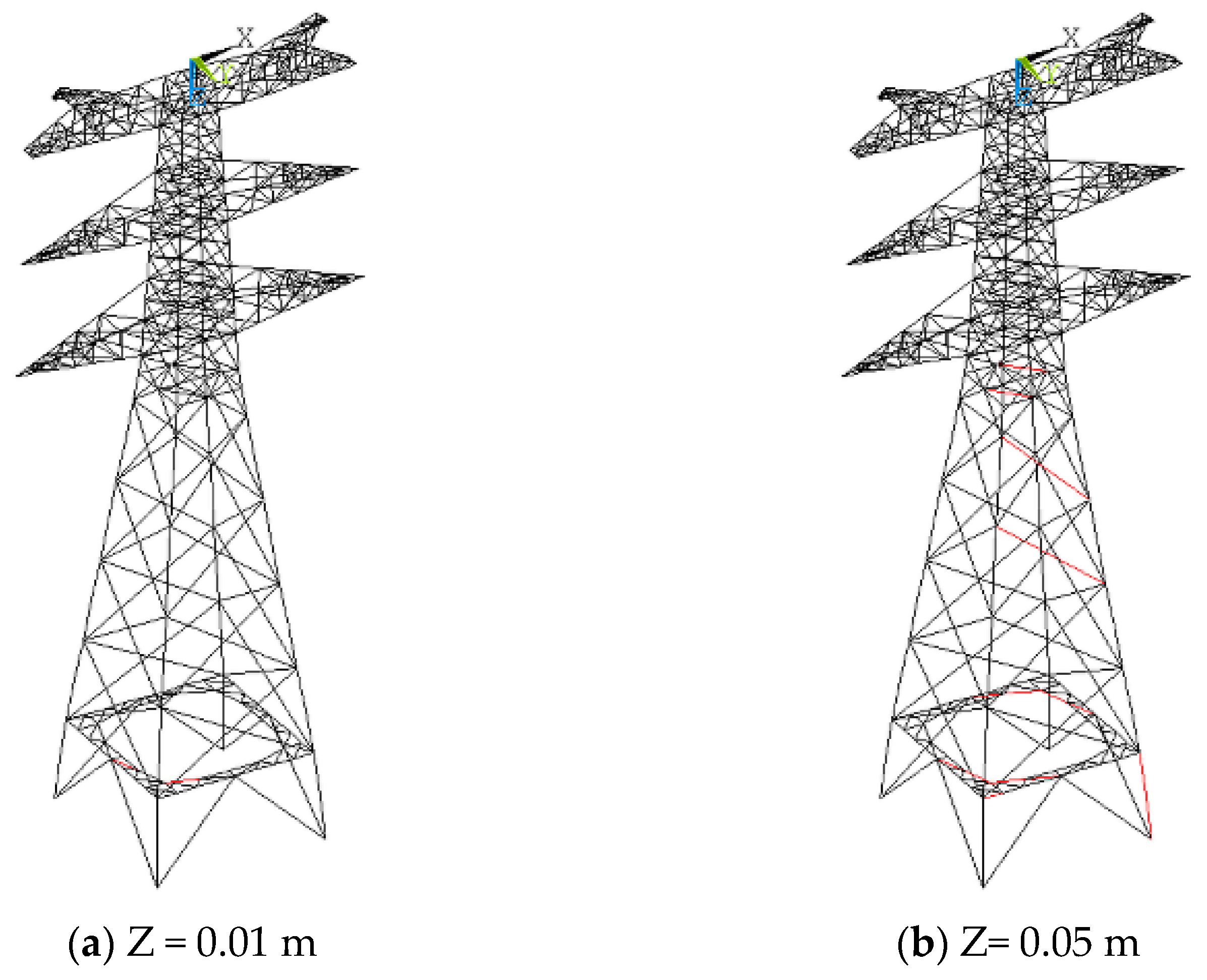
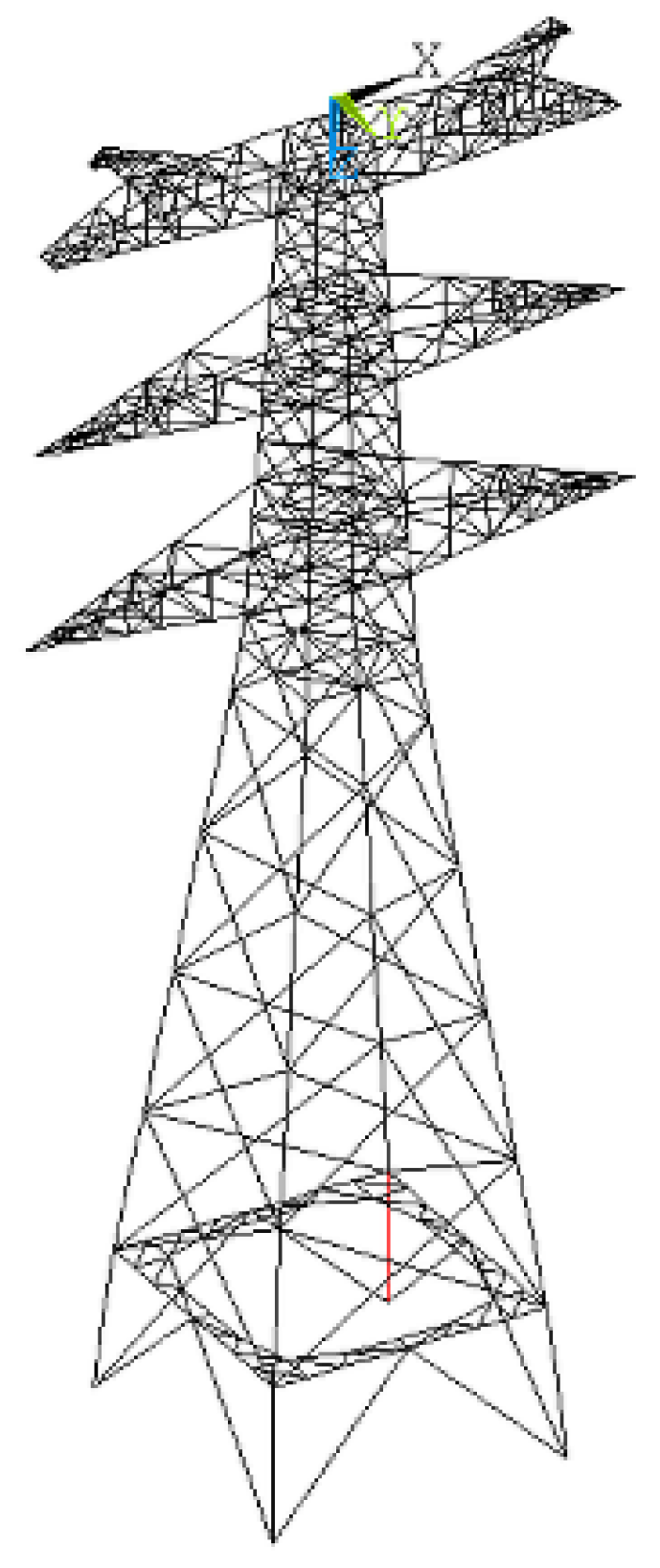
Failure path evolution was concentrated in the bottom part of the tower on the sliding side.
The simulation results show that, regardless of the displacement scenario, member failure consistently initiated at the junction between the bracing plane and the tower leg on the sliding side. It then progressively propagated to adjacent diagonal and main members, forming a failure chain characterized by a “bottom-to-top, local-to-global” evolution pattern.
- (2)
Single-foundation sliding poses greater risk than same-side simultaneous sliding.
Consistent with the accident back-analysis presented in
Section 3, the results in
Section 4 further confirm that, under the same displacement magnitude, single-foundation sliding triggered member failure at a smaller critical displacement and induced a more severe structural response compared to simultaneous sliding of foundations on the same side.
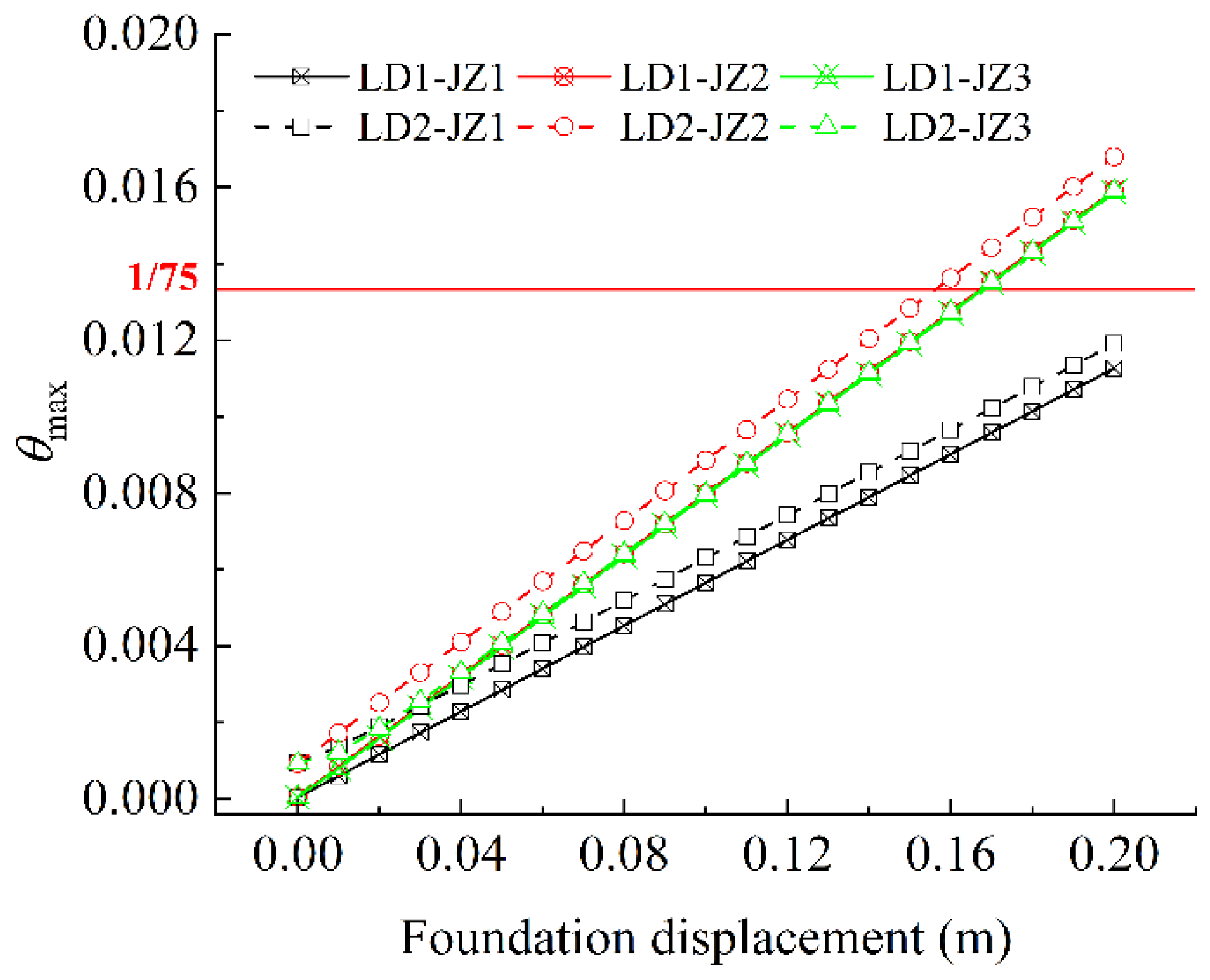
For example, under scenario JX1-LD2, the first bracing member of the transmission tower failed at a sliding displacement of 0.07 m, whereas under scenario JX2-LD2, failure was delayed until the foundation displacement reached 0.09 m.
This was primarily due to the severe asymmetric deformation caused by single-foundation sliding, which leads to localized overstressing and earlier buckling failure in components. Therefore, even minor single-foundation displacements warrant heightened engineering attention and preventive measures.
- (3)
The combined effect of wind loads and foundation sliding significantly amplifies structural risk.
The interaction between foundation sliding and wind loads exhibited a synergistic amplification effect, whereby the critical failure displacement under extreme-wind-load conditions was reduced by 10% to 30% compared to normal-wind-load conditions. Furthermore, the relative orientation between the sliding foundation and the wind direction influenced the failure path, with the most unfavorable scenario occurring when the foundation slid inward and aligns with the direction of wind.
- (4)
Safety warning thresholds for foundation sliding are proposed.
The critical collapse displacement of a transmission tower is primarily governed by the failure of its main structural members. Thus, using tower collapse as the criterion, the foundation displacement corresponding to the failure of main members is defined as the critical threshold for safety warning, as shown in
Table 9.
If the measured foundation lateral displacement or settlement exceeds the threshold values, and abnormal deformations are observed in the bracing members, an evaluation process should be initiated to determine whether the structural reinforcement or replacement of the transmission tower is necessary.