Review of the Discrete-Ordinates Method for Particle Transport in Nuclear Energy

Abstract

The advantages and recent advancements of the Discrete-Ordinates (S_N) Method have established its widespread adoption in particle transport calculations for nuclear energy systems. The mathematical foundations and diverse applications of the S_N method are comprehensively summarized in this review. Recent advances are critically evaluated, with particular emphasis placed on advanced discretization techniques, high-performance computing implementations, and hybrid coupling strategies with MC, MOC method, and so on. Despite these developments, challenges remain, including the need for high-fidelity simulations, optimization of computational performance, and the complexity introduced by temporal dependencies in dynamic radiation field calculations, which necessitates innovative numerical methods. Future developments of the S_N method are anticipated to address these challenges through enhanced high-fidelity numerical simulation, robust high-performance computing frameworks, multi-physics field coupling, and AI integration. These developments advance the industrial-scale implementation of the S_N method in nuclear energy applications, enabling efficient and accurate analyses of complex reactor systems.

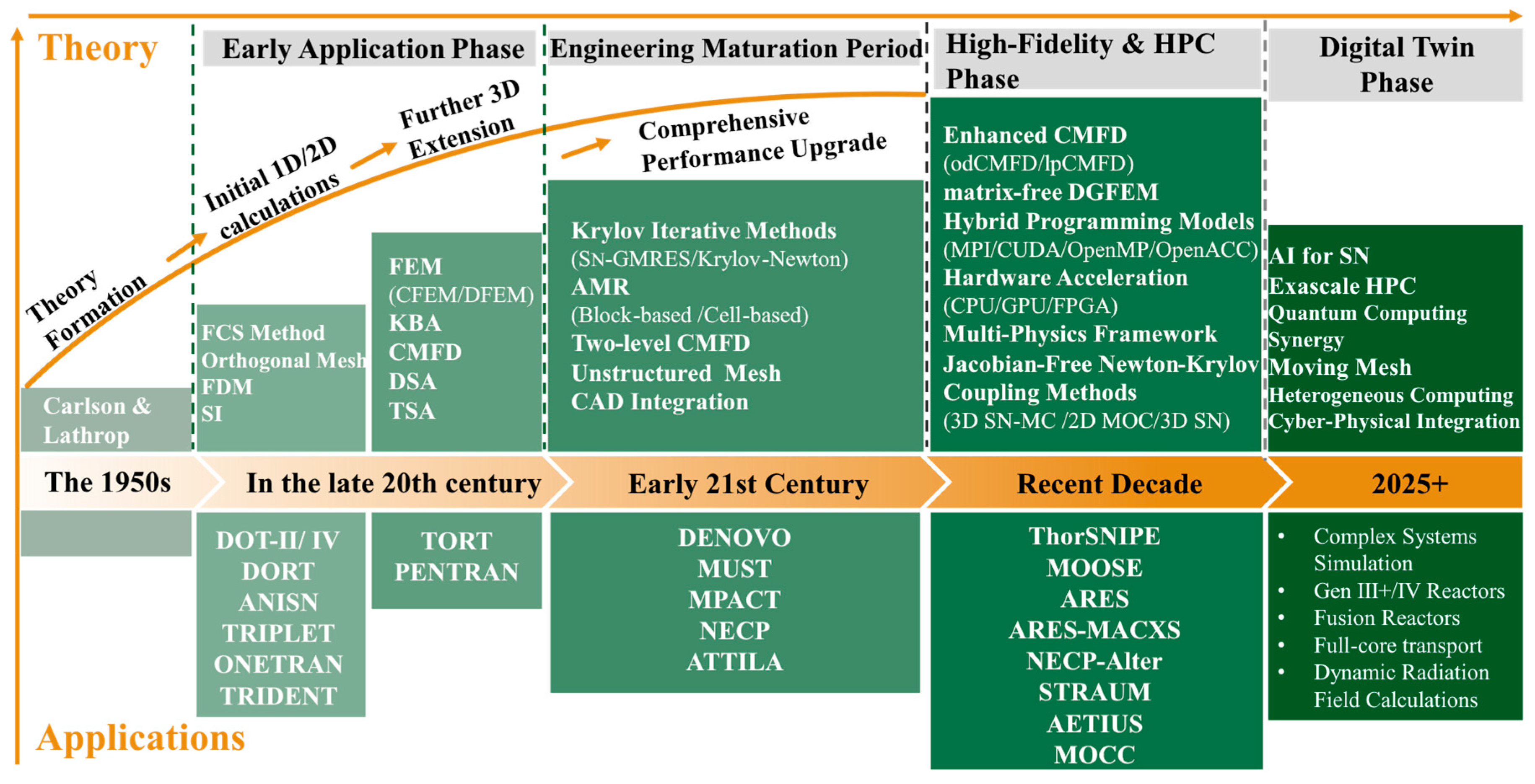
1. Introduction

The S_N method is a cornerstone numerical technique for solving particle transport equations. Here, ‘N’ represents the order of the angular quadrature, determining the number of discrete angular directions used in the calculation. Extensive application has been found in nuclear energy, particularly in core neutronics simulations and radiation shielding design. Its core principle involves directly discretizing angular variables, converting continuous angular space into quadrature sets composed of discrete directions and their corresponding weights. Concurrent discretization in energy and spatial domains transforms transport equations into linear algebraic systems, solved through source iteration (including inner and outer iterations) to determine the spatial distribution of particle flux. Owing to the independent discretization of each variable, formal independence among the spatial, angular, and energy variables is established in the resulting system, allowing separate treatment in the numerical solution process. This independence permits adjustment of the discretization direction as a parameter without necessitating algorithmic restructuring. This confers significant computational efficiency advantages, particularly in deep-penetration problems, and enhances its suitability for engineering applications.

The historical development of the S_N method can be traced back to the 1950s, when the mathematical framework was formalized by Carlson and Lathrop for reactor physics simulations [1,2]. Algorithms based on orthogonal coordinate systems and structured grids established theoretical foundations. The widespread adoption of the S_N method for nuclear reactor neutronics analysis was facilitated by its high efficiency and scalability. However, its application was initially restricted to low-dimensional problems due to the computational resources available at that time.

In the late 20th century, significant advancements in discretization techniques and high-performance computing (HPC) facilitated the extension of the S_N method to three-dimensional applications. Among these, the discontinuous finite element method (DFEM) is considered one of the most impactful, significantly influencing the all-variable discretization of the transport equations [3] (pp. 74–75). The DFEM, employing a segmented polynomial approximation of space and permitting weak continuity conditions at cell boundaries, was first integrated into the S_N framework by Reed and Hill. As a result, a substantial enhancement in the capability to model complex geometries was achieved [4,5,6]. The engineering applicability of S_N methods has been further expanded through the adoption of unstructured meshing and adaptive refinement techniques. Geometric accuracy is improved by these methods through flexible spatial discretization; nevertheless, increased memory overhead is introduced due to the storage requirements for cell adjacencies and vertex coordinates. Adaptive refinement dynamically optimizes mesh density based on local error estimation, reducing computational effort while maintaining accuracy; however, real-time meshing introduces additional overhead. To balance efficiency and accuracy, the Multi-level Octree Mesh (MLOM) is utilized to perform local refinement of the mesh, based on material properties or source strength, prior to sweeping the process of solving the transport equation along characteristic directions in sequence. This approach effectively minimizes computational costs while preserving computational accuracy. Additionally, acceleration methods such as diffusion synthesis acceleration (DSA) and coarse mesh finite difference (CMFD), combined with parallel strategies like the Koch–Baker–Alcouffe (KBA) algorithm and the MPI/OpenMP hybrid programming model, support the application of the S_N method to large-scale 3D problems.

In the past decade, architectural innovations in high-performance computing chips (CPU/GPU/FPGA) and advancements in exascale supercomputers have catalyzed a paradigm shift in nuclear energy research. A transition has occurred from traditional engineering-driven approaches to high-performance numerical simulations and digital twin-enabled applications. Advanced nuclear energy systems, including Generation III+ reactors, Generation IV reactors (sodium-cooled fast reactors, lead-bismuth-cooled reactors, molten salt reactors), and fusion reactors (such as ITER and EAST), necessitate (1) high-fidelity modeling of heterogeneous core structures, (2) transient safety analysis incorporating spatiotemporal coupling effects, (3) dynamic radiation field simulations, and (4) real-time virtual-reality coupling for digital twin platforms. These requirements present multidimensional challenges to the precision and efficiency of the S_N method while simultaneously driving its evolution toward cyber–physical integration, as illustrated in Figure 1.

This paper presents a systematic review of the S_N method in nuclear energy applications, spanning its theoretical underpinnings, practical implementations, and cutting-edge methodological innovations. The review is structured as follows: Section 2 presents the fundamental theory of the S_N method, including angular quadrature formulations, spatial discretization schemes, and iterative solution strategies. Section 3 provides a comprehensive review of S_N applications in nuclear energy. Section 4 examines advancements in S_N methodology, focusing on ray effect mitigation, enhanced discretization schemes, high-performance computing implementations, hybrid algorithmic frameworks, and coupling with other complementary methods for improved computational efficiency and accuracy. Section 5 analyzes current challenges and future directions in the S_N method. Section 6 presents concluding remarks.

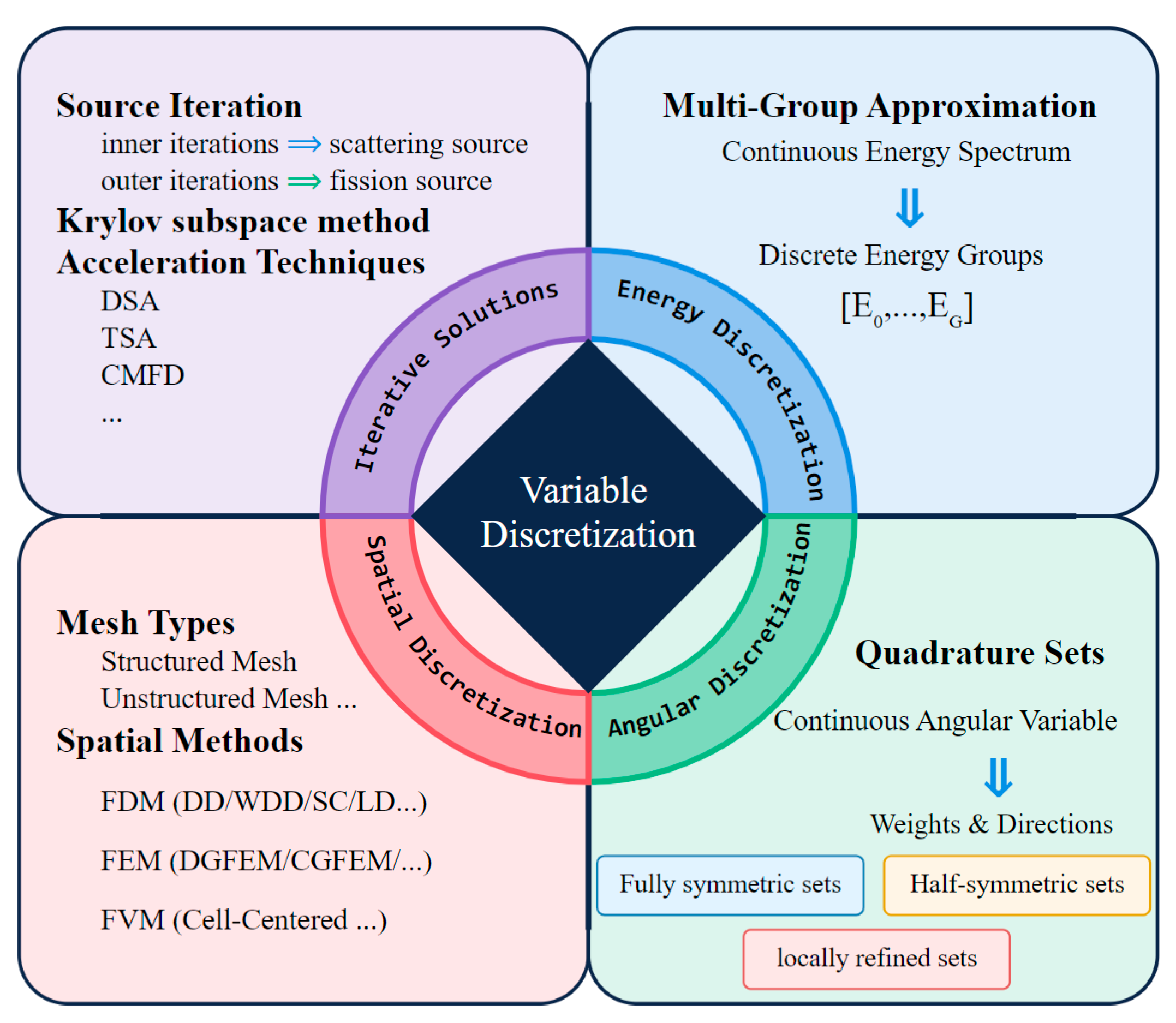
2. Fundamental Theory of the S_N Method

The S_N method is a cornerstone numerical technique for solving particle transport equations. In this section, the fundamental concept of the linear Boltzmann equation (LBE) is first introduced. The direct discretization of energy, angular, and spatial variables is then described, transforming the continuous problem into a system of linear algebraic equations. The theoretical framework is constructed through an examination of how Source Iteration (SI) and the principles of Krylov subspace methods are formulated and applied.

2.1. Linear Boltzmann Equation

The behavior of neutrons in a system is described by the linear Boltzmann equation, which characterizes their spatial distribution and temporal evolution. This equation is a function of time $t$, energy $E$, angle $\overrightarrow{\mathsf{\Omega }}\left(\theta ,\varphi \right)$, spatial variables $\overrightarrow{r}\left(x,y,z\right)$, and involves seven unknowns. This system is then solved to determine the neutron flux distribution $\psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E,t)$ within the core region. Additionally, the condition for the presence of a neutron-multiplying medium can be expressed as:

$$\begin{array}{l}{\displaystyle \frac{1}{v}}{\displaystyle \frac{\partial \psi }{\partial t}}(\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E,t)+\overrightarrow{\mathsf{\Omega }}\cdot \nabla \psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E,t)+{\mathsf{\Sigma }}_t(\overrightarrow{r},E)\psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E,t)=\\ {\displaystyle {\int }_{4\pi }{\displaystyle {\int }_0^{\infty }{\mathsf{\Sigma }}_s}}(\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{\prime }\to \overrightarrow{\mathsf{\Omega }},E^{\prime }\to E)\psi (\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{\prime },E^{\prime },t)\mathrm{d}{E}^{\prime }\mathrm{d}{\overrightarrow{\mathsf{\Omega }}}^{\prime }+\\ {\displaystyle \frac{\chi (\overrightarrow{r},E)}{4\pi }}{\displaystyle {\int }_{4\pi }{\displaystyle {\int }_0^{\infty }(1-\beta (\overrightarrow{r},E^{\prime })}})v{\mathsf{\Sigma }}_f(\overrightarrow{r},E^{\prime })\psi (\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{\prime },E^{\prime },t)\mathrm{d}{E}^{\prime }\mathrm{d}{\overrightarrow{\mathsf{\Omega }}}^{\prime }+\\ {\displaystyle \sum _{k=1}^{Ndg}\frac{{\chi }_k(\overrightarrow{r},E)}{4\pi }}{C}_k(\overrightarrow{r},t){\lambda }_k+{\displaystyle \frac{1}{4\pi }}Q(\overrightarrow{r},E,t)\end{array}$$

(1)

The boundary and initial conditions are specified as follows:

$$\begin{array}{l}\psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E,t)={\psi }^{boundary}(\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E,t),\overrightarrow{r}\in \partial V,\overrightarrow{\mathsf{\Omega }}\cdot \overrightarrow{n}<0,0<E<\infty ,0<t\\ \psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E,0)={\psi }^0(\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E),\overrightarrow{r}\in V,\overrightarrow{\mathsf{\Omega }}\in 4\pi ,0<E<\infty \\ C_k(\overrightarrow{r},0)=C_k^0(\overrightarrow{r}),\overrightarrow{r}\in V\end{array}$$

(2)

The main symbols and physical quantities appearing in the linear Boltzmann equation are summarized in

Table 1. Definitions of symbols in the linear Boltzmann equation.

Symbol	Description	Unit
$\nu$	neutron speed	$\mathrm{m}/\mathrm{s}$
${\mathsf{\Sigma }}_t$	macroscopic total cross-section	$\mathrm{c}{\mathrm{m}}^{-1}$
${\mathsf{\Sigma }}_s$	macroscopic scattering cross-section	$\mathrm{c}{\mathrm{m}}^{-1}$
${\mathsf{\Sigma }}_f$	macroscopic fission cross-section	$\mathrm{c}{\mathrm{m}}^{-1}$
$\chi (\overrightarrow{r},E)$	fission neutron energy spectrum (probability density at $r$ with energy within $\mathrm{d}E$ about $E$)	-
${\displaystyle \sum _{k=1}^{Ndg}\frac{{\chi }_k(\overrightarrow{r},E)}{4\pi }}{C}_k(\overrightarrow{r},t){\lambda }_k$	delayed neutron source	-
$N_{dg}$	delayed neutron groups (representing all delayed neutron precursors)	-
$C_k(\overrightarrow{r},t)$	concentration of the k-th group delayed neutron precursor	$\mathrm{c}{\mathrm{m}}^{-3}$
${\lambda }_k$	decay constant	${\mathrm{s}}^{-1}$
${\beta }_k$	delayed neutron yield of the k-th group	-
$\beta ={\displaystyle \sum _{k=1}^{Ndg}{\beta }_k}$	total delayed neutron yield	-

.

Additionally, the time-dependent concentration of the parent nuclei can be expressed as:

$${\displaystyle \frac{\partial C_k(\overrightarrow{r},t)}{\partial t}}={\displaystyle {\int }_{4\pi }{\displaystyle {\int }_0^{\infty }{\beta }_k(\overrightarrow{r},E^{\prime })}}v{\mathsf{\Sigma }}_f(\overrightarrow{r},E^{\prime })\psi (\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{\prime },E^{\prime },t)\mathrm{d}{E}^{\prime }\mathrm{d}{\overrightarrow{\mathsf{\Omega }}}^{\prime }-{\lambda }_k{C}_k(\overrightarrow{r},t)$$

(3)

When the delayed neutron precursor density reaches equilibrium and the inhomogeneous source term is omitted, the steady-state particle transport equation can be written in the following eigenvalue form:

$$\begin{array}{l}\overrightarrow{\mathsf{\Omega }}\cdot \nabla \psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E)+{\mathsf{\Sigma }}_t(\overrightarrow{r},E)\psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E)=\\ {\displaystyle {\int }_{4\pi }{\displaystyle {\int }_0^{\infty }{\mathsf{\Sigma }}_s}}(\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{\prime }\to \overrightarrow{\mathsf{\Omega }},E^{\prime }\to E)\psi (\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{\prime },E^{\prime })\mathrm{d}{E}^{\prime }\mathrm{d}{\overrightarrow{\mathsf{\Omega }}}^{\prime }+\\ {\displaystyle \frac{1}{k}}{\displaystyle \frac{\chi (\overrightarrow{r},E)}{4\pi }}{\displaystyle {\int }_0^{\infty }v{\mathsf{\Sigma }}_f(\overrightarrow{r},E^{\prime })\varphi (\overrightarrow{r},E^{\prime })\mathrm{d}{E}^{\prime }}\end{array}$$

(4)

Here, $k$ denotes the system eigenvalue, and the scalar flux is defined as:

$$\varphi (\overrightarrow{r},E^{\prime })={\displaystyle {\int }_{4\pi }\psi (\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{\prime },E^{\prime })\mathrm{d}{\overrightarrow{\mathsf{\Omega }}}^{\prime }}$$

(5)

High-performance computing and advanced numerical discretization methods are employed to obtain approximate solutions to the linear Boltzmann equation (LBE), which generally lacks analytical solutions in most practical scenarios, as illustrated in Figure 2. Detailed discussions of these computational approaches are provided in the subsequent sections.

2.2. Energy Discretization

Discretization of the energy variable is typically accomplished using the multi-group approximation, in which the continuous energy spectrum of the neutron flux density is partitioned into discrete energy groups, arranged in descending order of energy, as follows:

$$E_0=E_{\max }>E_1>\dots >E_g>\dots >E_{NG-1}>E_{NG}=E_{\min }$$

(6)

In the interval $E_{NG}<E<E_{NG-1}$, the following applies:

$${\psi }_g(\overrightarrow{r},\overrightarrow{\mathsf{\Omega }})={\displaystyle {\int }_{E_g}^{E_{g-1}}\psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E)dE}$$

(7)

$${\chi }_g(\overrightarrow{r})={\displaystyle {\int }_{E_g}^{E_{g-1}}\chi (\overrightarrow{r},E)dE}$$

(8)

$${\mathsf{\Sigma }}_{t,g}(\overrightarrow{r})={\displaystyle \frac{{\displaystyle {\int }_{E_g}^{E_{g-1}}{\mathsf{\Sigma }}_t(\overrightarrow{r},E){\displaystyle {\int }_{4\pi }\psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E)\mathrm{d}\mathsf{\Omega }\mathrm{d}E}}}{{\displaystyle {\int }_{E_g}^{E_{g-1}}{\displaystyle {\int }_{4\pi }\psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E)\mathrm{d}\mathsf{\Omega }\mathrm{d}}}E}}$$

(9)

$${\mathsf{\Sigma }}_{s,g^{\prime }\to g}(\overrightarrow{r})={\displaystyle \frac{{\displaystyle {\int }_{E_g}^{E_{g-1}}{\displaystyle {\int }_{E_g^{\prime }}^{{E^{\prime }}_{g-1}}{\mathsf{\Sigma }}_s(\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{\prime }\to \overrightarrow{\mathsf{\Omega }},E^{\prime }\to E)\varphi (\overrightarrow{r},E^{\prime })\mathrm{d}{E}^{\prime }\mathrm{d}E}}}{{\displaystyle {\int }_{E_g^{\prime }}^{{E^{\prime }}_{g-1}}\varphi (\overrightarrow{r},E^{\prime })\mathrm{d}{E}^{\prime }}}}$$

(10)

$${\mathsf{\Sigma }}_{f,g}(\overrightarrow{r})={\displaystyle \frac{{\displaystyle {\int }_{E_g}^{E_{g-1}}{\mathsf{\Sigma }}_f(\overrightarrow{r},E){\displaystyle {\int }_{4\pi }\psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E)\mathrm{d}\mathsf{\Omega }\mathrm{d}E}}}{{\displaystyle {\int }_{E_g}^{E_{g-1}}{\displaystyle {\int }_{4\pi }\psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }},E)\mathrm{d}\mathsf{\Omega }\mathrm{d}}}E}}$$

(11)

Thus, Equation (4) is transformed into a system of G energy group equations, expressed as:

$$\begin{array}{l}\overrightarrow{\mathsf{\Omega }}\cdot \nabla {\psi }_g(\overrightarrow{r},\overrightarrow{\mathsf{\Omega }})+{\mathsf{\Sigma }}_{t,g}(\overrightarrow{r}){\psi }_g(\overrightarrow{r},\overrightarrow{\mathsf{\Omega }})=\\ {\displaystyle \sum _{g^{\prime }\in G}{\displaystyle {\int }_{4\pi }{\mathsf{\Sigma }}_{s,g^{\prime }\to g}(\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{\prime }\to \overrightarrow{\mathsf{\Omega }}){\psi }_{g^{\prime }}(\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{\prime })\mathrm{d}{\overrightarrow{\mathsf{\Omega }}}^{\prime }}}+\\ {\displaystyle \frac{1}{k}}{\displaystyle \frac{{\chi }_g(\overrightarrow{r})}{4\pi }}{\displaystyle \sum _{g^{\prime }\in G}v{\mathsf{\Sigma }}_{f,g^{\prime }}(\overrightarrow{r}){\varphi }_{g^{\prime }}(\overrightarrow{r})}\end{array}$$

(12)

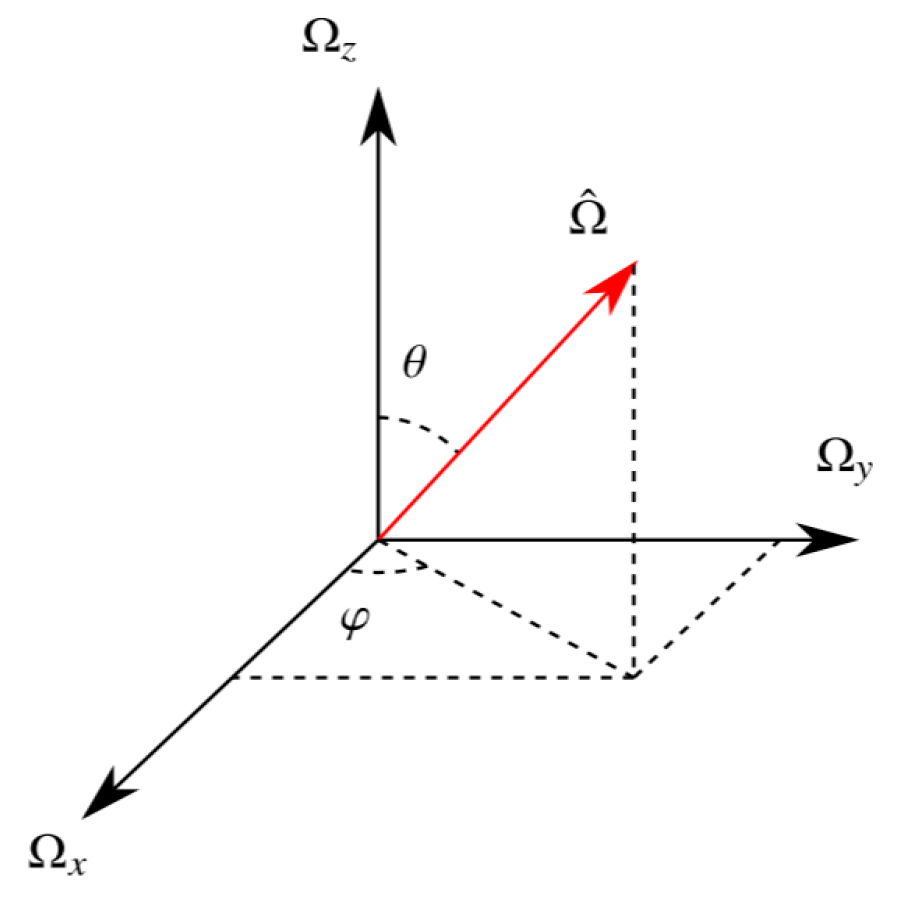
2.3. Angular Discretization

The discretization of the angular variable is achieved by replacing the continuous angular domain with a finite set of discrete directions $\overrightarrow{\mathsf{\Omega }}={\mathsf{\Omega }}_x\overrightarrow{i}+{\mathsf{\Omega }}_y\overrightarrow{j}+{\mathsf{\Omega }}_z\overrightarrow{k}$. $\mu$, $\eta$, and $\xi$ are commonly used to represent the discrete directions, satisfying ${\mu }^2+{\eta }^2+{\xi }^2=1$, with their magnitudes determined by the sine and cosine of the polar angle $\theta$ and the azimuthal angle $\phi$, as depicted in Figure 3.

$$\begin{array}{l}{\mathsf{\Omega }}_x=\mu =\cos \left(\phi \right)\sin \left(\theta \right)\\ {\mathsf{\Omega }}_y=\eta =\sin \left(\phi \right)\sin \left(\theta \right)\\ {\mathsf{\Omega }}_z=\xi =\cos \left(\theta \right)\end{array}$$

(13)

.

Each discrete direction is combined with its corresponding weight to form a quadrature set $\left\{{\overrightarrow{\mathsf{\Omega }}}^n,w_n,n=1,\dots ,N_G\right\}$, which comprises discrete angles and their corresponding weights, facilitating the numerical approximation of the angular dependence in the particle transport equation. The angular integration is approximated as:

$${\displaystyle {\int }_{4\pi }f(\overrightarrow{\mathsf{\Omega }})\mathrm{d}\mathsf{\Omega }\approx {\displaystyle \sum _{n=1}^N{w}_n}}f({\overrightarrow{\mathsf{\Omega }}}^n)$$

(14)

Additionally, the neutron flux, scalar flux, and macroscopic scattering cross-section can be expressed along the discrete directions as follows:

$$\begin{array}{c}{\psi }^n(\overrightarrow{r})=\psi (\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^n)\\ \varphi (\overrightarrow{r})={\displaystyle {\int }_{4\pi }\psi (\overrightarrow{r},\overrightarrow{\mathsf{\Omega }})}\mathrm{d}\mathsf{\Omega }\approx {\displaystyle \sum _{n=1}^N{w}_n}\psi (\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^n)={\displaystyle \sum _{n=1}^N{w}_n}{\psi }^n(\overrightarrow{r})\\ {\mathsf{\Sigma }}_{s,g^{\prime }\to g}^{n^{\prime }\to n}(\overrightarrow{r})={\mathsf{\Sigma }}_{s,g^{\prime }\to g}(\overrightarrow{r},{\overrightarrow{\mathsf{\Omega }}}^{n^{\prime }}\to {\overrightarrow{\mathsf{\Omega }}}^n)\end{array}$$

(15)

The appropriate selection of quadrature sets is critical to the computational accuracy of the S_N method. Based on symmetry and angular distribution principles, quadrature sets are classified into fully symmetric, half-symmetric, and locally refined types, designed to numerically integrate spherical harmonics through weighted discretization on the unit sphere. Fully symmetric sets (e.g., level symmetric quadrature set, LQ_N) exhibit complete symmetry in direction cosines and weights, with coefficients determined via moment equations or even-order moment conditions, though negative weights may occur at high discrete orders. Half-symmetric sets (e.g., half-symmetric Gaussian sets, Legendre–Chebyshev hybrid sets) maintain symmetry along the μ- and η-axes while preserving 90° rotational invariance along the ξ-axis, balancing symmetry and computational flexibility. For strongly anisotropic problems, locally refined sets enhance flux resolution by increasing discretization density in critical regions, achieving a balance between accuracy and efficiency.

The choice of quadrature sets affects solution accuracy, necessitating appropriate schemes in practical applications. The multi-group discrete form of the particle transport equation under angular discretization is expressed as:

$$\begin{array}{l}{\overrightarrow{\mathsf{\Omega }}}^n\cdot \nabla {\psi }_g^n(\overrightarrow{r})+{\mathsf{\Sigma }}_{t,g}(\overrightarrow{r}){\psi }_g^n(\overrightarrow{r})=\\ {\displaystyle \sum _{g^{\prime }\in G}{\displaystyle \sum _{n^{\prime }\in N}{\mathsf{\Sigma }}_{s,g^{\prime }\to g}^{n^{\prime }\to n}(\overrightarrow{r})w_n{\psi }_{g^{\prime }}(\overrightarrow{r})}}+\\ {\displaystyle \frac{1}{k}}{\displaystyle \frac{{\chi }_g(\overrightarrow{r})}{4\pi }}{\displaystyle \sum _{g^{\prime }\in G}v{\mathsf{\Sigma }}_{f,g^{\prime }}(\overrightarrow{r}){\displaystyle \sum _{n^{\prime }\in N}{w}_n{\psi }_{g^{\prime }}(\overrightarrow{r})}}\end{array}$$

(16)

2.4. Spatial Discretization

Spatial discretization is achieved by dividing the continuous domain into discrete grid cells, where numerical approximations to particle flux distributions are constructed while preserving conservation laws and boundary continuity. Two fundamental approaches are employed: differential equation discretization, which includes the finite difference method (FDM), finite volume methods, and nodal methods; and functional expansion methods, where intra-cell flux is represented by piecewise polynomials or basis functions. The coefficients in these expansions are determined through weighted residual or variational principles, as seen in finite element methods, which are further categorized into Rayleigh–Ritz, Galerkin, and least squares finite element methods. To illustrate these discretization approaches, the diamond difference (DD) scheme is presented as an example. For a three-dimensional Cartesian system with constant macroscopic total cross-section ${\mathsf{\Sigma }}_t$ in the orthogonal grid cell $V_{i,j,k}$, integration of the transport Equation (16) over $V_{i,j,k}$ yields:

$$\begin{array}{l}{\displaystyle \frac{{\mu }^n}{\mathsf{\Delta }{x}_i}}\left({\psi }_{i+1/2,j,k}^n-{\psi }_{i-1/2,j,k}^n\right)+{\displaystyle \frac{{\eta }^n}{\mathsf{\Delta }{y}_j}}\left({\psi }_{i,j+1/2,k}^n-{\psi }_{i,j-1/2,k}^n\right)+\\ {\displaystyle \frac{{\epsilon }^n}{\mathsf{\Delta }{z}_k}}{\mu }^n\left({\psi }_{i,j,k+1/2}^n-{\psi }_{i,j,k-1/2}^n\right)+{\mathsf{\Sigma }}_{t,ijk}\cdot {\overline{\psi }}_{i,j,k}^n=Q_{i,j,k}\end{array}$$

(17)

where the volume-averaged flux ${\overline{\psi }}_{i,j,k}^n$ and surface-averaged fluxes ${\psi }_{i\pm 1/2,j,k}^n$, ${\psi }_{i,j\pm 1/2,k}^n$, and ${\psi }_{i,j,k\pm 1/2}^n$ are, respectively, defined as:

$$\begin{array}{l}{\psi }_{i\pm 1/2,j,k}^n={\displaystyle \frac{1}{\mathsf{\Delta }{y}_j\mathsf{\Delta }{z}_k}}{\displaystyle {\int }_j{\displaystyle {\int }_k{\psi }^n\left(x_{i\pm 1/2},y,z\right)}}\mathrm{d}y\mathrm{d}z\\ {\psi }_{i,j\pm 1/2,k}^n={\displaystyle \frac{1}{\mathsf{\Delta }{x}_i\mathsf{\Delta }{z}_k}}{\displaystyle {\int }_i{\displaystyle {\int }_k{\psi }^n\left(x,y_{j\pm 1/2},z\right)}}\mathrm{d}x\mathrm{d}z\\ {\psi }_{i,j,k\pm 1/2}^n={\displaystyle \frac{1}{\mathsf{\Delta }{x}_i\mathsf{\Delta }{y}_j}}{\displaystyle {\int }_i{\displaystyle {\int }_k{\psi }^n\left(x,y,z_{k\pm 1/2}\right)}}\mathrm{d}x\mathrm{d}y\\ {\overline{\psi }}_{i,j,k}^n={\displaystyle \frac{1}{\mathsf{\Delta }{x}_i\mathsf{\Delta }{y}_j\mathsf{\Delta }{z}_k}}{\displaystyle {\int }_i{\displaystyle {\int }_j{\displaystyle {\int }_k{\psi }^n\left(x,y,z\right)}}}\mathrm{d}x\mathrm{d}y\mathrm{d}z\end{array}$$

(18)

The DD scheme achieves discretization by postulating the volume-averaged angular flux as the arithmetic means of adjacent upwind and downwind surface-averaged fluxes:

$$\begin{array}{cc}{\overline{\psi }}_{i,j,k}^n& ={\displaystyle \frac{1}{2}}({\psi }_{i+1/2,j,k}^n+{\psi }_{i-1/2,j,k}^n)\\ & ={\displaystyle \frac{1}{2}}({\psi }_{i,j+1/2,k}^n+{\psi }_{i,j-1/2,k}^n)\\ & ={\displaystyle \frac{1}{2}}({\psi }_{i,j,k+1/2}^n+{\psi }_{i,j,k-1/2}^n)\end{array}$$

(19)

Given the known upwind surface-averaged flux ${\psi }_{i+1/2,j,k}^n$, ${\psi }_{i,j+1/2,k}^n$, and ${\psi }_{i,j,k+1/2}^n$, the downwind surface flux is analytically expressed as:

$$\begin{array}{l}{\psi }_{i-1/2,j,k}^n=2{\overline{\psi }}_{i,j,k}^n-{\psi }_{i+1/2,j,k}^n\\ {\psi }_{i,j-1/2,k}^n=2{\overline{\psi }}_{i,j,k}^n-{\psi }_{i,j+1/2,k}^n\\ {\psi }_{i,j,k-1/2}^n=2{\overline{\psi }}_{i,j,k}^n-{\psi }_{i,j,k+1/2}^n\end{array}$$

(20)

Substitution of Equation (20) into Equation (17) to eliminate the downwind flux term results in the discretized equation for the first octant:

$$\begin{array}{l}{\overline{\psi }}_{i,j,k}^n={\displaystyle \frac{\frac{2{\mu }^n}{\mathsf{\Delta }{x}_i}{\psi }_{i+1/2,j,k}^n+\frac{2{\eta }^n}{\mathsf{\Delta }{y}_j}{\psi }_{i,j+1/2,k}^n+\frac{2{\epsilon }^n}{\mathsf{\Delta }{z}_k}{\psi }_{i,j,k+1/2}^n-Q_{i,j,k}}{\frac{2{\mu }^n}{\mathsf{\Delta }{x}_i}+\frac{2{\eta }^n}{\mathsf{\Delta }{y}_j}+\frac{2{\epsilon }^n}{\mathsf{\Delta }{z}_k}+{\mathsf{\Sigma }}_{t,ijk}}}\\ {\mu }^n\ge 0,\begin{array}{cc}& {\eta }^n\ge 0\end{array},\begin{array}{cc}& {\epsilon }^n\ge 0\end{array}\end{array}$$

(21)

The iterative solution process of the S_N method consists of two sweeping procedures: angular and spatial sweeping. The solution sequence, comprising initialization, directional sequencing, flux update, boundary propagation, and convergence criterion, proceeds through discrete directions sequentially. For each direction, spatial cells are solved systematically from the top boundary grid, followed by progression to the next discrete direction upon completion. Detailed discussion of these procedures follows in the next section.

2.5. Iterative Methods

The solution of transport equations predominantly relies on the source iteration concept, which achieves convergence through iterative updates of scattering and fission sources. For criticality problems, a dual-level iteration structure is employed: outer iterations update the fission source, while inner iterations resolve the scattering source. Fixed-source problems, however, only require scattering source convergence. The scattering source is decomposed into self-scattering ($S_{self}$, intra-group scattering), up-scattering ($S_{up}$, low-to-high energy group), and down-scattering ($S_{down}$, high-to-low energy group). Under isotropic scattering assumptions, Equation (16) simplifies to:

$$\overrightarrow{\mathsf{\Omega }}\cdot \nabla \psi +{\mathsf{\Sigma }}_t\psi ={\displaystyle \frac{1}{4\pi }}\left(S_{self}+S_{up}+S_{down}+{\chi }_{g}F\right)$$

(22)

where $F$ represents the fission source, which vanishes in photon transport. Initial guesses for $k_0$ and ${\psi }_0$ are required to compute $F^0$ and $S^0$.

$$F={\displaystyle \frac{1}{k}}{\displaystyle \sum _{g=1}^{NG}v{\mathsf{\Sigma }}_{f,g}}{\varphi }_g$$

(23)

During outer iterations, the fission source is updated from the previous inner iteration results, with energy groups processed in descending order. Inner iterations utilize either Jacobi or Gauss–Seidel iteration methods, as represented by Equations (24) and (25), respectively. In the Jacobi iteration method, both in-scattering sources are derived from the scalar flux of the previous iteration, resulting in:

$$\overrightarrow{\mathsf{\Omega }}\cdot \nabla {\psi }^{I+1}+{\mathsf{\Sigma }}_t{\psi }^{I+1}=S_{self}^{I+1}+S_{up}^I+S_{down}^I+F^I$$

(24)

Here, $I$ denotes the iteration index, and the Gauss–Seidel iteration method is represented as:

$$\overrightarrow{\mathsf{\Omega }}\cdot \nabla {\psi }^{I+1}+{\mathsf{\Sigma }}_t{\psi }^{I+1}=S_{self}^{I+1}+S_{up}^I+S_{down}^{I+1}+F^I$$

(25)

The Jacobi iteration requires full storage of prior results, resulting in high memory overhead, but excels in parallelism. In contrast, the Gauss–Seidel iteration calculates up-scattering without the need to revisit higher energy groups, facilitating the convergence of up-scatter sources in thermal energy regions where up-scattering is more common, thus referred to as “up-scatter iterations”. While both methods offer distinct advantages in handling multi-group transport problems, particularly with their slow convergence characteristics in scattering-dominated regimes, nonetheless, the increasing complexity of modern computational demands has driven the development of more sophisticated techniques.

Krylov subspace methods, a class of iterative algorithms for large-scale sparse linear systems, are characterized by high-dimensional problem-solving capability through progressive subspace expansion. Three main categories are distinguished based on matrix compatibility: symmetric, nonsymmetric, and normal equations. Each category contains specialized algorithms with distinct convergence properties and operational constraints, as systematically compared in

Table 2. Classification of Krylov subspace methods by matrix type and numerical characteristics.

Matrix Type	Method	Applicable Problem Types	Key Characteristics
Symmetric	CG	Symmetric positive definite systems (e.g., diffusion equations, Poisson problems)	Optimal convergence
	MINRES	Symmetric indefinite systems (including problems with negative eigenvalues)	Guaranteed residual monotonic decrease
	SYMMLQ	Symmetric indefinite systems (when minimal error solution is preferred over minimal residual)	Alternative to MINRES for specific cases
	SQMR	Symmetric indefinite systems (when avoiding transpose operations)	Symmetric version of BiCG
Nonsymmetric	CGS	Nonsymmetric systems (for fast convergence with possible oscillations)	Squared residual convergence
	BiCGSTAB	Nonsymmetric systems (when stable convergence is needed)	Stabilized version of CGS
	TFQMR	Nonsymmetric systems (when smooth convergence is preferred)	Alternative stabilized CGS variant
	GMRES	General nonsymmetric systems (e.g., transport equations, advection-diffusion problems)	Optimal residual reduction, high memory
	FOM	Nonsymmetric systems (when exact subspace solution is required)	Similar to GMRES without minimal residual guarantee
	BiCG	Nonsymmetric systems (when matrix transpose is available	$\mathrm{Requires} A^T$
	FGMRES	Nonsymmetric systems (with variable preconditioning)	Flexible GMRES variant
Normal Equations	CGLS	$\mathrm{Least} \mathrm{squares} \mathrm{problems} (A^{T}Ax=A^T\mathrm{b}$ formulation)	Implicit normal equations solver
	LSQR	Ill-conditioned least squares problems (when numerical stability is critical)	More stable than CGLS

.

Method selection is determined by both the mathematical structure of the coefficient matrix and computational requirements, including memory efficiency and stability tolerance. The implementation of its advanced search strategy within the constructed subspace results in superior convergence characteristics. These advantages are particularly evident when compared to conventional SI methods, especially within the context of particle transport equations, and are further highlighted in addressing complex problems characterized by strong scattering and anisotropic conditions. At its core, the method operates on a Krylov subspace of dimension m. In a representative Krylov method like GMRES, the algorithm proceeds by: (i) constructing the Krylov subspace, (ii) performing orthogonalization via the Arnoldi process, and (iii) solving a least squares problem to minimize the residual. For convenience, Equation (22) can be simplified as:

$$\begin{array}{l}L\psi =S\psi +Q\\ L=\overrightarrow{\mathsf{\Omega }}\cdot \nabla +{\mathsf{\Sigma }}_t\\ S=S_{self}+S_{up}+S_{down}\\ Q={\displaystyle \frac{1}{4\pi }}{\chi }_{g}F\end{array}$$

(26)

where $L$ represents the transport operator matrix (diagonally dominant), $S$ denotes the scattering source matrix (sparse non-diagonal), and $Q$ represents the fission source term. This can be arranged into a linear system: $A\psi =b$, where $A=L-S$ and $b=Q$.

The Krylov subspace methods approximate the solution by iteratively constructing the subspace ${\mathcal{K}}_m\left(A,r_0\right)$, which can be expressed as:

$${\mathcal{K}}_m\left(A,r_0\right)=\mathrm{span}\left\{r_0,A{r}_0,A^2{r}_0,\dots ,A^{m-1}{r}_0\right\},r_0=b-A{\psi }_0$$

(27)

where $r_0$ is initial residual and the iteration starts with an initial approximation ${\psi }_0$. This subspace construction enables the method to systematically explore optimal solution directions in the vector space.

The Arnoldi process serves as the fundamental algorithm for constructing orthogonal bases within the Krylov subspace. Through Gram–Schmidt orthogonalization, the vectors in the Krylov subspace are transformed into a set of orthonormal basis vectors, denoted as:

$$V_m=\left[v_1,v_2,\dots ,v_m\right]$$

(28)

which satisfy the condition:

$$V_m^T{V}_m=I$$

(29)

Orthonormal bases mitigate numerical instability, such as the accumulation of rounding errors in ill-conditioned problems, and provide a concise mathematical representation for projections. After m steps of iterations, the Arnoldi process is satisfied:

$$A{V}_m=V_{m+1}{\tilde{H}}_m$$

(30)

where ${\tilde{H}}_m$ is an $\left(m+1\right)\times m$ upper Hessenberg matrix, significantly smaller in scale than $A$.

$${\tilde{H}}_m=\left[\begin{array}{ccc}{h}_{1,1}& \dots & h_{1,m}\\ h_{2,1}& \dots & h_{2,m}\\ 0& \ddots & ⋮\\ 0& 0& h_{m+1,m}\end{array}\right]\in R^{\left(m+1\right)\times m}$$

(31)

The Arnoldi process allows Krylov subspace methods like GMRES, as employed here, to stably and efficiently solve discrete transport systems. By this means, the original problem $A\psi =b$ is projected onto a lower-dimensional Krylov subspace, resulting in an approximate problem.

$${\tilde{H}}_{m}y\approx {‖r_0‖}_2{e}_1$$

(32)

Due to the orthogonality of the columns of $V_m$, the computation of ${\tilde{H}}_m$ requires only the calculation of inner products:

$${\tilde{H}}_m=V_m^{T}A{V}_m$$

(33)

The objective function of GMRES is to minimize the residual norm ${‖b-A\psi ‖}_2$ projected onto the Krylov subspace ${\mathcal{K}}_m$. Utilizing the results of the Arnoldi process, the approximate solution ${\psi }_m$ can be expressed as:

$${\psi }_m={\psi }_0+V_m{y}_m,y_m\in R^m$$

(34)

where $y_m$ is the solution to the reduced-dimensional problem. Consequently, the minimization problem is transformed into:

$$y_m=\arg \underset{y}{\min }{‖{‖r_0‖}_2{e}_1-{\tilde{H}}_{m}y‖}_2$$

(35)

Based on the aforementioned least squares problem, the GMRES algorithm proceeds iteratively through the following steps: First, the optimal solution is obtained by solving the least squares problem within the current Krylov subspace. Subsequently, the approximate solution is updated accordingly. The residual is then computed and examined for convergence criteria satisfaction. If the convergence conditions are not met, the Krylov subspace is expanded, and the iterative procedure is continued until final convergence is achieved.

To accelerate scattering source convergence, low-order flux corrections can be implemented through diffusion synthetic acceleration (DSA), transport synthetic acceleration (TSA), or coarse mesh finite difference (CMFD) methods (see Section 4.3.1 for details). These techniques also serve effectively as preconditioners for Krylov subspace methods like GMRES. By leveraging low-order approximations, high-frequency errors are efficiently mitigated, and the conditioning of the coefficient matrix is improved, thereby enhancing overall convergence. Specifically, within the domain of transport applications, CMFD can serve as a global low-order flux correction during outer iterations, while Krylov subspace methods (e.g., GMRES) solve the CMFD-modified fine-mesh transport equations within inner iterations.

3. Applications of the S_N Method in Nuclear Energy

The establishment of the S_N method as a cornerstone for particle transport simulations in nuclear energy systems stems from its adaptability to complex geometries and compatibility with HPC architectures. The applications of the method have evolved along two primary domains: reactor physics calculations and shielding analyses, where its capabilities in resolving deep-penetration problems and complex geometric heterogeneities have proven instrumental.

The historical development of the S_N method reflects a systematic progression in computational capabilities. The initial two-dimensional implementation, DOT-II [7], established the foundational framework for practical shielding design. Subsequent enhancements through DOT-IV [8] and DORT [9] expanded both geometric modeling capabilities and computational efficiency. The practical utility of DORT was validated through comprehensive benchmarks, including the C5G7-MOX [10,11] and 172-group GE-13 assembly benchmarks [12]. In the 900 MWe PWR St. Laurent B1 unit tests, the DORT + DOTSYN system achieved calculated-to-measured (C/M) ratios within accepted uncertainty margins, with average values of 0.94 at in-vessel locations and 1.12 at ex-vessel dosimeter locations [13]. Its applications extended to specialized analyses, including the assessment of tungsten decay heat in ITER-simulated neutron fields at JAERI/FNS, with accuracy comparable to MCNP being achieved through the use of a self-shielding corrected 175-group multigroup library, whereas omission of self-shielding correction—particularly in coarser 46-group structures—results in underestimations of up to 40% [14]. Furthermore, DORT-TD has demonstrated the ability to accurately simulate neutronics processes over millisecond-to-second timescales, encompassing both slow and prompt supercritical transients, and has enabled detailed investigations of numerical errors, iteration strategies, time step control, and the influence of energy group structure [15].

The transition to three-dimensional capabilities marked a fundamental advancement in transport calculations. The DOORS discrete ordinates transport code system, integrating TORT [16,17], ANISN [18], and DOT/DORT [7], demonstrated remarkable accuracy in tests, including the 3D C5G7-MOX benchmarks [19] and pressure vessel of H.B. Robinson Unit 2 [20]. Moreover, the effectiveness of TORT in mitigating ray effects was validated through the initial collision source treatment conducted in ITER/EDA shielding gap streaming experiments utilizing the FNS D-T neutron source from JAERI [21]. Additionally, substantial performance improvements in computational speed were achieved. For example, in the IPEN/MB-01 reactor analysis, TORT reduced computation time by approximately a factor of 16 compared with MCNP [22]. Similar speedups were observed in the analysis of the BWR-4 KKM plant in Switzerland [23]. The success of TORT in addressing problems characterized by complex geometries and deep penetration [7] has significantly catalyzed the development of other specialized three-dimensional codes, including Ardra [24], AMTRN [25], TRITAC [26], ENSEMBLE [27], and PENTRAN [28], which are widely utilized in nuclear reactor design, radiation shielding analysis, and safety assessments of nuclear facilities.

Methodological advances in modern S_N implementations have been driven by the demands of increasingly complex nuclear systems. The PARTISN system introduced block-structured adaptive mesh refinement (AMR) [29] and employs generalized perturbation theory to enhance sensitivity analysis capabilities [30]; nevertheless, challenges in material interface modeling persisted [31], and extensions to ν, μ, and inter-nuclide covariances remain pending [32]. Parallel computing capabilities expanded significantly, as exemplified by the linear strong scaling of the DENOVO framework [33] and its efficient multigrid energy preconditioning [34,35], achieving high benchmark fidelity, notably, the C5 benchmark [36] and JET streaming benchmark [37]. Additionally, AMTRAN achieved substantial efficiency gains through MPI-threaded parallelism. Specifically, with 32 masters and 3000 processors, it demonstrated nearly linear scaling efficiency [38].

Geometric modeling capabilities have seen substantial enhancement through diverse approaches. The CAD integration of the ATTILA code demonstrates robust capabilities in particle transport simulations [39], with its ATLAS module enabling efficient angular distribution computations [40] while maintaining fusion neutronics accuracy standards [39,41]. Unstructured grid methods, implemented in MUST [42], AETIUS [43], and STRAUM [44], further enhanced these advances. The ARES further extended these capabilities through sophisticated domain decomposition [45], high-resolution solutions with enhanced computational efficiency [46], integration with the SALOME platform for streamlined geometry modeling and mesh generation [47], and adaptive discretization techniques [48].

The parallel computing landscape has been transformed by worldwide development efforts. The JSNT-S code pioneered hybrid MPI + threads approaches [49], while NECP-hydra implemented advanced KBA-based parallel computing with sophisticated acceleration methods [50]. Additionally, the ARES [45] achieved notable parallel efficiency, complemented by its ARES-MACXS extension for cross-section generation and analysis [51]. Furthermore, the Marvin code demonstrated comprehensive validation through multiple discretization methods and benchmark tests [52].

Integration with multi-physics frameworks represents a crucial advancement in application scope. Notably, the high-performance multi-physics S_N tool Osiris demonstrates robust computing capabilities for large-scale reactor core analysis [53]. Similarly, the MOOSE (Multiphysics Object-Oriented Simulation Environment) platform, coupled with HPC architectures [54,55], introduced specialized mesh generation for advanced reactor geometries [56,57]. Furthermore, practical applications expanded to include numerous areas, such as precise dose rate evaluations for radiation sources [58], radiation protection analyses [59], fuel behavior assessment during reactivity insertion transient periods [60], and various other nuclear engineering applications.

The limitations of S_N methods in complex geometries have been addressed through innovative hybrid approaches. Specifically, S_N-MC coupling methods have demonstrated substantial efficiency improvements while maintaining accuracy [61]. Additionally, the NECP-Alter coupling code, which combines NECP-Hydra [50] and NECP-MCX [62] capabilities, has further enhanced the treatment of large-scale reactor shielding problems [63].

In summary, the S_N method has been established as the predominant deterministic approach for core-level particle transport, with ongoing evolution from theoretical frameworks to industrial applications. The advancement of computational methodologies, parallel processing techniques, and hybrid approaches has systematically ameliorated historical limitations. The implementation of sophisticated algorithms and high-performance computing architectures has significantly enhanced the capabilities of these codes. Nevertheless, the full realization of industrial-scale applications remains an active area of development, with continued research focused on further optimization of computational efficiency and accuracy in complex geometries.

4. Advancements in S_N Methodology

The S_N method in particle transport simulations is challenged by ray effects and the limitations of traditional discretization techniques. This section provides a review of advancements in ray effect mitigation, discretization scheme enhancement, and high-performance computing architecture optimization. Additionally, the application of hybrid methods and machine learning within the S_N method is discussed.

4.1. Ray Effect Mitigation Schemes

Ray effects, non-physical ray-like artifacts inherent to angular discretization, arise from the enforced directional propagation of neutrons along discrete ordinates. These artifacts, exacerbated in geometries with localized sources or low scattering, manifest as angular flux oscillations with spurious peaks and troughs, degrading local solution accuracy despite preserved global quantities.

The mitigation of ray effects in S_N methods is systematically addressed through three technical strategies: ordinate refinement, segmented continuous function equivalence methodologies, and specialized source treatment. For ordinate refinement, localized angular enhancements are achieved via quadrature set optimization, such as the improved discrete ordinates method (IDOM) [64]. While the regional angular refinement (RAR) is effective for transport problems exhibiting strong angular correlation, its reliance on preselected refinement directions based on physical properties limits adaptability in complex scenarios [65,66]. To address this limitation, advanced dynamic angular adaptive methods iteratively optimize quadrature configurations through error analysis, thereby achieving a refined precision–efficiency balance [67]. Despite this, these methods substantially reduce computational efficiency, limiting their practical application.

Segmented continuous function equivalence methodologies are predominantly represented by two approaches: the fictitious source method [68] and angular finite element techniques [69]. In the fictitious source method, auxiliary fictitious source terms are introduced into discrete ordinates equations, enabling equivalence with spherical harmonic formulations (P_L approximations) for both 2D and 3D problems [27,70]. This category further includes specialized implementations such as the rotated S_N (rS_N) method, where periodic reorientation of ordinate sets through random-axis rotations is implemented, followed by interpolation-based solution transfers [71], and the artificial scattering S_N (as-S_N) method, which introduces forward-peaked angular diffusion operators to mitigate ray effects [72]. Angular finite element techniques, by contrast, employ distinct numerical frameworks for angular discretization [69]. While these equivalence methods effectively suppress ray effects, their implementation incurs significant computational overhead, reduced convergence rates, and the potential for numerical dispersion.

Within source treatment methodologies, the first collision source (FCS) method stands as the most widely adopted solution, with its theoretical framework established by Lathrop [73,74]. The method consists of three operational phases: (1) computing the uncollided flux density per cell using high-order transport or analytical methods, (2) generating first collision sources by coupling the uncollided flux with scattering cross-sections, and (3) solving fixed-source transport equations using the S_N method before superimposing the collided and uncollided components. This systematic approach has been standardized for 2D [75,76] and 3D [77,78] transport problems, and it has been further extended to electron [79] and photon transport [80]. For engineering optimizations, Denovo achieves optimized FCS processing through integrating ray tracing for point sources with parallel computing [33], while the ARES submodule, ARES_RayEffect, enhances computational accuracy of uncollided flux via correction factors [81]. To further enhance the effectiveness, the semi-analytic first collision source method strategically decomposes the flux into uncollided and collided components, with the former resolved analytically and the latter treated by the discrete ordinates method [82]. Additionally, the surface method resolves conservation limitations inherent in conventional internal-point approaches [83]. Moreover, the computational paradigm for uncollided flux has evolved into multiple branches, incorporating non-conservative mesh-center tracking, surface-averaged current balance schemes, and conservative characteristic-based numerical integration [84].

4.2. Enhanced Spatial Discretization Schemes

4.2.1. High-Order Spatial Discretization

The pursuit of accurate spatial discretization in S_N particle transport simulations remains fundamentally constrained by traditional methods’ limitations: the finite difference method (FDM) exhibits geometric inflexibility from structured grid dependence; the finite element method (FEM) suffers prohibitive computational scaling; and the finite volume method (FVM) oversimplifies flux representations in multi-physics coupling [4]. To address these challenges, high-order finite element methods (HO-FEMs) have been systematically developed. These methods leverage polynomial basis functions to enhance approximation fidelity while reducing mesh density. Domain decomposition, high-order basis function construction, and variational transformation into algebraic systems form the core of this framework. This approach enforces nodal continuity through Lagrange and Hermite functions (Equation (36)), with geometric adaptability proportional to the polynomial order.

$$N_j(x_i)={\varsigma }_{ij}=\left\{\begin{array}{ccc}0,& if& j\ne i,\\ 1,& if& j=i,\end{array}\right. for i,j=1,2,\dots ,N+1$$

(36)

The nodal method is characterized by a coarse mesh discretization strategy, in which the computational domain is divided into nodal elements. Within each node, high-order continuous polynomials, such as Legendre polynomials, are utilized to represent neutron flux distribution. Initially, average fluxes within each node are obtained by solving nodal equations. Finally, the detailed non-uniform flux distribution within the node is reconstructed using distribution reconstruction techniques. Thus, this high-order polynomial expansion significantly enhances flux approximation accuracy [85].

The nodal S_N method combines the high-order spatial accuracy of the nodal method with the angular discretization advantages of the S_N method. It is widely used in numerical calculations for light water reactors in Cartesian coordinates [86]. Moreover, compared to the FDM, it offers the advantage of improving computational accuracy in hexagonal-z (HEX-Z) geometries without increasing the number of computational points [87]. Nevertheless, existing nodal methods are heavily reliant on rectangular grids and HEX-Z geometries, and accuracy under complex geometric conditions remains a challenge.

To address this challenge, the use of triangular-z geometries has been proposed to enhance the geometric adaptability of the nodal S_N method. The DNTR3D code achieves the regularization of arbitrary triangular elements into equilateral triangles through coordinate transformation. This approach, combined with transverse integration techniques, significantly improves computational efficiency for triangular-z geometries [88]. Furthermore, the application of DSA techniques leads to further optimization of computational performance in the nodal S_N method [89]. In the realm of parallel computing, the SARAX code [90] employs an improved block Jacobi algorithm. By integrating interface prediction (IP) and inner iteration prediction (IIP) methods, it effectively reduces communication overhead and CPU idle time in unstructured mesh transport calculations. This strategy successfully addresses convergence degradation issues in parallel iterations, thereby substantially enhancing parallel computing efficiency [91].

While the nodal S_N methods require continuity of the solution within nodes, the discontinuous Galerkin finite element method (DGFEM) allows for discontinuities between elements. Originally introduced for neutron and photon transport problems [4], this flexibility in DGFEM offers distinct advantages in handling complex geometries and boundary conditions. It was initially implemented on 2D triangular meshes within the TRIPLET code [92], which was later extended to multi-group equations in TRIDENT [93]. Further advancements, including phase-space finite element formulations and explicit element-by-element algorithms, were incorporated into the ZEPHYR code [94], establishing foundational computational frameworks.

The DGFEM regained prominence due to its superior performance in solving first-order hyperbolic problems and compatibility with parallel computing. Its extension to three-dimensional unstructured meshes integrated source iteration and DSA, addressing scalability challenges [95]. Theoretical analyses identified two distinct diffusion limit behaviors: full-resolution DGFEM preserves discrete accuracy, whereas zero-resolution variants require lumped mass matrices to maintain numerical robustness [96]. Subsequent refinements incorporated anti-negative solutions while ensuring second-order accuracy and diffusion limit preservation, establishing a benchmark for high-order discretization [97].

Advancements in high-order methods have focused on optimizing basis functions. A scheme employing fourth-order hierarchical basis functions improved solution accuracy while mitigating numerical oscillations [98]. When combined with AMR and a modified interior penalty DSA scheme, computational efficiency was significantly enhanced [99]. Additionally, a self-lumped mass strategy based on Gauss–Lobatto quadrature enabled exact diagonalization, ensuring positive conservation across arbitrary polynomial orders [100]. This strategy was extended to problems with variable cross-sections [101], which provide theoretical support for multi-dimensional high-order discretization.

Developments in geometric adaptability have further expanded the applicability of DGFEM. The introduction of simplex decomposition facilitated high-order discretization on unstructured meshes [98], while Bergot-type pyramid elements demonstrated optimal convergence properties in singular geometries [102]. Specialized implementations have also extended to hexagonal elements, employing anisotropic basis functions aligned with honeycomb symmetry [103].

Recent research has emphasized hybrid methodologies to enhance computational efficiency. The p-CMFD accelerator significantly improved the efficiency of three-dimensional S_N-DGFEM by leveraging high-order partial current reconstruction [104]. The integration of B-spline wavelet basis functions in a DFEM framework enabled adaptive local accuracy adjustments via multi-resolution analysis [105]. Moreover, a hybrid characteristic-line-DFEM approach, which decouples axial and radial discretization, reduced computational errors in three-dimensional problems by an order of magnitude [106].

The latest advancements extend hybrid finite element discretization to the variable Eddington factor (VEF) equation, incorporating alternative Raviart–Thomas (RT) approaches to enhance compatibility with curved meshes and ensure robust convergence [107]. Furthermore, the development of an hp-adaptive DGFEM, combining mesh refinement (h-adaptivity) with polynomial order refinement (p-adaptivity), has unified spatial, angular, and energy discretization [108].

High-order DFEM continues to face several challenges: (1) balancing the construction of basic functions with integration efficiency in high-dimensional unstructured meshes; (2) ensuring the robustness of high-order schemes in strongly anisotropic scattering problems; and (3) optimizing the coupled refinement of discrete order and mesh size within the hp-adaptive strategy. Future research directions may include the development of intelligent basis functions based on neural networks, the design of non-tensor-product high-order elements, and the exploration of novel discretization paradigms within quantum computing architectures.

4.2.2. Mesh Refinement

In S_N transport methods, the influence of mesh structure on computational accuracy and stability is critical. Significant discretization errors and numerical deviations are caused by mismatches between mesh size and particle characteristic length. Particularly in multi-scale problems, excessive discretization in optically thin regions results from uniform mesh refinement, leading to resource wastage and increased computation time. To address these issues, the development of AMR has enabled the dynamic adjustment of local mesh resolution, allowing fine meshes in critical areas while permitting coarser meshes elsewhere, thus achieving a balance between precision and resource utilization [109].

The AMR process involves three core components: error estimation, adaptive strategy, and mesh refinement. Initially, the use of mesh optical thickness and flux gradients as error indicators was prevalent. The implementation of the Richardson-type truncation error estimation method through multi-component meshes established the theoretical foundation for AMR [110]. Subsequently, the development of a three-dimensional multi-level adaptive algorithm, utilizing pyramid data structures and angular flux spatial moments for error indicator construction, significantly enhanced the reliability and efficiency of S_N transport calculations [111]. Additionally, the introduction of a posteriori flux gradient estimation methods, employing relative surface net leakage as an evaluation criterion, provided effective tools for reactor core loading optimization [112].

The dual weighted residual (DWR) framework, among error estimation methods, offers distinct advantages. Mesh distribution optimization is achieved through adjoint problem solutions, allowing precise identification of key regions affecting objective functions in heterogeneous shielding problems, thereby enhancing computational efficiency [113]. For reactor physics eigenvalue problems, effective estimation of the $k_{eff}$ is facilitated by the DWR method, leading to reduced resource requirements through optimized mesh configurations [114]. These results confirm the adaptability and efficiency of the DWR method in complex particle transport problems.

AMR technology is categorized into block-based (patched) and cell-based (tree-based) types. In block-based AMR, structured mesh blocks are utilized, maintaining uniformity through integral refinement/coarsening, which simplifies load balancing and parallel processing [110,115]. Flexibility and scalability are enhanced by tile-clustering and cascading partitioning algorithms, which eliminate non-scalable communication [116]. The integration of the usability of multiblock methods with the flexibility of AMR in MB-AMR simplifies the implementation of the lattice Boltzmann method (LBM) in neutron transport [117]. However, mesh mismatching at boundaries and limited local refinement flexibility are potential issues in block-based AMR.

Conversely, cell-based AMR, based on tree structures like quadtrees/octrees, allows independent refinement of mesh cells. Although this increases complexity, significant advantages are demonstrated in handling complex geometries and local phenomena such as flux peaking near material interfaces and control rod positions [118]. The multi-level tree grid (MLTG) algorithm reduces mesh quantity and computational costs by constructing locally refined meshes before transport solutions, using hierarchical tree structures and mesh coarsening based on material consistency and source strength deviation [119]. A further reduction in computation time by 50% is achieved through the introduction of dynamic mode decomposition (DMD) in the DMD-MLTG method [120].

Additionally, in tree-based AMR, the use of space-filling curves (SFC) facilitates the management and operation of mesh elements. These curves assist in the creation, adaptation, partitioning, and balancing of meshes, as well as in the management of ghost layers, which are crucial for the accuracy and efficiency of numerical simulations. This approach reduces communication overhead between processors by minimizing the data exchange required, thereby enhancing overall computational performance [121,122]. The third generation Peano Software innovatively combines space-filling curves, such as Peano curves, with mesh traversal, achieving efficient mesh linearization and data management, which results in reduced memory usage and improved cache hit rates [123].

In AMR applications, the selection of appropriate acceleration methods is crucial: superior performance of DSA is observed in coarse meshes with high-order S_N approximations, while advantages of TSA are noted in fine meshes with low-order approximations [124]. Despite the efficiency gains of AMR, challenges remain, particularly in high-performance computing (HPC) environments, where dynamic mesh management introduces complexity and overhead in parallel storage, load balancing, and ghost element processing. As MPI task numbers increase, efficient dynamic mesh partitioning and random access remain technical challenges, necessitating further development of intelligent mesh management algorithms and parallel computing optimizations.

4.3. Acceleration Schemes and Techniques

4.3.1. Numerical Acceleration Methods

To alleviate computational demands, numerical acceleration methods such as DSA, TSA, and CMFD are often employed in solving particle transport equations.

The DSA method, initially proposed by Kopp in 1963 [125], accelerates SI convergence by solving a low-order diffusion approximation of the error equation. Its integration into S_N frameworks by Gelbard and Hageman [126] has resulted in superior convergence rates and stability compared to standard SI [127,128,129]. However, performance degradation in multidimensional problems with material discontinuities or high scattering ratios has been observed. To address these challenges, the development of Krylov-DSA hybrid methods has been undertaken to mitigate convergence deterioration [130].

Recent advancements in DSA implementation have targeted key engineering challenges, including AMR compatibility, parallel scalability, and robustness in heterogeneous media. The BAMR-DSA solver enhances geometric adaptability through AMR integration, resulting in improved performance over traditional TSA in 2D PARTISN benchmarks [131]. Despite these improvements, stability challenges associated with dynamic mesh refinement remain unresolved. In order to alleviate parallelization bottlenecks, the parallel DSA (PDSA) scheme has been introduced, which employs localized diffusion problem segmentation to improve scalability in distributed computing environments [132]. Robustness improvements have been investigated through various preconditioning strategies, including FMR-preconditioned conjugate gradient methods for stabilizing convergence under high scattering conditions [133], AMG-compatible heterogeneous preconditioners for optimizing performance in media with sharp cross-section transitions [134], and dual-partition additive preconditioners designed to mitigate the sensitivity of the condition number to mean free paths [135].

The TSA method avoids consistent differencing issues inherent to DSA by employing a low-order transport equation discretized identically to the high-order system [136]. Early limitations in handling anisotropic scattering, reflective boundaries, and optically thick media were partially resolved through boundary angular corrections and CG-accelerated TSA, achieving 20-fold speedup over source iteration in 2D assembly-level transport [137,138]. Nevertheless, TSA faces divergence risks in heterogeneous systems, as identified through Fourier analysis [139], and motivated the modified TSA (MTSA) algorithm with inexact parallel block Jacobi splitting for enhanced stability in optically thin subdomains [140]. Methodological flexibility has been enhanced through the integration of unified S_N/P_N low-order discretization with IF/AMG solvers, whereas Krylov–TSA hybrids remain under exploration for heterogeneous media.

The widespread adoption of the CMFD method [141,142] is attributed to its efficiency and ease of implementation. The core concept of CMFD involves the generation of an “equivalent” approximate diffusion problem through coarse mesh homogenization parameters and coupling correction factors prior to the convergence of the target computational grid. This equivalent problem is rapidly solved using coarse mesh differencing techniques, with the resulting neutron flux distribution subsequently utilized for the modification of neutron source terms across accelerated grid regions, thereby enhancing convergence rates. However, stability degradation in reactors with optically thick regions necessitates further refinement. Stability improvements have been achieved through mesh refinement, increased transport sweeps, artificial diffusion, and over-relaxation factors [143]. Building on fundamental relaxation techniques [144,145], pCMFD and odCMFD have demonstrated superior stability and convergence, leveraging partial current corrections and optimized artificial diffusion terms, respectively. pCMFD ensures unconditional stability in monoenergetic infinite homogeneous media [146], while odCMFD achieves higher convergence efficiency across all coarse mesh sizes through refined diffusion coefficients [147]. Two-level CMFD implementations further optimize computational performance. Alternating multi-group and two-group formulations accelerate fission/scattering source convergence with fewer iterations [148]. Stability is enhanced via fission-source-based coarse mesh acceleration within a local/global iteration framework [149]. Arbitrary-level CMFD improves efficiency and reduces memory requirements through space-energy coarsening [150], while novel local-global iteration frameworks enable advanced multi-group transport solutions [151]. Discretization compatibility advancements included FEM integration enabled by pseudo absorption cross section (PAXS) implementation [152]. Unconditional stability in 2D Cartesian coordinates was attained by linear prolongation CMFD (lpCMFD) through scalar flux linear interpolation at coarse mesh boundaries, effectively mitigating error propagation [153,154]. Subsequent development of SlpCMFD variants achieved enhanced convergence performance across wide optical thickness ranges via adaptive artificial diffusion factors [155]. The lp-pCMFD method effectively accelerated DGFEM-discretized neutron transport by incorporating the drift closure relations of pCMFD [156]. For unstructured grid applications, triangular-z-mesh CMFD streamlines coarse mesh generation by maintaining a unified fine/coarse grid topology [157]. Systematic performance evaluations of CMFD, odCMFD, and lpCMFD methods in two-dimensional fixed-source problems reveal distinct operational characteristics, as summarized in

Table 3. Applicable ranges and stability characteristics of CMFD, odCMFD, and lpCMFD methods in 2D fixed-source problems.

Method	Stability Characteristics	Optimal Optical Thickness (τ) Range	Performance Characteristics
Conventional CMFD	Conditionally stable (τ < 1)	<1	Non-convergence for τ > 2 under high scattering ratios
odCMFD	Unconditionally stable
lpCMFD	Unconditionally stable	>1	Superior convergence performance among variants at τ > 1
pCMFD	Unconditionally stable	Less efficient at intermediate thicknesses	Comparative underperformance for intermediate τ range

[158].

4.3.2. High-Performance Computing Architectures

The exponential rise in computational costs associated with the traditional S_N method for three-dimensional transport problems has necessitated systematic optimization. As illustrated in Figure 4, this optimization focuses on two key trade-offs: the mismatch between computational partitioning and hardware architecture, and the balance between communication overhead and computational load distribution. Addressing these challenges requires the maximization of independent computational units through dependency decoupling to enhance parallelism, and the minimization of data movement via optimized storage architectures and access patterns to improve efficiency [159].

In the context of structured grids, a pivotal advancement emerged with the KBA algorithm [160], which enabled 3D wavefront parallelization via 2D spatial decomposition, achieving high parallel efficiency in orthogonal grids and gaining widespread adoption in transport codes like Denovo [81], Marvin [52], and Hydra [83]. Building on this foundation, the integration of the Jacobian-Free Newton–Krylov (JFNK) framework with KBA in the comePSn_JFNK architecture [161] allowed for full decoupling of angular and energy dependencies, achieving a 20-fold acceleration over power iteration methods compared to comePSn. However, a reduction in the efficiency of KBA was observed in unstructured grids due to the absence of columnar decomposition.

To address these structural compatibility constraints, research has focused on three strategic directions:

(1)

The development of asynchronous message passing combined with dynamic task queue management [162] has been implemented to reduce communication latency and improve load balancing.

(2)

Advancements in grid allocation optimization have been made through scheduling strategies such as B-LEVEL, BFDS, DFDS, and DFHDS [163]. Notable contributions include the L-B-LEVEL algorithm, which minimizes global information dependency, and the STFC method, which reduces communication delays [164].

(3)

The refinement of task dependency graph (TDG) analysis has been achieved, as demonstrated by the PDT framework, which attains 68% parallel efficiency at a 1.5-million-thread scale, and the ARDRA system, which achieves 71% efficiency under similar conditions [142]. A particularly innovative development, the sweep plane data structure (SPDS) [165], integrates KBA with depth-of-graph (DOG) analysis and flux data structure (FLUDS), resolving cyclic dependencies while maintaining 80% efficiency across 100,000 processes in Chi-Tech simulations. Additionally, the unstructured overloading algorithm [166] has significantly improved high-concurrency efficiency through task density optimization.

The shift towards heterogeneous HPC nodes and the integration of high-throughput, low-latency cores in exascale architecture have increased demands on programming models. While dependency decoupling has proven effective in enhancing parallel computing efficiency (PCE) in multi-core and many-core architectures [159], sweep communication remains a critical bottleneck, highlighting the need for advanced intercommunication equation-solving strategies. Furthermore, performance limitations vary by architecture: for multi-core CPUs, the primary constraint is cache hierarchy optimization; for GPU-based structured grids, memory bandwidth is the dominant limitation; and for DGFEM on unstructured grids, device cache performance is crucial [167]. Moreover, achieving optimal performance on GPU architectures requires algorithms to expose additional concurrency. However, device memory bandwidth often serves as a limiting factor in GPU performance [167].

Current hybrid programming models (MPI/CUDA/OpenMP/OpenACC) face challenges in managing the multidimensional parallelism and dynamic memory requirements of wavefront algorithms like KBA [168]. Promising solutions include OpenACC-based asynchronous angular sweep parallelization with MPI domain decomposition [169], subdomain overloading with optimized sweep angle selection to improve discrete ordinates scalability [170], and OpenMP/CUDA implementations of implicit S_N discontinuous Galerkin methods, which demonstrate superior computational efficiency [171].

Additionally, the ThorSNIPE code achieved reliable shielding calculations through multithreaded grid sweep parallelization [172]. Traditionally, the parallelization of the S_N code has been concentrated on spatial dimensions, with the parallel potential in angular and energy group dimensions often neglected. To address this, an improved version of the SNAP (S_N application proxy) was developed, extending the parallelization capabilities to angular and energy group dimensions, thereby significantly enhancing the parallelism of the algorithm. Moreover, this enhancement was implemented using cross-platform programming frameworks such as OpenCL and OpenMP 4.0, ensuring efficient parallelization of the optimized S_N algorithm across various platforms [173]. Nevertheless, solver portability across heterogeneous architecture remains a challenge [167].

From a system perspective, HPC architecture comprises four fundamental elements, hardware infrastructure, software support, algorithmic optimization, and performance evaluation, as shown in Figure 5.

4.4. Coupling S_N with Complementary Methods

Practical nuclear reactor modeling and analysis face challenges regarding multi-scale effects, coupled multi-physical fields, and complex geometries. While the S_N method offers significant computational efficiency for many transport problems, its standalone application may encounter limitations when addressing these multifaceted challenges. By strategically coupling the S_N method with complementary numerical techniques, these limitations can be overcome. This coupling process gives rise to synergistic computational frameworks that can fully leverage the respective strengths of different methods. Such challenges can be ameliorated through hybrid algorithmic frameworks and coupling methods.

The coupling of S_N and MC methods represents a strategic integration aimed at leveraging the high efficiency of deterministic methods in homogeneous regions while maintaining MC accuracy in complex geometries. The development of S_N-MC coupling techniques was initially demonstrated through the first collision source method in DOMINO [174] and subsequently advanced with two-way data transfer mechanisms in DOMINO-II [175]. Additionally, further advancement was achieved through the integration with MCNP in PROBGON for 2D calculations [176]. Moreover, the S_N-MC coupling technology was further extended to 3D applications, which was successfully realized in DOT-DOMINO-MORSE code [177]. Building on this progress, the detector response calculation capabilities were significantly improved in RADSAT code [178]. Furthermore, the DISCO (deterministic–stochastic coupling operation) interface [179] facilitated the expansion of coupling capabilities across multiple coordinate systems. Notably, significant progress in three-dimensional applications has been marked by the development of S_N-MC and MC-S_N two-way coupling codes in both Cartesian and cylindrical coordinate systems [180]. Collectively, efficiency improvements of 2–10 times compared to pure MC methods in deep-penetration problems have been consistently demonstrated through these enhancements.

Beyond S_N-MC coupling, other coupling methods have been developed to address computational efficiency challenges in full 3D calculations. The 2D/1D coupling method, combining 2D MOC for radial calculations with 1D S_N for axial solutions, has been established as an effective transport methodology for core calculations, with implementations in CRX-3D [181], DeCART [182], nTRACER [183], etc. A significant advancement in this domain is represented by the VERA (virtual environment for reactor applications) core simulator [184], wherein MPACT, its primary deterministic neutron transport solver, is characterized by the decomposition of three-dimensional problems into axial stacks of two-dimensional radial planes [185,186]. Computational stability has been enhanced by incorporating transverse leakage splitting and relaxation factors [187]. Meanwhile, computational efficiency has been optimized through the utilization of azimuthal Fourier moments in axial solvers [188]. Furthermore, the integration of DGFEM-based S_N as an axial solver has been demonstrated to exhibit superior convergence characteristics across a wide range of optical thicknesses [189,190].

As an extension of the 2D/1D approach, the 2D/3D coupling method combines 2D MOC for complex fuel assembly modeling with 3D S_N for comprehensive spatial transport calculations [191]. This integration leverages the geometric flexibility of MOC and the computational efficiency of S_N. Technical advancements include cross-section correction factors for non-uniform problems [191] and bidirectional coupling through interfacial angular flux exchange [192].

Despite the significant advances achieved in coupling S_N with various complementary methods, several challenges remain to be addressed. Particularly, further improvements are needed in the fidelity of interface treatments between coupled methods, optimization of data transfer mechanisms, and enhancement of convergence characteristics for iterative coupling schemes. Future research should focus on developing more robust and efficient coupling strategies that preserve the accuracy advantages of individual methods while minimizing computational overhead. As reactor designs become increasingly complex, these coupled S_N-based approaches will play an essential role in balancing computational efficiency with simulation accuracy in next-generation nuclear applications.

5. Challenges and Future Directions

In summary, the S_N method remains an indispensable approach in nuclear energy applications, offering significant advantages in computational efficiency and accuracy. This discretized approach continues to be essential for reactor physics analysis, radiation shielding design, and criticality safety assessments. This comprehensive review has highlighted the S_N fundamental theory, diverse applications, and the significant advancements over recent decades that have further enhanced the capabilities of the S_N method, enabling more accurate and efficient particle transport simulations.

Despite these advancements, several significant challenges persist in advancing the S_N method. Specifically, when S_N-based solvers are applied to large-scale, industrial reactor analyses, both theoretical and practical limitations become particularly pronounced, directly impacting their feasibility and effectiveness. The critical balance between high-fidelity model and computational efficiency poses a persistent challenge in S_N applications. While advanced angular quadrature schemes and higher-order spatial discretization methods are essential for accurate solutions in complex systems, their deployment in industrial-scale problems often results in substantial computational burdens, which can hinder practical adoption. These challenges manifest particularly in the mitigation of ray effects and the preservation of solution positivity across domains with strong material discontinuities, requiring careful balance between numerical accuracy and computational feasibility. In large, heterogeneous reactor cores, these issues are further exacerbated by the scale and complexity of the system, making robust and efficient S_N solver deployment even more challenging. Furthermore, diverse reactor designs present varying requirements for cross-section data, with advanced reactor concepts necessitating specialized cross-section libraries and uncertainty quantification methodologies to address the unique neutron energy spectra and material compositions encountered in these systems. The lack of standardized, high-fidelity cross-section data for novel reactor types remains a practical barrier to the routine use of S_N-based solvers in industry, complicating both model setup and validation.

Full-core transport simulation presents significant computational efficiency challenges due to its extremely large problem size, often involving billions of unknowns. The application of existing acceleration techniques, despite their sophisticated design, fails to achieve sufficient performance gains for practical full-core analyses. This computational bottleneck is a major limitation for industrial deployment, where computational cost and resource limitations are key concerns. Memory bandwidth limitations severely restrict the effectiveness of domain decomposition methods and GPU-based implementations when applied to realistic reactor configurations. In unstructured mesh calculations, the near-unity dominance ratio significantly degrades iterative convergence rates, resulting in prohibitively long solution times despite the employment of advanced preconditioning strategies. These practical issues limit the scalability and efficiency of S_N-based solvers in industrial settings, making it difficult to meet the demands of large-scale reactor analysis.

The intrinsic geometric complexity of Generation III+ and Generation IV reactor designs presents significant modeling adaptation challenges. The sophisticated coolant channel architectures and non-uniform material distributions in these advanced reactor systems require specialized mesh adaptation capabilities that current tools inadequately address. Conventional mesh generation approaches exhibit limited flexibility in accurately representing curved boundaries and complex material interfaces, frequently resulting in either computational inefficiency through excessive mesh refinement or compromised geometric fidelity. This model adaptability limitation constitutes a critical barrier to the accurate and efficient implementation of S_N methods for next-generation reactor analysis.

Additionally, dynamic radiation field calculations, especially during transient scenarios like reactor scram events, necessitate time-dependent S_N formulations. Incorporating temporal dependencies is crucial for real-time tracking, but introduces significant computational complexities due to the need for coupled space-time discretization. The practical deployment of time-dependent solvers in industrial environments is further complicated by the stringent requirements for real-time performance. In summary, while S_N-based solvers offer high-fidelity modeling capabilities, their practical deployment in large-scale, industrial reactor analyses is fundamentally constrained by computational, numerical, data, geometric, and dynamic simulation challenges. Addressing these limitations is essential for the broader adoption of S_N-based solvers in industrial practice.

To address the challenges and advance the S_N method toward greater applicability in next-generation nuclear systems, research efforts are being strategically directed toward several interconnected domains:

(1)

High-fidelity numerical simulation of complex geometries and source terms: The enhancement of geometric fidelity through unstructured grids and adaptive discretization techniques represents a key frontier for accurately representing heterogeneous structures. These advanced meshing approaches enable precise modeling of complex fuel assembly configurations with intricate pin arrangements, multi-scale porous shielding materials containing randomly distributed microstructural features, and curved boundary interfaces between different materials. Simultaneously, the integration of spatially dependent source distributions is being improved through advanced mathematical formulations, such as moment-based expansions for angular-dependent fission sources and hybrid deterministic-stochastic approaches for localized source regions. The combination of these advanced geometric and source term representations is expected to significantly reduce discretization errors while maintaining computational feasibility for practical engineering applications.

(2)

Optimization of high-performance numerical computation: Modern computing architectures are being effectively utilized through GPU-accelerated transport sweeps with specialized memory access patterns, distributed memory parallelism via domain decomposition with optimized communication strategies, and heterogeneous computing approaches that leverage CPU–GPU synergies. Solution algorithms are simultaneously being reformulated to enhance scalability, focusing on communication-avoiding variants of traditional sweeping algorithms and asynchronous parallel iteration schemes that reduce synchronization barriers. While hardware optimization progresses, efforts are also directed toward parallel algorithm development to improve overall performance and efficiency. These efforts include sweeping algorithm optimization to restructure computational sequences and minimizing inter-processor communication, alongside asynchronous iteration schemes that allow processors to proceed without waiting at synchronization barriers. To fully leverage exascale computing capabilities, both fault-tolerant algorithms and advanced scheduling strategies are being implemented, dynamic load balancing systems are being developed, and data compression methods are being applied to overcome memory bandwidth constraints. With these computational breakthroughs, real-time solutions of large-scale transport problems at the million-energy cluster level are creating new possibilities for reactor digital twins and industrial-scale applications.

(3)

Coupling of multi-physics fields: The S_N method serves as the particle transport module, deeply integrated with thermal hydraulics and fuel mechanics modules. This integration facilitates the establishment of a comprehensive multi-physics coupling framework. To further advance this framework, specialized interface treatments should be pursued for the coupling of neutron transport calculations with thermal-hydraulics and fuel mechanics, encompassing the incorporation of temperature-dependent cross-section feedback mechanisms, the development of fluid–structure interaction modeling in advanced cooling systems, and the advancement of material property evolution simulation under radiation damage conditions. Additionally, the formulation of multi-time-scale coupling strategies will be essential for addressing the computational challenges presented by the coexistence of rapid neutronic transients with slower thermal-hydraulic phenomena. The realization of these anticipated advancements in multi-physics integration is expected to provide the foundation for high-fidelity whole-core analyses with comprehensive feedback mechanisms, thereby enabling the enhancement of reactor digital twin technologies and strengthening the design and safety assessment capabilities for next-generation nuclear energy systems.

(4)

AI for S_N: The application of artificial intelligence to S_N methods stands as a prominent frontier, representing a revolutionary transformation in computational particle transport. By learning complex input–output relationships from large datasets, AI techniques are being used to construct highly efficient surrogate models. Surrogate modeling, as a data-driven approach, provides fast approximations of S_N solutions, while reduced-order modeling focuses on simplifying the underlying physical models to lower computational complexity. These two approaches are complementary and can be integrated to further enhance computational efficiency. These AI-driven methods are advancing several key areas, including radiation field construction, neutron energy spectrum expansion, neutron and gamma field reconstruction, and acceleration of iterative convergence. In practical reactor analysis, surrogate models have been employed for the rapid prediction of specific reactor parameters such as core eigenvalues, assembly power distributions, and power peaking factors. Deep learning models trained on data from high-fidelity S_N simulations can significantly accelerate both steady-state and transient analyses. Furthermore, AI is being leveraged to enhance numerical convergence, for example, through reinforcement learning strategies for optimal selection of iteration parameters and the use of convolutional neural networks to provide improved initial flux estimates. Collectively, these developments are revolutionizing the efficiency and scope of S_N-based reactor analysis.

6. Conclusions

This review has comprehensively examined the evolution and applications of the S_N method in nuclear energy, with its fundamental mathematical principles and diverse applications being systematically presented. Based on this foundation, a thorough evaluation of recent methodological advancements has been conducted on ray effect mitigation, spatial discretization enhancement, acceleration techniques, and complementary method coupling as four essential aspects. Through this assessment, significant progress in angular discretization methodologies, spatial discretization approaches, acceleration techniques, and hybrid coupling mechanisms has been revealed, thereby leading to an expanded applicability of the S_N method to increasingly complex problems. Despite these advancements, persistent challenges have been identified in computational efficiency for full-core transport simulations, geometric representation of advanced reactor designs, and accurate modeling of transient phenomena, all of which warrant continued research attention. As part of this systematic review, promising future directions for the S_N method have been highlighted, with consideration given to high-performance computing integration, advanced geometric modeling capabilities, multi-physics coupling frameworks, and artificial intelligence applications, all of which are collectively pointing toward a new generation of S_N-based simulation tools. Overall, the continued evolution of the S_N method is deemed crucial in meeting the growing demands of nuclear energy simulations, ensuring both safety and efficiency in reactor design and operation.