1. Introduction
With the increasing consumption of fossil fuels, renewable energy sources have gained significant attention. Among them, PV generation has rapidly emerged as a research hotspot due to its low cost and environmental benefits [
1,
2,
3,
4]. However, the large-scale integration of high-penetration PV generation poses substantial challenges to power system operation. In particular, the stochastic and intermittent nature of PV output has profound impacts on voltage stability, reactive power balance, and network losses [
5,
6,
7,
8].
Accurate PV power forecasting plays a crucial role in enhancing grid stability, optimizing reactive power distribution in distribution networks, and improving power system dispatch efficiency [
9,
10,
11]. To address the challenges posed by PV output uncertainty—such as voltage stability issues and reactive power imbalance—improving PV forecasting accuracy and optimizing reactive power distribution in distribution networks have become active research areas. Traditional neural network models for PV forecasting [
12,
13,
14] are often constrained by the availability of power plant data and tend to overlook the influence of certain environmental factors on PV output [
15]. Additionally, conventional networks exhibit inherent limitations in handling long-term dependencies, feature analysis, and variable-length output generation, while also being highly dependent on meticulous hyperparameter tuning. PV power output is influenced by multiple factors, exhibiting complex nonlinear relationships with various environmental features, making precise modeling challenging. To accelerate model convergence, researchers have developed numerous optimization algorithms [
16,
17,
18]. However, slower convergence rates can lead to overfitting issues, limiting the general applicability of existing models under diverse operating conditions. Moreover, most existing approaches fail to adequately consider the time-varying characteristics of PV power, restricting improvements in forecasting accuracy. In response to these challenges, hybrid forecasting models have emerged, combining physical modeling with data-driven techniques to leverage the strengths of multiple technologies, thereby significantly improving forecasting accuracy and system reliability. For instance, Ref. [
19] proposes a hybrid model that integrates empirical mode decomposition (EMD), principal component analysis (PCA), and LSTM networks based on the methodology in Ref. [
20]. This model demonstrates superior performance in terms of spectral occupancy variation and effectively improves forecasting accuracy. Further research in Ref. [
21] demonstrated that global horizontal irradiance (GHI) is a key environmental factor influencing PV power generation, and that hybrid forecasting models outperform single models in terms of prediction accuracy.
On the basis of accurately forecasting distributed PV output, the rational coordination of reactive power distribution in high-penetration PV distribution networks can enhance grid operation efficiency, reduce energy consumption and losses, and provide technical support for integrating renewable energy into distribution networks. Reactive power optimization is a critical aspect of optimal power flow (OPF) in power systems and requires efficient optimization algorithms for its solution [
22,
23,
24,
25]. In recent years, artificial intelligence and machine learning algorithms have been widely applied to reactive power optimization, including Grey Wolf Optimization (GWO), Genetic Algorithm (GA), Multi-Objective Particle Swarm Optimization (MOPSO), and Whale Optimization Algorithm (WOA). However, these algorithms are prone to local optima, which affects their practical application. To address this issue, researchers have proposed various improvements. Ref. [
26] introduced a reactive power optimization method for distribution networks based on solid-state transformers, incorporating a dynamic search mechanism and entropy weight method to determine evaluation index weights, thereby enhancing the multi-objective wolf pack optimization algorithm. However, this method does not fully consider PV active power accommodation, which may lead to curtailment. Ref. [
27] proposed an improved differential evolution algorithm that dynamically adjusts the mutation and crossover factors to effectively mitigate the issue of local optima in the later stages of reactive power optimization. Ref. [
28] integrated an attention mechanism into the multi-objective particle swarm optimization algorithm to enhance PV accommodation, reduce network losses, and improve voltage quality. While the attention mechanism guides particle searches, it remains susceptible to local optima and suffers from slow convergence or difficulty in finding a global optimum in large-scale problems. Based on the traditional Whale Optimization Algorithm (WOA), Ref. [
29] introduced a local neighborhood search mechanism and established a reactive power optimization model aiming to minimize total active power losses and node voltage deviations across the distribution network. Furthermore, a novel adaptive threshold strategy was designed to enhance the global search capability of the algorithm, thereby balancing global exploration and local exploitation performance.
Conventional signal decomposition methods exhibit significant limitations when processing photovoltaic power data under transitional weather conditions, as they struggle to effectively capture abrupt changes and non-stationary characteristics. Meanwhile, existing reactive power optimization algorithms often suffer from slow convergence and a tendency to become trapped in local optima when dealing with complex grid conditions. Furthermore, current research on distribution network optimization rarely considers the impact of distributed generation forecasting, and systematic studies that integrate both aspects are scarce. Therefore, there is an urgent need to develop a novel coordinated optimization approach that simultaneously enhances forecasting accuracy and reactive power optimization performance.
Based on the above analysis, this study proposes a reactive power optimization method that integrates an improved FMD approach with a MOPSO algorithm, targeting reactive power dispatch in scenarios with high PV penetration. The main contributions are as follows:
- (1)
FMD-KPCA-LSTM Prediction Model. A hybrid FMD-KPCA-LSTM model is developed to predict the upper boundary of PV power output, which serves as a critical decision variable in reactive power optimization. The improved FMD [
30] method adaptively selects window functions to achieve finer decomposition according to different frequency characteristics, effectively capturing the cyclical fluctuations and trend features of PV output, thereby significantly enhancing prediction accuracy.
- (2)
Dimensionality Reduction and Time Series Modeling. KPCA is employed to extract high-contribution feature components, while a LSTM neural network is used to model the dynamic relationship between multivariate time series and PV output, improving the generalization capability of the prediction model.
- (3)
MOPSO Algorithm with Multi-Head Attention Mechanism. A multi-head attention mechanism is introduced into the MOPSO algorithm to dynamically guide the velocity updates of particles. This mechanism integrates the spatial distribution of particles’ historical best positions and their fitness differences, enabling adaptive adjustment of search direction and step size, thus enhancing the algorithm’s global search capability and convergence efficiency.
- (4)
Optimization of Reactive Power Compensation. The fluctuating PV output is incorporated as an optimization variable to guide the coordinated control of reactive power compensation devices. This approach contributes to improved PV utilization, reduced network losses, and enhanced voltage quality, offering a practical optimization strategy for the efficient integration of distributed renewable energy sources.
2. Reactive Power Optimization for High-PV Distribution Networks
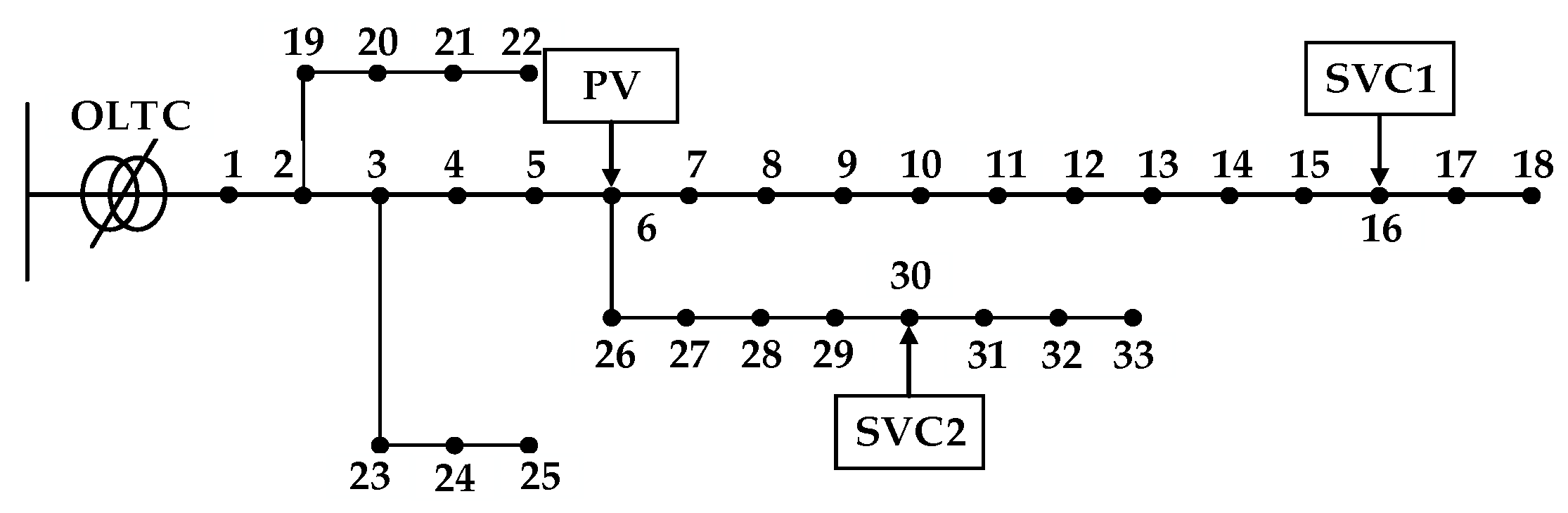
During periods of strong solar irradiation and low load demand, maximum PV output may cause voltage to rise at certain nodes, potentially exceeding permissible limits and threatening the safe operation of the distribution network. This issue is particularly pronounced in areas with weak network structures and insufficient reactive power regulation capability, where the indiscriminate integration of PV generation may result in voltage violations and system instability. Therefore, enhancing PV hosting capacity requires the effective participation of PV units in reactive power optimization. Common reactive power regulation methods include static var compensators (SVC), power capacitors, synchronous condensers, and on-load tap changers (OLTC). In this study, various reactive compensation devices are comprehensively coordinated within the distribution network to establish a reactive power optimization model tailored for high-penetration PV scenarios. The model aims to reduce voltage deviations and active power losses, thereby improving system stability and PV accommodation capability, and ultimately enhancing the overall operational efficiency of the distribution network.
2.1. Objective Function
(1) Active power loss of the distribution network
where
represents the number of nodes;
denotes the resistance between node
and node
;
and
represent the active power and reactive power, respectively, between node
and node
; and
is the voltage magnitude at node
.
(2) Voltage deviation of the distribution network
where
represents the voltage magnitude at node
at time
;
is the rated voltage of node
; and
and
represent the upper and lower voltage limits at node
, respectively.
(3) The photovoltaic (PV) absorption ratio of the distribution network
where
represents the photovoltaic power generation at time
and
is the photovoltaic absorption power at time
.
2.2. Constraints
The constraints in reactive power optimization typically include equality and inequality constraints. The equality constraints in this study primarily involve power flow equations, while the inequality constraints encompass current and voltage limits as well as decision variable constraints. The decision variables include the hourly PV power injected into the grid over a 24 h period, the compensation capacity of reactive power compensators, and the tap positions of on-load tap-changing (OLTC) transformers. In distribution network reactive power optimization, control variables generally consist of both continuous and discrete variables. Continuous variables include generator reactive power output and the output of SVC/STATCOM devices, while discrete variables include transformer tap positions and capacitor bank switching states. The optimization process can simultaneously account for both continuous and discrete variables to ensure comprehensive and efficient reactive power control.
(1) Power flow constraints
where
and
represent the active and reactive power injections at node
, respectively;
denotes the conductance between node
and node
;
is the susceptance between node
and node
;
and
represent the active and reactive power injected by the photovoltaic system at node
, respectively;
is the voltage phase angle difference between node
and node
; and
and
represent the nodes where the photovoltaic system and reactive power compensator are connected, respectively.
(2) Current and voltage constraints
where
represents the current flowing between nodes
and
at time
;
and
are the minimum and maximum current limits flowing between nodes
and
at time
, respectively;
is the voltage magnitude at node
at time
; and
and
are the minimum and maximum voltage limits at node
, respectively.
(3) Decision variable constraints
where
and
are the maximum and minimum reactive power injected by the photovoltaic system at node
, respectively;
and
are the maximum and minimum reactive power compensation capacities at node
, respectively;
is the tap ratio of the
-th OLTC transformer;
and
are the maximum and minimum tap ratio limits of the
-th on-load tap-changer transformer;
is the reactive power compensation capacity at node
; and
and
are the maximum and minimum reactive power compensation capacities at node
, respectively.
3. Forecasting Photovoltaic Power Generation
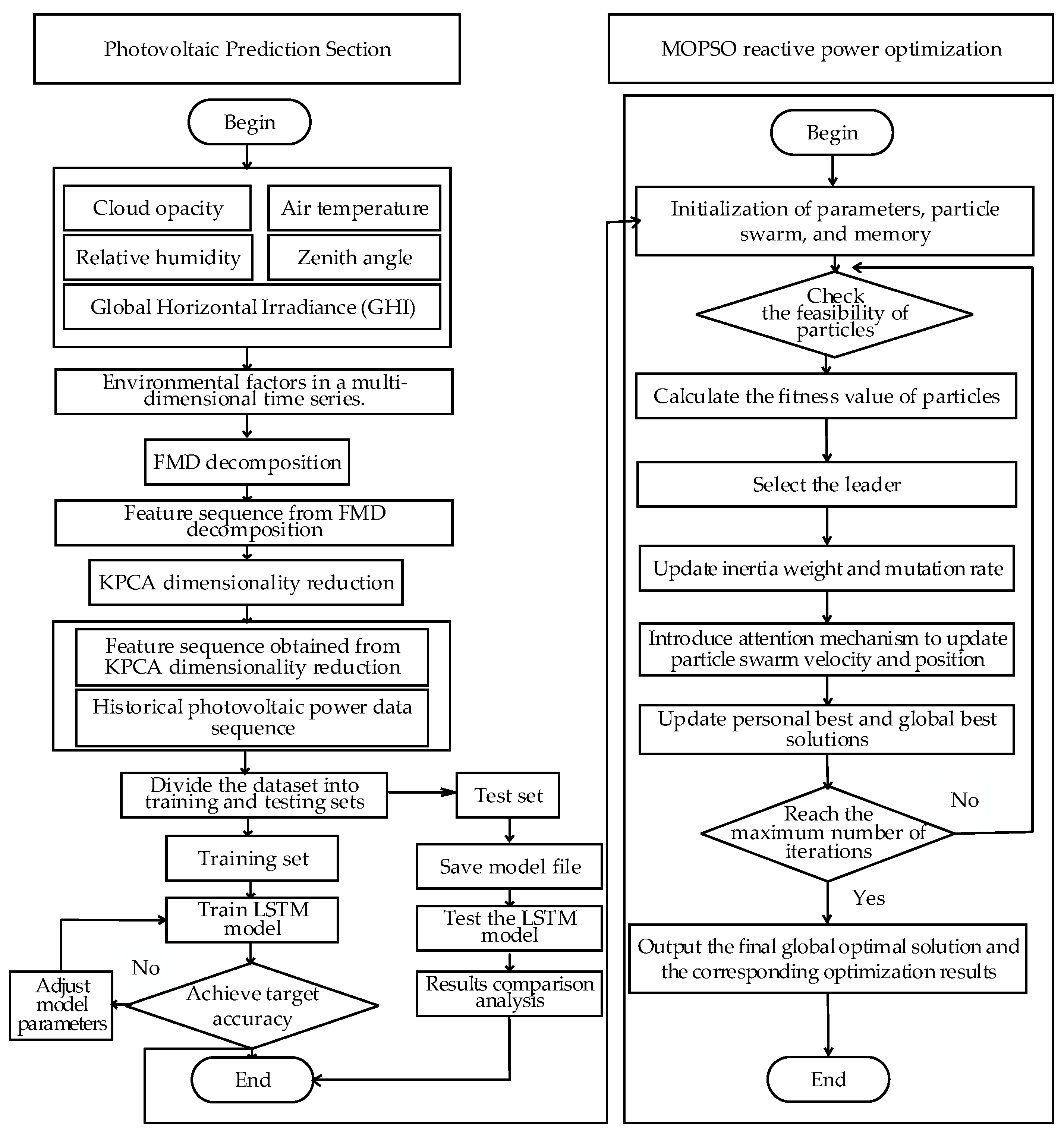
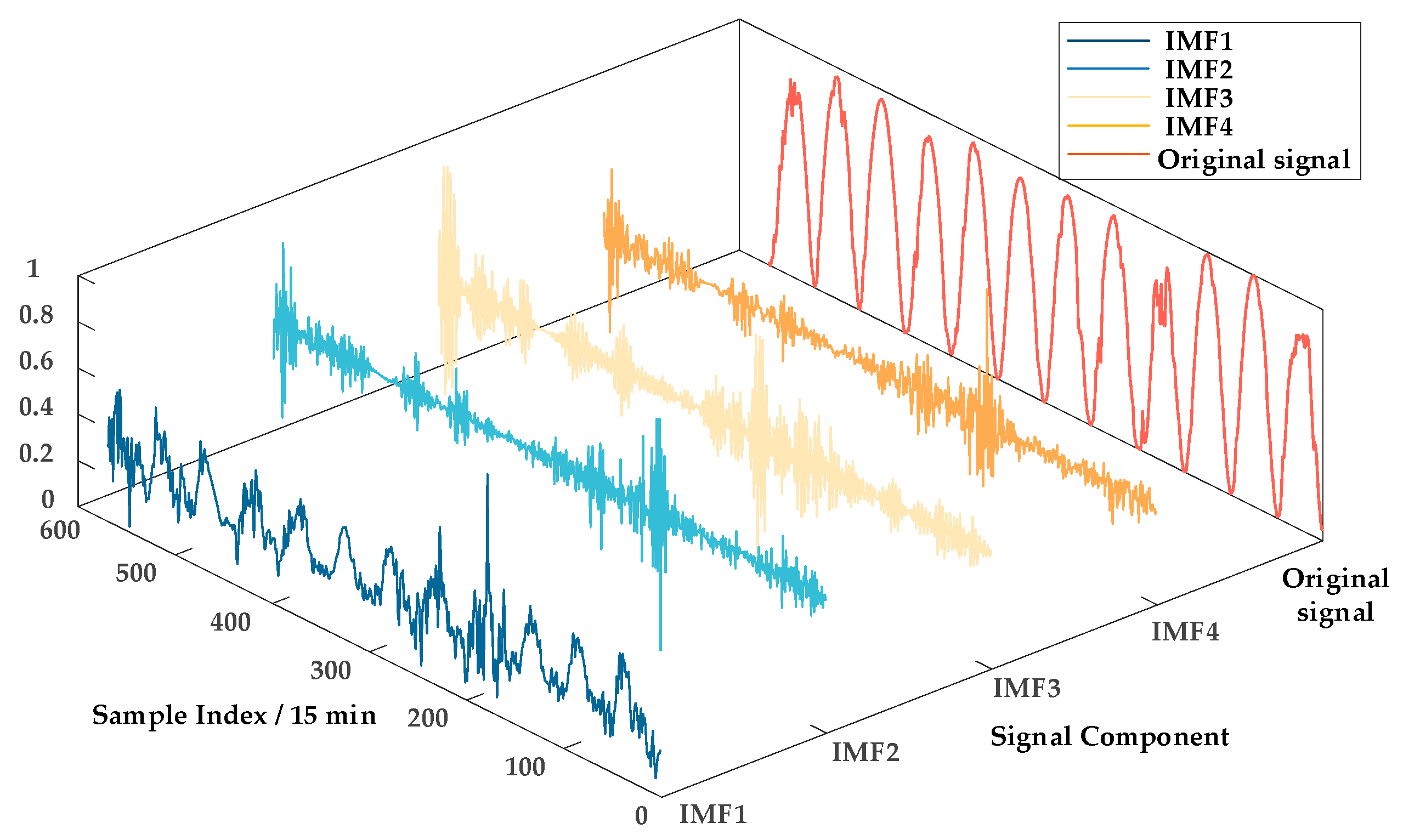
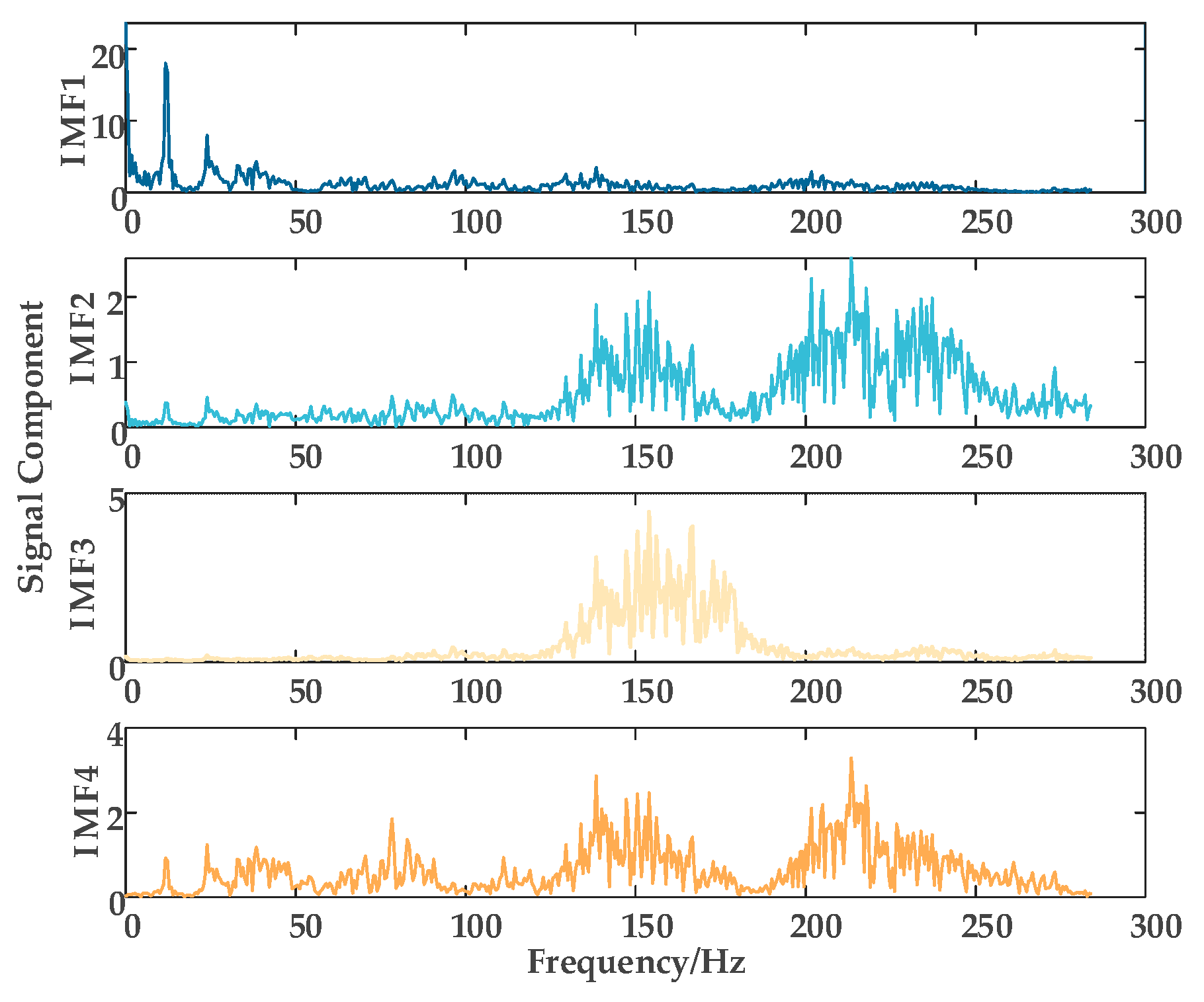
Short-term PV power forecasting provides critical support for enabling PV systems to participate in reactive power optimization. However, conventional signal decomposition methods, such as empirical mode decomposition (EMD) and variational mode decomposition (VMD), exhibit limitations when applied to non-stationary, multi-scale PV power signals. EMD is highly sensitive to noise and prone to mode mixing, resulting in decomposed components that lack clear physical interpretation. Although VMD can suppress mode mixing to some extent, it requires prior specification of the number of modes and penalty factors, which limits its adaptability and makes it less effective in handling complex spectral characteristics. To enhance the performance of hybrid forecasting models, this study first adopts an improved Feature Mode Decomposition (FMD) method to process environmental variables. Five environmental factors closely correlated with PV power output—global horizontal irradiance, air temperature, relative humidity, cloud optical depth, and solar zenith angle—are selected using Pearson correlation analysis. Each variable is decomposed into four modal components using the FMD approach. Subsequently, KPCA is applied to reduce the dimensionality of the high-dimensional feature space and extract the most informative characteristics. Finally, the dimensionally reduced features are fed into a LSTM network to achieve accurate PV power prediction.
3.1. Environmental Feature Decomposition Using an Improved FMD Model
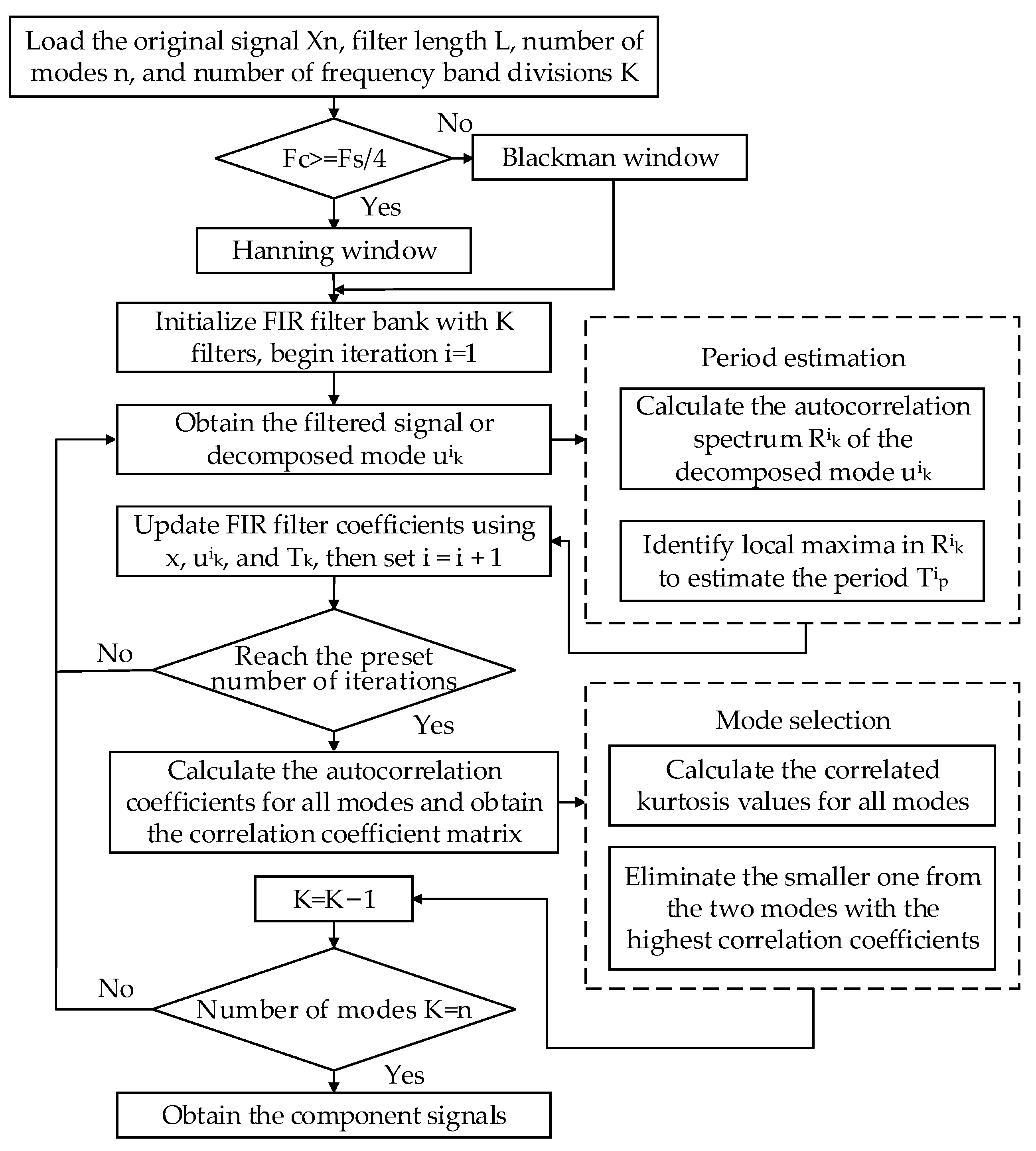
The FMD method demonstrates strong noise and interference resistance by simultaneously considering the impulsive and periodic characteristics of the signal. This method utilizes an adaptive FIR filter to extract decomposition modes, overcoming the limitations of traditional methods related to filter shape, bandwidth, and center frequency, thereby achieving a more thorough signal decomposition. To address the non-stationarity and multi-scale features of PV power data, this study improves the FMD method by introducing an adaptive window function selection mechanism. Based on the spectral distribution characteristics of each frequency band, the mechanism dynamically selects either the Hanning window or the Blackman window, enabling more precise separation of short-term fluctuations and long-term trends in PV power.
Correlated kurtosis (CK) is used as an indicator to construct constraint conditions and update the FIR filter coefficients, decomposing the original signal into
frequency bands, as defined by the following equation [
30]:
where
represents the
-th decomposition mode;
is the
-th FIR filter function;
denotes the index variable for the operation;
is the filter length;
represents the original signal with length
;
represents the photovoltaic fluctuation period; and
is the shift order,
.
The Hanning window and Blackman window are used to filter the low-frequency and high-frequency components of the signal, respectively. Under the constraint defined in the above Equation (7), the filter coefficients are updated iteratively with the maximum correlated kurtosis as the objective. The definition of the autocorrelation spectrum
is as follows [
30]:
where
is the lag coefficient.
First, the number of update iterations for the
-th filter is determined. Initial modal components are obtained through filter deconvolution. The correlation coefficients between the modal components are then calculated to identify the two pairs of modes with the highest correlation. Among these, the mode with the lower relative kurtosis is eliminated. After elimination, the filter coefficients of the remaining modes are updated, and the iteration continues until the number of modal components reaches the predefined value
, at which point the process is terminated. The relevant equations are given in Ref. [
30]:
where
and
represent the two mode components, and
and
are the average values of the
and
mode components, respectively. The following illustrates the procedure of the improved FMD method.
(1) Initialization: Load the original photovoltaic signal , input preset parameters such as sampling frequency, filter size, the number of frequency bands, the number of decomposition modes, and the maximum number of iterations as input information for initialization. Define the frequency band range for each band. Based on the frequency band characteristics, dynamically select the window function: use the Hanning window for the high-frequency components and the Blackman window for the low-frequency components. Design FIR filters . Set the initial iteration counter .
(2) Signal Decomposition: Filter the original signal
using the filter group. Perform convolution operations on the signal using the filter group
to obtain the filtered mode components.
Use the original signal , the decomposition mode components , and the estimated photovoltaic fluctuation period to update the filter coefficients. The photovoltaic fluctuation period is estimated by the autocorrelation spectrum at the moment when it reaches the local maximum after the zero-crossing point. After one iteration, set .
(3) Iteration Termination Check: Check whether the iteration count has reached the preset maximum iteration number. If it has not been reached, return to step 2 to continue the iteration. If it has been reached, proceed to step 4.
(4) Mode Component Selection: Use the Multiscale Decomposition Algorithm (MCKD) to decompose the signal into multiple modes (IMFs) and calculate the correlation coefficient between two modes:
where
is the covariance between signals
and
, and
and
are the standard deviations of signals
and
, respectively. This results in a matrix of size
, representing the pairwise signal correlations. The correlation kurtosis of the two signals with the highest correlation coefficient is compared, and the signal with the higher correlation kurtosis is retained. By updating the signals and filters, redundant signals are removed, and the final
modes are obtained. The improved FMD algorithm proposed in Ref. [
30] follows the procedure illustrated in
Figure 1.
3.2. Feature Dimensionality Reduction via KPCA
Excessively complex data can reduce the predictive performance of neural networks, making dimensionality reduction of the decomposed signals crucial to decrease computational complexity. Kernel Principal Component Analysis (KPCA) is an improvement on the PCA method. The core idea of KPCA is to map the data points in the input space to a feature space, where the data points in the feature space can be more easily processed and analyzed. Choosing an appropriate kernel function is critical for effective dimensionality reduction. Common kernel functions include linear kernel, polynomial kernel, and Gaussian kernel. Kernel functions also contain parameters that directly affect the degree of transformation, and these parameters can be determined through cross-validation. The explained variance method is used to evaluate the dimensionality reduction effect, and then the features obtained after KPCA fusion are ranked based on their contribution. The top few features whose total contribution reaches 90% of the overall contribution are selected as the reduced-dimensional data.
3.3. Long Short-Term Memory Network
LSTM is a deep learning algorithm based on an improved Recurrent Neural Network (RNN). The basic unit of LSTM is the memory block, which consists of three main stages: the forget stage, the input stage, and the output stage. Each stage has its specific operations, and the flow of information is controlled by different gating mechanisms.
3.4. Prediction Accuracy Evaluation
The model’s photovoltaic power prediction performance was evaluated using three metrics: Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and the coefficient of determination (R
2). The corresponding calculation formulas are provided in
Appendix A.1.
4. A Reactive Power Optimization Model for Distribution Networks Based on an Improved MOPSO Algorithm
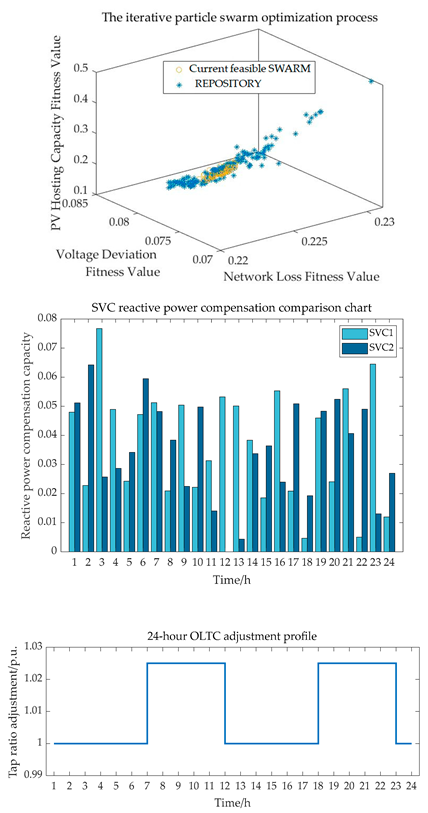
In the previous section, the PV forecasting model provided critical decision-making support for reactive power optimization by accurately predicting short-term photovoltaic generation. To further enhance the PV hosting capacity, this study develops a reactive power optimization model for distribution networks based on an improved multi-objective particle swarm optimization (MOPSO) algorithm. In this model, a multi-head attention mechanism is introduced into the particle velocity update process to enhance the algorithm’s global guidance and local exploration capabilities during the solution space search. The overall workflow is shown in
Figure 2.
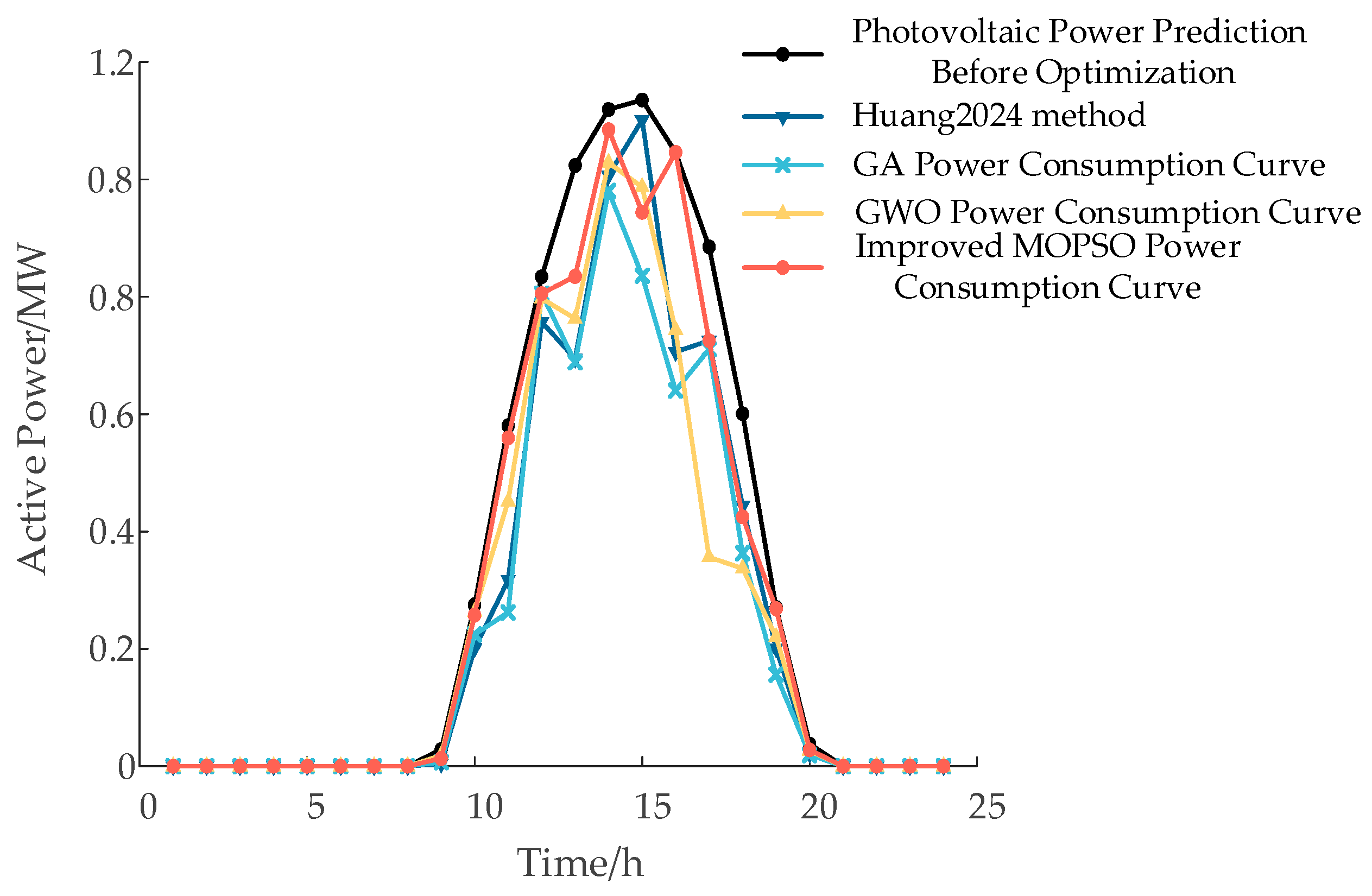
(1) After integrating static var compensators, photovoltaic generation, and on-load tap changers into the grid, the predicted photovoltaic output is used as the boundary for decision variables. Particle swarm initialization is performed, including acceleration coefficients, dynamic inertia weight, maximum iteration count, expansion rate, and dynamic mutation rate.
where
represents the dynamic inertia weight at iteration
;
and
denote the initial and final values of the inertia weight, respectively;
is the maximum number of iterations;
denotes the dynamic mutation rate at iteration
; and
represents the mutation rate.
The grid storage management is initialized, and individuals are assigned to the grid based on the objective function values.
where
represents the
objective function value;
and
denote the minimum and maximum values of the
objective function, respectively; and
represents the number of grids in each dimension.
(2) Based on the defined objective functions and constraints, the population and parameters are initialized to construct particle positions, update velocities, and assign attention weights.
where
represents the position vector of particle
, consisting of
components;
denotes the velocity vector of particle
; and
represents the attention weight of particle
.
(3) Fitness Value Calculation
The iterative loop calculates the fitness function based on the objective functions of each particle to ensure that the voltage magnitude remains within the allowable range while optimizing system performance.
where
represents the
-th fitness value of particle
.
A voltage violation penalty function is introduced into the network loss model to effectively constrain the voltage magnitude and enhance the stability and safety of the system.
where
represents the voltage violation penalty value;
is the voltage deviation at node
;
and
denote the lower and upper voltage limits at node
, respectively; and
is the penalty coefficient.
(4) The attention weight
is optimized using evolutionary strategies, and iterative evolution is achieved using methods such as parent selection and new solution generation. During this process, the attention weights are dynamically adjusted, considering both the distance between particles and the historical optimal solution as well as the differences in fitness. This approach enhances the algorithm’s exploration ability in the search space and improves its convergence performance.
where
represents the cognitive component attention weight of particle
;
denotes the social component attention weight of particle
;
is the position of particle
at iteration
;
represents the individual historical best position of particle
at iteration
; and
is the global best position of the population at iteration
. See
Appendix A.2 for the specific encapsulation formula.
(5) The particle velocity update employs an attention mechanism, where the cognitive and social coefficients are dynamically adjusted based on the historical best position and fitness values using multi-head attention weights, thereby updating the particle’s velocity and position.
where
represents the velocity of particle
at iteration
;
and
are random numbers;
is the dynamic cognitive coefficient; and
is the dynamic social coefficient.
(6) During the position update stage, boundary constraints are introduced to correct the particle’s position, ensuring it remains within the predefined reasonable range.
(7) The individual best position is updated by comparing the current fitness value with the individual best position.
(8) If the current particle is not dominated by other particles, the global best solution is updated, and the external storage mechanism is updated accordingly.
(9) Finally, the current iteration count is checked to see if it has reached the maximum value. If the maximum iteration has not been reached, the algorithm continues to iterate; otherwise, the global optimal solution and optimization results are output.
6. Conclusions
This paper addresses the issues caused by the high penetration of PV systems in distribution networks, such as uncertainty in PV power forecasting, limited PV absorption, and reactive power imbalance. An adaptive FMD-based coordinated reactive power–voltage optimization method is proposed to tackle these challenges. The main conclusions are as follows:
(1) The FMD based on an adaptive window function optimization enables more accurate extraction of the periodic fluctuations and long-term trends of photovoltaic (PV) output. Compared to the EMD-PCA-LSTM model reported in Ref. [
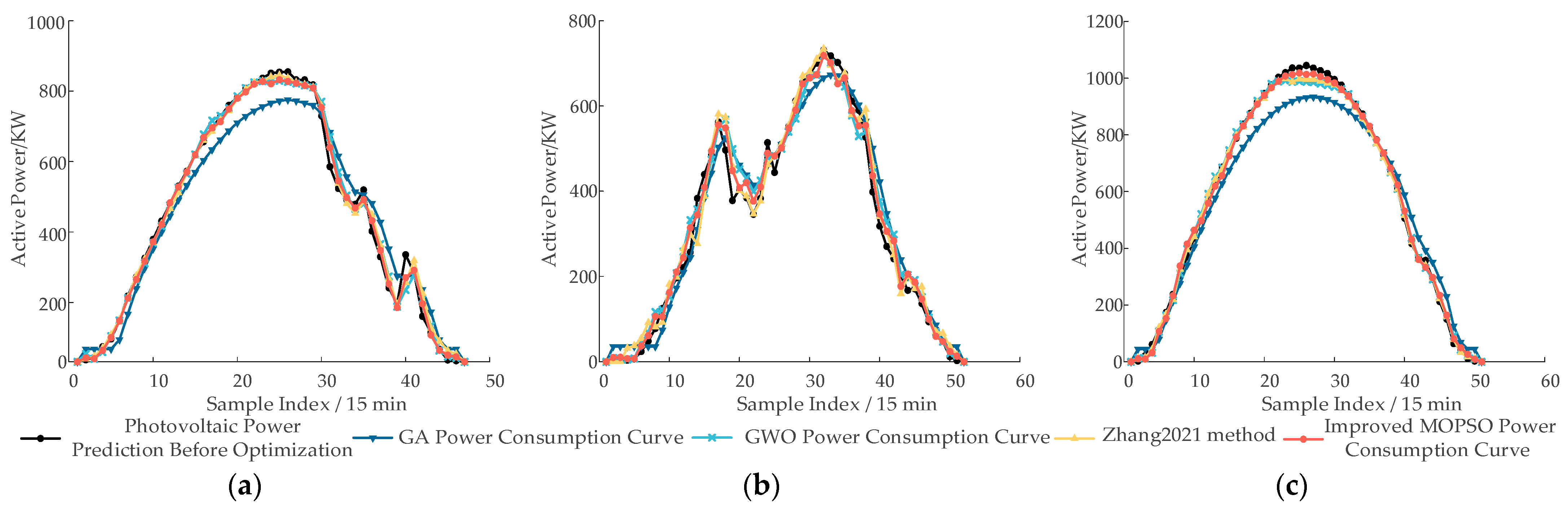
19], the improved FMD-KPCA-LSTM forecasting method reduces the RMSE from 2.9064, 4.2737, and 1.8598 to 2.2764, 3.2889, and 1.6647 under cloudy, variable, and sunny conditions, respectively. This corresponds to accuracy improvements of 21.70%, 23.03%, and 10.48%, providing high-quality data support for subsequent reactive power optimization.
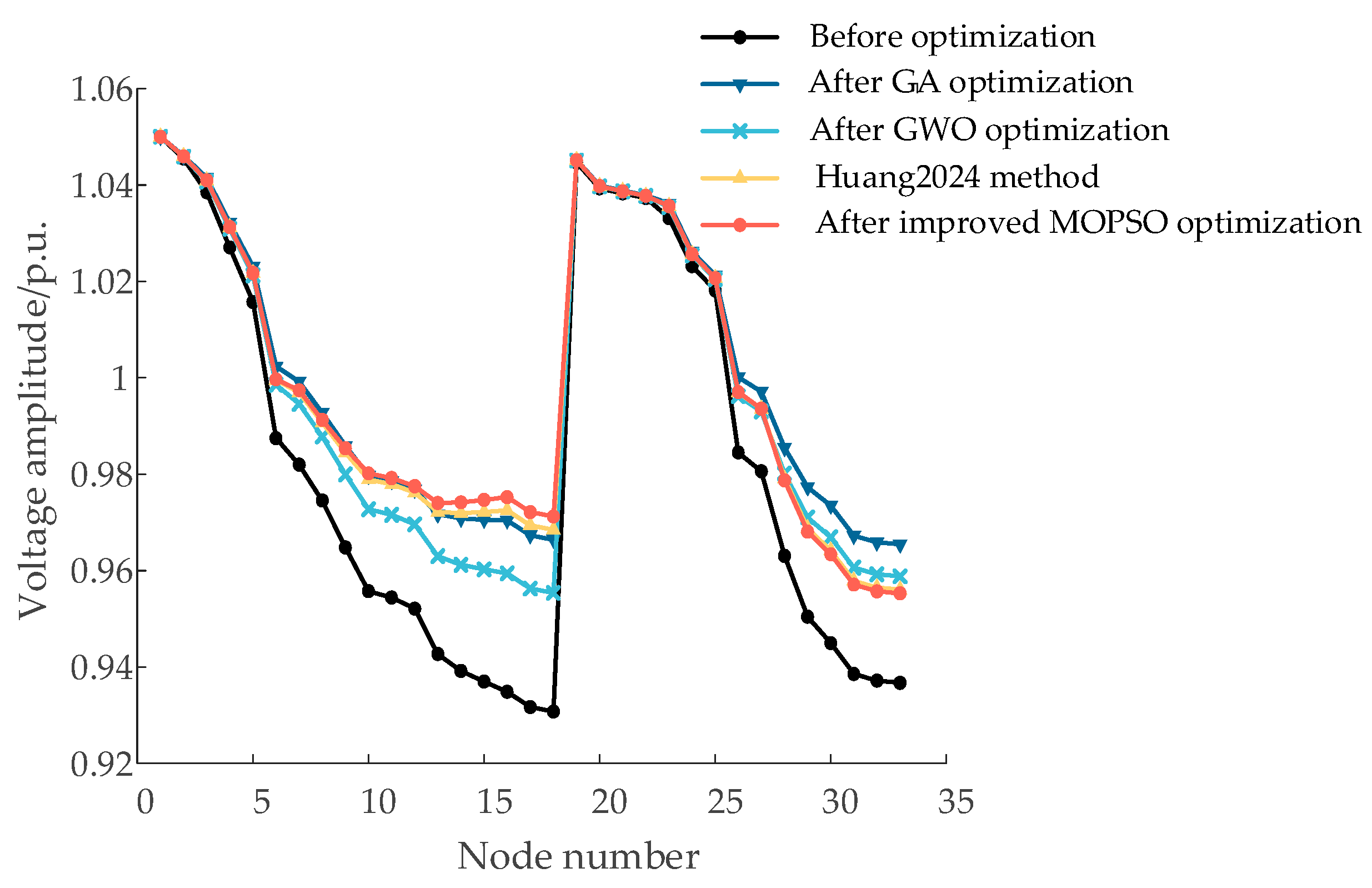
(2) A comprehensive objective function was constructed to coordinate the control of PV output, SVC, and OLTC, and solved using the improved MOPSO algorithm. Compared with the improved Whale Optimization Algorithm proposed in Ref. [
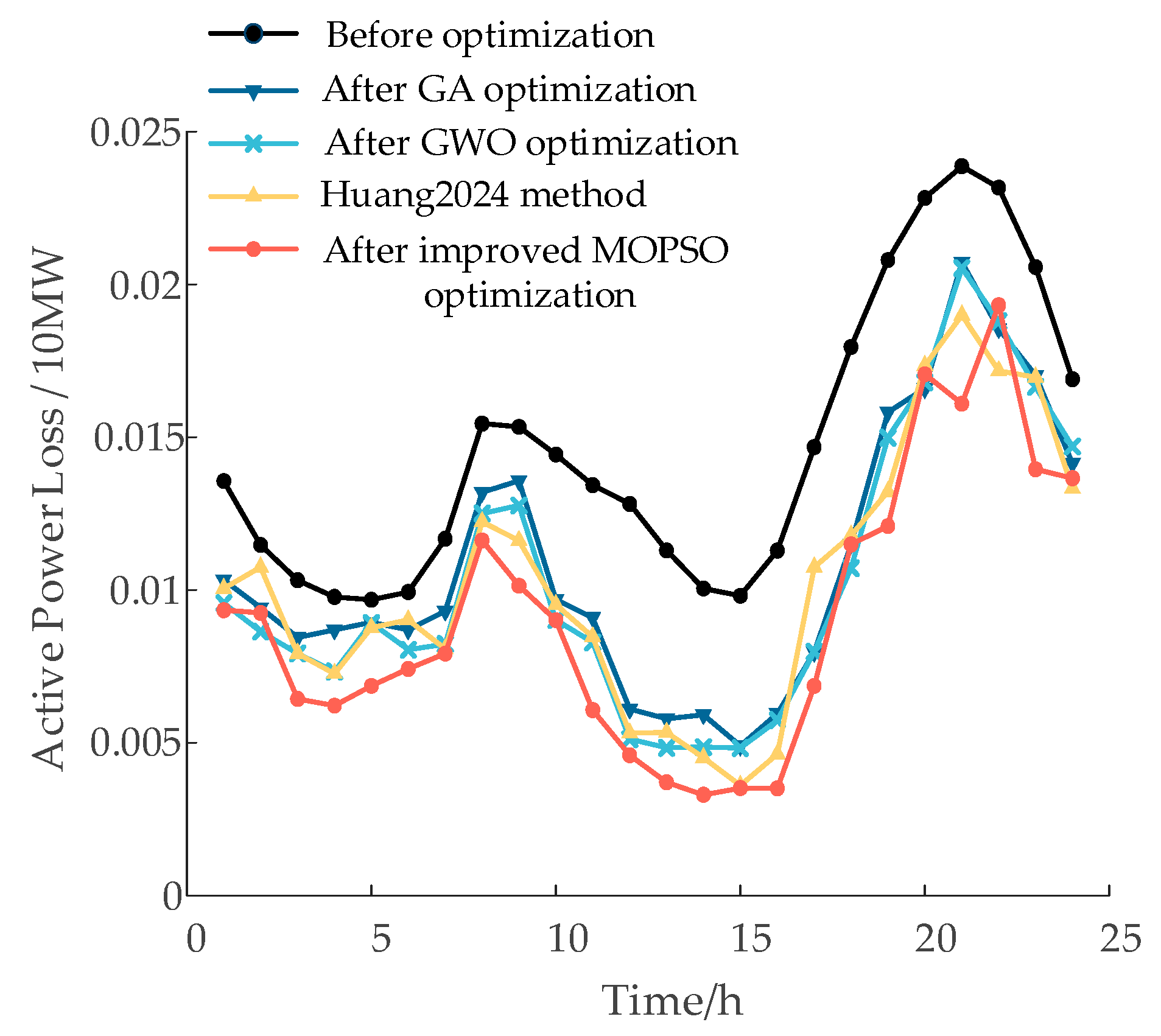
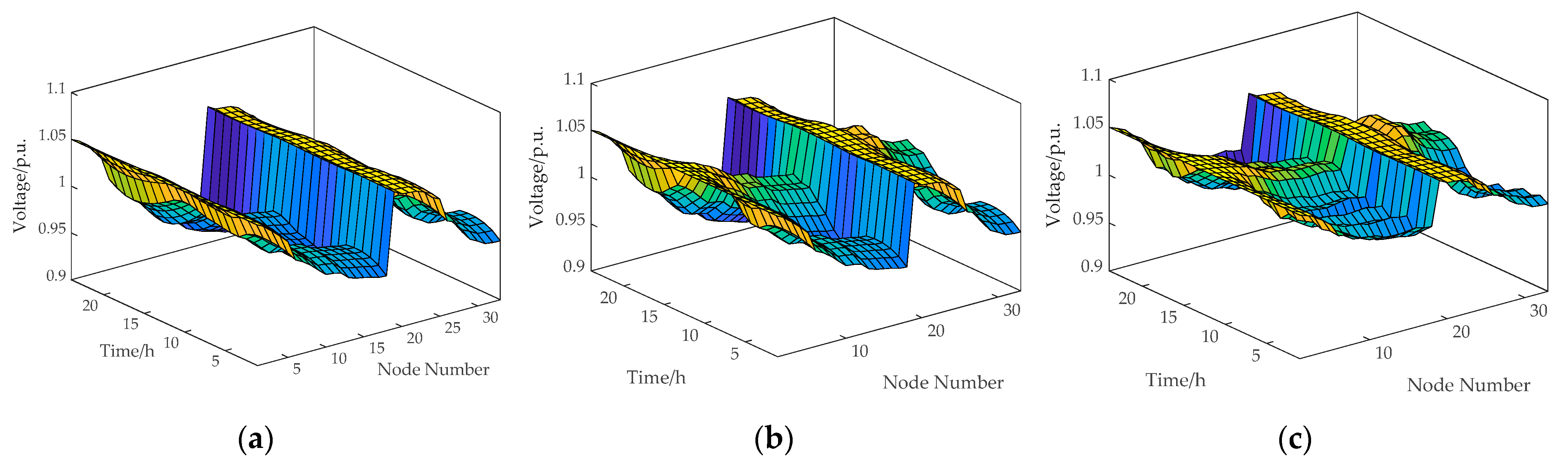
29], the proposed method achieves a 13.15% increase in PV utilization rate, a 2.86% reduction in voltage deviation, and an 11.01% decrease in active power losses. Under the scenario with typical load and optimized PV integration, active power losses and voltage deviation are reduced by 30.42% and 28.74%, respectively. These results verify the effectiveness of the proposed method in minimizing network losses, enhancing PV accommodation, and improving voltage quality while satisfying voltage constraint conditions.
(3) Case study validation shows that the proposed method demonstrates superior adaptability and computational accuracy, effectively enhancing the safety and economy of the distribution network, and further highlights the important role of photovoltaic power forecasting in reactive power optimization.
This study focuses on reactive power optimization in a distribution network based solely on day-ahead typical load profiles and PV forecast data with a one-hour resolution, without fully considering the dynamic uncertainties present in actual dispatching. Future research could integrate time-of-use pricing mechanisms and extreme PV fluctuation scenarios to develop multi-time-scale dynamic secondary reactive power optimization under source-load uncertainties, thereby further enhancing scheduling flexibility and economic efficiency.