An Acceleration-Observer-Based Position and Load Torque Estimation Method for Wind Turbine with Sensor Faults
Abstract
1. Introduction
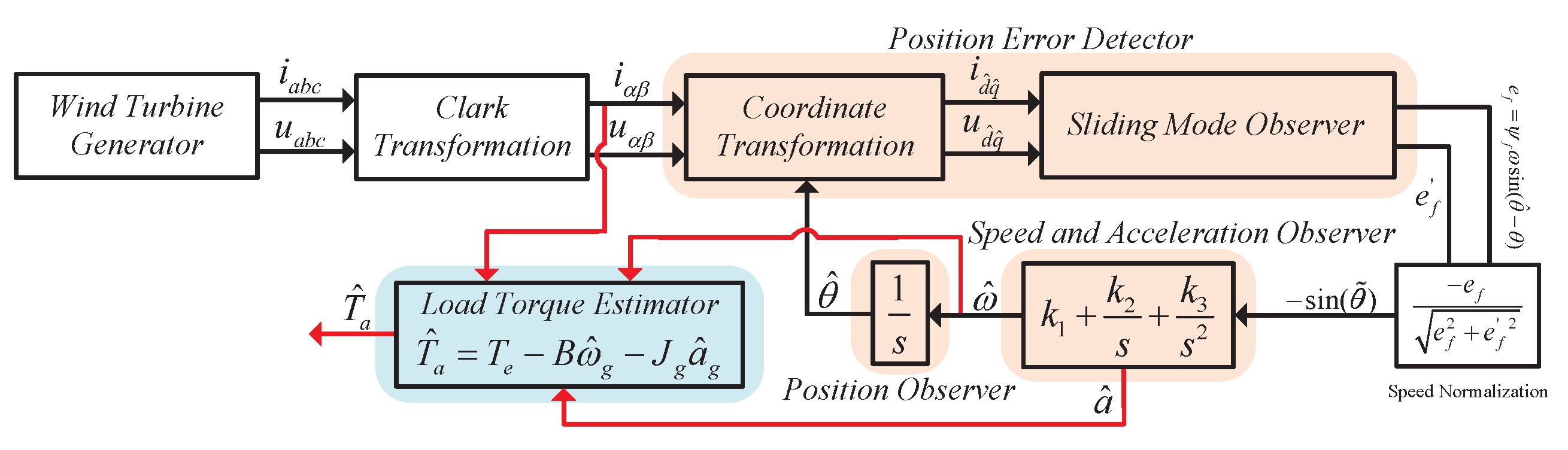
2. Proposed Position and Load Torque Estimation Method
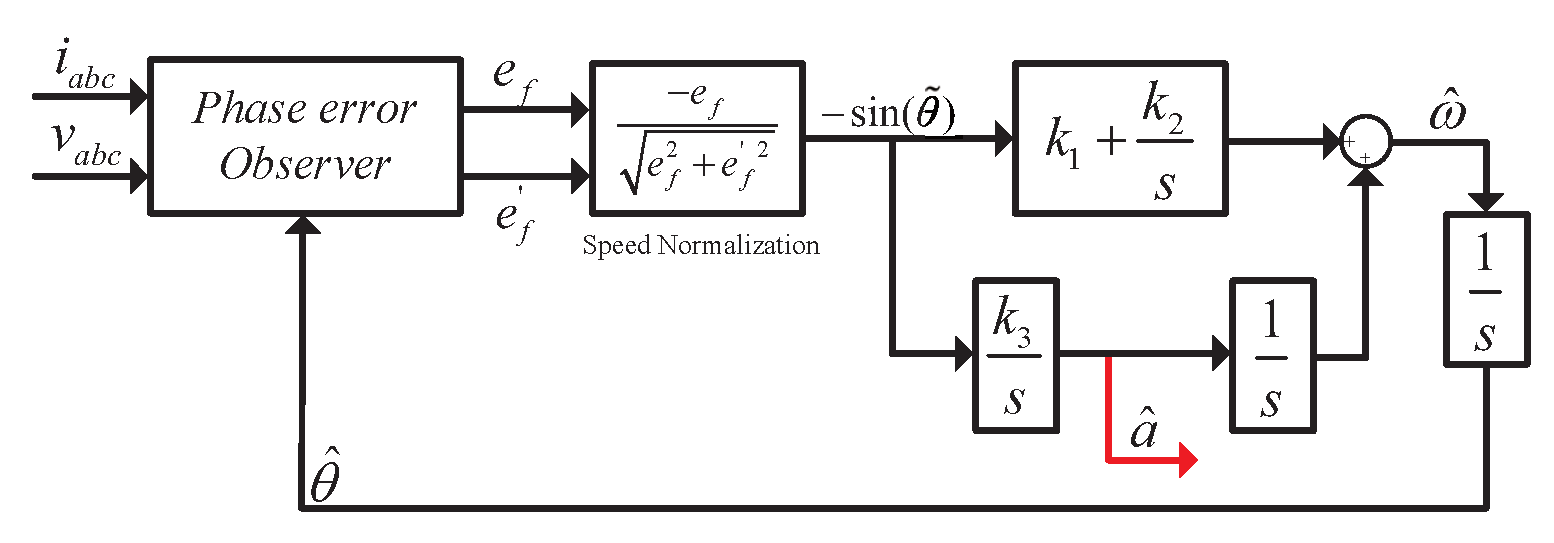
2.1. Position Error Detection
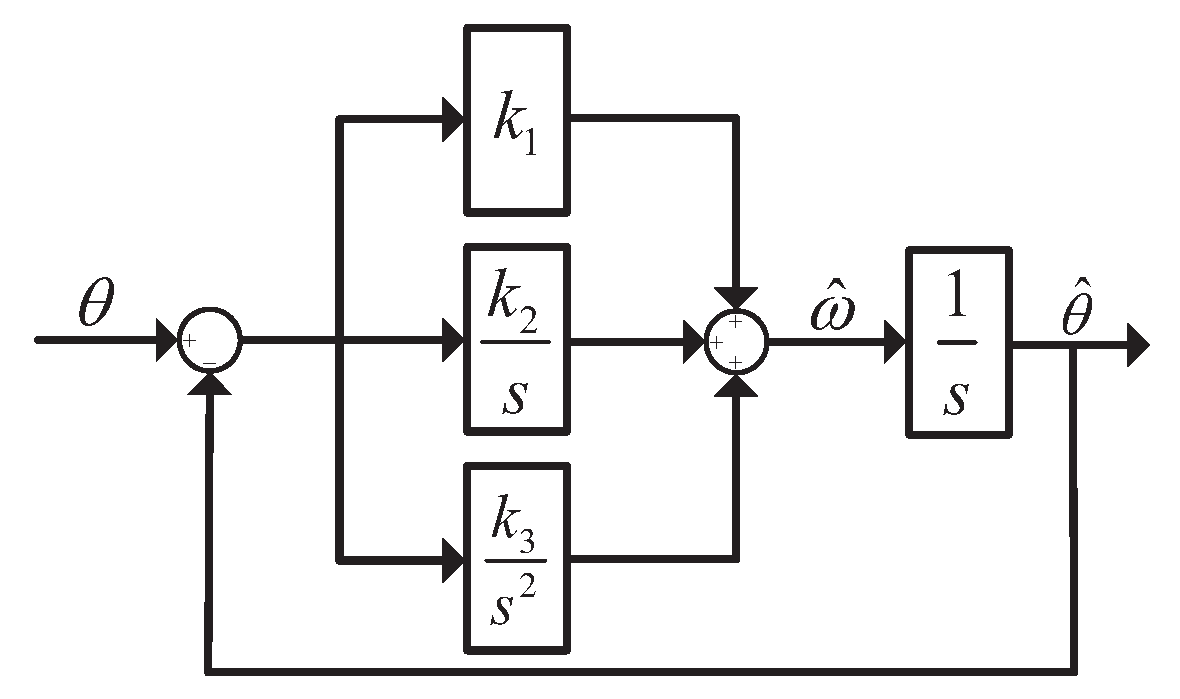
2.2. Speed, Position, and Acceleration Estimations
2.3. The Load Torque Estimation
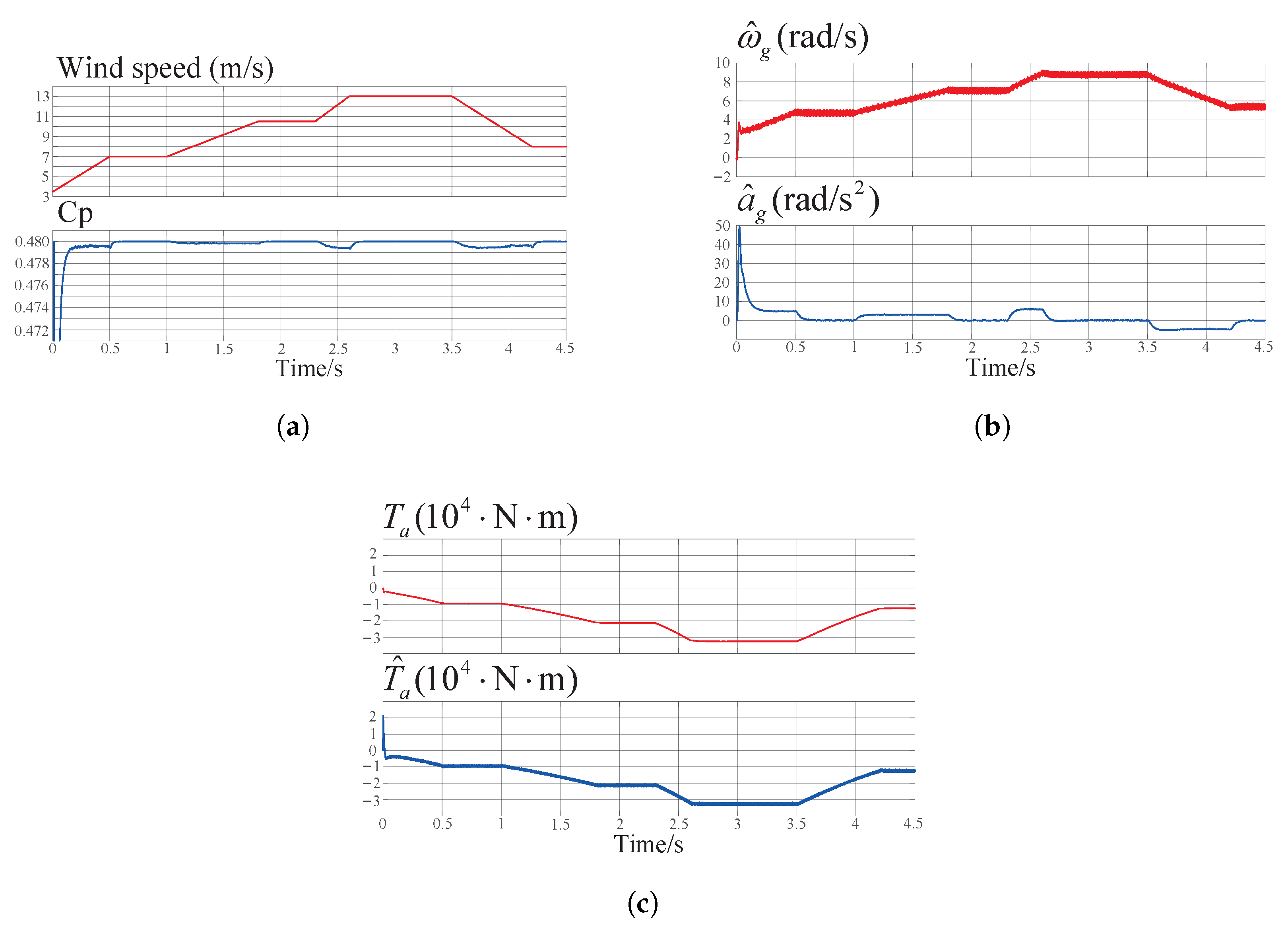
3. Numerical Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SMO | sliding mode observer |
| PMSG | permanent magnet synchronous generator |
| PLL | phase-locked loop |
| LF | loop filter |
References
- Rahideh, A.; Korakianitis, T. Analytical magnetic field distribution of slotless brushless machines with inset permanent magnets. IEEE Trans. Magn. 2011, 47, 1763–1774. [Google Scholar] [CrossRef]
- Vicknair, D.; Tansey, M.; O’Brien, T. Measuring fossil fuel reserves: A simulation and review of the U.S. Securities and Exchange Commission approach. Resour. Policy 2022, 79, 103028. [Google Scholar] [CrossRef]
- Pastore, L.; Basso, G.; Ricciardi, G.; de Santoli, L. Synergies between Power-to-Heat and Power-to-Gas in renewable energy communities. Renew. Energy 2022, 198, 1383–1397. [Google Scholar] [CrossRef]
- Yue, N.; Yang, C.; Li, S. The Influence of Reduced Frequency on H-VAWT Aerodynamic Performance and Flow Field Near Blades. Energies 2024, 17, 4760. [Google Scholar] [CrossRef]
- Zhang, C.; Li, J.; Liu, S.; Hu, P.; Feng, J.; Ren, H.; Zhang, R.; Jia, J. Coordinated Frequency Modulation Control Strategy of Wind Power and Energy Storage Considering Mechanical Load Optimization. Energies 2024, 17, 3198. [Google Scholar] [CrossRef]
- Njiri, J.G.; Söffker, D. State-of-the-art in wind turbine control: Trends and challenges. Renew. Sustain. Energy Rev. 2016, 60, 377–393. [Google Scholar] [CrossRef]
- Pao, L.Y.; Johnson, K.E. Control of wind turbines. IEEE Control Syst. Mag. 2011, 31, 44–62. [Google Scholar]
- Jung, C.; Sander, L.; Schindler, D. Future global offshore wind energy under climate change and advanced wind turbine technology. Energy Convers. Manag. 2024, 321, 119075. [Google Scholar] [CrossRef]
- Salic, T.; Charpentier, J.F.; Benbouzid, M.; Le Boulluec, M. Control strategies for floating offshore wind turbine: Challenges and trends. Electronics 2019, 8, 1185. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; University of Colorado at Boulder: Boulder, CO, USA, 2007. [Google Scholar]
- Pao, L.Y.; Johnson, K.E. A tutorial on the dynamics and control of wind turbines and wind farms. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 2076–2089. [Google Scholar]
- van Engelen, T.G. Design Model and Load Reduction Assessment for Multi-Rotational Mode Individual Pitch Control (Higher Harmonics Control); Technical Report ECN-RX–06-068; Energy Research Centre of the Netherlands (ECN): Petten, The Netherlands, 2006; Available online: https://publicaties.ecn.nl/PdfFetch.aspx?nr=ECN-RX--06-068 (accessed on 16 March 2025).
- Selvam, K. Individual Pitch Control for Large Scale Wind Turbines: A Multivariable Control Approach; Technical Report ECN-E–07-053; Energy Research Centre of the Netherlands (ECN): Petten, The Netherlands, 2007; Available online: http://www.ecn.nl/docs/library/report/2007/e07053.pdf (accessed on 18 March 2025).
- Shah, K.A.; Meng, F.; Li, Y.; Nagamune, R.; Zhou, Y.; Ren, Z.; Jiang, Z. A synthesis of feasible control methods for floating offshore wind turbine system dynamics. Renew. Sustain. Energy Rev. 2021, 151, 111525. [Google Scholar] [CrossRef]
- Cooperman, A.; Martinez, M. Load monitoring for active control of wind turbines. Renew. Sustain. Energy Rev. 2015, 41, 189–201. [Google Scholar] [CrossRef]
- Liu, X.; Bo, L.; Luo, H. Dynamical measurement system for wind turbine fatigue load. Renew. Energy 2016, 86, 909–921. [Google Scholar] [CrossRef]
- Martinez, M.; Fernandez, D.; Reigosa, D.; Guerrero, J.M.; Briz, F. Wireless torque pulsations measurement system for PMSMs. IEEE Trans. Ind. Appl. 2020, 56, 6467–6476. [Google Scholar] [CrossRef]
- Gao, J.; Li, C.; Dai, L.; Huang, S.; Xu, W. A practical analytical expression and estimation for average torque of high saturation permanent magnet synchronous motor for special vehicles. IEEE Trans. Veh. Technol. 2022, 72, 357–366. [Google Scholar] [CrossRef]
- Mohamed, M.; Jemli, M.; Gossa, M.; Jemli, K. Doubly fed induction generator (DFIG) in wind turbine modeling and power flow control. In Proceedings of the 2004 IEEE International Conference on Industrial Technology, Hammamet, Tunisia, 8–10 December 2004; pp. 580–584. [Google Scholar]
- Cardenas, R.; Pena, R.; Proboste, J.; Asher, G.; Clare, J. MRAS observer for sensorless control of standalone doubly fed induction generators. IEEE Trans. Energy Convers. 2005, 20, 710–718. [Google Scholar] [CrossRef]
- Payam, A.; Jalalifar, M. Robust speed sensorless control of doubly-fed induction machine based on input-output feedback linearization control using a sliding-mode observer. In Proceedings of the 2006 International Conference on Power Electronic, Drives and Energy Systems, New Delhi, India, 12–15 December 2006; pp. 1–5. [Google Scholar]
- Dendouga, A.; Abdessemed, R.; Bendaas, M.; Chaiba, A. Decoupled active and reactive power control of a doubly-fed induction generator (DFIG). In Proceedings of the 2007 Mediterranean Conference on Control & Automation, Athens, Greece, 27–29 June 2007; pp. 1–5. [Google Scholar]
- Benlaloui, I.; Drid, S.; Chrifi-Alaoui, L.; Ouriagli, M. Implementation of a new MRAS speed sensorless vector control of induction machine. IEEE Trans. Energy Convers. 2014, 30, 588–595. [Google Scholar] [CrossRef]
- Thomsen, S.; Rothenhagen, K.; Fuchs, F. Online parameter identification methods for doubly fed induction generators. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 2735–2741. [Google Scholar]
- Taherzadeh, M.; Hamida, M.A.; Ghanes, M.; Koteich, M. A New Torque Observation Technique for a PMSM Considering Unknown Magnetic Conditions. IEEE Trans. Ind. Electron. 2021, 68, 1961–1971. [Google Scholar] [CrossRef]
- Tang, S.; Cao, Y.; Shi, T.; Yan, Y.; Xia, C. Online Estimation of Load Torque and Moment of Inertia Incorporating Extended Disturbance Observer with Trigger. IEEE Trans. Power Electron. 2024, 40, 5731–5742. [Google Scholar] [CrossRef]



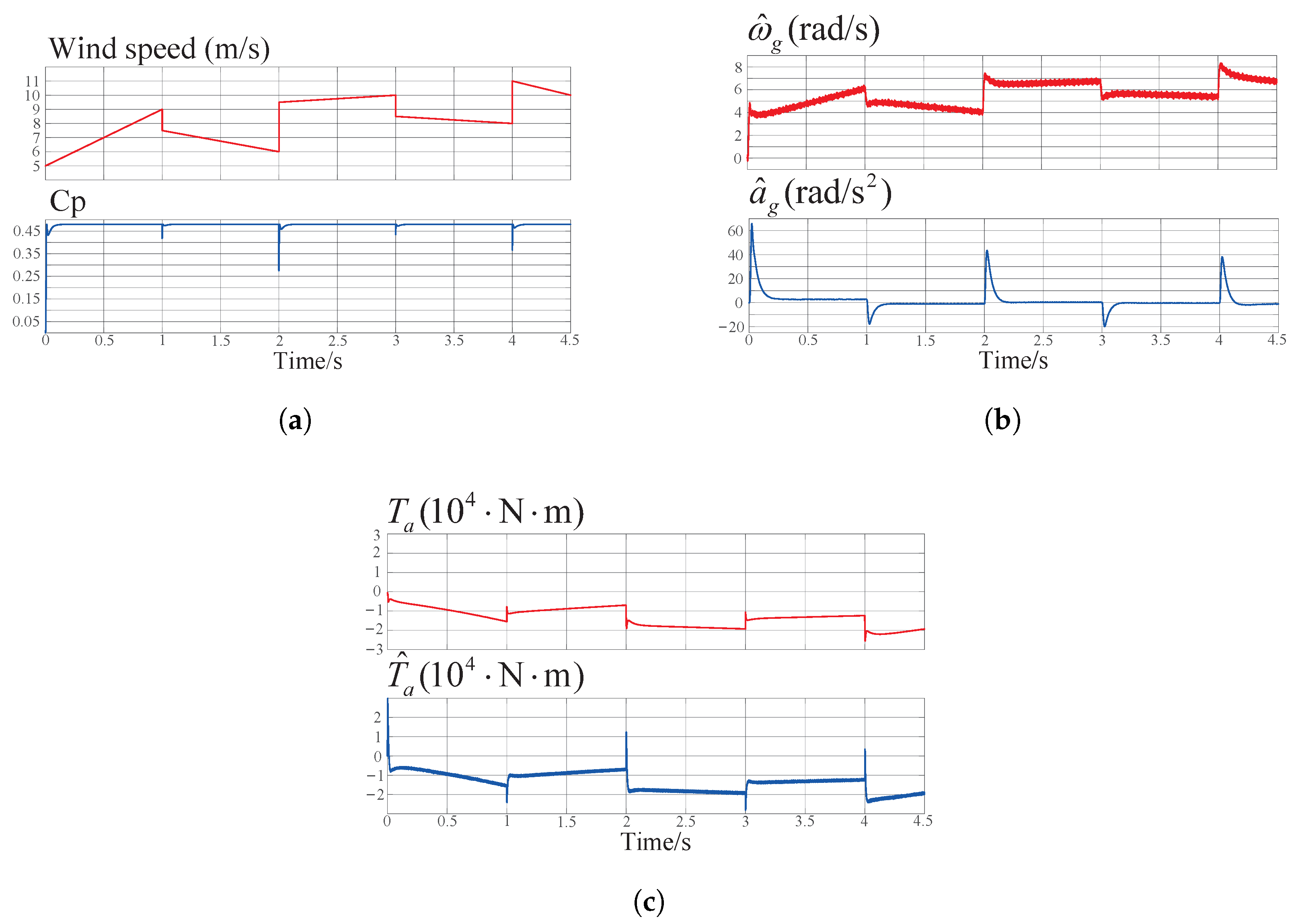
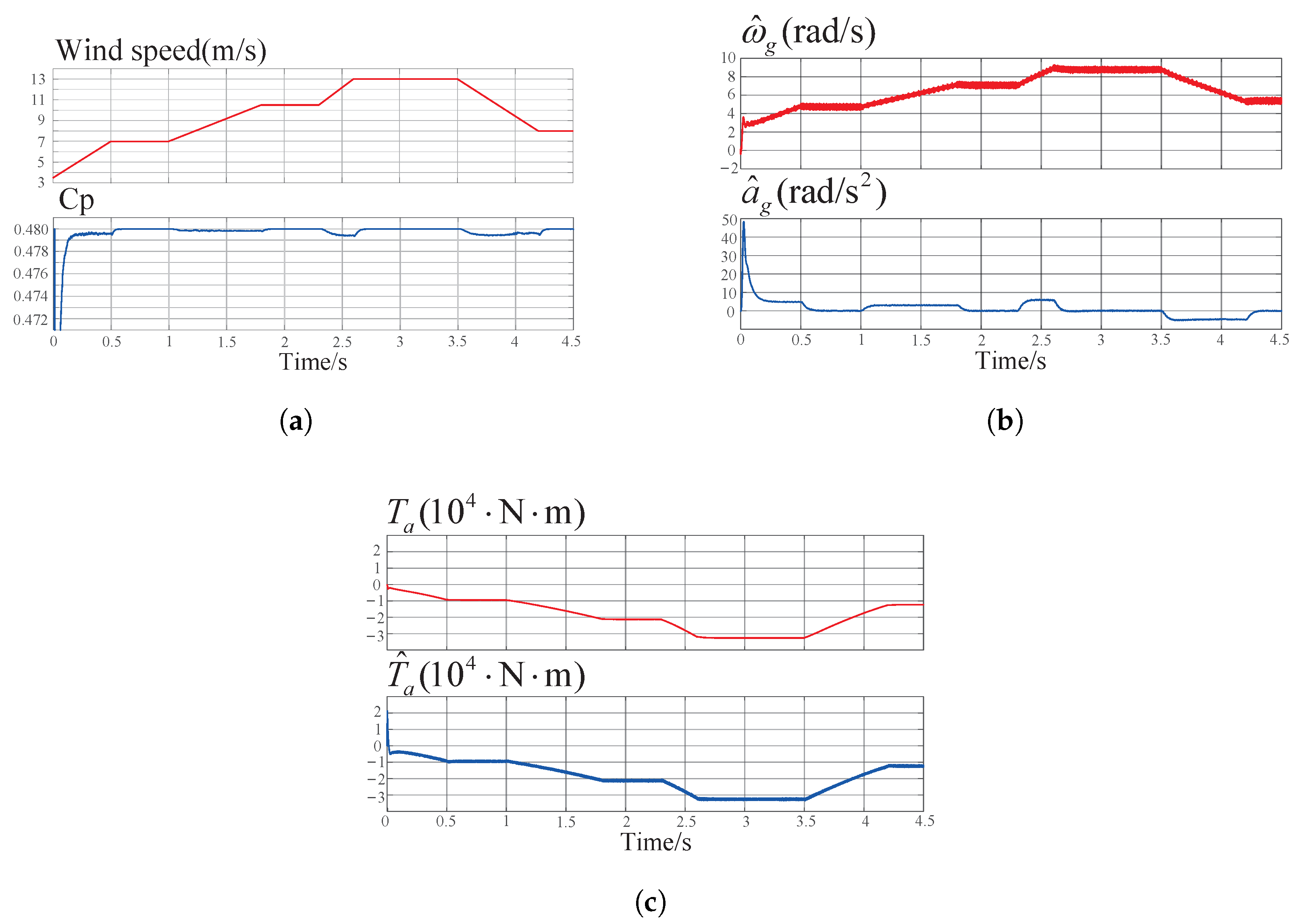
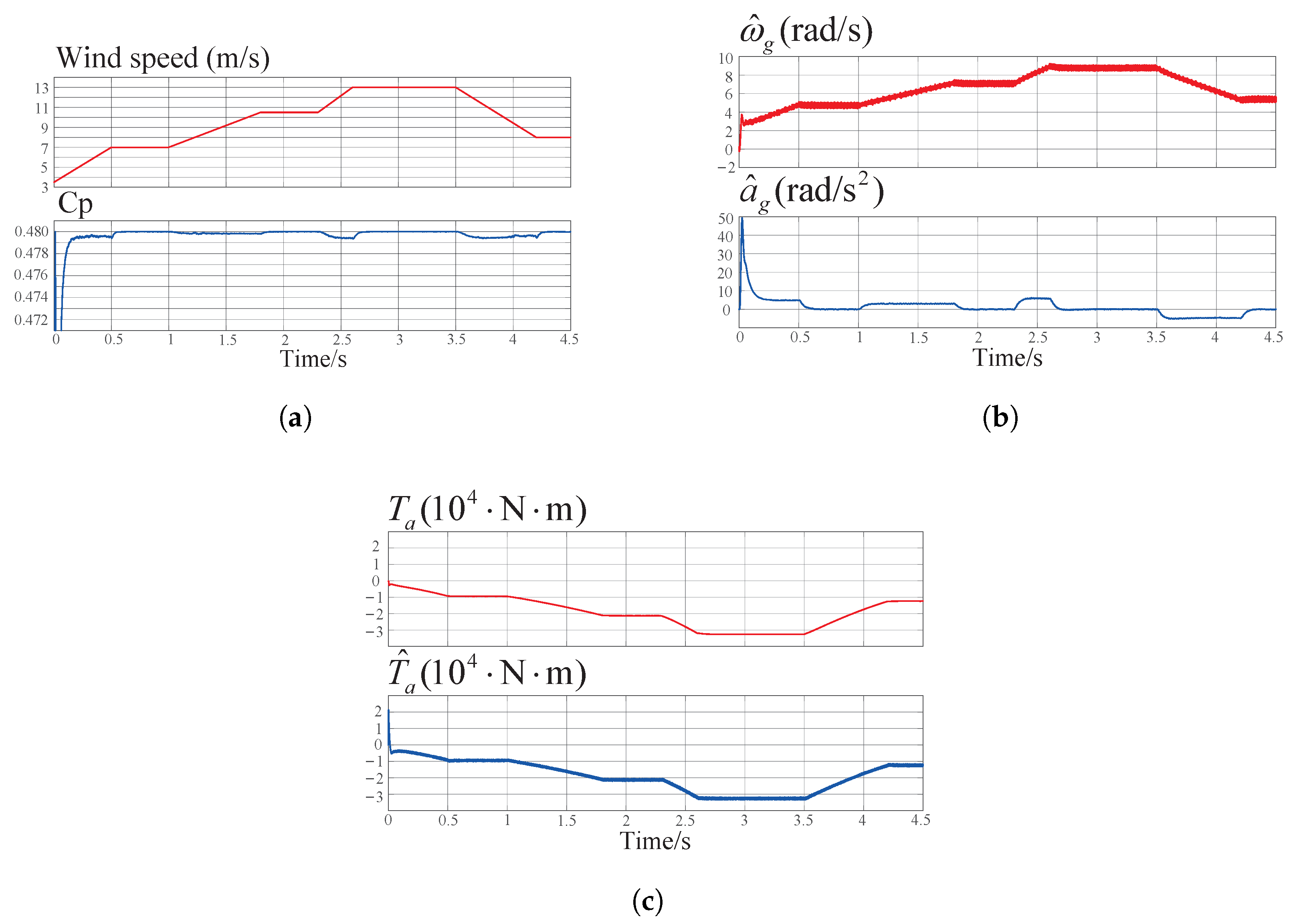
| Cases | Wind Conditions |
|---|---|
| Case A | Gradual staged increase or decrease of wind speed. |
| Case B | Continuous ramp-up and ramp-down of wind speed. |
| Case C | Variations with step changes of wind speed. |
| Case D | Gradual staged increase or decrease of wind speed with 10% variation of stator resistance and stator inductance of PMSG. |
| Case E | Gradual staged increase or decrease of wind speed with white noise in current and voltage signals |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Wang, X.; Ren, N.; Li, G.; Dai, Z. An Acceleration-Observer-Based Position and Load Torque Estimation Method for Wind Turbine with Sensor Faults. Energies 2025, 18, 2787. https://doi.org/10.3390/en18112787
Wu Z, Wang X, Ren N, Li G, Dai Z. An Acceleration-Observer-Based Position and Load Torque Estimation Method for Wind Turbine with Sensor Faults. Energies. 2025; 18(11):2787. https://doi.org/10.3390/en18112787
Chicago/Turabian StyleWu, Ziyun, Xuetong Wang, Na Ren, Guangqi Li, and Zhiyong Dai. 2025. "An Acceleration-Observer-Based Position and Load Torque Estimation Method for Wind Turbine with Sensor Faults" Energies 18, no. 11: 2787. https://doi.org/10.3390/en18112787
APA StyleWu, Z., Wang, X., Ren, N., Li, G., & Dai, Z. (2025). An Acceleration-Observer-Based Position and Load Torque Estimation Method for Wind Turbine with Sensor Faults. Energies, 18(11), 2787. https://doi.org/10.3390/en18112787





