Non-Uniformities in Heat Exchangers: A Two-Decade Review of Causes, Effects, and Mitigation Strategies
Abstract
1. Introduction to Non-Uniformities in HXs
1.1. Temperature Non-Uniformities
1.2. Flow Non-Uniformities
1.3. Refrigerant Non-Uniformities
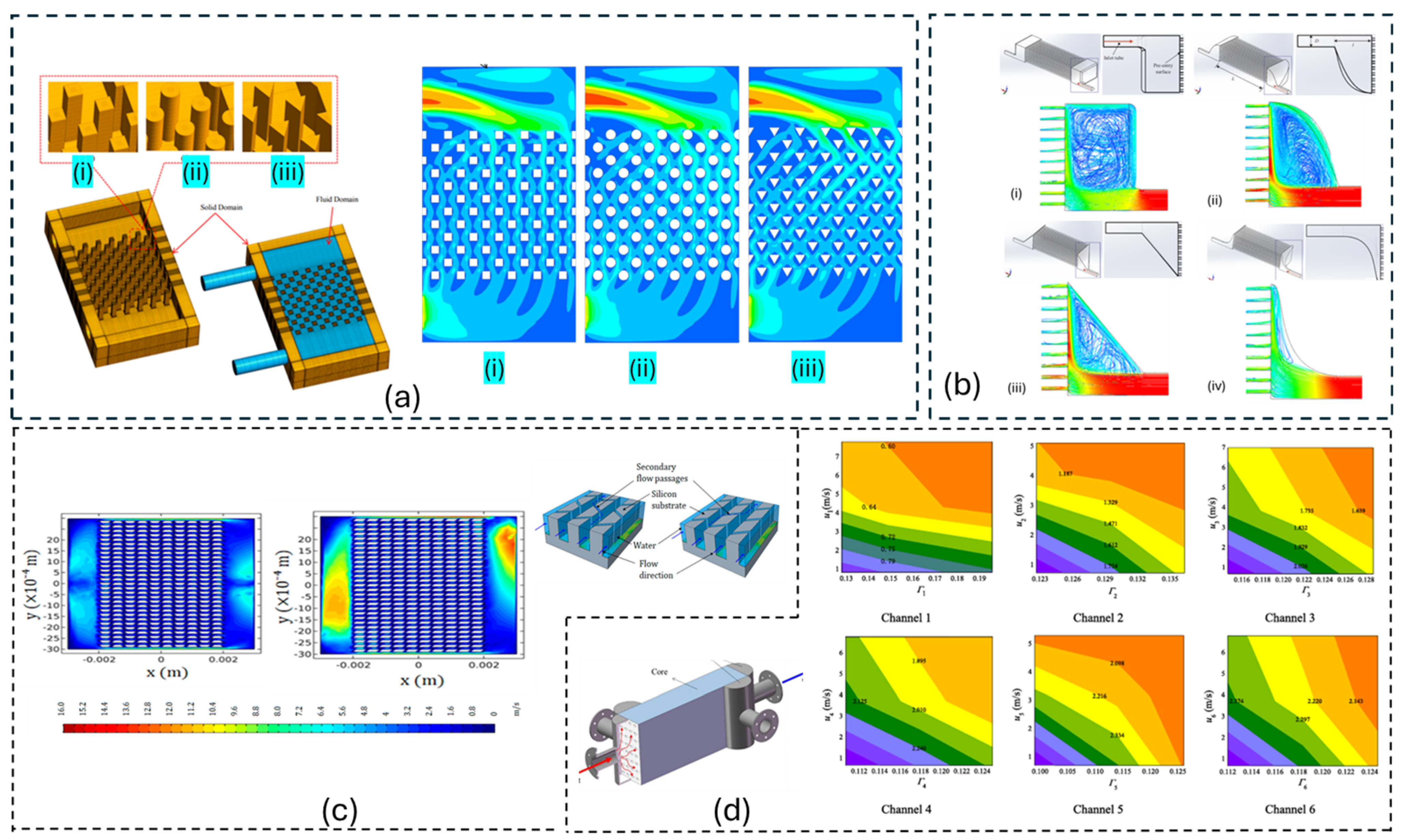
2. Impact of Non-Uniformities on PHX Performance: Causes and Mitigation Approaches
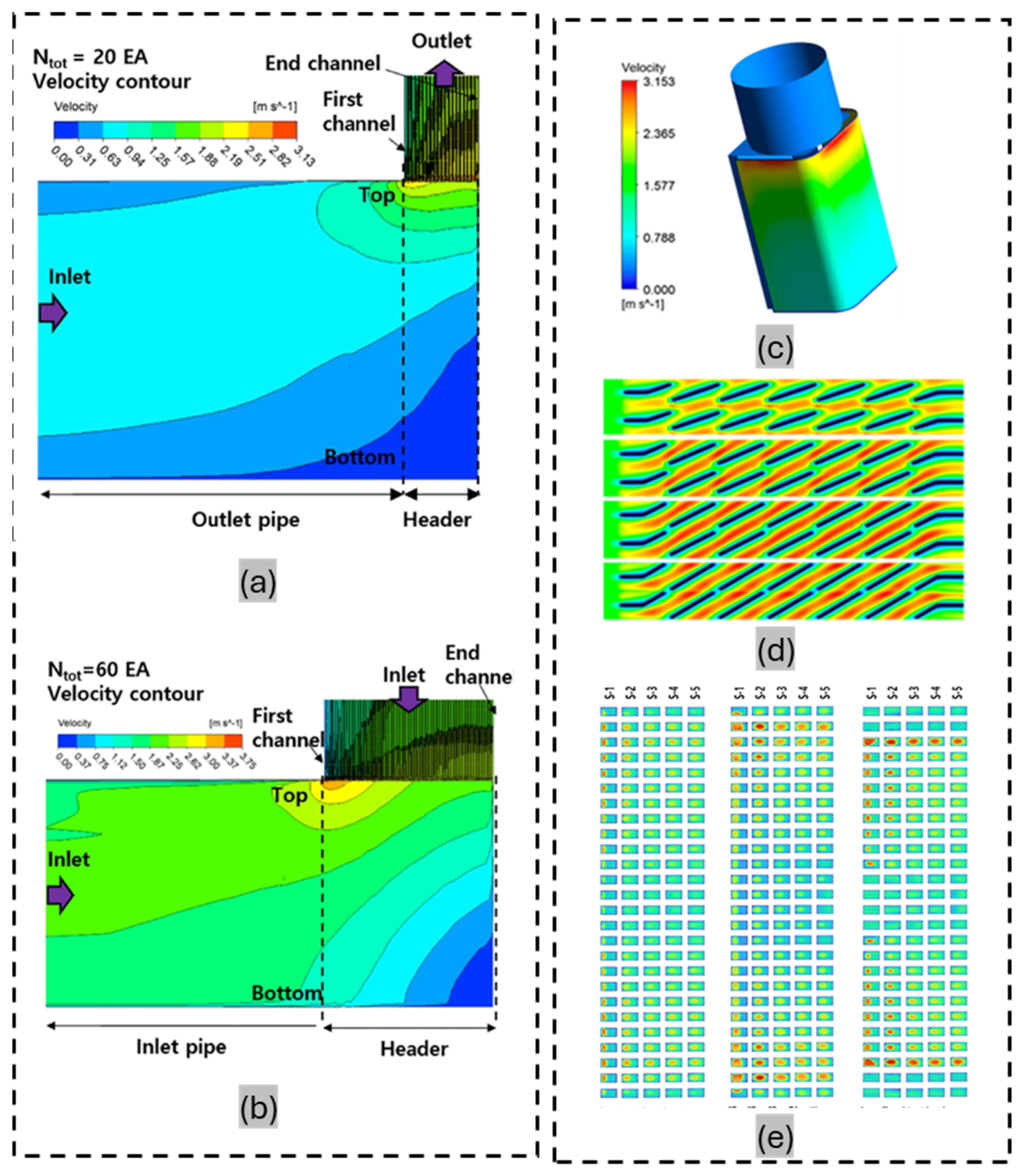
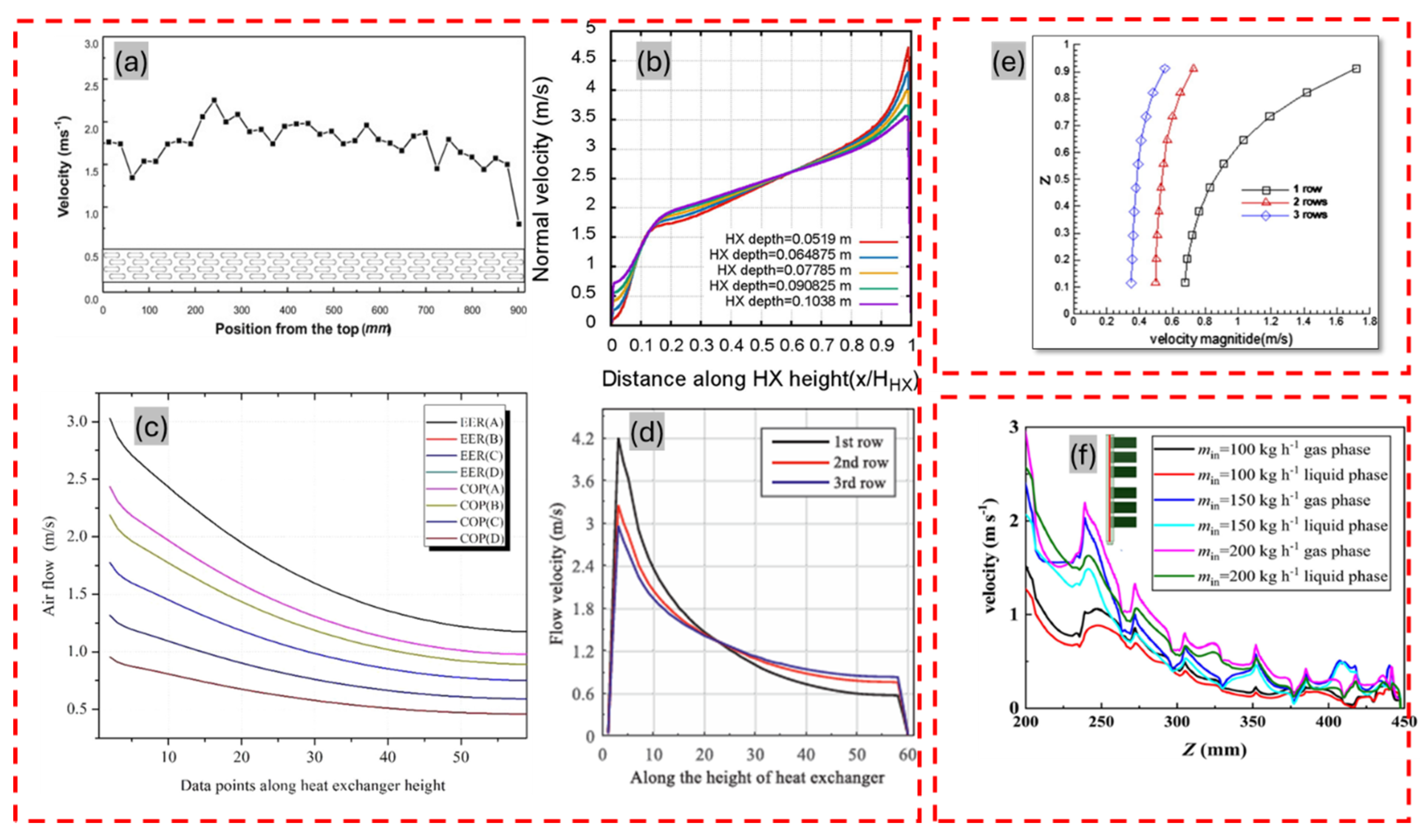
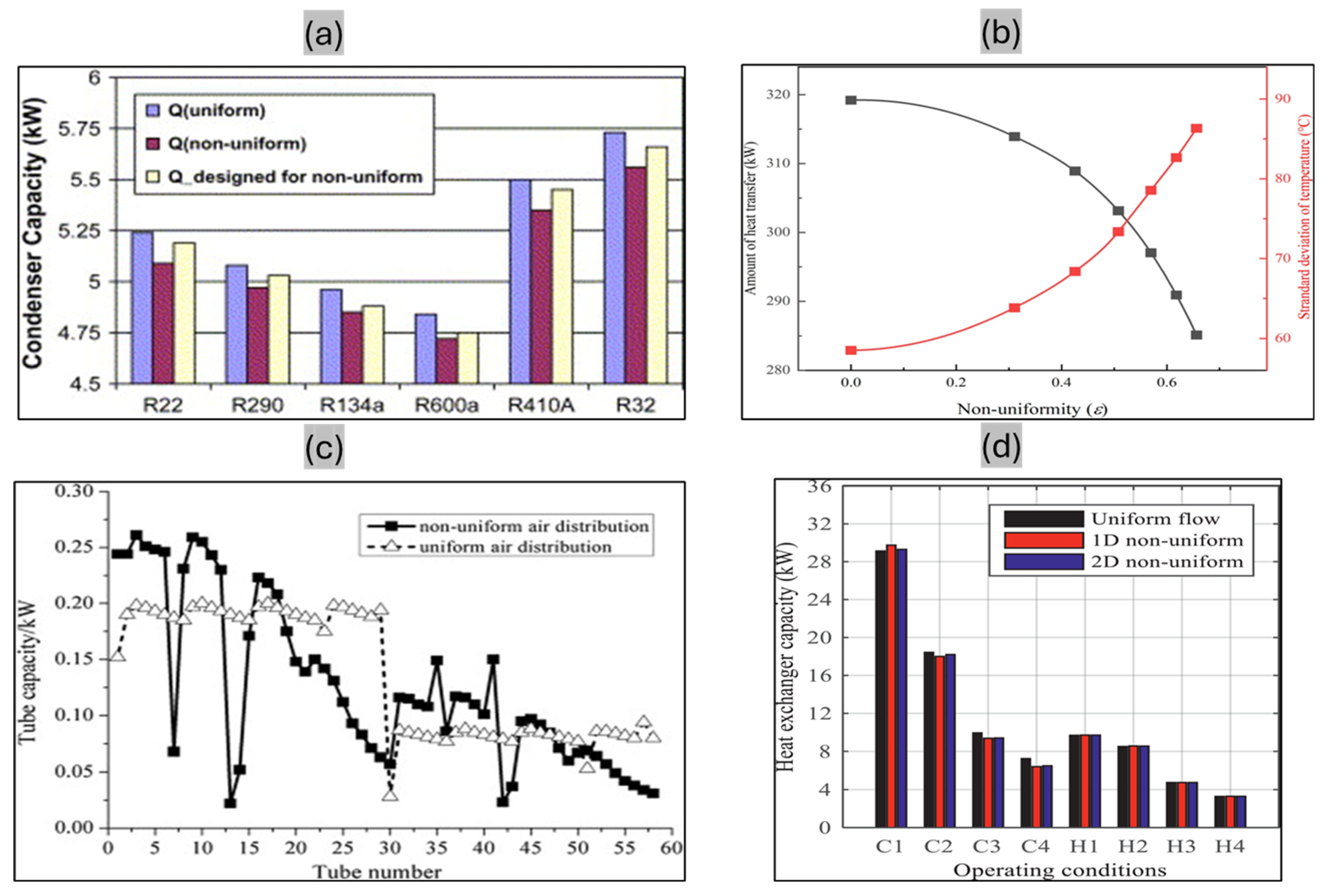
3. Impact of Non-Uniformities on FTHX Performance: Causes and Mitigation Strategies
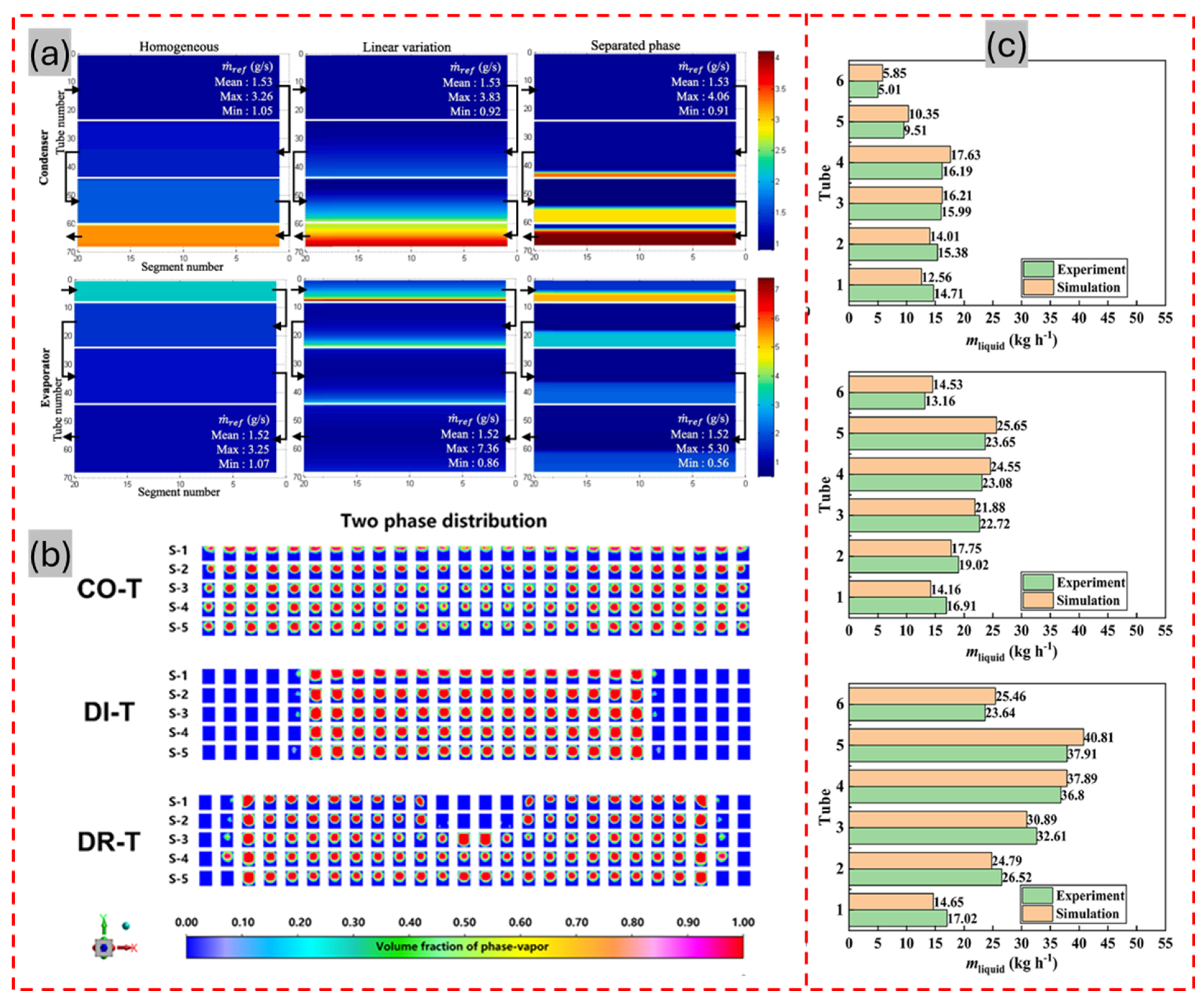
4. Impact of Non-Uniformities on MCHX and PCHX Performance: Causes and Mitigation Strategies
5. Mathematical Modeling of Non-Uniformities
6. Summary and Future Directions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HX | heat exchanger |
| PHX | plate heat exchanger |
| FTHX | finned and tube heat exchanger |
| MCHX | microchannel heat exchanger |
| CHX | compact heat exchanger |
| PCHX | printed circuit heat exchanger |
References
- Lu, X.; Yu, X.; Qu, Z.; Wang, Q.; Ma, T. Experimental investigation on thermoelectric generator with non-uniform hot-side heat exchanger for waste heat recovery. Energy Convers. Manag. 2017, 150, 403–414. [Google Scholar] [CrossRef]
- Chu, W.-X.; Bennett, K.; Cheng, J.; Chen, Y.-t.; Wang, Q.-w. Numerical study on a novel hyperbolic inlet header in straight-channel printed circuit heat exchanger. Appl. Therm. Eng. 2019, 146, 805–814. [Google Scholar] [CrossRef]
- Guo, X.; Li, Z.; Zhai, Y.; Wang, H. Flow maldistribution and its effect on the thermal performance of miniaturized devices: A perspective from thermal boundary condition. Energy Rev. 2024, 3, 100098. [Google Scholar] [CrossRef]
- Shao, H.; Zhang, M.; Zhao, Q.; Wang, Y.; Liang, Z. Study of improvements on flow maldistribution of double tube-passes shell-and-tube heat exchanger with rectangular header. Appl. Therm. Eng. 2018, 144, 106–116. [Google Scholar] [CrossRef]
- Menni, Y.; Chamkha, A.J.; Azzi, A.; Zidani, C.; Benyoucef, B. Study of air flow around flat and arc-shaped baffles in shell-and-tube heat exchangers. Math. Model. Eng. Probl. 2019, 6, 77–84. [Google Scholar] [CrossRef]
- Talebizadehsardari, P.; Mohammed, H.I.; Mahdi, J.M.; Gillott, M.; Walker, G.S.; Grant, D.; Giddings, D. Effect of airflow channel arrangement on the discharge of a composite metal foam-phase change material heat exchanger. Int. J. Energy Res. 2021, 45, 2593–2609. [Google Scholar] [CrossRef]
- Bishnoi, R.; Aharwal, K.R. Experimental evaluation of cooling characteristic, airflow distribution and mass transfer in a cold store. J. Food Process Eng. 2021, 44, e13609. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, B.; Wang, J.; Zhu, Z.; Li, T.; Guo, B.; Zhang, J.; Zhang, H.; Yang, Z. Effect of non-uniform airflow on the performance of a parallel-flow heat exchanger considering internal fluid distribution—Simulation studies and its experimental validation. Appl. Therm. Eng. 2020, 180, 115685. [Google Scholar] [CrossRef]
- Aasi, H.K.; Mishra, M. Influence of flow non-uniformity on the dynamic behaviour of three-fluid cross-flow compact heat exchanger. Int. J. Therm. Sci. 2020, 149, 106177. [Google Scholar] [CrossRef]
- Gao, T.; Geer, J.; Sammakia, B. Nonuniform temperature boundary condition effects on data center cross flow heat exchanger dynamic performance. Int. J. Heat. Mass. Transf. 2014, 79, 1048–1058. [Google Scholar] [CrossRef]
- Strobel, M.; Mortean, M.V.V. Pressure drop and fluid maldistribution analysis of a compact heat exchanger manufactured by 3D printing. Int. J. Therm. Sci. 2022, 172, 107331. [Google Scholar] [CrossRef]
- Li, B.; Hou, J.; Xu, K.; Gao, Q.; Zeng, M.; Wang, Q. Optimal designs for flow uniformity at inlet of microchannel flat tube heat exchanger. Appl. Therm. Eng. 2023, 226, 120300. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, W.; Shuai, W.; Song, X.; Shi, J.; Chen, J. Experimental and simulation study on the distributor design in plate evaporators. Int. J. Refrig. 2022, 143, 126–137. [Google Scholar] [CrossRef]
- Bobbili, P.R.; Sunden, B.; Das, S.K. Thermal analysis of plate condensers in presence of flow maldistribution. Int. J. Heat. Mass. Transf. 2006, 49, 4966–4977. [Google Scholar] [CrossRef]
- Zhang, L.Z. Flow maldistribution and thermal performance deterioration in a cross-flow air to air heat exchanger with plate-fin cores. Int. J. Heat. Mass. Transf. 2009, 52, 4500–4509. [Google Scholar] [CrossRef]
- Habib, M.A.; Ben-Mansour, R.; Said, S.A.M.; Al-Qahtani, M.S.; Al-Bagawi, J.J.; Al-Mansour, K.M. Evaluation of flow maldistribution in air-cooled heat exchangers. Comput. Fluids 2009, 38, 677–690. [Google Scholar] [CrossRef]
- Tereda, F.A.; Srihari, N.; Sunden, B.; Das, S.K. Experimental Investigation on Port-to-Channel Flow Maldistribution in Plate Heat Exchangers. Heat. Transf. Eng. 2007, 28, 435–443. [Google Scholar] [CrossRef]
- Rao, B.P.; Sunden, B.; Das, S.K. An Experimental and Theoretical Investigation of the Effect of Flow Maldistribution on the Thermal Performance of Plate Heat Exchangers. J. Heat. Transf. 2005, 127, 332. [Google Scholar] [CrossRef]
- Dwivedi, A.K.; Das, S.K. Dynamics of plate heat exchangers subject to flow variations. Int. J. Heat. Mass. Transf. 2007, 50, 2733–2743. [Google Scholar] [CrossRef]
- Hoffmann-Vocke, J.; Neale, J.; Walmsley, M. The effect of inlet conditions on the air side hydraulic resistance and flow maldistribution in industrial air heaters. Int. J. Heat. Fluid Flow. 2011, 32, 834–845. [Google Scholar] [CrossRef]
- Marchitto, A.; Fossa, M.; Guglielmini, G. The effect of the flow direction inside the header on two-phase flow distribution in parallel vertical channels. Appl. Therm. Eng. 2012, 36, 245–251. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, C.M.; Li, K.; Nawaz, K. Reducing the Flow Maldistribution in Heat Exchangers through a Novel Polymer Manifold: Numerical Evaluation. Energies 2023, 16, 7120. [Google Scholar] [CrossRef]
- Yang, H.; Wen, J.; Gu, X.; Liu, Y.; Wang, S.; Cai, W.; Li, Y. A mathematical model for flow maldistribution study in a parallel plate-fin heat exchanger. Appl. Therm. Eng. 2017, 121, 462–472. [Google Scholar] [CrossRef]
- Raul, A.; Bhasme, B.N.; Maurya, R.S. A Numerical Investigation of Fluid Flow Maldistribution in Inlet Header Configuration of Plate Fin Heat Exchanger. Energy Procedia 2015, 90, 267–275. [Google Scholar] [CrossRef]
- Mahvi, A.J.; Garimella, S. Visualization of flow distribution in rectangular and triangular header geometries. Int. J. Refrig. 2017, 76, 170–183. [Google Scholar] [CrossRef]
- Peng, X.; Qiu, C.; Li, J.; Jiang, S. Thermal Compensation Effect of Passage Arrangement Design for Inlet Flow Maldistribution in Multiple-Stream Plate-Fin Heat Exchanger. Heat. Transf. Eng. 2019, 40, 1239–1248. [Google Scholar] [CrossRef]
- Shokouhmand, H.; Hasanpour, M. Effect of flow maldistribution on the optimal design of plate heat exchanger using constrained multi objective genetic algorithm. Case Stud. Therm. Eng. 2020, 18, 100570. [Google Scholar] [CrossRef]
- Peng, X.; Li, D.; Li, J.; Jiang, S.; Gao, Q. Improvement of flow distribution by new inlet header configuration with splitter plates for plate-fin heat exchanger. Energies 2020, 16, 1323. [Google Scholar] [CrossRef]
- Ham, J.; Lee, G.; Kwon, O.; Bae, K.; Cho, H. Numerical study on the flow maldistribution characteristics of a plate heat exchanger. Appl. Therm. Eng. 2023, 224, 120136. [Google Scholar] [CrossRef]
- Brenk, A.; Pluszka, P.; Malecha, Z. Numerical study of flow maldistribution in multi-plate heat exchangers based on robust 2D model. Energies 2018, 11, 3121. [Google Scholar] [CrossRef]
- Ham, J.; Lee, G.; Oh, D.W.; Cho, H. Numerical study on non-uniform temperature distribution and thermal performance of plate heat exchanger. Energies 2021, 14, 8280. [Google Scholar] [CrossRef]
- Wang, C.C.; Yang, K.S.; Tsai, J.S.; Chen, I.Y. Characteristics of flow distribution in compact parallel flow heat exchangers, part II: Modified inlet header. Appl. Therm. Eng. 2011, 31, 3235–3242. [Google Scholar] [CrossRef]
- Wang, C.C.; Yang, K.S.; Tsai, J.S.; Chen, I.Y. Characteristics of flow distribution in compact parallel flow heat exchangers, part I: Typical inlet header. Appl. Therm. Eng. 2011, 31, 3226–3234. [Google Scholar] [CrossRef]
- Srihari, N.; Das, S.K. Experimental and Theoretical Analysis of Transient Response of Plate Heat Exchangers in Presence of Nonuniform Flow Distribution. J. Heat. Transf. 2008, 130, 051801. [Google Scholar] [CrossRef]
- Shaji, K.; Das, S.K. The effect of flow maldistribution on the evaluation of axial dispersion and thermal performance during the single-blow testing of plate heat exchangers. Int. J. Heat. Mass. Transf. 2010, 53, 1591–1602. [Google Scholar] [CrossRef]
- Siddiqui, O.K.; Al-Zahrani, M.; Al-Sarkhi, A.; Zubair, S.M. Flow Distribution in U- and Z-Type Manifolds: Experimental and Numerical Investigation. Arab. J. Sci. Eng. 2020, 45, 6005–6020. [Google Scholar] [CrossRef]
- Qi, D.; Li, A.; Li, S.; Zhao, C. Comparative analysis of earth to air heat exchanger configurations based on uniformity and thermal performance. Appl. Therm. Eng. 2021, 183, 116152. [Google Scholar] [CrossRef]
- Li, W.; Hrnjak, P. Effect of single-phase flow maldistribution on the thermal performance of brazed plate heat exchangers. Appl. Therm. Eng. 2023, 219, 119465. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Wen, J.; Ma, Y. Experimental investigation of header configuration on two-phase flow distribution in plate-fin heat exchanger. Int. Commun. Heat. Mass. Transf. 2010, 37, 116–120. [Google Scholar] [CrossRef]
- Song, X.; Huang, D.; Liu, X.; Chen, Q. Effect of non-uniform air velocity distribution on evaporator performance and its improvement on a residential air conditioner. Appl. Therm. Eng. 2012, 40, 284–293. [Google Scholar] [CrossRef]
- Peng, X.; Liu, Z.; Qiu, C. Effect-of-inlet-flow-maldistribution-on-the-passage-arrangement-design-of-multi-stream-plate-fin-heat-exchanger. Appl. Therm. Eng. J. 2016, 103, 67–76. [Google Scholar] [CrossRef]
- Tang, W.; Sun, L.; Liu, H.; Xie, G.; Mo, Z.; Tang, J. Improvement of flow distribution and heat transfer performance of a self-similarity heat sink with a modification to its structure. Appl. Therm. Eng. 2017, 121, 163–171. [Google Scholar] [CrossRef]
- Li, W.; Hrnjak, P. Modeling of two-phase refrigerant distribution in brazed plate heat exchangers. Int. J. Refrig. 2022, 136, 172–183. [Google Scholar] [CrossRef]
- Muneeshwaran, M.; Kim, H.J.; Tayyab, M.; Li, W.; Nawaz, K.; Yang, C.M. Flow maldistribution in plate heat exchangers—Impact, analysis, and solutions. Renew. Sustain. Energy Rev. 2025, 207, 114905. [Google Scholar] [CrossRef]
- Faraj, A.; Mortada, M.; Chahine, K.; Faraj, J.; Abdulhay, B.; Khaled, M. Experimental Study of the Effect of Non-Uniform Airflow Velocity Distribution on the Thermal Performance of a Water-Air Heat Exchanger. n.d. Available online: https://icerega.utbm.fr/wp-content/uploads/2021/05/ICEREGA2019-ID144.pdf (accessed on 8 December 2024).
- Khaled, M.; Mortada, M.; Faraj, J.; Chahine, K.; Lemenand, T.; Ramadan, H.; Ramadan, H.S. Effect of Airflow Non-Uniformities on the Thermal Performance of Water-Air Heat Exchangers-Experimental Study and Analysis. Energies 2022, 15, 8120. [Google Scholar] [CrossRef]
- Yashar, D.A.; Domanski, P.A. Air Flow Distribution through an A-Shaped Evaporator Under Dry and Wet Coil Conditions. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 12–15 July 2010; pp. 1–8. [Google Scholar]
- Choi, J.M.; Payne, W.V.; Domanski, P.A. Effects of Non-Uniform Refrigerant and Air Flow Distributions on Finned-Tube Evaporator Performance. In Proceedings of the International Conference of Refrigeration, Washington, DC, USA, 17–22 August 2003. [Google Scholar]
- Yashar, D.A.; Cho, H.H.; Domanski, P.A. Measurement of Air-Velocity Profiles for Finned Tube Heat Exchangers Using Particle Image Velocimetry. In Proceedings of the 12th International Refrigeration and Air-Conditioning Conference at Purdue, West Lafayette, IN, USA, 14–17 July 2008; pp. 1–8. [Google Scholar]
- Yashar, D.A.; Domanski, P.A.; Cho, H. An experimental and computational study of approach air distribution for slanted and A-shaped finned-tube heat exchangers. HVAC&R Res. 2014, 20, 498–507. [Google Scholar] [CrossRef]
- Yashar, D.A.; Lee, S.; Domanski, P.A. Rooftop air-conditioning unit performance improvement using refrigerant circuitry optimization. Appl. Therm. Eng. 2015, 83, 81–87. [Google Scholar] [CrossRef]
- Ishaque, S.; Kim, M.-H. Numerical modeling of an outdoor unit heat exchanger for residential heat pump systems with nonuniform airflow and refrigerant distribution. Int. J. Heat. Mass. Transf. 2021, 175, 121323. [Google Scholar] [CrossRef]
- Ishaque, S.; Kim, M.H. Refrigerant circuitry optimization of finned tube heat exchangers using a dual-mode intelligent search algorithm. Appl. Therm. Eng. 2022, 212, 118576. [Google Scholar] [CrossRef]
- Domanski, P.A.; Yashar, D. Optimization of finned-tube condensers using an intelligent system. Int. J. Refrig. 2007, 30, 482–488. [Google Scholar] [CrossRef]
- Domanski, P.A.; Yashar, D.; Kaufman, K. Finned-Tube Heat Exchanger Simulation Program with Refrigerant Circuitry Optimization Capability Program. 2008; pp. 1–8. Available online: https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=861600 (accessed on 8 December 2024).
- Lee, T.S.; Wu, W.C.; Chuah, Y.K.; Wang, S.K. An improvement of airflow and heat transfer performance of multi-coil condensers by different coil configurations. Int. J. Refrig. 2010, 33, 1370–1376. [Google Scholar] [CrossRef]
- Kennedy, I.J.; Spence, S.W.T.; Spratt, G.R.; Early, J.M. Investigation of heat exchanger inclination in forced-draught air-cooled heat exchangers. Appl. Therm. Eng. 2013, 54, 413–421. [Google Scholar] [CrossRef]
- Chin, W.M. The Effect of Combined Flow and Temperature Maldistribution on Heat Exchangers: Characteristics of Deterioration Factor Ratio, Y. J. Heat. Transf. 2013, 135, 121802. [Google Scholar] [CrossRef]
- Bach, C.K.; Groll, E.A.; Braun, J.E.; Horton, W.T. Mitigation of air flow maldistribution in evaporators. Appl. Therm. Eng. 2014, 73, 877–885. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; Wang, Y. A favorable face velocity distribution and a V-frame cell for power plant air-cooled condensers. Appl. Therm. Eng. 2015, 87, 1–9. [Google Scholar] [CrossRef]
- Chen, L.; Yang, L.; Du, X.; Yang, Y. A novel layout of air-cooled condensers to improve thermo-flow performances. Appl. Energy 2016, 165, 244–259. [Google Scholar] [CrossRef]
- She, X.; Yin, Y.; Dong, Y.; Zhang, X. Investigation on air flow patterns of evaporative cooling and dehumidification process for a hybrid refrigeration system. Appl. Therm. Eng. 2016, 95, 79–94. [Google Scholar] [CrossRef]
- Deepakkumar, R.; Jayavel, S. Air side performance of finned-tube heat exchanger with combination of circular and elliptical tubes. Appl. Therm. Eng. 2017, 119, 360–372. [Google Scholar] [CrossRef]
- Ramadan, M.; Khaled, M.; El Hage, H.; Harambat, F.; Peerhossaini, H. Effect of air temperature non-uniformity on water-air heat exchanger thermal performance—Toward innovative control approach for energy consumption reduction. Appl. Energy 2016, 173, 481–493. [Google Scholar] [CrossRef]
- Li, Z.; Ling, J.; Aute, V.C.; Aute, V. Purdue e-Pubs Tube-Fin Heat Exchanger Circuitry Optimization for Multiple Airflow Maldistribution Profiles. n.d. Available online: https://docs.lib.purdue.edu/iracc (accessed on 8 December 2024).
- Zhang, K.; Li, M.J.; Liu, H.; Xiong, J.G.; He, Y.L. A general and rapid method to evaluate the effect of flow maldistribution on the performance of heat exchangers. Int. J. Therm. Sci. 2021, 170, 107152. [Google Scholar] [CrossRef]
- Ishaque, S.; Siddiqui, M.I.H.; Kim, M.H. Effect of heat exchanger design on seasonal performance of heat pump systems. Int. J. Heat. Mass. Transf. 2020, 151, 119404. [Google Scholar] [CrossRef]
- Luo, B.; Li, F.; Wu, S.; Shi, K.; Ding, Y.; Zhao, R.; Huang, D.; Shi, W. Experimental and numerical research on a C-type heat exchanger in duct air conditioner under non-uniform airflow. Appl. Therm. Eng. 2025, 261, 125097. [Google Scholar] [CrossRef]
- Dirker, J.; Meyer, J.P.; Garach, D.V. Inlet flow effects in micro-channels in the laminar and transitional regimes on single-phase heat transfer coefficients and friction factors. Int. J. Heat. Mass. Transf. 2014, 77, 612–626. [Google Scholar] [CrossRef]
- Anbumeenakshi, C.; Thansekhar, M.R. Experimental investigation of header shape and inlet configuration on flow maldistribution in microchannel. Exp. Therm. Fluid Sci. 2016, 75, 156–161. [Google Scholar] [CrossRef]
- Ahmad, M.; Berthoud, G.; Mercier, P. General characteristics of two-phase flow distribution in a compact heat exchanger. Int. J. Heat. Mass. Transf. 2009, 52, 442–450. [Google Scholar] [CrossRef]
- Guo, W.; Zhao, R.; Hu, K.; Huang, D.; Zhao, Y. Two-phase refrigerant maldistribution and optimization design in novel alternatively-laminated-microchannel-tube (ALMT) heat exchangers with vertical headers. Int. J. Refrig. 2023, 151, 290–303. [Google Scholar] [CrossRef]
- Ham, S.; Choi, S.; Jeong, J.H. Two-phase flow distribution in a refrigerant distributor having four indoor-unit connections of a variable refrigerant flow system. Int. J. Refrig. 2021, 126, 246–258. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Huang, H.; Feng, Z. Effect of refrigerant flow direction and throttle opening in RAC unit using micro-channel evaporator. Int. J. Refrig. 2016, 70, 280–288. [Google Scholar] [CrossRef]
- Saad, S.B.; Clément, P.; Gentric, C.; Fourmigué, J.F.; Leclerc, J.P. Experimental distribution of phases and pressure drop in a two-phase offset strip fin type compact heat exchanger. Int. J. Multiph. Flow. 2011, 37, 576–584. [Google Scholar] [CrossRef]
- Vist, S.; Pettersen, J. Two-phase flow distribution in compact heat exchanger manifolds. Exp. Therm. Fluid Sci. 2004, 28, 209–215. [Google Scholar] [CrossRef]
- Ullah, N.; Ishaque, S.; Kim, M.H.; Choi, S. Modeling and Optimization of a Micro-Channel Gas Cooler for a Transcritical CO2 Mobile Air-Conditioning System. Machines 2022, 10, 1177. [Google Scholar] [CrossRef]
- Law, M.; Kanargi, O.B.; Lee, P.-S. Effects of varying oblique angles on flow boiling heat transfer and pressure characteristics in oblique-finned microchannels. Int. J. Heat. Mass. Transf. 2016, 100, 646–660. [Google Scholar] [CrossRef]
- Song, M.; Liu, S.; Deng, S.; Sun, Z.; Yan, H. Experimental investigation on reverse cycle defrosting performance improvement for an ASHP unit by evenly adjusting the refrigerant distribution in its outdoor coil. Appl. Therm. Eng. 2017, 114, 611–620. [Google Scholar] [CrossRef]
- Kim, C.H.; Kim, N.H. An experimental study of refrigerant distribution in an automotive condenser. Appl. Therm. Eng. 2021, 184, 116259. [Google Scholar] [CrossRef]
- Lee, W.J.; Lee, H.; Jeong, J.H. Numerical evaluation of the range of performance deterioration in a multi-port mini-channel heat exchanger due to refrigerant mal-distribution in the header. Appl. Therm. Eng. 2021, 185, 116429. [Google Scholar] [CrossRef]
- Cheng, H.; Yang, T.; Cheng, Q.; Zhao, Y.; Wang, L.; Yuan, W. Influence of Non-Uniform Airflow on Two-Phase Parallel-Flow Heat Exchanger in Data Cabinet Cooling System. Energies 2025, 18, 923. [Google Scholar] [CrossRef]
- Afaynou, I.; Faraji, H.; Choukairy, K.; Khallaki, K.; Akrour, D. Effectiveness of a PCM-based heat sink with partially filled metal foam for thermal management of electronics. Int. J. Heat. Mass. Transf. 2024, 235, 126196. [Google Scholar] [CrossRef]
- Zhu, H.; Xie, G.; Berrouk, A.S.; Saeed, M. Advanced modelling and iterative approach for high-accuracy PCHE design in SCO2 Brayton cycle. Appl. Therm. Eng. 2024, 236, 121657. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, S.; Guo, Y.; Li, X.; Wang, H.; Bao, W. Study on coupled heat transfer of pyrolytic kerosene and supercritical CO2 in zigzag-type PCHE used for hypersonic vehicle power generation system. Appl. Therm. Eng. 2024, 247, 123101. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, P.; Shi, H.; Chen, Y.; Wang, Q. Prediction of flow maldistribution in printed circuit heat exchanger. Int. J. Heat. Mass. Transf. 2020, 152, 119560. [Google Scholar] [CrossRef]
- Chiou, J.P. Thermal Performance Deterioration in Crossflow Heat Exchanger due to the Flow Nonuniformity. J. Heat. Transf. 1978, 100, 580–587. [Google Scholar] [CrossRef]
- Ranganayakulu, C.; Seetharamu, K.N.; Sreevatsan, K.V. The effects of inlet fluid flow nonuniformity on thermal performance and pressure drops in crossflow plate-fin compact heat exchangers. Int. J. Heat. Mass. Transf. 1997, 40, 27–38. [Google Scholar] [CrossRef]
- Ratts, E.B. Investigation of Flow Maldistribution in a Concentric-Tube, Counterflow, Laminar Heat Exchanger. Heat. Transf. Eng. 1998, 19, 65–75. [Google Scholar] [CrossRef]
- Ranganayakulu, C.; Seetharamu, K.N. The combined effects of longitudinal heat conduction, flow nonuniformity and temperature nonuniformity in crossflow plate-fin heat exchangers. Int. Commun. Heat. Mass. Transf. 1999, 26, 669–678. [Google Scholar] [CrossRef]
- Ranganayakulu, C.; Seetharamu, K.N. The combined effects of wall longitudinal heat conduction, inlet fluid flow nonuniformity and temperature nonuniformity in compact tube–fin heat exchangers: A finite element method. Int. J. Heat. Mass. Transf. 1999, 42, 263–273. [Google Scholar] [CrossRef]
- Roetzel, W.; Ranong, C.N. Consideration of maldistribution in heat exchangers using the hyperbolic dispersion model. Chem. Eng. Process. Process Intensif. 1999, 38, 675–681. [Google Scholar] [CrossRef]
- Lalot, S.; Florent, P.; Lang, S.K.; Bergles, A.E. Flow maldistribution in heat exchangers. Appl. Therm. Eng. 1999, 19, 847–863. [Google Scholar] [CrossRef]
- Sahoo, R.K.; Roetzel, W. Hyperbolic axial dispersion model for heat exchangers. Int. J. Heat. Mass. Transf. 2002, 45, 1261–1270. [Google Scholar] [CrossRef]
- Yuan, P. Effect of inlet flow maldistribution on the thermal performance of a three-fluid crossflow heat exchanger. Int. J. Heat. Mass. Transf. 2003, 46, 3777–3787. [Google Scholar] [CrossRef]
- Rao, B.P.; Das, S.K. An Experimental Study on the Influence of Flow Maldistribution on the Pressure Drop Across a Plate Heat Exchanger. J. Fluids Eng. 2004, 126, 680. [Google Scholar] [CrossRef]
- Bassiouny, M.K.; Martin, H. Flow distribution and pressure drop in plate heat exchangers-I U-type arrangement. Chem. Eng. Sci. 1984, 39, 693–700. [Google Scholar] [CrossRef]
- Bassiouny, M.K.; Martin, H. Flow distribution and pressure drop in plate heat exchangers-II Z-type arrangement. Chem. Eng. Sci. 1984, 39, 701–704. [Google Scholar] [CrossRef]
- Liu, J.; Wei, W.; Ding, G.; Zhang, C.; Fukaya, M.; Wang, K.; Inagaki, T. A general steady state mathematical model for fin-and-tube heat exchanger based on graph theory. Int. J. Refrig. 2004, 27, 965–973. [Google Scholar] [CrossRef]
- Mon, M.S.; Gross, U. Numerical study of fin-spacing effects in annular-finned tube heat exchangers. Int. J. Heat. Mass. Transf. 2004, 47, 1953–1964. [Google Scholar] [CrossRef]
- Srihari, N.; Rao, B.P.; Sunden, B.; Das, S.K. Transient response of plate heat exchangers considering effect of flow maldistribution. Int. J. Heat. Mass. Transf. 2005, 48, 3231–3243. [Google Scholar] [CrossRef]
- Mishra, M.; Das, P.K.; Sarangi, S. Effect of temperature and flow nonuniformity on transient behaviour of crossflow heat exchanger. Int. J. Heat. Mass. Transf. 2008, 51, 2583–2592. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Lu, Z.; Domigan, W.E.; White, A.D.; Benedict, M.W. Measurement of flow maldistribution in parallel channels and its application to ex-situ and in-situ experiments in PEMFC water management studies. Int. J. Heat. Mass. Transf. 2009, 52, 1741–1752. [Google Scholar] [CrossRef]
- Pacio, J.C.; Dorao, C.A. A study of the effect of flow maldistribution on heat transfer performance in evaporators. Nucl. Eng. Des. 2010, 240, 3868–3877. [Google Scholar] [CrossRef]
- Kærn, M.R.; Brix, W.; Elmegaard, B.; Larsen, L.F.S. Compensation of flow maldistribution in fin-and-tube evaporators for residential air-conditioning. Int. J. Refrig. 2011, 34, 1230–1237. [Google Scholar] [CrossRef]
- Kærn, M.R.; Brix, W.; Elmegaard, B.; Larsen, L.F.S. Performance of residential air-conditioning systems with flow maldistribution in fin-and-tube evaporators. Int. J. Refrig. 2011, 34, 696–706. [Google Scholar] [CrossRef]
- Chin, W.M.; Raghavan, V.R. On the adverse influence of higher statistical moments of flow maldistribution on the performance of a heat exchanger. Int. J. Therm. Sci. 2011, 50, 581–591. [Google Scholar] [CrossRef]
- Chin, W.M.; Raghavan, V.R. The influence of the moments of probability density function for flow maldistribution on the thermal performance of a fin-tube heat exchanger. Int. J. Therm. Sci. 2011, 50, 1942–1953. [Google Scholar] [CrossRef]
- Hsieh, C.T.; Jang, J.Y. Parametric study and optimization of louver finned-tube heat exchangers by Taguchi method. Appl. Therm. Eng. 2012, 42, 101–110. [Google Scholar] [CrossRef]
- Saad, S.B.; Clément, P.; Fourmigué, J.F.; Gentric, C.; Leclerc, J.P. Single phase pressure drop and two-phase distribution in an offset strip fin compact heat exchanger. Appl. Therm. Eng. 2012, 49, 99–105. [Google Scholar] [CrossRef]
- Mao, J.N.; Chen, H.X.; Jia, H.; Wang, Y.Z.; Hu, H.M. Effect of air-side flow maldistribution on thermalehydraulic performance of the multi-louvered fin and tube heat exchanger. Int. J. Therm. Sci. 2013, 73, 46–57. [Google Scholar] [CrossRef]
- Vocale, P.; Morini, G.L.; Spiga, M. Influence of outdoor air conditions on the air source heat pumps performance. Energy Procedia 2014, 45, 653–662. [Google Scholar] [CrossRef]
- Kumar, A.; Joshi, J.B.; Nayak, A.K.; Vijayan, P.K. 3D CFD simulation of air cooled condenser-I: Natural convection over a circular cylinder. Int. J. Heat. Mass. Transf. 2014, 78, 1265–1283. [Google Scholar] [CrossRef]
- Butler, C.; Grimes, R. The effect of wind on the optimal design and performance of a modular air-cooled condenser for a concentrated solar power plant. Energy 2014, 68, 886–895. [Google Scholar] [CrossRef]
- Niu, F.; Yu, Y.; Yu, D.; Li, H. Heat and mass transfer performance analysis and cooling capacity prediction of earth to air heat exchanger. Appl. Energy 2015, 137, 211–221. [Google Scholar] [CrossRef]
- Łopata, S.; Ocłoń, P. Numerical study of the effect of fouling on local heat transfer conditions in a high-temperature fin-and-tube heat exchanger. Energy 2015, 92, 100–116. [Google Scholar] [CrossRef]
- Wang, T.; Gu, B.; Wu, B.; Ma, H.; Qian, C. Modeling for multi-pass parallel flow condenser with the effect of refrigerant mal-distribution. Int. J. Refrig. 2015, 60, 234–246. [Google Scholar] [CrossRef]
- Yan, H.; Deng, S.; Chan, M. Developing and validating a dynamic mathematical model of a three-evaporator air conditioning (TEAC) system. Appl. Therm. Eng. 2016, 100, 880–892. [Google Scholar] [CrossRef]
- Datta, S.P.; Das, P.K.; Mukhopadhyay, S. Performance of a condenser of an automotive air conditioner with maldistribution of inlet air—Simulation studies and its experimental validation. Int. J. Heat. Mass. Transf. 2016, 98, 367–379. [Google Scholar] [CrossRef]
- Lee, W.J.; Jeong, J.H. Heat transfer performance variations of condensers due to non-uniform air velocity distributions. Int. J. Refrig. 2016, 69, 85–95. [Google Scholar] [CrossRef]
- Wang, D.; Liu, C.; Yu, D.; Chen, J. Influence factors of flow distribution and a feeder tube compensation method in multi-circuit evaporators. Int. J. Refrig. 2017, 73, 11–23. [Google Scholar] [CrossRef]
- Li, J.; Gao, Y.; Liu, C.; Yan, X.; Zhao, H.Q.; Xu, Y.; Meng, E. Effect of flow maldistribution on heat transfer performance and temperature field of plate-fin heat exchangers. Int. Commun. Heat. Mass. Transf. 2023, 149, 107135. [Google Scholar] [CrossRef]
- Li, H.; Guo, X.; Belotserkovsky, M.A.; Grigorchik, A.N.; Kukareko, V.A.; Bo, Z. A coupled modeling framework for investigating flow maldistribution in cross-flow-corrugated plate heat exchangers. Int. J. Fluid Eng. 2024, 1, 034301. [Google Scholar] [CrossRef]
- Yashar, D.; Domanski, P.; Cho, H.H. An experimental and computational study of approach air distribution for a finned-tube heat exchanger. HVAC&R Res. 2011, 17, 76–85. [Google Scholar] [CrossRef]
- Danckwerts, P. Continuous flow systems Distribution of residence times. Chem. Eng. Sci. 1953, 2, 1–13. [Google Scholar] [CrossRef]
- Wasewar, K.L.; Hargunani, S.; Atluri, P.; Naveen, K. CFD Simulation of Flow Distribution in the Header of Plate-Fin Heat Exchangers. Chem. Eng. Technol. 2007, 30, 1340–1346. [Google Scholar] [CrossRef]
- Chung, S.S.; Kim, N.; Jo, H.J. Effect of flow distribution on heat transfer in Printed Circuit Heat Exchangers using conjugate heat transfer model with a modified porous media approach. Appl. Therm. Eng. 2025, 266, 125540. [Google Scholar] [CrossRef]

| Authors | Nature of Domain | Numerical Details | Modeling Approach |
|---|---|---|---|
| Wang et al. [23] | Flow of gas–liquid refrigerant in a distributor | • Three-dimensional • Finite volume method • 400,000 cells • ANSYS Fluent | • Eulerian multiphase model • Standard k–ε turbulence model • Enhanced wall treatment • Pressure-based solver with the SIMPLE algorithm |
| Zhang et al. [60] | An air-cooled condenser in a steam-electric power plant | • Three-dimensional • Finite volume method • 3,820,000 cells • ANSYS Fluent | • Porous media model • Fan modeled as a moving reference frame • Standard k–ε turbulence model |
| Yashar et al. [124] | A FTHX | • Two-dimensional | |
| Ranganayakulu et al. [88] | A crossflow plate–fin compact HX | • Finite element method | • Mathematical model based on a Fourier series |
| Mishra et al. [102] | Crossflow HX | • Implicit finite difference method | • Governing equations and boundary conditions solved using the Gauss–Seidel iterative technique |
| Srihari and Das [34] | PHX | • Finite difference method • Comparison with analytical solution results | • Boundary conditions based on Danckwerts analysis [125] |
| Chin and Raghavan [108] | Thermal performance of a FTHX | • Two-dimensional • 10 × 10 grid | • Continuous probability density functions |
| Datta et al. [119] | A condenser in an automotive air conditioning system | • CoilDesigner software | • One-dimensional control volume energy balance for each port |
| Prabhakara Rao et al. [18] | PHX | • Control volume method • Multipass configuration modeled as multiple exchangers | • Governing energy equations formulated • Differential equations cast into a matrix form |
| Wasewar et al. [126] | Flow distribution in the header of a PHX | • Finite volume method • No-slip boundary conditions • 2,000,000 cells | • Single-phase model • Standard k–ε turbulence model • SIMPLE algorithm • Solved using the tridiagonal matrix algorithm |
| Mao et al. [111] | A multi-louvered FTHX | • One-dimensional steady-state • Finite volume method | • MATLAB-based custom code • Refrigerant properties from REFPROP |
| Chung et al. [127] | PCHXs | • Conjugate heat transfer model | • Modified porous media approach |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishaque, S.; Ullah, N.; Ali, Q.S.; Ullah, N.; Choi, S.; Kim, M.-H. Non-Uniformities in Heat Exchangers: A Two-Decade Review of Causes, Effects, and Mitigation Strategies. Energies 2025, 18, 2751. https://doi.org/10.3390/en18112751
Ishaque S, Ullah N, Ali QS, Ullah N, Choi S, Kim M-H. Non-Uniformities in Heat Exchangers: A Two-Decade Review of Causes, Effects, and Mitigation Strategies. Energies. 2025; 18(11):2751. https://doi.org/10.3390/en18112751
Chicago/Turabian StyleIshaque, Shehryar, Naveed Ullah, Qazi Shahzad Ali, Naveed Ullah, Sanghun Choi, and Man-Hoe Kim. 2025. "Non-Uniformities in Heat Exchangers: A Two-Decade Review of Causes, Effects, and Mitigation Strategies" Energies 18, no. 11: 2751. https://doi.org/10.3390/en18112751
APA StyleIshaque, S., Ullah, N., Ali, Q. S., Ullah, N., Choi, S., & Kim, M.-H. (2025). Non-Uniformities in Heat Exchangers: A Two-Decade Review of Causes, Effects, and Mitigation Strategies. Energies, 18(11), 2751. https://doi.org/10.3390/en18112751









