Multi-Objective Optimal Control of Variable Speed Alternating Current-Excited Pumped Storage Units Considering Electromechanical Coupling Under Grid Voltage Fault
Abstract
1. Introduction
- (1)
- A unified rotor current reference expression is developed by incorporating electromechanical coupling characteristics, which ensures consistent control across different fault scenarios and objectives;
- (2)
- A time-varying weighting factor mechanism is introduced to realize dynamic multi-objective optimization, enabling the control priorities to adaptively shift based on system operating conditions and fault severity;
- (3)
- A comprehensive LVRT control strategy is proposed for the VSACPSU under asymmetrical voltage faults, which simultaneously addresses active/reactive power oscillation suppression, torque fluctuation mitigation, and current unbalance reduction, leading to significantly improved grid fault adaptability and system stability.
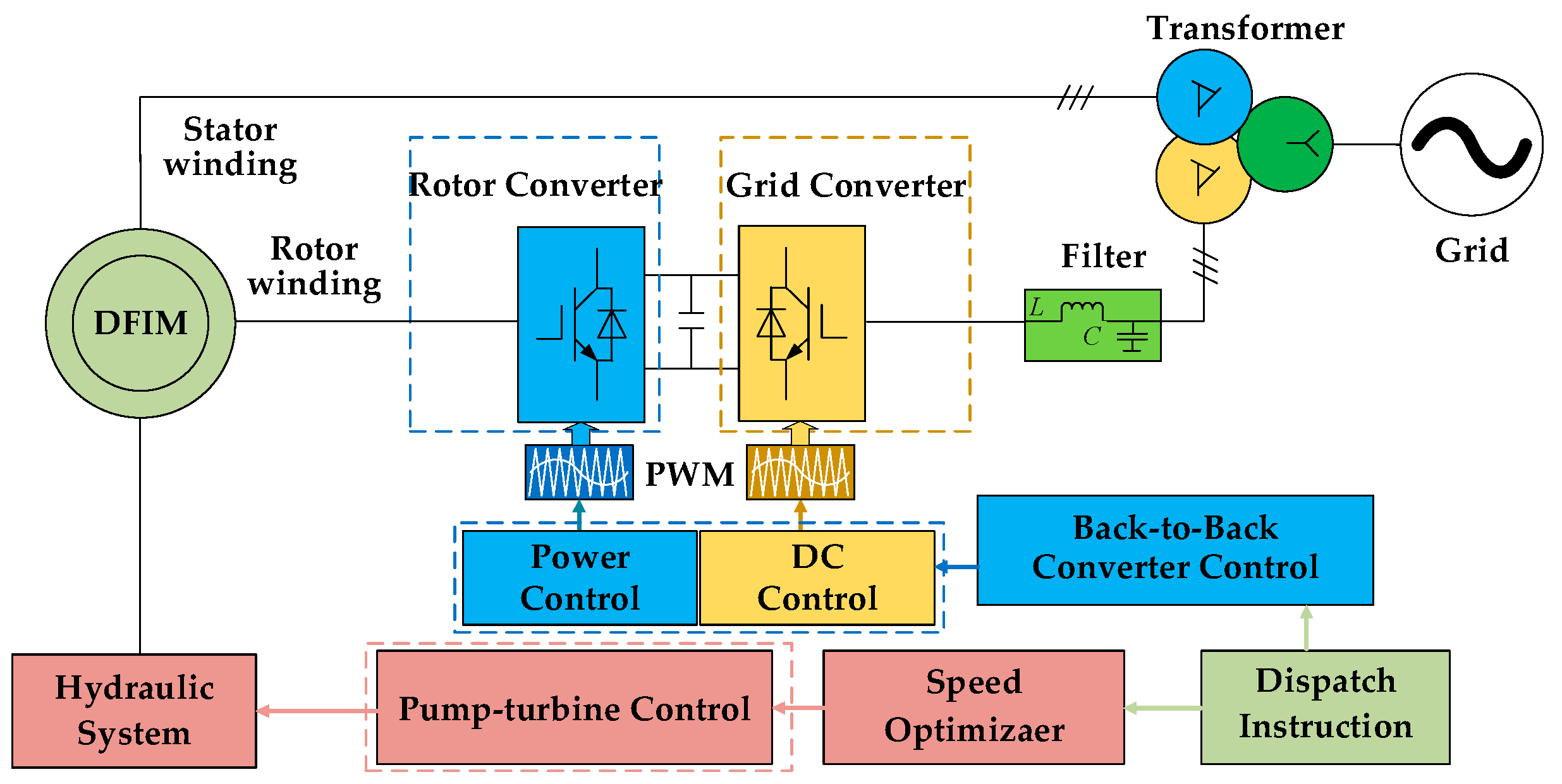
2. The System Configuration of Variable Speed AC-Excited Pumped Storage Units
3. Operating Characteristics of Variable Speed AC-Excited Pumped Storage Units Under Grid Voltage Faults
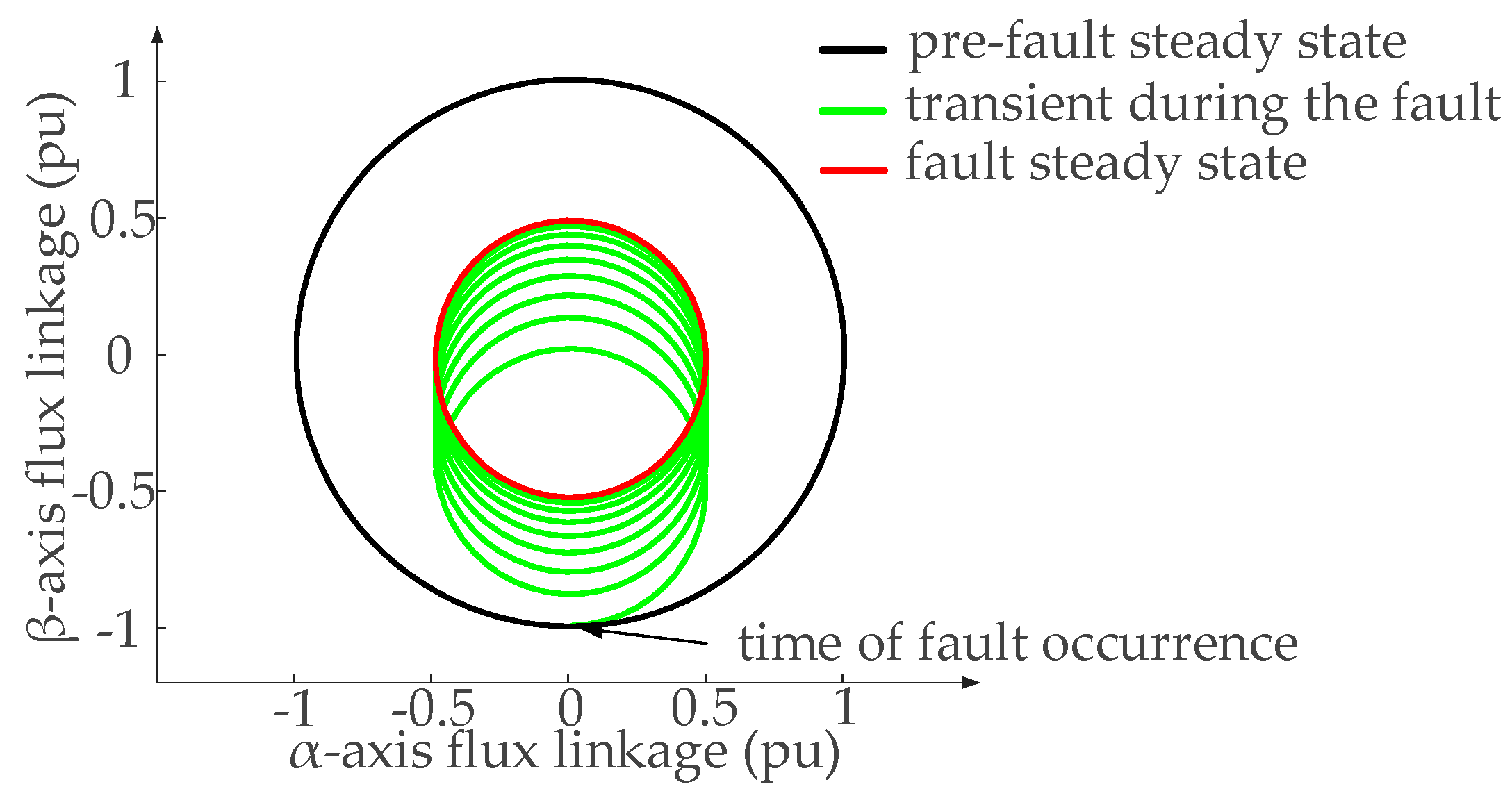
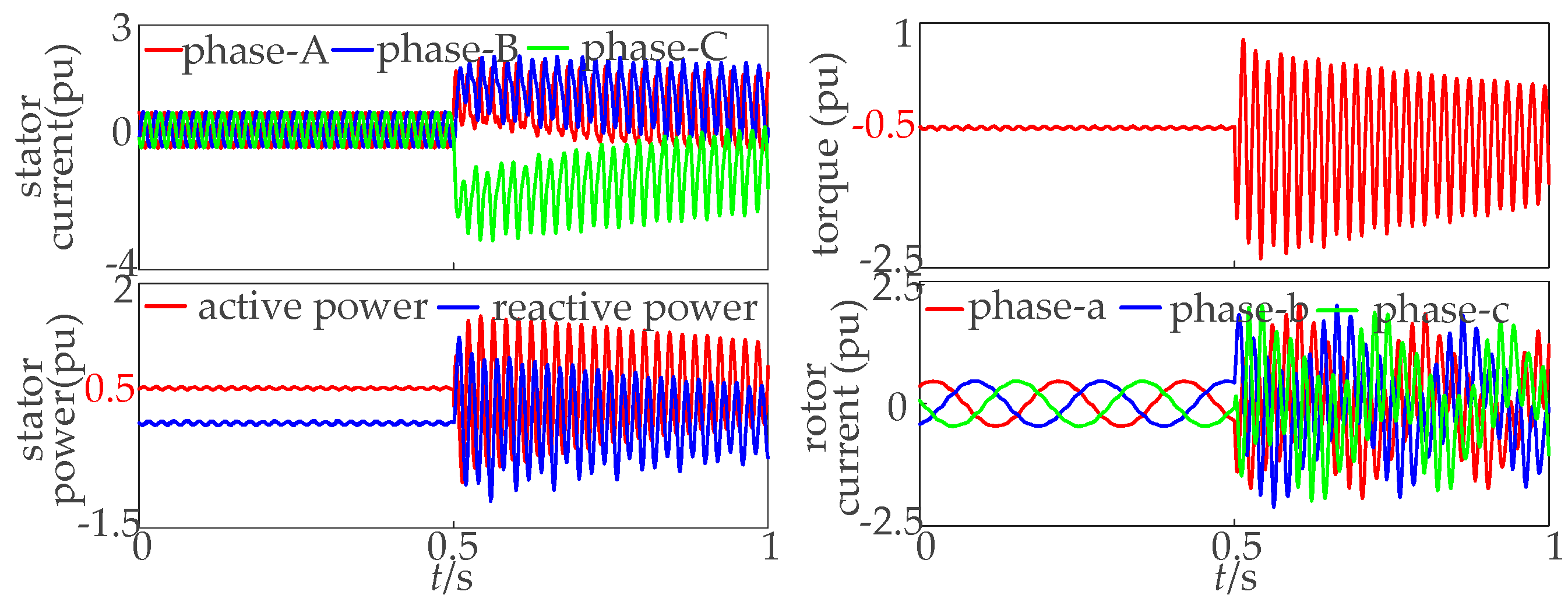
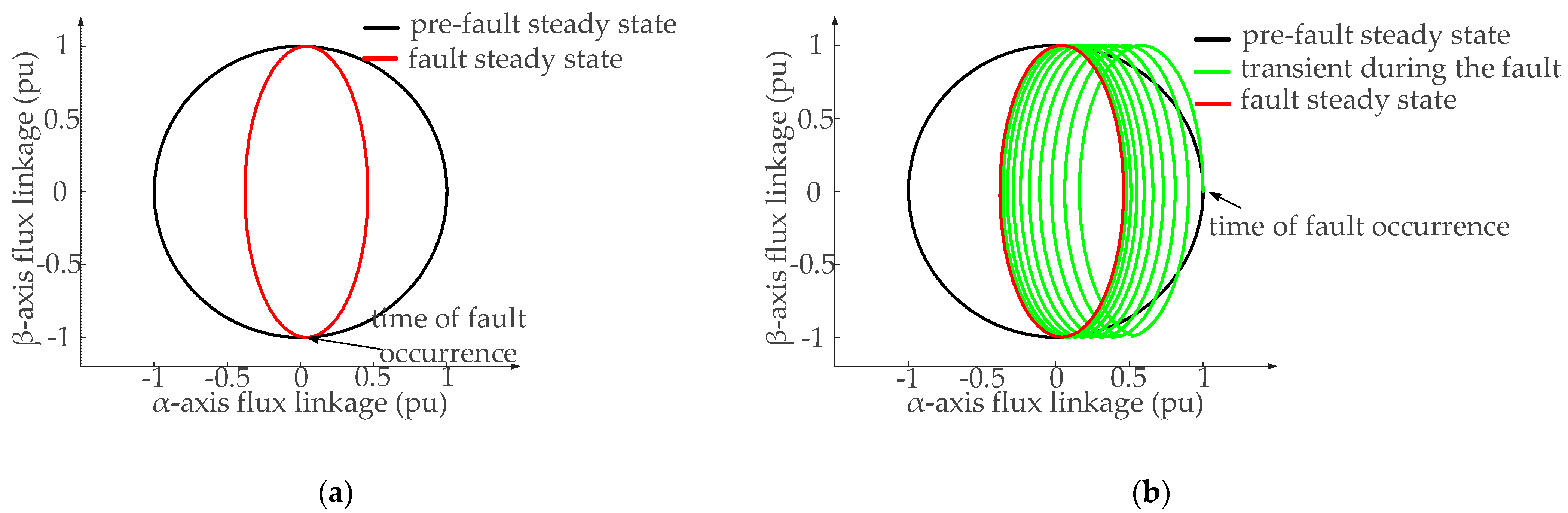
3.1. Operating Characteristics of DFIM Under a Symmetrical Grid Voltage Fault
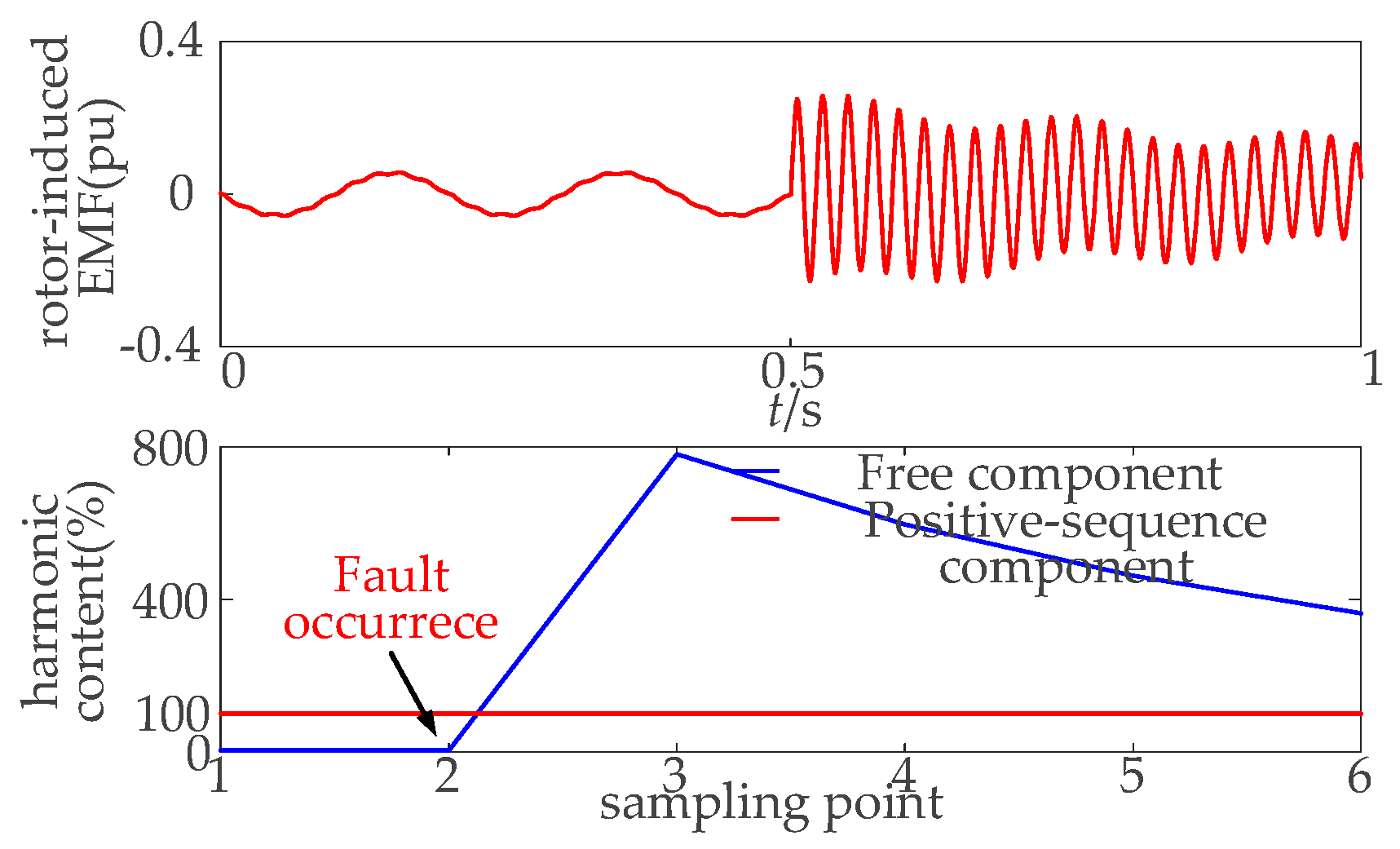
3.2. Operating Characteristics of DFIM Under a Symmetrical Grid Voltage Unbalanced Fault
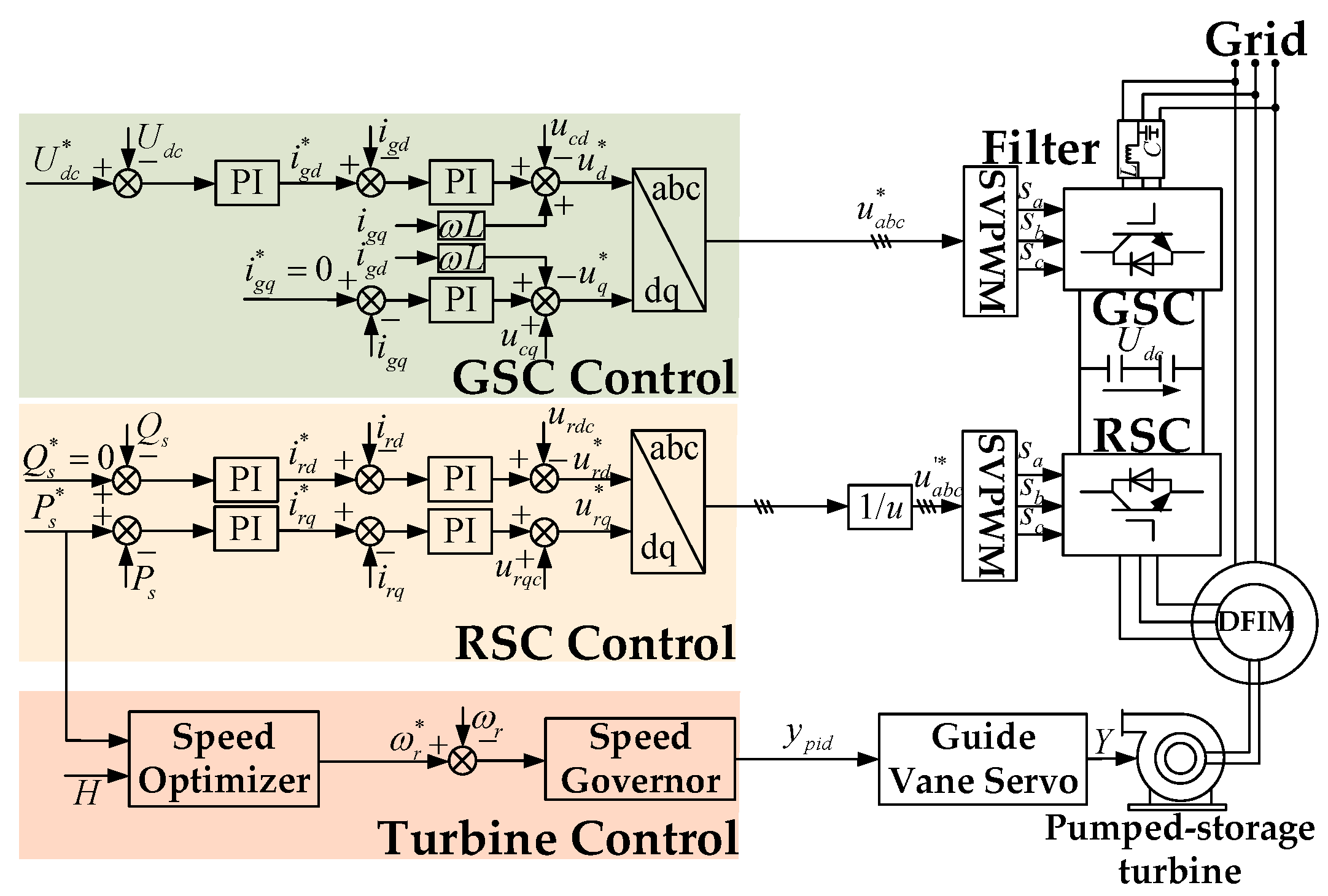
4. Multi-Objective Optimal Control of Variable Speed AC-Excited Pumped Storage Units Under a Grid Voltage Fault
4.1. Calculation of the Unified Rotor Reference Current
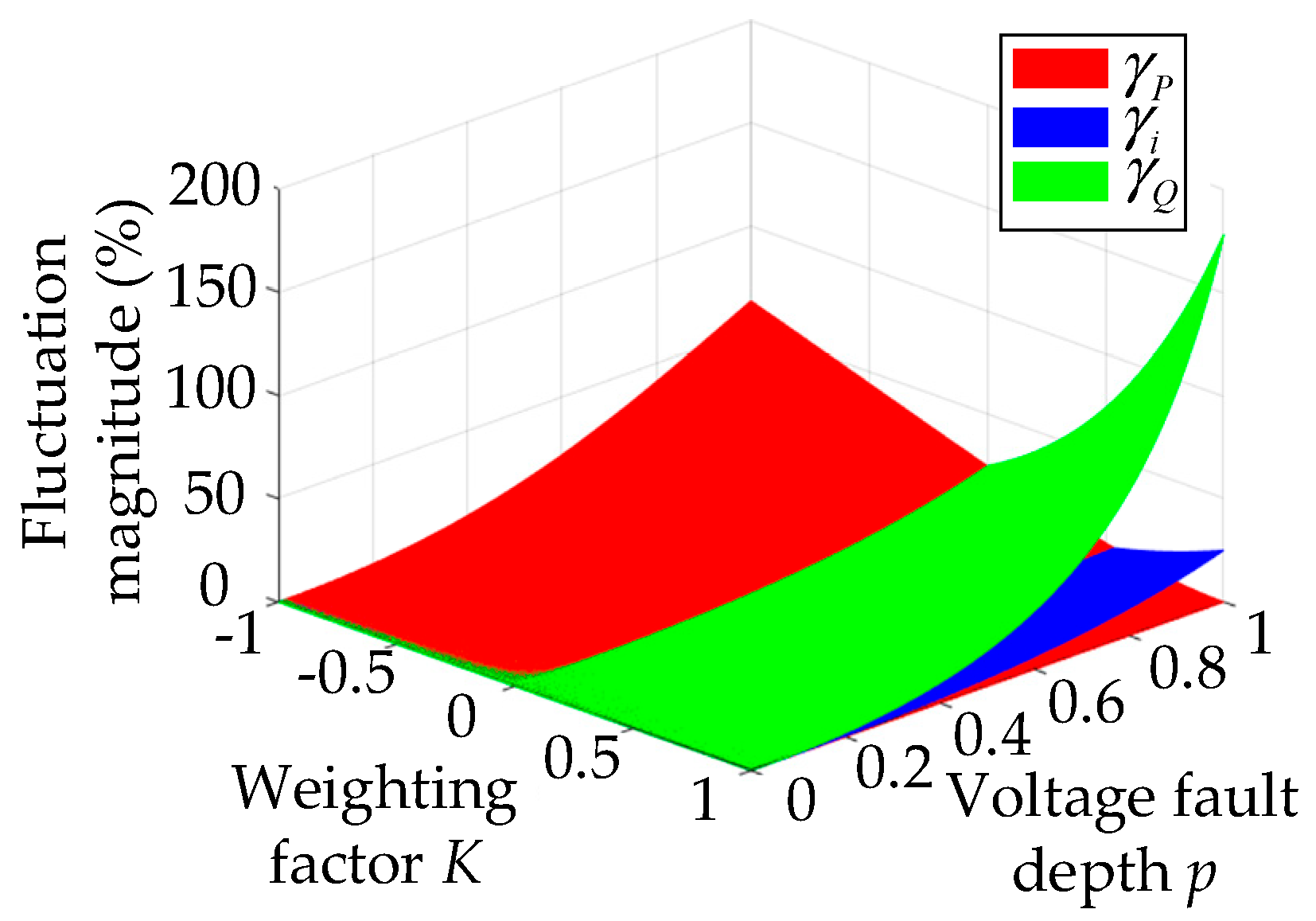
4.2. Construction of the Multi-Objective Optimization Model
4.3. Multi-Objective Coordinated Control Strategy Under Grid Voltage Faults
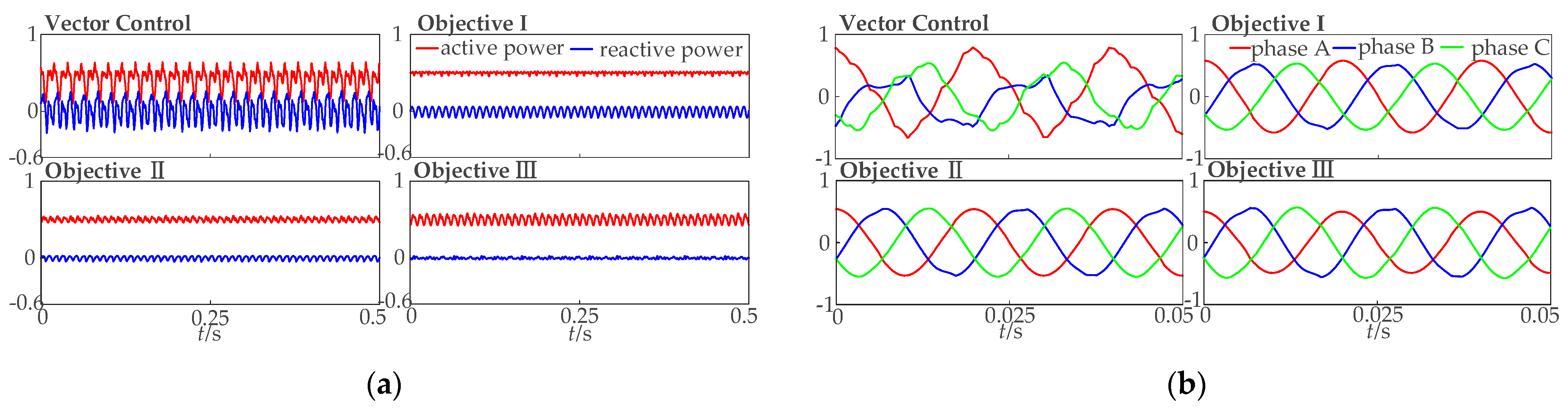
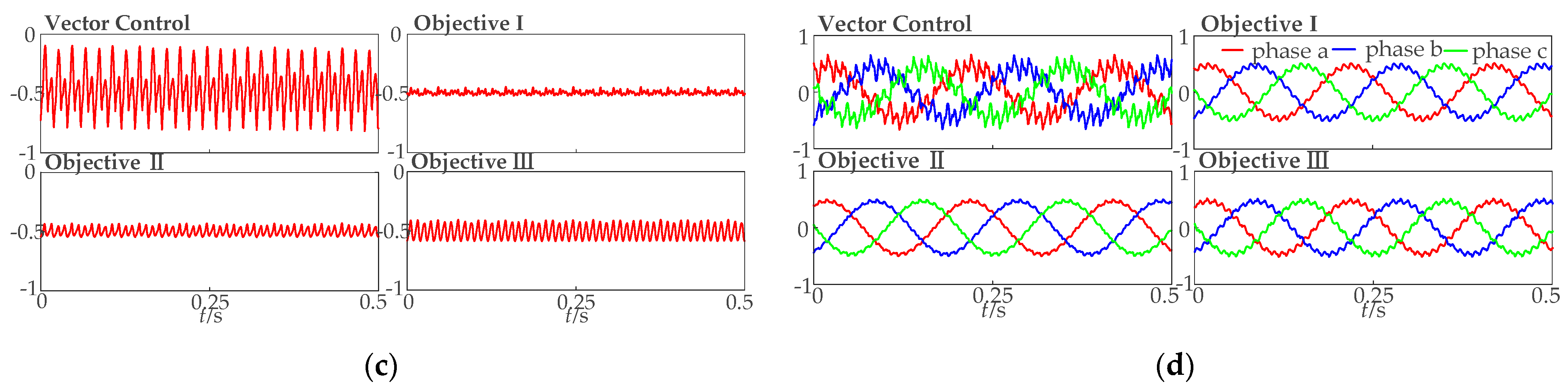
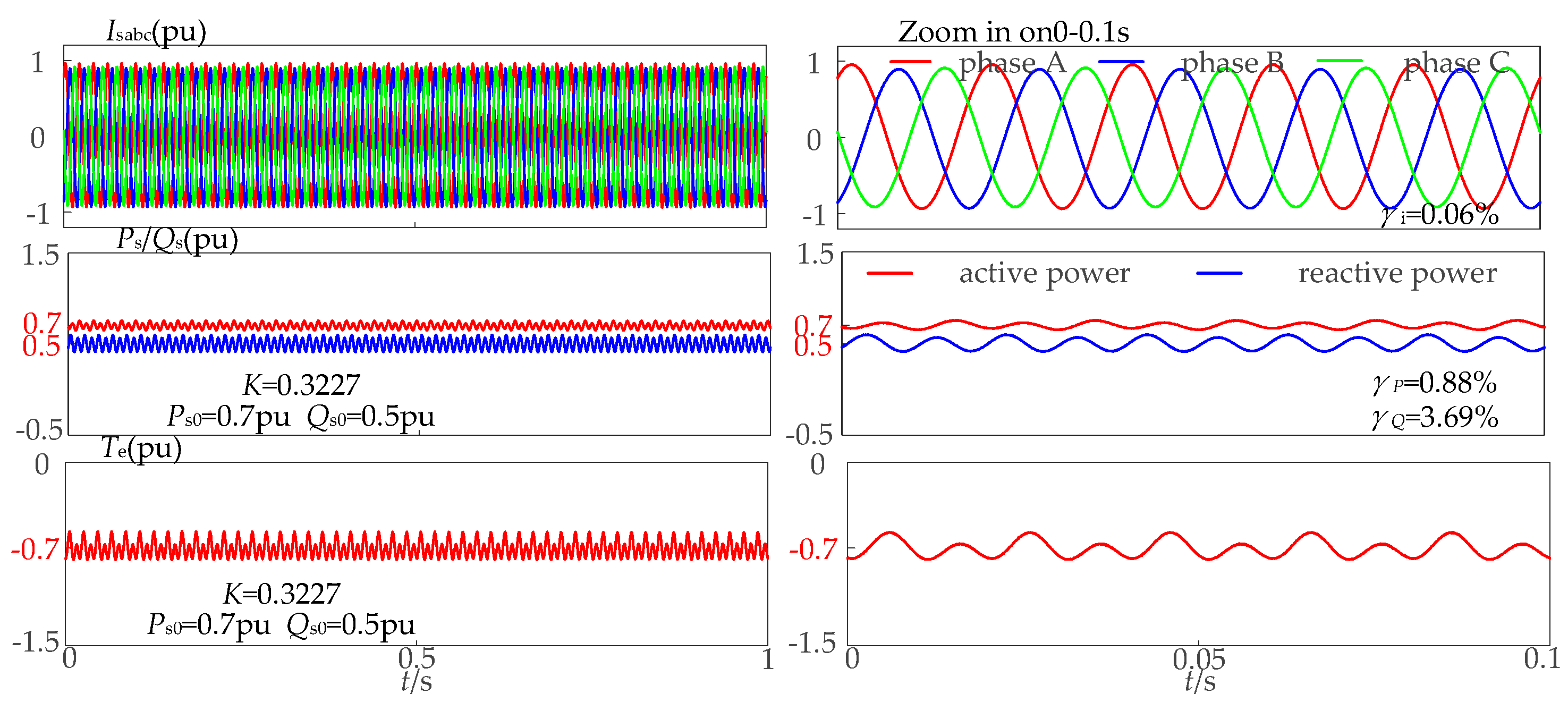
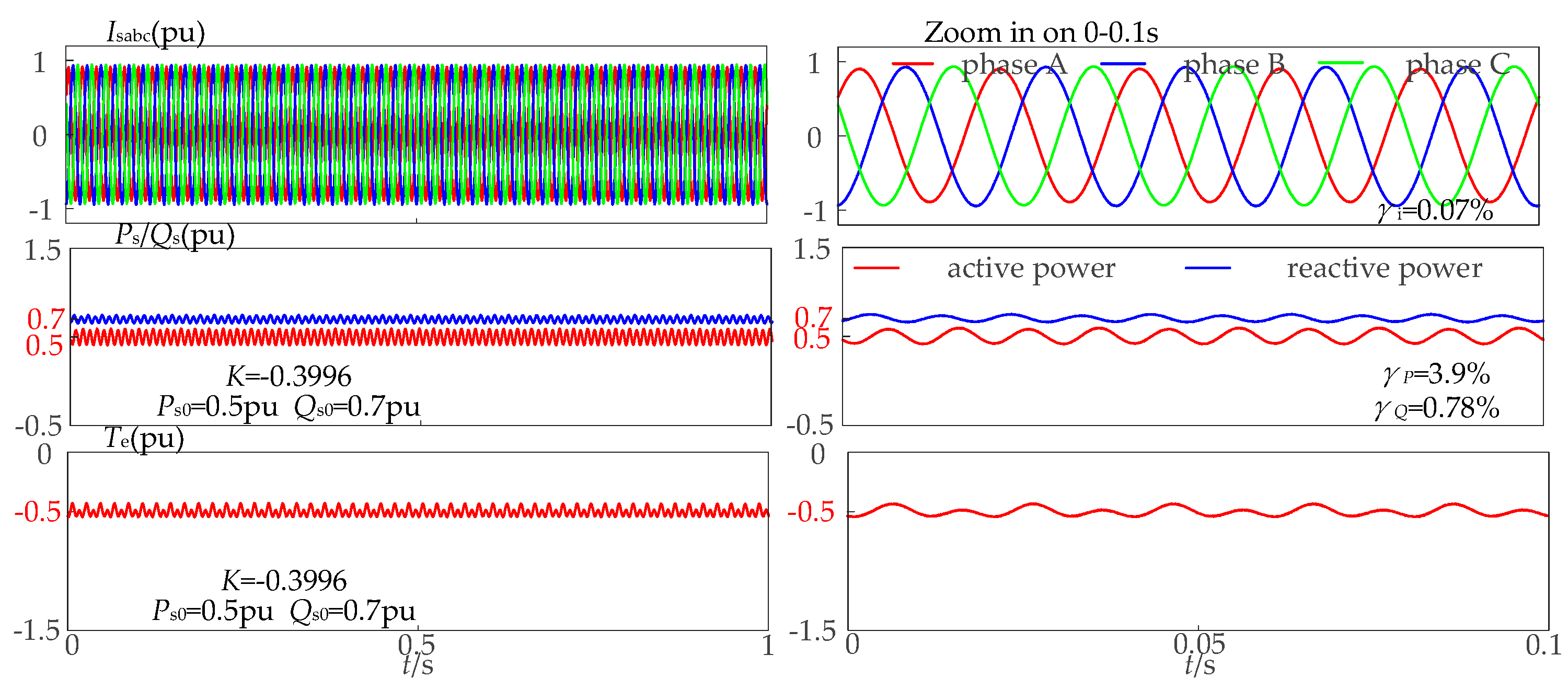
5. Simulation Analysis
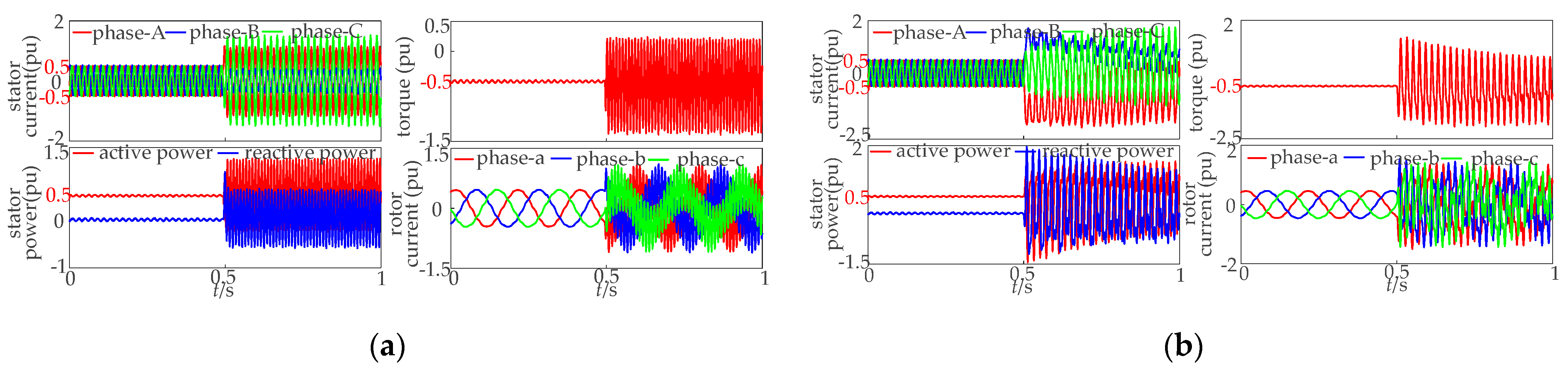
5.1. Simulation of the Conventional Control Strategy
5.2. Simulation of the Proposed Multi-Objective Control Strategy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PSU | Pumped Storage Unit |
| VSPSU | Variable Speed Pumped Storage Unit |
| VSACPSU | Variable Speed AC-excited Pumped Storage Unit |
| DFIM | Doubly-fed induction machine |
| FRT | Fault ride-through |
| LVRT | Low-voltage ride-through |
| RSC | Rotor-side converter |
| GSC | Grid-side converter |
| EMF | Electromotive force |
Appendix A
| Variable | Physical Meaning |
|---|---|
| vs1 | Positive-sequence component of stator three-phase voltage |
| vs2 | Negative-sequence component of stator three-phase voltage |
| vs0 | Zero-sequence component of stator three-phase voltage |
| is1 | Positive-sequence component of stator three-phase current |
| is2 | Negative-sequence component of stator three-phase current |
| ψs1 | Positive-sequence component of stator flux linkage |
| ψs2 | Negative-sequence component of stator flux linkage |
| ωs | Grid angular velocity |
| s | Slip ratio |
| Ps0 | Average value of stator active power |
| Ps cos | Double-frequency cosine component of stator active power |
| Ps sin | Double-frequency sine component of stator active power |
| Qs0 | Average value of stator reactive power |
| Qs cos | Double-frequency cosine component of stator reactive power |
| Qs sin | Double-frequency sine component of stator reactive power |
| λ | λ = vs2/vs1 |
| R | ) |
| D | ) |
References
- Zhu, Z.; Tan, X.; Lu, X.; Liu, D.; Li, C. Hopf Bifurcation and Parameter Sensitivity Analysis of a Doubly-Fed Variable-Speed Pumped Storage Unit. Energies 2022, 15, 204. [Google Scholar] [CrossRef]
- Grigorescu, A.; Ion, A.-E.; Lincaru, C.; Pirciog, S. Synergy Analysis of Knowledge Transfer for the Energy Sector within the Framework of Sustainable Development of the European Countries. Energies 2022, 15, 276. [Google Scholar] [CrossRef]
- Wenke, H. China’s Energy Transition: Progress and Outlook from the “14th Five-Year Plan” to the “15th Five-Year Plan”. China Oil Gas 2025, 32, 1–10. [Google Scholar]
- Esmaeilian, H.-R.; Fadaeinedjad, R.; Bakhshai, A. Performance Evaluation and MPPT Control of a Variable-Speed Pump-as-Turbine System. IEEE Syst. J. 2023, 17, 3117–3126. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, W.; Liu, Y.; Mao, Z. Dynamical Response Comparison Between Variable Speed and Synchronous Speed Pumped-Storage Units in Turbine Mode. IEEE Trans. Energy Convers. 2024, 39, 2490–2503. [Google Scholar] [CrossRef]
- Iliev, I.; Vedi, C.; Hlhaug, O.-G. Variable-speed operation of Francis turbines: A review of the perspectives and challenges. Renew. Sustain. Energy Rev. 2019, 103, 109–121. [Google Scholar] [CrossRef]
- Semwal, R.-R.; Joseph, A.; Chelliah, T.-R. Two-Stage Protection Circuit for a Multi-channeled Power Electronic Converter Fed Large Asynchronous Hydro generating Unit. IEEE Trans. Ind. Appl. 2019, 55, 5947–5959. [Google Scholar] [CrossRef]
- Damdoum, A.; Slama-Belkhodja, I.; Pietrzak-David, M.; Debbou, M. Low Voltage Ride-Through Strategies for Doubly Fed Induction Machine Pumped Storage System under Grid Faults. Renew. Energy 2016, 95, 248–262. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H. Short-circuit current of wind turbines with doubly fed induction generator. IEEE Trans. Energy Convers. 2007, 22, 174–180. [Google Scholar] [CrossRef]
- Pannell, G.; Atkinson, D.-J.; Zahawi, B. Minimum-Threshold Crowbar for a Fault-Ride-Through Grid-Code-Compliant DFIG Wind Turbine. IEEE Trans. Energy Convers. 2010, 25, 750–759. [Google Scholar] [CrossRef]
- Bidgoli, M.-A.; Mohammadpour, H.-A.; Bathaee, S.M.T. Advanced Vector Control Design for DFIM-Based Hydropower Storage for Fault Ride-Through Enhancement. IEEE Trans. Energy Convers. 2015, 30, 1449–1459. [Google Scholar] [CrossRef]
- Petersson, A.; Harnefors, L.; Thiringer, T. Evaluationof current control methods for wind turbines using doubly-fed in-duction machines. IEEE Trans. Power Electron. 2005, 20, 227–235. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, Z.; Hu, J.; Zou, X.; Kang, Y.; Guerrero, J.-M. Rethinking Fault Ride-Through Control of DFIG-Based Wind Turbines From New Perspective of Rotor-Port Impedance Characteristics. IEEE Trans. Sustain. Energy 2024, 15, 2050–2062. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, X.; Zhang, X.; Yang, X.; Wang, L. Improved ride-through control of DFIG during grid voltage swell. IEEE Trans. Ind. Electron. 2015, 62, 3584–3594. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Y. Dynamic modeling and control of DFIG-based wind turbines under unbalanced network conditions. IEEE Trans. Power Syst. 2007, 22, 314–323. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, W.; Liu, Y.; Bao, Z.; Mao, Z.; Rashad, E.-M. Modeling and Transient Response Analysis of Doubly-Fed Variable Speed Pumped Storage Unit in Pumping Mode. IEEE Trans. Ind. Electron. 2023, 70, 9935–9947. [Google Scholar] [CrossRef]
- Jinming, H.; Dajun, T.; Yutian, S.; Chunli, Z.; Guifen, L.; Gang, H. Analysis of Operating Characteristics of Variable Speed Pumped Storage Motor-Generator. IEEE Access. 2023, 11, 52117–52128. [Google Scholar] [CrossRef]
- Desingu, K.; Selvaraj, R.; Chelliah, T.-R.; Khare, D. Effective Utilization of Parallel-Connected Megawatt Three-Level Back-to-Back Power Converters in Variable Speed Pumped Storage Units. IEEE Trans. Ind. Appl. 2019, 55, 6414–6426. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, C.; Zhao, Y. Coordination Control Between Excitation and Hydraulic System During Mode Conversion of Variable Speed Pumped Storage Unit. IEEE Trans. Power Electron. 2021, 36, 10171–10185. [Google Scholar] [CrossRef]
- Zhu, Z.; Pan, W.; Liu, T.; Li, Y.; Liu, M. Dynamic Modeling and Eigen Analysis of Adjustable-Speed Pumped Storage Unit in Pumping Mode Under Power Regulation. IEEE Access 2021, 9, 155035–155047. [Google Scholar] [CrossRef]






| Name | Value |
|---|---|
| Rated voltage (kV) | 18 |
| Stator resistance (pu) | 0.001113 |
| Stator leakage reactance (pu) | 0.119 |
| Rotor resistance (pu) | 0.0012225 |
| Rotor leakage reactance (pu) | 0.141 |
| Magnetizing reactance (pu) | 2.468 |
| Turns ratio (stator to rotor) | 0.4287 |
| Synchronous speed (r/min) | 428.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Lu, Y.; Yang, X.; Man, Z.; Yan, W.; Liu, T.; Zhan, C.; Zhou, X.; Fang, T. Multi-Objective Optimal Control of Variable Speed Alternating Current-Excited Pumped Storage Units Considering Electromechanical Coupling Under Grid Voltage Fault. Energies 2025, 18, 2750. https://doi.org/10.3390/en18112750
Liu T, Lu Y, Yang X, Man Z, Yan W, Liu T, Zhan C, Zhou X, Fang T. Multi-Objective Optimal Control of Variable Speed Alternating Current-Excited Pumped Storage Units Considering Electromechanical Coupling Under Grid Voltage Fault. Energies. 2025; 18(11):2750. https://doi.org/10.3390/en18112750
Chicago/Turabian StyleLiu, Tao, Yu Lu, Xiaolong Yang, Ziqiang Man, Wei Yan, Teng Liu, Changjiang Zhan, Xingwei Zhou, and Tianyu Fang. 2025. "Multi-Objective Optimal Control of Variable Speed Alternating Current-Excited Pumped Storage Units Considering Electromechanical Coupling Under Grid Voltage Fault" Energies 18, no. 11: 2750. https://doi.org/10.3390/en18112750
APA StyleLiu, T., Lu, Y., Yang, X., Man, Z., Yan, W., Liu, T., Zhan, C., Zhou, X., & Fang, T. (2025). Multi-Objective Optimal Control of Variable Speed Alternating Current-Excited Pumped Storage Units Considering Electromechanical Coupling Under Grid Voltage Fault. Energies, 18(11), 2750. https://doi.org/10.3390/en18112750






