Comparison and Application of Pore Pressure Prediction Methods for Carbonate Formations: A Case Study in Luzhou Block, Sichuan Basin
Abstract
1. Introduction
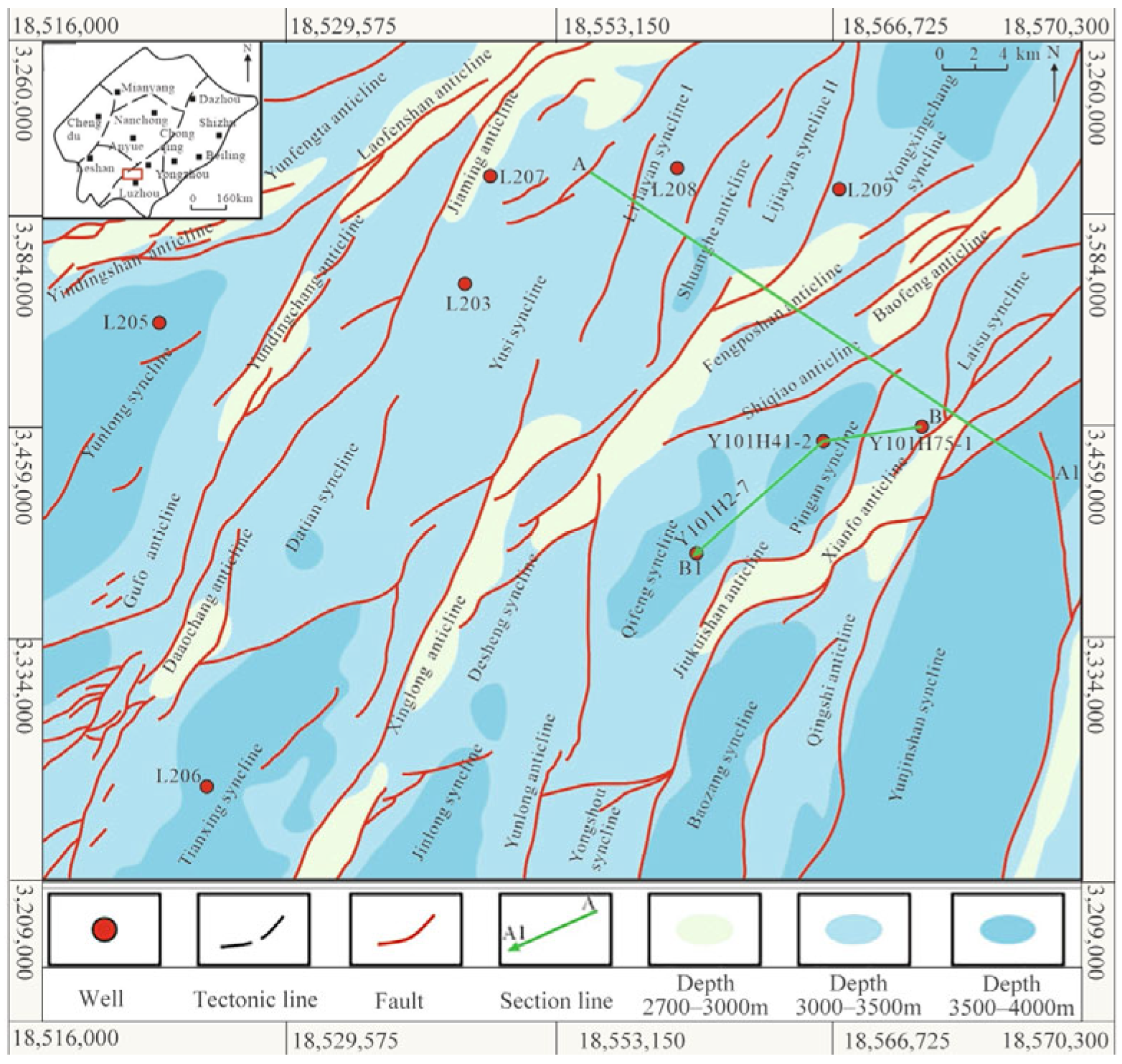
2. Geological Setting
3. Construction and Optimization of Pore Pressure Prediction Model
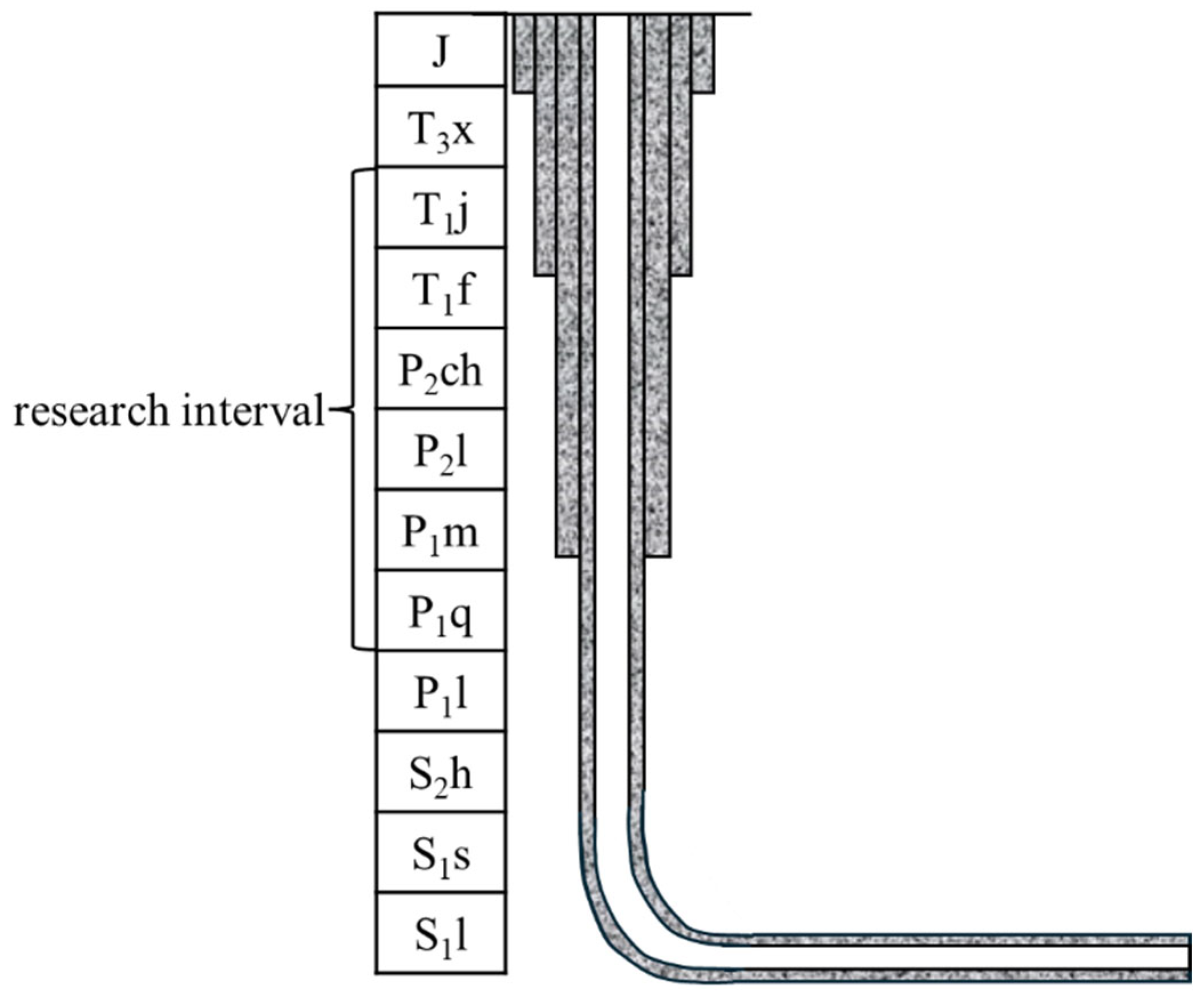
3.1. Equivalent Depth Method Model
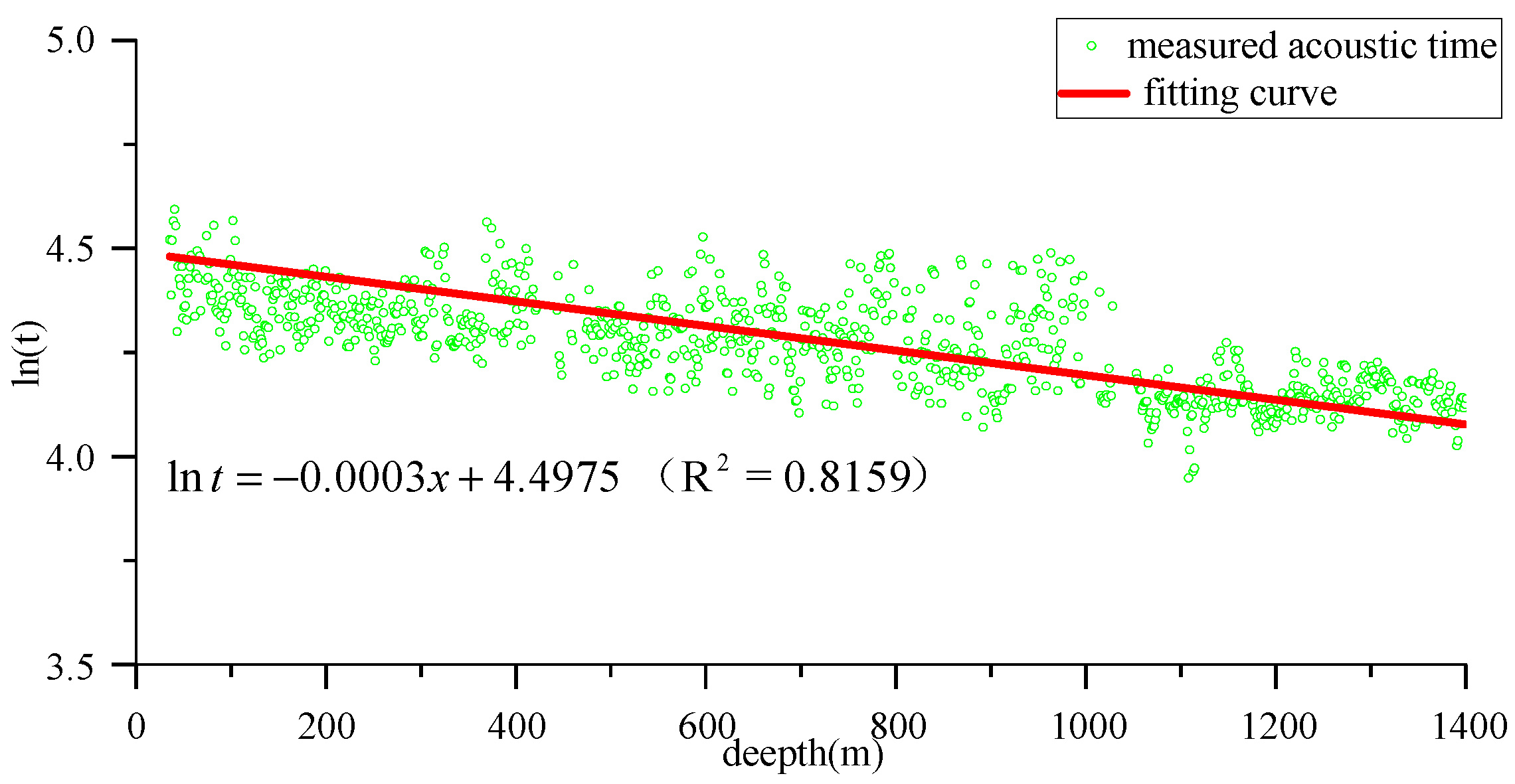
3.2. Eaton Method Model
- Compaction trend line establishment.
- 2.
- Determination of Eaton index “x”.
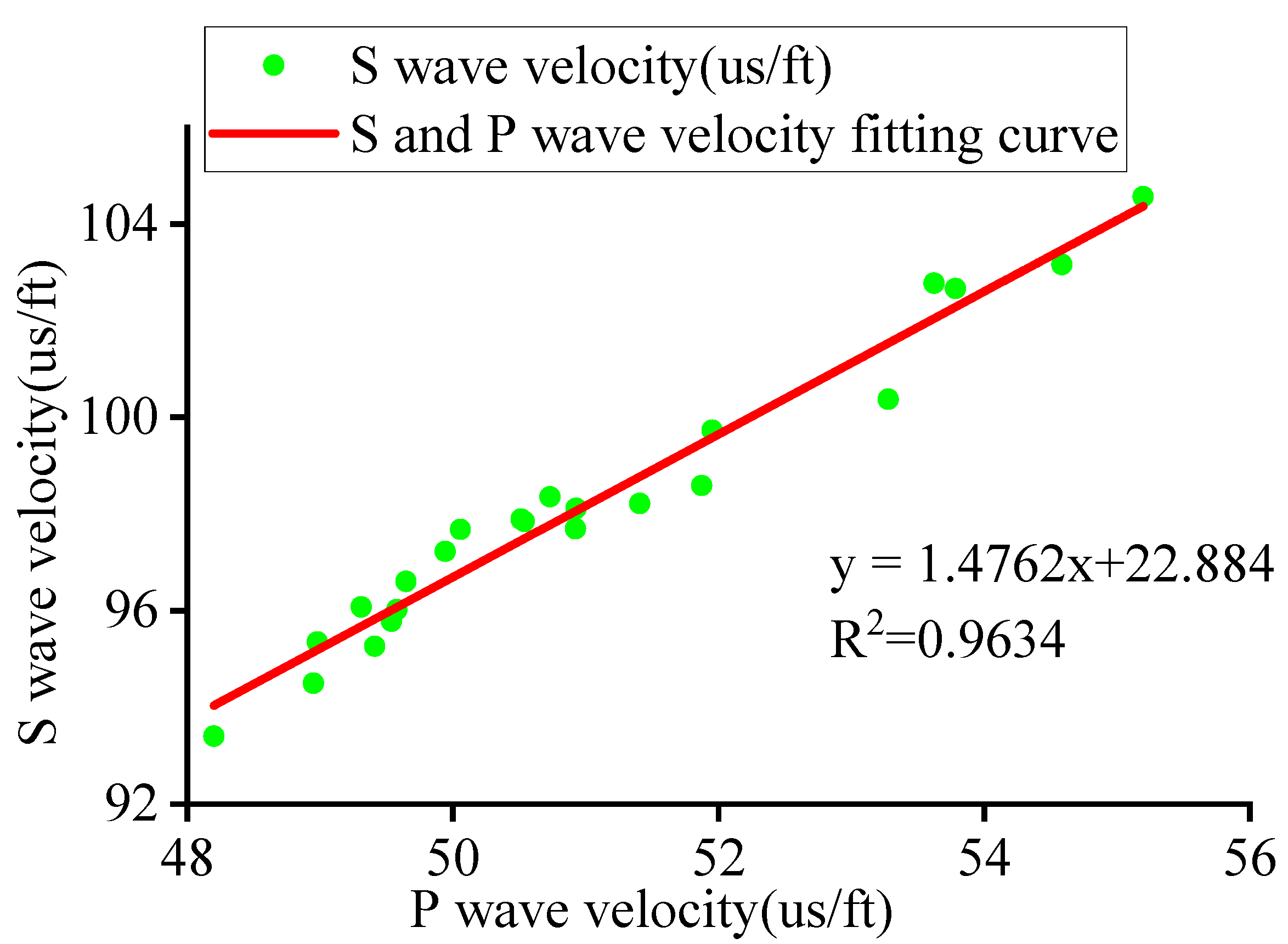
3.3. Effective Stress Method Model
4. Field Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full Term |
| J2s | Sha Ximiao Formation |
| J1l | Liang Gaoshan Formation |
| J1t | Zi Liujing Formation |
| T3x | Liang Gaoshan Formation |
| T1j | Jia Lingjiang Formation |
| T1f | Fei Xianguan Formation |
| P2ch | Chang Xing Formation |
| P2l | Long Tan Formation |
| P1m | Mao Kou Formation |
| P1q | Qi Xia Formation |
| P1l | Liang shan Formation |
| S2h | Shi Niulan Formation |
| S1s | Shi Niulan Formation |
| S1l | Long Maxi Formation |
References
- Polito Carmine, P.; Green Russell, A.; Lee, J. Pore Pressure Generation Models for Sands and Silty Soils Subjected to Cyclic Loading. J. Geotechnol. Geoenviron. Eng. 2008, 134, 1490–1500. [Google Scholar] [CrossRef]
- Ba, J.; Min, J.; Zhang, L.; Carcione, J.M. Effects of Stress on Transport Properties in Fractured Porous Rocks. Lithosphere 2024, 2024, lithosphere_2023_103. [Google Scholar] [CrossRef]
- Ghorbani, H.; Wood, D.A.; Moghadasi, J.; Choubineh, A.; Abdizadeh, P.; Mohamadian, N. Predicting liquid flow-rate performance through wellhead chokes with genetic and solver optimizers: An oil field case study. J. Pet. Explor. Prod. Technol. 2019, 9, 1355–1373. [Google Scholar] [CrossRef]
- Rashidi, S.; Mohamadian, N.; Ghorbani, H.; Wood, D.A.; Shahbazi, K.; Alvar, M.A. Shear modulus prediction of embedded pressurized salt layers and pinpointing zones at risk of casing collapse in oil and gas wells. J. Appl. Geophys. 2020, 183, 104205. [Google Scholar] [CrossRef]
- Zhang, G.; Lu, P.; Luo, P.; Sonnenthal, E.; Huang, Y.; Zhu, C. Effects of natural gas acidic components on local porosity generation in a carbonate reservoir: Insights from reactive transport modeling. AAPG Bull. 2019, 103, 2975–3001. [Google Scholar] [CrossRef]
- Reynolds, S.J.; Lister, G. Structural aspects of fluid-rock interactions in detachment zones. Geology 1987, 15, 362–366. [Google Scholar] [CrossRef]
- Conaway, J.G.; Bristow, Q.; Killeen, P.G. Optimization of gamma-ray logging techniques for uranium. Geophysics 1980, 45, 292–311. [Google Scholar] [CrossRef]
- Dahlberg, E.C. Formation Pressure Measurements and Data. In Applied Hydrodynamics in Petroleum Exploration; Dahlberg, E.C., Ed.; Springer: New York, NY, 1995; pp. 15–33. [Google Scholar]
- Stunes, S.D. Methods of Pore Pressure Detection from Real-time Drilling Data. Master’s Thesis, Norwegian University of Science and Technology, Ålesund, Norway, 2012. [Google Scholar]
- Adali, F.; Dosunmu, A.; Oriji, A. Real Time Optimization Model for Efficient Drilling Operations in the Oil and Gas Industry. Int. J. Sci. Eng. Res. 2020, 8, 38–47. [Google Scholar] [CrossRef]
- Kumar, R.; Al-Saeed, M.A.; Al-Kandiri, J.M.; Verma, N.K.; Al-Saqran, F. Seismic based pore pressure prediction in a West Kuwait field. In Proceedings of the 2010 SEG Annual Meeting, Denver, Colorado, 17–22 October 2010; pp. 2289–2293. [Google Scholar]
- Mahetaji, M.; Brahma, J. Prediction of Minimum Mud Weight for Prevention of Breakout Using New 3D Failure Criterion to Maintain Wellbore Stability. Rock Mech. Rock Eng. 2024, 57, 2231–2252. [Google Scholar] [CrossRef]
- Yao, Q.; Han, D.-H. Effect of Compaction History on Pore Pressure Prediction. In Proceedings of the Beijing 2009 International Geophysical Conference and Exposition, Beijing, China, 24–27 April 2009; Volume 28, pp. 2208–2212. [Google Scholar] [CrossRef]
- Atashbari, V.; Tingay, M. Pore Pressure Prediction in a Carbonate Reservoir. In Proceedings of the SPE Oil and Gas India Conference and Exhibition, Mumbai, India, 28–30 March 2012; Volume 1. [Google Scholar] [CrossRef]
- Eaton, B.A. Graphical method predicts geopressures worldwide. World Oil 1976, 183, 100–104. [Google Scholar]
- Manandhar, S.; Shrestha, U.; Yasufuku, N.; Omine, K.; Kobayashi, T. Safe bearing capacity evaluation of the bridge site along Syafrubesi-Rasuwagadhi road, Central Nepal. Bull. Dep. Geol. 2009, 12, 95–100. [Google Scholar] [CrossRef]
- Guo, Z.-H.; Lin, Y.-P. Selection of Normal Compaction Trend Line for Abnormal High Pressure Reservoirs in Fergana Basin. In Proceedings of the 8th International Field Exploration and Development Conference, IFEDC 2019, Chengdu, China, 16–18 October 2019; pp. 2076–2082. [Google Scholar]
- Shibo, H.; Wujun, J. Logging evaluation method for pore pressure of shale gas reservoirs-taking fuling area, Sichuan basin as an example. Open Pet. Eng. J. 2015, 8, 350–353. [Google Scholar] [CrossRef]
- Qiang, W.; Yaoting, L.; Gang, G.; Zhixian, G.; Zhendong, W.; Jiaqi, L. Research on Formation Pressure Prediction Method for Ultra-Deep Tight Sandstone Based on Collocated Cokriging. Process 2023, 11, 2010. [Google Scholar] [CrossRef]
- Kablan, O.A.B.K.; Chen, T. Shale Gas Reservoir Pore Pressure Prediction: A Case Study of the Wufeng–Longmaxi Formations in Sichuan Basin, Southwest China. Energies 2023, 16, 7280. [Google Scholar] [CrossRef]
- Hamid, O.; Al-Qahtani, A.; Albahrani, H.; Pamukcu, Y. A novel method for predicting 3D pore pressure in over-pressured carbonates. In Proceedings of the SPE Abu Dhabi International Petroleum Exhibition and Conference 2017, Abu Dhabi, United Arab Emirates, 13–16 November 2017. [Google Scholar]
- Shi, H.; Zhou, D.; Lu, D. Application of formation pressure prediction based on effective stress in Bohai BZ1 area. Pet. Geol. Eng. 2014, 28, 113–115. (In Chinese) [Google Scholar] [CrossRef]
- Eaton, B.A.; Eaton, T.L. Fracture gradient prediction for the new generation. SPE Repr. Ser. 1999, 49, 108–112. [Google Scholar]
- Oloruntobi, O.; Butt, S. The new formation bulk density predictions for siliciclastic rocks. J. Pet. Sci. Eng. 2019, 180, 526–537. [Google Scholar] [CrossRef]
- Tingay, M.R.P.; Hillis, R.R.; Swarbrick, R.E.; Morley, C.K.; Damit, A.R. Origin of overpressure and pore-pressure prediction in the Baram province, Brunei. AAPG Bull. 2009, 93, 51–74. [Google Scholar] [CrossRef]
- Osarogiagbon, A.U.; Oloruntobi, O.; Khan, F.; Venkatesan, R.; Gillard, P. Combining porosity and resistivity logs for pore pressure prediction. J. Pet. Sci. Eng. 2021, 205, 108819. [Google Scholar] [CrossRef]
- Li, H.; Tan, Q.; Deng, J.; Dong, B.; Li, B.; Guo, J.; Zhang, S.; Bai, W. A Comprehensive Prediction Method for Pore Pressure in Abnormally High-Pressure Blocks Based on Machine Learning. Processes 2023, 11, 2603. [Google Scholar] [CrossRef]
- Zhang, J. Effective stress, porosity, velocity and abnormal pore pressure prediction accounting for compaction disequilibrium and unloading. Mar. Pet. Geol. 2013, 45, 2–11. [Google Scholar] [CrossRef]
- López, J.L.; Rappold, P.M.; Ugueto, G.A.; Wieseneck, J.B.; Vu, C.K. Integrated shared earth model: 3D pore-pressure prediction and uncertainty analysis. Lead. Edge 2004, 23, 52–59. [Google Scholar] [CrossRef]
- Liu, L.; Shen, G.; Wang, Z.; Yang, H.; Han, H.; Cheng, Y. Abnormal formation velocities and applications to pore pressure prediction. J. Appl. Geophys. 2018, 153, 1–6. [Google Scholar] [CrossRef]
- Cheng, Y. Wellhead Stability during Development Process of Hydrate Reservoir in the Northern South China Sea: Evolution and Mechanism. Processes 2024, 13, 40. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Cao, H.; Wu, J.; Wang, F.; Wang, Y. The Crack Propagation Behaviour of CO2 Fracturing Fluid in Unconventional Low Permeability Reservoirs: Factor Analysis and Mechanism Revelation. Processes 2025, 13, 159. [Google Scholar] [CrossRef]
- Atashbari, V.; Tingay, M. Pore Pressure Prediction in Carbonate Reservoirs. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Mexico City, Mexico, 16–18 April 2012. [Google Scholar]
- Deng, S.; Fan, H.; Liu, Y.; He, Y.; Zhang, S.; Yang, J.; Fu, L. Two innovative pore pressure calculation methods for shallow deep-water formations. J. Appl. Geophys. 2017, 146, 208–213. [Google Scholar] [CrossRef]
- Osorio, J.G.; Muzzio, M. Correlation Between Microseismicity and Geomechanics Factors Affecting the Hydraulic Fracturing Performance in Unconventional Reservoirs—A Field Case in Neuquén, Argentina. In Proceedings of the 47th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 23–26 June 2013; pp. 1990–2002. [Google Scholar]
- Hutomo, P.S.; Rosid, M.S.; Haidar, M.W. Pore Pressure Prediction Using Eaton and Neural Network Method in Carbonate Field “X” Based on Seismic Data. IOP Conf. Ser. Mater. Sci. Eng. 2019, 546, 17–32. [Google Scholar] [CrossRef]
- LIU, Z.; Tang, X. On Predicting Formation Pore Pressure Method of Volcanic Rock with Log Data. Well Logging Technol. 2011, 3, 568–571. (In Chinese) [Google Scholar] [CrossRef]
- Luo, C.; Li, j.; Li, Z.; Zhang, D.; Tong, K.; Dai, Y.; Hu, X. Structural deformation characteristies and formation processof Luzhou Block in Sichuan Basin, China. J. Chengdu Univ. Technol. (Sci. Technol. Ed. ) 2022, 49, 665–673. (In Chinese) [Google Scholar] [CrossRef]
- Fan, C.; Nie, S.; Li, H.; Radwan, A.E.; Pan, Q.; Shi, X.; Li, J.; Liu, Y.; Guo, Y. Quantitative prediction and spatial analysis of structural fractures in deep shale gas reservoirs within complex structural zones: A case study of the Longmaxi Formation in the Luzhou area, southern Sichuan Basin, China. J. Asian Earth Sci. 2024, 263, 106025. [Google Scholar] [CrossRef]
- Jing, C. Pressure Predicting Methods Based on Overpressure Genetie Mechanisms and Its Application. Well Logging Technol. 2018, 42, 460–465. (In Chinese) [Google Scholar] [CrossRef]
- Eaton, B.A. The Effect of Overburden Stress on Geopressure Prediction from Well Logs. J. Pet. Technol. 1972, 24, 929–934. [Google Scholar] [CrossRef]
- Radwan, A.E. A multi-proxy approach to detect the pore pressure and the origin of overpressure in sedimentary basins: An example from the Gulf of Suez rift basin. Front. Earth Sci. 2022, 10, 967201. [Google Scholar] [CrossRef]
- Keshavarzi, R.; Jahanbakhshi, R.; Rashidi, M. Predicting Formation Fracture Gradient In Oil And Gas Wells: A Neural Network Approach. In Proceedings of the 45th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011; p. ARMA–11-114. [Google Scholar]
- Rizvi, A.; Saleh, S.T.; Williams, K. Automating Pore-Pressure Prediction in Subsalt Sediments. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2013; p. OTC–24159-MS. [Google Scholar]
- Xu, Y.; Pang, X.; Hu, T.; Xu, T.; Zheng, X. Seleetion of Formation Pressure Predietion Methods Based on Mudstone interval Transit Time. Spec. Oil Gas Reserv. 2018, 25, 46–50. (In Chinese) [Google Scholar] [CrossRef]
- Hossein, M.; Ali, R.M. A nonlinear approach for predicting pore pressure using genetic algorithm in one of the Iranian petroleum carbonate reservoirs. Arab. J. Geosci. 2020, 13, 688. [Google Scholar] [CrossRef]
- Xu, Y.; He, B.; Yang, L. Prediction Method of Formation Pore Pressure Driven by the Coupling of Depth Learning and Eaton Method. In Proceedings of the Computational and Experimental Simulations in Engineering, Shenzhen, China, 26–29 May 2023; pp. 89–102. [Google Scholar]
- Liang, H.; Fan, H.; Jia, L.; Wang, Y. New method of formation pore pressure detection by interval transit time. Oil Drill. Prod. Technol. 1998, 20, 1–5+110. (In Chinese) [Google Scholar] [CrossRef]
- Carcione, J.M.; Gei, D.; Picotti, S.; Qadrouh, A.N.; Alajmi, M.; Ba, J. Rock Acoustics of Diagenesis and Cementation. Pure Appl. Geophys. 2022, 179, 1919–1934. [Google Scholar] [CrossRef]
- Pommer, M.; Milliken, K. Pore types and pore-size distributions across thermal maturity, Eagle Ford Formation, southern Texas. AAPG Bull. 2015, 99, 1713–1744. [Google Scholar] [CrossRef]
- Deneale, S.; Bishop, N.A.; Buetikofer, L.B.; Sisson, R.; Sasthav, C.; Musa, M.; Wilcox, T.; Stewart, K.; Tingen, W.; Derolph, C.R. Hydropower Geotechnical Foundations: Current Practice and Innovation Opportunities for Low-Head Applications; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2020.
- Wang, Z.; Wang, R.; Shan, X.; Zang, Y.; Zhang, R.; Li, M. Uncertainty analysis of pore pressure prediction in carbonate formation using conventional methods. Zhongguo Shiyou Daxue Xuebao (Ziran Kexue Ban)/J. China Univ. Pet. (Ed. Nat. Sci.) 2014, 38, 96–101. [Google Scholar] [CrossRef]
- Cheng, Y.-F.; Shi, X.; Li, L.; Wu, L.-Y.; Mei, W. A novel pore pressure prediction model of carbonate formation with fracture development. Zhongguo Shiyou Daxue Xuebao (Ziran Kexue Ban)/J. China Univ. Pet. (Ed. Nat. Sci.) 2013, 37, 83–87+97. (In Chinese) [Google Scholar] [CrossRef]
- Khoshnevis-zadeh, R.; Hajian, A.; Larki, E. Pore Pressure Prediction and Its Relationship with Rock Strength Parameters and Weight on Bit in Carbonate Reservoirs (A Case Study, South Pars Gas Field). Arab. J. Sci. Eng. 2021, 46, 6939–6948. [Google Scholar] [CrossRef]
- Xia, H.; You, X.; Lin, Z.; Song, Y. Logging calculation for pore pressure on carbonate rock formation based on effectiveness stress method. Drill. Prod. Technol. 2005, 28, 28–30. (In Chinese) [Google Scholar] [CrossRef]

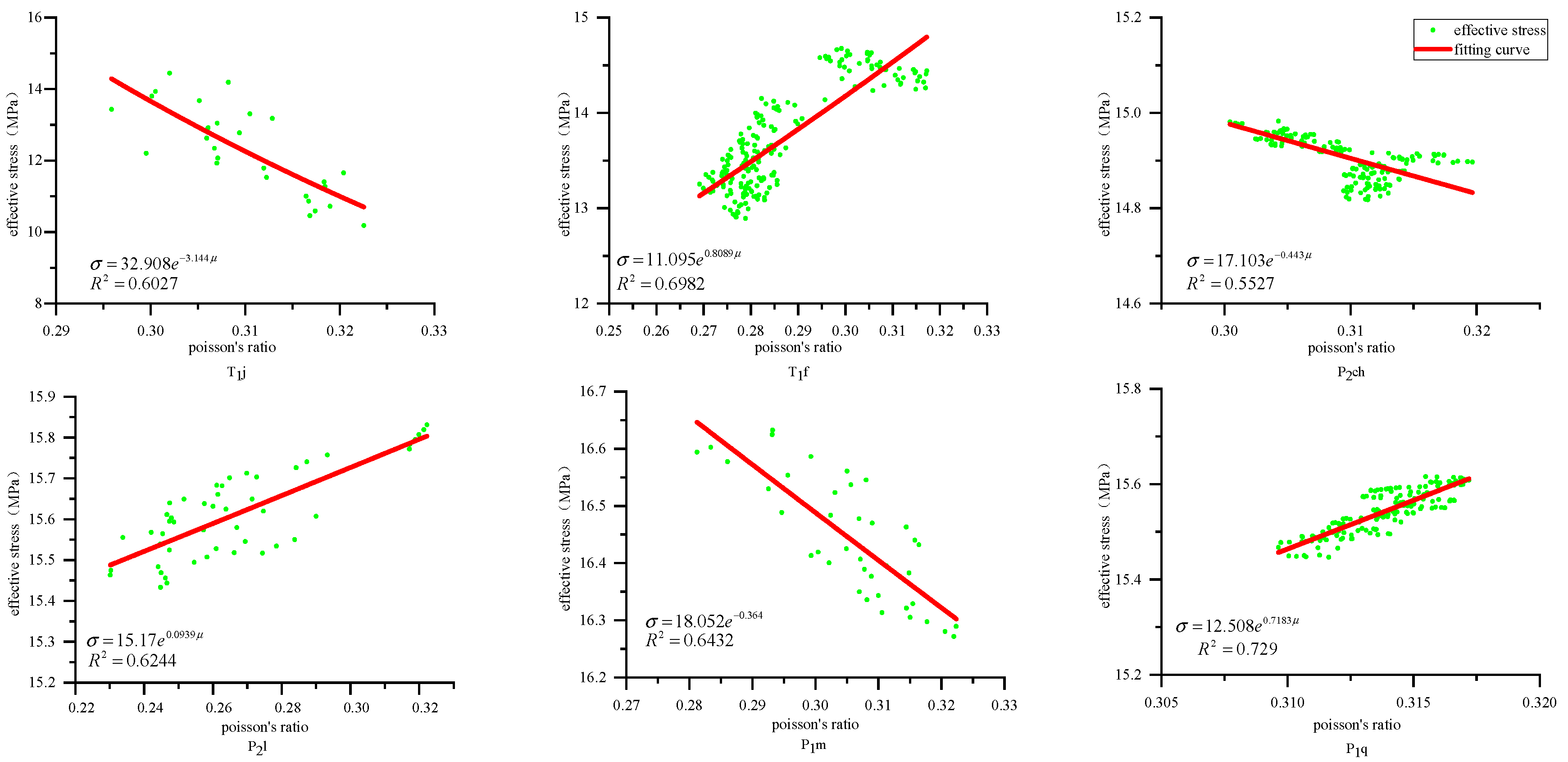
| Depth (m) | Measured Pore Pressure Pp (MPa) | Overburden Pressure P0 (MPa) | Hydrostatic Column Pressure Pg (MPa) | Normal Compaction Acoustic Time (Δtn) | Measured Acoustic Time (Δt) | Inverse Eaton Index “x” |
|---|---|---|---|---|---|---|
| 2171.8 | 36.22 | 54.97 | 21.94 | 46.80 | 68.88 | 1.46 |
| 2642.8 | 47.19 | 67.22 | 26.70 | 40.64 | 66.09 | 1.45 |
| 2810 | 50.17 | 71.57 | 28.39 | 38.65 | 62.50 | 1.46 |
| 3006 | 54.55 | 76.65 | 30.37 | 36.44 | 60.49 | 1.46 |
| 3135 | 57.51 | 80.03 | 31.68 | 35.06 | 58.88 | 1.47 |
| 1832 | 30.55 | 46.16 | 18.51 | 51.83 | 76.94 | 1.45 |
| 2272 | 40.56 | 57.84 | 22.96 | 45.42 | 73.66 | 1.45 |
| 2312 | 41.28 | 58.87 | 23.36 | 44.88 | 72.69 | 1.46 |
| 2427 | 48.09 | 61.79 | 24.52 | 43.35 | 86.28 | 1.45 |
| 2624 | 47.62 | 66.94 | 26.51 | 40.87 | 68.21 | 1.44 |
| 2718 | 49.86 | 69.41 | 27.46 | 39.73 | 67.07 | 1.46 |
| 1750 | 29.01 | 43.17 | 17.68 | 53.12 | 79.57 | 1.45 |
| 2235.9 | 40.58 | 56.16 | 22.59 | 45.91 | 77.93 | 1.45 |
| 2270 | 41.20 | 57.03 | 22.94 | 45.44 | 76.72 | 1.46 |
| 2410 | 43.74 | 60.51 | 24.35 | 43.58 | 74.20 | 1.44 |
| Layer | Fitting Curve |
|---|---|
| T1j | |
| T1f | |
| P2ch | |
| P2l | |
| P1m | |
| P1q |
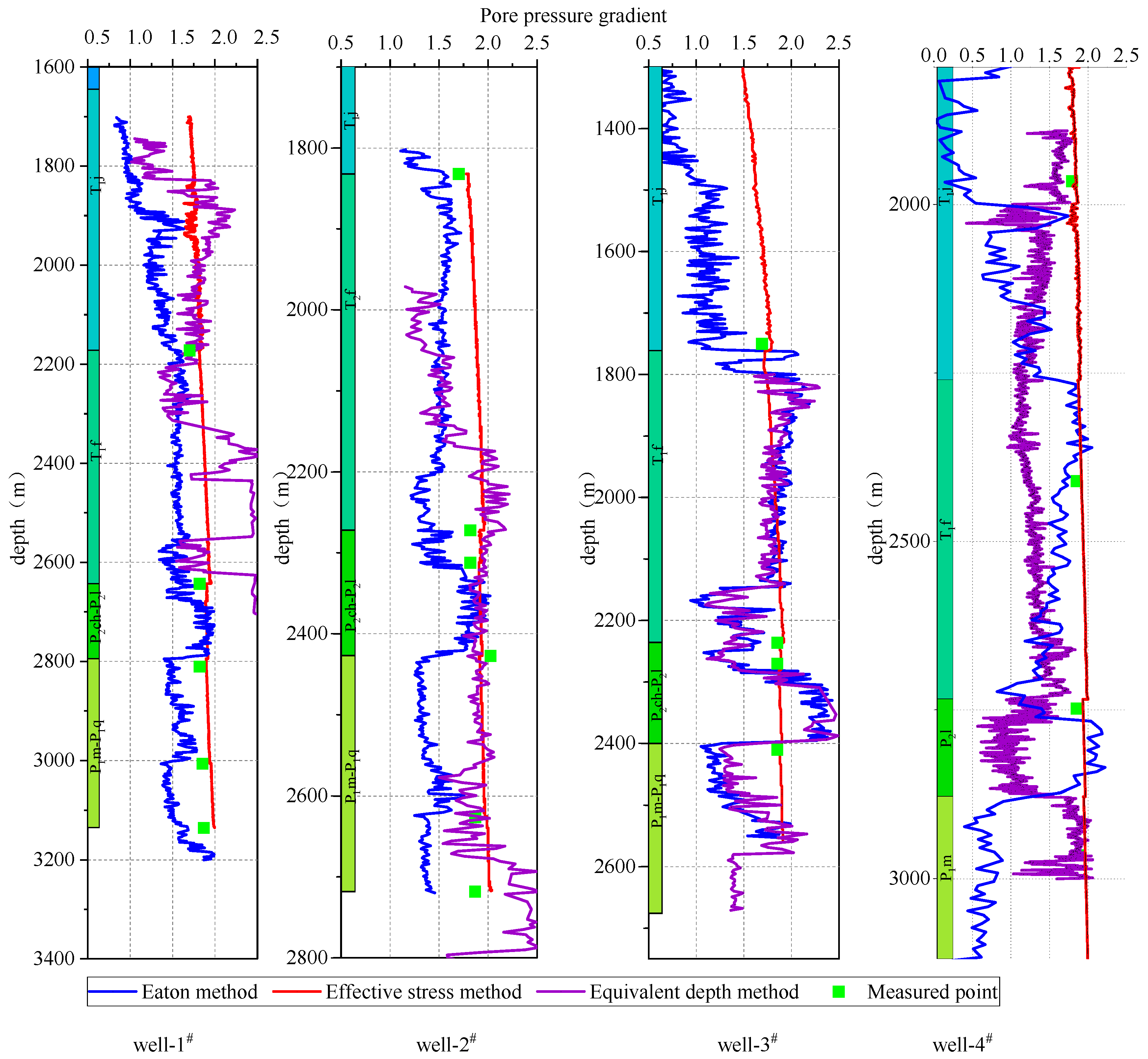
| Well | Depth/m | Measured Pore Pressure Gradient | Prediction of Pore Pressure and Error | |||||
|---|---|---|---|---|---|---|---|---|
| Equivalent Depth Method | Eaton Method | Effective Stress Method | ||||||
| Predicted Value | Error/% | Predicted Value | Error/% | Predicted Value | Error/% | |||
| (Well 1#) | 1832 | 1.70 | 1.95 | 14.6 | 1.57 | 7.8 | 1.8 | 5.6 |
| 2272 | 1.82 | 1.64 | 9.9 | 1.67 | 8.1 | 1.71 | 5.9 | |
| 2312 | 1.82 | 1.5 | 17.7 | 1.59 | 12.6 | 1.91 | 5.1 | |
| 2427 | 2.02 | 2.45 | 21.4 | 2.12 | 4.6 | 1.88 | 7.1 | |
| 2626 | 1.87 | 2.31 | 23.5 | 2.04 | 9.1 | 1.99 | 6.4 | |
| 2718 | 1.87 | 1.81 | 3.2 | 2.12 | 13.2 | 2.03 | 8.4 | |
| (Well 2#) | 2171.8 | 1.70 | 1.86 | 9.1 | 1.50 | 11.6 | 1.80 | 5.8 |
| 2642.8 | 1.82 | 1.55 | 14.6 | 1.71 | 6.1 | 1.94 | 6.6 | |
| 2794.4 | 1.83 | 1.72 | 5.7 | 1.52 | 17.1 | 1.91 | 4.4 | |
| 3006 | 1.85 | 1.53 | 17.1 | 1.63 | 11.9 | 1.95 | 5.3 | |
| 3135 | 1.87 | 2.13 | 13.7 | 1.69 | 9.6 | 1.99 | 6.4 | |
| (Well 3#) | 2235.9 | 1.75 | 1.54 | 11.9 | 1.58 | 9.9 | 1.64 | 6.5 |
| 2281.8 | 1.80 | 1.57 | 12.9 | 1.30 | 27.5 | 1.87 | 3.7 | |
| 2400 | 1.80 | 2.12 | 17.5 | 2.17 | 20.8 | 1.84 | 2.4 | |
| 2581 | 1.80 | 1.87 | 3.7 | 1.43 | 20.7 | 1.83 | 1.8 | |
| (Well 4#) | 1965 | 1.79 | 1.61 | 10.0 | 0.54 | 69.8 | 1.84 | 2.8 |
| 2140 | 1.85 | 1.27 | 31.3 | 1.68 | 9.2 | 1.91 | 3.2 | |
| 2474.5 | 1.85 | 1.34 | 27.5 | 1.28 | 30.8 | 1.93 | 4.3 | |
| 2965 | 1.89 | 1.87 | 1.0 | 0.89 | 52.9 | 1.96 | 3.7 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Luo, P.; Li, Y.; Zhou, J.; Hu, X.; Wang, Q.; He, Y.; Zhang, Y. Comparison and Application of Pore Pressure Prediction Methods for Carbonate Formations: A Case Study in Luzhou Block, Sichuan Basin. Energies 2025, 18, 2647. https://doi.org/10.3390/en18102647
Li W, Luo P, Li Y, Zhou J, Hu X, Wang Q, He Y, Zhang Y. Comparison and Application of Pore Pressure Prediction Methods for Carbonate Formations: A Case Study in Luzhou Block, Sichuan Basin. Energies. 2025; 18(10):2647. https://doi.org/10.3390/en18102647
Chicago/Turabian StyleLi, Wenzhe, Pingya Luo, Yatian Li, Jinghong Zhou, Xihui Hu, Qiutong Wang, Yiguo He, and Yi Zhang. 2025. "Comparison and Application of Pore Pressure Prediction Methods for Carbonate Formations: A Case Study in Luzhou Block, Sichuan Basin" Energies 18, no. 10: 2647. https://doi.org/10.3390/en18102647
APA StyleLi, W., Luo, P., Li, Y., Zhou, J., Hu, X., Wang, Q., He, Y., & Zhang, Y. (2025). Comparison and Application of Pore Pressure Prediction Methods for Carbonate Formations: A Case Study in Luzhou Block, Sichuan Basin. Energies, 18(10), 2647. https://doi.org/10.3390/en18102647