Resource Adequacy and Capital Cost Considerations Pertaining to Large Electric Grids Powered by Wind, Solar, Storage, Gas, and Nuclear

Abstract

The capacity and generation of wind, solar, storage, nuclear, and gas are estimated for large, idealized copper-plate electric grids. Wind and solar penetrations of 30% to 80% are considered together with different storage systems such as vanadium and lithium-ion batteries, pumped hydroelectric, compressed air, and hydrogen. In addition to a baseline dispatchable fleet without wind/solar, two bounding cases with wind/solar are analyzed: one without storage and one where the whole wind/solar fleet is connected to the storage system, hence providing a buffer between the wind/solar fleet and the grid. The reality will likely be somewhere between these bounding cases. The viability of a power grid with a large wind/solar penetration and no storage is not guaranteed but was nonetheless considered to provide a lower-bound capital cost estimate. Overall, the options that rely strongly on wind, solar, and storage could be significantly more capital-intensive than those that rely strongly on nuclear, depending on the amount of storage necessary to ensure grid stability. This is especially true in the long run because wind, solar, and storage assets have shorter lifetimes than nuclear plants and, consequently, need to be replaced more frequently. More analyses (e.g., grid stability and public acceptance) are necessary to determine which option is most likely to provide the path of least resistance to powering a clean, affordable, and reliable grid in a timely manner. Depending on the priorities, the path of least resistance may not necessarily be the one that is less capital intensive.

1. Introduction

Because of decreasing cost and supportive government policies, the deployment of wind turbines and solar photovoltaic (WS) on electric grids is rapidly growing worldwide. To ensure that the supply matches the demand in real time despite WS variability, grid operators must guarantee that there is enough dispatchable back-up power and, possibly, energy storage to smooth out WS variability. How this is achieved impacts significantly capital cost and resource utilization.

In this context, this paper presents some resource adequacy and capital cost considerations regarding the deployment of a large fleet of WS, and grid-scale storage on idealized greenfield power grids. Though simplified, this approach enables useful comparisons highlighting relative differences between options. More specifically, the objective is to highlight the differences in capital cost between power grids relying strongly on WS coupled with grid-scale storage, and power grids relying strongly on nuclear power. To reach this objective, a step-by-step, conceptualized, and rigorous approach is used that enables consistent comparisons of different power grids. The conceptualization of the grids makes it easier to grasp the root causes of the cost differences.

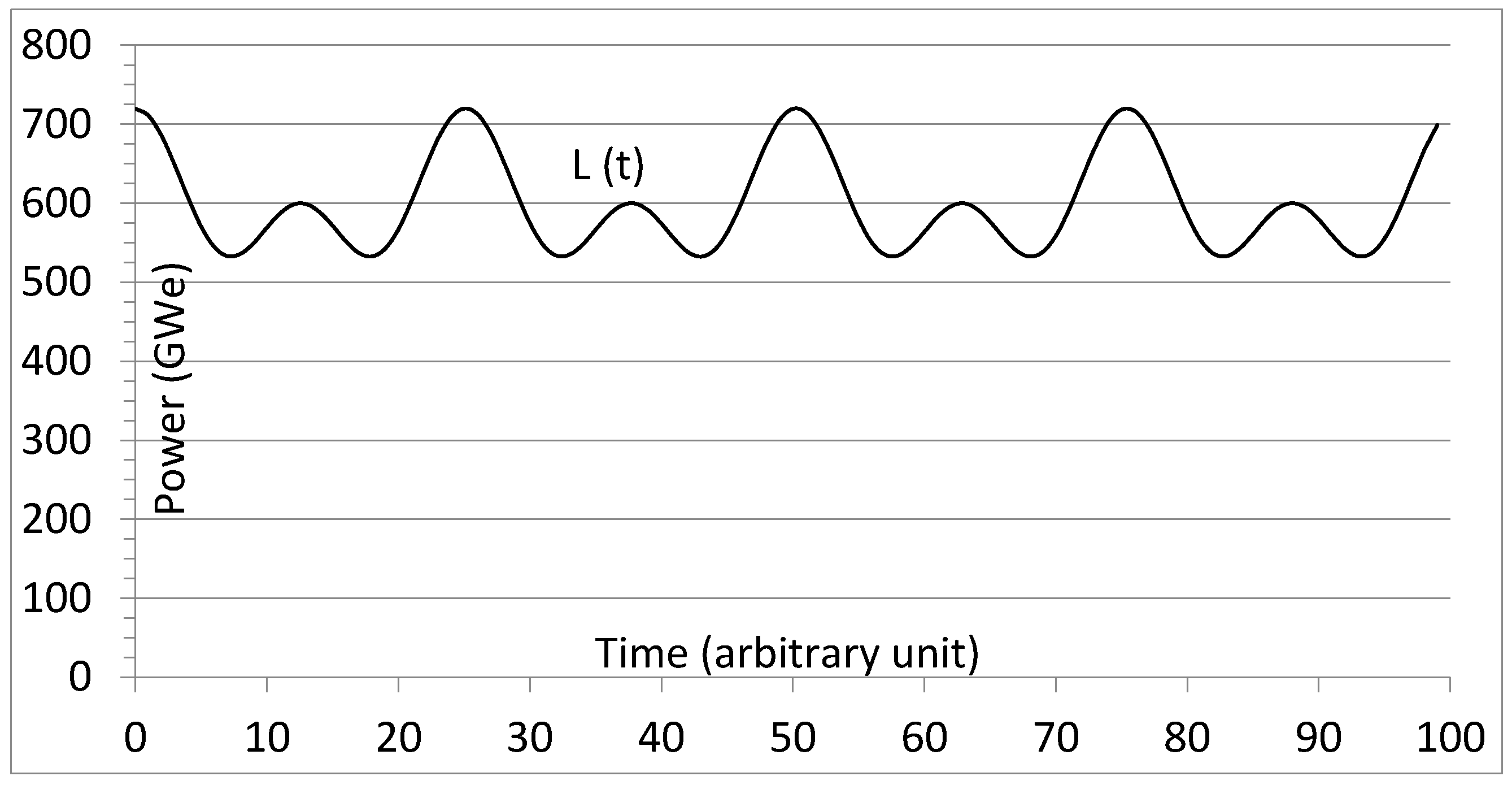
WS penetrations of 30 to 80% are considered. The WS fleets considered are scaled-up versions of the actual U.S. WS fleet, whose characteristics can be found on the U.S. Energy Information Administration (EIA) grid monitor portal. This idealized grid serves a large country, or a group of smaller countries or regions which need between 540 and 720 GW, with an average power of 600 GW (Figure 1).

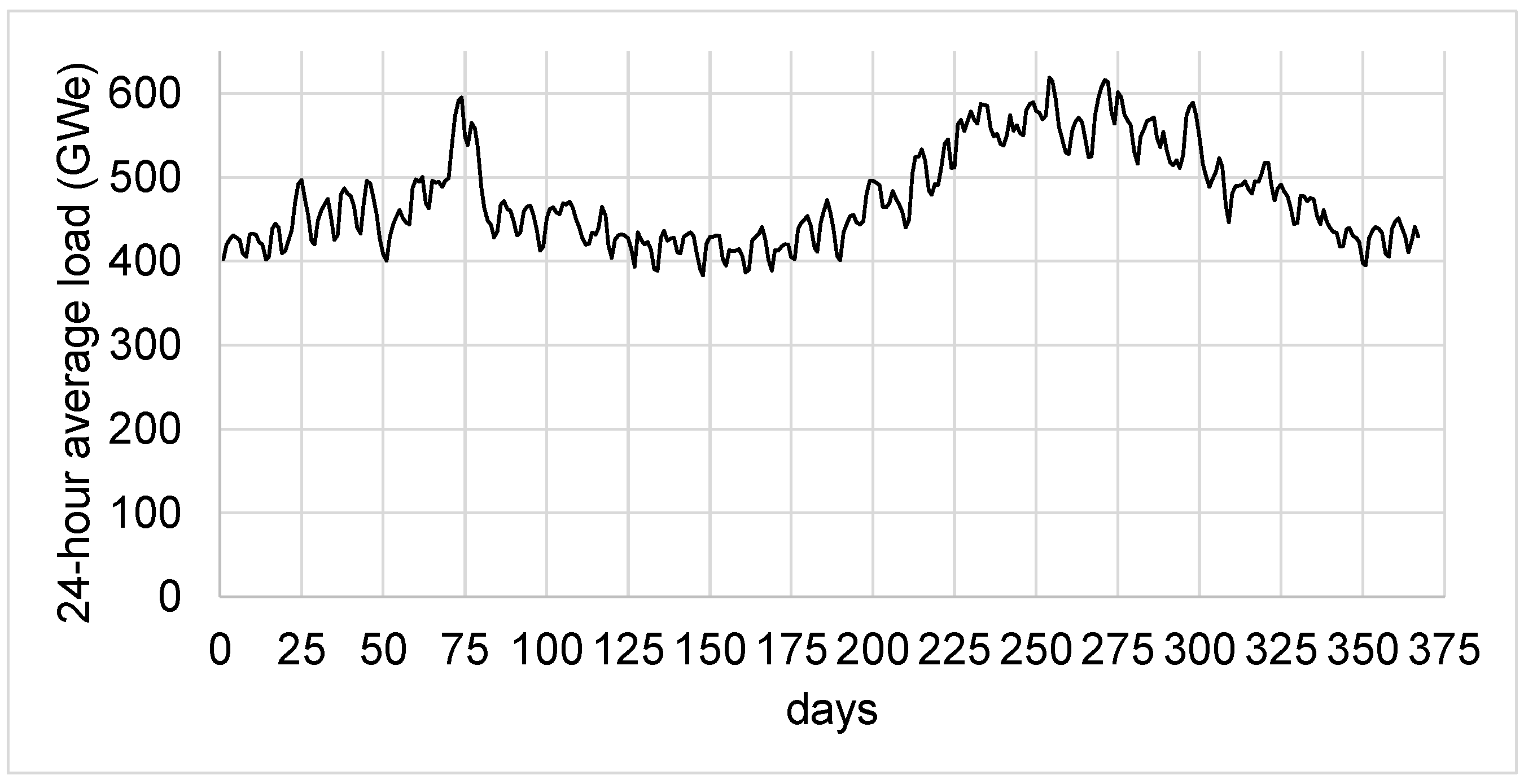
The corresponding annual electricity production is 5256 TWh or, equivalently, 600 GWy. This is about 25% more than what the U.S. currently needs (Figure 2). In its Annual Energy Outlook 2025 Reference Scenario, the EIA expects the U.S. demand to grow to that level by about 2045 [1].

The load, L, satisfies the following expressions:

$$540 \mathrm{G}\mathrm{W}={\mathrm{L}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le \mathrm{L}\left(\mathrm{t}\right)\le {\mathrm{L}}^{\mathrm{m}\mathrm{a}\mathrm{x}}=720 \mathrm{G}\mathrm{W}\mathrm{with} {\int }_{∆\mathrm{T}}\mathrm{L}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}=5256 \mathrm{T}\mathrm{W}\mathrm{h}, ∆\mathrm{T}=1 \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}$$

To simplify the discussion, the idealized grid is fully interconnected and without transmission losses (i.e., copper-plate grid), so that electricity can flow unhampered from high-quality WS locations to high-quality storage locations or directly to distant load centers. Practical WS deployment barriers such as geographical, material, or regulatory limitations were not considered at this point. This is an optimistic assumption and is central to enabling WS to contribute efficiently to the load. It is less important for the deployment of baseload power such as nuclear power plants. An actual grid will require more WS and storage capacity than this idealized grid to reach the same penetration.

Finally, the power system is assumed to be large enough to be considered an isolated system, i.e., supply and demand (i.e., load) must match without having recourse to an outside power grid either to export excess power or import power. The notion of an isolated system is important because it makes it necessary for the system designers and policy makers to fully internalize the consequences of the variability of the WS fleet. The U.S. grid almost satisfies this criterion because the exchanges of electricity with neighboring states (Canada and Mexico) are small compared to the electricity generated from within.

2. Baseline: No Wind, No Solar PV, Only Dispatchable Power

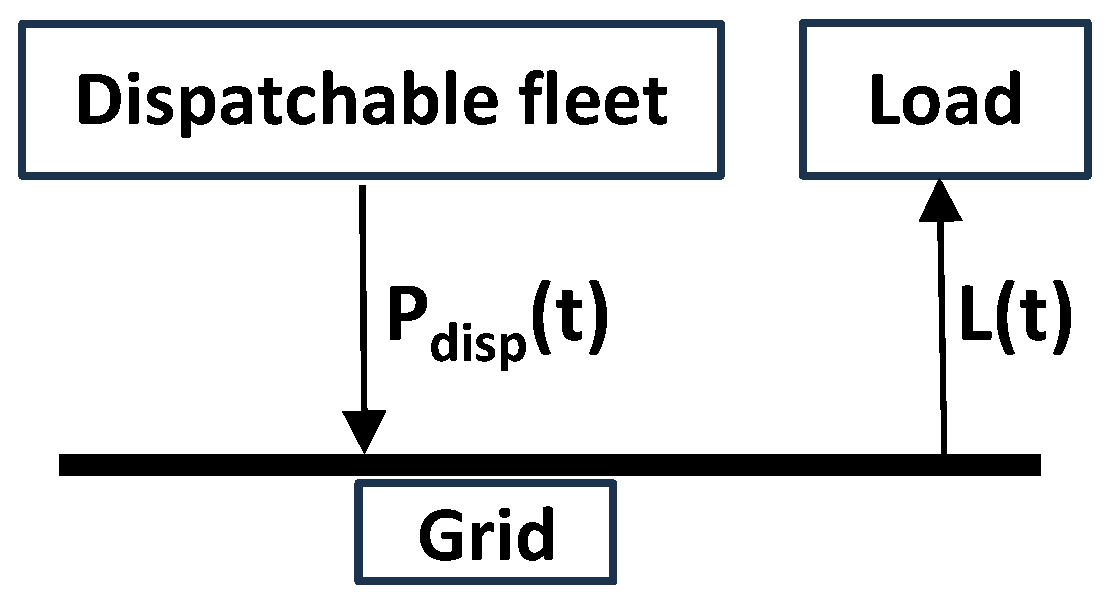
In the reference case, the load is met only with dispatchable thermal power generation such as fossil (coal and natural gas), nuclear, hydroelectric, or geothermal (Figure 3).

The power generated by the dispatchable fleet must satisfy the following in real time:

$${\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)=\mathrm{L}\left(\mathrm{t}\right)\mathrm{with} {\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)={\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}\times {\mathrm{a}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)\times {\mathrm{f}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)={\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}\times {\mathrm{c}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)$$

${\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ is the dispatchable nameplate capacity (the maximum power it can deliver to the grid), ${\mathrm{a}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)$ is the availability function at time t (fraction of the fleet that is available to generate power and not shut down because of planned or unplanned outages), and ${\mathrm{f}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)$ is the load-following function at time t (the fraction of the available fleet called on by the grid to deliver power). Availability factors depend on a range of factors such as the type of technology and how the plant operates. As a first approximation, it is assumed that, on average over any given year, the dispatchable power plants are unavailable 15% of the time and can generate their nominal power the rest of the time if needed. In other words, the yearly average of ${\mathrm{a}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)$ is 0.85. This is a reasonable assumption that could be revisited later to refine the results of the analysis. The load-following function ${\mathrm{f}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)$ is equal to 1 for baseload plants and varies between 0 and 1 for load-following plants. The instantaneous capacity factor of the dispatchable fleet, ${\mathrm{c}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)$, is equal to ${\mathrm{a}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)\times {\mathrm{f}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)$. With these assumptions, the yearly average capacity factor is 0.85 for baseload plants and less than 0.85 for load-following plants. Actual yearly average capacity factors for different technologies can be found, for example, in reference [2] (Table 4.8A).

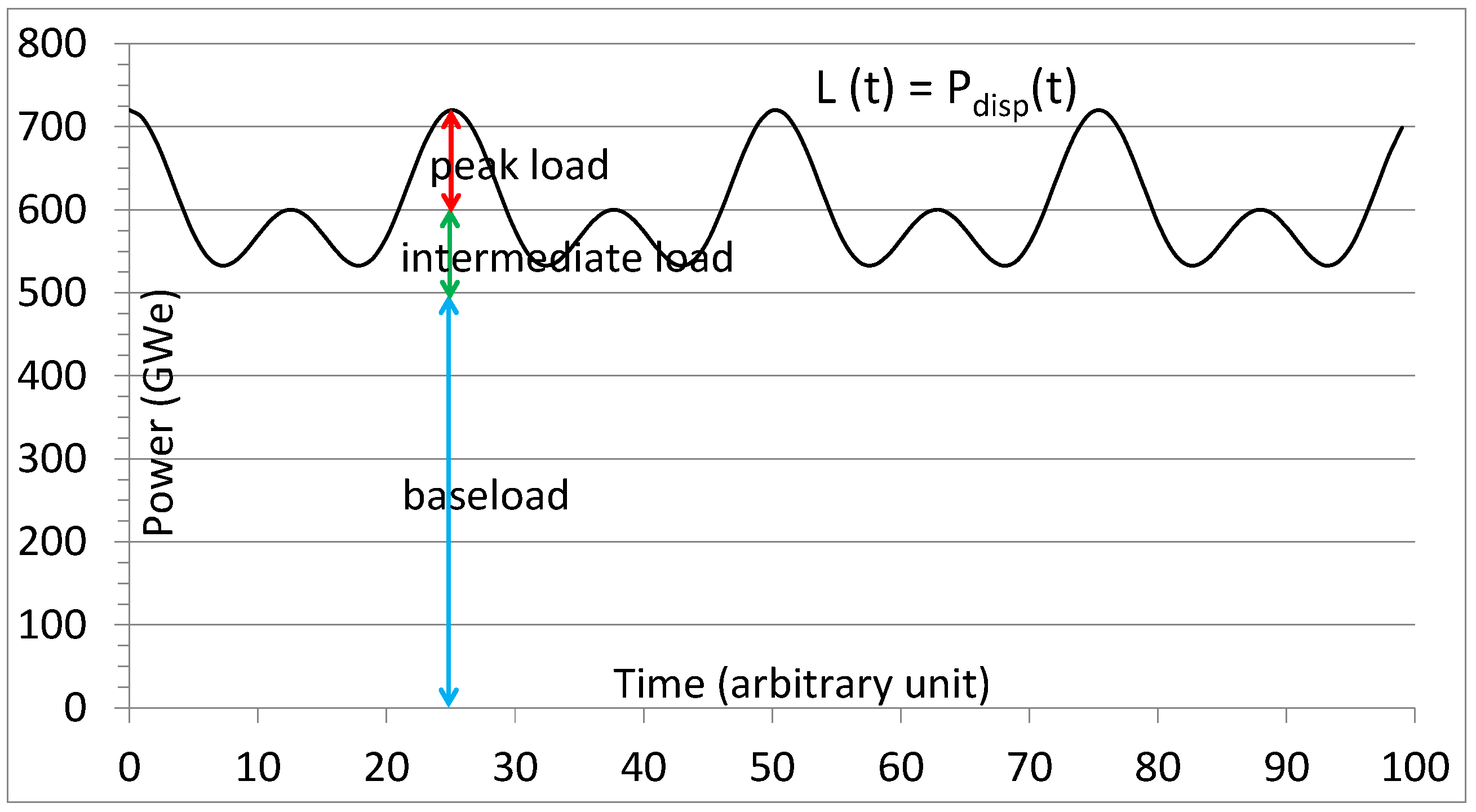
At $\mathrm{t}$ = ${\mathrm{t}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$, when the load is at its maximum, ${\mathrm{f}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left({\mathrm{t}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$ is, by definition, equal to 1 for all the power plants, i.e., ${\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left({\mathrm{t}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)={\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}\times {\mathrm{a}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left({\mathrm{t}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)=\mathrm{L}\left({\mathrm{t}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)=720 \mathrm{G}\mathrm{W}$. If, as a first approximation, ${\mathrm{a}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left({\mathrm{t}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$ is substituted by the average ${\mathrm{a}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)$ value, i.e., 0.85, then ${\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}=720/0.85=847 \mathrm{G}\mathrm{W}$.

Under these assumptions, 847 GW of dispatchable plants (${\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$) are necessary to ensure that the 720 GW peak load is covered with sufficient confidence. In practice, more detailed analyses are of course necessary to determine the size of the fleet needed to meet the appropriate grid reliability criteria. As already mentioned, the load is assumed to vary between 540 and 720 GW with an average of 600 GW. One part of the fleet operates as baseload while the other follows the load. For instance, 588 GW of baseload plants could cover the load up to 500 GW (500/0.85) and 259 GW of load-following plants between 500 and 720 GW (220/0.85) (see Figure 4).

The CO₂ emission of a dispatchable fleet depends on the proportions of fossil fuel generation (coal, gas) and CO₂-free generation (e.g., hydro, nuclear, geothermal). Overnight capital costs estimated by the U.S. EIA, natural resource consumption of coal, gas and nuclear power plants are shown in

Table 1. Thermal power plants’ characteristics.

Natural Resource	Techno.	Lifetime (Years)	Net Efficiency (%) [4]	Nat. Resource Consumption (MT A/GWy)	Overnight Cap. Cost [4] (USD B/GW)	Capital Cost Over 60 yrs (USD B/GW/60 y)
Coal	USC B	50	39.5	3.4 million	4.1	4.9
Gas	CT C/CC D	35	37.3/54.4	1.8/1.2 million	0.84/0.92 E	1.4/1.6 E
Uranium	PWR F	60	32.2	150–210 G	7.9	7.9

(^A) Metric Ton = 1000 kg. (^B) Ultra-supercritical. (^C) Combustion turbine, single cycle. (^D) Combined cycle. (^E) The average values are considered for the cost estimations in the next sections, i.e., USD 0.88 B/GW and USD 1.5 B/GW/60 y. (^F) Large pressurized water reactor (PWR), such as, for example, the AP1000 [5]. (^G) U enrichment = 4.95%, average fuel burnup at discharge = 55–60 MWd/kg [6], U tail enrichment = 0.10–0.25%.

. The lifetime of combined-cycle gas power plants is nominally 25–30 years, but many operators intend to extend it to 40–45 years [3]. A lifetime of 35 years was considered for gas power plants. Nuclear power plants are expected to operate for at least 60 years and modern coal power plants for 50–60 years.

To account for the lifetimes of each technology, capital costs necessary for 60 years of operation are also presented in Table 1, assuming a zero discount rate and no credit for potential recycling of systems and components with lifetimes shorter than 60 years. The rationale for using a zero discount rate is presented in the next section. Sixty years of operation was chosen as a useful benchmark because it corresponds to the longest asset lifetime, i.e., that of nuclear plants. With this approach, the capital cost expenditure over 60 years is simply the initial capital cost multiplied by [60 years ÷ asset lifetime]. For example, if an asset has a lifetime of 30 years and an overnight capital cost of USD 1.5 B/GW, the estimated capital cost expenditure over 60 years is USD 3.0 B/GW/60 y. This simplified approach has the benefit of providing a lower and upper estimate of the capital cost expenditure with assets having different lifetimes.

If all 588 GW of baseload capacity is provided by nuclear power plants, and all 259 GW of load-follow from gas power plants, the grid is 83% CO₂-free and the capital cost is USD 4.9 T, i.e., USD 5.0 T/60 y (

Table 2. Installed capacity and annual electricity generation of the reference dispatchable-only fleet.

	Capacity (GW)	Gene (GWy)
Baseload (nuclear)	588	500
Load-follow (gas)	259	100
Total fleet	847	600
% CO2-free	83
Initial capital cost (USD T)	4.9
60-year capital cost (USD T/60 y)	5.0

). This dispatchable fleet provides a useful benchmark to compare the other fleets with. Most importantly, this dispatchable low-CO₂ fleet provides a reference point to determine whether less capital-intensive fleets are possible by introducing WS and storage. It is noteworthy that, for the past 40 years, the feasibility of a grid relying strongly on nuclear has been consistently demonstrated at scale in one of the largest world economies, France. However, it is also true that some countries have been experiencing difficulties deploying nuclear power plants on time and on budget.

3. The Zero Discount Rate Rationale

The analysis in this example assumes a reference discount rate of zero for three reasons. First, because the purpose of the example is to focus on resource utilization and not financial consequences to a specific entity, the analysis is ownership agnostic so that the insights do not reflect a particular ownership regime. Second, the cost data used in the analysis, obtained from the U.S. Department of Energy, is the overnight cost of capital for each evaluation alternative. Third, the analysis is projected over a sufficiently long time horizon such that a non-zero discount rate would obfuscate the resource utilization impact. To illustrate this point, a couple cases will also be evaluated with a 7% discount rate.

Assuming a non-zero discount rate implies subjective value in the concept of the time value of money, which is not the intent of the example. If discounting is applied and the time value of money represented, then one must decide whose value is to be represented. The choice of which discount rate should be applied in an analysis is a topic of considerable debate in the literature [7]. Economic reasoning suggests that identifying the purpose of the discount rate is a necessary but not sufficient condition [8]. For example, discounting public sector investments requires different assumptions than those underlying the discount rate choice for private sector investments [9]. Discounting in the private sector using the notion of weighted average cost of capital (WACC) requires different assumptions than discounting for public investments. Ramsey’s seminal work identified that the discount rate is a function of time preference and assumptions about future economic growth [10]. Whereas computing the WACC can be made based on assumptions of equity and debt, the public sector discount rate requires assumptions about society [11]. In either private or public sector analysis, the discount rate adjusts cash flows for the effects of financial risk and opportunity cost, neither of these can be identified without defining whose risk and cost.

The second assumption underlying the zero-discount assumption in the paper has to do with the cost data utilized. Overnight cost of capital is the convention adopted to focus on the cost of resource utilization void of financing implications. The analysis utilizes this data to measure the marginal impact of adding the next GW of capacity to the energy system. The cash flow approach is not employed, consequently neither is discounted cash flow analysis because the profile of cash flow is not necessary in the analytical comparison. Instead, the analysis focuses on the marginal impact of installing the next GW of capacity. The monetary units represent the quantity of resources used over the lifetime of the project.

Finally, since the analysis is aimed at resource utilization over a 60-year period, a non-zero discount rate would obscure the total life cycle impact. The literature on climate change identifies the difficulty in choosing the discount rate over long time horizons for exactly this reason. Depending on the aim of the analysis and underlying assumptions, zero-discounting can be appropriate [12].

4. Deploying the WS Fleet Without Storage

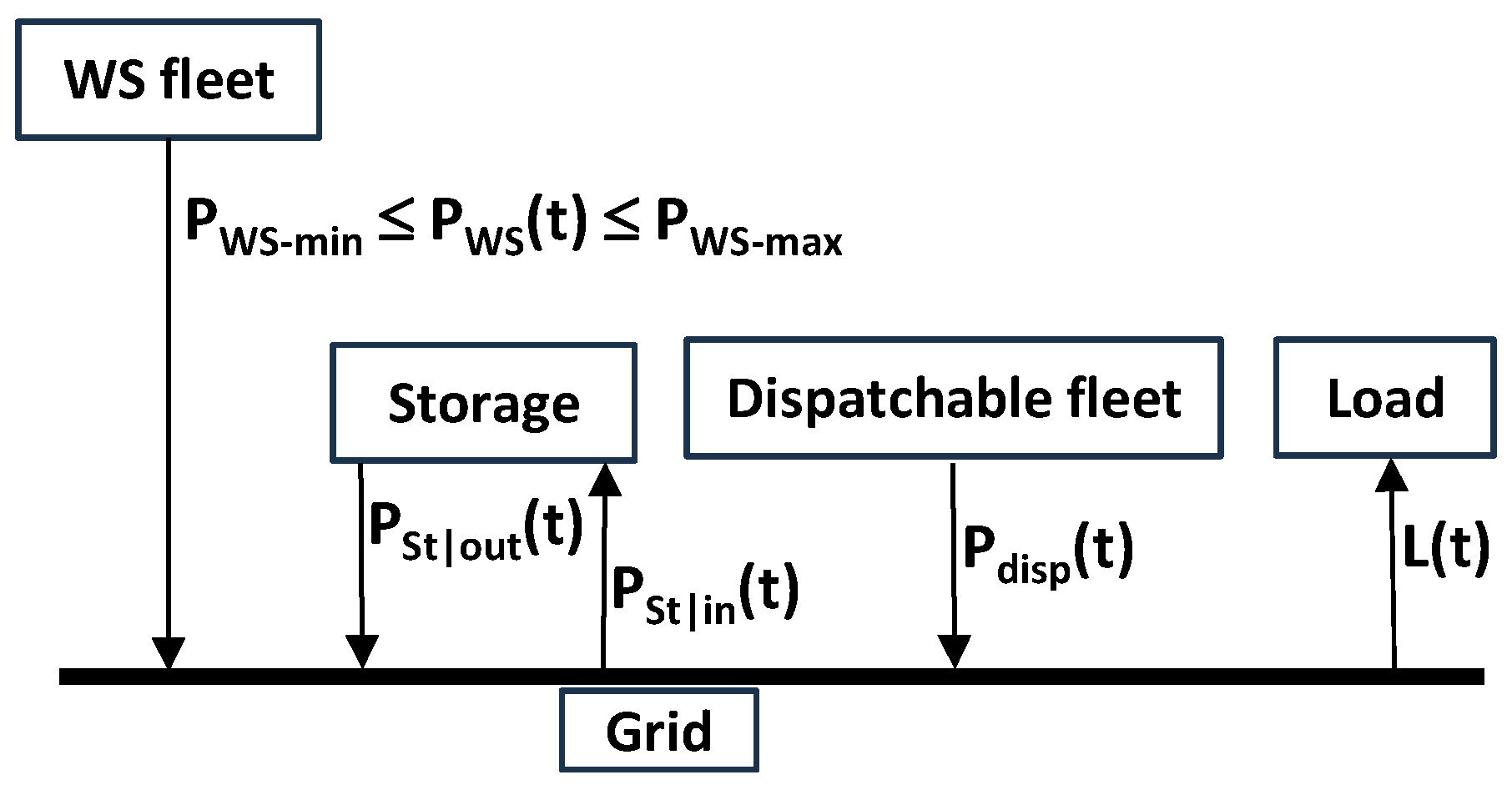
The power generated by the WS and dispatchable fleets (Figure 5) must satisfy the following in real time:

$${\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)=\mathrm{L}\left(\mathrm{t}\right)\mathrm{with} {\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)={\mathrm{a}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)\times {\mathrm{b}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)\times {\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}={\mathrm{c}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)\times {\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$$

${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ is the WS nameplate capacity (the maximum power that it can deliver to the grid), ${\mathrm{a}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$ is the WS fleet availability function (fraction of the WS fleet that is available to generate power and not shut down for maintenance), and ${\mathrm{b}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$ is the fraction of the available WS fleet delivering power to the grid. The instantaneous capacity factor of the WS fleet, ${\mathrm{c}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$, is equal to ${\mathrm{a}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)\times {\mathrm{b}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$. The assumed yearly average capacity factor of the WS fleet is 30%, analogous to that of the actual U.S. WS fleet (in 2023, the yearly average capacity factors of the ~150 GW wind fleet and of the ~125 GW solar PV fleet were 33% and 23%, respectively) [2] (Table 4.8B).

$$0\le {\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le {\mathrm{c}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)\le {\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}\le 1 \mathrm{with\; an\; assumed\; yearly\; average\; equal\; to}$$

$${\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}={\int }_{∆\mathrm{T}}[{\mathrm{c}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)/∆\mathrm{T}]\mathrm{d}\mathrm{t}=0.30 (∆\mathrm{T}=1 \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r})$$

In other words, ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}={\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}\times {\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$, ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}={\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\times {\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$, and ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}={\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}\times {\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$.

Grid stability aspects are not explicitly treated here, but it is important to note that the viability of a power grid with a large WS penetration and no storage is not guaranteed. The reason is that ensuring that the power delivered by the dispatchable fleet, ${\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)$, matches the residual load, $\mathrm{L}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$, in real time is more challenging than just ensuring that it matches the actual load, $\mathrm{L}\left(\mathrm{t}\right)$, as for the reference case without WS. The no-storage cases were nonetheless considered to provide lower-bound capital cost estimates.

The assumed yearly average capacity of our WS fleet is 30%. This could be, for example, a WS fleet with equal installed capacity of wind and solar where ${\mathrm{c}}_{\mathrm{W}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ = 0.35 and ${\mathrm{c}}_{\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ = 0.25. The estimated lifetime of both wind turbines and PV systems is about 30 years [13,14]. Capital cost is about USD 1.5 B/GW for both PV and onshore wind turbines [4]. Consequently, using the approach described in Section 2, the 60-year capital expenditure is USD 3.0 B/GW/60 y. Note that the cost of PV and onshore wind turbines (USD 1.5 B/GW) corresponds to 2024 estimates [4]. It may decrease further with technological advancement.

The extent of ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$ fluctuations, the [${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$–${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$] range, depends on factors such as the location of the WS fleet and its composition (i.e., the respective fractions of wind and solar). This is a crucial attribute of the WS fleet because it strongly impacts the composition and size of the dispatchable fleet needed to ensure an appropriate power supply to the grid. The WS penetrations considered here (30–80%) are larger than the current one (15%). Consequently, the dispatchable fleet needs to accommodate higher ramp rates than is currently the case to compensate for the variability of the WS fleet. This has consequences for the power plants that are not addressed here. It is assumed that the dispatchable fleet will adjust accordingly.

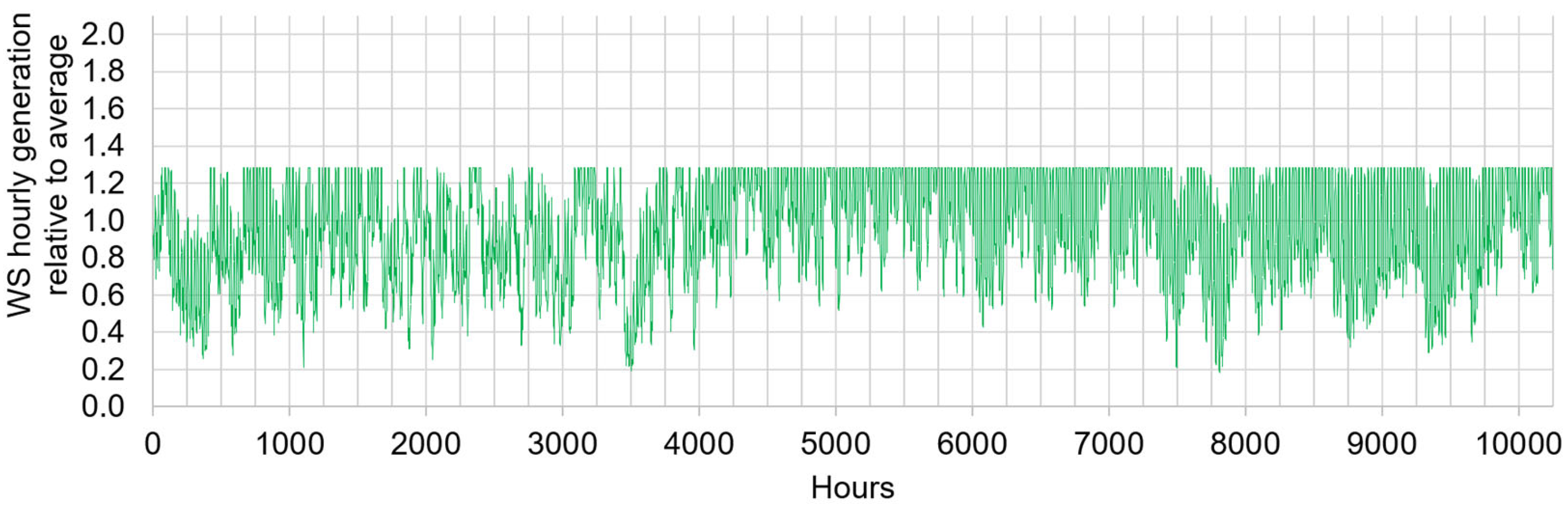
An indication of the potential [${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}–{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$] range can be found in the U.S. electric grid data maintained by the EIA [15]. The data corresponding to the actual U.S. WS fleet between 01 September 2023 and 31 October 2024 is shown in Figure 6. During that time, it produced on average 72 GW (50 GW from W; 22 GW from S) with maximum and minimum hourly averages of 150 GW (18 June 2024 @ 2 p.m. EST) and 13 GW (22 July 2024 @ 7 a.m. EST), respectively. In other words, the maximum and minimum hourly average were 2.1× and 0.18× the average, respectively. Applying these factors to our WS fleet, neglecting the intra-hour fluctuations as a first approximation, the instantaneous capacity factor varies between ${\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ = 0.054 (0.18 × ${\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$) and ${\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ = 0.63 (2.1 × ${\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$). This is of course only a first order approximation as it assumes that every year is similar to our sample year. It does not consider, for example, the long-term impact of changes in extreme weather frequency caused by climate change on the statistical characteristics of wind and solar power output.

As mentioned above, the [${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}–{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$] range has important consequences for the dispatchable fleet. The larger it is, the more baseload it displaces and the larger the ramp rate of the load-following plants is. In this respect, curtailment could be useful to minimize the [${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}–{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$] range. A curtailed WS fleet, WS*, satisfies the following:

$${\int }_{∆\mathrm{T}}{\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}=\mathsf{\alpha }{\int }_{∆\mathrm{T}}{\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t} \mathrm{with} \Delta T ~1 \mathrm{year}$$

$$\mathrm{with} {\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }\left(\mathrm{t}\right)={\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)\mathrm{when} {\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)<\mathsf{\beta }{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$$

$$\mathrm{and} {\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }\left(\mathrm{t}\right)=\mathsf{\beta }{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}\mathrm{when} {\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)\ge \mathsf{\beta }{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$$

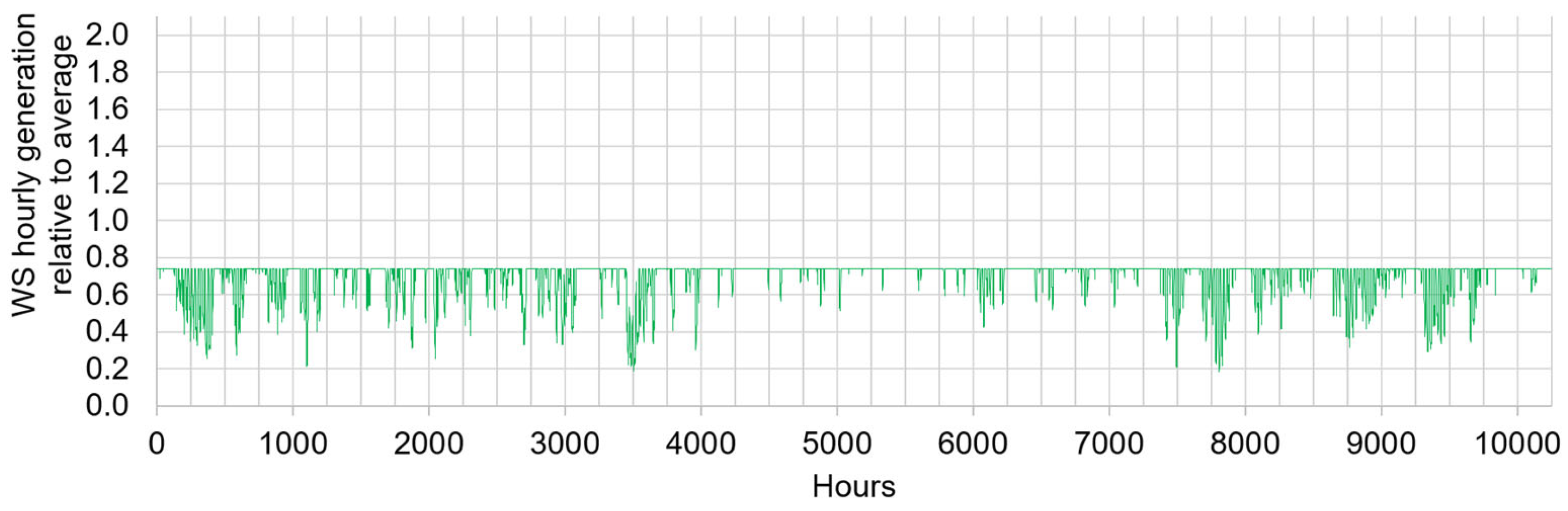
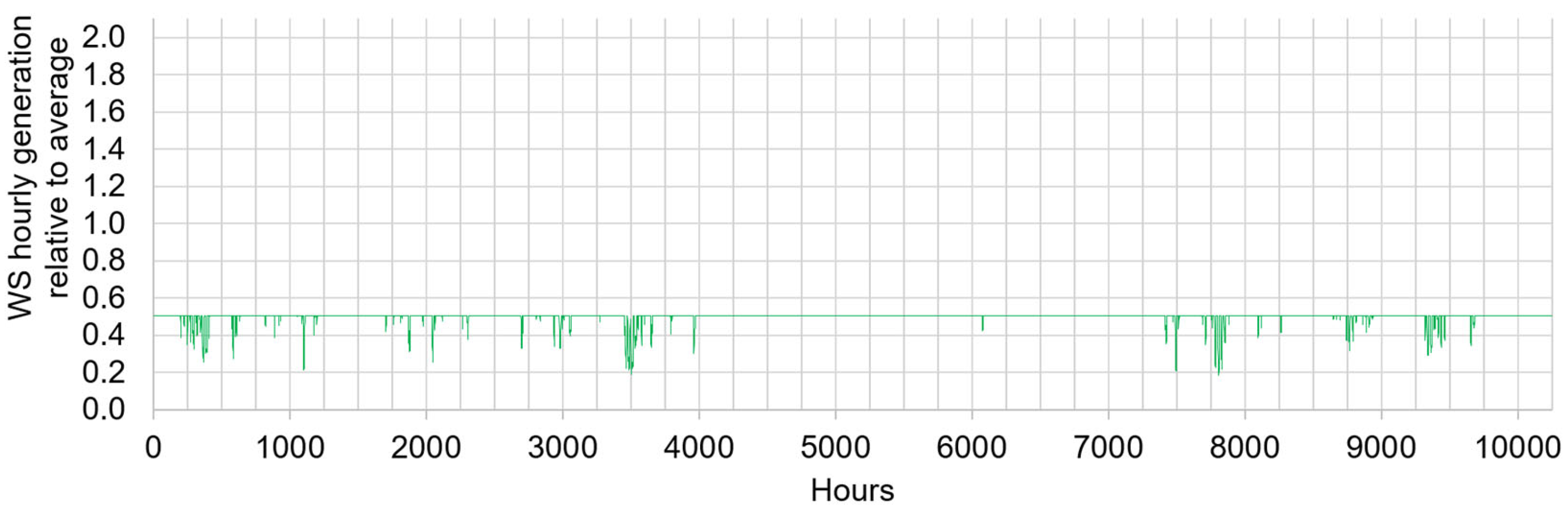
The α/β couples obtained from the reference U.S. WS data are shown in Figure 7. For example, the couple 0.95/1.3 satisfies the equations above. In other words, if the reference U.S. WS fleet was curtailed when its power exceeded 1.3${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$, it would still deliver to the grid 95% of the electricity generated by the reference, non-curtailed fleet. The [${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}–{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$] range is reduced by 42% ([1.3 − 0.18] ÷ [2.1 − 0.18]) compared to that of the non-curtailed case for a 5% loss of generation. The time series corresponding to three curtailed WS* fleets are shown in Figure 8, Figure 9 and Figure 10 as examples.

It is noteworthy that the WS* power delivered to the grid becomes more predictable as the level of curtailment increases. For example, ${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }\left(\mathrm{t}\right)$ equals $1.3{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ 22% of the time when the curtailment threshold is $1.3{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$. When the curtailment threshold is $0.74{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$, ${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }\left(\mathrm{t}\right)$ equals ${0.74\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ 75% of the time. And when the curtailment threshold is ${0.51\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$, ${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }\left(\mathrm{t}\right)$ equals $0.51{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ 93% of the time. The benefits of increased predictability should be weighed against the energy lost due to curtailment. Ideally, the energy generated by the WS fleet when it exceeds the grid curtailment threshold would be used for off-grid applications better suited to cope with large power fluctuations, assuming such applications exist.

5. Deploying the WS Fleet with Storage

The energy storage systems of interest should be scalable to 100 s of GW. The whole WS fleet is assumed to be connected to it, as illustrated in Figure 11.

The energy storage system acts as a buffer, or integrator, between the WS fleet and the grid. It also contributes to grid stability. Just like curtailment, energy storage mitigates the rate and amplitude of the fluctuations of the power delivered to the grid and, consequently, makes it more predictable. Since curtailment and energy storage both increase predictability, it seems reasonable to expect that a curtailed WS fleet may require less energy storage than a non-curtailed WS fleet to reach the same level of predictability.

The underlying assumption is that, as WS penetration increases, future WS operators will be required to contribute some degree of firmness to the grid by using storage. The degree of firmness increases with the storage duration as well as with the curtailment level. The round-trip efficiency (RTE) of a storage system is defined as the kWh-out/kWh-in ratio. The storage system and the dispatchable fleet satisfy the following requirements:

$${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)=\mathrm{L}\left(\mathrm{t}\right)$$

$$\mathrm{with} {{\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le {\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)=\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{i}\mathrm{n}}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{and} {\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\right)=\mathrm{R}\mathrm{T}\mathrm{E}\times {\int }_{∆\mathrm{t}}{[\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)/∆\mathrm{t}]\mathrm{d}\mathrm{t}$$

${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{i}\mathrm{n}}\left(\mathrm{t}\right)$ is the power used to charge the storage system; it is equal to ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$. ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\right)$ is the power delivered to the grid by the storage system. Δt is the storage duration (4, 24, and 100 h were considered). ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\right)$ fluctuates less and less as the storage duration increases. In other words, the degree of firmness of the storage system increases with its duration, and, consequently, its ability to replace dispatchable thermal power plants also increases. ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\right)$ is more predictable than ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right),$ and, consequently, it is less challenging to ensure that the power delivered by the dispatchable fleet, ${\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)$, matches $\mathrm{L}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\right)$ in real time than to ensure it matches $\mathrm{L}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$, as when there is no storage.

From an operational standpoint, an important consequence of increased storage duration is that fewer fuel-inefficient fast-ramping load-following single-cycle gas power plants may be needed. Indeed, with storage durations in the 24 to 100 h range, grid operators may be able to plan for generation capacity sufficiently in advance for other power plant technologies such as fuel-efficient combined-cycle gas power plants or nuclear power plants to contribute to load-following. This important aspect is not treated explicitly here as the focus is on resource adequacy.

However, the inevitable inefficiencies of the storage systems require increasing the size of the WS fleet by a factor of 1/RTE compared to the WS fleet without storage to deliver the same energy to the grid. The power delivered to the grid by the storage system during an interval Δt is:

$${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\to \mathrm{t}+∆\mathrm{t}\right)={\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}} \times {\mathrm{c}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\to \mathrm{t}+∆\mathrm{t}\right)=\mathrm{R}\mathrm{T}\mathrm{E}\times {\int }_{\mathrm{t}-∆\mathrm{t}}^{\mathrm{t}}[{\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)/∆\mathrm{t}]\mathrm{d}\mathrm{t}$$

$${\mathrm{c}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\to \mathrm{t}+∆\mathrm{t}\right)={\mathrm{a}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\to \mathrm{t}+∆\mathrm{t}\right)\times {\mathrm{f}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\to \mathrm{t}+∆\mathrm{t}\right)\le 1$$

For example, if Δt = 24 h, the average power delivered by the storage system on any given day is equal to the average power generated by the WS fleet the day before multiplied by the storage system RTE (assuming there is no residual from previous days).

In the previous equation, ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ is the storage nameplate capacity, i.e., the maximum power it can deliver to the grid; ${\mathrm{c}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\to \mathrm{t}+∆\mathrm{t}\right)$ is the fraction of the storage nameplate capacity delivering power to the grid between t and t + Δt; ${\mathrm{a}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\to \mathrm{t}+∆\mathrm{t}\right)$ is the availability function of the storage power conversion system between t and t + Δt (fraction of the storage fleet that it is available to generate power); ${\mathrm{f}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\to \mathrm{t}+∆\mathrm{t}\right)$ is the fraction of the available storage nameplate capacity called on by the grid to deliver power between t and t + Δt. The availability function’s yearly average is assumed to be 0.85. The storage nameplate capacity, ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$, depends on the system characteristics. Four types of storage are possible (A, B, C, D).

• Type-A can charge with ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{i}\mathrm{n}}\left(\mathrm{t}\right)\gg {\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ and charge/discharge concurrently. Storage systems, such as pumped hydro (PHS), compressed air energy storage (CAES), or power-to-hydrogen-to-power (P2H2P) (see Section 6), have separate charge and discharge processes and subsystems, and, consequently, either are type-A or could, in principle, be modified to be type-A. In the time interval Δt, when the storage system delivers its maximum power, ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$, by definition, ${\mathrm{f}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}$ is equal to 1. If, as a first approximation, ${\mathrm{a}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}$ is substituted by its average value of 0.85, then, the nameplate capacity can be expressed as ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}={\mathrm{P}}_{\mathrm{S}\mathrm{t}\left|\mathrm{o}\mathrm{u}\mathrm{t}\right|\mathrm{A}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}=[1/0.85]\times \mathrm{RTE}\times \max \left[{\int }_{∆\mathrm{t}}[{\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)/∆\mathrm{t}]\mathrm{d}\mathrm{t}\right]$. Storage system A must be able to store up to ${{\mathrm{E}}_{\mathrm{S}\mathrm{t}\left|\mathrm{A}\right|∆\mathrm{t}}=\mathrm{P}}_{\mathrm{S}\mathrm{t}\left|\mathrm{o}\mathrm{u}\mathrm{t}\right|\mathrm{A}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}\times ∆\mathrm{t}$.
• Type-B can charge with ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{i}\mathrm{n}}\left(\mathrm{t}\right)\gg {\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ but cannot charge/discharge concurrently. Consequently, the type-A storage system must be doubled, with the nameplate capacity as follows: ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}={\mathrm{P}}_{\mathrm{S}\mathrm{t}\left|\mathrm{o}\mathrm{u}\mathrm{t}\right|\mathrm{B}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}=2\times {\mathrm{P}}_{\mathrm{S}\mathrm{t}\left|\mathrm{o}\mathrm{u}\mathrm{t}\right|\mathrm{A}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$. Storage system B must be able to store up to ${{\mathrm{E}}_{\mathrm{S}\mathrm{t}\left|\mathrm{B}\right|∆\mathrm{t}}=2\times \mathrm{E}}_{\mathrm{S}\mathrm{t}\left|\mathrm{A}\right|∆\mathrm{t}}$.
• Type-C cannot charge with ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{i}\mathrm{n}}\left(\mathrm{t}\right)\gg {\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ but can charge/discharge concurrently. In this case, the nameplate capacity must be equal to ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{i}\mathrm{n}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$, i.e., ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ divided by the availability of the storage system: ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}={\mathrm{P}}_{\mathrm{S}\mathrm{t}\left|\mathrm{o}\mathrm{u}\mathrm{t}\right|\mathrm{C}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}=[1/0.85]\times {\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}=1.176\times {\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$. Storage system C must be able to store up to ${{\mathrm{E}}_{\mathrm{S}\mathrm{t}\left|\mathrm{C}\right|∆\mathrm{t}}=\mathrm{E}}_{\mathrm{S}\mathrm{t}\left|\mathrm{A}\right|∆\mathrm{t}}$.
• Type-D cannot charge with ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{i}\mathrm{n}}\left(\mathrm{t}\right)\gg {\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ and cannot charge/discharge concurrently. Consequently, the type-C storage system must be doubled. Batteries typically belong to this category. The nameplate capacity is ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}={\mathrm{P}}_{\mathrm{S}\mathrm{t}\left|\mathrm{o}\mathrm{u}\mathrm{t}\right|\mathrm{D}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}=2\times {\mathrm{P}}_{\mathrm{S}\mathrm{t}\left|\mathrm{o}\mathrm{u}\mathrm{t}\right|\mathrm{C}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}=2.353\times {\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$. Storage system D must be able to store up to ${{\mathrm{E}}_{\mathrm{S}\mathrm{t}\left|\mathrm{D}\right|∆\mathrm{t}}={2\times \mathrm{E}}_{\mathrm{S}\mathrm{t}\left|\mathrm{C}\right|∆\mathrm{t}}=2\times \mathrm{E}}_{\mathrm{S}\mathrm{t}\left|\mathrm{A}\right|∆\mathrm{t}}$.

Finally, it is noteworthy that the storage configuration of interest (Figure 11) is conceptually and operationally different from how most storage systems currently operate (Figure 12).

In this case, the storage system does not act as a buffer between the WS fleet and the grid and is mainly used for energy arbitrage. With typically only one cycle/day, it is also used less intensively than in Figure 11. This configuration satisfies the following equation:

$${\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)=\mathrm{L}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{i}\mathrm{n}}\left(\mathrm{t}\right)$$

6. Energy Storage System Considerations

6.1. Short-Duration Storage

For storage systems capable of storing energy for up to 4 h, RTEs of 0.50–0.85 were considered. This range is representative of various technologies, such as CAES (RTE ~0.5) [16], vanadium flow batteries energy storage (BES) (RTE = 0.65) [17], PHS (RTE = 0.80) [18], and lithium-ion BES using a lithium iron phosphate (LFP) cathode (RTE = 0.85) [19].

The U.S. has 43 PHS plants with an estimated energy storage capacity of 553 GWh; the largest (Bath County) has a maximum generation capacity of 3 GW and a total storage capacity of 24 GWh. A resource assessment performed by the National Renewable Energy Laboratory (NREL) concluded that there are sufficient sites in the contiguous U.S. to generate up to 27 TWh [20] (2700 GW for 10 h) with PHS, equivalent to 49× the current capacity.

As of September 2024, the U.S. also had about 21 GW of utility-scale lithium-ion BES with an estimated energy storage capacity of 56 GWh [21]. Until it was recently destroyed by a fire, the largest LFP BES (Moss Landing, California) had a maximum generation capacity of 0.75 GW and total storage capacity of 3 GWh. Among the critical materials required, LFP BES require about 0.08 kgLi/kWh [22], or 0.08 million metric tons of lithium per TWh. For comparison, recent estimates of worldwide lithium resources and annual production are approximately 105 and 0.18 million metric tons, respectively [23].

There is currently no vanadium BES in the U.S. to speak of. The largest vanadium flow BES (Dalian, China) has a maximum generation capacity of 0.1 GW and a total storage capacity of 0.4 GWh [24]. Vanadium flow BES have a typical power density of 20 kWh/m³ and vanadium concentration of 1–3 M (51–153 kgV/m³) [25]. Expressed differently, a vanadium flow BES system requires about 2.5–7.7 million metric tons of vanadium per TWh. For comparison, recent estimates of world vanadium resource and annual production are about 63 and 0.10 million metric tons, respectively [26]. Hence, vanadium BES are more resource limited than lithium BES.

Several small-scale CAES facilities have been built and operated around the world, including in the U.S. The largest one is currently located in Hubei, China. It has a maximum generation capacity of 0.3 GW, a total storage capacity of 1.5 GWh, and a claimed RTE of 0.64 [27]. The 0.11 GW McIntosh plant in Alabama has a total storage capacity of 2.6 GWh but is not entirely CO₂-free as it also burns natural gas.

6.2. Long-Duration Storage

For storage systems capable of storing energy for 24 to 100 h, a range of long-duration energy storage (LDES) technologies [28] was considered, with RTEs of 0.30–0.80. This includes PHS, CAES, and P2H2P (RTE ~0.3) [29]. The P2H2P process considered here is commonly referred to as green hydrogen because it uses only WS electricity to power low-temperature electrolyzers. High-temperature electrolysis consumes less electricity, but it also requires a high-temperature heat source that typically comes from a non-WS source. This was not considered here. The 24 h and 100 h durations are long compared to the current mainstay 4 h storage. Much longer durations (months) would, however, be necessary to get rid of most of the dispatchable power.

Assuming a power conversion system efficiency (gas turbine [30] or fuel cells) of 50%, 1 kg of hydrogen generates 16.7 kWh of electricity, whereas it takes about 45–55 kWh to create this kg through low-temperature water electrolysis. This corresponds to a P2H2P RTE of 0.30 to 0.37 (these values do not include losses during storage and transportation). The largest hydrogen electrolyzer (the P2H part of the P2H2P system) was manufactured by the Shuangliang Group (Shanghai, China) and inaugurated in October 2024. It has the capacity to produce about 450 kg of hydrogen per hour (up to 3.94 million metric tons per year if operated 24/7) [31]. A resource assessment performed by NREL concluded that 9.8 million metric tons of pure hydrogen could be stored in existing U.S. underground gas storage facilities [32]. The largest hydrogen geological storage facility (in Utah) can store up to 11,000 metric tons [33].

6.3. Assets Lifetime

PHS and CAES both have an estimated lifetime of 60 years. For continuous baseload operation, the expected P2H2P electrolyzer stack lifetimes are 60,000 to 80,000 h (7–9 years) of operation for proton exchanging membrane (PEM) and alkaline electrolyzers [34]. However, studies have shown that flexible operation, such as when powered by WS, may lead to a shorter stack lifetime. The U.S. Department of Energy has set ultimate targets for fuel cell system lifetime under realistic operating conditions at 80,000 h (9 years) for distributed power systems [35]. Based on the information provided in the two previous references, and as a first approximation, a 9-year lifetime was considered for the P2H2P storage system.

For 4 h storage, lithium-ion LFP BES have an estimated lifetime of 7300 cycles [36]. This corresponds to a 7.8-year lifetime for the operating conditions of interest here, i.e., 3 cycles per day (24 ÷ [2 × 4]) and an availability of 0.85 (7300 ÷ [3 × 365 × 0.85]). Many references give longer BES lifetimes because they consider only one cycle per day, implying that the BES is mainly used for arbitrage purposes and not as a buffer between the WS fleet and the grid. The DOE Technology Strategy Assessments referenced previously yield a comparable lifetime estimate: 2640 cycles for 10 h storage lithium-ion LFP BES. This corresponds to a 7.1-year lifetime for 1.2 cycles per day (24 ÷ [2 × 10]) and an availability of 0.85 (2640 ÷ [1.2 × 365 × 0.85]). For 10 h storage, vanadium BES are rated at 10,000 cycles (i.e., ~25,000 cycles for 4 h storage). The corresponding vanadium BES operational lifetime is 27 years.

It is noteworthy that, since only PHS has been deployed at scale, the uncertainties in the lifetime of the other storage technologies are large.

6.4. Storage Capital Cost

Representative storage overnight capital costs, estimated by the U.S. Pacific Northwest National Laboratory for large 1 GW facilities in 2030, are presented in

Table 3. Storage overnight capital costs (USD B/GW) for different storage technologies and durations (4–100 h).

	4	10	24	100	Lifetime (yrs)	RTE
PHS	1.7	2.2	2.9	6.9	60	0.80
CAES	1.1	1.1	1.2	1.6	60	0.50
P2H2P	-	1.0	1.1	1.5	9	0.30
Li-BES	1.1	2.5	-	-	8	0.85
V-BES	1.6	3.0	6.4	-	27	0.65

for storage durations of 4–100 h [37].

Table 4. Storage capital costs expenditure over 60 years (USD B/GW/60 y) for different storage technologies and durations (4–100 h).

	0% Discount Rate				7% Discount Rate
	4	10	24	100	4	10	24	100
PHS	1.7	2.2	2.9	6.9	1.7	2.2	2.9	6.9
CAES	1.1	1.1	1.2	1.6	1.1	1.1	1.2	1.6
P2H2P	-	6.7	7.3	10.0	-	2.2	2.4	3.2
Li-BES	8.3	18.8	-	-	2.6	5.9	-	-
V-BES	3.6	6.7	14.2	-	1.9	3.5	7.5	-

shows the storage 60-year capital expenditure (USD B/GW/60 y) using the reference 0% discount rate approach described in Section 3. The values obtained with a 7% discount rate are also shown to illustrate the sensitivity. P2H2P and Li-BES are particularly penalized economically due to their short lifetimes. Since only PHS has been deployed at scale, the cost uncertainties for the other storage technologies are significant.

7. Wind/Solar Penetration of 30%

A 30% WS penetration corresponds to approximately twice the current WS penetration of the U.S. grid. Power systems without storage and with storage are successively discussed.

7.1. No Energy Storage

The WS fleet delivers a yearly average of 180 GW to the grid, i.e., 30% of the average load of 600 GW. Since the yearly average WS capacity factor, ${\mathrm{c}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$, is also 30%, the WS fleet nameplate capacity, ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$, is 600 GW.

$${\int }_{∆\mathrm{T}}{\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}=0.3\times {\int }_{∆\mathrm{T}}\mathrm{L}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t} \mathrm{and} {\int }_{∆\mathrm{T}}{\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}=0.7\times {\int }_{∆\mathrm{T}}\mathrm{L}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t} \mathrm{f}\mathrm{o}\mathrm{r}∆\mathrm{T}=1 \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}$$

As mentioned in Section 4, based on existing data, it is assumed that the power delivered by our 600 GW WS fleet fluctuates between ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}=0.63 {\times \mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}=378 \mathrm{G}\mathrm{W}$ and ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}=0.054{ \times \mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}=32.4 \mathrm{G}\mathrm{W}$. Since ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}<{\mathrm{L}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, curtailment is not necessary. If it is deemed sufficiently unlikely that ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$ could be lower than this ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ value, then it can be considered a firm capacity and, consequently, replace 38 GW of baseload power (32.4/0.85). Furthermore, 407 GW of baseload power must be replaced by 407 GW of fast-ramping load-following plants ([378 − 32.4]/0.85) to compensate for potentially large and rapid fluctuations of the WS fleet. Out of the original 588 GW of baseload power (see Table 2), there remain 588 – 407 − 38 = 143 GW. If it cannot be ruled out with sufficient certainty that ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ could happen concomitantly with peak load, then the same 259 GW of load -following plants as before are needed to cover the load between 500 and 720 GW.

The resulting 1409 GW fleet is made up of 600 GW WS and 809 GW of dispatchable power (666 GW of load-following plants and 143 GW nuclear baseload). It is 50% CO₂-free (30% WS + 20% nuclear). Gas power plants would likely provide most of the necessary 666 GW of fast ramping load-following capacity generating the other 50% of the electricity needed by the grid. The capital cost for this fleet is about USD 2.6 T (0.90 T WS, 0.59 T gas power plants, 1.1 T nuclear power plants) or USD 3.9 T/60 y.

The 809 GW dispatchable fleet could, in principle, meet the load without the WS fleet. The potential benefit of the WS fleet is that it may enable less fossil fuel consumption and, consequently, fewer CO₂ emissions may result. This, however, is not necessarily the case. Indeed, even highly efficient power plants such as combined-cycle gas turbines (CCGT) see their efficiency drop when they operate outside their range of optimal nominal operation. Consequently, they burn more fuel and emit more CO₂ per kWh [38,39]. In other words, replacing highly efficient CCGT baseload power plants with a combination of WS and fast ramping gas power plants may not necessarily reduce CO₂ emissions, even if the fast-ramping power plants generate overall fewer kWh than the baseload power plants that they replaced.

As discussed in Section 4, curtailment can be used to manage supply and demand. For example, if the power generated by a 632 GW WS fleet were curtailed when it exceeded 1.3× its average (189 GW), it would still generate, on average, 95% of the non-curtailed fleet, i.e., 180 GW. In this case, the curtailed 632 GW WS* fleet fluctuates between ${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{a}\mathrm{x}}=0.39{ \times \mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}=246 \mathrm{G}\mathrm{W}$ and ${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{i}\mathrm{n}}=0.054{ \times \mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}=34 \mathrm{G}\mathrm{W}$. As before, if this ${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{i}\mathrm{n}}$ value can be considered a firm capacity, then 40 GW of baseload power (34/0.85) can be retired. Furthermore, 249 GW of baseload power must be replaced by 249 GW of fast-ramping load-following plants ([246 − 34]/0.85) to compensate for the fluctuations of the WS fleet. Out of the original 588 GW of baseload power (see Table 2), there remain 588 – 249 − 40 = 299 GW. As previously, 259 GW of load-following plants is needed to cover the load between 500 and 720 GW. In this example, curtailing 5% of the WS production enables doubling the nuclear baseload from 143 to 299 GW. Consequently, the CO₂-free percentage increases from 50% to 72%. The capital cost for this fleet is about USD 3.8 T (0.95 T WS, 0.45 T gas power plants, 2.4 T nuclear power plants) or USD 5.0 T/60 y.

7.2. With Energy Storage

The storage system delivers a yearly average of 180 GW to the grid, i.e., 30% of the average load of 600 GW.

$${\int }_{∆\mathrm{T}}{\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}=0.30\times {\int }_{∆\mathrm{T}}\mathrm{L}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t} \mathrm{and} {\int }_{∆\mathrm{T}}{\mathrm{P}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}=0.7\times {\int }_{∆\mathrm{T}}\mathrm{L}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}, ∆\mathrm{T}=1 \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}$$

7.2.1. With 4-Hour Storage

RTEs of 0.50–0.85 were considered representative of a range of technologies, such as vanadium flow BES, lithium-ion BES, PHS, and CAES. The range of fluctuations of ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}\left(\mathrm{t}\right)$ depends on the ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$ 4 h averages. Indications of the possible range of fluctuations can be found, for example, by averaging the reference hourly time series of Figure 6 over 4 h intervals. It results in a maximum and minimum 4 h average of 2.0× and 0.20× the average. For the 5% curtailed case of Figure 8, the maximum and minimum 4 h averages are 1.3× and 0.20× the reference non-curtailed average.

As discussed in Section 5, ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ is proportional to either the maximum 4 h average ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$ (type-A) or to the maximum instantaneous ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}\left(\mathrm{t}\right)$ (type-D), the two of which are approximately 2× and 1.3× ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ for the reference WS fleet and the 5% curtailed fleet, respectively. Hence, harvesting the entirety of the WS generation in the storage system, instead of only 95% of it, requires 54% (2/1.3) more storage power capacity, i.e., ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$. The rest of the discussion considers only the 5% curtailed WS* fleet.

With neither storage nor curtailment, ${\mathrm{P}}_{\mathrm{W}\mathrm{S}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ = 600 GW (see Section 7.1). With storage and 5% curtailment, additional capacity must be deployed. Consequently, depending on the storage RTE, ${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ = 743–1263 GW to enable the storage system to deliver, on average, ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ = 180 GW to the grid (743 × 0.3 × 0.95 × 0.85 or 1263 × 0.3 × 0.95 × 0.50). The corresponding capital cost is about USD 1.1–1.9 T or USD 2.2–3.6 T/60 y.

The curtailed WS* maximum and minimum 4 h average capacity factors are 39% (1.3 × 30%) and 6.0% (0.20 × 30%). During the 4 h time periods when the capacity factor is 39%, the 743–1263 GW WS* fleet delivers, on average, 290–493 GW to the storage system, which then, 4 h later, delivers ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ = 246 GW to the grid (290 × 0.85 or 493 × 0.50). During the very few 4 h time periods when the capacity factor is only 6%, the storage system coupled to the 743–1263 GW WS* fleet would deliver only ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ = 38 GW to the grid (743 × 0.06 × 0.85 or 1263 × 0.06 × 0.50).

As mentioned previously, the storage nameplate capacity depends on whether it is a type A, B, C, or D (see Section 4). Assuming only type-A storage systems, such as PHS, are used, ${\mathrm{P}}_{\mathrm{S}\mathrm{t}\left|\mathrm{o}\mathrm{u}\mathrm{t}\right|\mathrm{A}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ = 289 GW to ensure ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ = 246 GW can be delivered to the grid (with assumed availability of 0.85). Type-A storage systems should be able to store up to 1.2 TWh (289 GW × 4 h), i.e., 2.1× the current U.S. PHS capacity. Assuming only type-D storage systems, such as lithium-ion or vanadium flow BES, are used, the required storage nameplate capacities are, for example, ${\mathrm{P}}_{\mathrm{S}\mathrm{t}\left|\mathrm{o}\mathrm{u}\mathrm{t}\right|\mathrm{D}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ = 682 GW for lithium-ion BES (RTE = 0.85) or ${\mathrm{P}}_{\mathrm{S}\mathrm{t}\left|\mathrm{o}\mathrm{u}\mathrm{t}\right|\mathrm{D}}^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ = 892 GW for vanadium flow BES (RTE = 0.65) (see Section 4). Type-D storage systems should be able to store up to 2.4 TWh, i.e., 43× the current U.S. lithium-ion BES storage capacity. The capital cost for 289 GW of 4 h PHS is USD 0.49 T (USD 0.49 T/60 y), the capital cost for 682 GW of lithium-ion BES is USD 0.75 T (USD 5.7 T/60 y), and the capital cost for 892 GW of vanadium flow BES is USD 1.4 T (USD 3.2 T/60 y).

Hence, the yearly average power delivered to the grid by the combination of the 743–1263 GW WS* fleet and of the 289–892 GW storage system is 180 GW, but it can vary between 38 and 246 GW. If the minimum power delivered by the storage system (38 GW) can be considered a firm capacity, 45 GW of baseload power can be retired (38/0.85). Furthermore, because the power delivered by the storage system varies between 38 GW and 246 GW, 245 GW of baseload plants must be replaced by 245 GW of load-following plants ([246 − 38]/0.85). Out of the original 588 GW of baseload power (see Table 2), there remains 588 − 245 − 45 = 298 GW. If it cannot be ruled out that ${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ could happen at the same time as the peak load, then the same 259 GW of load-following plants as in the reference fleet without WS is needed to cover the load between 500 and 720 GW, bringing the total load-following capacity to 504 GW (259 + 245).

The resulting 1881–2666 GW fleet consists of 743–1263 GW of WS*, coupled with 289–892 GW of storage and 802 GW of dispatchable power (504 GW of load-following plants and 298 GW of nuclear baseload). The resulting power grid is 72% CO₂-free (30% WS*/storage + 42% baseload nuclear). An important difference from the previous case without storage is the increased predictability of the power delivered by the storage system compared to that delivered directly by the WS* fleet.

The capital cost of the dispatchable fleet is about USD 2.8 T (USD 0.4 T gas + USD 2.4 T for nuclear) or USD 3.1 T/60 y. The capital cost of the WS* fleet + storage depends on the storage technology: USD 1.7 T for WS*/PHS (USD 1.2 T WS*, USD 0.49 T PHS), USD 1.9 T for WS*/LiBES (USD 1.1 T WS*, USD 0.75 T LiBES), and USD 2.9 T for WS*/VaBES (USD 1.5 T WS*, USD 1.4 T VaBES). Hence, the capital cost for the total fleet is USD 4.5-USD 5.7 T depending on the 4 h storage technology. Considering the lifetimes USD 2.9 T/60 y for WS*/PHS, USD 7.9 T/60 y for WS*/LiBES, and USD 6.1 T/60 y for WS*/VaBES, the corresponding total capital expenditure over 60 years is USD 6.0–11.0 T/60 y. The results are summarized in Table 5.

7.2.2. With LDES (24–100 H)

The assumed RTEs for LDES are 0.30–0.80, representative of a range of LDES technologies (e.g., CAES, PHS, P2H2P). Only type-A storage systems are considered. The corresponding 5% curtailed WS fleet nameplate capacity (${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$) is 789–2105 GW to enable the storage system to deliver, on average, 180 GW to the grid.

Averaging the hourly time series shown in Section 4 over 24 h and 100 h intervals shows that the U.S. WS fleet’s daily generation varied between 1.3× and 0.30× the non-curtailed average, whereas the 100 h average generation varied between 1.2× and 0.46× the non-curtailed average. Applying these factors to our WS/C fleet, the maximum and minimum 24 h average capacity factors are 39% and 9% whereas the maximum and minimum 100 h average capacity factors are 36% and 14%. The methodology is the same as before and is not reproduced here. The results are summarized in Table 5.

7.3. Summary of the 30% WS Penetration Case

The results obtained in the previous sections with the 5% curtailed WS* fleet are summarized in Table 5 for the no-storage case, and for the 4, 24, and 100 h storage cases. The reality will likely lie somewhere between these bounding cases.

The size of the nuclear baseload fleet is only weakly dependent on the nature and duration of the storage system: 298 GW for the no-storage case and 321 GW for the 100 h storage case. On the other hand, the size of the WS fleet (632–2105 GW) and that of the storage system (0–892 GW) depend strongly on the nature of the latter because of the difference in RTEs. The estimated overnight capital cost is USD 3.8–6.5 T, depending on the size and nature of the storage system. Considering the different technology lifetimes, the estimated capital expenditure over 60 years is USD 5.0–12.2 T/60 y. These fleets are 72–75% CO₂-free. As discussed in Section 2, the capital cost of the reference 83% CO₂-free dispatchable-only fleet relying on nuclear plants for the entirety of baseload power is USD 4.9 T, or, equivalently, USD 5.0 T/60 y. Hence, depending on the amount of storage needed to guarantee grid stability, the WS/storage/nuclear/gas fleets may be more capital-intensive than the reference 83% CO₂-free nuclear/gas fleet. This is especially true in the long run because WS and storage assets have shorter lifetimes than nuclear plants and, consequently, need to be replaced more frequently.

As mentioned in Section 1, the grid considered here is assumed to be fully interconnected and without transmission losses (i.e., a copper-plate grid), which enables WS to contribute most efficiently to the load. Upgrading the current grid so that it more closely approximates this idealized copper-plate grid will require capital investment in addition to the capital necessary to deploy the WS and storage fleets. This aspect was not considered here. The copper-plate grid assumption is less important for the reference dispatchable-only fleet and, consequently, less capital may be needed to upgrade the current grid compared to the cases with large contributions from WS and storage.

Table 5. Installed capacity and annual electricity generation of the fleet with 30% WS* penetration, assuming a 5% curtailment.

	0 h Storage		4 h Storage		24 h Storage		100 h Storage
Representative Storage Technology	-		BES (Li-Ion, V-Flow), PHS, CAES		PHS, P2H2P, CAES		PHS, P2H2P, CAES
WS* capacity factor	0.3 × 0.95 = 0.285		0.3 × 0.95 = 0.285		0.3 × 0.95 = 0.285		0.3 × 0.95 = 0.285
Storage RTE	-		0.85 ↔ 0.50		0.80 ↔ 0.30		0.80 ↔ 0.30
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ (GW)	632		743 ↔ 1263		789 ↔ 2105		789 ↔ 2105
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{a}\mathrm{v}\mathrm{e}}$ (GW)	180		212 ↔ 360		225 ↔ 600		225 ↔ 600
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{i}\mathrm{n}}$ (GW)	34		40 ↔ 68		43 ↔ 114		43 ↔ 114
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{a}\mathrm{x}}$ (GW)	246		290 ↔ 493		308 ↔ 821		308 ↔ 821
${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ (GW)	-		180		180		180
${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$/${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ (GW)	-		38/246		57/246		88/227
	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)
Baseload (nuclear)	298	253	298	253	299	254	321	273
Load-follow (gas)	509 A	167	504 B	167	481 B	166	423 B	147
WS*	632	180	743–1263	-	789–2105	-	789–2105	-
Storage	-	-	289 C1 682 C2–892 C3	180	289 D	180 E	267 F	180 E
Total fleet	1438	600	1881–2666	600	1858–3174	600	1800–3116	600
% CO2-free	WS* alone = 30 WS* + Bsld = 72		WS*/St alone = 30 WS*/St + Bsld = 72		WS*/St alone = 30 WS*/St + Bsld = 72		WS*/St alone = 30 WS*/St + Bsld = 75
Initial capital cost (USD T)	3.8		4.5/5.0 − PHS/CAES 4.7/5.7 − Li/V BES		4.8/5.0 − PHS/CAES 6.3 − P2H2P		5.9/5.2 − PHS/CAES 6.5 − P2H2P
60-year capital cost (USD T/60 y) − 0% DiRa	5.0		6.0/7.2 − PHS/CAES 11.0/9.2 − Li/V BES		6.3/7.2 − PHS/CAES 11.5 − P2H2P		7.4/7.4 − PHS/CAES 12.2 − P2H2P

(^A) Mostly fast-ramping, single-cycle gas power plants. (^B) The storage system delivers more predictable power to the grid and, consequently, may enable nuclear and combined-cycle gas power plants to contribute to load following. (^C1) Only type-A storage, such as PHS or CAES; 1.2 TWh of storage needed (289 GW × 4 h) ≡ 2.1× the total U.S. PHS. (^C2) Only lithium-ion BES (type-D storage, RTE = 0.85); 2.3 TWh of storage needed ≡ 41× the total U.S. lithium-ion BES. (^C3) Only vanadium flow BES (type-D storage, RTE = 0.65); 2.3 TWh of storage needed. (^D) Only type-A storage considered; 6.9 TWh of storage needed (289 GW × 24 h) ≡ 12× the total U.S. PHS or 0.42 million metric tons of hydrogen. (^E) The generation of 180 GWy (1577 TWh) per year requires 94 million metric tons of hydrogen per year. (^F) Only type-A storage considered; 27 TWh of storage needed (267 GW × 100 h) ≡ 48× the total U.S. PHS ≡ estimated total U.S. PHS resource; or 1.6 million metric tons of hydrogen.

Table 5. Installed capacity and annual electricity generation of the fleet with 30% WS* penetration, assuming a 5% curtailment.

	0 h Storage		4 h Storage		24 h Storage		100 h Storage
Representative Storage Technology	-		BES (Li-Ion, V-Flow), PHS, CAES		PHS, P2H2P, CAES		PHS, P2H2P, CAES
WS* capacity factor	0.3 × 0.95 = 0.285		0.3 × 0.95 = 0.285		0.3 × 0.95 = 0.285		0.3 × 0.95 = 0.285
Storage RTE	-		0.85 ↔ 0.50		0.80 ↔ 0.30		0.80 ↔ 0.30
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ (GW)	632		743 ↔ 1263		789 ↔ 2105		789 ↔ 2105
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{a}\mathrm{v}\mathrm{e}}$ (GW)	180		212 ↔ 360		225 ↔ 600		225 ↔ 600
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{i}\mathrm{n}}$ (GW)	34		40 ↔ 68		43 ↔ 114		43 ↔ 114
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{a}\mathrm{x}}$ (GW)	246		290 ↔ 493		308 ↔ 821		308 ↔ 821
${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ (GW)	-		180		180		180
${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$/${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ (GW)	-		38/246		57/246		88/227
	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)
Baseload (nuclear)	298	253	298	253	299	254	321	273
Load-follow (gas)	509 A	167	504 B	167	481 B	166	423 B	147
WS*	632	180	743–1263	-	789–2105	-	789–2105	-
Storage	-	-	289 C1 682 C2–892 C3	180	289 D	180 E	267 F	180 E
Total fleet	1438	600	1881–2666	600	1858–3174	600	1800–3116	600
% CO2-free	WS* alone = 30 WS* + Bsld = 72		WS*/St alone = 30 WS*/St + Bsld = 72		WS*/St alone = 30 WS*/St + Bsld = 72		WS*/St alone = 30 WS*/St + Bsld = 75
Initial capital cost (USD T)	3.8		4.5/5.0 − PHS/CAES 4.7/5.7 − Li/V BES		4.8/5.0 − PHS/CAES 6.3 − P2H2P		5.9/5.2 − PHS/CAES 6.5 − P2H2P
60-year capital cost (USD T/60 y) − 0% DiRa	5.0		6.0/7.2 − PHS/CAES 11.0/9.2 − Li/V BES		6.3/7.2 − PHS/CAES 11.5 − P2H2P		7.4/7.4 − PHS/CAES 12.2 − P2H2P

(^A) Mostly fast-ramping, single-cycle gas power plants. (^B) The storage system delivers more predictable power to the grid and, consequently, may enable nuclear and combined-cycle gas power plants to contribute to load following. (^C1) Only type-A storage, such as PHS or CAES; 1.2 TWh of storage needed (289 GW × 4 h) ≡ 2.1× the total U.S. PHS. (^C2) Only lithium-ion BES (type-D storage, RTE = 0.85); 2.3 TWh of storage needed ≡ 41× the total U.S. lithium-ion BES. (^C3) Only vanadium flow BES (type-D storage, RTE = 0.65); 2.3 TWh of storage needed. (^D) Only type-A storage considered; 6.9 TWh of storage needed (289 GW × 24 h) ≡ 12× the total U.S. PHS or 0.42 million metric tons of hydrogen. (^E) The generation of 180 GWy (1577 TWh) per year requires 94 million metric tons of hydrogen per year. (^F) Only type-A storage considered; 27 TWh of storage needed (267 GW × 100 h) ≡ 48× the total U.S. PHS ≡ estimated total U.S. PHS resource; or 1.6 million metric tons of hydrogen.

8. Wind/Solar Penetration of 60%

The characteristics of the fleets were assessed using the same methodology discussed in the previous sections. The individual calculations are not reproduced here. The results obtained for the 5% curtailed WS* fleet are summarized in

Table 6. Installed capacity and annual electricity generation of the fleet with 60% WS* penetration, assuming a 5% curtailment.

	0 h Storage		4 h Storage		24 h Storage		100 h Storage
Representative Storage Technologies	-		BES (Li-Ion, V-Flow), PHS, CAES		PHS, P2H2P, CAES		PHS, P2H2P, CAES
WS* capacity factor	0.3 × 0.95 = 0.285		0.3 × 0.95 = 0.285		0.3 × 0.95 = 0.285		0.3 × 0.95 = 0.285
Storage RTE	-		0.85 ↔ 0.50		0.80 ↔ 0.30		0.80 ↔ 0.30
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ (GW)	1263		1486 ↔ 2526		1579 ↔ 4211		1579 ↔ 4211
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{a}\mathrm{v}\mathrm{e}}$ (GW)	360		424 ↔ 720		450 ↔ 1200		450 ↔ 1200
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{i}\mathrm{n}}$ (GW)	68		80 ↔ 136		85 ↔ 227		85 ↔ 227
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{a}\mathrm{x}}$ (GW)	493		580 ↔ 985		616 ↔ 1642		616 ↔ 1642
${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ (GW)	-		360		360		360
${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$/${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ (GW)	-		76/492		114/492		176/454
	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)
Baseload (nuclear)	8	7	9	8	9	8	54	46
Load-follow (gas)	758 A	233	748 B	232	704 B	232	586 B	194
WS*	1263	360	1486–2526	-	1579–4211	-	1579–4211	-
Storage	-	-	579 C1 1364 C2–1783 C3	360	579 D	360 E	534 F	360 E
Total fleet	2030	600	2915–4484	600	2871–5502	600	2753–5385	600
% CO2-free	WS* alone = 60 WS* + Bsld = 61		WS*/St alone = 60 WS*/St + Bsld = 61		WS*/St alone = 60 WS*/St + Bsld = 61		WS*/St alone = 60 WS*/St + Bsld = 68
Initial capital cost (USD T)	2.6		4.1/5.2 − PHS/CAES 4.5/6.5 − Li/V BES		4.7/5.2 − PHS/CAES 7.6 − P2H2P		7.0/5.6 − PHS/CAES 8.1 − P2H2P
60-year capital cost (USD T/60 y) − 0% DiRa	5.0		6.9/9.4 − PHS/CAES 17.0/13.4 − Li/V BES		7.5/9.4 − PHS/CAES 18.0 − P2H2P		9.7/9.7 − PHS/CAES 19.3 − P2H2P
60-year capital cost (USD T/60 y) − 7% DiRa	2.9		4.4/5.7 − PHS/CAES 6.8/7.5 − Li/V BES		5.1/5.7 − PHS/CAES 9.3 − P2H2P		7.3/6.1 − PHS/CAES 9.8 − P2H2P

(^A) Mostly fast-ramping, single-cycle gas power plants. (^B) The storage system delivers more predictable power to the grid and, consequently, may enable nuclear and combined-cycle gas power plants to contribute to load following. (^C1) Only type-A storage, such as PHS or CAES; 2.3 TWh of storage needed (579 GW × 4 h) ≡ 4.2× the total U.S. PHS. (^C2) Only lithium-ion BES (type-D storage, RTE = 0.85); 4.6 TWh of storage needed ≡ 83× the total U.S. lithium-ion BES. (^C3) Only vanadium flow BES (type-D storage, RTE = 0.65); 4.6 TWh of storage needed. (^D) Only type-A storage considered; 14 TWh of storage needed (579 GW × 24 h) ≡ 25× the total U.S. PHS or 0.83 million metric tons of hydrogen. (^E) The generation of 360 GWy (3154 TWh) per year requires 189 million metric tons of hydrogen per year. (^F) Only type-A storage considered; 53 TWh of storage needed (534 GW × 100 h) ≡ 97× the total U.S. PHS ≡ 2× estimated total U.S. PHS resource; or 3.2 million metric tons of hydrogen.

for the no-storage case, and for the 4, 24, and 100 h storage cases. As before, the reality will likely be somewhere between these bounding cases.

In this case the nuclear baseload fleet is reduced to almost nothing (8–54 GW) because the fluctuations of the WS* fleet force baseload power into retirement. The size of the WS* fleet varies between 1263 and 4211 GW, and that of the storage system between 0 and 1783 GW, depending on the nature of the latter. The estimated overnight capital cost is USD 2.6–8.1 T depending on the size and nature of the storage system. Considering the different technology lifetimes, the estimated 60-year capital expenditure is USD 5.0–19.2 T/60 y with the reference 0% discount rate. The 60-year capital expenditure was also estimated with a 7% discount rate to quantify the sensitivity: USD 2.9–9.8 T/60 y. Note that the WS and gas power plants 60-year capital expenditures were also adjusted to reflect the 7% discount rate (USD 1.7 B/60 y for WS and 0.94 B/60 y for gas).

These fleets are 61–68% CO₂-free and almost nuclear-free. As previously, depending on the amount of storage needed to guarantee grid stability, the WS/storage/gas fleets may be more capital intensive than the reference 83% CO₂-free nuclear/gas fleet. Each option has its pros and cons, and more analyses (including grid stability, resource availability, and public acceptance) would of course be necessary to determine which one is most likely to provide the path of least resistance to powering a clean, affordable, and reliable grid in a timely manner.

As stated previously, the predictability of a WS* fleet generation increases with the level of curtailment and, consequently, less long duration storage may be needed compared to a non-curtailed fleet. For this reason, the impact of curtailment was evaluated. The results obtained for a 30% curtailed WS* fleet (see time series in Figure 9) are summarized in

Table 7. Installed capacity and annual electricity generation of the fleet with 60% WS* penetration, assuming a 30% curtailment.

	0 h Storage		4 h Storage		24 h Storage		100 h Storage
Representative Storage Technology	-		BES (Li-Ion, V-Flow), PHS, CAES		PHS, P2H2P, CAES		PHS, P2H2P, CAES
WS* capacity factor	0.3 × 0.7 = 0.21		0.3 × 0.7 = 0.21		0.3 × 0.7 = 0.21		0.3 × 0.7 = 0.21
Storage RTE	-		0.85 ↔ 0.50		0.80 ↔ 0.30		0.80 ↔ 0.30
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ (GW)	1714		2017 ↔ 3429		2143 ↔ 5714		2143 ↔ 5714
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{a}\mathrm{v}\mathrm{e}}$ (GW)	360		424 ↔ 720		450 ↔ 1200		450 ↔ 1200
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{i}\mathrm{n}}$ (GW)	93		109 ↔ 185		116 ↔ 309		116 ↔ 309
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{a}\mathrm{x}}$ (GW)	381		448 ↔ 761		476 ↔ 1269		476 ↔ 1269
${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ (GW)	-		360		360		360
${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$/${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ (GW)	-		103/377		155/377		221/377
	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)
Baseload (nuclear)	140	119	145	123	145	123	145	123
Load-follow (gas)	598 A	121	581 B	117	520 B	117	443 B	117
WS*	1714	360	2017–3429	-	2143–5714	-	2143–5714	-
Storage	-	-	443 C1 1054 C2–1378 C3	360	443 D	360 E	443 F	360 E
Total fleet	2452	600	3312–4741	600	3251–6822	600	3173–6745	600
% CO2-free	WS* alone = 60 WS* + Bsld = 80		WS*/St alone = 60 WS*/St + Bsld = 80		WS*/St alone = 60 WS*/St + Bsld = 80		WS*/St alone = 60 WS*/St + Bsld = 80
Initial capital cost (USD T)	4.2		5.6/7.3 − PHS/CAES 5.8/7.8 − Li/V BES		6.1/7.3 − PHS/CAES 10.7 − P2H2P		7.8/7.4 − PHS/CAES 10.8 − P2H2P
60-year capital cost (USD T/60 y) − 0% DiRa	7.1		9.2/12.8 − PHS/CAES 16.8/14.9 − Li/V BES		9.6/12.7 − PHS/CAES 22.3 − P2H2P		11.2/12.7 − PHS/CAES 23.3 − P2H2P

(^A) Mostly fast-ramping, single-cycle gas power plants. (^B) The storage system delivers more predictable power to the grid and, consequently, may enable nuclear and combined-cycle gas power plants to contribute to load following. (^C1) Only type-A storage, such as PHS or CAES; 1.8 TWh of storage needed (443 GW × 4 h) ≡ 3.2× the total U.S. PHS. (^C2) Only lithium-ion BES (type-D storage, RTE = 0.85); 3.5 TWh of storage needed ≡ 63× the total U.S. lithium-ion BES. (^C3) Only vanadium flow BES (type-D storage, RTE = 0.65); 3.5 TWh of storage needed. (^D) Only type-A storage considered; 11 TWh of storage needed (443 GW × 24 h) ≡ 19× the total U.S. PHS or 0.64 million metric tons of hydrogen. (^E) The generation of 360 GWy (3154 TWh) per year requires 189 million metric tons of hydrogen per year. (^F) Only type-A storage considered; 44 TWh of storage needed (443 GW × 100 h) ≡ 80× the total U.S. PHS ≡ 1.6× total U.S. PHS estimated resource or 2.7 million metric tons of hydrogen.

for the no-storage case, and for the 4, 24, and 100 h storage cases.

Compared to the 5% curtailment case, the increased curtailment level enables more nuclear baseload (140–145 GW) to contribute to the load. The size of the WS* fleet varies between 1714 and 5714 GW, and that of the storage system varies between 0 and 1378 GW, depending on the nature of the latter. The estimated overnight capital cost is USD 4.2–10.8 T, depending on the size and nature of the storage system. Considering the different technology lifetimes, the estimated capital expenditure over 60 years is USD 7.1–23.3 T/60 y. These fleets are 80% CO₂-free compared to only 60% CO₂-free in the previous case with a 5% curtailment. Here, again, depending on the amount of storage needed to guarantee grid stability, the WS/storage/gas fleets may be more capital-intensive than the reference 83% CO₂-free nuclear/gas fleet.

9. 80% Wind/Solar Penetration

The results presented in Table 7 indicate that the grid can still accommodate 140–145 GW of baseload power at 60% WS* penetration if 30% of WS* output is curtailed. The next logical step is to increase the WS* capacity until all baseload power has been displaced. This results in an 80% WS* penetration. The results are summarized in

Table 8. Installed capacity and annual electricity generation of the fleet with 80% WS* penetration, assuming a 30% curtailment.

	0 h Storage		4 h Storage		24 h Storage		100 h Storage
Representative Storage Technologies	-		BES (Li-Ion, V-Flow), PHS, CAES		PHS, P2H2P, CAES		PHS, P2H2P, CAES
WS* capacity factor	0.3 × 0.7 = 0.21		0.3 × 0.7 = 0.21		0.3 × 0.7 = 0.21		0.3 × 0.7 = 0.21
Storage RTE	-		0.85 ↔ 0.50		0.80 ↔ 0.30		0.80 ↔ 0.30
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{n}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{t}}$ (GW)	2253		2677 ↔ 4551		2845 ↔ 7586		2845 ↔ 7586
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{a}\mathrm{v}\mathrm{e}}$ (GW)	473		562 ↔ 956		597 ↔ 1593		597 ↔ 1593
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{i}\mathrm{n}}$ (GW)	122		145 ↔ 246		154 ↔ 410		154 ↔ 410
${\mathrm{P}}_{\mathrm{W}\mathrm{S}\ast }^{\mathrm{m}\mathrm{a}\mathrm{x}}$ (GW)	500		594 ↔ 1010		632 ↔ 1684		632 ↔ 1684
${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{a}\mathrm{v}\mathrm{e}}$ (GW)	-		478		478		478
${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$/${\mathrm{P}}_{\mathrm{S}\mathrm{t}|\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ (GW)	-		137/500		205/500		293/500
	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)	Capacity (GW)	Gene. (GWy)
Baseload (nuclear)	0	0	0	0	0	0	0	0
Load-follow (gas)	704 A	127	686 B	122	606 B	122	503 B	122
WS*	2253	473	2677–4551	-	2845–7586	-	2845–7586	-
Storage	-	-	588 C1 1399 C2–1829 C3	478	588 D	478 E	588 F	478 E
Total fleet	2957	600	4119–6016	600	4038–8779	600	3935–8676	600
% CO2-free	WS* alone = 79		WS*/St alone = 80		WS*/St alone = 80		WS*/St alone = 80
Initial capital cost (USD T)	4.0		5.9/8.1 − PHS/CAES 6.2/8.8 − Li/V BES		6.5/8.1 − PHS/CAES 12.6 − P2H2P		8.8/8.2 − PHS/CAES 12.7 − P2H2P
60-year capital cost (USD T/60 y) − 0% DiRa	7.8		10.6/15.3 − PHS/CAES 20.7/18.1 − Li/V BES		11.1/15.3 − PHS/CAES 28.0 − P2H2P		13.3/15.3 − PHS/CAES 29.4 − P2H2P
60-year capital cost (USD T/60 y) − 7% DiRa	4.5		6.5/9.0 − PHS/CAES 8.8/10.1 − Li/V BES		7.1/9.0 − PHS/CAES 14.9 − P2H2P		9.4/9.1 − PHS/CAES 15.2 − P2H2P

(^A) Mostly fast-ramping, single-cycle gas power plants. (^B) The storage system delivers more predictable power to the grid and, consequently, may enable nuclear and combined-cycle gas power plants to contribute to load following. (^C1) Only type-A storage, such as PHS or CAES; 2.4 TWh of storage needed (588 GW × 4 h) ≡ 4.2× the total U.S. PHS. (^C2) Only lithium-ion BES (type-D storage, RTE = 0.85); 4.7 TWh of storage needed ≡ 84× the total U.S. lithium-ion BES. (^C3) Only vanadium flow BES (type-D storage, RTE = 0.65); 4.7 TWh of storage needed. (^D) Only type-A storage considered; 14 TWh of storage needed (588 GW × 24 h) ≡ 26× the total U.S. PHS or 0.85 million metric tons of hydrogen. (^E) The generation of 478 GWy (4187 TWh) per year requires 251 million metric tons of hydrogen per year. (^F) Only type-A storage considered; 59 TWh of storage needed (588 GW × 100 h) ≡ 106× the total U.S. PHS ≡ 2.2× total U.S. PHS estimated resource or 3.5 million metric tons of hydrogen.

.

The size of the WS* fleet varies between 2253 and 7586 GW, and that of the storage system between 0 and 1829 GW, depending on the nature of the latter. The estimated overnight capital cost is USD 4.0–12.7 T depending on the size and nature of the storage system. Considering the different technology lifetimes, the estimated 60-year capital expenditure is USD 7.8–29.4 T/60 y with the reference 0% discount rate and USD 4.5–15.2 T/60 y with the 7% discount rate. These fleets are 80% CO₂-free and 100% nuclear-free. As before, depending on the amount of storage needed to guarantee grid stability, the WS/storage/gas fleets may be more capital-intensive than the reference 83% CO₂-free nuclear/gas fleet (USD 4.9 T, USD 5.0 T/60 y). To reiterate what was said earlier, more analyses would, of course, be necessary to determine which option is the most likely to provide the path of least resistance to powering a clean, affordable and reliable grid in a timely manner. Depending on the priorities, the path of least resistance may not necessarily be the less capital-intensive.

10. Summary

This paper presents some resource adequacy and capital cost considerations regarding the deployment of a large fleet of WS and storage on an idealized power grid. The yearly average capacity factor of the WS fleet is 30% without curtailment. WS penetrations of 30 to 80% were analyzed. A range of storage technologies was considered (lithium-ion and vanadium flow BES, CAES, PHS, and P2H2P) together with three storage durations (4, 24, and 100 h). Nuclear power plants provide baseload power whenever the grid can accommodate it, whereas gas power plants provide load-following capacity.

The average load is 600 GW, and it varies between 540 GW and 720 GW. The corresponding total annual electricity production is 5256 TWh. This is about 25% more than current U.S. power generation. In its Annual Energy Outlook 2023, the EIA expects U.S. demand to grow to that level by about 2045.

Overnight capital costs for each technology were obtained from appropriate references. Furthermore, to account for the lifetimes of each technology, capital costs necessary for 60 years of operation were estimated assuming a reference zero discount rate and no credit for potential recycling of systems and components with shorter lifetimes than 60 years. Two cases were also evaluated with a 7% discount rate to quantify sensitivity. The 60 years of operation was chosen as a useful benchmark because it corresponds to the longest asset lifetime, which is that of nuclear plants.

The baseline fleet does not include WS. It is made up of 847 GW of dispatchable power plants: 588 GW operate as baseload and 259 GW follow the load. If all baseload generation is from nuclear power plants, and load follow from gas power plants, the grid is 83% CO₂-free and the capital cost is USD 4.9 T. Considering the different technology operational lifetimes, the estimated 60-year capital expenditure is USD 5.0 T/60 y.

In addition to the baseline dispatchable fleet, two bounding WS cases are analyzed for each WS penetration level: one without storage and one where the whole WS fleet is connected to the storage system, hence providing a buffer between the WS fleet and the grid. The reality will likely be somewhere between these bounding cases. The viability of a power grid with a large WS penetration and no storage is not guaranteed but was nonetheless considered to provide a lower-bound capital cost estimate.

In the 30% WS penetration case, a 5% curtailment was used to facilitate grid integration. The size of the dispatchable fleet is only weakly dependent on the nature and duration of the storage system: 298–321 GW of nuclear baseload and 423–509 GW of load-following gas power plants. On the other hand, the size of the WS fleet (632–2105 GW) and that of the storage system (0–892 GW) depend strongly on the nature of the latter because of the difference in RTEs. The estimated overnight capital cost is USD 3.8–6.5 T depending on the size and nature of the storage system, i.e., USD 5.0–12.2 T/60 y. Between WS and nuclear, these fleets are 72–75% CO₂-free.

In the 60% WS penetration case, 5% and 30% curtailment were used to evaluate the impact of curtailment level. In the 5% curtailment case, the nuclear baseload fleet is reduced to almost nothing because the fluctuations of the WS fleet force baseload power into retirement. The size of the WS fleet varies between 1263 and 4211 GW, and that of the storage system between 0 and 1783 GW, depending on the nature of the latter. About 586–758 GW of load-following gas power plants are also needed. The estimated overnight capital cost is USD 2.6–8.1 T depending on the size and nature of the storage system which corresponds to USD 5.0–19.3 T/60 y with the reference 0% discount rate and USD 2.9–9.8 T/60 y with a 7% discount rate. Between WS and nuclear, these fleets are 61–68% CO₂-free. Increasing curtailment up to 30% enables more nuclear baseload to contribute to the load (140–145 GW). The size of the WS fleet varies between 1714 and 5714 GW, and that of the storage system between 0 and 1378 GW, depending on the nature of the latter. About 443–598 GW of load-following gas power plants are also needed. The estimated overnight capital cost is USD 4.2–10.8 T depending on the size and nature of the storage system, i.e., USD 7.1–23.3 T/60 y. Between WS and nuclear, these fleets are 80% CO₂-free.

In the 80% WS penetration case, a 30% curtailment was assumed. The size of the WS fleet varies between 2253 and 7586 GW, and that of the storage system between 0 and 1829 GW, depending on the nature of the latter. About 503–704 GW of load-following gas power plants are also needed. The estimated overnight capital cost is USD 4.0–12.7 T depending on the size and nature of the storage system which corresponds to USD 7.8–29.4 T/60 y with the reference 0% discount rate and USD 4.5–15.2 T/60 y with a 7% discount rate. These fleets are 80% CO₂-free and 100% nuclear-free.

The results are summarized graphically in Figure 13.

11. Conclusions and Future Work

Depending on the amount of storage needed to guarantee grid stability, the options that rely strongly on WS could be significantly more capital intensive than those that rely strongly on nuclear. This is especially true in the long run because WS and storage assets have shorter lifetimes than nuclear plants and, consequently, need to be replaced more frequently. More analyses (including grid stability, resource availability, and public acceptance) would be necessary to determine which one is the most likely to provide the path of least resistance to powering a clean, affordable and reliable grid in a timely manner. Depending on the priorities, the path of least resistance may not necessarily be the less capital-intensive one.

The grids discussed in this paper are large enough to be essentially isolated systems. This is typically the case for large economic and geographic entities such as the U.S., Europe, or China, for example. It is also the case for remote islands. These grids have in common that the amount of electricity generated from within is much larger than that exported to or imported from neighboring states.

As a first step, idealized fully interconnected grids without transmission losses are analyzed. This is an optimistic assumption. Actual grids will require more WS and storage capacity than this idealized grid to reach the same penetration. That said, the conclusions are still expected to apply qualitatively to real grids.

However, the conclusions cannot be expected to apply quantitatively to actual grids for the reasons just mentioned. Describing actual grids with more detailed models than used in this paper would be the next logical step to inform policy with actionable quantitative conclusions.

To reflect actual grids, it would be necessary to consider the following: (1) sensitivity and uncertainty; (2) technology-specific availability factors; (3) energy mix deployed on the grid, i.e., wind, solar, storage, and dispatchable; (4) grid constraints such as frequency control, congestion, and losses; (5) practical deployment barriers to storage systems such as geographical, material, or regulatory; (6) the effect of variable WS power on the performances of the storage systems; (7) ways to use the curtailed WS power for off-grid applications.