Generalized Predictive Control for a Single-Phase, Three-Level Voltage Source Inverter
Abstract
:1. Introduction
- A proposal for a GPC controller applied to a multilevel VSI in off-grid operation mode;
- CCS–MPC real-time implementation with a vast prediction horizon, without increasing the computational cost;
- A complete integration of the entire control strategy within a single control device, eliminating the need for additional filters or intermediate devices.
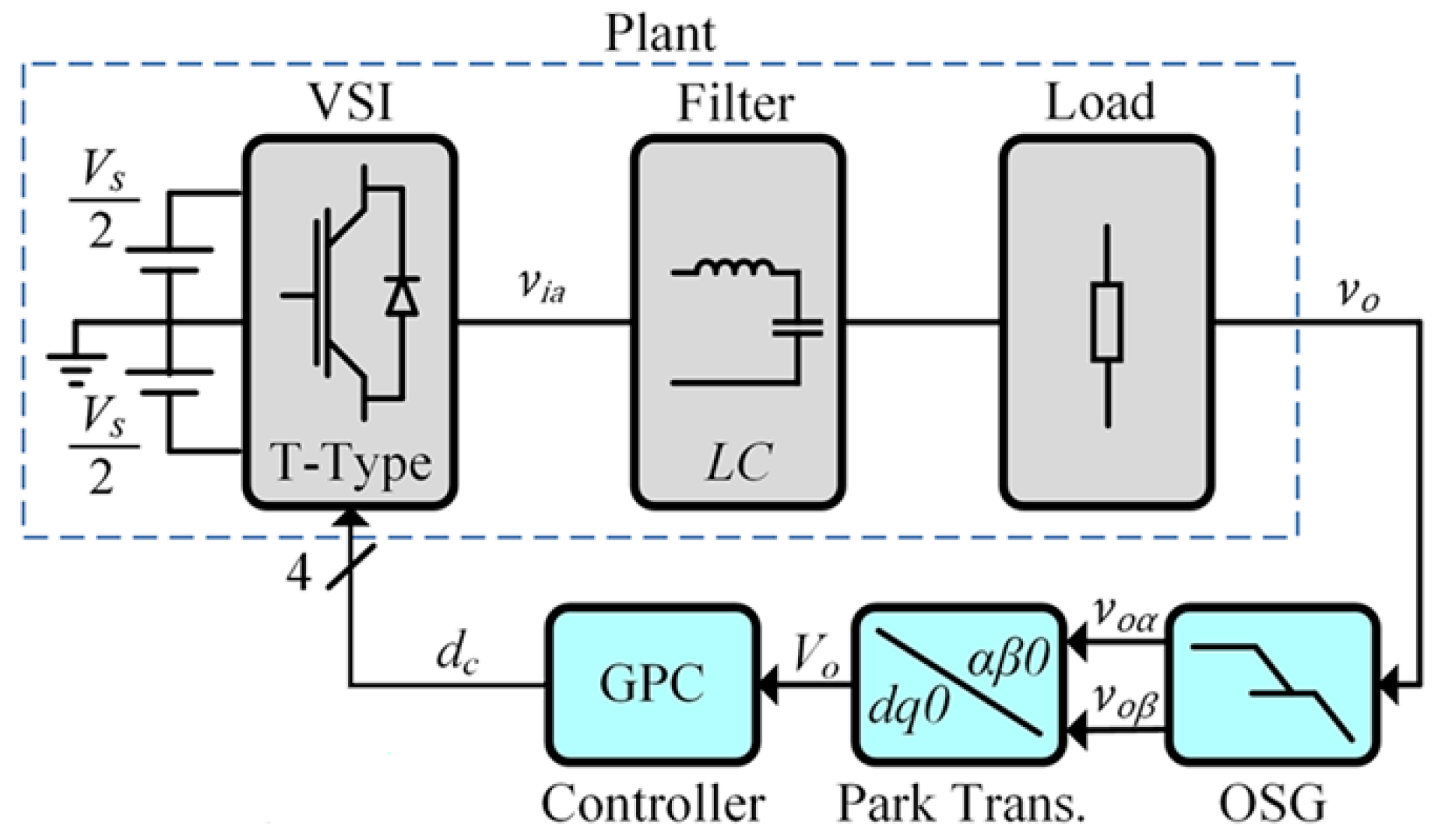
2. System Modeling
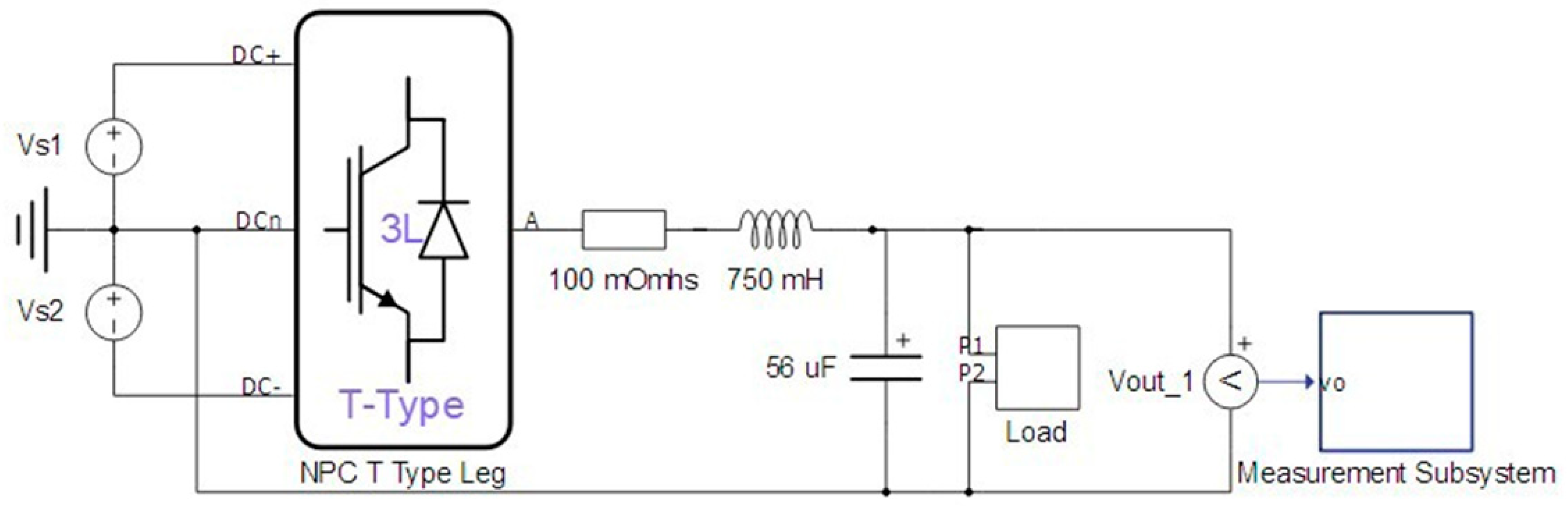
2.1. Single-Phase T-Type NPC Voltage Source Inverter
2.2. Orthogonal Signal Generator
2.3. Generalized Predictive Control
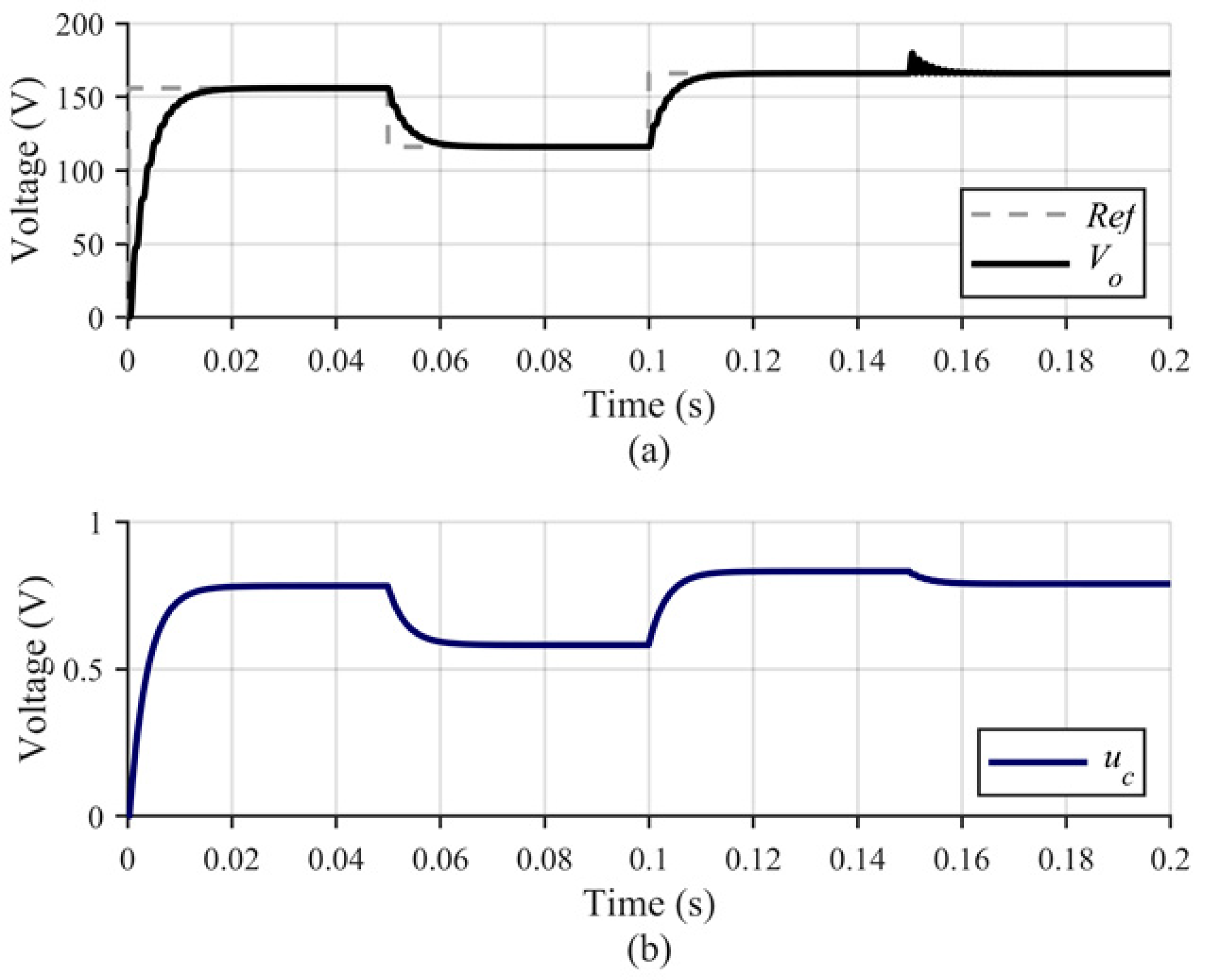
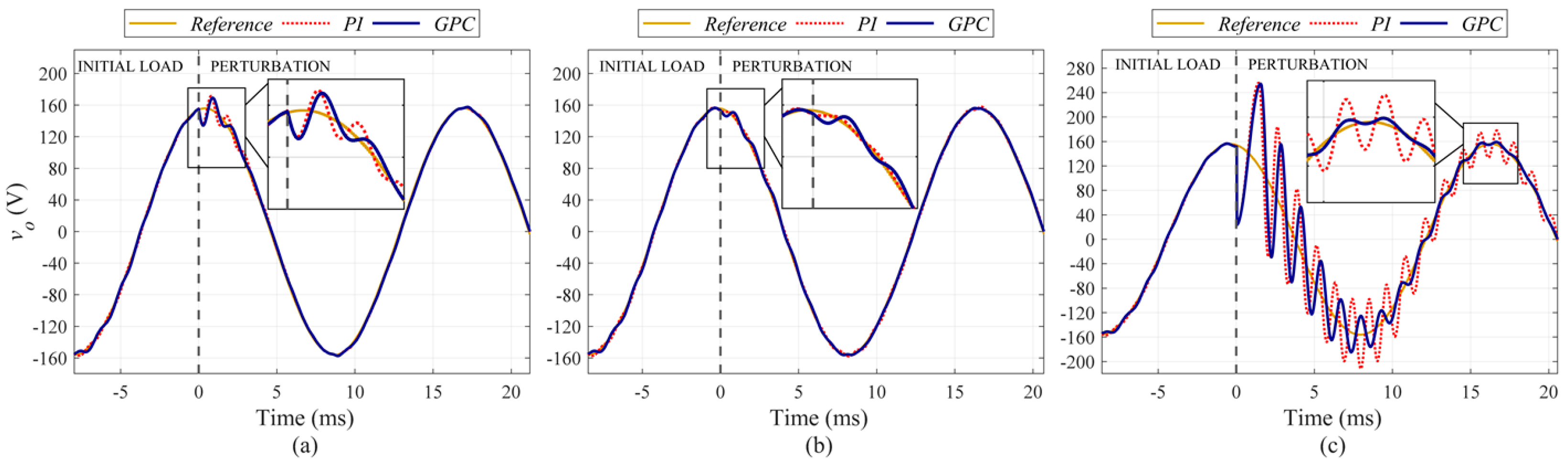
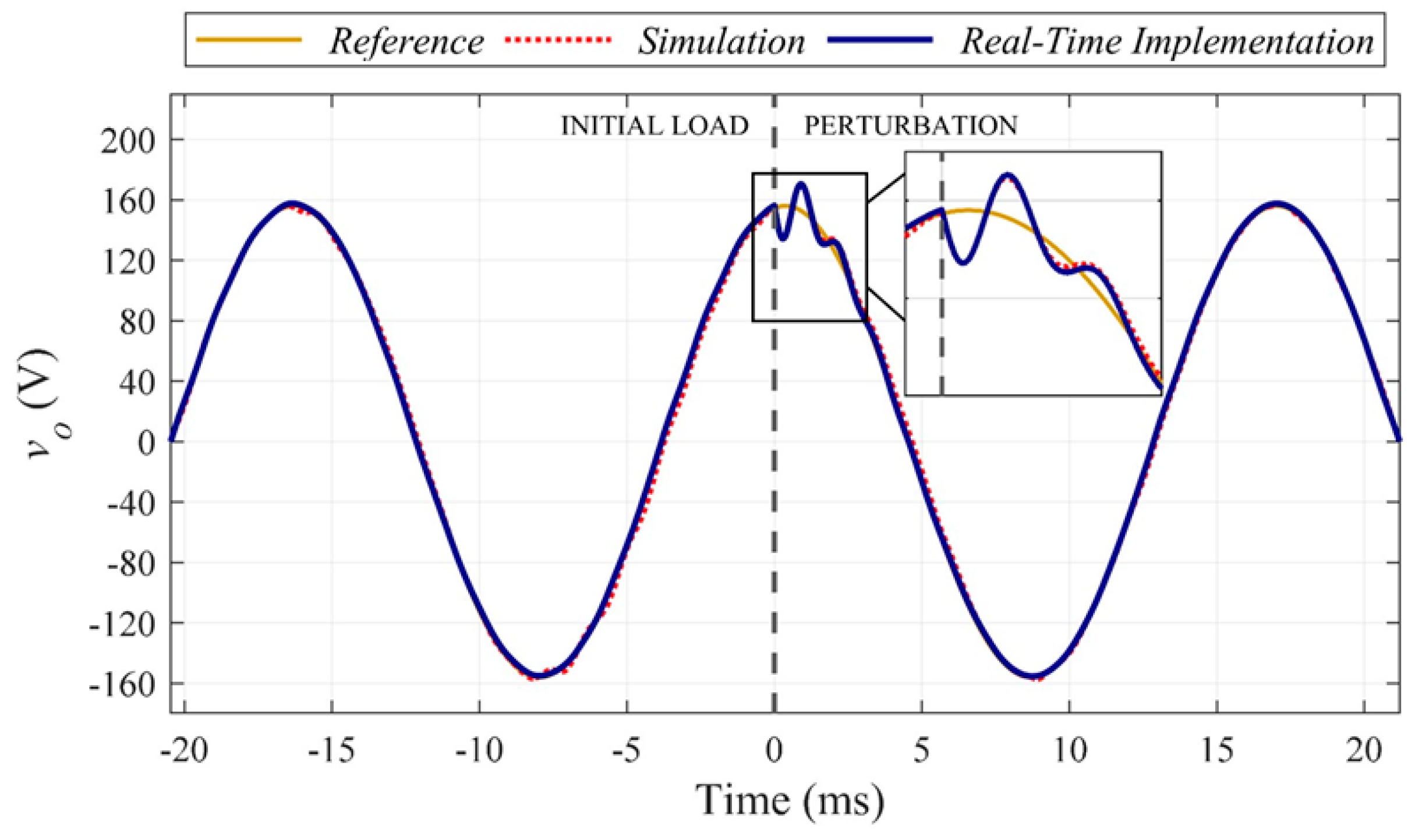
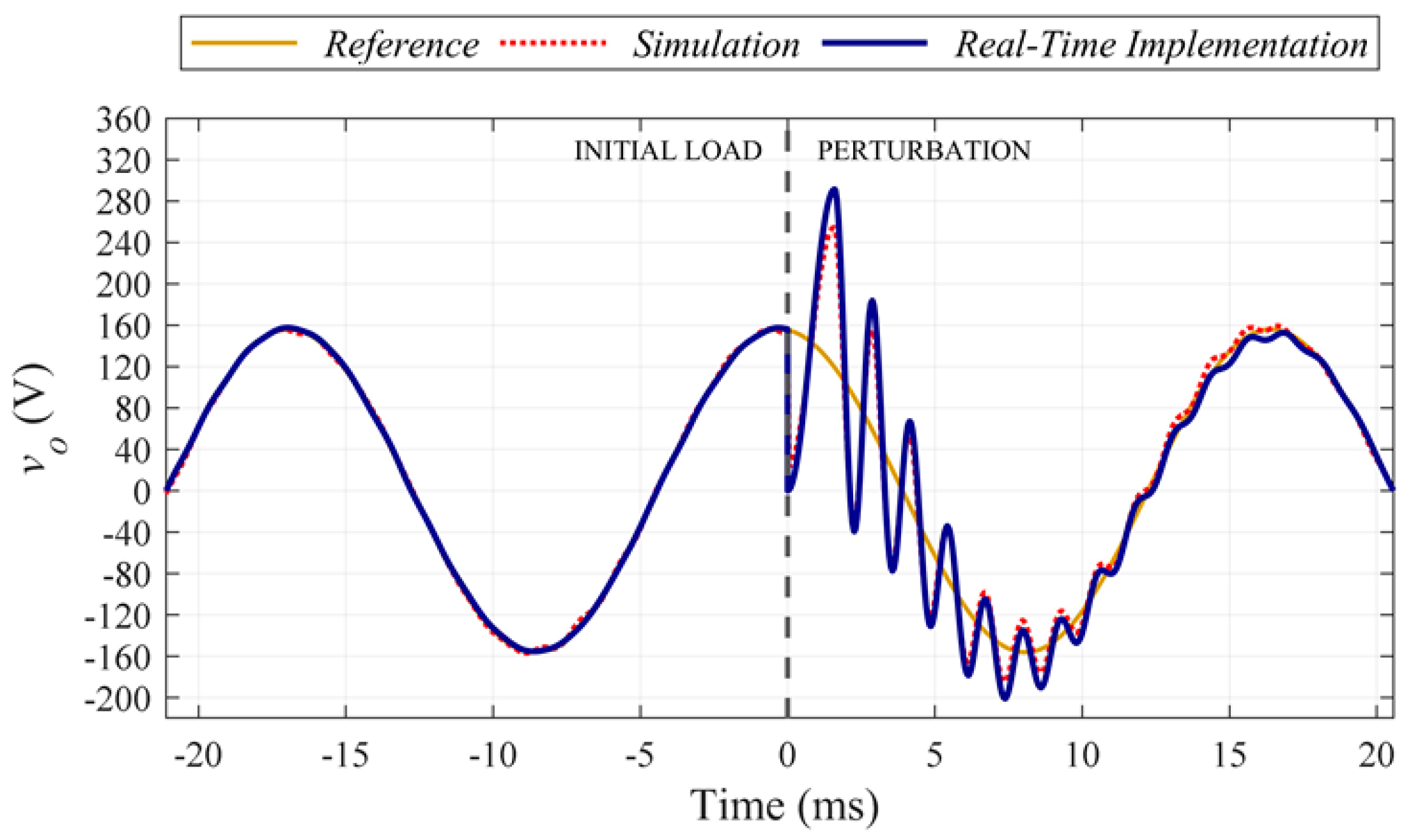
3. Simulation Results
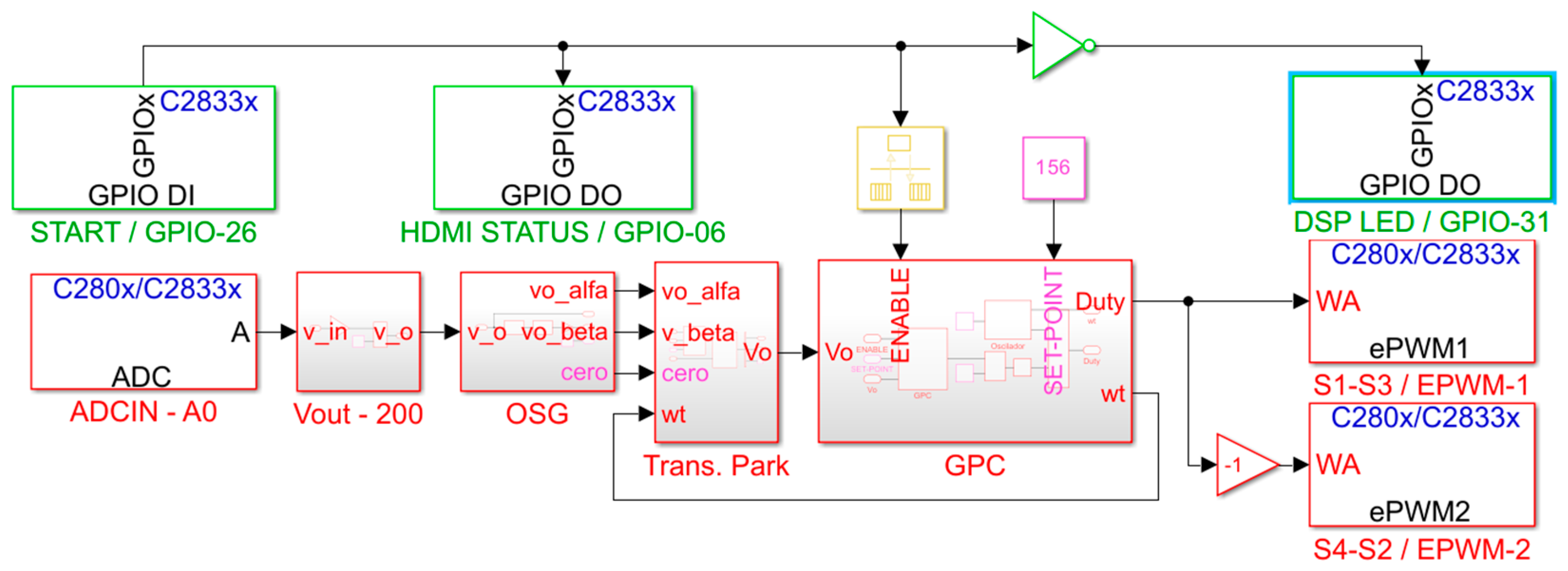
4. System Implementation and Results
5. Conclusions
- An experimental validation and efficiency analysis of the proposed approach involving a real T-type NPC VSI;
- Apply restrictions to the GPC cost function and improve the control technique for NL loads;
- Perform a comprehensive study of various metaheuristic and machine learning methods for controlling a T-type NPC VSI.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. World Energy Outlook 2022; International Energy Agency: Paris, France, 2022. [Google Scholar]
- Meral, M.E.; Çelík, D. A comprehensive survey on control strategies of distributed generation power systems under normal and abnormal conditions. Annu. Rev. Control 2019, 47, 112–132. [Google Scholar] [CrossRef]
- Memon, M.A.; Mekhilef, S.; Mubin, M.; Aamir, M. Selective harmonic elimination in inverters using bio-inspired intelligent algorithms for renewable energy conversion applications: A review. Renew. Sustain. Energy Rev. 2018, 82, 2235–2253. [Google Scholar] [CrossRef]
- Sultana, W.R.; Sahoo, S.K.; Sukchai, S.; Yamuna, S.; Venkatesh, D. A review on state of art development of model predictive control for renewable energy applications. Renew. Sustain. Energy Rev. 2017, 76, 391–406. [Google Scholar] [CrossRef]
- Mohamed, A.A.S.; Metwally, H.; El-Sayed, A.; Selem, S.I. Predictive neural network based adaptive controller for grid-connected PV systems supplying pulse-load. Sol. Energy 2019, 193, 139–147. [Google Scholar] [CrossRef]
- Silva, F.A. Advanced DC\/AC Inverters: Applications in Renewable Energy. IEEE Ind. Electron. Mag. 2013, 7, 68–69. [Google Scholar] [CrossRef]
- Amin, M.R.; Zulkifli, S.A. A framework for selection of grid-inverter synchronisation unit: Harmonics, phase-angle and frequency. Renew. Sustain. Energy Rev. 2017, 78, 210–219. [Google Scholar] [CrossRef]
- Andishgar, M.H.; Gholipour, E.; Hooshmand, R. An overview of control approaches of inverter-based microgrids in islanding mode of operation. Renew. Sustain. Energy Rev. 2017, 80, 1043–1060. [Google Scholar] [CrossRef]
- Khooban, M.-H. Secondary Load Frequency Control of Time-Delay Stand-Alone Microgrids With Electric Vehicles. IEEE Trans. Ind. Electron. 2018, 65, 7416–7422. [Google Scholar] [CrossRef]
- Hassan, A.; Yang, X.; Chen, W.; Houran, M.A. A State of the Art of the Multilevel Inverters with Reduced Count Components. Electronics 2020, 9, 1924. [Google Scholar] [CrossRef]
- Rana, R.A.; Patel, S.A.; Muthusamy, A.; Lee, C.W.; Kim, H.-J. Review of Multilevel Voltage Source Inverter Topologies and Analysis of Harmonics Distortions in FC-MLI. Electronics 2019, 8, 1329. [Google Scholar] [CrossRef]
- Aly, M.; Ahmed, E.M.; Shoyama, M. Modulation Method for Improving Reliability of Multilevel T-Type Inverter in PV Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1298–1309. [Google Scholar] [CrossRef]
- Trabelsi, M.; Alquennah, A.N.; Vahedi, H. Review on Single-DC-Source Multilevel Inverters: Voltage Balancing and Control Techniques. IEEE Open J. Ind. Electron. Soc. 2022, 3, 711–732. [Google Scholar] [CrossRef]
- Basha, S.G.; Mani, V.; Mopidevi, S. Single-phase thirteen-level dual-boost inverter based shunt active power filter control using resonant and fuzzy logic controllers. CSEE J. Power Energy Syst. 2020, 8, 849–863. [Google Scholar] [CrossRef]
- Das, S.R.; Mishra, A.K.; Sahoo, A.K.; Hota, A.P.; Viriyasitavat, W.; Alghamdi, N.S.; Dhiman, G. Fuzzy Controller Designed-Based Multilevel Inverter for Power Quality Enhancement. IEEE Trans. Consum. Electron. 2024, 70, 4839–4847. [Google Scholar] [CrossRef]
- Trabelsi, M.; Ben-Brahim, L.; Gastli, A.; Abu-Rub, H. Enhanced Deadbeat Control Approach for Grid-Tied Multilevel Flying Capacitors Inverter. IEEE Access 2022, 10, 16720–16728. [Google Scholar] [CrossRef]
- Ramaiah, S.L.N.; Mishra, M.K. Loss Modulated Deadbeat Control for Grid Connected Inverter System. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3715–3725. [Google Scholar] [CrossRef]
- Stonier, A.A.; Murugesan, S.; Samikannu, R.; Venkatachary, S.K.; Kumar, S.S.; Arumugam, P. Power Quality Improvement in Solar Fed Cascaded Multilevel Inverter With Output Voltage Regulation Techniques. IEEE Access 2020, 8, 178360–178371. [Google Scholar] [CrossRef]
- Makhamreh, H.; Trabelsi, M.; Kukrer, O.; Abu-Rub, H. An Effective Sliding Mode Control Design for a Grid-Connected PUC7 Multilevel Inverter. IEEE Trans. Ind. Electron. 2020, 67, 3717–3725. [Google Scholar] [CrossRef]
- Anssari, O.M.H.; Badamchizadeh, M.; Ghaemi, S. Designing of a PSO-Based Adaptive SMC With a Multilevel Inverter for MPPT of PV Systems Under Rapidly Changing Weather Conditions. IEEE Access 2024, 12, 41421–41435. [Google Scholar] [CrossRef]
- Andino, J.; Ayala, P.; Llanos-Proano, J.; Naunay, D.; Martinez, W.; Arcos-Aviles, D. Constrained Modulated Model Predictive Control for a Three-Phase Three-Level Voltage Source Inverter. IEEE Access 2022, 10, 10673–10687. [Google Scholar] [CrossRef]
- Huo, X.; Li, P. Parameter-free ultralocal model-based predictive current control method for grid-tied inverters using extremum seeking control. Control Eng. Pract. 2025, 157, 106253. [Google Scholar] [CrossRef]
- Azizi, A.; Akhbari, M.; Danyali, S.; Tohidinejad, Z.; Shirkhani, M. A review on topology and control strategies of high-power inverters in large- scale photovoltaic power plants. Heliyon 2025, 11, e42334. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Acuna, P.; Aguilera, R.P.; Jiang, J.; Wei, S.; Fletcher, J.E.; Lu, D.D. Model Predictive Control for DC–DC Boost Converters With Reduced-Prediction Horizon and Constant Switching Frequency. IEEE Trans. Power Electron. 2018, 33, 9064–9075. [Google Scholar] [CrossRef]
- Judewicz, M.G.; González, S.A.; Fischer, J.R.; Martínez, J.F.; Carrica, D.O. Generalised predictive current-mode control of passive front-end boost-type converters. IET Power Electron. 2021, 14, 666–679. [Google Scholar] [CrossRef]
- De Oliveira, H.A.; Torrico, B.C.; De, S.D.; Barbosa, S.G.; De Almeida Filho, M.P. Predictive Control Applied to a Single-Stage, Single-Phase Bidirectional AC-DC Converter. IEEE Access 2022, 10, 34984–34995. [Google Scholar] [CrossRef]
- Shao, M.; Deng, Y.; Li, H.; Liu, J.; Fei, Q. Robust Speed Control for Permanent Magnet Synchronous Motors Using a Generalized Predictive Controller With a High-Order Terminal Sliding-Mode Observer. IEEE Access 2019, 7, 121540–121551. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Generalized Predictive Control. In Model Predictive Control of Microgrids. Advances in Industrial Control, 2nd ed.; Springer: London, UK, 2007; Volume 4, pp. 47–79. [Google Scholar] [CrossRef]
- Bordons, C.; Garcia-Torres, F.; Ridao, M.A. Microgrids Power Quality Enhancement. In Model Predictive Control of Microgrids. Advances in Industrial Control, 2nd ed.; Springer: London, UK, 2020. [Google Scholar] [CrossRef]
- Franco, R.A.P.; Cardoso, Á.A.; Filho, G.L.; Vieira, F.H.T. MIMO auto-regressive modeling-based generalized predictive control for grid-connected hybrid systems. Comput. Electr. Eng. 2022, 97, 107636. [Google Scholar] [CrossRef]
- Cerón, C.E.P.; Lourenço, L.F.N.; Solís-Chaves, J.S.; Filho, A.J.S. A Generalized Predictive Controller for a Wind Turbine Providing Frequency Support for a Microgrid. Energies 2022, 15, 2562. [Google Scholar] [CrossRef]
- Šimek, P.; Valouch, V. Generalized predictive power control for grid-connected converter. Int. J. Electr. Power Energy Syst. 2021, 125, 106380. [Google Scholar] [CrossRef]
- Wang, T.; Zhu, Z.Q.; Freire, N.M.A.; Stone, D.A.; Foster, M.P. Generalized Predictive dc-Link Voltage Control for Grid-Connected Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1489–1506. [Google Scholar] [CrossRef]
- Tran, T.V.; Kim, K.-H.; Lai, J.-S. Optimized Active Disturbance Rejection Control With Resonant Extended State Observer for Grid Voltage Sensorless LCL -Filtered Inverter. IEEE Trans. Power Electron. 2021, 36, 13317–13331. [Google Scholar] [CrossRef]
- Lunardi, A.; Conde, D.E.R.; de Assis, J.; Fernandes, D.A.; Filho, A.J.S. Model Predictive Control with Modulator Applied to Grid Inverter under Voltage Distorted. Energies 2021, 14, 4953. [Google Scholar] [CrossRef]
- Zamani, H.; Abbaszadeh, K.; Karimi, M.; Gyselinck, J. Offset free generalized model predictive control for 3-phase LCL-filter based grid-tied inverters. Int. J. Electr. Power Energy Syst. 2023, 153, 109351. [Google Scholar] [CrossRef]
- Judewicz, M.G.; Gonzalez, S.A.; Echeverria, N.I.; Fischer, J.R.; Carrica, D.O. Generalized Predictive Current Control (GPCC) for Grid-Tie Three-Phase Inverters. IEEE Trans. Ind. Electron. 2016, 63, 4475–4484. [Google Scholar] [CrossRef]
- Judewicz, M.G.; Gonzalez, S.A.; Fischer, J.R.; Martinez, J.F.; Carrica, D.O. Inverter-Side Current Control of Grid-Connected Voltage Source Inverters With LCL Filter Based on Generalized Predictive Control. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1732–1743. [Google Scholar] [CrossRef]
- Memeghani, M.J.; Ghamari, S.M.; Jouybari, T.Y.; Mollaee, H.; Wheeler, P. Generalised predictive controller (GPC) design on single-phase full-bridge inverter with a novel identification method. IET Control Theory Appl. 2023, 17, 284–294. [Google Scholar] [CrossRef]
- Lunardi, A.; Conde, E.; Assis, J.; Meegahapola, L.; Fernandes, D.A.; Filho, A.J.S. Repetitive Predictive Control for Current Control of Grid-Connected Inverter Under Distorted Voltage Conditions. IEEE Access 2022, 10, 16931–16941. [Google Scholar] [CrossRef]
- Cordero, R.; Estrabis, T.; Brito, M.A.; Gentil, G. Development of a Resonant Generalized Predictive Controller for Sinusoidal Reference Tracking. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1218–1222. [Google Scholar] [CrossRef]
- Naunay, D.; Ayala, P.; Andino, J.; Martinez, W.; Llanos, J.; Arcos-Aviles, D. Generalized predictive control strategy applied to a single-phase T-type voltage source inverter in stand-alone operation mode. In Proceedings of the 22nd Workshop on Control and Modelling of Power Electronics (COMPEL), Cartagena, Colombia, 2–5 November 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Boussada, Z.; Elbeji, O.; Benhamed, M. Modeling of diode clamped inverter using SPWM technique. In Proceedings of the International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Prabaharan, N.; Palanisamy, K. A comprehensive review on reduced switch multilevel inverter topologies, modulation techniques and applications. Renew. Sustain. Energy Rev. 2017, 76, 1248–1282. [Google Scholar] [CrossRef]
- Sebaaly, F.; Kanaan, H.Y.; Moubayed, N. Three-level neutral-point-clamped inverters in transformerless PV systems—State of the art. In Proceedings of the MELECON 2014—2014 17th IEEE Mediterranean Electrotechnical Conference, Beirut, Lebanon, 13–16 April 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Mishra, P.; Maheshwari, R. Design, Analysis, and Impacts of Sinusoidal LC Filter on Pulsewidth Modulated Inverter Fed-Induction Motor Drive. IEEE Trans. Ind. Electron. 2020, 67, 2678–2688. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, L.; Xing, Y.; Zhang, Z.; Zhao, H.; Ge, H. Generalized Clarke Transformation and Enhanced Dual-Loop Control Scheme for Three-Phase PWM Converters Under the Unbalanced Utility Grid. IEEE Trans. Power Electron. 2022, 37, 8935–8947. [Google Scholar] [CrossRef]
- O’Rourke, C.J.; Qasim, M.M.; Overlin, M.R.; Kirtley, J.L. A Geometric Interpretation of Reference Frames and Transformations: dq0, Clarke, and Park. IEEE Trans. Energy Convers. 2019, 34, 2070–2083. [Google Scholar] [CrossRef]
- Tan, G.; Sun, X. Analysis of Tan-Sun Coordinate Transformation System for Three-Phase Unbalanced Power System. IEEE Trans. Power Electron. 2018, 33, 5386–5400. [Google Scholar] [CrossRef]
- Bamigbade, A.; Khadkikar, V.; Zeineldin, H.H.; El Moursi, M.S.; Al Hosani, M. A Novel Power-Based Orthogonal Signal Generator for Single-Phase Systems. IEEE Trans. Power Deliv. 2021, 36, 469–472. [Google Scholar] [CrossRef]
- Bertoluzzo, M.; Giacomuzzi, S.; Kumar, A. Design and Experimentation of a Single-Phase PLL With Novel OSG Method. IEEE Access 2022, 10, 33393–33407. [Google Scholar] [CrossRef]
- Kang, Y.G.; Reigosa, D.D. Improving Harmonic Rejection Capability of OSG Based on n-th Order Bandpass Filter for Single-Phase System. IEEE Access 2021, 9, 81728–81739. [Google Scholar] [CrossRef]
- Lamo, P.; Pigazo, A.; Azcondo, F.J. Evaluation of Quadrature Signal Generation Methods with Reduced Computational Resources for Grid Synchronization of Single-Phase Power Converters through Phase-Locked Loops. Electronic 2020, 9, 2026. [Google Scholar] [CrossRef]
- Madgula, S.; Veeramsetty, V.; Durgam, R. Signal processing approaches for power quality disturbance classification: A comprehensive review. Results Eng. 2025, 25, 104569. [Google Scholar] [CrossRef]
- Chen, W.; Bazzi, A.M. Model-Based Voltage Quality Analysis and Optimization in Post-Fault Reconfigured N-Level NPC Inverter. IEEE Trans. Power Electron. 2021, 36, 13706–13715. [Google Scholar] [CrossRef]
- Arranz-Gimon, A.; Zorita-Lamadrid, A.; Morinigo-Sotelo, D.; Duque-Perez, O. A Review of Total Harmonic Distortion Factors for the Measurement of Harmonic and Interharmonic Pollution in Modern Power Systems. Energies 2021, 14, 6467. [Google Scholar] [CrossRef]
- IEEE Std 519-2014 (Revision IEEE Std 519-1992); 519-2014—IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2014; pp. 1–29. [CrossRef]
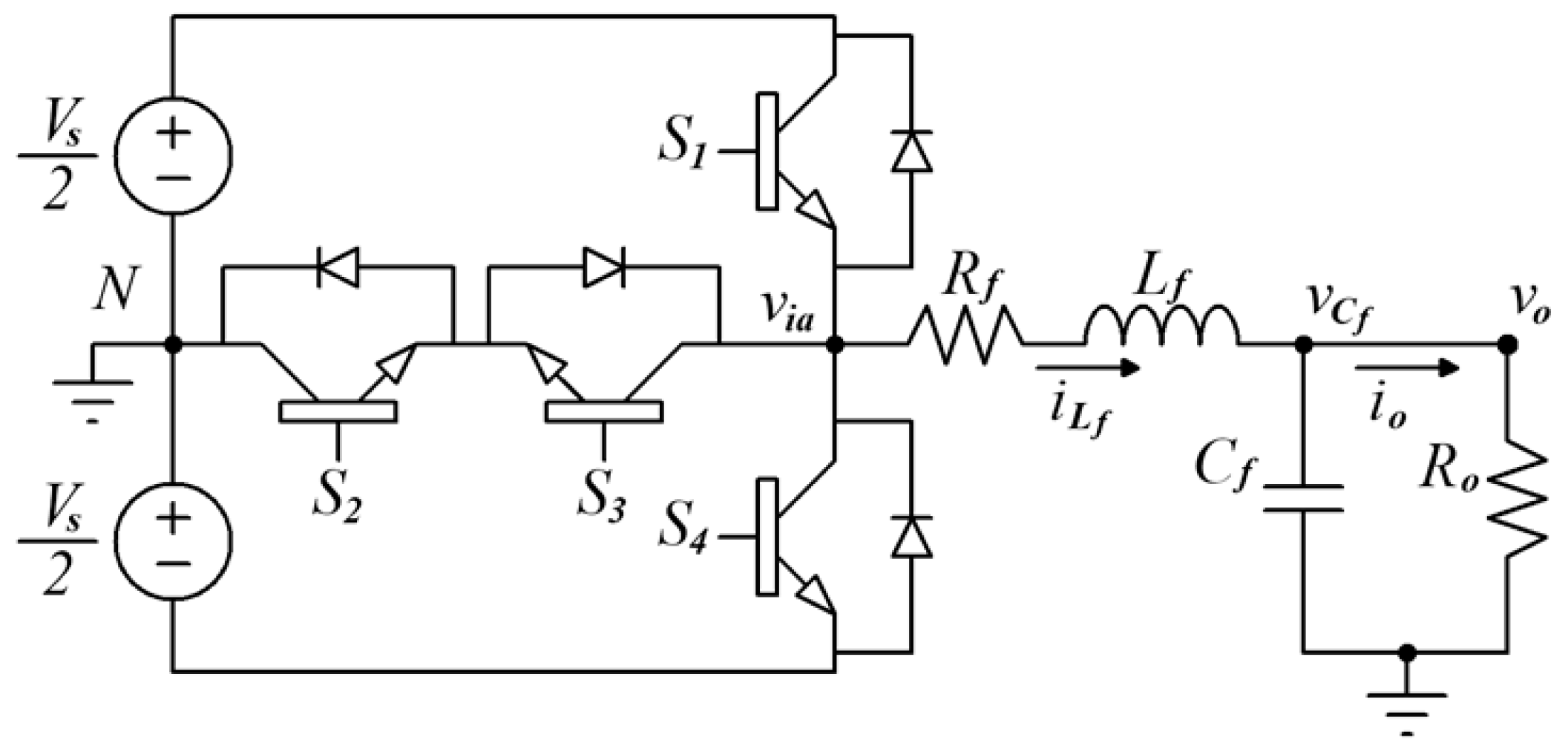



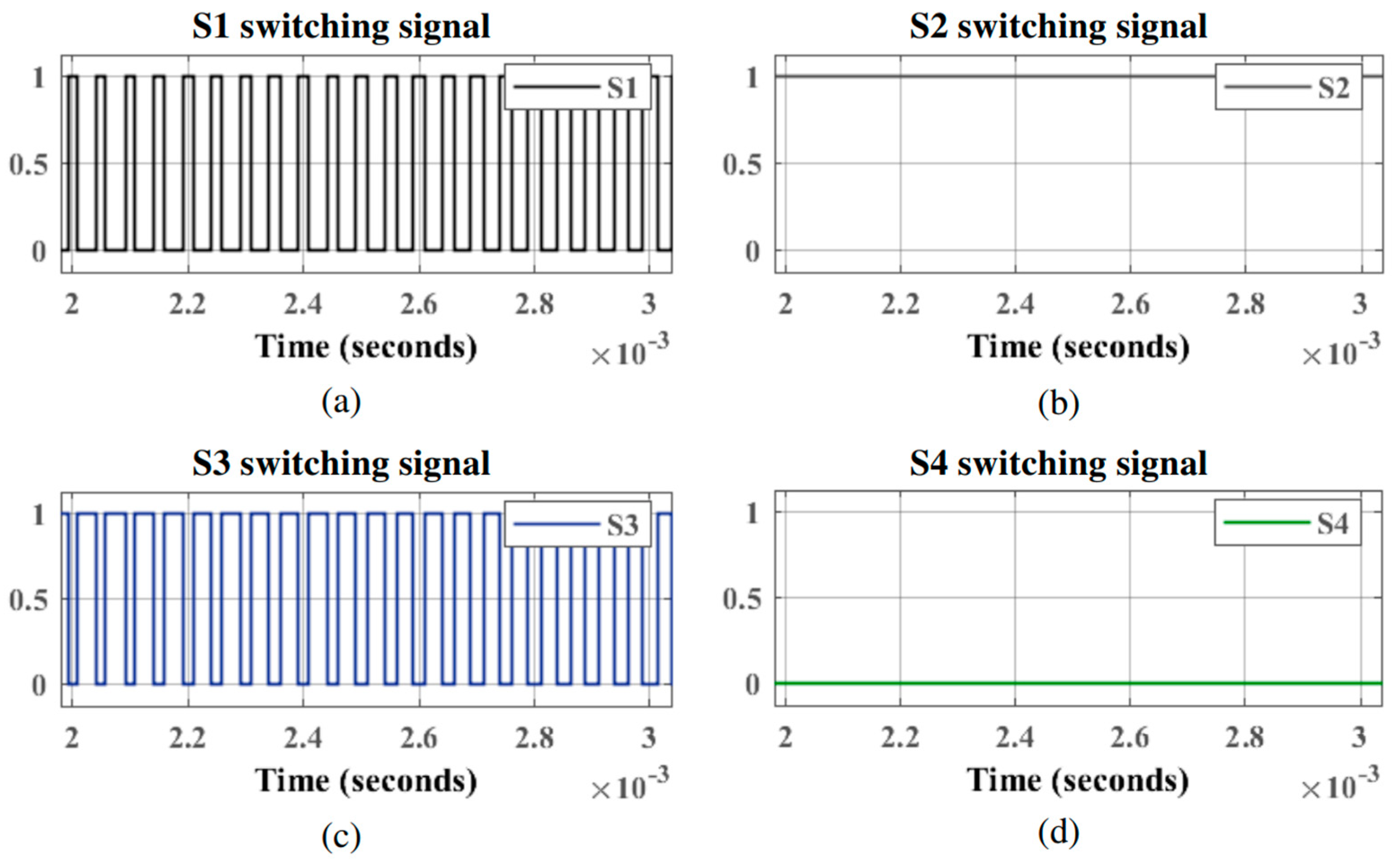
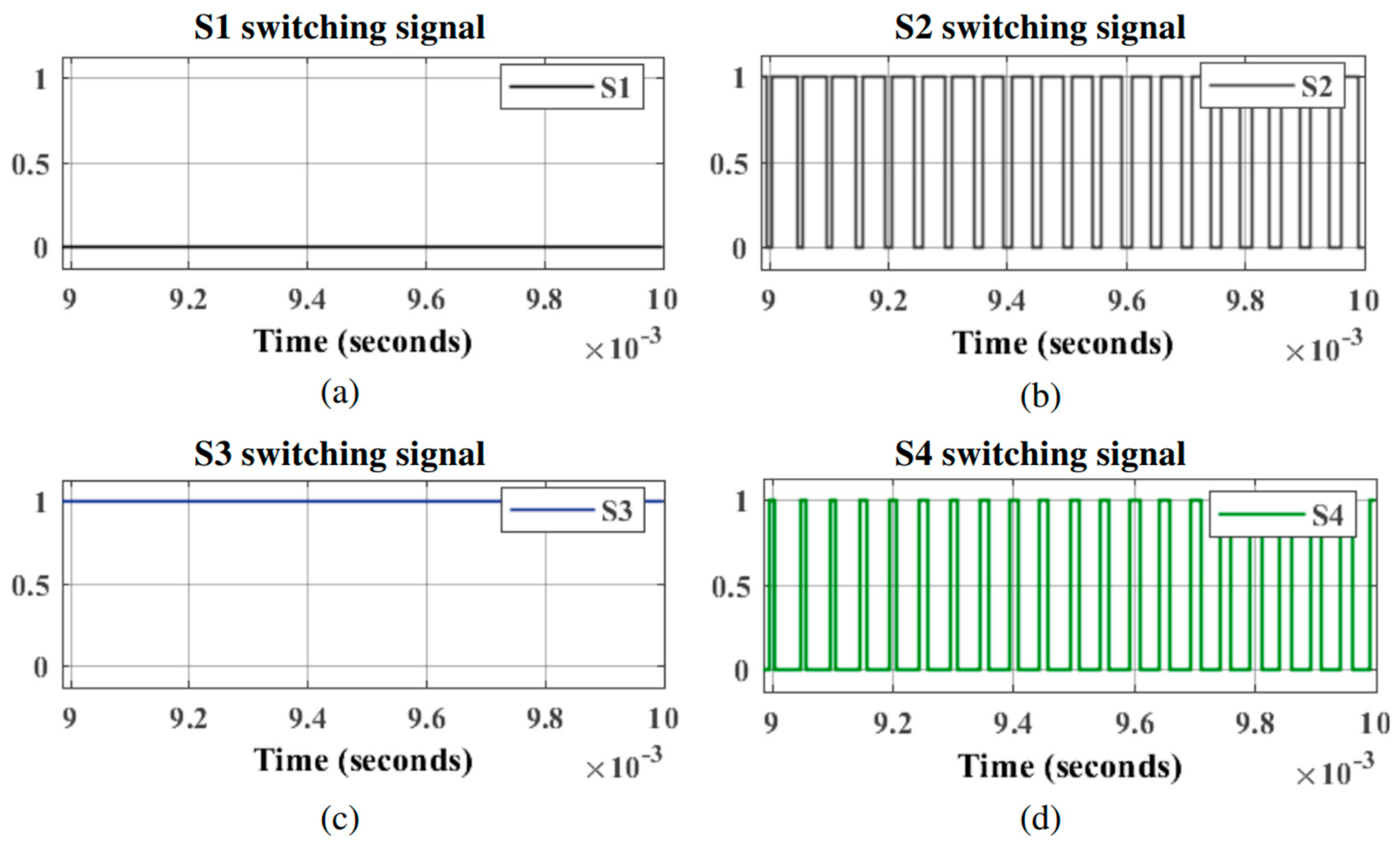



| u | S1 | S2 | S3 | S4 | Via |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | +Vs/2 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| −1 | 0 | 0 | 1 | 1 | −Vs/2 |
| Parameter | Definition | Value | Unit |
|---|---|---|---|
| Vs | DC-link voltage | 400 | V |
| vo | Nominal AC-link voltage | 110 | VRMS |
| fn | Nominal frequency | 60 | Hz |
| fs | Switching frequency | 20 | kHz |
| Ts | Sampling time | 50 | μs |
| Lf | Filter inductance | 750 | μH |
| Rf | Inductance resistance | 100 | mΩ |
| Cf | Filter capacitance | 56 | μF |
| Ro | Output load | 40 | Ω |
| Control | THD (%) | ||||
|---|---|---|---|---|---|
| R = 5.5 Ω | R = 20 Ω | R = 50 Ω | R = 500 Ω | R = 1000 Ω | |
| GPC | 0.29 | 0.66 | 1.41 | 2.40 | 2.58 |
| PI | 0.29 | 0.74 | 1.25 | 144.27 | 154.14 |
| Control | THD (%) | ||
|---|---|---|---|
| Case 1 R = 50 Ω, L = 10 mH | Case 2 R = 50 Ω, L = 20 mH | Case 3 R = 50 Ω, L = 50 mH | |
| GPC | 1.51 | 1.80 | 1.91 |
| PI | 3.65 | 94.02 | 161.90 |
| Control | THD (%) | ||
|---|---|---|---|
| Case 1 C = 330 μF, R = 100 Ω | Case 2 C = 330 μF, R = 200 Ω | Case 3 C = 330 μF, R = 500 Ω | |
| GPC | 9.43 | 6.40 | 3.58 |
| PI | 8.51 | 7.08 | 5.26 |
| GPC | THD (%) | ||||
|---|---|---|---|---|---|
| R = 5.5 Ω | R = 20 Ω | R = 50 Ω | R = 500 Ω | R = 1000 Ω | |
| IMP | 0.83 | 0.79 | 0.89 | 1.02 | 0.99 |
| SIM | 0.29 | 0.66 | 1.41 | 2.40 | 2.58 |
| GPC | THD (%) | ||
|---|---|---|---|
| Case 1 R = 50 Ω, L = 10 mH | Case 2 R = 50 Ω, L = 20 mH | Case 3 R = 50 Ω, L = 50 mH | |
| IMP | 0.99 | 1.06 | 1.15 |
| SIM | 1.51 | 1.80 | 1.91 |
| GPC | THD (%) | ||
|---|---|---|---|
| Case 1 C = 330 μF, R = 100 Ω | Case 2 C = 330 μF, R = 200 Ω | Case 3 C = 330 μF, R = 500 Ω | |
| IMP | 9.30 | 6.39 | 3.81 |
| SIM | 9.43 | 6.40 | 3.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naunay, D.; Ayala, P.; Andino, J.; Martinez, W.; Arcos-Aviles, D. Generalized Predictive Control for a Single-Phase, Three-Level Voltage Source Inverter. Energies 2025, 18, 2541. https://doi.org/10.3390/en18102541
Naunay D, Ayala P, Andino J, Martinez W, Arcos-Aviles D. Generalized Predictive Control for a Single-Phase, Three-Level Voltage Source Inverter. Energies. 2025; 18(10):2541. https://doi.org/10.3390/en18102541
Chicago/Turabian StyleNaunay, Diego, Paul Ayala, Josue Andino, Wilmar Martinez, and Diego Arcos-Aviles. 2025. "Generalized Predictive Control for a Single-Phase, Three-Level Voltage Source Inverter" Energies 18, no. 10: 2541. https://doi.org/10.3390/en18102541
APA StyleNaunay, D., Ayala, P., Andino, J., Martinez, W., & Arcos-Aviles, D. (2025). Generalized Predictive Control for a Single-Phase, Three-Level Voltage Source Inverter. Energies, 18(10), 2541. https://doi.org/10.3390/en18102541







