Design for Loss Reduction in a Compact AFPM Electric Water Pump with a PCB Motor

Abstract

A PCB stator axial flux permanent magnet (AFPM) motor is presented that overcomes the manufacturing challenges associated with the complex geometry of conventional stators by employing a PCB substrate. Traditionally, AFPM motors are produced by winding coils around the stator teeth, a process that requires specialized winding machinery and is both labor intensive and time consuming, ultimately incurring considerable manufacturing costs and delays. In contrast, PCB substrates offer significant advantages in manufacturability and mass production, effectively resolving these issues. Furthermore, the primary material used in PCB substrates, FR-4, exhibits a permeability similar to that of air, resulting in negligible electromagnetic cogging torque. Cogging torque arises from the attraction between permanent magnets and stator teeth, creating forces that interfere with motor rotation and generate unwanted vibration, noise, and potential mechanical collisions between the rotor and stator. In the PCB stator design, the conventional PCB circuit pattern is replaced by the motor’s coil configuration, and the absence of stator teeth eliminates these interference issues. Consequently, a slotless motor configuration with minimal vibration and noise is achieved. The PCB AFPM motor has been applied to a vehicle-mounted electric water pump (EWP), where mass production and space efficiency are critical. In an EWP, which integrates the impeller with the motor, it is essential that vibrations are minimized since excessive vibration could compromise impeller operation and, due to fluid resistance, require high power input. Moreover, the AFPM configuration facilitates higher torque generation compared to a conventional radial flux permanent magnet synchronous motor (RFPM). In a slotless AFPM motor, the absence of stator teeth prevents core flux saturation, thereby further enhancing torque performance. AC losses occur in the conductors as a result of the magnetic flux produced by the permanent magnets, and similar losses arise within the PCB circuits. Therefore, an optimized PCB circuit design is essential to reduce these losses. The Constant Trace Conductor (CTC) PCB circuit design process is proposed as a viable solution to mitigate AC losses. A 3D finite element analysis (3D FEA) model was developed, analyzed, fabricated, and validated to verify the proposed solution.

1. Introduction

Currently, there is a trend toward transitioning from mechanical systems to electrified systems, with particularly active shifts in automotive applications. In conventional internal combustion engines, a mechanical water pump was used solely for engine cooling; however, beginning with hybrid (HEV) or plug-in hybrid (PHEV) vehicles, an electric water pump (EWP) has been introduced that is capable of cooling the engine, the motor, and the battery simultaneously. In an electric vehicle (EV), an EWP is required not only for the drive motor and battery but also for the autonomous driving controller. Consequently, HEV and EV vehicles incorporate a greater number of EWP units.

Due to spatial constraints in vehicles, an increase in the number of EWP units necessitates a reduction in their individual sizes. With a conventional radial flux permanent magnet (RFPM) motor, reducing the size leads to a decrease in output, thereby approaching a technical limitation. PCB motors offer a significant reduction in axial size, thereby facilitating easier accommodation in confined spaces. Accordingly, recent research on motors utilizing PCB stator technology has intensified. Current research topics on PCB motors include, for example, the use of Halbach magnets to reduce leakage flux and enhance air-gap flux density [1], investigations of eddy current losses related to trace width and circulating current losses with respect to the number of layers [2,3], PCB stators composed of concentrated windings [4] and distributed windings [5], comparative studies employing magnetic equivalent circuits [6,7], research on reducing eddy current losses by incorporating slits in the traces [8], studies utilizing flexible PCB with Halbach magnets for RFPM applications [9], and thermal design investigations considering PCB vias and pads [10]. In commercially available RFPM motors, numerous design techniques have been actively researched, including rotor shape design for cogging torque reduction [11], studies on permanent magnet geometry in RFPM [12,13], design investigations on permanent magnet geometry in axial flux permanent magnet (AFPM) configurations [14], research applying dual-skew to permanent magnets in AFPM [11,15], and stator shape design research [16,17]. However, completely eliminating cogging torque with these design approaches is challenging, as achieving total elimination requires replacement of the traditional coil-winding structure. Such a replacement involves a highly complex process that hinders single-step manufacturing and results in poor manufacturability. A promising solution to this challenge is the substitution of the coil with a PCB circuit. PCB substrates are well suited for rapid mass production and obviate the need for winding coils on a bobbin. Nevertheless, applying a PCB circuit in place of a coil to a rotating motor requires multiple validations. Therefore, the design process was conducted in stages.

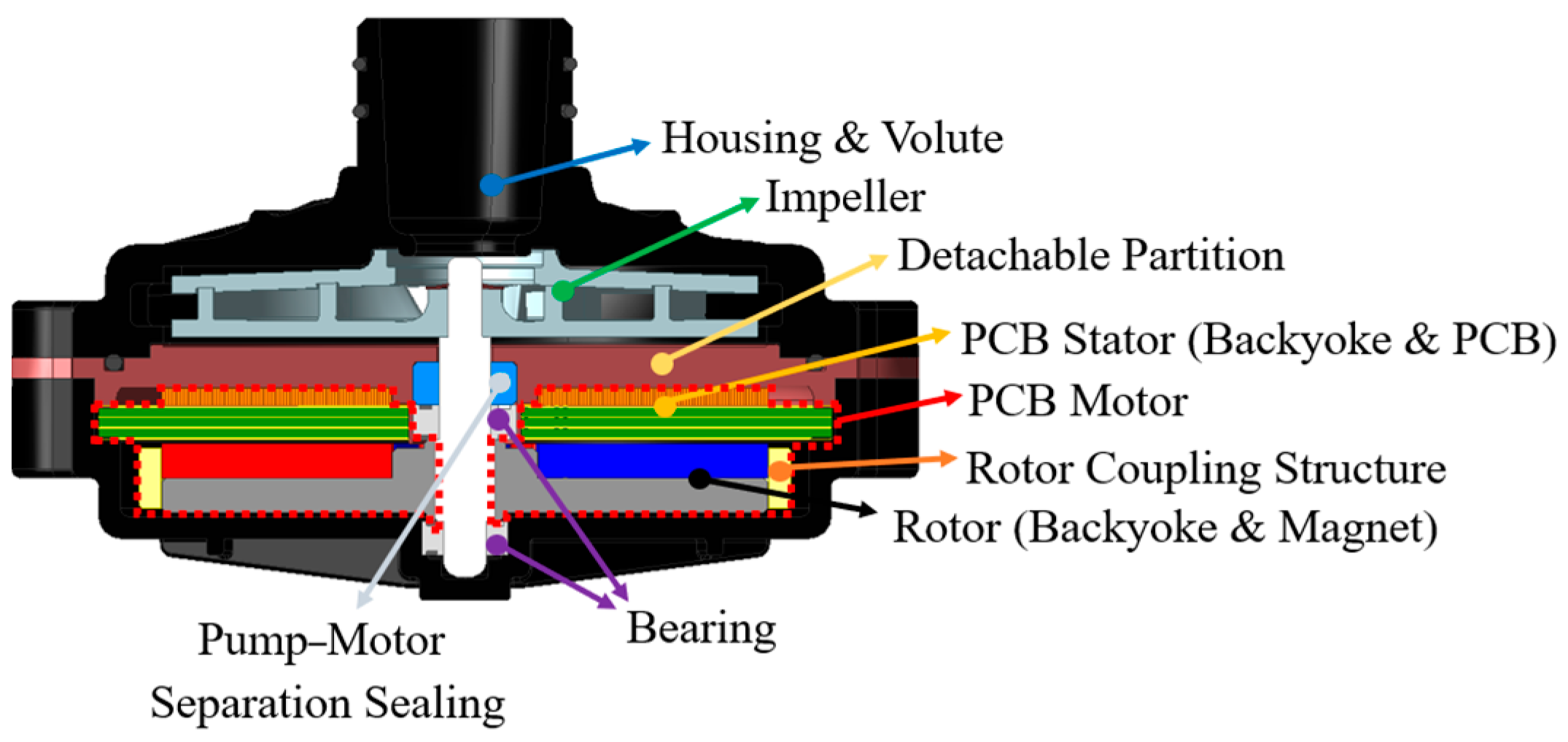
Figure 1 is a cross-sectional view of an axial flux permanent magnet (AFPM) electric water pump (EWP) incorporating a PCB stator. The proposed invention implements a single-rotor type PCB AFPM to improve manufacturability. In this design, the PCB substrate is directly affixed to a stator backyoke, which is fabricated from a material with high thermal conductivity. Rather than using coolant to directly cool the motor by allowing coolant to enter the motor’s interior, the design employs an indirect cooling approach. The stator backyoke, together with a separated external wall, is engineered to conduct the heat generated in the PCB circuit away from the motor. Instead, coolant flows on the pump side of the separated wall, indirectly cooling the PCB stator assembly. This construction allows the entire mechanical assembly, including the housing, to function as an integrated heat dissipation structure. In addition, the PCB is fabricated with a parallel-layer architecture that offers excellent thermal performance. This design advantage eliminates the need for a separate rotor can, thereby minimizing the air gap. Since an increased air gap degrades electromagnetic performance and reduces output, minimizing the air gap through mechanical design is essential for reducing the overall motor size. The structure of the PCB EWP is divided into a pump section and a motor section. A detachable partition separates these sections to prevent water ingress into the motor. Moreover, additional sealing measures are incorporated between the pump and motor sections to mitigate potential leakage from the shaft. The primary advantage of the PCB motor lies in its ultra-thin construction and extremely short shaft length. As a result, a compact design is achieved by positioning the large-diameter PCB stator close to the impeller and securing the PCB stator to the housing, which in turn enhances structural stability.

2. Design Process of Single Rotor Type PCB Motor

Figure 2 presents the design process for an axial flux permanent magnet (AFPM) motor incorporating a PCB stator, as proposed in this study. First, the magnetic equivalent circuit of the PCB AFPM is implemented and formulated into analytical equations to calculate the required torque. In a 12 V electric water pump (EWP) system for vehicles, the target speed is 4500 rpm, and the output specification requires a torque of 0.22 Nm. Using magnetic equivalent circuit calculations, the external diameter necessary to achieve the target torque is determined. At this stage, the type and grade of the permanent magnet are selected and the airgap flux density is computed. Based on the calculated torque, the rotor’s inner and outer diameters are chosen. In the proposed PCB motor, the use of distributed windings leads to protruding end turns; thus, the rotor’s external diameter is designed smaller than the overall motor external diameter. This aspect is further addressed in the finite element analysis (FEA) model design section. For the PCB substrate, FR-4 is selected as it is widely used in commercial applications and is suitable for motor operation, with a heat resistance of approximately 100–120 °C [3,18]. The thickness of the circuit pattern is specified in ounces (oz), where 1 oz corresponds to 0.035 mm. A thicker coil reduces electrical resistance and decreases AC loss within the conductor; therefore, a copper thickness of at least 2 oz is considered appropriate. Next, the selection of the number of turns and layers is critical. In the basic design to meet the target torque, a key parameter is the total number of turns in series, which is determined by both the number of turns per layer and the number of layers. For a three-phase AC motor, the PCB motor must use a number of layers that is a multiple of three, since each set of layers corresponds to parallel current paths. Given the copper thickness of 2 oz employed in the PCB circuit pattern, a 6-layer board is deemed suitable. Although increasing the number of layers provides additional parallel current paths, it also significantly raises manufacturing costs and increases the overall thickness of the PCB, potentially leading to greater magnetic leakage. Based on magnetic equivalent circuit calculations, an approximate total series turn count required to meet the target torque is derived, and the number of turns and layers are determined while considering these factors. An increase in the number of turns also results in higher electrical resistance in the PCB substrate. To mitigate this, multiple 6-layer boards can be connected in series; typically, stacking two 6-layer boards is referred to as a 12 layer configuration. Note that this configuration does not imply 12 parallel current paths but rather two series connections of 6 parallel paths each. The next design focus is resistance reduction. Increasing the outer end-turn thickness of the PCB circuit reduces the rotor’s external diameter, given that the overall motor external diameter is fixed. Although a thicker outer end-turn minimizes the PCB circuit resistance, it concurrently decreases the rotor’s external diameter, thereby reducing the no-load back electromotive force (EMF) and resulting in an increased applied current. All these factors are carefully considered when selecting the optimal design parameters. For the PCB motor, 3D FEA is required. Due to the thin coil thickness characteristic of the PCB circuit, a large number of mesh elements is necessary, rendering the FEA time-consuming. Consequently, an interpolation method based on key design variables is employed to simplify the process. Once the external diameter of the PCB motor and the outer end-turn thickness of the PCB circuit are determined, an optimized design is achieved by adjusting the permanent magnet thickness variable (MagT) and the Constant Trace Conductor (CTC) width variable (CTCW). Since 3D FEA demands extensive computational time, interpolation based on these two variables is used to evaluate all design points [3]. Ultimately, an FEA design model that satisfies the voltage limitations was derived, fabricated, and validated against experimental data.

Figure 3 compares the conventional electric water pump (EWP) motor with the PCB EWP motor, while

Table 1. Design specifications for conventional EWP motor.

Parameter	Value	Unit
Pole/Slot	6/9	-
Stator Diameter	56	mm
Rotor Diameter	21.5	mm
Airgap length	1.5	mm
Stack length (Active)	24.4 (18)	mm
Coil Turns	31	-
Parallel Number	3	-
Magnet	N45UH	-
Coil	Copper	-
Core	50PN270	-
Pole/Slot	6/9	-

presents the specifications of the conventional motor. The conventional motor’s active part is defined by an outer diameter of 56 mm and a shaft length of 24.4 mm; these dimensions pertain only to the motor itself and do not include the overall packaging. In contrast, when the total packaged volume is taken into account, the PCB motor is considerably more compact. The rated operating speed is 4500 rpm, and the required torque to meet the target output is 0.22 Nm. Additionally, the supply voltage is 12 V.

$$T_{RFM}=({\displaystyle \frac{\pi }{4}}{K}_w{B}_{g1}ac\cos \beta ){D^2}_g{L}_{stk}$$

(1)

Equation (1) is the torque equation of the RFM.

$$T_{AFM}=\{({\displaystyle \frac{1}{8}}ac{K}_{w1}{B}_{avg})(1-{K^2}_d)\}{D^3}_{out}$$

(2)

Equation (2) represents the torque equation for the axial flux motor (AFM). In Equation (2), TRFM denotes the torque of the radial flux motor (RFM); kw is the winding factor, Bg1 indicates the flux density per pole, and ac represents the average flux per unit area on the air gap surface. The angle β is defined as the angle between the current vector and the flux vector, with cos β quantifying the phase difference between them. Dg corresponds to the rotor’s outer diameter, and Lstk is the length of the motor’s active shaft. In Equation (3), TAFM denotes the torque produced by the AFM. Here, ac again denotes the average flux per unit area on the air gap surface, and kw1 is the winding factor for the fundamental (first harmonic) component used to analyze ideal performance while excluding harmonic effects. Bavg is the average air gap flux density, and Kd is the motor torque coefficient; a larger Kd implies a decrease in torque. Dout represents the outer diameter of the AFM rotor, which is also the overall motor diameter. For the RFM, when the magnetic and electric fluxes are equivalent, the generated torque is proportional to D2gLstk. Therefore, reducing Lstk results in a proportional decrease in output performance. In contrast, the AFM generates torque that is proportional to the cube of the rotor diameter, enabling higher torque in applications requiring a short shaft and large diameter. In other words, the torque of the AFM increases cubically with respect to the diameter compared to the RFM. Since an increased effective magnetic flux area enhances both torque and output, the AFM exhibits superior torque characteristics and achieves a higher output density within the same volume as the RFM. Consequently, the AFM is well suited for applications requiring high torque and compact structures [6,18].

3. Structural Characterization of PCB-Based Motor Architecture

Figure 4a shows the occurrence of eddy current loss in the core and demonstrates that cutting the laminations can effectively reduce the eddy current paths. Figure 4b depicts the teeth of a conventional AFM stator; due to their complex geometry, it is extremely challenging to fabricate the teeth by rolling electrical steel laminations, as shown in Figure 4a. Figure 4c presents the application of this concept to the electrical steel of an AFM stator within the PCB stator design, along with the corresponding fabrication method. As is evident in Figure 4b, the lamination of a conventional AFM stator is technically demanding and requires a complex manufacturing process. To implement the stator teeth, steel sheets with progressively increasing outer diameters must be produced and subsequently rolled to form the teeth, onto which the coils are wound. This intricate stator design poses significant challenges for mass production. Moreover, since conventional AFMs require the coils to be wound directly on the stator teeth, sufficient shaft length is necessary to accommodate the physical dimensions, thereby limiting further miniaturization. To address these manufacturing challenges, one solution is to eliminate the stator teeth and provide an alternative structure for coil winding. For example, the coils may be wound independently or secured using non-magnetic injection plastics. However, these alternatives involve additional fabrication steps and do not lend themselves well to mass production. In contrast, the PCB stator features a cylindrical stator backyoke that can be manufactured by uniformly rolling electrical steel, thereby significantly simplifying the production process and enhancing mass production feasibility.

Figure 5 depicts a conventional printed circuit board (PCB), on which circuits are laid out and semiconductor devices are mounted. The PCB electrically connects the semiconductor devices using copper foils, which also facilitate interconnection with external wiring.

Figure 6 depicts the application of the PCB stator to the final model of the PCB AFPM EWP. Although printed circuit boards are conventionally used to mount semiconductor devices and electrically interconnect them using copper foils to form circuits, the copper foil itself can serve as a coil. A printed circuit board without any mounted components is referred to as a bare PCB. A bare PCB generally consists of copper foil and FR-4, the insulating material of the PCB substrate. FR-4 is a glass epoxy material with a magnetic permeability similar to that of air, resulting in a structure essentially equivalent to an air-wound coil. This PCB stator enables a slotless AFPM design that eliminates the stator teeth. Since a bare PCB is composed solely of a copper circuit without additional semiconductor devices, it offers significant advantages in terms of manufacturability and mass production. Moreover, the extremely thin profile of printed circuit boards facilitates the realization of a motor with an ultra-thin design [19].

Figure 7 shows a comparison between the EWP RFM and the EWP PCB AFM, taking the housing into account. In particular, for an EWP, the existence of a volute serving as the fluid channel inevitably increases a portion of the external diameter. This means that even if the motor’s external diameter is small, space must still be reserved for the volute. In the case of an RFM, the shaft length is also long, imposing additional spatial limitations. However, the PCB AFM proposed in this paper features an ultra-thin structure that dramatically reduces the size in the axial direction. Moreover, because the PCB stator does not have teeth, magnetic saturation is minimal, allowing for a greater usage of permanent magnets to achieve high output density. Since the AFM has a large rotor diameter, it is easier to use many permanent magnets to generate a high output density. Therefore, this paper proposes a PCB AFM design process that replaces the conventional EWP RFM with a PCB stator applied AFM to realize an ultra-thin EWP and overcome spatial limitations. However, the model proposed in this paper was analyzed under vacuum conditions, whereas in a real EWP, the hydraulic section, including the impeller, is flooded with cooling water, so it would operate at a lower current density.

4. Magnetic Equivalent Circuit and PCB AC Loss Generation in PCB AFPM

Figure 8a presents the magnetic equivalent circuit of the PCB-based AFM, while Figure 8b is an FEA plot that demonstrates the occurrence of AC loss. The magnetic equivalent circuit of a motor is constructed based on its flux paths. In Figure 8a, the excitation flux emerging from the permanent magnets flows toward the air gap and encounters the magnetic reluctance of that gap. The flux then traverses the magnetic reluctance of the PCB substrate and reaches the stator backyoke. Because the stator backyoke is stationary, the time-varying flux from the rotor’s permanent magnets is conveyed to the stator. Since this time-varying flux gives rise to eddy current losses, the stator backyoke is fabricated using skewed laminated electrical steel. Although the core’s high permeability yields a magnetic reluctance that is often negligible, it is included here to achieve an accurate equivalent circuit. The flux passes through the stator backyoke, then through the PCB and the air gap, and finally circulates toward the S-pole of the pole-combined permanent magnets before reaching the rotor backyoke. Under sinusoidal current excitation and synchronous operation, no iron loss occurs in the rotor backyoke because it rotates at synchronous speed. The absence of iron loss in the rotor backyoke implies that a non-laminated solid core may be used instead of a laminated core. Consequently, the rotor is typically fabricated from a cost-effective steel such as S45C, since skewed laminated electrical steel cores are expensive. Although the rotor backyoke is designed to provide a flux path and is generally composed of a material with high permeability relative to air, rendering its magnetic reluctance nearly negligible, it is still taken into account in the equivalent circuit [5,6]. Furthermore, the leakage flux in the PCB, as observed in Figure 8a, comprises rapidly time-varying components that directly affect the AC losses within the PCB circuit. Along the flux path, several magnetic reluctances are encountered. R_m denotes the magnetic reluctance of the permanent magnet, Rpcb represents the magnetic reluctance of the PCB, and Rg corresponds to the magnetic reluctance of the air gap.

Figure 9 shows the variation in the number of effective conductors as a function of the pole count. In the proposed PCB AFM, the coil is wound in a distributed manner with a pole-to-slot ratio of 1:3. As the number of poles increases, the number of slots likewise increases, leading to a substantial rise in the total series turns. Although the back electromotive force (BEMF) also increases as a consequence, the increased number of effective conductors contributes to higher AC losses in the coil [5]. With a lower pole count, the reduction in the total series turns diminishes the phase back EMF, thereby necessitating a higher applied current; however, the shortened current path results in lower resistance. Conversely, with an increased pole count, the total series turns become greater, which yields a higher phase back EMF and subsequently reduces the applied current. Nevertheless, the lengthened current path results in increased resistance. Moreover, an elevation in the number of effective conductors amplifies the sources of AC loss, thereby further increasing these losses. Taking all factors into consideration, the most efficient combination of poles and slots is selected.

5. Fundamental Concepts and Principles of PCB Circuit Structures

Figure 10a depicts the principle of time-varying flux generated by rotor rotation. In this figure, as the rotor rotates, the flux emitted from the permanent magnets, fluctuates over time, inducing eddy currents in the conductive copper. Figure 10b identifies the regions where AC losses predominantly occur in a conventional coil and in the PCB stator trace. In conventional coils, these losses primarily arise from the rapidly fluctuating flux between the poles acting on the PCB conductors. Although one mitigation strategy involves introducing slits into the conductor [8], such modifications do not effectively suppress the principal regions where eddy currents are generated. Consequently, a design that maintains equal inner and outer trace widths—thereby substantially minimizing the regions susceptible to eddy current generation—is preferred. This design is defined as the Constant Trace Conductor (CTC). Figure 10c presents an FEA plot comparing the AC losses in the PCB circuit as a function of the CTC width. In conventional conductors, AC losses result not only from the proximity effect but also from the rapidly varying flux between the poles. In a one-turn PCB circuit, the wide spacing between conductors significantly reduces the impact of the proximity effect, thereby highlighting the loss mechanism driven by the rapidly fluctuating flux between the poles.

$$\delta =\sqrt{{\displaystyle \frac{1}{\pi f\mu \sigma }}}$$

(3)

Equation (3) represents the skin depth equation, where δ is the skin depth, f is the current frequency, μ is the permeability of the conductor, and σ is the electrical conductivity. The skin effect refers to the tendency of an alternating current (AC) to concentrate near the conductor surface due to the induced eddy currents arising from a time-varying magnetic field.

In a PCB motor, the rotor’s permanent magnets produce a time-varying flux that directly couples into the PCB coil, since the stator lacks a ferromagnetic core (such as stator teeth). This time-varying flux is the fundamental driver of the eddy currents, responsible for both the skin effect and the proximity effect. The proximity effect occurs when multiple conductors or coil turns are arranged close to one another and share the same time-varying magnetic field. In such a configuration, the magnetic fields generated by the induced currents in one conductor distort the current distribution in its neighbors, forcing currents to redistribute and further increasing AC losses. Thus, the time-varying flux itself does not function as a separate or additional proximity phenomenon; rather, it triggers the underlying eddy currents that give rise to both the skin and proximity effects.

A central challenge in designing PCB axial flux motors involves balancing copper conduction loss and AC loss. While increasing the conductor thickness or trace width can reduce DC resistance by enlarging the cross-sectional area available for current flow, such measures may also amplify AC losses. This occurs because additional surface area accentuates the skin and proximity effects. Moreover, increasing conductor thickness can raise manufacturing costs and enlarge the air gap, reducing overall flux linkage.

As the rotor speed rises, the magnitude and rate of change in the time-varying flux intensify, causing AC loss to become more significant. Because the copper foil dimensions in a PCB are generally fixed at the design stage, one way to mitigate AC loss is to adjust trace width. The trace width is tied to the number of turns; fewer turns allow for wider traces, thus reducing DC resistance. However, a trace that is too wide can inflate AC losses, negating the benefits of lower DC resistance. Figure 10c demonstrates that reducing the effective surface area in regions where AC loss is dominant leads to improved motor efficiency. Consequently, an optimal design requires a careful balance between conduction (copper) loss and AC loss, ensuring minimal impact from the skin and proximity effects [5].

Figure 11a depicts the multi-layer structure of a single PCB in the PCB stator, whereas Figure 11b presents the configuration attainable by stacking multiple PCBs. Figure 11c demonstrates how the effective number of layers increases in the finite element analysis (FEA) model with the addition of extra boards. As shown in Figure 11a, a single PCB employs a multi-layer design that permits parallel current conduction. This parallel conduction is facilitated by via holes that create vertical pathways through the PCB, allowing current to transfer from one layer to another. When current is distributed across multiple layers, the overall high current density is spread out, thereby preventing excessive heat generation in any one layer. However, stacking additional layers increases the overall thickness of the PCB. This increase in thickness enlarges the magnetic gap between the permanent magnets and the stator, consequently enhancing the leakage flux. In the multi-layer structure, the extremely thin copper foil used in the PCB has a significant impact on the coil resistance. Unlike a conventional motor, in which resistance increases linearly with the number of turns, the PCB configuration can exhibit a nonlinear increase in resistance as the number of turns grows. In this paper, after careful consideration of these factors, a design employing a single-layer current path per PCB has been selected and an overall six-layer configuration has been implemented. This arrangement is referred to as one 6-layer board; when two boards are employed, the structure becomes 12 layers, and with three boards, it is configured as 18 layers. The boards are connected in series such that when the configuration changes from 6 to 12 layers, the total number of series turns is doubled. Although a simple count of the series turns might suggest that the back electromotive force (EMF) should double, the increased PCB stator thickness results in a wider magnetic gap and enhanced leakage flux. Consequently, as the number of layers increases, the leakage effect becomes more pronounced, leading to a nonlinear impact on performance. The basic model must therefore be selected by carefully assessing the electromagnetic performance in relation to the number of turns and layers to meet the target voltage.

Figure 12 depicts the effect of increasing the outer end-turn thickness of the PCB circuit. In PCB circuits, the coil is inherently very thin, which results in high resistance. This condition underscores the need for resistance reduction, typically achieved by increasing the conductor’s cross-sectional area. When the outer diameter of the coil is fixed, the outer end-turn thickness becomes the primary design variable for maximizing the cross-sectional area. Although increasing this thickness yields a significant gain in cross-sectional area and hence reduces resistance, it also reduces the rotor’s outer diameter, resulting in a lower back electromotive force (EMF). A reduction in back EMF implies that, to meet the target output, a higher applied current is required. Therefore, by analyzing electromagnetic performance trends, the most efficient design point can be identified.

6. Optimal Design of EWP AFPM with PCB Stator

Figure 13 and Figure 14 present comparative models for selecting the optimum number of turns and layers in the electromagnetic design of a PCB motor. For a PCB motor design with a DC-link voltage of 12 V, two turn/layer configurations were evaluated, namely 1 Turn/18 Layer and 2 Turn/12 Layer. In this context, the 1 Turn/18 Layer configuration corresponds to a total series turn count of 90, while the 2 Turn/12 Layer configuration yields a total of 120 series turns. It was observed that the electrical resistance of the PCB circuit does not increase proportionally with the number of turns; specifically, the resistance in the 2 Turn configuration increases by more than twice that of the 1 Turn configuration. Consequently, despite the lower series turn count, the 1 Turn configuration exhibits considerably lower resistance, which in turn leads to enhanced overall efficiency. Furthermore, for a slotless motor, where the rotor operates at synchronous speed, iron losses are nearly negligible, and the effect of the armature flux on the eddy current loss of the permanent magnets is minimal. Additionally, since the stator back yoke is constructed from rolled electrical steel cores, iron losses remain very low. Thus, in the PCB motor, the impact of copper loss and AC loss arising from factors such as the permanent magnet thickness and CTC width is a critical determinant of overall performance. Based on these considerations, the 1 Turn/18 Layer configuration was selected as the optimal design.

Figure 15 shows performance data for a 1 Turn/18 Layer PCB circuit as a function of the outer end-turn thickness. Subfigure (a) compares the no-load line voltage and current density; this design was developed considering the voltage utilization limitations of a 12 V EWP motor system. Subfigure (b) compares the no-load back electromotive force (EMF) with the input current, indicating that a decrease in no-load back EMF requires an increase in input current to meet the target output. Subfigure (c) compares the motor losses and efficiency. It was found that when the outer end-turn thickness is set to 4.5 mm, the voltage utilization is maximized, leading to a reduction in the applied current and, consequently, achieving maximum efficiency. Therefore, the outer end-turn thickness was determined to be 4.5 mm.

Figure 16 presents the variation in loss and efficiency as a function of the CTC width for the selected 1 Turn/18 Layer PCB motor. The PCB motor is extremely sensitive to electrical resistance and AC loss due to the inherently thin copper foil in the PCB circuit. To identify the optimal design point, it is desirable to review all design points similar to those presented in Figure 13. For intuitive understanding, Figure 16 depicts the relationship between loss and efficiency using a graph. Because a CTC width that is too narrow adversely affects the copper thickness and via hole dimensions during manufacturing, a CTC width of 1.3 mm was chosen. Regarding the permanent magnet thickness, although efficiency increases with a thicker magnet, the associated increase in axial length and potential impacts on mechanical stability necessitated selecting a thickness of 4 mm.

Figure 17 shows the current density distribution as a function of the permanent magnet thickness and the CTC width for the selected 1 turn, 6-parallel-layer PCB AFM applied to the EWP. The 6-parallel-layer structure distributes the current, resulting in thermal characteristics equivalent to those of conventional motor even at current densities approximately 4–5 times higher than those of a conventional motor. Consequently, the design point is chosen based on the current density, which is inherently dependent on both the CTC width and the permanent magnet thickness. The current density was calculated using the conventional RFM, and, considering manufacturability, the design point was constrained to be within 30 A/mm².

Figure 18 presents the outer diameter, axial length dimensions, and the three-phase PCB circuit phase pattern of the final finite element analysis (FEA) model of the PCB motor. The phase pattern proposed in this study employs a design that facilitates efficient current flow within a parallel-structure PCB. Regarding dimensional considerations, the outer diameter is minimally affected by the spatial constraints imposed by the EWP volute structure; consequently, reducing the axial length proves advantageous for space-saving applications. With the adoption of the PCB stator, the active axial length of a conventional motor can be reduced from 24.4 mm to 14.4 mm, which corresponds to an approximate 41% reduction. Given that EWP are installed in large numbers in vehicles, space conservation is critical. Due to the constraints of the volute structure in accommodating the outer diameter, reducing the axial length becomes essential. This significant reduction not only facilitates space saving but, by shortening the winding process tact time, substantially reduces the production time for vehicle EWP, thereby enabling efficient mass production in line with the high production demand for EV. Figure 19 is the flux density saturation plot of the final PCB motor FEA model under load conditions, showing that the maximum flux density in the core reaches 1.73T.

Table 2. Comparing 3D finite element analysis (3D FEA) data.

PARAMETER	Unit	CONVENTIONAL MODEL	PCB Final MODEL
Back EMF	Vrms	2.48	3.4
Rated Speed	rpm	4500	4500
Load Torque	Nm	0.22	0.22
L2L Max(+IR)	Vpeak	8.05	9.6
Current	Arms	14	9.35
Current Density	$\mathrm{A}/{\mathrm{m}\mathrm{m}}^2$	14.06	27.35
Copper Loss	W	20.34	14.39
Core Loss	W	1.08	1.45
AC Loss	W	0	7.26
Output Power	W	102.59	102.22
Efficiency	%	82.62	81.57

presents a comparison of the 3D FEA analyses between the conventional EWP RFPM and the PCB AFPM final FEA models. In the proposed PCB stator, current flows through parallel layers, enabling the design of a current density that is 4–5 times higher than that of conventional designs. However, for stability, the increase was limited to a twofold value. Although an AC loss reduction design was implemented, the efficiency was approximately 1% lower than that of the conventional design due to AC losses. Considering that the target efficiency of the FEA model was over 80%, the model achieving this efficiency was derived using 2 oz copper. Moreover, since the PCB AFPM does not include stator teeth, no cogging torque is theoretically generated, and torque ripple is negligible due to the slotless motor characteristics, resulting in stable operation; consequently, both cogging torque and torque ripple were excluded from the analysis.

Figure 20 presents the measurement of the line-to-line resistance of the manufactured 1-turn/18-layer PCB stator. The line resistance was determined to be 106.82 mΩ, while the phase resistance measured 53.41 mΩ. In the FEA model, which incorporates manufacturing considerations such as via plating, the phase resistance was calculated as 52.05 mΩ. The discrepancy between the measured resistance and the FEA model prediction was approximately 2.55%.

Figure 21 shows the PCB motor test unit incorporating the Constant Trace Conductor. The test motor was evaluated and validated using the test environment described below.

Figure 22 presents a comparison of the no-load back EMF data between the FEA model and the prototype model. At a rated speed of 4500 rpm, the FEA model yielded a value of 3.28 Vrms, whereas the prototype model produced 3.31 Vrms, corresponding to an error of 0.91%.

7. Conclusions

Due to the technical limitations of the conventional radial-flux motor used in EWP, further reduction in the axial length was not feasible. However, the PCB axial-flux motor incorporating a PCB stator overcomes these limitations and enables the realization of an extremely thin, compact motor. Although the thin copper in the PCB circuit is susceptible to AC and copper losses, the design process and the application of the Constant Trace Conductor (CTC) proposed in this study allow the PCB motor to achieve performance equivalent to that of conventional motor. By implementing a loss-optimized design using a CTC PCB, equivalent output and efficiency were obtained while reducing the axial length by up to 41% compared to conventional motor. This revolutionary reduction in axial length offers a significant advantage by maximizing the available interior space in vehicles. If applied to other automotive components, it could result in unprecedented space savings. Further innovation is demonstrated by adopting a 1:3 pole-to-slot distributed-winding topology, which yields a unity winding factor that maximizes back-EMF and minimizes air-gap harmonic content. End-turn cross-section is leveraged to minimize current density reduced to 27.35 Arms/mm² for mechanical and thermal stability—and validated via high-fidelity 3D FEA. Slotless construction ensures theoretically zero cogging torque and negligible ripple. Additionally, indirect cooling through the stator back-yoke and detachable housing partition exploits the PCB parallel-layer heat paths to manage thermal stress. Together, these features confirm that the PCB AFM design not only achieves a compact form factor but also meets or exceeds the performance, efficiency, and reliability benchmarks set by conventional EWP motors.