Abstract
Power system state estimation (PSSE) is critical for accurately monitoring and managing electrical networks, especially with the increasing integration of renewable energy sources (RESs). This review aims to explicitly evaluate and compare state estimation techniques specifically adapted to handle RES-related uncertainties, providing both theoretical insights and clear practical guidance. It categorizes and analytically compares physical-model-based, forecasting-aided, and neural network-based approaches, summarizing their strengths, limitations, and ideal application scenarios. The paper concludes with recommendations for method selection under different practical conditions, highlighting opportunities for future research.
1. Introduction
The climate change issue draws the attention of governments all over the world to make proposals to reduce carbon emissions. One such proposal is the decarbonization of power systems by introducing large-scale integration of renewable generation, such as wind turbine generators (WTGs) and photovoltaic (PV) systems. It is becoming increasingly difficult to monitor the system and ensure the quality of the power supply due to these new elements in the system, and power system operators must respond to changes in the network consistently and correctly. Introduced in the 1970s, the power system state estimation (PSSE) is a tool to monitor the state of the system based on the available measurement infrastructure to help power system operators make energy management decisions [1,2,3]. The weighted least square (WLS) algorithm was the first proposed PSSE algorithm, which is still effective as the most widely used method of PSSE. However, the influence of renewable energy resources (RESs) on the accuracy of PSSE cannot be addressed solely by WLS. The discussion of addressing this challenge has intensified as the installed capacity of RES generation has increased globally significantly and consistently.
To support both academic research and real-world operations in coping with these challenges, a variety of commercial and open-source tools have been developed for PSSE and network analysis. Among the commercial offerings, Siemens PSS®E and GE Grid Solutions’ Power System Analysis Toolbox (PSAT) are widely adopted by utilities for their robust, scalable state estimation and contingency analysis capabilities [4,5]. DIgSILENT PowerFactory provides a comprehensive suite of state estimation and dynamic simulation modules, particularly popular across European transmission and distribution networks [6,7]. On the open-source and research side, MATPOWER (developed at Cornell University) serves as a flexible MATLAB-based platform for algorithm development and benchmarking, while OpenDSS (supported by EPRI) focuses on detailed distribution system modeling with built-in state estimation functions [8,9]. More recently, platforms such as GridLAB-D have emerged to simulate complex smart grid environments, integrating advanced state estimation with demand response and distributed energy resource models [10,11].
The approaches to addressing this issue can be divided into three categories: (1) by integrating models to describe the renewable generation process into PSSE problem formulations (physical-model-aided approach), (2) by using forecasting algorithms to generate more accurate pseudo-measurements (forecasting-aided state estimation (FASE) approach), and (3) by using a neural network to perform PSSE (neural network (NN)-based PSSE approach). Some review articles are available in the literature that discuss recent developments and trends in PSSE [12,13], or provide an overview of PSSE problem formulations and emerging technologies [14,15,16,17,18]. Some review articles discuss RESs’ impact on PSSE in particular, such as Section 7 of [14], Section 5.2 of [15], and Section 2.C of [16]. However, these papers do not provide a detailed description and comparison of the algorithms specifically designed for tackling the challenges introduced by RESs; rather, these papers provide an overview of the entire field of PSSE.
In contrast to the existing review papers on PSSE, this paper places RESs at the core of the review, assessing and comparing all PSSE technologies that are tailored for renewable-rich grids. The differences between models, and the merits and demerits of different methods are discussed, along with providing suggestions for future research. Hence, the primary goal of this review is to provide a clear comparative evaluation of state estimation methodologies adapted for renewable-rich grids. It seeks to offer explicit practical recommendations, addressing not only theoretical aspects but also practical challenges faced by system operators and researchers in selecting appropriate algorithms.
The following sections of this paper are organized as follows: Section 2 briefly introduces the formulation of the PSSE problem. Table 1 and Figure 1 provide a ‘big picture’ of the various RES-based DSSE methods from the three aforementioned categories of ‘physical-model-based’, ‘forecasting-aided’, and ‘NN-based’ methods, while a detailed description and explanation of the methods belonging to the three categories are provided in Section 3, Section 4, and Section 5, respectively. Section 6 provides discussions of the findings of different papers and provides suggestions for future research. Section 7 concludes this paper.

Table 1.
Classification of algorithms in this paper.
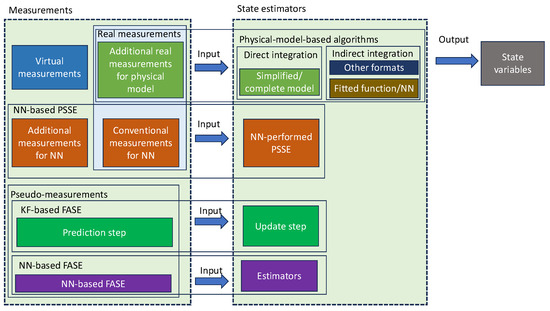
Figure 1.
Flowchart of Algorithmic Approaches.
2. Problem Formulation
The PSSE problem aims to estimate the voltage magnitudes and angles, called state variables, of all the buses (or nodes) in the power network. The objective of PSSE is to provide reasonably accurate estimates for these state variables based on a limited number of measurements. The error of these measurements is usually assumed to follow Gaussian distribution with mean values, , and standard deviations, . The loss function of the measurement errors (that is, the difference between the measurements and their actual values) is formed based on the assumption of independence of measurements, that is [19],
where is the likelihood function of the m-dimensional measurement vector, z, and is the normal probability density function of the ith measurement, . is defined as . By taking the natural logarithm of the above function, the log-likelihood function is identified as follows:
Maximizing (2) is equivalent to minimizing:
where the mean, , is the expected value, , of , and is the standard deviation of the error of the ith measurement. Considering a nonlinear function, , which relates the ith state variable, , to the ith measurement, , the residual between and is defined as follows:
The loss function in (3) can be rewritten in matrix format as follows:
where is the residual matrix, which is the covariance matrix of the measurement error, , and , , and are column vectors of , , and , respectively.
There are many approaches for solving the loss function in PSSE, among which WLS is the most widely used algorithm and is described as follows.
Applying Taylor’s expansion to (6), and ignoring terms that have an order higher than one, the above equation is rewritten as follows:
where and . Reformulating the above equation gives
By solving the equation below iteratively, accurate estimations of state vector can be provided:
where is the difference between and . Although several PSSE algorithms have been proposed since the 1970s, WLS is still widely applied to solve PSSE problems.
2.1. Pseudo-Measurement
Pseudo-measurement is a concept proposed to help solve PSSE if a required measurement is not available. As mentioned previously, a limited number of measurements are usually available in a power system, and we can have a scenario in which the available measurements are not sufficient to solve PSSE. In this case, pseudo-measurements are added to the set of measurements in lieu of the required but unavailable measurements.
The problem of having sufficient measurements is mathematically described using observability. If the state vectors of a bus in the system can be estimated using available measurements, then the bus is called observable. It is desirable that all buses are observable so that the power system operators can obtain a complete picture of the status of the system. For a system with one or more unobservable buses, such pseudo-measurements are added to the set of measurements such that all the buses in the system become observable. Additionally, for an already observable system, adding pseudo-measurements can improve the redundancy of measurements, making PSSE more robust to bad data. Hence, when bad data pollute multiple measurements, it is still possible to ensure accurate estimation because of redundant measurements.
Pseudo-measurements are usually derived from the historical load or generation profile at a bus, which gives typical values for generation or load throughout the year for that bus. Pseudo-measurements should be applied with a carefully selected weight, or . Since the weight normalizes the residual between actual measured and estimated values, applying a large weight to an inaccurate measurement will result in a large estimation error in the final estimation results. Hence, the weight assigned to pseudo-measurements is usually small and depends on the variance of this pseudo-measurement. The higher the variance, the smaller the weight will be.
2.2. Virtual Measurement
Virtual measurements refer to measurements not obtained from physical sensors, but instead derived from known network conditions, topology, or operational constraints. Typical examples include zero-injection buses (nodes without local load or generation), open switches with zero power flow, closed switches having negligible voltage drops, and fixed reference bus angles assigned for computational purposes. Virtual measurements are integrated into state estimation algorithms either as pseudo-measurements with very high confidence (low variance) or explicitly as equality constraints via methods such as Lagrange multipliers, thus enhancing observability, redundancy, and overall numerical stability of estimation solutions. Their role is particularly critical in distribution systems with high renewable energy penetration, where the accuracy of pseudo-measurements derived from forecasts can be adversely impacted by generation variability. By enforcing known network conditions, virtual measurements significantly improve state estimation reliability under these challenging conditions.
3. Physical-Model-Based Algorithms
In the DSSE problem, measurement redundancy and observability are essential factors that make state estimation robust and accurate. However, only a limited number of variables measured at the grid level are usually included, such as power injections and voltage magnitudes. If the measured variables are extended outside the networks of transmission and distribution, the observability can be changed. This is the essential idea of the physical-model-aided approach, the first category of DSSE algorithms in Table 1. The term ‘physical-model-aided’ indicates that new states are included based on RESs’ physical model and the corresponding extended measurements. As shown in Figure 1, the physical-model-based approach introduces new measurements and also integrates new elements from physical models in state estimators. In other words, the physical-model-based algorithm changes observability by taking additional measurements and states from RES-installed buses to obtain accurate and robust state estimates of the whole system.
3.1. Direct Integration of Physical Models into PSSE
The most straightforward approach that introduces equations related to RESs is by introducing these directly into the Jacobian matrix. The RX model, which is the simplified model of asynchronous generators, is used in [20] to include WTGs that are based on asynchronous machines in PSSE problems. Similar approaches can also be applied using further simplifications of the RX model, as in [21,22]. In [23] (in contrast to [20]), different types of WTGs are included using detailed models, which are more advanced than the RX model. This kind of direct approach could also be applied to PV as well; for instance, the five-parameter model of PV is used to build an extended estimator in [24]. Other types of distributed generators (DGs) used in PSSE are discussed in [25], which are not limited to renewable generators but extend to fuel cells and gas turbines.
Although the direct approach is considered to be the most straightforward way to extend the state space of the state estimators, some undesirable issues could be introduced in this approach [2]. The new measurement redundancy and observability at and outside the network level must be evaluated to make sure that they are improved; otherwise, convergence issues can arise. Furthermore, new parameters and variables are required to form the measurement functions (measurements expressed as functions of states) but may not be available, possibly making these algorithms impractical for real-world applications. The complexity of the Jacobian matrix is another concerning factor, which will increase with the application of new measurements. The difficulties of implementing these algorithms due to the higher complexity of the Jacobian matrix can also be an obstacle.
3.2. Integrating Fitted Functions of Generation Models into PSSE
Considering the challenges of direct integration of the physical model, another approach has been proposed in the literature, which addresses the three issues mentioned earlier. Rather than introducing the complete and detailed physical models, the physical model is fitted using several functions or neural networks before model integration (See Figure 1). The fitted function replacing the five-parameter PV model is expressed as follows [26]:
where , and t are parameters fitted based on historical data; G and T represent the solar irradiance and temperature, respectively, and and represent the output voltage and current of PV power arrays, respectively. The fitted function requires only two extra accessible variables, temperature and irradiance, to relate voltage and current. However, the fitted functions have been applied only to some parts of the PV system; for example, they are not applied to power converters, implying a partial solution as the converter model is still required. Another example is [23], where neural networks and fitted functions are used for WTGs without a detailed model used in the algorithm. The selected neural network in [23] is referred to as the back-propagation neural network (BPNN). The differentiability of this neural network is supported by the back-propagation algorithm, which calculates the gradient of the loss function concerning the weights and biases of the network layer by layer based on chain rules. This helps in directly obtaining the Jacobian matrix elements required for PSSE.
Using fitted functions and neural networks requires fewer measurements than detailed models, which partially solves the issue of unavailable measurements. The concern about the difficulty of performing differentiation for obtaining the elements of the Jacobian matrix is also addressed. The BPNN and fitted function gradients could be obtained in a straightforward and accurate manner without requiring detailed system models. It is also easier to derive the gradient of the fitted function than deriving it using the detailed model because the complexity of the fitted function is reduced. However, a large amount of data is required to derive the fitted functions and neural networks, which is the primary challenge of this approach. Additionally, these data are generator- and site-specific and cannot be easily applied to other locations.
3.3. DSSE Problem in Alternative Forms
The DSSE problem can be reformulated into various forms beyond the standard equations presented in Section 2 (9), although it still falls within the physical-model-based category depicted in Figure 1. For example, Chapter 6 of [19] discusses the optimization approach, where the objective is to minimize the difference between the estimated value and the measurement z to find the optimal state variable x. Reformulating the DSSE problem as an optimization problem is advantageous because physical models can be incorporated as constraints. This approach is demonstrated in [27], where the loss function is defined as follows:
where is the objective function of DSSE, and are the equality and inequality constraints from generation units of RESs and other units of the system, respectively. and are the penalty coefficients. and are the numbers of equality and inequality constraints, respectively. is the new loss function of the optimization problems formulated from the original DSSE problem. The optimization problem is solved using the combination of particle swarm optimization and Nelder–Mead simplex search, which is called PSO-NM in [27]. Similarly, in [28,29], the estimation problem is framed as an optimization problem and solved using the modified firefly algorithm and mutated two-loop particle swarm optimization algorithm, respectively, with DG models included as constraints.
Additionally, DSSE can be formulated in other ways. Interval state estimation (ISE) is one such form, where the goal is to determine the interval of state variables rather than their exact values, as in conventional DSSE. ISE employs the Krawczyk operator and its variants (modified Krawczyk operator (MKO)), which are numerical algorithms used to find guaranteed enclosures or approximations of solutions to systems of equations. For instance, ref. [30] proposes a modified Krawczyk operator to handle the ISE problem while considering DGs. This approach is similar to the algorithms discussed in Section III.A, which introduce an extended estimator directly using physical models.
Both approaches reformulate the DSSE problem into alternative forms other than the one given in Section 2. When the DSSE problem is cast in an optimization form, incorporating a detailed physical model as constraint may introduce measurement and parametric issues. Additionally, these optimization forms typically encounter fewer convergence problems because most optimization algorithms are inherently convergent. Moreover, these algorithms are versatile and can be applied to various types of RESs.
3.4. Comparative Analysis and Summary of Physical-Model-Based Categories
The physical-model-based DSSE approaches from Section 3 can be grouped into three categories: direct integration of RES models, surrogate modeling via fitted functions/NNs, and alternative optimization/interval formulations. Table 2 compares these categories.

Table 2.
Category-level summary of physical-model–based DSSE methods.
Category-Level Recommendations:
- Use direct integration when detailed RES dynamic models and parameters are available and maximum observability is required.
- Choose surrogate modeling if historical RES data are abundant but detailed physical parameters are unavailable.
- Apply alternative formulations when robust convergence under constraints is critical, accepting higher computational cost.
3.5. Summary
The physical-model-based approach aims to extend estimation to the observable internal parts of the generators rather than limit it to the transmission and distribution networks. This extends the DSSE problem to include measurements other than conventional network measurements and provides algorithms capable of handling issues related to RESs.
4. Forecasting-Aided Approach
As introduced in Section II.A, DSSE usually applies pseudo-measurements generated from historical data. However, forecasted generation or load could be used for generating pseudo-measurements, instead of using historial data. The second category of the DSSE algorithms utilises forecasting techniques to provide appropriate values of pseudo-measurements to aid the state estimation process rather than changing the model of the estimators, as shown in Figure 1. This kind of approach of DSSE is usually identified as FASE [31,32].
4.1. Kalman-Filter-Based Algorithms
The Kalman filter is a mathematical algorithm used to estimate and predict the state of a dynamic system by integrating measurements or observations with predictions based on the system’s mathematical model. Thanks to its predictive capabilities, the Kalman filter and its variants have been extensively applied in various fields, including DSSE, as depicted in Figure 2. In the Kalman-filter-based DSSE algorithm, the prediction step generates pseudo-measurements for DSSE, while the update steps incorporate these measurements to perform the DSSE. It has been demonstrated that Kalman-filter-based forecasting-aided DSSE outperforms WLS in [33]. Numerous Kalman filter variants have been proposed in the power system literature to address the diverse characteristics of DSSE problems and power systems.
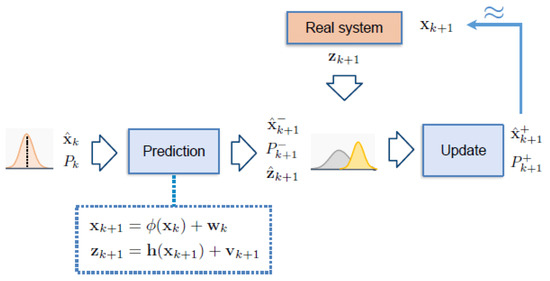
Figure 2.
Kalman filter scheme [34].
Convergence issues are a primary concern in both DSSE and Kalman filtering, prompting the development of modified Kalman filter algorithms. For instance, the photovoltaic-assisted interleaved extended Kalman filter (PV-IEKF) addresses potential ill-conditioning problems of the Kalman innovation matrix due to zero injection, as highlighted in [35]. These zero injections may result from low solar irradiance affecting PV generation and zero-injection buses. A novel block-wise inverse computation algorithm based on the Schur complement is proposed for PV-IEKF to tackle this ill-conditioning issue.
The performance of KF-based FASE algorithms relies heavily on the accuracy of Kalman filter predictions. In [36], a data-driven unscented Kalman filter (UKF) is introduced to address low forecasting accuracy due to decoupling between bus transitions. A non-diagonal matrix derived from historical data replaces the diagonal transition matrix in the prediction step, enhancing forecasting accuracy. Similarly, a past-aware state estimation (PASE) using an ensemble Kalman filter (EnKF) is applied in [37], incorporating the latest state into the EnKF ensemble to account for past states.
Rather than addressing internal Kalman filter issues, the robust ensemble Kalman filter (REnKF) in [38] considers system noise and bad data. The projection statistics (PS) technique, used to detect bad data in DSSE in [39], is applied to the innovation matrix in REnKF, creating a new measurement error covariance for bad data and enhancing the algorithm’s robustness. The system process noise is also accounted for by updating its Gaussian variance, which benefits state tracking and forecasting performance. The PS technique’s ability to manage bad data and update system noise contributes to the robustness of the Kalman filter in REnKF. Robustness is also a focus in [37,40], which use modified EKF and EnKF, respectively.
Different Kalman filter algorithms have unique strengths and weaknesses and can be integrated to achieve superior performance. For example, the UKF and EKF are combined to form a hybrid algorithm known as the adaptive extended Kalman filter (AEKF) in [41], which surpasses both UKF and EKF in convergence speed and estimation accuracy.
Using the Kalman filter steps to generate pseudo-measurements and perform DSSE is logical because the prediction and update steps provide pseudo-measurements, which are then used in DSSE. Additionally, Kalman filtering is grounded in mature theory and robust mathematical foundations, offering numerous variants that can inspire novel DSSE algorithms. Consequently, it may be more reliable than neural network approaches, which are often seen as black boxes. However, deriving the Kalman filter parameters requires data, similar to neural network approaches. Furthermore, additional steps to address specific problems, such as the ill-conditioning issue in [35], can increase computational costs and slow down the process.
4.2. Neural Network-Based Algorithms for Generating Pseudo-Measurements
NNs are widely utilized in various engineering domains due to their capability to handle nonlinear problems, such as forecasting power generation [42,43,44]. These forecasted values can directly serve as pseudo-measurements in conventional DSSE algorithms, as illustrated in Figure 1. In [45,46], it is demonstrated that a basic two-layer feedforward artificial neural network (ANN), without additional mechanisms, generates more accurate pseudo-measurements compared to those derived from load profiles.
Similar to KF-based FASE, enhancing forecasting performance is a key strategy for improving FASE accuracy. A sophisticated approach proposed in [47] leverages the extreme learning machine (ELM), which is a single-layer feedforward neural network where hidden layer node weights are randomly initialized and only output weights are adjusted during training. In [47], ELM is utilized for forecasting to provide enhanced pseudo-measurements for DSSE. To optimize ELM performance, two additional steps are introduced: selecting training data using Grey relation analysis, which assesses similarity between sequences based on weather conditions to prevent overfitting, and tuning hyperparameters using genetic algorithms. In another innovative approach, WaveNet and long short-term memory (LSTM) architectures are combined to create WaveNet-LSTM in [48]. This hybrid model effectively captures complex patterns in power injections, including those from RESs.
The benefits of employing NNs directly for generating pseudo-measurements include straightforward implementation, high accuracy, and rapid computation speed post-training. However, different from the Kalman filter, NNs suffer from low explainability regarding their internal operations. Moreover, like the Kalman filter’s reliance on data, NNs also necessitate extensive datasets for training and validation. This data-intensive requirement poses a significant challenge for practical applications in power systems, where obtaining sufficient and timely data can be constrained by measurement infrastructure limitations [49].
4.3. Other Approaches
There are also other approaches to produce pseudo-measurements to aid the DSSE process, which are not generated using KF and NNs. In [50], pseudo-measurements of demand-response-enabled load (DREL), including load-aggregating PVs, are generated using discrete-time linear models, which characterize and track the dynamics of DREL online based on sampling. An optimization model has been introduced in [50] to simulate the self-adjust behavior of DREL considering the time of use price and physical constraints.
4.4. Comparative Analysis and Summary of Forecasting-Aided Categories
To provide a clearer comparison among the forecasting-aided approaches presented in Section 4.1, Section 4.2, Section 4.3, Table 3 summarizes their main strengths, weaknesses, and ideal application contexts.

Table 3.
Comparative summary of forecasting-aided DSSE methods.
Category-Level Recommendations:
- KF–based methods when measurement noise characteristics are known and moderate computational resources are available.
- NN–based methods if rich historical datasets exist and sub-second estimation is required.
- Other approaches for quick, low-complexity implementations in data-scarce scenarios.
4.5. Summary
Forecasting-aided algorithms strive to generate precise pseudo-measurements to assist in the estimation process. One category includes KF-based algorithms, where the KF is employed for both forecasting and estimation. Therefore, KF-based algorithms can concentrate on directly enhancing forecasting and estimation accuracy. In contrast, NN-based algorithms do not utilize NNs for estimation but improve estimation performance solely through input measurements. Additionally, there are alternative FASE approaches that do not rely on KF or NNs for forecasting and generating pseudo-measurements for DSSE.
5. NN-Performed DSSE
A single NN can potentially replace conventional DSSE algorithms like WLS for computing state vectors from measurements. Such algorithms defy easy classification since they neither introduce extended estimators through physical models and additional states (as discussed in Section 3) nor rely on forecasted or predicted values (as discussed in Section 4). Consequently, they can be categorized separately (see Figure 1). For instance, a basic approach involves using a feedforward ANN for state estimation, demonstrated in [51]. Similarly, ref. [52] proposes an algorithm involving dataset pre-processing, focusing on measurements, states, and topology, utilizing the K-nearest neighbor (KNN) method. NNs can also emulate DSSE solvers, such as the prox-linear net presented in [53]. Additionally, ref. [54] introduces the unobservable state estimation neural network (USENN) to handle estimation challenges in distribution systems with low observability.
Bayesian neural networks (BNNs) represent another NN category widely applied for addressing the DSSE problem due to their well-founded Bayesian theory, which enhances explainability. In the conventional approach, for instance, [55] employs an exact modeling estimator to handle non-Gaussian measurement uncertainties. However, this approach does not yield deterministic improvements and typically incurs higher computational costs. In [56,57], BNNs are utilized to address non-Gaussian measurements and observability issues in distribution systems with sparse measurement setups.
Traditional DSSE algorithms are tightly bound by the power system’s physical models, a constraint absent in NN results, which can lead to discrepancies with power-flow models or system element characteristics. For instance, DSSE outcomes might show power generation values exceeding generators’ rated outputs.
A novel category of NNs, discussed in [58], integrates physical principles into NNs, termed physics-informed neural networks (PINNs) or physics-guided neural networks (PGNNs). PINNs are recognized as promising tools for solving diverse problems, including flow dynamics, optics, and electromagnetic problems, as highlighted in [59]. One approach involves incorporating physical equations into the loss function, preserving model simplicity and accuracy [60,61]. Another variant modifies network architecture, such as the graph neural network (GNN), introduced for DSSE in [62,63,64]. GNN integrates physical equations into connections between and within neurons, mimicking power system topology. Each neuron represents a power system bus, and connections symbolize transmission lines between buses, resulting in a physically guided structure offering enhanced accuracy compared to traditional PINNs. However, implementing and interpreting GNNs can be complex due to their intricate structure, though they can be partitioned into subsystems to enhance computational efficiency, as detailed in [65,66].
The advantages of NN-performed DSSE include user-friendliness, high accuracy, and rapid computation post-training. However, they often suffer from greater interpretability challenges than NN-based FASE algorithms, as they may discard physical equations and constraints in favor of a black-box modeling approach. While NN-based FASE algorithms utilize NN-generated pseudo-measurements, the DSSE results are still derived using traditional DSSE methods, thereby remaining subject to power system physical models and constraints—unlike NN-performed DSSE, which may disregard such constraints. PINNs mitigate some of these physical constraint issues by embedding physical laws within NNs, yet they also require substantial data for training, reflecting the inherent data dependency of NNs.
Comparative Analysis and Summary of NN-Performed DSSE Categories
The NN-performed DSSE methods of Section 5 fall into four categories: standard ANNs, Bayesian NNs, physics-informed NNs, and other hybrid architectures. Table 4 provides a category-level comparison.

Table 4.
Category-level summary of NN-performed DSSE methods.
Category-Level Recommendations:
- Employ standard ANNs for very fast, large-scale deployments when uncertainty quantification is not critical.
- Use Bayesian NNs in applications where robust uncertainty estimates and non-Gaussian handling are required.
- Opt for physics-informed NNs to enforce power-flow and equipment constraints within the learning process.
- Consider hybrid architectures for scenarios with low observability or bespoke robustness needs.
6. Discussion and Suggestions for Future Work
In the preceding sections, three categories of DSSE algorithms incorporating RES were discussed. This section explores potential future research directions in this field.
In DSSE, observability and measurement uncertainties are critical factors influencing the solvability of DSSE problems. Integrating RES physical models into the estimation process can enhance observability and align estimation results more closely with these models, contingent upon the availability of accurate physical model data. Future research in the first category of algorithms may focus on leveraging advanced optimization techniques to tackle robustness challenges, as exemplified in [27,28,29]. Established optimization theories offer numerous avenues for robust estimation solutions, such as the Osprey optimization algorithm [67] and the Coati optimization algorithm [68].
The second category can enhance DSSE’s measurement matrix by introducing additional pseudo-measurements to restore observability, improve measurement redundancy, and address missing data. However, the feasibility of applying these FASE algorithms heavily relies on the availability of comprehensive datasets. Modifications to the estimation step of KF-based FASE algorithms can also enhance performance in specific contexts, as demonstrated in [37,38,40]. Additionally, KF-based algorithms can draw insights from other established algorithms to tackle specific DSSE challenges; for example, the Schur complement to handle ill-conditioning issues in [35].
NNs have demonstrated efficacy in RES generation forecasting [44], paving the way for NN-based FASE implementations. Advanced RES generation forecasting techniques, such as machine learning and statistical hybrid models [69] and recurrent neural network models like dynamic fitness Al-Biruni earth radius [70], can potentially enhance NN-based FASE. However, the practical implementation of these approaches necessitates careful consideration of data availability and the trade-offs between cost and efficiency.
The application of NNs for DSSE represents a growing area that warrants further exploration. Following the introduction of PINNs to address DSSE challenges, the issue of interpretability has been mitigated by constraining outputs to align with power flow and other relevant models. The evolving landscape of NNs offers promising avenues for performing DSSE, exemplified by innovations such as the Kolmogorov–Arnold network [71] and Lagrangian neural networks [72]. Moreover, the Bayesian physics-informed neural network (BPINN) proposed in [73] presents a compelling approach for DSSE, leveraging the robustness and safety features of Bayesian and physics-informed techniques. The future application of BPINN to perform DSSE seems a promising approach.
Finally, unbalanced network conditions—common in low-voltage distribution feeders due to uneven single-phase loads, asymmetrical line impedances, and nonuniform DER integration—significantly increase the SE problem dimension, intensify phase coupling, and exacerbate observability challenges under sparse instrumentation, leading to reduced accuracy, slower or failed convergence, and heightened sensitivity to initialization [74,75]. To mitigate these effects, current research has extended classical WLS to robust three-phase formulations that explicitly model asymmetry [75], employ dynamic Kalman filter variants to leverage temporal correlations and fill in data gaps [76], and adopt physics-informed machine learning models embedding power-flow constraints for rapid, reliable estimation despite limited sensing [46]. Future work should focus on hybrid SE frameworks that seamlessly combine physical models with data-driven learning for greater adaptability, on strategic sensor placement and multi-source data fusion to bolster observability, and on advanced uncertainty quantification—such as probabilistic, interval, and forecast-aided estimation—to robustly manage DER variability and dynamic load conditions [40].
7. Conclusions
Starting from the viewpoint of algorithms, this paper has reviewed articles on DSSE problems considering RESs’ uncertainties in three categories: generation-model-aided, forecasting-aided, and neural network-based approaches. The main difference between categories one and two is the introduction of an extended state estimator based on models other than the standard power-flow models, while NNs are directly used to perform DSSE in the third category. This paper provides insight into the practical application of DSSE algorithms. For instance, if a researcher needs to address the DSSE problem in an RES-penetrated network and has access to a large volume of historical data of RESs, the researcher may refer to the fitted function and NN approach in Section 3.2 and the algorithms in Section 4.1 and Section 4.2 and develop their own approach for target scenario. Directions for future research have also been identified, which can be helpful to researchers who would like to have insights into this field. A summary of the mentioned PSSE algorithms has been tabulated in Table 5.
Author Contributions
Conceptualization, H.Q.; investigation, H.Q.; writing—original draft preparation, H.Q.; writing—review and editing, A.K.S. and E.B.; supervision, A.K.S. and E.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| WTG | Wind Turbine Generator |
| PV | Photovoltaics |
| PSSE | Power System State Estimation |
| WLS | Weighted Least Square |
| RESs | Renewable Energy Resources |
| PSAT | Power System Analysis Toolbox |
| DSSE | Distribution System State Estimation |
| FASE | Forecasting-Aided State Estimation |
| NNs | Neural Networks |
| BPNN | Back-Propagation Neural Network |
| ANN | Artificial Neural Network |
| ISE | Interval State Estimation |
| MKO | Modified Krawczyk Operator |
| KF | Kalman Filter |
| PV-IEKF | Photovoltaic-Assisted Interleaved Extended Kalman Filter |
| UKF | Unscented Kalman Filter |
| EnKF | Ensemble Kalman Filter |
| REnKF | Robust Ensemble Kalman Filter |
| AEKF | Adaptive Extended Kalman Filter |
| ELM | Extreme Learning Machine |
| GA | Genetic Algorithm |
| LSTM | Long Short-Term Memory |
| DREL | Demand-Response-Enabled Load |
| KNN | K-Nearest Neighbor |
| USENN | Unobservable State Estimation Neural Network |
| BNN | Bayesian Neural Network |
| PINN | Physics-Informed Neural Network |
| GNN | Graph Neural Network |
| MV | Medium Voltage |
| NM | Nelder–Mead (Simplex Search) |
| PSO | Particle Swarm Optimization |
| DLM-PSO | Mutated Two-Loop Particle Swarm Optimization |
| PASE | Past-Aware State Estimation |
| PS | Projection Statistics |
| PGNN | Physics-Guided Neural Network |
| ML | Machine Learning |
References
- Schweppe, F.C.; Wildes, J. Power System Static-State Estimation, Part I: Exact Model. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 120–125. [Google Scholar] [CrossRef]
- Schweppe, F.C.; Rom, D.B. Power System Static-State Estimation, Part II: Approximate Model. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 125–130. [Google Scholar] [CrossRef]
- Schweppe, F.C. Power System Static-State Estimation, Part III: Implementation. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 130–135. [Google Scholar] [CrossRef]
- PSS®E; Power Transmission System Planning Software; Siemens Industry, Inc.: Munich, Germany, 2025. Available online: https://www.siemens.com/global/en/products/energy/grid-software/planning/pss-software/pss-e.html (accessed on 12 May 2025).
- PSAT; Power System Analysis Toolbox; GE Grid Solutions: Boulogne-Billancourt, France, 2025. Available online: https://www.gegridsolutions.com/ (accessed on 12th May 2025).
- DIgSILENT PowerFactory; Power System Analysis Software; DIgSILENT GmbH: Gomaringen, Germany, 2025. Available online: https://www.digsilent.de/en/powerfactory.html (accessed on 12 May 2025).
- Gonzalez-Longatt, F.M.; Rueda, J.L. PowerFactory Applications for Power System Analysis; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2010, 26, 12–19. [Google Scholar] [CrossRef]
- OpenDSS. The Open Distribution System Simulator; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2010; Available online: https://www.epri.com/pages/sa/opendss (accessed on 12 May 2025).
- Chassin, D.P.; Fuller, J.C.; Djilali, N. GridLAB-D: An agent-based simulation framework for smart grids. J. Appl. Math. 2014, 2014, 492320. [Google Scholar] [CrossRef]
- Chassin, D.P.; Schneider, K.; Gerkensmeyer, C. GridLAB-D: An open-source power systems modeling and simulation environment. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, G.; Giannakis, G.B.; Chen, J.; Sun, J. Distribution system state estimation: An overview of recent developments. Front. Inf. Technol. Electron. Eng. 2019, 20, 4–17. [Google Scholar] [CrossRef]
- Jin, X.B.; Robert Jeremiah, R.J.; Su, T.L.; Bai, Y.T.; Kong, J.L. The New Trend of State Estimation: From Model-Driven to Hybrid-Driven Methods. Sensors 2021, 21, 2085. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Wang, Z.; Wang, J.; Yuan, Y.; Bu, F. A survey on state estimation techniques and challenges in smart distribution systems. IEEE Trans. Smart Grid 2018, 10, 2312–2322. [Google Scholar] [CrossRef]
- Fotopoulou, M.; Petridis, S.; Karachalios, I.; Rakopoulos, D. A Review on Distribution System State Estimation Algorithms. Appl. Sci. 2022, 12, 11073. [Google Scholar] [CrossRef]
- Primadianto, A.; Lu, C.N. A review on distribution system state estimation. IEEE Trans. Power Syst. 2016, 32, 3875–3883. [Google Scholar] [CrossRef]
- Wu, F.F. Power system state estimation: A survey. Int. J. Electr. Power Energy Syst. 1990, 12, 80–87. [Google Scholar] [CrossRef]
- Ahmad, F.; Rasool, A.; Ozsoy, E.; Sekar, R.; Sabanovic, A.; Elitaş, M. Distribution System state estimation—A step towards smart grid. Renew. Sustain. Energy Rev. 2018, 81, 2659–2671. [Google Scholar] [CrossRef]
- Abur, A.; Exposito, A.G. Power System State Estimation: Theory and Implementation; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Sun, G.Q.; Wei, Z.N.; Pang, B. Power System State Estimation Containing Wind Generators. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Sun, G.Q.; Wei, Z.N.; Pang, B. Impact of wind generators on power system state estimation. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Wei, Z.; Yang, X.; Sun, G.; Sun, Y.; Ju, P. Wind power system state estimation with automatic differentiation technique. Int. J. Electr. Power Energy Syst. 2013, 53, 297–306. [Google Scholar] [CrossRef]
- Miranda-Blanco, B.N.; Díaz-Dorado, E.; Carrillo, C.; Cidrás, J. State estimation for wind farms including the wind turbine generator models. Renew. Energy 2014, 71, 453–465. [Google Scholar] [CrossRef]
- Ranković, A.; Sarić, A.T. Modeling of photovoltaic and wind turbine based distributed generation in state estimation. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. LS2b.2-1–LS2b.2-6. [Google Scholar] [CrossRef]
- Ranković, A.; Maksimović, B.M.; Sarić, A.T. A three-phase state estimation in active distribution networks. Int. J. Electr. Power Energy Syst. 2014, 54, 154–162. [Google Scholar] [CrossRef]
- Fang, Z.; Lin, Y.; Song, S.; Song, C.; Lin, X.; Cheng, G. Active distribution system state estimation incorporating photovoltaic generation system model. Electr. Power Syst. Res. 2020, 182, 106247. [Google Scholar] [CrossRef]
- Niknam, T.; Firouzi, B.B. A practical algorithm for distribution state estimation including renewable energy sources. Renew. Energy 2009, 34, 2309–2316. [Google Scholar] [CrossRef]
- Khorshidi, R.; Shabaninia, F.; Niknam, T. A new smart approach for state estimation of distribution grids considering renewable energy sources. Energy 2016, 94, 29–37. [Google Scholar] [CrossRef]
- Shaghaghi, A.; Zahedi, R.; Ghorbani, M.; Ranjbar, Z.; Arzhangi, S.S.; Keshavarzzadeh, M.; Alipour, H. State estimation for distribution power systems by applying an advanced optimization approach. Expert Syst. Appl. 2024, 240, 122325. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Li, Z. Interval State Estimation With Uncertainty of Distributed Generation and Line Parameters in Unbalanced Distribution Systems. IEEE Trans. Power Syst. 2020, 35, 762–772. [Google Scholar] [CrossRef]
- Do Coutto Filho, M.B.; de Souza, J.C.S. Forecasting-aided state estimation—Part I: Panorama. IEEE Trans. Power Syst. 2009, 24, 1667–1677. [Google Scholar] [CrossRef]
- Do Coutto Filho, M.B.; Stacchini de Souza, J.C.; Freund, R.S. Forecasting-Aided State Estimation—Part II: Implementation. IEEE Trans. Power Syst. 2009, 24, 1678–1685. [Google Scholar] [CrossRef]
- Nishiya, K.; Hasegawa, J.; Koike, T. Dynamic state estimation including anomaly detection and identification for power systems. IEE Proc. C (Gener. Transm. Distrib.) 1982, 129, 192–198. [Google Scholar] [CrossRef]
- Servadio, S. High Order Filters for Relative Pose Estimation of an Uncooperative Target. Master Thesis, Politecnico di Milano, Milan, Italy, 2017. [Google Scholar]
- Barchi, G.; Macii, D. A photovoltaics-aided interlaced extended Kalman filter for distribution systems state estimation. Sustain. Energy Grids Netw. 2021, 26, 100438. [Google Scholar] [CrossRef]
- Huang, M.; Wei, Z.; Sun, G.; Sun, Y.; Zang, H.; Cheung, K.W. A historical data-driven unscented Kalman filter for distribution system state estimation. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Carquex, C.; Rosenberg, C.; Bhattacharya, K. State Estimation in Power Distribution Systems Based on Ensemble Kalman Filtering. IEEE Trans. Power Syst. 2018, 33, 6600–6610. [Google Scholar] [CrossRef]
- Huang, M.; Wei, Z.; Zhao, J.; Jabr, R.A.; Pau, M.; Sun, G. Robust Ensemble Kalman Filter for Medium-Voltage Distribution System State Estimation. IEEE Trans. Instrum. Meas. 2020, 69, 4114–4124. [Google Scholar] [CrossRef]
- Mili, L.; Cheniae, M.; Vichare, N.; Rousseeuw, P. Robust state estimation based on projection statistics [of power systems]. IEEE Trans. Power Syst. 1996, 11, 1118–1127. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Dinavahi, V. Robust Forecasting-Aided State Estimation for Power System Against Uncertainties. IEEE Trans. Power Syst. 2020, 35, 691–702. [Google Scholar] [CrossRef]
- Yem Souhe, F.G.; Boum, A.T.; Ele, P.; Mbey, C.F.; Foba Kakeu, V.J. A novel smart method for state estimation in a smart grid using smart meter data. Appl. Comput. Intell. Soft Comput. 2022, 2022, 7978263. [Google Scholar] [CrossRef]
- Hu, H.; Wang, L.; Lv, S.X. Forecasting energy consumption and wind power generation using deep echo state network. Renew. Energy 2020, 154, 598–613. [Google Scholar] [CrossRef]
- Zhu, H.; Li, X.; Sun, Q.; Nie, L.; Yao, J.; Zhao, G. A Power Prediction Method for Photovoltaic Power Plant Based on Wavelet Decomposition and Artificial Neural Networks. Energies 2016, 9, 11. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Artificial neural networks in renewable energy systems applications: A review. Renew. Sustain. Energy Rev. 2001, 5, 373–401. [Google Scholar] [CrossRef]
- Manitsas, E.; Singh, R.; Pal, B.C.; Strbac, G. Distribution System State Estimation Using an Artificial Neural Network Approach for Pseudo Measurement Modeling. IEEE Trans. Power Syst. 2012, 27, 1888–1896. [Google Scholar] [CrossRef]
- Zamzam, A.S.; Fu, X.; Sidiropoulos, N.D. Data-Driven Learning-Based Optimization for Distribution System State Estimation. IEEE Trans. Power Syst. 2019, 34, 4796–4805. [Google Scholar] [CrossRef]
- Cheng, G.; Song, S.; Lin, Y.; Huang, Q.; Lin, X.; Wang, F. Enhanced state estimation and bad data identification in active power distribution networks using photovoltaic power forecasting. Electr. Power Syst. Res. 2019, 177, 105974. [Google Scholar] [CrossRef]
- Alduhaymi, M.; Singh, R.; Nazir, F.U.; Pal, B.C. Deep Learning Based Forecasting-Aided State Estimation in Active Distribution Networks. arXiv 2023, arXiv:2310.13817. [Google Scholar]
- Stowell, D.; Kelly, J.; Tanner, D.; Taylor, J.; Jones, E.; Geddes, J.; Chalstrey, E. A harmonised, high-coverage, open dataset of solar photovoltaic installations in the UK. Sci. Data 2020, 7, 394. [Google Scholar] [CrossRef]
- Liu, J.; Singh, R.; Pal, B.C. Distribution system state estimation with high penetration of demand response enabled loads. IEEE Trans. Power Syst. 2021, 36, 3093–3104. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K.; Kashef, H. A novel smart grid state estimation method based on neural networks. IJIMAI 2018, 5, 92–100. [Google Scholar] [CrossRef]
- Weng, Y.; Negi, R.; Faloutsos, C.; Ilić, M.D. Robust Data-Driven State Estimation for Smart Grid. IEEE Trans. Smart Grid 2017, 8, 1956–1967. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, G.; Giannakis, G.B. Real-Time Power System State Estimation and Forecasting via Deep Unrolled Neural Networks. IEEE Trans. Signal Process. 2019, 67, 4069–4077. [Google Scholar] [CrossRef]
- Tian, G.; Gu, Y.; Shi, D.; Fu, J.; Yu, Z.; Zhou, Q. Neural-network-based Power System State Estimation with Extended Observability. J. Mod. Power Syst. Clean Energy 2021, 9, 1043–1053. [Google Scholar] [CrossRef]
- Vanin, M.; Van Acker, T.; D’hulst, R.; Van Hertem, D. Exact Modeling of Non-Gaussian Measurement Uncertainty in Distribution System State Estimation. IEEE Trans. Instrum. Meas. 2023, 72, 9002911. [Google Scholar] [CrossRef]
- Pegoraro, P.A.; Angioni, A.; Pau, M.; Monti, A.; Muscas, C.; Ponci, F.; Sulis, S. Bayesian approach for distribution system state estimation with non-Gaussian uncertainty models. IEEE Trans. Instrum. Meas. 2017, 66, 2957–2966. [Google Scholar] [CrossRef]
- Mestav, K.R.; Luengo-Rozas, J.; Tong, L. Bayesian state estimation for unobservable distribution systems via deep learning. IEEE Trans. Power Syst. 2019, 34, 4910–4920. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, Q.; Jin, S. Physics-guided Deep Learning for Power System State Estimation. J. Mod. Power Syst. Clean Energy 2020, 8, 607–615. [Google Scholar] [CrossRef]
- Stiasny, J.; Misyris, G.S.; Chatzivasileiadis, S. Physics-Informed Neural Networks for Non-linear System Identification for Power System Dynamics. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Pagnier, L.; Chertkov, M. Physics-informed graphical neural network for parameter & state estimations in power systems. arXiv 2021, arXiv:2102.06349. [Google Scholar]
- Wu, Z.; Wang, Q.; Liu, X. State Estimation for Power System Based on Graph Neural Network. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 1431–1436. [Google Scholar] [CrossRef]
- Habib, B.; Isufi, E.; van Breda, W.; Jongepier, A.; Cremer, J.L. Deep statistical solver for distribution system state estimation. IEEE Trans. Power Syst. 2023, 39, 4039–4050. [Google Scholar] [CrossRef]
- Zamzam, A.S.; Sidiropoulos, N.D. Physics-aware neural networks for distribution system state estimation. IEEE Trans. Power Syst. 2020, 35, 4347–4356. [Google Scholar] [CrossRef]
- Tran, M.Q.; Zamzam, A.S.; Nguyen, P.H.; Pemen, G. Multi-area distribution system state estimation using decentralized physics-aware neural networks. Energies 2021, 14, 3025. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovskỳ, P. Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems. Front. Mech. Eng. 2023, 8, 1126450. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovskỳ, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- AlKandari, M.; Ahmad, I. Solar power generation forecasting using ensemble approach based on deep learning and statistical methods. Appl. Comput. Informatics 2024, 20, 231–250. [Google Scholar] [CrossRef]
- Karim, F.K.; Khafaga, D.S.; Eid, M.M.; Towfek, S.; Alkahtani, H.K. A novel bio-inspired optimization algorithm design for wind power engineering applications time-series forecasting. Biomimetics 2023, 8, 321. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov-arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Cranmer, M.; Greydanus, S.; Hoyer, S.; Battaglia, P.; Spergel, D.; Ho, S. Lagrangian neural networks. arXiv 2020, arXiv:2003.04630. [Google Scholar]
- Yang, L.; Meng, X.; Karniadakis, G.E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys. 2021, 425, 109913. [Google Scholar] [CrossRef]
- Ullah, Z.; Elkadeem, M.R.; Wang, S.; Radosavljević, J. A novel PSOS-CGSA method for state estimation in unbalanced DG-integrated distribution systems. IEEE Access 2020, 8, 113219–113229. [Google Scholar] [CrossRef]
- Song, S.; Xiong, H.; Lin, Y.; Huang, M.; Wei, Z.; Fang, Z. Robust three-phase state estimation for PV-Integrated unbalanced distribution systems. Appl. Energy 2022, 322, 119427. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, X.; Zhang, X.; Wang, C.; Chiang, H.D.; Li, P. Adaptive dynamic state estimation of distribution network based on interacting multiple model. IEEE Trans. Sustain. Energy 2021, 13, 643–652. [Google Scholar] [CrossRef]
- Saric, A.; Ciric, R. Integrated fuzzy state estimation and load flow analysis in distribution networks. IEEE Trans. Power Deliv. 2003, 18, 571–578. [Google Scholar] [CrossRef]
- Sarić, A.T.; Ranković, A. Load reallocation based algorithm for state estimation in distribution networks with distributed generators. Electr. Power Syst. Res. 2012, 84, 72–82. [Google Scholar] [CrossRef]
- Boris, A. Alcaide Moreno, Claudio R. Fuerte Esquivel, L.M.C.; Cárdenas, E.A.Z. Generalized State Estimation of Flexible AC Power Systems Considering Wind Generators and Primary Frequency Control. Electr. Power Components Syst. 2015, 43, 1534–1547. [Google Scholar] [CrossRef]
- Sotavento—Parque Eólico Experimental, 2020. Available online: https://www.sotaventogalicia.com/en/ (accessed on 12 May 2025).
- Resources—IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 12 May 2025).
- Das, D.; Kothari, D.; Kalam, A. Simple and efficient method for load flow solution of radial distribution networks. Int. J. Electr. Power Energy Syst. 1995, 17, 335–346. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).