Modeling and Analysis of Current-Carrying Coils Versus Rotating Magnet Transmitters for Low-Frequency Electrodynamic Wireless Power Transmission
Abstract
1. Introduction
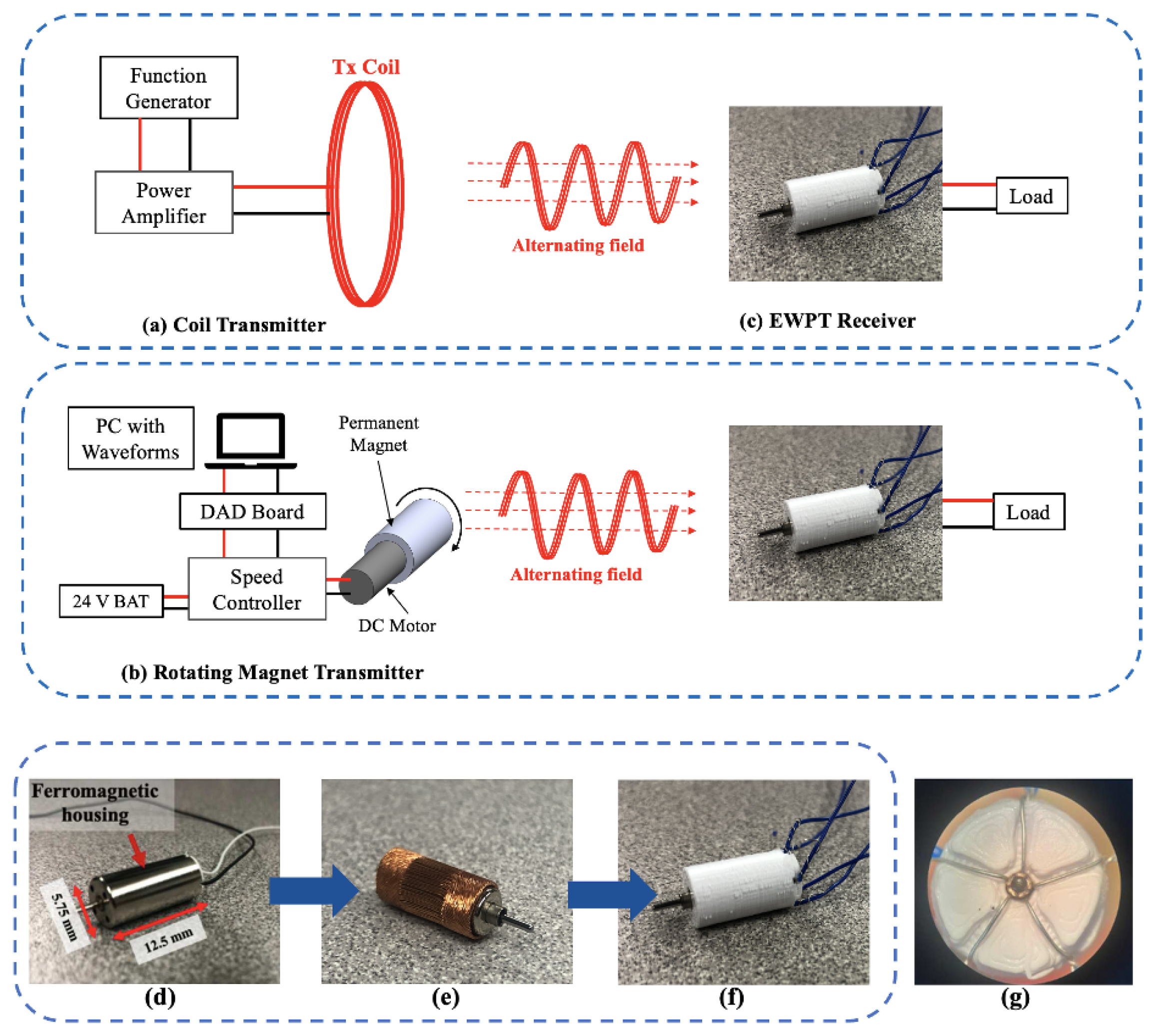
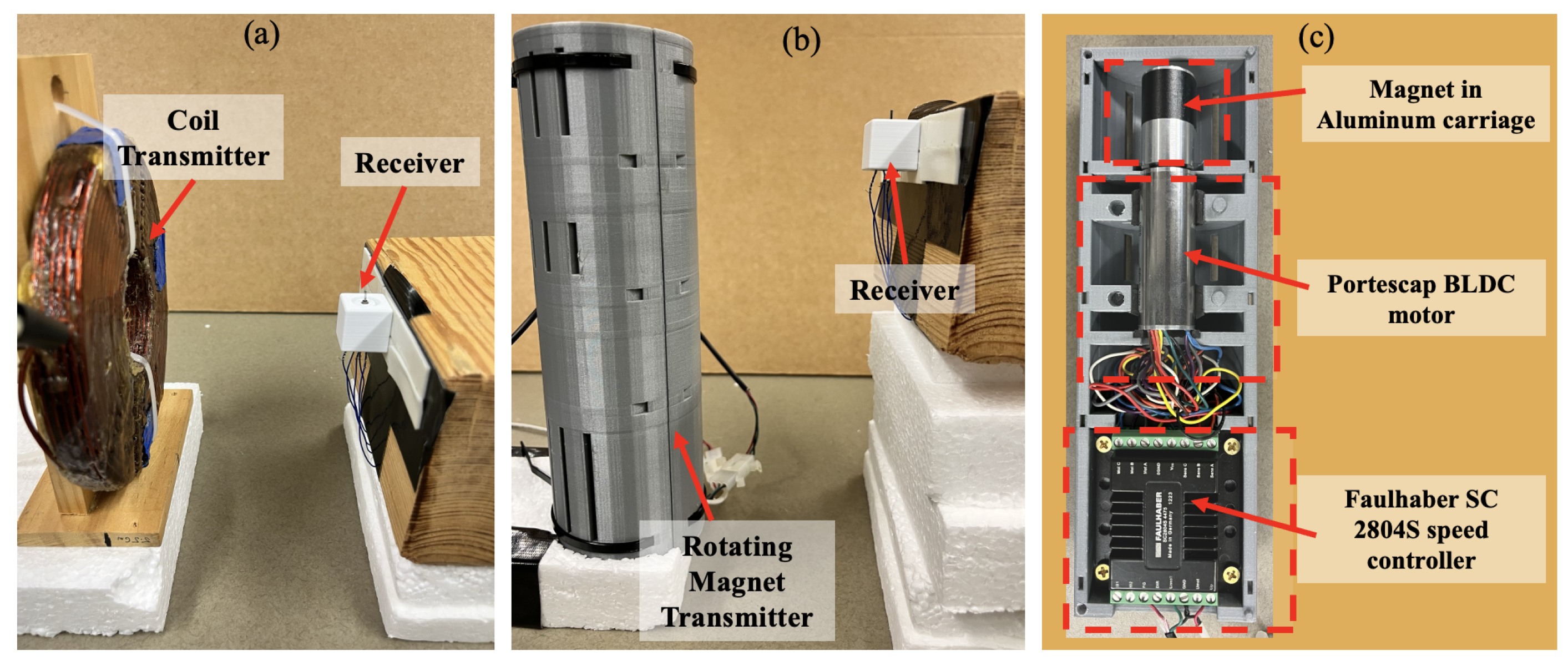
2. Methods and Materials
3. Modeling and Simulation
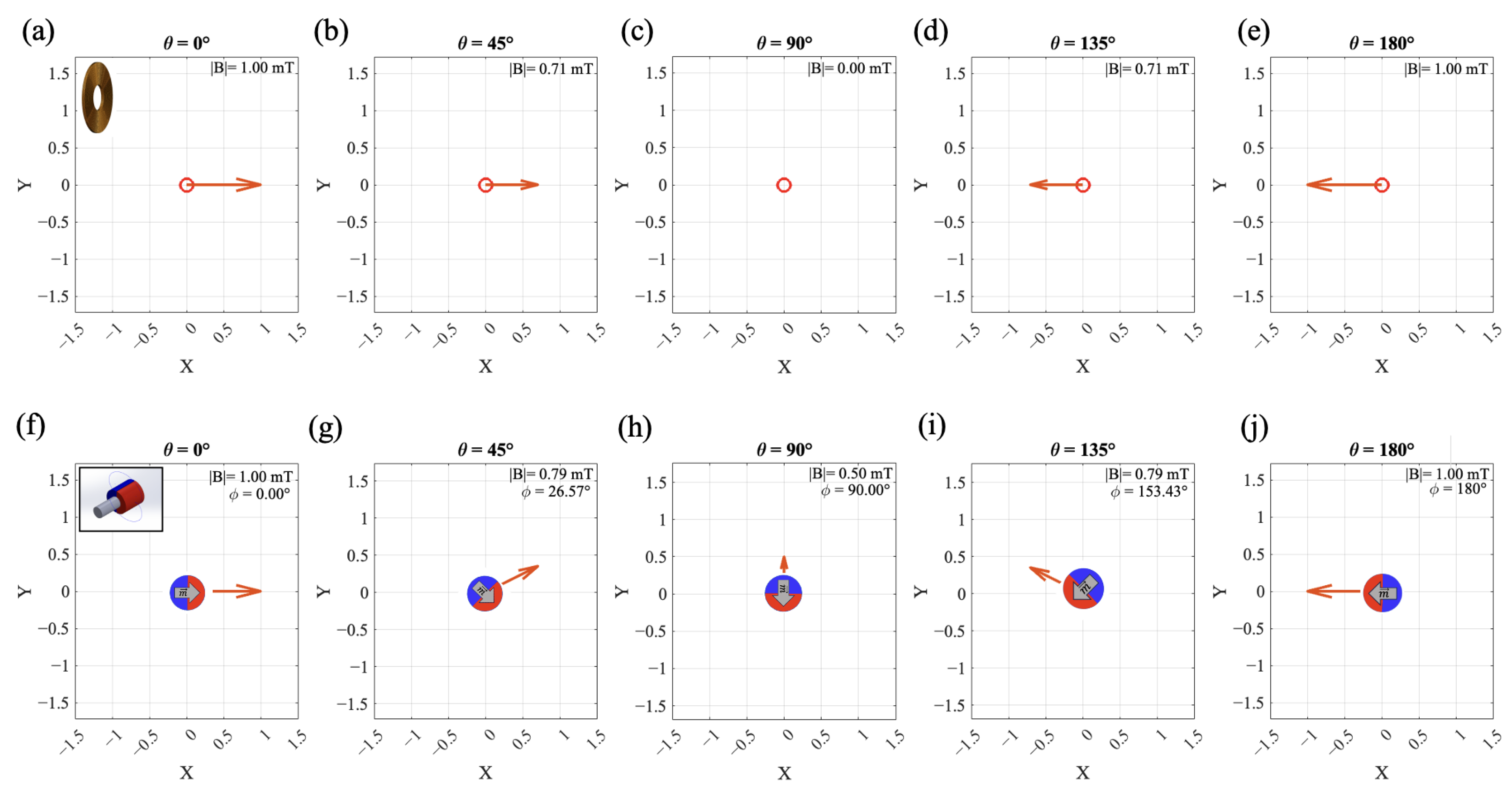
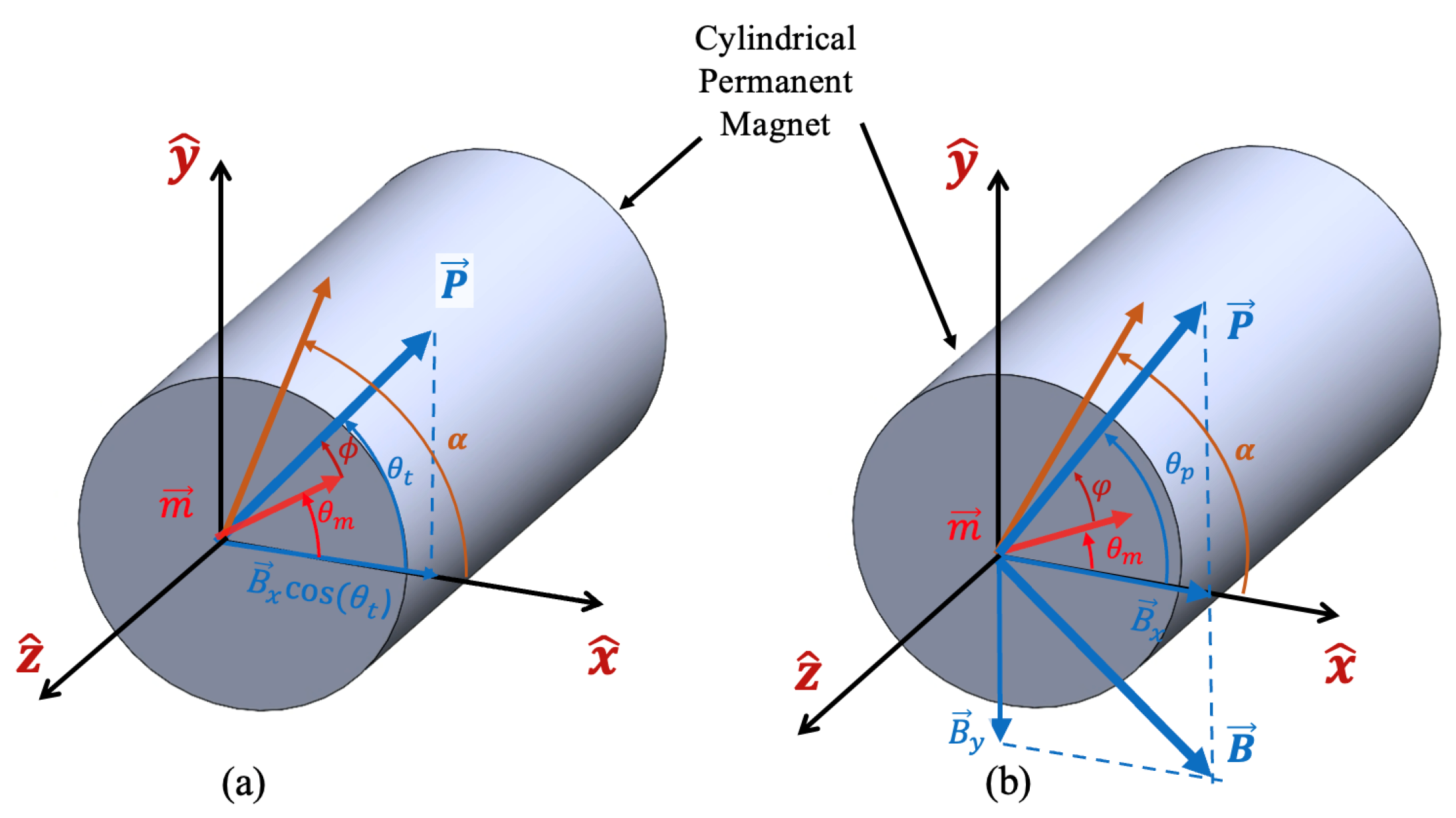
3.1. Theory
3.1.1. Uniaxial Field Case
3.1.2. Biaxial Field Case
3.2. Analytical Solution
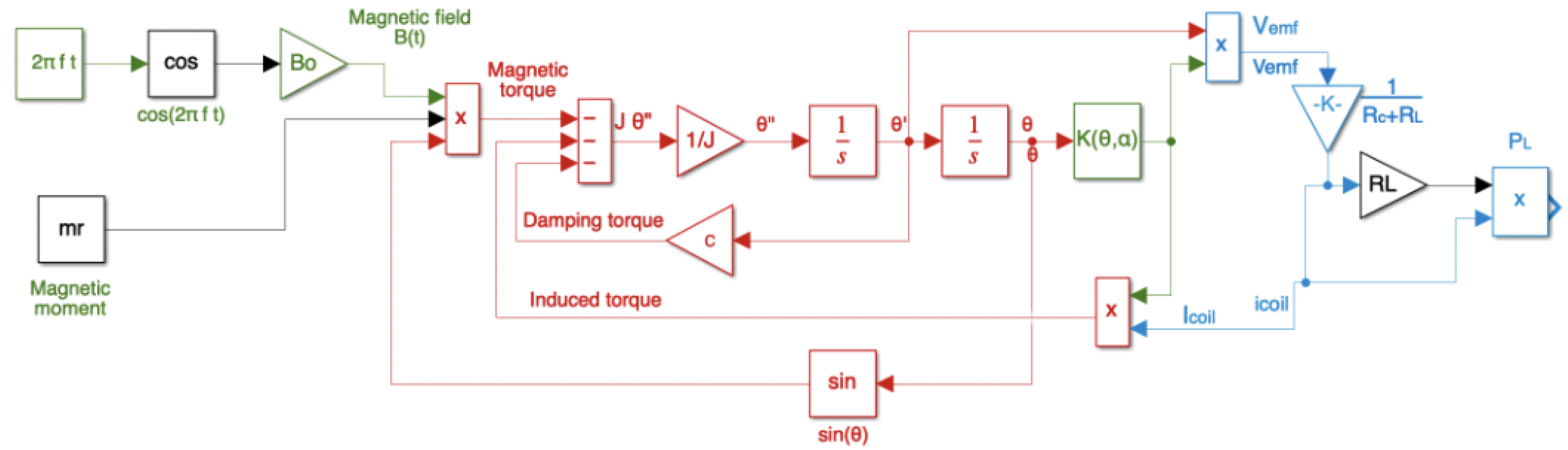
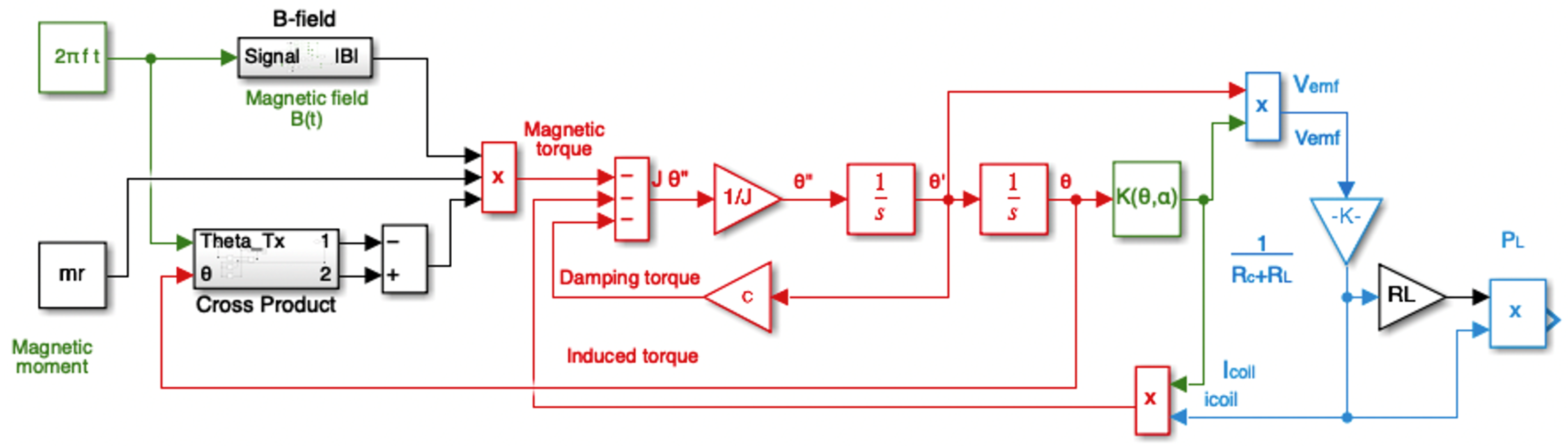
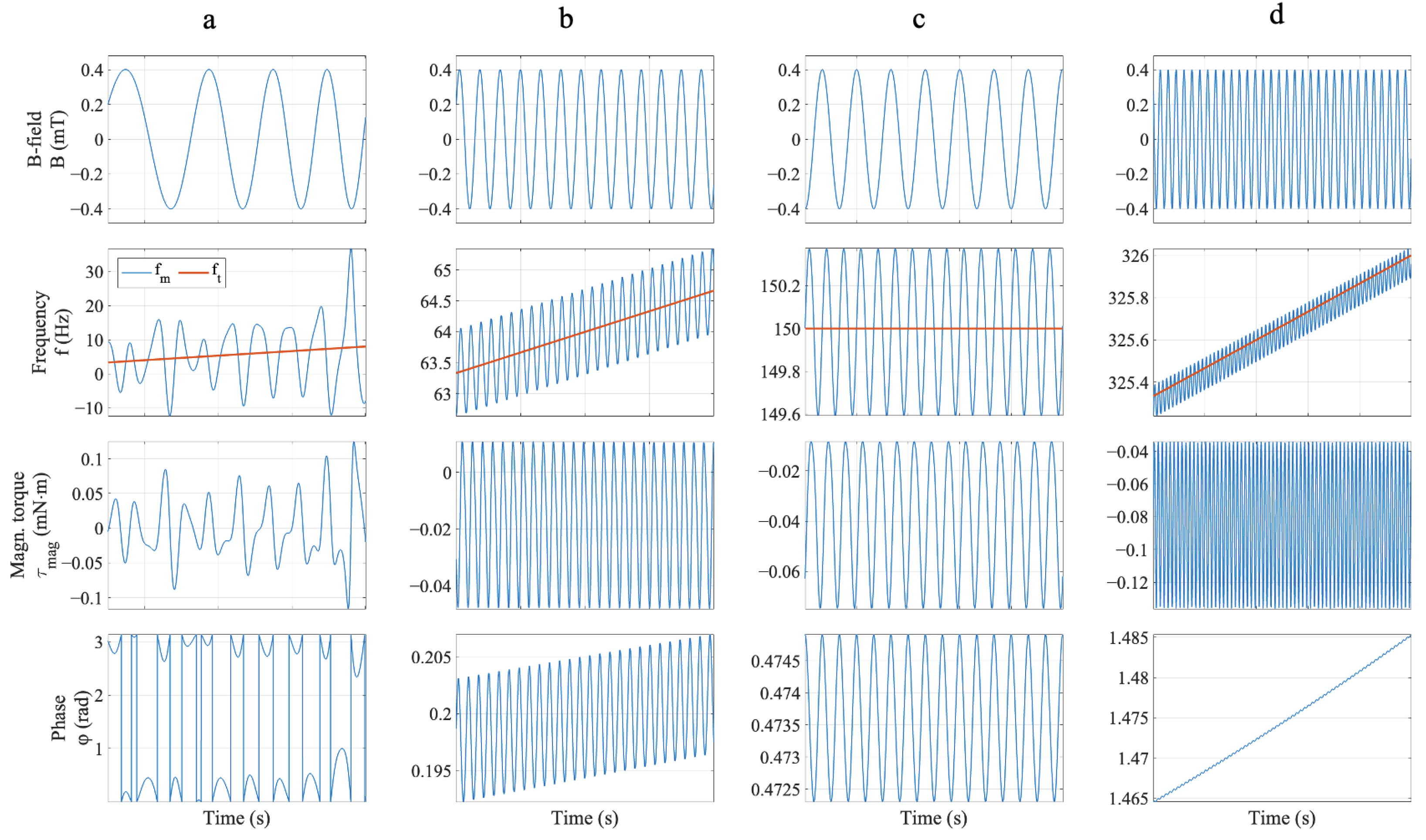
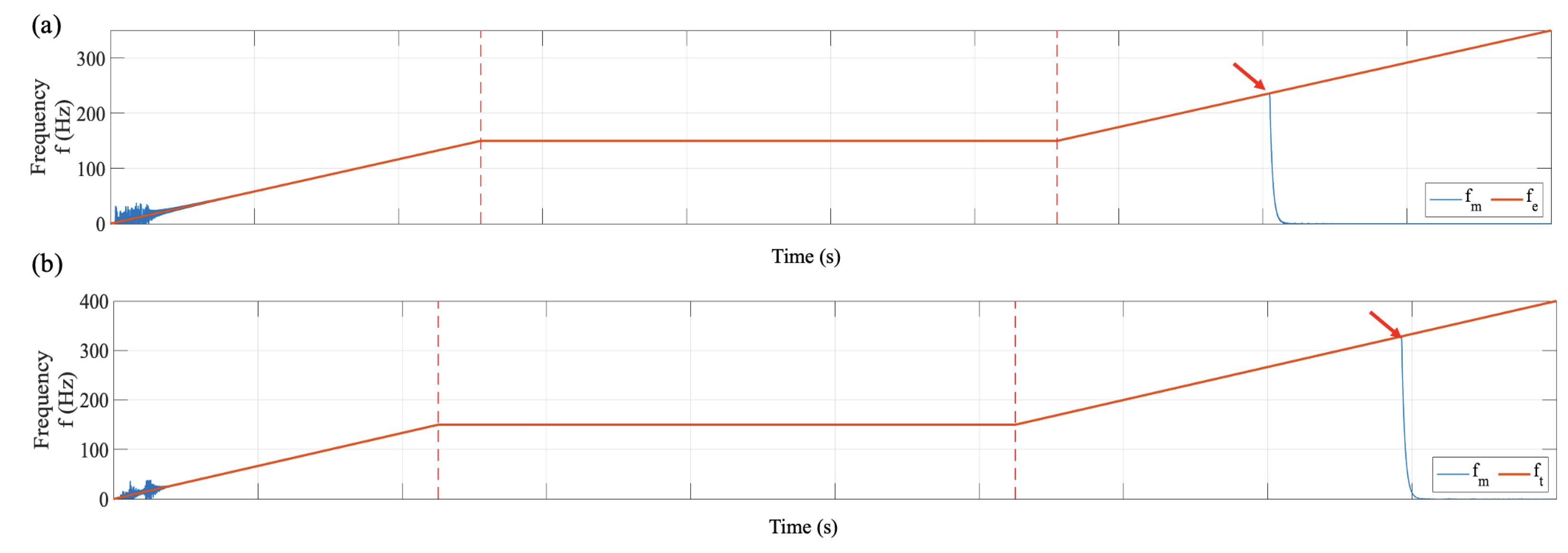
3.3. Simulink Modeling
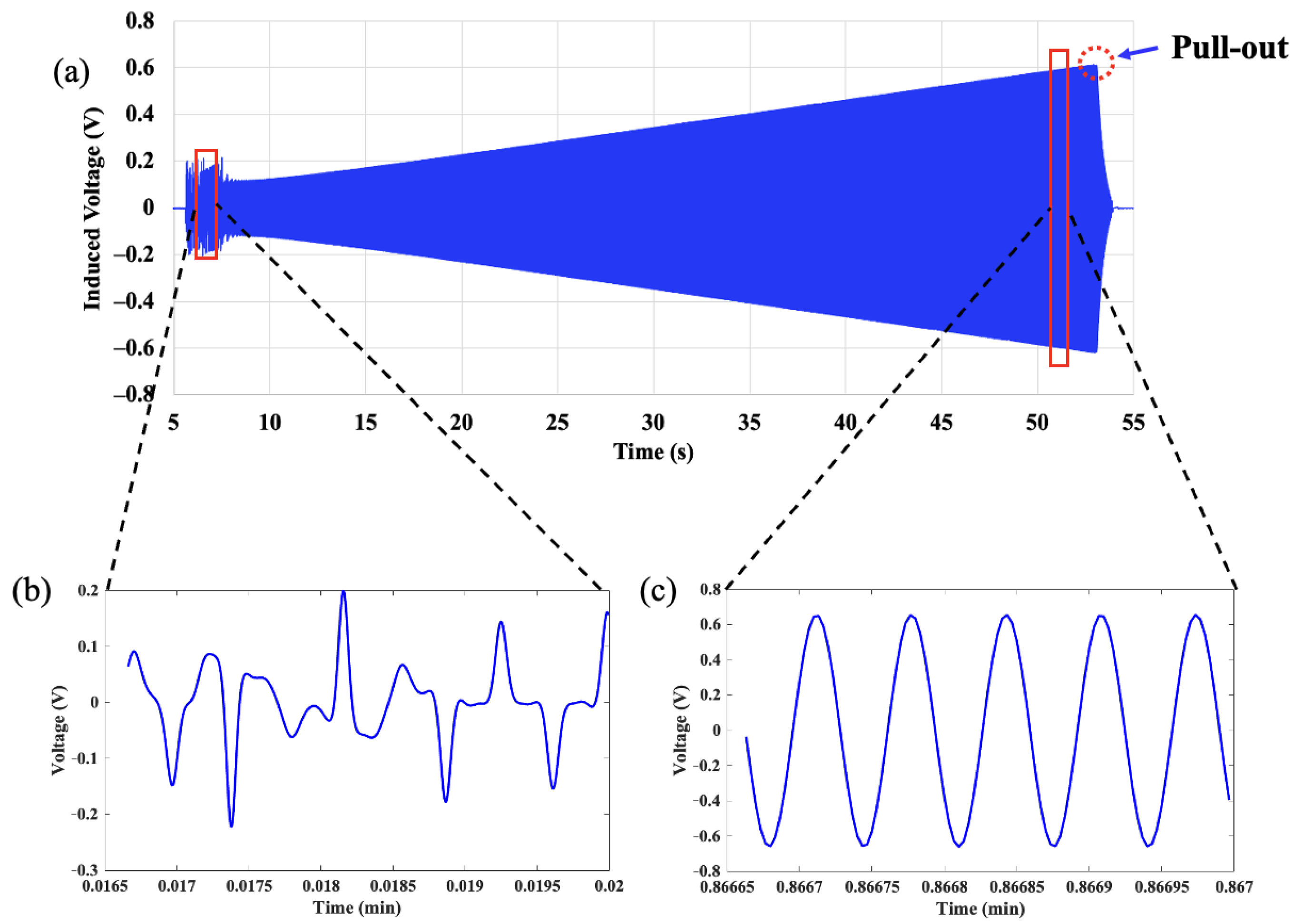
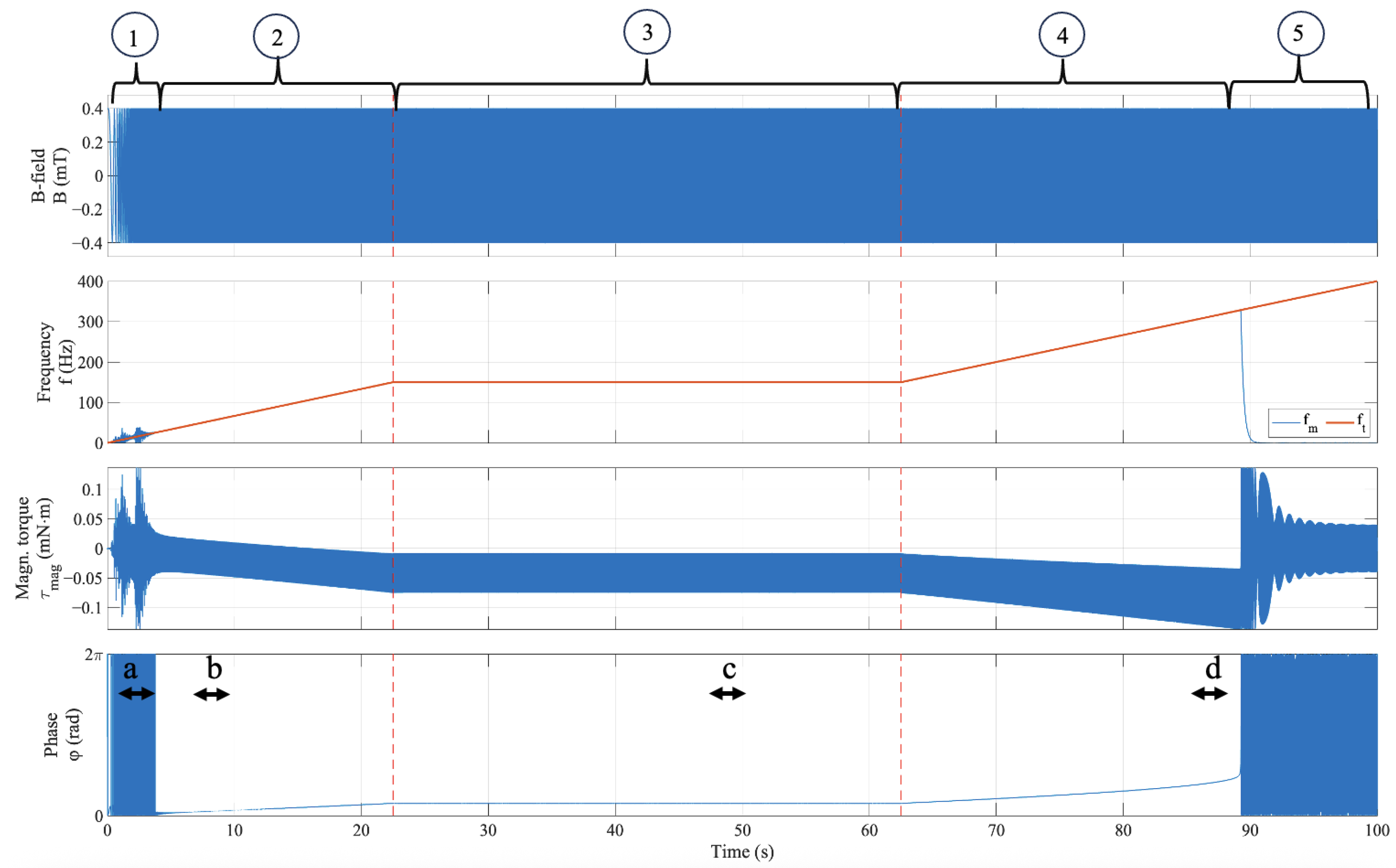
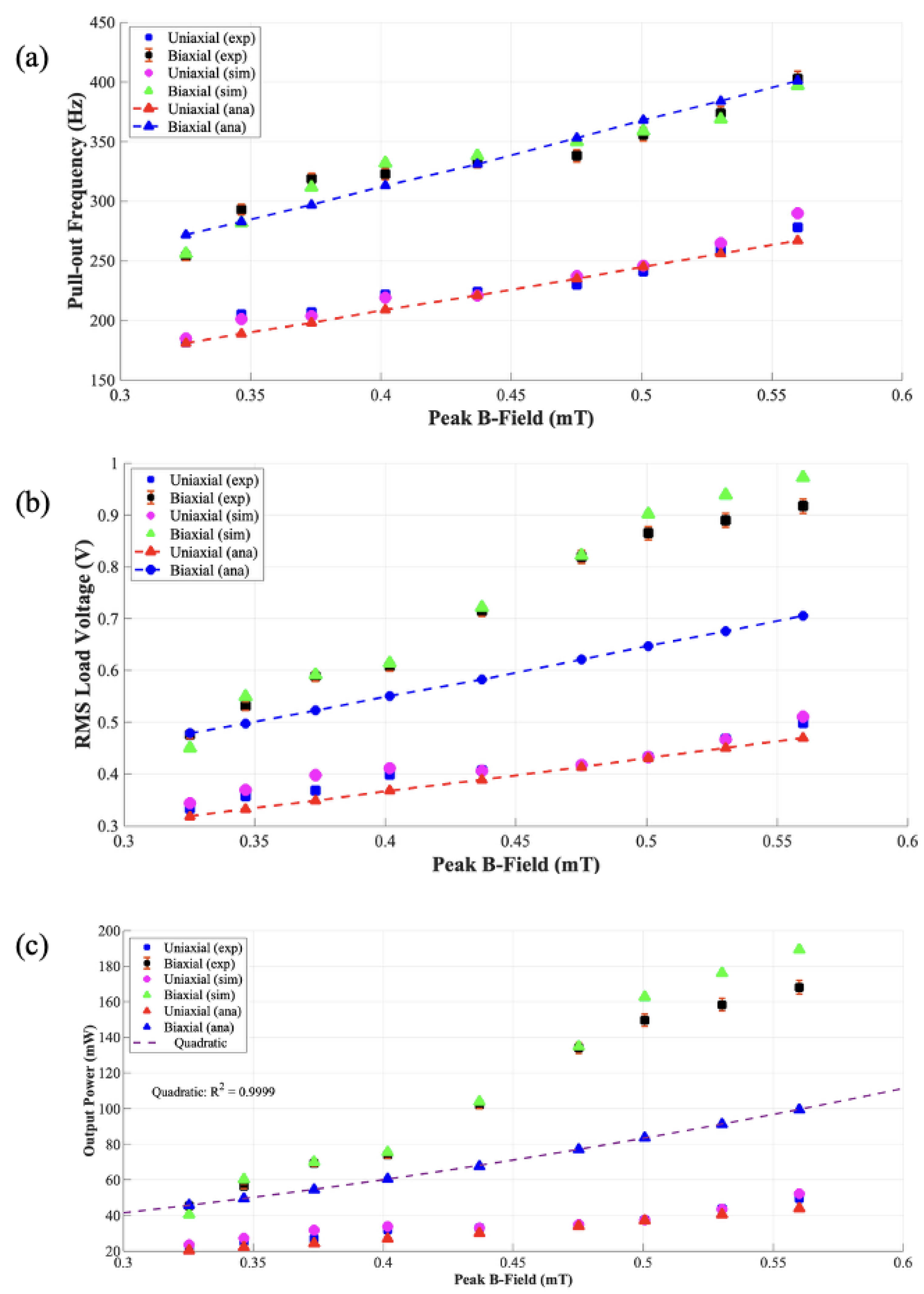
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WPT | Wireless Power Transfer |
| EWPT | Electrodynamic Wireless Power Transfer |
| PD | Power Density |
| NPD | Normalized Power Density |
References
- Niu, S.; Xu, H.; Sun, Z.; Shao, Z.; Jian, L. The state-of-the-arts of wireless electric vehicle charging via magnetic resonance: Principles, standards and core technologies. Renew. Sustain. Energy Rev. 2019, 114, 109302. [Google Scholar] [CrossRef]
- Li, W. High Efficiency Wireless Power Transmission at Low Frequency Using Permanent Magnet Coupling. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2009. [Google Scholar] [CrossRef]
- Du, S.; Chan, E.K.; Wen, B.; Hong, J.; Widmer, H.; Wheatley, C.E. Wireless Power Transfer Using Oscillating Magnets. IEEE Trans. Ind. Electron. 2018, 65, 6259–6269. [Google Scholar] [CrossRef]
- Singer, A.; Dutta, S.; Lewis, E.; Chen, Z.; Chen, J.C.; Verma, N.; Avants, B.; Feldman, A.K.; O’Malley, J.; Beierlein, M.; et al. Magnetoelectric Materials for Miniature, Wireless Neural Stimulation at Therapeutic Frequencies. Neuron 2020, 107, 631–643.e5. [Google Scholar] [CrossRef] [PubMed]
- Barrett, C.; Fu, H.; Theodossiades, S. Electrodynamic Wireless Power and Data Transfer for Implanted Medical Devices. In Proceedings of the 2023 IEEE SENSORS, Vienna, Austria, 29 October–1 November 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Garraud, N.; Alabi, D.; Chyczewski, S.; Varela, J.D.; Arnold, D.P.; Garraud, A. Extending the range of wireless power transmission for bio-implants and wearables. J. Phys. Conf. Ser. 2018, 1052, 012023. [Google Scholar] [CrossRef]
- Garraud, N.; Alessandri, B.; Gasnier, P.; Arnold, D.; Boisseau, S. Optimization of a Magnetodynamic Receiver for Versatile Low-Frequency Wireless Power Transfer. In Proceedings of the 2019 19th International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS), Krakow, Poland, 2–6 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, J.; Lan, D.; Chao, K.K.; Liou, S.; Shahnasser, H.; Fechter, R.; Hirose, S.; Harrison, M.; Roy, S. A Low-Frequency Versatile Wireless Power Transfer Technology for Biomedical Implants. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 526–535. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Yuan, H.; Zhang, R.; Yang, A.; Wang, X.; Rong, M. Low-Frequency Wireless Power Transfer Via Rotating Permanent Magnets. IEEE Trans. Ind. Electron. 2022, 69, 10656–10665. [Google Scholar] [CrossRef]
- Crasto, V.S.; Stormant, M.G.; Arnold, D.P. Electrodynamic Wireless Power Transfer to High-Performance Rotating Magnet Receivers. In Proceedings of the 2023 IEEE 22nd International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS), Abu Dhabi, United Arab Emirates, 11–14 December 2023; pp. 33–36. [Google Scholar] [CrossRef]
- Garraud, N.; Garraud, A.; Munzer, D.; Althar, M.; Arnold, D.P. Modeling and experimental analysis of rotating magnet receivers for electrodynamic wireless power transmission. J. Phys. D Appl. Phys. 2019, 52, 185501. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crasto, V.S.; Garraud, N.; Stormant, M.G.; Arnold, D.P. Modeling and Analysis of Current-Carrying Coils Versus Rotating Magnet Transmitters for Low-Frequency Electrodynamic Wireless Power Transmission. Energies 2025, 18, 2506. https://doi.org/10.3390/en18102506
Crasto VS, Garraud N, Stormant MG, Arnold DP. Modeling and Analysis of Current-Carrying Coils Versus Rotating Magnet Transmitters for Low-Frequency Electrodynamic Wireless Power Transmission. Energies. 2025; 18(10):2506. https://doi.org/10.3390/en18102506
Chicago/Turabian StyleCrasto, Vernon S., Nicolas Garraud, Matthew G. Stormant, and David P. Arnold. 2025. "Modeling and Analysis of Current-Carrying Coils Versus Rotating Magnet Transmitters for Low-Frequency Electrodynamic Wireless Power Transmission" Energies 18, no. 10: 2506. https://doi.org/10.3390/en18102506
APA StyleCrasto, V. S., Garraud, N., Stormant, M. G., & Arnold, D. P. (2025). Modeling and Analysis of Current-Carrying Coils Versus Rotating Magnet Transmitters for Low-Frequency Electrodynamic Wireless Power Transmission. Energies, 18(10), 2506. https://doi.org/10.3390/en18102506







