An Adaptive Control Strategy for a Better Performance of the Paralleled PV-BES-VSG Power System
Abstract
1. Introduction
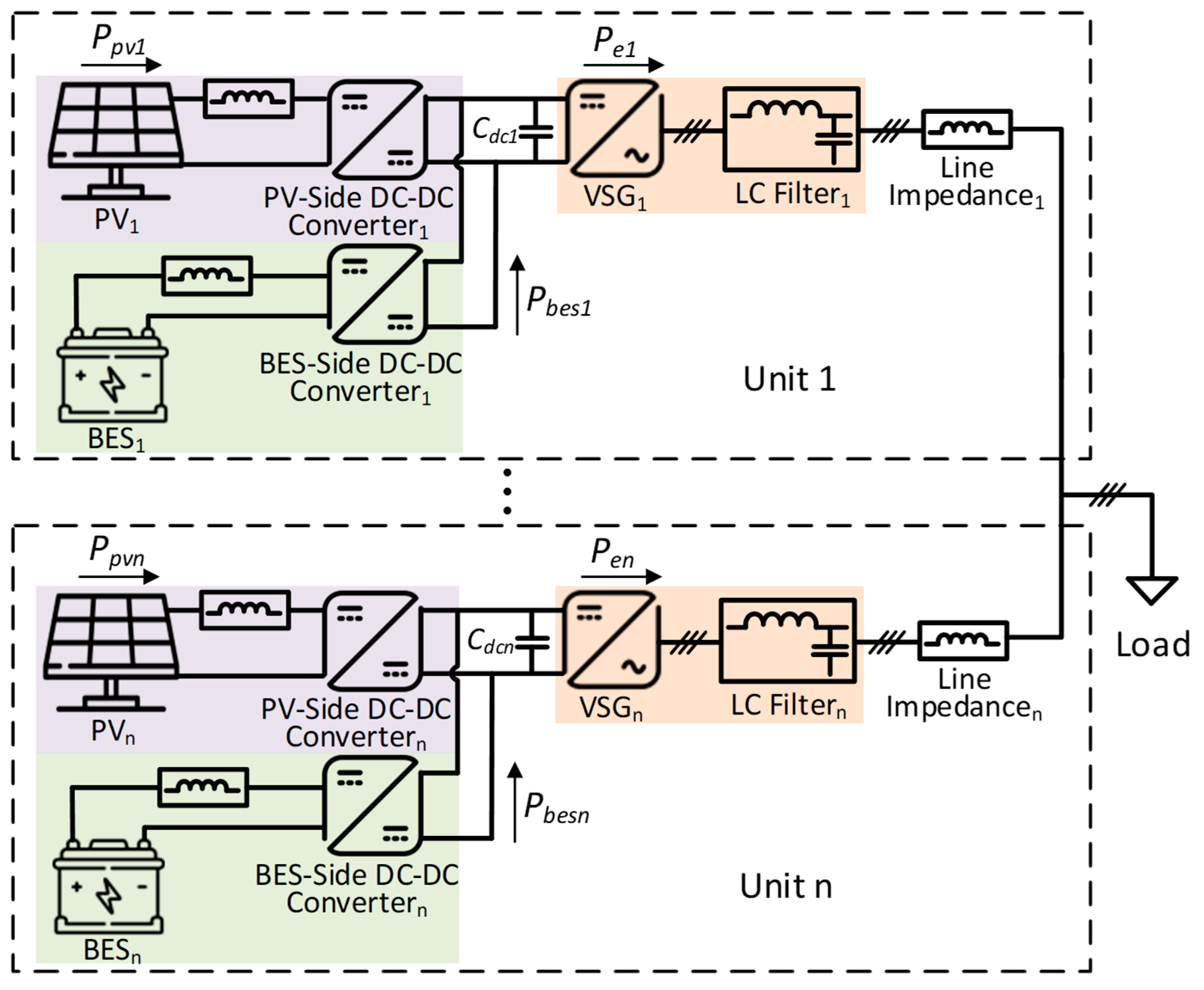
2. Typical Structure of a Paralleled PV-BES-VSG Power System
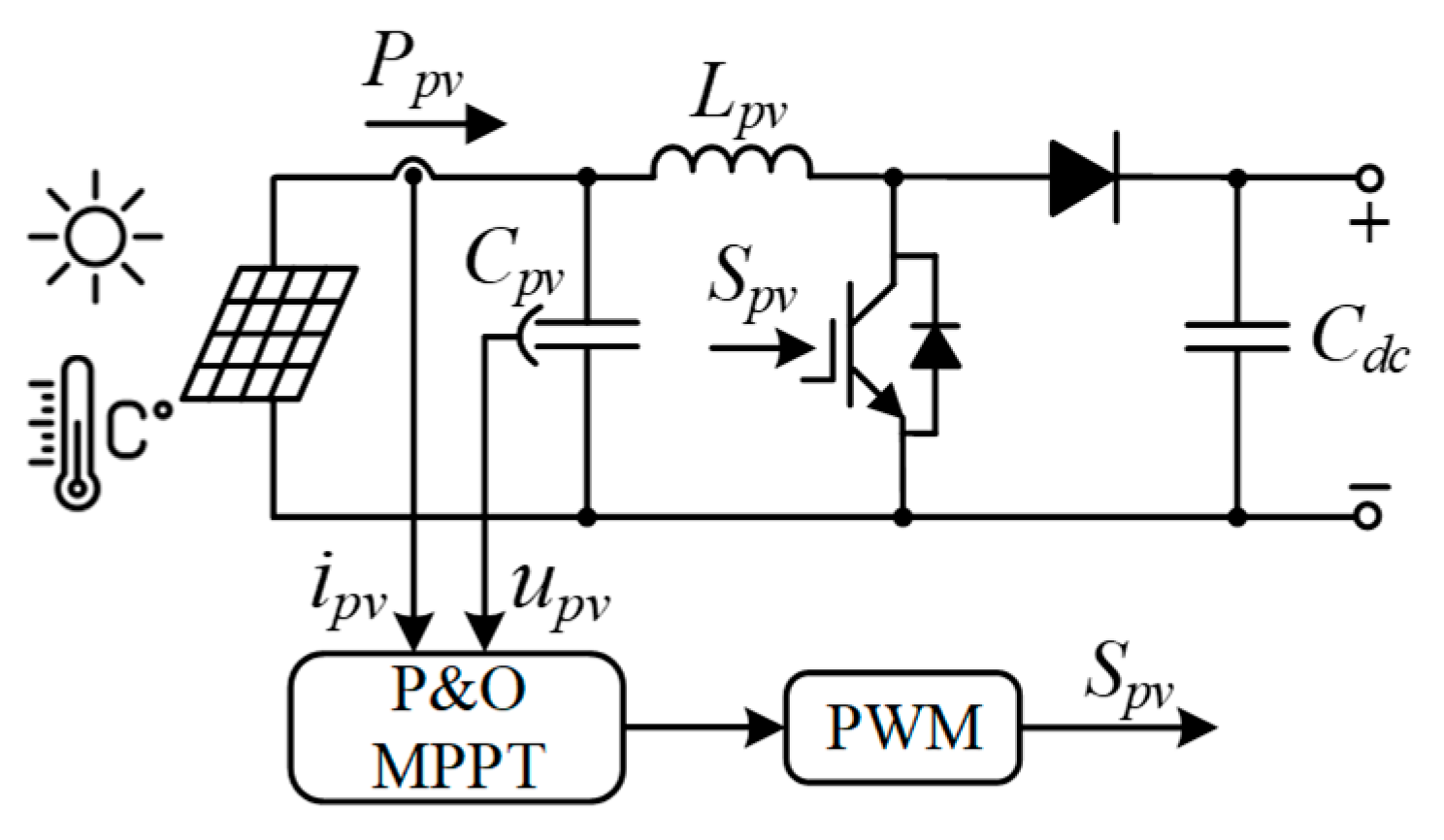
2.1. PV-Side DC-DC Converter
2.2. BES-Side DC-DC Converter
2.3. DC-AC Converter
3. Adaptive Control Strategy Considering SoC Balancing
4. Simulation Results
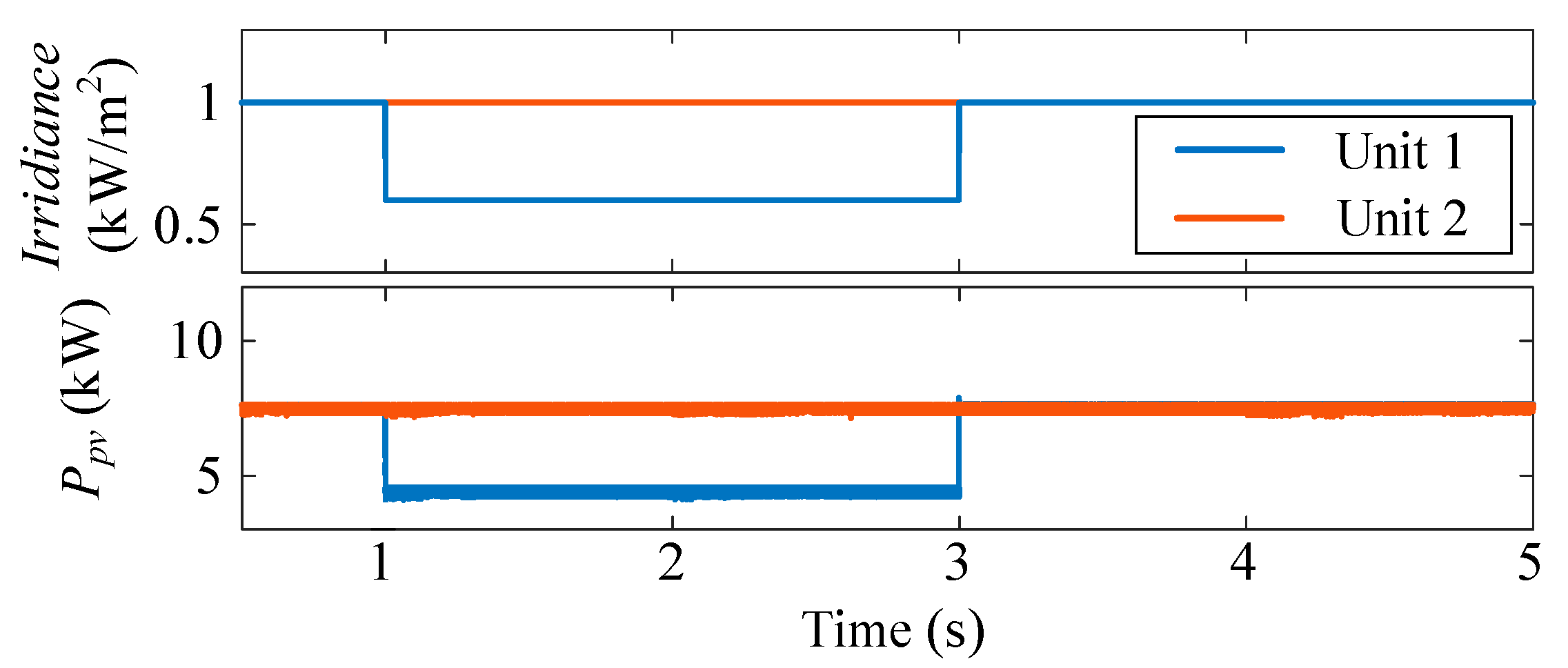
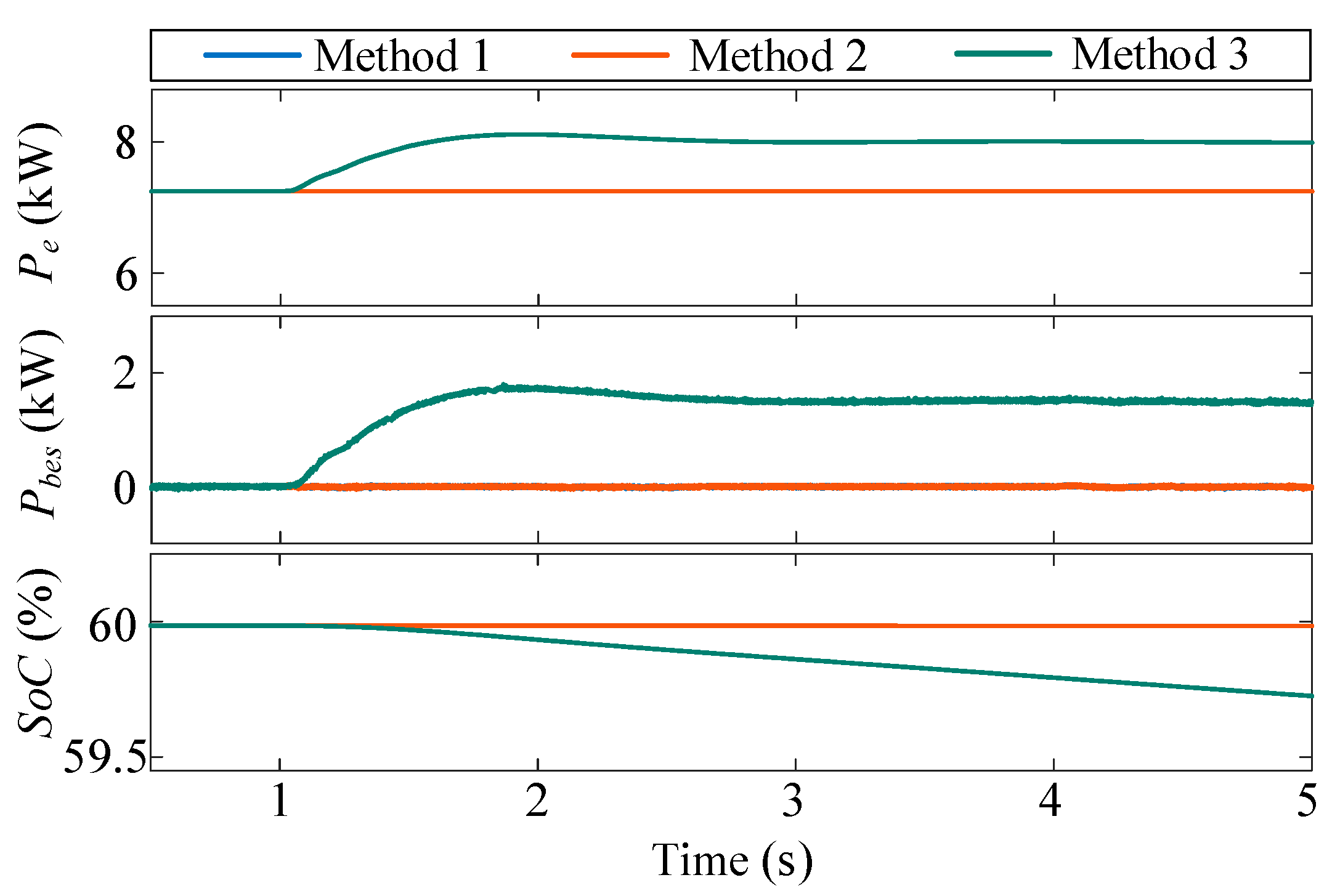
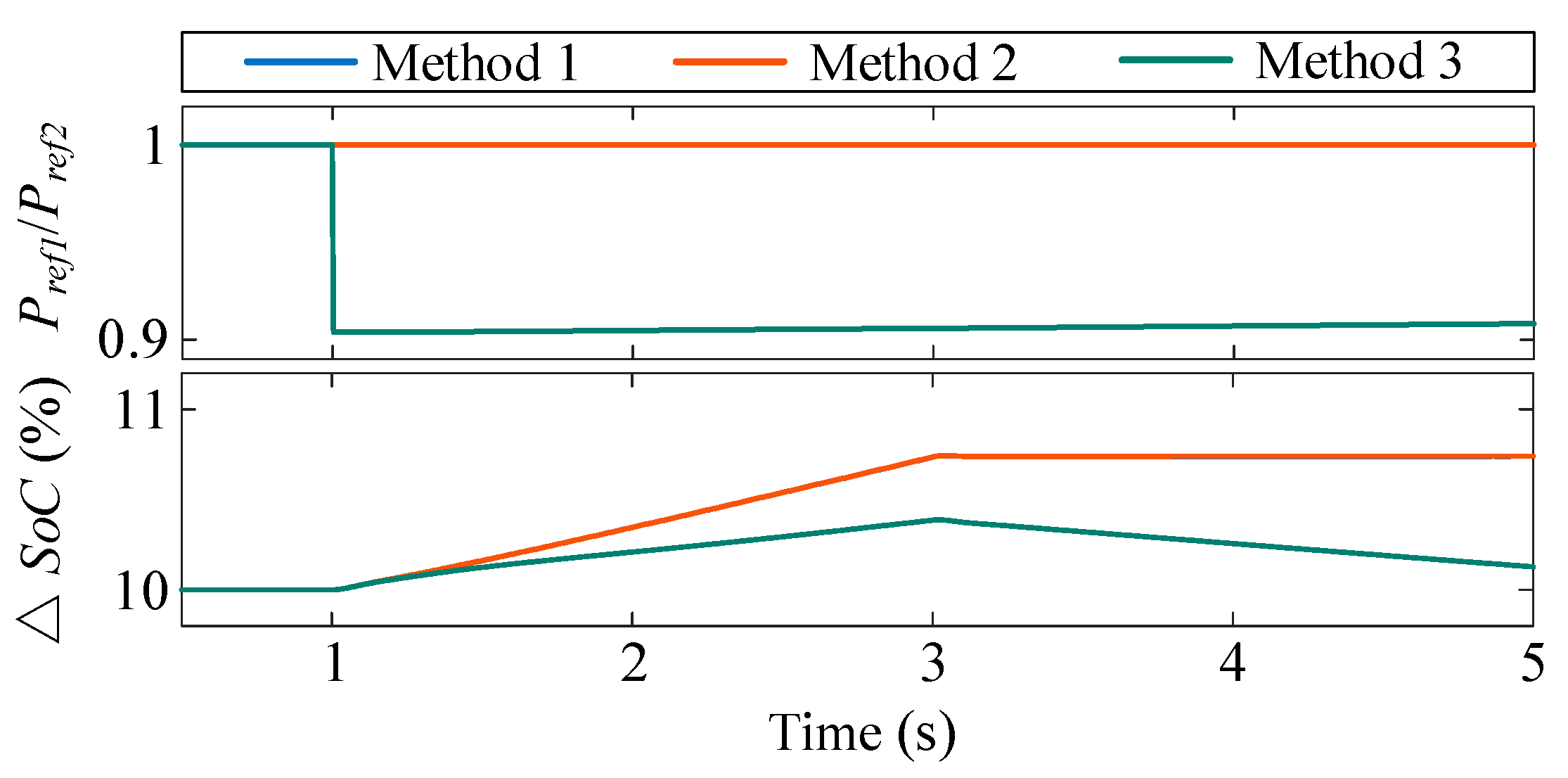
4.1. Irradiance Variation
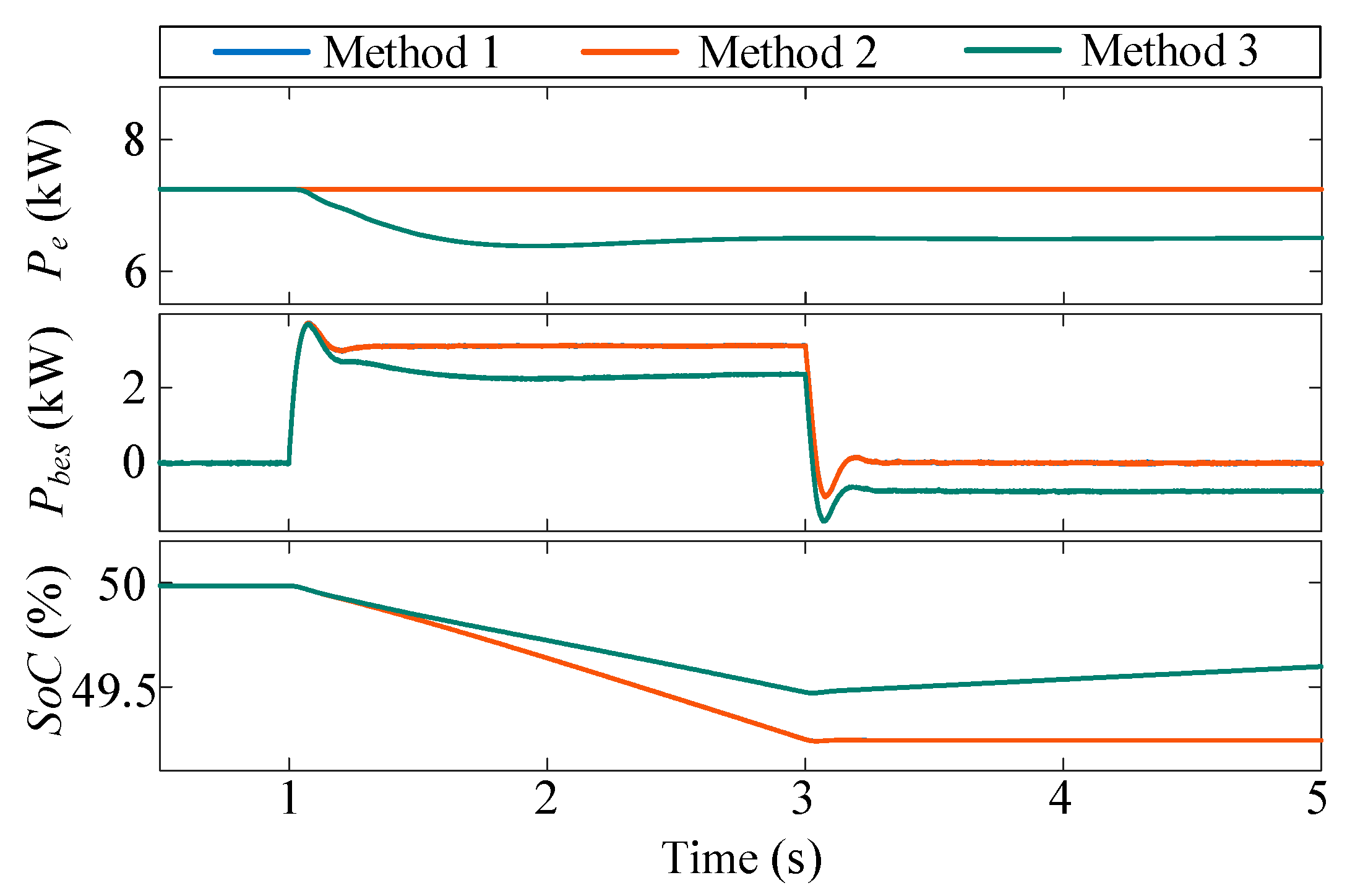
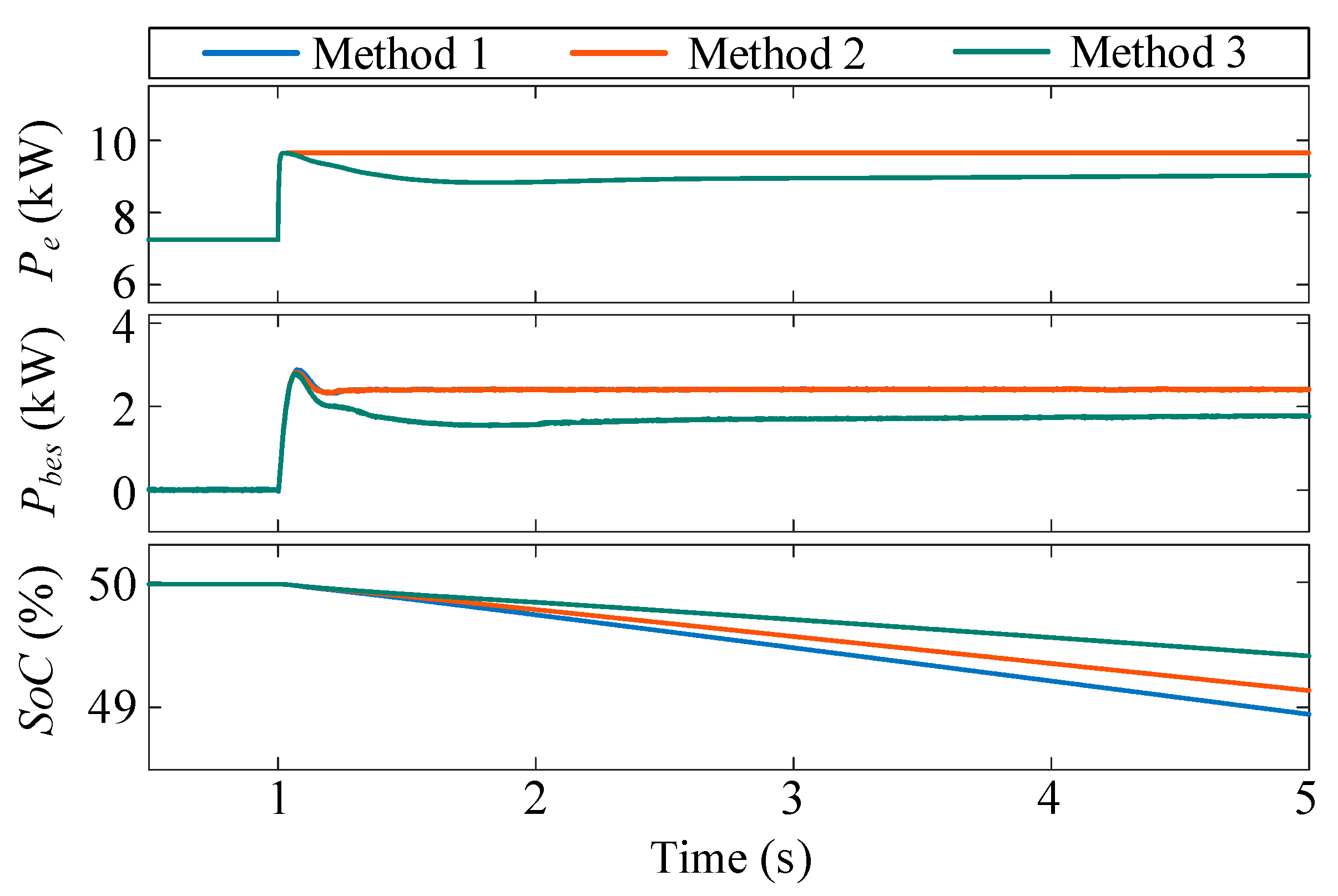
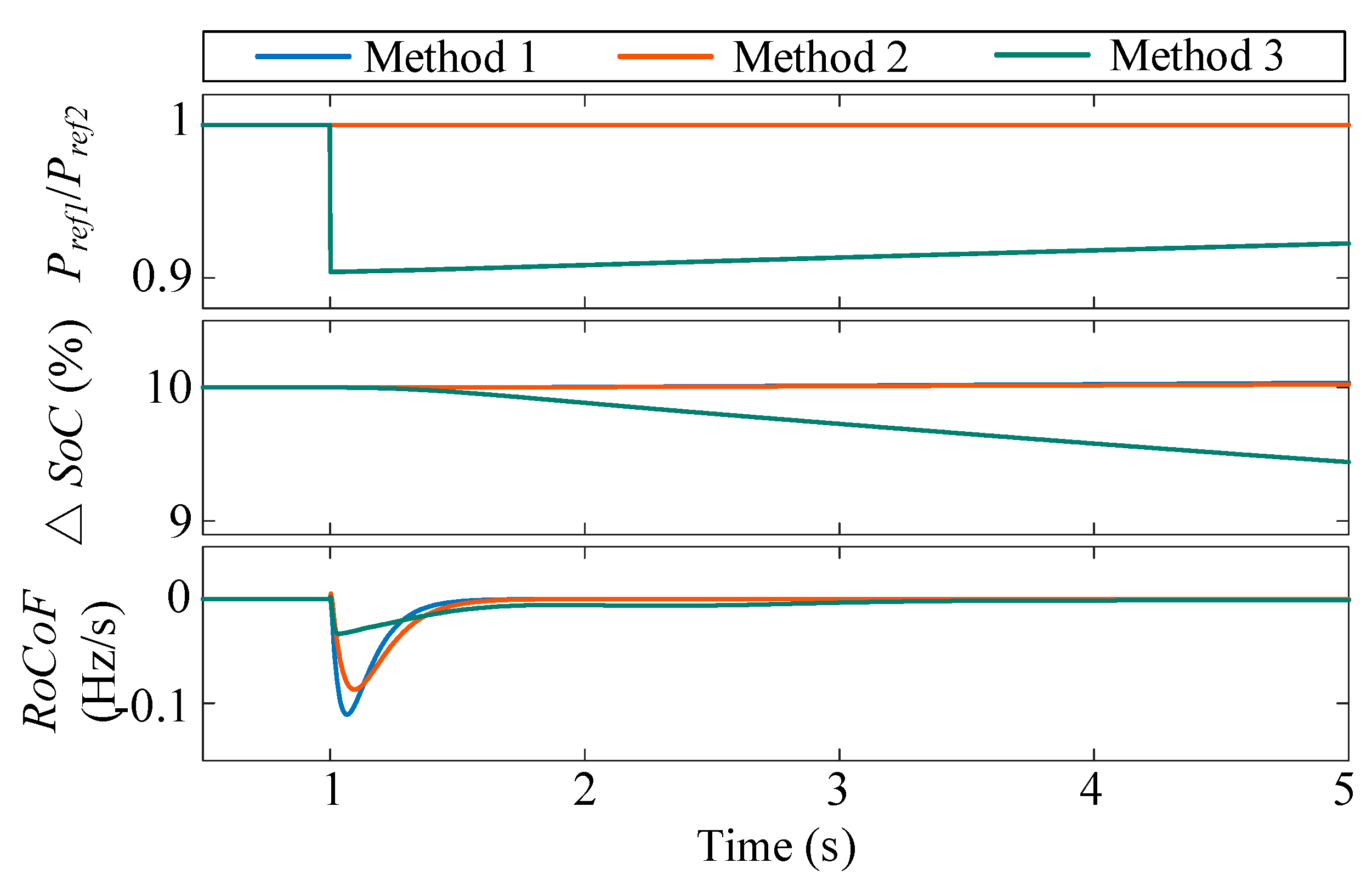
4.2. Load Step
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blaabjerg, F.; Yang, Y.; Yang, D.; Wang, X. Distributed power-generation systems and protection. Proc. IEEE. 2017, 105, 1311–1331. [Google Scholar] [CrossRef]
- Paris Agreement, United Nations Framework Convention on Climate Change, Tech. Rep. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement (accessed on 5 April 2024).
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed power system virtual inertia implemented by grid-connected power converters. IEEE Trans. Power Electron. 2018, 33, 8488–8499. [Google Scholar] [CrossRef]
- Peng, Q.; Jiang, Q.; Yang, Y.; Liu, T.; Wang, H.; Blaabjerg, F. On the stability of power electronics-dominated systems: Challenges and potential solutions. IEEE Trans. Ind. Appl. 2019, 55, 7657–7670. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Blaabjerg, F. Active Power Oscillation Damping Based on Acceleration Control in Paralleled Virtual Synchronous Generators System. IEEE Trans. Power Electron. 2021, 36, 9501–9510. [Google Scholar] [CrossRef]
- Yu, Y.; Chaudhary, S.K.; Tinajero, G.D.A.; Xu, L.; Bakar, N.N.B.A.; Vasquez, J.C.; Guerrero, J.M. A reference-feedforward-based damping method for virtual synchronous generator control. IEEE Trans. Power Electron. 2022, 37, 7566–7571. [Google Scholar] [CrossRef]
- Li, M.; Yu, P.; Hu, W.; Wang, Y.; Shu, S.; Zhang, Z.; Blaabjerg, F. Phase feedforward damping control method for virtual synchronous generators. IEEE Trans. Power Electron. 2022, 37, 9790–9806. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Yuan, H.; Wang, G.; Ju, P. Damping effect of virtual synchronous machines provided by a dynamical virtual impedance. IEEE Trans. Energy Convers. 2020, 36, 570–573. [Google Scholar] [CrossRef]
- Li, M.; Huang, W.; Tai, N.; Yang, L.; Duan, D.; Ma, Z. A dual-adaptivity inertia control strategy for virtual synchronous generator. IEEE Trans. Power Syst. 2019, 35, 594–604. [Google Scholar] [CrossRef]
- Perez, F.; Damm, G.; Verrelli, C.M.; Ribeiro, P.F. Adaptive virtual inertia control for stable microgrid operation including ancillary services support. IEEE Trans. Contr. Syst. Technol. 2023, 31, 1552–1564. [Google Scholar] [CrossRef]
- Shintai, T.; Miura, Y.; Ise, T. Oscillation damping of a distributed generator using a virtual synchronous generator. IEEE Trans. Power Deliv. 2014, 29, 668–676. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Q.; Lin, S.; Bian, X.Y. A self-adaptive inertia and damping combination control of VSG to support frequency stability. IEEE Trans. Energy Conver. 2016, 32, 397–398. [Google Scholar] [CrossRef]
- Wang, Z.; Meng, F.; Zhang, Y.; Wang, W.; Li, G.; Ge, J. Cooperative Adaptive Control of Multi-Parameter Based on Dual-Parallel Virtual Synchronous Generators System. IEEE Trans. Energy Convers. 2023, 38, 2396–2408. [Google Scholar] [CrossRef]
- Yu, Y.; Chaudhary, S.K.; Tinajero, G.D.A.; Xu, L.; Vasquez, J.C.; Guerrero, J.M. Active Damping for Dynamic Improvement of Multiple Grid-Tied Virtual Synchronous Generators. IEEE Trans. Ind. Electron. 2024, 71, 3673–3683. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Y.; Han, H.; Shi, G.; Guan, Y.; Guerrero, J.M. Dynamic frequency performance analysis and improvement for parallel VSG systems considering virtual inertia and damping coefficient. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 478–489. [Google Scholar] [CrossRef]
- Gao, X.; Zhou, D.; Anvari-Moghaddam, A.; Blaabjerg, F. An adaptive control strategy with a mutual damping term for paralleled virtual synchronous generators system. Sustain. Energy Grids Netw. 2024, 38, 101308. [Google Scholar] [CrossRef]
- Kumar, A.W.; din Mufti, M.U.; Zargar, M.Y. Fuzzy based virtual inertia emulation in a multi-area wind penetrated power system using adaptive predictive control based flywheel storage. Sustain. Energy Technol. Assess. 2022, 53, 102515. [Google Scholar] [CrossRef]
- Ma, Y.; Cao, W.; Yang, L.; Wang, F.; Tolbert, L.M. Virtual synchronous generator control of full converter wind turbines with short-term energy storage. IEEE Trans. Ind. Electron. 2017, 64, 8821–8831. [Google Scholar] [CrossRef]
- Hasabelrasul, H.; Cai, Z.; Sun, L.; Suo, X.; Matraji, I. Two-stage converter standalone PV-battery system based on VSG control. IEEE Access 2022, 10, 39825–39832. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Wang, M.; Xu, Z.; Peng, Y.; Li, M. Coordinated VSG control of photovoltaic/battery system for maximum power output and grid supporting. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 12, 301–309. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. A sensorless power reserve control strategy for two-stage grid-connected PV systems. IEEE Trans. Ind. Electron. 2017, 32, 8559–8569. [Google Scholar] [CrossRef]
- Peng, Q.; Tang, Z.; Yang, Y.; Liu, T.; Blaabjerg, F. Event-triggering virtual inertia control of PV systems with power reserve. IEEE Trans. Ind. Appl. 2021, 57, 4059–4070. [Google Scholar] [CrossRef]
- Fang, J.; Tang, Y.; Li, H.; Li, X. A battery/ultracapacitor hybrid energy storage system for implementing the power management of virtual synchronous generators. IEEE Trans. Power Electron. 2018, 33, 2820–2824. [Google Scholar] [CrossRef]
- Sarojini, R.K.; Palanisamy, K.; Sanjeevikumar, P.; Nielsen, J.B.H. Inertia emulation control technique based frequency control of grid-connected single-phase rooftop photovoltaic system with battery and supercapacitor. IET Renew. Power Gen. 2020, 14, 1156–1163. [Google Scholar] [CrossRef]
- Quan, X.; Yu, R.; Zhao, X.; Lei, Y.; Chen, T.; Li, C.; Huang, A.Q. Photovoltaic synchronous generator: Architecture and control strategy for a grid-forming PV energy system. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 936–948. [Google Scholar] [CrossRef]
- Liu, J.; Hou, Y.; Guo, J.; Liu, X.; Liu, J. A Cost-Efficient Virtual Synchronous Generator System Based on Coordinated Photovoltaic and Supercapacitor. IEEE Trans. Power Electron. 2023, 38, 16219–16229. [Google Scholar] [CrossRef]
- Huang, Y.; Lv, Q.; Zhang, Z.; Dong, H. Virtual Synchronous Generator Adaptive Control of Energy Storage Power Station Based on Physical Constraints. Energy Eng. 2023, 120, 1401–1420. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, W.; Jiang, W. Fuzzy-controlled energy storage VSG control strategy. In Proceedings of the 2022 International Conference on Artificial Intelligence and Computer Information Technology (AICIT), Yichang, China, 16–18 September 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Mao, M.; Qian, C.; Ding, Y. Decentralized coordination power control for islanding microgrid based on PV/BES-VSG. CPSS Trans. Power Electron. Appl. 2018, 3, 14–24. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, C.; Peng, X.; Zhang, S. Configuration of an energy storage system for primary frequency reserve and inertia response of the power grid. IEEE Access 2021, 9, 41965–41975. [Google Scholar] [CrossRef]
- Chen, J.; Liu, M.; Milano, F.; O’Donnell, T. Adaptive virtual synchronous generator considering converter and storage capacity limits. CSEE J. Power Energy Syst. 2022, 8, 580–590. [Google Scholar] [CrossRef]
- Li, C.; Coelho, E.A.A.; Dragicevic, T.; Guerrero, J.M.; Vasquez, J.C. Multiagent-based distributed state of charge balancing control for distributed energy storage units in AC microgrids. IEEE Trans. Ind. Appl. 2016, 53, 2369–2381. [Google Scholar] [CrossRef]
- Kumar, R.R.; Bharatiraja, C.; Udhayakumar, K.; Devakirubakaran, S.; Sekar, K.S.; Mihet-Popa, L. Advances in batteries, battery modeling, battery management system, battery thermal management, SoC, SOH, and charge/discharge characteristics in EV applications. IEEE Access 2023, 11, 105761–105809. [Google Scholar] [CrossRef]
- Fagundes, T.A.; Fuzato, G.H.F.; Ferreira, P.G.B.; Biczkowski, M.; Machado, R.Q. Fuzzy Controller for Energy Management and SoC Equalization in DC Microgrids Powered by Fuel Cell and Energy Storage Units. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 90–100. [Google Scholar] [CrossRef]
- Fagundes, T.A.; Fuzato, G.H.F.; Silva, L.J.R.; dos Santos Alonso, A.M.; Vasquez, J.C.; Guerrero, J.M.; Machado, R.Q. Battery Energy Storage Systems in Microgrids: A Review of SoC Balancing and Perspectives. IEEE Open J. Ind. Electron. Soc. 2024, 5, 961–992. [Google Scholar] [CrossRef]
- Diaz, N.L.; Luna, A.C.; Vasquez, J.C.; Guerrero, J.M. Centralized control architecture for coordination of distributed renewable generation and energy storage in islanded AC microgrids. IEEE Trans. Power Electron. 2016, 32, 5202–5213. [Google Scholar] [CrossRef]
- Buchinskiy, N.; Saitoh, H. SoC Balancing Mechanism to Improve Active Power Sharing Among Multiple ESS Units in Low-Inertia Power Systems. In Proceedings of the 2023 IEEE PES Innovative Smart Grid Technologies-Asia (ISGT Asia), Auckland, New Zealand, 21–24 November 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, D.; Ma, T.; Su, X. Adaptive cooperative terminal sliding mode control for distributed energy storage systems. IEEE Trans. Circuits Sys. I Regul. Pap. 2020, 68, 434–443. [Google Scholar] [CrossRef]
- Xu, D.; Tang, L.; Jiang, B.; Pan, T.; Liu, J.; Hua, W. Cooperative Adaptive Command Filtered Backstepping Control for EVs to UPS-Microgrid via Virtual Synchronous Generator. IEEE Trans. Cybern. 2024, 54, 5369–5380. [Google Scholar] [CrossRef]
- Wu, Q.; Chu, X.; Fan, Y.; Liu, L.; Sun, X. Consistency Algorithm-Based SOC Balancing Scheme of Retired Non-equal Capacity Lithium Battery in Virtual Synchronous Generator Controlled Microgrids. IEEE Access. 2025, 13, 9073–9088. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Blaabjerg, F. A Decentralized Adaptive SOC Balancing Strategy in VSG-based Islanded Power System. In Proceedings of the 47th Annual Conference of the IEEE Industrial Electronics Society (IECON), Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Y.; Kim, K.A.; Ding, T. Modeling and control of PV systems. In Control of Power Electronic Converters and Systems; Academic Press: Amsterdam, The Netherlands, 2018; pp. 243–268. [Google Scholar]
- Zhao, L.; Liu, Z.; Ji, G. Lithium-ion battery state of charge estimation with model parameters adaptation using H∞ extended Kalman filter. Control Eng. Pract. 2018, 81, 114–128. [Google Scholar] [CrossRef]
- Ng, K.S.; Moo, C.S.; Chen, Y.P.; Hsieh, Y.C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Huang, W.; Qahouq, J.A.A. An online battery impedance measurement method using DC–DC power converter control. IEEE Trans. Ind. Electron. 2014, 61, 5987–5995. [Google Scholar] [CrossRef]
- El Mejdoubi, A.; Oukaour, A.; Chaoui, H.; Gualous, H.; Sabor, J.; Slamani, Y. State-of-Charge and State-of-Health Lithium-Ion Batteries’ Diagnosis According to Surface Temperature Variation. IEEE Trans. Ind. Electron. 2016, 63, 2391–2402. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, G.; Lin, M.; Wu, J.; Zheng, G. A Novel Estimation Method for the State of Health of Lithium-Ion Battery Using Prior Knowledge-Based Neural Network and Markov Chain. IEEE Trans. Ind. Electron. 2019, 66, 7706–7716. [Google Scholar] [CrossRef]
- Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.; Stroe, D.I.; Stroe, A.I.; Teodorescu, R. An overview and comparison of online implementable SOC estimation methods for lithium-ion battery. IEEE Trans. Ind. Appl. 2017, 54, 1583–1591. [Google Scholar] [CrossRef]
- Gao, X.; Zhou, D.; Anvari-Moghaddam, A.; Blaabjerg, F. Stability Analysis of Grid-Following and Grid-Forming Converters Based on State-Space Model. IEEE Trans. Ind. Appl. 2024, 60, 4910–4920. [Google Scholar] [CrossRef]






| Description | Symbol | Value |
|---|---|---|
| Maximum power of PV modules | PPV1, PPV2 | 7.6 kW, 7.6 kW |
| Inductor and capacitor of PV-side DC-DC converter | Lpv, Cpv | 2 mH, 10 μF |
| Rated capacity of batteries | Cbes1, Cbes2 | 1 Ah, 1 Ah |
| Inductor and capacitor of BES-side DC-DC converter | Lbes, Cbes | 2 mH, 10 μF |
| Initial SoCs of batteries | SoC1, SoC2 | 50%, 60% |
| DC-link capacitor | Cdc | 10 mF |
| Rated power of VSGs | SVSG1, SVSG2 | 15.8 kVA, 15.8 kVA |
| LC filter of VSGs | Lf, Cf | 3 mH, 10 μF |
| Load power | Pload | 15 kW |
| Case | Description |
|---|---|
| Method 1 | Traditional VSG control method with fixed moment of inertia and damping coefficient [6], as shown in (2) |
| Method 2 | Adaptive moment of inertia and damping coefficient, with a mutual damping term [18], as shown in (5) |
| Method 3 | The adaptive control strategy with SoC balancing mechanism proposed in this study, as shown in (9) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Zhou, D.; Anvari-Moghaddam, A.; Blaabjerg, F. An Adaptive Control Strategy for a Better Performance of the Paralleled PV-BES-VSG Power System. Energies 2025, 18, 2505. https://doi.org/10.3390/en18102505
Gao X, Zhou D, Anvari-Moghaddam A, Blaabjerg F. An Adaptive Control Strategy for a Better Performance of the Paralleled PV-BES-VSG Power System. Energies. 2025; 18(10):2505. https://doi.org/10.3390/en18102505
Chicago/Turabian StyleGao, Xian, Dao Zhou, Amjad Anvari-Moghaddam, and Frede Blaabjerg. 2025. "An Adaptive Control Strategy for a Better Performance of the Paralleled PV-BES-VSG Power System" Energies 18, no. 10: 2505. https://doi.org/10.3390/en18102505
APA StyleGao, X., Zhou, D., Anvari-Moghaddam, A., & Blaabjerg, F. (2025). An Adaptive Control Strategy for a Better Performance of the Paralleled PV-BES-VSG Power System. Energies, 18(10), 2505. https://doi.org/10.3390/en18102505







