Kinetic Analysis of Construction, Renovation, and Demolition (CRD) Wood Pyrolysis Using Model-Fitting and Model-Free Methods via Thermogravimetric Analysis
Abstract
1. Introduction
2. Theory, Materials, and Methods
2.1. Foundational Derivation
2.2. Model-Fitting and Model-Free TGA Methods Rooting from Foundational Equations
2.2.1. Model-Fitting Methods
| Reaction Model | Type/Mechanism | Denotation | f(α) | g(α) |
|---|---|---|---|---|
| Chemical | First-order | F1 | 1 − α | −ln(1 − α) |
| Second-order | F2 | (1 − α)2 | (1 − α)−1 − 1 | |
| Third-order | F3 | (1 − α)3 | [(1 − α)−2 − 1]/2 | |
| Diffusion | One-dimensional | D1 | 0.5α | α2 |
| Two-dimensional | D2 | [−ln(1 − α)]−1 | (1 − α)ln(1 − α) + α | |
| Three-dimensional Jander (J) | D3 | 1.5(1 − α)2/3[1 − (1 − α)1/3]−1 | [1 − (1 − α)1/3]2 | |
| Three-dimensional Ginstling-Brounshtein (GB) | D4 | 1.5[(1 − α)−1/3 − 1]−1 | (1 − 2α/3) − (1 − α)2/3 | |
| Interfacial Phase | One-dimensional | R1 | 1 | α |
| Two-dimensional | R2 | 2(1 − α)1/2 | 1 − (1 − α)1/2 | |
| Three-dimensional | R3 | 3(1 − α)2/3 | 1 − (1 − α)1/3 | |
| Nucleation and growth | Two-dimensional | A2 | 2(1 − α)[-ln(1 − α)]1/2 | [−ln(1 − α)]1/2 |
| Three-dimensional | A3 | 3(1 − α)[−ln(1 − α)]2/3 | [−ln(1 − α)]1/3 |
Arrhenius Model
Coats-Redfern (CR) Model
2.2.2. Model-Free or Iso-Conversional Methods
2.3. Thermodynamic Study
2.4. CRD Wood Biomass Sample Preparation for Characterization and Kinetic Analysis
2.5. Physicochemical Characterization
2.6. Composition Analysis
2.7. FTIR
2.8. TGA
3. Results and Discussion
3.1. Physicochemical Properties of CRD Wood—Comparative Analysis with Other Biomass Feedstock
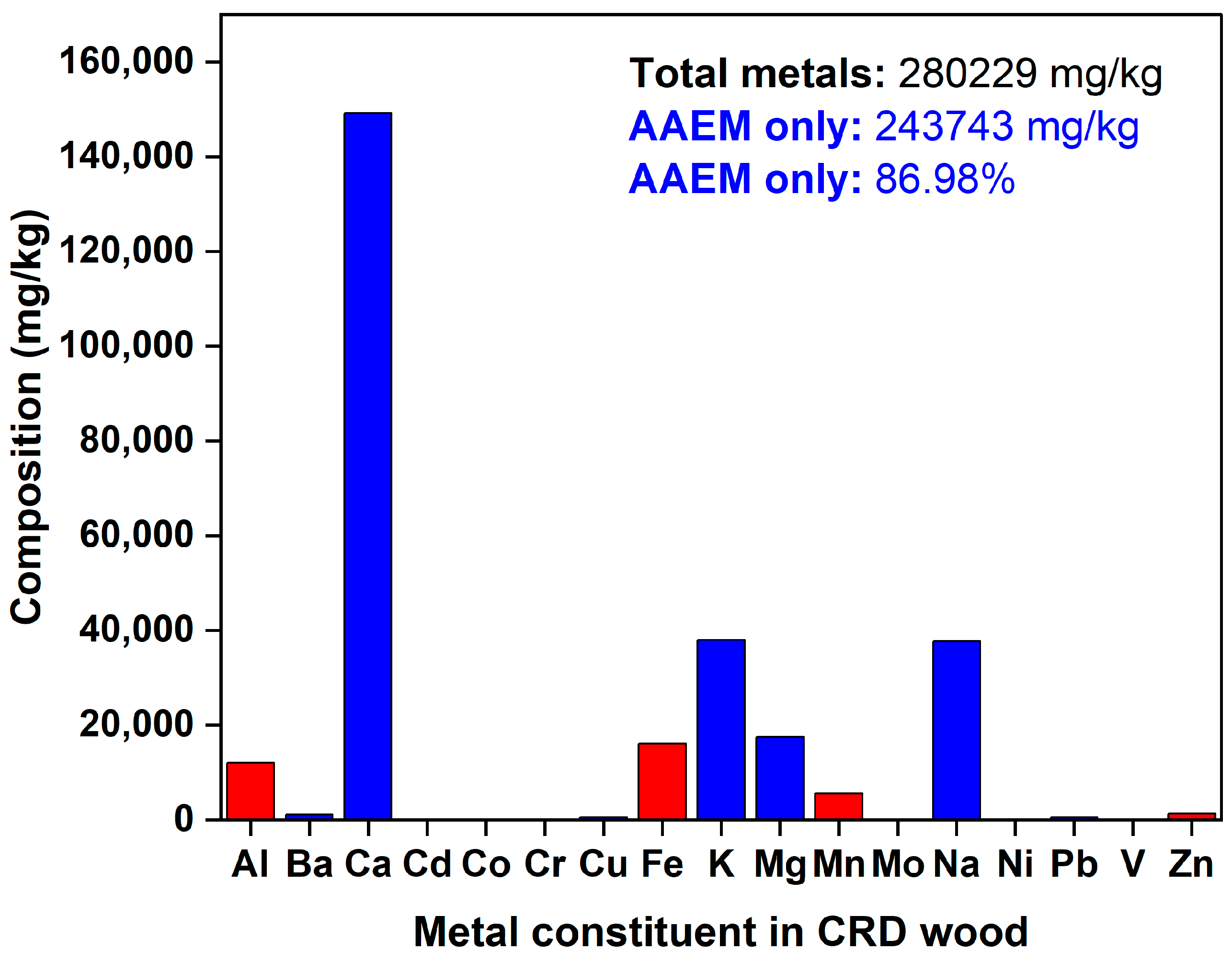
3.2. CRD Wood Compositional Analysis
3.3. FTIR Spectroscopy Analysis
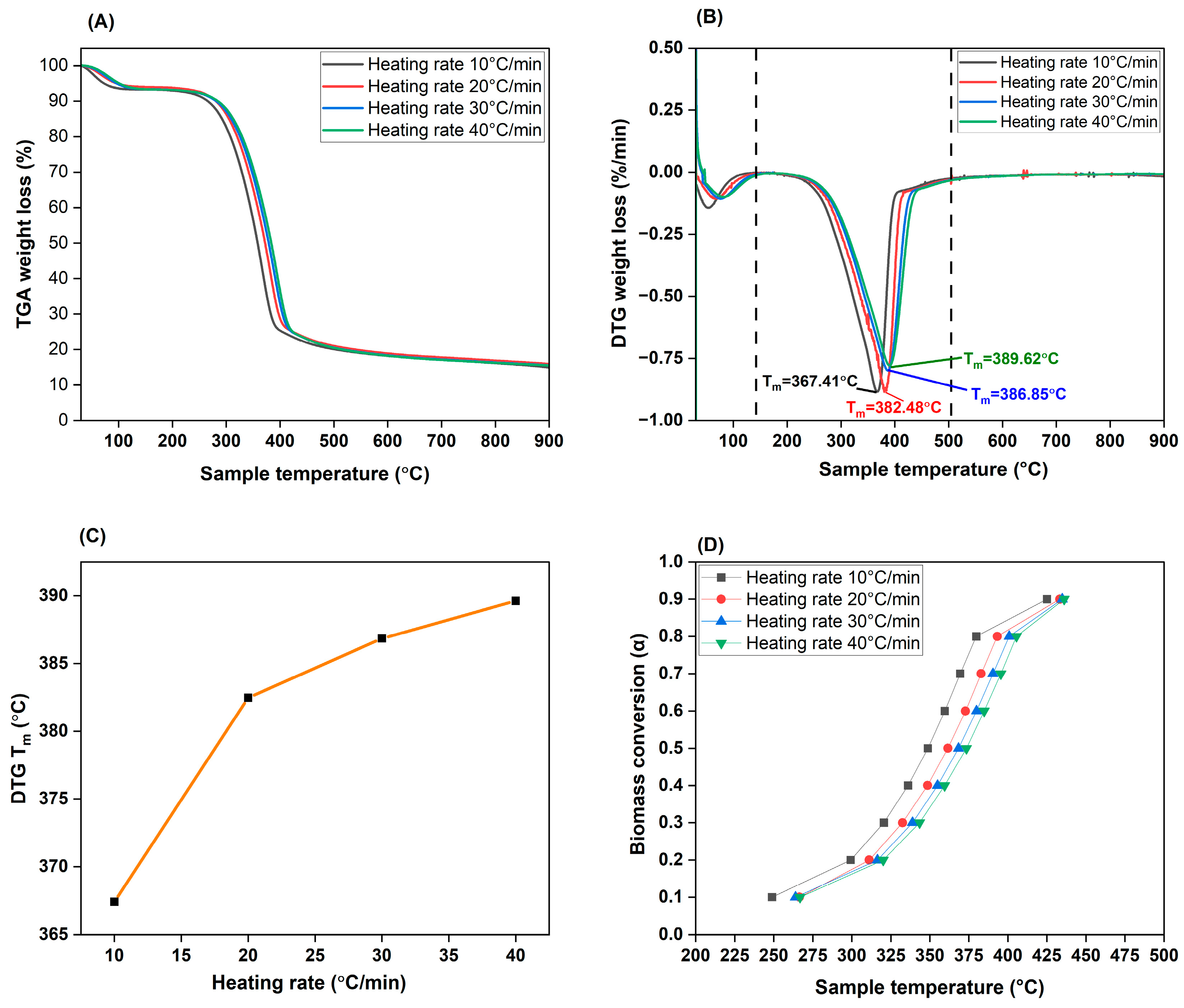
3.4. TGA Analysis and Effect of Heating Rate
3.5. Kinetic Analysis of CRD Wood Pyrolysis
3.5.1. Model-Fitting Method
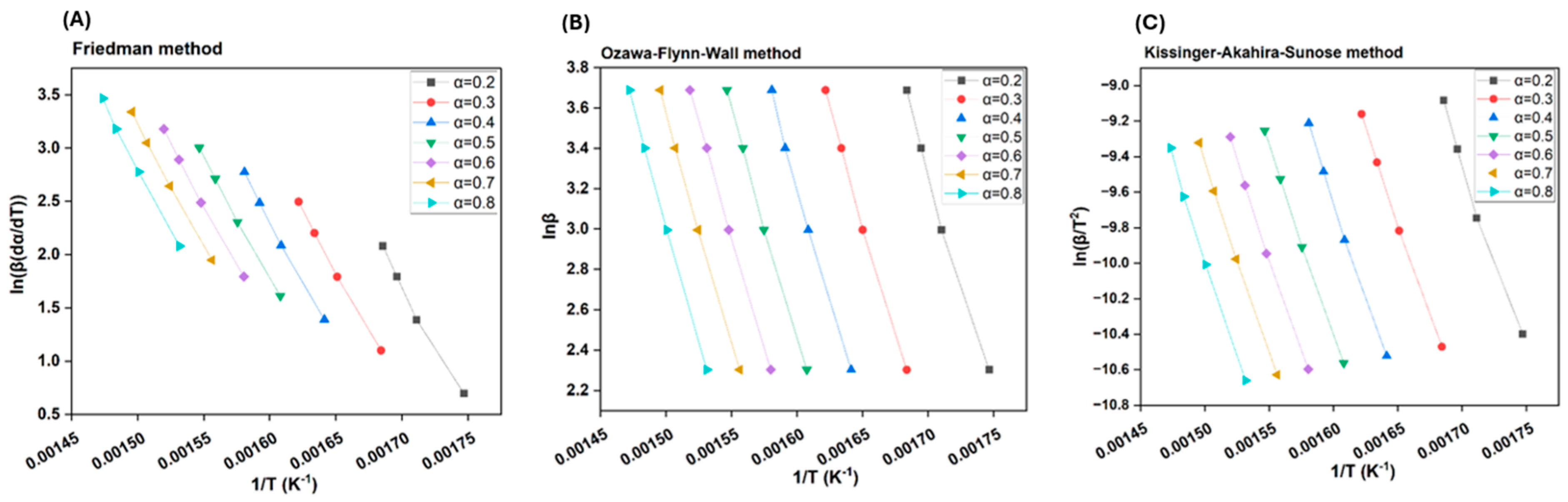
3.5.2. Model-Free Methods
3.6. Thermodynamic Parameters
3.7. Summary
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AAEM | Alkaline and alkaline earth metal. |
| BRT | Biomass residence time. |
| CCA | Copper, chromium, and arsenic. |
| CR | Coats–Redfern. |
| CRD | Construction, renovation, and demolition. |
| DB | Dry basis. |
| DTG | Differential thermogram. |
| FC | Fixed carbon. |
| FM | Friedman. |
| FTIR | Fourier Transform Infrared. |
| GHGs | Greenhouse gases. |
| HHV | Higher heating value. |
| HTC | Hydrothermal carbonization. |
| KAS | Kissinger–Akahira–Sunose. |
| MP-AES | Microwave Plasma Atomic Emission Spectrometer. |
| Mt | Million tons. |
| OFW | Ozawa–Flynn–Wall. |
| PAH | Polyaromatic hydrocarbon. |
| TGA | Thermogravimetric analysis. |
| VC | Volatile carbon. |
| Wt% | Weight percent (used interchangeably with %). |
References
- Laadila, M.A.; LeBihan, Y.; Caron, R.F.; Vaneeckhaute, C. Construction, renovation and demolition (CRD) wastes contaminated by gypsum residues: Characterization, treatment and valorization. Waste Manag. 2021, 120, 125–135. [Google Scholar] [CrossRef] [PubMed]
- Kumar, I.; Tirlangi, S.; Kathiresan, K.; Sharma, V.; Madhu, P.; Sathish, T.; Ağbulut, Ü.; Murugan, P. Co-pyrolysis of furniture wood with mixed plastics and waste tyres: Assessment of synergistic effect on biofuel yield and product characterization under different blend ratio. Sci. Rep. 2024, 14, 24584. [Google Scholar] [CrossRef] [PubMed]
- Ganesan, A.; Rezazgui, O.; Langlois, S.; Boussabbeh, C.; Barnabé, S. Pyrolytic conversion of construction, renovation, and demolition (CRD) wood wastes in Québec to biochar: Production, characterization, and identifying relevant stability indices for carbon sequestration. Sci. Total Environ. 2025, 965, 178650. [Google Scholar] [CrossRef] [PubMed]
- Gmar, M.; Bouafif, H.; Bouslimi, B.; Braghiroli, F.L.; Koubaa, A. Pyrolysis of chromated copper arsenate-treated wood: Investigation of temperature, granulometry, biochar yield, and metal pathways. Energies 2022, 15, 5071. [Google Scholar] [CrossRef]
- O’Dwyer, J.; Walshe, D.; Byrne, K.A. Wood waste decomposition in landfills: An assessment of current knowledge and implications for emissions reporting. Waste Manag. 2018, 73, 181–188. [Google Scholar] [CrossRef]
- Kizha, A.R.; Han, H.S. Processing and sorting forest residues: Cost, productivity and managerial impacts. Biomass Bioenergy 2016, 93, 97–106. [Google Scholar] [CrossRef]
- Ganesan, A.; Rezazgui, O.; Burgos, J.B.; Mangin, P.J.; Barnabé, S. Valorization of lignocellulosic biomass forest residues in quebec via the integrated hydropyrolysis and hydroconversion (IH2) technology: A review. Biomass Bioenergy 2025, 193, 107516. [Google Scholar] [CrossRef]
- Rao, Y.K.; Dhanalakshmi, C.S.; Vairavel, D.K.; Surakasi, R.; Kaliappan, S.; Patil, P.P.; Socrates, S.; Lalvani, J.I.J. Investigation on forestry wood wastes: Pyrolysis and thermal characteristics of Ficus religiosa for energy recovery system. Adv. Mater. Sci. Eng. 2022, 2022, 3314606. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, Y.; Li, S.; Yuan, Y.; Zhang, D.; Wu, Y.; Xie, H.; Brindhadevi, K.; Pugazhendhi, A.; Xia, C. A review of biomass pyrolysis gas: Forming mechanisms, influencing parameters, and product application upgrades. Fuel 2023, 347, 128461. [Google Scholar] [CrossRef]
- Guedes, R.E.; Luna, A.S.; Torres, A.R. Operating parameters for bio-oil production in biomass pyrolysis: A review. J. Anal. Appl. Pyrolysis 2018, 129, 134–149. [Google Scholar] [CrossRef]
- Mouneir, S.M.; El-Shamy, A.M. A review on harnessing the energy potential of pyrolysis gas from scrap tires: Challenges and opportunities for sustainable energy recovery. J. Anal. Appl. Pyrolysis 2024, 177, 106302. [Google Scholar] [CrossRef]
- Peters, J.F.; Iribarren, D.; Dufour, J. Biomass pyrolysis for biochar or energy applications? A life cycle assessment. Environ. Sci. Technol. 2015, 49, 5195–5202. [Google Scholar] [CrossRef]
- Ibitoye, S.E.; Loha, C.; Mahamood, R.M.; Jen, T.C.; Alam, M.; Sarkar, I.; Das, P.; Akinlabi, E.T. An overview of biochar production techniques and application in iron and steel industries. Bioresour. Bioprocess. 2024, 11, 65. [Google Scholar] [CrossRef]
- Hasan, M.; Chakma, S.; Liang, X.; Sutradhar, S.; Kozinski, J.; Kang, K. Engineered Biochar for Metal Recycling and Repurposed Applications. Energies 2024, 17, 4674. [Google Scholar] [CrossRef]
- Legan, M.; Gotvajn, A.Ž.; Zupan, K. Potential of biochar use in building materials. J. Environ. Manag. 2022, 309, 114704. [Google Scholar] [CrossRef]
- Han, H.; Buss, W.; Zheng, Y.; Song, P.; Rafiq, M.K.; Liu, P.; Mašek, O.; Li, X. Contaminants in biochar and suggested mitigation measures–a review. Chem. Eng. J. 2022, 429, 132287. [Google Scholar] [CrossRef]
- Mlonka-Mędrala, A.; Magdziarz, A.; Dziok, T.; Sieradzka, M.; Nowak, W. Laboratory studies on the influence of biomass particle size on pyrolysis and combustion using TG GC/MS. Fuel 2019, 252, 635–645. [Google Scholar] [CrossRef]
- Adhikari, S.; Moon, E.; Paz-Ferreiro, J.; Timms, W. Comparative analysis of biochar carbon stability methods and implications for carbon credits. Sci. Total Environ. 2024, 914, 169607. [Google Scholar] [CrossRef]
- Altıkat, A.; Alma, M.H.; Altıkat, A.; Bilgili, M.E.; Altıkat, S. A Comprehensive Study of Biochar Yield and Quality Concerning Pyrolysis Conditions: A Multifaceted Approach. Sustainability 2024, 16, 937. [Google Scholar] [CrossRef]
- Ranzi, E.; Debiagi, P.E.A.; Frassoldati, A. Mathematical modeling of fast biomass pyrolysis and bio-oil formation. Note I: Kinetic mechanism of biomass pyrolysis. ACS Sustain. Chem. Eng. 2017, 5, 2867–2881. [Google Scholar] [CrossRef]
- Silva, J.; Teixeira, S.; Teixeira, J. A review of biomass thermal analysis, kinetics and product distribution for combustion modeling: From the micro to macro perspective. Energies 2023, 16, 6705. [Google Scholar] [CrossRef]
- Branca, C.; Galgano, A. Kinetic Modelling of Biomass Pyrolysis Processes. Processes 2024, 12, 706. [Google Scholar] [CrossRef]
- Thejaswini, N.; Annapureddy, P.K.R.; Rammohan, D.; Kishore, N. Kinetics and thermodynamics of non-isothermal pyrolysis of Terminalia chebula branches at different heating rates. Int. J. Chem. Kinet. 2023, 55, 673–687. [Google Scholar] [CrossRef]
- Zhong, Y.; Ding, Y.; Lu, K.; Mao, S.; Li, C. Kinetic parameters and reaction mechanism study of biomass pyrolysis by combined kinetics coupled with a heuristic optimization algorithm. Fuel 2023, 334, 126622. [Google Scholar] [CrossRef]
- Rambhatla, N.; Panicker, T.F.; Mishra, R.K.; Manjeshwar, S.K.; Sharma, A. Biomass pyrolysis for biochar production: Study of kinetics parameters and effect of temperature on biochar yield and its physicochemical properties. Results Eng. 2024, 25, 103679. [Google Scholar] [CrossRef]
- Fanezouné, C.K.; Dhahak, A.; Peixinho, J.; El Bari, H. Thermogravimetric analysis and kinetic modeling for empty fruit bunch date palm pyrolysis. Bioresour. Technol. Rep. 2024, 27, 101916. [Google Scholar] [CrossRef]
- Patidar, K.; Singathia, A.; Vashishtha, M.; Sangal, V.K.; Upadhyaya, S. Investigation of kinetic and thermodynamic parameters approaches to non-isothermal pyrolysis of mustard stalk using model-free and master plots methods. Mater. Sci. Energy Technol. 2022, 5, 6–14. [Google Scholar] [CrossRef]
- Zsinka, V.; Tarcsay, B.L.; Miskolczi, N. Determination of Kinetic and Thermodynamic Parameters of Biomass Gasification with TG-FTIR and Regression Model Fitting. Energies 2024, 17, 1875. [Google Scholar] [CrossRef]
- Arenas, C.N.; Navarro, M.V.; Martínez, J.D. Pyrolysis kinetics of biomass wastes using isoconversional methods and the distributed activation energy model. Bioresour. Technol. 2019, 288, 121485. [Google Scholar] [CrossRef]
- Postawa, K.; Fałtynowicz, H.; Szczygieł, J.; Beran, E.; Kułażyński, M. Analyzing the kinetics of waste plant biomass pyrolysis via thermogravimetry modeling and semi-statistical methods. Bioresour. Technol. 2022, 344, 126181. [Google Scholar] [CrossRef]
- White, J.E.; Catallo, W.J.; Legendre, B.L. Biomass pyrolysis kinetics: A comparative critical review with relevant agricultural residue case studies. J. Anal. Appl. Pyrolysis 2011, 91, 1–33. [Google Scholar] [CrossRef]
- Pecha, M.B.; Arbelaez, J.I.M.; Garcia-Perez, M.; Chejne, F.; Ciesielski, P.N. Progress in understanding the four dominant intra-particle phenomena of lignocellulose pyrolysis: Chemical reactions, heat transfer, mass transfer, and phase change. Green Chem. 2019, 21, 2868–2898. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, C.; Tang, C.; Wang, Y. Morphological control of biochar with emerging functionalities by thermodynamic and kinetic approaches. Acc. Mater. Res. 2022, 3, 525–539. [Google Scholar] [CrossRef]
- Pfersich, J.; Arauzo, P.J.; Modugno, P.; Titirici, M.M.; Kruse, A. Evaluation of the Char Formation During the Hydrothermal Treatment of Wooden Balls. Glob. Chall. 2023, 7, 2300169. [Google Scholar] [CrossRef]
- Mishra, R.K.; Mohanty, K. Pyrolysis kinetics and thermal behavior of waste sawdust biomass using thermogravimetric analysis. Bioresour. Technol. 2018, 251, 63–74. [Google Scholar] [CrossRef]
- Mahmood, H.; Shakeel, A.; Abdullah, A.; Khan, M.I.; Moniruzzaman, M. A comparative study on suitability of model-free and model-fitting kinetic methods to non-isothermal degradation of lignocellulosic materials. Polymers 2021, 13, 2504. [Google Scholar] [CrossRef]
- Mian, I.; Li, X.; Jian, Y.; Dacres, O.D.; Zhong, M.; Liu, J.; Ma, F.; Rahman, N. Kinetic study of biomass pellet pyrolysis by using distributed activation energy model and Coats Redfern methods and their comparison. Bioresour. Technol. 2019, 294, 122099. [Google Scholar] [CrossRef]
- Wang, L.; Lei, H.; Liu, J.; Bu, Q. Thermal decomposition behavior and kinetics for pyrolysis and catalytic pyrolysis of Douglas fir. RSC Adv. 2018, 8, 2196–2202. [Google Scholar] [CrossRef]
- Chen, L.; Hu, J.; Han, Q.; Xie, A.; Zhou, Z.; Yang, J.; Tang, Q.; Mi, B.; Wu, F. Application of distributed activation energy model and Coats-Redfern integration method in the study of industrial lignin pyrolysis kinetics. Biomass Convers. Biorefinery 2022, 1–11. [Google Scholar] [CrossRef]
- Altynbaeva, D.; Astafev, A.; Tabakaev, R. Kinetics of biomass low-temperature pyrolysis by coats–redfern method. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 194, p. 01058. [Google Scholar]
- Emiola-Sadiq, T.; Zhang, L.; Dalai, A.K. Thermal and kinetic studies on biomass degradation via thermogravimetric analysis: A combination of model-fitting and model-free approach. ACS Omega 2021, 6, 22233–22247. [Google Scholar] [CrossRef]
- Najafi, H.; Golrokh Sani, A.; Sobati, M.A. Thermogravimetric and thermo-kinetic analysis of sugarcane bagasse pith: A comparative evaluation with other sugarcane residues. Sci. Rep. 2024, 14, 2076. [Google Scholar] [CrossRef] [PubMed]
- Mishra, R.K.; Mohanty, K.; Wang, X. Pyrolysis kinetic behavior and Py-GC–MS analysis of waste dahlia flowers into renewable fuel and value-added chemicals. Fuel 2020, 260, 116338. [Google Scholar] [CrossRef]
- Li, J.; Shang, Y.; Wei, W.; Liu, Z.; Qiao, Y.; Qin, S.; Tian, Y. Comparative study on pyrolysis kinetics behavior and high-temperature fast pyrolysis product analysis of coastal zone and land biomasses. ACS Omega 2022, 7, 10144–10155. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.K.; Patil, T.; Pandey, D.; Sawarkar, A.N. Pyrolysis of mustard oil residue: A kinetic and thermodynamic study. Bioresour. Technol. 2021, 339, 125631. [Google Scholar]
- Armynah, B.; Tahir, D.; Tandilayuk, M.; Djafar, Z.; Piarah, W.H. Potentials of biochars derived from bamboo leaf biomass as energy sources: Effect of temperature and time of heating. Int. J. Biomater. 2019, 2019, 3526145. [Google Scholar] [CrossRef]
- Nzediegwu, C.; Naeth, M.A.; Chang, S.X. Elemental composition of biochars is affected by methods used for its determination. J. Anal. Appl. Pyrolysis 2021, 156, 105174. [Google Scholar] [CrossRef]
- Channiwala, S.A.; Parikh, P.P. A unified correlation for estimating HHV of solid, liquid and gaseous fuels. Fuel 2002, 81, 1051–1063. [Google Scholar] [CrossRef]
- Sluiter, A.; Ruiz, R.; Scarlata, C.; Sluiter, J.; Templeton, D. Determination of Extractives in Biomass: Laboratory Analytical Procedure (LAP); National Renewable Energy Laboratory: Golden, CO, USA, 2008. Available online: https://docs.nrel.gov/docs/gen/fy08/42619.pdf (accessed on 1 May 2025).
- Sluiter, A.; Hames, B.; Ruiz, R.; Scarlata, C.; Sluiter, J.; Templeton, D.; Crocker, D. Determination of Structural Carbohydrates and Lignin in Biomass: Laboratory Analytical Procedure (LAP); National Renewable Energy Laboratory: Golden, CO, USA, 2008. Available online: https://docs.nrel.gov/docs/gen/fy13/42618.pdf (accessed on 1 May 2025).
- Maaoui, A.; Trabelsi, A.B.H.; Abdallah, A.B.; Chagtmi, R.; Lopez, G.; Cortazar, M.; Olazar, M. Assessment of pine wood biomass wastes valorization by pyrolysis with focus on fast pyrolysis biochar production. J. Energy Inst. 2023, 108, 101242. [Google Scholar] [CrossRef]
- Chakravarty, K.H.; Sadi, M.; Chakravarty, H.; Andersen, J.; Choudhury, B.; Howard, T.J.; Arabkoohsar, A. Pyrolysis kinetics and potential utilization analysis of cereal biomass by-products; an experimental analysis for cleaner energy productions in India. Chemosphere 2024, 353, 141420. [Google Scholar] [CrossRef]
- Giglio, E.; Vitaali, G.; Lanzini, A.; Santarelli, M. Integration between biomass gasification and high-temperature electrolysis for synthetic methane production. Biomass Bioenergy 2021, 148, 106017. [Google Scholar] [CrossRef]
- Radojević, M.; Janković, B.; Jovanović, V.; Stojiljković, D.; Manić, N. Comparative pyrolysis kinetics of various biomasses based on model-free and DAEM approaches improved with numerical optimization procedure. PLoS ONE 2018, 13, e0206657. [Google Scholar] [CrossRef] [PubMed]
- Fischer, O.; Lemaire, R.; Bensakhria, A. Thermogravimetric analysis and kinetic modeling of the pyrolysis of different biomass types by means of model-fitting, model-free and network modeling approaches. J. Therm. Anal. Calorim. 2024, 149, 10941–10963. [Google Scholar] [CrossRef] [PubMed]
- Szufa, S.; Piersa, P.; Adrian, Ł.; Czerwińska, J.; Lewandowski, A.; Lewandowska, W.; Sielski, J.; Dzikuć, M.; Wróbel, M.; Jewiarz, M.; et al. Sustainable drying and torrefaction processes of miscanthus for use as a pelletized solid biofuel and biocarbon-carrier for fertilizers. Molecules 2021, 26, 1014. [Google Scholar] [CrossRef]
- Thiru, S.; Kola, R.; Thimmaraju, M.K.; Dhanalakshmi, C.S.; Sharma, V.; Sakthi, P.; Maguluri, L.P.; Ranganathan, L.; Lalvani, J.I.J. An analytical characterization study on biofuel obtained from pyrolysis of Madhuca longifolia residues. Sci. Rep. 2024, 14, 14745. [Google Scholar] [CrossRef]
- Paredes, R.; Castells, B.; Tascón, A. Thermogravimetric Assessment of Biomass: Unravelling Kinetic, Chemical Composition and Combustion Profiles. Fire 2024, 7, 396. [Google Scholar] [CrossRef]
- Punsuwan, N.; Tangsathitkulchai, C. Product Characterization and Kinetics of Biomass Pyrolysis in a Three-Zone Free-Fall Reactor. Int. J. Chem. Eng. 2014, 2014, 986719. [Google Scholar] [CrossRef]
- Gani, A.; Desvita, H.; Munawar, E.; Mamat, R.; Nizar, M.; Darnas, Y.; Sarjono, R.E. Comparative analysis of HHV and LHV values of biocoke fuel from palm oil mill solid waste. Case Stud. Chem. Environ. Eng. 2024, 9, 100581. [Google Scholar] [CrossRef]
- Uwaoma, R.C.; Schröer, B.J.; Strydom, C.A.; Bunt, J.R.; Matjie, R.H.; Mphahlele, K.; Meyer, J.A. Kinetics, thermodynamics, and thermal decomposition characteristics of co-pyrolysis of municipality solid waste residue hydrochar and <1.5 g/cm3 fraction of South African discarded fine coal. Bioresour. Technol. Rep. 2022, 18, 100998. [Google Scholar]
- Wang, W.; Lemaire, R.; Bensakhria, A.; Luart, D. Analysis of the catalytic effects induced by alkali and alkaline earth metals (AAEMs) on the pyrolysis of beech wood and corncob. Catalysts 2022, 12, 1505. [Google Scholar] [CrossRef]
- Cao, J.; Yu, Y.; Wu, H. Primary release and transformation of inorganic and organic sodium during fast pyrolysis of sodium-loaded lignin. Proc. Combust. Inst. 2023, 39, 3439–3446. [Google Scholar] [CrossRef]
- Liu, N.; Huang, H.; Feng, J.; Li, R.; Huang, X.; Wu, Y. Effects of alkali and alkaline earth metals in biomass on co-pyrolysis characteristics and product distribution of coal and biomass. Fuel 2025, 389, 134551. [Google Scholar] [CrossRef]
- Grafmüller, J.; Böhm, A.; Zhuang, Y.; Spahr, S.; Müller, P.; Otto, T.N.; Bucheli, T.D.; Leifeld, J.; Giger, R.; Tobler, M.; et al. Wood ash as an additive in biomass pyrolysis: Effects on biochar yield, properties, and agricultural performance. ACS Sustain. Chem. Eng. 2022, 10, 2720–2729. [Google Scholar] [CrossRef]
- Elhenawy, Y.; Fouad, K.; Mansi, A.; Bassyouni, M.; Gadalla, M.; Ashour, F.; Majozi, T. Experimental analysis and numerical simulation of biomass pyrolysis. J. Therm. Anal. Calorim. 2024, 149, 10369–10383. [Google Scholar] [CrossRef]
- Nhuchhen, D.R.; Afzal, M.T. HHV predicting correlations for torrefied biomass using proximate and ultimate analyses. Bioengineering 2017, 4, 7. [Google Scholar] [CrossRef]
- Li, J.; Sun, W.; Lichtfouse, E.; Maurer, C.; Liu, H. Life cycle assessment of biochar for sustainable agricultural application: A review. Sci. Total Environ. 2024, 951, 175448. [Google Scholar] [CrossRef]
- Yildiz, M.J.; Wurzer, C.; Robinson, T.; Wietecha, J.; Mašek, O. Biochar from pellets: Influence of binders and pyrolysis temperature on physical properties of pyrolyzed pellets. Sustain. Mater. Technol. 2025, 43, e01327. [Google Scholar]
- Dhyani, V.; Bhaskar, T. A comprehensive review on the pyrolysis of lignocellulosic biomass. Renew. Energy 2018, 129, 695–716. [Google Scholar] [CrossRef]
- Gurtner, D.; Kresta, M.; Hupfauf, B.; Götz, P.; Nussbaumer, R.; Hofmann, A.; Pfeifer, C. Mechanical strength characterisation of pyrolysis biochar from woody biomass. Energy 2023, 285, 129366. [Google Scholar] [CrossRef]
- Dufourny, A.; Van De Steene, L.; Humbert, G.; Guibal, D.; Martin, L.; Blin, J. Influence of pyrolysis conditions and the nature of the wood on the quality of charcoal as a reducing agent. J. Anal. Appl. Pyrolysis 2019, 137, 1–13. [Google Scholar] [CrossRef]
- Xia, C.; Cai, L.; Zhang, H.; Zuo, L.; Shi, S.Q.; Lam, S.S. A review on the modeling and validation of biomass pyrolysis with a focus on product yield and composition. Biofuel Res. J. 2021, 29, 1296–1315. [Google Scholar] [CrossRef]
- Johnston, C.T. 18 Biochar analysis by Fourier-transform infra-red spectroscopy. In Biochar: A Guide to Analytical Methods; CRC Press: Boca Raton, FL, USA, 2017; p. 199. [Google Scholar]
- Nanda, S.; Mohanty, P.; Pant, K.K.; Naik, S.; Kozinski, J.A.; Dalai, A.K. Characterization of North American lignocellulosic biomass and biochars in terms of their candidacy for alternate renewable fuels. Bioenergy Res. 2013, 6, 663–677. [Google Scholar] [CrossRef]
- Mukherjee, A.; Okolie, J.A.; Tyagi, R.; Dalai, A.K.; Niu, C. Pyrolysis kinetics and activation thermodynamic parameters of exhausted coffee residue and coffee husk using thermogravimetric analysis. Can. J. Chem. Eng. 2021, 99, 1683–1695. [Google Scholar] [CrossRef]
- Raza, M.; Abu-Jdayil, B.; Inayat, A. Pyrolytic kinetics and thermodynamic analyses of date seeds at different heating rates using the Coats–Redfern method. Fuel 2023, 342, 127799. [Google Scholar] [CrossRef]
- Almusafir, R.; Smith, J.D. Thermal Decomposition and Kinetic Parameters of Three Biomass Feedstocks for the Performance of the Gasification Process Using a Thermogravimetric Analyzer. Energies 2024, 17, 396. [Google Scholar] [CrossRef]
- Apaydın Varol, E.; Mutlu, Ü. TGA-FTIR analysis of biomass samples based on the thermal decomposition behavior of hemicellulose, cellulose, and lignin. Energies 2023, 16, 3674. [Google Scholar] [CrossRef]
- Gonzalez-Aguilar, A.M.; Cabrera-Madera, V.P.; Vera-Rozo, J.R.; Riesco-Ávila, J.M. Effects of heating rate and temperature on the thermal pyrolysis of expanded polystyrene post-industrial waste. Polymers 2022, 14, 4957. [Google Scholar] [CrossRef]
- Călin, C.; Sîrbu, E.E.; Tănase, M.; Győrgy, R.; Popovici, D.R.; Banu, I. A Thermogravimetric Analysis of Biomass Conversion to Biochar: Experimental and Kinetic Modeling. Appl. Sci. 2024, 14, 9856. [Google Scholar] [CrossRef]
- Dhaundiyal, A.; Singh, S.B.; Hanon, M.M.; Rawat, R. Determination of kinetic parameters for the thermal decomposition of parthenium hysterophorus. Environ. Clim. Technol. 2018, 22, 5–21. [Google Scholar] [CrossRef]
- Monir, M.U.; Shovon, S.M.; Akash, F.A.; Habib, M.A.; Techato, K.; Abd Aziz, A.; Chowdhury, S.; Prasetya, T.A.E. Comprehensive characterization and kinetic analysis of coconut shell thermal degradation: Energy potential evaluated via the Coats-Redfern method. Case Stud. Therm. Eng. 2024, 55, 104186. [Google Scholar] [CrossRef]
- Saleem, M.; Bahadar, A. In-Depth Study on Synergic Interactions and Thermo-Kinetic Analysis of (Wheat Straw and Woody Sawdust) Biomass Co-Pyrolysis over Mussel Shell-Derived CaO Catalyst Using Coats–Redfern Method. Catalysts 2024, 14, 655. [Google Scholar] [CrossRef]
- Hadey, C.; Malika, A.; Mohammed, A.; Fatima, B. A study on the biomass wastes’ combustion process and their biochar. Res. Sq. 2020. [Google Scholar] [CrossRef]
- Hassan, A.M.M.; Asif, M.; Hussain, T.; Sajjad, R.; Yasmin, F.; Khandaker, M.U. Pyrolysis of municipal solid waste: Kinetics and thermodynamic parameters via Coats-Redfern method. Appl. Chem. Eng. 2024, 7, 1872. [Google Scholar] [CrossRef]
- Tariq, R.; Saeed, S.; Riaz, M.; Saeed, S. Kinetic and thermodynamic evaluation of almond shells pyrolytic behavior using Coats–Redfern and pyrolysis product distribution model. Energy Sources Part A Recovery Util. Environ. Eff. 2023, 45, 4446–4462. [Google Scholar] [CrossRef]
- Sobek, S.; Werle, S. Kinetic modelling of waste wood devolatilization during pyrolysis based on thermogravimetric data and solar pyrolysis reactor performance. Fuel 2020, 261, 116459. [Google Scholar] [CrossRef]
- Shrivastava, D.K.; Singh, A.K.; Chakraborty, J.P. Model-free isoconversional methods to determine the intrinsic kinetics and thermodynamic parameters during pyrolysis of boiled banana peel: Influence of inorganic species. Bioresour. Technol. Rep. 2023, 24, 101676. [Google Scholar] [CrossRef]
- Bisen, D.; Chouhan, A.P.S.; Sarma, A.K.; Rajamohan, S.; Elumalai, P.V.; Balasubramanian, D.; Cherie, A. Thermogravimetric analysis of rice husk and low-density polyethylene co-pyrolysis: Kinetic and thermodynamic parameters. Sci. Rep. 2024, 14, 31798. [Google Scholar] [CrossRef]
- Shagali, A.A.; Hu, S.; Li, H.; Chi, H.; Qing, H.; Xu, J.; Jiang, L.; Wang, Y.; Su, S.; Xiang, J. Thermal behavior, synergistic effect and thermodynamic parameter evaluations of biomass/plastics co–pyrolysis in a concentrating photothermal TGA. Fuel 2023, 331, 125724. [Google Scholar] [CrossRef]
- Tabal, A.; Barakat, A.; Aboulkas, A. Pyrolysis of ficus nitida wood: Determination of kinetic and thermodynamic parameters. Fuel 2021, 283, 119253. [Google Scholar] [CrossRef]
- Patil, Y.; Ku, X.; Vasudev, V. Pyrolysis characteristics and determination of kinetic and thermodynamic parameters of raw and torrefied Chinese fir. ACS Omega 2023, 8, 34938–34947. [Google Scholar] [CrossRef]
- Lei, J.; Ye, X.; Wang, H.; Zhao, D. Insights into pyrolysis kinetics, thermodynamics, and the reaction mechanism of wheat straw for its resource utilization. Sustainability 2023, 15, 12536. [Google Scholar] [CrossRef]




| Model-Free Method | Equation | Procedure for Plotting | |
|---|---|---|---|
| OFW | (1) | Plot versus to obtain a straight line with a negative slope of to calculate Ea. Using this and an assumed reaction model/mechanism for g(α), A can be calculated from the y-axis intercept, . | |
| KAS | (2) | Plot versus to obtain a straight line with a negative slope of to calculate Ea. Using this and an assumed reaction model/mechanism for g(α), A can be calculated from the y-axis intercept, . | |
| FM | (or) | (3) | Plot or versus to obtain a straight line with a negative slope of to calculate Ea. Using this and an assumed reaction model/mechanism for f(α), A can be calculated from the y-axis intercept, . |
| Biomass | Pinewood | Rice Husk | Beech | Wheat Straw | Miscanthus * | Madhuca Longifolia | Poplar Sawdust * | Palm Kernel * | MSW | CRD Wood * |
|---|---|---|---|---|---|---|---|---|---|---|
| Proximate analysis | ||||||||||
| Moisture (wt%) | 4.01 | 10.10 | 15.20 | 11.63 | --- | 5.98 | --- | --- | 2.75 | --- |
| Volatiles (wt%) | 64.37 | 52.30 | 84.87 | 65.32 | 83.30 | 71.26 | 83.60 | 79.68 | 51.13 | 82.35 |
| FC (wt%) | 24.89 | 23.40 | 14.53 | 15.17 | 14.40 | 18.24 | 15.40 | 16.78 | 37.86 | 16.48 |
| Ash (wt%) | 6.73 | 14.20 | 0.60 | 7.88 | 2.30 | 4.50 | 1.00 | 3.54 | 8.26 | 1.17 |
| Ultimate analysis | ||||||||||
| C (wt%) | 54.53 | 34.99 | 49.38 | 44.12 | 47.50 | 47.20 | 49.47 | 43.84 | 76.26 | 49.88 |
| H (wt%) | 6.56 | 4.58 | 6.17 | 6.34 | 6.10 | 5.90 | 5.89 | 6.13 | 6.88 | 6.12 |
| S (wt%) | 0.09 | --- | 0.01 | --- | 0.10 | 1.20 | 0.05 | 0.06 | 0.28 | 0.10 |
| N (wt%) | 0.94 | 1.95 | 0.28 | 0.63 | 1.00 | 3.60 | 1.40 | 3.11 | 3.32 | 0.99 |
| O (wt%) | 31.14 | 34.18 | 43.55 | 39.99 | 45.30 | 42.10 | 43.12 | 46.86 | 13.25 | 41.74 |
| Van-Krevelen parameters | ||||||||||
| H/C | 1.44 | 1.57 | 1.50 | 1.72 | 1.54 | 1.50 | 1.43 | 1.68 | 1.07 | 1.47 |
| O/C | 0.43 | 0.73 | 0.66 | 0.68 | 0.72 | 0.67 | 0.65 | 0.80 | 0.13 | 0.63 |
| Calorific value | ||||||||||
| HHV (MJ/kg) | 22.33 | 14.09 | 19.3 | 15.29 | 15.82 | --- | 19.50 | 16.83 | 29.70 | 20.28 |
| Reference | [51] | [52] | [53] | [54] | [55,56] | [57] | [58] | [59,60] | [61] | Present study |
| Biomass Constituents | Lot 1 | Lot 2 | Lot 3 | Lot 4 |
|---|---|---|---|---|
| Hot Water Extractives (wt%) | 3.2 | 2.0 | 3.1 | 2.7 |
| Ethanol Extractives (wt%) | 3.7 | 3.0 | 2.8 | 4.0 |
| Total extractives (wt%) | 6.9 | 5.0 | 5.9 | 6.7 |
| Insoluble Lignin (wt%) | 19.7 | 20.5 | 26.1 | 25.3 |
| Total Lignin (wt%) | 24.9 | 26.2 | 30.2 | 29.7 |
| Glucan (wt%) | 50.9 | 44.2 | 46.9 | 53.1 |
| Xylan (wt%) | 19.2 | 23.2 | 8.0 | 10.1 |
| Arabinan (wt%) | 0.0 | 0.1 | 0.9 | 1.3 |
| Galactan (wt%) | 0.6 | 0.8 | 2.5 | 2.4 |
| Mannan (wt%) | 2.0 | 2.3 | 9.7 | 10.0 |
| Total holocellulose (wt%) | 72.7 | 70.6 | 68.0 | 76.9 |
| Reaction Model | Type/Mechanism | Heating Rate = 10 °C/min | Heating Rate = 20 °C/min | Heating Rate = 30 °C/min | Heating Rate = 40 °C/min | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Activation Energy, Ea (kJ/mol) | Pre-Exponential Factor, A (min−1) | R2 from Plot | Activation Energy, Ea (kJ/mol) | Pre-Exponential Factor, A (min−1) | R2 from Plot | Activation Energy, Ea (kJ/mol) | Pre-Exponential Factor, A (min−1) | R2 from Plot | Activation Energy, Ea (kJ/mol) | Pre-Exponential Factor, A (min−1) | R2 from Plot | ||
| Chemical | First-order (F1) | 65.82 | 5.0873 × 104 | 0.9882 | 67.34 | 1.0329 × 105 | 0.9888 | 66.40 | 1.0953 × 105 | 0.9881 | 66.40 | 1.3118 × 105 | 0.9864 |
| Second-order (F2) | 94.62 | 3.0881 × 107 | 0.9559 | 94.62 | 6.1763 × 107 | 0.9563 | 96.89 | 9.7105 × 107 | 0.9563 | 95.55 | 6.9599 × 107 | 0.9524 | |
| Third-order (F3) | 129.70 | 6.4717 × 1010 | 0.9217 | 129.70 | 1.29434 × 1011 | 0.9219 | 132.90 | 2.1212 × 1011 | 0.9219 | 131.05 | 1.2162 × 1011 | 0.9172 | |
| Diffusion | One-dimensional (D1) | 98.06 | 1.2944 × 107 | 0.9992 | 98.06 | 2.5889 × 107 | 0.9993 | 100.22 | 3.9199 × 107 | 0.9993 | 99.07 | 2.8758 × 107 | 0.9997 |
| Two-dimensional (D2) | 110.51 | 1.0282 × 108 | 0.9993 | 110.51 | 2.0565 × 108 | 0.9996 | 112.97 | 3.1433 × 108 | 0.9996 | 111.67 | 2.1457 × 108 | 0.9992 | |
| Three-dimensional J (D3) | 125.69 | 6.4219 × 108 | 0.9958 | 125.69 | 1.2844 × 109 | 0.9963 | 128.54 | 1.9907 × 109 | 0.9963 | 127.04 | 1.2459 × 109 | 0.9949 | |
| Three-dimensional GB (D4) | 115.52 | 6.8969 × 107 | 0.9986 | 115.52 | 1.3794 × 108 | 0.9989 | 118.12 | 2.1179 × 108 | 0.9989 | 116.75 | 1.4021 × 108 | 0.9981 | |
| Phase interfacial | One-dimensional (R1) | 43.95 | 3.3309 × 102 | 0.9990 | 43.95 | 6.6618 × 102 | 0.9990 | 44.93 | 9.9444 × 102 | 0.9990 | 44.26 | 9.6170 × 102 | 0.9995 |
| Two-dimensional (R2) | 54.03 | 1.7353 × 103 | 0.9977 | 54.03 | 3.4705 × 103 | 0.9977 | 55.25 | 5.2249 × 103 | 0.9982 | 54.56 | 4.7584 × 103 | 0.9970 | |
| Three-dimensional (R3) | 57.76 | 2.7237 × 103 | 0.9953 | 57.76 | 5.4473 × 103 | 0.9953 | 59.08 | 8.2295 × 103 | 0.9958 | 58.24 | 7.3348 × 103 | 0.9943 | |
| Nucleation and growth | Two-dimensional (A2) | 27.83 | 16.139 | 0.9845 | 27.83 | 3.2278 × 101 | 0.9845 | 28.48 | 48.360 | 0.9853 | 27.92 | 49.806 | 0.9819 |
| Three-dimensional (A3) | 15.17 | 0.799 | 0.9784 | 15.17 | 1.5984 | 0.9784 | 15.53 | 2.3829 | 0.9795 | 15.14 | 2.6205 | 0.9739 | |
| Conversion Rate, α | OFW Method | KAS Method | FM Method | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Activation Energy, Ea (kJ/mol) | Pre-Exponential Factor, A (min−1) | R2 from Plot | Activation Energy, Ea (kJ/mol) | Pre-Exponential Factor, A (min−1) | R2 from Plot | Activation Energy, Ea (kJ/mol) | Pre-Exponential Factor, A (min−1) | R2 from Plot | |
| 0.1 | 8.85 | 49.51005146 | 0.414 | 135.06 | 2.08822 × 1012 | 0.599 | 144.09 | 2.9616 × 1014 | 0.637 |
| 0.2 | 172.87 | 8.40043 × 1014 | 0.990 | 176.05 | 1.6275 × 1015 | 0.987 | 185.71 | 2.15137 × 1017 | 0.988 |
| 0.3 | 176.61 | 7.47933 × 1014 | 0.997 | 174.12 | 4.35321 × 1014 | 0.998 | 185.27 | 8.42214 × 1016 | 0.998 |
| 0.4 | 178.65 | 6.27054 × 1014 | 0.996 | 179.28 | 6.85439 × 1014 | 0.996 | 189.54 | 1.17277 × 1017 | 0.997 |
| 0.5 | 179.77 | 4.95313 × 1014 | 0.997 | 177.02 | 2.79223 × 1014 | 0.999 | 188.26 | 6.43149 × 1016 | 0.999 |
| 0.6 | 178.33 | 2.6664 × 1014 | 0.999 | 178.91 | 2.85704 × 1014 | 0.997 | 189.77 | 6.86145 × 1016 | 0.998 |
| 0.7 | 179.97 | 2.79517 × 1014 | 0.999 | 178.44 | 1.98226 × 1014 | 0.998 | 189.92 | 6.3583 × 1016 | 0.998 |
| 0.8 | 184.86 | 5.32708 × 1014 | 0.999 | 185.41 | 5.66593 × 1014 | 0.997 | 196.47 | 2.06678 × 1017 | 0.997 |
| 0.9 | 522.38 | 7.94663 × 1039 | 0.927 | 470.58 | 4.06828 × 1035 | 0.901 | 482.38 | 1.04521 × 1038 | 0.905 |
| Ea and A Estimated from OFW Method | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Conversion Rate, α | Heating Rate = 10 °C/min Tm = 367.41 | Heating Rate = 20 °C/min Tm = 382.48 | Heating Rate = 30 °C/min Tm = 386.85 | Heating Rate = 40 °C/min Tm = 389.62 | ||||||||
| ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | |
| 0.1 | 3.52 | −109.52 | 176.48 | 3.40 | −112.44 | 176.68 | 3.36 | −113.28 | 176.73 | 3.34 | −113.82 | 175.99 |
| 0.2 | 167.54 | 216.73 | −76.79 | 167.42 | 217.64 | −76.60 | 167.38 | 217.90 | −76.55 | 167.36 | 218.07 | −76.23 |
| 0.3 | 171.28 | 219.86 | −75.83 | 171.16 | 220.75 | −75.64 | 171.12 | 221.00 | −75.58 | 171.10 | 221.17 | −75.26 |
| 0.4 | 173.32 | 220.96 | −74.36 | 173.20 | 221.82 | −74.17 | 173.16 | 222.08 | −74.11 | 173.14 | 222.23 | −73.80 |
| 0.5 | 174.44 | 220.82 | −72.40 | 174.32 | 221.66 | −72.21 | 174.28 | 221.90 | −72.15 | 174.26 | 222.05 | −71.85 |
| 0.6 | 173.00 | 216.08 | −67.25 | 172.88 | 216.85 | −67.06 | 172.84 | 217.07 | −67.00 | 172.82 | 217.20 | −66.72 |
| 0.7 | 174.64 | 217.97 | −67.65 | 174.52 | 218.74 | −67.45 | 174.48 | 218.96 | −67.40 | 174.46 | 219.10 | −67.12 |
| 0.8 | 179.53 | 226.30 | −73.01 | 179.40 | 227.14 | −72.81 | 179.37 | 227.39 | −72.76 | 179.35 | 227.54 | −72.45 |
| 0.9 | 517.05 | 872.53 | −554.95 | 516.93 | 880.64 | −554.76 | 516.89 | 883.00 | −554.71 | 516.87 | 884.49 | −552.39 |
| Ea and A Estimated from KAS Method | ||||||||||||
| Conversion Rate, α | Heating Rate = 10 °C/min Tm = 367.41 | Heating Rate = 20 °C/min Tm = 382.48 | Heating Rate = 30 °C/min Tm = 386.85 | Heating Rate = 40 °C/min Tm = 389.62 | ||||||||
| ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | |
| 0.1 | 129.73 | 146.98 | −26.93 | 129.61 | 147.14 | −26.31 | 129.57 | 147.18 | −26.14 | 129.55 | 147.21 | −26.03 |
| 0.2 | 170.72 | 223.44 | −82.29 | 170.60 | 224.43 | −80.40 | 170.56 | 224.71 | −79.87 | 170.54 | 224.89 | −79.54 |
| 0.3 | 168.79 | 214.48 | −71.33 | 168.66 | 215.30 | −69.69 | 168.63 | 215.54 | −69.23 | 168.61 | 215.69 | −68.94 |
| 0.4 | 173.95 | 222.06 | −75.10 | 173.83 | 222.94 | −73.38 | 173.79 | 223.19 | −72.89 | 173.77 | 223.36 | −72.59 |
| 0.5 | 171.70 | 215.02 | −67.64 | 171.57 | 215.79 | −66.08 | 171.54 | 216.01 | −65.64 | 171.51 | 216.15 | −65.37 |
| 0.6 | 173.58 | 217.03 | −67.83 | 173.46 | 217.80 | −66.27 | 173.42 | 218.02 | −65.83 | 173.40 | 218.17 | −65.55 |
| 0.7 | 173.11 | 214.61 | −64.79 | 172.98 | 215.33 | −63.30 | 172.95 | 215.54 | −62.88 | 172.93 | 215.68 | −62.62 |
| 0.8 | 180.08 | 227.18 | −73.52 | 179.96 | 228.03 | −71.83 | 179.92 | 228.28 | −71.35 | 179.90 | 228.44 | −71.06 |
| 0.9 | 465.26 | 768.12 | −472.81 | 465.13 | 774.99 | −461.94 | 465.10 | 776.98 | −458.88 | 465.07 | 778.25 | −456.96 |
| Ea and A Estimated from FM Method | ||||||||||||
| Conversion Rate, α | Heating Rate = 10 °C/min Tm = 367.41 | Heating Rate = 20 °C/min Tm = 382.48 | Heating Rate = 30 °C/min Tm = 386.85 | Heating Rate = 40 °C/min Tm = 389.62 | ||||||||
| ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | ΔH (kJ/mol) | ΔG (kJ/mol) | ΔS (J/mol·K) | |
| 0.1 | 138.76 | 182.40 | −68.13 | 138.64 | 183.18 | −67.93 | 138.60 | 183.40 | −67.88 | 138.58 | 183.54 | −67.59 |
| 0.2 | 180.38 | 259.11 | −122.90 | 180.26 | 260.71 | −122.71 | 180.22 | 261.17 | −122.65 | 180.20 | 261.47 | −122.14 |
| 0.3 | 179.94 | 253.67 | −115.11 | 179.81 | 255.15 | −114.91 | 179.78 | 255.58 | −114.86 | 179.75 | 255.86 | −114.38 |
| 0.4 | 184.22 | 259.71 | −117.86 | 184.09 | 261.24 | −117.67 | 184.06 | 261.68 | −117.61 | 184.03 | 261.96 | −117.12 |
| 0.5 | 182.94 | 255.23 | −112.86 | 182.81 | 256.68 | −112.67 | 182.77 | 257.10 | −112.62 | 182.75 | 257.37 | −112.14 |
| 0.6 | 184.44 | 257.08 | −113.40 | 184.32 | 258.54 | −113.21 | 184.28 | 258.96 | −113.15 | 184.26 | 259.23 | −112.68 |
| 0.7 | 184.60 | 256.83 | −112.77 | 184.47 | 258.28 | −112.58 | 184.44 | 258.70 | −112.52 | 184.41 | 258.97 | −112.05 |
| 0.8 | 191.14 | 269.65 | −122.57 | 191.01 | 271.25 | −122.38 | 190.98 | 271.71 | −122.32 | 190.95 | 272.00 | −121.81 |
| 0.9 | 477.05 | 809.47 | −518.94 | 476.93 | 817.04 | −518.75 | 476.89 | 819.23 | −518.69 | 476.87 | 820.62 | −516.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ganesan, A.; Barnabé, S.; Bareha, Y.; Langlois, S.; Rezazgui, O.; Boussabbeh, C. Kinetic Analysis of Construction, Renovation, and Demolition (CRD) Wood Pyrolysis Using Model-Fitting and Model-Free Methods via Thermogravimetric Analysis. Energies 2025, 18, 2496. https://doi.org/10.3390/en18102496
Ganesan A, Barnabé S, Bareha Y, Langlois S, Rezazgui O, Boussabbeh C. Kinetic Analysis of Construction, Renovation, and Demolition (CRD) Wood Pyrolysis Using Model-Fitting and Model-Free Methods via Thermogravimetric Analysis. Energies. 2025; 18(10):2496. https://doi.org/10.3390/en18102496
Chicago/Turabian StyleGanesan, Aravind, Simon Barnabé, Younès Bareha, Simon Langlois, Olivier Rezazgui, and Cyrine Boussabbeh. 2025. "Kinetic Analysis of Construction, Renovation, and Demolition (CRD) Wood Pyrolysis Using Model-Fitting and Model-Free Methods via Thermogravimetric Analysis" Energies 18, no. 10: 2496. https://doi.org/10.3390/en18102496
APA StyleGanesan, A., Barnabé, S., Bareha, Y., Langlois, S., Rezazgui, O., & Boussabbeh, C. (2025). Kinetic Analysis of Construction, Renovation, and Demolition (CRD) Wood Pyrolysis Using Model-Fitting and Model-Free Methods via Thermogravimetric Analysis. Energies, 18(10), 2496. https://doi.org/10.3390/en18102496







