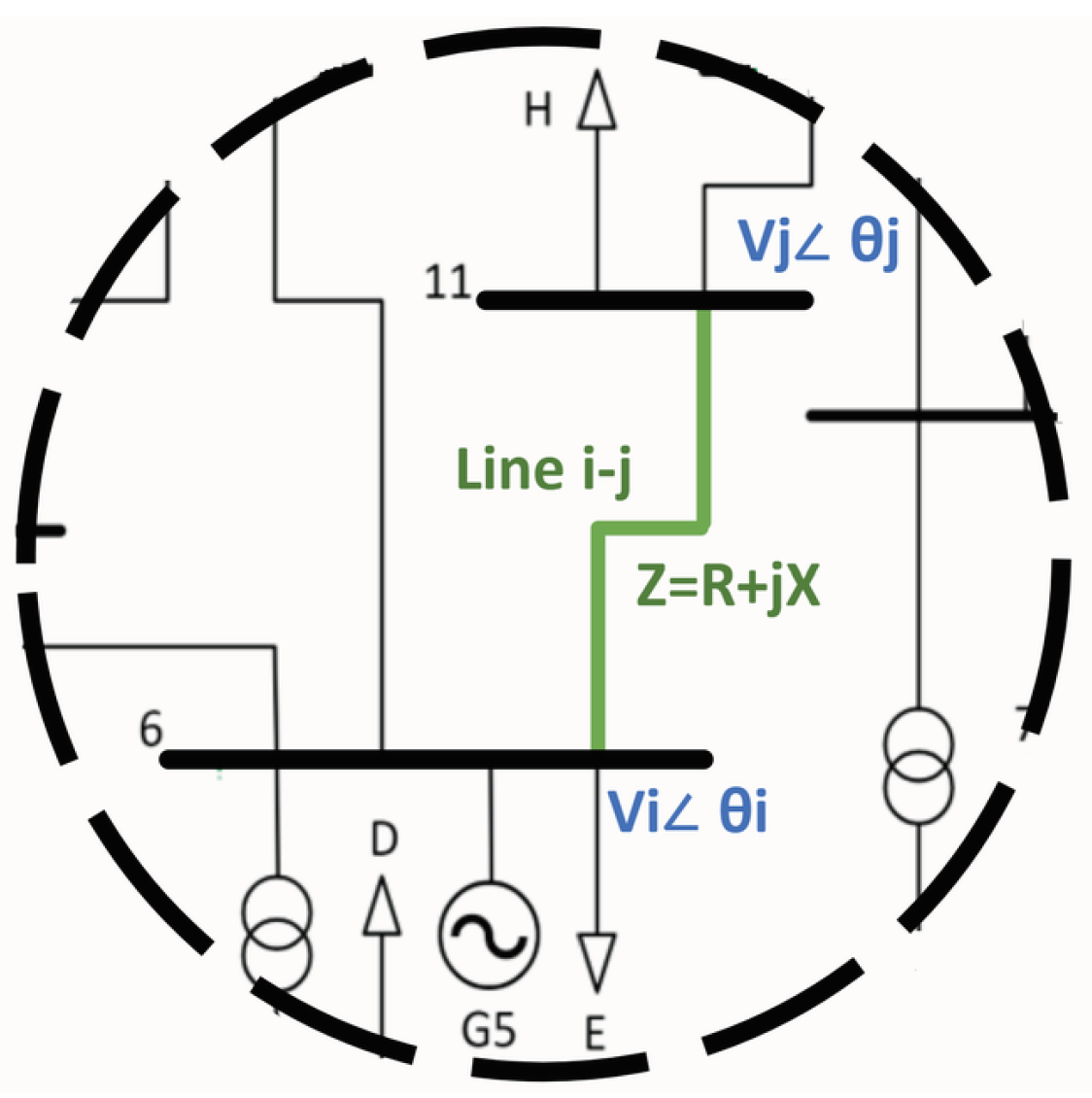
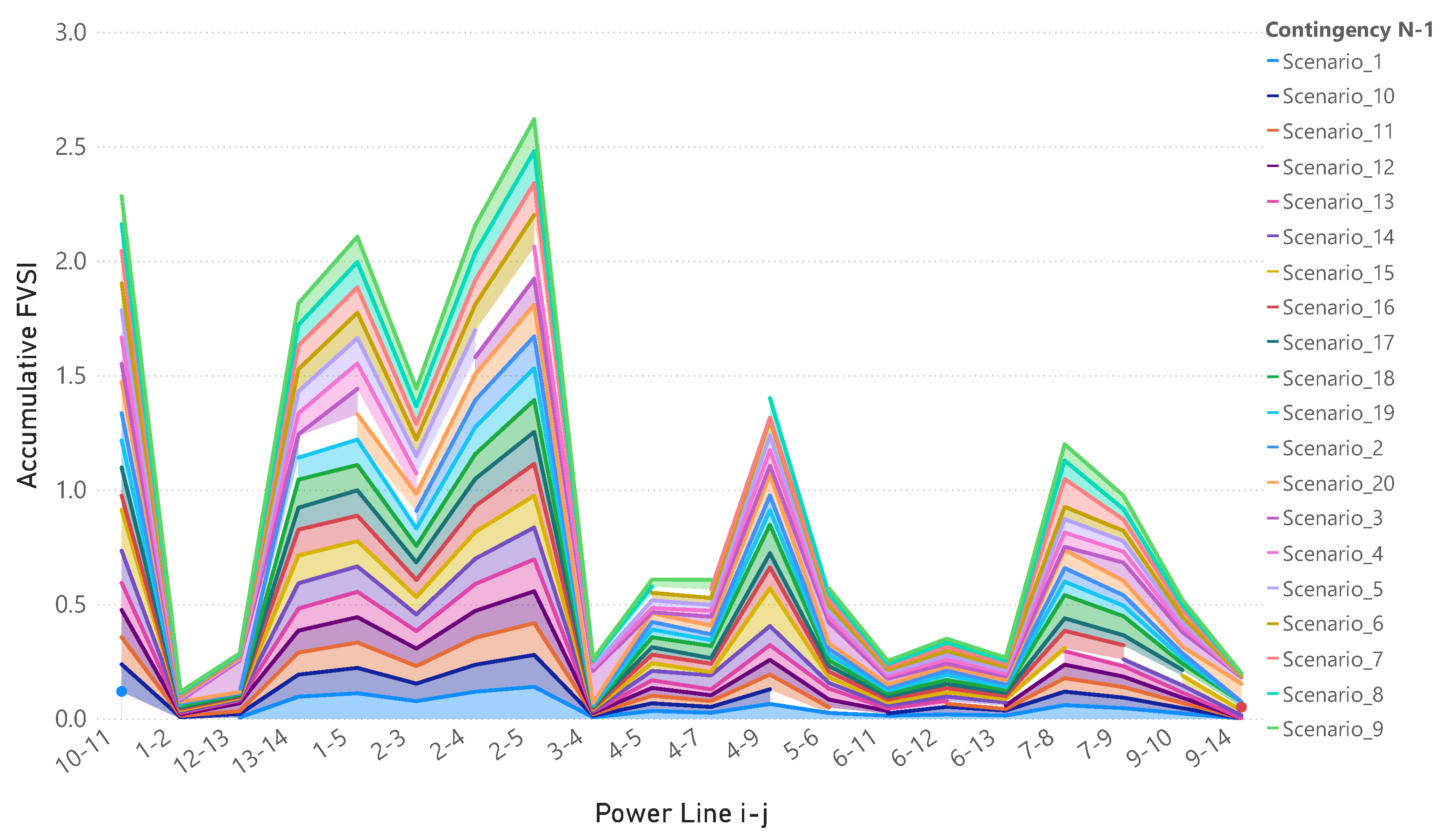
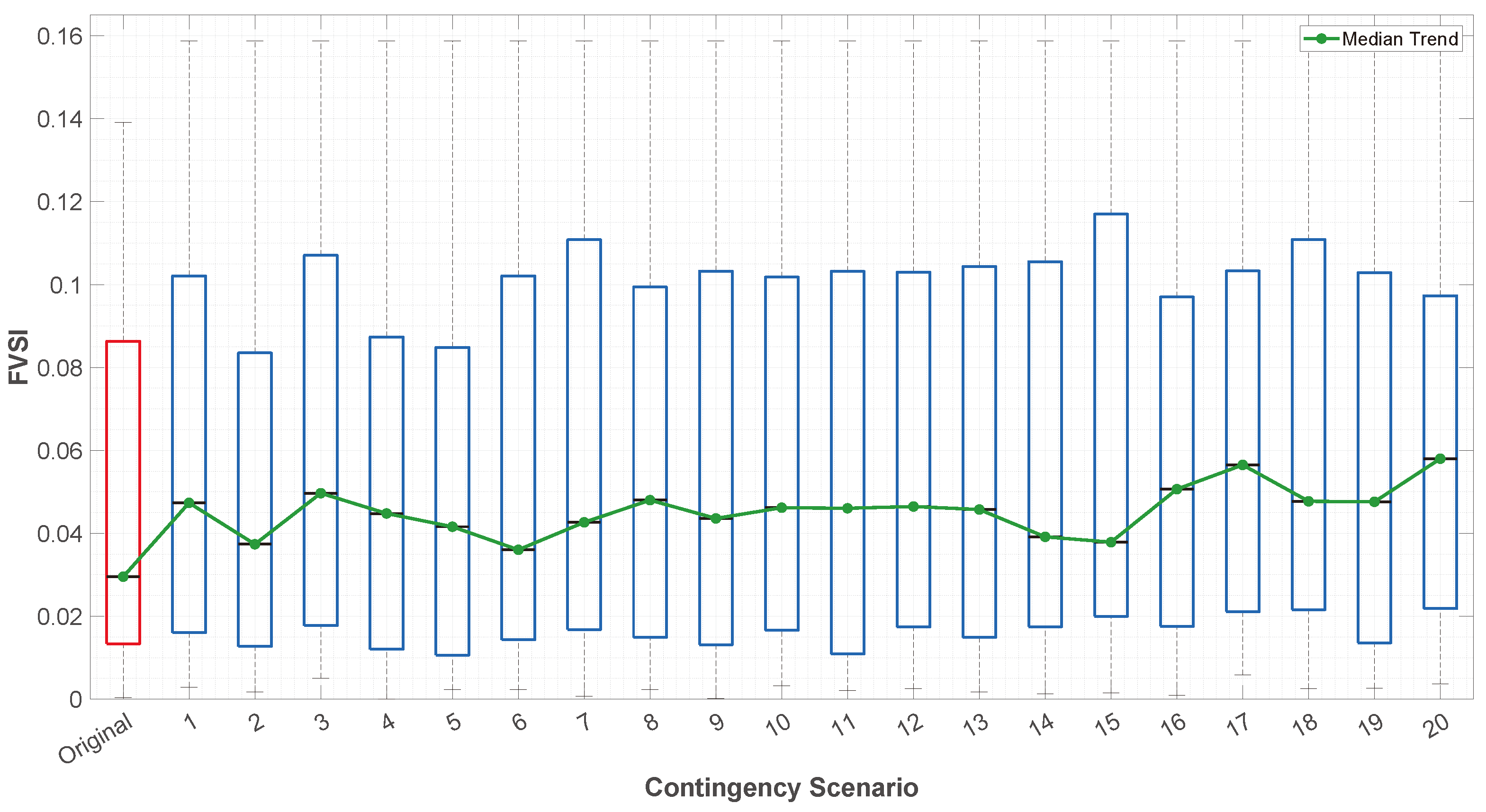
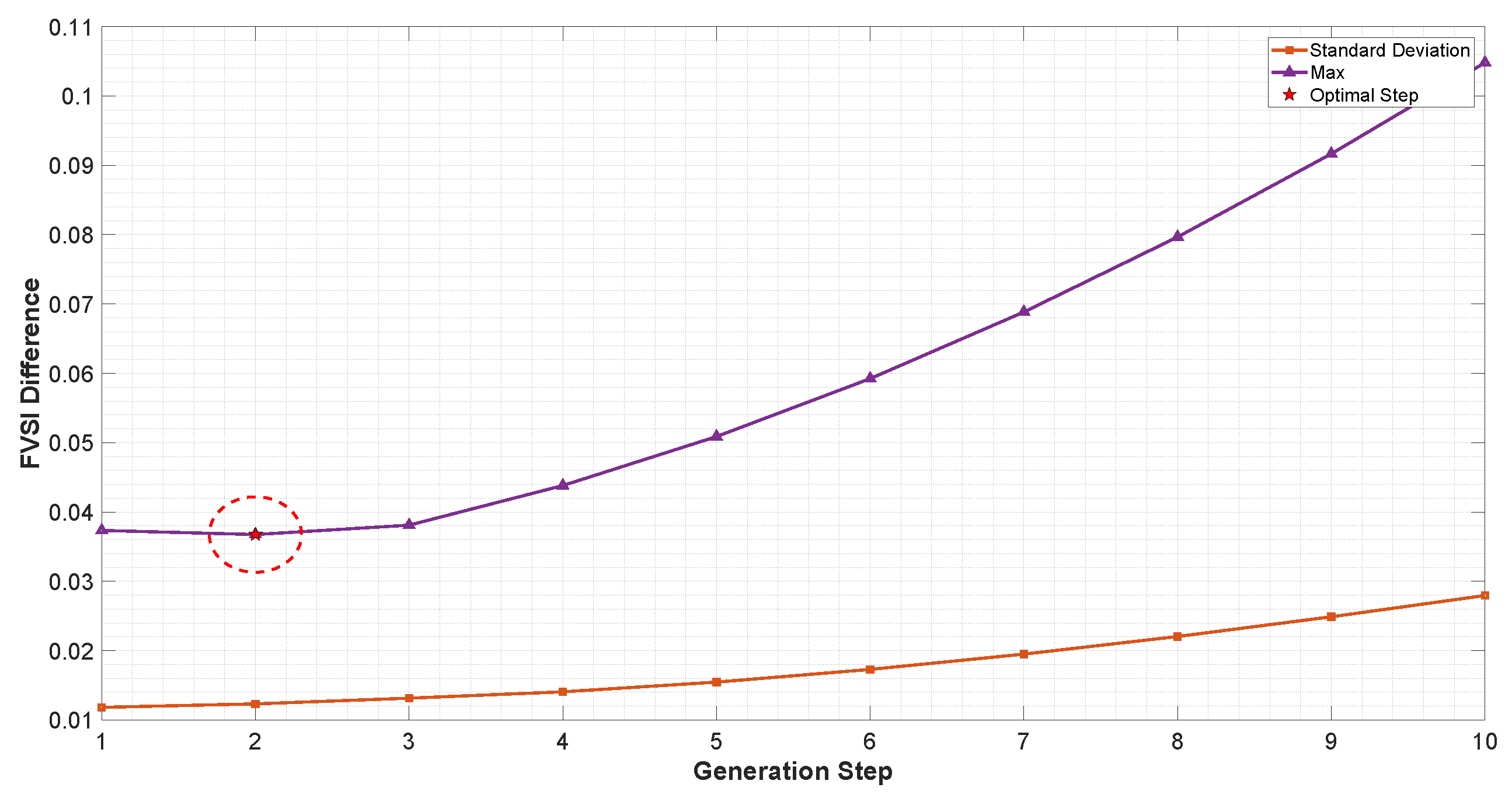
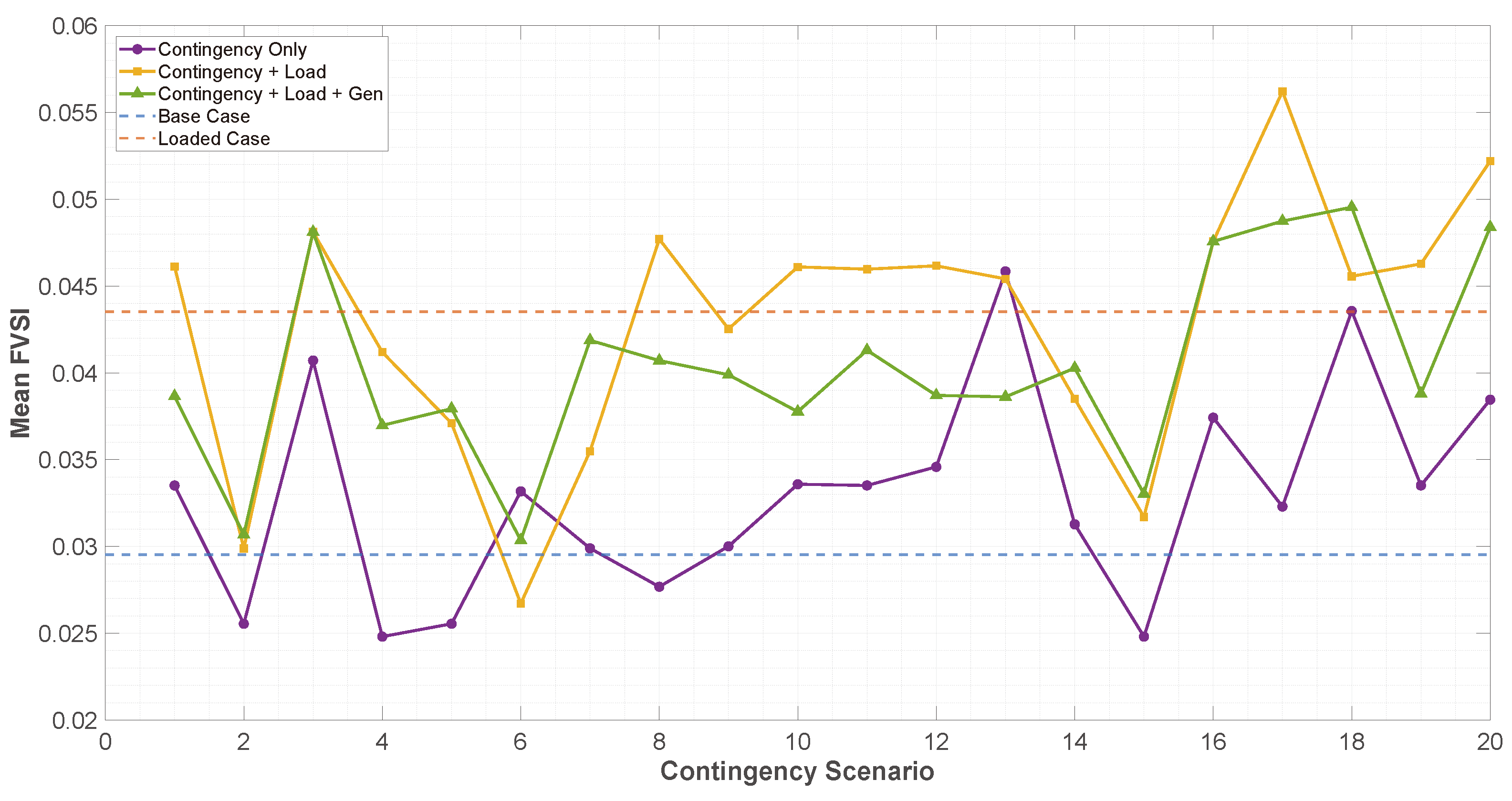
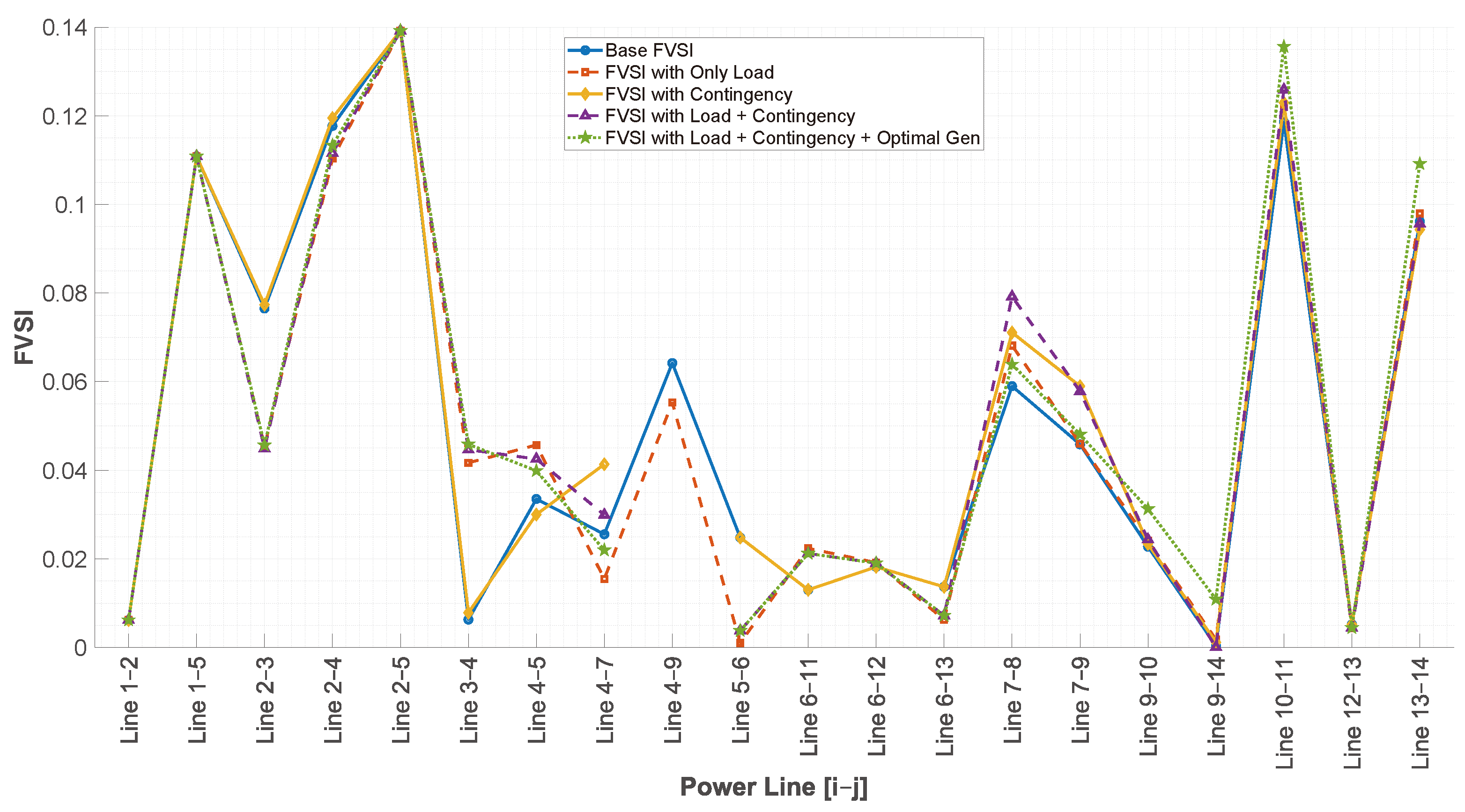
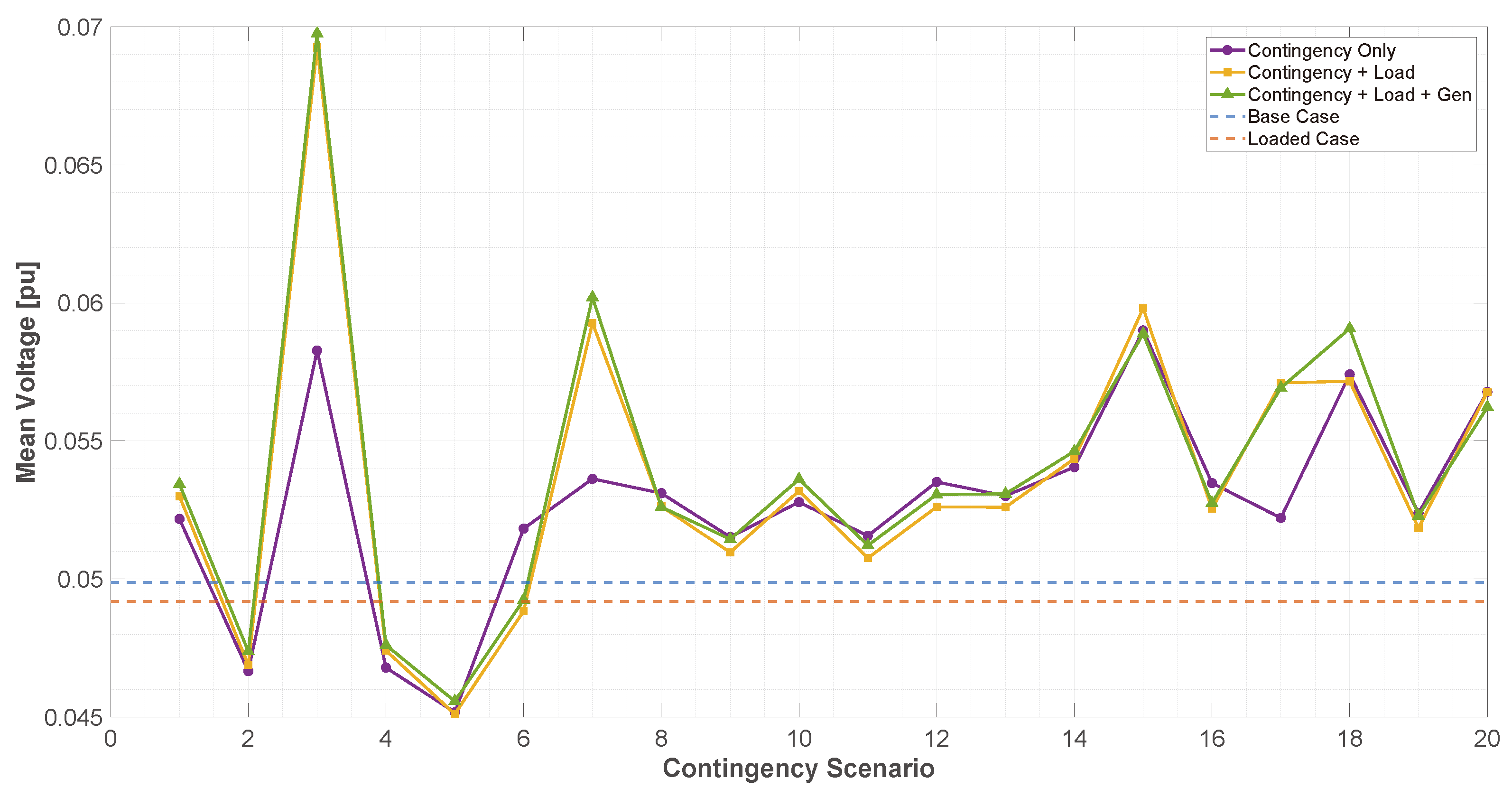
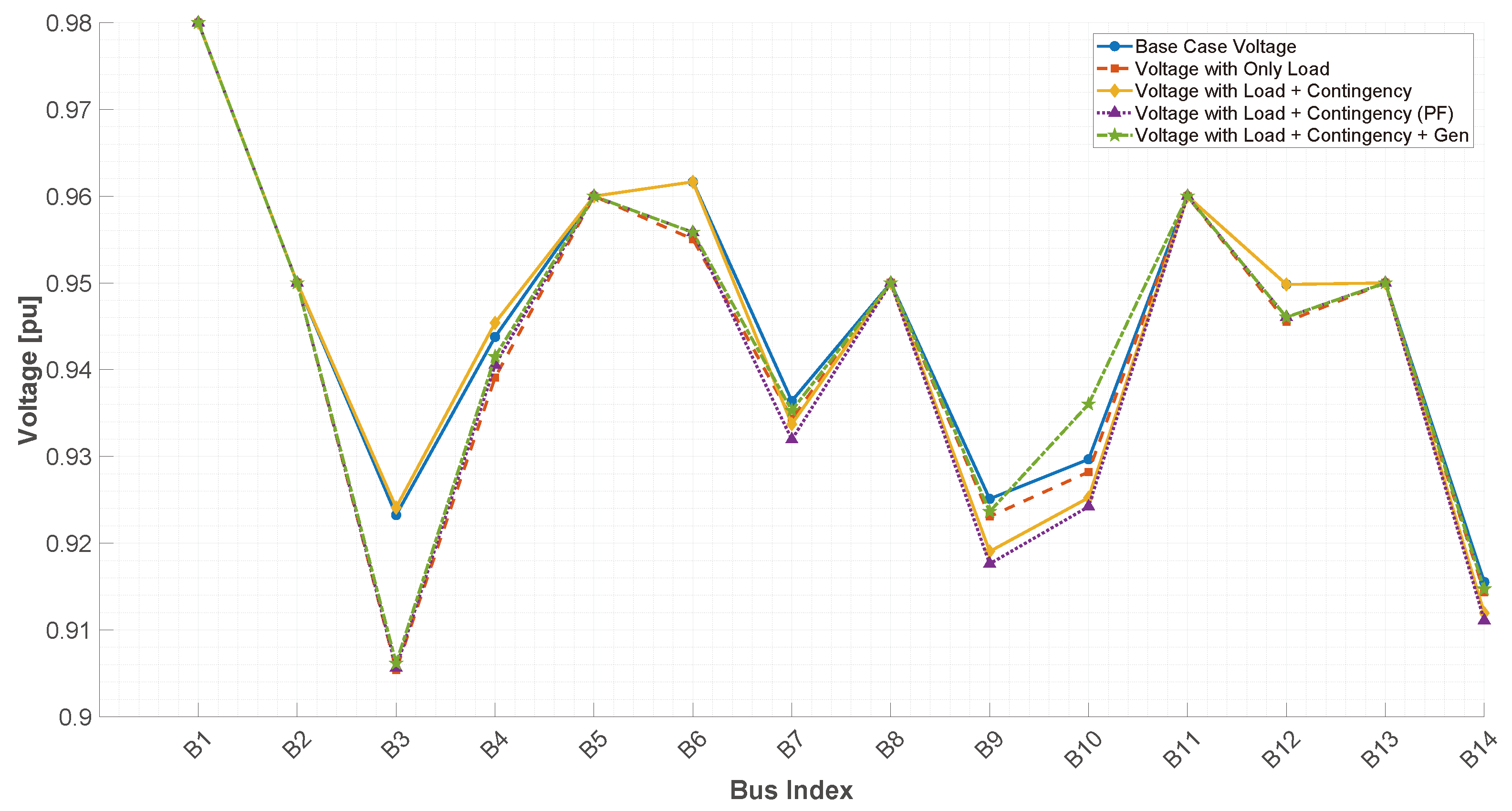
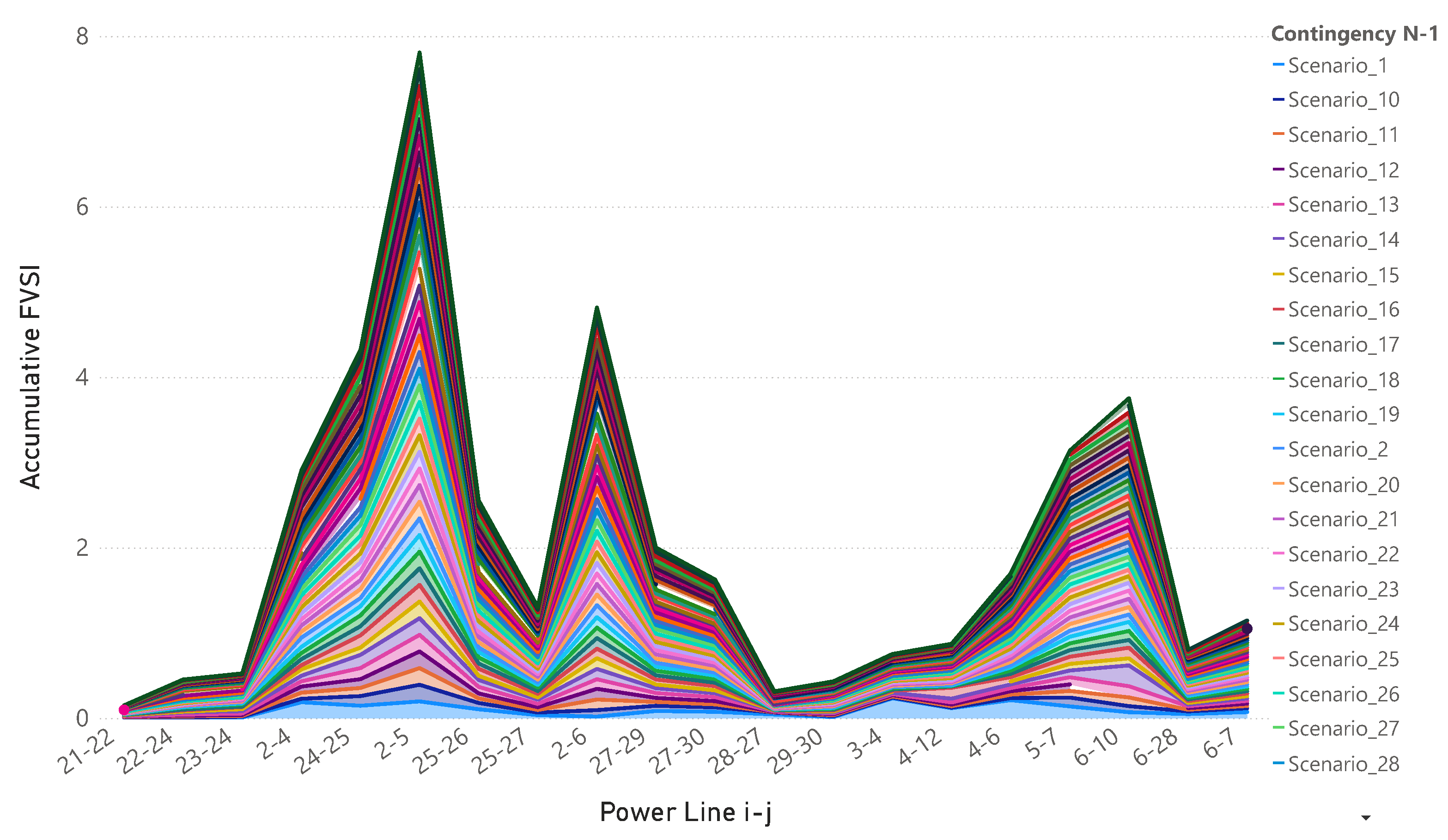
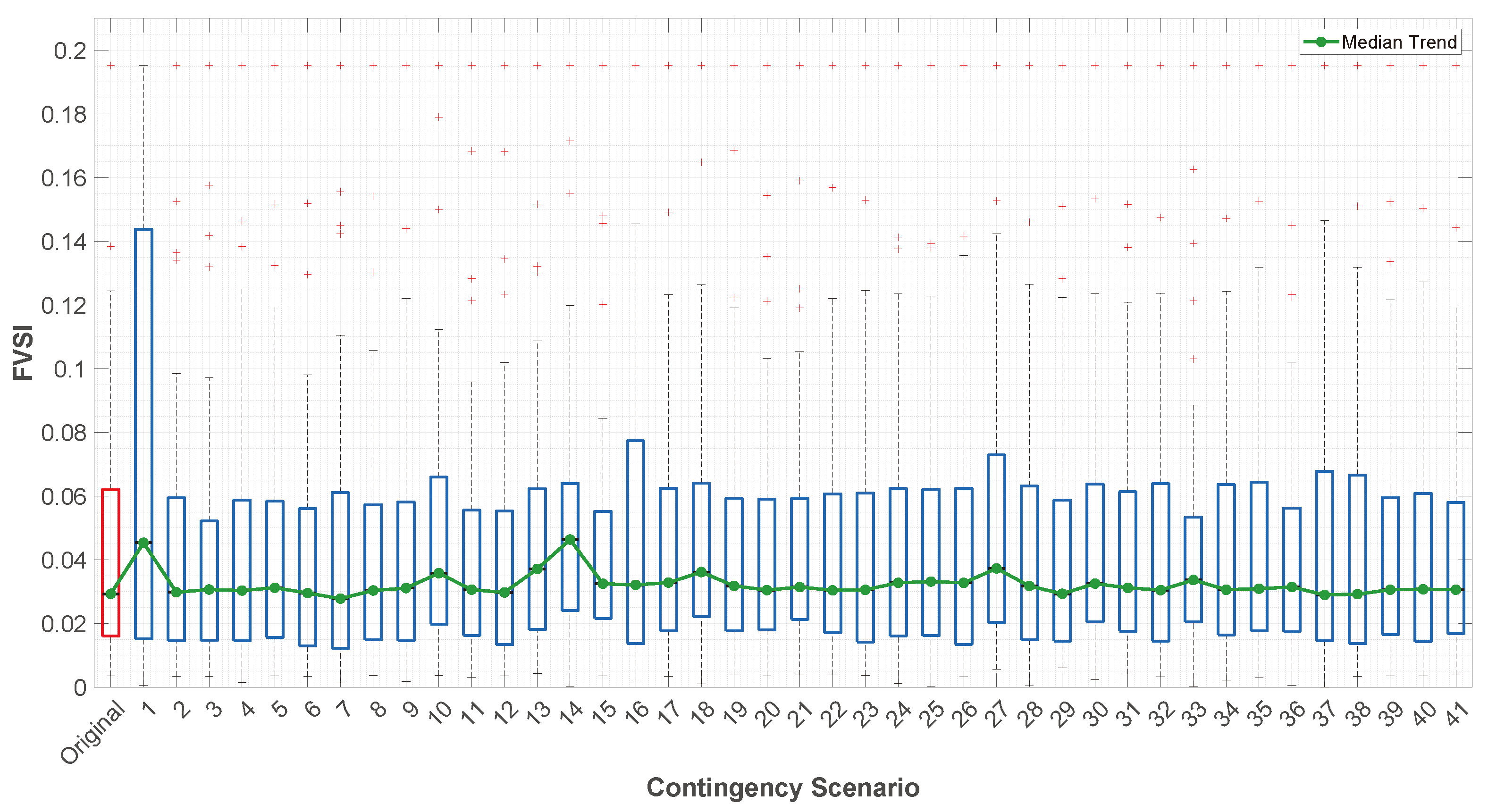
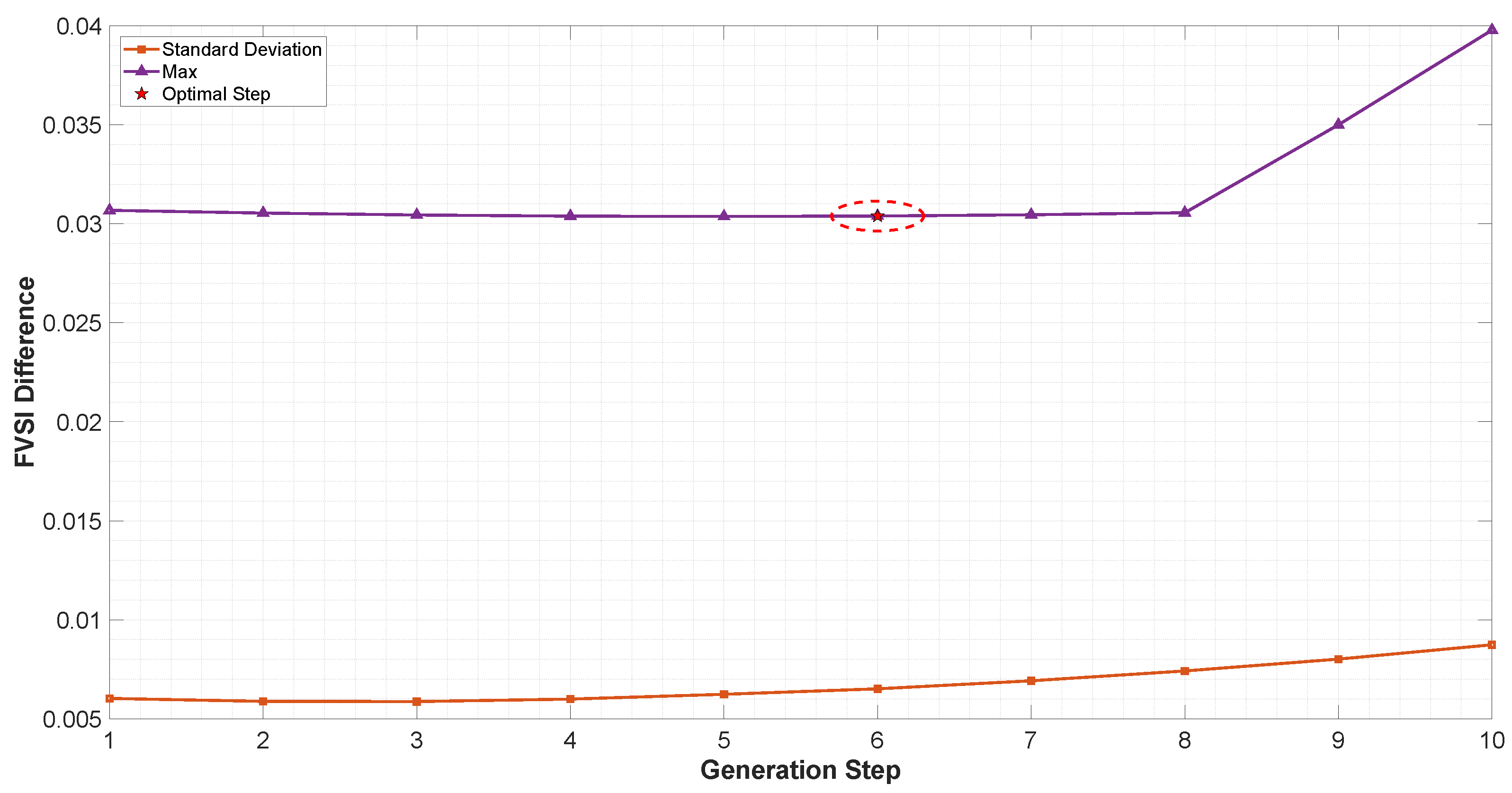
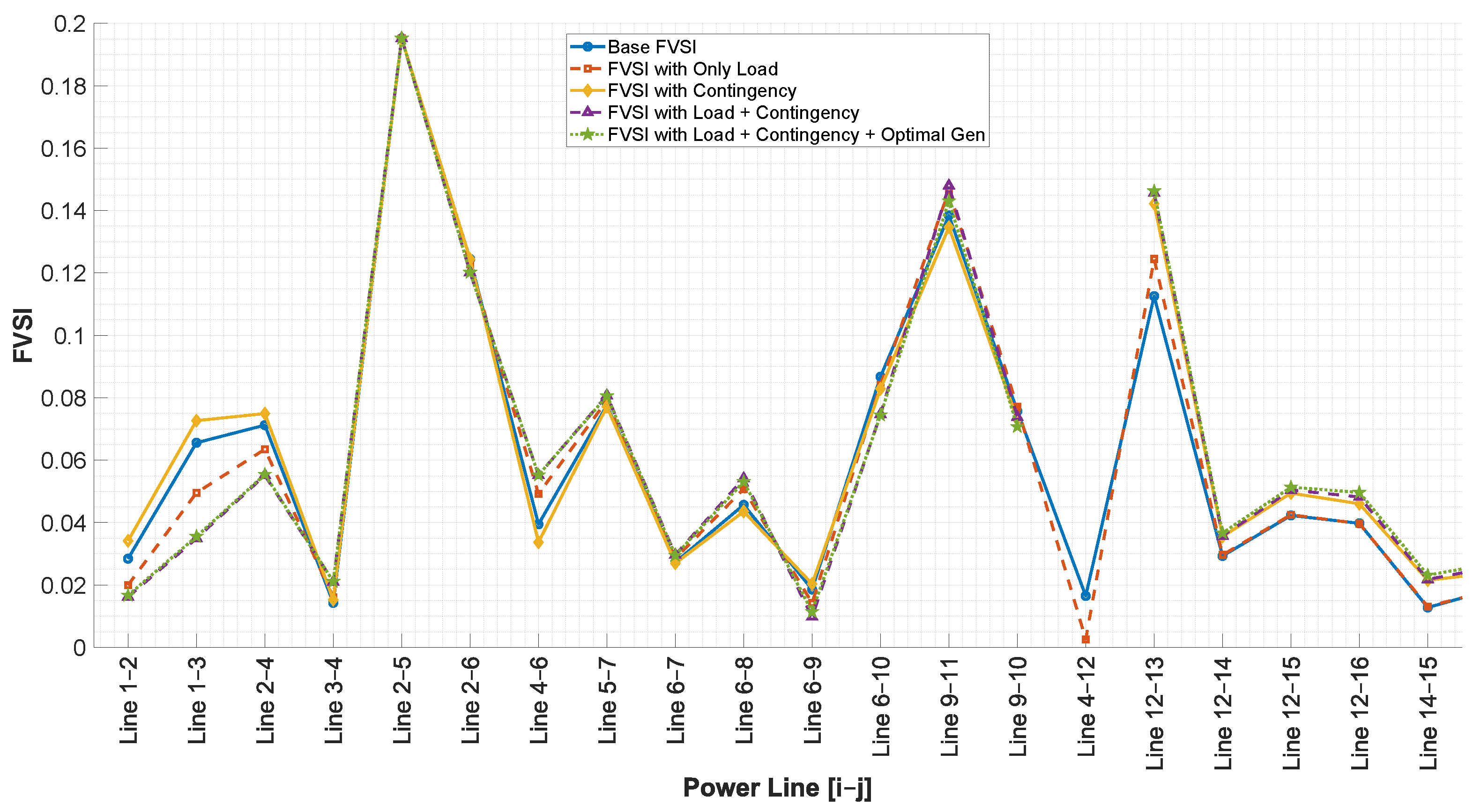
Though existing literature proposes heuristic approaches and optimization models for voltage profile enhancement, they mainly focus on FVSI monitoring, overlooking active decision-making for corrective action planning, such as determining the size and location of auxiliary generation units for contingency scenarios. While some heuristic approaches to optimize voltage profiles have been put forth, very few incorporate multi-scenario FVSI behavioral analysis into the optimization framework to create systematic decision structures.
In this regard, this work proposes a methodology where the analysis region is extended to include contingency and overload conditions to identify the critical lines and weak busbars and optimally position a single auxiliary distributed generator averted to the determined sensitive loading conditions. To the best of our knowledge, the difference between this study and others is that the proposal is tested using three IEEE systems (14, 30, and 118 busbars) and implements decision strategies derived from FVSI statistical inflection point analysis. The approach enhances voltage profiles while FVSI peak values almost halve, proving a cost-efficient scalable solution to operate electrical systems safely under critical conditions.
1.1. Literature Review
This section presents the most relevant works in the review of the state of the art that have used the Fast Voltage Stability Index (FVSI) to improve stability in electrical power systems by connecting active or reactive power.
Researches in [
1] propose the optimal allocation of solar PV and wind generators on the IEEE 33-bus system using the Fast Voltage Stability Index (FVSI) to identify the three most critical buses (buses 6, 3, and 28). Simulations in MATLAB R2023b. and MATPOWER 7.1 showed that allocating three solar PV units reduced power loss from 0.20 MW to 0.093 MW (a 53.5% reduction), while three wind generators reduced it further to 0.049 MW (75.5% reduction). The voltage at the weakest bus (bus 18) improved from 0.90 to 0.98 p.u. Wind generators outperformed solar PV due to their additional reactive power contribution. This paper presented an FVSI strategy to allocate generation while stabilizing voltage profiles.
The study presented in [
2] proposed a Genetic Algorithm (GA)-based method to determine the optimal placement of Thyristor-Controlled Series Capacitor (TCSC) devices to improve voltage profiles in power systems. Using the IEEE 30 bus-bar test system, the methodology identified weak buses via the Fast Voltage Stability Index (FVSI) and applied GA to minimize voltage deviation and enhance system stability. Results showed that optimal TCSC placement reduced real power loss by 15.67% and improved minimum bus voltage from 0.91 to 0.963 p.u. The approach outperformed traditional methods in both convergence speed and voltage profile enhancement.
Authors in [
3] propose a voltage control strategy for radial distribution systems (RDS) integrating electric vehicles (EVs) by leveraging reactive power procurement as an ancillary service. Using the IEEE 14 bus-bar radial system, the methodology involves optimal DG placement (Bus 9, 58 MW) via FVSI and voltage constraints, followed by iterative reactive power estimation to restore voltage profiles under EV loading scenarios. Three EV case studies show voltage dips (e.g., 0.9 p.u. at Bus 3) and successful compensation without grid support in Case 1. In Cases 2 and 3, additional reactive power was required. Results support cost-based reactive compensation to maintain stability amid EV-induced load stress.
Researches in [
4] propose a multi-objective optimization method using the Marine Predators Algorithm (MPA) for optimal allocation of hybrid electric vehicle charging stations (EVCS) and renewable distributed generators (RDGs) in the IEEE 69 bus-bar system. The objective functions minimize active power loss (APL) and improve voltage stability indices (VSI, FVSI, LPQ, PVSI). Results show that the EVCS-WTDG case outperformed all others, reducing active/reactive power losses by 96.27% and 91.51%, respectively, and improving minimum bus voltage to 0.991 p.u. The MPA algorithm consistently performed better than other algorithms like SMA, GWO, and POA.
The study presented by [
5] developed an Artificial Neural Network (ANN)-based method to estimate voltage stability indices (FVSI and LMN) using synthetic Phasor Measurement Unit (PMU) data for IEEE 14, 30, and 57 bus-bar systems. The methodology involved optimal PMU placement via Mixed Integer Linear Programming and ANN training using 70% of the dataset. The results showed strong prediction accuracy, with MSE values as low as 1.05 × 10
−6 (IEEE 30 LMN) and correlation coefficients R greater than 0.998. Critical lines were identified in IEEE 57 (with FVSI = 1.45 and LMN = 2.22). The ANN achieved results almost identical to Newton-Raphson-based calculations.
Paper presented in [
6] proposes an Arithmetic Optimization Algorithm (AOA) for optimal placement and sizing of DSTATCOM units in distribution systems, targeting minimization of active power loss (APL) and enhancement of voltage stability indices (VSI, FVSI, LPQ, PVSI). Applied to IEEE 33 and 69 bus-bar systems, results showed APL reductions of 32.24% and 33.09%, respectively, with three DSTATCOMs. Voltage profiles improved significantly, with minimum voltages raised to 0.9359 p.u. (33-bus) and 0.9275 p.u. (69-bus). The AOA converged in under 50 iterations, proving highly efficient and effective for enhancing voltage stability and minimizing losses in distribution networks.
Authors in [
7] compare two techniques—Power Stability Index (PSI) and Fast Voltage Stability Index (FVSI)—for optimal placement of Static VAR Compensator (SVC) devices in the IEEE 14-bus system. Using Newton-Raphson power flow in MI Power, buses 10 and 11 were identified as optimal candidates. SVC placement at bus 10 (FVSI) reduced active power loss by 20.45% and reactive loss by 52.9%, while placement at bus 11 (PSI) reduced active loss by 27.3% and reactive loss by 51.3%. Both techniques improved voltage profiles, with FVSI offering better overall system stability through reactive power flow reduction.
Researchers in [
8] introduce a new line stability index (NLSI-1) for predicting voltage collapse in power systems, applied to the 28-bus, 330 kV Nigerian National Grid. The index incorporates voltage angle differences and a switching logic to improve accuracy over conventional indices like FVSI and Lmn. The simulation results in the base and contingency scenarios show that NLSI-1 matches existing indices with an error of less than 2.4% and identifies Bus 16 as the weakest, with a critical line at 16–19 and a maximum reactive load of 139.5 MVAr. NLSI-1 proves computationally efficient and effective for real-time voltage stability assessment.
Research in [
9] introduced and evaluated a new voltage stability index, namely the Modern Stability Assessment Index (MSAI), comparing its effectiveness against established indices, including NCPI, MVSI, Lmn, FVSI, LQP, NLSI, NVSI, and VSLI. Numerical analyses were conducted using IEEE 30-bus, 57-bus, and 118-bus test systems under various loading scenarios, including heavy reactive power loads, combined active and reactive power loads, and
and
contingency conditions. The advantages and limitations of each evaluated index were thoroughly discussed, highlighting MSAI’s superior ability to approach the stability limit accurately (index value 1.00), thus reliably predicting voltage collapse points and identifying critical system lines. The numerical results provide valuable insights into each index’s performance, supporting the recommendation of MSAI as a highly suitable tool for effective and accurate monitoring of power system stability.
The study in [
10] proposed a Novel Collapse Prediction Index (NCPI) to accurately predict voltage collapse and rank contingencies in power systems. NCPI was tested against established indices such as Lmn, FVSI, LQP, NLSI, and VSLI through comprehensive numerical studies on IEEE 30-bus and IEEE 118-bus systems. The analysis included heavy active/reactive power loading scenarios and various
and
contingency conditions. Results indicated NCPI’s superior performance, accurately reaching stability limits (1.00) and reliably identifying critical lines and weak buses. NCPI provided more precise predictions and robust performance under diverse conditions, outperforming existing indices by considering critical assumptions overlooked by others.
The study by [
11] proposed a generalized voltage stability index to accurately evaluate voltage stability in both transmission and distribution (T&D) networks, considering their interactions and the effect of line length (long, medium, and short lines). Unlike existing indices, the proposed method assesses stability in T&D networks individually or combined, including the impacts of distributed generation (DG) and tap-changers. Numerical evaluations confirmed its superior performance over established indices, indicating it could effectively replace multiple indices currently required for different scenarios.
Researches in [
12] comprehensively reviewed voltage stability monitoring and improvement methods in renewable energy-integrated deregulated power systems. It evaluated traditional assessment techniques like continuation power flow (CPF), modal analysis, and voltage stability indices (VSIs), alongside emerging machine learning approaches, such as Artificial Neural Networks (ANN), Fuzzy Logic, Decision Trees, and Support Vector Machines. The research highlighted the critical roles of FACTS devices, including STATCOM, SVC, and UPFC, for enhancing voltage stability under renewable energy penetration.
The paper presented in [
13] analyzed voltage stability enhancement in distribution networks integrated with a squirrel cage induction generator (SCIG) wind turbine using voltage stability indices (FVSI and Lmn) and the continuation power flow (CPF) technique. The CPF method identified the optimal location for the wind generator, improving voltage profiles and system loadability from 1.7 to 1.72 p.u. Voltage stability indices determined the weakest lines and buses, guiding the proper placement of STATCOM and SSSC FACTS devices. Simulation results indicated that STATCOM performed better than SSSC in restoring voltage stability under three-phase fault conditions, providing quicker reactive power support and system stabilization.
The study by [
14] proposed a Modern Voltage Stability Index (MVSI) designed to accurately predict voltage collapse and estimate maximum loadability for identifying weak buses and critical lines in power systems. The MVSI partially considers line resistance, addressing inaccuracies from completely ignoring it, which can cause prediction errors exceeding 70%. The proposed index was evaluated against established indices like Lmn, FVSI, LQP, NLSI, VSLI, and NVSI on the IEEE 30-bus system under various load conditions (heavy active, reactive, and apparent power). Results demonstrated MVSI’s superior performance, consistently achieving values close to the stability limit (1.00).
Research in [
15] focuses on enhancing voltage stability in high wind energy penetration power systems. The authors identify weak nodes within the system and quantify their short-circuit ratio (SCR) requirements under voltage safety constraints. They propose a third-order dynamic model of a virtual synchronous generator (VSG) and design a virtual transient reactance to meet these SCR requirements. Simulations demonstrate that under the proposed control strategy, grid-forming wind turbines can effectively enhance voltage stability by optimizing transient reactance, thereby improving the system’s voltage support capabilities.
The paper presented in [
16] presented a congestion management method utilizing the Fast Voltage Stability Index (FVSI) for identifying congested lines, combined with Particle Swarm Optimization (PSO) to determine the optimal sizing and placement of FACTS devices. FVSI assessed voltage stability conditions across power lines, identifying critical lines when reactive loads at selected buses reached maximum loadability. Tests on the IEEE 30-bus system identified congestion on specific lines (e.g., line 20 at bus 14 with an FVSI of 0.9751). Subsequent optimal placement and sizing of FACTS devices significantly reduced system losses and improved voltage profiles, demonstrating the effectiveness of the proposed congestion management technique.
Authors in [
17] proposed a New Voltage Stability Pointer (NVSP) to assess line contingency ranking and identify vulnerable lines in power systems. The NVSP was derived from a simplified 2-bus network model and tested on the IEEE 14-bus system. Simulation results demonstrated NVSP’s capability to accurately rank line contingencies by incrementally varying reactive power loads until maximum loadability was reached. Compared with existing indices (Lmn, FVSI), NVSP provided enhanced accuracy and faster computational performance. The results indicated that NVSP effectively identified the most critical lines approaching voltage collapse (values near unity), demonstrating its practical application for real-time voltage stability monitoring and contingency planning.
Authors in [
18] improved the resilience of power grids against extreme events through strategic placement of distributed generation (DG). The research addressed voltage stability challenges caused by multiple line or generator outages using a two-stage method involving Voltage Stability Constrained Optimal Power Flow (VSCOPF) and Integer Programming (IP). Evaluations on the IEEE 118-bus system showed the method effectively maintained system stability under 40 extreme scenarios, requiring DG placements at buses 21, 44, 52, and 95. Specifically, single DG placement stabilized 32 scenarios, while paired DG placements were necessary for the remaining 8, demonstrating the strategy’s effectiveness in significantly reducing the likelihood of voltage instability.
The study presented by [
19] proposes a methodology to enhance voltage stability under
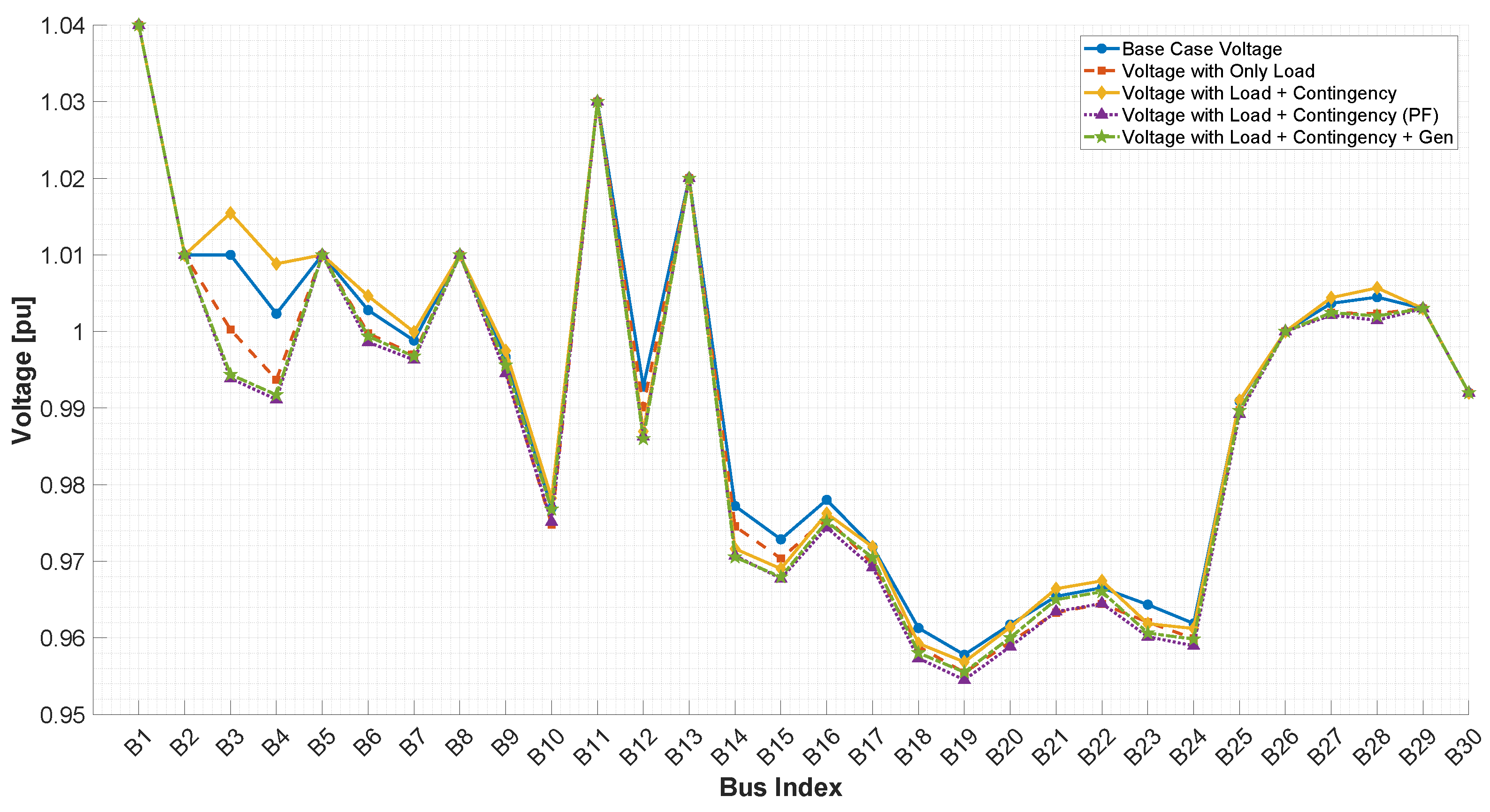
contingencies by optimally placing and sizing a static VAR compensator (SVC) based on the Fast Voltage Stability Index (FVSI). Using Newton-Raphson power flow and brute-force simulation across all line outages, the algorithm locates the most critical line. It determines the SVC size (5–100 Mvar range) needed to restore FVSI and voltage profiles. Results on IEEE 14, 30, and 118-bus systems showed 100% accuracy in restoring FVSI values to pre-contingency levels, with average FVSI reductions up to 20.33% and full voltage profile recovery using a single SVC installation. However, that work did not include generator-based optimization, statistical trend analysis, or load stress modeling, which are the focus of the present study.
Author in [
20] aimed to enhance stability assessment (SA) in new power systems (NPS) dominated by renewable energy and power electronics. The research presents a framework comparing traditional and deep learning-driven SA methods, analyzing over 100 studies. Results show that transient stability accounts for 77% of research, while voltage stability is only 17%, indicating a research gap. Time-series data analysis grew by 38%, emphasizing dynamic modeling needs. Deep learning methods, especially LSTM and CNN, outperform traditional SVM and DT in accuracy and scalability but face deployment challenges due to high communication and computational requirements. Future trends favor edge computing and spatial-temporal analysis.
The study proposed by [
21] developed an ANFIS-based predictive model to assess voltage stability using the Novel Line Stability Index (NLSI) and Critical Boundary Index (CBI). Input features included resistance, reactance, load levels, voltage, and angle differences. Tested on IEEE 14 and 118 bus systems, the model achieved a Mean Absolute Percentage Error (MAPE) as low as 0.361% for CBI and 3.15% for NLSI, with RRMSE below 2% for CBI. The correlation coefficient R exceeded 0.998 for CBI across all simulations, confirming superior predictive performance. Results validate CBI as a robust, accurate, real-time voltage stability monitoring tool.
Researches in [
22] reviews power system optimization approaches to mitigate voltage instability using Particle Swarm Optimization (PSO). It surveys over 30 voltage stability indices (e.g., FVSI, Lmn, LQP, NLSI), analyzing their pros and cons. The methodology highlights PSO’s application in optimal FACTS placement, reactive power compensation, and distributed generation sizing. Results from multiple IEEE test systems report significant voltage profile improvement and power loss reductions exceeding 20% in some cases. The paper emphasizes PSO’s fast convergence, robustness, and ease of implementation, positioning it as a key technique for voltage stability enhancement in modern power systems.
Despite the extensive use of the FVSI index in power system monitoring and the integration of optimization methods for voltage support, several gaps remain in the literature. Most studies focus on voltage profile enhancement without formulating statistical decision frameworks based on the behavior of FVSI across multiple contingency scenarios. Furthermore, many optimization methods rely on multi-generator or FACTS-based reinforcement, which, while effective, lack cost-efficiency and often neglect the implications of parameter uncertainties or variability in system behavior. Additionally, inflection point analysis as a strategy for determining optimal generator size and placement is rarely, if ever, explored in existing works.
This paper addresses the above gaps by introducing a novel data-driven methodology that combines FVSI frequency analysis, load stress simulations, and a statistical inflection point detection algorithm to determine the optimal sizing and placement of a single distributed generator (DG). The proposed approach enables low-cost voltage stability reinforcement in critical areas under contingencies and overload conditions. Unlike prior work, our method offers quantified FVSI improvements, voltage profile recovery, and a detailed comparative analysis across three benchmark test systems, validating its scalability and practical applicability.
To further highlight the novelty and practical relevance of this study, a direct comparison with representative traditional approaches is presented in
Table 1. This comparison highlights the methodological differences in the decision-making strategy, cost-effectiveness, robustness under contingencies, and scalability of the system. By contrasting key characteristics, it becomes evident how the proposed framework builds upon and extends existing literature through a statistically grounded and minimally intrusive reinforcement strategy.