Robust Data-Driven State of Health Estimation of Lithium-Ion Batteries Based on Reconstructed Signals
Abstract
1. Introduction
- Closed-form signal reconstruction: We present a non-iterative closed-form solution for the signal reconstruction of noisy measurements.
- Novel data-driven health indicators: We introduce five noise-resilient features derived from the reconstructed voltage and temperature discharge profiles.
- Robust data-driven state of health estimation: In this work, we use the Huber cost function to improve the accuracy of the regression model by reducing the impact of outliers, providing an alternative to removing outliers from the dataset.
2. Materials and Methods
2.1. Proposed Approach
- (1)
- Signal Reconstruction: This stage estimates a vector from noisy voltage and temperature profiles , where corresponds to the battery discharge voltage profile and represents the battery discharge temperature profile. The signal reconstruction employs the proposed closed-form, non-iterative mathematical expression formulated in Equation (8).
- (2)
- Feature Extraction: From the reconstructed voltage and temperature discharge profiles, five new data-driven health indicators are extracted, which are conditionally correlated with the battery aging process.
- (3)
- SoH Estimation: A Huber regression model was employed for SoH estimation, demonstrating robustness against outliers.
- Further details of each stage will be explained in the following sections.
2.1.1. Proposed Signal Reconstruction Stage
Signal Reconstruction Based on Tikhonov Regularization
Signal Reconstruction Based on LASSO Regularization
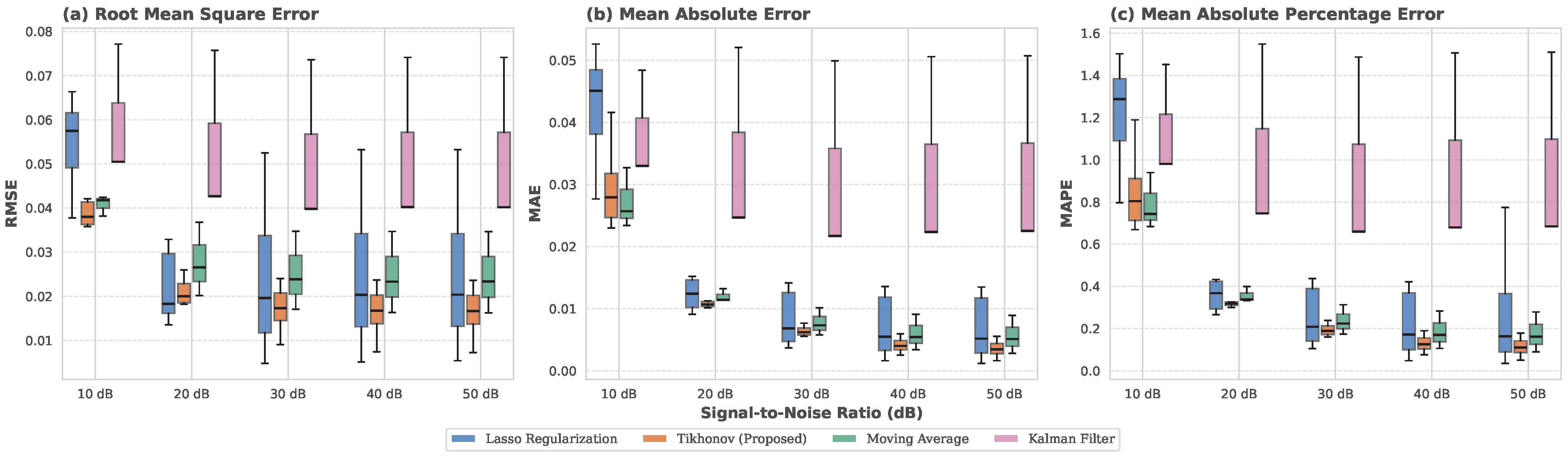
- For highly corrupted signals (SNR < 10 dB), larger values () are recommended to enhance noise suppression.
- For signals with minimal noise contamination (SNR > 10 dB), lower values () preserve original signal details.
2.1.2. Proposed Feature Extraction Stage
- Identification of discharge cycle.
- Extraction of voltage features.
- Extraction of temperature features.
- Minimum discharge voltage (): This is the lowest voltage reached during the discharge cycle (cutoff voltage). As a battery ages, its internal impedance increases due to factors such as lithium inventory loss and conductive degradation [40]. An increment in the impedance leads to a more pronounced voltage drop () during discharge [41]. According to the Shepherd model, the terminal voltage V at discharge time t can be modeled as follows [42]:where is the theoretical initial open-circuit voltage under specific working conditions, represents the internal ohmic resistance of the battery , i is the discharge current in amperes (A), assumed positive, and Q is the actual full capacity of the battery in ampere-hours (), in which eventually, with aging, its experiment capacity will fade. is the remaining capacity in the battery at discharge time t and K is the polarization resistance coefficient . Thus, the minimum discharge voltage is sensitive to internal resistance growth, and to the battery’s full capacity Q. In this work, we found that tracking the time to minimum discharge voltage can be used as a feature to estimate SoH in data-driven models.
- Time to minimum voltage (): This is the duration between the beginning of discharge and the minimum voltage. A healthy battery with full capacity can sustain the discharge current longer before reaching the voltage limit, whereas an aged battery with capacity fade will hit the minimum voltage sooner [43].
- Minimum temperature at the beginning of discharge (): The baseline temperature at the beginning of discharge, establishing a reference point.
- Maximum discharge temperature (): The peak temperature reached during discharge, reflecting internal resistance and exothermic reactions. As the battery degrades and its internal resistance increases, it produces more heat for the same discharge current, resulting in a higher peak temperature [44].
- Time elapsed between minimum and maximum temperature (): The aged battery’s temperature climbs to its maximum in a shorter time than in a new battery, which heats more slowly due to its lower internal resistance [45].
2.1.3. State of Health (SoH) Estimation
2.2. Datasets
2.2.1. NASA Data Overview
2.2.2. SNL Data Overview
2.3. Accuracy Evaluation Metrics
- Mean Absolute Percentage Error (MAPE) quantifies the relative error as a percentage, making it easy to interpret and compare across different datasets or models, and is defined as follows:Note that MAPE can be misleading when actual values are close to zero, as the percentage error becomes disproportionately large.
- Mean Absolute Error (MAE) measures the average magnitude of absolute deviations between the estimated and actual SoH values. Lower MAE values indicate higher prediction accuracy. Mathematically, it is expressed as follows:Note that MAE is less sensitive to outliers compared to metrics like Root Mean Squared Error (RMSE), as it does not square the error.
- Root Mean Square Error (RMSE) evaluates the standard deviation of prediction errors, heavily penalizing large deviations. RMSE is computed as follows:Note that RMSE is sensitive to outliers.where is the estimated SoH, is the ground truth SoH, and n is the total number of SoH observations.
3. Numerical Results and Discussion
3.1. Experimental Setup
3.2. Sensitivity Analysis of Signal Reconstruction
3.3. Sensitivity and Correlation Analysis of Proposed Features
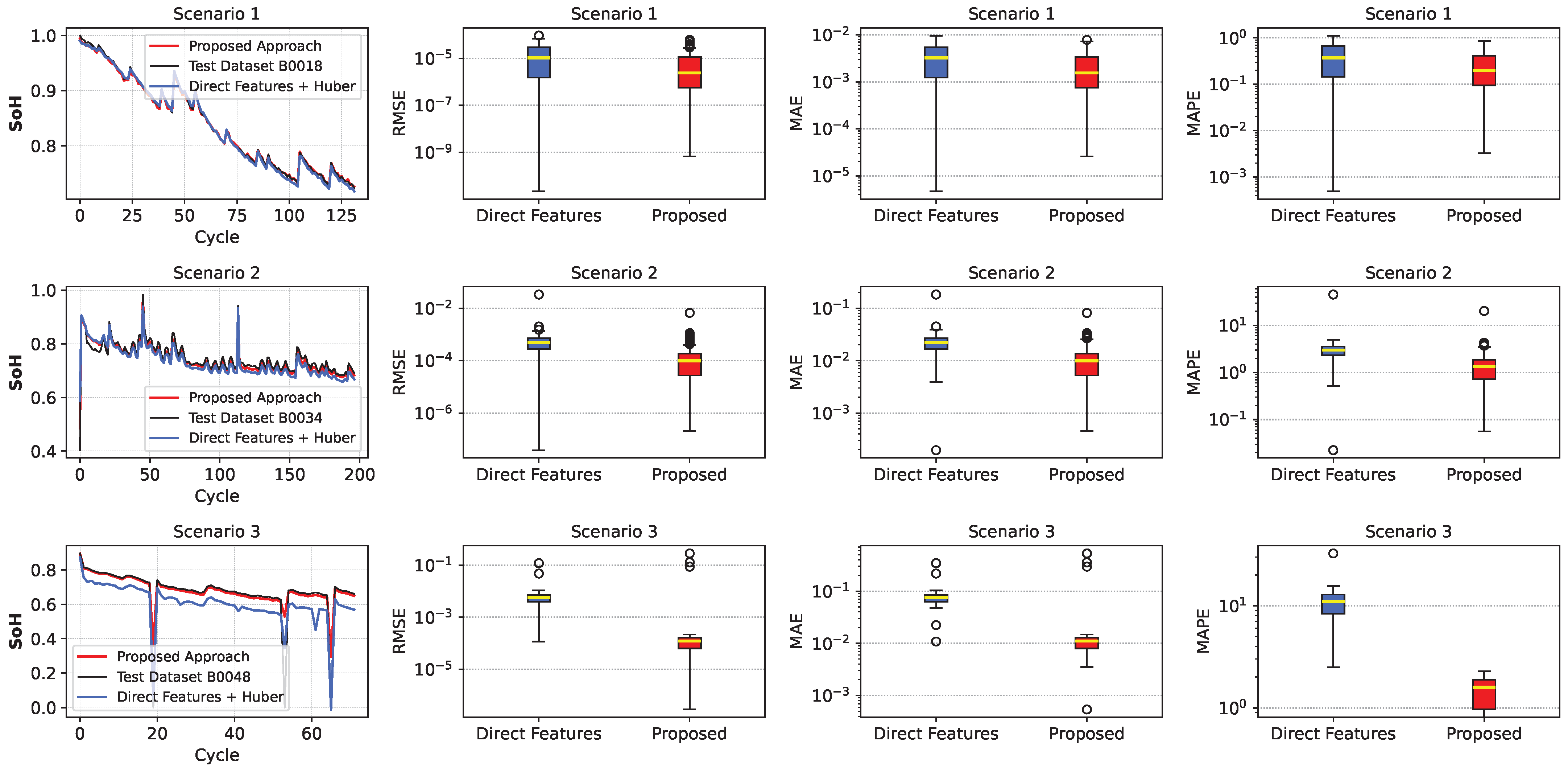
3.4. Comparison of Feature Selection: Direct Features vs Proposed
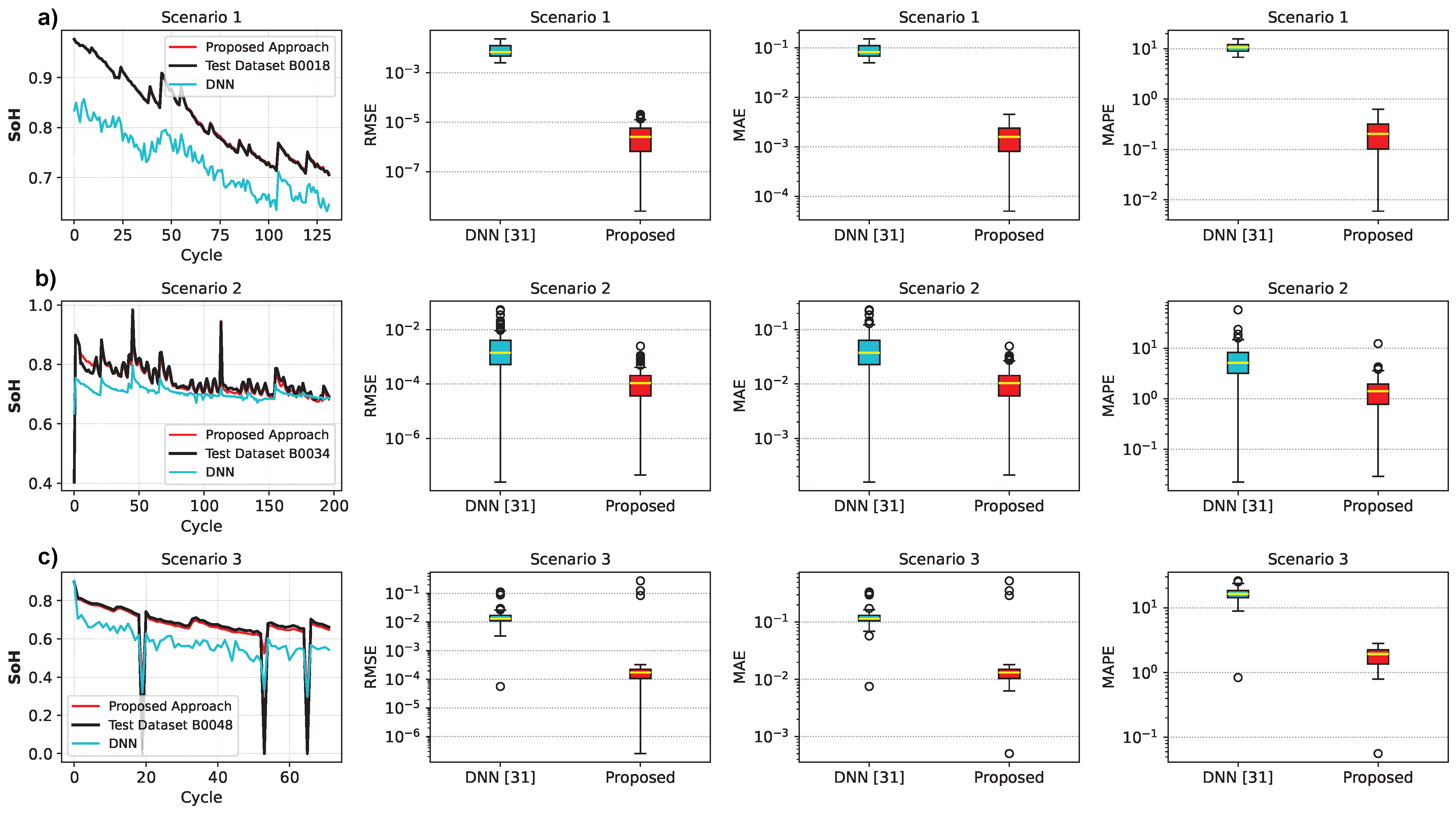
3.5. Data-Driven Robustness Comparison
3.5.1. DNN
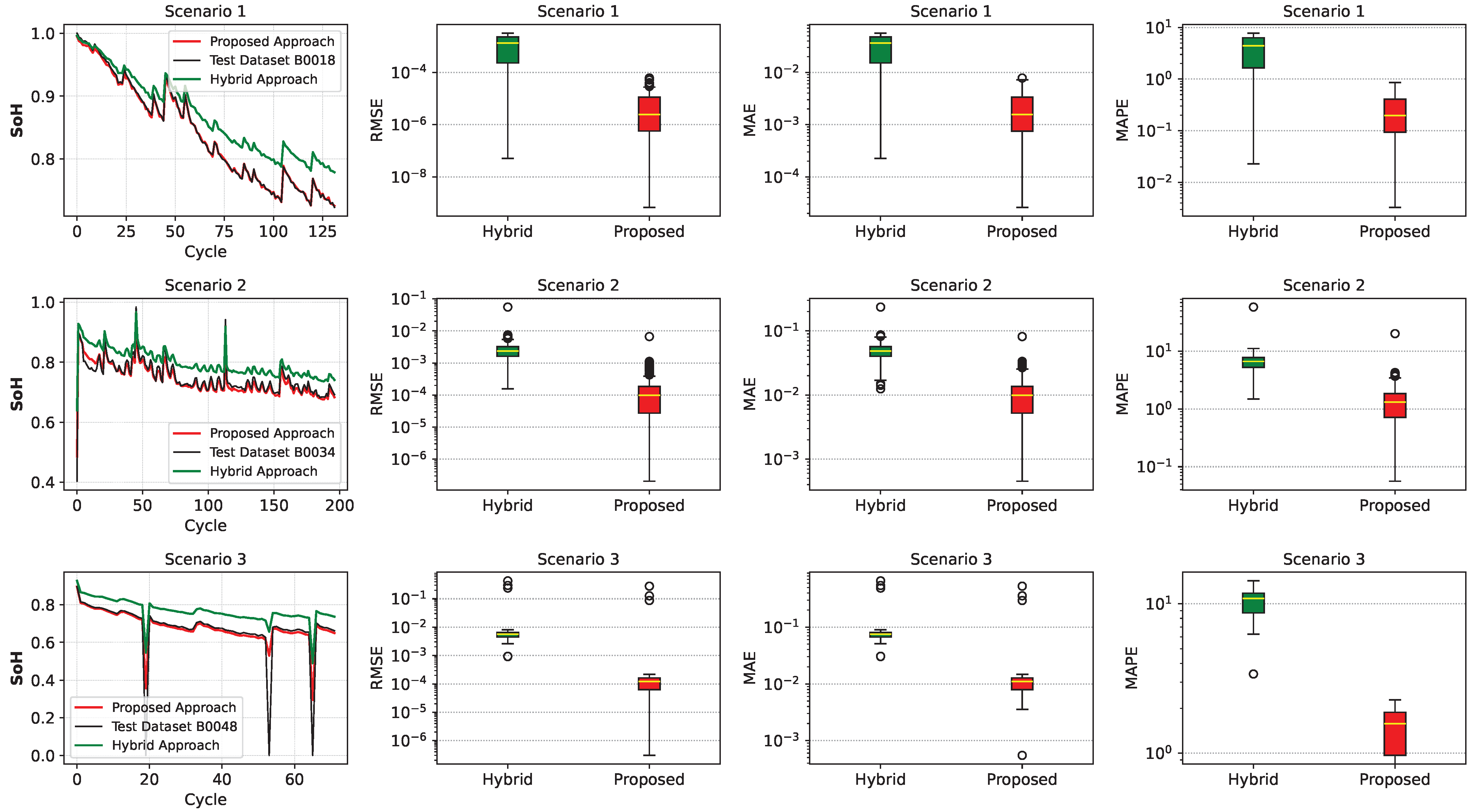
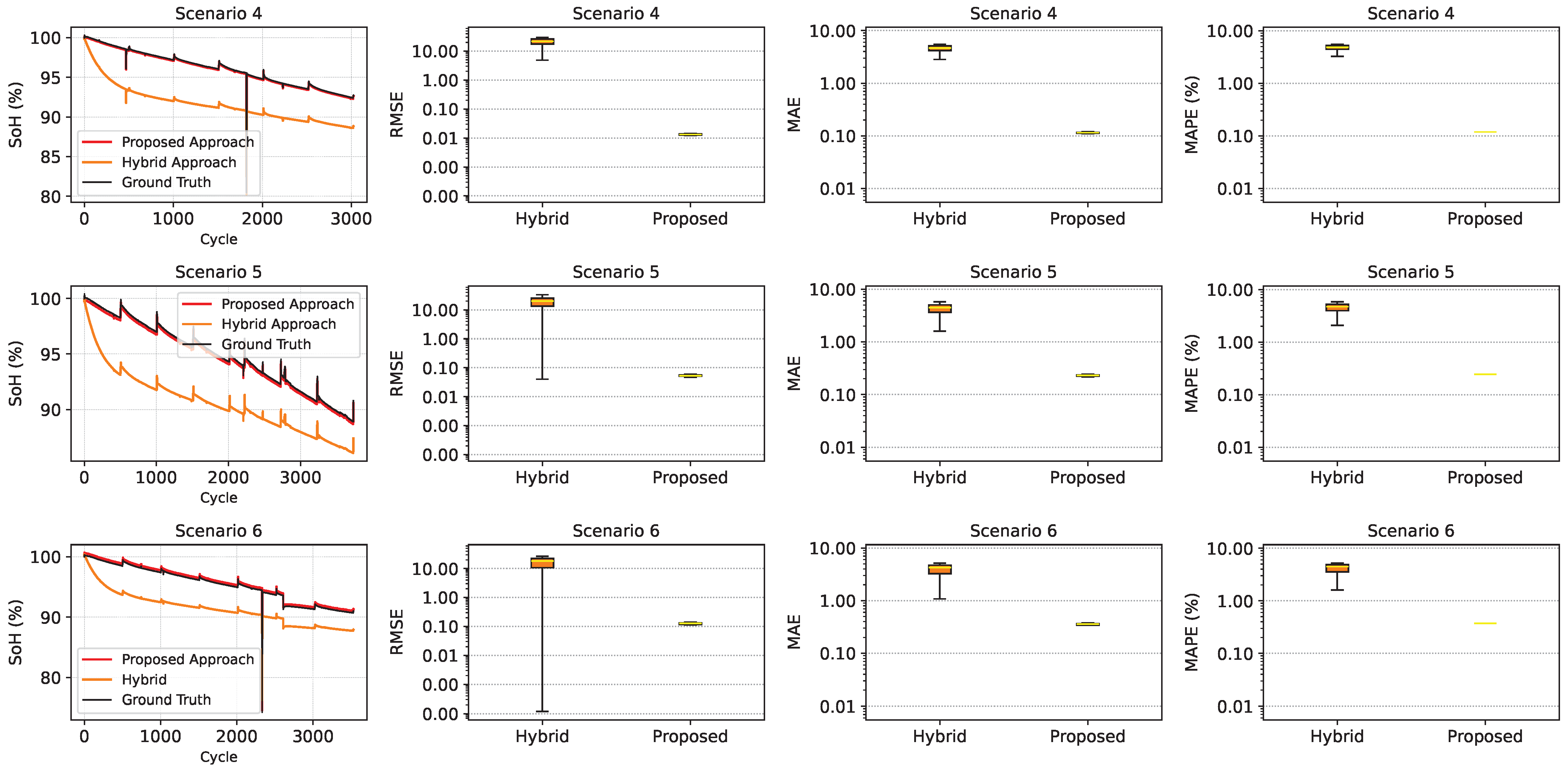
3.6. Comparison with Hybrid Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Greim, P.; Solomon, A.; Breyer, C. Assessment of lithium criticality in the global energy transition and addressing policy gaps in transportation. Nat. Commun. 2020, 11, 4570. [Google Scholar] [CrossRef]
- Lagrange, A.; de Simón-Martín, M.; González-Martínez, A.; Bracco, S.; Rosales-Asensio, E. Sustainable microgrids with energy storage as a means to increase power resilience in critical facilities: An application to a hospital. Int. J. Electr. Power Energy Syst. 2020, 119, 105865. [Google Scholar] [CrossRef]
- Department of Energy. DOE Global Energy Storage Database, 2023. Available online: https://gesdb.sandia.gov/ (accessed on 8 September 2023).
- Stroe, D.I.; Schaltz, E. Lithium-ion battery state-of-health estimation using the incremental capacity analysis technique. IEEE Trans. Ind. Appl. 2019, 56, 678–685. [Google Scholar] [CrossRef]
- Kallel, A.Y.; Petrychenko, V.; Kanoun, O. State-of-health of Li-ion battery estimation based on the efficiency of the charge transfer extracted from impedance spectra. Appl. Sci. 2022, 12, 885. [Google Scholar] [CrossRef]
- Oji, T.; Zhou, Y.; Ci, S.; Kang, F.; Chen, X.; Liu, X. Data-driven methods for battery soh estimation: Survey and a critical analysis. IEEE Access 2021, 9, 126903–126916. [Google Scholar] [CrossRef]
- John, J.; Kudva, G.; Jayalakshmi, N. Secondary life of electric vehicle batteries: Degradation, state of health estimation using incremental capacity analysis, applications and challenges. IEEE Access 2024, 12, 63735–63753. [Google Scholar] [CrossRef]
- Gharebaghi, M.; Rezaei, O.; Li, C.; Wang, Z.; Tang, Y. A Survey on Using Second-Life Batteries in Stationary Energy Storage Applications. Energies 2024, 18, 42. [Google Scholar] [CrossRef]
- Zhang, J.; Li, K. State-of-Health Estimation for Lithium-Ion Batteries in Hybrid Electric Vehicles—A Review. Energies 2024, 17, 5753. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Y.; Lai, X. Data Science-Based Full-Lifespan Management of Lithium-Ion Battery: Manufacturing, Operation and Reutilization; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Tian, J.; Xiong, R.; Shen, W. A review on state of health estimation for lithium ion batteries in photovoltaic systems. ETransportation 2019, 2, 100028. [Google Scholar] [CrossRef]
- Wilhelm, J.; Seidlmayer, S.; Keil, P.; Schuster, J.; Kriele, A.; Gilles, R.; Jossen, A. Cycling capacity recovery effect: A coulombic efficiency and post-mortem study. J. Power Sources 2017, 365, 327–338. [Google Scholar] [CrossRef]
- Bayoumi, E.H.; De Santis, M.; Awad, H. A Brief Overview of Modeling Estimation of State of Health for an Electric Vehicle’s Li-Ion Batteries. World Electr. Veh. J. 2025, 16, 73. [Google Scholar] [CrossRef]
- Andersson, M.; Streb, M.; Ko, J.Y.; Klass, V.L.; Klett, M.; Ekström, H.; Johansson, M.; Lindbergh, G. Parametrization of physics-based battery models from input–output data: A review of methodology and current research. J. Power Sources 2022, 521, 230859. [Google Scholar] [CrossRef]
- Iurilli, P.; Brivio, C.; Carrillo, R.E.; Wood, V. Physics-Based SoH Estimation for Li-Ion Cells. Batteries 2022, 8, 204. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Zhang, Y.; Wang, L.; Wang, K. Summary of health-state estimation of lithium-ion batteries based on electrochemical impedance spectroscopy. Energies 2023, 16, 5682. [Google Scholar] [CrossRef]
- Tran, M.K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Velasco-Arellano, H.; Castillo-Magallanes, N.; Visairo-Cruz, N.; Núñez-Gutiérrez, C.A.; Lázaro, I. Parametric Correlation Analysis between Equivalent Electric Circuit Model and Mechanistic Model Interpretation for Battery Internal Aging. World Electr. Veh. J. 2024, 15, 291. [Google Scholar] [CrossRef]
- Lu, J.; Wu, T.; Amine, K. State-of-the-art characterization techniques for advanced lithium-ion batteries. Nat. Energy 2017, 2, 1–13. [Google Scholar] [CrossRef]
- Ren, Z.; Du, C. A review of machine learning state-of-charge and state-of-health estimation algorithms for lithium-ion batteries. Energy Rep. 2023, 9, 2993–3021. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, D.; Du, J.; Sun, H.; Li, L.; Wang, L.; Wang, K. A review of SOH prediction of Li-ion batteries based on data-driven algorithms. Energies 2023, 16, 3167. [Google Scholar] [CrossRef]
- Gong, J.; Xu, B.; Chen, F.; Zhou, G. Predictive Modeling for Electric Vehicle Battery State of Health: A Comprehensive Literature Review. Energies 2025, 18, 337. [Google Scholar] [CrossRef]
- Nuroldayeva, G.; Serik, Y.; Adair, D.; Uzakbaiuly, B.; Bakenov, Z. State of health estimation methods for lithium-ion batteries. Int. J. Energy Res. 2023, 2023, 4297545. [Google Scholar] [CrossRef]
- Alamin, K.S.S.; Daghero, F.; Pollo, G.; Pagliari, D.J.; Chen, Y.; Macii, E.; Poncino, M.; Vinco, S. Model-Driven Dataset Generation for Data-Driven Battery SOH Models. In Proceedings of the 2023 IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED), Vienna, Austria, 7–8 August 2023; pp. 1–6. [Google Scholar]
- Bamati, S.; Chaoui, H. Developing an online data-driven state of health estimation of lithium-ion batteries under random sensor measurement unavailability. IEEE Trans. Transp. Electrif. 2022, 9, 1128–1141. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Meng, X.; Zhang, L.; Li, X.; Zhang, W. A Novel Feature Engineering-Based SOH Estimation Method for Lithium-Ion Battery with Downgraded Laboratory Data. Batteries 2024, 10, 139. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, R.; Liu, X.; Zhang, C.; Sun, G.; Zhou, Y.; Yang, Z.; Liu, X.; Chen, S.; Dong, X.; et al. Advanced State-of-Health Estimation for Lithium-Ion Batteries Using Multi-Feature Fusion and KAN-LSTM Hybrid Model. Batteries 2024, 10, 433. [Google Scholar] [CrossRef]
- Lu, X.; Qiu, J.; Lei, G.; Zhu, J. Degradation mode knowledge transfer method for LFP batteries. IEEE Trans. Transp. Electrif. 2022, 9, 1142–1152. [Google Scholar] [CrossRef]
- Lu, X.; Qiu, J.; Lei, G.; Zhu, J. State of health estimation of lithium iron phosphate batteries based on degradation knowledge transfer learning. IEEE Trans. Transp. Electrif. 2023, 9, 4692–4703. [Google Scholar] [CrossRef]
- Alhazmi, R.M. State of health prediction in electric vehicle batteries using a deep learning model. World Electr. Veh. J. 2024, 15, 385. [Google Scholar] [CrossRef]
- Driscoll, L.; de la Torre, S.; Gomez-Ruiz, J.A. Feature-based lithium-ion battery state of health estimation with artificial neural networks. J. Energy Storage 2022, 50, 104584. [Google Scholar] [CrossRef]
- Khumprom, P.; Yodo, N. A data-driven predictive prognostic model for lithium-ion batteries based on a deep learning algorithm. Energies 2019, 12, 660. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, C.; Gao, X.; Tian, S. State of health estimation for lithium-ion battery based on the coupling-loop nonlinear autoregressive with exogenous inputs neural network. Electrochim. Acta 2021, 393, 139047. [Google Scholar] [CrossRef]
- Fan, Y.; Xiao, F.; Li, C.; Yang, G.; Tang, X. A novel deep learning framework for state of health estimation of lithium-ion battery. J. Energy Storage 2020, 32, 101741. [Google Scholar] [CrossRef]
- Zhou, D.; Li, Z.; Zhu, J.; Zhang, H.; Hou, L. State of health monitoring and remaining useful life prediction of lithium-ion batteries based on temporal convolutional network. IEEE Access 2020, 8, 53307–53320. [Google Scholar] [CrossRef]
- Acurio, B.A.A.; Barragán, D.E.C.; Amezquita, J.C.L.; Rider, M.J.; Da Silva, L.C.P. Design and Implementation of a Machine Learning State Estimation Model for Unobservable Microgrids. IEEE Access 2022, 10, 123387–123398. [Google Scholar] [CrossRef]
- Rufino Júnior, C.A.; Sanseverino, E.R.; Gallo, P.; Amaral, M.M.; Koch, D.; Kotak, Y.; Diel, S.; Walter, G.; Schweiger, H.G.; Zanin, H. Unraveling the degradation mechanisms of lithium-ion batteries. Energies 2024, 17, 3372. [Google Scholar] [CrossRef]
- Wei, Y.; Yao, Y.; Pang, K.; Xu, C.; Han, X.; Lu, L.; Li, Y.; Qin, Y.; Zheng, Y.; Wang, H.; et al. A comprehensive study of degradation characteristics and mechanisms of commercial Li (NiMnCo) O2 EV batteries under vehicle-to-grid (V2G) services. Batteries 2022, 8, 188. [Google Scholar] [CrossRef]
- Yagci, M.C.; Feldmann, T.; Bollin, E.; Schmidt, M.; Bessler, W.G. Aging characteristics of stationary lithium-ion battery systems with serial and parallel cell configurations. Energies 2022, 15, 3922. [Google Scholar] [CrossRef]
- Edge, J.S.; O’Kane, S.; Prosser, R.; Kirkaldy, N.D.; Patel, A.N.; Hales, A.; Ghosh, A.; Ai, W.; Chen, J.; Yang, J.; et al. Lithium ion battery degradation: What you need to know. Phys. Chem. Chem. Phys. 2021, 23, 8200–8221. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Z.; Xie, S. Influence of Overdischarge Depth on the Aging and Thermal Safety of LiNi0.5Co0.2Mn0.3O2/Graphite Cells. Battery Energy 2025, e70008. [Google Scholar] [CrossRef]
- Li, S.; Ke, B. Study of battery modeling using mathematical and circuit oriented approaches. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011; pp. 1–8. [Google Scholar]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Shen, W.; Wang, N.; Zhang, J.; Wang, F.; Zhang, G. Heat generation and degradation mechanism of lithium-ion batteries during high-temperature aging. ACS Omega 2022, 7, 44733–44742. [Google Scholar] [CrossRef]
- Huang, R.; Xu, Y.; Wu, Q.; Chen, J.; Chen, F.; Yu, X. Simulation study on heat generation characteristics of lithium-ion battery aging process. Electronics 2023, 12, 1444. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, Y.; Zhao, K.; Tian, Y. A comprehensive survey of loss functions in machine learning. Ann. Data Sci. 2020, 9, 187–212. [Google Scholar] [CrossRef]
- Mangasarian, O.L.; Musicant, D.R. Robust linear and support vector regression. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 950–955. [Google Scholar] [CrossRef]
- Huber, P.J. Robust estimation of a location parameter. In Breakthroughs in Statistics: Methodology and Distribution; Springer: Berlin/Heidelberg, Germany, 1992; pp. 492–518. [Google Scholar]
- Saha, B.; Goebel, K. Battery data set. In NASA AMES Prognostics Data Repository; NASA Ames Research Center: Moffett Field, CA, USA, 2007. Available online: https://www.nasa.gov/intelligent-systems-division/discovery-and-systems-health/pcoe/pcoe-data-set-repository/ (accessed on 1 January 2023).
- Preger, Y.; Barkholtz, H.M.; Fresquez, A.; Campbell, D.L.; Juba, B.W.; Romàn-Kustas, J.; Ferreira, S.R.; Chalamala, B. Degradation of commercial lithium-ion cells as a function of chemistry and cycling conditions. J. Electrochem. Soc. 2020, 167, 120532. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Battery Archive. Battery Archive, 2025. Available online: https://www.batteryarchive.org/ (accessed on 6 March 2025).
- Lipu, M.S.H.; Mamun, A.A.; Ansari, S.; Miah, M.S.; Hasan, K.; Meraj, S.T.; Abdolrasol, M.G.; Rahman, T.; Maruf, M.H.; Sarker, M.R.; et al. Battery management, key technologies, methods, issues, and future trends of electric vehicles: A pathway toward achieving sustainable development goals. Batteries 2022, 8, 119. [Google Scholar] [CrossRef]
- Python Software Foundation. Python Programming Language; Python Software Foundation: Wilmington, DE, USA, 1991–2024; Available online: https://www.python.org/ (accessed on 1 January 2023).
- Lucu, M.; Martinez-Laserna, E.; Gandiaga, I.; Camblong, H. A critical review on self-adaptive Li-ion battery ageing models. J. Power Sources 2018, 401, 85–101. [Google Scholar] [CrossRef]
- Engelberg, S. Implementing Moving Average Filters Using Recursion [Tips & Tricks]. IEEE Signal Process. Mag. 2023, 40, 78–80. [Google Scholar]
- Kim, Y.; Bang, H. Introduction to Kalman filter and its applications. In Introduction and Implementations of the Kalman Filter; IntechOpen: Rijeka, Croatia, 2018. [Google Scholar]
- Jiang, N.; Zhang, J.; Jiang, W.; Ren, Y.; Lin, J.; Khoo, E.; Song, Z. Driving behavior-guided battery health monitoring for electric vehicles using extreme learning machine. Appl. Energy 2024, 364, 123122. [Google Scholar] [CrossRef]
- Lin, M.; Zeng, X.; Wu, J. State of health estimation of lithium-ion battery based on an adaptive tunable hybrid radial basis function network. J. Power Sources 2021, 504, 230063. [Google Scholar] [CrossRef]
- Deng, L.M.; Hsu, Y.C.; Li, H.X. An improved model for remaining useful life prediction on capacity degradation and regeneration of lithium-ion battery. In Proceedings of the Annual Conference of the PHM Society, Jeju, Republic of Korea, 2–5 October 2017; Volume 9. [Google Scholar]
- Liang, J.; Liu, H.; Xiao, N.C. A hybrid approach based on deep neural network and double exponential model for remaining useful life prediction. Expert Syst. Appl. 2024, 249, 123563. [Google Scholar] [CrossRef]

| Data-Driven Method | Number of Input Features | Robustness | Trainable Parameters | Performance Metric |
|---|---|---|---|---|
| Proposed Approach | 5 proposed features based on signal reconstruction | Our proposed signal reconstruction approach can handle noise and outliers in the measurement data | 6 polynomial parameters trained with Huber cost function | RMSE = , MAE = , MAPE = 1% |
| Deep Neural Network [31] | 3 (Direct features) | The reported approach requires preparing the data by removing significant outliers manually | 2 hidden layers with 30 and 15 neurons, respectively, as well as Sigmoid and Tanh activation functions | RMSE = 1.9 ×, MAPE = 1.39% |
| Deep Neural Network [32] | 6 (Direct features) | The paper does not discuss a dedicated noise handling mechanism | 217 trainable parameters | RMSE = 0.004758%, MAE = 0.534% |
| Nonlinear Autoregressive Exogenous Neural Network [33] | 8 (Model-based features) | The paper does not discuss a dedicated noise handling mechanism | Hidden neurons = 50, Feedback delays = 8 | MAE = 0.72%, MaxE = 4.69% |
| Gated Recurrent Unit Network [34] | 3 (Direct features) | Gaussian noise injection with a mean of 0 and a standard deviation of 1–2% into the voltage, current, and temperature measurements (works on less noise-corrupted signals) | Hidden neurons = 256 (GRU), convolution number = 64, size of each convolution layer 32 × 1 | MAE = 1.03%, MaxE = 4.11% |
| Convolutional Neural Network [35] | 1 (Preprocessed features) | The reported approach is sensitive to noise and outliers | Number of convolution kernels = 256, size of the kernel = 3 × 1 | RMSE = 1.1%, MAE = 0.9% |
| Battery ID | End Voltage (V) | Ambient Temperature (°C) | Nominal Capacity (Ah) | Discharge Current (A) | End of Life Criteria (Ah) | No. of Cycles |
|---|---|---|---|---|---|---|
| B0005 | 2.7 | 4 to 40 | 2 | 2 | 1.4 | 168 |
| B0007 | 2.2 | 4 to 40 | 2 | 2 | 1.4 | 168 |
| B0018 | 2.5 | 4 to 40 | 2 | 2 | 1.4 | 132 |
| B0033 | 2.0 | 24 | 2 | 4 | 1.6 | 198 |
| B0034 | 2.2 | 24 | 2 | 4 | 1.6 | 198 |
| B0046 | 2.2 | 4 | 2 | 1 | 1.4 | 72 |
| B0047 | 2.5 | 4 | 2 | 1 | 1.4 | 72 |
| B0048 | 2.7 | 4 | 2 | 1 | 1.4 | 72 |
| Cathode Chemistry | ||
|---|---|---|
| NCA | NMC | |
| Manufacturer | Panasonic | LG Chem |
| Manufacturer City—Country | Osaka—Japan | Seoul—Republic of Korea |
| Manufacturer PN | NCR18650B | 18650HG2 |
| Battery type | 18650 | 18650 |
| Nominal capacity [Ah] | 3.2 | 3 |
| Nominal voltage [V] | 3.6 | 3.6 |
| Voltage range [V] | 2.5–4.2 | 2.0–4.2 |
| Max discharge current [A] | 6 | 20 |
| Temperature range [°C] | 0–45 | −5–50 |
| Charge C-rate | 0.5C | 0.5C |
| Discharge C-rate | 0.5C/1C/2C | 0.5C/1C/2C |
| Test temperature [°C] | 15/25/35 | 15/25/35 |
| Depth of discharge | 0–100% | 0–100% |
| Metrics | Method | SNR (dB) | Average | ||||
|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | |||
| RMSE | Tikhonov | 0.0404 | 0.0210 | 0.0172 | 0.0165 | 0.0164 | 0.0223 |
| MA | 0.0408 | 0.0278 | 0.0252 | 0.0248 | 0.0248 | 0.0287 | |
| Lasso | 0.0547 | 0.0248 | 0.0240 | 0.0247 | 0.0248 | 0.0306 | |
| Kalman | 0.0594 | 0.0537 | 0.0511 | 0.0515 | 0.0515 | 0.0534 | |
| MAE | Tikhonov | 0.0295 | 0.0112 | 0.0064 | 0.0041 | 0.0035 | 0.0109 |
| MA | 0.0273 | 0.0120 | 0.0077 | 0.0060 | 0.0056 | 0.0117 | |
| Lasso | 0.0427 | 0.0144 | 0.0104 | 0.0091 | 0.0088 | 0.0171 | |
| Kalman | 0.0381 | 0.0338 | 0.0311 | 0.0318 | 0.0319 | 0.0334 | |
| MAPE (%) | Tikhonov | 0.8497 | 0.3295 | 0.1940 | 0.1299 | 0.1133 | 0.3233 |
| MA | 0.7894 | 0.3566 | 0.2369 | 0.1866 | 0.1764 | 0.3492 | |
| Lasso | 1.2197 | 0.4241 | 0.3164 | 0.2809 | 0.2719 | 0.5026 | |
| Kalman | 1.1377 | 1.0139 | 0.9360 | 0.9553 | 0.9601 | 1.0006 | |
| Proposed Features | RMSE | MAE | MAPE (%) | R2 | Time (s) | ||||
|---|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | |||||
| ✓ | ✓ | ✓ | ✓ | ✓ | 0.0862 | 0.0732 | 0.5987 | 0.923523 | 0.0259 |
| - | ✓ | ✓ | ✓ | ✓ | 0.233401 | 0.1855705 | 1.2169 | 0.913716 | 0.01905 |
| ✓ | - | ✓ | ✓ | ✓ | 1.0651395 | 0.8038405 | 2.60585 | 0.628143 | 0.0176 |
| ✓ | ✓ | - | ✓ | ✓ | 0.2290405 | 0.181089 | 0.70005 | 0.922905 | 0.01785 |
| ✓ | ✓ | ✓ | - | ✓ | 0.230986 | 0.18282 | 0.64605 | 0.9241995 | 0.01835 |
| ✓ | ✓ | ✓ | ✓ | - | 0.2297205 | 0.181146 | 0.73265 | 0.923476 | 0.01975 |
| ✓ | - | - | - | - | 1.393372 | 1.171515 | 8.9394 | −1.454 | 0.0076 |
| - | ✓ | - | - | - | 0.231793 | 0.1860235 | 1.22655 | 0.9275805 | 0.0086 |
| - | - | ✓ | - | - | 1.1681775 | 0.862342 | 4.66665 | 0.08354 | 0.0079 |
| - | - | - | ✓ | - | 1.1566025 | 0.8757905 | 6.4991 | −0.63832 | 0.0067 |
| - | - | - | - | ✓ | 1.364249 | 1.157678 | 3.33345 | 0.4079215 | 0.00895 |
| Proposed Features | Train | Test | Overall |
|---|---|---|---|
| : minimum discharge voltage | −0.1465 | −0.2116 | −0.1791 |
| : time to minimum voltage | 0.9689 | 0.9627 | 0.9658 |
| : minimum temperature at the start of discharge | −0.0340 | 0.2752 | 0.1206 |
| : maximum discharge temperature | 0.0357 | −0.0601 | −0.0122 |
| : time elapsed between minimum and maximum temperature | 0.9625 | 0.9305 | 0.9465 |
| Scenario | Method | RMSE | MAE | MAPE (%) |
|---|---|---|---|---|
| 1 | Proposed | 0.0029 | 0.0022 | 0.2546 |
| DNN | 0.018239 | 0.015416 | 1.9341 | |
| Direct Features | 0.0042 | 0.0034 | 0.4231 | |
| Hybrid | 2.277851 | 1.922806 | 2.5100 | |
| 2 | Proposed | 0.0140 | 0.0110 | 1.4985 |
| DNN | 0.103690 | 0.097540 | 12.8129 | |
| Direct Features | 0.0274 | 0.0238 | 3.2878 | |
| Hybrid | 2.845887 | 1.890512 | 2.6018 | |
| 3 | Proposed | 0.0835 | 0.0261 | 1.4191 |
| DNN | 0.178465 | 0.174136 | 23.8429 | |
| Direct Features | 0.0883 | 0.0793 | 10.6426 | |
| Hybrid | 10.205681 | 3.207709 | 1.7226 | |
| 4 | Proposed | 0.0640 | 0.0567 | 0.06 |
| DNN | 9.3996 | 9.3972 | 9.78 | |
| Direct Features | 4.5677 | 0.5558 | 0.58 | |
| Hybrid | 4.5398 | 4.4670 | 4.65 | |
| 5 | Proposed | 0.0830 | 0.0757 | 0.08 |
| DNN | 0.4271 | 0.3912 | 0.41 | |
| Direct Features | 4.6395 | 0.5065 | 0.53 | |
| Hybrid | 4.2480 | 4.1490 | 4.37 | |
| 6 | Proposed | 0.2696 | 0.2676 | 0.28 |
| DNN | 22.5040 | 22.4926 | 23.58 | |
| Direct Features | 5.5194 | 2.2520 | 2.36 | |
| Hybrid | 4.2111 | 4.1170 | 4.30 | |
| Average | Proposed | 0.0862 | 0.0732 | 0.5987 |
| DNN | 5.4385 | 5.4280 | 12.0616 | |
| Direct Features | 2.4744 | 0.5701 | 2.96725 | |
| Hybrid | 4.72140 | 3.2923 | 3.3591 |
| Scenario | Charge C-Rate | Discharge C-Rate | Ambient Temperature (°C) | RMS | MAE | MAPE (%) |
|---|---|---|---|---|---|---|
| 1 | ∼0.75C (CC-CV) | 1C | 4 to 40 | 0.002021 | 0.001711 | 0.2182 |
| 2 | ∼0.75C (CC-CV) | 1C | 24 | 0.013571 | 0.011308 | 1.5269 |
| 3 | ∼0.75C (CC-CV) | 2C | 4 | 0.083121 | 0.028124 | 1.8028 |
| 4 | ∼0.75C (CC-CV) | 1C | 25 | 0.1148 | 0.1147 | 0.12 |
| 5 | 0.5C (CC) | 0.5C (CC) | 15 | 0.2309 | 0.2308 | 0.24 |
| 6 | 0.5C (CC) | 2C (CC) | 25 | 0.3568 | 0.3566 | 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acuña Acurio, B.A.; Chérrez Barragán, D.E.; Rodríguez, J.C.; Grijalva, F.; Pereira da Silva, L.C. Robust Data-Driven State of Health Estimation of Lithium-Ion Batteries Based on Reconstructed Signals. Energies 2025, 18, 2459. https://doi.org/10.3390/en18102459
Acuña Acurio BA, Chérrez Barragán DE, Rodríguez JC, Grijalva F, Pereira da Silva LC. Robust Data-Driven State of Health Estimation of Lithium-Ion Batteries Based on Reconstructed Signals. Energies. 2025; 18(10):2459. https://doi.org/10.3390/en18102459
Chicago/Turabian StyleAcuña Acurio, Byron Alejandro, Diana Estefanía Chérrez Barragán, Juan Carlos Rodríguez, Felipe Grijalva, and Luiz Carlos Pereira da Silva. 2025. "Robust Data-Driven State of Health Estimation of Lithium-Ion Batteries Based on Reconstructed Signals" Energies 18, no. 10: 2459. https://doi.org/10.3390/en18102459
APA StyleAcuña Acurio, B. A., Chérrez Barragán, D. E., Rodríguez, J. C., Grijalva, F., & Pereira da Silva, L. C. (2025). Robust Data-Driven State of Health Estimation of Lithium-Ion Batteries Based on Reconstructed Signals. Energies, 18(10), 2459. https://doi.org/10.3390/en18102459







