Aggregation Method and Bidding Strategy for Virtual Power Plants in Energy and Frequency Regulation Markets Using Zonotopes
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contributions
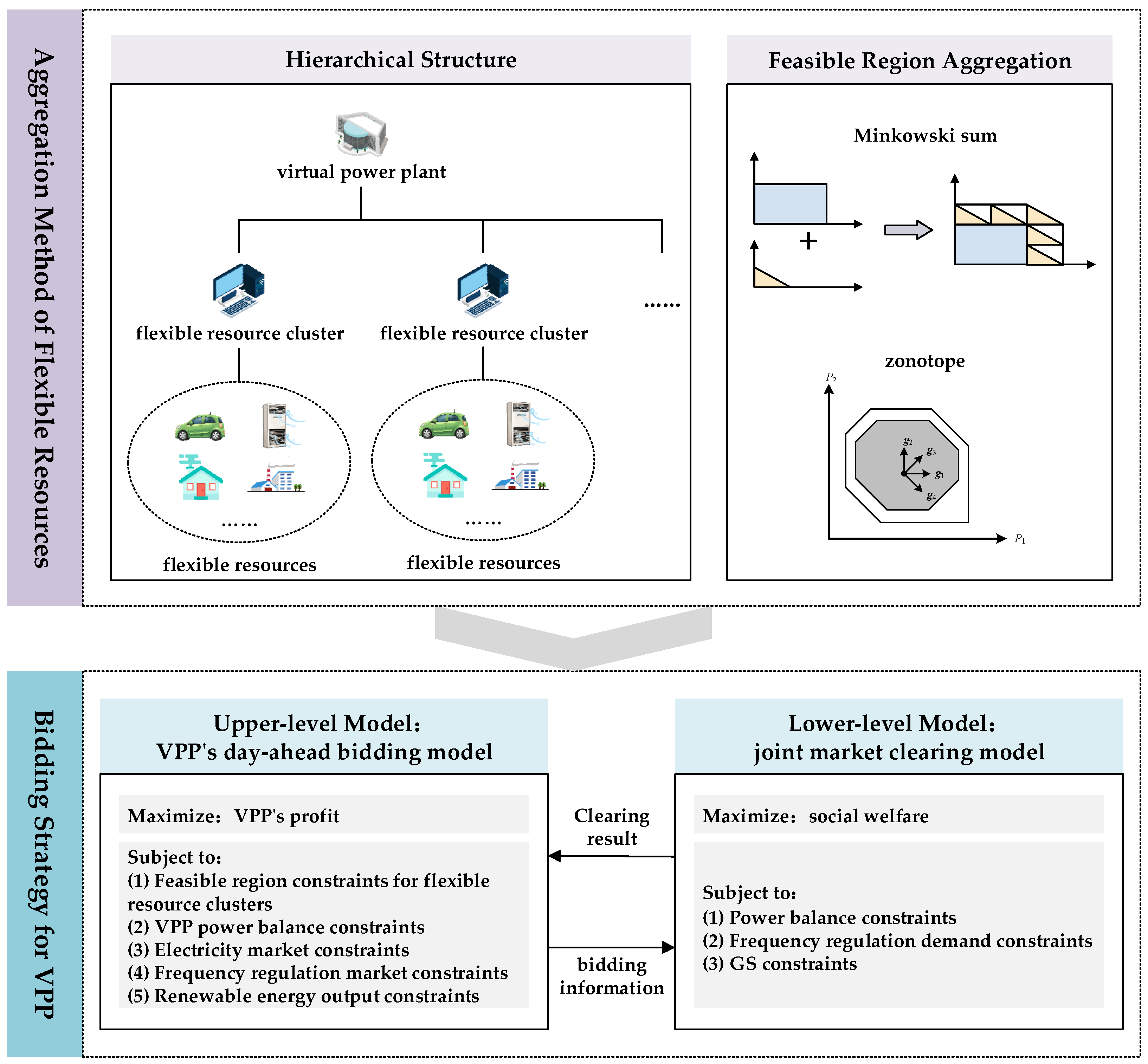
2. Research Methodology
3. Aggregation Method of Flexible Resources Based on Zonotope
3.1. Feasible Region of Flexible Resources
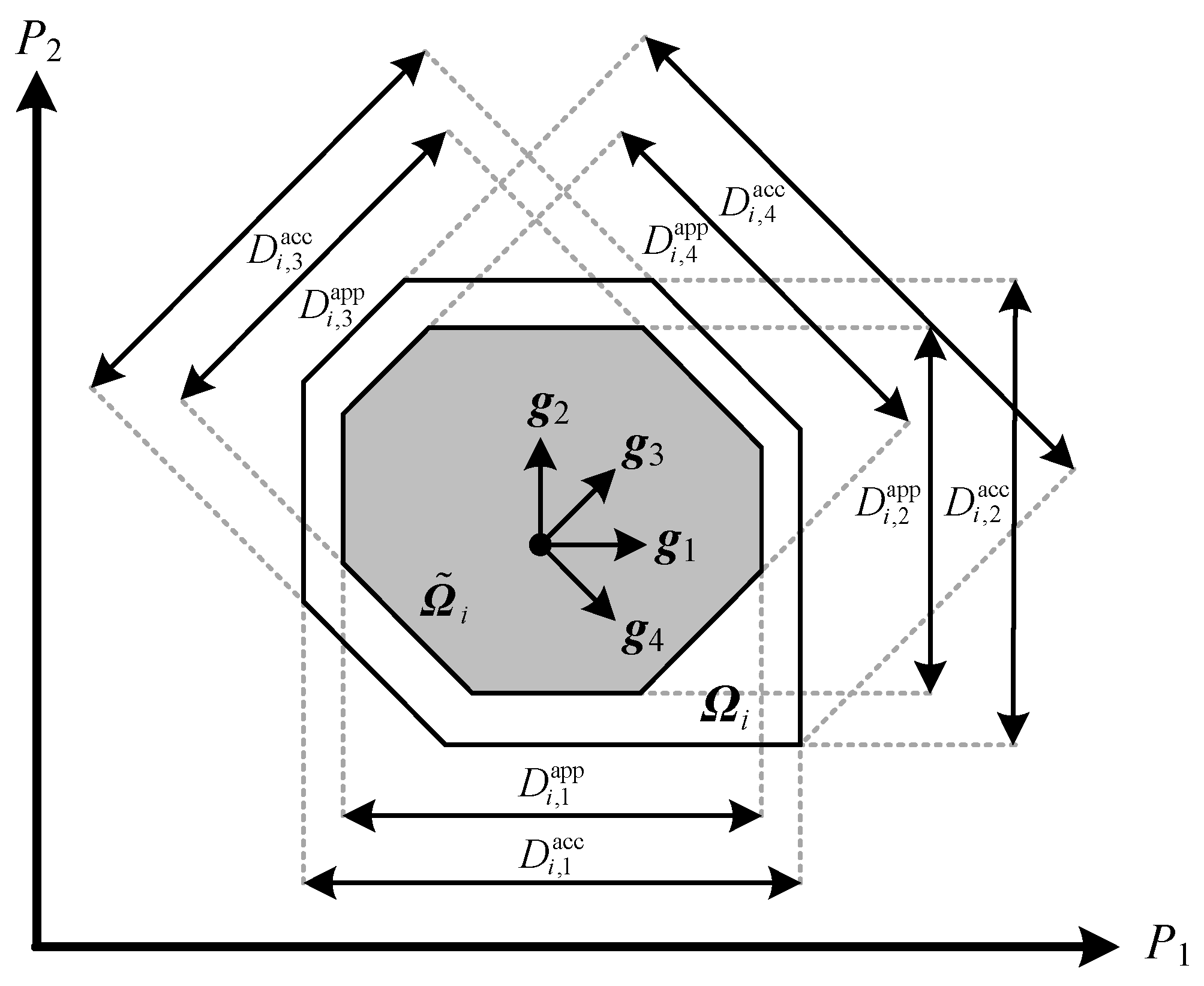
3.2. Zonotope
3.3. Zonotope-Based Feasible Region Aggregation Method
3.4. Conversion of Zonotope to Half-Space Representation
4. Day-Ahead Bidding Model for VPPs Participating in Electricity and Frequency Regulation Markets
4.1. Operational Framework and Trading Mechanism
4.2. Optimization Model
4.2.1. Upper-Level Model Objective Function
- Electricity market revenue:
- 2.
- Frequency regulation market revenue:
- 3.
- Flexible resource dispatch compensation cost:
- 4.
- WT/PV curtailment penalty cost:
4.2.2. Upper-Level Model Constraints
- Feasible region constraints for flexible resource clusters
- 2.
- VPP power balance constraints
- 3.
- Electricity market constraints
- 4.
- Frequency regulation market constraints
- 5.
- Renewable energy output constraints
4.2.3. Lower-Level Model Objective Function
4.2.4. Lower-Level Model Constraints
- Power balance constraints
- 2.
- Frequency regulation demand constraints
- 3.
- GS constraints
4.3. Model Solution Method
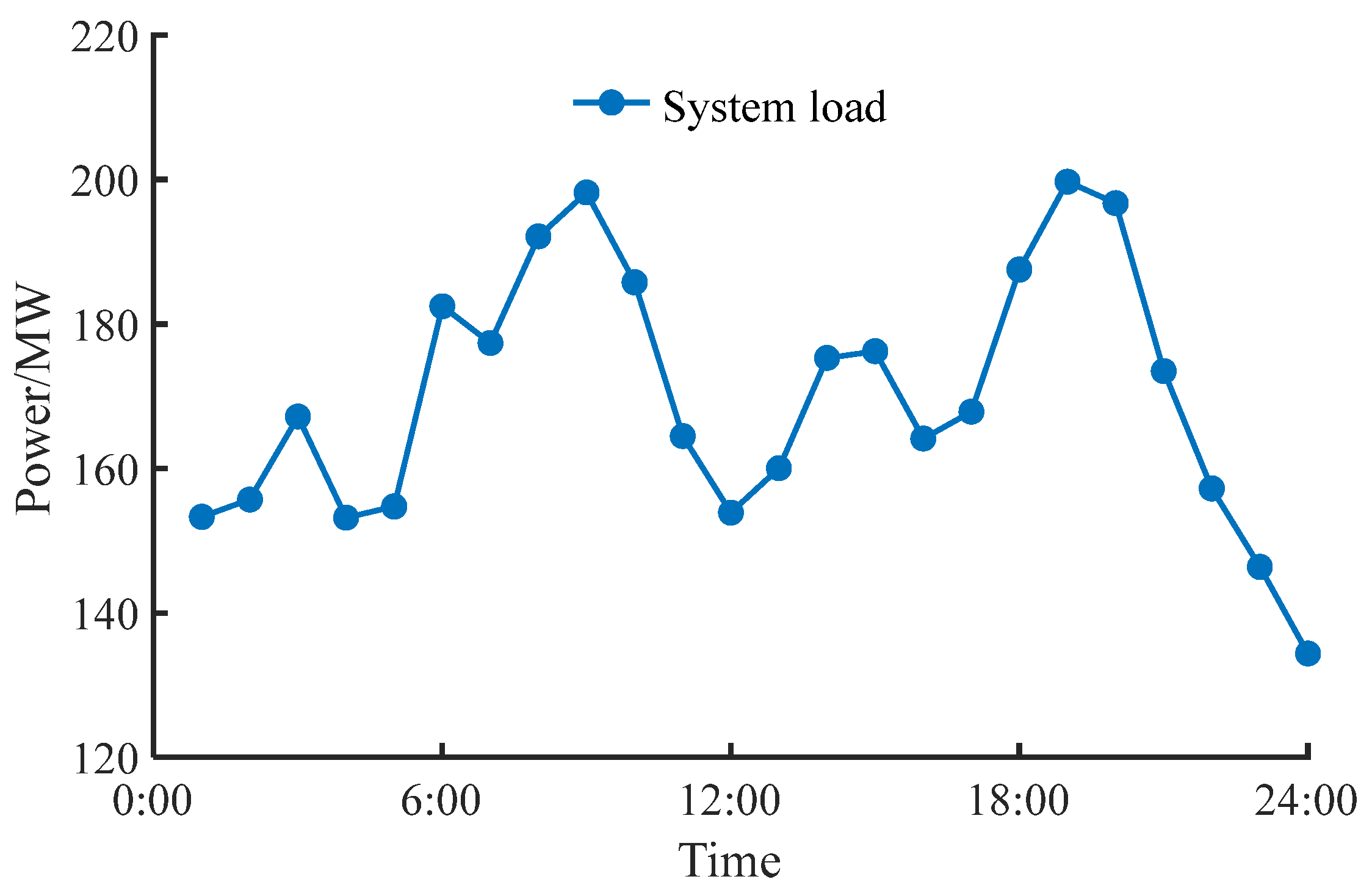
5. Case Study
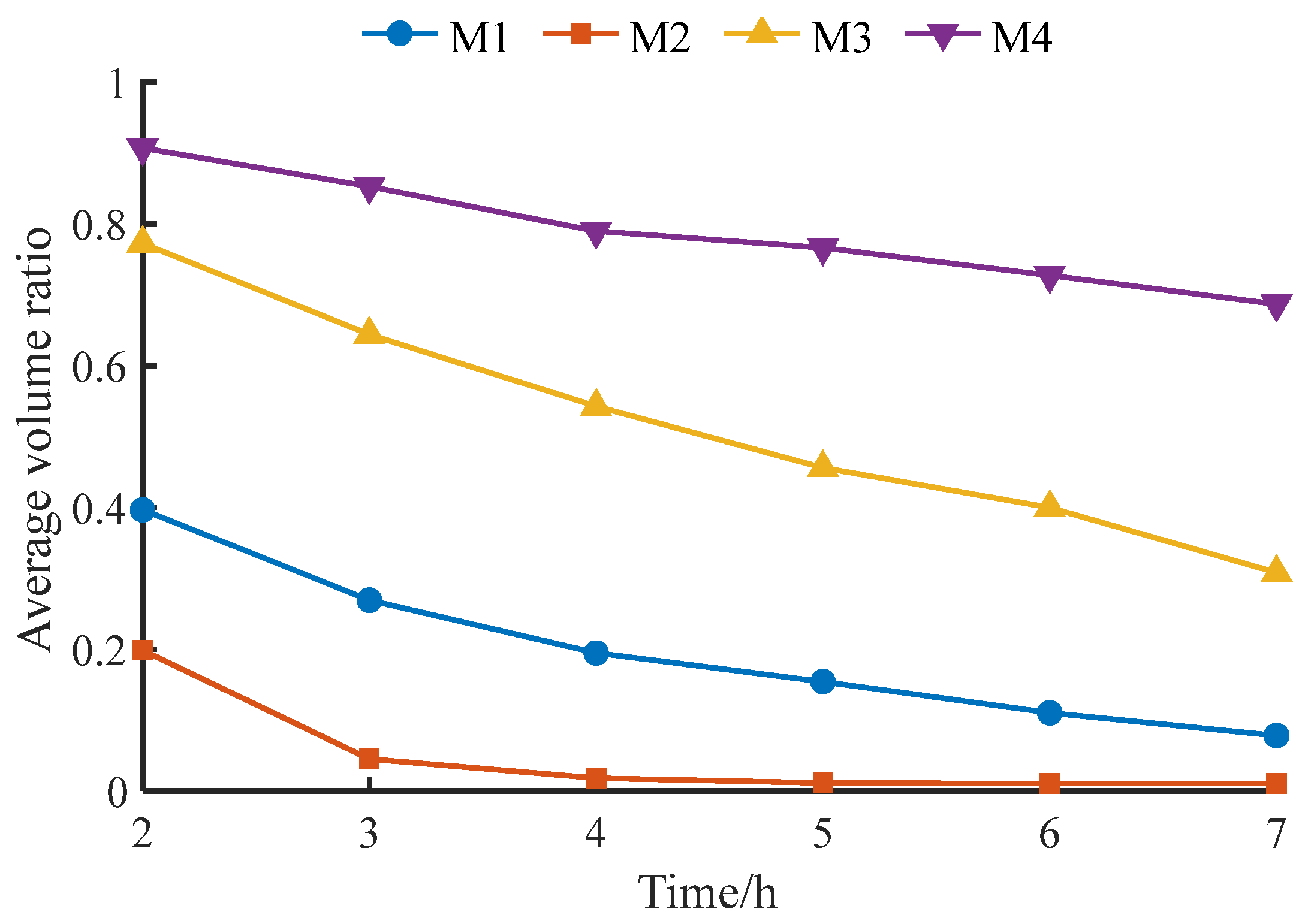
5.1. Comparative Analysis of Aggregation Methods
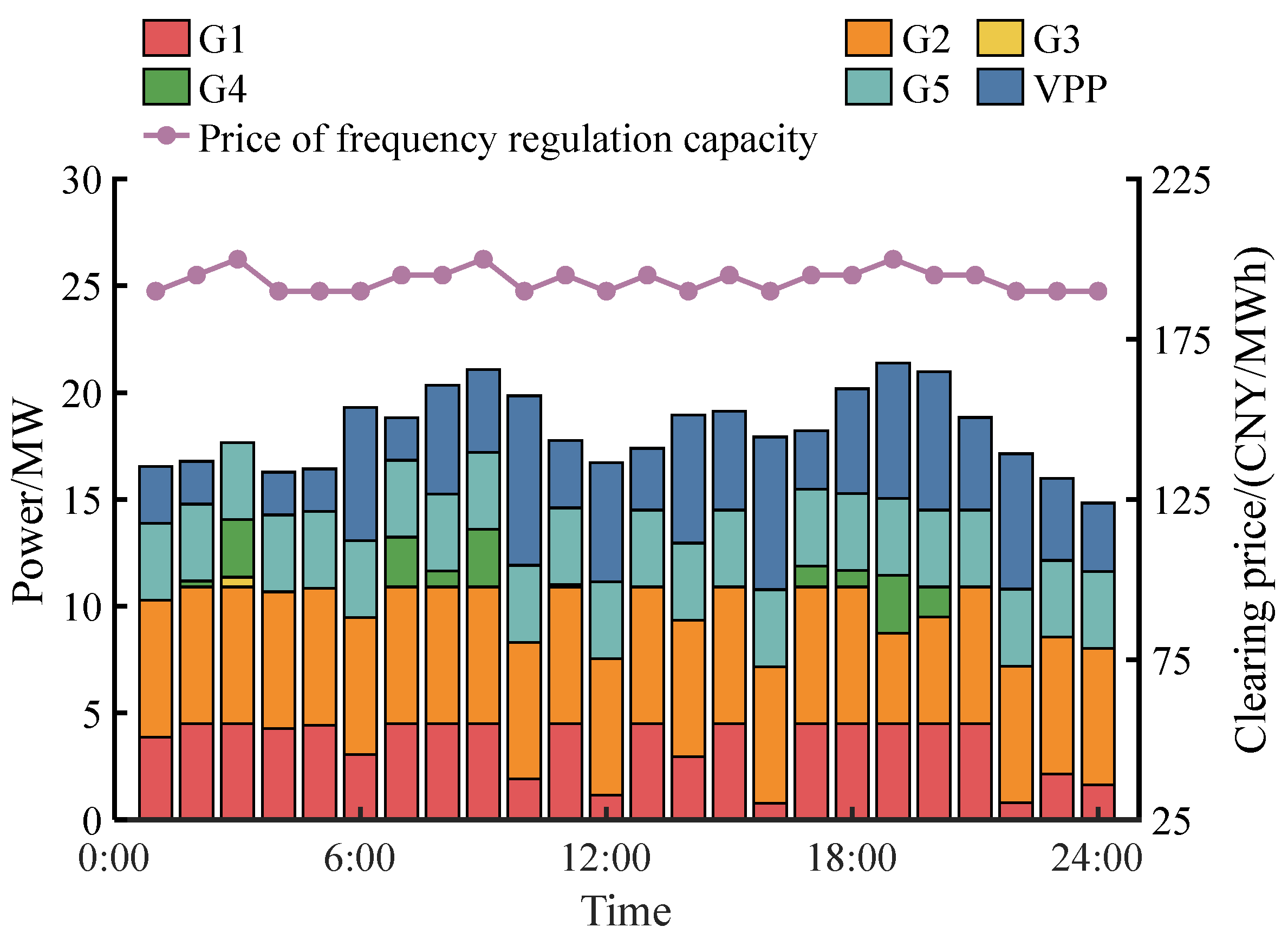
5.2. Analysis of Day-Ahead Optimization Results
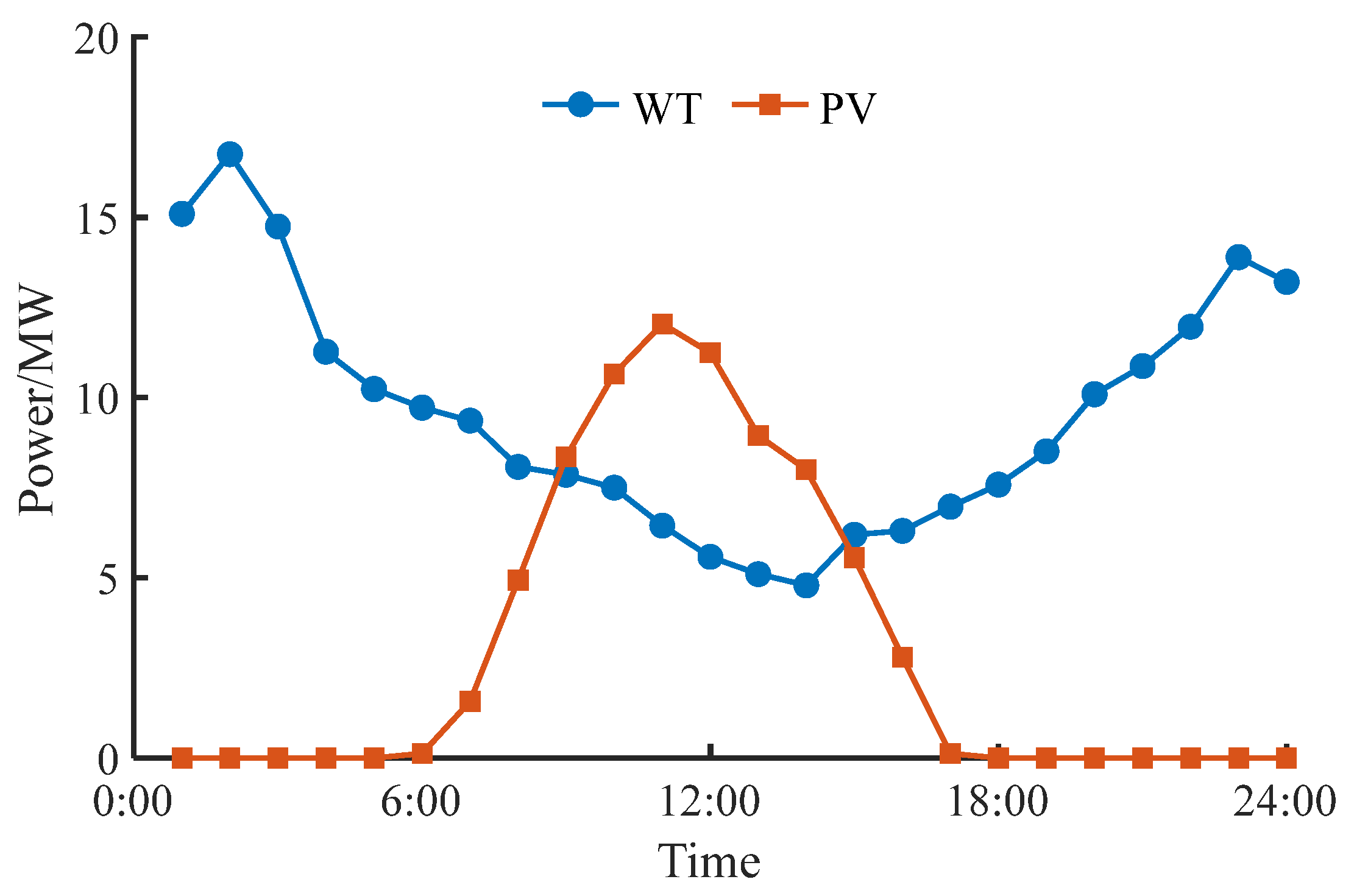
5.2.1. Case Data
5.2.2. Analysis of Day-Ahead Market-Clearing Results
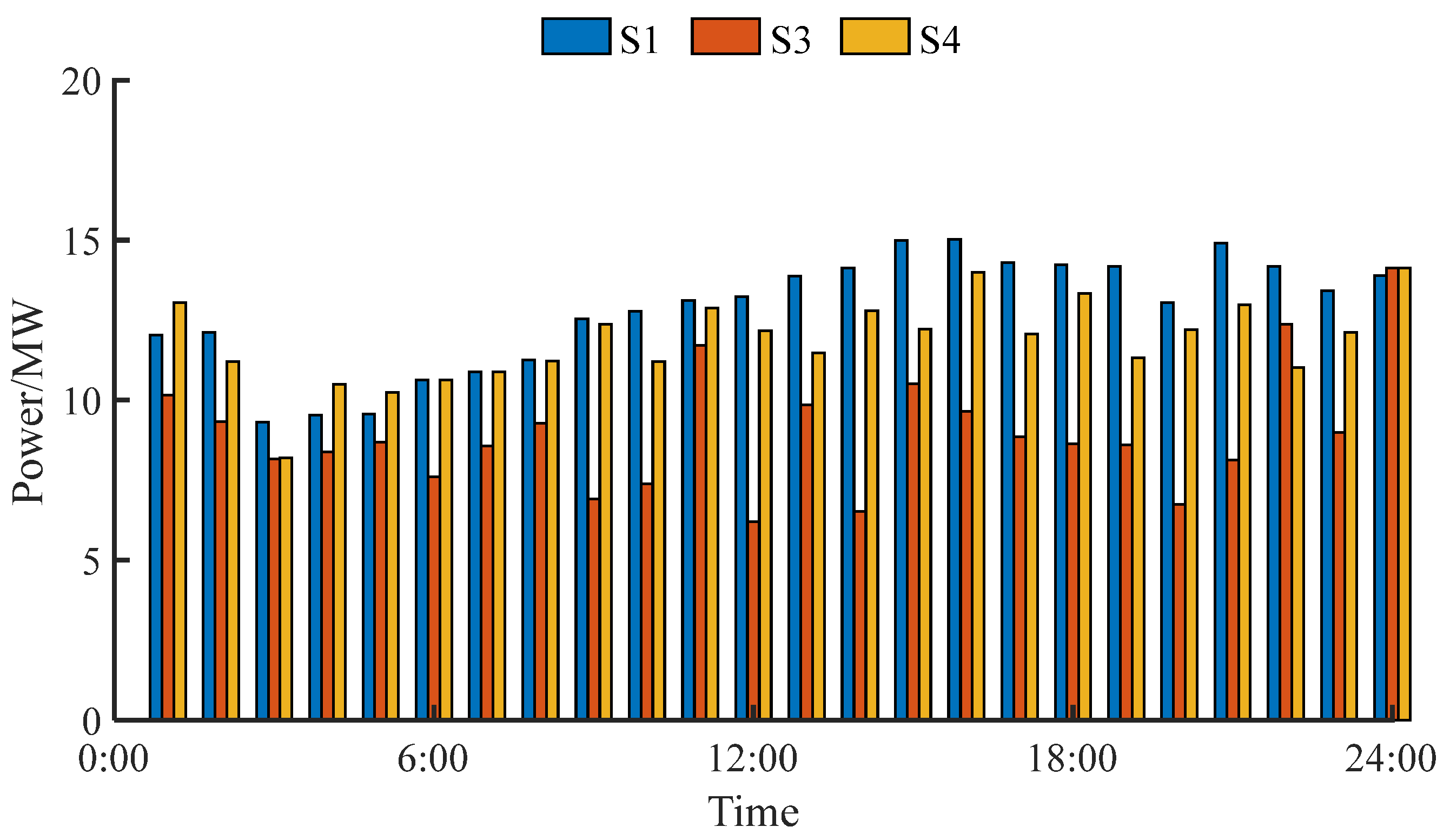
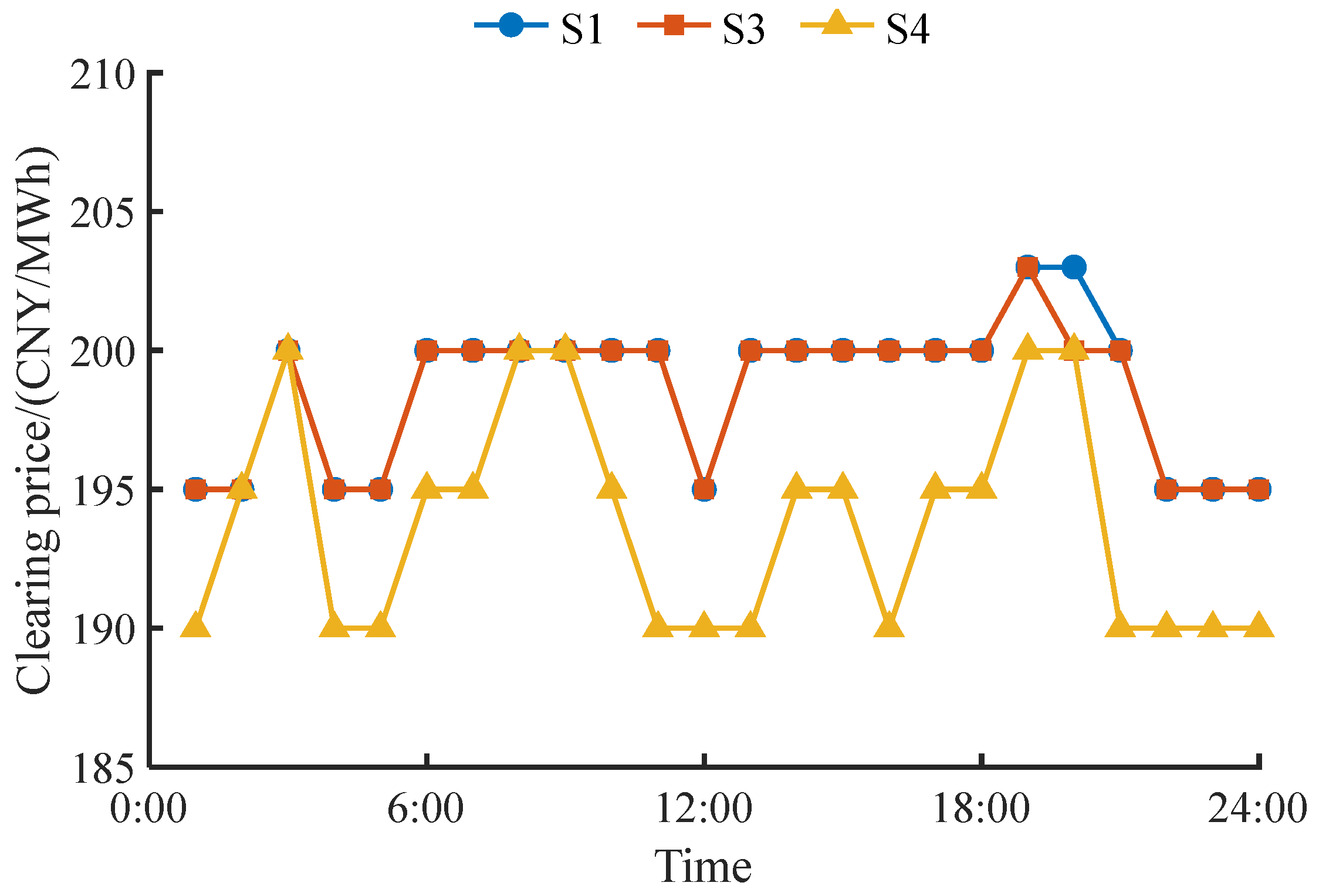
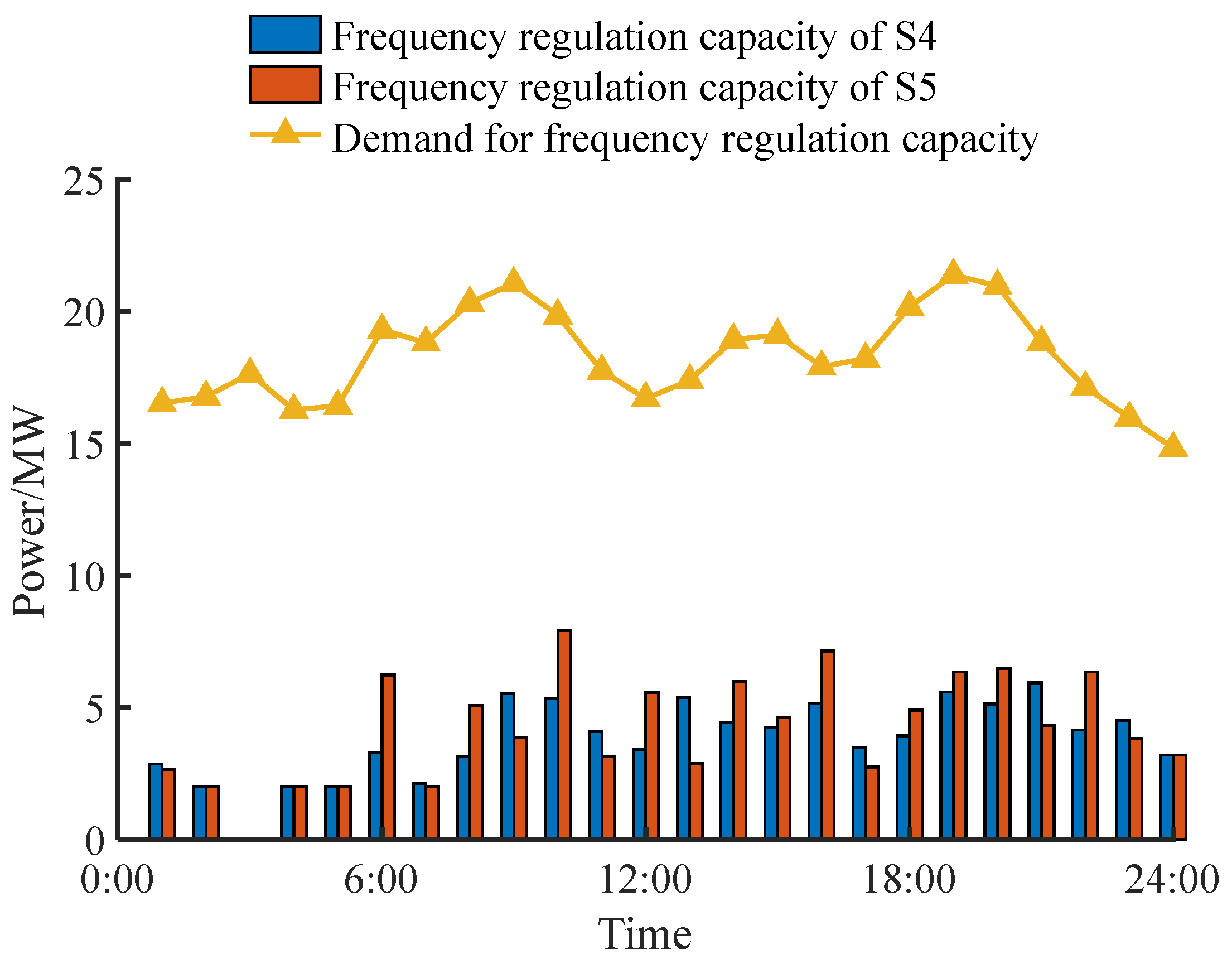
5.2.3. Comparative Analysis
6. Conclusions
- The improved zonotope-based feasible region approximation method enhanced the approximation accuracy, improved the frequency regulation capability of flexible resources, and increased the VPP revenue.
- The proposed day-ahead optimization model guided the VPP to participate in electricity and frequency regulation ancillary service markets, optimally scheduling internal flexible resources and renewable energy to maximize revenue.
- VPP participation in the frequency regulation market reduced the clearing prices and alleviated the frequency regulation resource demand pressure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Liu, Z.; Guo, G.; Gong, D.; Xuan, L.; He, F.; Wan, X.; Zhou, D. Bi-Level Game Strategy for Virtual Power Plants Based on an Improved Reinforcement Learning Algorithm. Energies 2025, 18, 374. [Google Scholar] [CrossRef]
- Wang, K.; Xue, Y.; Shahidehpour, M.; Chang, X.; Li, Z.; Zhou, Y.; Sun, H. Resilience-Oriented Two-Stage Restoration Considering Coordinated Maintenance and Reconfiguration in Integrated Power Distribution and Heating Systems. IEEE Trans. Sustain. Energy 2025, 16, 124–137. [Google Scholar] [CrossRef]
- Yang, N.; Zhu, L.; Wang, B.; Fu, R.; Qi, L.; Jiang, X.; Sun, C. A Master–Slave Game-Based Strategy for Trading and Allocation of Virtual Power Plants in the Electricity Spot Market. Energies 2025, 18, 442. [Google Scholar] [CrossRef]
- Qi, J.; Ying, A.; Zhang, B.; Zhou, D.; Weng, G. Distributed Frequency Regulation Method for Power Grids Considering the Delayed Response of Virtual Power Plants. Energies 2025, 18, 1361. [Google Scholar] [CrossRef]
- Gao, Y.; Ai, Q. Novel Optimal Dispatch Method for Multiple Energy Sources in Regional Integrated Energy Systems Considering Wind Curtailment. CSEE J. Power Energy Syst. 2024, 10, 2166–2173. [Google Scholar] [CrossRef]
- Barot, S.; Taylor, J.A. A Concise, Approximate Representation of a Collection of Loads Described by Polytopes. Int. J. Electr. Power Energy Syst. 2017, 84, 55–63. [Google Scholar] [CrossRef]
- Tong, Y.; Hu, J.; Du, H.; Chen, C.; Zeng, W. Feasible Region Aggregation Method for Load Regulation of Minkowski Heat Pump Based on External Approximation of VB Model. Dianwang Jishu/Power Syst. Technol. 2024, 48, 3340–3349. [Google Scholar] [CrossRef]
- Wen, Y.; Hu, Z.; You, S.; Duan, X. Aggregate Feasible Region of DERs: Exact Formulation and Approximate Models. IEEE Trans. Smart Grid 2022, 13, 4405–4423. [Google Scholar] [CrossRef]
- Li, Z.; Li, T.; Wu, W.; Zhang, B.; Jiang, F.; Cui, D. Minkowski Sum Based Flexibility Aggregating Method of Load Dispatching for Heat Pumps. Dianli Xitong Zidonghua/Autom. Electr. Power Syst. 2019, 43, 14–21. [Google Scholar] [CrossRef]
- Chen, X.; Dall’Anese, E.; Zhao, C.; Li, N. Aggregate Power Flexibility in Unbalanced Distribution Systems. IEEE Trans. Smart Grid 2020, 11, 258–269. [Google Scholar] [CrossRef]
- Wang, S.; Wu, W. Aggregation Reference Model and Quantitative Metric System of Flexible Energy Resources. Dianli Xitong Zidonghua/Autom. Electr. Power Syst. 2024, 48, 1–9. [Google Scholar] [CrossRef]
- Müller, F.L.; Szabó, J.; Sundström, O.; Lygeros, J. Aggregation and Disaggregation of Energetic Flexibility from Distributed Energy Resources. IEEE Trans. Smart Grid 2019, 10, 1205–1214. [Google Scholar] [CrossRef]
- Hreinsson, K.; Scaglione, A.; Alizadeh, M.; Chen, Y. New Insights from the Shapley-Folkman Lemma on Dispatchable Demand in Energy Markets. IEEE Trans. Power Syst. 2021, 36, 4028–4041. [Google Scholar] [CrossRef]
- Chen, X.; Li, N. Leveraging Two-Stage Adaptive Robust Optimization for Power Flexibility Aggregation. IEEE Trans. Smart Grid 2021, 12, 3954–3965. [Google Scholar] [CrossRef]
- Li, J.; Ai, Q. Operation Mode of Virtual Power Plant Considering Peak Regulation Auxiliary Service. Dianli Zidonghua Shebei/Electr. Power Autom. Equip. 2021, 41, 1–7. [Google Scholar] [CrossRef]
- Qing, Z.; An, R.; Gao, H.; Gao, Y.; Wang, C.; Yang, J.; Liu, J. Intelligent Peak Regulation Pricing for Virtual Power Plant Considering Interactive Response of Distributed Resources. Dianli Zidonghua Shebei/Electr. Power Autom. Equip. 2023, 43, 96–103. [Google Scholar] [CrossRef]
- Lee, J.; Won, D. Optimal Operation Strategy of Virtual Power Plant Considering Real-Time Dispatch Uncertainty of Distributed Energy Resource Aggregation. IEEE Access 2021, 9, 56965–56983. [Google Scholar] [CrossRef]
- Li, X.; Zhan, Z.; Li, F.; Zhang, L. Bidding Strategy for Battery Swapping Station Participating in Electricity Energy and Frequency Regulation Market Considering Demand Response of Battery Swapping. Dianli Xitong Zidonghua/Autom. Electr. Power Syst. 2024, 48, 207–215. [Google Scholar] [CrossRef]
- Xiao, F.; Cui, Y.; Zhu, J.; Qiao, Y.; Li, Z.; Ai, Q. A Load-Side Resource Aggregation Method Based on Minkowski Sum. J. Phys. Conf. Ser. 2024, 2728, 012073. [Google Scholar] [CrossRef]
- Tiwary, H.R. On the Hardness of Computing Intersection, Union and Minkowski Sum of Polytopes. Discret. Comput. Geom. 2008, 40, 469–479. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Y.; Chen, Y.; Wang, Z.; Qu, S.; He, K. Demand Side Feasible Region Aggregation Considering Flexibility Revenue. Electr. Power 2022, 55, 56–63. [Google Scholar]
- Yi, Z.; Xu, Y.; Gu, W.; Yang, L.; Sun, H. Aggregate Operation Model for Numerous Small-Capacity Distributed Energy Resources Considering Uncertainty. IEEE Trans. Smart Grid 2021, 12, 4208–4224. [Google Scholar] [CrossRef]





| Flexible Resource | Downward Regulation Rate/(kW/h) | Upward Regulation Rate/(kW/h) |
|---|---|---|
| 1 | 3.5 | 3.5 |
| 2 | 4.8 | 4.8 |
| 3 | 5.4 | 5.4 |
| 4 | 5.0 | 5.0 |
| 5 | 4.0 | 4.0 |
| 6 | 6.6 | 6.6 |
| 7 | 5.2 | 5.2 |
| 8 | 5.1 | 5.1 |
| 9 | 5.4 | 5.4 |
| 10 | 5.2 | 5.2 |
| GS | Minimum Technical Output/MW | Maximum Technical Output/MW |
|---|---|---|
| G1 | 15 | 55 |
| G2 | 20 | 75 |
| G3 | 15 | 55 |
| G4 | 10 | 35 |
| G5 | 10 | 45 |
| GS | Capacity/MW | Price/(CNY/MWh) | ||||
|---|---|---|---|---|---|---|
| Segment 1 | Segment 2 | Segment 3 | Segment 1 | Segment 2 | Segment 3 | |
| G1 | 20 | 15 | 15 | 370 | 455 | 548 |
| G2 | 35 | 20 | 15 | 350 | 440 | 530 |
| G3 | 25 | 10 | 15 | 361 | 464 | 559 |
| G4 | 10 | 10 | 10 | 371 | 460 | 565 |
| G5 | 20 | 10 | 10 | 360 | 445 | 540 |
| GS | Frequency Regulation Capacity | Frequency Regulation Mileage | ||
|---|---|---|---|---|
| Capacity/MW | Price/(CNY/MWh) | Capacity/MW | Price/(CNY/MWh) | |
| G1 | 4.5 | 190 | 45 | 19 |
| G2 | 6.4 | 185 | 64 | 18.5 |
| G3 | 4.5 | 200 | 45 | 20 |
| G4 | 2.7 | 195 | 27 | 19.5 |
| G5 | 3.6 | 180 | 36 | 18 |
| Scenarios | VPP Revenues/CNY | Market Clearing Costs/CNY | Solution Time/s |
|---|---|---|---|
| S1 | −3970.56 | 1,769,808 | 3.61 |
| S2 | 31,645.02 | 1,770,069 | 1427.27 |
| S3 | −2054.60 | 1,770,364 | 3.95 |
| S4 | 28,709.30 | 1,769,699 | 5.73 |
| S5 | 31,006.84 | 1,769,732 | 5.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, J.; Huang, M.; Sun, X.; Chen, Z.; Zhang, Y.; Xie, X.; Chen, Y.; Qiao, Y.; Ai, Q. Aggregation Method and Bidding Strategy for Virtual Power Plants in Energy and Frequency Regulation Markets Using Zonotopes. Energies 2025, 18, 2458. https://doi.org/10.3390/en18102458
Zhan J, Huang M, Sun X, Chen Z, Zhang Y, Xie X, Chen Y, Qiao Y, Ai Q. Aggregation Method and Bidding Strategy for Virtual Power Plants in Energy and Frequency Regulation Markets Using Zonotopes. Energies. 2025; 18(10):2458. https://doi.org/10.3390/en18102458
Chicago/Turabian StyleZhan, Jun, Mei Huang, Xiaojia Sun, Zuowei Chen, Yubo Zhang, Xuejing Xie, Yilin Chen, Yining Qiao, and Qian Ai. 2025. "Aggregation Method and Bidding Strategy for Virtual Power Plants in Energy and Frequency Regulation Markets Using Zonotopes" Energies 18, no. 10: 2458. https://doi.org/10.3390/en18102458
APA StyleZhan, J., Huang, M., Sun, X., Chen, Z., Zhang, Y., Xie, X., Chen, Y., Qiao, Y., & Ai, Q. (2025). Aggregation Method and Bidding Strategy for Virtual Power Plants in Energy and Frequency Regulation Markets Using Zonotopes. Energies, 18(10), 2458. https://doi.org/10.3390/en18102458






