Experimental and Numerical Study of the Heat Dissipation of the Electronic Module in an Air Conditioner Outdoor Unit
Abstract
1. Introduction
2. Experiments
3. Numerical Simulation
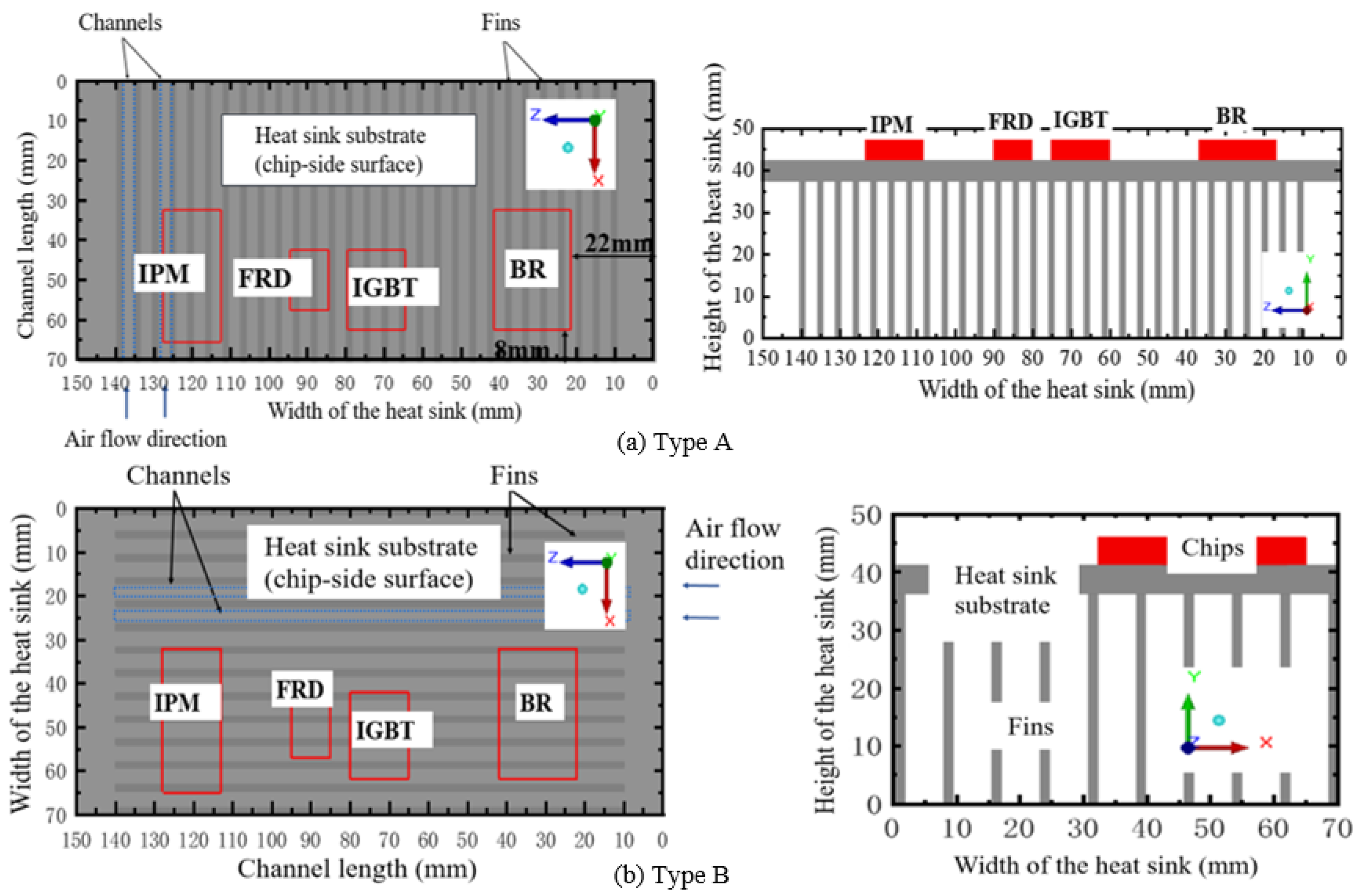
3.1. Model of Plate-Fin Heat Sink
- (1)
- The physical property parameters are assumed to be constant [17].
- (2)
- The effects of viscous dissipation and gravity are neglected.
- (3)
- The flow can be thought of as a continuum.
- (4)
- When analyzing the heat dissipation process of the equipment, the heat conduction and forced convection heat transfer of the equipment are mainly considered [12].
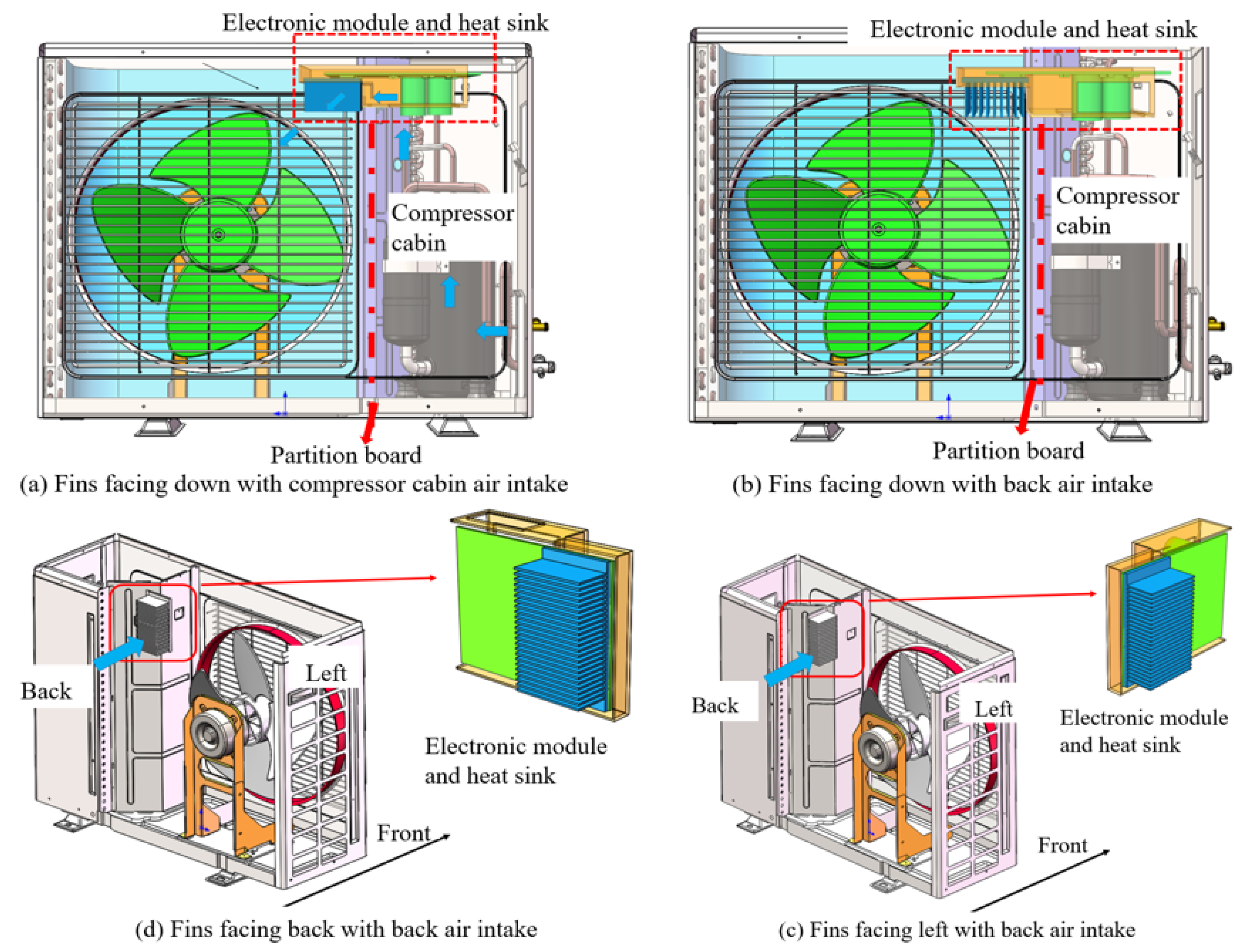
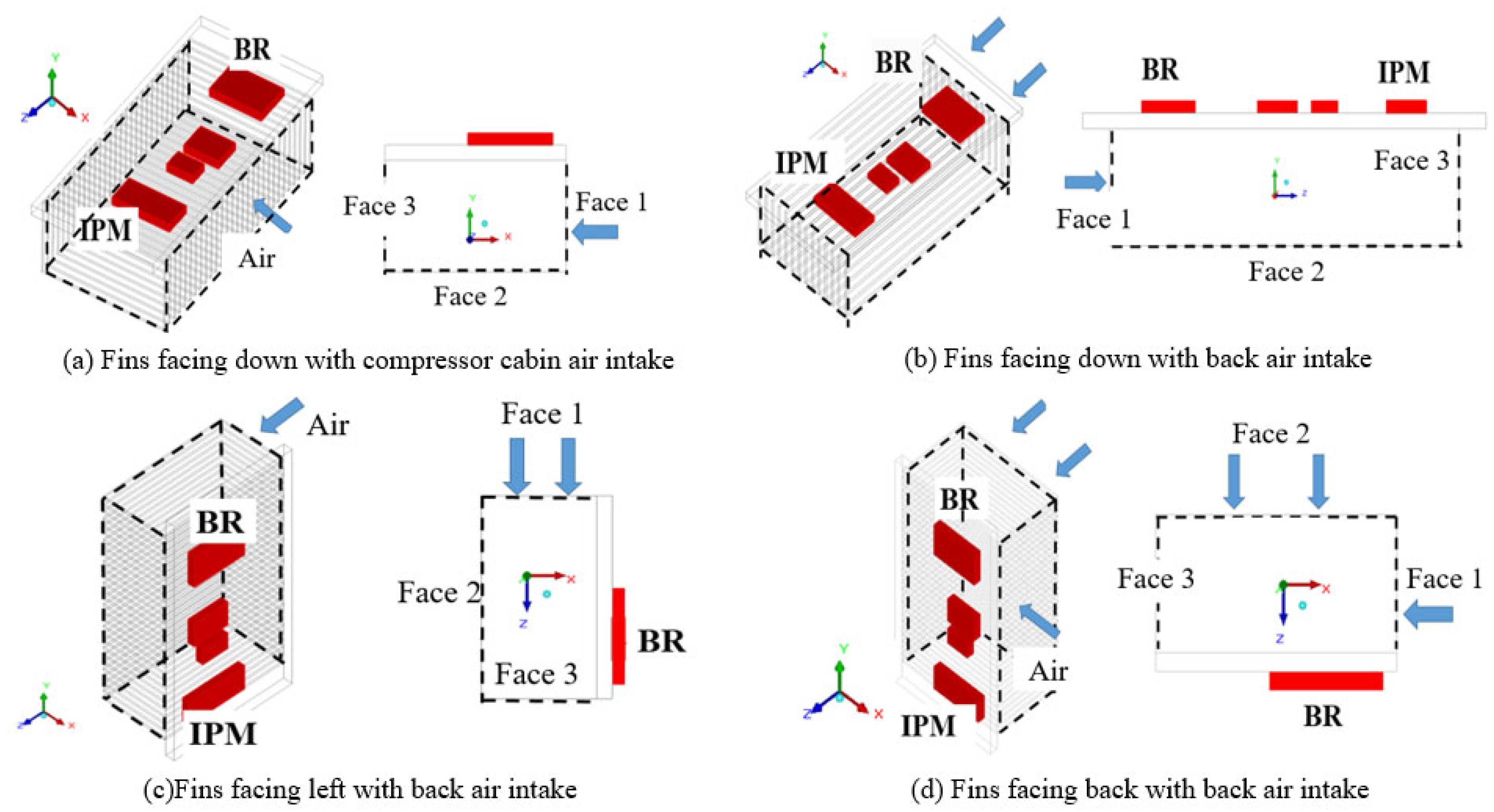
3.2. Different Heat Dissipation Cases for the Electronic Module
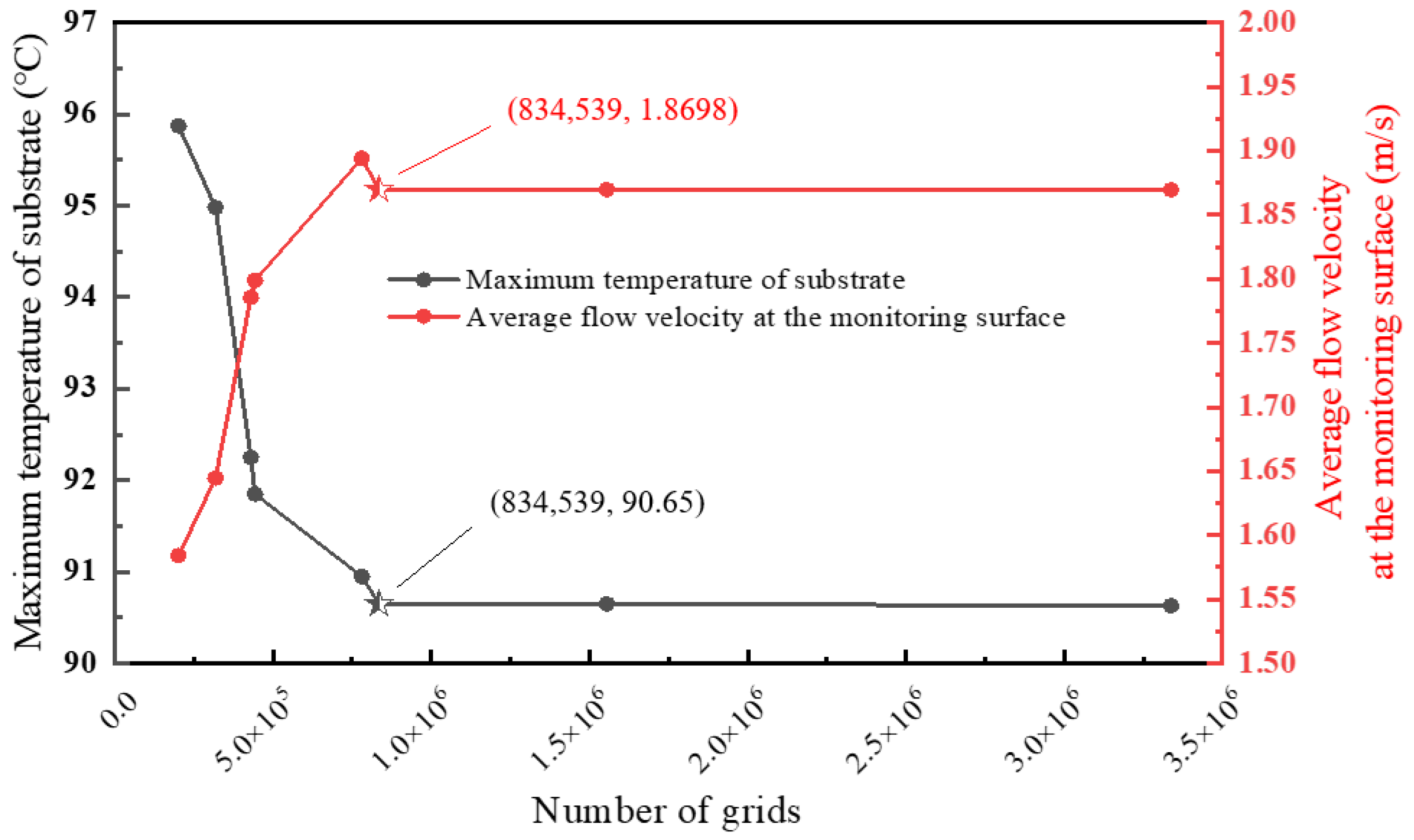
3.3. Computation Domain, Boundary Conditions, and Grid Independency
4. Results and Discussion
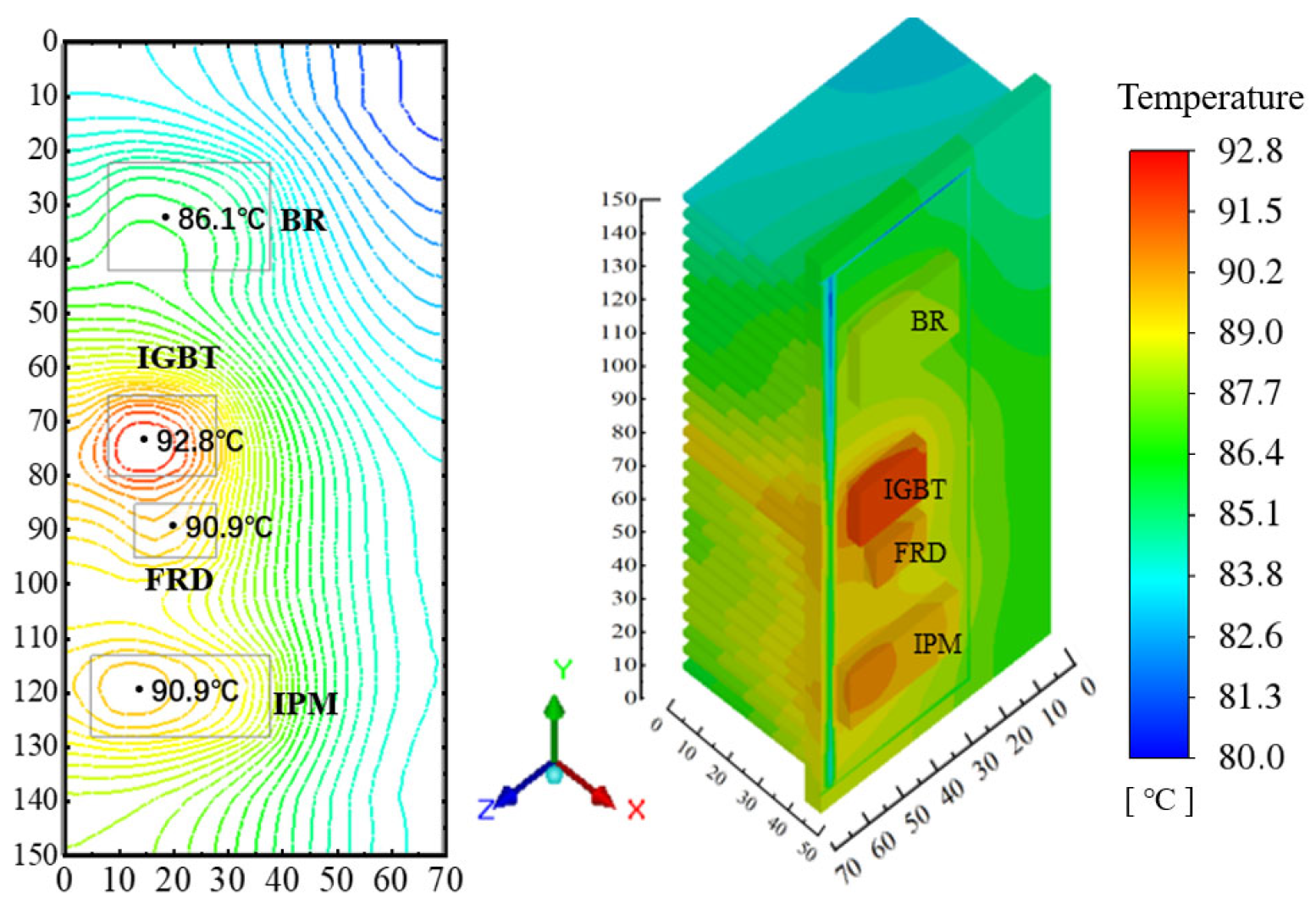
4.1. Validation of the Simulation Model
4.2. Comparative Analysis of Heat Transfer Coefficients
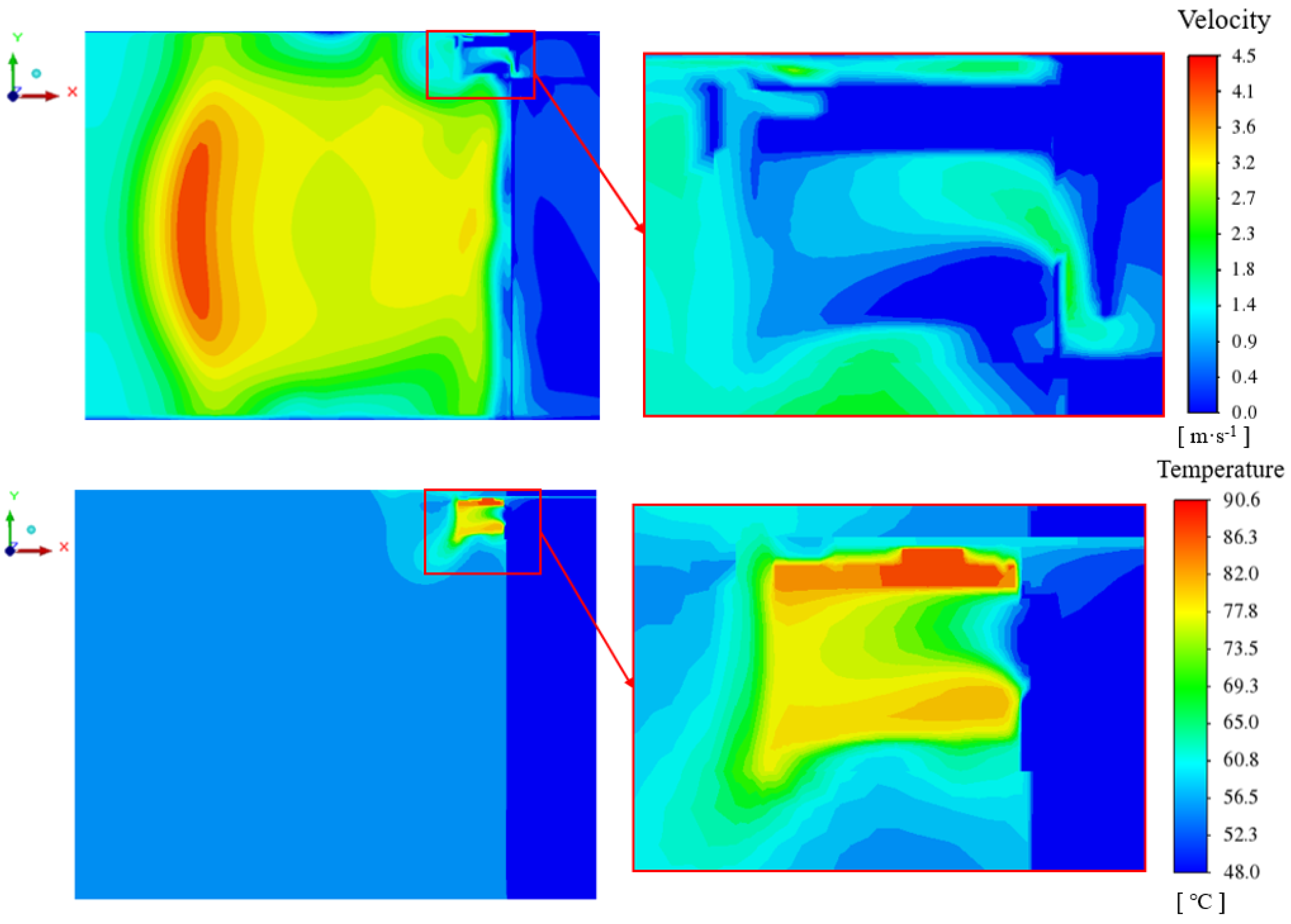
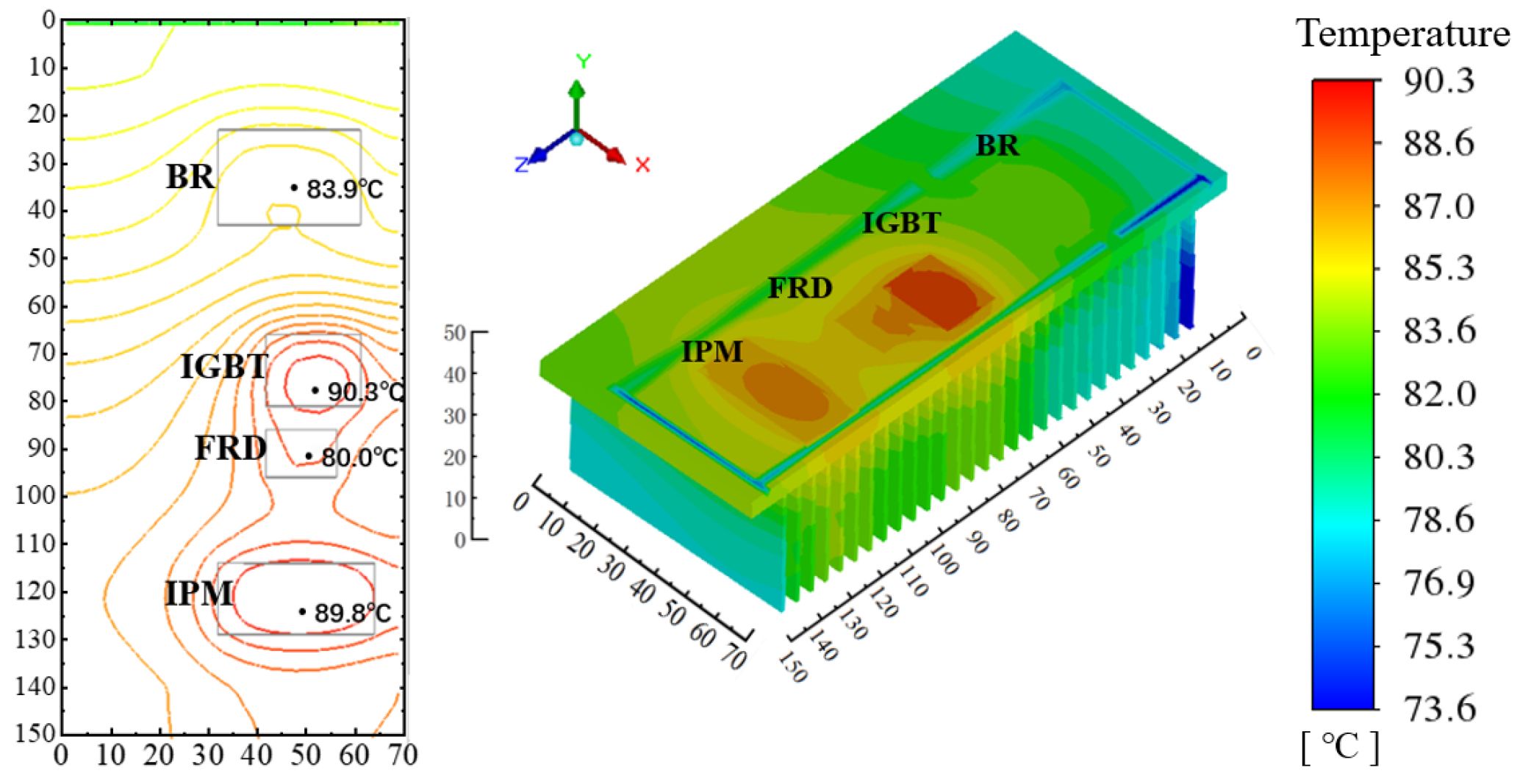
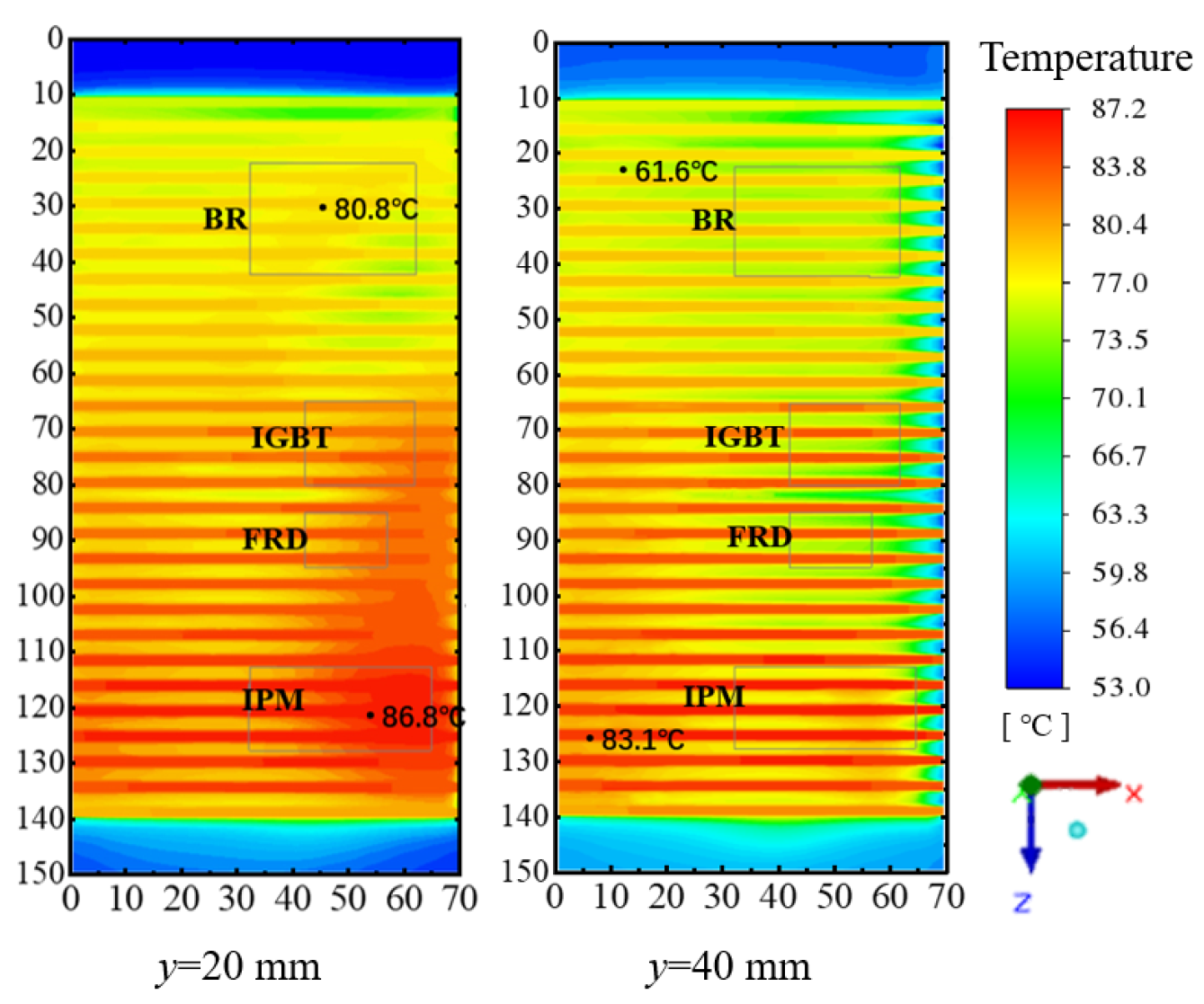
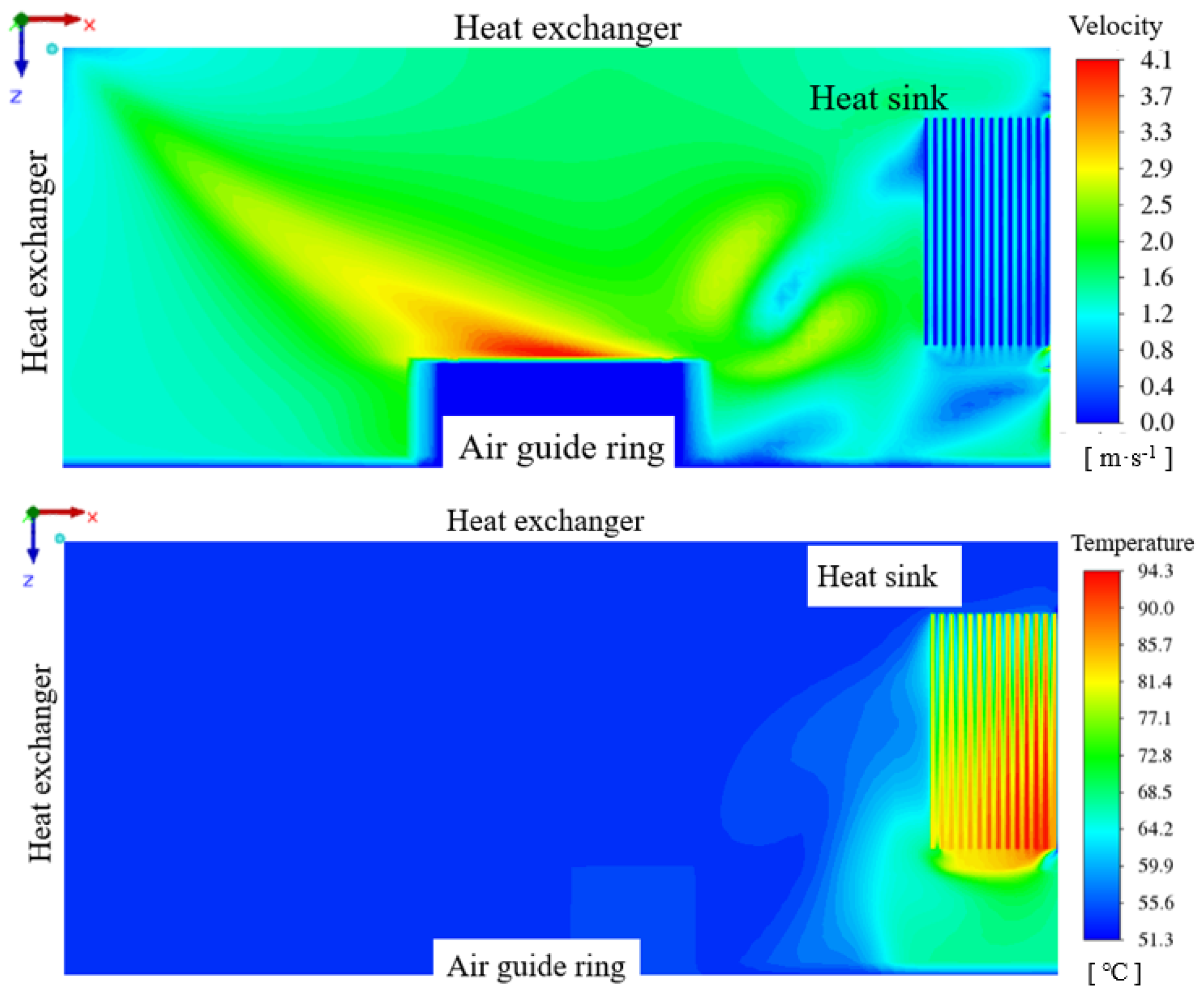
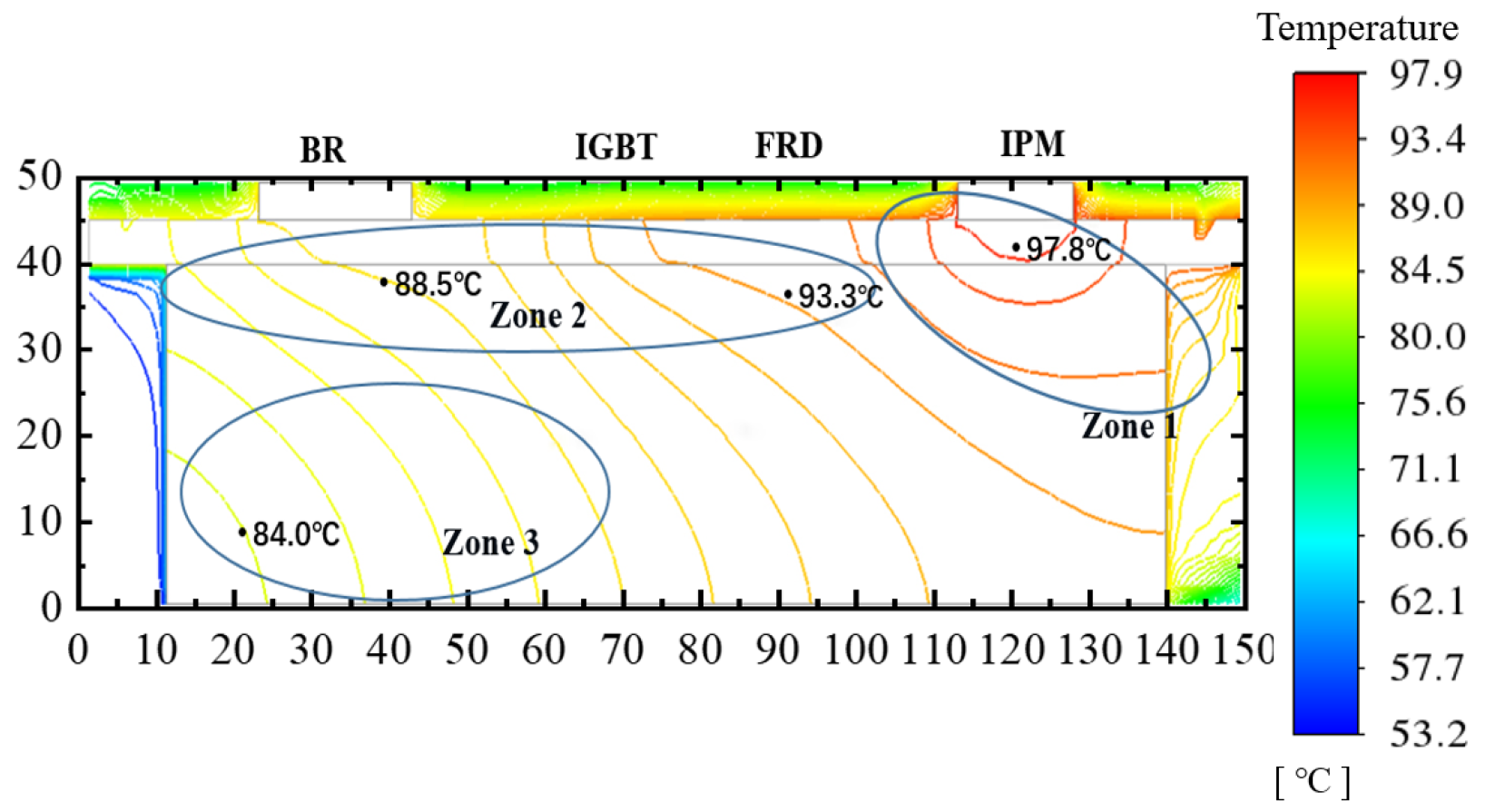
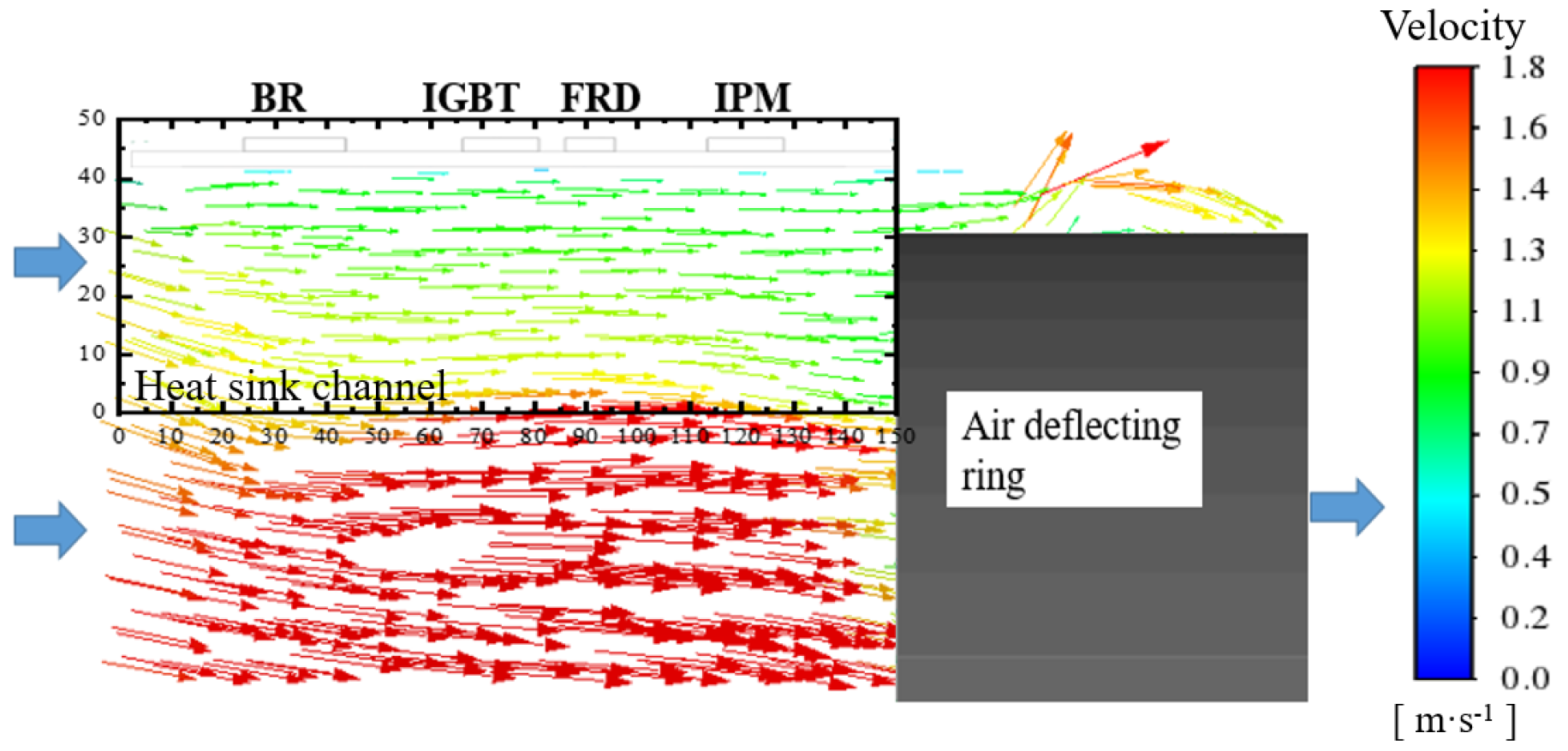
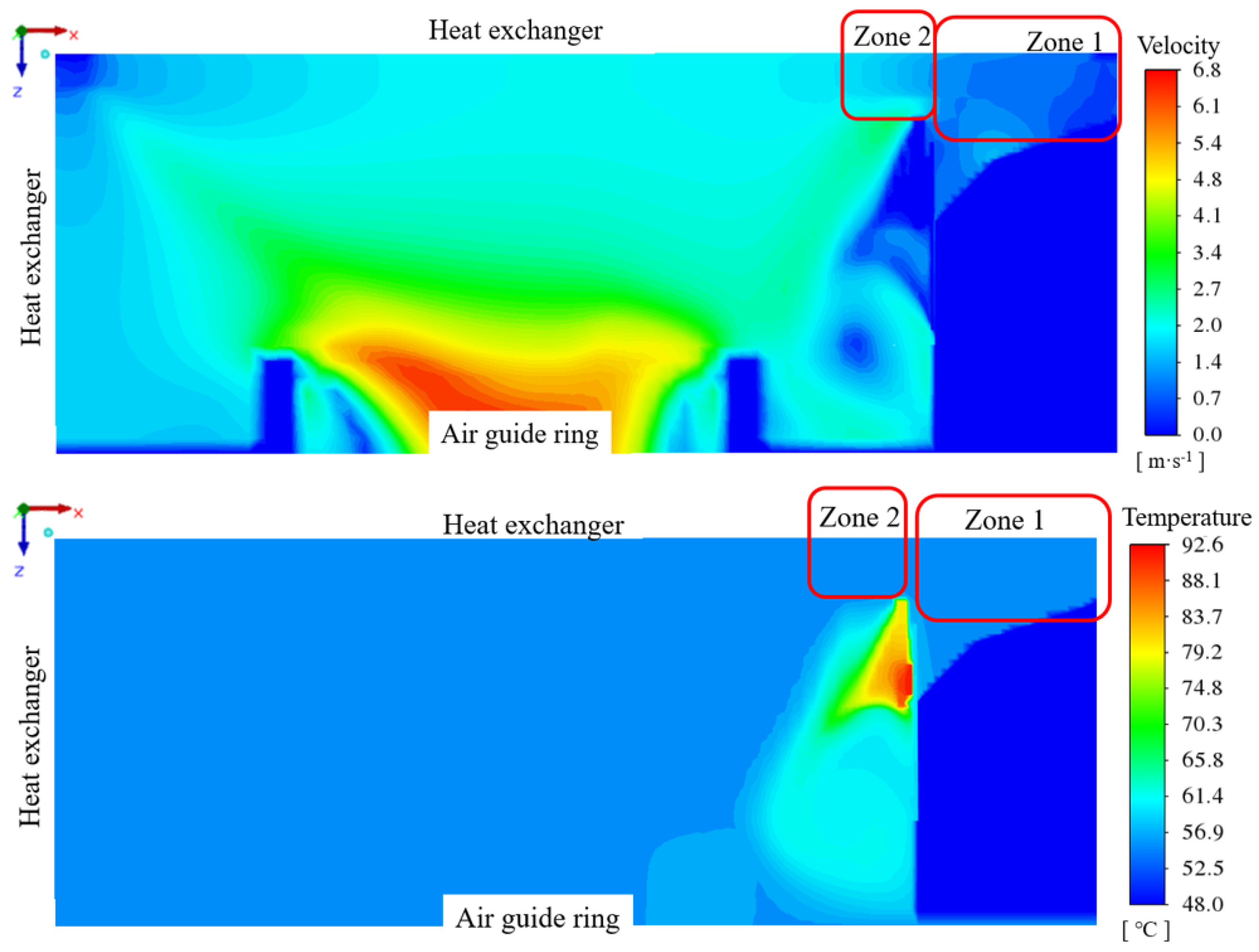
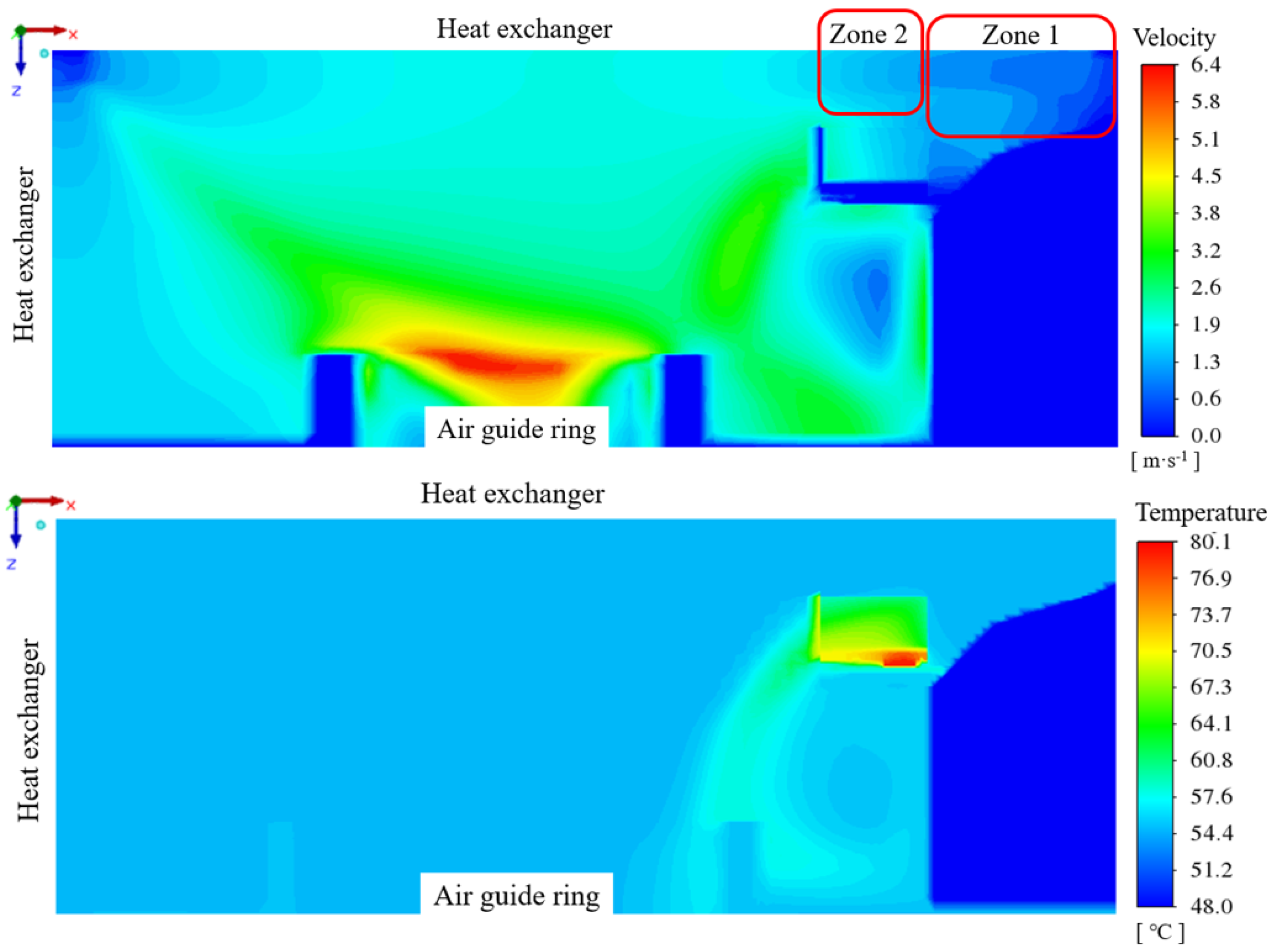
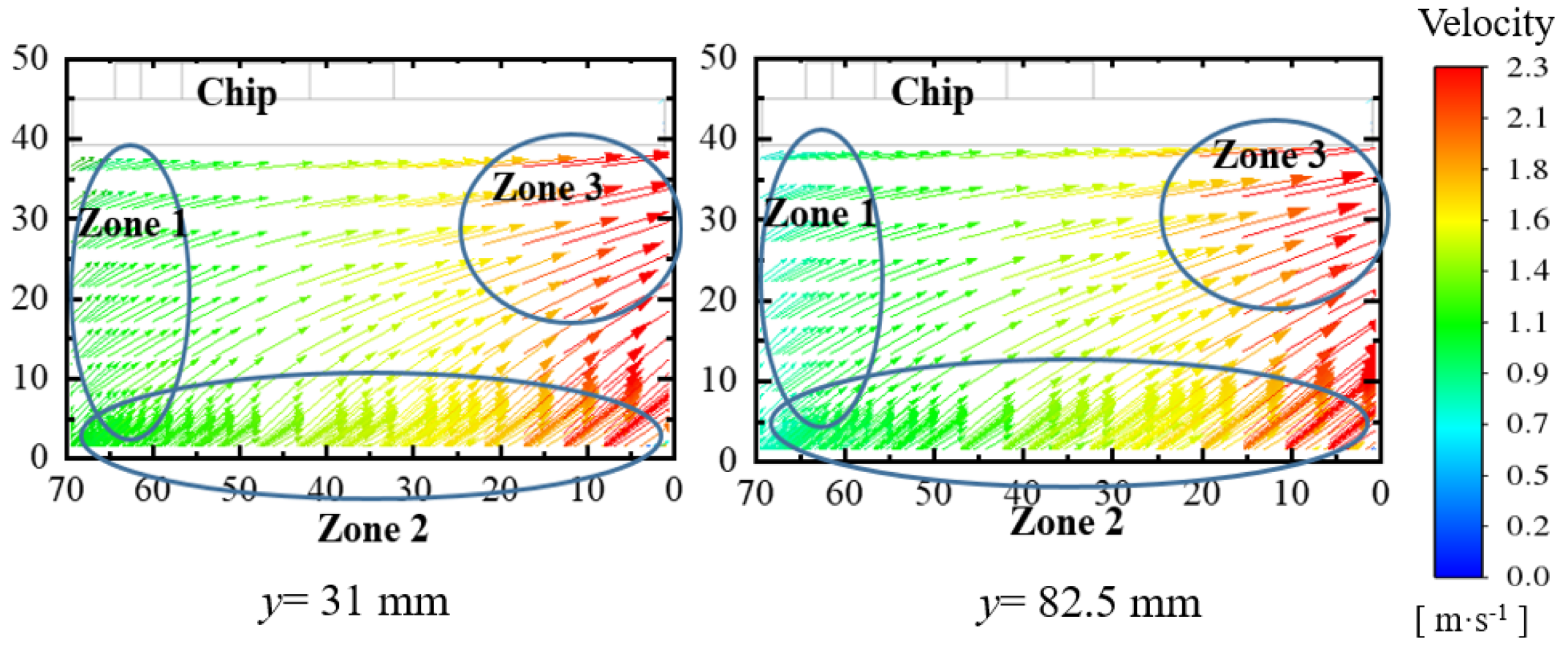
4.3. Fins Facing Down with Air Intake from Compressor Compartment
4.4. Fins Facing Down with Back Air Intake
4.5. Fins Facing Left with Back Air Intake
4.6. Fins Facing Back with Back Air Intake
4.7. Comparison of Four Cases
5. Conclusions
- (1)
- Multiple chips are arranged on the same heat sink substrate, and the heat dissipation process of the chips will be coupled with each other. The placement of the chip on the circuit board has an important effect on the heat dissipation of the chip. The optimization of multi-chip placement on the substrate is an important research topic in the future.
- (2)
- Case IV indeed demonstrates the most favorable thermal performance and is recommended as the optimal configuration for the electronic control module in variable frequency air conditioner outdoor units. Case IV has the highest HTC at 316.5 W·m−2·°C−1, outperforming case I by 6.9%, case II by 13.9%, and case III by 56.8%. The air impact jet is very beneficial to the heat dissipation process of the heat sink. The flow rate and temperature of the effective cooling air entering the heat sink play an important role in strengthening the heat dissipation of the heat sink.
- (3)
- Under the condition that the structural parameters of the heat sink are unchanged, the effect of heat transfer can be enhanced by changing the installation position of the heat sink and the direction between the heat sink and the air flow. The total effective cooling air mass flow rate in case IV exhibits a 238% increase compared to case I. In case IV, the maximum chip temperature is more than 10 °C lower than that in cases I and III. The effect is obvious.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Area (mm2) |
| H | Height of the heat sink (mm) |
| HTC | Heat transfer coefficient (W·m−2·°C−1) |
| L | Length of the heat sink (mm) |
| Mass flow rate (kg·s−1) | |
| P | Power consumption (W) |
| Q̇ | Heat transfer rate dissipated from the fin (W) |
| Rjh | Thermal resistance between heat source junction and heat sink (°C·W−1) |
| Rja | Thermal resistance between junction and ambient air (°C·W−1) |
| Tf,out | Heat sink outlet air average temperature (°C) |
| Tf,in | Heat sink inlet air average temperature (°C) |
| W | Width of the heat sink (mm) |
| δ | Uncertainty |
| AC | Alternating current |
| BR | Bridge rectifier |
| DC | Direct current |
| FRD | Fast recovery diode |
| FS | Full-scale |
| IGBT | Insulated gate bipolar transistor |
| IPM | Intelligent power module |
| PCB | Printed circuit board |
| PV | Photovoltaic |
| RH | Relative humidity |
References
- Aggarwal, V.; Meena, C.S.; Kumar, A.; Alam, T.; Kumar, A.; Ghosh, A.; Ghosh, A. Potential and Future Prospects of Geothermal Energy in Space Conditioning of Buildings: India and Worldwide Review. Sustainability 2020, 12, 8428. [Google Scholar] [CrossRef]
- Bar-Cohen, A.; Iyengar, M. Design and Optimization of Air-Cooled Heat Sinks for Sustainable Development. IEEE Trans. Compon. Packag. Technol. 2002, 25, 584–591. [Google Scholar] [CrossRef]
- Li, Z.; Luo, H.; Jiang, Y.; Liu, H.; Xu, L.; Cao, K.; Wu, H.; Gao, P.; Liu, H. Comprehensive Review and Future Prospects on Chip-Scale Thermal Management: Core of Data Center’s Thermal Management. Appl. Therm. Eng. 2024, 251, 123612. [Google Scholar] [CrossRef]
- Ayers, C.W.; Conklin, J.C.; Hsu, J.S.; Lowe, K.T. A Unique Approach to Power Electronics and Motor Cooling in a Hybrid Electric Vehicle Environment. In Proceedings of the 2007 IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; Volumes 1 and 2, pp. 102–106. [Google Scholar]
- Whelan, B.P.; Kempers, R.; Robinson, A.J. A Liquid-Based System for Cpu Cooling Implementing a Jet Array Impingement Waterblock and a Tube Array Remote Heat Exchanger. Appl. Therm. Eng. 2012, 39, 86–94. [Google Scholar] [CrossRef]
- Vittorini, D.; Cipollone, R. Fin-Cooled Photovoltaic Module Modeling—Performances Mapping and Electric Efficiency Assessment under Real Operating Conditions. Energy 2019, 167, 159–167. [Google Scholar] [CrossRef]
- Kazem, H.A.; Al-Waeli, A.A.; Chaichan, M.T.; Sopian, K.; Ahmed, A.-A.; Roslam, W.I.W.N. Enhancement of Photovoltaic Module Performance Using Passive Cooling (Fins): A Comprehensive Review. Case Stud. Therm. Eng. 2023, 49, 103316. [Google Scholar] [CrossRef]
- Zaghloul, H.; Abdelrahman, M.A.; Rabbo, M.F.A.; Emam, M. Passive Thermal Control of a Triple-Junction Solar Cell at High Concentrations Using Various Finned Heat Sink Configurations. J. Clean. Prod. 2023, 387, 135844. [Google Scholar] [CrossRef]
- Johnston, E.; Szabo, P.S.B.; Bennett, N.S. Cooling Silicon Photovoltaic Cells Using Finned Heat Sinks and the Effect of Inclination Angle. Therm. Sci. Eng. Prog. 2021, 23, 100902. [Google Scholar] [CrossRef]
- Adhikari, R.C.; Wood, D.H.; Pahlevani, M. An Experimental and Numerical Study of Forced Convection Heat Transfer from Rectangular Fins at Low Reynolds Numbers. Int. J. Heat Mass Transf. 2020, 163, 120418. [Google Scholar] [CrossRef]
- Meng, X.; Zhu, J.; Wei, X.; Yan, Y. Natural Convection Heat Transfer of a Straight-Fin Heat Sink. Int. J. Heat Mass Transf. 2018, 123, 561–568. [Google Scholar] [CrossRef]
- Moradikazerouni, A.; Afrand, M.; Alsarraf, J.; Wongwises, S.; Asadi, A.; Nguyen, T.K. Investigation of a Computer Cpu Heat Sink under Laminar Forced Convection Using a Structural Stability Method. Int. J. Heat Mass Transf. 2019, 134, 1218–1226. [Google Scholar] [CrossRef]
- Kim, T.; Han, Y.-S.; You, H.; Kim, C.; Kim, M.; Choi, B.-I.; Do, K.H. Pressure Drop and Thermal Resistance Characteristics of Plain-Fin Heat Sink with Impingement Flow. Int. J. Therm. Sci. 2023, 194, 108598. [Google Scholar] [CrossRef]
- Mehryan, S.A.M.; Kashkooli, F.M.; Soltani, M. Comprehensive Study of the Impacts of Surrounding Structures on the Aero-Dynamic Performance and Flow Characteristics of an Outdoor Unit of Split-Type Air Conditioner. Build. Simul. 2017, 11, 325–337. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, J.; Wang, C.; Zhang, Z. Experimental and Numerical Study of Electronic Module-Cooling Heat Sinks Used in a Variable Frequency Air-Conditioner Outdoor Unit. Int. J. Refrig. 2014, 38, 10–21. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the Uncertainties in Experimental Results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Q.; Jiang, X.; Dong, X.; Zou, W.; Zhang, X. Numerical Simulation of Elastocaloric Cooling Thermal Control System for Electronic Chips. J. Refrig. 2024, 45, 85–92. [Google Scholar]
- Tal, Y. An Improved Two-Resistors Compact Thermal Model by Means of Modified Top-Surface-Area. In Proceedings of the Eighteenth Annual IEEE Semiconductor Thermal Measurement and Management Symposium, Proceedings 2002, San Jose, CA, USA, 12–14 March 2002; pp. 64–70. [Google Scholar]
- Dang, H.; Lu, Y.; Du, Y.; Zhang, X.; Zhang, Q.; Ma, W.; Zhang, X. A Detailed Thermal Resistance Network Analysis of Fcbga Package. J. Therm. Sci. 2023, 33, 18–28. [Google Scholar] [CrossRef]
- Lee, D.; Ji, H.Y.; Chung, D.-Y.; Kim, W.D.; Kang, C.; Kim, J.-Y. Numerical Study on the Thermal Fluid of Multi-Chip Test Chamber with Guide Vane. Case Stud. Therm. Eng. 2024, 53, 103851. [Google Scholar] [CrossRef]







| Equipment | Type | Measuring Range | Uncertainty |
|---|---|---|---|
| Thermocouple | T | −200 °C~350 °C | ±0.2 °C |
| Standard DC power supply | GWINSTEK GPS-3303C | 0 V~30 V 0 A~3 A | ±0.01% FS ±0.01% FS |
| Digital differential pressure measuring instrument | Testo 512 | 0 Pa~200 Pa | ±0.5% FS |
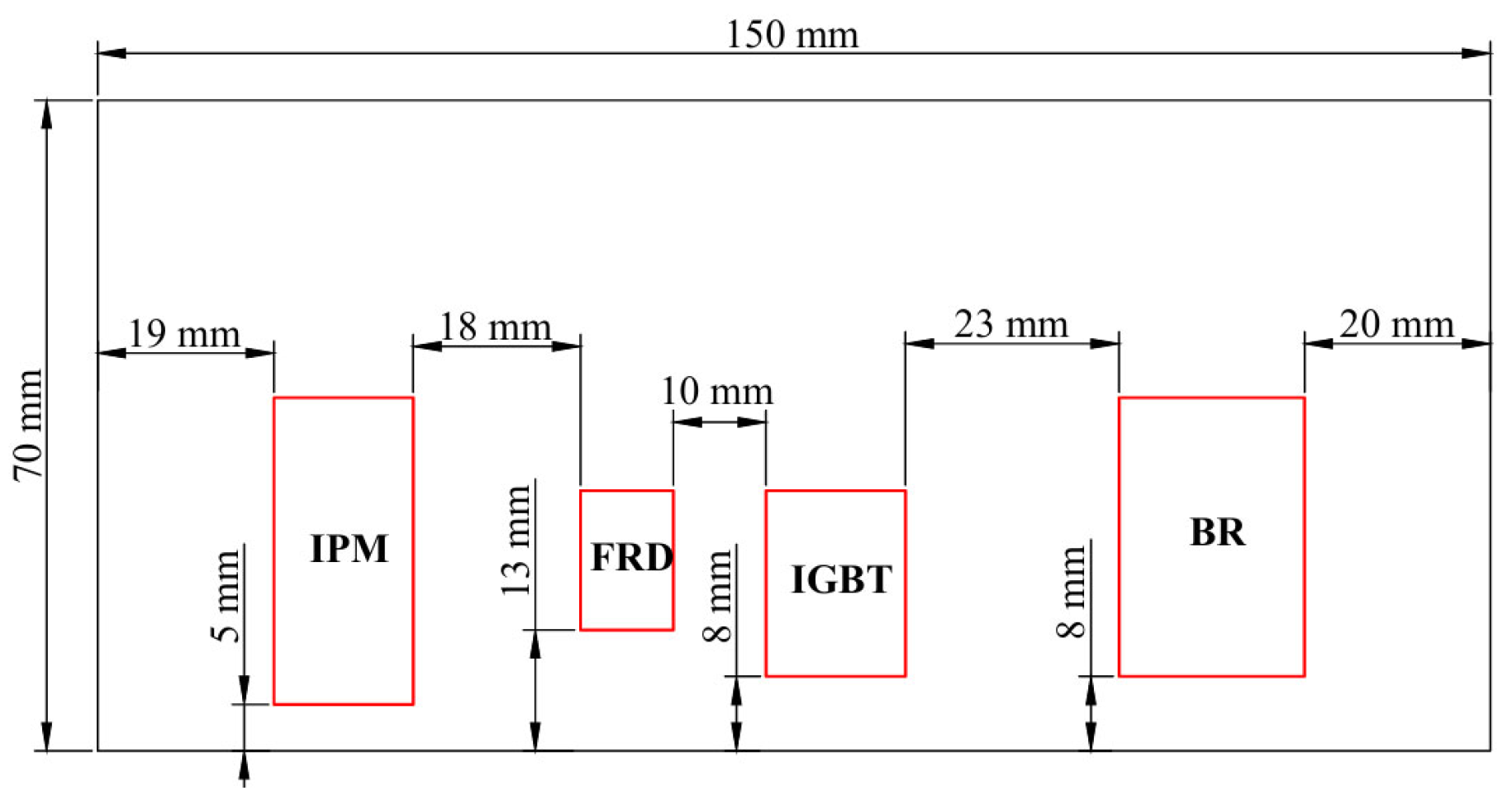
| Type of Chips | Rjh (°C·W−1) | Rja (°C·W−1) | Q̇ (W) | L (mm) | W (mm) | H (mm) | Supplier |
|---|---|---|---|---|---|---|---|
| IPM | 0.47 | 12.50 | 32.6 | 33 | 15 | 4 | Silan |
| FRD | 0.25 | 40.00 | 10.0 | 15 | 10 | 4 | Vishay |
| IGBT | 0.45 | 40.00 | 33.0 | 20 | 15 | 4 | Infineon |
| BR | 0.80 | 22.00 | 24.0 | 30 | 20 | 4 | ASEMI |
| Heat Sink Type | Type A | Type B |
|---|---|---|
| Substrate thickness (mm) | 5 | 5 |
| Total height (mm) | 42 | 42 |
| Width (mm) | 150 | 70 |
| Channel length (mm) | 70 | 150 |
| Fin thickness (mm) | 1.5 | 1.5 |
| Fin spacing (mm) | 3 | 3.7 |
| Number of fins | 29 | 14 |
| Case | I | II | III | IV |
|---|---|---|---|---|
| Heat sink | Type A | Type B | Type A | Type A |
| Distance from the outdoor heat exchanger (mm) | 27 | 27 | 23 | 43 |
| Distance from the front panel of the outdoor unit (mm) | 63 | 63 | 147 | 155 |
| Distance from the cover plate of the outdoor unit (mm) | 15 | 15 | 10 | 10 |
| The distance from the left plate of the outdoor unit (mm) | 205 | 205 | 208 | 203 |
| Case No. | Temperature of Various Chips (°C) | Tf,in | Tf,out | HTC | |||
|---|---|---|---|---|---|---|---|
| IPM | FRD | IGBT | BR | (°C) | (°C) | (W·m−2·°C−1) | |
| I | 90.8 | 89.7 | 90.7 | 83.9 | 48.0 | 86.0 | 296.1 |
| II | 99.5 | 97.9 | 98.5 | 90.7 | 53.0 | 93.9 | 277.9 |
| III | 92 | 92 | 94.1 | 86.9 | 53.0 | 65.6 | 201.8 |
| IV | 79.6 | 78.9 | 80.7 | 74.9 | 53.0 | 63.3 | 316.5 |
| Parameters | Face 1 | Face 2 | Face 3 | Total |
|---|---|---|---|---|
| Cases | g·s−1 | g·s−1 | g·s−1 | g·s−1 |
| I | 2.5 | 0.1 | −2.6 | 2.6 |
| II | 2.3 | −1.2 | −1.1 | 2.3 |
| III | 7.8 | −6.8 | −1.0 | 7.8 |
| Ⅳ | 2.6 | 6.2 | −8.8 | 8.8 |
| Case No. | I | II | III | IV |
|---|---|---|---|---|
| Experimental | 90.8 | 99.5 | 94.1 | 80.7 |
| Simulated | 90.3 | 99.1 | 92.8 | 80.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Du, S.; Bie, Q.; Wang, D.; Song, Q.; Zhou, S. Experimental and Numerical Study of the Heat Dissipation of the Electronic Module in an Air Conditioner Outdoor Unit. Energies 2025, 18, 2439. https://doi.org/10.3390/en18102439
Peng Y, Du S, Bie Q, Wang D, Song Q, Zhou S. Experimental and Numerical Study of the Heat Dissipation of the Electronic Module in an Air Conditioner Outdoor Unit. Energies. 2025; 18(10):2439. https://doi.org/10.3390/en18102439
Chicago/Turabian StylePeng, Yi, Su Du, Qingfeng Bie, Dechang Wang, Qinglu Song, and Sai Zhou. 2025. "Experimental and Numerical Study of the Heat Dissipation of the Electronic Module in an Air Conditioner Outdoor Unit" Energies 18, no. 10: 2439. https://doi.org/10.3390/en18102439
APA StylePeng, Y., Du, S., Bie, Q., Wang, D., Song, Q., & Zhou, S. (2025). Experimental and Numerical Study of the Heat Dissipation of the Electronic Module in an Air Conditioner Outdoor Unit. Energies, 18(10), 2439. https://doi.org/10.3390/en18102439






