Moisture Localization and Diagnosis Method for Power Distribution Cables Based on Dynamic Frequency Domain Reflectometry
Abstract
1. Introduction
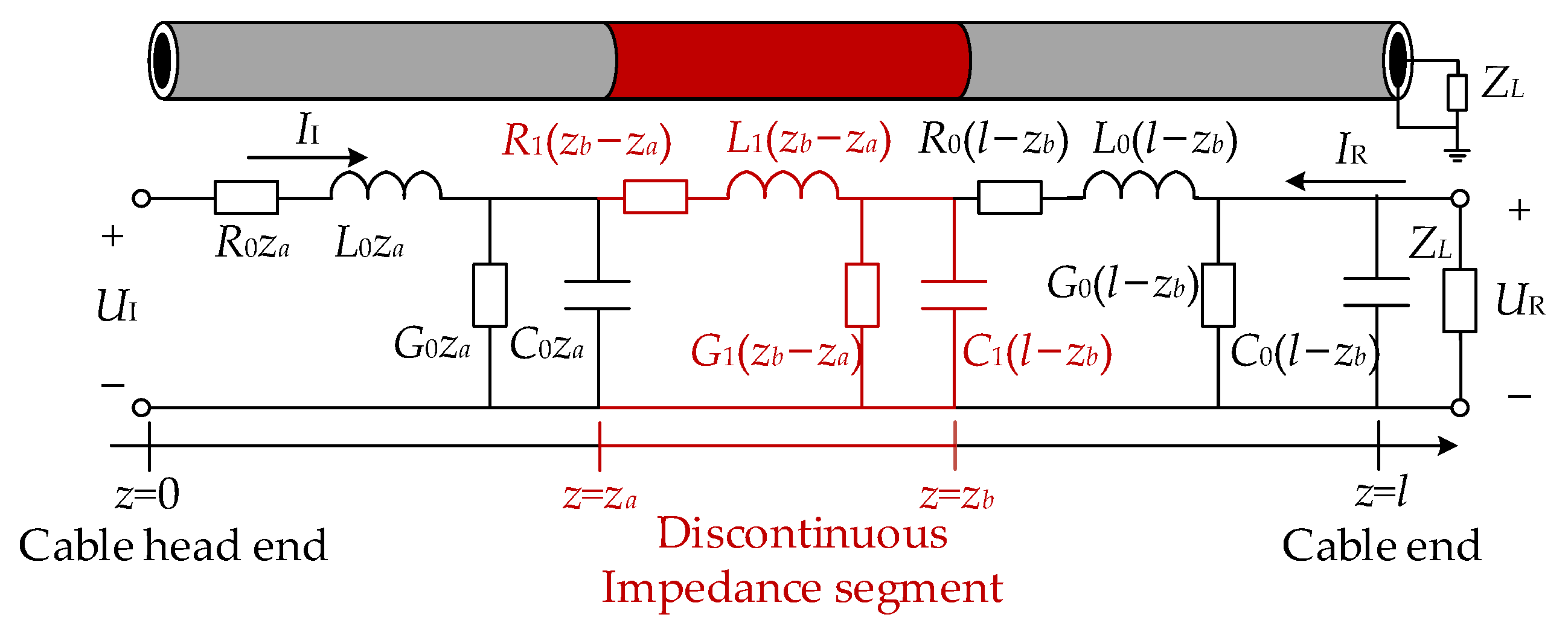
2. Principle of Defect Localization Using Frequency Domain Reflectometry
2.1. Cable Reflection Coefficient Spectrum
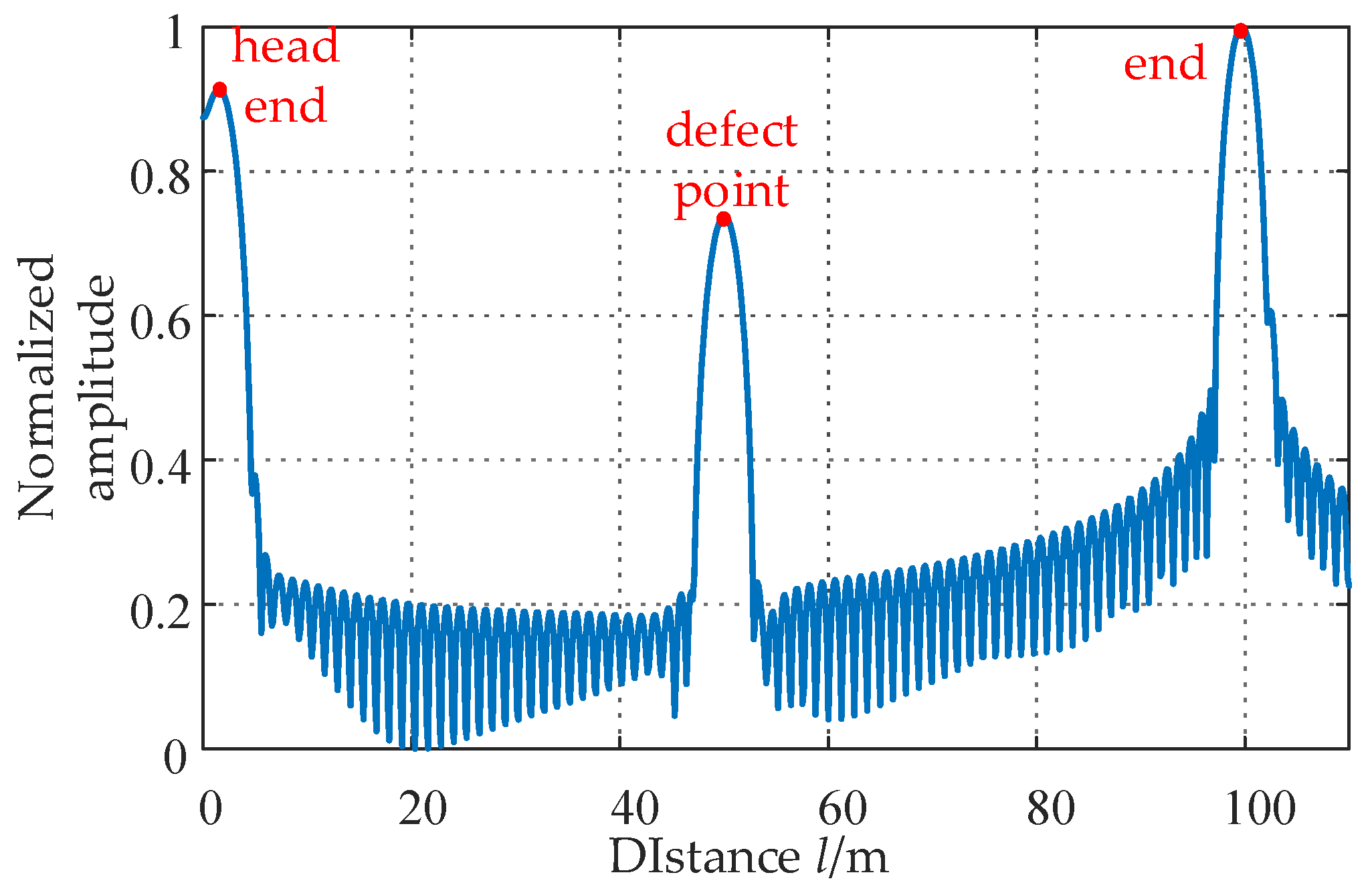
2.2. Defect Localization Principle
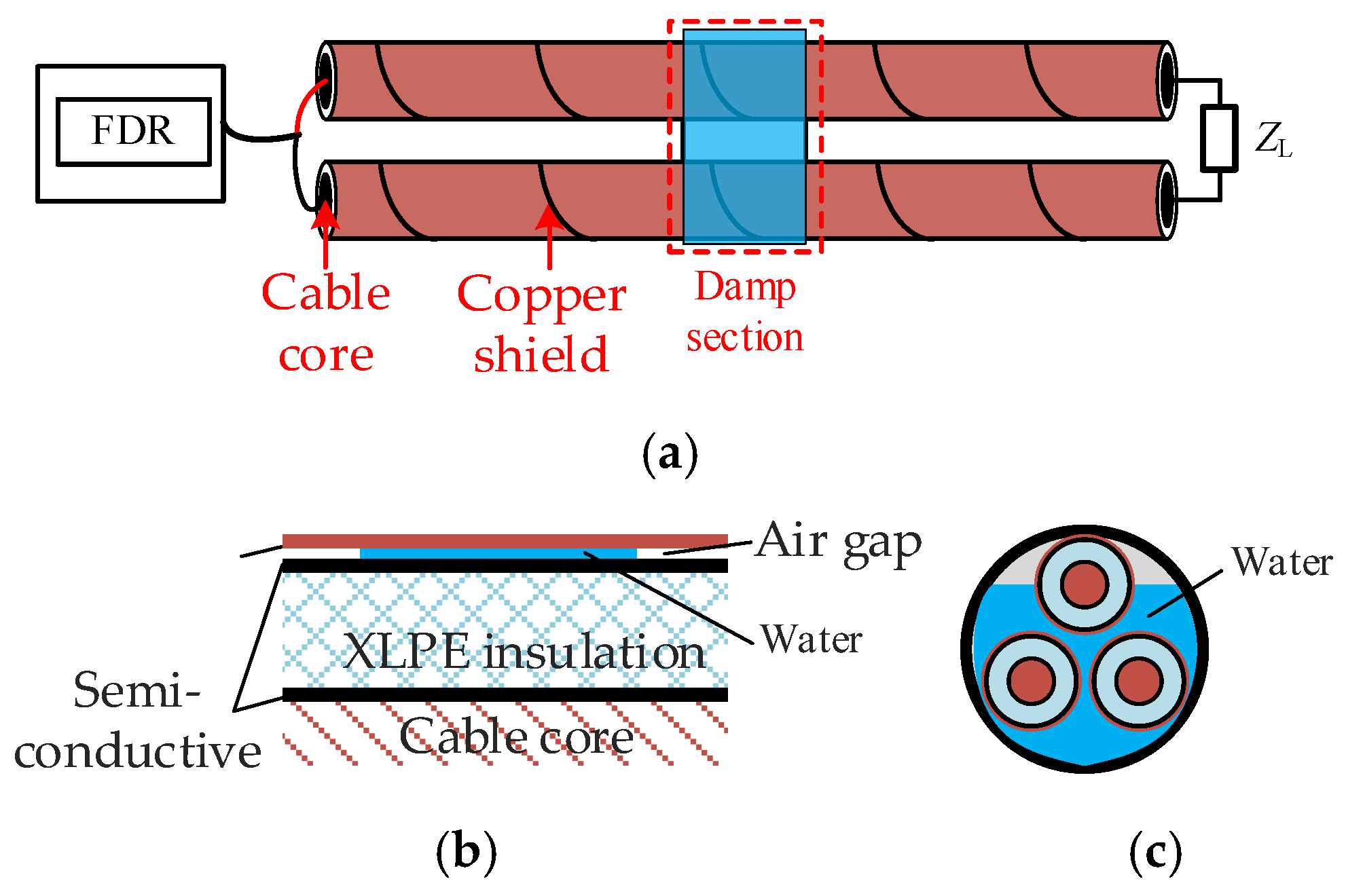
3. Dynamic FDR-Based Moisture Localization and Diagnosis Method for Cables
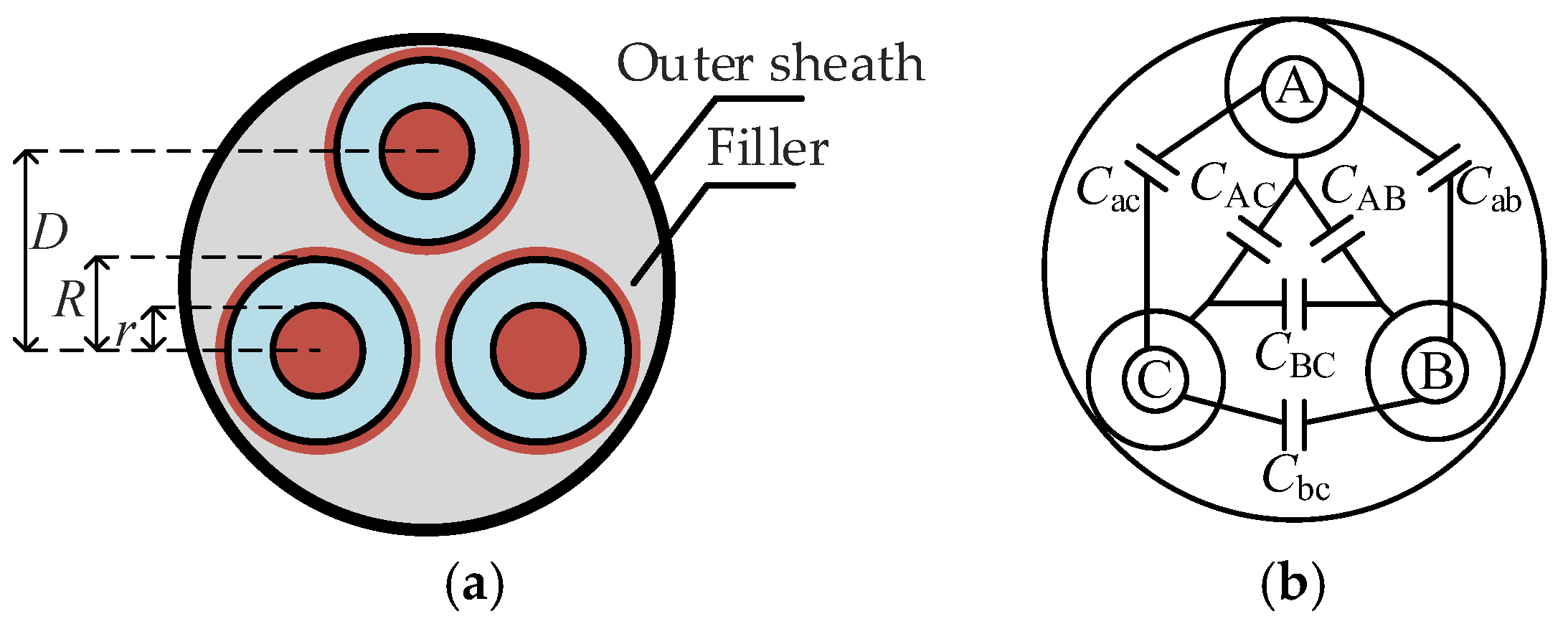
3.1. Moisture Characteristics and Capacitance Changes in Three-Core Cables
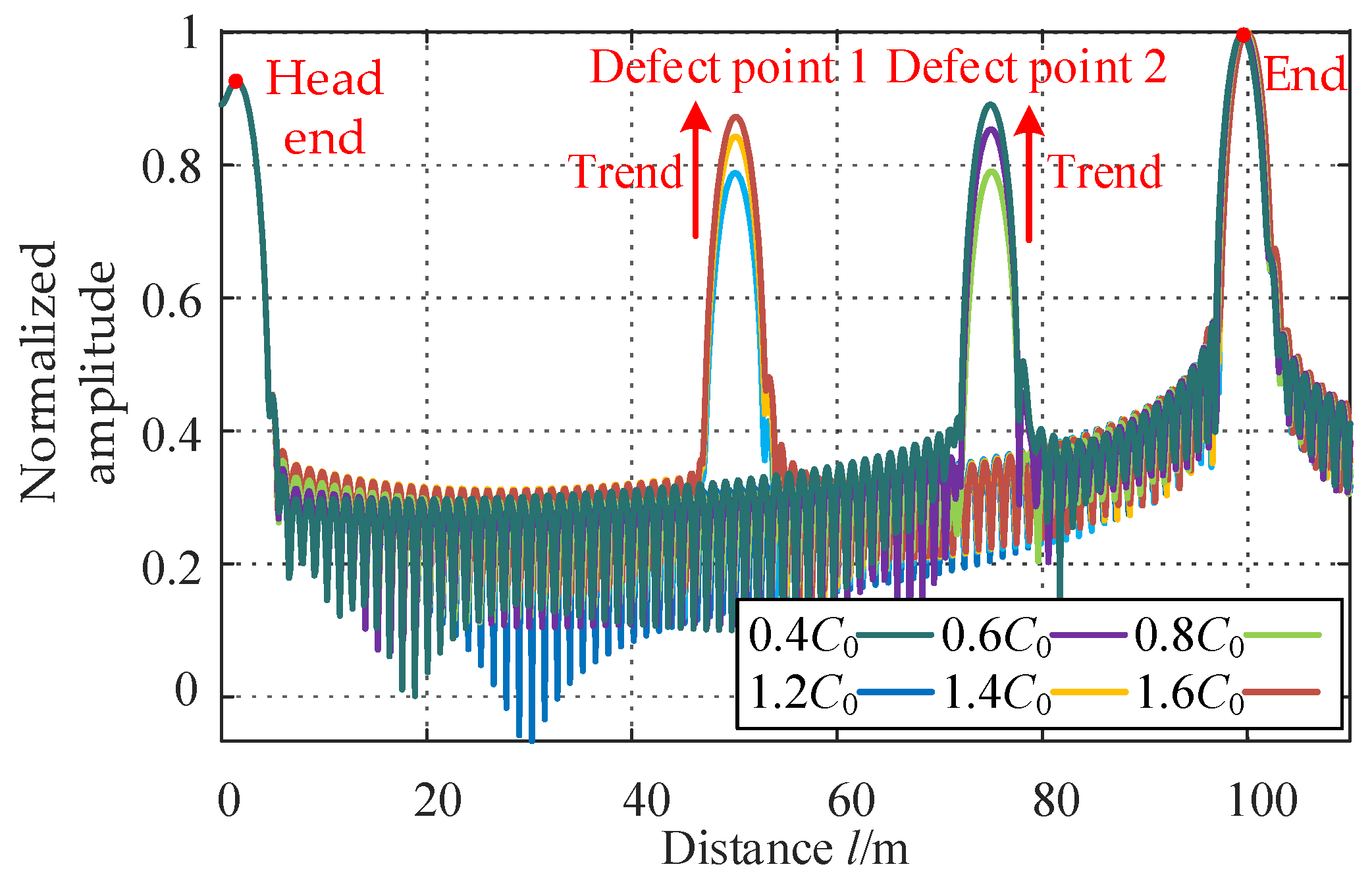
3.2. Dynamic Gradient on the Dynamic FDR Frequency Domain Localization Map
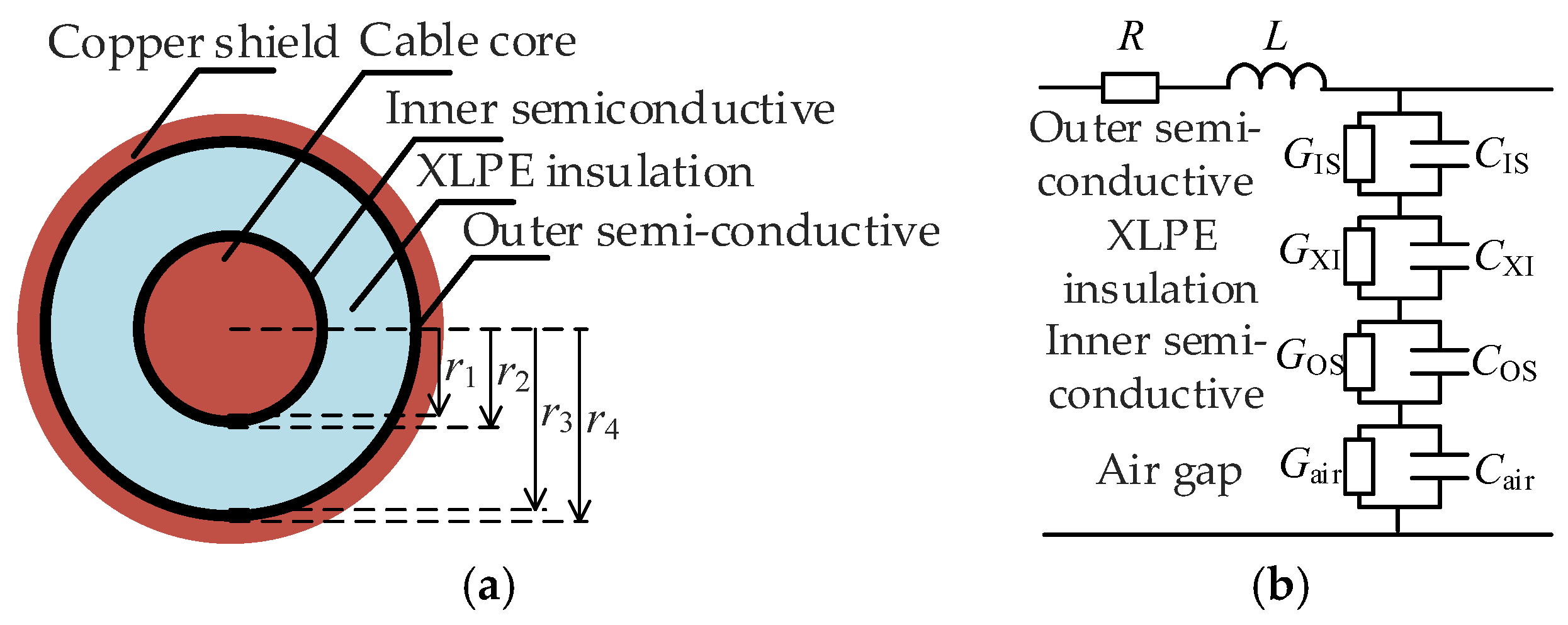
4. Temperature Response of Distributed Capacitance in Cable Moisture Defects
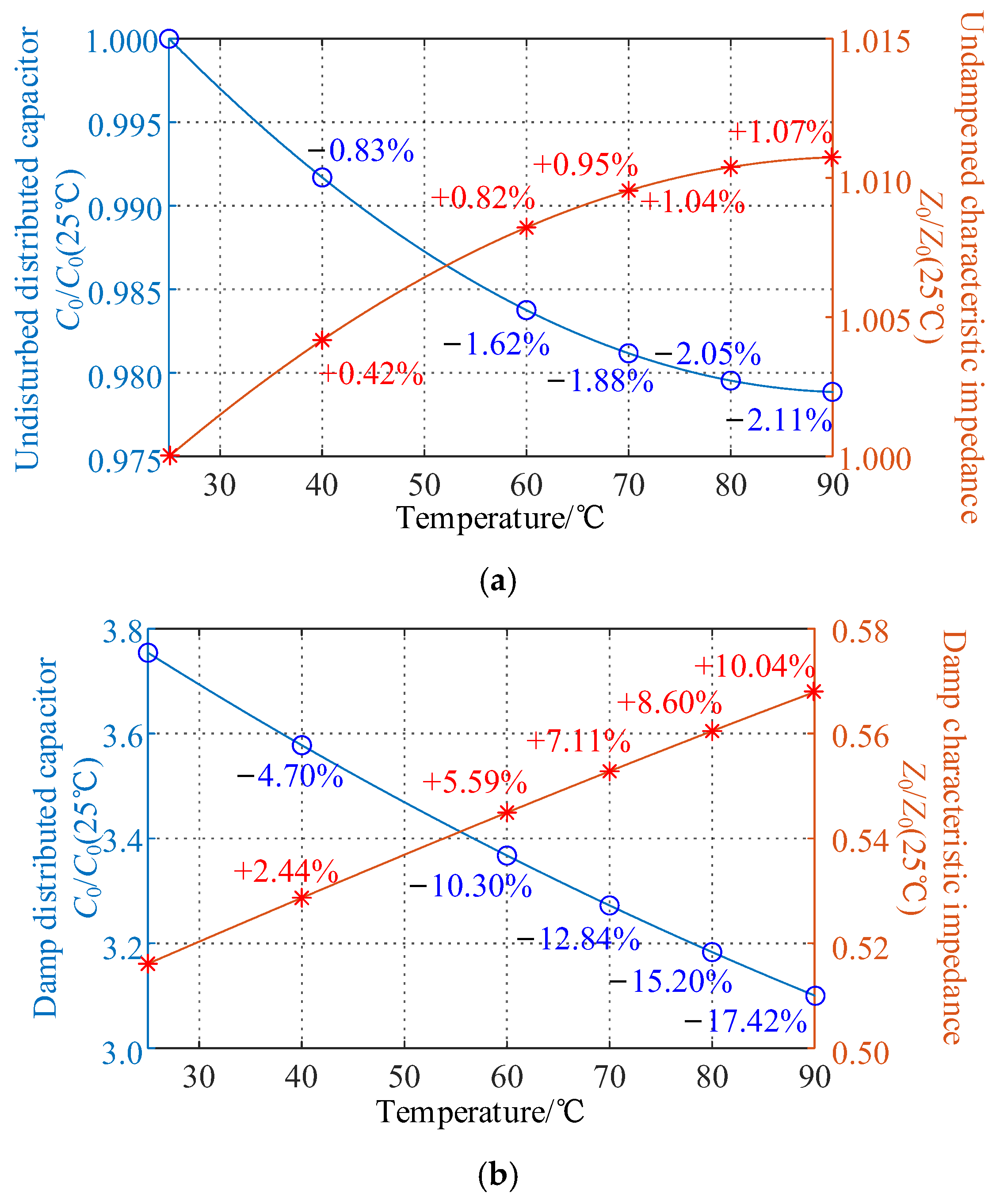
4.1. Temperature Response of Dielectric Constants in Moisture Defects
4.2. Computational Analysis of Temperature Response in Moisture-Affected Cable Capacitance
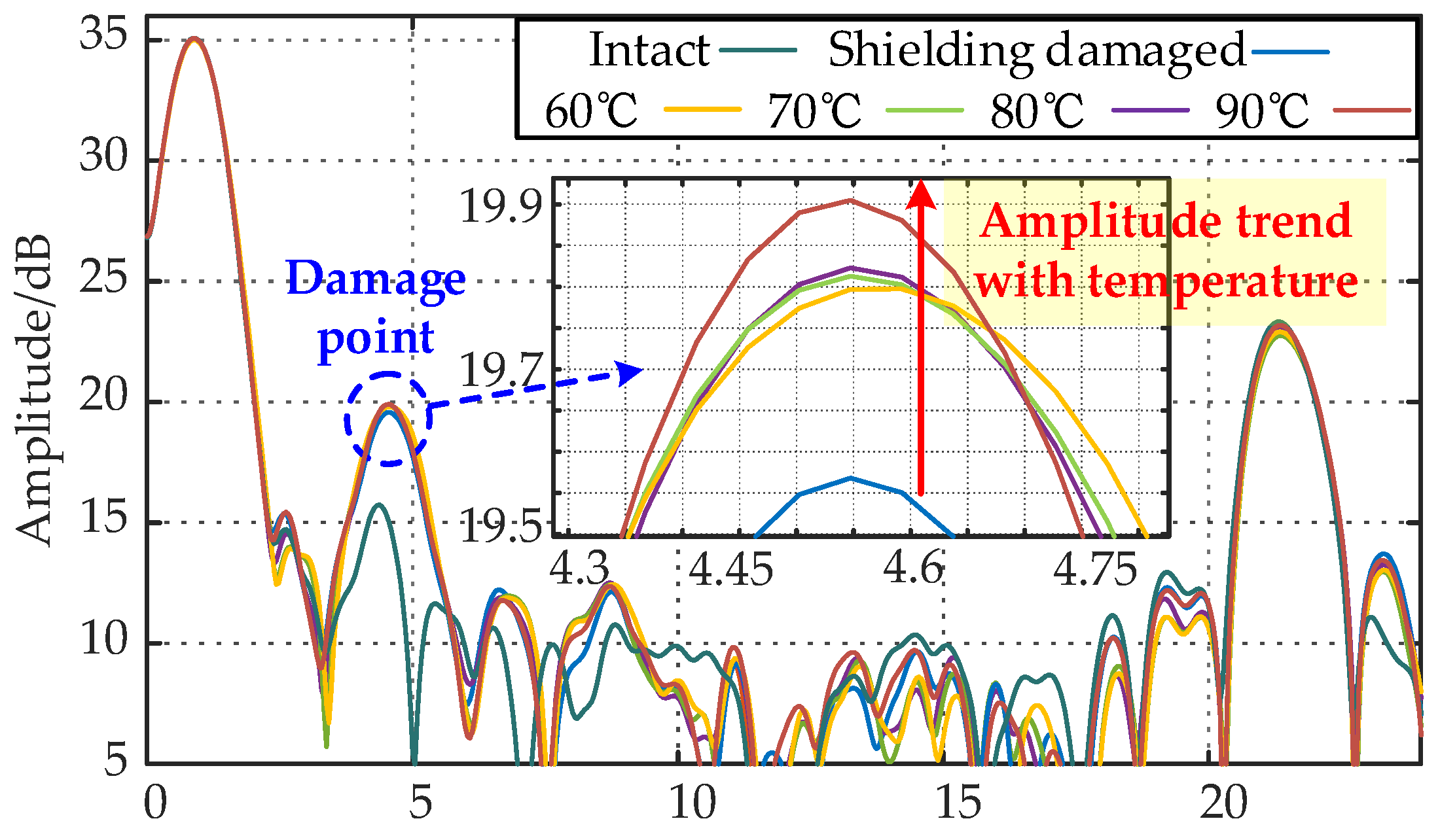
5. Experimental Validation
5.1. Experimental Design
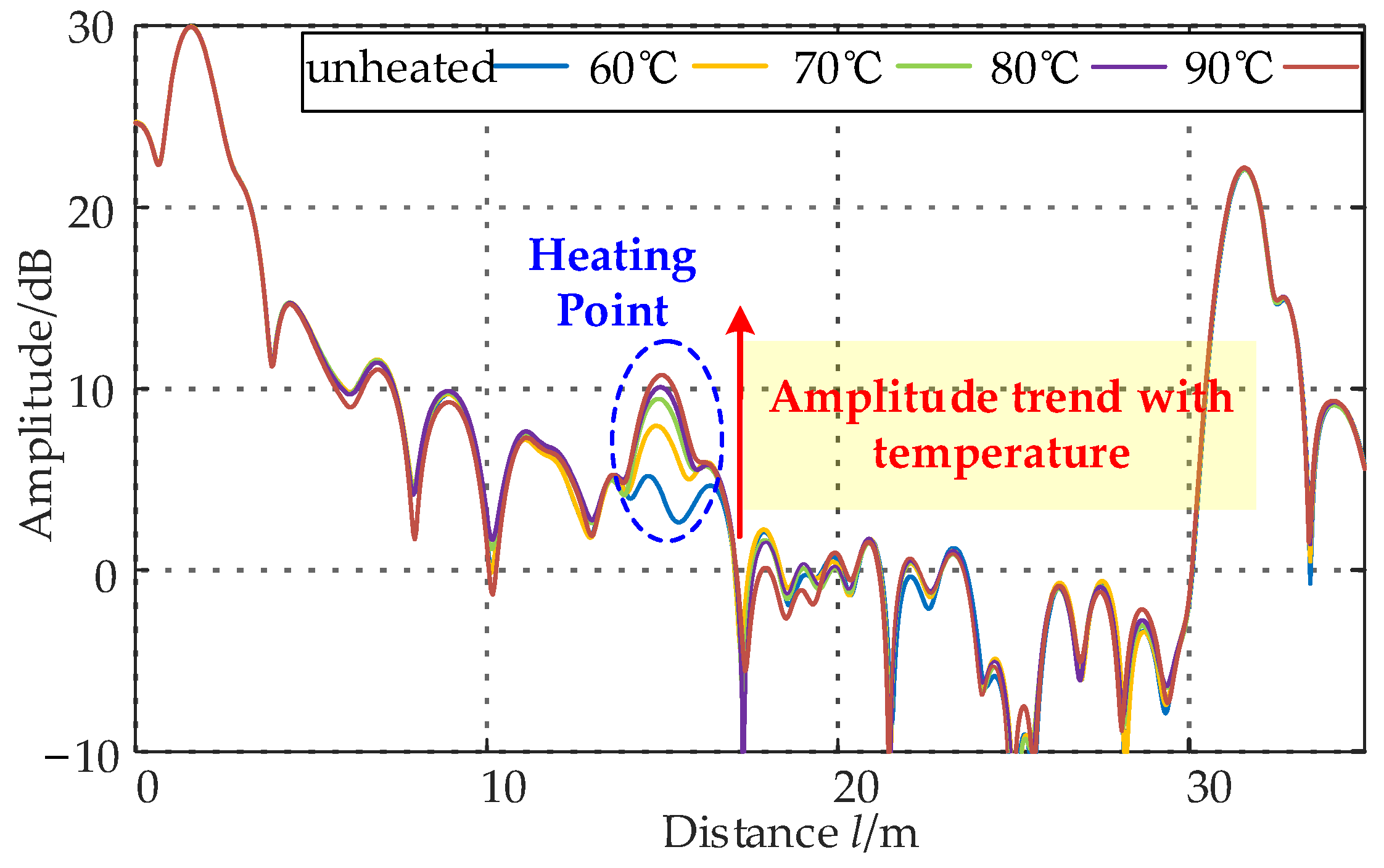
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDR | Frequency domain reflectometry |
| D-FDR | Dynamic frequency domain reflectometry |
| FT | Fourier transform |
References
- Zhu, B.; Jia, Z.D.; Yuan, Y.; Lu, G.; Fan, W.N.; Guan, Z.C. Research on the insulation properties of 10 kV XLPE damp cable. In Proceedings of the 2015 IEEE 11th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Sydney, NSW, Australia, 19–22 July 2015; pp. 592–595. [Google Scholar]
- Adebomi, A.J.; Putter, H.T.; Legler, P. Contemporary Techniques and Case Studies in Offline Condition Assessment of MV Underground Power Cables. In Proceedings of the 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athens, Greece, 10–13 September 2018; pp. 1–6. [Google Scholar]
- Jeon, S.-S.; Joung, J.M.; Lee, C.-K.; Kim, Y.-D. Cable fault and assessment using multiple frequency autoencoder regression-based reflectometry. IEICE Electron. Express 2022, 19, 20220113. [Google Scholar] [CrossRef]
- Khamlichi, A.; Garnacho, F.; Simón, P. New Synthetic Partial Discharge Calibrator for Qualification of Partial Discharge Analyzers for Insulation Diagnosis of HVDC and HVAC Grids. Sensors 2023, 23, 5955. [Google Scholar] [CrossRef] [PubMed]
- Arcones, E.; Álvarez, F.; Khamlichi, A.; Garnacho, F. Scale Modular Test Platform for the Characterization of PD Measuring Systems Using HFCT Sensors. Sensors 2024, 24, 1363. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Liu, Y.; Huang, Y.; Xin, Y.; Han, T.; Du, B. Defect Identification of XLPE Power Cable Using Harmonic Visualized Characteristics of Grounding Current. Electronics 2024, 13, 1159. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, H.; Su, G.; Shi, X. Defect Diagnosis Method of Cable Shielding Layer Based on Frequency Domain Reflection Coefficient Spectrum. IEEE Trans. Electromagn. Compat. 2023, 65, 114–125. [Google Scholar] [CrossRef]
- Ohki, Y.; Hirai, N.; Yamada, T.; Kumagai, S. Highly sensitive location method of an abnormal temperature point in a cable by frequency domain reflectometry. In Proceedings of the 2013 IEEE International Conference on Solid Dielectrics (ICSD), Bologna, Italy, 30 June–4 July 2013; pp. 117–120. [Google Scholar]
- Guo, M.; Xu, J.; Zhang, Y.; Xiao, X.; Yang, Z.; Wu, Z. A Partial Discharge Localization Method for AC XLPE Cable Based on Improved GCC Algorithm. IEEE Open Access J. Power Energy 2023, 10, 605–616. [Google Scholar] [CrossRef]
- Zhu, G.; Liu, Z.; Zhou, K.; Wang, Z.; Lu, L.; Li, Y.; Meng, P. A Novel Dampness Diagnosis Method for Distribution Power Cables Based on Time-Frequency Domain Conversion. IEEE Trans. Instrum. Meas. 2022, 71, 3510609. [Google Scholar] [CrossRef]
- Chen, H.; Wang, L.; Xu, H.; Yang, S. Research on blind spot elimination of spread spectrum time domain reflectometry based on signal separation. Chin. J. Sci. Instrum. 2024, 45, 280–289. (In Chinese) [Google Scholar]
- Möhring, B.N.; Siart, U.; Eibert, T.F. Fast Chirp Frequency-Modulated Continuous-Wave Reflectometer for Monitoring Fast Varying Discontinuities on Transmission Lines. IEEE Trans. Instrum. Meas. 2021, 70, 8005611. [Google Scholar] [CrossRef]
- Zou, X.Y.; Mu, H.B.; Zhang, H.T.; Qu, L.Q.; He, Y.F.; Zhang, G.J. An Efficient Cross-Terms Suppression Method in Time–Frequency Domain Reflectometry for Cable Defect Localization. IEEE Trans. Instrum. Meas. 2022, 71, 3511610. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, D.; He, J.; Li, M. Local degradation diagnosis for cable insulation based on broadband impedance spectroscopy. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2097–2107. [Google Scholar] [CrossRef]
- Xie, M.; Zhou, K.; Zhao, S.; He, M.; Zhang, F. A new location method of local defects in power cables based on reflection coefficient spectrum. Power Syst. Technol. 2017, 41, 3083–3089. (In Chinese) [Google Scholar]
- Rong, L.I.; Kai, Z.H.O.U.; Xianjie, R.A.O. Localization of Damp Defects and Analysis of Moisture Characteristics for Cable Body in the Distribution Grid. Proc. CSEE 2021, 45, 825–832. (In Chinese) [Google Scholar]
- Rao, X.; Xu, Z.; Guan, H.; Ding, Y.; Yang, X.; Yang, Y. Cable Defect Location by Using Frequency Domain Reflectometry with Synchrosqueezing Generalized S-Transform. In Proceedings of the 2023 Panda Forum on Power and Energy (PandaFPE), Chengdu, China, 27–30 April 2023; pp. 1178–1182. [Google Scholar]
- Mu, H.B.; Zhang, H.T.; Zou, X.Y.; Zhang, D.N.; Lu, X.; Zhang, G.J. Sensitivity Improvement in Cable Faults Location by Using Broadband Impedance Spectroscopy with Dolph-Chebyshev Window. IEEE Trans. Power Deliv. 2022, 37, 3846–3854. [Google Scholar] [CrossRef]
- Nazrin, A.; Kuan, T.M.; Mansour, D.E.A.; Farade, R.A.; Ariffin, A.M.; Abd Rahman, M.S.; Wahab, N.I.B.A. Innovative Approaches for Augmenting Dielectric Properties in Cross-Linked Polyethylene (XLPE): A Review. Heliyon 2024, 10, e34737. [Google Scholar] [CrossRef] [PubMed]
- Nyamupangedengu, C.; Sotsaka, M.; Mlangeni, G.; Ndlovu, L.; Munilal, S. Effect of Temperature Variations on Wave Propagation Characteristics in Power Cables. SAIEE Afr. Res. J. 2015, 106, 28–38. [Google Scholar] [CrossRef]
- Xiaoyan, B.; Qibin, Z.; Yang, F. Numerical Method for Capacitance Matrix of Coaxial Cables of Finite Length. High Volt. Eng. 2009, 35, 1920–1926. (In Chinese) [Google Scholar]
- Fanggao, C.; Saunders, G.A.; Hampton, R.N.; Moody, S.M.; Clark, A.M. The effect of hydrostatic pressure and temperature on the permittivity of crosslinked polyethylene. In Proceedings of the Seventh International Conference on Dielectric Materials, Measurements and Applications (Conf. Publ. No. 430), Bath, UK, 23–26 September 1996; pp. 267–270. [Google Scholar]
- Huang, J.; Zhou, K.; Xu, Y.; Meng, P.; Tang, Z.; Liang, Z. Upper Sweeping Frequency Selection for Cable Defect Location Based on STFT. IEEE Trans. Instrum. Meas. 2023, 72, 3521109. [Google Scholar] [CrossRef]
- Mo, S.; Zhang, D.; Li, Z.; Wan, Z. The Possibility of Fault Location in Cross-Bonded Cables by Broadband Impedance Spectroscopy. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 1416–1423. [Google Scholar] [CrossRef]



| Temperature (°C) | εXLPE | ∆ε |
|---|---|---|
| 25 | 2.608 | 0% |
| 40 | 2.551 | 2.16% |
| 60 | 2.498 | 4.20% |
| 70 | 2.481 | 4.86% |
| 80 | 2.470 | 5.27% |
| 90 | 2.466 | 5.44% |
| Temperature (°C) | εwater | ∆ε |
|---|---|---|
| 25 | 78.30 | 0% |
| 40 | 73.15 | 6.58% |
| 60 | 66.81 | 14.67% |
| 70 | 63.86 | 18.45% |
| 80 | 61.03 | 22.06% |
| 90 | 58.32 | 25.52% |
| Parameter | Value |
|---|---|
| Core radius rC | 3.35 mm |
| Half conductive layer thickness rSC | 1 mm |
| Insulation thickness rXLPE | 4 mm |
| Gap thickness rgap | 0.1 mm |
| Shielding layer radius rS | 9.5 mm |
| Cable core distance D | 21 mm |
| Cable core (aluminum) resistivity ρC | 2.83 × 108 Ω∙m |
| Shielding layer resistivity ρS | 1.75 × 108 Ω∙m |
| Vacuum permeability μ0 | 4π × 107 H/m |
| Semiconducting layer εSC | 1000 |
| Filler εFL | 2.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhou, K.; Ren, X.; Xu, Y. Moisture Localization and Diagnosis Method for Power Distribution Cables Based on Dynamic Frequency Domain Reflectometry. Energies 2025, 18, 2430. https://doi.org/10.3390/en18102430
Zhang H, Zhou K, Ren X, Xu Y. Moisture Localization and Diagnosis Method for Power Distribution Cables Based on Dynamic Frequency Domain Reflectometry. Energies. 2025; 18(10):2430. https://doi.org/10.3390/en18102430
Chicago/Turabian StyleZhang, Hongzhou, Kai Zhou, Xiang Ren, and Yefei Xu. 2025. "Moisture Localization and Diagnosis Method for Power Distribution Cables Based on Dynamic Frequency Domain Reflectometry" Energies 18, no. 10: 2430. https://doi.org/10.3390/en18102430
APA StyleZhang, H., Zhou, K., Ren, X., & Xu, Y. (2025). Moisture Localization and Diagnosis Method for Power Distribution Cables Based on Dynamic Frequency Domain Reflectometry. Energies, 18(10), 2430. https://doi.org/10.3390/en18102430





