Comprehensive Control Strategy for Hybrid Energy Storage System Participating in Grid Primary Frequency Regulation
Abstract
1. Introduction
- (1)
- Current control strategies do not fully leverage the characteristics of ESSs and fundamental control methods;
- (2)
- Control coefficients for ESS output are fixed or only based on SOC without considering output variations under different operating conditions, while a more reasonable output curve is lacking.
- (3)
- The potential for SOC recovery within the PFR dead zone is not fully utilized.
2. PFR Control Model Based on HESS
2.1. Primary Frequency Regulation Model
2.2. Three Control Strategies
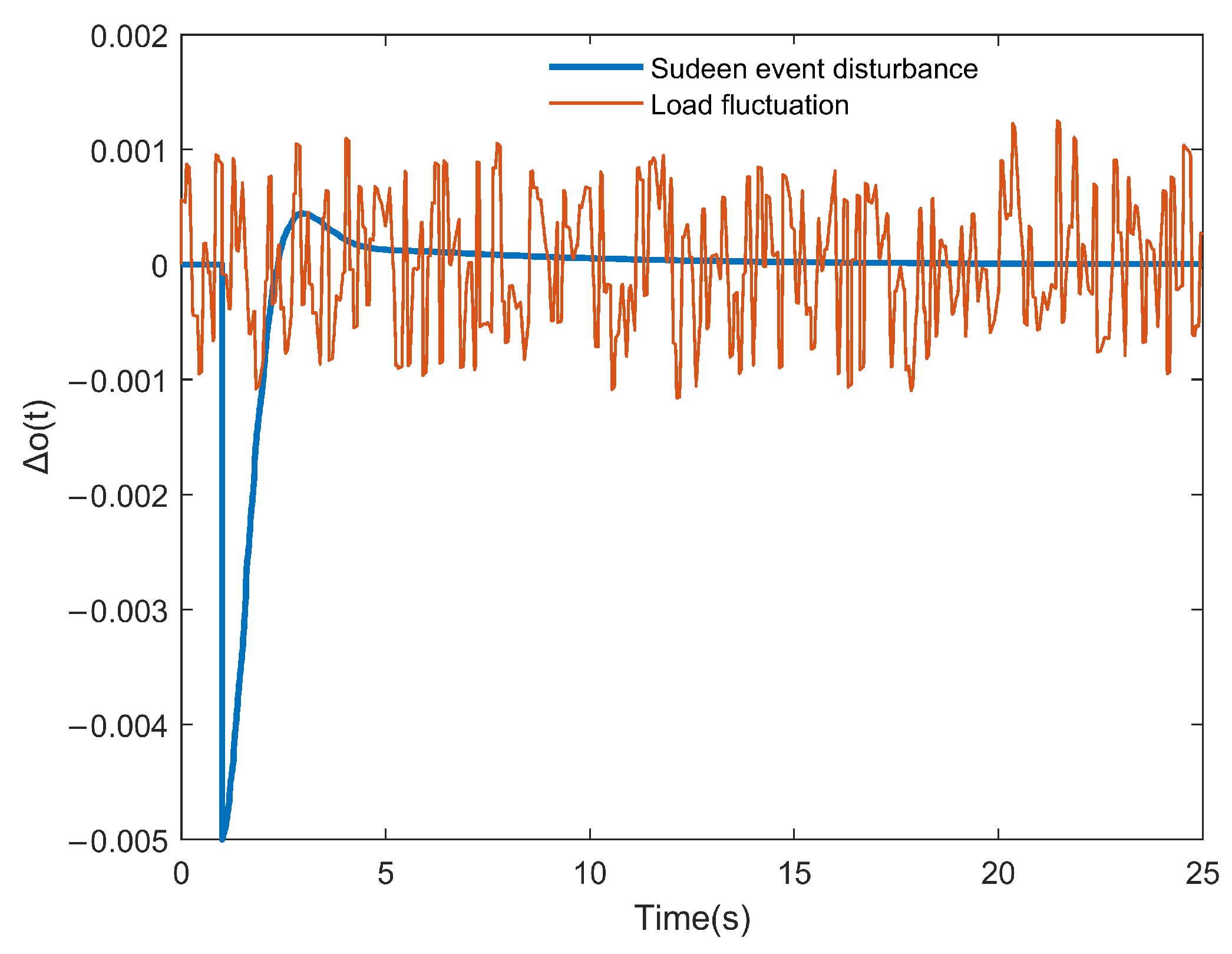
2.3. Analysis of Load Disturbance Types
3. Control Strategies for ESS Participation in PFR
3.1. Coordinated Control Based on Supercapacitor-Battery HESS
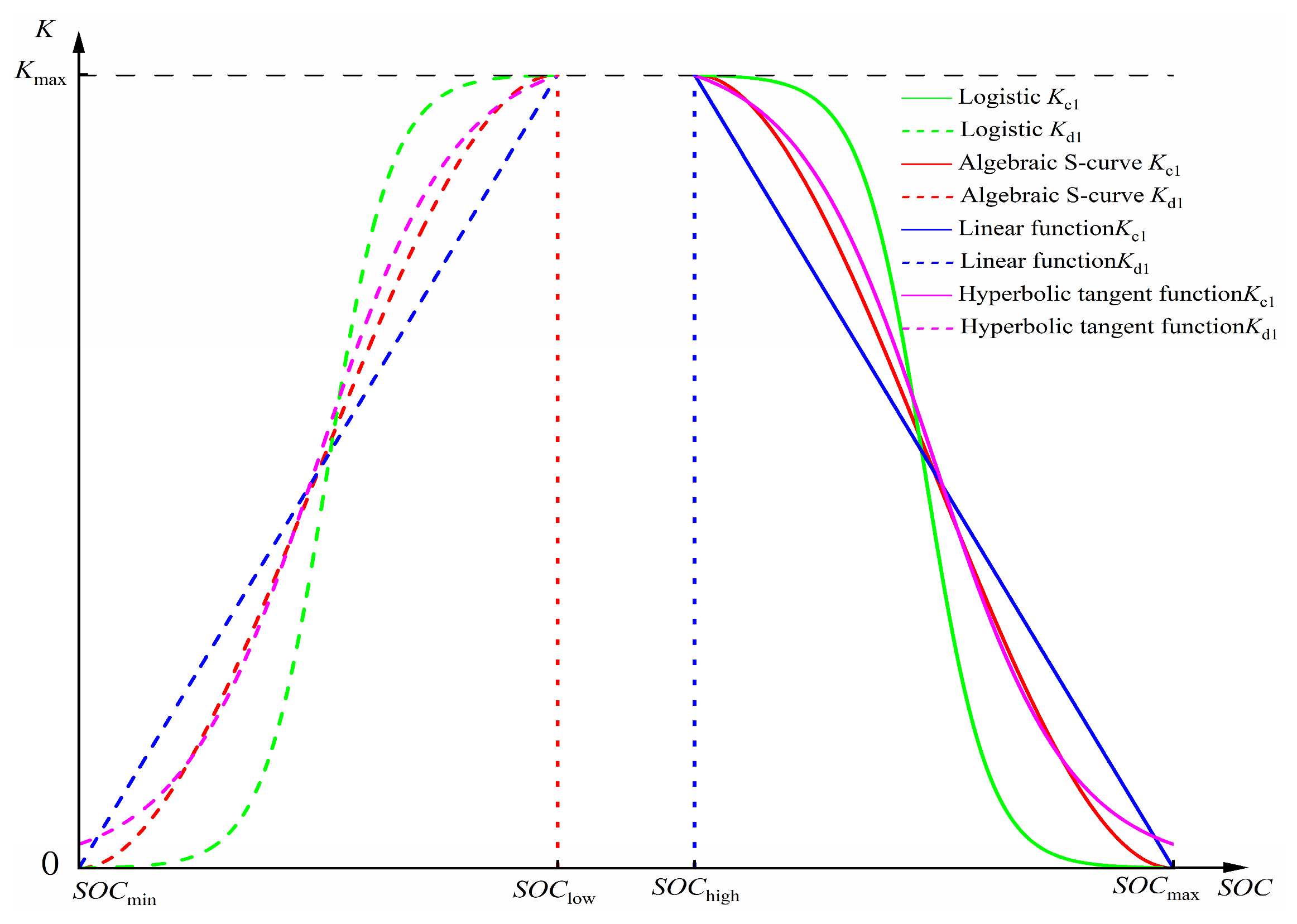
3.2. Adaptive Droop Coefficient Based on SOC Feedback
3.3. Adaptive Inertia Coefficient Based on Disturbance Type and SOC
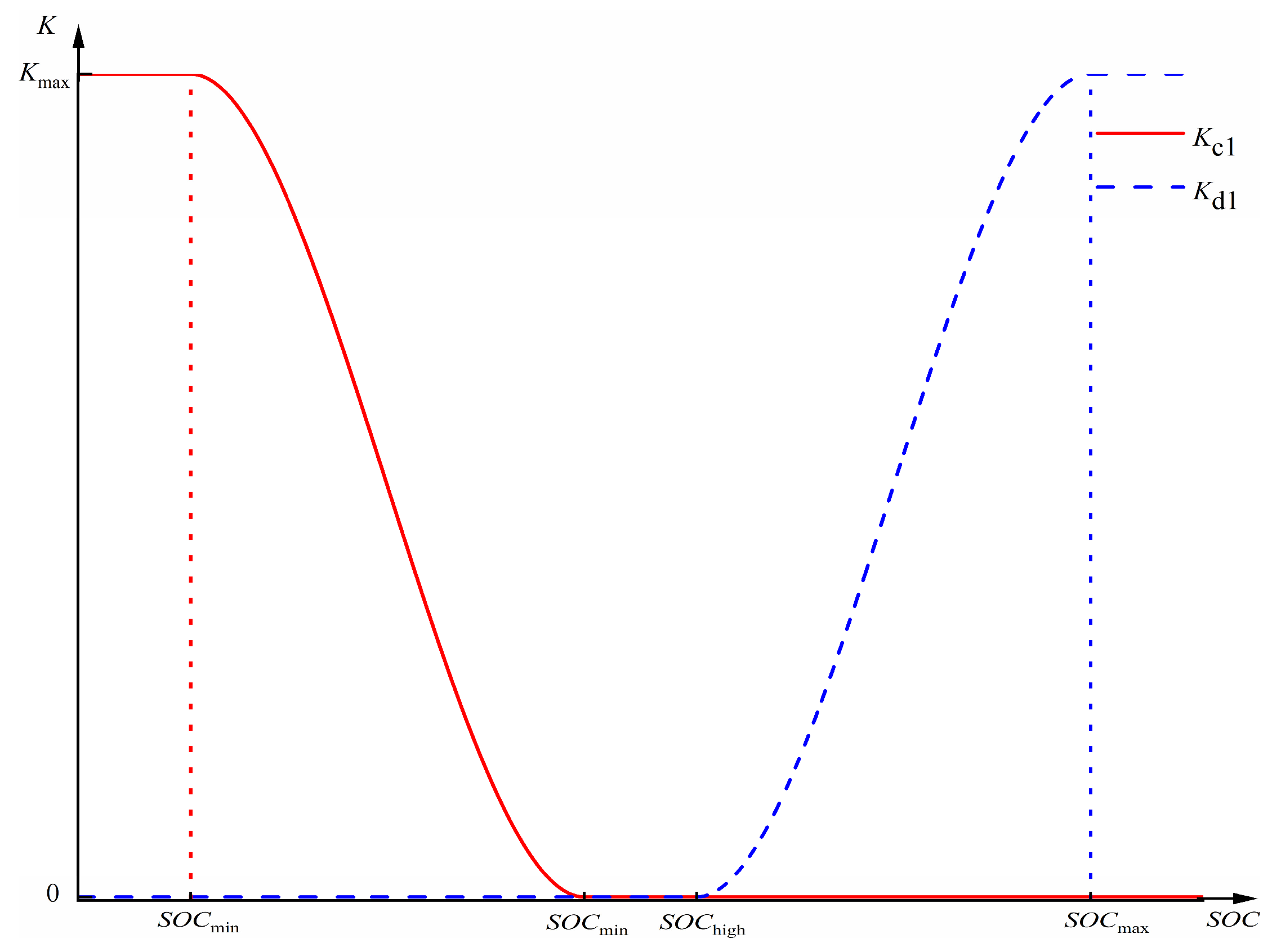
3.4. SOC Recovery Within the BESS Frequency Regulation Dead Zone
3.4.1. Recovery Demand Coefficient Determination Based on SOC
3.4.2. Recovery Constraint Coefficient Based on Δf
3.4.3. Determination of the Recovery Coefficient
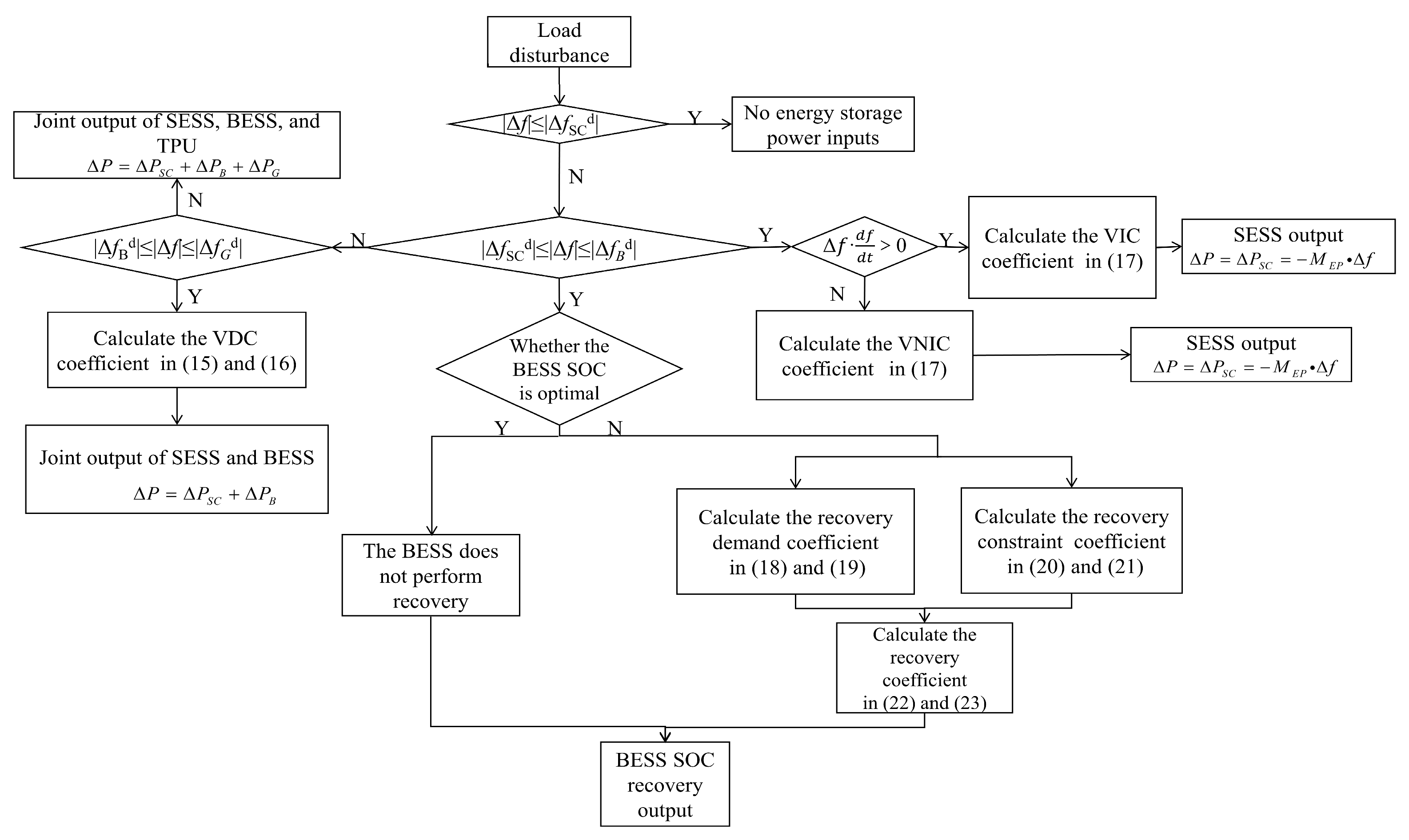
4. Comprehensive Control Strategy and Evaluation Metrics
4.1. Comprehensive Control Strategy
- (1)
- When Δf < ΔfSCd, the FD lies within a safe range, so no frequency regulation is required.
- (2)
- When ΔfSCd ≪ Δf ≪ ΔfBd, the SESS is employed for frequency regulation, while the BESS decides whether to restore its SOC based on its current status.
- (a)
- When dΔf/dt > 0: At this stage, the FD and its rate of change are in the same direction, indicating a worsening frequency condition. The SESS determines the VIC coefficient based on (17) and applies adaptive VIC to mitigate frequency deterioration.
- (b)
- When dΔf/dt ≪ 0: Here, the FD and its rate of change are in opposite directions, indicating a frequency recovery phase. The SESS determines the VNIC coefficient based on (17) and employs adaptive VNIC to speed up frequency recovery.
- (a)
- When the SOC of the BESS is in a satisfactory condition, the recovery of SOC is deemed unnecessary.
- (b)
- When the SOC of the BESS is suboptimal, the recovery demand coefficient is determined based on (18) and (19), while the recovery constraint coefficient is calculated based on (20) and (21). Considering both the recovery demand and recovery constraint, the recovery coefficient is determined according to Equations (22) and (23), which is then used to calculate the SOC recovery power output of the BESS.
- (3)
- For ΔfBd ≪ Δf ≪ ΔfGd, the SESS and BESS collaborate for frequency regulation. The BESS participates in grid frequency regulation using VDC, with the VDC coefficient calculated according to (15) and (16). While the SESS continues to apply positive or negative inertia control based on the product of the FD and its rate of change.
- (4)
- For Δf > ΔfGd, the FD is large, and the HESS collaborates with the TPU to generate power.
4.2. Evaluation Metrics
5. Simulation Verification
5.1. Simulation Model
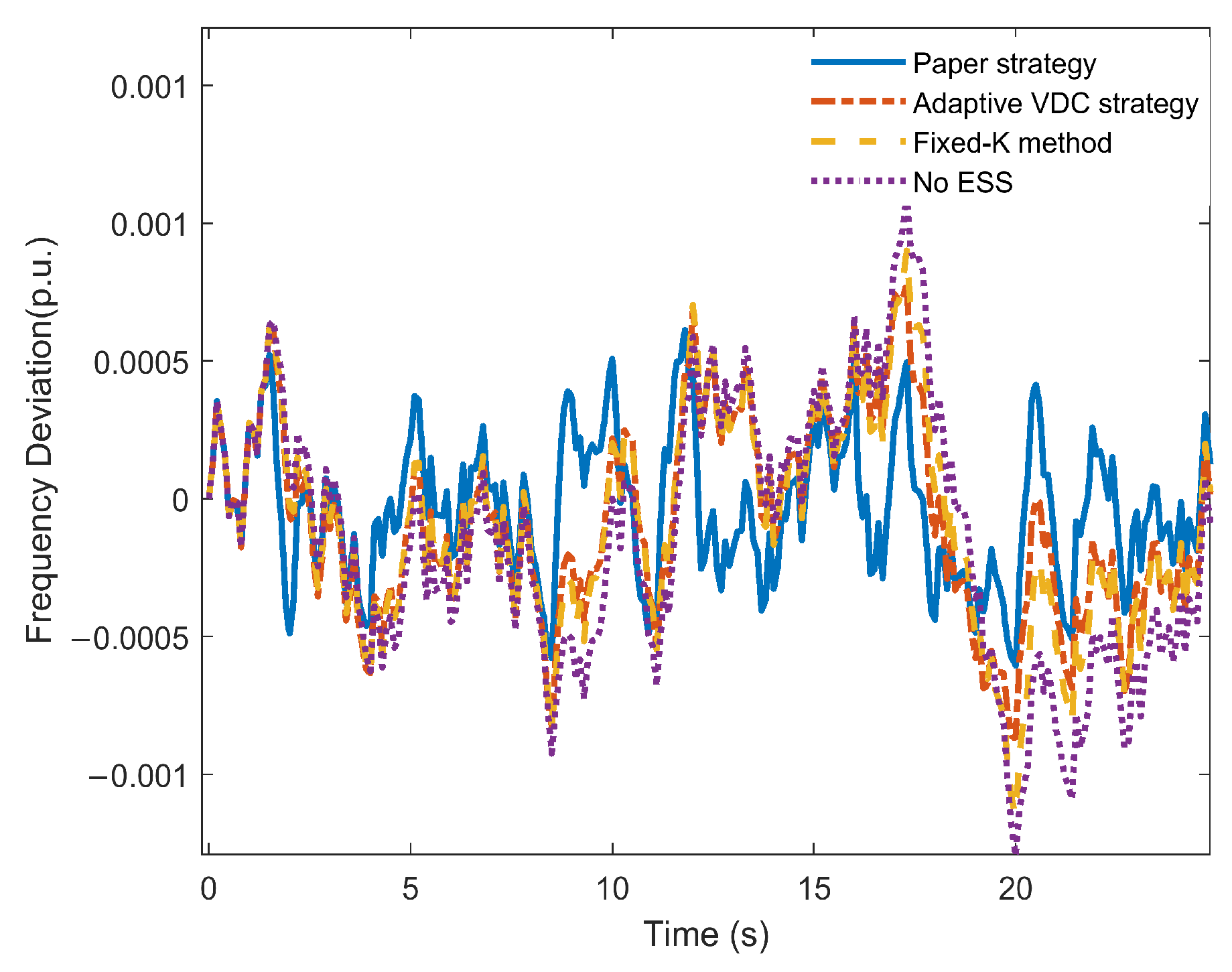
5.2. Simulation and Analysis of Step Load Disturbance
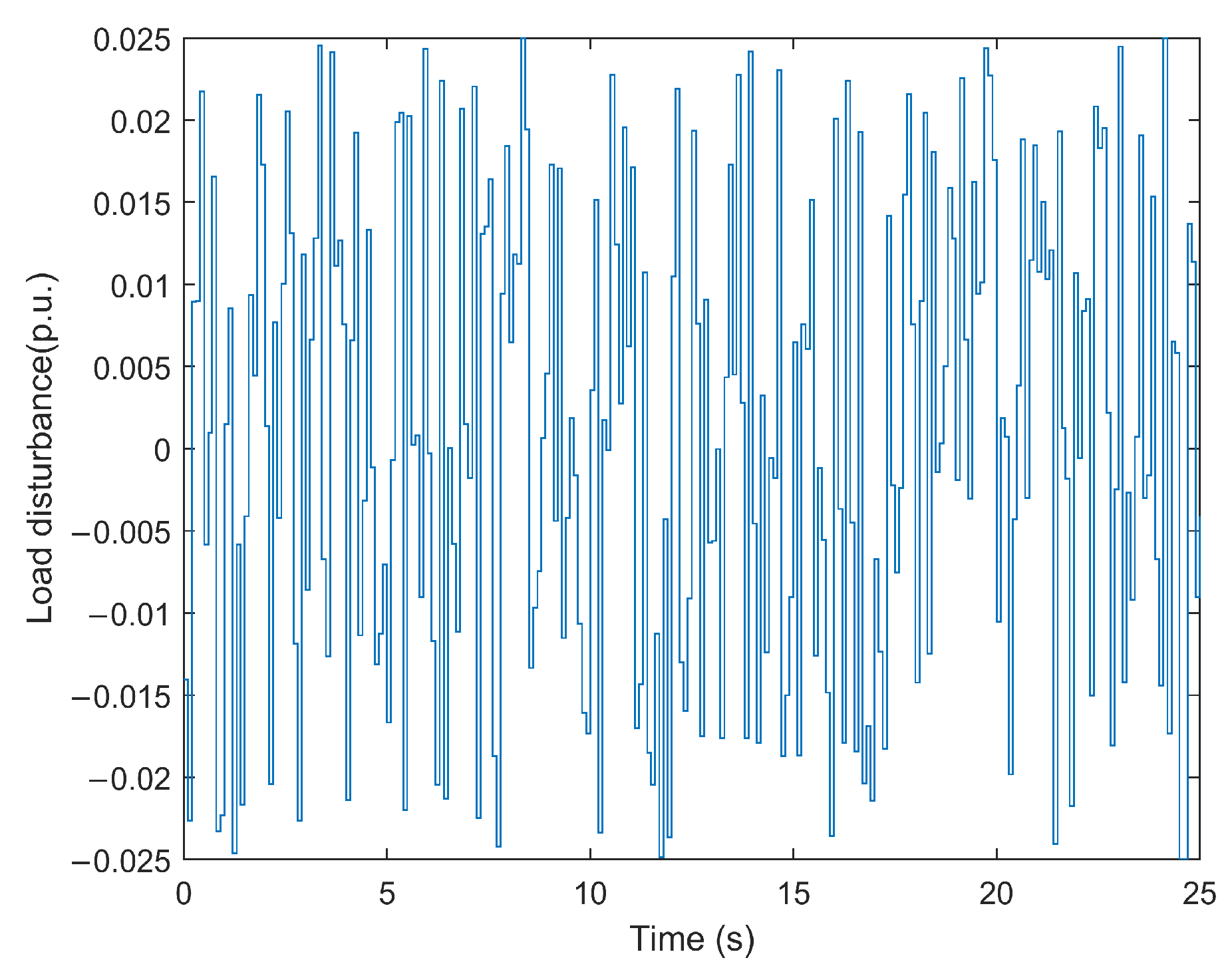
5.3. Simulation Analysis of Continuous Load Disturbance
5.4. Simulation Analysis of Combined Disturbances
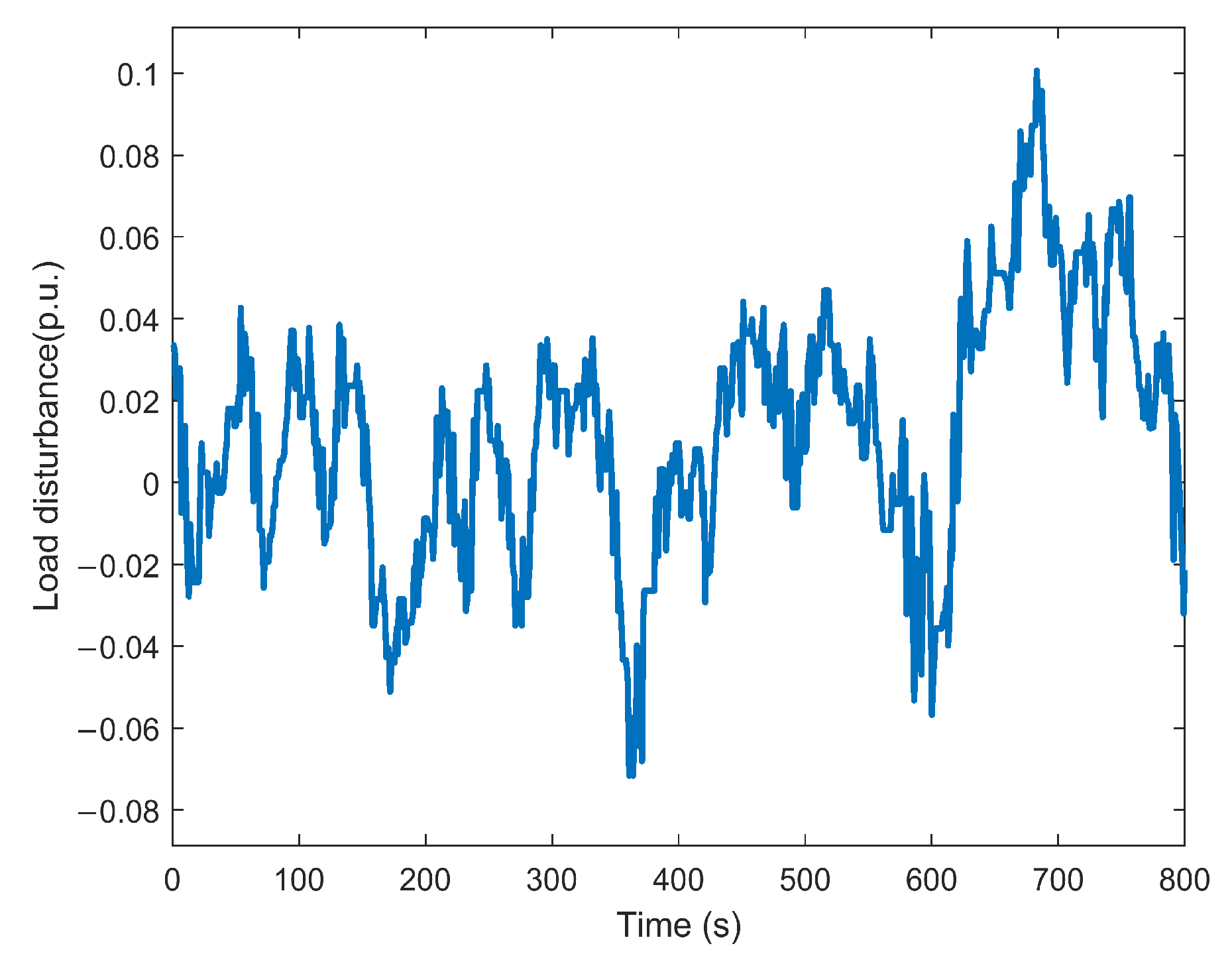
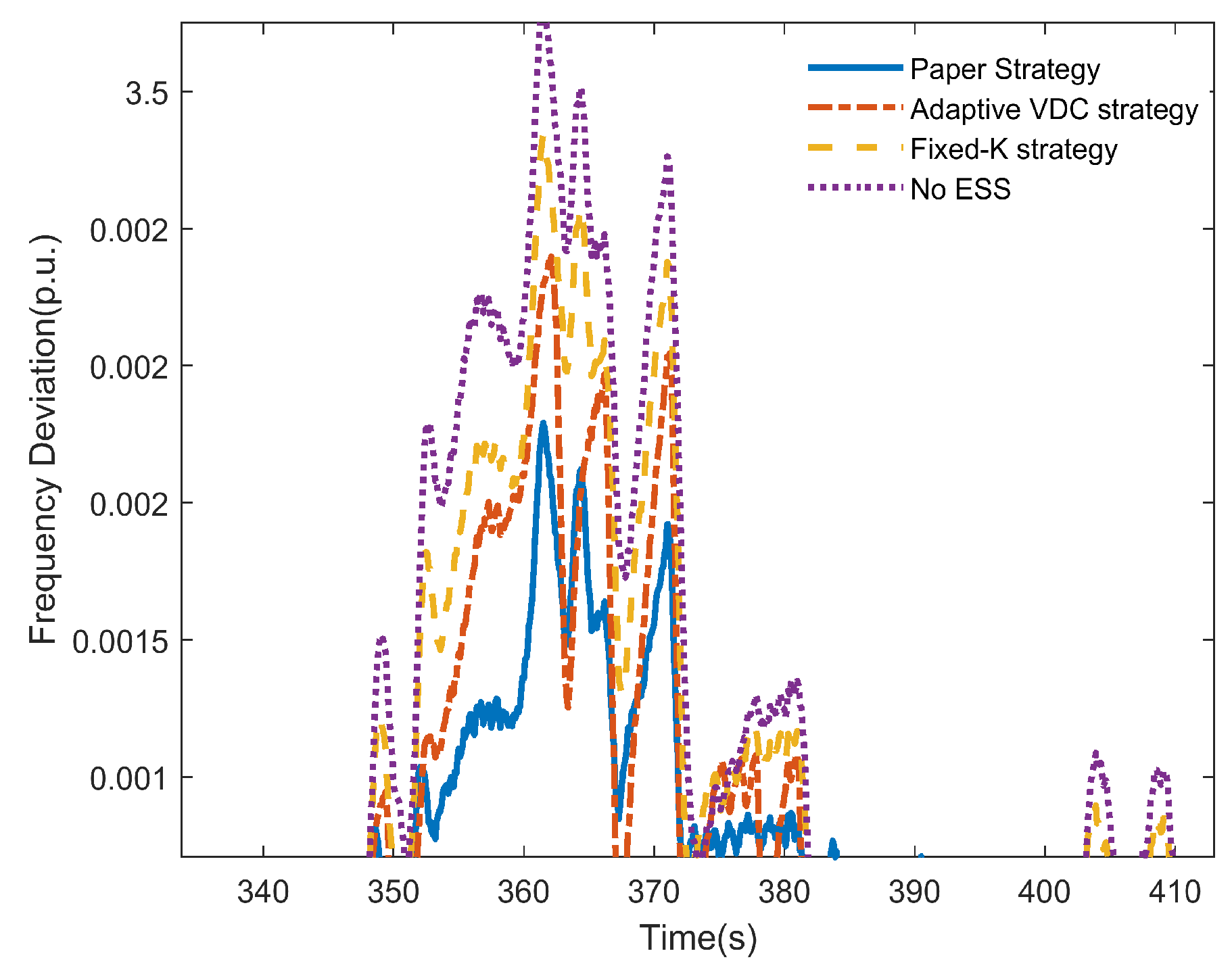
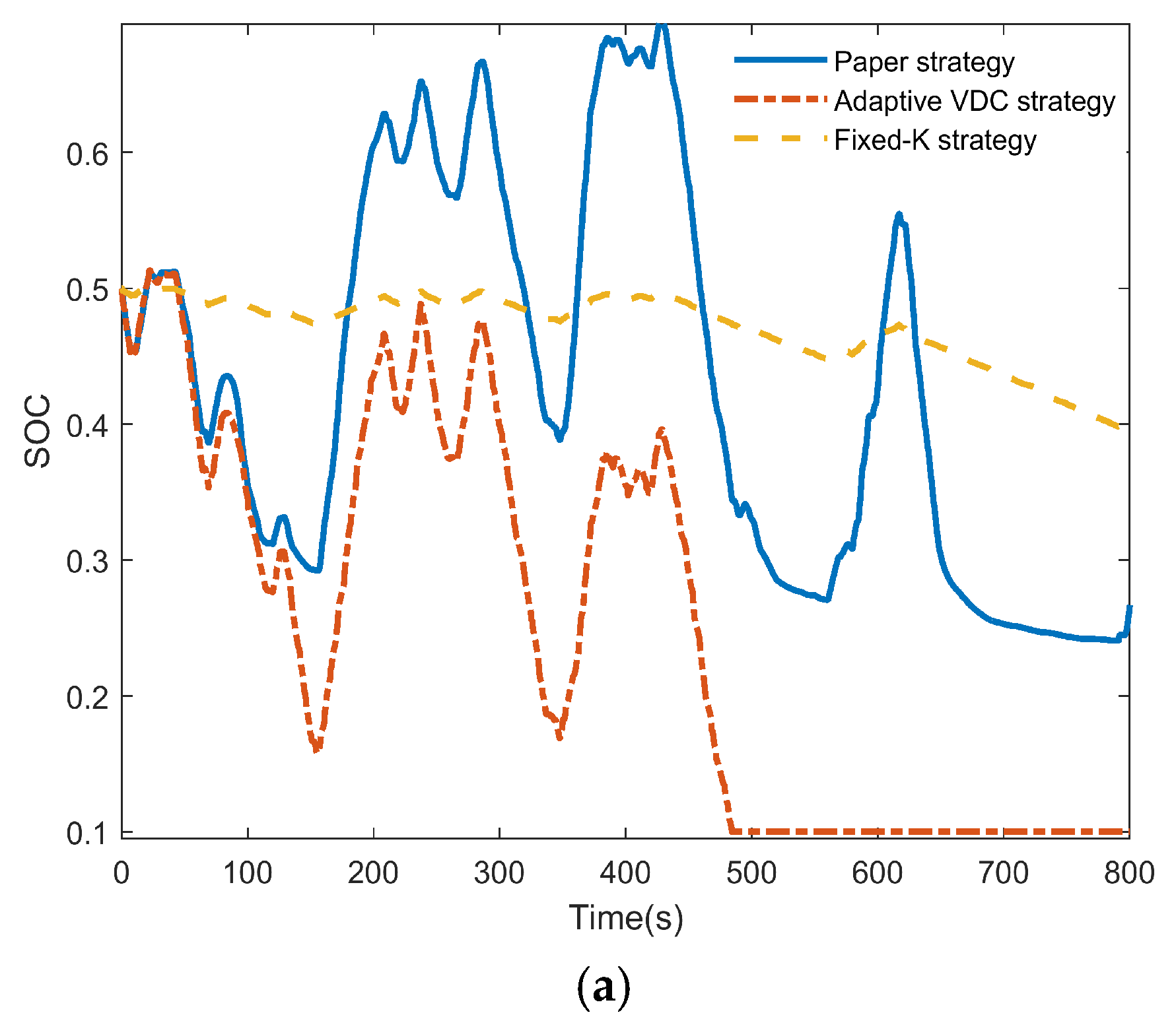
5.5. Simulation Analysis of Commercial Load Disturbance
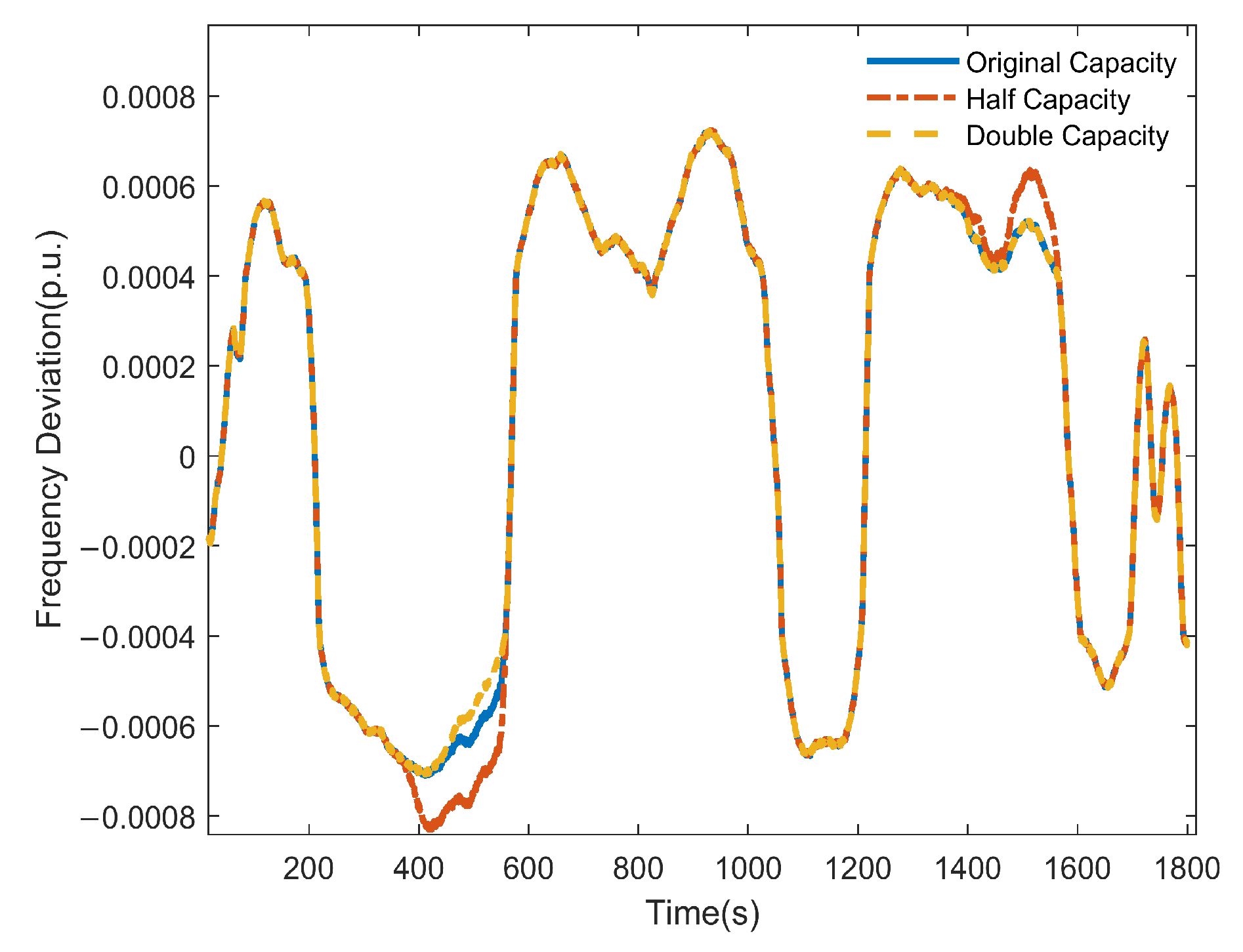
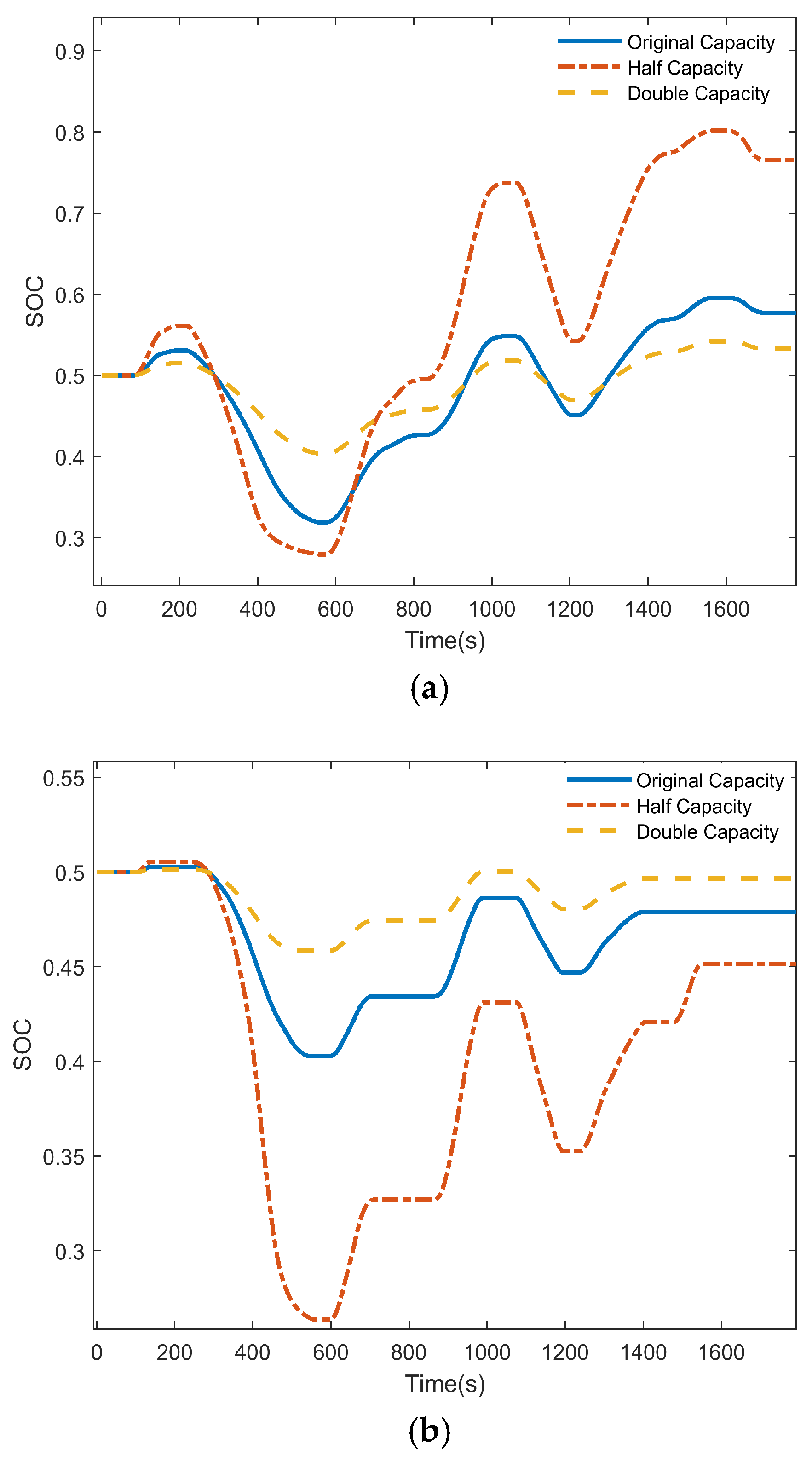
5.6. Simulation Analysis of Different Capacity Configurations
5.7. Economic Analysis
5.8. Discussion on Simulation Verification
6. Conclusions
- (1)
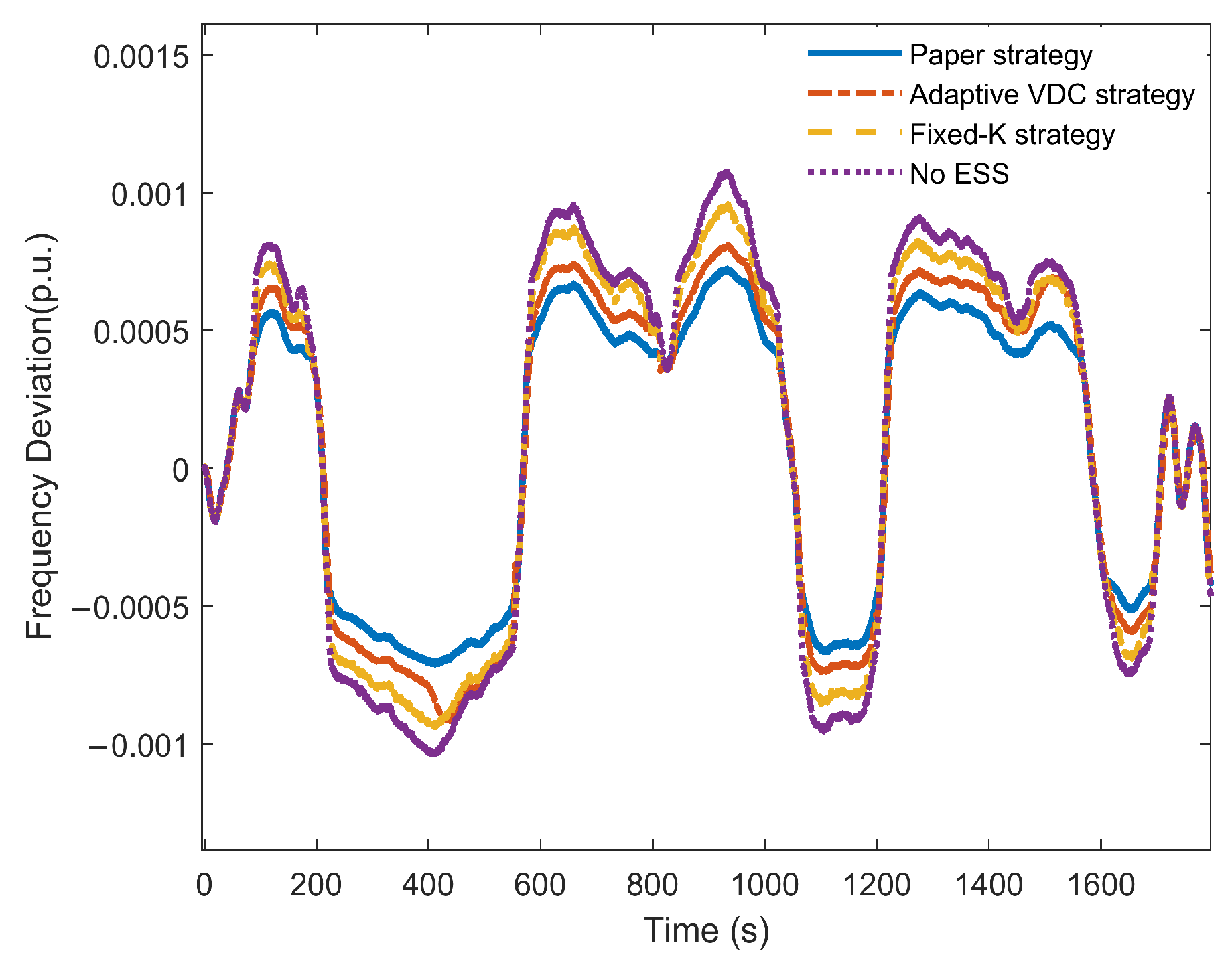
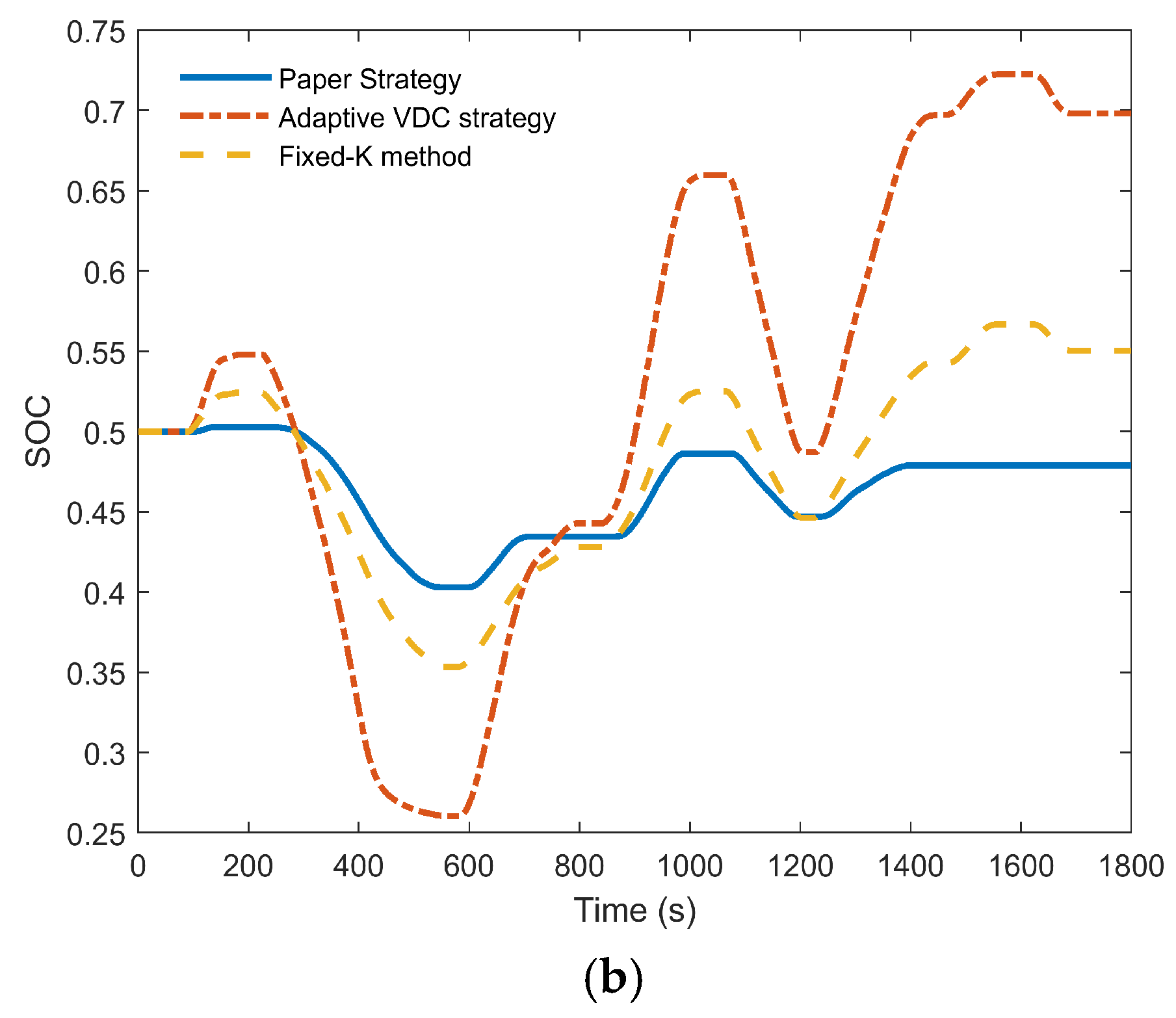
- The proposed control combines the advantages of VDC and VIC with the distinct characteristics of power-type and energy-type storage systems. The high-power SESS is designed to respond to inertial control signals, while the high-capacity BESS responds to VDC signals. Compared to the conventional strategy, the proposed control strategy reduces the frequency drop rate by 17.43% under step disturbance. Under compound disturbances, the RMS of frequency deviation decreases by 13.34% and the RMS of BESS’s SOC decreases by 68.61%. The economic benefit of this strategy is 3.212 times that of the single-energy-storage scheme. This approach maximizes the advantages of different ESSs, exhibits superior performance in PFR and economic benefits, strengthens frequency stability of the, power grid, supports greater integration of renewable energy sources, and contributes to reducing fossil fuel dependence and carbon emissions.
- (2)
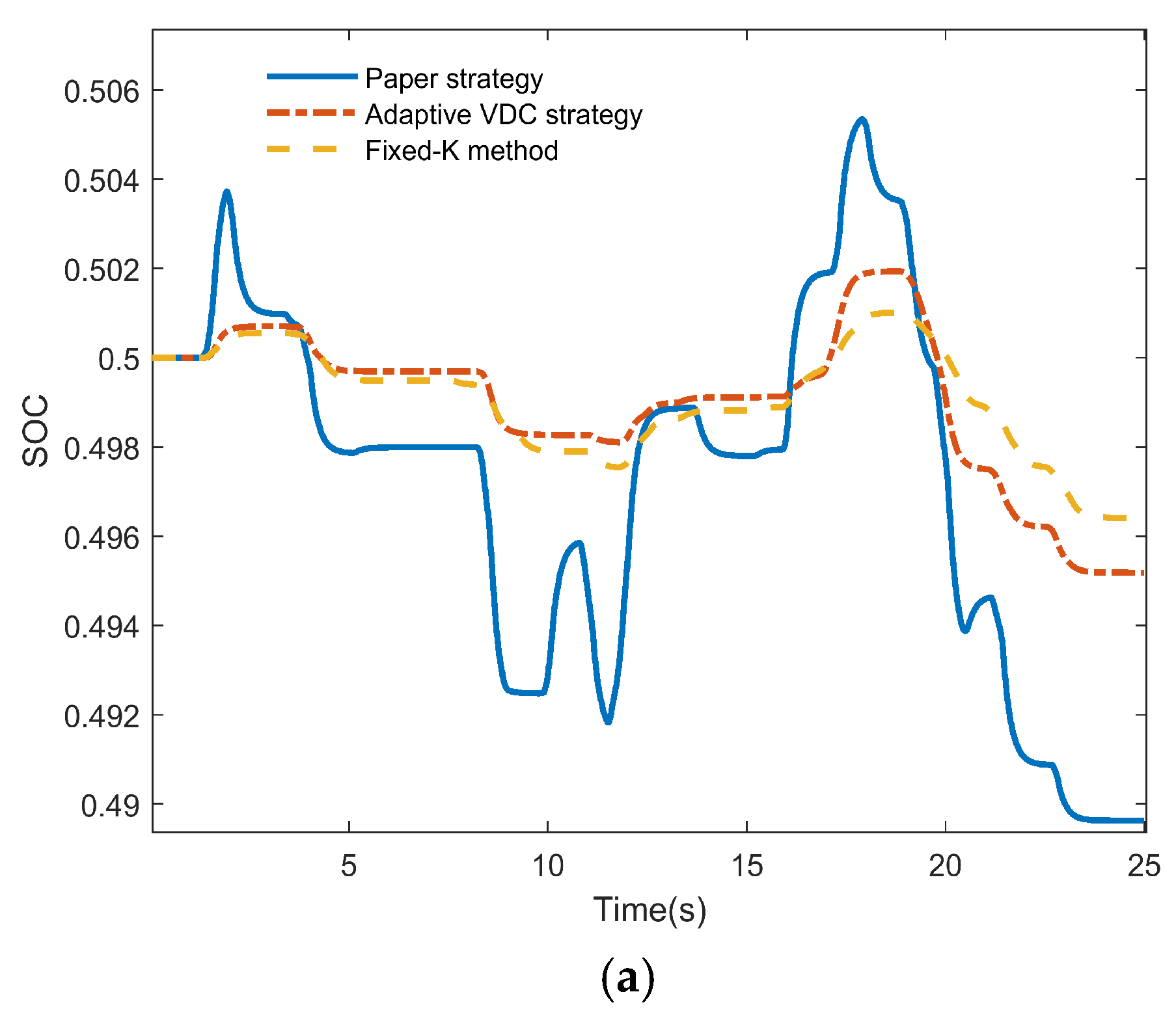
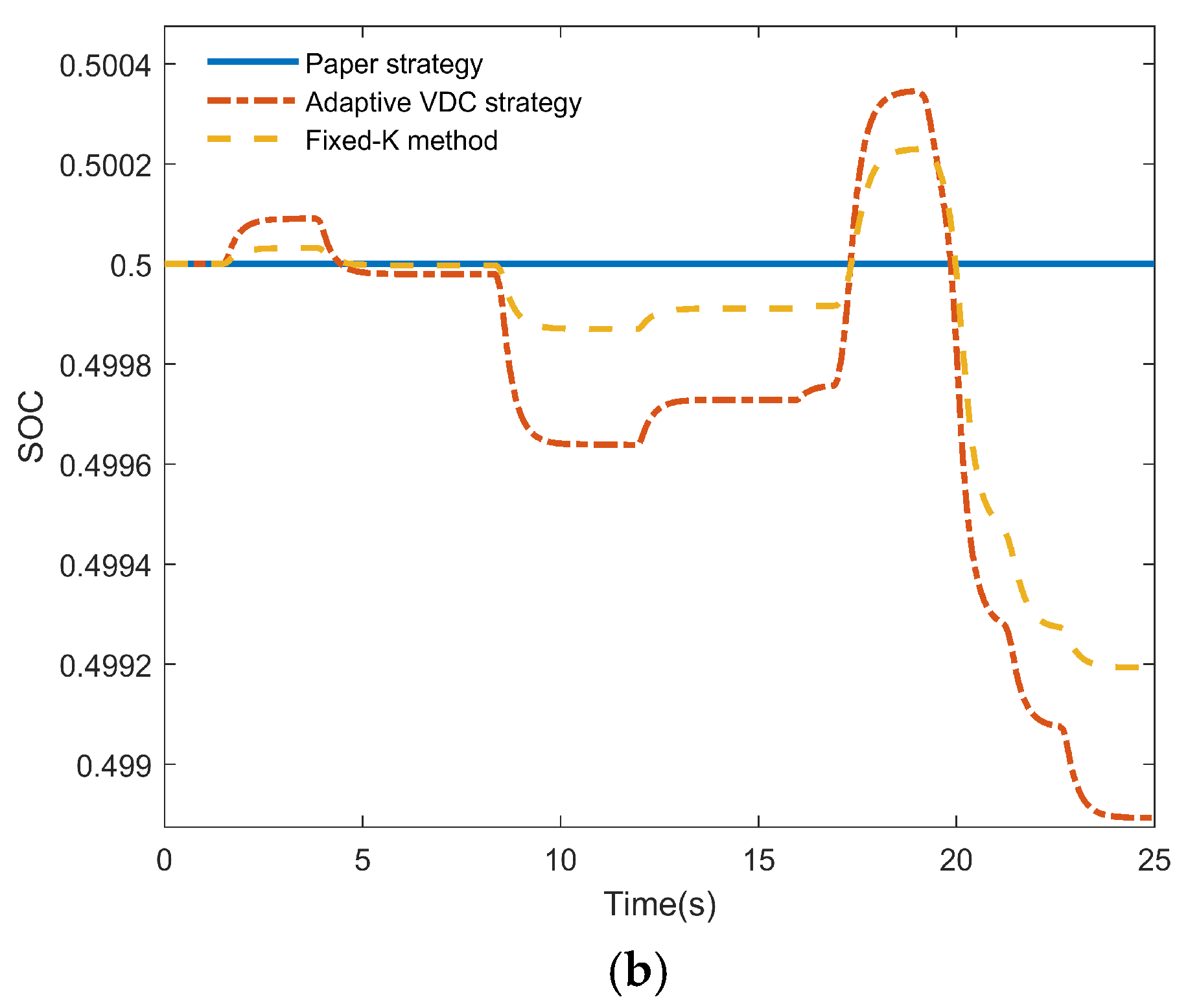
- The strategy effectively protects the lifespan of ESSs, reduces the start/stop frequency of the TPU, and reduces the costs associated with BESS replacement, disposal of retired BESS, and TPU maintenance. By appropriately setting dead zones, the SESS is prioritized for output following the BESS, with the TPU acting as a last resort. This approach leverages the long cycle life of SESS, avoiding excessive BESS charge–discharge cycles and start/stop frequency of TPU. Additionally, to prevent over-charging and over-discharging, which could irreversibly damage the storage system, the output coefficient of ESS is adaptively controlled according to the SOC. Compared with the fixed-K method, the proposed strategy better maintains the SOC of ESSs.
- (3)
- The proposed control strategy better adapts to the impact of different loads. The inertia coefficient and the dead zone of the ESS are flexibly adjusted according to the load type, enhancing adaptability to various operating conditions.
- (4)
- The proposed control strategy fully utilizes SOC recovery within the dead zone for the BESS. During the SOC recovery phase of the BESS, it introduces a recovery demand coefficient determined by the SOC and a recovery constraint coefficient determined by the FD. These coefficients are used to establish an SOC recovery coefficient within the frequency dead zone, ensuring effective SOC recovery while preventing secondary frequency drops. Simulations demonstrate no occurrence of secondary frequency drops, and the SOC remains in good condition.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HESS | hybrid energy storage system |
| SOC | state of charge |
| TPUs | thermal power units |
| ESSs | energy storage systems |
| PFR | primary frequency regulation |
| FD | frequency deviation |
| VDC | virtual droop control |
| VIC | virtual inertia control |
| BESSs | battery energy storage systems |
| VNIC | virtual negative inertia control |
| SESS | supercapacitor energy storage system |
| RMS | root mean square |
| DoD | depth-of-discharge |
References
- Yan, G.G.; Li, D.Y.; Liu, J.H.; Mao, G. A Cost Accounting Method of the Li-ion Battery Energy Storage System for Frequency Regulation Considering the Effect of Life Degradation. Prot. Control Mod. Power Syst. 2018, 3, 1–9. [Google Scholar] [CrossRef]
- Ma, Y.X.; Hu, Z.C.; Song, Y.H. Hour-Ahead Optimization Strategy for Shared Energy Storage of Renewable Energy Power Stations to Provide Frequency Regulation Service. IEEE Trans. Sustain. Energy 2022, 13, 2331–2342. [Google Scholar] [CrossRef]
- Dang, J.; Seuss, J.; Suneja, L.; Harley, R.G. SoC Feedback Control for Wind and ESS Hybrid Power System Frequency Regulation. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 79–86. [Google Scholar] [CrossRef]
- Li, P.Q.; Tan, Z.X.; Zhou, Y.J.; Li, C.B.; Li, R.; Qi, X.Z. Secondary Frequency Regulation Strategy With Fuzzy Logic Method and Self-Adaptive Modification of State of Charge. IEEE Access 2018, 6, 43575–43585. [Google Scholar] [CrossRef]
- Delille, G.; François, B.; Malarange, G. Dynamic Frequency Control Support by Energy Storage to Reduce the Impact of Wind and Solar Generation on Isolated Power System’s Inertia. IEEE Trans. Sustain. Energy 2012, 3, 931–939. [Google Scholar] [CrossRef]
- Chen, W.; Sun, N.; Ma, Z.C.; Liu, W.F.; Dong, H.Y. A Two-Layer Optimization Strategy for Battery Energy Storage Systems to Achieve Primary Frequency Regulation of Power Grid. Energies 2023, 16, 2811. [Google Scholar] [CrossRef]
- Yan, L.; Jiang, P.P.; Li, W.; Xu, Y.S.; Yang, Z.T.; Zhang, B.H.; Mao, C.X. A Mathematical Model of Versatile Energy Storage System and Its Modeling by Power System Analysis Software Package. Power Syst. Technol. 2012, 36, 51–57. [Google Scholar]
- Mu, Y.F.; Wu, J.Z.; Ekanayake, J.; Jenkins, N.; Jia, H.J. Primary Frequency Response From Electric Vehicles in the Great Britain Power System. IEEE Trans. Smart Grid 2013, 4, 1142–1150. [Google Scholar] [CrossRef]
- Feng, Y.H. Research on Energy Storage Battery Participating in Primary Frequency Control Strategy of Power System. Master’s Thesis, Hunan University, Changsha, China, 2019. [Google Scholar]
- Knap, V.; Chaudhary, S.K.; Stroe, D.I.; Swierczynski, M.; Craciun, B.I.; Teodorescu, R. Sizing of an Energy Storage System for Grid Inertial Response and Primary Frequency Reserve. IEEE Trans. Power Syst. 2016, 31, 3447–3456. [Google Scholar] [CrossRef]
- Yang, P.H.; Dong, X.L.; Li, Y.; Kuang, L.; Zhang, J.H.; He, B.; Wang, Y. Research on Primary Frequency Regulation Control Strategy of Wind-thermal Power Coordination. IEEE Access 2019, 7, 144766–144776. [Google Scholar] [CrossRef]
- Gao, S.; Li, J.; Song, H.; Ding, L.; Zhang, C. An integrated thermal power-energy storage system for improving primary frequency regulation performance of thermal power units. Power Syst. Prot. Control 2023, 51, 116–125. [Google Scholar]
- Shui, T. Research on Integrated Control Strategy Considering Hybrid Energy Storage Participation in Grid Frequency Regulation. Master’s Thesis, Shanxi University, Taiyuan, China, 2023. [Google Scholar]
- Zhang, J.C. Research on Optimal Control Strategy of Electrochemical Energy Storage System Participating in Power Grid Primary Frequency Regulation. Master’s Thesis, Changsha University of Science and Technology, Changsha, China, 2022. [Google Scholar]
- He, L.; Guo, L.Q.; Tan, Z.X.; Chen, C.Y.; Li, X.R.; Huang, J.Y.; Li, X.Y. Dynamic Performance Improving Strategy for Primary Frequency Regulation With Energy Storages in High Penetration of RESs Power System. IEEE Access 2024, 12, 139560–139572. [Google Scholar] [CrossRef]
- Yan, L.Q.; Shui, T.; Xue, T.L.; Wang, M.; Ma, N.; Li, K.Y. Comprehensive Control Strategy Considering Hybrid Energy Storage for Primary Frequency Modulation. Energies 2022, 15, 4079. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Chen, M.R.; Xie, B.; Ban, M.F. Integrated control strategy of BESS in primary frequency modulation considering SOC recovery. IET Renew. Power Gener. 2024, 18, 875–886. [Google Scholar] [CrossRef]
- Huang, J.Y.; Li, X.R.; Cao, Y.J.; Liu, W.J. Capacity Allocation of Energy Storage System Considering Its Action Moment and Output Depth in Rapid Frequency Regulation. Trans. China Electrotech. Soc. 2015, 30, 454–464. [Google Scholar]
- Fang, C.X.; Tang, Y.C.; Ye, R.; Lin, Z.S.; Zhu, Z.S.; Wen, B.Y.; Ye, C.T. Adaptive Control Strategy of Energy Storage System Participating in Primary Frequency Regulation. Processes 2020, 8, 687. [Google Scholar] [CrossRef]
- Li, X.R.; Cui, X.W.; Huang, J.Y.; Li, S.J.; Meng, Y.P. The Self-Adaption Control Strategy of Energy Storage Batteries Participating in the Primary Frequency Regulation. Trans. China Electrotech. Soc. 2019, 34, 3897–3908. [Google Scholar]
- Lopes, J.A.P.; Almeida, P.M.R.; Soares, F.J. Using Vehicle-to-Grid to Maximize the Integration of Intermittent Renewable Energy Resources in Islanded Electric Grids. In Proceedings of the 2009 International Conference on Clean Electrical Power (ICCEP 2009), Capri, Italy, 9–11 June 2009. [Google Scholar]
- Wu, Q.F.; Song, X.L.; Zhang, J.R.; Yu, H.F.; Huang, J.D.; Dai, H.Y. Study on Self-Adaptation Comprehensive Strategy of Battery Energy Storage in Primary Frequency Regulation of Power Grid. Power Syst. Technol. 2020, 44, 3829–3836. [Google Scholar]
- Li, X.R.; Deng, T.; Huang, J.Y.; Li, S.J.; Yang, J.; Deng, M. Battery Energy Storage System Self-Adaptation Control Strategy in Fast Frequency Regulation. High Volt. Eng. 2017, 43, 2362–2369. [Google Scholar]
- Ma, J.; Pan, J.; Wu, Y.; Wang, H.; Zhang, P. Improved flexible virtual inertial control considering SOC of energy storage and characteristics of frequency recovery. Electr. Power Autom. Equip. 2020, 40, 100–107. [Google Scholar]
- Wei, W.; Bin, H.; Ai, F.Z.; Chen, Z.F.; Xu, R.J.; Ren, Y.F. Research on battery energy storage in cooperation with thermal power units to participate in system frequency regulation control strategy. China Meas. Test 2022, 48, 1–7. [Google Scholar]
- Tian, S.J. Research on Control Strategy of Battery Energy Storage System Under Primary Frequency Regulation of Power Grid and Unbalanced Grid Voltage. Master’s Thesis, North China Electric Power University, Baoding, China, 2022. [Google Scholar]
- Zhao, X.L.; Zhang, D.H.; Gui, Y.; Li, P.; Tan, S.Y. An Integrated Control Strategy for Energy Storage Participating in Primary Frequency Regulation Considering State of Charge Constraint. Mod. Electr. Power 2022, 39, 95–103. [Google Scholar]
- Bi, L. Optimal Control Strategy of Energy Storage Assisting Wind for Power Grid in the Primary Frequency Regulation. Master’s Thesis, North China Electric Power University, Baoding, China, 2020. [Google Scholar]
- Zhang, Z.Y.; Ding, T.; Zhou, Q.; Sun, Y.G.; Qu, M.; Zeng, Z.Y.; Ju, Y.T.; Li, L.; Wang, K.; Chi, F.D. A review of technologies and applications on versatile energy storage systems. Renew. Sust. Energ. Rev. 2021, 148, 31. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuña, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids-A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Yoon, M.; Lee, J.; Song, S.; Yoo, Y.; Jang, G.; Jung, S.; Hwang, S. Utilization of Energy Storage System for Frequency Regulation in Large-Scale Transmission System. Energies 2019, 12, 3898. [Google Scholar] [CrossRef]
- Liu, Z.L. Research on Frequency Regulation Characteristics of Hybrid Energy Storage Assisted Heating Units. Master’s Thesis, North China Electric Power University, Baoding, China, 2023. [Google Scholar]
- Man, Y. Research on Primary Frequency Modulation Control Method of New Energy Power Station Assisted by “Flywheel +Lithium” Hybrid Energy Storage System. Master’s Thesis, Shandong University, Jinan, China, 2023. [Google Scholar]
- Fang, H.Y. Research on Control Strategies for Hybrid Energy Storage in System Frequency Regulation. Master’s Thesis, Qingdao University, Qingdao, China, 2022. [Google Scholar]
- Liu, H.; Liu, J.; Zhao, L.; Li, Y. Adaptive Control Strategy for Primary Frequency Modulation of Hybrid Energy Storage Considering State of Charge Recovery. In Proceedings of the 2022 International Conference on Energy Materials and Electrical Engineering (ICEMEE 2022), Guilin, China, 22–24 July 2022. [Google Scholar]
- Elkasem, A.H.A.; Kamel, S.; Khamies, M.; Nasrat, L. Frequency regulation in a hybrid renewable power grid: An effective strategy utilizing load frequency control and redox flow batteries. Sci. Rep. 2024, 14, 33. [Google Scholar] [CrossRef]
- Zhao, X.L.; Li, P.; Fu, B. Frequency Regulation Method Assisted by Energy Storage Based on Frequency Response Characteristics. Electr. Power Eng. Technol. 2024, 43, 41–49. [Google Scholar]
- GB/T 15945-2008; Power Quality—Frequency Deviation for Power System. Standards Press of China: Beijing, China, 2008.
- Sun, H.D.; Xu, T.; Guo, Q.; Li, Y.L.; Lin, W.F.; Yi, J.; Li, W.F. Analysis on Blackout in Great Britain Power Grid on August 9th, 2019 and Its Enlightenment to Power Grid in China. Proc. CSEE 2019, 39, 6183–6192. [Google Scholar]
- Meng, Y.; Li, X.R.; Liu, X.L.; Cui, X.W.; Xu, P.A.; Li, S.J. A Control Strategy for Battery Energy Storage Systems Participating in Primary Frequency Control Considering the Disturbance Type. IEEE Access 2021, 9, 102004–102018. [Google Scholar] [CrossRef]
- Li, L.; Liu, X.P. Study on Frequency Modulation Control Strategy of Energy Storage Auxiliary Thermal Power Unit Considering Frequency Difference Zone. J. North China Electr. Power Univ. 2024, 51, 126–133+142. [Google Scholar]
- Wei, N.; Yan, X.; Han, X.; Ma, X.; Cui, J.; Sun, W. Research on Control Strategy of Hybrid Energy Storage System Participating in Primary Frequency Regulation of Power Grid. J. Phys. Conf. Ser. 2023, 2592, 012061. [Google Scholar] [CrossRef]
- Li, J.H.; Guo, Z.; Yang, H.; Li, L.; Sun, B.X.; Fan, X.K. Primary Frequency Regulation Control Strategy of Energy Storage Based on Dynamic Droop Coefficient and SOC Reference. Power Syst. Prot. Control 2021, 49, 1–10. [Google Scholar]
- Xu, Y.H.; Li, H.Q.; Qin, J.X.; Wang, K.C.; Han, J.H. Frequency Control of Hybrid Energy Storage Assisted Thermal Power Units Based on SOC State. Autom. Appl. 2023, 64, 78–83. [Google Scholar]
- Li, P.Q.; Fu, Y.H.; Liu, X.R.; Tan, Z.Z.; Yang, B.; Han, J.Y. Control Strategy for Energy Storage Battery Participating in Primary Frequency Regulation of Power Grid Considering Ultra-short-term Load Forecasting. Autom. Electr. Power Syst. 2019, 43, 87–93. [Google Scholar]
- Ma, Z.H.; Li, X.R.; Tang, Z.X.; Huang, J.Y.; Li, H. Integrated Control of Primary Frequency Regulation Considering Dead Band of Energy Storage. Trans. China Electrotech. Soc. 2019, 34, 2102–2115. [Google Scholar]
- Wuraola, A.; Patel, N.; Nguang, S.K. Efficient Activation Functions for Embedded Inference Engines. Neurocomputing 2021, 442, 73–88. [Google Scholar] [CrossRef]
- Fang, Y.; Hu, J.Y.; Liu, W.H.; Shao, Q.Q.; Qi, J.; Peng, Y.H. Smooth and Time-Optimal S-Curve Trajectory Planning for Automated Robots and Machines. Mech. Mach. Theory 2019, 137, 127–153. [Google Scholar] [CrossRef]
- Liu, T.Y.; Cui, J.K.; Li, Y.H.; Gao, S.Y.; Zhu, M.C.; Chen, L.H. Time-Optimal Asymmetric S-Curve Trajectory Planning of Redundant Manipulators under Kinematic Constraints. Sensors 2023, 23, 3074. [Google Scholar] [CrossRef]
- Liu, Y.P.; Tian, S.J.; Liang, H.P.; Xie, Y.; Huo, Q.D.; Tang, X.J. Control Strategy of a Battery Energy Storage System Considering SOC in Primary Frequency Regulation of Power Grid. Power Syst. Prot. Control 2022, 50, 107–118. [Google Scholar]
- Deng, X.; Sun, W.; Xiao, H.W. Integrated Control Method of Battery Energy Storage Participating in Primary Frequency Regulation. High Volt. Eng. 2018, 44, 1157–1165. [Google Scholar]
- Wang, Y.F.; Yang, M.C.; Xue, H.; Zhang, Y.H.; Mi, Y. Adaptive Integrated Control Strategy for Battery Energy Storage System Considering SOC in Primary Frequency Regulation. Electr. Power Autom. Equip. 2021, 41, 192–198, 219. [Google Scholar]
- Ju, P.; Li, H.Y.; Gan, C.; Liu, Y.; Yu, Y.P.; Liu, Y.L. Analytical Assessment for Transient Stability Under Stochastic Continuous Disturbances. IEEE Trans. Power Syst. 2018, 33, 2004–2014. [Google Scholar] [CrossRef]
- Huang, J.Y.; Li, X.R.; Chang, M.; Li, S.J.; Liu, W.J. Capacity Allocation of Battery Energy Storage System in Primary Frequency Regulation Considering Its Technical-Economic Model. High Volt. Eng. 2017, 32, 112–121. [Google Scholar]
- Li, J.H.; Tao, H.; Mu, G.; Yan, G.; Li, C.; He, D.C. Primary frequency regulation strategy with energy storage system based on weight factors and state of charge recovery. Autom. Electr. Power Syst. 2020, 44, 63–72. [Google Scholar]
- Liu, J. Hybrid Energy Storage for Frequency Modulation Cooperative Control of Power Grid. Master’s Thesis, North China Electric Power University, Baoding, China, 2022. [Google Scholar]
- Zhou, D.; Zou, Z.W.; Dan, Y.Q.; Wang, C.X.; Teng, C.Y.; Zhu, Y.L. An Integrated Strategy for Hybrid Energy Storage Systems to Stabilize the Frequency of the Power Grid Through Primary Frequency Regulation. Energies 2025, 18, 246. [Google Scholar] [CrossRef]
- Fang, H.Y.; Ma, P. Adaptive Droop Control Strategy Considering Frequency Modulation Dead Band of Hybrid Energy Storage. J. Electr. Eng. 2021, 16, 213–222. [Google Scholar]
- Zhang, Q.; Li, X.R.; Yang, M.; Cao, Y.J.; Li, P.Q. Capacity Allocation Method of Hybrid Energy Storage System for Smoothing Wind Power Fluctuations with Maximum Net Benefit. Trans. China Electrotechn. Soc. 2016, 31, 40–48. [Google Scholar]
- Zizlavsky, O. Net Present Value Approach: Method for Economic Assessment of Innovation Projects. In Proceedings of the 19th International Scientific Conference on Economics and Management (ICEM), Riga, Latvia, 23–25 April 2014. [Google Scholar]
- Ye, L.; Wang, K.F.; Lai, Y.N.; Chen, H.; Zhao, Y.N.; Xu, X.; Lu, P.; Jin, Y.F. Analysis of Frequency Characteristics and Control Strategies of Battery Energy Storage Frequency Regulation in Power Systems Under Low Inertia. Power Syst. Technol. 2023, 47, 446–464. [Google Scholar]
- Huang, J.Y.; Li, X.R.; Cao, Y.J.; Zhang, Q.; Liu, W.J. Simulation Model of Battery Energy Storage System for Grid Frequency Regulation. Autom. Electr. Power Syst. 2015, 39, 20–24, 74. [Google Scholar]
- Vermeer, W.; Mouli, G.R.C.; Bauer, P. A Comprehensive Review on the Characteristics and Modeling of Lithium-Ion Battery Aging. IEEE Trans. Transp. Electrif. 2022, 8, 2205–2232. [Google Scholar] [CrossRef]
- Deng, X.Y.; Mo, R.; Wang, P.L.; Chen, J.R.; Nan, D.L.; Liu, M.Y. Review of RoCoF Estimation Techniques for Low-Inertia Power Systems. Energies 2023, 16, 3708. [Google Scholar] [CrossRef]
- Jabari, M.; Ekinci, S.; Izci, D.; Bajaj, M.; Zaitsev, I. Efficient DC Motor Speed Control Using a Novel Multi-Stage FOPD(1 + PI) Controller Optimized by the Pelican Optimization Algorithm. Sci. Rep. 2024, 14, 22442. [Google Scholar] [CrossRef] [PubMed]
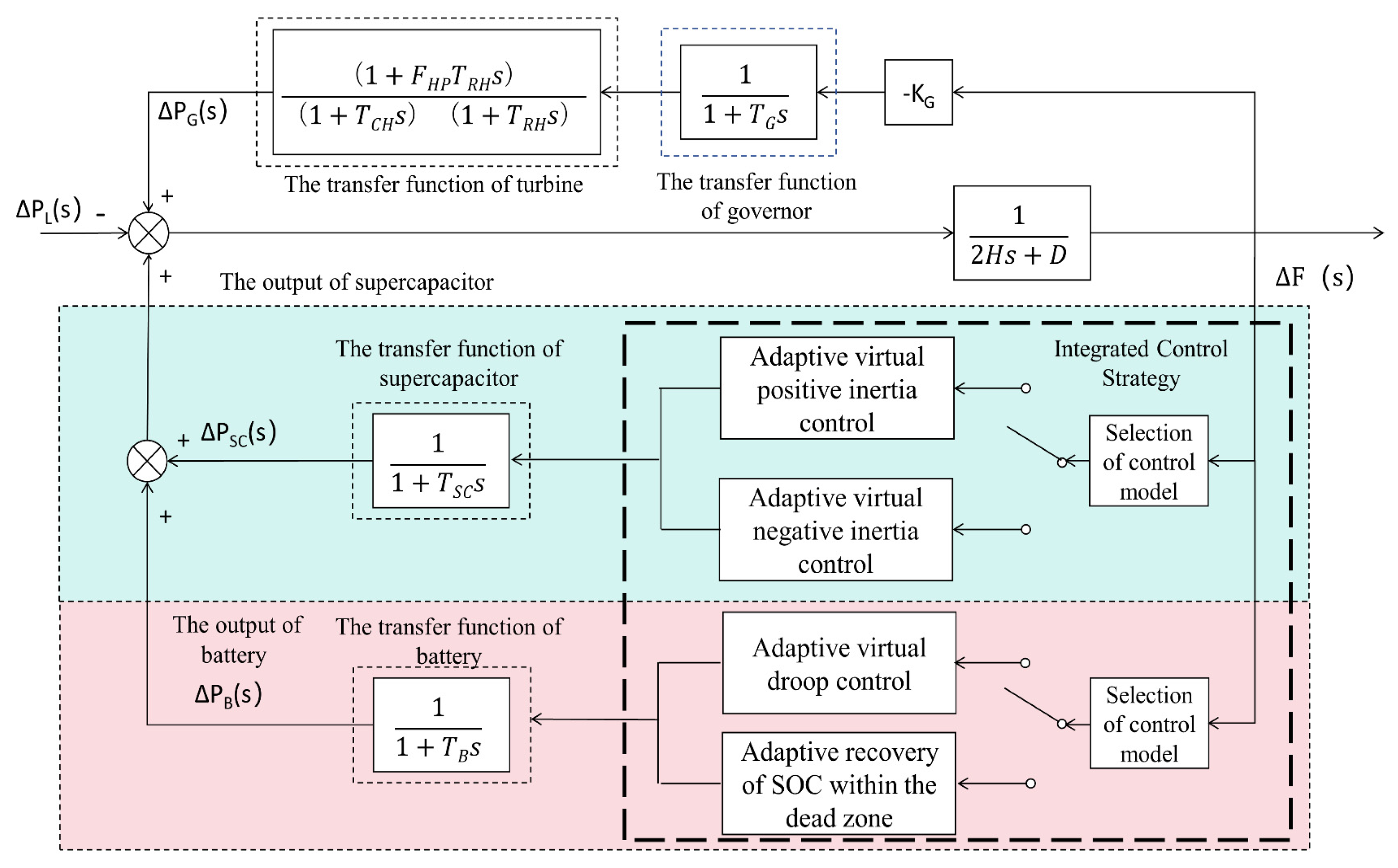









| Parameters | Definition | Unit |
|---|---|---|
| ΔPG(s) | PFR output of the TPU | MW |
| ΔPSC(s) | SESS PFR power out | MW |
| ΔPB(s) | BESS PFR power out | MW |
| ΔPL(s) | Load disturbance | MW |
| KG | PFR factor for TPU | - |
| H | Inertia TC of the power grid | - |
| D | Load damping coefficient | - |
| FHP | Reheater gain | - |
| TG | Governor TC of the TPU | s |
| TRH | Reheater TC | s |
| TCH | Turbine TC | s |
| TSC | Inertia TC of SESS | s |
| TB | Inertia TC of BESS | s |
| Control Policies | |Δfm|/10−3 p.u. | tm | |Δfs|/10−3 p.u. | ts | vm/10−3 |
|---|---|---|---|---|---|
| Paper strategy | 2.739 | 3.443 | 1.981 | 20.885 | 0.796 |
| Adaptive VDC strategy | 1.649 | 1.710 | 1.999 | 23.571 | 0.964 |
| Fixed-K method | 2.946 | 2.616 | 2.001 | 23.946 | 1.126 |
| No ESS | 3.665 | 2.491 | 2.313 | 24.274 | 1.471 |
| Control Policies | findex/10−4 p.u. | SOCSCindex | SOCBindex/10−4 |
|---|---|---|---|
| Paper strategy | 2.9478 | 0.0049 | 0 |
| Adaptive VDC strategy | 4.0143 | 0.0019 | 4.3488 |
| Fixed-K method | 4.4223 | 0.0015 | 2.9782 |
| No ESS | 5.4207 | - | - |
| Control Policies | findex/10−4 p.u. | SOCSCindex | SOCBindex |
|---|---|---|---|
| Paper strategy | 5.1355 | 0.0809 | 0.0458 |
| Adaptive VDC strategy | 5.9258 | 0.0224 | 0.1459 |
| Fixed-K method | 6.5755 | 0.0217 | 0.0652 |
| No ESS | 7.2071 | - | - |
| Control Policies | findex/p.u. | SOCSCindex | SOCBindex |
|---|---|---|---|
| Paper strategy | 0.0012 | 0.1606 | 0.1156 |
| Adaptive VDC strategy | 0.0013 | 0.2808 | 0.1470 |
| Fixed-K method | 0.0015 | 0.0039 | 0.1514 |
| No ESS | 0.0018 | - | - |
| BESS in HESS | BESS in HESS | BESS Only | |
|---|---|---|---|
| CLCC/USD | 7.8426 ×107 | 1.728 × 107 | 9.857 × 107 |
| NRES/USD | 2.0394 × 108 | 5.1281 × 108 | 2.9188 × 108 |
| PNET/USD | 1.2551 × 108 | 4.9553 × 108 | 1.9331 × 108 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Han, K.; Bao, W.; Li, Y. Comprehensive Control Strategy for Hybrid Energy Storage System Participating in Grid Primary Frequency Regulation. Energies 2025, 18, 2423. https://doi.org/10.3390/en18102423
Jiang H, Han K, Bao W, Li Y. Comprehensive Control Strategy for Hybrid Energy Storage System Participating in Grid Primary Frequency Regulation. Energies. 2025; 18(10):2423. https://doi.org/10.3390/en18102423
Chicago/Turabian StyleJiang, Haorui, Kuihua Han, Weiyu Bao, and Yahui Li. 2025. "Comprehensive Control Strategy for Hybrid Energy Storage System Participating in Grid Primary Frequency Regulation" Energies 18, no. 10: 2423. https://doi.org/10.3390/en18102423
APA StyleJiang, H., Han, K., Bao, W., & Li, Y. (2025). Comprehensive Control Strategy for Hybrid Energy Storage System Participating in Grid Primary Frequency Regulation. Energies, 18(10), 2423. https://doi.org/10.3390/en18102423






