Economic Optimization of Hybrid Energy Storage Capacity for Wind Power Based on Coordinated SGMD and PSO
Abstract
1. Introduction
2. Energy Storage Configuration Strategy Considering Peak-Shaving Effectiveness
2.1. Peak-Shaving Power Curve of Hybrid Energy Storage System
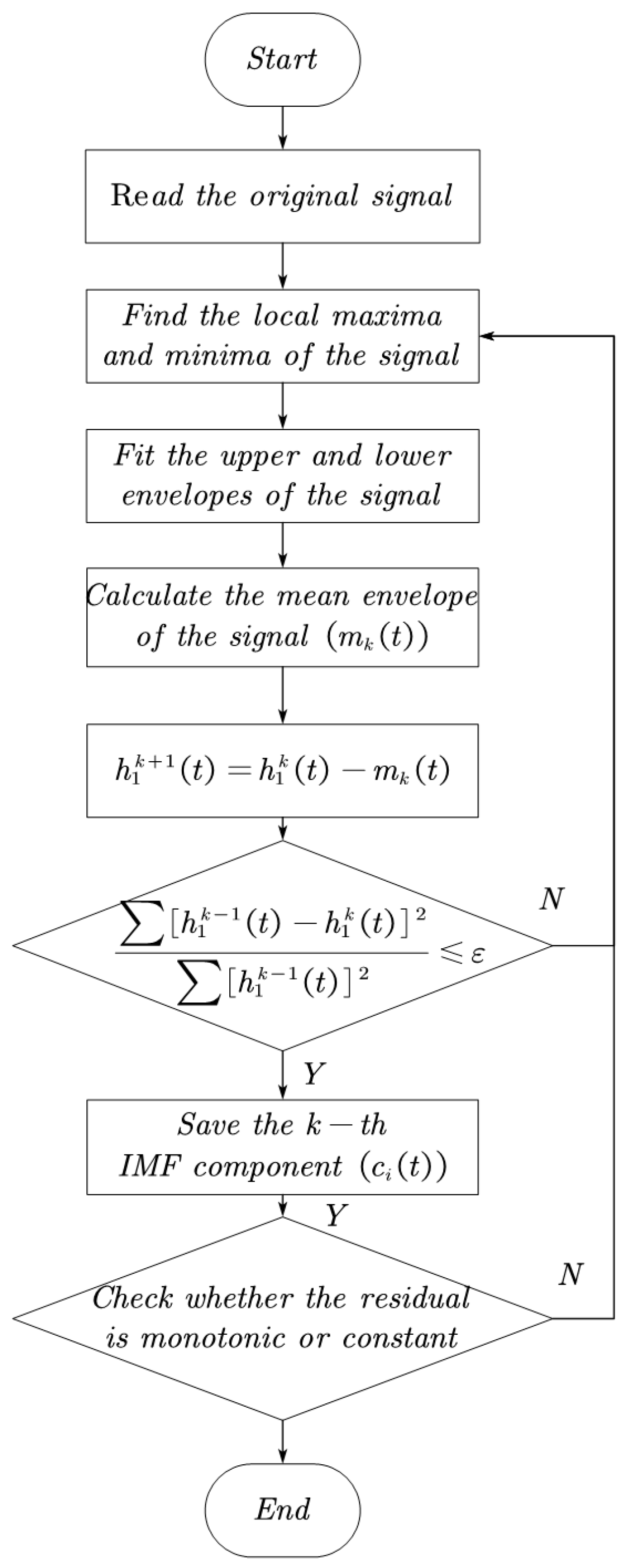
2.2. Empirical Mode Decomposition Algorithm
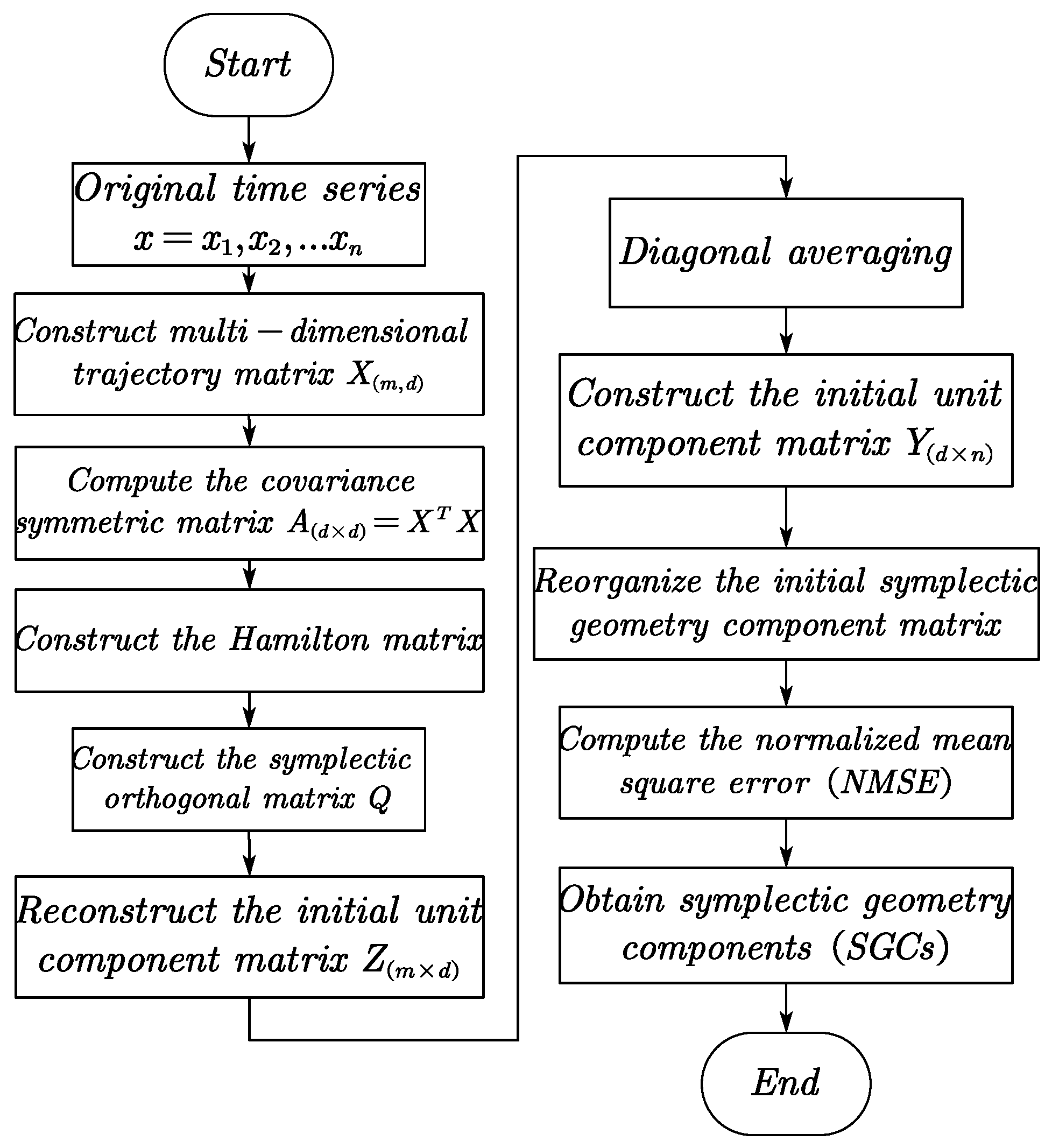
2.3. Symplectic Geometry Mode Decomposition Algorithm
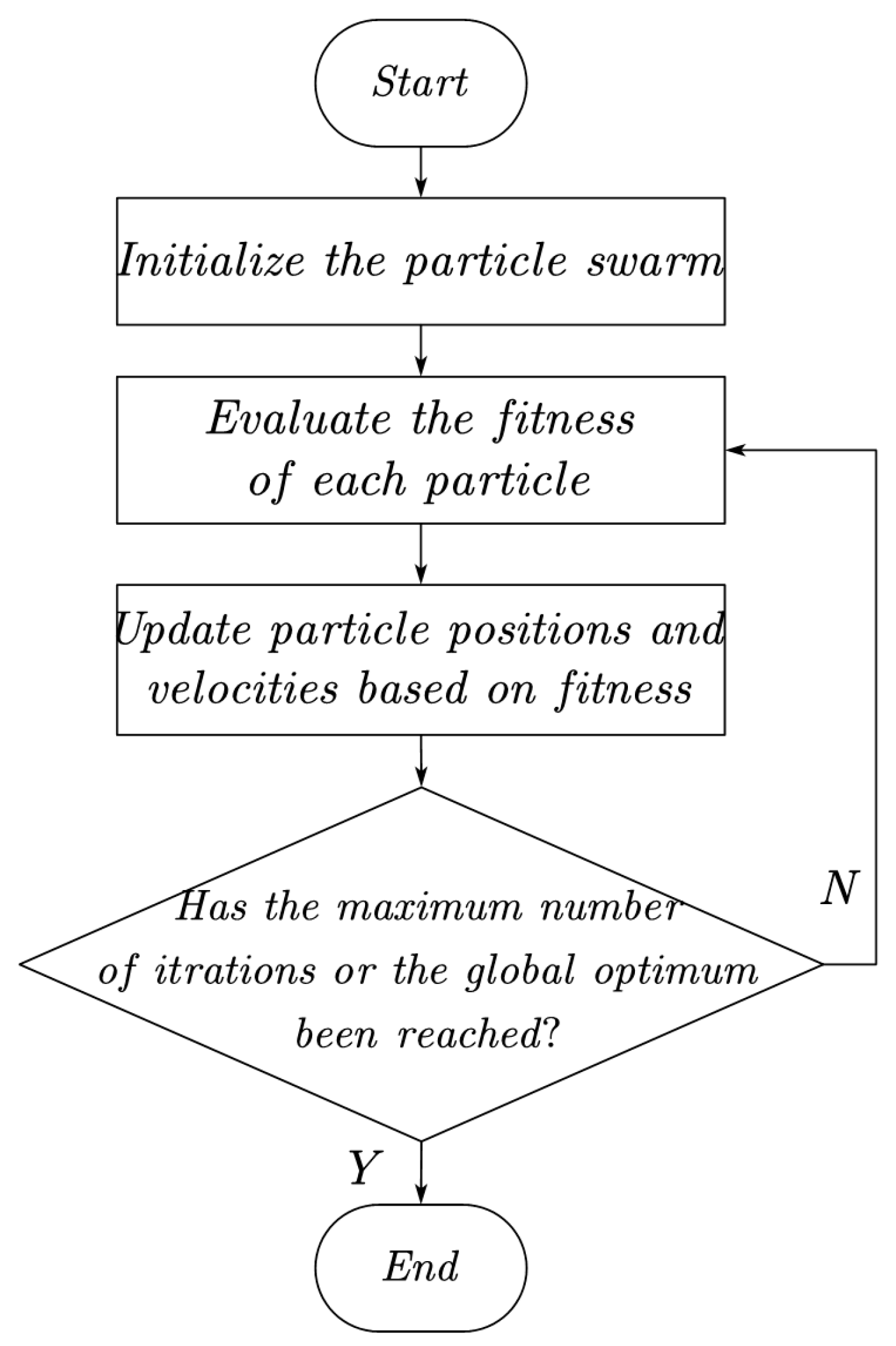
2.4. Particle Swarm Optimization
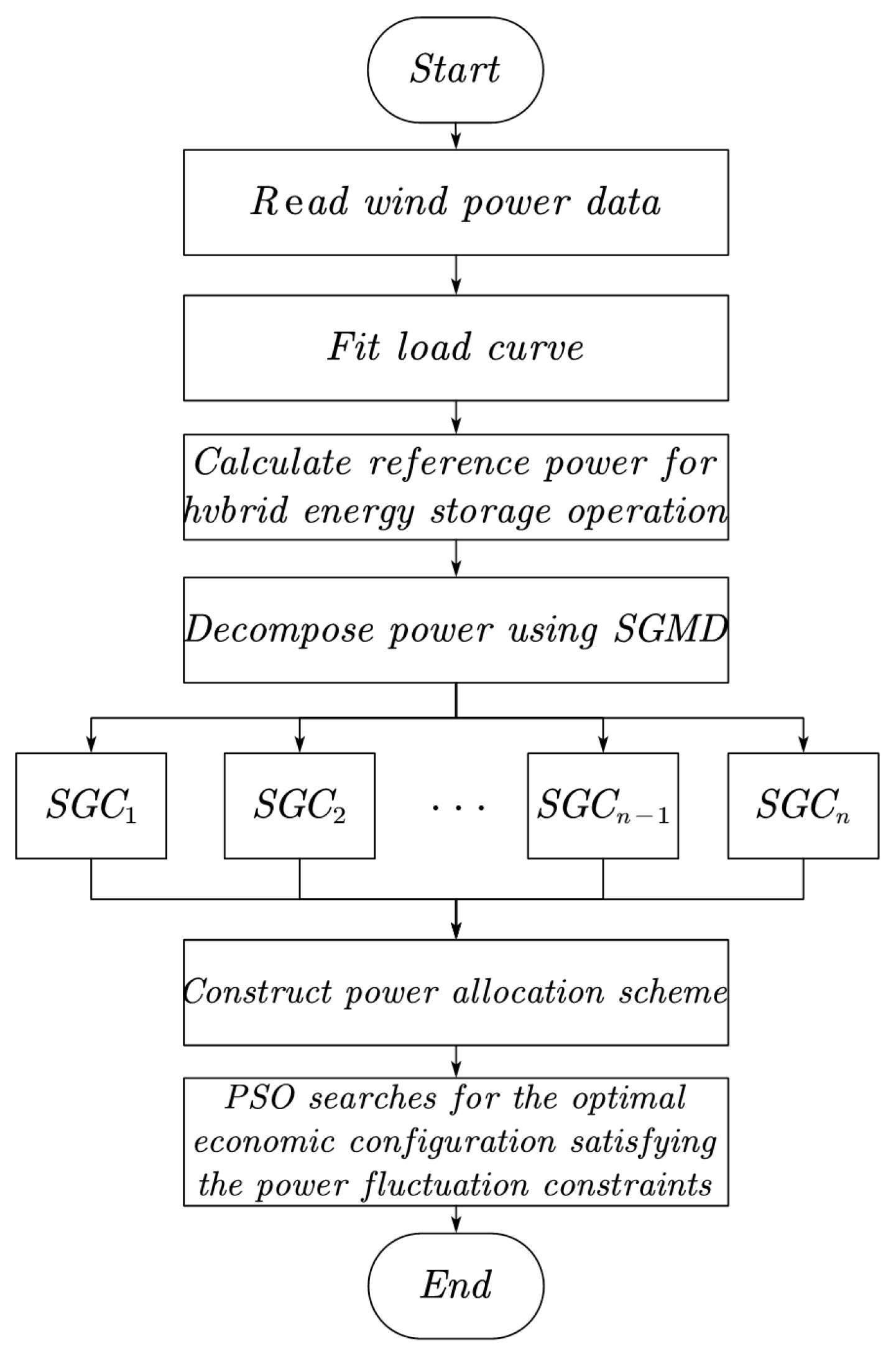
3. Peak Regulation Control and Economic Optimization Strategy for Hybrid Energy Storage Systems
3.1. Hybrid Energy Storage System Configuration
3.2. Construction of an Optimization Model for Hybrid Energy Storage System Configuration
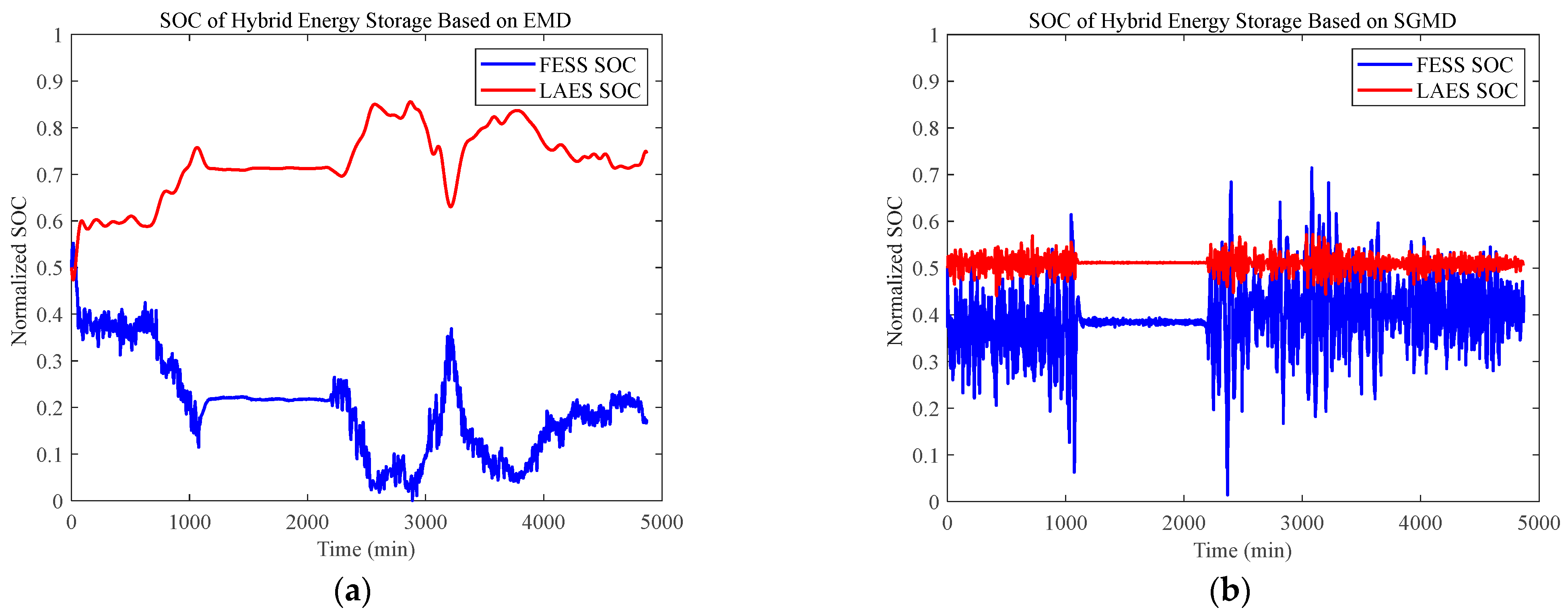
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, X.X.; Zhao, Q.; Zhang, Y.Q.; Yang, H.H. Analysis on the Development Trend of China’s Energy and Power System under “Dual-Carbon” Goals: Green Electricity and Green Hydrogen Substitution. Proc. CSEE 2024, 44, 6707–6721. [Google Scholar]
- Liu, Y.; Qiao, Y.; Han, S.; Xu, Y.; Geng, T.; Ma, T. Quantitative Evaluation Methods of Cluster Wind Power Output Volatility and Source–Load Timing Matching in Regional Power Grid. Energies 2021, 14, 5214. [Google Scholar] [CrossRef]
- Rocky Mountain Institute. The Economics of Battery Energy Storage; Rocky Mountain Institute: Basalt, CO, USA, 2017. [Google Scholar]
- Li, X.; Pan, L.Y.; Zhang, J.K.; Jin, Z.; Jiang, W.Z.; Wang, Y.F.; Liu, L.; Tang, R.L.; Lai, J.G.; Yang, X.G.; et al. A Novel Capacity Allocation Method for Hybrid Energy Storage System for Electric Ship Considering Life Cycle Cost. J. Energy Storage 2025, 116, 116070. [Google Scholar] [CrossRef]
- Zheng, H.; Xie, L.R.; Ye, L.; Lu, P.; Wang, K.F. Hybrid Energy Storage Strategy Considering Dual Evaluation Indexes for Smoothing Photovoltaic Output Fluctuations. Trans. China Electrotech. Soc. 2021, 36, 1805–1817. [Google Scholar]
- Liu, Y.B.; Wu, H.; Liu, T.J.; Yang, Z.Y.; Liu, J.Y.; Li, Q.H. User-Side Net Load Forecasting Algorithm Integrating Empirical Mode Decomposition and Deep Learning. Autom. Electr. Power Syst. 2021, 45, 57–64. [Google Scholar]
- Shen, J.; Huang, S.; Liu, C.; Li, S.; Wu, J. Optimal Configuration Method of Wind Farm Hybrid Energy Storage Based on EEMD-EMD and Grey Relational Degree Analysis. Front. Energy Res. 2023, 10, 1021189. [Google Scholar] [CrossRef]
- Nguyen, C.L.; Lee, H.H. A Novel Dual-Battery Energy Storage System for Wind Power Applications. IEEE Trans. Ind. Electron. 2016, 63, 6136–6147. [Google Scholar] [CrossRef]
- Yan, Q.M.; Liu, Y.C.; Dong, X.Z.; Ma, Y.X. Optimal Hybrid Energy Storage Capacity Allocation for Smoothing Photovoltaic Output Based on CEEMDAN-HT. Power Syst. Prot. Control 2022, 50, 43–53. [Google Scholar]
- Zhang, P.; Li, Y.Q.; Xing, H.L. Optimal Hybrid Energy Storage Capacity Allocation for Wind Power Fluctuation Smoothing Based on Variational Mode Decomposition. Power Gener. Technol. 2025, 1–10. Available online: http://kns.cnki.net/kcms/detail/33.1405.TK.20250317.1620.004.html (accessed on 4 May 2025).
- Shi, L.J.; Duanmu, C.R.; Yang, D.M.; Feng, W. Energy Storage Capacity Optimization for Wind Farms Based on Group Control Strategy. Acta Energiae Solaris Sin. 2024, 45, 340–349. [Google Scholar] [CrossRef]
- GB/T 19963.1-2021; Technical Regulations for Connecting Wind Farms to Power Systems, Part 1: Onshore Wind Power. China Standards Press: Beijing, China, 2021.
- Liang, Y.; Zhang, D.; Zhang, J.; Hu, H.G. A State-of-the-Art Analysis on Decomposition Method for Short-Term Wind Speed Forecasting Using LSTM and a Novel Hybrid Deep Learning Model. Energy 2024, 313, 133826. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, X.; Niu, D. A New Framework for Ultra-Short-Term Electricity Load Forecasting Model Using IVMD–SGMD Two–Layer Decomposition and INGO–BiLSTM–TPA–TCN. Appl. Soft Comput. 2024, 167, 112311. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, S.; Li, Y.; Qian, H.; Jia, Q.; Xiao, S.; Huang, Y. Constrained Multi-objective Particle Swarm Optimization for Bistatic RFID Network Planning with Distributed Antennas. Swarm Evol. Comput. 2025, 94, 101882. [Google Scholar] [CrossRef]
- Shunhe, Z.; Keqilao, M.; Rihan, H.; Teng, W. Sensorless DPMSM Sliding Mode Control Based on Particle Swarm Optimized EKF. Modular Mach. Tool Autom. Manuf. Technol. 2022, 7, 66–70. [Google Scholar]
- Ren, J.P.; Ma, H.W.; Yao, M.Q. Coordinated Control Strategy for Flywheel Array Based on Particle Swarm Optimization. Trans. China Electrotech. Soc. 2021, 36, 381–388. [Google Scholar]
- Toughzaoui, Y.; Elkhatib, R.; Kaoutari, T.; Louahlia, H.; Chaoui, H.; Gualous, H. Advances in hospital energy systems: Genetic algorithm optimization of a hybrid solar and hydrogen fuel cell combined heat and power. Int. J. Hydrogen Energy 2024, 86, 1310–1325. [Google Scholar] [CrossRef]
- Suresh, M.; Meenakumari, R. An improved genetic algorithm-based optimal sizing of solar photovoltaic/wind turbine generator/diesel generator/battery connected hybrid energy systems for standalone applications. Int. J. Ambient Energy 2019, 42, 1136–1143. [Google Scholar] [CrossRef]
- Tong, Y.; Li, X. Ant Colony Algorithm for Time Optimal Load Balancing Scheduling Problem Strategy. J. Phys. Conf. Ser. 2021, 2010, 012045. [Google Scholar] [CrossRef]
- Gao, J.Y.; Li, W.Y.; Ma, R. Variable Time Constant Smoothing Strategy Based on Wind Power Flattening Index. In Proceedings of the 15th IEEE Conference on Industrial Electronics and Applications (ICIEA 2020), Kristiansand, Norway, 9–13 November 2020; pp. 500–505. [Google Scholar]
- Li, X. Fuzzy Adaptive Kalman Filter for Wind Power Output Smoothing with Battery Energy Storage System. IET Renew. Power Gener. 2012, 6, 340–347. [Google Scholar] [CrossRef]
- Wan, C.; Qian, W.; Zhao, C.; Song, Y.; Yang, G. Probabilistic Forecasting-Based Sizing and Control of Hybrid Energy Storage for Wind Power Smoothing. IEEE Trans. Sustain. Energy 2021, 12, 1841–1852. [Google Scholar] [CrossRef]
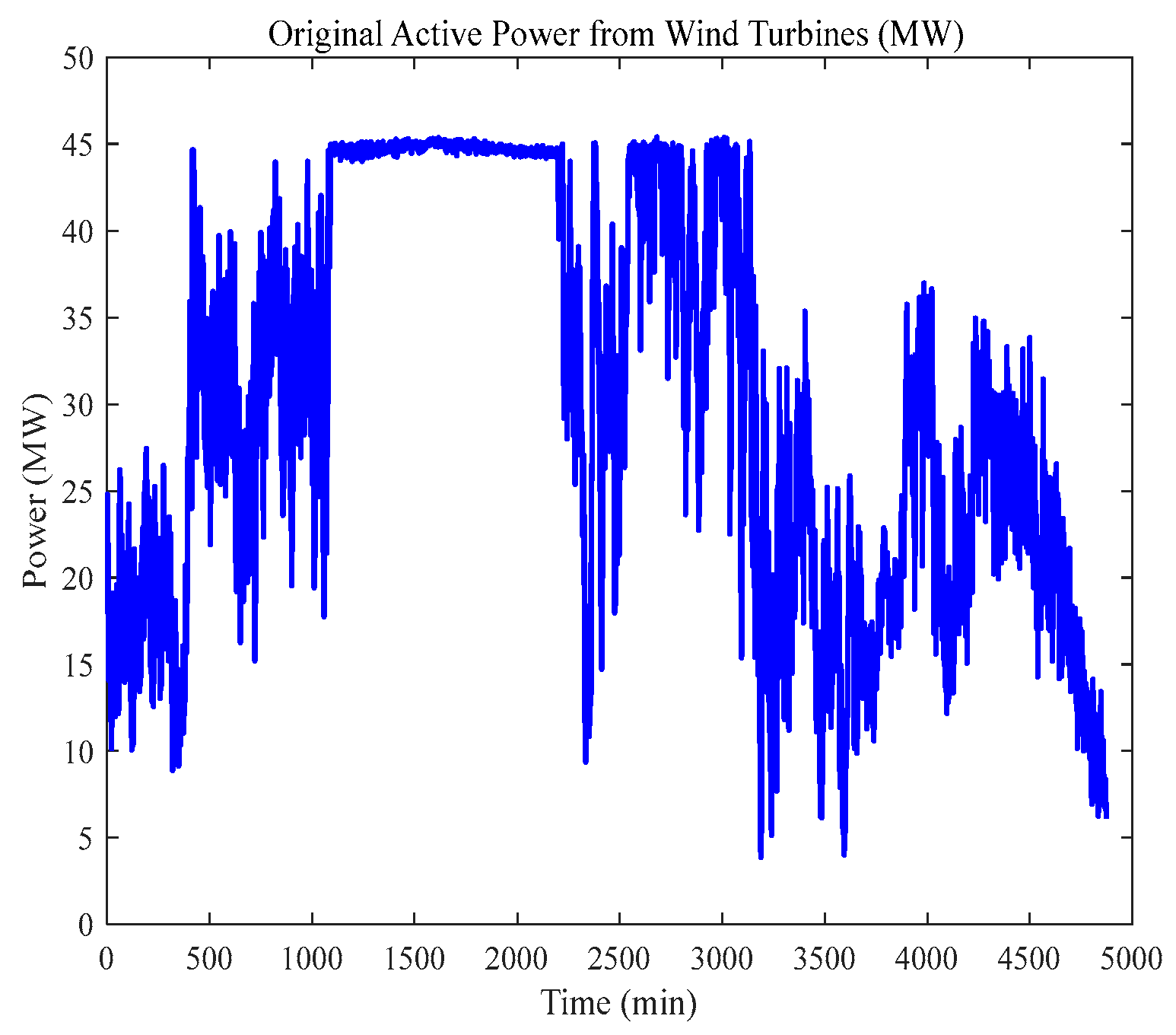
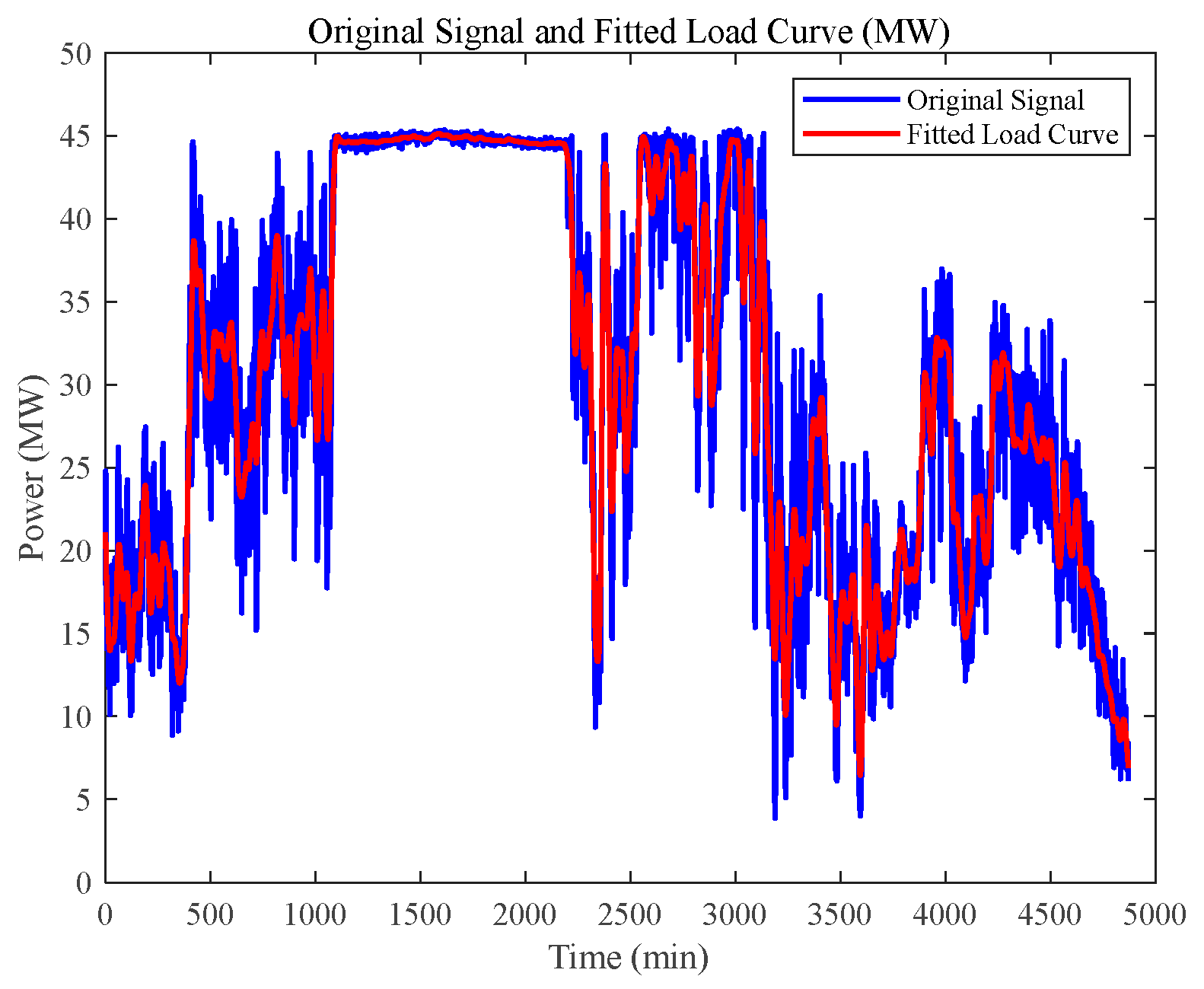
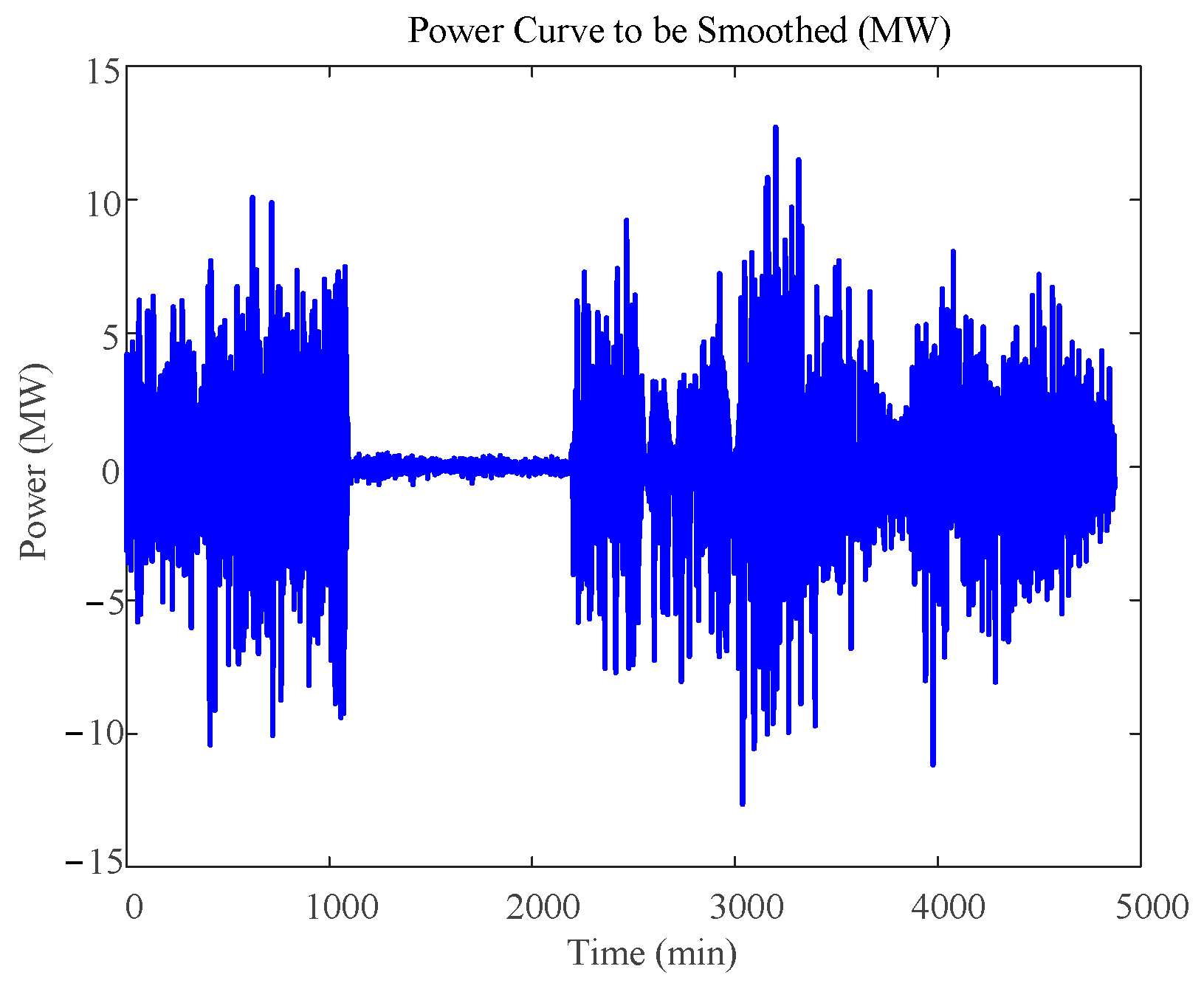


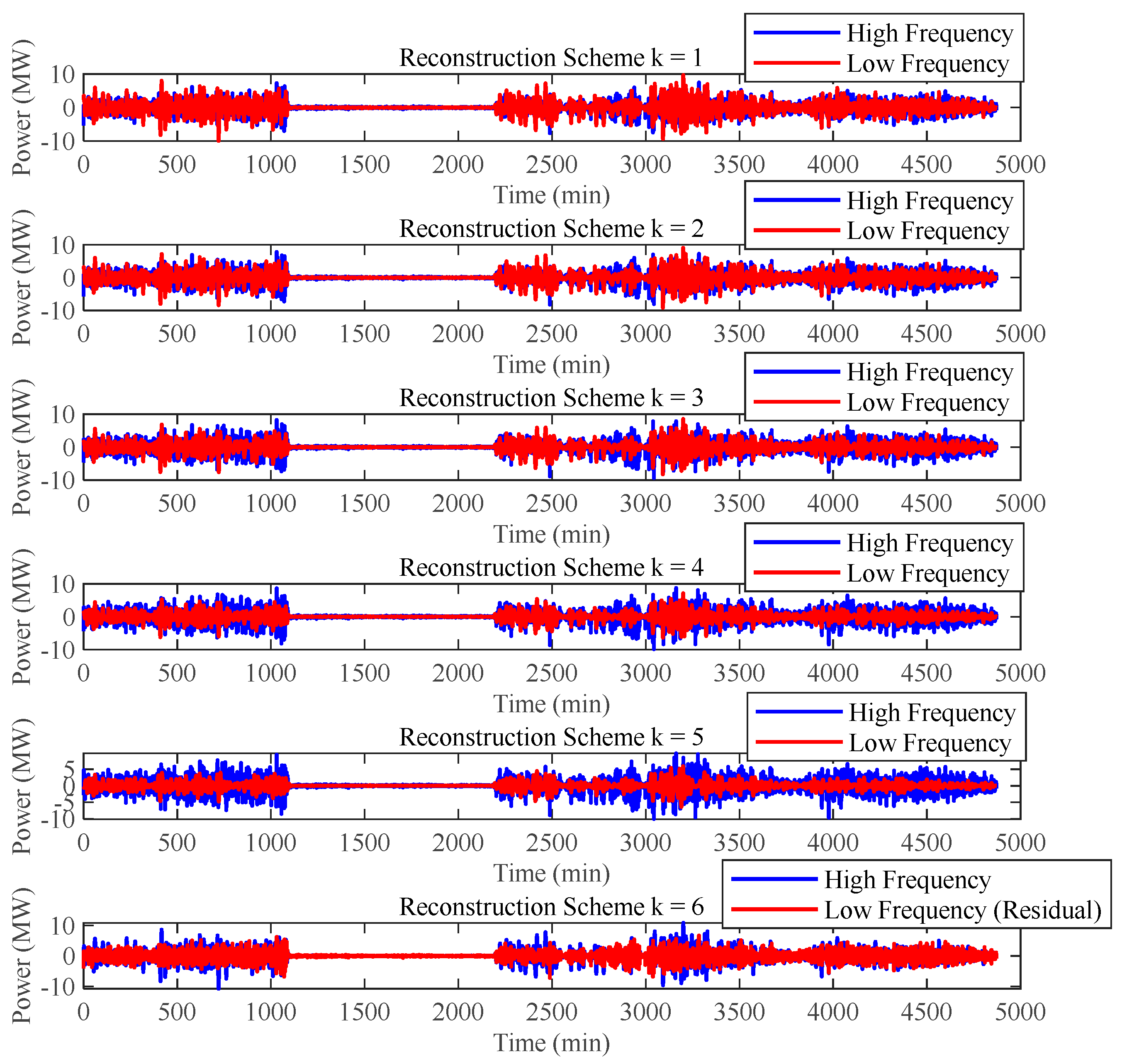
| ) | 10-Min Maximum Active Power Variation/MW | 1-Min Maximum Active Power Variation/MW |
|---|---|---|
| Storage Type | Discharge Duration | Main Advantages | Power Cost (CNY/kW) | Energy Cost (CNY/kWh) | Operation and Maintenance Cost (CNY/kWh) |
|---|---|---|---|---|---|
| Flywheel Energy Storage | Seconds to Minutes | Fast response, long service life, excellent stability, and high power density. | 3000–6000 | 3000–8000 | 0.008 |
| Pumped Hydro Storage | 4–10 h | Large storage capacity, long service life, and rapid load response, but significantly constrained by geographical conditions. | 5200–6480 | 200–1200 | 0.006 |
| Liquefied Compressed Air Energy Storage | Minutes–28 h | High energy density, relatively fast response, long service life, and low-cost storage using atmospheric pressure in liquefied tanks. | 1500–3000 | 400–1000 | 0.033 |
| Lithium-Ion Battery | 1–4 h | Fast charging and discharging capability and high energy density but a relatively limited service life. | 2000–4000 | 1000–2500 | 0.010 |
| Lead–Acid Battery Energy Storage | 6–10 h | Short service life, but offers the advantage of low costs. | 800–1500 | 600–1000 | 0.020 |
| Superconducting Magnetic Energy Storage | Virtually unlimited | Fast response time and high operational efficiency. | 4000–8000 | 2000–4000 | 0.006 |
| Energy Storage Configuration | EMD-Based Scheme | SGMD-Based Scheme |
|---|---|---|
| FESS Power (MW) | 12.17 | 6.70 |
| FESS Capacity (MWh) | 8.94 | 0.61 |
| LAES Power (MW) | 2.23 | 9.99 |
| LAES Capacity (MWh) | 10.69 | 10.00 |
| Total Configuration Cost (CNY·104) | 12,371.85 | 9172.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, K.; Meng, K.; Meng, X.; Zhao, F.; Lü, Y. Economic Optimization of Hybrid Energy Storage Capacity for Wind Power Based on Coordinated SGMD and PSO. Energies 2025, 18, 2417. https://doi.org/10.3390/en18102417
Qi K, Meng K, Meng X, Zhao F, Lü Y. Economic Optimization of Hybrid Energy Storage Capacity for Wind Power Based on Coordinated SGMD and PSO. Energies. 2025; 18(10):2417. https://doi.org/10.3390/en18102417
Chicago/Turabian StyleQi, Kai, Keqilao Meng, Xiangdong Meng, Fengwei Zhao, and Yuefei Lü. 2025. "Economic Optimization of Hybrid Energy Storage Capacity for Wind Power Based on Coordinated SGMD and PSO" Energies 18, no. 10: 2417. https://doi.org/10.3390/en18102417
APA StyleQi, K., Meng, K., Meng, X., Zhao, F., & Lü, Y. (2025). Economic Optimization of Hybrid Energy Storage Capacity for Wind Power Based on Coordinated SGMD and PSO. Energies, 18(10), 2417. https://doi.org/10.3390/en18102417






