Synergistic Framework for Fuel Cell Mass Transport Optimization: Coupling Reduced-Order Models with Machine Learning Surrogates
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Assumptions
2.2. Governing Equations
2.3. Electrochemical Model
2.4. Source Terms and Phase Changes
3. Coupled Solution and Verification of the Model
3.1. Boundary and Initial Conditions
- (1)
- Boundary Conditions
- (2)
- Initial Conditions
3.2. Numerical Application of the Model and Validation of Its Effectiveness
- (1)
- Application Process of the Model
- (2)
- Validation Process of the Model
4. Analysis and Optimization of Mass Transfer Property Parameters in the FC
4.1. Selection of Parameters to Be Optimized and Their Sensitivity Analysis
4.2. Building a Neural Network Proxy Model
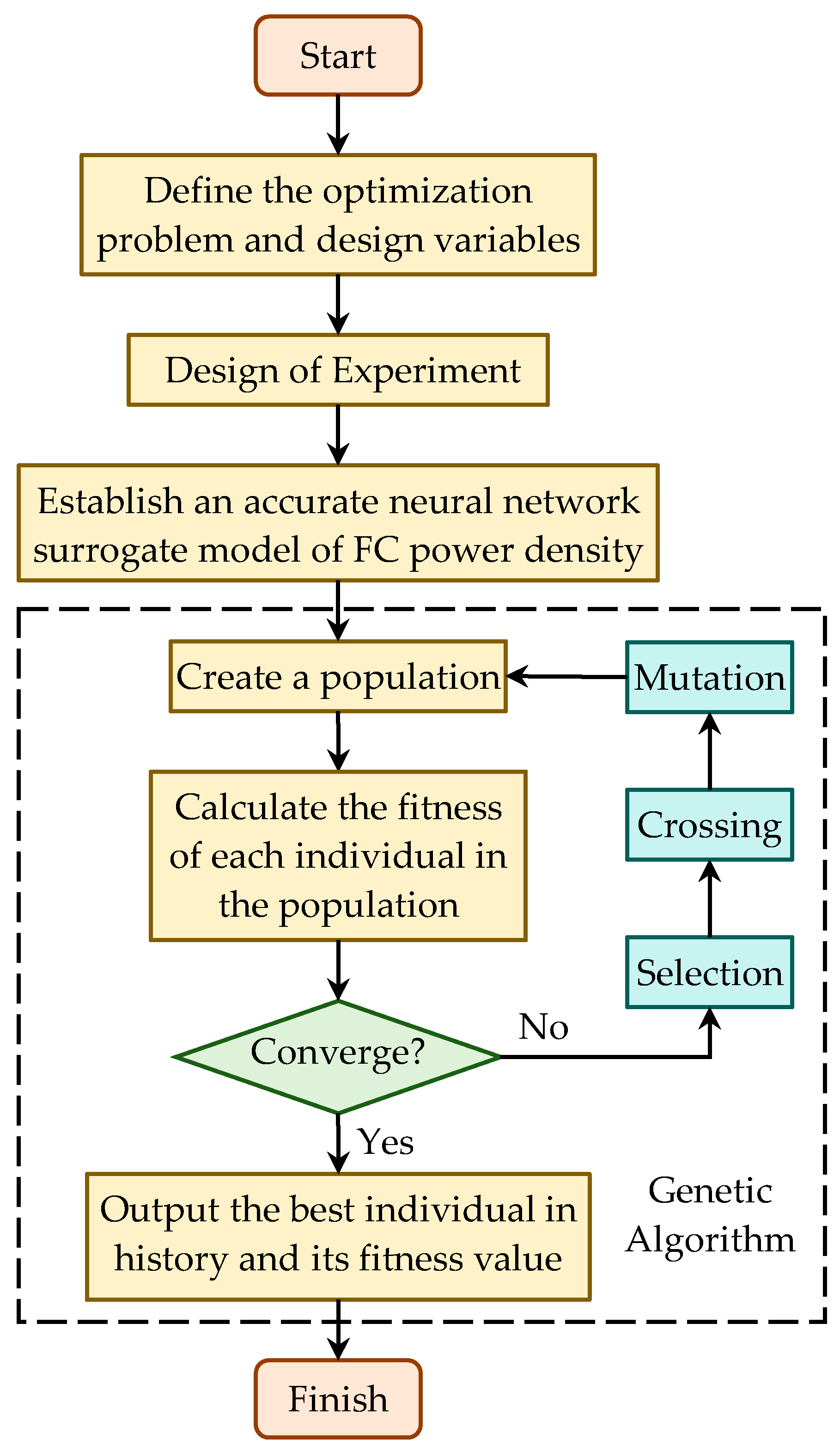
4.3. Optimization Process Based on the Genetic Algorithm
5. Analysis of the Impact of Heat and Mass Transfer Properties on the Internal State and Performance of the FC
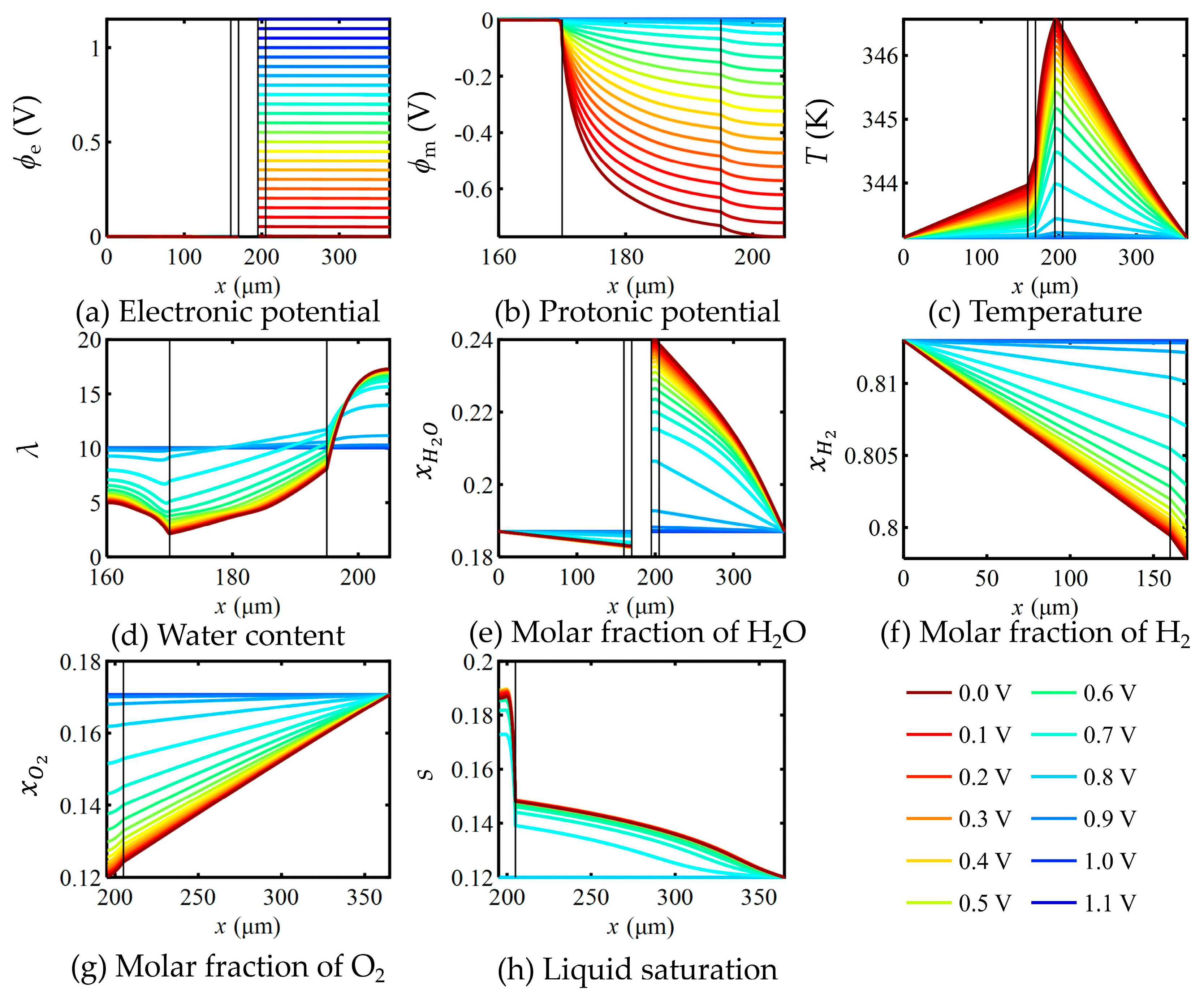
5.1. Distribution of Important Independent Variables Within the FC
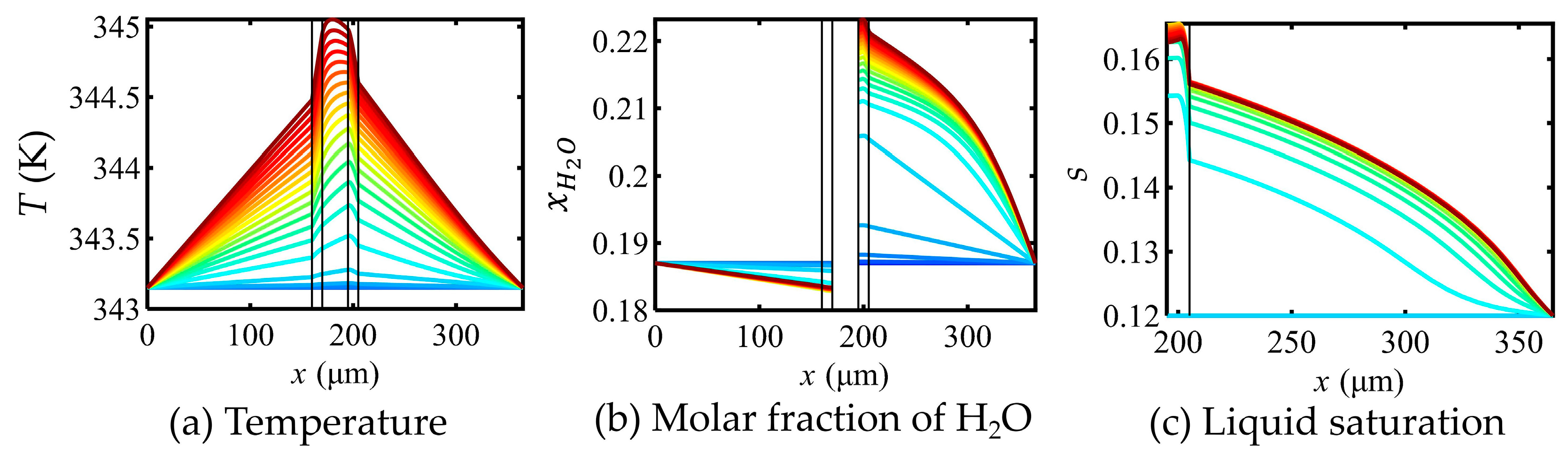
5.2. Effects of Mass Transfer Parameters on Key Variables in the FC
5.3. Impact of Optimizing Mass Transfer Parameters on FC Performance
6. Conclusions
- (1)
- The 1D two-phase non-isothermal parametric model established in this study can capture the distribution of key variables within the FC and predict its output performance. Compared with the experimental results, the error was within 3.87%. Additionally, it requires minimal computational resources and time, demonstrating high practical value.
- (2)
- Sensitivity analysis revealed that kPEM is negatively correlated with Pd, while other parameters are positively correlated. The parameter kAGDL had the most significant impact on Pd, followed by kCGDL, κGDL, , and . Remaining parameters exhibited negligible influence.
- (3)
- The ANN surrogate model achieved high accuracy, with the error between predicted and actual values remaining below 0.15%. When combined with the genetic algorithm, it could rapidly perform global optimization across multiple parameters within seconds, significantly improving the optimization efficiency.
- (4)
- The MEA’s mass transfer properties primarily affect the internal heat and mass transfer in the FC by influencing the temperature, gaseous water, and liquid water distributions. These adjustments improve the concentration polarization region, thereby enhancing electrochemical process and output performance.
- (5)
- The optimized mass transfer properties increased the net Pd of the FC by 5.51%. Through the combined optimization design process of the 1D model, ANN surrogate model, and genetic algorithm, an optimal solution can be obtained in a short time, which has certain reference significance for guiding the design process of the MEA.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| ACL | Anode catalyst layer |
| AGC | Anode gas channel |
| ANN | Artificial neural network |
| CCL | Cathode catalyst layer |
| CGC | Cathode gas channel |
| CL | Catalyst layer |
| EW | Equivalent weight |
| FC | Fuel cell |
| GDL | Gas diffusion layer |
| GC | Gas channel |
| HOR | Hydrogen oxidation reaction |
| LBM | Lattice Boltzmann method |
| MEA | Membrane electrode assembly |
| ORR | Oxygen reduction reaction |
| PDEs | Partial differential equations |
| PEM | Proton exchange membrane |
| PEMFC | Proton exchange membrane fuel cell |
| RH | Relative humidity |
| Symbols | |
| a | Water activity |
| aa,d | Ad-/desorption mass transfer coefficient (m·s−1) |
| alg | Effective liquid–gas interface area density ratio factor (m−1) |
| A | Electrochemical active area of catalyst layer (m−1) |
| C | Total interstitial gas concentration (mol·m−3) |
| D | Diffusion coefficient (m2·s−1) |
| f | Water volume fraction in ionomer |
| F | Faraday constant (C·mol−1) |
| ΔH | Enthalpy of formation of liquid water (J·mol−1) |
| Had | Water adsorption/desorption enthalpy (J·mol−1) |
| Hec | Evaporation/condensation enthalpy (J·mol−1) |
| i | Electrochemical reaction rate (A·m−3) |
| i0 | Exchange current density (A·m−2) |
| I | Cell current density (A·m−2) |
| j | Flux |
| k | Thermal conductivity (W·K−1) |
| ka,d | Water adsorption/desorption transfer coefficient (m·s−1) |
| kc,e | Water condensation/evaporation transfer coefficient (m·s−1) |
| L | Layer thickness (m) |
| Mw | Molar mass of water (kg·mol−1) |
| n | Interfacial unit normal vector |
| nd | Electrophoretic resistance coefficient |
| p | Partial pressure (Pa) |
| pc | Capillary pressure (Pa) |
| P | Pressure (Pa) |
| Pd | Power density (W·cm−2) |
| R | Universal gas constant (J·mol−1·K−1) |
| s | Liquid water saturation |
| S | Source term |
| ΔS | Reaction entropy (J·mol−1·K−1) |
| T | Temperature (K) |
| Vcell | Cell voltage (V) |
| Vm | Equivalent volume of membrane (m3·mol−1) |
| Vw | Molar volume of liquid water (m3·mol−1) |
| x | Mole fraction of species i |
| Greek letters | |
| α | Mole fraction of species i in dry fuel gas |
| β | Transfer coefficient |
| γe,c | Water evaporation/condensation rate (s−1) |
| εp | Porosity |
| εi | Volume fraction of ionomer |
| η | Activation overpotential (V) |
| θc | Contact angle (°) |
| κ | Hydraulic permeability (m2) |
| λ | Membrane water content |
| μ | Dynamic viscosity of liquid (Pa·s) |
| ρ | Density (kg·m−3) |
| σ | Conductivity (S·m−1) |
| τ | Pore tortuosity |
| ϕ | Potential (V) |
| Δϕ | Galvani potential difference (V) |
| Δϕ0 | Reversible potential difference (V) |
| Subscripts and superscripts | |
| a | Anode |
| abs | Absolute value |
| c | Cathode |
| e | Electronic phase |
| eq | Equilibrium value |
| m | Protonic phase |
| i | Species H2, O2 and H2O |
| red | Reduced value |
| ref | Reference value |
| sat | Saturation value |
| H2 | Hydrogen |
| O2 | Oxygen |
| H2O | Water |
References
- Zuo, Q.; Wang, G.; Shen, Z.; Ma, Y.; Ouyang, Y.; Yang, D.; Lei, S.; Ouyang, M. Performance evaluation and field synergy analysis of PEMFC with novel snake coil flow field. Int. J. Heat Mass Transf. 2025, 238, 126470. [Google Scholar] [CrossRef]
- Lee, S.H.; Nam, J.H.; Kim, C.J.; Kim, H.M. Numerical investigation of effective thermal conductivity of gas diffusion layer of the PEM fuel cell. Numer. Heat Transf. Part A Appl. 2024, 85, 1356–1378. [Google Scholar] [CrossRef]
- Froning, D.; Wirtz, J.; Hoppe, E.; Lehnert, W. Flow Characteristics of Fibrous Gas Diffusion Layers Using Machine Learning Methods. Appl. Sci. 2022, 12, 12193. [Google Scholar] [CrossRef]
- Xiao, L.; Yin, Z.; Bian, M.; Bevilacqua, N.; Zeis, R.; Yuan, J.; Sui, P. Microstructure reconstruction using fiber tracking technique and pore-scale simulations of heterogeneous gas diffusion layer. Int. J. Hydrog. Energy 2022, 47, 20218–20231. [Google Scholar] [CrossRef]
- Ye, S.; Hou, Y.; Li, X.; Jiao, K.; Du, Q. Pore-Scale Investigation of Coupled Two-Phase and Reactive Transport in the Cathode Electrode of Proton Exchange Membrane Fuel Cells. Trans. Tianjin Univ. 2023, 29, 1–13. [Google Scholar] [CrossRef]
- He, Y.; Bai, M.; Hao, L. Pore-Scale Simulation of Effective Transport Coefficients in the Catalyst Layer of Proton Exchange Membrane Fuel Cells. J. Electrochem. Soc. 2023, 170, 044501. [Google Scholar] [CrossRef]
- Park, S.; Akbar, A.; Lee, J.; Kim, Y.; Um, S. Nanoscopic Post-Compression Effects on Transport Phenomena and Electrochemical Utilization in Quaternion Catalyst Layers for Fuel Cell Applications. Int. J. Precis. Eng. Manuf.-Green Technol. 2024, 11, 463–479. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, R.; Kang, Q.; Tao, W. Pore-scale study of pore-ionomer interfacial reactive transport processes in proton exchange membrane fuel cell catalyst layer. Chem. Eng. J. 2020, 391, 123590. [Google Scholar] [CrossRef]
- Liu, Q.; Lan, F.; Chen, J.; Wang, J.; Zeng, C. Effect of anisotropic transport properties of porous layers on the dynamic performance of proton exchange membrane fuel cell. Int. J. Hydrog. Energy 2023, 48, 10982–11002. [Google Scholar] [CrossRef]
- Zhang, G.; Qu, Z.; Yang, H.; Mu, Y.; Wang, Y. A one-dimensional model of air-cooled proton exchange membrane fuel cell stack integrating fan arrangement and operational characteristics. Appl. Therm. Eng. 2024, 249, 123353. [Google Scholar] [CrossRef]
- Trinh, D.H.; Kim, Y.; Yu, S. One-dimensional dynamic model of a PEM fuel cell for analyzing through-plane species distribution and irreversible losses under various operating conditions. Case Stud. Therm. Eng. 2024, 60, 104815. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, L.; Zheng, W.; Hu, Z.; Shao, Y.; Li, J.; Ouyang, M. Characterizing the two-phase flow effect in gas channel of proton exchange membrane fuel cell with dimensionless number. Int. J. Hydrog. Energy 2023, 48, 5250–5265. [Google Scholar] [CrossRef]
- Khemili, F.; Najjari, M. Numerical Modeling of the Influence of Gas Diffusion Layer Properties on Liquid Water Transport and Transient Responses in a Proton Exchange Membrane Fuel Cell. Microgravity Sci. Technol. 2023, 35, 42. [Google Scholar] [CrossRef]
- Liu, Q.; Lan, F.; Wang, J.; Chen, Y.; Chen, J. Multi-objective optimization of helical baffle flow field structure for fuel cell under multiple performance indicator constraints. Renew. Energy 2025, 241, 122349. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, D.; Chen, Q.; Zhang, Y.; Jiang, X.; Yang, X.; Cao, J.; Deng, Q.; Chen, B.; Liu, Q.; et al. Three-dimensional full-morphology numerical simulation of PEM fuel cells: Spatial distribution characteristics of “gas–water-electricity” considering circular dot matrix gas distribution zones. Chem. Eng. J. 2025, 505, 159199. [Google Scholar] [CrossRef]
- Neyerlin, K.C.; Gu, W.; Jorne, J.; Gasteiger, H.A. Determination of Catalyst Unique Parameters for the Oxygen Reduction Reaction in a PEMFC. J. Electrochem. Soc. 2006, 153, A1955. [Google Scholar] [CrossRef]
- Neyerlin, K.C.; Gu, W.; Jorne, J.; Gasteiger, H.A. Study of the Exchange Current Density for the Hydrogen Oxidation and Evolution Reactions. J. Electrochem. Soc. 2007, 154, B631. [Google Scholar] [CrossRef]
- Vetter, R.; Schumacher, J.O. Free open reference implementation of a two-phase PEM fuel cell model. Comput. Phys. Commun. 2019, 234, 223–234. [Google Scholar] [CrossRef]
- Liu, Q.; Lan, F.; Chen, J.; Wang, J.; Zeng, C. Flow field structure design modification with helical baffle for proton exchange membrane fuel cell. Energy Convers. Manag. 2022, 269, 116175. [Google Scholar] [CrossRef]
- Liu, Q. Study of Diffusion Layer Pore Characteristics and Helical Baffle Flow Field Improvement for Fuel Cell Mass Transfer Capability Enhancement. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2023. [Google Scholar]
- Weber, A.Z.; Borup, R.L.; Darling, R.M.; Das, P.K.; Dursch, T.J.; Gu, W.; Harvey, D.; Kusoglu, A.; Litster, S.; Mench, M.M.; et al. A Critical Review of Modeling Transport Phenomena in Polymer-Electrolyte Fuel Cells. J. Electrochem. Soc. 2014, 161, F1254. [Google Scholar] [CrossRef]
- Raghunath, K.V.; Reddy, B.K.; Muliankeezhil, S.; Aparna, K. Non-isothermal One-Dimensional Two-Phase Model of Water Transport in Proton Exchange Membrane Fuel Cells with Micro-porous Layer. Arab. J. Sci. Eng. 2023, 48, 8543–8556. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, H.; Sun, H.; Hu, Z.; Li, J.; Xu, L.; Ouyang, M. Analysis and Optimization of Commercial Scale PEMFCs with Different Flow Channels Prepared by Ultrafast Laser Fabrication Technique. Automot. Innov. 2024, 7, 225–235. [Google Scholar] [CrossRef]
- Tao, J.; Wei, X.; Ming, P.; Wang, X.; Jiang, S.; Dai, H. Order reduction, simplification and parameters identification for cold start model of PEM fuel cell. Energy Convers. Manag. 2022, 274, 116465. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Ji, X.; Liu, F.; And Hao, D. Sensitivity analysis of structural parameters for PEMFCs based on 1D transient model and elementary effect method. Int. J. Green Energy 2024, 21, 87–101. [Google Scholar] [CrossRef]
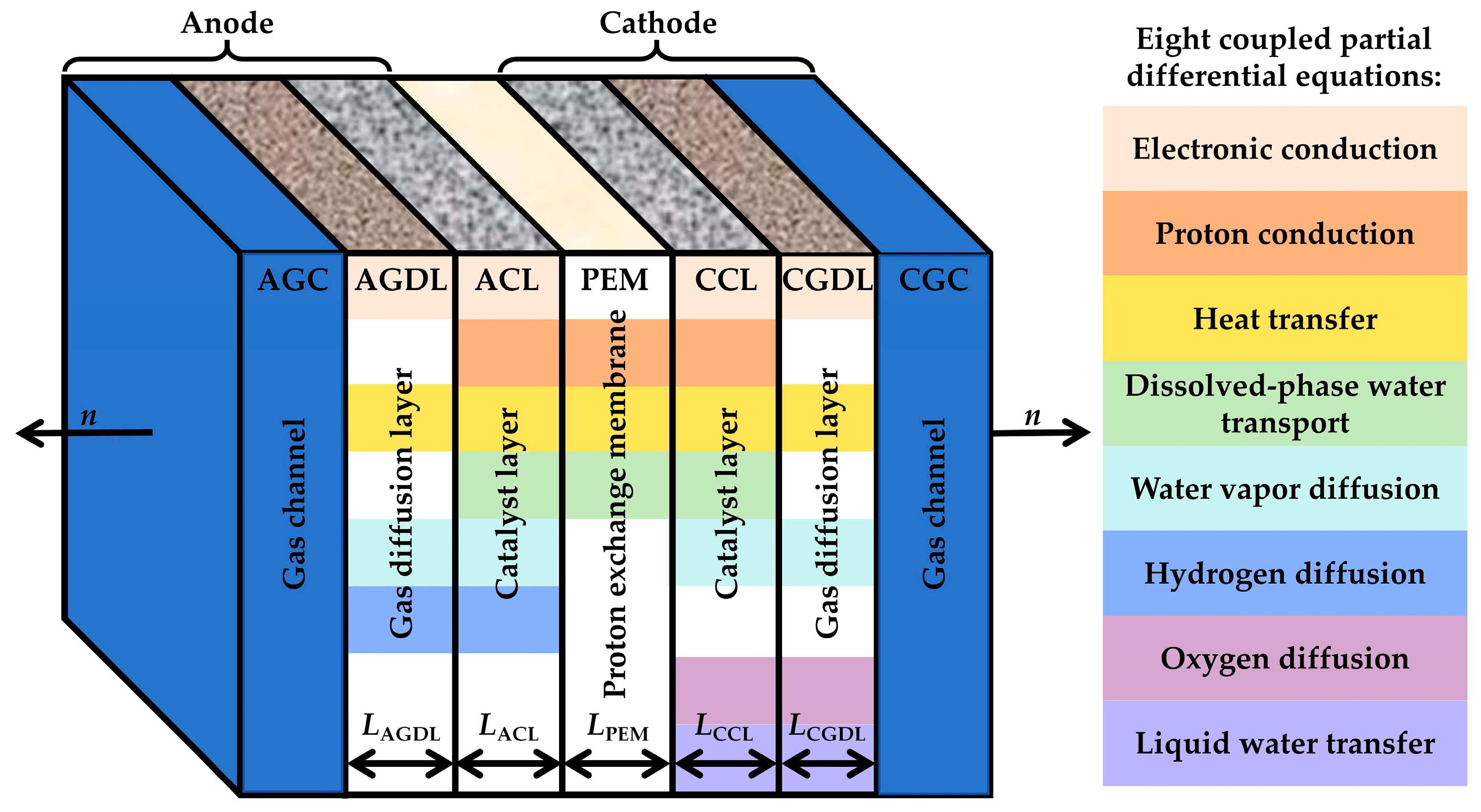




| Name | Variable | Flux | Continuity Equation |
|---|---|---|---|
| Electronic conduction | |||
| Proton conduction | |||
| Heat transfer | T | ||
| Water transport in ionomers | λ | ||
| Water vapor diffusion | |||
| Hydrogen diffusion | |||
| Oxygen diffusion | |||
| Liquid water transfer | s |
| Source Terms | AGDL | ACL | PEM | CCL | CGDL |
|---|---|---|---|---|---|
| Se | 0 | −i | - | i | 0 |
| Sm | - | i | 0 | −i | - |
| ST | |||||
| Sλ | - | Sad | 0 | i/2F + Sad | - |
| 0 | −Sad | - | −Sad − Sec | −Sec | |
| 0 | −i/2F | - | - | - | |
| - | - | - | −i/4F | 0 | |
| Ss | - | - | - | Sec | Sec |
| Property/Unit | Expression | Property/Unit | Expression |
|---|---|---|---|
| Saturated pressure of water vapor/Pa | Dynamic viscosity of liquid water/mPa·s | ||
| Water vapor mass transfer coefficient in the membrane/m·s−1 | The volume fraction of water in the ionomer/- | ||
| Capillary pressure/Pa | Electrophoretic resistance coefficient/- | ||
| Equilibrium water content of the ionomer/- | Water activity/- | ||
| Concentration of interstitial gas/mol·m−3 | C = P/RT | Hydraulic permeability/m² | |
| Water diffusion rate in the ionomer/m²·s−1 | Fickean gas diffusion rate/m²·s−1 | ||
| Evaporation and condensation rates/s−1 | Hertz–Knudsen mass transfer coefficient/m·s−1 | ||
| Ion conductivity of the membrane/S·m−1 | Reduced saturation/- |
| Parameters/Symbols | Value/Unit | Parameters/Symbols | Value/Unit |
|---|---|---|---|
| The equivalent volume of dry film/Vm | 517.766/cm3·mol−1 | The molar volume of liquid water/Vw | 18.405/cm3·mol−1 |
| Latent heat of evaporation/condensation/Had,ec | 42/kJ·mol−1 | Transfer coefficient/β | 0.5/− |
| Adsorption mass transfer coefficient/aa | 3.53 × 10−5/m·s−1 | Desorption mass transfer coefficient/ad | 1.42 × 10−4/m·s−1 |
| Entropy value of the anode half-reaction/∆SHOR | 0.104/J (mol K)−1 | Entropy value of the cathode half-reaction /∆SORR | −163.3/J (mol K)−1 |
| The electrochemically active area of anode CL/Aa | 1 × 107/m−1 | The electrochemically active area of the cathode CL/Ac | 3 × 107/m−1 |
| Effective liquid-gas interface area density ratio factor/alg | 2 × 106/m−1 | The molar mass of water/Mw | 18/g·mol−1 |
| Variable | AGC/AGDL | AGDL/ACL | ACL/PEM | PEM/CCL | CCL/CGDL | CGDL/CGC |
|---|---|---|---|---|---|---|
| ϕe | Continuity | Continuity | ||||
| ϕm | - | Continuity | Continuity | - | ||
| T | T = Ta | Continuity | Continuity | Continuity | Continuity | T = Tc |
| λ | - | Continuity | Continuity | - | ||
| Continuity | Continuity | |||||
| Continuity | - | - | - | |||
| - | - | - | Continuity | |||
| s | - | - | - | Continuity |
| Symbol | Explanation | Unit | AGDL and CGDL | ACL and CCL | PEM |
|---|---|---|---|---|---|
| L | Thickness | μm | 160 | 10 | 25 |
| εi | Volume fraction of ionomer | - | - | 0.3 | 1 |
| εp | Porosity | - | 0.76 | 0.4 | - |
| k | Thermal conductivity | W·(m·K)−1 | 1.6 | 0.27 | 0.3 |
| τ | Pore tortuosity | - | 1.6 | 1.6 | - |
| κabs | Absolute permeability | m2 | 6.15 × 10−12 | 1 × 10−13 | - |
| σe | Electrical conductivity | S·m−1 | 1250 | 350 | - |
| θc | Contact angle | ° | 120 | 100 | - |
| Parameters to Be Optimized | Symbol | Range of Values | Unit |
|---|---|---|---|
| A/CGDL Thermal conductivity | kA/CGDL | [0.5, 3.5] | W·(m·K)−1 |
| A/CGDL Electrical conductivity | [500, 2000] | S·m−1 | |
| CGDL Permeability | κCGDL | [3, 9] | ×10−12 m2 |
| A/CCL Thermal conductivity | kA/CCL | [0.1, 0.4] | W·(m·K)−1 |
| A/CCL Electrical conductivity | [100, 700] | S·m−1 | |
| CCL Permeability | κCCL | [2, 20] | ×10−14 m2 |
| PEM Thermal conductivity | kPEM | [0.05, 0.5] | W·(m·K)−1 |
| Parameters | Optimal Values | Rounded Values | Unit |
|---|---|---|---|
| GDL Thermal conductivity | Anode: 3.49751 Cathode: 0.50111 | Anode: 3.50 Cathode: 0.50 | W·(m·K)−1 |
| GDL Electrical conductivity | Anode: 1528.99781 Cathode: 1999.77377 | Anode: 1529.00 Cathode: 2000.00 | S·m−1 |
| CGDL Permeability | 8.94163 | 8.94 | ×10−12 m2 |
| CL Thermal conductivity | Anode: 0.39898 Cathode: 0.39815 | Anode: 0.40 Cathode: 0.40 | W·(m·K)−1 |
| CL Electrical conductivity | Anode: 699.28924 Cathode: 699.39099 | Anode: 699.29 Cathode: 699.39 | S·m−1 |
| CCL Permeability | 2.52221 | 2.52 | ×10−14 m2 |
| PEM Thermal conductivity | 0.05071 | 0.05 | W·(m·K)−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Liu, Q.; Chen, Y. Synergistic Framework for Fuel Cell Mass Transport Optimization: Coupling Reduced-Order Models with Machine Learning Surrogates. Energies 2025, 18, 2414. https://doi.org/10.3390/en18102414
Li S, Liu Q, Chen Y. Synergistic Framework for Fuel Cell Mass Transport Optimization: Coupling Reduced-Order Models with Machine Learning Surrogates. Energies. 2025; 18(10):2414. https://doi.org/10.3390/en18102414
Chicago/Turabian StyleLi, Shixin, Qingshan Liu, and Yisong Chen. 2025. "Synergistic Framework for Fuel Cell Mass Transport Optimization: Coupling Reduced-Order Models with Machine Learning Surrogates" Energies 18, no. 10: 2414. https://doi.org/10.3390/en18102414
APA StyleLi, S., Liu, Q., & Chen, Y. (2025). Synergistic Framework for Fuel Cell Mass Transport Optimization: Coupling Reduced-Order Models with Machine Learning Surrogates. Energies, 18(10), 2414. https://doi.org/10.3390/en18102414





