Novel Multi-Stage Phasor Measurement Unit Placement on Critical Buses with Observability Assessment

Abstract

Phasor measurement units (PMUs) provide synchronized measurements to enhance power system monitoring, strategically placed to achieve full network observability with minimal cost. In this paper, the PMU placement problem for critical buses is addressed using integer linear programming, taking into account both PMU contingencies and the impact of zero-injection buses. The primary contribution is the development of a multi-stage approach to place PMUs on critical buses. Moreover, it is demonstrated that considering PMU contingencies inherently accounts for line contingencies. Furthermore, a new performance metric, the Bus Coverage Index (BCI), is proposed to evaluate the effectiveness of the placement strategy. This index overcomes the limitations of existing indices, such as the Sum of Redundancy Index (SORI) and Bus Observability Index (BOI). The results are tested on various IEEE benchmark systems under four different cases, showing significantly improved results in terms of network observability and minimized number of PMUs. In Case 1, SORI values improved significantly for the IEEE 7 and IEEE 118 bus systems, while in Case 2, enhancements were observed in the IEEE 30 and IEEE 118 systems. Case 3 demonstrated consistency in results across systems. Notably, in Case 4, the number of required PMUs was reduced in the IEEE 30, IEEE 57, IEEE 118, and New England 39 bus systems, with complete network observability.

1. Introduction

A power system deals with electrical energy that is transferred from the source to the load through transmission and distribution networks. Conventionally, voltage, current, and frequency are typically monitored using supervisory control and data acquisition (SCADA) systems. However, SCADA has limitations of lacking phase angle information and slow measurement speed in meeting the demands of the wide area monitoring system (WAMS). A WAMS ensures network observability and stability. It enables dynamic control, especially in cross-border areas with stability challenges [1]. The phasor measurement units (PMUs) are essential in WAMSs to mitigate inter-area oscillations, as shown in the Greek–Bulgarian oscillation case study [2]. PMUs not only overcome the constraints of SCADA but also provide synchronized measurements of voltage and current magnitudes, along with their phasor values, using a common time source. Despite their advantages, the installation of PMUs incurs substantial costs, especially when deployed on every bus in the network. Using Kirchhoff’s laws, it is possible to place PMUs strategically on some buses to minimize costs while ensuring complete network observability. This process is called the optimal PMU placement (OPP).

The OPP problem for achieving complete network observability was initially addressed using integer linear programming (ILP) [3]. A wide range of optimization techniques has been employed to solve the OPP problem for complete network observability, including the greedy algorithm [4], nonlinear programming [5], graph theory [6], genetic algorithm [7], and particle swarm optimization [8]. Researchers have been working on OPP problems for more than three decades. Through an extensive literature review by Ahmed et al., the following inferences for OPP can be stated [9]: First, the OPP problem is NP-complete, and ILP remains the most suitable method for solving it. Second, various objective functions and constraints have been proposed to address the computational complexity inherent in this problem.

In the OPP problem, the strategy of placing PMUs plays a vital role. Broadly, two strategies have been identified: considering economic aspects, ref. [10] or buses with better connectivity [11,12]. Ahmed et al. [13] proposed a strategy for the OPP problem using a normalized degree of centrality in the objective function, combining the benefits of the strategies mentioned above into a single objective function. It improved both placement results and observability. This paper extends the work of Ahmed et al., who addressed zero-injection buses (ZIBs) and the contingency of PMU. However, line contingency and phasing of PMUs are not considered. This paper demonstrates that line contingency is inherently addressed when PMU contingency is considered in the OPP problem, as the line contingency is a subset of PMU contingency. Furthermore, a novel multi-stage installation of PMUs on critical buses is also proposed. These efforts primarily aim to enhance measurement redundancy and minimize the number of PMUs for complete network observability. Subsequent research has expanded on this foundation of complete network observability; addressing various practical constraints and considerations in the literature is the effect of conventional measurements and channel capacity in the OPP problem [14,15,16,17,18].

The performance of OPP solutions obtained through different optimization techniques is often evaluated using indices such as the Observability Reliability Index (OR), Loss of Data Expectation Index (LODE), Unobservability Index (UI), Bus Observability Index (BOI), and the Sum of Redundancy Index (SORI). The OR and LODE indices account for potential PMU failures and quantify the expected data loss directly [19]. The complexity of the first increases when the number of possible system states is increased, and the second is highly dependent on the accuracy of the Observability Reliability Index. The UI was proposed to adapt the OPP based on line contingencies [20]. The drawback of this index is that balancing confidence and cost can be complex. The results of the OPP problem were found using degree and neighborhood degree, and the results were evaluated on the BOI and SORI indices [21]. Both indices help select a solution out of multiple solutions with greater redundancy. The drawback is that they address system redundancy but fail to guarantee complete network observability. Therefore, there is a need for an index to evaluate whether the proposed OPP solution also guarantees complete network observability, which is addressed in this paper. A new observability index, called the Bus Coverage Index (BCI), is proposed. It overcomes the limitations of BOI and SORI indices. It quantifies system observability for its state estimation and gives information that the network has complete or incomplete observability. The key contributions of this paper are as follows:

• The OPP problem is solved using a normalized degree of centrality approach considering PMU contingency and the impact of zero-injection buses.
• It is proved that single-line contingency is inherently encompassed within a single PMU contingency, eliminating the need for separate analysis.
• A novel multi-stage installation strategy for critical buses is proposed, extending the methodology of Ahmed et al. [13] to improve network planning and flexibility.
• The new metric, the Bus Coverage Index (BCI), is proposed for assessing and validating complete network observability.

This paper is organized into multiple sections. Section 2 highlights a unique PMU placement method considering the normalized degree of centrality with constraints like PMU or line contingency, the effect of ZIBs, and the phasing of PMUs for multi-stage installation. Section 3 proposes a new measure to evaluate the observability status of the placement solution called the Bus Coverage Index. Section 4 deals with a thorough discussion of four different cases to solve the OPP on various IEEE benchmark systems using different optimization algorithms. Finally, in Section 5, the conclusion provides a summary of the key findings and discusses their implications.

2. Optimal PMU Placement Considering Normalized Degree of Centrality

Strategically placing PMUs for complete network observability is called optimal PMU placement. If the strategy to place PMU is formulated on the basis of the normalized degree of centrality, then it improves the system observability while concurrently reducing overall costs [13]. The degree of centrality is computed for the objective function, as indicated by the following formula:

$$D_i=\sum _{j=1}^n(a_{ij}-{\delta }_{ij})$$

(1)

The following formula is used to obtain the normalized degree of centrality, or zeta ${\displaystyle \zeta }$:

$${\displaystyle {\zeta }_i}={\displaystyle \frac{D_i}{{\sum }_{i=1}^n{D}_i}}$$

(2)

The mid-range normalized degree of centrality is a measure that serves as a benchmark for analyzing the distribution of centrality values across all buses. The formula for calculating it is given in Equation (3). Critical buses have a degree of centrality above mid-range. Their PMU placement should be prioritized for better observability and control. The critical network buses for different IEEE test bed systems are shown in Figure 1a–f.

$$\overline{\zeta }={\displaystyle \frac{{\zeta }_{\max }+{\zeta }_{\min }}{2}}$$

(3)

Normalized degree centrality solves the OPP by multiplying decision variable $X_i$ with factor ${\displaystyle 1-{\zeta }_i}$ for each bus. This factor helps to convert maximization to a minimization problem. The subsequent expression represents the mathematical formulation of normalized degree centrality within the objective function:

$$min\sum _{i=1}^{n}C·(1-{\zeta }_i)·X_i$$

(4)

Subject to

$$AX\ge Y$$

(5)

$$(1-{\zeta }_i)\to \left\{\begin{array}{cc}1\hfill & \mathrm{As} {\zeta }_i\to 0 (\mathrm{the} \mathrm{bus} \mathrm{that} \mathrm{has} \mathrm{the} \mathrm{least} \mathrm{potential} \mathrm{for} \mathrm{PMU})\hfill \\ 0\hfill & \mathrm{As} {\zeta }_i\to 1 (\mathrm{the} \mathrm{bus} \mathrm{that} \mathrm{has} \mathrm{the} \mathrm{most} \mathrm{potential} \mathrm{for} \mathrm{PMU})\hfill \end{array}\right.$$

This formulation identifies key vertices for PMU placement. The proposed formulation is solved using binary integer linear programming (ILP). It is an optimization method employed to address issues in which decision variables are constrained to take on integer values. The branch and bound methodology encompasses several essential steps: A binary ILP is first formulated to examine all potential PMU locations, and the objective function is then resolved. If the solution produces integer results, the optimal solution is revised; if not, the procedure advances to branching. In the branching step, sub-problems are generated utilizing non-integer decision variables, which are assigned values of 0 or 1. Each sub-problem is resolved by LP relaxation, and if the relaxed solution found is inferior to the optimal integer solution present, the branch is eliminated; otherwise, results are revised. This process is repeated until all sub-problems are resolved or meet the termination criteria, as shown in Figure 2. The optimal integer solution is determined to guarantee the full observability of the power system. After solving simple OPP, different constraints are solved separately as well as cumulatively, like the $N-1$ contingency and effect of ZIBs. After addressing these constraints, an OPP solution is used to place PMUs in different phases. The details of the constraints and phasing proposed are discussed below.

2.1. $N-1$ PMU Contingency

The OPP problem requires a minimum of one PMU to monitor each bus. If any device unexpectedly fails, the system becomes unmonitored. Therefore, each bus must be monitored by at least two PMUs. This reliability condition is referred to as the $N-1$ contingency criterion, which extends beyond the basic observability requirement but is crucial for ensuring network reliability. It helps to improve the network’s information redundancy, real-time monitoring under fault scenarios, enhanced observability for critical operations, and compliance with industry standards like North American Electric Reliability Corporation (NERC) or European Network of Transmission System Operators for Electricity (ENTSO-E) [22,23]. This work addresses the $N-1$ contingency of PMU only. To incorporate PMU contingency, the formula for N operational PMU devices and K failed PMU devices is

$$AX\ge K+1$$

(6)

2.2. $N-1$ PMU Contingency Incorporates a Single Line Contingency

In the literature, line outages are treated separately to PMU outages [24], and they are considered the same as PMU outages [25]. This work demonstrates that $N-1$ PMU contingency encompasses $N-1$ line contingency. However, to address multiple line failures, $N-1$ PMU contingency is insufficient; therefore, redundant PMUs are required. The following assumptions are made to prove this statement: Let $G=(V,E)$ be a graph representing the power system, where V is the set of vertices (substations) and E is the set of edges (transmission lines). Let $P\subseteq V$ be the set of vertices where PMUs are placed. A PMU at vertex $v\in V$ monitors vertex v and all adjacent vertices connected to v, i.e., the set $P_i$, where it is the set of adjacent vertices (neighbors). The above rules are demonstrated using the IEEE 7 bus system, represented as a graph with the following adjacency matrix:

$$A={\left[\begin{array}{ccccccc}1& 1& 0& 0& 0& 0& 0\\ 1& 1& 1& 0& 0& 1& 1\\ 0& 1& 1& 1& 0& 1& 0\\ 0& 0& 1& 1& 1& 0& 1\\ 0& 0& 0& 1& 1& 0& 0\\ 0& 1& 1& 0& 0& 1& 0\\ 0& 1& 0& 1& 0& 0& 1\end{array}\right]}_{7\times 7}$$

(7)

In this matrix, $a_{i,j}=1$ indicates that there is an edge $e_{ij}$ between vertices $v_i$ and $v_j$. The graph represents the connections between the seven buses and will show how the contingency of PMU in OPP ensures the observability of the network under single line failures. When $N-1$ PMU contingency is considered, PMUs are placed at buses 1, 2, 3, 4, and 5 to ensure redundancy and full observability in the event of any single PMU failure, as shown in Figure 3. Now, the PMUs monitor the following buses given in

Table 1. PMU locations and their corresponding monitored buses under $N-1$ PMU contingency.

PMU Location (Bus)	Monitored Buses
1	1, 2
2	1, 2, 3, 6, 7
3	2, 3, 4, 6
4	3, 4, 5, 7
5	4, 5

.

2.2.1. Single Line Failure

Statement: If a single line fails, the system remains observable if PMUs are placed according to $N-1$ PMU contingency.

Let $e_{ij}=(v_i,v_j)\in E$ be a transmission line that fails. The failure of the line e removes the edge between vertices $v_i$ and $v_j$. For the system to remain observable, both vertices $v_i$ and $v_j$ must still be observable via other PMUs or connections. Let $O\left(N\right)$ represent the set of observable vertices under N number of PMUs. For a single line failure between two vertices $v_i$ and $v_j$:

$$O\left(N\right)=V$$

(8)

The above equation gives full observability under $N-1$ contingency. When a single line $e_{ij}\in E$ fails, the PMUs at $v_i$ and $v_j$ can still be observed through PMUs on them or other adjacent PMU vertices, as

$$O(N,e_{ij})=O\left(N\right)=V$$

(9)

Let us assume the failure of the transmission line between buses 2 and 6 (edge $(2,6)$): Bus 2 has its own PMU, so it remains observable. Bus 6 also connects with bus 3, a PMU bus, so that it can be monitored via adjacent bus 3. Thus, the system remains fully observable even though a line has failed. In any other single line failure scenario (such as between buses 3 and 6, buses 2 and 7, buses 4 and 7, or any others), the PMU redundancy ensures that both vertices connected by the failed line still have observability through their own PMUs or adjacent PMUs. Since each bus is either directly observed by its PMU or covered by an adjacent PMU, the failure of any one line does not affect the overall observability of the network.

2.2.2. Multiple Line Failures

Statement: If more than one line fails, the system may become unobservable unless redundant PMUs are placed.

Consider the case where two lines $e_{ij}=(v_i,v_j)$ and $e_{lm}=(v_l,v_m)$ fail. The PMUs at vertices $v_i$, $v_j$, $v_l$, and $v_m$ can no longer monitor their respective incident lines because multiple edges are lost. Let $E^{\prime }\subseteq E$ represent the set of failed lines, where $2\le |E^{\prime }|\le |E|$. The system remains observable if and only if the total number of PMUs N can still monitor all vertices. However, in the case of multiple line failures, some vertices may lose connectivity to the rest of the graph. When two lines fail, any vertices $v_i$, $v_j$, $v_l$, or $v_m$ may no longer be monitored because there is no redundancy for the lines connecting them. Without redundant PMUs at neighboring vertices, the set of observable vertices $O(N,E^{\prime })$ will be strictly smaller than V, meaning an unobservable system:

$$O(N,E^{\prime })\subset V$$

(10)

$$2\le |E^{\prime }|\le |E|$$

(11)

$$O(N,E^{\prime })<V$$

(12)

Let us assume the failure of the transmission line between buses 2 and 6 (edge $(2,6)$) and the transmission line between buses 3 and 6 (edge $(3,6)$) simultaneously; bus 6 will lose observability unless PMUs is placed redundantly on bus 6. In this case, the PMU at bus 2 can no longer observe bus 6 due to the failure of the line $(2,6)$. The PMU at bus 3 can no longer observe bus 6 due to the failure of the line $(3,6)$. Thus, the system requires additional redundancy through $N-1$ PMU contingency to handle multiple line failures. This example of the IEEE 7 bus system demonstrates that $N-1$ PMU contingency incorporates single-line contingency, and multiple line failures require additional redundancy for full observability.

2.3. Zero-Injection Bus

In the context of optimal PMU placement, a significant consideration is the effect of zero-injection buses (ZIBs). It reduces the required number of PMUs. ZIBs can be incorporated into the formulation through specific rules [26]: the first rule is that unobserved buses must either belong to or be adjacent to a ZIB cluster, and the second rule is that for a zero-injection bus i, where $P_i$ represents the set of adjacent buses and $Q_i=P_i\cup \left\{i\right\}$, no more than one bus in the set $Q_i$ is permitted to remain unobserved. Zero-injection buses have generic formulation, as follows:

$$A_m{X}_m\ge U$$

(13)

$$u_j=1\hspace{0.5em} \forall j\notin \bigcup _{z=1}^{\mathcal{Z}}{Q}_z$$

(14)

$$\sum _{k\in Q_i}{u}_k\ge \left|P_i\right|\hspace{0.5em} \forall i\in \mathcal{Z}$$

(15)

where:

$$u_i=\left\{\begin{array}{cc}1\hfill & \mathrm{If} \mathrm{bus} i \mathrm{is} \mathrm{observed}\hfill \\ 0\hfill & \mathrm{Otherwise}\hfill \end{array}\right.$$

The constraint specified in Equation (14) requires that buses that are not directly connected to the ZIB be monitored, ensuring the ZIB adjacent bus’s observability. The application of Ohm’s law stipulates that installing a PMU on a bus renders its adjacent buses observable, thereby facilitating complete network observability through strategic PMU placement [27]. This study adopts the positioning guidelines proposed by Ahmed et al. [13] to achieve this goal. Specifically, when a PMU is connected to a bus, Rule 1 for complete network observability says that the current measurements of all connected branches, as well as the voltage of the bus itself, are directly obtainable. Furthermore, suppose the given current phasor and given bus voltage data at one branch are terminal; it becomes feasible to compute the bus voltage with its phasor at the opposite terminal, as illustrated in Figure 4a (pseudo-measurement). In addition, Rule 2 for complete observability says that bus voltages given at both ends of a selected branch allow for determining the current and its phasor for the chosen branch, depicted in Figure 4b as another pseudo-measurement.

A ZIB is characterized by its lack of active or reactive power injection or withdrawal [18,28]. The following rules ensure comprehensive network observability for ZIBs:

• Kirchhoff’s current law enables the determination of the unknown branch current phasor, provided that the current of all linked lines, except for the line connected to the zero-injection bus, is known, as shown in Figure 4c.
• If the voltages of all buses directly connected to the ZIB are known except for one, Kirchhoff’s voltage law can be used to calculate the voltage of the unknown bus. KVL states that the sum of voltage differences around a closed circuit must equal zero. This principle allows us to incorporate the known voltages to solve for the unknown voltage values, as illustrated in Figure 4d.
• When the voltage as well as phasors of neighboring buses and the current, as well as phasors, of the branches connected to a group of ZIBs are known, it can be inferred that an adjacent ZIBs group exists, enabling the determination of their bus voltage and branch current as well as phasors. It is possible to calculate unknown branch currents and bus voltages for a group of ZIBs, given that current and phasor for all branches except one and voltage, as well as phasors, for all affected buses except one are known. This calculation is depicted in Figure 4e. The extended measurements refer to those obtained through the above-stated ZIB rules.

2.4. Phasing of PMUs for Multi-Stage Installation

In OPP, multi-stage installation of PMUs is performed to maximize system observability; PMUs are deployed over a number of stages. This process is known as the phasing of PMUs. Utilities can control costs and gradually guarantee sufficient system coverage by installing PMUs gradually and prioritizing crucial places. Given the set of buses $V=\{v_1,v_2,v_3,\dots ,v_n\}$ and the normalized degree of centrality values ${\zeta }_i$ for each bus $v_i$, the phasing of PMUs in different stages can be formulated as:

Let

$$S_{\mathrm{PMU}}=\{{\widehat{v}}_1,{\widehat{v}}_2,\dots ,{\widehat{v}}_N\}\mid S_{\mathrm{PMU}}\subseteq V$$

(16)

The sorted set $S{S}_{\mathrm{PMU}}$ based on the ${\zeta }_{\pi \left(i\right)}$ where $\pi \left(i\right)$ is the permutation that sorts the bus locations in descending order of their normalized degree of centrality ${\zeta }_i$ is derived as follows:

$$S{S}_{\mathrm{PMU}}=\{{\widehat{v}}_{\pi \left(1\right)},{\widehat{v}}_{\pi \left(2\right)},{\widehat{v}}_{\pi \left(3\right)},\dots ,{\widehat{v}}_{\pi \left(N\right)}\}\mid {\zeta }_{\pi \left(1\right)}\ge {\zeta }_{\pi \left(2\right)}\ge \cdots \ge {\zeta }_{\pi \left(N\right)}$$

(17)

We aim to divide $S{S}_{\mathrm{PMU}}$ into three phases, as shown in Figure 5. Phases are represented as $I_1$, $I_2$, and $I_3$

Given that:

$$I_1\cup I_2\cup I_3=S{S}_{\mathrm{PMU}}\mid \hspace{0.5em}\hspace{0.5em}{I}_1\cap I_2=I_1\cap I_3=I_2\cap I_3=\varnothing$$

(18)

To distribute PMUs to phases, the number of PMUs is calculated using $k=⌊\mathrm{mod}(n,3)⌋$ and $r=⌈\mathrm{mod}(n,3)⌉$ are used in the proposed formulation below:

$$I_1=\{{\widehat{v}}_{\pi \left(1\right)},{\widehat{v}}_{\pi \left(2\right)},\dots ,{\widehat{v}}_{\pi (\lfloor k\rfloor +\lceil {\displaystyle \frac{r}{2}}\rceil )}\}$$

(19)

$$I_2=\{{\widehat{v}}_{\pi (\lfloor k\rfloor +\lceil {\displaystyle \frac{r}{2}}\rceil +1)},{\widehat{v}}_{\pi (\lfloor k\rfloor +\lceil {\displaystyle \frac{r}{2}}\rceil +2)},\dots ,{\widehat{v}}_{\pi (2\left(\lfloor k\rfloor \right)+\lceil {\displaystyle \frac{r}{2}}\rceil )}\}$$

(20)

$$I_3=\{{\widehat{v}}_{\pi (2\left(\lfloor k\rfloor \right)+\lceil {\displaystyle \frac{r}{2}}\rceil +1)},{\widehat{v}}_{\pi (2\left(\lfloor k\rfloor \right)+\lceil {\displaystyle \frac{r}{2}}\rceil +2)},\dots ,{\widehat{v}}_{\pi \left(N\right)}\}$$

(21)

3. Proposed Bus Coverage Index

In OPP, results are compared using performance indices. The Bus Observability Index (BOI) and the Sum of Redundancy Index (SORI) are the key indicators in PMU-based power network monitoring [26]. The number of PMUs that observe bus data is its BOI. For a bus i, it is calculated as

$$BO{I}_i=\sum _{j=1}^N{B}_{ij}$$

(22)

$$b_{ij}=\left\{\begin{array}{cc}1\hfill & \mathrm{If} \mathrm{PMU} \mathrm{at} \mathrm{bus} j \mathrm{can} \mathrm{gather} \mathrm{data} \mathrm{from} \mathrm{the} \mathrm{bus} i.\hfill \\ 0\hfill & \mathrm{Otherwise}.\hfill \end{array}\right.$$

Large BOIs reveal well-positioned PMUs to monitor the bus. The SORI measures total observability redundancy. The Bus Observability Index for each network bus is taken from [13] to calculate SORI.

$$SORI=\sum _{i=1}^n{BOI}_i$$

(23)

The solution with a large SORI value is more suitable among many possible solutions of OPP as it gives well-positioned PMUs to monitor the network. BOI shows how often a bus is spotted, whereas SORI shows the overall number of observations across the network. However, these indices only indicate bus or system redundancy, not network observability.

Therefore, in this paper, an innovative method for assessing the observability coverage efficacy of PMU installations in a power network is provided. This new performance index, known as the Bus Coverage Index (BCI), gives information about whether that network is completely observed or not. It considers the positioning of PMUs and the network’s bus connectivity. The BCI is mathematically formulated as follows:

Initialize:

$$M=\{S_{PMU}\cup Q_Z\}$$

(24)

$$P_i=\left\{j\right|A(i,j)=1\}$$

(25)

Add the adjacent buses to the set M:

$$O\left(N\right)=M\cup P_i$$

(26)

Calculate the Bus Coverage Index (BCI) as the ratio of the number of buses in set $O\left(N\right)$ to the total number of buses n:

$$\mathrm{BCI}={\displaystyle \frac{\left|O\right(N\left)\right|}{n}}$$

(27)

Scenario: Complete network observability

The connectivity matrix A given in Equation (7) for the IEEE 7 bus system helps to solve this scenario. Assume that PMUs are placed on buses 2 and 4, represented by the binary array $X=[0,1,0,1,0,0,0]$, and apply the BCI formula without considering ZIBs: Initialize

$$M=\{2,4\}$$

Add adjacent buses iteratively to the set M: For bus 2, adjacent buses are 1, 3, 6, and 7. For bus 4, adjacent buses are 3, 5, and 7. Thus, update the set $O\left(N\right)$:

$$O\left(N\right)=\{2,1,3,6,7,4,5\}$$

Calculate BCI:

$$\mathrm{BCI}={\displaystyle \frac{\left|O\right(N\left)\right|}{n}}={\displaystyle \frac{7}{7}}=1$$

Scenario: Incomplete network observability

Assuming that PMUs are placed on buses 2 and 3, represented by the binary array $X=[0,1,1,0,0,0,0]$, apply the BCI formula without considering ZIBs:

Initialize

$$M=\{2,3\}$$

Add adjacent buses iteratively to the set M: For bus 2, the adjacent buses are $1,3,6,$ and 7. For bus 3, the adjacent buses are $2,4,$ and 6. Thus, update the set $O\left(N\right)$:

$$O\left(N\right)=\{2,1,3,6,7,4\}$$

Calculate BCI:

$$\mathrm{BCI}={\displaystyle \frac{\left|O\right(N\left)\right|}{n}}={\displaystyle \frac{6}{7}}\approx 0.857$$

In the first scenario, where the BCI is 1, the PMU placement on buses 2 and 4 results in complete observability of the entire IEEE 7 bus system, whereas in the second scenario, the BCI is approximately 0.857, indicating that while the PMUs on buses 2 and 3 contribute significantly to network observability, they do not cover all buses. This provides a thorough evaluation of the level of coverage that a PMU placement plan achieves. Both the direct placement of PMUs and the indirect coverage achieved by watching nearby buses are considered. This strategy is consistent with Kirchhoff’s current law, which states that observations of one bus allow for observations of its neighboring buses. Traditional performance indexes frequently only include direct placements and may ignore the indirect advantages of watching over nearby buses. The suggested BCI’s improved accuracy and efficacy in determining the network observability and reliability are demonstrated by comparisons with existing indices in

Table 2. Analysis of PMU placement ensuring complete observability.

Bus System	IEEE_14			IEEE_30			New England 39			IEEE_57			IEEE_118
Parameters	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI
EBS [10,29]	4	1	19	10	1	50	13	1	52	-	-	-	-	-	-
PSO [8]	4	1	19	10	1	52	-	-	-	17	1	71	31	0.974	148
GA [7]	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Proposed ILP	4	1	19	10	1	52	13	1	52	17	1	72	32	1	164
Phase 1 PMUs	2,6			2,6,10,12			2,6,10,13,14			1,4,6,9,15,38			5,12,15,17,37,49,56,70,85,92,100
Phase 2 PMUs	9			4,15,27			17,19,22,23			20,24,32,36,41			3,25,34,40,62,68,89,96,105,110
Phase 3 PMUs	7			9,20,25			9,20,25,29			25,28,47,50,53,57			9,21,29,45,53,64,71,76,79,86,114

,

Table 3. Analysis of PMU placement ensuring complete observability under $N-1$ contingency.

Bus System	IEEE_14			IEEE_30			New England 39			IEEE_57			IEEE_118
Parameters	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI
EBS [10,29]	9	1	39	21	1	83	-	-	-	33	1	130	68	1	308
PSO [8]	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
GA [7]	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
Proposed ILP	9	1	39	21	1	85	28	1	52	33	1	130	68	1	309
Phase 1 PMUs	2,4,5			2,4,6,10,12,15,27			2,3,6,8,10,11,13, 14,16,26			1,3,4,6,9,11,12,15, 38,41,56			5,11,12,15,17,19,27,32,37,49, 54,56,59,70,75,77,80,85,92,94, 96,100,105
Phase 2 PMUs	6,7,9			1,5,9,22,24,25,28			9,17,19,20,22,23, 25,29,39			19,20,22,24,25,27, 28,29,32,36,37			1,3,24,25,30,31,34,40,42,45,46, 51,61,62,64,66,68,71,83,89, 106,110
Phase 3 PMUs	8,11,13			11,13,17,19,20,26,30			30,31,32,33,34,35, 36,37,38			30,33,35,39,44,46, 47,50,51,53,54			6,9,10,21,22,29,36,44,50,52,73, 76,79,86,87,91,101,108,111,112, 115,116,117

,

Table 4. Analysis of PMU placement ensuring complete observability under ZIBs.

Bus System	IEEE_14			IEEE_30			New England 39			IEEE_57			IEEE_118
Parameters	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI
EBS [10,29]	3	1	16	7	1	39	8	1	44	-	-	-	-	-	-
PSO [8]	3	1	16	7	1	34	-	-	-	13	1	64	29	1	155
GA [7]	3	1	16	7	1	41	8	0.92	45	11	1	61	29	1	161
Proposed ILP	3	1	16	7	1	41	8	1	44	11	1	61	29	1	161
Phase 1 PMUs	2			10,12,27			3,6,16			1,6,9,15,38			5,12,15,17,32,49,56,75,77,80
Phase 2 PMUs	6			3,24			13,23,25			14,32,36,56			27,34,40,62,65,85,94,105,110
Phase 3 PMUs	9			5,18			20,29,39			20,25,27,51,53			3,8,21,31,45,53,72,86,90,102

and

Table 5. Analysis of PMU placement ensuring complete observability under $N-1$ contingency and ZIBs.

Bus System	IEEE_14			IEEE_30			New England 39			IEEE_57			IEEE_118
Parameters	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI	PMU	BCI	SORI
EBS [10,29]	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
PSO [8]	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
GA [7]	7	1	34	14	1	60	15	0.97	63	25	1	112	61	1	277
Proposed ILP	7	1	34	13	1	57	14	1	58	23	1	97	59	1	280
Phase 1 PMUs	2,4,5			2,4,10,12,15			2,6,8,16,26			1,4,9,12,14,38,41,56			11,12,15,17,32,49,54,56,59,69,70, 75,77,80,85,92,94,96,100,105
Phase 2 PMUs	6,9			1,7,24,27			13,23,25,29			2,18,20,25,29,32,36			3,8,19,24,25,27,31,34,40,42,45, 46,51,62,66,83,89,106,110
Phase 3 PMUs	11,13			13,17,19,20			20,34,36,37,38			27,30,33,50,51,53,54			1,6,21,22,29,35,44,50,52,76,78, 86,87,90,101,108,111,112,114,117

. It has applications for planners and operators, as it assists in making more informed decisions about PMU placements by considering both direct and indirect monitoring. Optimal PMU placement strategies that maximize the BCI can help to improve network observability and overall system dependability.

4. Results and Discussion

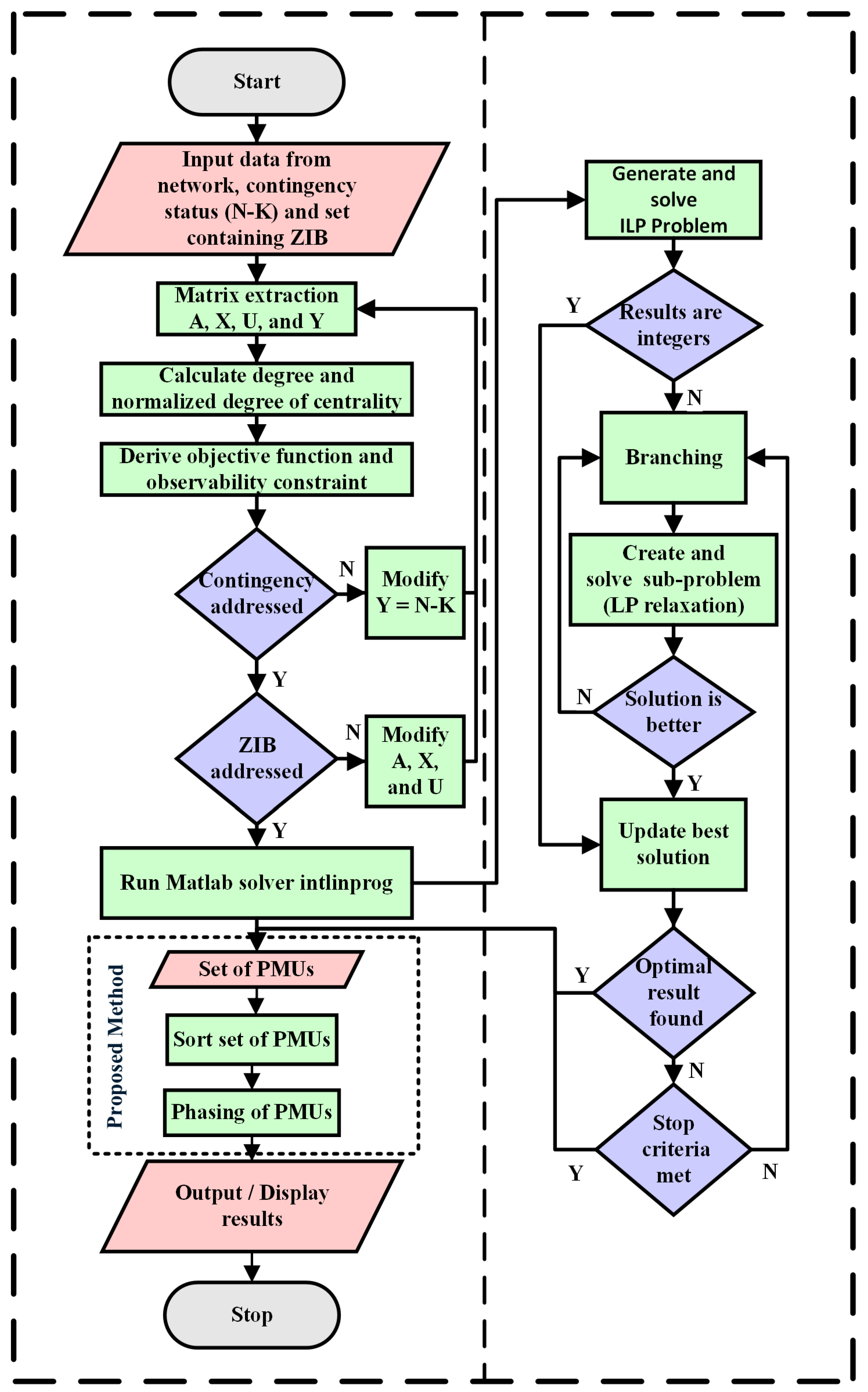
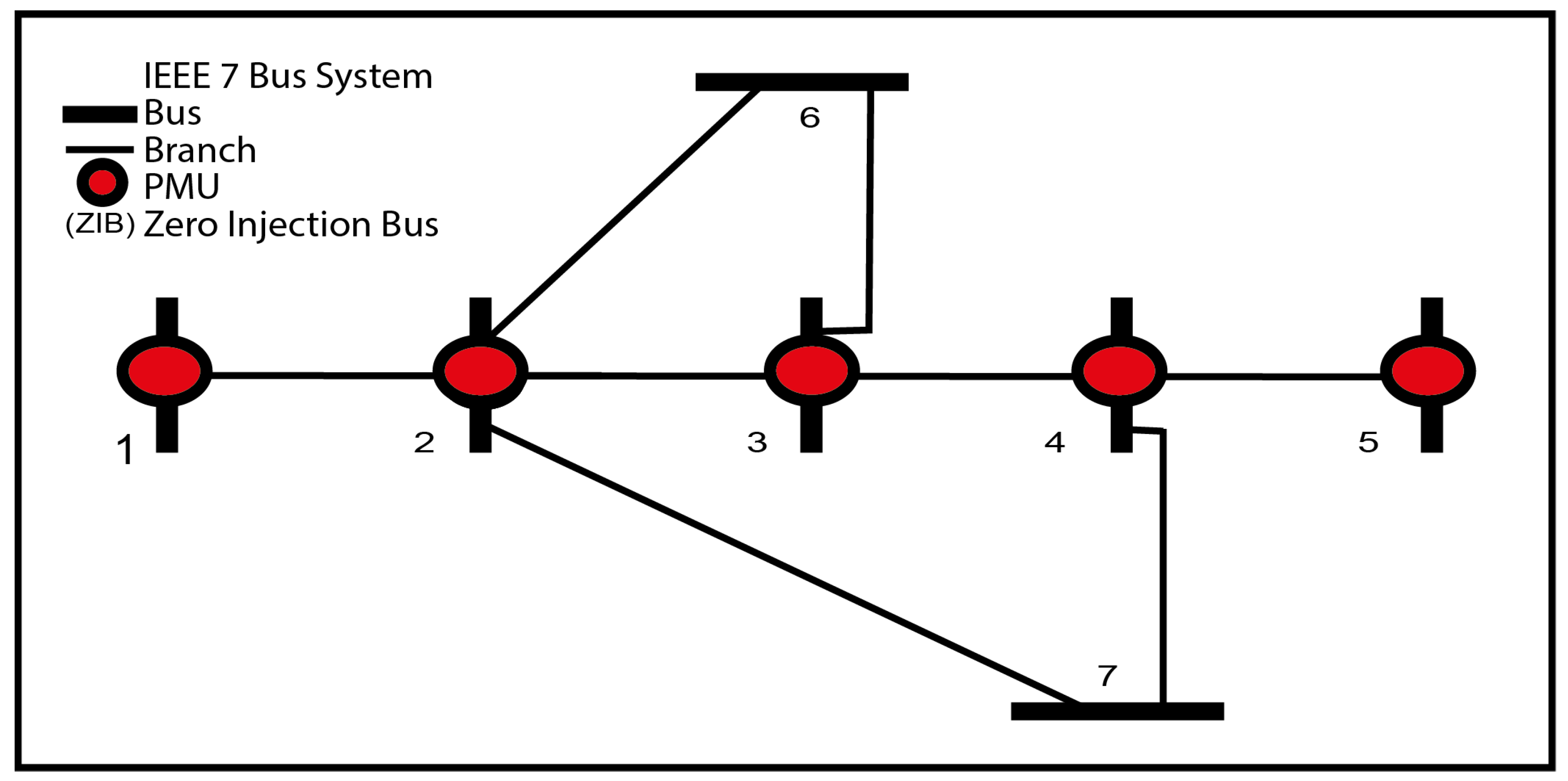
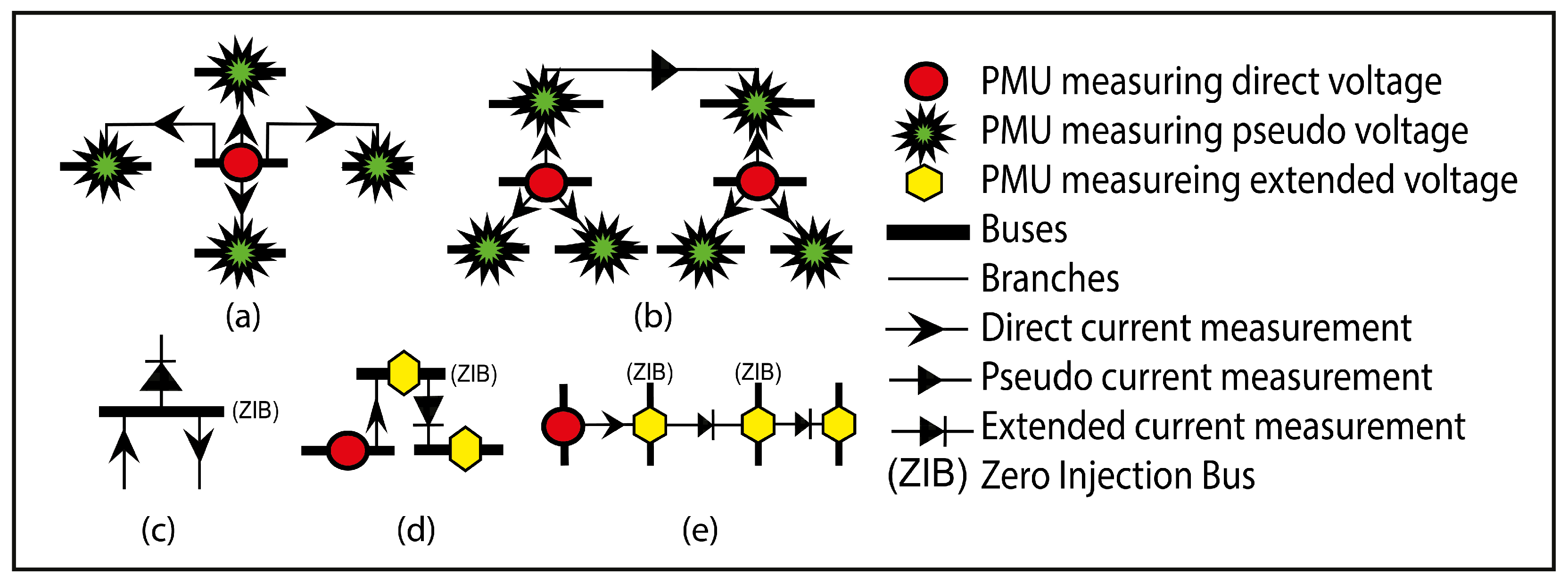
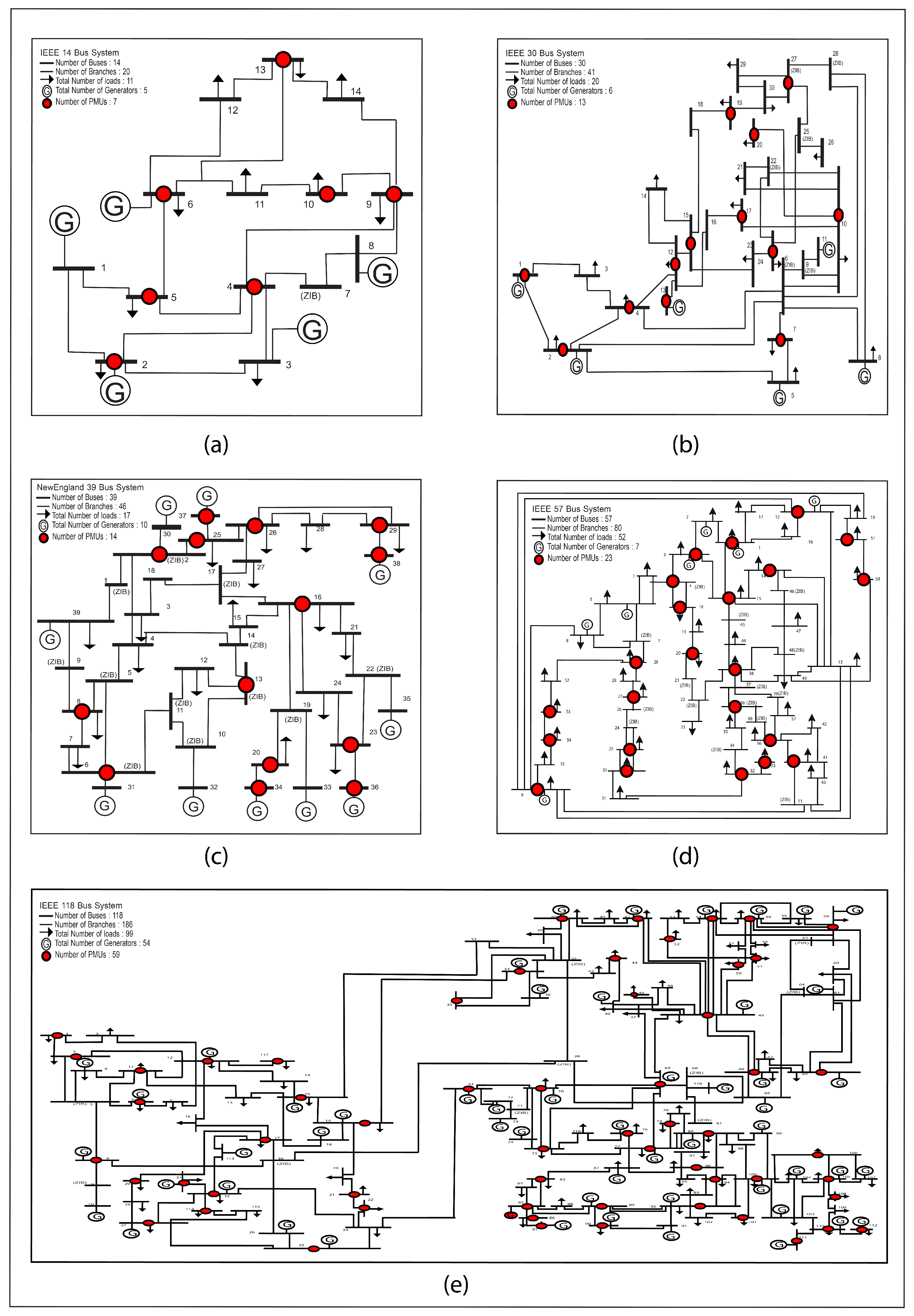
The multi-stage installation of PMUs uses a phased approach to deploy PMUs across power systems, allowing for incremental monitoring and performance assessment. This strategy helps operators prioritize high-impact areas based on factors like bus criticality and system topology, ultimately managing costs more effectively while minimizing disruptions. With each phase, utilities gain valuable feedback and data, enabling them to adjust future installations based on real-time observations, leading to a more efficient monitoring network.

The performance of various optimization algorithms for PMU allocation is analyzed across multiple IEEE bus systems, including IEEE 14, IEEE 30, New England 39, IEEE 57, and IEEE 118. The primary metrics considered were the number of PMUs required for complete network observability, the BCI to evaluate whether the network is completely observed or not, and the SORI to evaluate redundant observations within the network. These metrics reflect the effectiveness of each algorithm in achieving full observability of the power grid. The performance of four optimization methods (exhaustive binary search (EBS) [10,29], particle swarm optimization (PSO) [8], genetic algorithm (GA) [7], and the proposed integer linear programming (ILP)) are compared for PMU placement across several IEEE test bus systems. 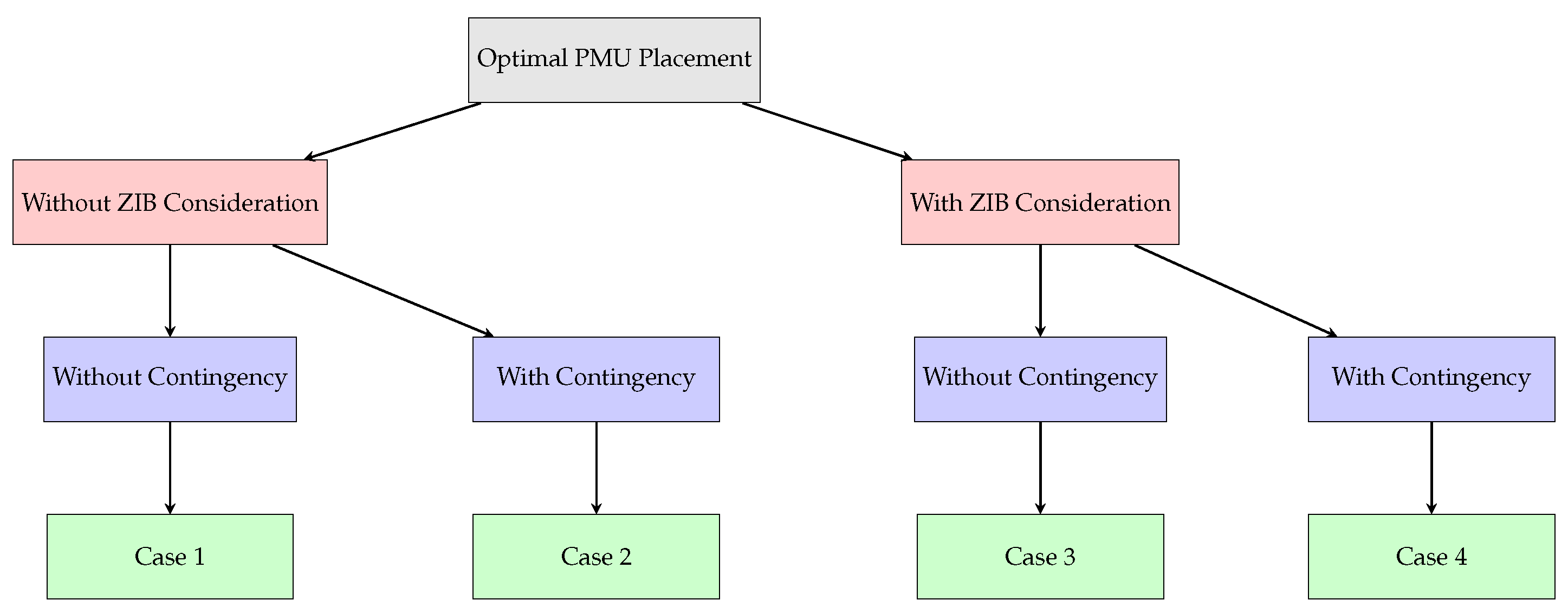This work examines the results under four different cases, as shown in Figure 6. The results of the phasing, number of PMUs, BCI, and SORI of four different cases of OPP solved using the proposed ILP approach are shown in Table 2, Table 3, Table 4 and Table 5.

4.1. PMU Allocation with Comprehensive Observability Constraint

PMU allocation with an observability constraint only is the first case for comparing different methods and test bus systems. Table 2 provides the following inferences. In terms of the number of PMUs, fewer devices indicate a more efficient result. Across all test systems (New England 39, IEEE 14, 30, 57, and 118), the proposed ILP method consistently uses the same PMUs as EBS and PSO. In the IEEE 118 bus system, PSO gives 31 PMUs, but, as can be seen from the value of BCI in Table 2, the system is not completely observed.

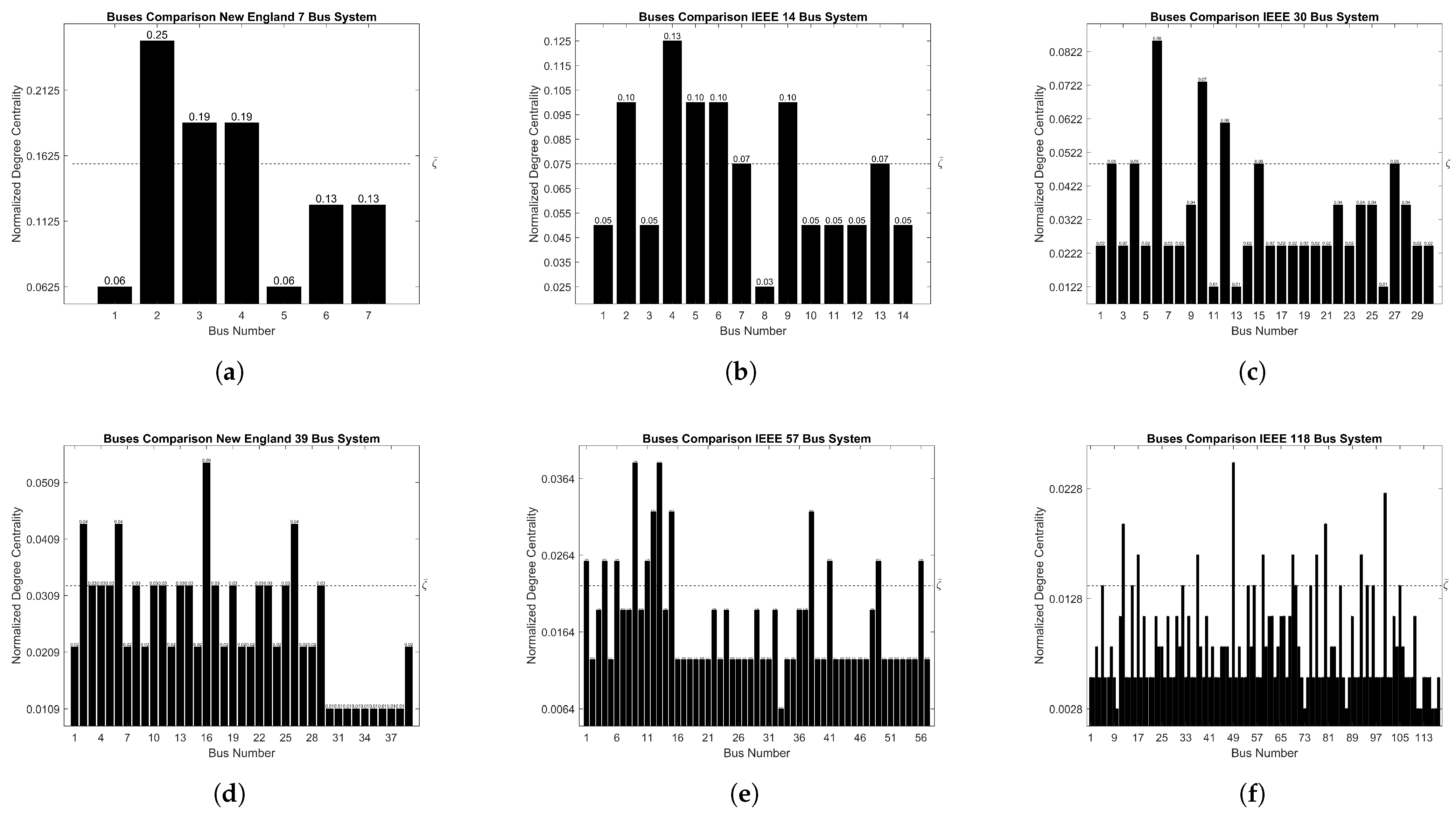
The BCI indicates how well each bus in the system is covered, with a value closer to 1 being optimal. In the IEEE 14, IEEE 30, New England 39, and IEEE 57, algorithms EBS, PSO, and proposed ILP achieved similar BCI values equal to 1, indicating that all buses are well covered. In the last IEEE 118, the algorithm PSO, [8] failed to have a value equal to 1, which means that the system is not completely observed. They claimed to have PMUs at locations (3, 5, 9, 12, 15, 17, 21, 23, 28, 30, 36, 40, 44, 46, 51, 54, 57, 62, 64, 68, 71, 75, 80, 85, 86, 91, 94, 101, 105, 110, and 114). The unobserved buses were found to be (76, 78, and 82) using the proposed index BCI. However, for the IEEE 118 network, the ILP method achieved a BCI of 1, matching the best result, which indicates that the entire network was covered efficiently with the least number of PMUs.

The SORI is highest when system redundancy is maximized. The ILP method performed competitively in all cases, achieving similar or higher SORI values compared to EBS and PSO, especially in cases where the number of PMUs was the same. For example, in the IEEE 118 system, the ILP method achieved an SORI of 164, which was higher than the PSO’s 148. Given that the result found using the proposed ILP is highly efficient.

4.2. PMU Allocation with Comprehensive Observability and Contingency Constraint

The allocation of PMUs with observability and contingency constraints is the second case for comparing different methods and test bus systems, as it ensures reliability in PMU placement. The following insights are derived from the results presented in Table 3. In this scenario, the goal is to ensure system observability, even in the case of a single PMU or branch failure. The proposed ILP method consistently used the same PMUs as EBS. The BCI values for the proposed ILP method were consistently equal to 1, indicating good bus coverage even under contingency scenarios. For contingency scenarios, a high SORI value indicates better redundancy, especially when the number of PMUs is equal. In the IEEE (30 and 118) bus systems, ILP had a slightly higher SORI than EBS, with the same number of PMUs reflecting better performance.

4.3. PMU Allocation with Comprehensive Observability and ZIB Constraint

The allocation of PMUs with observability and ZIB constraints is the third case for comparing various methods and test bus systems, as ZIBs help reduce the number of PMUs required. The following insights are drawn from the results presented in Table 4.

Introducing ZIBs reduces the number of PMUs needed to maintain observability. The proposed ILP method and GA showed equal PMUs in all networks compared to other EBS and PSO. For the IEEE 57 bus system, the proposed ILP and GA lead the other two techniques by using fewer PMUs.

The BCI values for all the methods are equal to 1 except for GA in one network. Castro et al. [7] claimed to have complete network observability in the New England 39 bus system and placed PMUs at locations (2, 5, 8, 10, 16, 19, 23, 26) but failed to observe buses (12, 14, and 18) found using the proposed BCI, meaning that the algorithm needs further tuning to ensure a BCI value equal to 1.

Although the SORI was slightly lower in some systems, the number of PMUs was also reduced, making the ILP method more optimal overall. For example, in the IEEE 57 bus system, the ILP method achieved an SORI of 61 with 11 PMUs, compared to PSO’s 64, but using 13 PMUs made the ILP solution more efficient.

4.4. PMU Allocation with Comprehensive Observability, Contingency, and ZIB Constraint

The allocation of PMUs with observability, contingency, and ZIB constraints is the fourth case for comparing different methods and test bus systems. ZIBs help reduce the number of required PMUs, while contingency constraints ensure the system’s observability under failures. The following insights are derived from the results shown in Table 5. The optimal results found considering this case are presented in Figure 7 so that results can be directly seen.

In the most complex scenario, considering both contingencies and ZIBs, the ILP method again showed its effectiveness. In the New England 39, IEEE 30, 57, and 118 bus systems, the ILP method used fewer PMUs, giving the best result when compared to GA.

The BCI values achieved by the ILP method were optimal across all systems, maintaining near-total observability despite the additional constraints. Castro et al. [7] claimed complete observability by placing PMUs at locations (1, 2, 3, 4, 7, 8, 10, 11, 16, 19, 20, 22, 23, 26, 29) but failed to observe bus (37) found using the proposed BCI, which means that the proposed ILP is superior.

Meanwhile, the SORI values for ILP were comparable to those of other methods. Although the SORI was slightly lower in some systems, the number of PMUs was also reduced, making the ILP method more optimal overall. In the IEEE 118 system, ILP improved SORI and reduced the number of PMUs. It achieved an SORI of 280 with 59 PMUs, outperforming other methods.

4.5. Algorithm-Specific Observations

The EBS algorithm consistently achieved a minimal number of PMUs across various bus systems. Chakrabarti et al. [10,29] claimed that EBS outperforms PSO, GA, and ILP despite being more computationally intensive. While this assertion holds for PSO and GA, it is not entirely accurate for ILP. When properly formulated, ILP can provide optimal solutions without imposing excessive computational demands on the system and is better than the EBS algorithm.

The PSO algorithm performed comparably to EBS in terms of the number of PMUs required. However, its ability to maintain SORI varied slightly, particularly in larger bus systems. Ahmadi et al. [8] claimed to have optimal results, but when a comparison between the conventional method solved using PSO and the proposed formulation solved using ILP is made, it is revealed that PSO-based solutions have a lower SORI value. Therefore, the proposed formulation is more effective than the conventional approach for solving the PMU placement problem using the ILP algorithm.

The results from the GA showed more significant variability in both the number of PMUs and observability metrics. Castro et al. [7] claimed to have complete network observability, but it failed in the New England 39 bus system found using the proposed BCI. Its performance was inconsistent, indicating a need for further tuning or modifications to improve scalability. Additionally, GA struggled to achieve complete network observability, highlighting an area that requires improvement. Therefore, ILP leads, when the proposed formulation is solved, to the GA.

It is inferred from the above discussion that the EBS algorithm consistently achieved lower PMU counts while maintaining high observability across all bus systems. PSO delivered similar results but showed variability in SORI, suggesting a balance between redundancy and PMU count. GA performed well in smaller networks but required optimization for larger systems. Overall, the ILP method outperformed or matched PSO, GA, and EBS in minimizing PMUs while ensuring high SORI and BCI values of 1. Its robust performance across different IEEE test systems, including the larger 118 bus system, highlights its effectiveness for practical PMU placement under varying constraints.

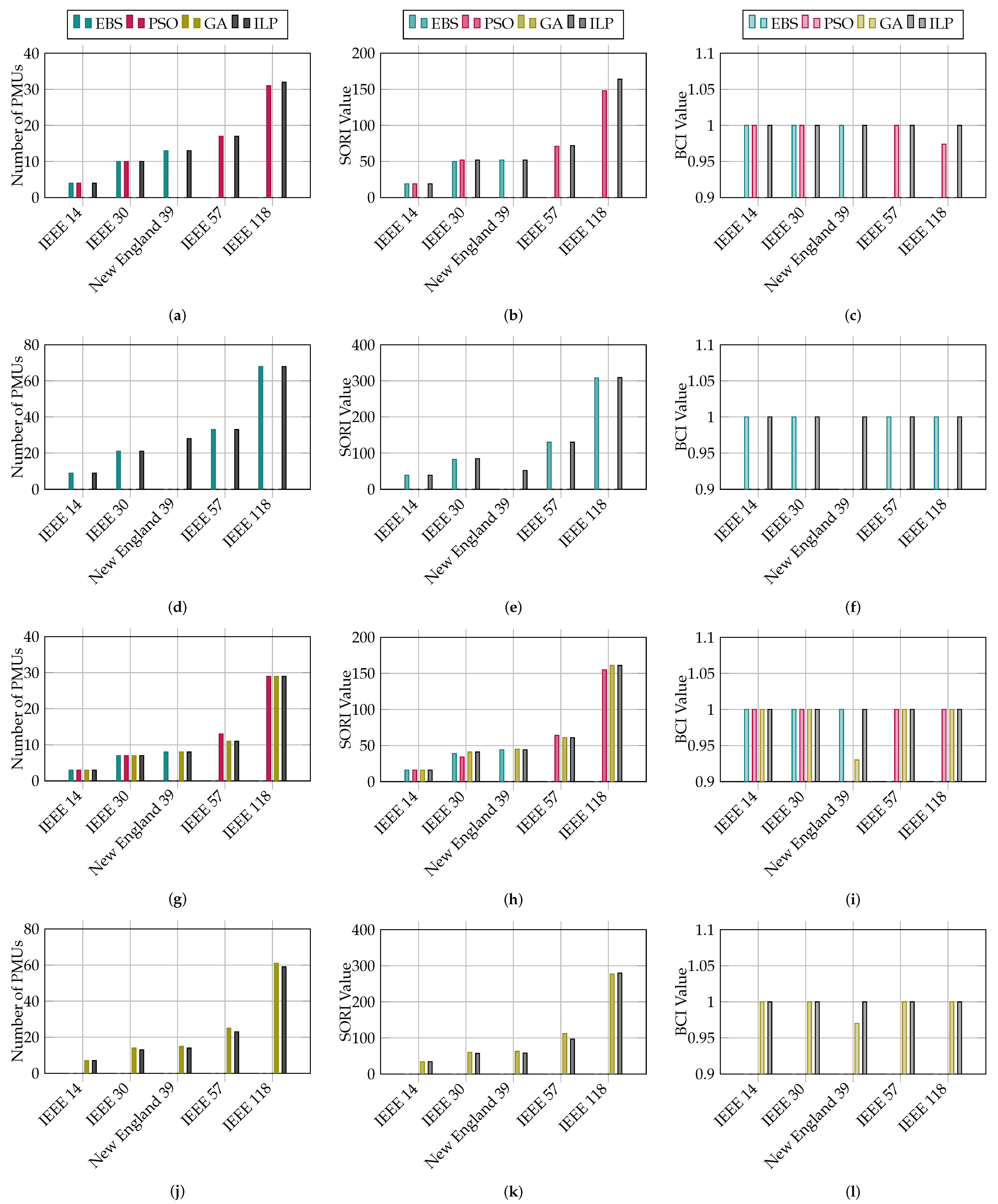
The comparative analysis of all four cases is presented in Figure 8. The twelve sub-figures present the results of evaluating four methods (EBS, PSO, GA, and the proposed ILP) across four cases, focusing on three key metrics: the number of PMUs required, the SORI value, and the BCI value. Overall, it can be seen that ILP always provides full system observability with the same number of PMUs while also obtaining the highest SORI and BCI score for large networks of Case 1, as shown in Figure 8a–c. In Case 2, ILP performed better in terms of SORI than EBS in IEEE 30 and IEEE 118 bus systems, as can be seen in Figure 8d–f. In Case 3, the results are the same as GA, but better than EBS and PSO. In this case, for New England, the test bed system GA fails to have complete network observability, but ILP techniques give PMUs that completely monitor the network, as can be seen in Figure 8g–i. In the last case, where contingency and ZIB effects are considered for complete network observability, a direct comparison is made between the proposed ILP and GA, as other algorithm results were not available. It reveals that ILP outperformed in reducing the number of PMUs in IEEE 30, New England 39, IEEE 57, and IEEE 118 bus systems, satisfying complete network observability, as can be seen in Figure 8j–l.

The simulations were conducted on a system equipped with an Intel(R) Core(TM) i7-5500U CPU running at a base speed of 2.40 GHz, featuring two cores and four logical processors. The system also included 12 GB of DDR3 RAM and an Intel(R) HD Graphics 5500 GPU. This setup provided a robust environment for efficiently handling the computational demands of the optimization problem. The times consumed by different cases are presented below in

Table 6. Computation times for OPP under different scenarios for IEEE test bed systems.

Test Systems	Case 1	Case 2	Case 3	Case 4
IEEE 14	1.0 s	1.1 s	1.5 s	1.9 s
IEEE 30	2.1 s	2.3 s	2.2 s	2.9 s
New England 39	1.5 s	1.8 s	2.0 s	2.5 s
IEEE 57	2.0 s	2.8 s	3.5 s	3.6 s
IEEE 118	2.8 s	3.1 s	5.1 s	5.8 s

.

From the above results and discussion, it is found that placing PMUs based on the normalized degree of centrality is an optimal way to enhance observability. By focusing on the most connected buses, it is possible to strategically position PMUs to cover the maximum area with fewer units. The simulations show a significant reduction in the number of PMUs needed compared to traditional methods, improving both observability and efficiency. This approach also strengthens the system’s resilience during contingencies, as PMUs at central vertices maintain observability even if parts of the network fail. Additionally, it aligns well with zero-injection bus (ZIB) considerations, allowing for effective monitoring of nearby ZIBs and further reducing PMU requirements. When compared to other methods like EBS, PSO, and GA, this strategy consistently delivers solid performance metrics, including high SORI and BCI values, making it especially effective for larger networks where achieving comprehensive observability is crucial.

The main limitation of this study is that the results of EBS, PSO, and GA are compared with ILP, but they are based on different formulations. The ILP method uses a normalized degree of centrality-based formulation that combines cost and critical buses. In contrast, the EBS, PSO, and GA methods are based on a traditional formulation that focuses only on reducing PMU installation costs. Because of this difference, the comparison between the algorithms is not entirely direct. In future work, EBS, PSO, and GA should be solved using the same normalized degree of centrality-based formulation. It will allow for a fair and direct comparison of all algorithms under the same mathematical framework.

5. Conclusions

This study presented an integer linear programming (ILP) approach for optimal phasor measurement unit (PMU) placement, focusing on critical buses and employing a new multi-stage installation strategy based on critical buses to enhance monitoring and resilience in larger networks. This methodology is better than the conventional method to solve OPP, as it focuses on critical nodes with more connections. This research demonstrates that single PMU contingencies account for single line failures, eliminating the need for separate analyses; however, multiple line outages require independent evaluation. By integrating PMU contingencies and zero-injection buses, the ILP approach outperformed existing algorithms in minimizing PMU counts while ensuring high network observability, as measured by the proposed Bus Coverage Index and the existing Sum of Redundancy Index. This research highlights the need for future work to develop PMU contingency constraints that encompass both single and multiple line failures to enhance PMU placement reliability further.