DEM-CFD Simulation Analysis of Heat Transfer Characteristics for Hydrogen Flow in Randomly Packed Beds
Abstract
1. Introduction
2. Physical Model and Numerical Method
2.1. Physical Model
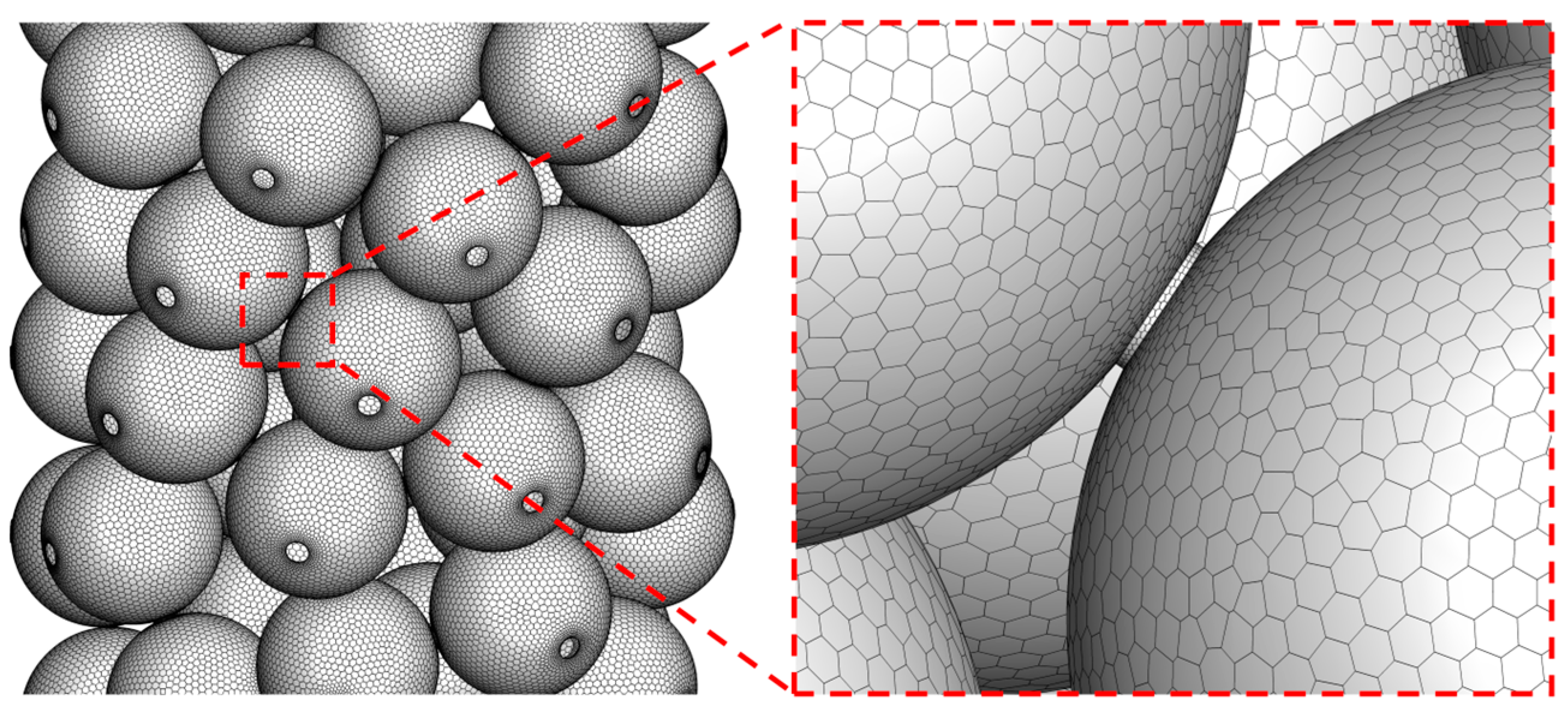
2.2. Meshing Scheme
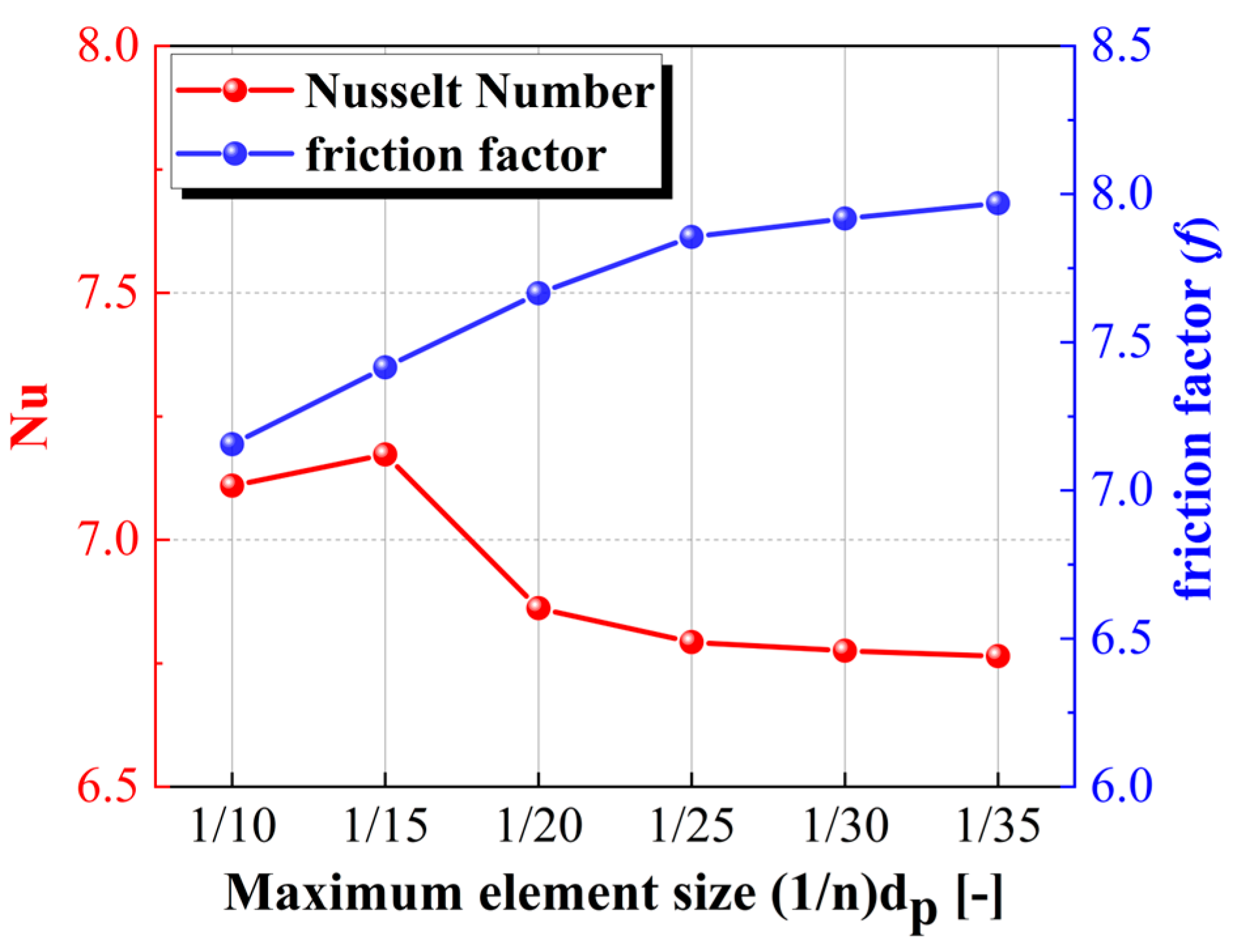
2.3. Validation of Grid Independence
2.4. Governing Equations
2.5. Boundary Conditions
2.6. Hydrogen Properties
2.7. Definitions of Dimensionless Parameter
3. Model Validation
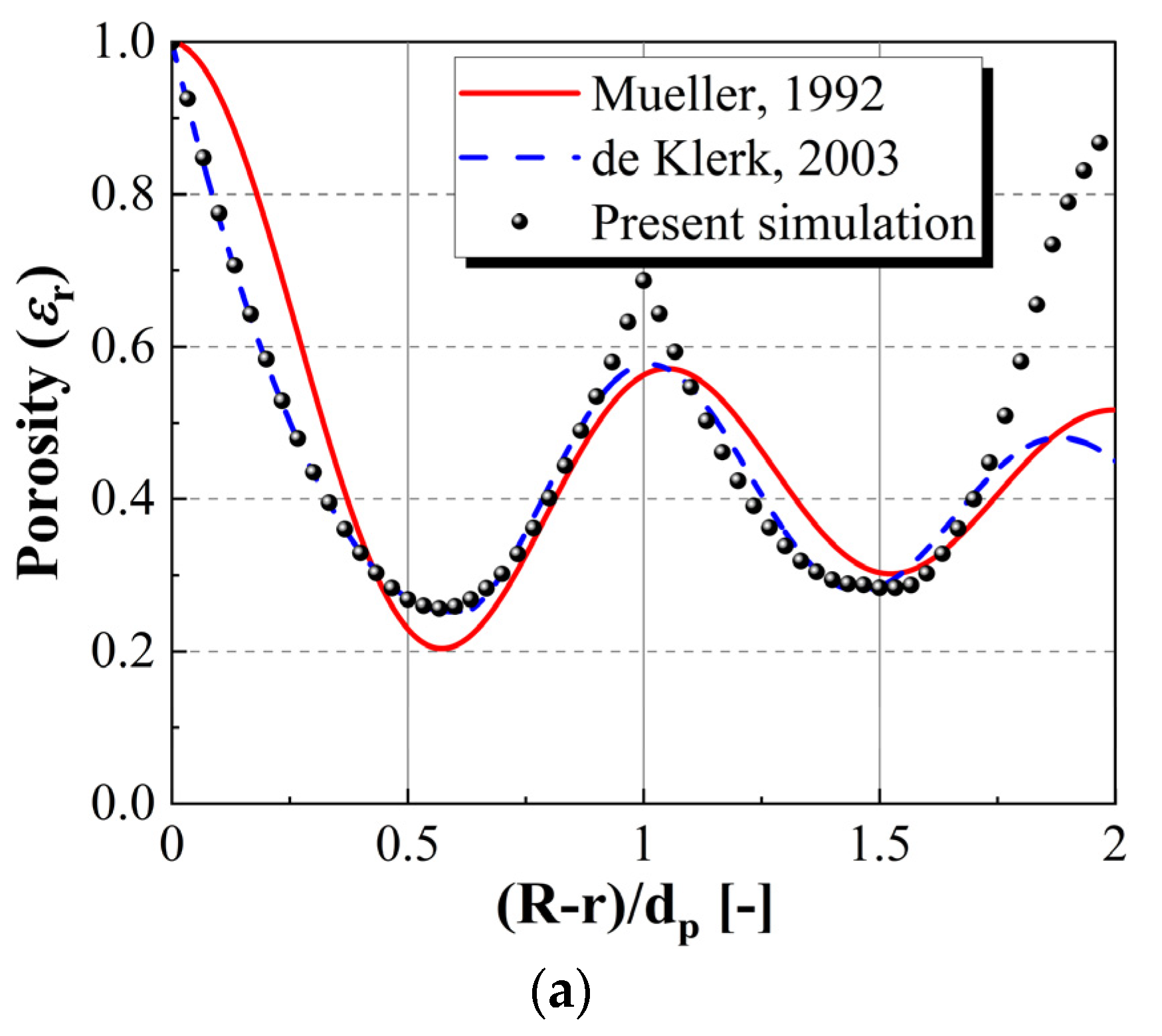
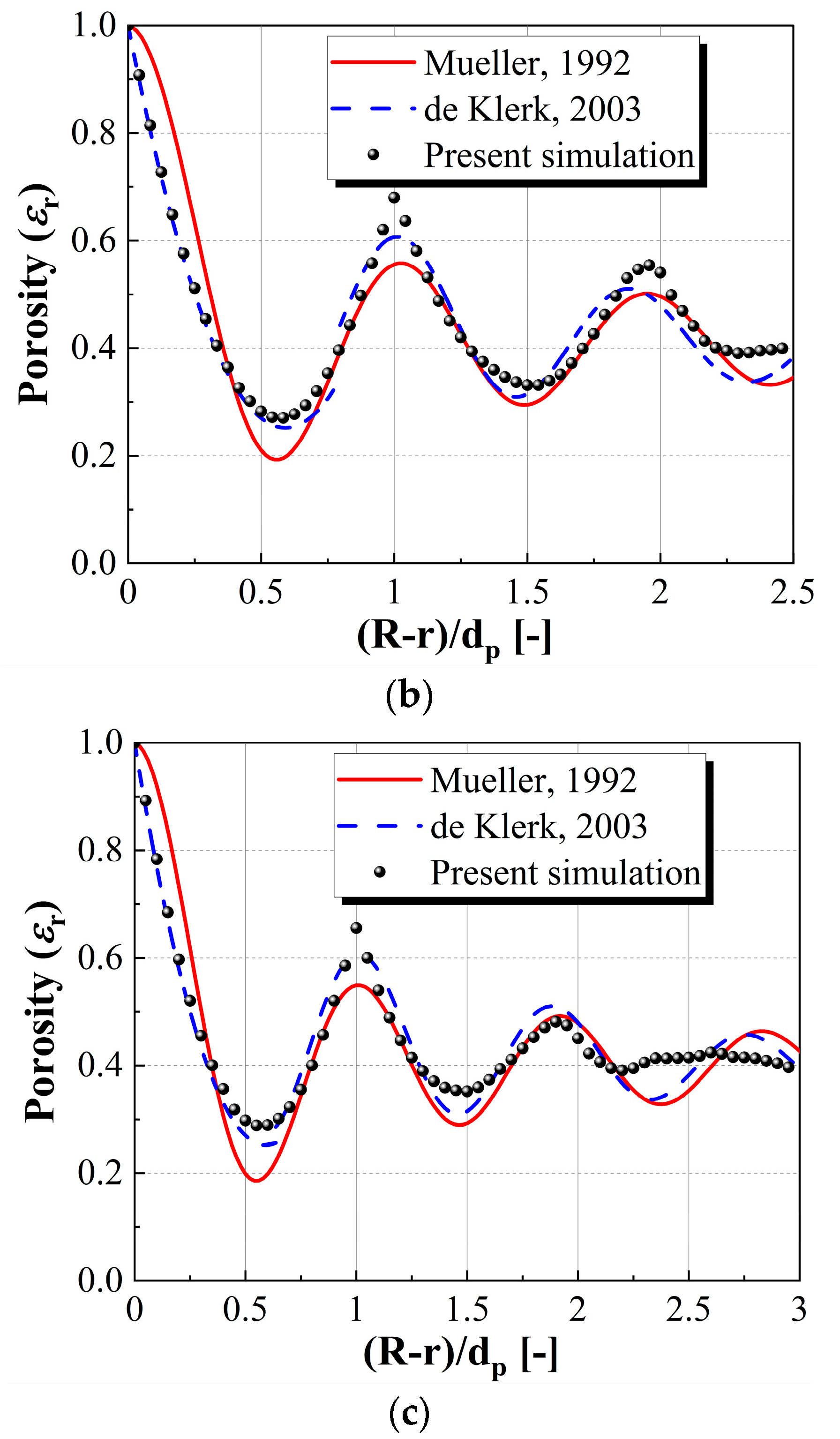
3.1. Validation of the Packing Structure
3.2. Validation of the Heat Transfer Model
4. Results and Discussion
4.1. Analysis of Friction Factor in Packed Bed
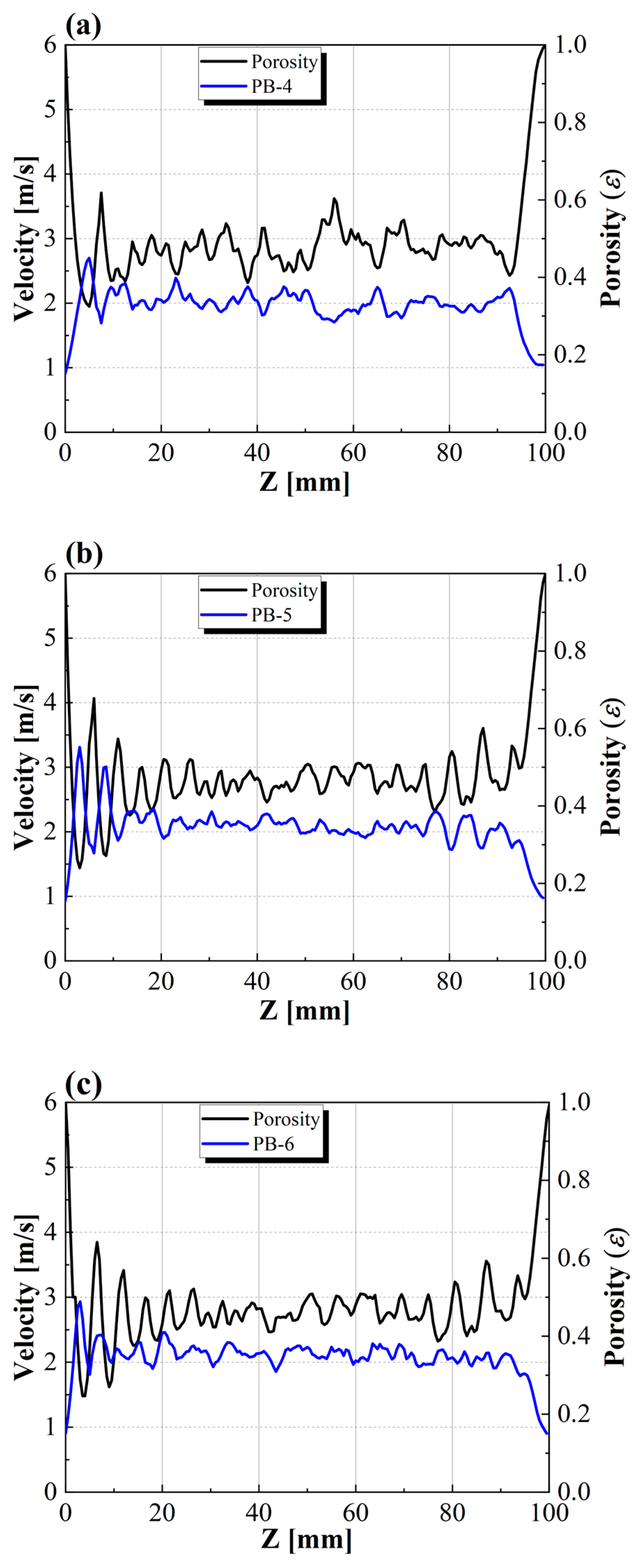
4.2. Characteristics of Flow and Heat Transfer in Packed Bed
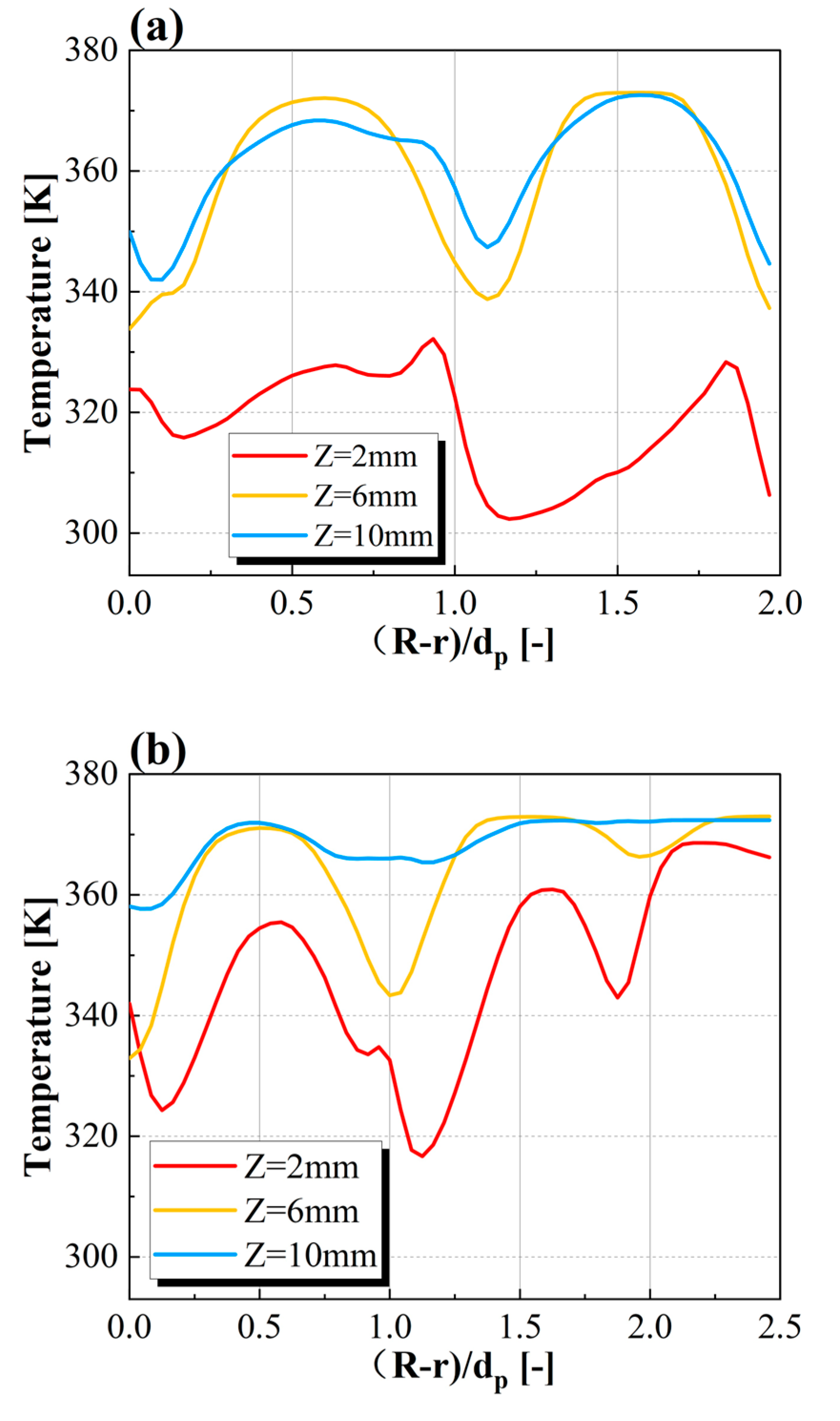
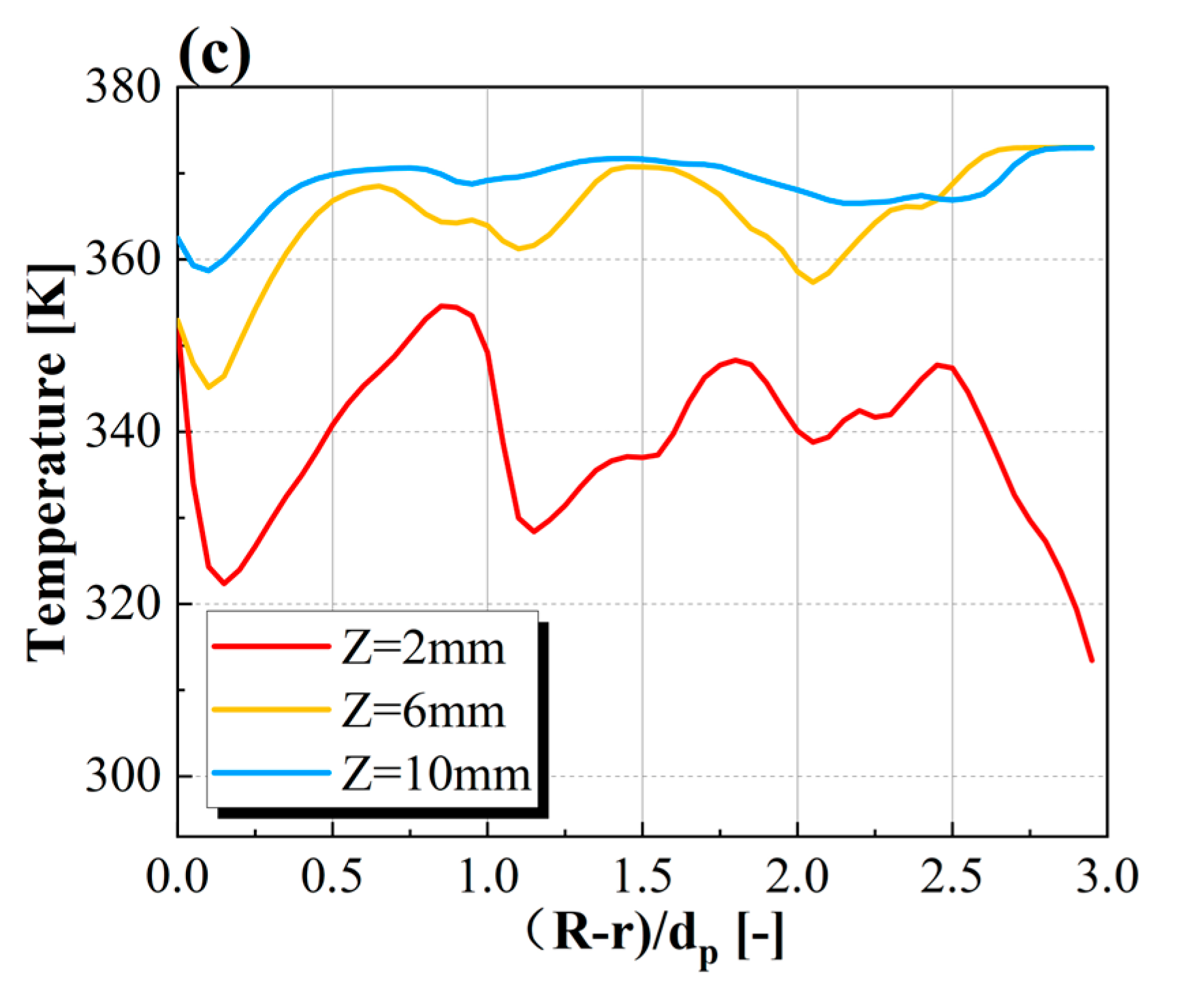
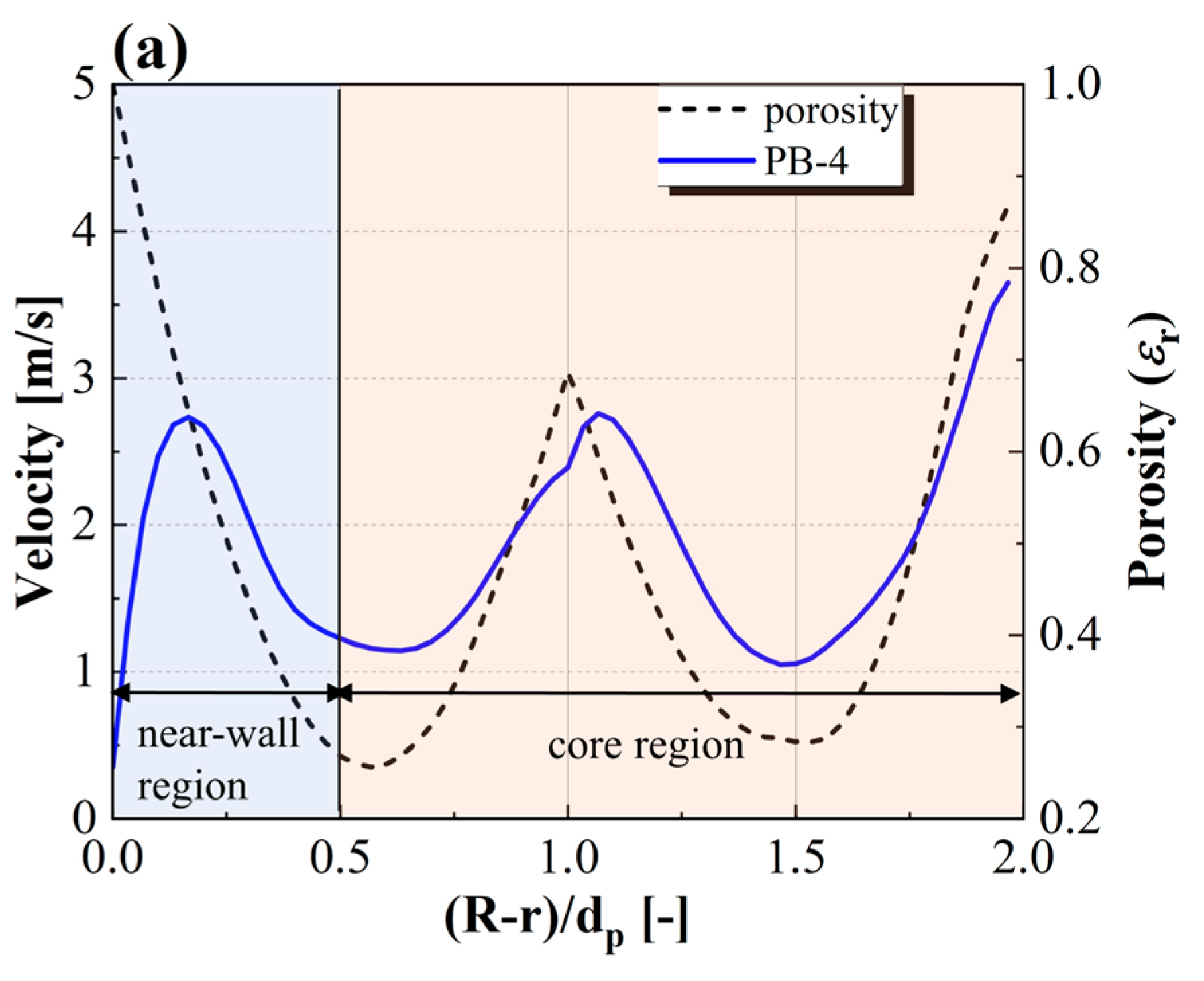
4.3. The Influence of the Wall Effect
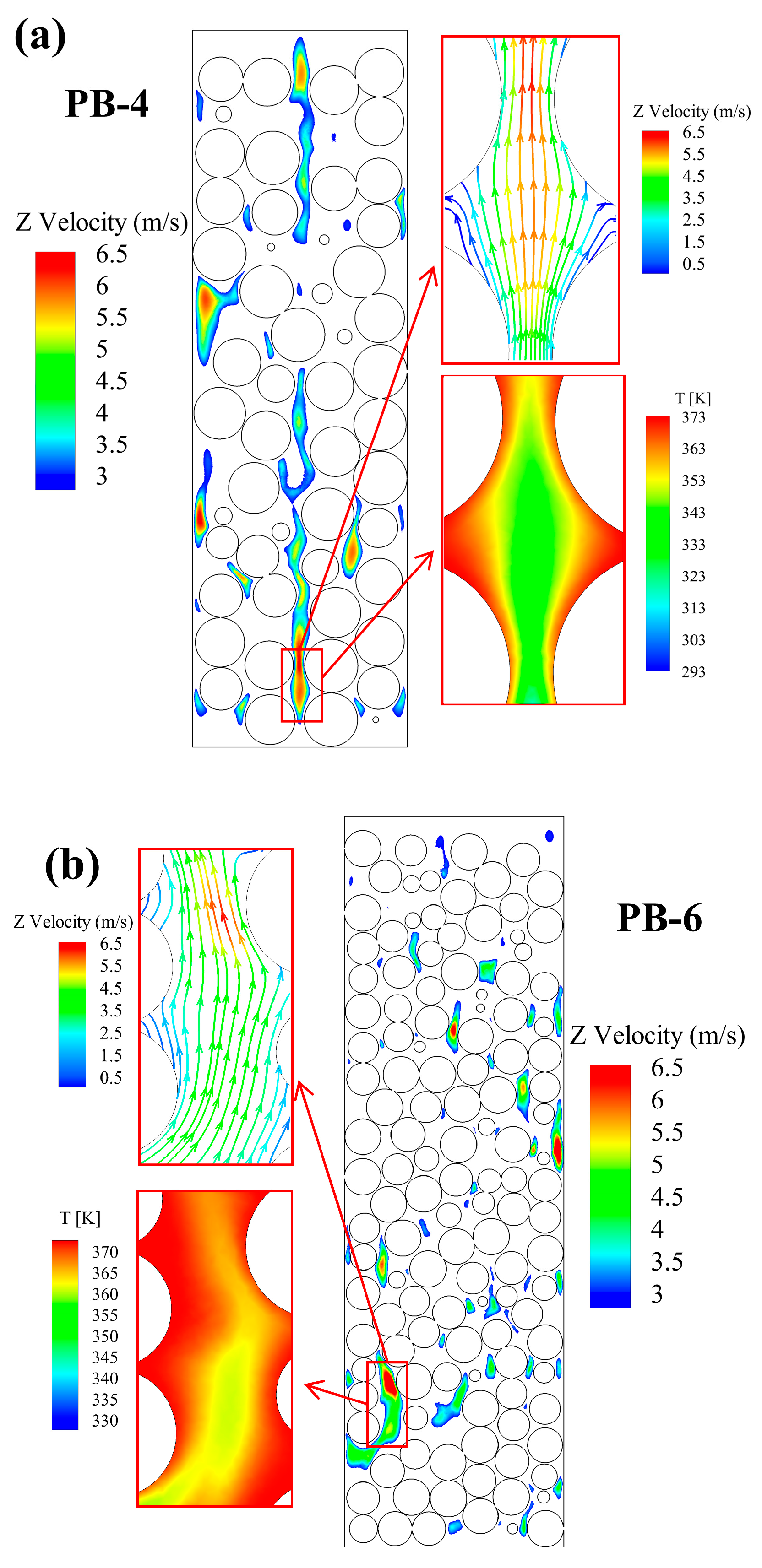
4.4. Analysis of Local High-Speed Fluid Channels
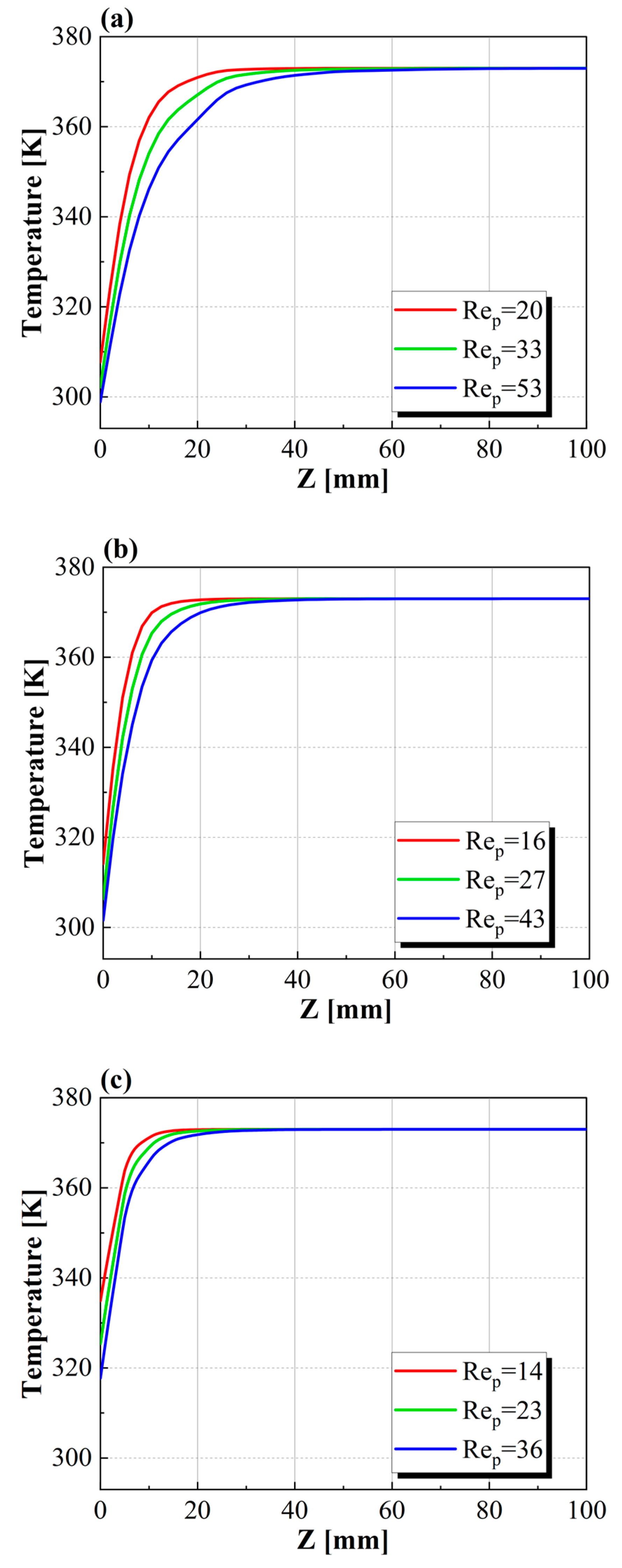
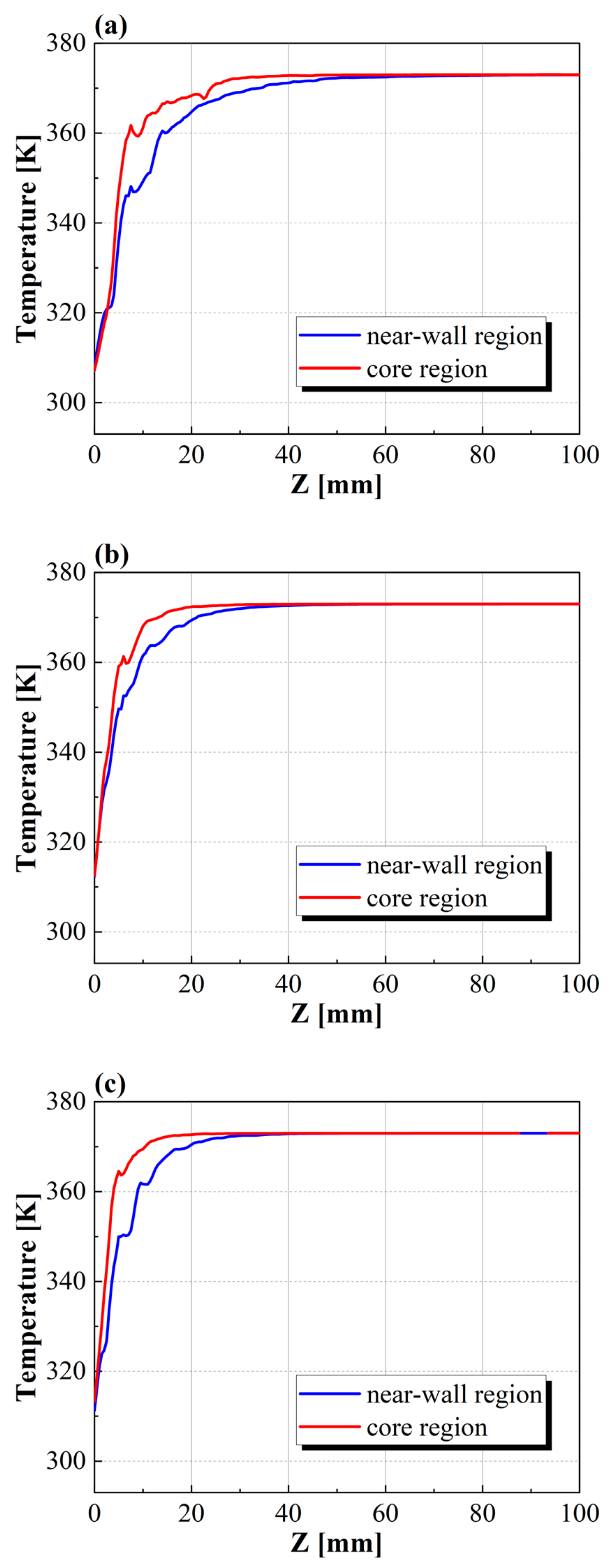
4.5. Characteristics of Axial Local Nusselt Number in Packed Bed
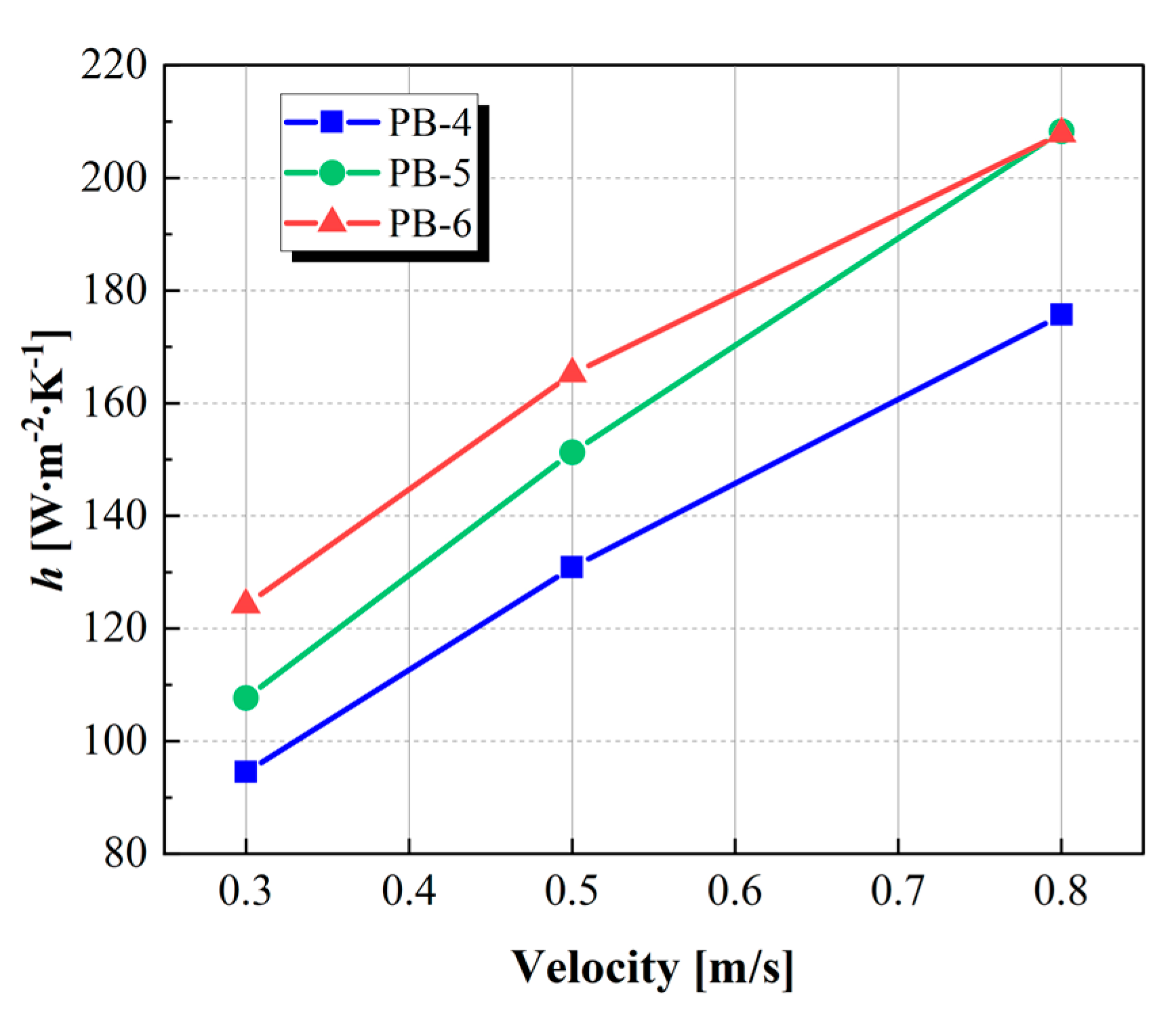
4.6. Evaluation of Heat Transfer Coefficient for the Three Packed Beds
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| cp | specific heat at constant pressure (J/(kg∙K)) | Tf | fluid temperature (K) |
| Tin | inlet temperature (K) | ||
| D | tube diameter (mm) | Tout | outlet temperature (K) |
| db | bridge column diameter (mm) | Tp | particle surface temperature (K) |
| dh | hydraulic diameter (mm) | Greek symbols | |
| dp | particle diameter (mm) | ε | porosity |
| f | friction factor | λ | thermal conductivity (W/(m∙K)) |
| L1 | length of entrance region (mm) | μ | viscosity (kg/m·s) |
| L2 | length of packing region (mm) | ρ | density (kg/m3) |
| L3 | length of outlet region (mm) | Abbreviations | |
| Nu | Nusselt number | PB−4 | packed bed with a tube-to-particle diameter ratio of 4 |
| Pr | Prandtl number | PB−5 | packed bed with a tube-to-particle diameter ratio of 5 |
| R | radius of tube (mm) | PB−6 | packed bed with a tube-to-particle diameter ratio of 6 |
| Re | Reynolds number | Subscripts | |
| Rep | pore Reynolds number | b | bridge |
| r | radial coordinate (mm) | r | radial |
References
- Zhang, Z.Y.; Dong, Y.J.; Li, F.; Zhang, Z.M.; Wang, H.T.; Huang, X.J.; Li, H.; Liu, B.; Wu, X.X.; Wang, H.; et al. The Shandong Shidao bay 200 mwe high-temperature gas-cooled reactor pebble-bed module (HTR-PM) demonstration power plant: An engineering and technological innovation. Engineering 2016, 2, 112–118. [Google Scholar] [CrossRef]
- Huang, R.; Cheng, L.; Qiu, K.; Zheng, C.; Luo, Z. Low-calorific gas combustion in a two-layer porous burner. Energy Fuels 2016, 30, 1364–1374. [Google Scholar] [CrossRef]
- Zhang, B.; Dai, H.; Dai, H.; Wang, Z. Inhomogeneous packed bed burner for improving the utilization of low-concentration methane. Environ. Prog. Sustain. 2022, 41, e13921. [Google Scholar] [CrossRef]
- Kumar, A.; Saha, S.K. Performance analysis of a packed bed latent heat thermal energy storage with cylindrical-shaped encapsulation. Int. J. Energy. Res. 2021, 45, 13130–13148. [Google Scholar] [CrossRef]
- Guo, W.; He, Z.; Meng, Z.; Zhang, P. A comprehensive investigation of the mathematical models for a packed bed latent heat thermal energy storage system. Int. J. Energy. Res. 2021, 45, 15005–15021. [Google Scholar] [CrossRef]
- Berrhazi, S.; Ouammi, A.; Benchrifa, R. Thermo-physical effect of solid filler on the performance of a packed-bed thermal storage. Therm. Sci. Eng. Prog. 2020, 20, 100716. [Google Scholar] [CrossRef]
- Agalit, H.; Zari, N.; Maalmi, M.; Maaroufi, M. Numerical investigations of high temperature packed bed TES systems used in hybrid solar tower power plants. Sol. Energy 2015, 122, 603–616. [Google Scholar] [CrossRef]
- Jurtz, N.; Kraume, M.; Wehinger, G.D. Advances in fixed-bed reactor modeling using particle-resolved computational fluid dynamics (CFD). Rev. Chem. Eng. 2019, 35, 139–190. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Flaischlen, S. Computational fluid dynamics modeling of radiation in a steam methane reforming fixed-bed reactor. Ind. Eng. Chem. Res. 2019, 58, 14410–14423. [Google Scholar] [CrossRef]
- Thaker, A.H.; Karthik, G.M.; Buwa, V.V. PIV measurements and CFD simulations of the particle-scale flow distribution in a packed bed. Chem. Eng. J. 2019, 374, 189–200. [Google Scholar] [CrossRef]
- Theuerkauf, J.; Witt, P.; Schwesig, D. Analysis of particle porosity distribution in fixed beds using the discrete element method. Powder Technol. 2006, 165, 92–99. [Google Scholar] [CrossRef]
- Wu, Y.; Hou, Q.; Yu, A. Pore-scale study of fluid flow and drag force in randomly packed beds of different porosities. Ind. Eng. Chem. Res. 2019, 58, 5041–5053. [Google Scholar] [CrossRef]
- Afgan, I.; Kahil, Y.; Benhamadouche, S.; Ali, M.; Alkaabi, A.; Sofiane Berrouk, A.; Sagaut, P. Cross flow over two heated cylinders in tandem arrangements at subcritical Reynolds number using large eddy simulations. Int. J. Heat. Fluid. Flow. 2023, 100, 109115. [Google Scholar] [CrossRef]
- Wu, J.; Li, L.; Yin, Z.; Li, Z.; Wang, T.; Tan, Y.; Tan, D. Mass transfer mechanism of multiphase shear flows and interphase optimization solving method. Energy 2024, 292, 130475. [Google Scholar] [CrossRef]
- Ge, M.; Zheng, G. Fluid–Solid Mixing Transfer Mechanism and Flow Patterns of the Double-Layered Impeller Stirring Tank by the CFD-DEM Method. Energies 2024, 17, 1513. [Google Scholar] [CrossRef]
- Wijesooriya, K.; Mohotti, D.; Lee, C.-K.; Mendis, P. A technical review of computational fluid dynamics (CFD) applications on wind design of tall buildings and structures: Past, present and future. J. Build. Eng. 2023, 74, 106828. [Google Scholar] [CrossRef]
- Calis, H.P.A.; Nijenhuis, J.; Paikert, B.C.; Dautzenberg, F.M.; van den Bleek, C.M. CFD modelling and experimental validation of pressure drop and flow profile in a novel structured catalytic reactor packing. Chem. Eng. Sci. 2001, 56, 1713–1720. [Google Scholar] [CrossRef]
- Guardo, A.; Coussirat, M.; Larrayoz, M.A.; Recasens, F.; Egusquiza, E. CFD flow and heat transfer in nonregular packings for fixed bed equipment design. Ind. Eng. Chem. Res. 2004, 43, 7049–7056. [Google Scholar] [CrossRef]
- Kuroki, M.; Ookawara, S.; Street, D.; Ogawa, K. High-fidelity CFD modeling of particle-to-fluid heat transfer in packed bed reactors. In Proceedings of the European Congress of Chemical Engineering (ECCE-6), Copenhagen, Denmark, 16–20 September 2007; pp. 16–21. [Google Scholar]
- Eppinger, T.; Seidler, K.; Kraume, M. DEM-CFD simulations of fixed bed reactors with small tube to particle diameter ratios. Chem. Eng. J. 2011, 166, 324–331. [Google Scholar] [CrossRef]
- Dixon, A.G.; Nijemeisland, M.; Stitt, E.H. Systematic mesh development for 3D CFD simulation of fixed beds: Contact points study. Comput. Chem. Eng. 2013, 48, 135–153. [Google Scholar] [CrossRef]
- Bu, S.S.; Yang, J.; Zhou, M.; Li, S.Y.; Wang, Q.W.; Guo, Z.X. On contact point modifications for forced convective heat transfer analysis in a structured packed bed of spheres. Nucl. Eng. Des. 2014, 270, 21–33. [Google Scholar] [CrossRef]
- Fernengel, J.; Hinrichsen, O. Influence of material properties on voidage of numerically generated random packed beds. Chem. Eng. Sci. 2021, 233, 116406. [Google Scholar] [CrossRef]
- Dong, Y.; Sosna, B.; Korup, O.; Rosowski, F.; Horn, R. Investigation of radial heat transfer in a fixed-bed reactor: CFD simulations and profile measurements. Chem. Eng. J. 2017, 317, 204–214. [Google Scholar] [CrossRef]
- Guo, Z.; Sun, Z.; Zhang, N.; Ding, M.; Zhou, Y. Influence of flow guiding conduit on pressure drop and convective heat transfer in packed beds. Int. J. Heat Mass Transf. 2019, 134, 489–502. [Google Scholar] [CrossRef]
- Liu, H.B.; Zhao, C.Y. Effect of radial porosity oscillation on the thermal performance of packed bed latent heat storage. Engineering 2021, 7, 515–525. [Google Scholar] [CrossRef]
- Cohen, Y.; Metzner, A.B. Wall effects in laminar flow of fluids through packed beds. AIChE J. 1981, 27, 705–715. [Google Scholar] [CrossRef]
- Yang, J.; Wu, J.; Zhou, L.; Wang, Q. Computational study of fluid flow and heat transfer in composite packed beds of spheres with low tube to particle diameter ratio. Nucl. Eng. Des. 2016, 300, 85–96. [Google Scholar] [CrossRef]
- Cheng, L.-C.; Wong, S.-C. Pore-scale numerical simulation and LTNE analysis for fully-developed forced convective heat transfer in packed beds of mono-sized rough spheres covering near-wall and core regions. Int. J. Heat Mass Transf. 2023, 208, 124047. [Google Scholar] [CrossRef]
- Guo, X.; Dai, R. Numerical simulation of flow and heat transfer in a random packed bed. Particuology 2010, 8, 293–299. [Google Scholar] [CrossRef]
- Jadidi, M.; Param, H.K.; Revell, A.; Mahmoudi, Y. Large eddy simulations of turbulent heat transfer in packed bed energy storage systems. J. Energy Storage 2023, 59, 106449. [Google Scholar] [CrossRef]
- Liu, L.; Deng, J.; Zhang, D.; Wang, C.; Qiu, S.; Su, G.H. Experimental analysis of flow and convective heat transfer in the water-cooled packed pebble bed nuclear reactor core. Prog. Nucl. Energy 2020, 122, 103298. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, L.; Zhang, M.; Feng, J.; Dong, H. Experimental investigation of flow and exergy transfer characteristics in the air-cooled randomly packed particle bed based on second law analysis. Int. J. Heat Mass Transf. 2022, 185, 122360. [Google Scholar] [CrossRef]
- Al-Hasan, M.; Al-Odat, M.Q.; Al-Busoul, M. An experimental investigation of forced convection heat transfer from a coiled heat exchanger embedded in a packed bed. Exp. Heat Transf. 2012, 25, 363–376. [Google Scholar] [CrossRef]
- Wu, Z.; Wu, Y.; Wang, C.; Tang, S.; Liu, D.; Qiu, S.; Su, G.H.; Tian, W. Experimental and numerical study on helium flow characteristics in randomly packed pebble bed. Ann. Nucl. Energy 2019, 128, 268–277. [Google Scholar] [CrossRef]
- Dawood, F.; Anda, M.; Shafiullah, G.M. Hydrogen production for energy: An overview. Int. J. Hydrog. Energy 2020, 45, 3847–3869. [Google Scholar] [CrossRef]
- Griffiths, S.; Sovacool, B.K.; Kim, J.; Bazilian, M.; Uratani, J.M. Industrial decarbonization via hydrogen: A critical and systematic review of developments, socio-technical systems and policy options. Energy Res. Soc. Sci. 2021, 80, 102208. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, X.R.; Li, T.; Zhang, J.; Gao, J.; Sun, Z.Y. Hydrogen and ethanol: Production, storage, and transportation. Int. J. Hydrog. Energy 2021, 46, 27330–27348. [Google Scholar] [CrossRef]
- Gibreel, M.; Zhang, X.; Elmouazen, H. Enhancement of heat transfer and hydrogen fuel flow characteristics in a wavy cooling channel with secondary branch design. Int. J. Therm. Sci. 2023, 193, 108513. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Kobayashi, H.; Naruo, Y.; Takesaki, Y.; Sato, T. Investigation of boiling hydrogen heat transfer characteristics under low-pressure conditions. Cryogenics 2023, 131, 103652. [Google Scholar] [CrossRef]
- Tong, J.; Fu, W.; Yang, W.; Wang, S.; Shen, F.; Zhou, B.; Lin, L.; Yu, C.; Zheng, H.; Yao, C.; et al. Numerical simulation of heat transfer characteristics of supercritical liquid hydrogen through triangular U-tube in moderator. Cryogenics 2023, 132, 103698. [Google Scholar] [CrossRef]
- Huber, M.L.; Lemmon, E.W.; Bell, I.H.; McLinden, M.O. The NIST REFPROP Database for highly accurate properties of industrially important fluids. Ind. Eng. Chem. Res. 2022, 61, 15449–15472. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Yu, Q.; Wang, C.; Tian, W.; Su, G.; Qiu, S. Heat transfer of hydrogen with variable properties in a heated tube. Int. J. Heat Mass Transf. 2023, 209, 124128. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Dixon, A.G.; Walls, G.; Stanness, H.; Nijemeisland, M.; Stitt, E.H. Experimental validation of high Reynolds number CFD simulations of heat transfer in a pilot-scale fixed bed tube. Chem. Eng. J. 2012, 200–202, 344–356. [Google Scholar] [CrossRef]
- Bear, J.; Corapcioglu, M.Y. Fundamentals of Transport Phenomena in Porous Media; Springer Science & Business Media: Boston, MA, USA, 1984; Volume 82, pp. 201–258. [Google Scholar]
- Hassanpouryouzband, A.; Joonaki, E.; Edlmann, K.; Heinemann, N.; Yang, J. Thermodynamic and transport properties of hydrogen containing streams. Sci. Data 2020, 7, 222. [Google Scholar] [CrossRef] [PubMed]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0; National Institute of Standards and Technology, Standard Reference Data Program: Gaithersburg, MD, USA, 2018. [Google Scholar] [CrossRef]
- Romkes, S.J.P.; Dautzenberg, F.M.; van den Bleek, C.M.; Calis, H.P.A. CFD modelling and experimental validation of particle-to-fluid mass and heat transfer in a packed bed at very low channel to particle diameter ratio. Chem. Eng. J. 2003, 96, 3–13. [Google Scholar] [CrossRef]
- Mueller, G.E. Radial void fraction distributions in randomly packed fixed beds of uniformly sized spheres in cylindrical containers. Powder Technol. 1992, 72, 269–275. [Google Scholar] [CrossRef]
- de Klerk, A. Voidage variation in packed beds at small column to particle diameter ratio. AIChE J. 2003, 49, 2022–2029. [Google Scholar] [CrossRef]
- Wakao, N.; Kaguei, S.; Funazkri, T. Effect of fluid dispersion coefficients on particle-to-fluid heat transfer coefficients in packed beds. Chem. Eng. Sci. 1979, 34, 325–336. [Google Scholar] [CrossRef]
- Tavassoli, H.; Kriebitzsch, S.H.L.; van der Hoef, M.A.; Peters, E.A.J.F.; Kuipers, J.A.M. Direct numerical simulation of particulate flow with heat transfer. Int. J. Multiph. Flow 2013, 57, 29–37. [Google Scholar] [CrossRef]
- Chen, Y.; Müller, C.R. Lattice Boltzmann simulation of gas-solid heat transfer in random assemblies of spheres: The effect of solids volume fraction on the average Nusselt number for Re ≤ 100. Chem Eng J. 2019, 361, 1392–1399. [Google Scholar] [CrossRef]
- Sun, B.; Tenneti, S.; Subramaniam, S. Modeling average gas–solid heat transfer using particle-resolved direct numerical simulation. Int. J. Heat Mass Transf. 2015, 86, 898–913. [Google Scholar] [CrossRef]
- Foumeny, E.A.; Benyahia, F.; Castro, J.A.A.; Moallemi, H.A.; Roshani, S. Correlations of pressure drop in packed beds taking into account the effect of confining wall. Int. J. Heat Mass Transf. 1993, 36, 536–540. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Chem. Eng. Res. Des. 1997, 75, S32–S48. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89. [Google Scholar]
- Harrison, L.D.; Brunner, K.M.; Hecker, W.C. A combined packed-bed friction factor equation: Extension to higher reynolds number with wall effects. AIChE J. 2013, 59, 703–706. [Google Scholar] [CrossRef]
- Ranz, W. Evaporation from drops: Part II. Chem. Eng. Prog. 1952, 48, 173–180. [Google Scholar]
- Gunn, D.J. Transfer of heat or mass to particles in fixed and fluidised beds. Int. J. Heat Mass Transfer. 1978, 21, 467–476. [Google Scholar] [CrossRef]




| Property | Unit | Value |
|---|---|---|
| Particle diameter | m | 0.0005, 0.006, 0.0075 |
| Poisson ratio | - | 0.24 |
| Density | kg/m3 | 3750 |
| Shear Modulus | pa | 1.37E9 |
| Coefficient of Restitution | - | 0.5 |
| Coefficient of Static Friction | - | 0.154 |
| Coefficient of Rolling Friction | - | 0.1 |
| Specific heat at constant | J/(kg∙K) | 780 |
| Thermal conductivity | W/(m·K) | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Xia, Y.; Cheng, Z.; Quan, X. DEM-CFD Simulation Analysis of Heat Transfer Characteristics for Hydrogen Flow in Randomly Packed Beds. Energies 2024, 17, 2226. https://doi.org/10.3390/en17092226
Zhang Q, Xia Y, Cheng Z, Quan X. DEM-CFD Simulation Analysis of Heat Transfer Characteristics for Hydrogen Flow in Randomly Packed Beds. Energies. 2024; 17(9):2226. https://doi.org/10.3390/en17092226
Chicago/Turabian StyleZhang, Quanchen, Yongfang Xia, Zude Cheng, and Xin Quan. 2024. "DEM-CFD Simulation Analysis of Heat Transfer Characteristics for Hydrogen Flow in Randomly Packed Beds" Energies 17, no. 9: 2226. https://doi.org/10.3390/en17092226
APA StyleZhang, Q., Xia, Y., Cheng, Z., & Quan, X. (2024). DEM-CFD Simulation Analysis of Heat Transfer Characteristics for Hydrogen Flow in Randomly Packed Beds. Energies, 17(9), 2226. https://doi.org/10.3390/en17092226








