Novel Self-Organizing Probability Maps Applied to Classification of Concurrent Partial Discharges from Online Hydro-Generators
Abstract
1. Introduction
2. Background on Partial Discharges
2.1. Partial Discharges in Hydro-Generators
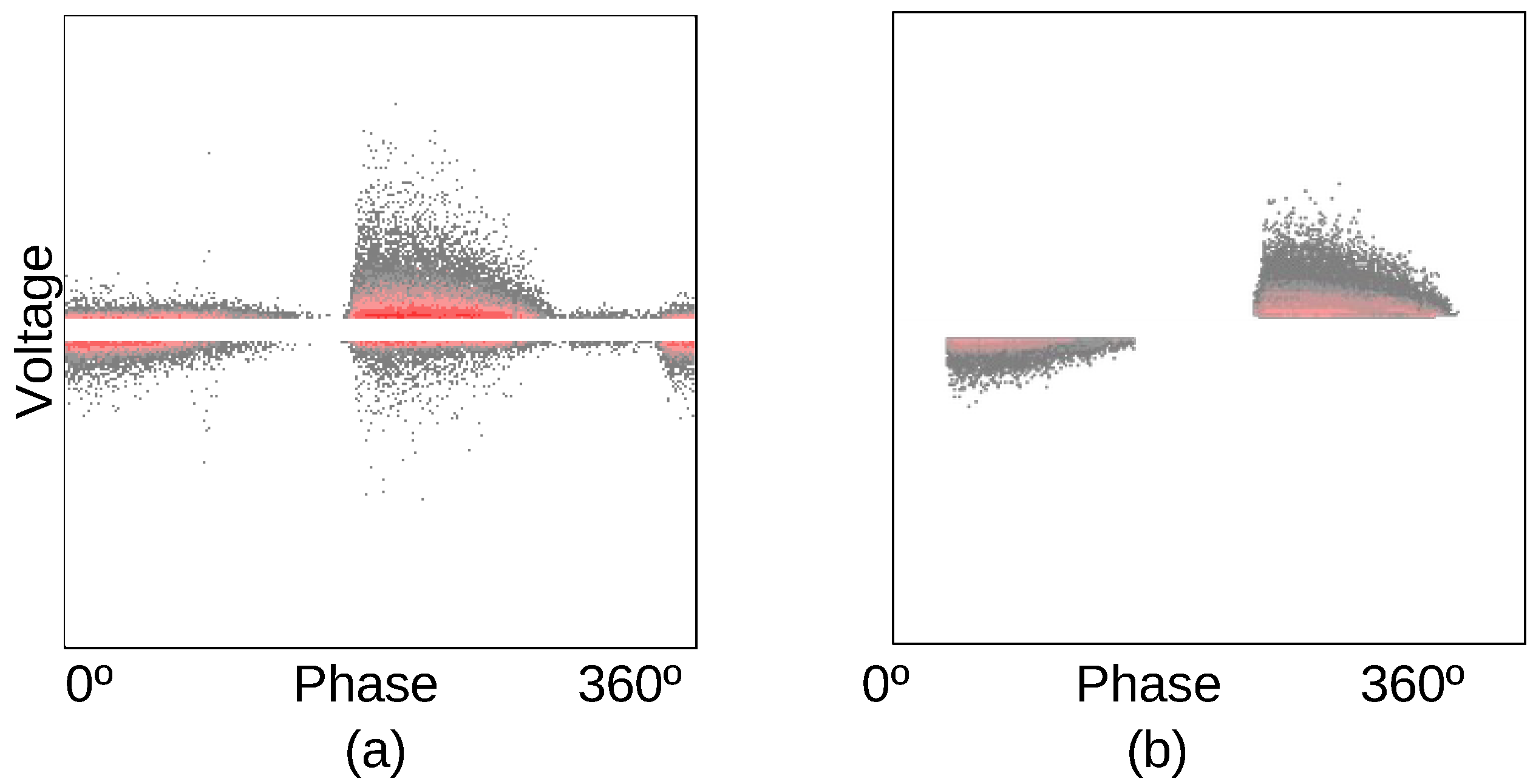
2.2. PRPD Denoising and Feature Extraction
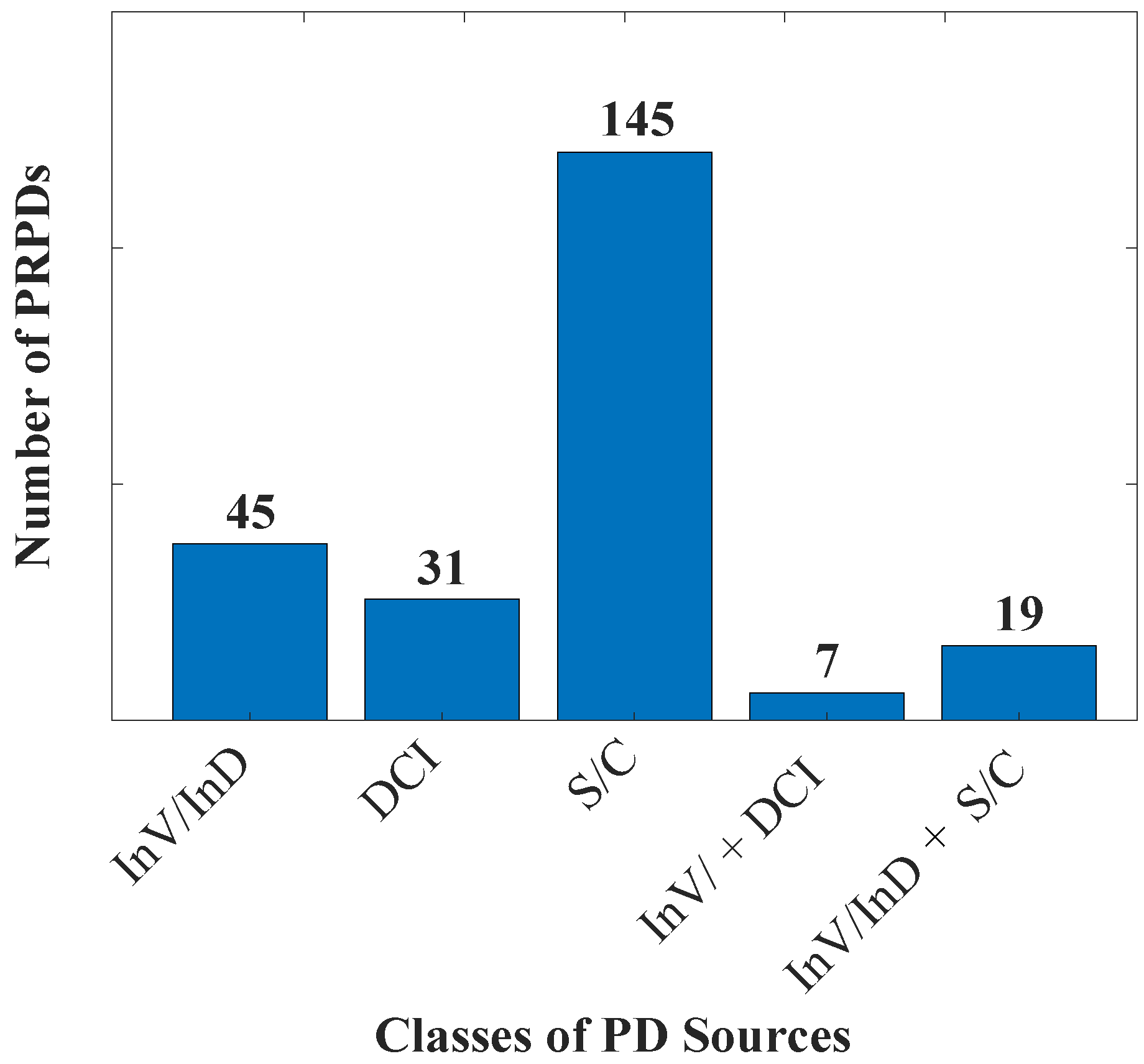
3. The Data Set Obtained from the On-Line Hydro-Generators
4. Review of Kohonen Self-Organizing Maps (SOMs)
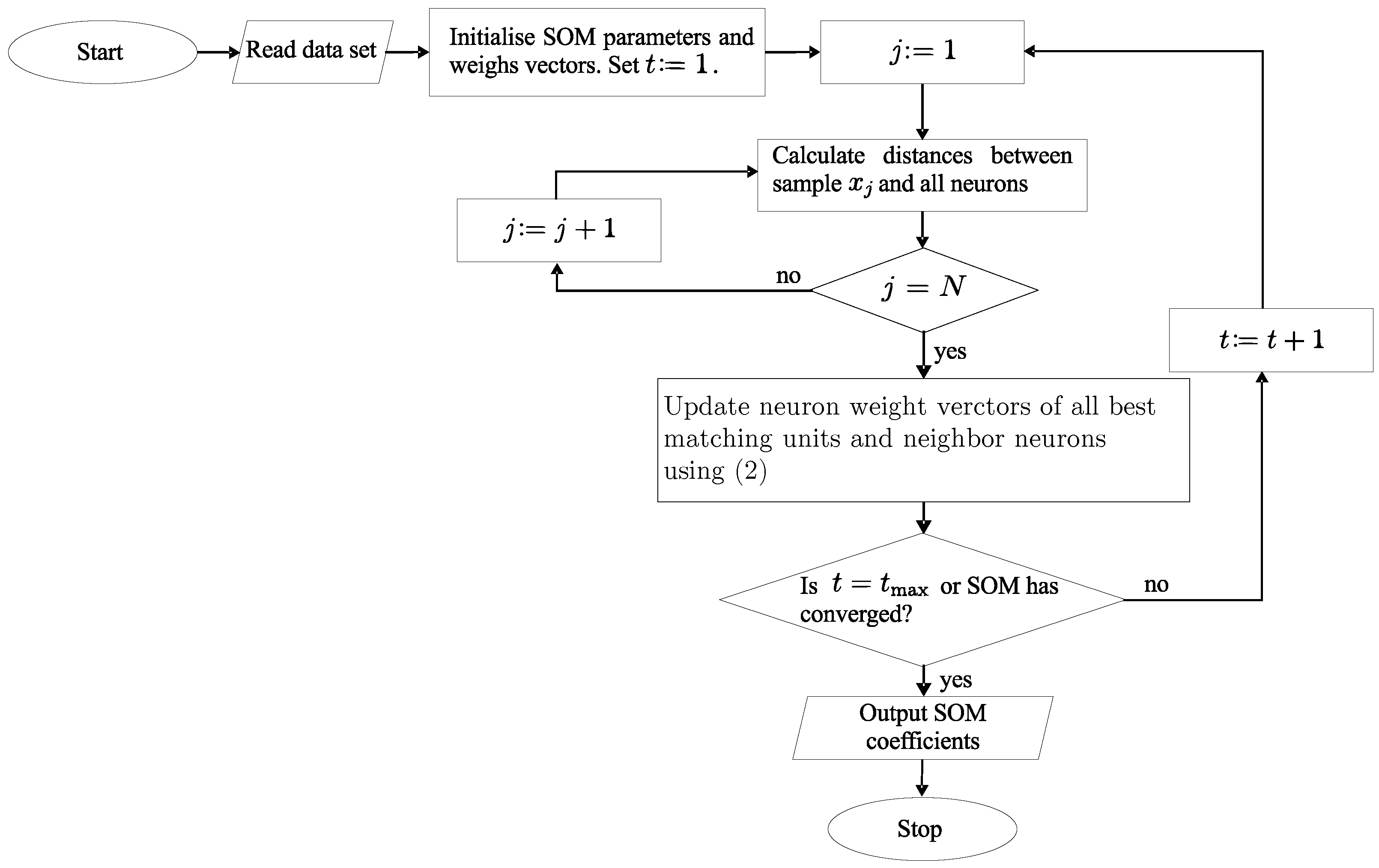
4.1. Training SOM Networks
4.2. Metrics for SOM Evaluation
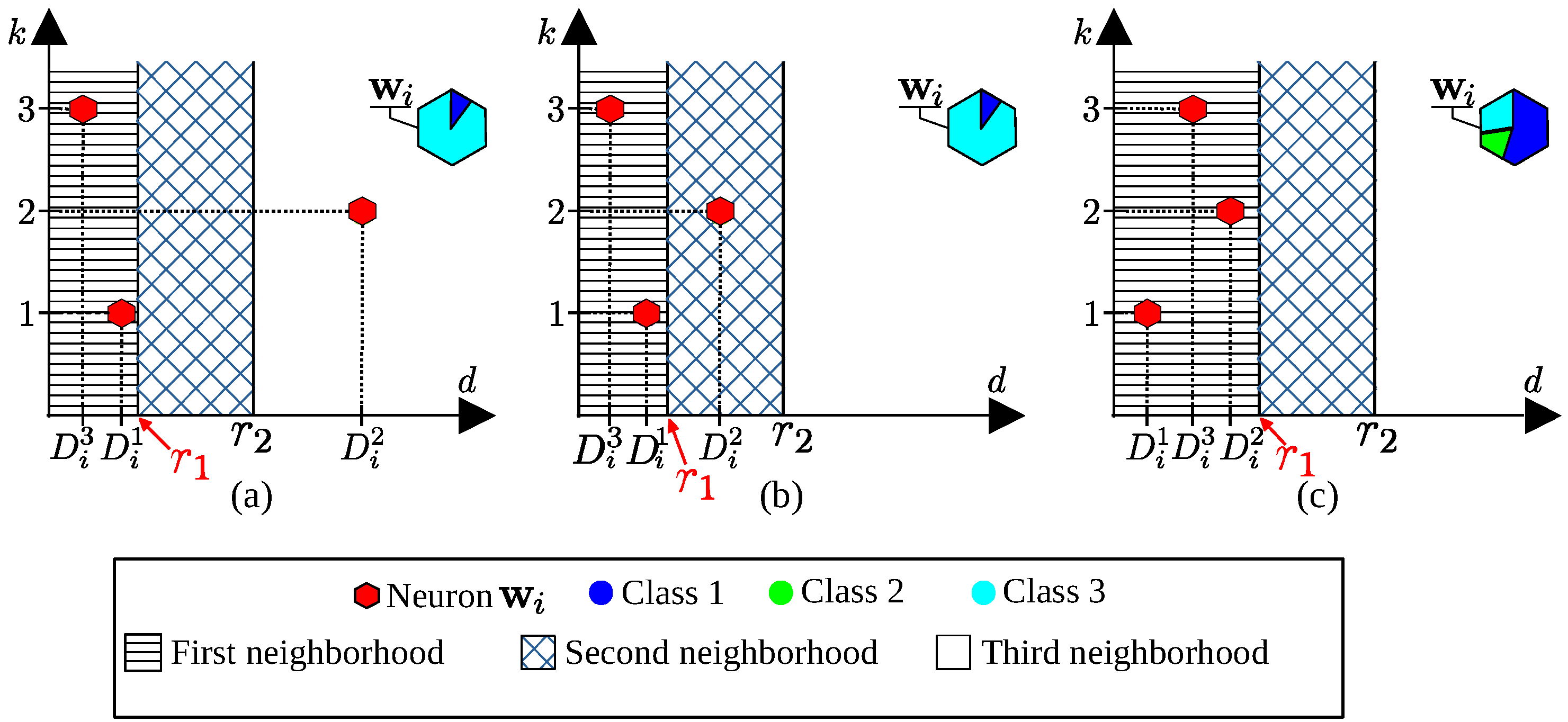
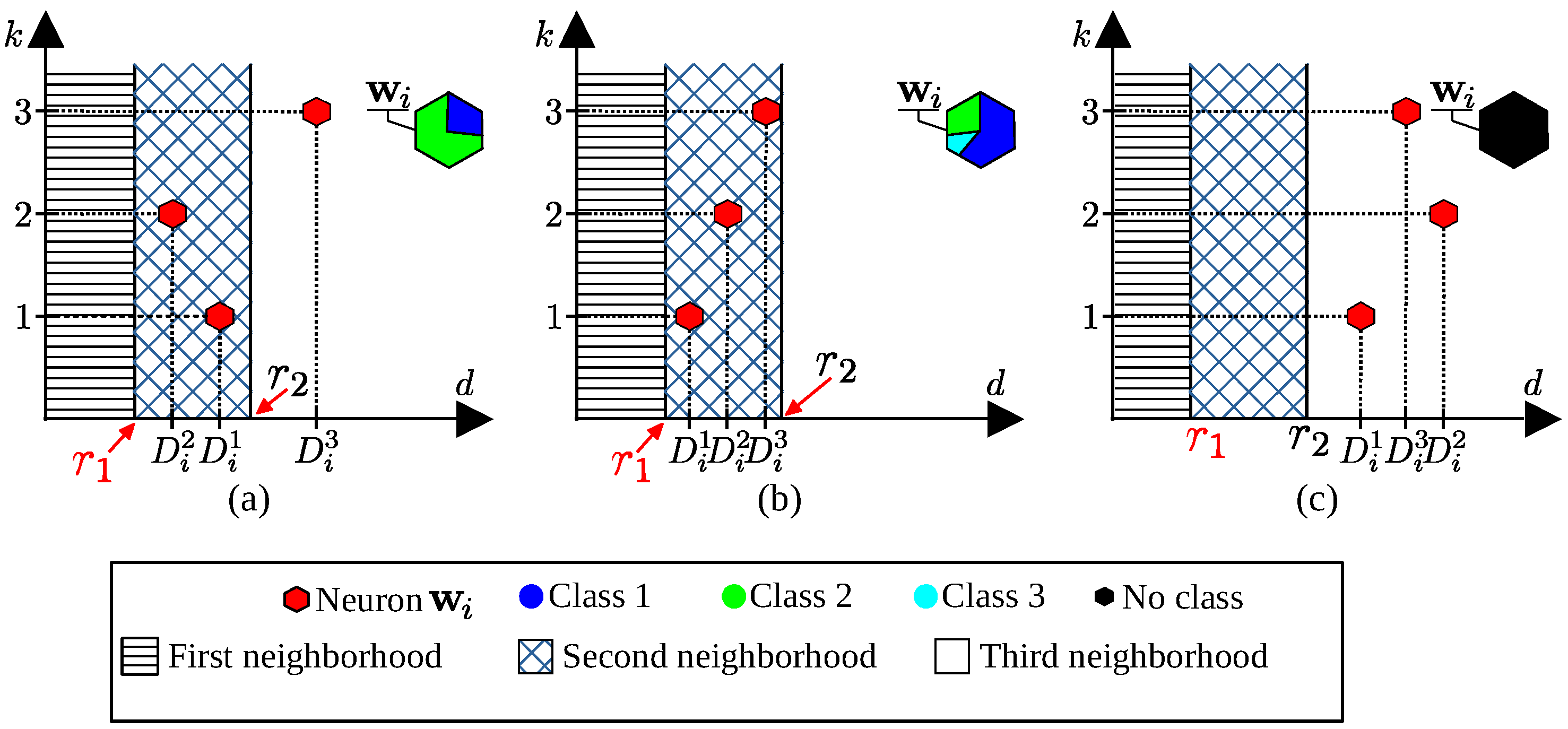
5. The Novel Self-Organizing Probability Maps (SOPMs)
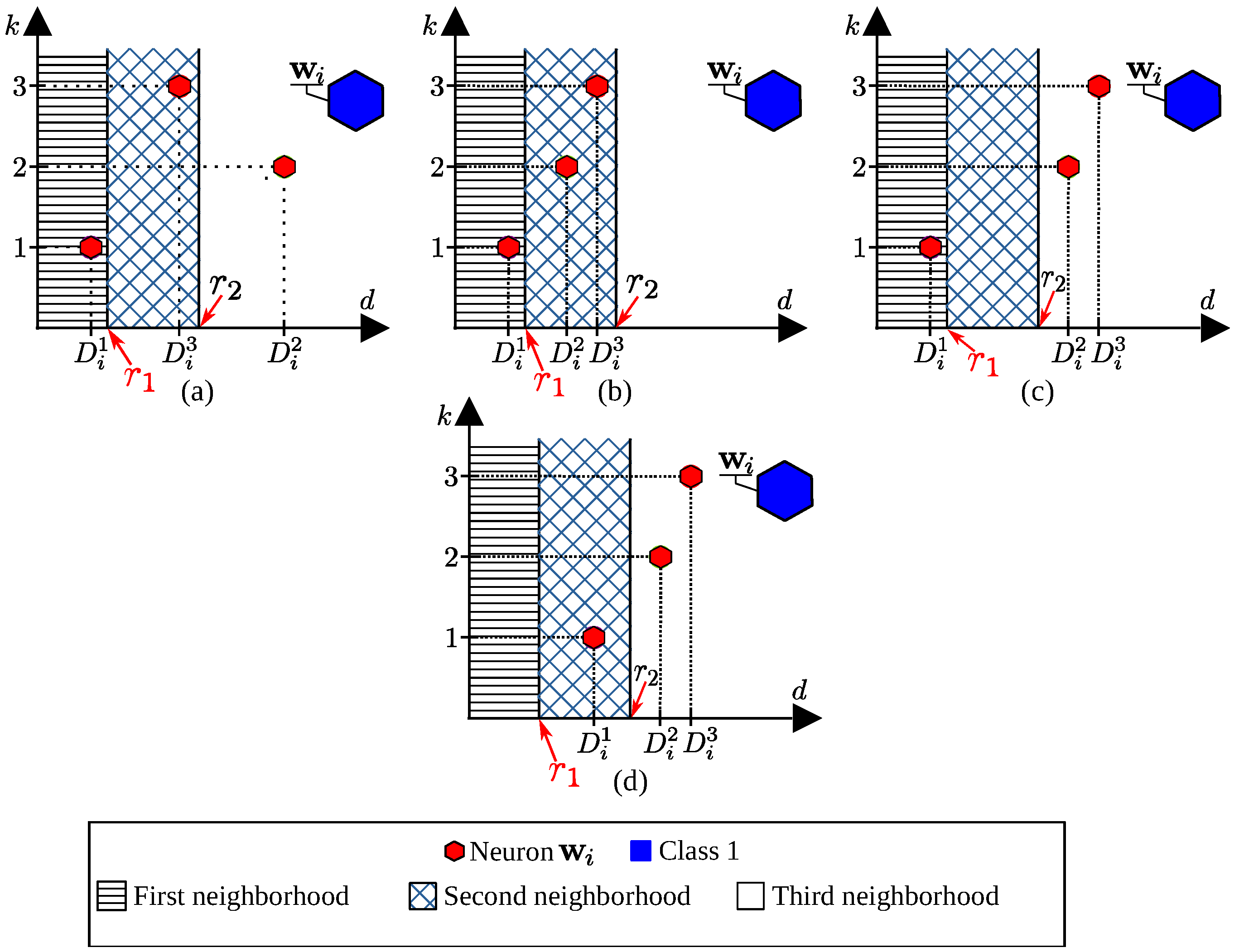
5.1. Calculation of
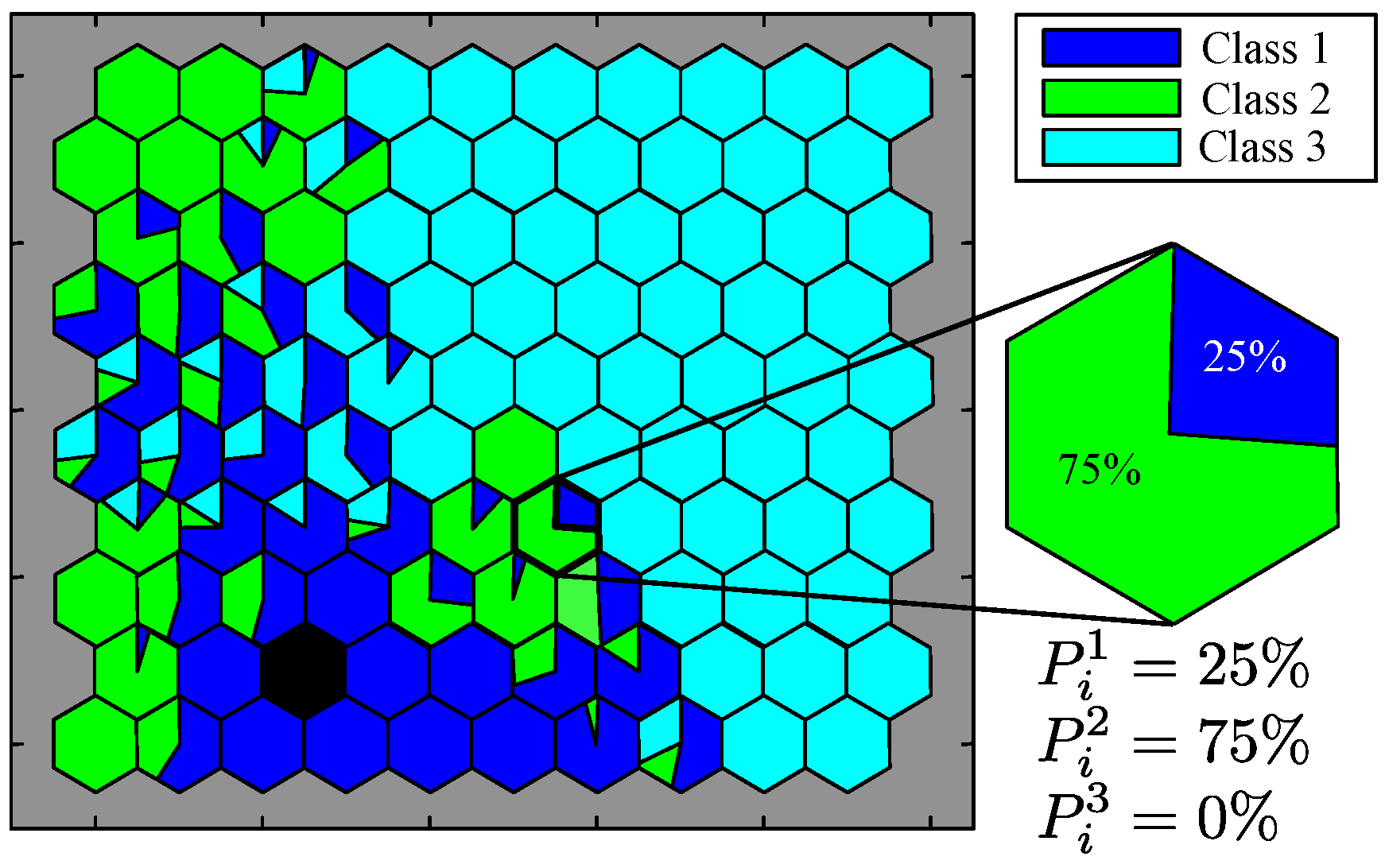
5.2. Calculation of Classification Probabilities
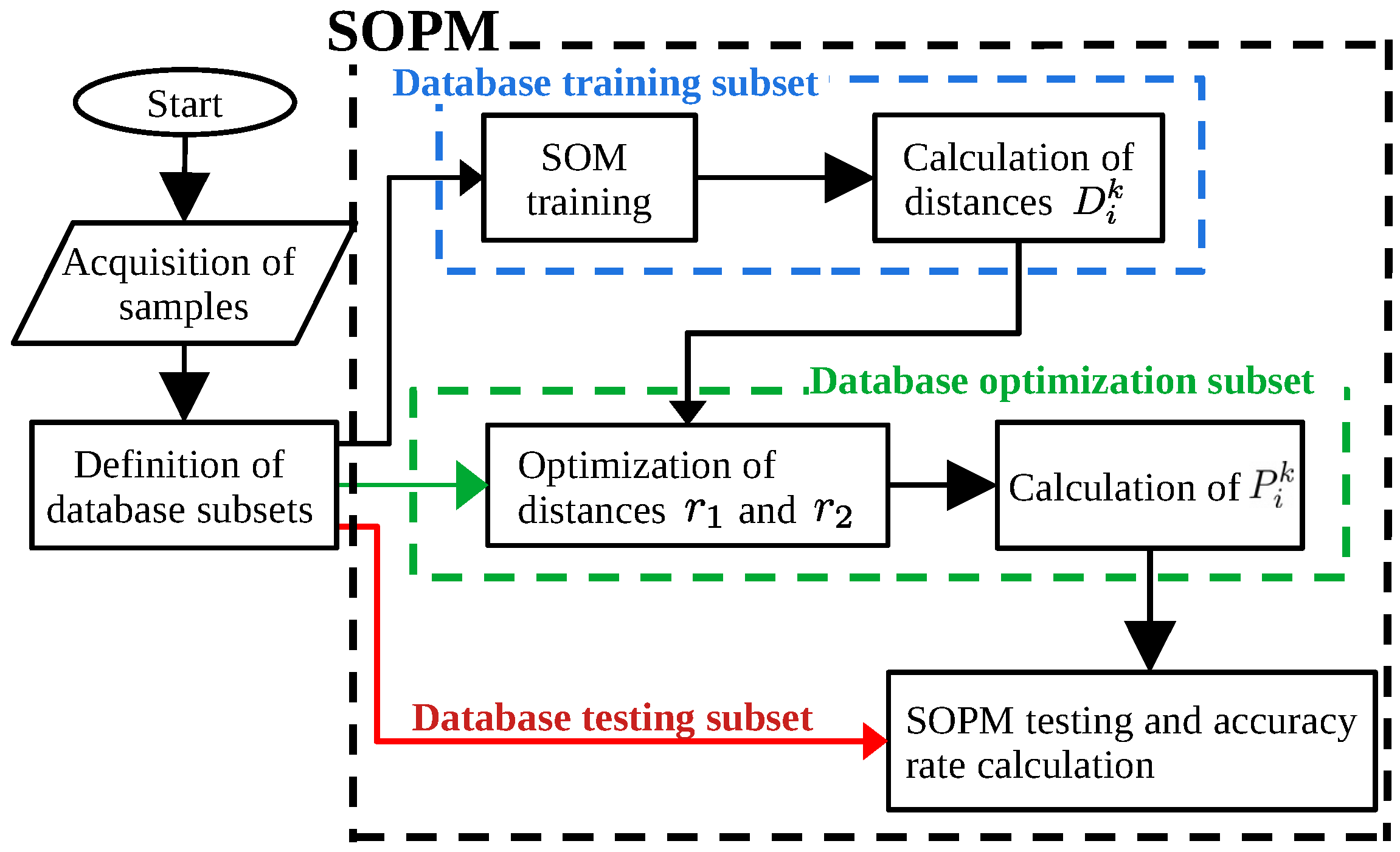
6. The SOPM Algorithm
7. Results and Discussion
7.1. SOM Classification Results
7.2. SOPM Classification Results
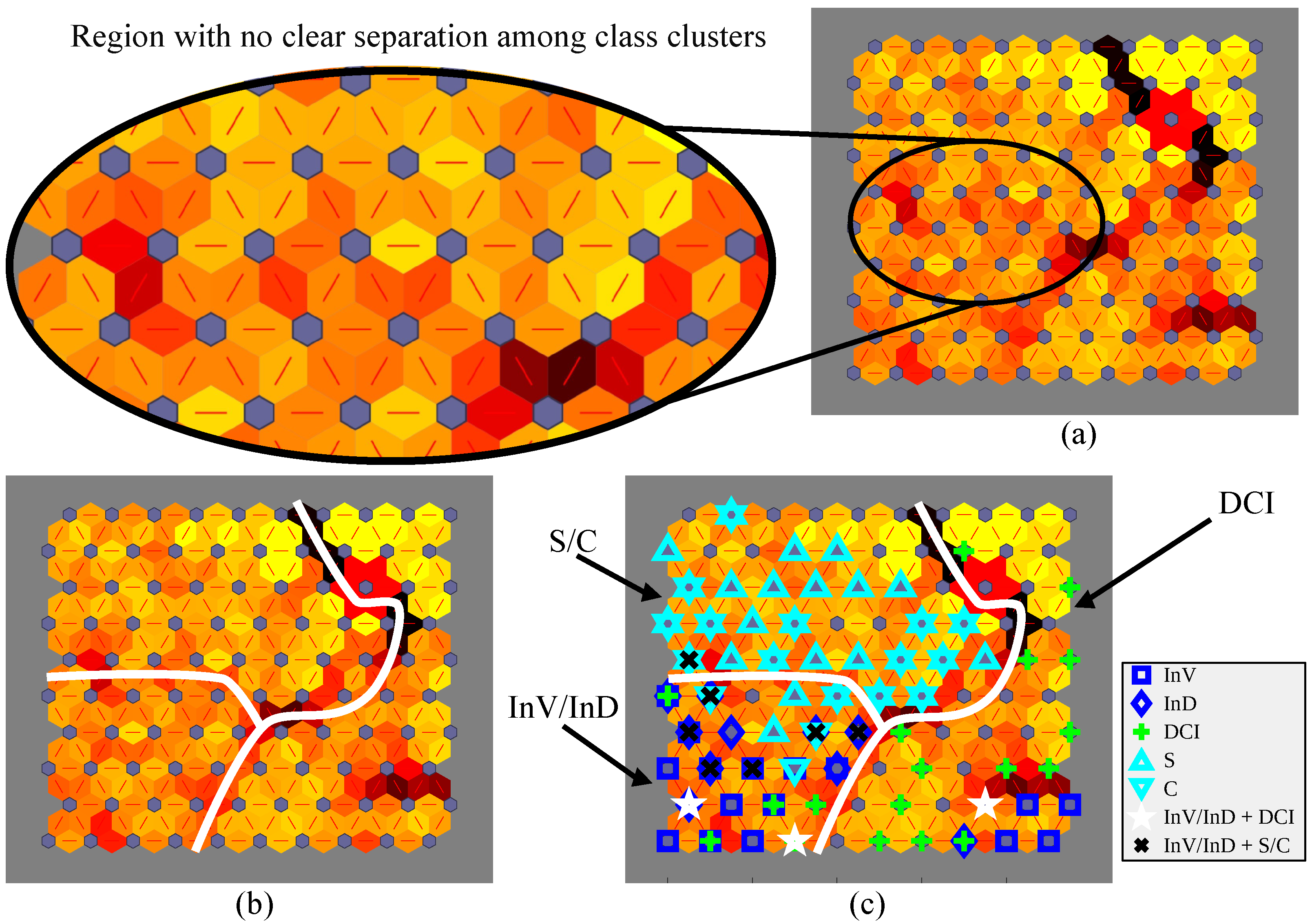
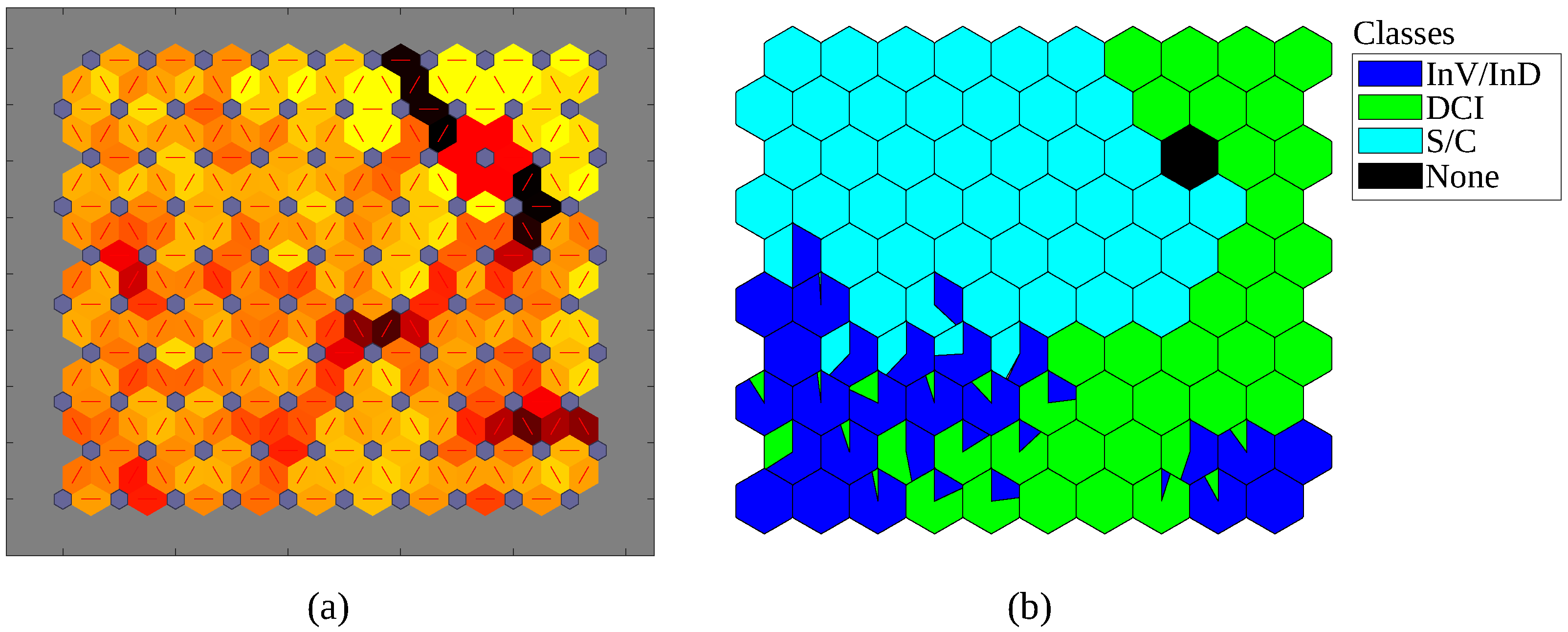
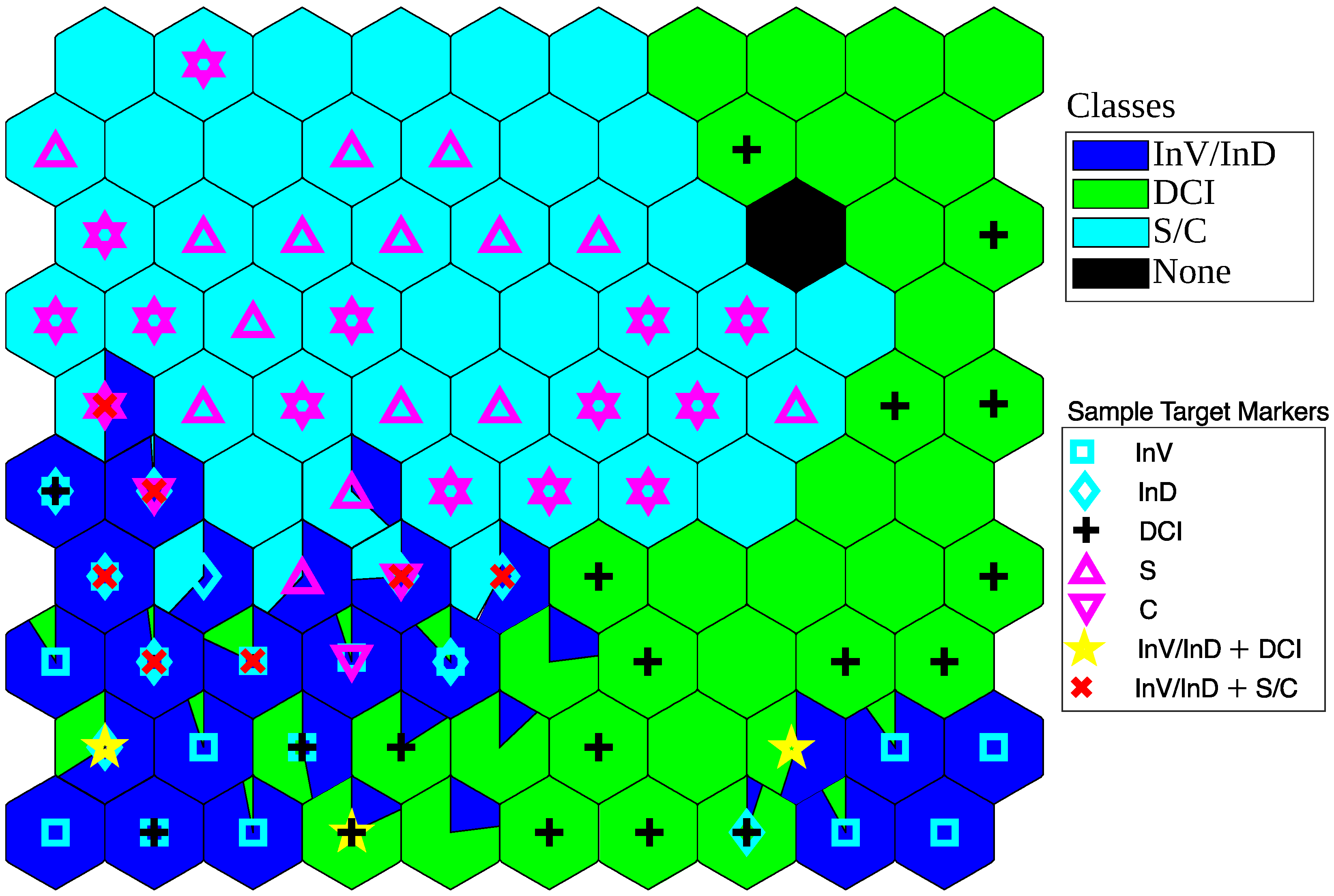
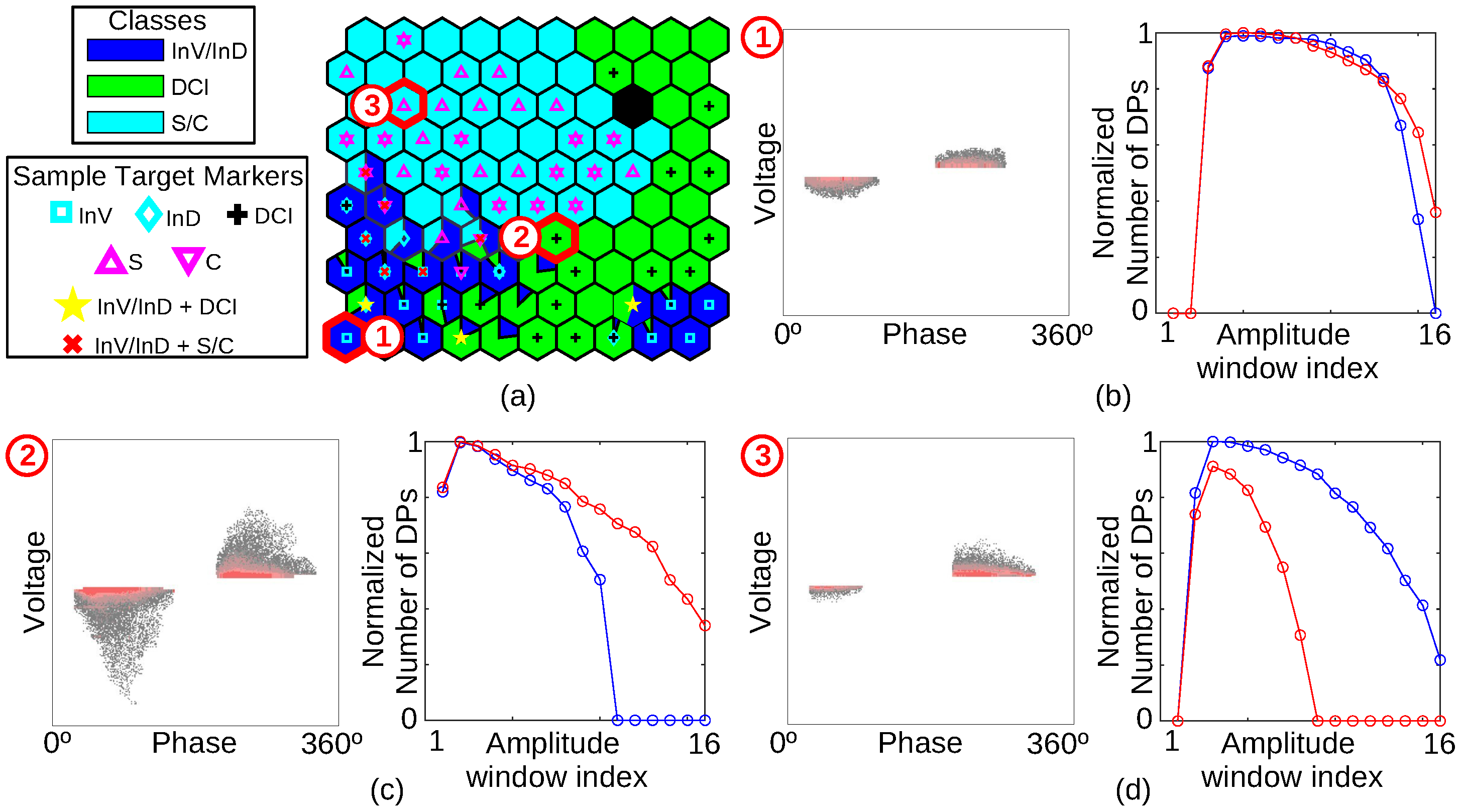
7.3. Discussion on Features of Samples Mapped on SOPM
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEC TS 60034-27:2006; Rotating Electrical Machines—Part 27-2: On-Line Partial Discharge Measurements On The Stator Winding Insulation Of Rotating Electrical Machines. IEC: Geneva, Switzerland, 2006.
- Stone, G.C.; Culbert, I.; Boulter, E.A.; Dhirani, H. Electrical Insulation for Rotating Machines, 2nd ed.; IEEE Press Series on Power Engineering; Wiley-Blackwell: Hoboken, NJ, USA, 2012. [Google Scholar]
- Stone, G.C.; Cavallini, A.; Behrmann, G.; Serafino, C.A. Practical Partial Discharge Measurement on Electrical Equipment; Wiley-IEEE Press: New York, NY, USA, 2023. [Google Scholar]
- Cruz, J.S.; Fruett, F.; Lopes, R.R.; Takaki, F.L.; Tambascia, C.A.; Lima, E.R.; Giesbrecht, M. Partial Discharges Monitoring for Electric Machines Diagnosis: A Review. Energies 2022, 15, 7966. [Google Scholar] [CrossRef]
- Machado, G.d.O.; Gomes, L.C.; da Silveira, A.W.F.V.; Tavares, C.E.; de Andrade, D.A. Impacts of Harmonic Voltage Distortions on the Dynamic Behavior and the PRPD Patterns of Partial Discharges in an Air Cavity Inside a Solid Dielectric Material. Energies 2022, 15, 2650. [Google Scholar] [CrossRef]
- Lalitha, E.; Satish, L. Wavelet analysis for classification of multi-source PD patterns. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 40–47. [Google Scholar] [CrossRef]
- Krivda, A.; Gulski, E. Neural networks as a tool for recognition of partial discharges. In Proceedings of the 1993 International Conference on Partial Discharge, Canterbury, UK, 28–30 September 1993; pp. 84–85. [Google Scholar]
- Araújo, R.C.F.; de Oliveira, R.M.S.; Brasil, F.S.; Barros, F.J.B. Novel Features and PRPD Image Denoising Method for Improved Single-Source Partial Discharges Classification in On-Line Hydro-Generators. Energies 2021, 14, 3267. [Google Scholar] [CrossRef]
- Lopes, F.H.; Zampolo, R.F.; Oliveira, R.M.; Dmitriev, V. Evaluation of transfer learning approaches for partial discharge classification in hydrogenerators. In Proceedings of the 2022 Workshop on Communication Networks and Power Systems (WCNPS), Fortaleza, Brazil, 17–18 November 2022; pp. 1–6. [Google Scholar]
- Pardauil, A.C.N.; Nascimento, T.P.; Siqueira, M.R.S.; Bezerra, U.H.; Oliveira, W.D. Combined Approach Using Clustering-Random Forest to Evaluate Partial Discharge Patterns in Hydro Generators. Energies 2020, 13, 5992. [Google Scholar] [CrossRef]
- Zemouri, R.; Lévesque, M.; Kokoko, O.; Hudon, C. Generative Adversarial Networks used for latent space Optimization: A comparative study for the Classification of Partial Discharge Sources. In Proceedings of the PHM Society European Conference, Prague, Czech Republic, 3–5 July 2021; Volume 6, p. 10. [Google Scholar]
- Zemouri, R.; Lévesque, M. Ensemble Deep-Learning Model for Phase-Resolved Partial Discharge Diagnosis in Hydrogenerators. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 2394–2401. [Google Scholar] [CrossRef]
- Dang, N.Q.; Ho, T.T.; Vo-Nguyen, T.D.; Youn, Y.W.; Choi, H.S.; Kim, Y.H. Supervised Contrastive Learning for Fault Diagnosis Based on Phase-Resolved Partial Discharge in Gas-Insulated Switchgear. Energies 2024, 17, 4. [Google Scholar] [CrossRef]
- Florkowski, M. Classification of Partial Discharge Images Using Deep Convolutional Neural Networks. Energies 2020, 13, 5496. [Google Scholar] [CrossRef]
- Basharan, V.; Siluvairaj, W.I.M.; Velayutham, M.R. Recognition of multiple partial discharge patterns by multi-class support vector machine using fractal image processing technique. IET Sci. Meas. Technol. 2018, 12, 1031–1038. [Google Scholar] [CrossRef]
- Castro Heredia, L.C.; Rodrigo Mor, A. Density-based clustering methods for unsupervised separation of partial discharge sources. Int. J. Electr. Power Energy Syst. 2019, 107, 224–230. [Google Scholar] [CrossRef]
- Hudon, C.; Belec, M. Partial discharge signal interpretation for generator diagnostics. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 297–319. [Google Scholar] [CrossRef]
- Stone, G.C.; Warren, V. Objective methods to interpret partial-discharge data on rotating-machine stator windings. IEEE Trans. Ind. Appl. 2006, 42, 195–200. [Google Scholar] [CrossRef]
- de Oliveira, R.M.S.; Araújo, R.C.F.; Barros, F.J.B.; Segundo, A.P.; Zampolo, R.F.; Fonseca, W.; Dmitriev, V.; Brasil, F.S. A system based on artificial neural networks for automatic classification of hydro-generator stator windings partial discharges. J. Microwaves Optoelectron. Electromagn. Appl. 2017, 16, 628–645. [Google Scholar] [CrossRef]
- Stone, G.C. A perspective on online partial discharge monitoring for assessment of the condition of rotating machine stator winding insulation. IEEE Electr. Insul. Mag. 2012, 28, 8–13. [Google Scholar] [CrossRef]
- Leffler, J.; Trnka, P. Failures of Electrical Machines-Review. In Proceedings of the 2022 8th International Youth Conference on Energy (IYCE), Eger, Hungary, 6–9 July 2022; pp. 1–4. [Google Scholar]
- Raymond, W.J.K.; Illias, H.A.; Mokhlis, H. Partial discharge classifications: Review of recent progress. Measurement 2015, 68, 164–181. [Google Scholar] [CrossRef]
- Luo, Y.; Li, Z.; Wang, H. A review of online partial discharge measurement of large generators. Energies 2017, 10, 1694. [Google Scholar] [CrossRef]
- Araújo, R.C.F.; de Oliveira, R.M.S.; Barros, F.J.B. Automatic PRPD Image Recognition of Multiple Simultaneous Partial Discharge Sources in On-Line Hydro-Generator Stator Bars. Energies 2022, 15, 326. [Google Scholar] [CrossRef]
- Stone, G.C. Partial discharge diagnostics and electrical equipment insulation condition assessment. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 891–904. [Google Scholar] [CrossRef]
- Kohonen, T. Analysis of a simple self-organizing process. Biol. Cybern. 1982, 44, 135–140. [Google Scholar] [CrossRef]
- Haykin, S.O. Neural Networks and Learning Machines, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Vesanto, J. SOM-based data visualization methods. Intell. Data Anal. 1999, 3, 111–126. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps; Springer Science & Business Media: New York, NY, USA, 2012; Volume 30. [Google Scholar]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira, V.Y.M.; de Oliveira, R.M.S.; Affonso, C.M. Cuckoo Search approach enhanced with genetic replacement of abandoned nests applied to optimal allocation of distributed generation units. IET Gener. Transm. Distrib. 2018, 12, 3353–3362. [Google Scholar] [CrossRef]
- Han, Y.; Song, Y. Using improved self-organizing map for partial discharge diagnosis of large turbogenerators. IEEE Trans. Energy Convers. 2003, 18, 392–399. [Google Scholar] [CrossRef]
- Darabad, V.; Vakilian, M.; Blackburn, T.; Phung, B. An efficient PD data mining method for power transformer defect models using SOM technique. Int. J. Electr. Power Energy Syst. 2015, 71, 373–382. [Google Scholar] [CrossRef]






| Papers | Algorithms | Classification Probabilities | Input Features and Metrics |
|---|---|---|---|
| Krivda and Gulski [7] | Kohonen | No | Pulse count and amplitude distributions |
| Araújo et al. [8] | MLP | No | Histograms (Normalized) |
| Lopes et al. [9] | CNN | No | Histograms |
| Pardauil et al. [10] | K-means and RF | No | Histograms |
| Zemouri et al. [11] | GAN | No | 2D PDA |
| Zemouri et al. [12] | Deep Learning | No | Edge Detection Filter, Statistical Features |
| Dang et al. [13] | Supervised contrastive learning (SCL) | No | t-distributed stochastic neighbor embedding (t-SNE) |
| This work | SOPM (novel) | Yes (concurrent PD classification) | Amplitude Histograms, sample-neuron distances in the space of features |
| True Class | Predicted Class | ||
|---|---|---|---|
| Inv/InD | DCI | S/C | |
| Inv/InD | 80.00% | 20.00% | 0.00% |
| DCI | 13.33% | 86.67% | 0.00% |
| S/C | 13.33% | 0.00% | 86.67% |
| True Class | Predicted Class | ||
|---|---|---|---|
| Inv/Ind | DCI | S/C | |
| Inv/Ind | 92.59% | 7.41% | 0.00% |
| DCI | 53.85% | 46.15% | 0.00% |
| S/C | 14.17% | 0.00% | 85.83% |
| True Class | Predicted Class | ||
|---|---|---|---|
| Inv/InD | DCI | S/C | |
| Inv/InD | 97.00% | 2.93% | 0.07% |
| DCI | 2.60% | 97.40% | 0.00% |
| S/C | 0.00% | 0.00% | 100% |
| True Class | Predicted Class | ||
|---|---|---|---|
| Inv/InD | DCI | S/C | |
| Inv/InD | 93.50% | 4.11% | 2.39% |
| DCI | 2.17% | 97.83% | 0.00% |
| S/C | 0.00% | 0.00% | 100% |
| True Class | Predicted Class | ||||
|---|---|---|---|---|---|
| Inv/InD | DCI | S/C | Inv/InD + DCI | Inv/InD + S/C | |
| Inv/InD | 86.75% | 8.88% | 4.37% | 0.00% | 0.00% |
| DCI | 24.23% | 75.77% | 0.00% | 0.00% | 0.00% |
| S/C | 6.84% | 0.00% | 91.37% | 1.79% | 0.00% |
| Inv/InD + DCI | 0.00% | 0.00% | 0.00% | 100% | 0.00% |
| Inv/InD + S/C | 0.00% | 3.44% | 9.69% | 0.00% | 86.87% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Oliveira, R.M.S.; Fernandes, F.C.; Barros, F.J.B. Novel Self-Organizing Probability Maps Applied to Classification of Concurrent Partial Discharges from Online Hydro-Generators. Energies 2024, 17, 2208. https://doi.org/10.3390/en17092208
de Oliveira RMS, Fernandes FC, Barros FJB. Novel Self-Organizing Probability Maps Applied to Classification of Concurrent Partial Discharges from Online Hydro-Generators. Energies. 2024; 17(9):2208. https://doi.org/10.3390/en17092208
Chicago/Turabian Stylede Oliveira, Rodrigo M. S., Filipe C. Fernandes, and Fabrício J. B. Barros. 2024. "Novel Self-Organizing Probability Maps Applied to Classification of Concurrent Partial Discharges from Online Hydro-Generators" Energies 17, no. 9: 2208. https://doi.org/10.3390/en17092208
APA Stylede Oliveira, R. M. S., Fernandes, F. C., & Barros, F. J. B. (2024). Novel Self-Organizing Probability Maps Applied to Classification of Concurrent Partial Discharges from Online Hydro-Generators. Energies, 17(9), 2208. https://doi.org/10.3390/en17092208






