Abstract
Recent increases in gas-fired power generation have engendered increased interdependencies between natural gas and power transmission systems. These interdependencies have amplified existing vulnerabilities in gas and power grids, where disruptions can require the curtailment of load in one or both systems. Although typically operated independently, coordination of these systems during severe disruptions can allow for targeted delivery to lifeline services, including gas delivery for residential heating and power delivery for critical facilities. To address the challenge of estimating maximum joint network capacities under such disruptions, we consider the task of determining feasible steady-state operating points for severely damaged systems while ensuring the maximal delivery of gas and power loads simultaneously, represented mathematically as the nonconvex joint Maximal Load Delivery (MLD) problem. To increase its tractability, we present a mixed-integer convex relaxation of the MLD problem. Then, to demonstrate the relaxation’s effectiveness in determining bounds on network capacities, exact and relaxed MLD formulations are compared across various multi-contingency scenarios on nine joint networks ranging in size from 25 to 1191 nodes. The relaxation-based methodology is observed to accurately and efficiently estimate the impacts of severe joint network disruptions, often converging to the relaxed MLD problem’s globally optimal solution within ten seconds.
1. Introduction
Between 2022 and 2050, global electric power generation capacity is projected to increase from million gigawatt hours (GWh) to million GWh. Of this, natural gas-fired generation is projected to increase from to million GWh [1]. These projections suggest the continued sensitivity of power systems to upstream disruptions in gas pipelines. At a high level, Figure 1 illustrates the gas-fired generation interdependencies that link natural gas pipelines and power transmission networks. Additionally, Figure 2 illustrates interstate and intrastate natural gas pipelines in the contiguous United States [2], exemplifying the reach of these pipelines and their potential grid interdependencies.
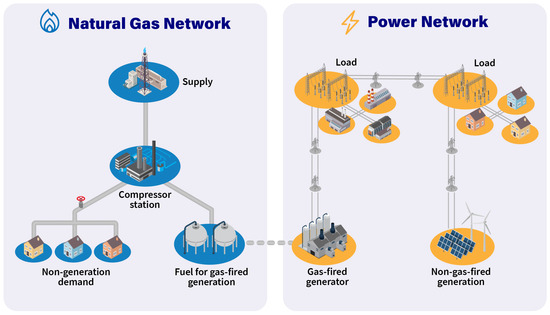
Figure 1.
Illustration of a highly simplified natural gas pipeline network, power transmission network, and a gas-fired generation interdependency that links the two networks together.
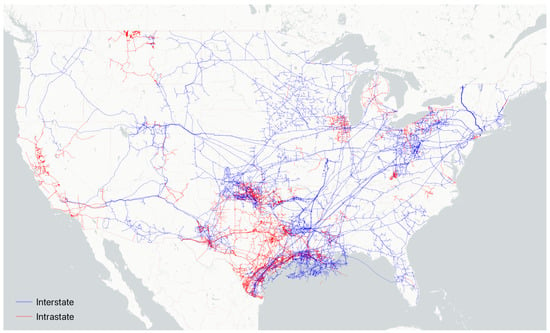
Figure 2.
Interstate and intrastate natural gas pipelines in the contiguous United States [2].
One notable example of this interdependency is the February 2021 Texas power crisis, where the Electric Reliability Council of Texas suffered a loss of nearly GW () of its generation capacity. Around half of this loss was associated with a lack of gas-fired power generation [3]. Other examples include the 2014 polar vortex, where curtailments in gas delivery resulted in nearly of generation outages throughout the Pennsylvania-New Jersey-Maryland Interconnection [4]. Disruptions in the gas grid can additionally inhibit the transport of fuel required for residential heating. This highlights an important tradeoff between gas delivery and power delivery during network disruptions. Understanding these interdependencies is critical for the resilience of gas and power delivery systems.
In Figure 3, we illustrate a simplified natural gas pipeline system and the potential effects of disruptions on downstream consumers. Here, fuel from various sources on the left is transported through the pipeline system to ultimately reach three types of consumers: (i) a gas-fired generator, (ii) an industrial consumer, and (iii) a distribution system that transports fuel for residential heating. Hypothetical disruptions appear in the form of (i) a natural hazard that disrupts extraction from a natural gas well and (ii) a man-made disruption on a pipeline that serves the industrial consumer. These disruptions nonlinearly affect the delivery of fuel to gas-fired generators in the power system and residential heating units.
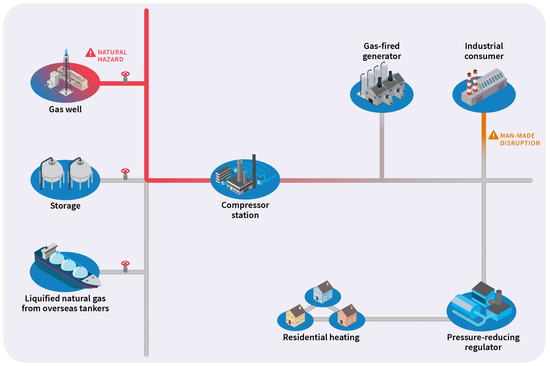
Figure 3.
Illustration of a hypothetical simplified natural gas pipeline system experiencing a natural hazard and man-made disruption, both of which ultimately inhibit the delivery of fuel to consumers.
The contingency response measures considered in this paper are illustrated in Figure 4. Given a severe disruption, (i) gas and/or power load deliveries decrease as gas and/or power network elements are impaired and effects begin to cascade, while existing linepack in operational pipelines begins to deplete. By (ii), cascading effects have subsided, and a new stable operating point is realized. After (ii), load can gradually be restored via operational methods until (iii) network repairs begin. These restorative actions are performed until (iv) all gas and power loads can be delivered. Repairs continue until (v) all gas and power network components are operational. This paper focuses on estimating the transport capacity of a joint gas–power system between events of types (ii) and (iv), i.e., maximizing gas and power load delivery in the surviving gas–power system. In this paper, this task is formalized as the steady-state joint Maximal Load Delivery (MLD) problem. The problem is informally stated as follows: Given severely damaged gas and power networks, in which multiple components have become nonoperational, maximize the amounts of prioritized gas and active power loads that can be served simultaneously in the damaged joint network, subject to steady-state natural gas and alternating current (AC) power network physics. The nonconvex physics and discrete nature of operations in the joint network (e.g., the opening and closing of valves in the gas network) render this a challenging mixed-integer nonlinear program (MINLP). For the purpose of providing real-time situational awareness during disruptive events, this MINLP is unsuitable due to its intractability. Thus, to increase analytical tractability, we develop a mixed-integer convex programming (MICP) relaxation of the MLD. The MICP is found to be an effective means for bounding maximum total deliverable gas and power loads.
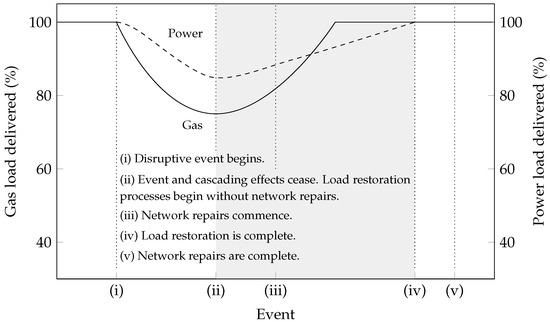
Figure 4.
Illustration of gas and power network responses to a hypothetical disruption. The shaded region comprises points in the disruption and restoration timeline that are studied in this paper using an optimization-based assessment of damaged network capacities.
This paper expands upon existing MLD methods for independent gas [5] and power networks [6], as well as approaches from joint network modeling [7], to formulate and solve the gas–power MLD problem. The contributions of this work are as follows:
- The first formulation of the joint gas–power MLD problem;
- An efficient and accurate MICP relaxation of the MLD problem;
- Proof-of-concept analyses of MLD gas–power tradeoffs.
The remainder of this paper proceeds as follows. Section 2 reviews gas, power, and joint steady-state optimization models that appear in the literature and then formulates the requirements for AC power and gas pipeline operational feasibility as an MINLP; Section 3 formulates the MLD problem as an MINLP and then proposes an MICP relaxation; Section 4 benchmarks the MINLP and MICP formulations across multiple joint gas–power networks of various sizes and then provides proofs of concept for joint multi-contingency analysis using the MLD method; and Section 5 concludes this paper.
2. Background for Network Modeling
The past decade has seen remarkable theoretical and algorithmic advances in the independent fields of power and natural gas network optimization. A survey of relaxations and approximations used in power system optimization was presented in [8]. The study of power most related to this paper can be found in [6], where the AC MLD problem was introduced and various relaxations were proposed to increase its tractability. The MLD problem was also used in [9], where it was applied within a bilevel optimization for balancing wildfire risk and power outages. Finally, an implementation of the power MLD problem was given in [10], in which software was provided via the PowerModelsRestoration package.
As with power, the growing utilization of gas networks has led to a variety of optimization studies. A summary of works related to the optimization-based assessment of gas network capacities was provided in [11]. Steady-state models and approximations of gas network components amenable to optimization applications were provided in [12]. A growing body of literature has been motivated by proposed projects to blend hydrogen produced by excess renewables into existing pipelines. Simulation and optimization modeling studies [13,14,15], as well as reviews of technical and regulatory challenges [16,17], have investigated the feasibility of such projects. However, the study of gas most related to this paper can be found in [5], in which the steady-state gas MLD problem and an MICP relaxation were developed.
An even more recent body of literature has examined the optimal coordination of gas and power infrastructures. A review of joint gas and power planning was given in [18]. Other studies have focused on market coordination and energy pricing problems [19,20]. Many studies have assumed the networks to be fully coordinated, examining the optimal scheduling of generator dispatching and gas compressor operations [21]. Recent studies have expanded upon these earlier joint “optimal gas–power flow” problems, developing specialized formulations and algorithms for related applications [22,23,24].
Compared to prior studies like Jiang et al. [23], our work differs in a few important aspects. For example, Jiang et al. [23] focused on a single-objective problem that minimizes the economic cost of operating the joint system, whereas we devise a multi-objective problem that maximizes the simultaneous delivery of gas and power. Furthermore, Jiang et al. [23] posed a time-discretized scheduling problem and developed a specialized algorithm, whereas we consider a single-period problem and develop new convex relaxations to render it more tractable. Lastly, Jiang et al. [23] assessed their methods on one small joint network, whereas we design nine joint networks of various sizes to evaluate our methods.
Most importantly, the applications of studies like Jiang et al. [23] and our work are fundamentally different. The goal of Jiang et al. [23] was the economic scheduling of a joint system under nominal conditions, but our work aims to estimate joint network capacities under severe disruptions. The latter requires modeling considerations that are different from those of the former, such as the use of additional continuous and discrete variables to ensure feasibility with respect to physical constraints, as well as multiple objectives to model the tradeoff between maximizing natural gas delivery and power delivery.
A smaller number of studies have considered joint problems related to restoration, e.g., the scheduling of general large-scale interdependent infrastructures in [25]. The remaining subsections build upon previous studies to define the requirements for modeling the steady-state operations of a damaged joint gas–power network.
2.1. Power Transmission Network Modeling
2.1.1. Notations for Sets
A power network is represented by an arbitrarily directed graph , where is the set of buses, is the set of forward-directed branches (or lines), and is the set of branches in their reverse orientation. The sets of generators (producers), loads (consumers), and shunts are denoted by , , and , respectively, which are attached to existing buses . The subsets of these components attached to are denoted by , , and . Next, we define the decision variables and constraints required to model a damaged AC power network’s steady-state operations.
2.1.2. Power Network Modeling Requirements
The MINLP formulation for AC power network feasibility, as defined for AC MLD analysis, is presented in Constraints (1a)–(1i) and detailed in [6]. Here, Constraints (1a) and (1b) model Ohm’s law for lines, where denotes the variable power along each line; and are constants denoting the line admittance and line charging; denotes the variable voltage at bus ; and denotes constant transformer properties. Constraint (1c) models power balance from Kirchhoff’s current law for each bus, where denotes the variable power supplied by generator ; denotes the maximum power that can be delivered at load ; and denotes the admittance of bus shunt . Note that , allows each load to vary between zero and its predefined maximum, and allows for continuous shedding of fixed bus shunts from the network. These modeling modifications ensure that power balance constraints will be satisfied in damaged power networks.
Constraints (1d)–(1i) impose engineering limits. Constraint (1d) bounds the apparent power flow on each line, representing thermal limits. Constraint (1e) ensures that each voltage phase angle difference is limited by predefined lower and upper bounds, and , respectively. Constraint (1f) bounds the voltage magnitude at each bus, where and denote lower and upper bounds, respectively. Here, is a variable allowing each bus to become de-energized when isolated from load or generation. Similarly, Constraint (1g) bounds the power generation, where and denote lower and upper bounds, respectively, and allows for each generator to become uncommitted when required to satisfy Constraints (1a) and (1b).
Much of the justification for this model is provided in [6]. As in that study, in our work, we estimate the maximum amount of deliverable load after a damage scenario has occurred. Because we are interested only in the longer-horizon steady-state transport capacity, we forgo modeling transient dynamics that may occur immediately after event (i) in Figure 4. Additionally, to limit the scope of this study, we forgo time-discretized dynamic restoration or economic scheduling of the damaged system. Nonetheless, the presented model could serve as a valuable building block for future multiperiod restoration problems.
2.2. Natural Gas Transmission Network Modeling
2.2.1. Notations for Sets
A gas pipeline network is modeled using a directed graph , where is the set of nodes (i.e., junctions) and is the set of components that connect two nodes. The sets of receipts (producers) and deliveries (consumers) are denoted by and , respectively. These components are considered to be attached to junctions . The subset of receipts attached to is denoted by , and the subset of deliveries is denoted by . The sets of horizontal and short pipes are denoted by and , respectively; the set of resistors is denoted by ; the sets of valves and pressure-reducing regulators are denoted by and , respectively; and the set of compressors is denoted by . Additionally, the set of node-connecting components incident to , where i is the tail (respectively, head) of the arc, is denoted by (respectively, ). Next, we define the decision variables and constraints required to model the engineering limits and physics of a damaged gas network’s steady-state operations.
2.2.2. Gas Network Modeling Requirements
The MINLP formulation for gas network feasibility, as defined for MLD analysis, is presented in Constraints (2a)–(2v) and detailed in [5]. Constraint (2a) models nodal physics, i.e., mass conservation at junctions . Here, denotes the variable mass flow along each node-connecting component, denotes the variable supply at receipt , and denotes the variable demand at delivery .
Constraints (2b)–(2u) model the physics of the node-connecting components. Constraint (2b) models the pressure–flow relationship for steady-state flow in a gas pipeline for each horizontal pipe, . Here, denotes the variable pressure at junction , and denotes the constant mass flow resistance of the pipe. This constraint is the most frequent source of nonconvex nonlinearity in modeling the gas pipeline network.
Constraint (2c) models short pipes in the network, which provide resistanceless mass transport between two junctions. Constraint (2d) models resistors in the network, which act as surrogate components capable of modeling pressure losses elsewhere from pipes. Here, pressure loss is modeled according to the Darcy–Weisbach equation, where is the resistance, which is a function of the resistor’s drag factor and (possibly artificial) diameter. Like Constraint (2b), this constraint is nonconvex nonlinear.
Constraints (2e)–(2g) model controllable valves in the network. Here, the operating status of each valve, , is modeled using a discrete variable, , where indicates an open valve and indicates a closed valve. Constraint (2e) prohibits flow across each valve when . Constraints (2f) and (2g) ensure that when a valve is open, the pressures at connecting junctions are equal. These constraints also disjunctively model the decoupling of junction pressures when the valve is closed.
Constraints (2h)–(2k) model regulators (i.e., pressure-reducing valves) in the network. Similar to valves, the status of each regulator is modeled using a discrete variable, , where and indicate active and inactive statuses, respectively. Constraint (2h) prohibits mass flow across each regulator when . Constraint (2i) ensures that mass flow across each regulator is in the same direction as the loss in pressure. Constraints (2j) and (2k) model the remaining pressure relationships. Here, each regulator has a corresponding scaling factor, . This factor models the relationship between junction pressures when the regulator is active, i.e., . The factor is further limited by the bounds . Constraints (2j) and (2k) require that when a regulator is active, pressures are defined according to the scaling relationship. Otherwise, the pressures at the junctions connected by the regulator are decoupled from one another.
Constraints (2l)–(2s) model compressors in the network. Each compressor models an increase in pressure at junction by a variable scalar . Without loss of generality, bidirectional compression is not considered, although each compressor may allow for uncompressed flow in the opposite direction. These different behaviors of compressors are modeled by employing three different sets of constraints. The first is Constraint (2l) for compressors that prohibit reverse flow, where and are minimum and maximum pressure ratios. The second set includes Constraints (2m) and (2n) for compressors where reverse flow is allowed and . Note that here, if , then . Finally, Constraints (2o)–(2s) model compressors where uncompressed reverse flow is allowed and . In this case, the behavior of each compressor is disjunctive in its flow direction. To model this disjunction, discrete variables are introduced in Constraint (2o) to model the direction of flow through each compressor. Here, indicates that flow is transported from i to j, and indicates flow from j to i. Constraints (2p)–(2s) model the pressures and pressure differences between junctions per the specified flow direction and compression ratio bounds.
The remaining Constraints (2t)–(2v) define variable bounds. Constraint (2t) specifies mass flow bounds, Constraint (2u) specifies pressure bounds, and Constraint (2v) specifies receipt and delivery bounds. Note that Constraint (2v) differs from the typical assumption of fixed supply and demand. These modifications ensure mass conservation is satisfied in damaged networks.
Finally, we remark that, unlike power systems where physical phenomena evolve on time scales of seconds or less, it can require minutes to hours for the effects of a disruption to propagate through a natural gas system. This suggests that a transient model of gas flow is required to appropriately model maximum load delivery in natural gas systems. However, we emphasize that the MLD described in this paper determines the best-case, sustainable capacity of a damaged joint network, and, as is common in many pipeline planning applications, is computable from steady injections and withdrawals [26]. Additional justification for this modeling choice, as well as a derivation of the steady-state equations from transient partial differential equations, appears in Section 2.1 of [5].
Nonetheless, generalization to the transient regime would be useful for applications requiring greater spatiotemporal accuracy. The modeling of transient flow through natural gas pipelines is well established and has recently been considered in optimal control contexts [27,28]. Because transient models are computationally intensive even in a simulation setting, reduced-order models have been developed [29] and applied within optimal control contexts [30]. In [31], a framework for integrated gas and power uncertainty management was introduced that stressed the importance of modeling transient intraday dynamics, showing promise on a robust scheduling problem. Extending our methods to the transient regime would likely require (i) reframing the MLD in a multiperiod setting, leveraging these recent advances, and (ii) developing new convex reduced-order models of the gas dynamics to ensure our methods scale to large networks. We leave these extensions to future work.
2.3. Interdependency Modeling
As in [19,32], gas and power systems are interconnected via heat rate curve models for gas-fired power generators, i.e.,
Each constraint links the real power generated at possibly multiple generators with a single gas delivery. Here, are coefficients of the heat rate curve for , and is the set of linkages between gas-fired generators in and their corresponding gas delivery points in . Furthermore, for all , and thus the left-hand side is always a convex function. However, note that Constraint (3) is nonlinear nonconvex when . Finally, the presence of ensures that when , the intercept of the heat rate curve, and thus both the generation and gas required for generation, will be zero when a generator is uncommitted from the dispatch scenario.
A diagrammatic illustration of the joint network model is illustrated in Figure 5. Here, gas and power systems are linked by the single interdependency , which relates the delivery to the generator . Contributions to the gas and power delivery objectives, which are later described in Section 3.1, are represented by green and red nodes, respectively.
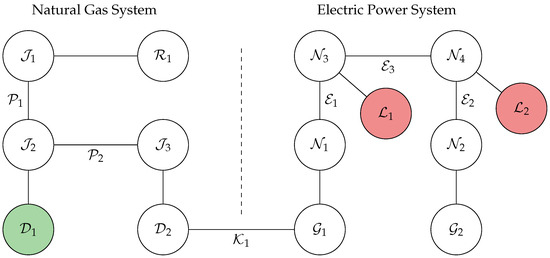
Figure 5.
Diagrammatic representation of a small, hypothetical joint gas–power network. Here, contributes to the objective term , and and contribute to . Contributions to the gas and power delivery objectives are represented by green and red nodes, respectively. The linkage between gas and power systems occurs at the interdependency .
2.4. Challenges
Although independent gas and power MLD models were explored in [5,6], respectively, the joint MLD problem that includes Constraints (1a)–(1i), (2a)–(2v), and (3) is more challenging. Most importantly, the nonlinearities that appear in gas and power network constraints arise primarily from different sources: Constraints (1a)–(1i) include nonlinear equations with bilinear variable products, whereas Constraints (2a)–(2v) include more manageable quadratic nonlinear equations. These modeling differences suggest potentially incompatible numerical methods and solving technologies.
3. Maximal Load Delivery Formulations
This section derives the joint gas–power MLD formulations used throughout the remainder of this paper. First, Section 3.1 defines the competing objectives of the joint MLD problem. Section 3.2 poses lexicographic and weighted MLD formulations that prioritize the gas–power delivery tradeoff in different ways. Section 3.3 derives MICP relaxations of the MINLP MLD formulations. Finally, Section 3.4 summarizes the naming conventions used for these MLD formulations, which are empirically compared in Section 4.
3.1. Objectives of the Maximum Load Delivery Problem
The objective of the MLD problem is to maximize the amount of nongeneration gas and active power load delivered simultaneously under a multi-contingency scenario. Note that the maximization of nongeneration gas, specifically, allows the model to decouple the practical objectives of the gas system (e.g., the delivery of fuel for residential heating) from practical objectives of the power system. However, because the delivery of the nongeneration gas load can inhibit the amount of active power generation and thus the total active power delivered, there exists an important tradeoff between these two objectives. For notational ease, we first write the two objective functions as
Equation (4a) denotes the normalized sum of all prioritized nongeneration gas demands, where (i.e., the set of all nongeneration gas deliveries), and is a predefined restoration priority for delivery . Similarly, Equation (4b) denotes the normalized sum of all prioritized active power loads. Note that for all of the experiments considered in this study, for simplicity, we set for all .
The tradeoff between nongeneration gas and active power load naturally lends the MLD problem to the broader category of multi-objective optimization. A thorough survey of multi-objective optimization methods in engineering was presented in [33], which described a number of techniques for specifying preferences among multiple objective functions. These include weighted sum, lexicographic, and bounded objective optimization methods. In Section 3.2, we define lexicographic and weighted sum variants of the MLD problem.
3.2. Lexicographic and Weighted MLD Formulations
To explore the gas–power tradeoff, we introduce three MLD models that prioritize gas and power delivery in different ways. The first is a lexicographic formulation that maximizes the amount of nongeneration gas load delivered first. This situation is representative of common contractual requirements for gas grid operators. Here, the MLD is written as the mathematical program
where is the optimal objective when maximizing gas delivery alone. The second MLD is a similar formulation that maximizes the amount of active power load delivered first. This mathematical program is written as
The last model is a single-level formulation that parametrically weights the normalized sums of nongeneration gas and active power delivery, i.e.,
where is a weighting parameter that models the objective tradeoff.
Note that (5), (6), and (7) are mixed-integer nonlinear nonconvex programs. The nonconvexities arise from three sources: (i) discrete operations of controllable components (e.g., for generator commitment); (ii) bilinear products that appear in gas and power network physics (e.g., in Ohm’s law); and (iii) nonlinear equations that model physical relations (e.g., pressure-flow equations for pipes). In the following sections, we employ a number of relaxations to render these problems more tractable.
3.3. Relaxation of Bilinear Products and Nonlinear Equations
3.3.1. Convexification of Power Physics
The primary sources of nonconvexity in Constraints (1a)–(1i) are bilinear products that appear in Constraints (1a)–(1c) (e.g., ). A wealth of literature has developed relaxations for similar terms. For a comprehensive review, we refer the reader to [8]. In this paper, we develop a model using a second-order cone (SOC) relaxation of the AC power flow equations, first presented in [34] and used for power MLD analysis in [6].
The primary insight of the SOC formulation is that variable products ( and ) can be lifted into a higher-dimensional variable space ( and , respectively). This renders terms involving these products linear, and the relaxation in the new W-space is ultimately strengthened via
This is a convex SOC constraint, which lends the formulation its name.
3.3.2. Convexification of Gas Physics
Many nonconvexities in Constraints (2a)–(2v) appear in the form of nonlinear equations (e.g., Constraint (2b)) and bilinear variable products (e.g., Constraint (2i)). To resolve both, direction variables are introduced for each node-connecting component . We also introduce variables to denote squared pressures for . This first enables a partial linearization of the pressure-flow equations, i.e.,
Then, variables for are introduced to model the difference in squared pressures across each pipe. The introduction of y, , and ℓ, as well as convexly relaxing the equality in Constraint (9), gives rise to the relaxation
Note that Constraint (10d) defines the primary physical relaxations. This constraint states that pressure-flow equations need not be satisfied with equality.
Convexification of the remaining nonlinear nonconvex terms in Constraints (2a)–(2v) is accomplished in a similar manner to the above. Here, for brevity, we omit the derivation of the full mixed-integer convex relaxation used throughout the remainder of this study. However, for a complete derivation and description of the relaxed mixed-integer convex model, we refer the reader to [5].
3.3.3. Convexification of Gas-Fired Generation
3.4. Summary of Formulations
The remainder of this paper compares two MLD formulations of (5), (6), and (7), which model physics differently:
These formulations provide different tradeoffs between model accuracy and computational performance. An evaluation of both allows us to quantify the effects of the relaxations, as well as guide our subsequent MLD analyses.
4. Computational Evaluation
In the following, Section 4.1 describes the networks, computational resources, and parameters used throughout the experiments; Section 4.2 compares the efficacy of exact and relaxed MLD formulations across randomized multi-contingency scenarios; Section 4.3 evaluates the runtime performance of formulations over the same experimental sets; Section 4.4 provides a proof-of-concept MLD analysis, illustrating the tradeoffs when lexicographically maximizing gas and power load delivery; and Section 4.5 provides a proof-of-concept Pareto analysis of load delivery on a single joint network.
4.1. Benchmark Datasets and Experimental Setup
The computational experiments in this paper consider gas and power networks of various sizes that have appeared in the literature or have been derived by subject matter experts. These networks are summarized in Table 1. The networks in this table are named according to the number of junctions in the natural gas network (e.g., NG11) and the number of buses in the electric power network (e.g., EP14). The references from which the gas, power, and/or joint network properties were derived appear in the second column of this table. The numbers of gas and power system components of the joint networks vary substantially and are specified in the third column on in Table 1. For networks that reference [35], heavily loaded variants of the corresponding electric power network datasets are used.

Table 1.
Summary of joint network datasets used in this study.
Joint gas–power network properties are summarized in the last column of Table 1. Here, NG25-EP14 uses the linking and heat rate properties of the joint network instance developed by [38], and NG146-EP36 uses the properties of the instance developed by [32]. Linkages within the NG247-EP240 network were derived from open data, and heat rate curves were estimated in a manner similar to [32]. The remaining networks combine instances from GasLib and PGLib-OPF to create new joint networks of various sizes. The purpose of these new instances is twofold: (i) to explore the tractability of joint MLD instances as network sizes grow and (ii) to explore the tradeoffs involved in maximizing gas versus power delivery. Note that these networks use synthetically generated linkages between GasLib and PGLib-OPF instances, and these linkages are not necessarily reflective of real-world datasets. They are, however, instances where gas and power interdependencies are consequential, which, in turn, allows for a meaningful exploration of the MLD method.
All of the MLD formulations considered in this paper were implemented in the Julia programming language using the mathematical modeling layer JuMP, version 0.21 [40]; version 0.9 of GasModels (https://github.com/lanl-ansi/GasModels.jl accessed on 21 April 2024), a package for steady-state and transient natural gas network optimization; version 0.6 of PowerModelsRestoration, a package that implements the steady-state power MLD model [10]; and version 0.4 of GasPowerModels (https://github.com/lanl-ansi/GasPowerModels.jl, accessed on 21 April 2024), a package for joint steady-state gas–power network optimization. Our multi-infrastructure software modeling approach using InfrastructureModels is detailed in [7], which also includes MLD examples from this work. For the exact nonconvex nonlinear representation of Constraints (1a)–(1i) in Problems (5), (6), and (7), the polar form of the AC power flow equations introduced in [41] was used. For the exact representation of Constraints (2a)–(2v), the mixed-integer nonlinear nonconvex formulation described in [5] was used.
Each optimization experiment was prescribed a wall-clock time limit of one hour on a node containing two Intel Xeon E5-2695 v4 processors, each with 18 cores at 2.10 GHz and 125 GB of memory. For solutions of (7), version 0.7 of the open-source Juniper MINLP solver was used [42]. Within Juniper, Ipopt 3.12 was leveraged as the nonlinear programming solver [43], using a feasibility tolerance of and the underlying linear system solver MA57 [44]. Note that Juniper does not provide global optimality guarantees for (7), and feasible solutions obtained from the solver thus serve only as lower bounds on the true amount of maximum deliverable load. For solutions of (5)-R, (6)-R, and (7)-R, Gurobi 9.1 was used with its default parameterization. Here, since each problem is a mixed-integer convex program, globally optimal solutions to the problem are obtained. However, since each problem is a relaxation, a globally optimal solution corresponds only to an upper bound on the objective of (5), (6), or (7).
4.2. Multi-Contingency Damage Scenarios
This section examines the robustness and accuracy of the exact and relaxed weighted MLD formulations, (7) and (7)-R, respectively, with . Specifically, it studies these properties across large sets of randomized multi-contingency or scenarios, where k indicates the number of components simultaneously removed from the joint gas–power network. These scenarios are intended to capture the effects of severe multimodal network outages across joint systems. In each scenario, a random selection of node-connecting components was assumed to be damaged (i.e., ). Through a parameter sensitivity study, we observed that this proportion of outages appeared to generate challenging MLD scenarios while providing interesting gas and power delivery tradeoffs among the coupled networks. For each network, one thousand such scenarios were generated.
Table 2 compares statistics of solver termination statuses across all scenarios for each network and formulation. Here, “Conv.” corresponds to the percentage of cases where the solver converged, “Lim.” to cases where the solver time or other solver limit was reached, and “Inf.” to cases that were (possibly incorrectly) classified as infeasible by the solver. Although both formulations were typically capable of converging for cases containing tens of nodes, for larger networks, (7)-R clearly outperformed (7), solving nearly all instances. The results are especially dramatic for the three largest networks, where only one of three thousand (7) cases converged but all (7)-R cases converged.

Table 2.
Comparison of solver termination statuses across multi-contingency scenarios.
Note that three (7)-R cases were classified as infeasible due to numerical difficulties. It is likely that (i) using a different MICP solver, (ii) using a newer version of Gurobi, or (iii) adjusting the Gurobi solver parameters (e.g., setting NumericFocus=3), as recommended in the solver output, would resolve these alleged infeasibilities. We also remark that many more (7) cases were classified as infeasible due to the MINLP formulation and solver’s greater tendency to converge to locally infeasible points.
While Table 2 demonstrated the numerical reliability of exact and relaxed MLD formulations, Table 3 compares the solution quality of the relaxed formulations with feasible lower bounds obtained from (7). Here, “# Compared” corresponds to the number of cases used in each comparison, “Mean Obj.” is the mean objective value obtained by (7) over all compared instances, “Mean” is the mean relative gap between objective values of (7) and (7)-R, and “Median” is the median relative gap between objective values. In each such measurement, the relative gap is computed as
where is the objective value obtained when solving (7)-R (an upper bound) and is the objective value when solving (7) (a lower bound).

Table 3.
Comparison of solution quality across multi-contingency scenarios.
We note that for NG25-EP30, five instances were excluded from the comparison: the three infeasible (7)-R instances and two instances that implied a negative relative gap. Proceeding with the analysis, the mean objective values for all sets of feasible solutions indicate that between around and of gas and power loads were delivered across all multi-contingency scenarios. Furthermore, the mean relative gap between the feasible solutions obtained by (7) and the upper bounds obtained by (7)-R was sometimes large, with the largest being across all NG134-EP162 damage scenarios.
These extreme gaps have only two sources from which they can arise. First, a feasible solution obtained by Juniper for a (7) instance is not guaranteed to be near the globally optimal solution. That is, the optimal (7) objective value is potentially much larger than what Juniper reported at termination. Second, since (7)-R is a relaxation, it upper-bounds the globally optimal objective value of (7). The median column in Table 3 reports measures of centrality without the outliers that likely arose from the first source of discrepancy. Through these measurements, it can be observed that (7)-R often provided reliable and tight bounds on the optimal objective of (7), with relative gaps most often ranging from nearly zero to less than . This indicates that the relaxation is capable of providing tight upper bounds on maximum capacities of damaged networks.
4.3. Computational Performance
This section compares the performance of (7) and (7)-R using the instances described in Section 4.2. The performance profiles for these cases are depicted in Figure 6 and divided into three categories: (S) networks containing tens of nodes; (M) networks containing hundreds of nodes; and (L) networks containing more than a thousand nodes (i.e., NG603-EP588). Across all categories, it is shown that the (7)-R formulation was able to solve substantially more problems compared to (7) in significantly shorter amounts of time. For joint networks with tens of nodes, both formulations were able to solve many instances within the one-hour time limit. For networks with hundreds of nodes, (7)-R was capable of solving most instances within ten seconds, whereas (7) required hundreds or thousands of seconds to solve only a small proportion. For networks with thousands of nodes, (7)-R solved all instances within ten seconds, whereas (7) did not solve any. The efficiency of (7)-R compared to (7) highlights its applicability to (i) real-time multi-contingency analysis and (ii) analyses that would require distributions of many multi-contingency scenarios.
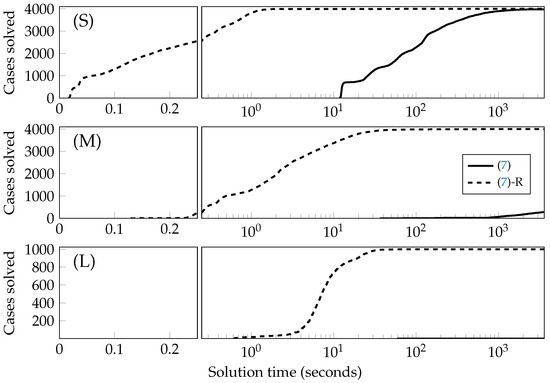
Figure 6.
Performance profiles comparing the efficiency of (7) and (7)-R across the instances described in Section 4.2. Here, the performance profiles are partitioned into three categories: (S) networks containing tens of nodes; (M) networks containing hundreds of nodes; and (L) networks containing more than a thousand nodes.
4.4. Proof-of-Concept Maximum Load Delivery Analysis
While Section 4.2 and Section 4.3 studied the computational and accuracy tradeoffs between (7) and (7)-R, this section provides a proof-of-concept MLD analysis using the (5)-R and (6)-R formulations across the same set of damage scenarios. Figure 7 and Figure 8 display 18 histograms that evaluate the proportions of gas and power loads delivered across the solved damage scenarios for the nine joint networks using the two problem specifications. Here, the green bars correspond to the histogram frequencies obtained from analyzing results of (5)-R solutions (i.e., gas prioritization), and the red bars correspond to (6)-R solutions (i.e., power prioritization). The brown, overlapping bars correspond to frequencies that appear in both the (6)-R and (5)-R histograms. These results indicate qualitative differences in the hypothetical robustness of each joint network. They also display the extreme tradeoffs between prioritizing gas versus power delivery in the presence of severe outages. Finally, they indicate the sensitivity of each gas or power network to the interdependencies that link them. These histograms serve as basic proofs of concept for real-world MLD analyses.
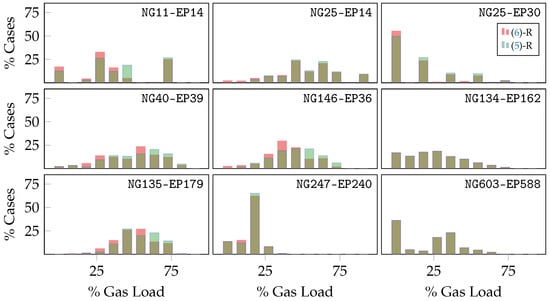
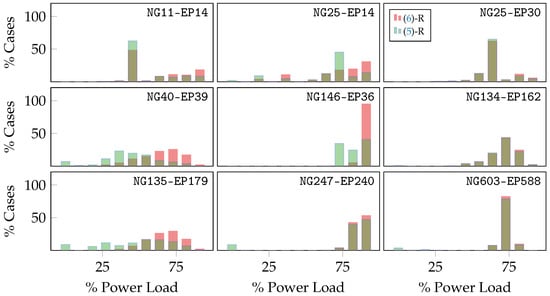
Figure 8.
Histograms comparing the proportion of active power delivered across the solved scenarios, using the same experimental and analytical settings as in Figure 7.
Figure 7 displays histograms of maximum gas load delivered in the presence of severe outages. First, note that these histograms display a variety of load distributions across the cases and networks considered. Some networks, e.g., NG25-EP30, NG247-EP240, and NG603-EP588, suggest gas grids that are highly sensitive to the outages considered, with large proportions of damaged networks often incapable of delivering more than of gas load. Other networks, e.g., NG40-EP39, NG146-EP36, and NG135-EP179, show less severe but still substantial sensitivities to these outages. The remaining networks display gas network sensitivities somewhere between these extremes.
The overlapping histograms also display the tradeoffs encountered when prioritizing gas versus power delivery. In the three joint networks NG25-EP14, NG134-EP162, and NG603-EP588, gas and power interdependencies are mostly inconsequential, and prioritizing either gas or power barely affects the maximum gas capacity. This is likely a result of excess generation capacity in the corresponding power networks. Other networks, e.g., NG40-EP39, NG146-EP36, and NG135-EP179, show more interesting tradeoffs, where prioritizing either gas or power results in substantial changes in the overall maximum load distributions. The remaining networks show less interesting tradeoffs, although NG11-EP14 displays large tradeoffs, likely due to the drastic effects that even minor outages can have on the relatively small network.
Figure 8 displays histograms of maximum active power delivered in the presence of the outages considered. First, the four networks, NG25-EP30, NG134-EP162, NG247-EP240, and NG603-EP588, appear robust to outages in the joint network and are often capable of delivering more than of the original power load. The remaining networks exhibit greater variety in their maximum load distributions. While some networks, e.g., NG25-EP30, NG134-EP162, and NG603-EP588, appear less reliant on gas-fired power generators, the remaining networks exhibit more dramatic changes when prioritizing gas versus power delivery. The most extreme example appears to be NG146-EP36, which is often capable of delivering a large amount of power across all cases when power is prioritized but also often loses more than of its total capacity when gas delivery is prioritized.
We remark that to solve (5)-R and (6)-R, inner- and outer-level problems of the lexicographic maximization are solved sequentially. For example, to solve (5)-R, (i) the inner-level problem maximizing is solved, yielding a solution , and then (ii) is maximized, subject to the relaxed forms of Constraints (1a)–(1i), (2a)–(2v), (3), and . The latter ensures that nongeneration gas load delivered in the outer level is at least that of the inner level, minus some tolerance , taken in this study to be . A similar algorithm is used for (6)-R. We note that the general algorithm is not as numerically reliable as (7)-R and does not solve 469 of the cases considered in this subsection. This could potentially be alleviated with a larger , the use of multi-objective modeling features natively available in some solver libraries (e.g., Gurobi), or the modification of the solver parameters to promote greater numerical accuracy (e.g., setting NumericFocus=3 in Gurobi).
4.5. Proof-of-Concept Pareto Analysis
Together, (5)-R, (6)-R, and (7)-R allow for a variety of prioritizations of gas versus power load. As such, they serve as powerful tools for exploring the wide range of possible MLD solutions based on the relative importance of gas versus power delivery. This can provide gas and power grid managers with best-case capacity estimates depending on the type of coordination between systems. In turn, this enables a better understanding of the complex yet practically important tradeoffs encountered during the operation of a damaged joint network. While Section 4.2, Section 4.3 and Section 4.4 focused on analyzing the performance and qualitative aspects of MLD analyses across a large number of joint networks, this section focuses on providing a proof-of-concept Pareto analysis of a single joint network, NG146-EP36.
Figure 9 shows a linearly interpolated approximation of the convex hull of the Pareto front for mean active power versus gas delivery across the same set of scenarios from the previous sections. Here, the upper-left and lower-right endpoints correspond to means obtained from the (6)-R and (5)-R problem formulations, respectively. The interior points correspond to means obtained from the (7)-R formulation, where the tradeoff parameter was varied to determine interesting and distinct points on the Pareto front.
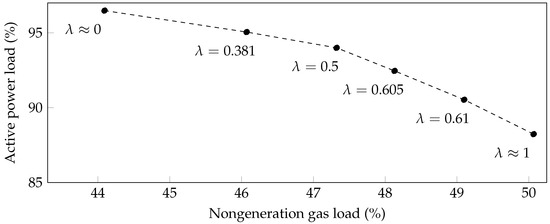
Figure 9.
Convex hull of the Pareto front for mean total active power load versus mean nongeneration gas load delivered over one thousand NG146-EP36 damage scenarios.
First, note that when prioritizing power delivery, on average, of active power is delivered but less than of nongeneration gas is delivered. When gas delivery is prioritized, of power is delivered, while of gas is delivered. Between these two extremes, the amount of gas and power increases and decreases, respectively, with increases in . For , active power decreases more slowly as a function of , and for , the rate of decrease appears larger. In this case, happens to represent a value where (7)-R begins to prefer maximization of gas delivery over power delivery. In practice, a point near this value of could be one that maximizes simultaneous delivery while having practically equal prioritizations.
5. Conclusions
Gas-fired power generation amplifies interdependencies between natural gas and power transmission systems. These interdependencies have engendered greater vulnerabilities in gas and power grids, where natural or man-made disruptions can require the curtailment of load in one or both systems. To address the challenge of estimating maximum joint network capacities under these disruptions, this study considered the task of determining feasible steady-state operating points for severely damaged joint networks while ensuring the maximal delivery of gas and power loads simultaneously. Mathematically, this task was represented as the mixed-integer nonlinear nonconvex joint MLD problem, which is difficult to solve directly.
Three variants of the MLD problem were formulated: one that prioritizes gas delivery, one that prioritizes power delivery, and one that assumes a linear tradeoff between the two objectives. To increase the tractability of these problems, a mixed-integer convex relaxation of the joint network’s physical constraints was proposed. The relaxation was found to be a fast and reliable method for determining bounds on the capacities of damaged joint networks containing up to around a thousand nodes. Multiple proofs of concept show that the efficacy of the relaxation-based MLD method makes it a potentially valuable tool for complex real-world decision-support applications, including identifying critical network components given a forecasted natural hazard or prioritizing restoration efforts to enable the maximal delivery of load after a disruption has occurred.
Future work will focus on extending the MLD approaches developed in this paper. First, additional gas and power relaxations should be considered to more accurately and efficiently scale to joint networks containing many thousands of nodes. Preprocessing routines, such as optimization-based bound tightening, may also aid in improving relaxations. Second, the current problem assumes full coordination between gas and power systems when deciding operations that maximize load delivery. The modeling of bidding mechanisms that drive both systems could provide more accurate capacity estimates. Additionally, although difficult to obtain and curate, the availability of real-world and historical joint network data could prove useful for validating our general methodology. Capturing transient dynamics in gas networks is sometimes crucial for understanding the effects of network disruptions, which may be realized long after the disruption occurs. Future work should consider these transient effects when modeling load delivery in the gas network.
Finally, this study considers the effects of severe contingencies in a single-period setting that assumes known supplies and demands. In practice, supply and demand may change during peak usage periods due to variations in renewable generation or in response to disruptions. Future studies could extend this work to include these temporal variations and uncertainties. For example, one could consider supply and demand uncertainty, along with damage uncertainty, in the joint distribution from which contingency scenarios are sampled. Additionally, like Rhodes et al. [10] leveraged Coffrin et al. [6], our work could be applied in a multiperiod context. This could be useful for capturing temporal changes in supply, demand, and component outages while maximizing deliverable load. It could also facilitate other applications, such as scheduling restoration actions.
Author Contributions
Conceptualization, B.T., C.C. and R.B.; Methodology, B.T., C.C. and R.B.; Software, B.T., C.C. and R.B.; Validation, B.T., C.C. and R.B.; Investigation, B.T., C.C. and R.B.; Data curation, C.C.; Writing—original draft, B.T.; Writing—review and editing, B.T., C.C. and R.B.; Visualization, B.T.; Supervision, C.C. and R.B.; Project administration, C.C.; Funding acquisition, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was conducted under the auspices of the National Nuclear Security Administration of the U.S. Department of Energy at Los Alamos National Laboratory under Contract No. 89233218CNA000001. This work was funded by the U.S. Department of Energy’s Office of Electricity Advanced Grid Modeling (AGM) project “Joint Power System and Natural Gas Pipeline Optimal Expansion Planning”.
Data Availability Statement
Data and software are detailed in Section 4.1. Most joint network models were derived from publicly available datasets. The NG247-EP240 joint network model is available upon request, subject to approval. All MLD formulations were implemented in GasPowerModels, an open-source Julia package, where an example MLD analysis is described in examples/README.md. Examples based on Section 4.5 also appear in [7], which details our general multi-infrastructure software modeling approach. Finally, a snapshot containing the network models, damage scenarios, optimization modeling implementation, experimental results, and analysis scripts used in the production of this study are available upon request, subject to approval.
Acknowledgments
Earlier versions of this work appear in the form of a preprint [45] and in Chapter 8 of the first author’s dissertation [46]. The authors gratefully acknowledge David Fobes and Kaarthik Sundar at Los Alamos National Laboratory for their contributions to the InfrastructureModels software packages. The authors also thank Sarah Tasseff at Los Alamos National Laboratory for her assistance with the production of Figure 1 and Figure 3.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- U.S. DOE Energy Information Administration. International Energy Outlook 2023; Technical Report; U.S. DOE Energy Information Administration: Washington, DC, USA, 2023.
- U.S. DOE Energy Information Administration. U.S. Natural Gas Pipelines. 2018. Available online: https://hifld-geoplatform.opendata.arcgis.com/datasets/geoplatform::natural-gas-pipelines/about (accessed on 23 March 2024).
- ERCOT. Review of February 2021 Extreme Cold Weather Event; ERCOT: Austin, TX, USA, 2021. [Google Scholar]
- PJM Interconnection. Analysis of Operational Events and Market Impacts During the January 2014 Cold Weather Events; Technical Report; PJM Interconnection: Norristown, PA, USA, 2014. [Google Scholar]
- Tasseff, B.; Coffrin, C.; Bent, R.; Sundar, K.; Zlotnik, A. Natural gas maximal load delivery for multi-contingency analysis. Comput. Chem. Eng. 2022, 168, 108032. [Google Scholar] [CrossRef]
- Coffrin, C.; Bent, R.; Tasseff, B.; Sundar, K.; Backhaus, S. Relaxations of AC Maximal Load Delivery for Severe Contingency Analysis. IEEE Trans. Power Syst. 2019, 34, 1450–1458. [Google Scholar] [CrossRef]
- Bent, R.; Tasseff, B.; Coffrin, C. InfrastructureModels: Composable Multi-infrastructure Optimization in Julia. Informs J. Comput. 2023, 36, 305–704. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Hiskens, I.A. A Survey of Relaxations and Approximations of the Power Flow Equations. Found. Trends Electr. Energy Syst. 2019, 4, 1–221. [Google Scholar] [CrossRef]
- Rhodes, N.; Ntaimo, L.; Roald, L. Balancing Wildfire Risk and Power Outages Through Optimized Power Shut-Offs. IEEE Trans. Power Syst. 2021, 36, 3118–3128. [Google Scholar] [CrossRef]
- Rhodes, N.; Fobes, D.M.; Coffrin, C.; Roald, L. PowerModelsRestoration.jl: An open-source framework for exploring power network restoration algorithms. Electr. Power Syst. Res. 2021, 190, 106736. [Google Scholar] [CrossRef]
- Hiller, B.; Koch, T.; Schewe, L.; Schwarz, R.; Schweiger, J. A System to Evaluate Gas Network Capacities: Concepts and Implementation. Eur. J. Oper. Res. 2018, 270, 797–808. [Google Scholar] [CrossRef]
- Schmidt, M.; Steinbach, M.C.; Willert, B.M. High Detail Stationary Optimization Models for Gas Networks: Validation and Results. Optim. Eng. 2016, 17, 437–472. [Google Scholar] [CrossRef]
- Cheli, L.; Guzzo, G.; Adolfo, D.; Carcasci, C. Steady-state analysis of a natural gas distribution network with hydrogen injection to absorb excess renewable electricity. Int. J. Hydrogen Energy 2021, 46, 25562–25577. [Google Scholar] [CrossRef]
- Kazi, S.R.; Sundar, K.; Srinivasan, S.; Zlotnik, A. Modeling and optimization of steady flow of natural gas and hydrogen mixtures in pipeline networks. Int. J. Hydrogen Energy 2024, 54, 14–24. [Google Scholar] [CrossRef]
- Zlotnik, A.; Kazi, S.R.; Sundar, K.; Gyrya, V.; Baker, L.; Sodwatana, M.; Brodskyi, Y. Effects of Hydrogen Blending on Natural Gas Pipeline Transients, Capacity, and Economics. In Proceedings of the PSIG Annual Meeting, San Antonio, TX, USA, 16–19 May 2023. [Google Scholar]
- Tang, D.; Tan, G.L.; Li, G.W.; Liang, J.G.; Ahmad, S.M.; Bahadur, A.; Humayun, M.; Ullah, H.; Khan, A.; Bououdina, M. State-of-the-art hydrogen generation techniques and storage methods: A critical review. J. Energy Storage 2023, 64, 107196. [Google Scholar] [CrossRef]
- Erdener, B.C.; Sergi, B.; Guerra, O.J.; Lazaro Chueca, A.; Pambour, K.; Brancucci, C.; Hodge, B.M. A review of technical and regulatory limits for hydrogen blending in natural gas pipelines. Int. J. Hydrogen Energy 2023, 48, 5595–5617. [Google Scholar] [CrossRef]
- Farrokhifar, M.; Nie, Y.; Pozo, D. Energy systems planning: A survey on models for integrated power and natural gas networks coordination. Appl. Energy 2020, 262, 114567. [Google Scholar] [CrossRef]
- Byeon, G.; Van Hentenryck, P. Unit Commitment With Gas Network Awareness. IEEE Trans. Power Syst. 2020, 35, 1327–1339. [Google Scholar] [CrossRef]
- Mitridati, L.; Kazempour, J.; Pinson, P. Heat and electricity market coordination: A scalable complementarity approach. Eur. J. Oper. Res. 2020, 283, 1107–1123. [Google Scholar] [CrossRef]
- Zlotnik, A.; Roald, L.; Backhaus, S.; Chertkov, M.; Andersson, G. Coordinated Scheduling for Interdependent Electric Power and Natural Gas Infrastructures. IEEE Trans. Power Syst. 2017, 32, 600–610. [Google Scholar] [CrossRef]
- Wang, C.; Wei, W.; Wang, J.; Bai, L.; Liang, Y.; Bi, T. Convex Optimization Based Distributed Optimal Gas-Power Flow Calculation. IEEE Trans. Sustain. Energy 2018, 9, 1145–1156. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, J.; Sun, Y.; Wei, C.; Wang, J.; Liao, S.; Ke, D.; Li, X.; Yang, J.; Peng, X. Coordinated operation of gas-electricity integrated distribution system with multi-CCHP and distributed renewable energy sources. Appl. Energy 2018, 211, 237–248. [Google Scholar] [CrossRef]
- Mirzaei, M.A.; Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Zare, K.; Marzband, M.; Anvari-Moghaddam, A. A Novel Hybrid Framework for Co-Optimization of Power and Natural Gas Networks Integrated With Emerging Technologies. IEEE Syst. J. 2020, 14, 3598–3608. [Google Scholar] [CrossRef]
- Abeliuk, A.; Aziz, H.; Berbeglia, G.; Gaspers, S.; Kalina, P.; Mattei, N.; Peters, D.; Stursberg, P.; Van Hentenryck, P.; Walsh, T. Interdependent Scheduling Games. arXiv 2016, arXiv:1605.09497. [Google Scholar]
- Ríos-Mercado, R.Z.; Borraz-Sánchez, C. Optimization problems in natural gas transportation systems: A state-of-the-art review. Appl. Energy 2015, 147, 536–555. [Google Scholar] [CrossRef]
- Zlotnik, A.; Chertkov, M.; Backhaus, S. Optimal control of transient flow in natural gas networks. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 4563–4570. [Google Scholar] [CrossRef]
- Zlotnik, A.; Sundar, K.; Rudkevich, A.M.; Beylin, A.; Li, X. Optimal Control for Scheduling and Pricing Intra-day Natural Gas Transport on Pipeline Networks. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019. pp. 4887–4884. [Google Scholar] [CrossRef]
- Grundel, S.; Hornung, N.; Klaassen, B.; Benner, P.; Clees, T. Computing Surrogates for Gas Network Simulation Using Model Order Reduction. In Surrogate-Based Modeling and Optimization: Applications in Engineering; Koziel, S., Leifsson, L., Eds.; Springer: New York, NY, USA, 2013; pp. 189–212. [Google Scholar] [CrossRef]
- Zlotnik, A.; Dyachenko, S.; Backhaus, S.; Chertkov, M. Model Reduction and Optimization of Natural Gas Pipeline Dynamics. In Proceedings of the ASME 2015 Dynamic Systems and Control Conference, Columbus, OH, USA, 28–30 October 2015. [Google Scholar] [CrossRef]
- Roald, L.A.; Sundar, K.; Zlotnik, A.; Misra, S.; Andersson, G. An Uncertainty Management Framework for Integrated Gas-Electric Energy Systems. Proc. IEEE 2020, 108, 1518–1540. [Google Scholar] [CrossRef]
- Bent, R.; Blumsack, S.; Van Hentenryck, P.; Borraz-Sánchez, C.; Shahriari, M. Joint Electricity and Natural Gas Transmission Planning With Endogenous Market Feedbacks. IEEE Trans. Power Syst. 2018, 33, 6397–6409. [Google Scholar] [CrossRef]
- Marler, R.; Arora, J. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Jabr, R. Radial distribution load flow using conic programming. IEEE Trans. Power Syst. 2006, 21, 1458–1459. [Google Scholar] [CrossRef]
- Babaeinejadsarookolaee, S.; Birchfield, A.; Christie, R.D.; Coffrin, C.; DeMarco, C.; Diao, R.; Ferris, M.; Fliscounakis, S.; Greene, S.; Huang, R.; et al. The Power Grid Library for Benchmarking AC Optimal Power Flow Algorithms. arXiv 2021, arXiv:1908.02788. [Google Scholar]
- Schmidt, M.; Aßmann, D.; Burlacu, R.; Humpola, J.; Joormann, I.; Kanelakis, N.; Koch, T.; Oucherif, D.; Pfetsch, M.E.; Schewe, L.; et al. GasLib—A Library of Gas Network Instances. Data 2017, 2, 40. [Google Scholar] [CrossRef]
- De Wolf, D.; Smeers, Y. The Gas Transmission Problem Solved by an Extension of the Simplex Algorithm. Manag. Sci. 2000, 46, 1454–1465. [Google Scholar] [CrossRef]
- Sánchez, C.B.; Bent, R.; Backhaus, S.; Blumsack, S.; Hijazi, H.; van Hentenryck, P. Convex Optimization for Joint Expansion Planning of Natural Gas and Power Systems. In Proceedings of the 2016 49th Hawaii International Conference on System Sciences (HICSS), Koloa, HI, USA, 5–8 January 2016; pp. 2536–2545. [Google Scholar] [CrossRef]
- Price, J.E.; Goodin, J. Reduced network modeling of WECC as a market design prototype. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Dunning, I.; Huchette, J.; Lubin, M. JuMP: A Modeling Language for Mathematical Optimization. SIAM Rev. 2017, 59, 295–320. [Google Scholar] [CrossRef]
- Carpentier, J. Contribution to the economic dispatch problem. Bull. Soc. Fr. Electr. 1962, 3, 431–447. [Google Scholar]
- Kröger, O.; Coffrin, C.; Hijazi, H.; Nagarajan, H. Juniper: An Open-Source Nonlinear Branch-and-Bound Solver in Julia. In Integration of Constraint Programming, Artificial Intelligence and Operations Research; van Hoeve, W.J., Ed.; Springer: Cham, Switzerland, 2018; pp. 377–386. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Duff, I.S. MA57—A code for the solution of sparse symmetric definite and indefinite systems. ACM Trans. Math. Softw. 2004, 30, 118–144. [Google Scholar] [CrossRef]
- Tasseff, B.; Coffrin, C.; Bent, R. Convex Relaxations of Maximal Load Delivery for Multi-contingency Analysis of Joint Electric Power and Natural Gas Transmission Networks. arXiv 2021, arXiv:2108.12361. [Google Scholar]
- Tasseff, B. Optimization of Critical Infrastructure with Fluids. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2021. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).