Research on Hybrid Rectifier for High Power Electrolytic Hydrogen Production Based on Modular Multilevel Converter

Abstract

Aiming at the problem that silicon-controlled rectifiers (SCR) and pulse width modulation (PWM) rectifiers cannot balance high power levels, high hydrogen production efficiency, and high grid connected quality in the current research on rectifier power supplies for electrolytic hydrogen production, a new hybrid rectifier topology based on a modular multilevel converter (MMC) is proposed. The hybrid topology integrates a silicon-controlled rectifier (SCR) with an auxiliary power converter, wherein the SCR is designated as the primary power source for electrolytic hydrogen production. The auxiliary converter employs a cascaded modular multilevel converter (MMC) and an input-series-output-parallel (ISOP) phase-shifted full-bridge (PSFB) arrangement. This configuration allows the auxiliary converter to effectively mitigate AC-side harmonics and minimize DC-side ripple, concurrently transmitting a small amount of power. The effectiveness of the hybrid rectifier in achieving low ripple and harmonic distortion outputs was substantiated through hardware-in-the-loop experiments. Notably, the hybrid topology is characterized by its enhanced electric-to-hydrogen conversion efficiency, elevated power density, cost efficiency, and improved grid compatibility.

1. Introduction

Hydrogen holds great potential as a future energy source due to its cleanliness, high energy density, and efficient conversion. Electrolytic hydrogen production using renewable energy sources provides high purity and zero carbon emissions while effectively integrating fluctuating renewable energy and minimizing grid impact [1,2,3,4]. However, power consumption remains a significant consideration. In a renewable energy electrolytic hydrogen production system with an AC bus structure, the power supply quality of the AC-DC converter is crucial for optimizing the electrolytic stack’s efficiency and overall hydrogen production efficiency [5].

In recent years, studies have investigated the impact of converter output current quality on electrolytic hydrogen production efficiency. It has been found that the quantity of hydrogen produced is influenced by the average value of the supply current. However, the presence of current ripple leads to additional power losses in the electrolyzer, reducing hydrogen production efficiency [6,7,8,9,10,11,12]. For instance, the influence of different characteristics of the supply current on the efficiency of the Proton Exchange Membrane (PEM) electrolyzer was evaluated in [6]. The results indicated that as the ripple coefficient of the supply current increased, there was a corresponding upward trend in the average power consumption of the electrolyzer. Ursúa connected power sources based on thyristors and IGBTs to a 5 kW alkaline electrolyzer to test system efficiency and power consumption. The results demonstrated that the thyristor-based power supply exhibited a high ripple content in its output, achieving a maximum efficiency of 70.9% when coupled with the electrolyzer. In contrast, the IGBT-based power supply, operating at higher frequencies, facilitated nearly pure DC waveforms in the electrolyzer voltage and current, with a measured maximum efficiency of 77.6%, which is nearly 7% higher than that of the thyristor-based source [9,10]. Dobó analyzed a laboratory-scale alkaline water electrolyzer and discovered that a stable direct current could maximize the reduction of efficiency losses in the electrolyzer [11]. The presence of ripple current in electrolyzer increases the internal equivalent resistance, leading to additional energy losses. This phenomenon is particularly prominent in high-power applications of hydrogen production through electrolysis. According to the aforementioned studies, the development of an electrolytic hydrogen rectifier that can adapt to large power applications, minimize the impact of ripple currents, and maintain relatively low cost has become a focal point of research innovation.

Grid-connected AC-DC converters commonly utilize two main current topologies: silicon-controlled rectifiers (SCRs) and pulse-width modulation (PWM) rectifiers [13]. SCRs are widely used in high-power industrial applications due to their simple structure and low cost. However, they suffer from significant harmonic distortion and a low power factor. Additionally, SCRs are semi-controlled devices and require additional circuitry to implement turn-off capabilities. Although harmonic contamination can be effectively mitigated through the use of filters or multi-pulse rectification techniques, these solutions also lead to an increased size and cost of the converters [14,15,16]. On the other hand, PWM rectifiers offer excellent control characteristics and high power factors. They effectively reduce harmonic content using high-frequency modulation techniques. However, the fully-controlled power devices used in PWM rectifiers are expensive and not suitable for large-scale electrolytic hydrogen production [17,18,19,20]. For example, in [17], a Vienna rectifier is employed as the interface between the AC grid and the electrolyzer. Since the electrolyzer operates at a lower voltage than the DC bus voltage, an additional synchronous step-down converter is required to regulate power transmission. However, this additional conversion process results in increased power losses and costs. Additionally, Muyeen cascaded a two-level PWM rectifier with a Buck converter for use in a wind-powered hydrogen production system and proposed a coordinated control scheme to absorb fluctuations in wind power. However, the ripple in the system’s output current is constrained by the inductance, making it unsuitable for large-scale power applications in hydrogen electrolysis [20].

For large-capacity electrolytic hydrogen production, the limitations of SCRs and PWM rectifiers can be addressed by employing a hybrid rectifier configuration. This hybrid rectifier integrates an uncontrolled rectifier, such as a diode rectifier, or a controlled rectifier, such as an SCR, in parallel with a PWM rectifier either at the input or output stage. The design philosophy centers on optimizing both AC and DC power quality through precise control of the PWM rectifier section while maintaining system cost-effectiveness. This configuration not only reduces the harmonic content of the rectifier grid-side current and improves the system power factor but also significantly decreases the output ripple of the rectifier. Consequently, the hybrid rectifier meets the stringent requirements for high power quality in efficient electrolytic hydrogen production processes. Hence, the hybrid rectifier can more precisely respond to the dynamic changes in the electrical grid and the hydrogen production load, facilitating a more efficient and stable electrolytic hydrogen production process [21,22,23,24,25,26]. For instance, Bintz has designed a high-current, low-voltage hybrid rectifier topology for use in electrolytic hydrogen production. This design effectively reduces thermal losses in the electrolysis cell, thereby enhancing the efficiency of hydrogen production. However, the PWM rectifier lacks electrical isolation on both the AC and DC sides, which results in lower system reliability [23]. In [25,26], a parallel electrolytic hydrogen production hybrid rectifier is proposed which incorporates an auxiliary converter. The auxiliary converter’s main objective is to improve the quality of the grid current and suppress output current ripple. However, it is important to note that the auxiliary converter is connected to the low-voltage AC bus. In scenarios involving large-scale hydrogen production, even though the auxiliary converter handles only a portion of the power, it still carries a significant amount of current. This increases manufacturing complexity and cost.

To fulfill the demands of large-scale, high-efficiency, and cost-effective electrolytic hydrogen production, this paper proposes a hybrid rectifier topology based on a modular multilevel converter (MMC). In this topology, the SCR operates in parallel with the auxiliary power converter, with the SCR serving as the primary power source for the electrolytic hydrogen production load. The auxiliary power converter consists of a cascaded configuration of the MMC and ISOP-PSFB, where ISOP-PSFB refers to a phase-shifted full-bridge (PSFB) converter group featuring an input-series-output-parallel (ISOP) structure [27,28,29,30,31,32,33]. Through the implementation of an integrated control strategy, the auxiliary power converter not only transfers a portion of the power but also mitigates AC-side harmonics and compensates for DC-side ripple. As a result, the hybrid rectifier exhibits minimal DC-side ripple, which significantly enhances the efficiency of electricity-to-hydrogen conversion. Furthermore, the rectifier ensures low current distortion on the grid side, thereby maintaining grid compatibility.

2. Topology of Hybrid Rectifier

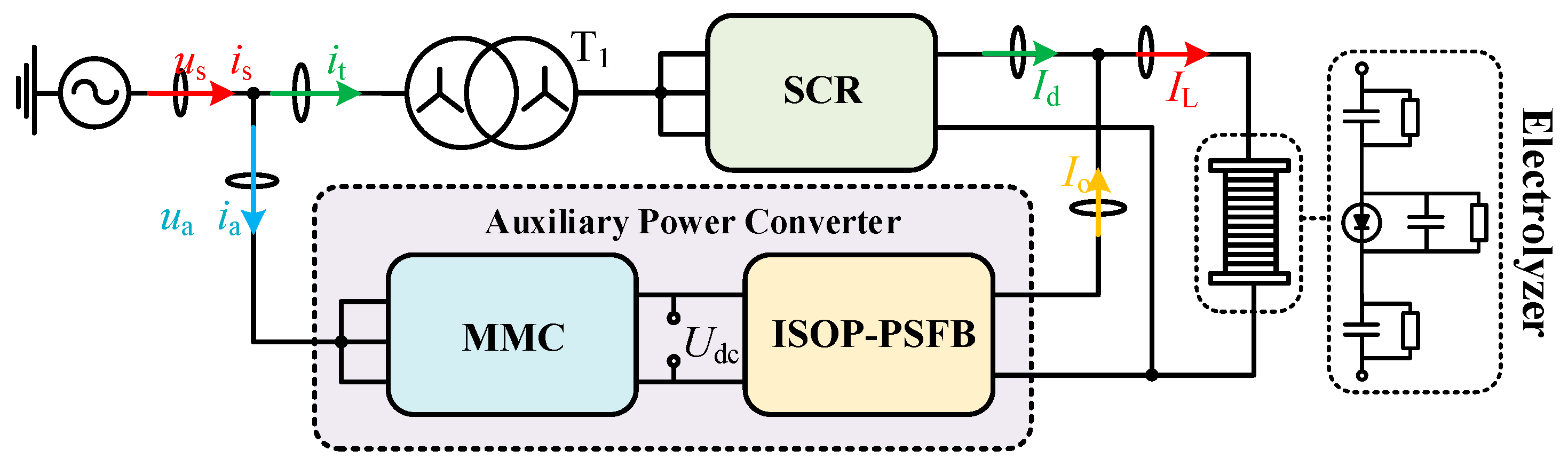
The proposed hybrid rectifier topology, as shown in Figure 1, comprises an SCR and an auxiliary power converter. The electrolyzer, serving as the load for the hybrid rectifier, utilizes an equivalent circuit model based on a diode and an RC parallel circuit [34]. The SCR converts the high-voltage grid voltage u_s, which is stepped down by the transformer T₁ with a high reduction ratio, and serves as the input for the SCR, providing the main power to the electrolyzer. The power unit for the SCR can be flexibly selected, with commonly used options being 6-pulse and 12-pulse wave thyristor rectifiers. This study will employ a 6-pulse thyristor rectifier for investigation.

The high-voltage AC bus is directly connected to the AC side of the auxiliary power converter. The MMC is employed to absorb harmonics and reactive components from the grid-connected current of the thyristor rectifier while maintaining the stability of the common DC bus voltage in the auxiliary power converter. During normal operation of the hybrid rectifier, the grid-side current is the sum of the primary side current of the transformer and the input current of the auxiliary power converter, denoted as i_s = i_t + i_a. This configuration optimizes the quality of the grid-connected current. The ISOP-PSFB converter is utilized to transfer a portion of the power and compensate for the DC ripple component of the thyristor rectifier. 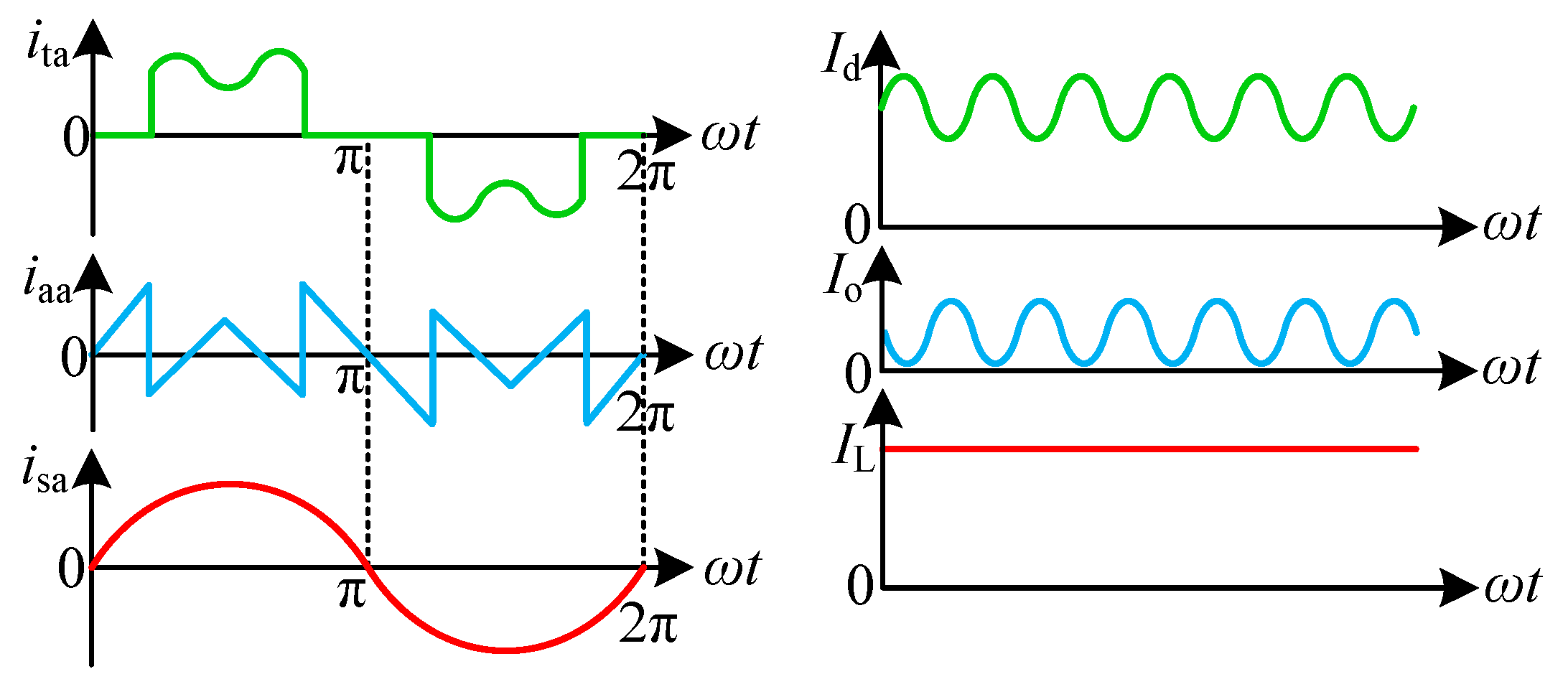As a result, the supply current to the electrolyzer is the sum of the output currents from the thyristor rectifier and the ISOP-PSFB, denoted as I_L = I_d + I_o. This characteristic ensures that the output current of the hybrid rectifier exhibits low ripple, thus improving the efficiency of electrolytic hydrogen production. The schematic diagram of the key current waveforms on the AC and DC sides of the hybrid rectifier is shown in Figure 2.

2.1. The Topology of MMC

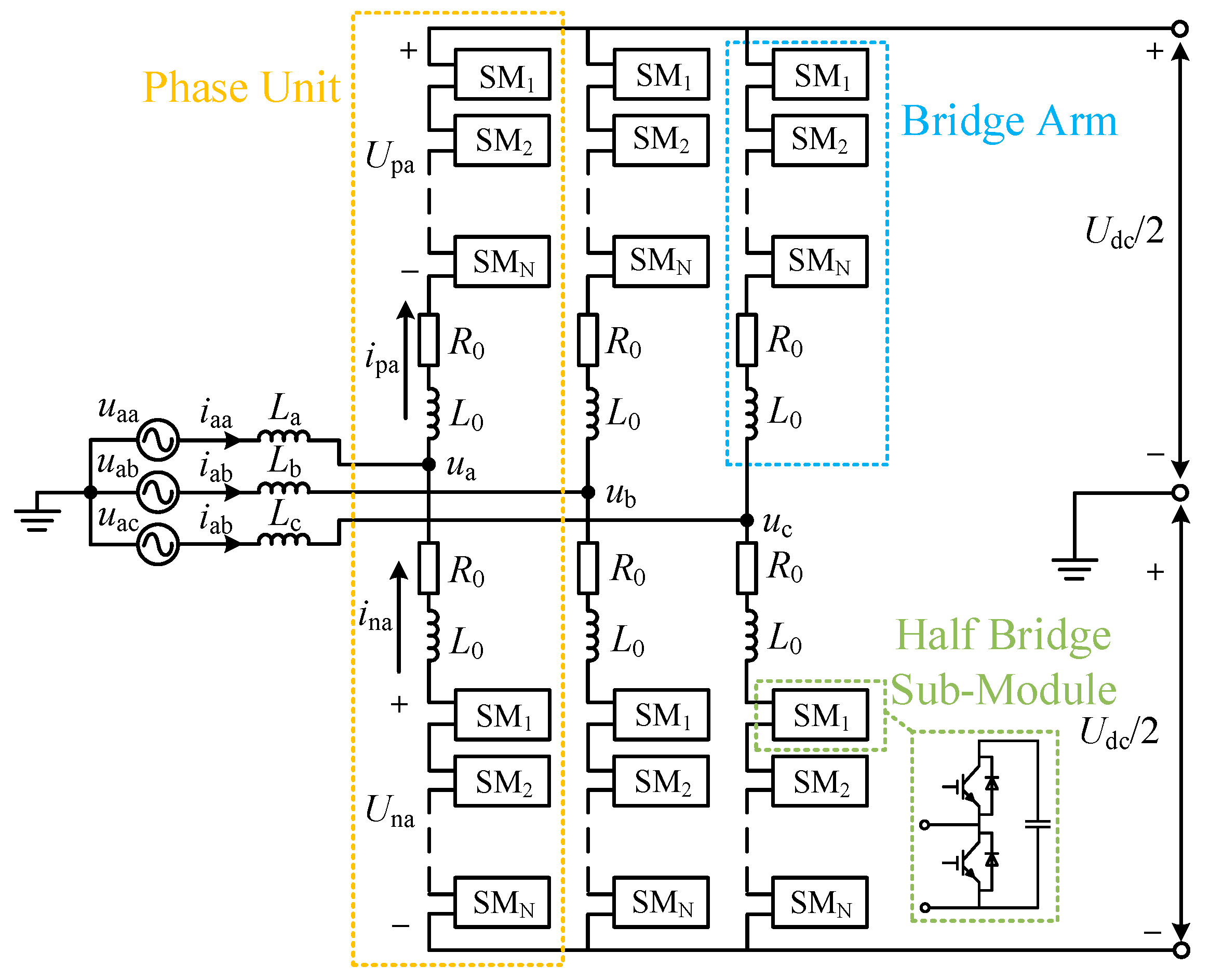
The topology of the MMC using a half bridge sub-module is shown in Figure 3. It comprises three phases and six bridge arms, exhibiting a highly symmetrical structure. Each bridge arm is composed of interconnected and identical sub-modules connected in series with the bridge arm inductance L₀ and bridge arm resistance R₀. The upper and lower bridge arms form a phase unit. During the normal operation of the MMC, the number of sub-modules invested in each phase should be equal to the number of sub-modules within the bridge arm. The flexibility of the MMC design allows N, the number of sub-modules, to be adjusted to accommodate expansion requirements.

Focusing on analyzing phase A when the MMC works in rectification mode, the simplified equivalent circuit diagram of phase A is shown in Figure 4. The voltage across the bridge arm is dependent on the number of sub-modules connected to it, rendering it equivalent to a controlled voltage source. Specifically, U_ap and U_an represent the voltages across the upper and lower bridge arms, respectively. U_a represents the voltage of this point to ground, U_dc signifies the DC voltage, and U_sa and i_a correspond to the AC-side voltage and current of phase A, respectively. Additionally, i_ap and i_an represent the currents flowing through the upper and lower bridge arms, respectively. Neglecting the voltage drop across the bridge arms’ impedance, the application of KVL yields the following expression:

$$U_{\mathrm{a}}=\frac{U_{\mathrm{dc}}}{2}-U_{\mathrm{ap}}$$

(1)

$$U_{\mathrm{a}}=-\frac{U_{\mathrm{dc}}}{2}+U_{\mathrm{an}}$$

(2)

By combining (1) and (2), we can derive the following expressions:

$$U_{\mathrm{dc}}=U_{\mathrm{ap}}+U_{\mathrm{an}}=N_{\mathrm{ap}}{U}_{\mathrm{c}}+N_{\mathrm{an}}{U}_{\mathrm{c}}=N{U}_{\mathrm{c}}$$

(3)

$$U_{\mathrm{a}}=\frac{U_{\mathrm{an}}-U_{\mathrm{ap}}}{2}=(N_{\mathrm{an}}-N_{\mathrm{ap}})\frac{U_{\mathrm{c}}}{2}$$

(4)

N_ap and N_an represent the number of sub-modules connected to the upper and lower bridge arms, respectively, while U_c denotes the voltage value of each sub-module. Equation (3) reveals that the DC output voltage of the MMC is the summation of the voltages across the upper and lower bridge arms. The MMC achieves multilevel rectification control by adjusting the addition and removal of sub-modules in the upper and lower bridge arms.

To analyze the mathematical relationship between the voltages and currents within the rectifier more clearly, it is necessary to establish a mathematical model of the MMC. Based on Figure 4, the KVL and KCL equations can be written as follows:

$$\left\{\begin{array}{l}\frac{U_{\mathrm{dc}}}{2}-U_{\mathrm{ap}}+R_0{i}_{\mathrm{ap}}+L_0\frac{d{i}_{\mathrm{ap}}}{dt}+L_{\mathrm{s}}\frac{d{i}_{\mathrm{a}}}{dt}-U_{\mathrm{sa}}=0\\ -\frac{U_{\mathrm{dc}}}{2}+U_{\mathrm{an}}-R_0{i}_{\mathrm{an}}-L_0\frac{d{i}_{\mathrm{an}}}{dt}+L_{\mathrm{s}}\frac{d{i}_{\mathrm{a}}}{dt}-U_{\mathrm{sa}}=0\\ i_{\mathrm{a}}=i_{\mathrm{ap}}-i_{\mathrm{an}}\end{array}\right.$$

(5)

From (4), it is known that U_a can be expressed as (U_an − U_ap)/2. By adding the first two equations in the system of (5) and substituting U_a accordingly, we can derive:

$$\frac{R_0}{2}{i}_{\mathrm{a}}+(\frac{L_0}{2}+L_{\mathrm{s}})\frac{d{i}_{\mathrm{a}}}{dt}=U_{\mathrm{sa}}-U_{\mathrm{a}}$$

(6)

By defining R = R₀/2 and L = L₀/2 + L_s, we can substitute these expressions into (6) to obtain the dynamic equation of the MMC:

$$R{i}_j(t)+L\frac{d{i}_j(t)}{dt}=U_{\mathrm{s}j}(t)-U_j(t)$$

(7)

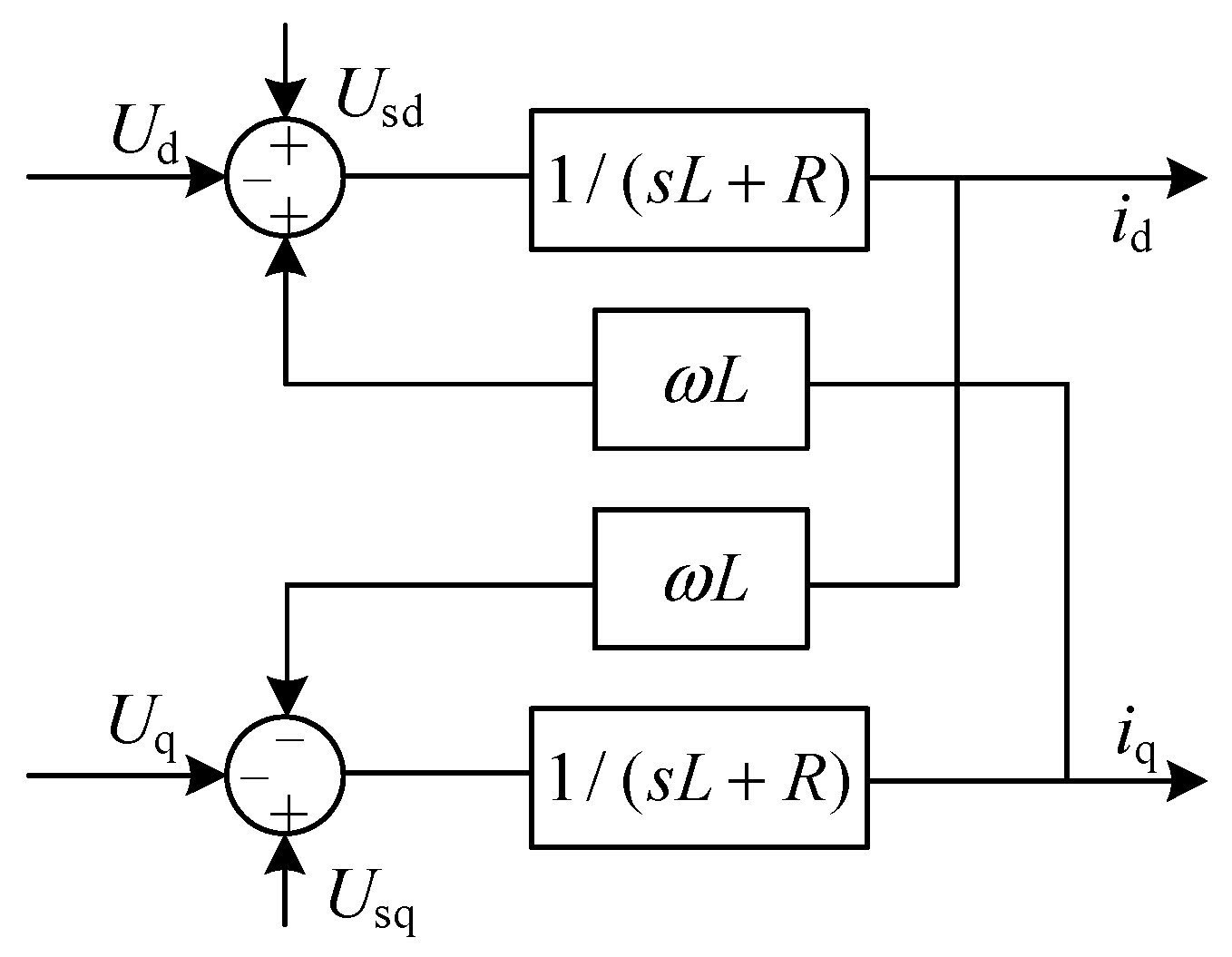
where j = a, b, and c. From (7), it is evident that the mathematical structure of the MMC is similar to that of the conventional voltage source converter (VSC), thus making the VSC control strategy applicable to the MMC. In order to facilitate MMC control, coordinate transformation and Laplace transformation are applied to the physical quantities within the MMC, converting them into DC quantities. Consequently, the MMC input-output model can be expressed as follows:

$$\left\{\begin{array}{l}(sL+R)i_{\mathrm{d}}=U_{\mathrm{sd}}-U_{\mathrm{d}}+\omega L{i}_{\mathrm{q}}\\ (sL+R)i_{\mathrm{q}}=U_{\mathrm{sq}}-U_{\mathrm{q}}+\omega L{i}_{\mathrm{d}}\end{array}\right.$$

(8)

where U_sd, U_sq, i_d, and i_q represent the components of the MMC grid-side voltage and current in the d-q coordinate system. U_d and U_q represent the components of the MMC equivalent output voltage in the d-q coordinate system. Based on (8), the mathematical model of the MMC’s AC side in the d-q coordinate system is illustrated in Figure 5:

2.2. The Topology of ISOP-PSFB

For the case where the auxiliary power converter has a high-voltage common DC bus and a low-voltage high-current output, the PSFB can adopt an input-series output-parallel structure, as shown in Figure 6. The main function of ISOP-PSFB is to convert the high-voltage DC output from the MMC to low-voltage DC and to compensate for the output ripple of the thyristor rectifier. Meanwhile, the PSFB also realizes the function of electrical isolation between the high-voltage side and the low-voltage side. By serially connecting the power modules on the input side, the high voltage is distributed among the individual units, effectively reducing the voltage level of each unit. Similarly, on the output side, the power modules are connected in parallel to mitigate the current flowing through each unit.

3. Integrated Control Strategy of Hybrid Rectifier

The thyristor rectifier employs a proportional-integral (PI) controller to regulate the trigger angle α and generate a variable DC current. However, the specific details of the control structure are not further elaborated in this context. The subsequent discussion focuses on the control strategy applied to the auxiliary power converter.

3.1. Modulation of the MMC

Carrier phase shift modulation is widely used in modular multilevel converters due to its ease of implementation and high equivalent switching frequency. The specific principle behind modulation is that for each set of N sub-modules in the bridge arm, their corresponding triangular carriers are successively delayed by 1/N of a carrier period. By comparing these carriers with the sinusoidal modulating waveform of the bridge arm, N driving signals are generated to control the insertion and removal of the sub-modules. Figure 7 presents the schematic of the carrier phase shift modulation principle for a five-level half-bridge MMC. Carrier phase shift modulation is easy to implement and can achieve a higher equivalent switching frequency effect at lower switching frequencies, optimizing harmonic performance.

3.2. Double Closed-Loop Control of the MMC

To ensure the stability of the DC bus voltage of the auxiliary power converter and to achieve unity power factor operation of the hybrid rectifier, the MMC requires the implementation of a double closed-loop control strategy. Additionally, the MMC needs to absorb the AC-side harmonics and reactive power from the thyristor rectifier. Therefore, it is also necessary to extract the harmonic components of the thyristor rectifier and incorporate them as part of the current reference in the double closed-loop control, aiming to reduce the total harmonic distortion (THD) of the hybrid rectifier’s AC output. The block diagram of the double closed-loop control for the MMC is presented in Figure 8.

In the diagram, i_tj (where j = a, b, and c) represents the three-phase current on the AC side of the thyristor rectifier. i_td and i_tq are the components of i_tj in the d-q coordinate system. i_td0 and i_tq0 denote the fundamental components of i_td and i_tq, respectively, obtained through a low pass filter (LPF). i_tdh and i_tqh represent the harmonic components of i_td and i_tq, respectively. i_d* and i_q* represent the fundamental component outputs generated by the voltage outer loop controller. Consequently, based on the direction of the AC-side current of the hybrid rectifier, the total reference for the inner-loop current of the MMC is obtained as:

$$\left\{\begin{array}{l}{i}_{\mathrm{ad}}^{\ast }=i_{\mathrm{d}}^{\ast }-i_{\mathrm{tdh}}\\ i_{\mathrm{aq}}^{\ast }=i_{\mathrm{q}}^{\ast }-i_{\mathrm{tqh}}\end{array}\right.$$

(9)

For a 6-pulse thyristor rectifier, its AC-side current mainly contains harmonics of 6n ± 1 (where n = 1, 2), which are transformed into 6n harmonics in the d-q coordinate system. While PI control is capable of quickly tracking the desired current, it tends to struggle with lower harmonic currents. To address this limitation, a repetition controller G_RC with a delay time of T₀/6 is introduced. G_RC is connected in parallel with the PI controller to form the current regulator G_c, allowing effective tracking of specific order harmonic currents while maintaining system dynamics. The expression of G_RC in the discrete domain is as follows:

$$G_{\mathrm{RC}}(z)=\frac{z^{-T_0/6}\cdot G_{\mathrm{f}}(z)}{1-Q(z)\cdot z^{-T_0/6}}$$

(10)

where $z^{-T_0/6}$ represents the delay element, T₀ denotes the fundamental period, and Q(z) is typically chosen as a LPF or a constant slightly below 1 to improve system stability. The amplitude phase compensator G_f(z), is expressed as K_r·z^k·S(z), where K_r represents the gain of the repetition control, z^k represents the phase lead element, and S(z) represents a filter.

3.3. Sub-Module Capacitor Voltage Control of the MMC

During normal operation of the MMC, the sub-module capacitors undergo continuous charging and discharging, leading to fluctuations in sub-module voltages around their reference values. This can cause voltage imbalances across the sub-module capacitors, resulting in inconsistent output voltages across the converter’s bridge arms and the generation of substantial circulating currents. Therefore, the MMC must implement sub-module capacitor voltage control to maintain system balance. The basic modulation wave produced by the MMC’s double closed-loop control is combined with the modulation wave correction component from the sub-module capacitor voltage control to form the overall modulating waveform. This waveform is then input into the carrier phase-shift modulation module to generate the drive signals for each sub-module.

3.3.1. Bridge Arm Energy Equalization Control

Bridge arm energy equalization control aims to maintain the average voltage of the capacitors in each sub-module of a phase aligned with its reference value, ensuring that energy is evenly distributed among the phases. It also helps to suppress bridge arm circulating currents, which is beneficial for the stable operation of the system. Taking phase A of the MMC as an example, the block diagram for bridge arm energy equalization control is shown in Figure 9. U_cref represents the reference voltage of the sub-module energy storage capacitor, while U_cav denotes the average voltage of all sub-module energy storage capacitors within the phase unit. The output of the average capacitor voltage controller G_{PI_av} serves as the reference value for the loop current i_{cir_ref}. By comparing i_{cir_ref} with the phase A loop current i_acir, the loop current controller G_{PI_cir} generates the modulating wave deviation u_a1, effectively regulating the magnitude of the bridge arm loop current.

3.3.2. Sub-Module Capacitor Voltage Equalization Control

Bridge arm energy equalization control can maintain stable average voltages across the sub-modules in a bridge arm, but it does not ensure that the voltage of each sub-module on the bridge arm tracks its reference value. Therefore, it is necessary to introduce sub-module capacitor voltage equalization control. The block diagram of the sub-module capacitor voltage equalization control is illustrated in Figure 10. Considering phase A as an example, the actual capacitor voltage U_caj, of each sub-module is compared to the reference value U_cref. If the actual voltage is lower than the reference value, a positive control signal is generated by the proportional regulator K₁. The direction factor K₂ of the bridge arm current is then utilized to determine the modulating wave deviation u_a2. A positive u_a2 leads to an increase in the sub-module capacitor charging time, thereby raising the sub-module capacitor voltage. Conversely, a negative u_a2 reduces the sub-module capacitor discharge time, preventing further decrease in the sub-module capacitor voltage.

3.4. Control Strategy of ISOP-PSFB

The PSFB converter is chosen for power transfer in the auxiliary power converter due to its simple structure, low voltage stress on the switching devices, and wide output regulation range. However, since the parameters of each component in the ISOP-PSFB power module cannot be perfectly matched, a control strategy is necessary to ensure output current equalization and enhance system stability. In the auxiliary power converter, the ISOP-PSFB module is primarily responsible for compensating the ripple component of the thyristor rectifier’s output current. Therefore, a relatively simple common duty cycle control structure is employed to achieve equalization of the output current across all units. Furthermore, the PSFB converter’s internal adjustment mechanism is utilized to achieve input voltage equalization. The block diagram of the ISOP-PSFB current control is depicted in Figure 11.

Initially, the ripple component I_ripple of the thyristor rectifier’s output current I_dc is extracted using the ripple detection unit. The total current reference value I_oref for the ISOP-PSFB is obtained by adding I_ripple to the DC offset component I_offset, where I_offset is set to be greater than I_ripple/2 to ensure that I_oref is greater than 0. The current deviation quantity I_c is obtained by comparing the sampled total output current I₀ of the PSFB converter with the total current reference value I_oref. This deviation signal I_c is then fed into the output current controller G_ioc. After processing in G_ioc, the deviation signal I_c is transformed into the final deviation signal d. The PWM module utilizes this deviation signal d to generate the necessary switching device drive signals, which are subsequently distributed to each sub-module. This ensures that all sub-modules maintain a consistent duty cycle. In the event of a disturbance causing a decrease in the input voltage of the PSFB_i module, each module, operating with the same duty cycle, will experience a corresponding decrease in input current. Consequently, the current flowing into the capacitor of the affected module will increase, leading to a gradual rise in the capacitor voltage until equalization is restored.

Since the ISOP-PSFB is required to compensate for the ripple component of the 6-pulse thyristor rectifier’s output current at a frequency of 300 Hz, an output current controller G_ioc is designed to regulate the ripple current. To achieve this, a quasi-resonant controller with a resonant angular frequency of 6ω is employed in parallel with a PI controller. The combined expression for G_ioc is as follows:

$$G_{i\mathrm{oc}}(s)=K_{\mathrm{p}}+\frac{K_{\mathrm{i}}}{s}+\frac{2K_{\mathrm{R}}{\omega }_{\mathrm{c}}s}{s^2+2{\omega }_{\mathrm{c}}s+{(6\omega )}^2}$$

(11)

where K_p and K_i are the proportional and integral coefficients of the PI controller, respectively, K_R is the gain of the quasi-resonant controller, ω is the system angular frequency, and ω_c is the resonant angular frequency.

4. Experimental Results

This study conducts Hardware-In-the-Loop (HIL) experiments using the RT-LAB real-time simulation platform to validate the effectiveness of the hybrid rectifier under high-power application conditions. The RT-LAB platform consists of hardware components including a host computer, an RT-LAB real-time simulator, and integrated I/O boards. Data exchange between the host computer and RT-LAB is facilitated through TCP/IP Ethernet. Users can construct system simulation circuit models within the Matlab/Simulink environment on the host computer and load them into the RT-LAB simulator to simulate the real-time operating state of the controlled object. The controller receives real-time simulated signals provided by the simulator through the I/O boards, executes control algorithms, and then feeds back the control signals to the simulator to form a closed-loop system. Additionally, signal waveforms can be monitored in real-time using an oscilloscope.

The physical picture of the hardware-in-the-loop experimental platform is shown in Figure 12.

Table 1. Experimental Parameters.

Parameter	Value
Grid voltage us	10 kV
Grid frequency f	50 Hz
Transformer T1 turns ratio k	20:1
Auxiliary power converter DC bus voltage Vdc	20 kV
Number of MMC sub-modules N1	10
MMC sub-module capacitor reference voltage Uc	2000 V
MMC sub-module capacitor C	2200 μF
MMC Bridge Arm Inductor L0	0.05 mH
MMC carrier modulation frequency fc	1000 Hz
Number of ISOP-PSFB power modules N2	10
ISOP-PSFB power module input capacitor Cin	2200 μF
ISOP-PSFB switching frequency fp	10 kHz
ISOP-PSFB output filter inductor Lo	2 mH
ISOP-PSFB output filter capacitor Co	230 μF
Hybrid rectifier capacity	4 MW
Auxiliary power converter capacity	800 kW

presents the experimental parameters employed in the study.

Figure 13 shows the DC side current waveform of the hybrid rectifier during steady-state operation. From the figure, it can be observed that I_d is a 6-pulse DC current containing significant ripple components. The ripple amplitude of I_d is 500 A, resulting in a ripple factor of 18.2%. By using an auxiliary power converter to compensate for the ripple component of the output current from the thyristor rectifier, the total output current of the hybrid rectifier is stabilized as a direct current. After compensation, the ripple amplitude of current I_L is reduced to 8 A, which is a 98.4% decrease compared to before compensation, with a calculated ripple factor for I_L of 0.26%. These experimental results verify the functionality of the auxiliary power converter in compensating for DC ripple, as well as the effectiveness of the ISOP-PSFB control strategy. The low ripple current is crucial for enhancing the efficiency of hydrogen production in high-power electrolytic hydrogen production scenarios.

Figure 14 presents the AC-side voltage and current waveforms of the hybrid rectifier during steady-state operation. The figure illustrates that the phase difference between the input voltage and current of the hybrid rectifier is nearly zero, indicating that the hybrid rectifier operates at a unity power factor. Furthermore, the input current of the thyristor rectifier, i_ta, contains a significant harmonic content, leading to severe distortion of the current waveform. After compensation of the harmonic components by the auxiliary power converter, the waveform of the grid-connected current, i_sa, is significantly improved and approaches an ideal sinusoidal shape. These results validate the effectiveness of the auxiliary power converter in suppressing AC-side harmonics, highlighting its significant role in enhancing the quality of the grid-connected current of the hybrid rectifier.

5. Conclusions

For large-scale electrolytic hydrogen production systems powered by renewable energy, this study innovatively proposes a hybrid rectifier topology based on an MMC and its control strategy, validated through HIL experiments. This topology employs a parallel configuration of a thyristor rectifier and an auxiliary power converter, where the thyristor rectifier primarily handles power transmission to the electrolyzer load, while the auxiliary power converter not only supplies additional power but also absorbs AC harmonics and reactive components, and compensates for DC ripple components, thus optimizing the power quality on both the AC and DC sides of the hybrid rectifier. Compared to traditional SCR and PWM rectifiers used in electrolytic hydrogen production, the MMC-based hybrid rectifier proposed in this study achieves high-quality grid-connected current at high power levels, and its low-ripple output effectively enhances the efficiency and cost-effectiveness of hydrogen production. This research provides an innovative solution for the design and study of high-power rectification sources for electrolytic hydrogen production, contributing to the advancement of the high-power electrolytic hydrogen production field.