Abstract
Fault problems associated with submarine cables caused by variations in their burial depth are becoming increasingly prominent. To address the difficulty of detecting the burial depth of submarine cables and trends in its variation, a prediction model for submarine cable burial depth was proposed which considers the dynamic characteristics of thermal resistance. First, a parallel thermal circuit model of a three-core submarine cable was established, and a formula for calculating the submarine cable’s burial depth was derived based on a formula for calculating the submarine cable’s core temperature. Then, the calculation result was corrected by considering the dynamic characteristics of the thermal resistance of the submarine cable’s structural materials. On this basis, feature vectors associated with the seabed cable burial depth calculation data and time nodes were mined by a convolutional neural network and used as the input parameters of a long short-term memory network for optimization and training, and a prediction model for trends in seabed cable burial depth variation was obtained. Finally, an example analysis was carried out based on the actual electrical parameter data of submarine cables buried by an offshore oil and gas platform. The results showed that the prediction model for trends in variations in the burial depth of submarine cables based on the CNN-LSTM neural network can achieve high prediction accuracy and prediction efficiency.
1. Introduction
In recent years, with the continuous exploitation and use of onshore energy, countries around the world have gradually shifted their focus on energy development to the marine field. The operating state of submarine cables directly affects the safety and stability of the production environment in cross-sea projects [1]. The main parts of submarine cables are often buried in the seabed. Under the long-term influence of external factors such as ocean current scouring, earthquakes, and production and development, continuous variations in the burial depth of submarine cables easily occur [2,3]. When the burial depth decreases, that is, the closer to the seabed surface a submarine cable is, the higher the probability of the direct exposure of the submarine cable to the marine environment is. The direct exposure of a submarine cable exposes it to impacts such as seawater erosion and bites from marine animals, thereby causing physical damage to the cable. When the ultimate load capacity of a submarine cable is abnormal or faulty due to the influence of environmental thermal resistance characteristics, it is difficult to locate the abnormal fault position, limiting maintenance work and deployment and further increasing accident risk and loss.
Many scholars have conducted research on technology for the detection of submarine cable burial depth, and technology for detecting submarine cable burial depth based on acoustics and magnetism has developed rapidly [4]. At present, acoustic detection is a commonly used detection technology in the field of submarine cable burial depth detection; it mainly comprises four kinds of equipment, including side-scan sonar, multi-beam sonar, shallow formation profiling, and synthetic aperture sonar equipment, and it mainly uses ocean “trawl fish” and underwater robots as the main means of detection [5,6]. Magnetic detection is also a widely used and effective method of detecting submarine cable burial depth which can be divided into passive detection and active detection; among these, passive detection can be subdivided into the absolute magnetic field method and the metal detection method [7,8]. At present, the detection of submarine cable burial depth mainly relies on external hardware equipment, which has problems such as its high labor cost, long detection cycle, limited detection effect, and so on. Moreover, defects and faults caused by changes in submarine cable burial depth cannot be found in time; thus, there is a greater risk of danger and economic loss. Therefore, it is necessary to study real-time methods of predicting the burial depth of submarine cables, realize the online monitoring of the burial depth of submarine cables with high precision, and ensure the safe and stable operation of submarine cables.
In view of the above problems, existing studies mainly use the composite single-mode fibers inside submarine cables as temperature-measuring media to obtain the temperature of submarine cable cores and further obtain the thermal characteristics of cables in buried environments through temperature inversion. According to the IEC 60287 standard [9], in [10], a steady-state thermal circuit model of a power cable is built, and the steady-state current-carrying capacity of the power cable under general conditions is calculated by considering the influence of the external environment on the temperature of the cable. At the same time, the accuracy of the calculated value is verified using finite element simulation results, and the error value is only about 1%. In combination with the IEC 60287 standard, in [11], based on the thermal circuit model of the power cable body, research was further extended to a complete thermal circuit model of a power cable in a tunnel, and the steady-state current carrying-capacity of the power cable in the tunnel environment was calculated. At the same time, the accuracy of the calculated value was verified by an experiment involving the steady-state temperature increase in the power cable, and the error value was within only 5%. However, these calculation methods do not consider the dynamic characteristics of thermal resistance of the structural materials of each layer of the submarine cable, and there are certain differences in the thermal resistance parameters of the submarine cable under different submarine cable core temperatures. Therefore, a more accurate determination of the burial depth of submarine cables can be obtained by conducting fiber temperature measurements inside the cable to determine the thermal characteristics of the buried environment. Additionally, through the use of the thermal circuit model under the joint influence of the cable and the environment, the calculation parameters of the thermal circuit model can be corrected. However, burial depth data calculated in this way exhibit little fluctuation between adjacent time points; hence, early warnings of variations in the burial depth of submarine cables cannot be achieved, nor can trends in their development be reflected. Deep learning involves learning the inherent rules and representation levels of sample data, and the information obtained in this learning process is of great help to the interpretation of data such as words, images, and sounds [12,13]. A convolutional neural network is a type of feedforward neural network which includes computing convolution, which is one of the representative algorithms of deep learning [14,15]. A convolutional neural network has two learning modes, namely supervised learning and unsupervised learning, and convolution kernel parameter sharing and inter-layer connections enable the convolutional neural network to compare lattice features, such as pixels and audio, with little computation, few computation requirements, a stable effect, and no additional feature engineering requirements regarding the data [16,17].
In this paper, a three-core submarine cable parallel thermal circuit model is first built, and then, considering the dynamic characteristics of the thermal resistance of submarine cable structural materials, a formula for calculating submarine cable burial depth is derived and revised. Next, a CNN is used to mine the feature vectors associated with seabed cable burial depth calculation data and time nodes, which are used as input parameters for an LSTM neural network for optimization and training. Then, a prediction model of the trend in seabed cable burial depth variation is obtained. Finally, an actual submarine cable laid by an offshore oil and gas platform is used as an example to verify that the prediction model for trends in submarine cable burial depth variation based on a CNN-LSTM neural network has a high prediction accuracy and prediction efficiency.
2. Thermal Circuit Model of a Submarine Cable
2.1. Submarine Cable Structure
At present, most submarine cables are cross-linked polyethylene (XLPE) cables. XLPE-insulated fiber composite submarine cables have similar structures. However, some details of the structural components are slightly different according to the different types of submarine cables. In this paper, an HYJQF41-F 20 kV XLPE fiber composite submarine cable is chosen as an example. Based on the superposition of the IEC standard and a three-core conductor structure, a parallel thermal circuit model of a submarine cable is established.
The structural profile of the cable is shown in Figure 1. The cable is composed of three conductive wire cores and three twisted optical fiber units. The inner parts of the wire core, from the outside to the inside, include the polyethylene (PE) sheath, alloy sheath, water-blocking semiconductive layer, copper tape shield layer, insulation shield, XLPE insulation, conductor screen, and water-blocking copper conductor. The wire core and optical fiber unit are wrapped in the filling layer, and the outer layer comprises the cable belt, armor cushion, galvanized steel wire armor layer, and outer layer.
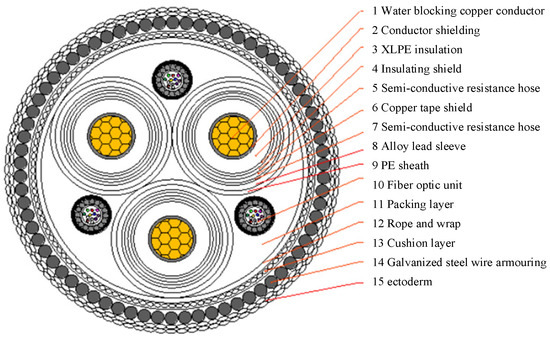
Figure 1.
Schematic diagram of submarine cable structure.
2.2. A Parallel Thermal Circuit Model of a Submarine Cable
The heat transfer characteristics of submarine cables can be analyzed using a thermal circuit and heat flow. Based on the similarity between the heat flow field and the current field, the method of calculating the physical quantities in the heat flow field can refer to the method of calculating the physical quantities in the current field. Metal materials have no hindering effect on heat transfer and can be equivalent to heat sources, while other materials have a hindering effect on heat transfer and can be equivalent to thermal resistance. In particular, since the insulating material also produces a certain loss, it is equivalent to a heat source with thermal resistance. When constructing the parallel thermal circuit model of a submarine cable, structural layers which have similar heat transfer coefficients and are in contact with each other can be merged to reduce the complexity of the model. The simplified internal thermal resistance of the submarine cable is mainly due to its insulation layer, lining layer, and outer layer; the external thermal resistance is mainly due to seabed soil; and the internal heat source is mainly due to the conductor, insulation layer, alloy lead sleeve, and galvanized steel wire armor. Thus, a parallel thermal circuit model of submarine cable [18] is constructed as shown in Figure 2.
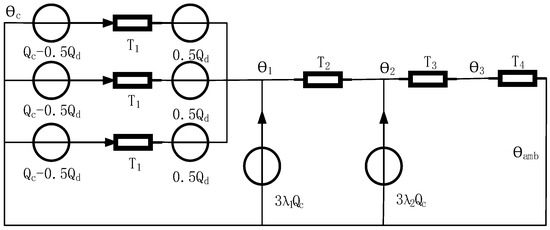
Figure 2.
Model of parallel thermal circuit of submarine cable.
The formula for the calculation of the core temperature of the submarine cable is as follows:
where θc is the cable’s core temperature, θamb is the ambient temperature, T1 is the thermal resistance of the insulation layer, T2 is the thermal resistance of the lining layer, T3 is the thermal resistance of outer layer, and T4 is the environmental thermal resistance. R is the AC resistance, I is the carrying capacity, λ1 is the loss factor of the alloy lead sleeve, λ2 is the loss factor of the galvanized steel wire armor, and Qd is the insulating layer loss. The values of each parameter are shown in Table 1.

Table 1.
HYJQF41-F cable parameter values.
The ambient thermal resistance T4 is calculated as follows:
where ρ4 is the thermal resistance coefficient of the seabed soil, L is the burial depth, and De is the outer diameter of the outer coat.
It can be seen that there must be a correlation between the temperature of the submarine cable core θc and the laying depth L of the submarine cable. The burial depth value of a submarine cable can be calculated by building a parallel thermal circuit model of the submarine cable and combining the structural parameters of each layer of the submarine electric cable.
3. Calculation of Submarine Cable Burial Depth Considering the Dynamic Characteristics of Thermal Resistance
3.1. Sensitivity Analysis of Thermal Resistance Coefficient of Submarine Cables
According to the normalized sensitivity formula shown in Equation (3), combined with the formula for the calculation of the submarine cable’s core temperature, the normalized sensitivity of the cable’s core temperature θc to the thermal resistance of the insulation layer T1, the thermal resistance of the lining layer T2, and the thermal resistance of the outer layer T3 of the submarine cable can be obtained, as shown in Equations (4)–(6), respectively:
In the formula above, T1, T2, and T3 can be calculated using Equations (7)–(9):
where G1 and G2 are geometric factors. ρ1 is the thermal resistance coefficient of the insulation layer, ρ2 is the thermal resistance coefficient of the lining layer, and ρ3 is the thermal resistance coefficient of the outer coating layer. d is the thickness of the outer sheath, and D is the outer diameter of the armor layer.
Based on the above contents, the sensitivity of the cable’s core temperature to the thermal resistance coefficient of the insulating layer, the thermal resistance coefficient of the lining layer and the thermal resistance coefficient of the outer layer of the submarine cable can be calculated under different operating carrying currents, as shown in Table 2.

Table 2.
The sensitivity of the cable’s core temperature to the thermal resistance coefficient of each structural layer under different operating current-carrying rates.
The sensitivity classification standards for the submarine cable’s thermal resistance coefficient [19] are shown in Table 3.

Table 3.
Sensitivity classification of thermal resistance coefficient.
According to a sensitivity classification analysis of the thermal resistance coefficient of each structural layer of the submarine cable, when the other physical parameters are unchanged, the sensitivity of the thermal resistance coefficient of each structural layer of the submarine cable increases with an increase in the cable’s core temperature, as shown in Figure 3.
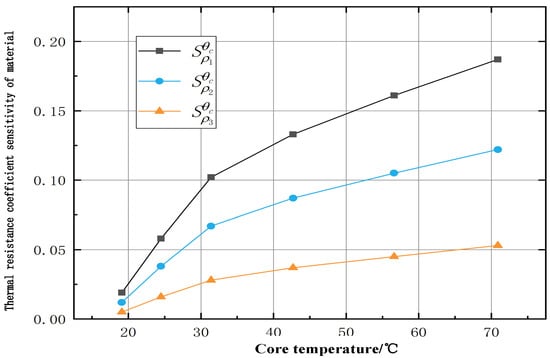
Figure 3.
Temperature–thermal resistance sensitivity.
When the temperature of the insulation layer increases from 19.1 °C to 70.9 °C, the sensitivity of the thermal resistance coefficient increases from 0.019 to 0.187; that is, when the conductor current is within 100 A, the layer is a class I layer, that is, “insensitive”, and the remaining layers are class II layers, that is, they are of “medium sensitivity”. When the inner layer temperature increases from 19.1 °C to 70.9 °C, the thermal resistance coefficient sensitivity increases from 0.012 to 0.122, and the conductor current increases to more than 200 A; therefore, this layer is classified as a class II layer, that is, it demonstrates “medium sensitivity”. When the temperature of the outer coating layer increases from 19.1 °C to 70.9 °C, the sensitivity of the thermal resistance coefficient increases from 0.005 to 0.053, and the conductor current increases to 600 A; therefore, the layer is a class II layer, that is, it shows “medium sensitivity”. The thermal resistance coefficient of each layer inside the submarine cable varies with the temperature variation in the structural layer. It can be seen that the thermal resistance coefficient of each structural layer will change with the change in temperature. It can be seen that the thermal resistance coefficient of each layer of the submarine cable will change with a change in temperature, and its sensitivity level may also increase from “insensitive” to “moderately sensitive”. Therefore, a change in the operating carrying capacity of the submarine cable will directly lead to a change in the temperature of the cable’s core, thus causing a dynamic change in the thermal resistance coefficient of each layer of the submarine cable.
When using the IEC standard thermal circuit model to calculate the temperature of each layer of the submarine cable, the dynamic characteristics of the thermal resistance of each layer of the submarine cable’s structural materials are not taken into account, so the thermal resistance coefficient of each layer of the submarine cable is fixed. In view of the fact that the inner layers of the submarine cable are mainly composed of a crystalline polymer, the crystallinity of the crystalline polymer will change with an increase in the operating temperature of the submarine cable. When the operating temperature increases, the crystallinity value decreases, and the thermal resistance coefficient of the material also decreases. Now, a curve of the relationship between the operating temperature of the submarine cable and the thermal resistance coefficient of the material is established, as shown in Figure 4. Therefore, when using the IEC standard thermal circuit model to calculate the temperature of each layer of a submarine cable, it is necessary to dynamically determine the thermal resistance coefficient of each layer of the submarine cable so as to reduce data error and improve the subsequent accuracy of predicting submarine cable burial depth.
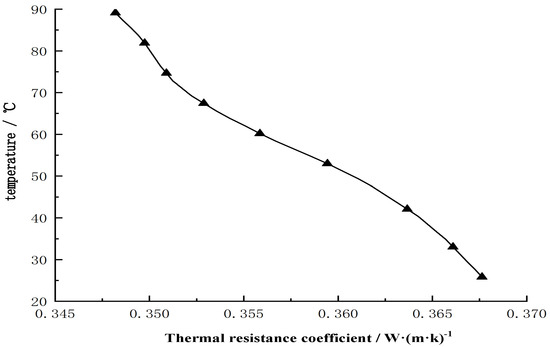
Figure 4.
Temperature-thermal resistance relationship.
3.2. Temperature–Depth Calculation Considering the Dynamic Characteristics of Thermal Resistance
A temperature–burial depth calculation process for submarine cables is constructed, as shown in Figure 5. Firstly, the thermal resistance coefficient of each structural layer of the submarine cable is determined according to the temperature of the cable’s core, and then the environmental thermal resistance is calculated by inputting the real-time operation carrying capacity of the submarine cable into the parallel thermal circuit model of the three-core submarine cable. Finally, the burial depth of the submarine cable is calculated according to the outer diameter of the submarine cable.
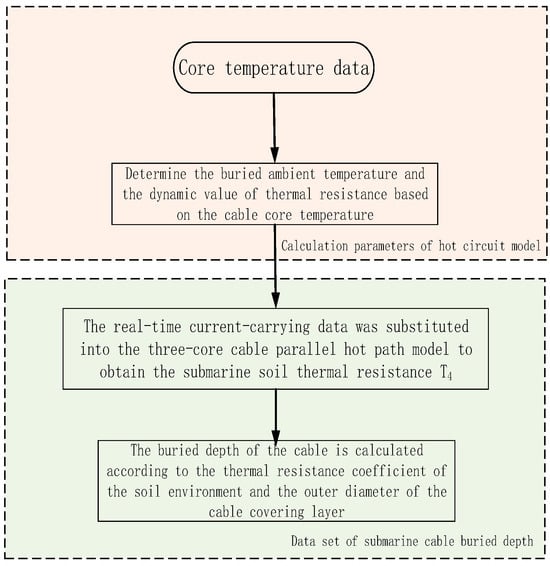
Figure 5.
Calculation processes for cable temperature and burial depth.
To analyze the accuracy of the submarine cable burial depth calculation method based on the dynamic characteristics of its thermal resistance, the temperature monitoring data and burial depth detection data of an oil and gas platform are selected as an example. The error between the calculated value and the measured value of the submarine cable burial depth during the sampling time is calculated, and the results are shown in Figure 6.
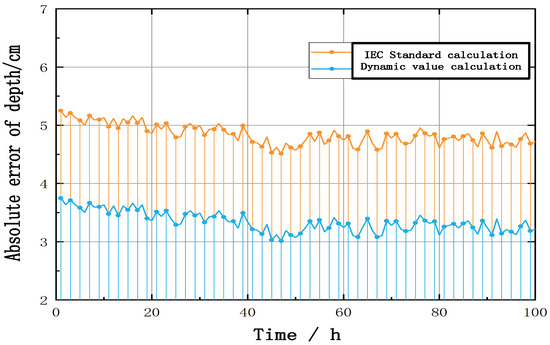
Figure 6.
Time-varying curve of the absolute error of the submarine cable burial depth.
It can be seen from Figure 6 that there is an absolute error of about 5 cm between the burial depth of the submarine cable calculated according to the IEC standards and its actual burial depth, and there is an absolute error of about 3.5 cm between the burial depth of the submarine cable calculated according to the dynamic value of its thermal resistance and the actual burial depth. Therefore, it is proved that the method of calculating submarine cable depth based on the dynamic characteristics of its thermal resistance has high accuracy.
4. Prediction Model of Submarine Cable Burial Depth Based on CNN-LSTM
4.1. CNN Neural Network
A CNN is a feedforward neural network with an excellent data feature learning ability. It is mainly composed of an input layer, a convolution layer, a pooling layer, a fully connected layer, and an output layer. The structure is shown in Figure 7.
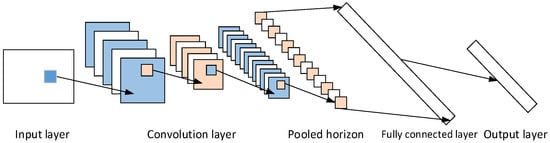
Figure 7.
CNN structure.
Based on the temperature–burial depth calculation process for submarine cables proposed in the previous section, a seabed cable burial depth dataset can be calculated. However, this dataset has a huge amount of data and strong nonlinearity, so it is necessary to extract effective information from the seabed cable burial depth calculation dataset to provide reliable data sources for subsequent burial depth predictions. In this paper, the CNN convolutional layer’s convolution kernel mechanism is used to extract the features of the seabed cable burial depth calculation dataset so as to obtain the local features of the burial depth calculation data and establish a dense and complete feature vector.
4.2. LSTM Neural Network
LSTM is a modified recurrent neural network. The LSTM structure is shown in Figure 8. Compared with CNNs, LSTM introduces the concept of a “gate” in the internal structure to control the internal unit. The LSTM network contains three gate structures: an input gate, a forget gate, and an output gate. By combining the extracted feature vector Xt, the state memory cell Ct−1, and the hidden layer state ht−1 with the forget gate ft, the parts of the state memory cell Ct−1 that need to be forgotten are determined. The eigenvector Xt in the input gate determines the vector to be retained in the state memory cell Ct−1 after the σ and tanh activation functions are applied [20].
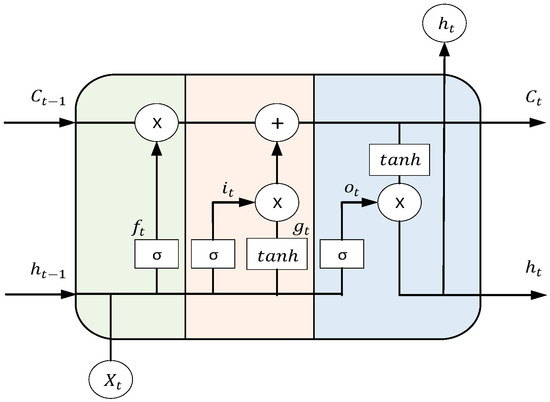
Figure 8.
Structure of LSTM.
In this paper, a CNN neural network is used to mine the feature vectors associated with the seabed cable burial depth calculation data and time nodes, which are used as the input parameters of an LSTM neural network for optimization and training. Finally, a burial depth prediction value for the seabed cable is obtained, and changes in the burial depth of the seabed cable in the future in the short term can be plotted based on a large amount of burial depth prediction data.
4.3. Prediction Model
When a submarine cable is in a normal state of operation, due to the influence of ocean currents or silt deposition, the burial depth of the submarine cable is in a state of slow variation for a long time; even if there are sudden abnormal conditions, such as trawling, anchor dragging, and fishing activities, the submarine cable will remain in a single state after more obvious variations. When an electrical fault occurs in a submarine cable, the temperature of the cable’s core at the fault location will suddenly and sharply increase, and it will drive the temperature of the cable’s core to change along the fault location. When a submarine cable short-circuit fault occurs, the temperature of the cable’s core at the fault location will suddenly increase greatly, driving a change in the temperature of the cable’s core within a range of tens of meters along the fault location. When a submarine cable leakage fault occurs, the temperature of the cable’s core at the fault location will suddenly increase in a small range, driving a change in the temperature of the cable’s core within a range of several meters along the fault location, as shown in Figure 9. Because the variation in the cable’s core temperature caused by the variation in the burial depth of the submarine cable is much smaller than that caused by an electrical fault in the submarine cable, a sudden variation in the cable’s core temperature of the submarine cable can effectively eliminate the influence of the electrical fault in the submarine cable.
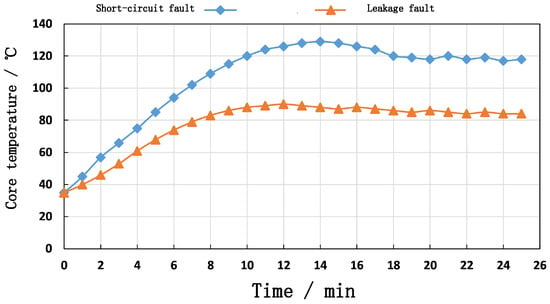
Figure 9.
The effect of an electrical fault on the cable’s core temperature.
Based on the above analysis, in this paper, the overall process of calculating and correcting a submarine cable’s burial depth is designed, as shown in Figure 10.
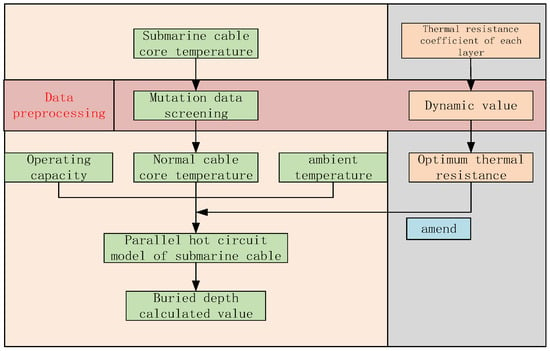
Figure 10.
Submarine cable burial depth prediction and correction process.
Due to high labor costs and the many problems associated with the actual detection of submarine cable burial depths, regular detection is usually conducted every few months or half a year in actual submarine cable projects. Therefore, there are few measured submarine cable burial depth data, and these data are very discrete and cannot be used as a prediction sample for the neural network prediction model. Considering that the calculation error of the submarine cable burial depth is small, the calculation data of the submarine cable burial depth are chosen as a forecast dataset. First, a CNN neural network is used to extract the features of the burial depth calculation dataset, extract the internal relationship between the time nodes and the burial depth of the submarine cable, construct a one-dimensional feature vector of the time series, and then input it into the LSTM neural network for optimization training, obtaining a prediction model for the trend in the variation of the burial depth of a submarine cable. The training process of the prediction model is shown in Figure 11.
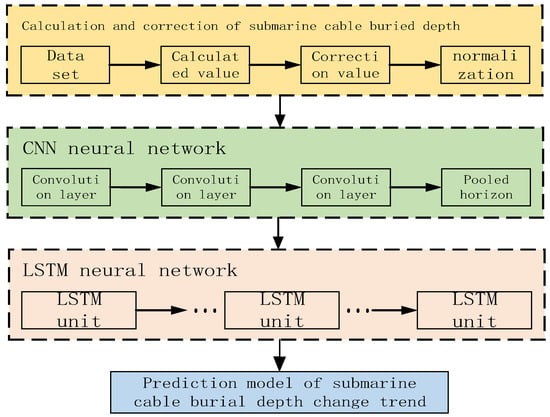
Figure 11.
Flow of predicting submarine cable burial depth based on CNN-LSTM.
5. Example Analysis
5.1. CNN Neural Network
- (1)
- Data selection:
In order to verify the feasibility and correctness of the prediction model for the trend in submarine cable burial depth changes established in this paper, temperature monitoring data for a submarine cable core belonging to an offshore oil and gas platform were obtained for a total of 190 days from 1 March 2019 to 6 September 2019, with a collection interval of 5 h.
- (2)
- Data normalization processing:
The burial depth calculation dataset of submarine cable was normalized so that the whole dataset changed in the range of [0, 1], and the specific conversion function is as follows:
where x′ is the normalized values, xmin is the minimum value of the dataset, and xmax is the maximum value of the dataset. After the input buried depth data were normalized to the maximum value, the whole data series was distributed in the interval [0, 1].
5.2. Indicators of Evaluation
In this paper, the mean absolute error (MAE), root mean square (RMSE), and mean absolute percentage error (MAPE) are adopted as evaluation indices for the results of the submarine cable burial prediction. The specific calculation formula is shown in Equations (11)–(13):
where xi is the calculated value of the submarine cable burial depth, is the predicted value of the submarine cable burial depth, and n is the length of the buried seabed cable dataset.
5.3. Prediction and Analysis of Submarine Cable Burial Depth
In order to further understand the burial depth of the submarine cable in the future in the short term, based on the characteristics of the cable’s core temperature data, two different types of cable core temperature datasets were selected to calculate the burial depth of the submarine cable. Then, the calculated burial depth value was preprocessed and used as input data for the CNN neural network, LSTM neural network, and CNN-LSTM neural network so as to obtain the trend in the burial depth changes of the submarine cable via different prediction models. The results are shown in Figure 12 and Figure 13.
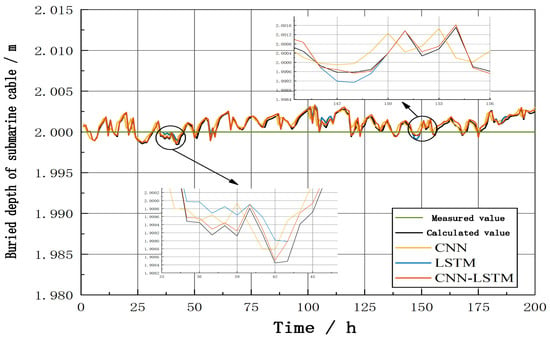
Figure 12.
Comparison of prediction results for burial depth change trend (Group 1).
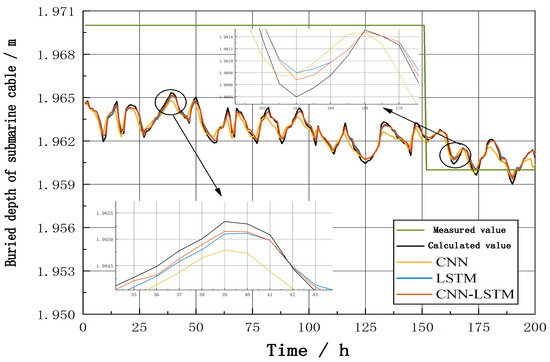
Figure 13.
Comparison of prediction results for burial depth change trend (Group 2).
According to Figure 12 and Table 4, the MAEs of the CNN-LSTM neural network model decreased by 0.234 and 0.040, the RMSEs decreased by 0.353 and 0.047, and the MAPEs decreased by 11.69% and 2.02%, compared with those of the single-CNN and single-LSTM models, respectively.

Table 4.
Comparison of different prediction models (Group 1).
Figure 13 and Table 5 show that the MAEs of the CNN-LSTM neural network models decreased by 0.194 and 0.028, the RMSEs decreased by 0.256 and 0.025, and the MAEs decreased by 9.86% and 1.39% compared with those of the single-CNN and single-LSTM models, respectively. In addition, the prediction accuracy and prediction efficiency of the CNN-LSTM neural network model in Figure 13 are greater compared with those in Figure 12, indicating that the CNN-LSTM neural network model has a better prediction effect when the burial depth of a submarine cable changes in a large range.

Table 5.
Comparison of different prediction models (Group 2).
In summary, on the basis of nearly identical model training and debugging times, the CNN-LSTM-based submarine cable burial depth variation trend prediction model proposed in this paper achieves a higher prediction accuracy and greatly improves prediction efficiency compared with a single model; the submarine cable burial depth values of future time nodes can subsequently be predicted.
6. Conclusions
In this paper, a prediction model for the burial depth trend of submarine cables considering the dynamic characteristics of thermal resistance is proposed. Firstly, a parallel thermal circuit model of a three-core submarine cable is built, and calculated results of the submarine cable’s burial depth are derived and revised considering the dynamic characteristics of the thermal resistance of the submarine cable’s structural materials. Then, a CNN is used to explore in depth the internal relationship between the burial depth calculation dataset and the time node, and the results are input to an LSTM neural network for optimized training, resulting in a prediction model for trends in the variation in the submarine cable’s burial depth. The following conclusions can be drawn from this paper:
- (1)
- There is an inevitable correlation between the temperature of the submarine cable core and the burial depth of the submarine cable. By building a thermal circuit model of the submarine cable and combining it with the structural parameters of the submarine cable, the burial depth of the submarine cable can be calculated.
- (2)
- The error of the submarine cable burial depth value calculated according to the IEC standard is obviously larger than that calculated according to the dynamic value of its thermal resistance, which proves that the method of calculating submarine cable burial depth based on the dynamic characteristics of thermal resistance has high calculation accuracy.
- (3)
- A CNN is used to explore the internal relationship between the burial depth calculation dataset and the time node in depth; the results are input to an LSTM neural network for optimization and training, and a prediction model for trends in burial depth variation in submarine cables is obtained.
- (4)
- Compared with single artificial intelligence prediction models such as a CNN neural network and an LSTM neural network, the prediction model for submarine cable burial depth change trends based on a CNN-LSTM network proposed in this paper has a higher prediction accuracy and greatly improves prediction efficiency.
Author Contributions
Conceptualization, Z.H. and X.Y.; methodology, Z.H., X.Y. and X.L.; writing—original draft preparation, H.Z., M.H., J.L. and Q.L.; writing—review and editing, Z.H., X.Y., X.L. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project “study on section optimization of new energy power cable based on cable transient current carrying capacity ” (grant number SWEPDI-FG-KXF-2023-0080).
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding authors.
Acknowledgments
The authors are thankful for comments from the reviewers of this article. The authors would like to take this opportunity to thank their data collection assistants and the anonymous respondents who responded to the questionnaire.
Conflicts of Interest
Authors Zhenxing Hu, Xueyong Ye, Xiaokang Luo and Hao Zhang were employed by the company Southwest Electric Power Design Institute Co., Ltd. of China Power Engineering Consulting Group. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Jiang, Z.; Yu, Q.; Li, L.; Liu, Y. Expansion Planning Method of Offshore Multiplatform Power System with Wind Power Considering Cable Size Selection. IEEE Access 2021, 9, 129796–129809. [Google Scholar] [CrossRef]
- Zhang, T.; Du, A.; Li, L.; Wei, R.; Tan, H.; Wang, K.; Li, Z. Analysis of Three-core Composite Submarine Cable Damage due to Ship Anchor. IEEE Access 2022, 10, 93910–93920. [Google Scholar] [CrossRef]
- Duraisamy, N.; Gooi, H.B.; Ukil, A. Ampacity Estimation for Submarine Power Cables Installed in Saturated Seabed—Experimental Studies. IEEE Trans. Ind. Appl. 2020, 56, 6229–6237. [Google Scholar] [CrossRef]
- Ji, D.X.; Zhou, J.L.; Qian, J.H.; Shao, J.; Zhang, H. Current Development Review of Submarine Cable Detection Methods. South. Power Syst. Technol. 2021, 15, 36–49. [Google Scholar]
- Asakawa, K.; Shirasaki, Y.; Iwamoto, Y. Metal Detector for Tracing Submarine Telecommunication Cables. IEEE Trans. Instrum. Meas. 1983, 32, 477–483. [Google Scholar] [CrossRef]
- Zhang, J.; Xiang, X.; Li, W. Advances in Marine Intelligent Electromagnetic Detection System, Technology, and Applications: A Review. IEEE Sens. J. 2021, 23, 4312–4326. [Google Scholar] [CrossRef]
- Qin, X.; Luo, X.; Wu, Z.; Shang, J.; Zhao, D. Deep Learning-Based High Accuracy Bottom Tracking on 1-D Side-Scan Sonar Data. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Foresti, G.L. Visual inspection of sea bottom structures by an autonomous underwater vehicle. IEEE Trans. Syst. Man Cybern. Part B 2001, 31, 691–705. [Google Scholar] [CrossRef]
- IEC 60287-1-1; Electric Cables-Calculation of the Current Rating Part 1-1, Current Rating Equations (100% Load Factor) and Calculation of Losses. HIS: Geneva, Switzerland, 2006.
- Hao, Y.; Huang, J.; Yang, L.; Fu, M.; Zhou, R. Analytical Calculation Method of Steady-State Current Capacity of HVDC Cables. Power Syst. Technol. 2016, 40, 1283–1288. [Google Scholar]
- Jiayin, B.; Yonglan, L.; Luping, S. Analysis of Steady-state Heat Path Model and Calculation of Current Carrying Capacity for 500 kV Power Cable. Insul. Mater. 2019, 52, 96–101. [Google Scholar]
- Duan, R.; Peng, X.; Li, C.; Yang, Z.; Jiang, Y.; Li, X.; Liu, S. A Hybrid Three-Staged, Short-Term Wind-Power Prediction Method Based on SDAE-SVR Deep Learning and BA Optimization. IEEE Access 2022, 10, 123595–123604. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, H.; Sun, X. Residual Life Prediction of Bearings Based on SENet-TCN and Transfer Learning. IEEE Access 2022, 10, 123007–123019. [Google Scholar] [CrossRef]
- Yang, H.F.; Dillon, T.S.; Chen, Y.P.P. Optimized structure of the traffic flow forecasting model with a deep learning approach. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2371–2381. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Li, R.; Tang, H.; Liu, Y.; Wan, X.; Dong, X.; Saripan, M.I.; Lan, X.; Song, H.; Zhou, Y. Task-State EEG Signal Classification for Spatial Cognitive Evaluation Based on Multiscale High-Density Convolutional Neural Network. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 1041–1051. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Tan, E.; Li, L.; Wang, G.; Wang, J.; Wang, P. Hybrid traffic forecasting model with fusion of multiple spatial toll collection data and remote microwave sensor data. IEEE Access 2018, 6, 79211–79221. [Google Scholar] [CrossRef]
- Park, K.; Choi, Y.; Choi, W.J.; Ryu, H.-Y.; Kim, H. LSTM-Based Battery Remaining Useful Life Prediction with Multi-Channel Charging Profiles. IEEE Access 2020, 8, 20786–20798. [Google Scholar] [CrossRef]
- Li, J.; Zhang, A.; Li, Q.; Huang, B. Prediction Model of Submarine Cable Burial Depth Trend Based on CNN-LSTM. In Proceedings of the 2022 IEEE 6th Conference on Energy Internet and Energy System Integration (EI2), Chengdu, China, 11–13 November 2022; pp. 2332–2336. [Google Scholar]
- Lenhart, T.; Eckhardt, K.; Fohrer, N.; Frede, H.-G. Comparison of two different approaches of sensitivity analysis. Phys. Chem. Earth Parts A/B/C 2002, 27, 645–654. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Song, J. Short-term orbit prediction based on LSTM neural network. Syst. Eng. Electron. 2022, 44, 939–947. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).