The Reliability and Profitability of Virtual Power Plant with Short-Term Power Market Trading and Non-Spinning Reserve Diesel Generator
Abstract
1. Introduction
2. Literature Review
- -
- -
- Techno-economic optimization models (stochastic): In addition to unit commitment [18] and economic dispatch, stochastic-based optimization models uncertainties in renewable energy generation [19], generation forecasting [20], demand load forecasting [21], and market price uncertainty [22]. Chance-constraint optimization, scenario-based optimization, and stochastic robust optimization are among three well-known VPP operating optimization methods under uncertainty [23].
- -
- -
- Unlike previous research, which has focused on energy storage (supply or discharge), this study utilizes energy storage along with a diesel generator (produce) to reduce uncertainty. To cap CO2 emissions, this study proposes a non-spinning reserve DG. The proposed DG’s operation is limited based on two additional constraints: (I) minimum running time and (II) maximum number of switching times per day.
- -
- Moreover, this study suggests a mixed integer optimization model to support electric market participants in choosing the most profitable market between the DA and ID markets. The market selection is figured out in terms of power income in both markets, selling surplus power, shortage costs, and the operation costs of technologies.
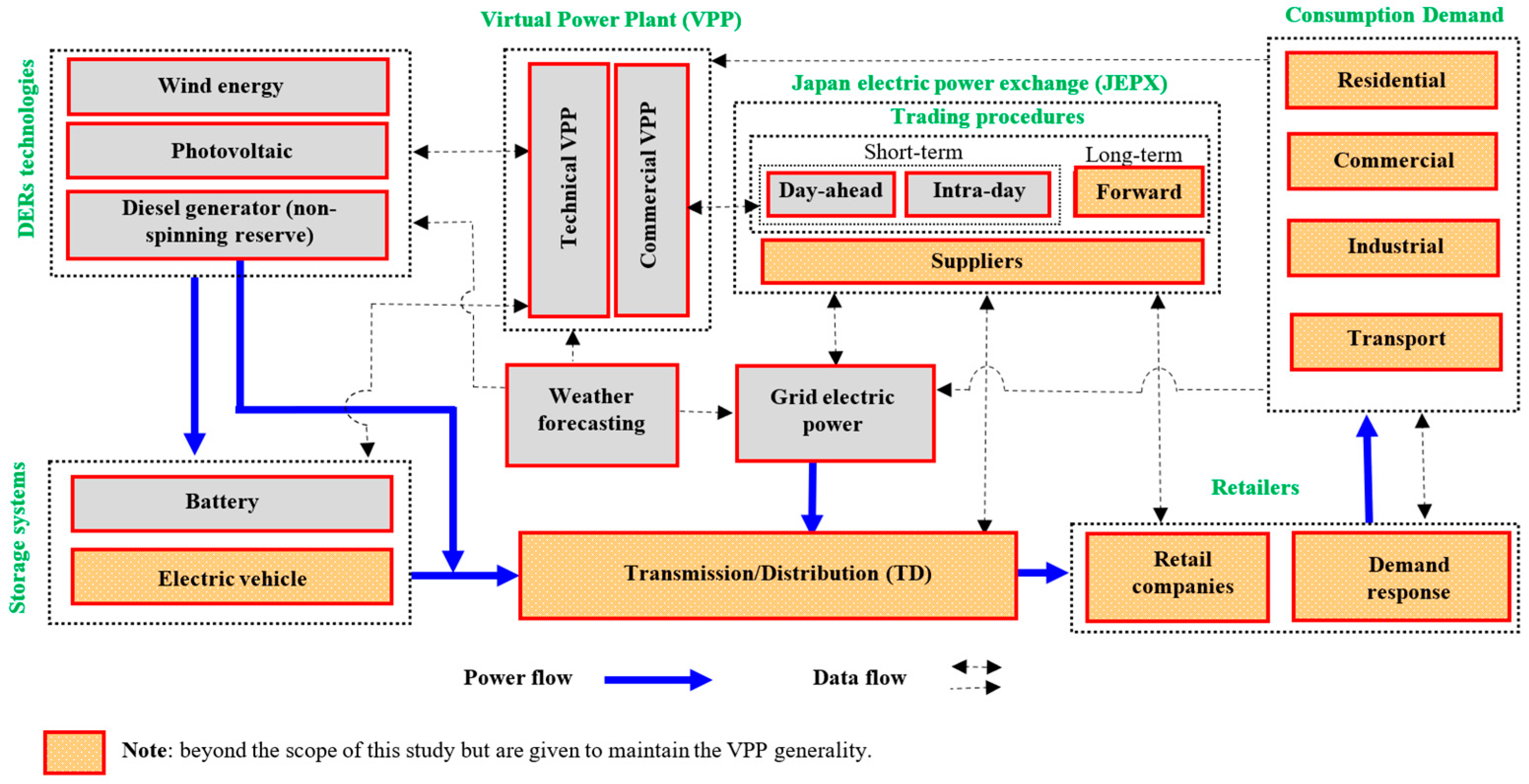
3. Materials and Methods
- -
- The estimated VPP power supply does not meet the minimum tradable amount of the DA market, or
- -
- The optimization model suggests the ID market.
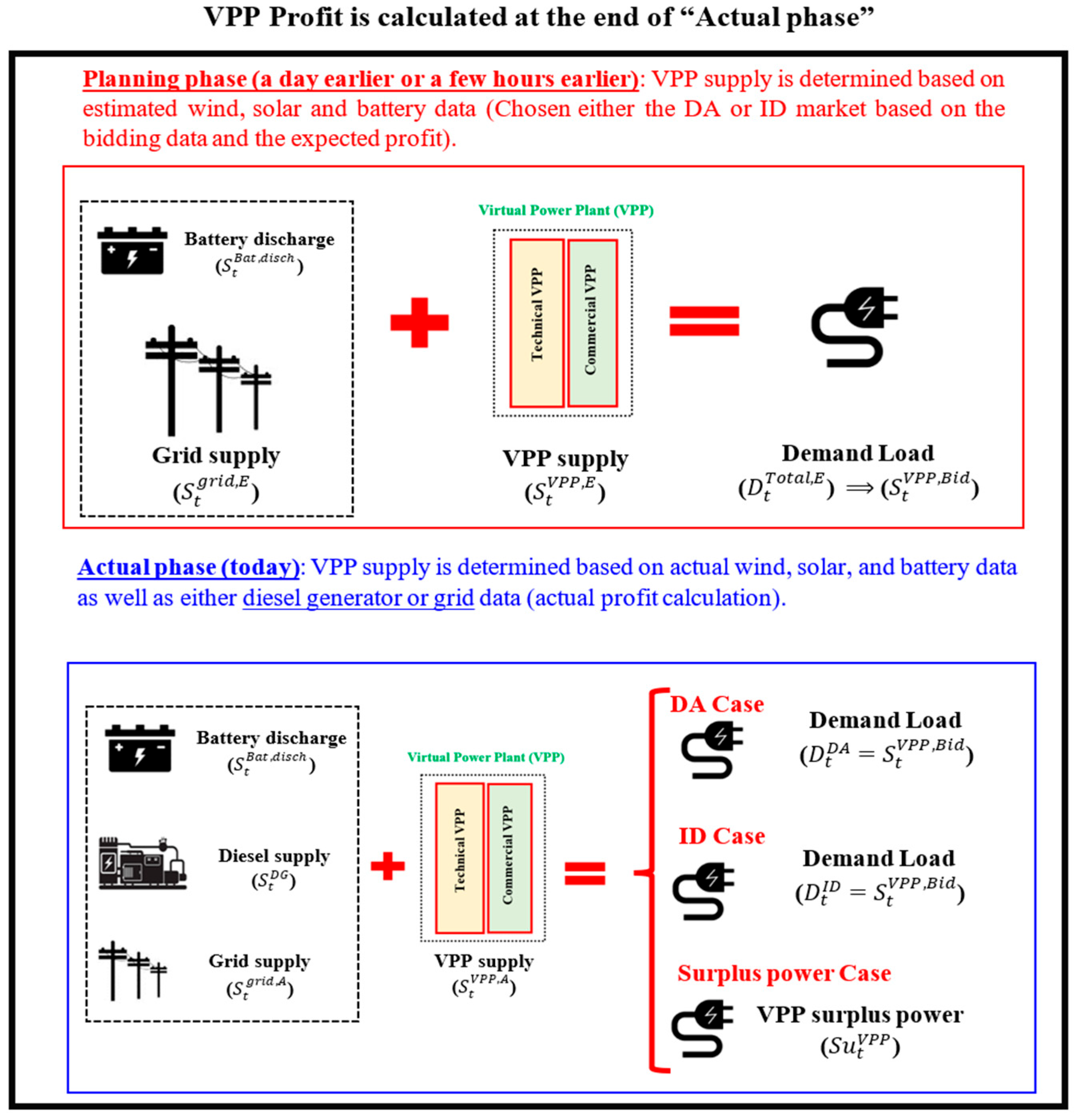
3.1. Descriptions of VPP Models
- -
- The actual power supply by the VPP () is equal to : In this case, the actual profit is the same as the expected profit,
- -
- : In this case, the actual profit will be greater than the expected profit due to selling the surplus power. The generation cost of surplus power should be deducted from the selling price,
- -
- : In this case, the unmet demand should be supplied by energy storage and either a non-spinning reserve DG or grid power. The actual profit decreases in terms of power purchases from the grid, diesel operation costs, and a drop in the selling price compared to the planning price ().
3.2. VPP Mathematical Model
3.2.1. VPP Objective Function
3.2.2. VPP Constraints
- A.
- Supply–demand balancing constraint:
- -
- Charging power into the battery and surplus power, or
- -
- Discharging power from the battery and either the grid or DG power supply.
- B.
- Technological constraints of DERs:
- C.
- Energy storage constraints:
- D.
- Non-spinning reserve diesel generator constraint:
- E.
- Additional constraints to adjust the actual profit objective function:
- The initial binary variable of the DG becomes one, or : Equations (27) and (28) assign a binary value for the initial DG indicator by which the DG’s operation is tracked.
- Minimum running time of the DG, or : The minimum running time is used to avoid starting the DG on and off frequently because of inefficient fuel burning in the startup, warmup, unload, and cool-down phases. The minimum running time depends on several factors, such as fuel price, diesel capacity, the control unit of the VPP, and so on (at least 30 min is required because the startup and warmup phases take at least 4 minutes, and the shutdown and cool-down phases take more than or equal to 6 min) [38,39], but 30 min is the lowest value. Equation (33) finds the startup time for the DG via the variable if the DG is called on. Equations (29)–(32) count the number of consecutive settlement periods to ensure that their cumulative values are greater than or equal to L. The terms and calculate the count and cumulative sum of the consecutive settlement periods. The middle binary variable of the DG, , represents if the DG meets the minimum running time constraint. The ε and M2 indicate the epsilon (small value) and a big value (upper bound), respectively. This study sets 0.0005 and 48 for ε and M2, respectively.
- Maximum switching on/off times per day, or : Equations (33)–(36) figure out if the number of GD switching times is less or equal to its threshold. The variable adds up the cumulative sum until its value is less than the value using the middle binary variable of the DG. The final binary variable of the DG, , specifies the settlement periods in which the DG is allowed to operate based on the maximum switching times’ condition. Equation (36) finally calculates the DG indicator, which represents which settlement period is turned on.
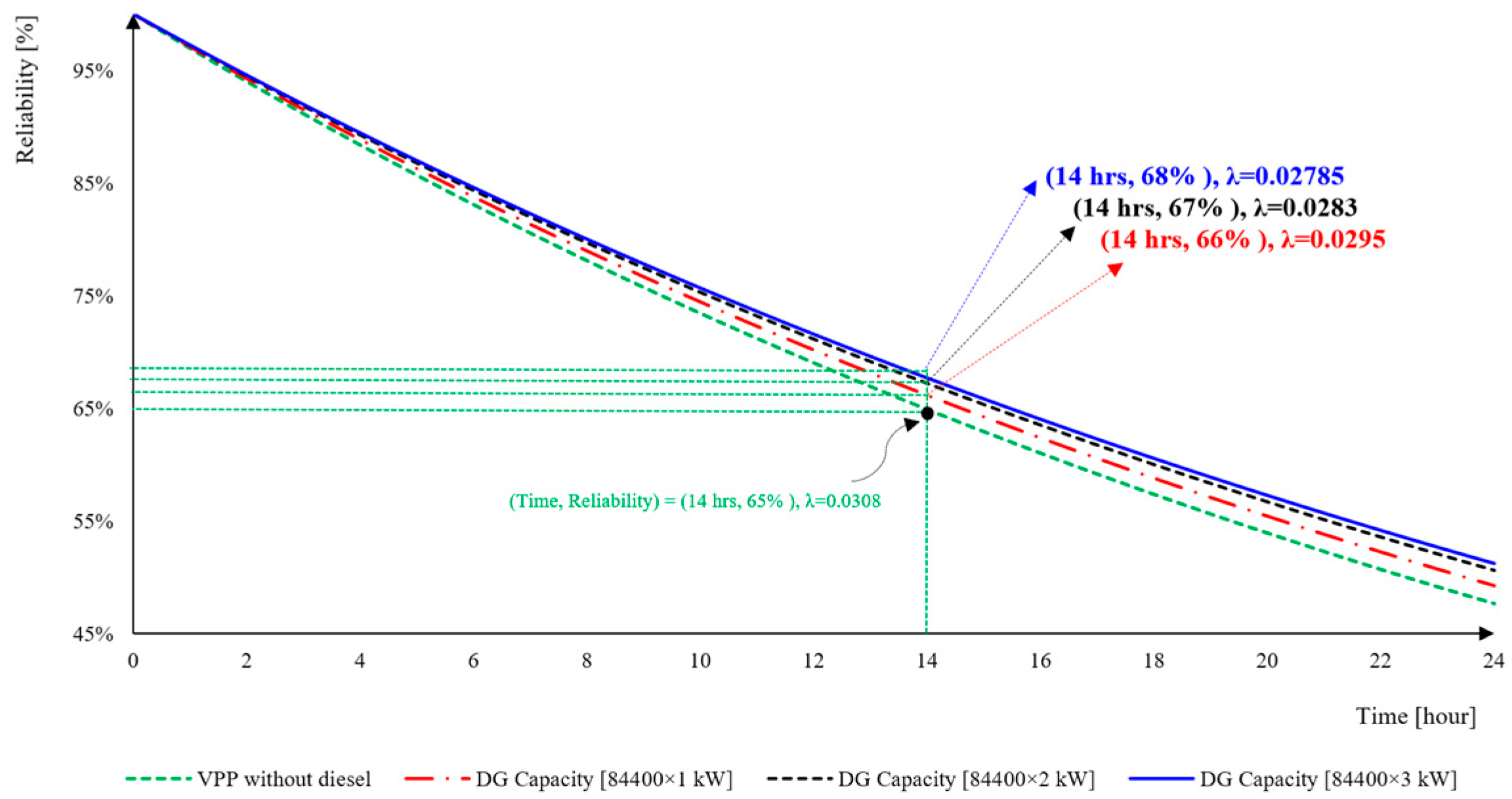
3.3. Reliability and Profitability of the VPP System
3.4. Model Data
4. Results
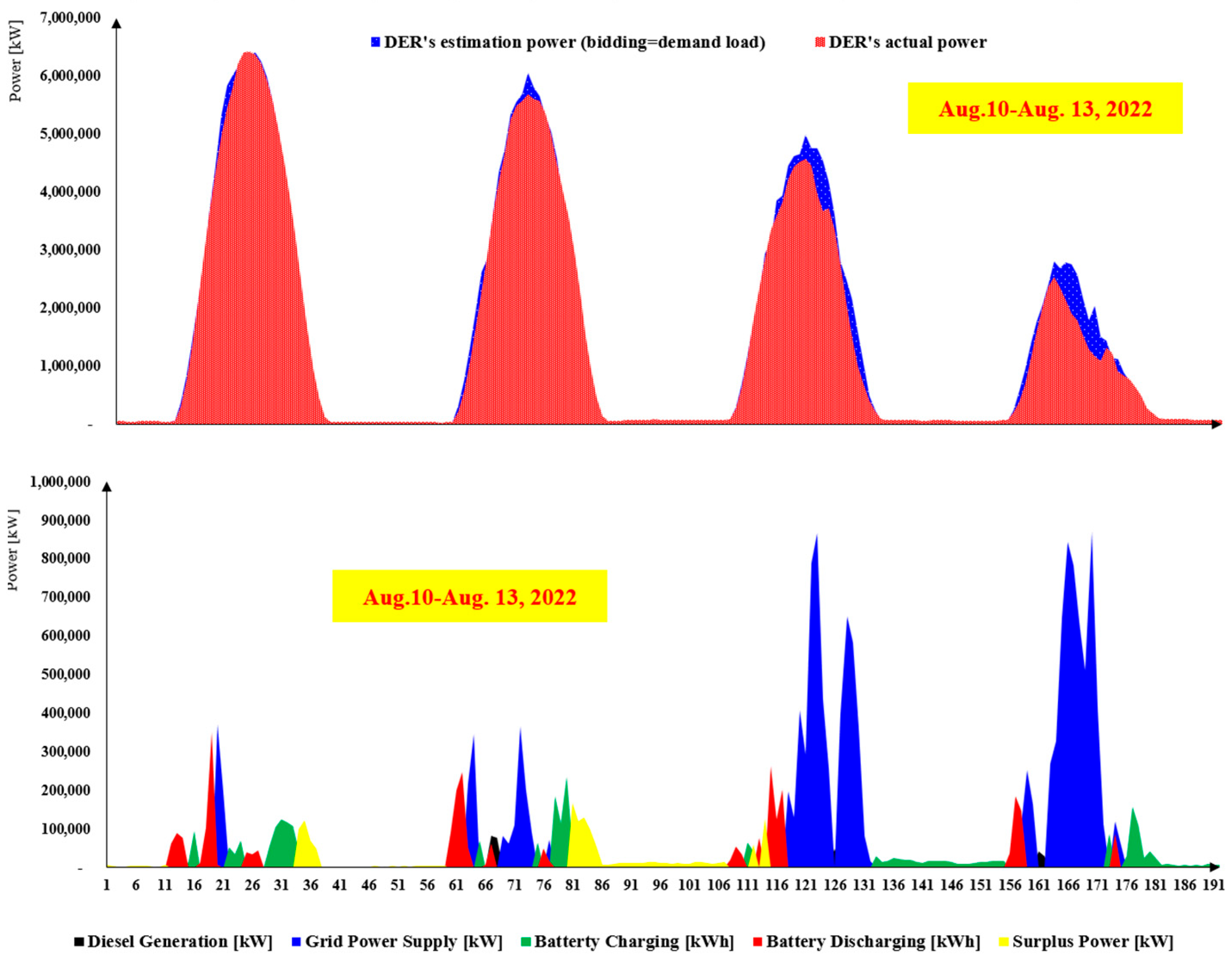
4.1. VPP Optimization Model’s Results
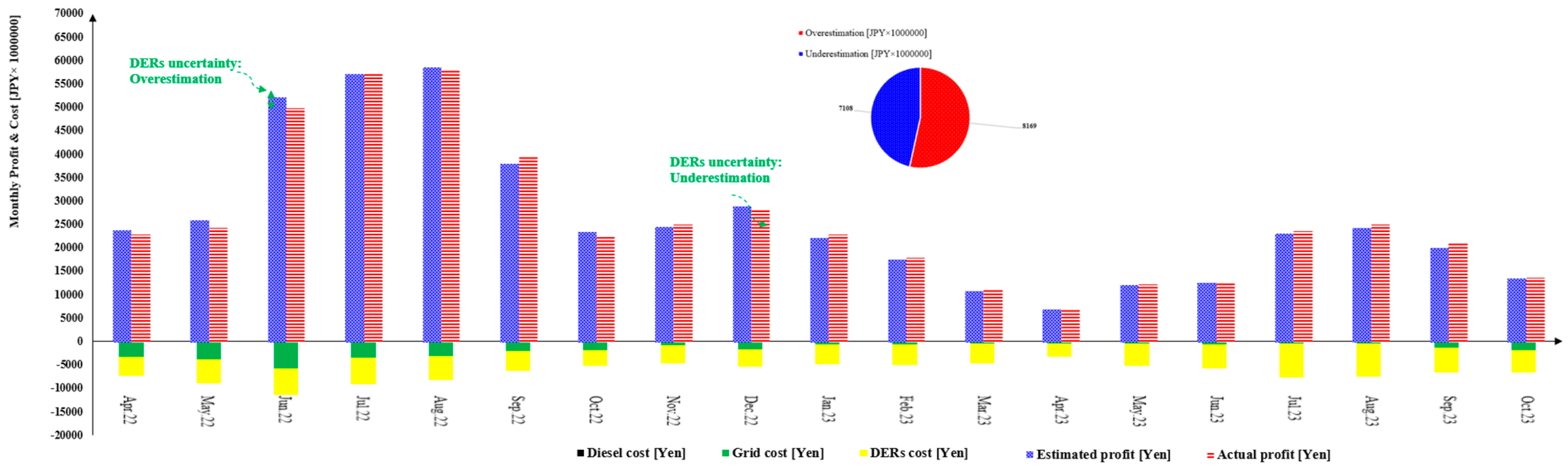
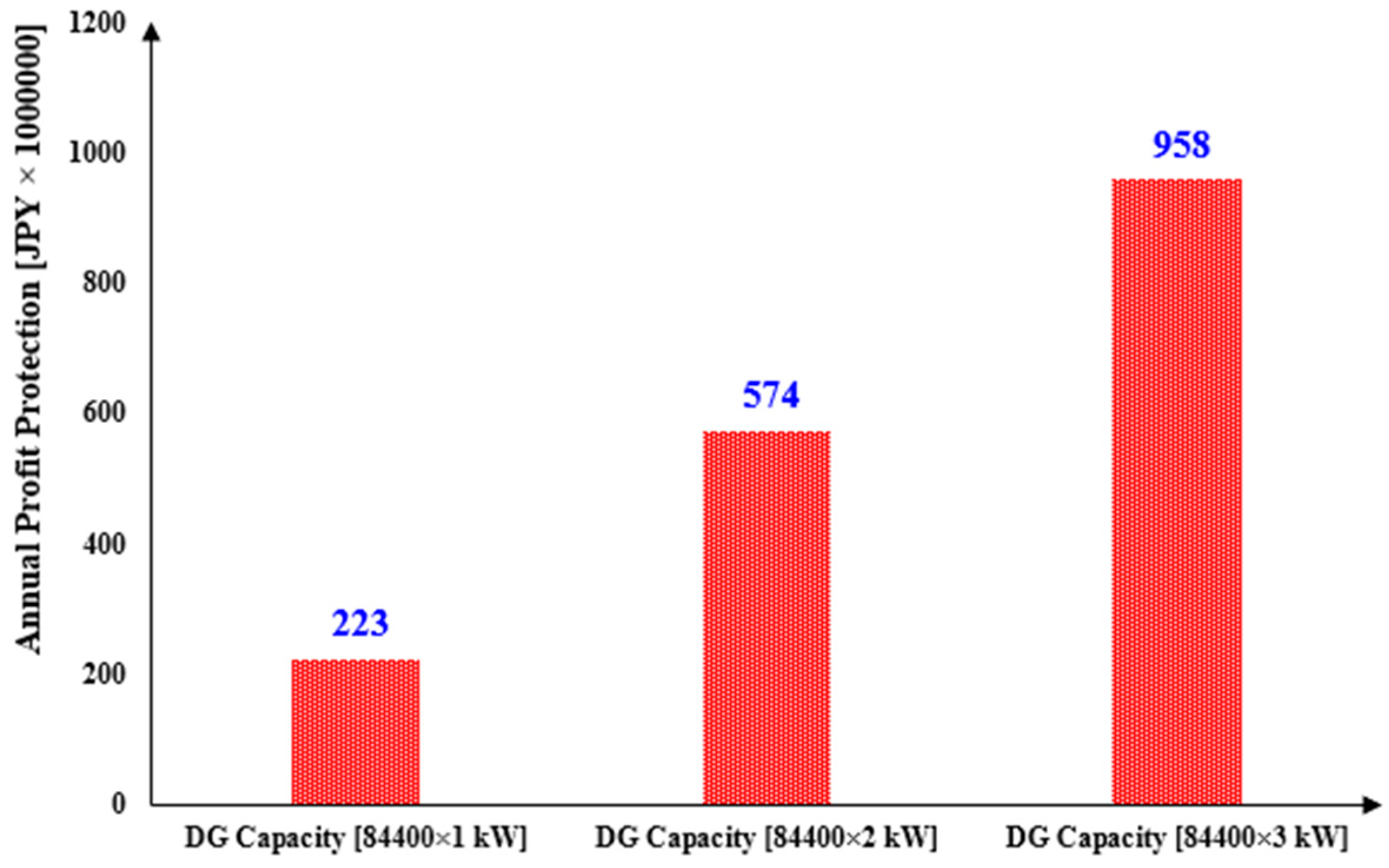
4.2. VPP Reliability and Profitability Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | ||
| Majority of variables’ format: A refers to Demand, Generation, Supply, Price, Surplus, State of charge (SOC), Cost, Integer/Binary/Slack variables, B specifies source of power supply (technology), demand sources, market types, share of selling power, negative/positive slack variable C indicates settlement period, minimum or maximum capacity for a technology, and D represents additional information such as estimated or actual power supply, For example, : represent estimated grid supply power at settlement period t. | ||
| Input Variables | Description | Unit |
| Total estimated demand load at period t | kW | |
| VPP day-ahead (DA) demand load at period t | kW | |
| VPP intra-day (ID) demand load at period t | kW | |
| Actual power generation by wind turbine at period t | kW | |
| Estimated power generation by wind turbine at period t | kW | |
| Actual power generation by solar panel at period t | kW | |
| Estimated power generation by solar panel at period t | kW | |
| Power generation by tDG at period t | kW | |
| Day-ahead power price at period t | $/kW | |
| Intra-day power price at period t | $/kW | |
| Estimated VPP power supply at period t | kW | |
| VPP power supply based on bid data at period t | kW | |
| Actual VPP power supply at period t | kW | |
| Intermediate Variables | Description | Unit |
| Battery state of charge at period t | kW | |
| Decision variable | Description | Unit |
| Continuous | ||
| Discharging power from battery at period t | kW | |
| Charging power into battery at period t | kW | |
| Estimated supply power by grid at period t | kW | |
| Possible supply power by grid at period t | kW | |
| Actual supply power by grid at period t | kW | |
| Maximum between and at period t | kW | |
| Possible supply power by DG at period t | kW | |
| Actual supply power by DG at period t | kW | |
| VPP surplus power at period t | kW | |
| Maximum between and at period t | kW | |
| Binary | ||
| Binary variable for day-ahead market | ||
| Binary variable for grid power selling at period t | ||
| Binary variable for surplus power selling at period t | ||
| Binary variable for DG at period t | ||
| Initial binary variable for operation of DG at period t | ||
| Middle binary variable for operation of DG at period t | ||
| Final binary variable for operation of DG at period t | ||
| Binary variable for battery charging at period t | ||
| Binary variable for battery discharging at period t | ||
| Integer | ||
| Counting number of running times for each possible operation period at period t | ||
| Cumulative sum of running times for a day until period t | ||
| Cumulative sum of maximum switching on/off times until period t per day | ||
| Minimum running time of DG operation (minute) | ||
| Maximum number of DG switching on/off times per day | ||
| Slack variable | Description | Unit |
| Negative slack variable at period t | kW | |
| Positive slack variable at period t | kW | |
| Model Parameters | Description | Unit |
| Maximum discharging power from battery at period t | kW | |
| Maximum SOC of battery (80% of battery capacity) | kWh | |
| Minimum SOC of battery (20% of battery capacity) | kWh | |
| Operation cost of DG | $/kW∆t | |
| Operation cost of VPP | $/kW∆t | |
| Maximum power generation capacity of DG | kW | |
| Max power generation capacity of wind turbine | kW | |
| Max power generation capacity of solar panel | kW | |
| Minimum power generation of DG | kW | |
| Share of selling surplus power in ID market | % | |
| Other symbols | Description | |
| VPP system reliability at hour h | % | |
| VPP system failure rate at period t | % | |
| Failure rate of the VPP system | % | |
| Settlement period (here 30 min) | minute | |
| Epsilon or small value (here | ||
| M1 | Big number or Big-M (here M1 = 589,200) | |
| M2 | Big number or Big-M (here M2 = 48) | |
| T | Time horizon of optimization (Number of days × settlement periods) | |
| Minimum tradable amount in DA market | kW | |
| Minimum tradable amount in ID market | kW | |
References
- Naval, N.; Yusta, J.M. Virtual power plant models and electricity markets—A review. Renew. Sustain. Energy Rev. 2021, 149, 111393. [Google Scholar] [CrossRef]
- Hobbs, B.F. Optimization methods for electric utility resource planning. Eur. J. Oper. Res. 1995, 83, 1–20. [Google Scholar] [CrossRef]
- Bukar, A.L.; Hamza, M.F.; Ayub, S.; Abobaker, A.K.; Modu, B.; Mohseni, S.; Brent, A.C.; Ogbonnaya, C.; Mustapha, K.; Idakwo, H.O. Peer-to-peer electricity trading: A systematic review on current developments and perspectives. Renew. Energy Focus 2023, 44, 317–333. [Google Scholar] [CrossRef]
- JEPX. Japan Wholesale Electric Power Exchange Trading Guide; JEPX: Tokyo, Japan, 2019. [Google Scholar]
- The Electric Power Industry in Japan 2023. Japan Electric Power Information Center (JEPIC). Available online: https://www.jepic.or.jp/en/data/epijpdf.html (accessed on 5 December 2023).
- JEPX Trading Market Data. Japan Electric Power Exchange, 28 November 2003. Available online: https://www.jepx.jp/electricpower/market-data/spot/ (accessed on 10 November 2023).
- Mashhour, E.; Masoud, M.-T.S. Bidding Strategy of Virtual Power Plant for Participating in Energy and Spinning Reserve Markets—Part I: Problem Formulation. IEEE Trans. Power Syst. 2011, 26, 949–956. [Google Scholar] [CrossRef]
- Rouzbahani, H.M.; Karimipour, H.; Lei, L. A review on virtual power plant for energy management. Sustain. Energy Technol. Assess. 2021, 47, 101370. [Google Scholar] [CrossRef]
- Zhu, J.; Ihara, S. The market for spinning reserve and its impacts on energy prices. In Proceedings of the IEEE Power Engineering Society Winter Meeting, Singapore, 23–27 January 2000. [Google Scholar]
- Yu, S.; Fang, F.; Liu, Y.; Liu, J. Uncertainties of virtual power plant: Problems and countermeasures. Appl. Energy 2019, 239, 454–470. [Google Scholar] [CrossRef]
- Ko, R.; Kang, D.; Joo, S.-K. Mixed Integer Quadratic Programming Based Scheduling Methods for Day-Ahead Bidding and Intra-Day Operation of Virtual Power Plant. Energies 2019, 12, 1410. [Google Scholar] [CrossRef]
- Dielmann, K.-P.; Velden, A.V.D. Virtual power plants (VPP)—A new perspective for energy generation? In Proceedings of the 9th International Scientific and Practical Conference of Students, Post-Graduates Modern Techniques and Technologies, Tomsk, Russia, 7–11 April 2003. [Google Scholar]
- Hasankhani, A.; Vahidi, B.; Riahy, G.H. Replacing Diesel Generator with Wind Turbine & LI-ION Battery in Virtual Power Plant. Sci. Int. 2014, 26, 583–587. [Google Scholar]
- Elwan, A.A.; Habibuddin, M.H.; Arief, Y.Z.; Sharan, S.N.A.M.; Mokhtar, A.S.B.; Idris, R.B.M. Optimization of Distributed Generators in a Virtual Power Plan Using Mixed Integer Linear Programming Method. In Renewable Power for Sustainable Growth; Springer: Singapore, 2024. [Google Scholar]
- Abiodun, K.; Hood, K.; Cox, J.L.; Newman, A.M.; Zolan, A.J. The value of concentrating solar power in ancillary services markets. Appl. Energy 2023, 334, 120518. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, C.; Ding, Y.; Xydis, G.; Wang, J.; Østergaard, J. Review of real-time electricity markets for integrating distributed energy resources and demand response. Appl. Energy 2015, 138, 695–706. [Google Scholar] [CrossRef]
- Haugen, M.; Farahmand, H.; Jaehnert, S.; Fleten, S. Representation of uncertainty in market models models for operational planning and forecasting in renewable power systems: A review. Energy Syst. 2023. [Google Scholar] [CrossRef]
- Wozabal, D.; Rameseder, G. Optimal bidding of a virtual power plant on the Spanish day-ahead and intraday market for electricity. Eur. J. Oper. Res. 2020, 280, 639–655. [Google Scholar] [CrossRef]
- Nadimi, R.; Tokimatsu, K. Applying consumption time analysis to measure fundamental energy needs: A method to quantify households’ energy services. MRS Energy Sustain. 2022, 9, 501–517. [Google Scholar] [CrossRef]
- Gomes, I.; Pousinho, H.; Melício, R.; Mendes, V. Stochastic coordination of joint wind and photovoltaic systems with energy storage in day-ahead market. Energy 2017, 124, 310–320. [Google Scholar] [CrossRef]
- Zamani, A.G.; Zakariazadeh, A.; Jadid, S. Day-ahead resource scheduling of a renewable energy based virtual power plant. Appl. Energy 2016, 169, 324–340. [Google Scholar] [CrossRef]
- Valitov, N.; Maier, A. Asymmetric information in the German intraday electricity market. Energy Econ. 2020, 89, 104785. [Google Scholar] [CrossRef]
- Epexspot. European Market Coupling. Available online: https://www.epexspot.com/en/marketcoupling#single-day-ahead-coupling-sdac (accessed on 12 December 2023).
- Le, H.L.; Ilea, V.; Bovo, C. Integrated European intra-day electricity market: Rules, modeling and analysis. Appl. Energy 2019, 238, 258–273. [Google Scholar] [CrossRef]
- TEPCO Power Grid. TEPCO. Available online: https://www.tepco.co.jp/en/forecast/html/download-e.html (accessed on 1 November 2023).
- Wang, H.; Riaz, S.; Mancarella, P. Integrated techno-economic modeling, flexibility analysis, and business case assessment of an urban virtual power plant with multi-market co-optimization. Appl. Energy 2019, 259, 114142. [Google Scholar] [CrossRef]
- Cavazzini, G.; Benato, A.; Pavesi, G.; Ardizzon, G. Techno-economic benefits deriving from optimal scheduling of a Virtual Power Plant: Pumped hydro combined with wind farms. J. Energy Storage 2021, 37, 102461. [Google Scholar] [CrossRef]
- Abdullah, W.S.W.; Osman, M.; Kadir, M.Z.A.A.; Verayiah, R.; Aziz, N.F.A.; Rasheed, M.A. Techno-economics analysis of battery energy storage system (BESS) design for virtual power plant (VPP)—A case study in Malaysia. J. Energy Storage 2021, 83, 102568. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, H.; Xu, Y.; Li, Z.; Lin, Z.; Liang, Z. A mixed-integer SDP solution to distributionally robust unit commitment with second order moment constraints. CSEE J. Power Energy Syst. 2020, 6, 374–383. [Google Scholar]
- Ahmadian, A.; Ponnambalam, K.; Almansoori, A.; Elkamel, A. Optimal Management of a Virtual Power Plant Consisting of Renewable Energy Resources and Electric Vehicles Using Mixed Integer Linear Programming and Deep Learning. Energies 2023, 16, 1000. [Google Scholar] [CrossRef]
- Sharadga, H.; Hajimirza, S.; Balog, R.S. Time series forecasting of solar power generation for large-scale photovoltaic plants. Renew. Energy 2020, 150, 797–807. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, Z.; Huang, M.; Yang, S.; Zhu, J.; Zhang, M.; Chen, D. Research on day-ahead optimal dispatching of virtual power plants considering the coordinated operation of diverse flexible loads and new energy. Energy 2024, 297, 131235. [Google Scholar] [CrossRef]
- Baringo, A.; Baringo, L. A Stochastic Adaptive Robust Optimization Approach for the Offering Strategy of a Virtual Power Plant. IEEE Trans. Power Syst. 2017, 32, 3492–3504. [Google Scholar] [CrossRef]
- Naughton, J.C. A Modelling Framework for Virtual Power Plants under Uncertainty. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2022. [Google Scholar]
- Liu, X.; Ni, Y.; Sun, Y.; Wang, J.; Wang, R.; Sun, Q. Multi-VPPs power-carbon joint trading optimization considering low-carbon operation mode. J. Energy Storage 2024, 83, 110786. [Google Scholar] [CrossRef]
- Yan, X.; Gao, C.; Jiang, H.; Francois, B. Multi-objective optimization and profit allocation of virtual power plant considering the security operation of distribution networks. J. Energy Storage 2024, 89, 111607. [Google Scholar] [CrossRef]
- Song, H.; Gu, M.; Liu, C.; Amani, A.M.; Jalili, M.; Meegahapola, L.; Yu, X.; Dickeson, G. Multi-objective battery energy storage optimization for virtual power plant applications. Appl. Energy 2023, 352, 121860. [Google Scholar] [CrossRef]
- Lambert, M.; Hassani, R. Diesel genset optimization in remote microgrids. Appl. Energy 2023, 340, 121036. [Google Scholar] [CrossRef]
- Nadimi, R.; Goto, M.; Tokimatsu, K. The impact of diesel operation time constraint on total cost of diesel-based hybrid renewable power system simulation model. Renew. Energy Focus 2023, 44, 40–55. [Google Scholar] [CrossRef]
- Kwag, H.-G.; Kim, J.-O. Reliability modeling of demand response considering uncertainty of customer behavior. Appl. Energy 2014, 122, 24–33. [Google Scholar] [CrossRef]
- Goudarzi, A.; Li, Y.; Xiang, J. Efficient energy management of renewable resources in microgrids. In Renewable Energy Microgeneration Systems; Academic Press: Cambridge, MA, USA, 2021; pp. 285–321. [Google Scholar]
- GlobalPetrolPrices.com. Available online: https://www.globalpetrolprices.com/natural_gas_prices/ (accessed on 13 December 2023).
- About Wind Energy—The Facts. Available online: https://www.wind-energy-the-facts.org/operation-and-maintenance-costs-of-wind-generated-power.html (accessed on 12 December 2023).
- Kikuchi, Y.; Ishihara, T. Assessment of capital expenditure for fixed-bottom offshore wind farms using probabilistic engineering cost model. Appl. Energy 2023, 341, 120912. [Google Scholar] [CrossRef]
- Yamazaki, M.; NEDO; Ikki, O.; RTS Corporation. National Survey Report of PV Power Applications in Japan; NEDO: Kawasaki, Japan, 2020. [Google Scholar]
- International Renewable Energy Agency. Energy Profile Japan. 2020. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Statistics/Statistical_Profiles/Asia/Japan_Asia_RE_SP.pdf (accessed on 25 March 2024).
- Kimura, K. Solar Power Generation Costs in Japan Current Status and Future Outlook; Renewable Energy Institute: Tokyo, Japan, 2019. [Google Scholar]
- ISEP. Share of Electricity from Renewable Energy Sources in Japan (Preliminary). Institute for Sustainable Energy Policies. 2022. Available online: https://www.isep.or.jp/en (accessed on 12 December 2023).
- Jackson, N.D.; Gunda, T.; Gayoso, N.; Desai, J.; Walker, A. Operations, Maintenance, and Costconsiderations for PV+Storage in the United States; Sandia National Laboratories: Albuquerque, NM, USA, 2022. [Google Scholar]
- Yang, Z.; Radchenko, M.; Andrii, R.; Mikielewicz, D.; Radchenko, R. Gas Turbine Intake Air Hybrid Cooling Systems and a New Approach to Their Rational Designing. Energies 2022, 15, 1474. [Google Scholar] [CrossRef]
- Radchenko, M.; Radchenko, A.; Radchenko, R.; Kantor, S.; Konovalov, D.; Kornienko, V. Rational loads of turbine inlet air absorption-ejector cooling systems. J. Power Energy 2022, 236, 450–462. [Google Scholar] [CrossRef]
- Beal, L.D.R.; Hill, D.C.; Martin, R.A.; Hedengren, J.D. GEKKO Optimization Suite. Processes 2018, 6, 106. [Google Scholar] [CrossRef]

| Data | Type of Data | Data Collected Period | Data Resolution | Reference |
|---|---|---|---|---|
| Demand load | Estimated | 1 April 2022–31 October 2023 | 30-min | [37] |
| Actual | ||||
| Renewable power generation | Estimated | |||
| Actual | ||||
| Non-renewable power generation | Estimated | |||
| Actual | ||||
| Electric power prices | Day-ahead | 1 April 2022–31 October 2023 | 30-min | [6] |
| Intra-day | ||||
| Electric power volume | Day-ahead | |||
| Intra-day |
| Unit | Parameters | Initial Value | Reference |
|---|---|---|---|
| Battery | Initial SOC [kWh] | 117,840 | Assumed |
| Max discharge * [kWh] | 196,400 | Assumed | |
| Capacity * [kWh] | 589,200 | Estimated | |
| Diesel | Maximum capacity [kW] | 84,400 | Estimated |
| Min power generation [kW] | 0.3 × 84,400 | [41] | |
| Natural gas fuel cost [JPY/kWh] | 9.75587 ** | [42] | |
| Min diesel running time [min] | L × ∆t = 30 | [38] | |
| Warmup and cool-down time [min] | 10 | ||
| Max switching on/off per day | 2 | Assumed | |
| VPP | Supply cost [JPY/kWh] | 2.6208 | Estimated |
| Market | Minimum DA requirement [kW] | 1000 | [4] |
| Surplus power | Selling surplus power in ID market [%] | 100 | Assumed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadimi, R.; Takahashi, M.; Tokimatsu, K.; Goto, M. The Reliability and Profitability of Virtual Power Plant with Short-Term Power Market Trading and Non-Spinning Reserve Diesel Generator. Energies 2024, 17, 2121. https://doi.org/10.3390/en17092121
Nadimi R, Takahashi M, Tokimatsu K, Goto M. The Reliability and Profitability of Virtual Power Plant with Short-Term Power Market Trading and Non-Spinning Reserve Diesel Generator. Energies. 2024; 17(9):2121. https://doi.org/10.3390/en17092121
Chicago/Turabian StyleNadimi, Reza, Masahito Takahashi, Koji Tokimatsu, and Mika Goto. 2024. "The Reliability and Profitability of Virtual Power Plant with Short-Term Power Market Trading and Non-Spinning Reserve Diesel Generator" Energies 17, no. 9: 2121. https://doi.org/10.3390/en17092121
APA StyleNadimi, R., Takahashi, M., Tokimatsu, K., & Goto, M. (2024). The Reliability and Profitability of Virtual Power Plant with Short-Term Power Market Trading and Non-Spinning Reserve Diesel Generator. Energies, 17(9), 2121. https://doi.org/10.3390/en17092121








