Geometrical Optimization of Segmented Thermoelectric Generators (TEGs) Based on Neural Network and Multi-Objective Genetic Algorithm
Abstract
1. Introduction
2. Methods
2.1. Model and Boundary Conditions
2.2. Governing Equations
2.3. Neural Network Dataset Generation and Training
2.4. Multi-Objective Optimization with Constraint Condition
3. Results and Discussion
3.1. Neural Network Prediction
3.2. Optimization Results
3.3. Comparison Results
4. Conclusions
- A trade-off analysis between V and P is more in line with practical industrial requirements. Only through comprehensive consideration can the most suitable design solution be found.
- The computation time for 5000 sets of finite element models was 167 h, while the optimization process of the NSGA-II genetic algorithm took only 12 min. The RBF neural network model can rapidly predict the maximum output power of segmented TEGs with trapezoidal legs, thereby accelerating their structural optimization process.
- For the optimized segmented TEG with trapezoidal legs, when the range of V was from 52.8 to 216.2 mm3, as V increased, the optimal Sn,c, Sp,c, Kn, and Kp values remained basically unchanged. In this range, the geometric parameter Wc played an important role in the output performance of the segmented TEG with trapezoidal legs.
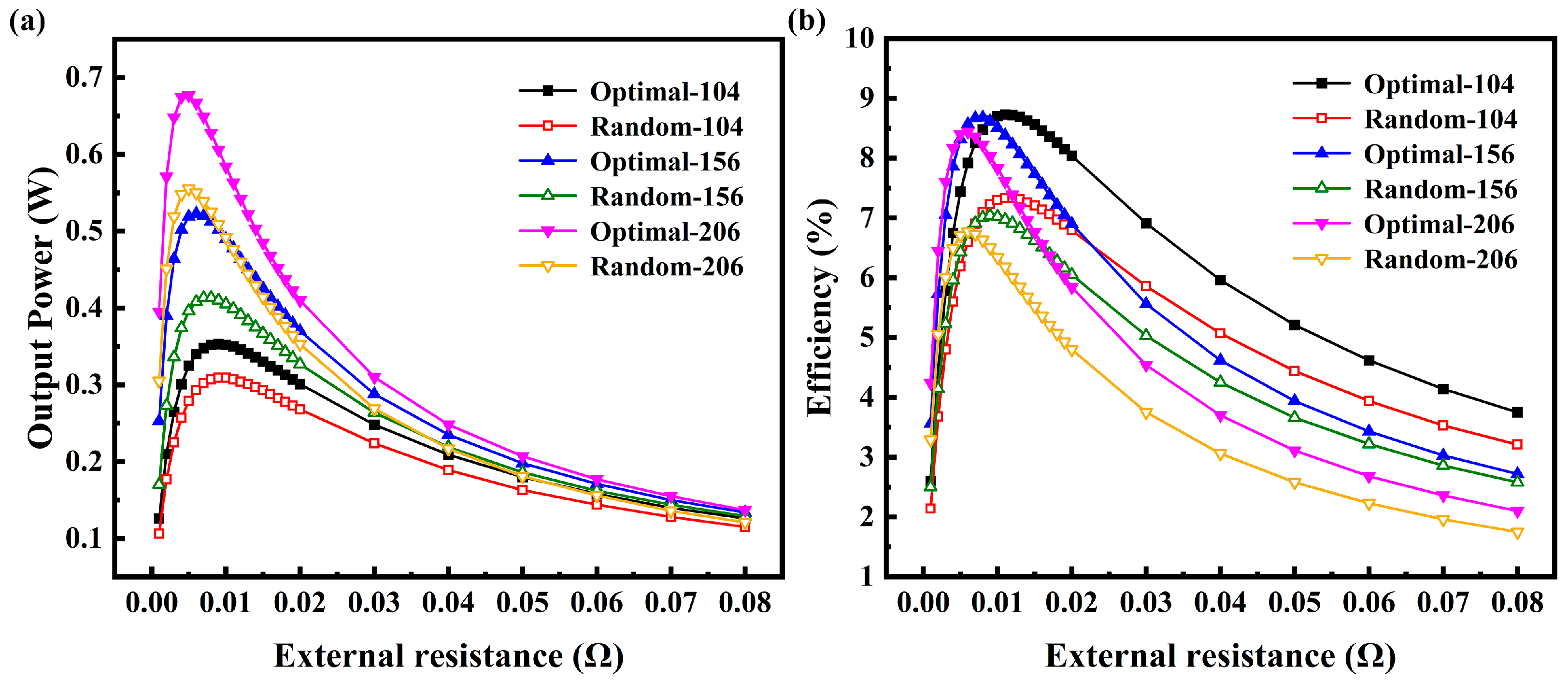
- When V was 104, 156, and 206 mm3, the optimized output power was increased by 14.2%, 26.6%, and 22%, respectively. The optimized conversion efficiency was also improved by 19.1%, 23.3%, and 24.7% respectively. The geometry before optimization is randomly generated, and another randomly selected non-optimized geometry (one for each volume) may yield either better or worse results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aydin, G. Production modeling in the oil and natural gas industry: An application of trend analysis. Pet. Sci. Technol. 2014, 32, 555–564. [Google Scholar] [CrossRef]
- Champier, D. Thermoelectric generators: A review of applications. Energy Convers. Manag. 2017, 140, 167–181. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Y.; Mei, D.; Chen, Z. Wearable thermoelectric generator to harvest body heat for powering a miniaturized accelerometer. Appl. Energy 2018, 215, 690–698. [Google Scholar] [CrossRef]
- Demir, M.E.; Dincer, I. Performance assessment of a thermoelectric generator applied to exhaust waste heat recovery. Appl. Therm. Eng. 2017, 120, 694–707. [Google Scholar] [CrossRef]
- Shittu, S.; Li, G.; Zhao, X.; Ma, X. Review of thermoelectric geometry and structure optimization for performance enhancement. Appl. Energy 2020, 268, 115075. [Google Scholar] [CrossRef]
- Cai, L.; Li, P.; Luo, Q.; Zhai, P.; Zhang, Q. Geometry optimization of a segmented thermoelectric generator based on multi-parameter and nonlinear optimization method. J. Electron. Mater. 2017, 46, 1552–1566. [Google Scholar] [CrossRef]
- Kishore, R.A.; Sanghadasa, M.; Priya, S. Optimization of segmented thermoelectric generator using taguchi and anova techniques. Sci. Rep. 2017, 7, 16746. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Shuai, J.; Mao, J.; Wang, Y.; Wang, Z.; Cai, W.; Sui, J.; Ren, Z. Effects of antimony content in MgAg0.97Sbx on output power and energy conversion efficiency. Acta Mater. 2016, 102, 17–23. [Google Scholar] [CrossRef]
- Zhou, X.; Yan, Y.; Lu, X.; Zhu, H.; Han, X.; Chen, G.; Ren, Z. Routes for high performance thermoelectric materials. Mater. Today 2018, 21, 974–988. [Google Scholar] [CrossRef]
- Cai, B.; Hu, H.; Zhuang, H.L.; Li, J.-F. Promising materials for thermoelectric applications. J. Alloys Compd. 2019, 806, 471–486. [Google Scholar] [CrossRef]
- Yang, J.; Liu, G.; Shi, Z.; Lin, J.; Ma, X.; Xu, Z.; Qiao, G. An insight into β-Zn4Sb3 from its crystal structure, thermoelectric performance, thermal stability and graded material. Mater. Today Energy 2017, 3, 72–83. [Google Scholar] [CrossRef]
- Lavric, E.D. Sensitivity analysis of thermoelectric module performance with respect to geometry. Chem. Eng. Trans. 2010, 21, 133–138. [Google Scholar]
- Meng, J.H.; Zhang, X.X.; Wang, X.D. Characteristics analysis and parametric study of a thermoelectric generator by considering variable material properties and heat losses. Int. J. Heat Mass Transf. 2015, 80, 227–235. [Google Scholar] [CrossRef]
- Maduabuchi, C.; Fagehi, H.; Alatawi, I.; Alkhedher, M. Predicting the optimal performance of a concentrated solar segmented variable leg thermoelectric generator using neural networks. Energies 2022, 15, 6024. [Google Scholar] [CrossRef]
- Fabian-Mijangos, A.; Min, G.; Alvarez-Quintana, J. Enhanced performance thermoelectric module having asymmetrical legs. Energy Convers. Manag. 2017, 148, 1372–1381. [Google Scholar] [CrossRef]
- Sahin, A.Z.; Yilbas, B.S. The thermoelement as thermoelectric power generator: Effect of leg geometry on the efficiency and power generation. Energy Convers. Manag. 2013, 65, 26–32. [Google Scholar] [CrossRef]
- Liu, H.B.; Wang, S.L.; Yang, Y.R.; Chen, W.H.; Wang, X.D. Theoretical analysis of performance of variable cross-section thermoelectric generators: Effects of shape factor and thermal boundary conditions. Energy 2020, 201, 117660. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, K.; Niu, Z.; Diao, H.; Du, Q.; Tian, H.; Shu, G. Power and efficiency factors for comprehensive evaluation of thermoelectric generator materials. Int. J. Heat Mass Transf. 2016, 93, 1034–1037. [Google Scholar] [CrossRef]
- Shittu, S.; Li, G.; Zhao, X.; Ma, X.; Akhlaghi, Y.G.; Ayodele, E. High performance and thermal stress analysis of a segmented annular thermoelectric generator. Energy Convers. Manag. 2019, 184, 180–193. [Google Scholar] [CrossRef]
- Liu, H.B.; Meng, J.H.; Wang, X.D.; Chen, W.H. A new design of solar thermoelectric generator with combination of segmented materials and asymmetrical legs. Energy Convers. Manag. 2018, 175, 11–20. [Google Scholar] [CrossRef]
- Ge, Y.; Liu, Z.; Sun, H.; Liu, W. Optimal design of a segmented thermoelectric generator based on three dimensional numerical simulation and multi-objective genetic algorithm. Energy 2018, 147, 1060–1069. [Google Scholar] [CrossRef]
- Zhu, Y.; Newbrook, D.W.; Dai, P.; de Groot, C.H.K.; Huang, R. Artificial neural network enabled accurate geometrical design and optimisation of thermoelectric generator. Appl. Energy 2022, 305, 117800. [Google Scholar] [CrossRef]
- Shen, Z.G.; Liu, X.; Chen, S.; Wu, S.Y.; Xiao, L.; Chen, Z.X. Theoretical analysis on a segmented annular thermoelectric generator. Energy 2018, 157, 297–313. [Google Scholar] [CrossRef]
- Liu, J.P.; Sun, Y.J.; Chen, G.; Zhai, P.C. Performance Analysis of Variable Cross-Section TEGs under Constant Heat Flux Conditions. Energies 2023, 16, 4473. [Google Scholar] [CrossRef]
- Ferreira, T.S.; Pereira, A.M. Geometrical optimization of a thermoelectric device: Numerical simulations. Energy Convers. Manag. 2018, 169, 217–227. [Google Scholar] [CrossRef]
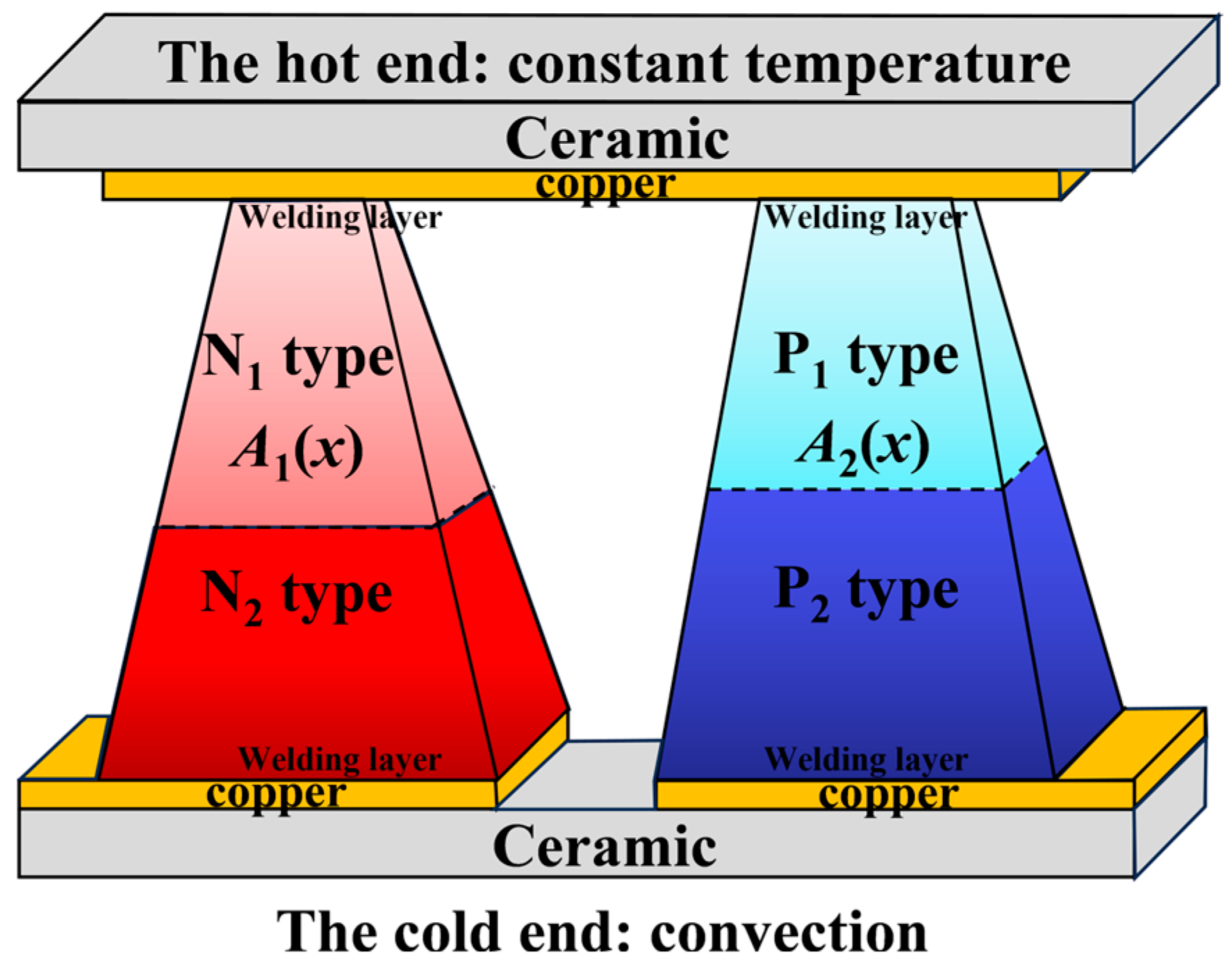
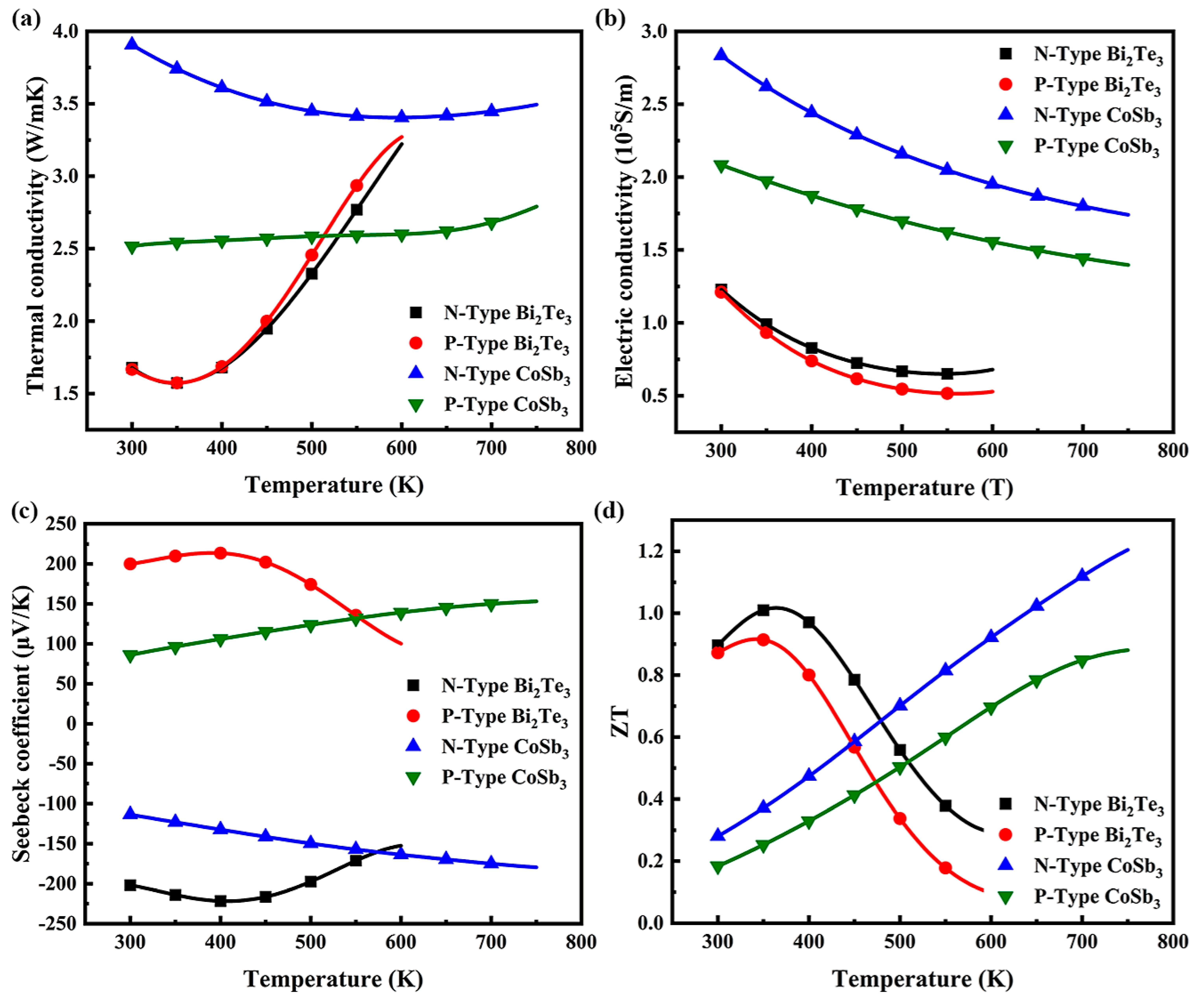
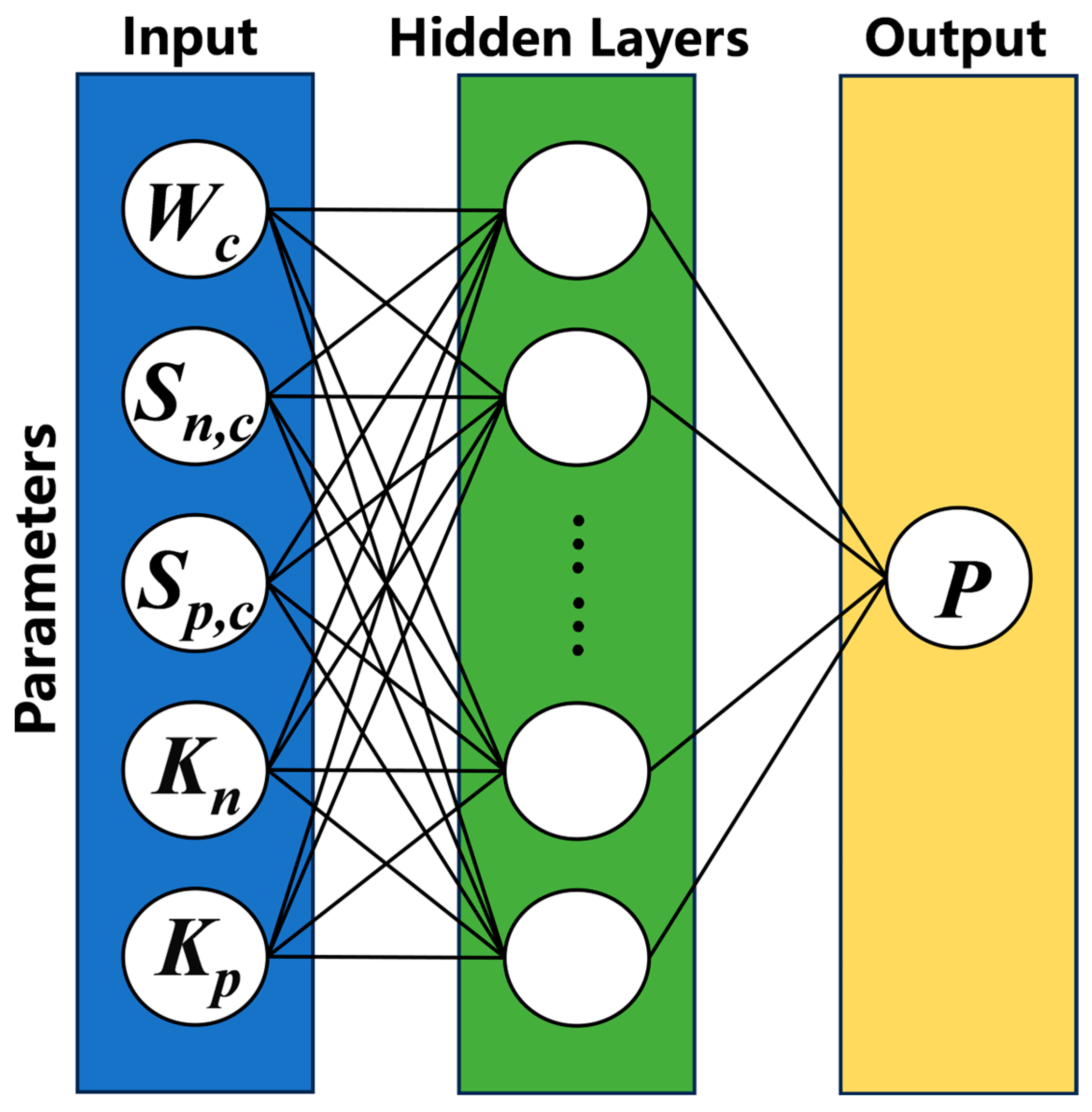
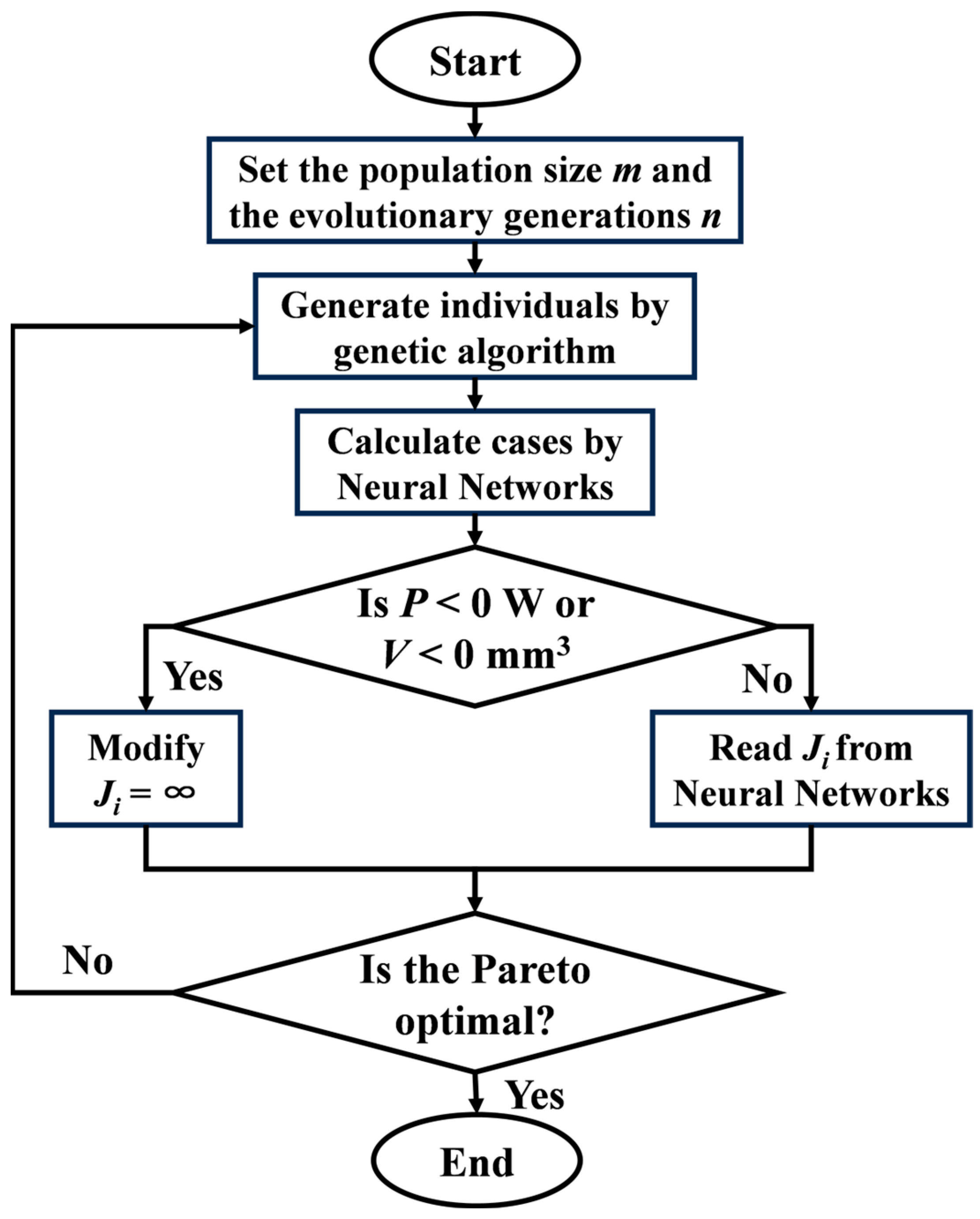



| Geometric Parameter | Value Range | Resolution |
|---|---|---|
| Width of cold end TE leg Wc | 3–6 mm | 0.1 mm |
| Ratio of cold-segment length to total length n-leg Sn,c (Sn,c = Ln,c/L) | 0.10–0.60 | 0.01 |
| Ratio of cold-segment length to total length p-leg Sp,c (Sp,c = Lp,c/L) | 0.10–0.60 | 0.01 |
| Width ratio between hot end and cold end n-leg Kn (Kn = Wn,h/Wc) | 0.10–1 | 0.01 |
| Width ratio between hot end and cold end p-leg Kp (Kp = Wp,h/Wc) | 0.10–1 | 0.01 |
| Width of hot end n-leg Wn,h | 0.3–6 mm | |
| Width of hot end p-leg Wp,h | 0.3–6 mm |
| Geometric Parameter | Performance | ||||||
|---|---|---|---|---|---|---|---|
| Wc (mm) | Sn,c | Sp,c | Kn | Kp | V (mm3) | P (W) | |
| Value | 3 | 0.27 | 0.27 | 0.47 | 0.54 | 52.8 | 0.183 |
| Model | Volume | Wc (mm) | Sn,c | Sp,c | Kn | Kp |
|---|---|---|---|---|---|---|
| Optimal-104 | 104 | 4.1 | 0.26 | 0.27 | 0.52 | 0.57 |
| Random-104 | 104 | 3.7 | 0.13 | 0.44 | 0.72 | 0.76 |
| Optimal-156 | 156 | 5 | 0.28 | 0.27 | 0.54 | 0.57 |
| Random-156 | 156 | 4.3 | 0.53 | 0.34 | 0.84 | 0.83 |
| Optimal-206 | 206 | 5.6 | 0.27 | 0.27 | 0.52 | 0.55 |
| Random-206 | 206 | 5 | 0.12 | 0.41 | 0.93 | 0.68 |
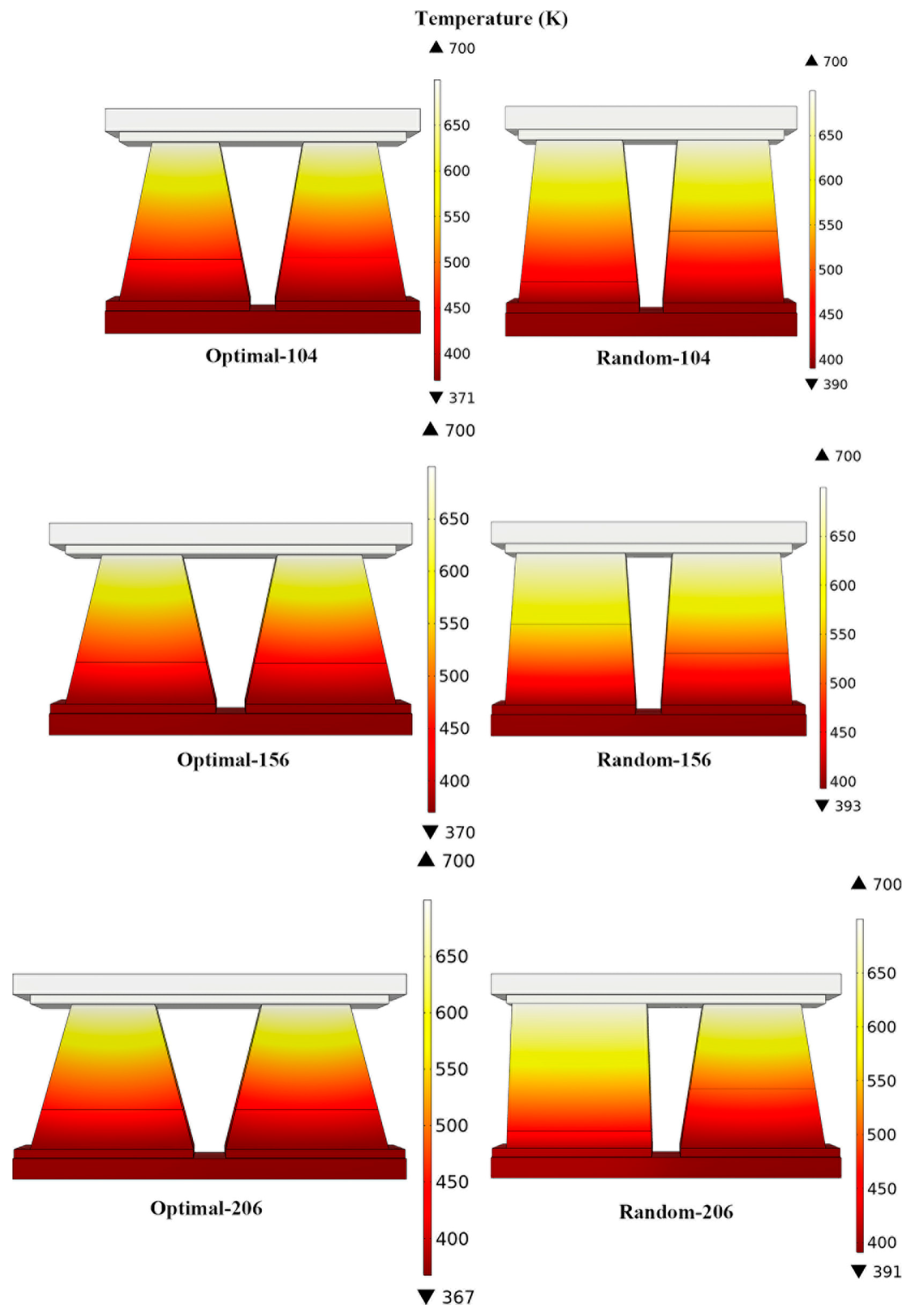
| Model | Volume (mm3) | Temperature Difference (K) |
|---|---|---|
| Optimal-104 | 104 | 329 |
| Random-104 | 104 | 310 |
| Optimal-156 | 156 | 330 |
| Random-156 | 156 | 307 |
| Optimal-206 | 206 | 333 |
| Random-206 | 206 | 309 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Wen, P.; Zhu, S.; Zhai, P. Geometrical Optimization of Segmented Thermoelectric Generators (TEGs) Based on Neural Network and Multi-Objective Genetic Algorithm. Energies 2024, 17, 2094. https://doi.org/10.3390/en17092094
Sun W, Wen P, Zhu S, Zhai P. Geometrical Optimization of Segmented Thermoelectric Generators (TEGs) Based on Neural Network and Multi-Objective Genetic Algorithm. Energies. 2024; 17(9):2094. https://doi.org/10.3390/en17092094
Chicago/Turabian StyleSun, Wei, Pengfei Wen, Sijie Zhu, and Pengcheng Zhai. 2024. "Geometrical Optimization of Segmented Thermoelectric Generators (TEGs) Based on Neural Network and Multi-Objective Genetic Algorithm" Energies 17, no. 9: 2094. https://doi.org/10.3390/en17092094
APA StyleSun, W., Wen, P., Zhu, S., & Zhai, P. (2024). Geometrical Optimization of Segmented Thermoelectric Generators (TEGs) Based on Neural Network and Multi-Objective Genetic Algorithm. Energies, 17(9), 2094. https://doi.org/10.3390/en17092094






