Study on Hydrocarbon Fuel Ignition Characterization Based on Optimized BP Neural Network
Abstract
1. Introduction
2. Methodology
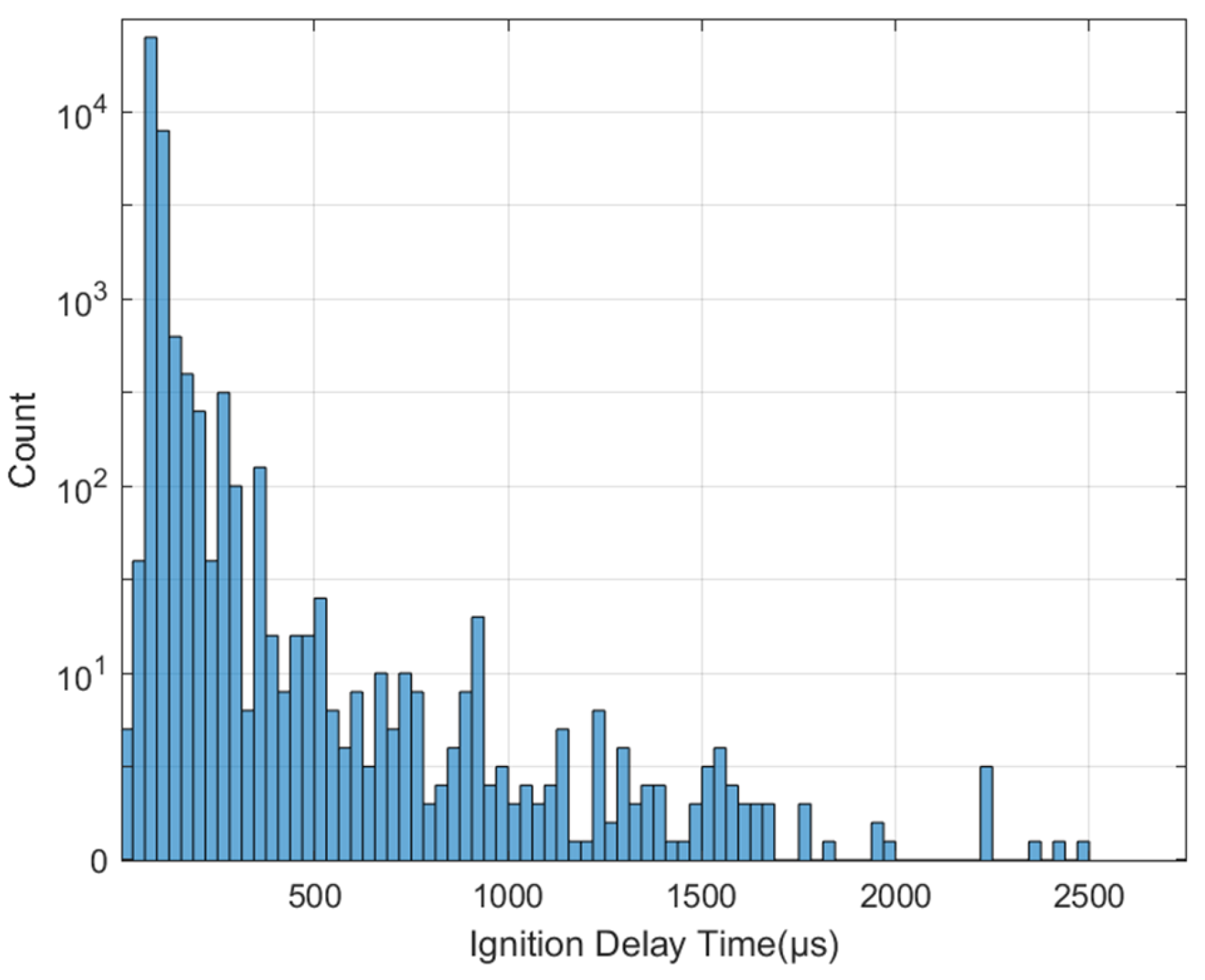
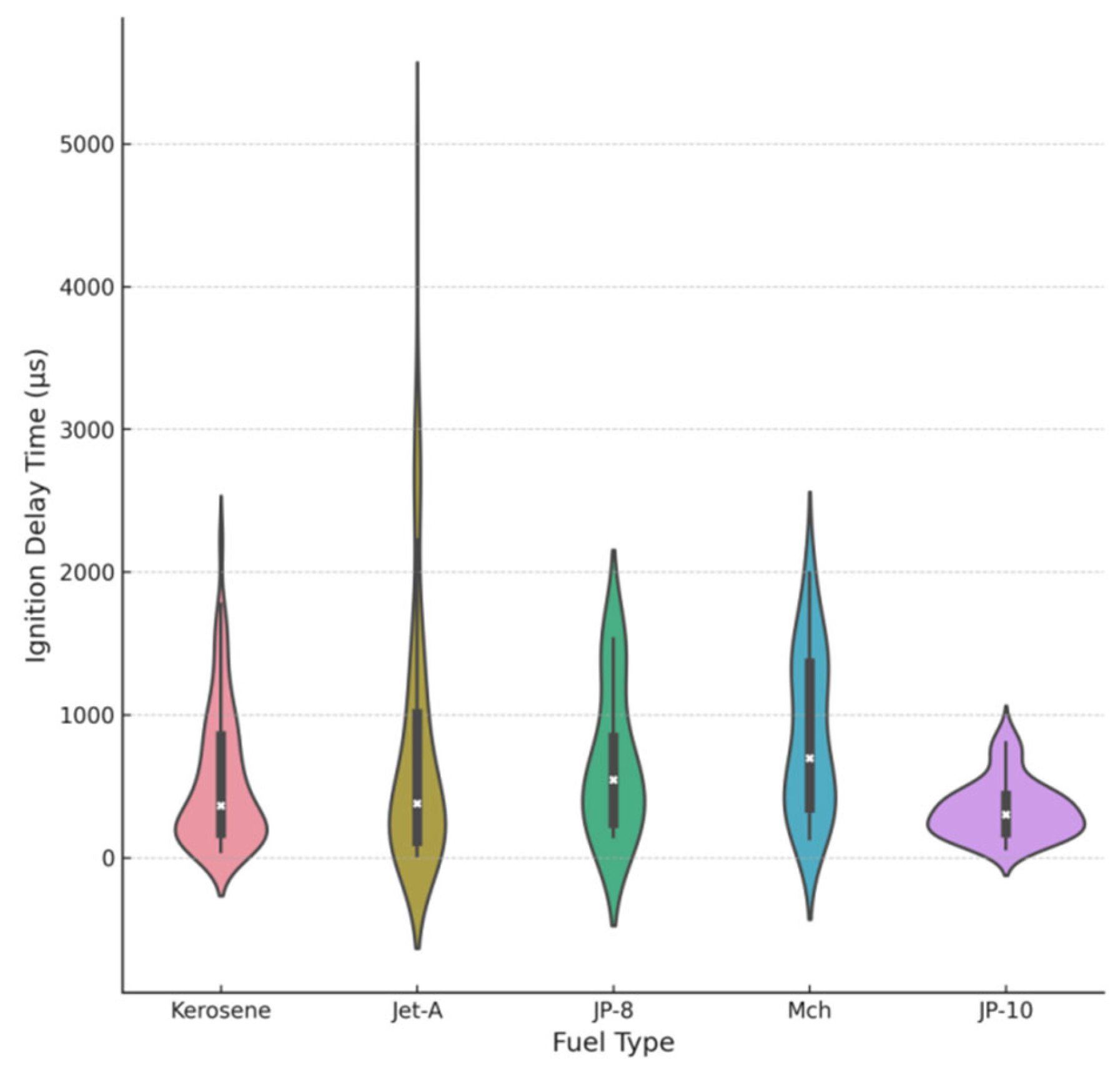
2.1. Acquisition of Data
2.2. Creation of Data Sets
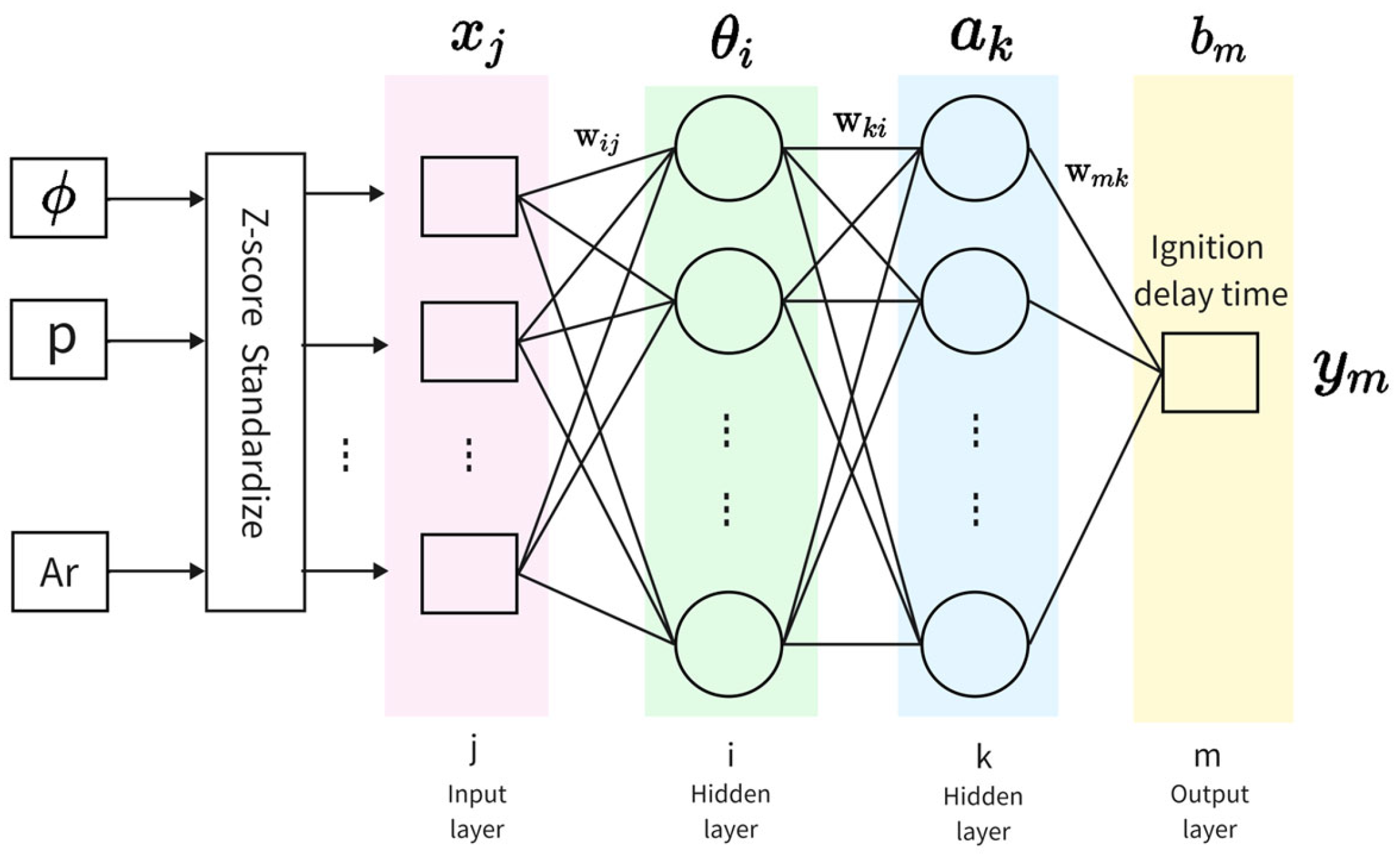
2.3. BP Neural Networks
3. Improvement of the BP Algorithm
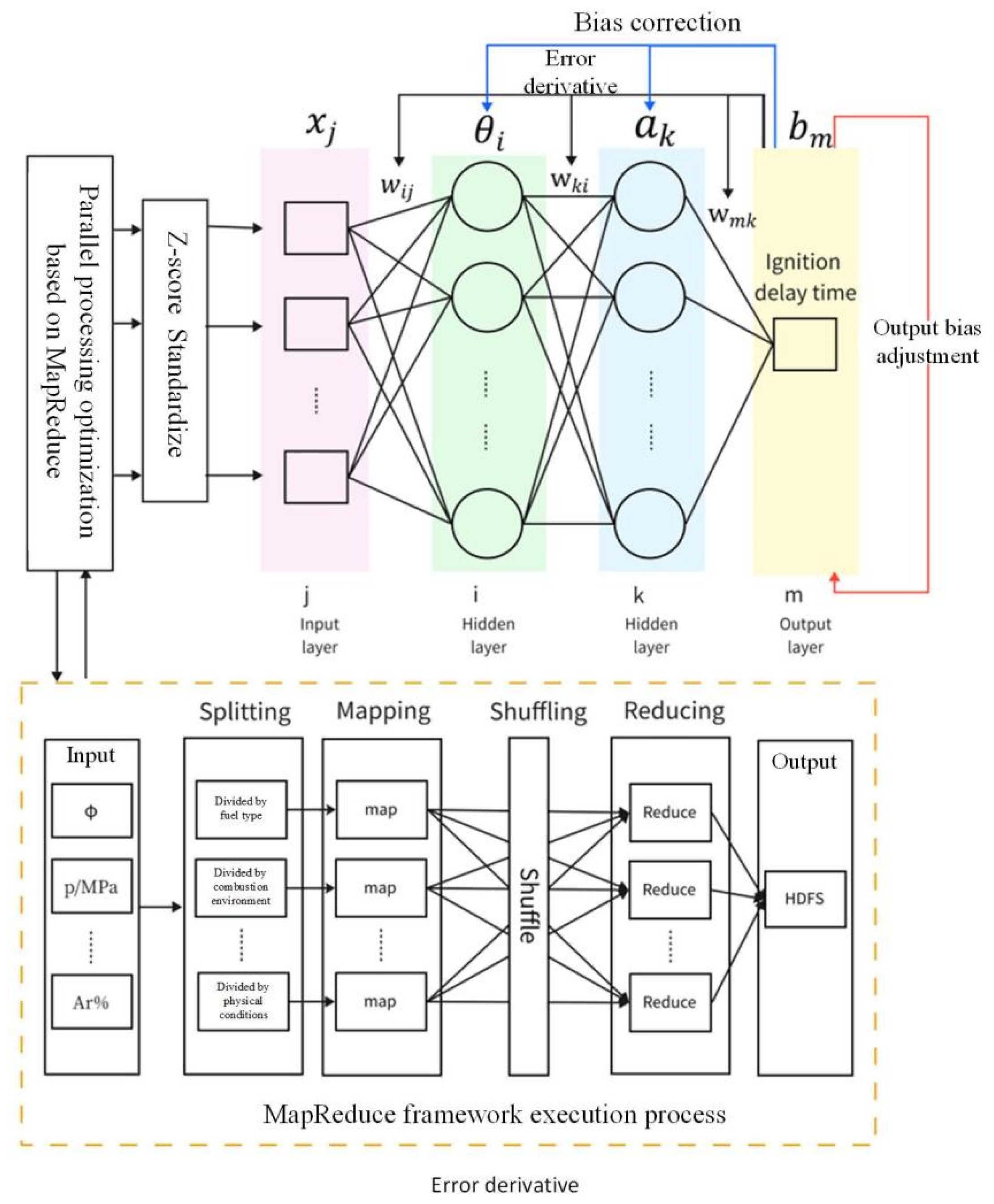
3.1. MapReduce-Based Parallel Processing Optimization
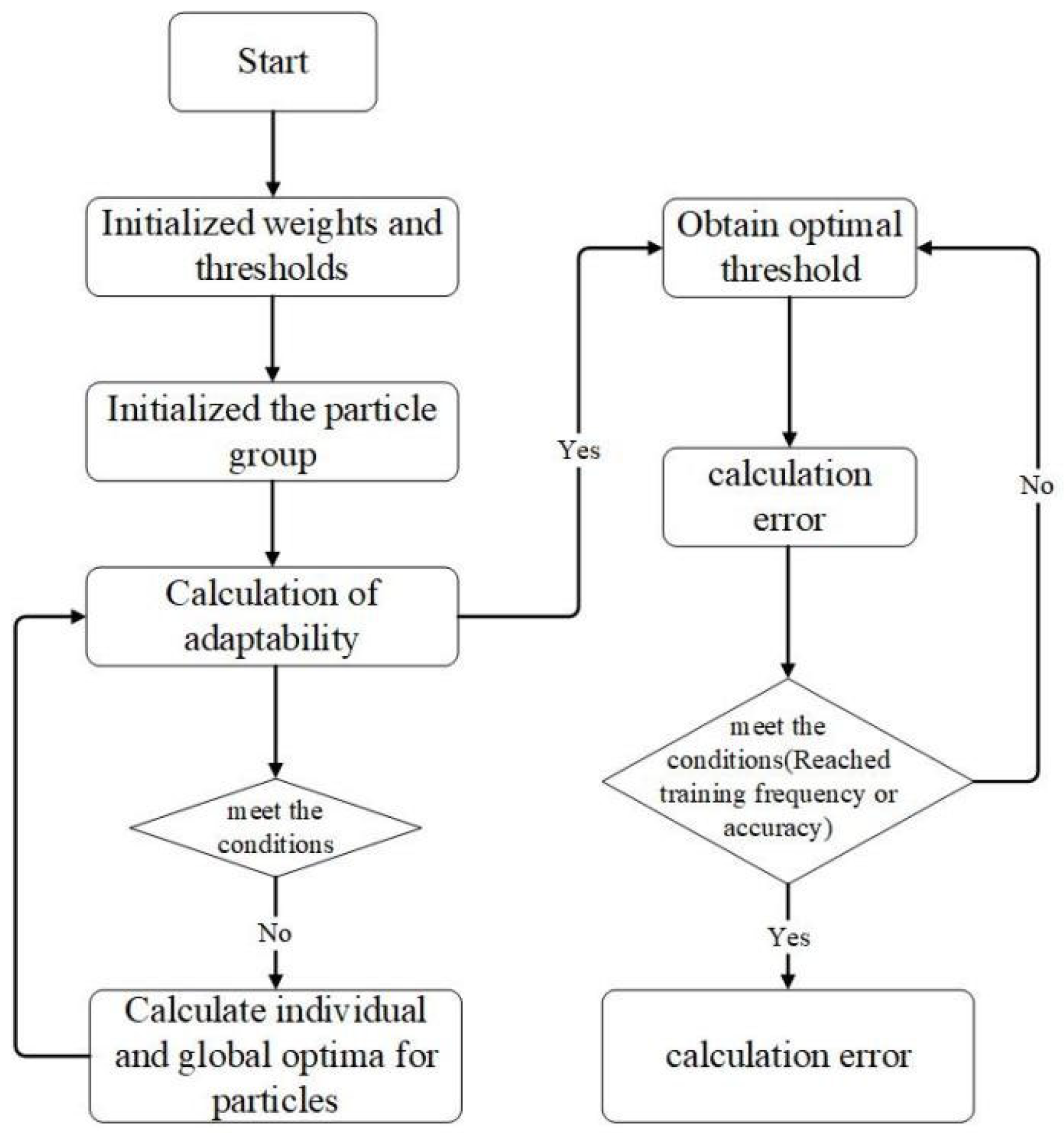
3.2. Particle Swarm Optimization (PSO) Algorithm Integration
3.3. BP-MRPSO Neural Network Modeling
4. Prediction and Analysis of Fuel Ignition Delay Characteristics
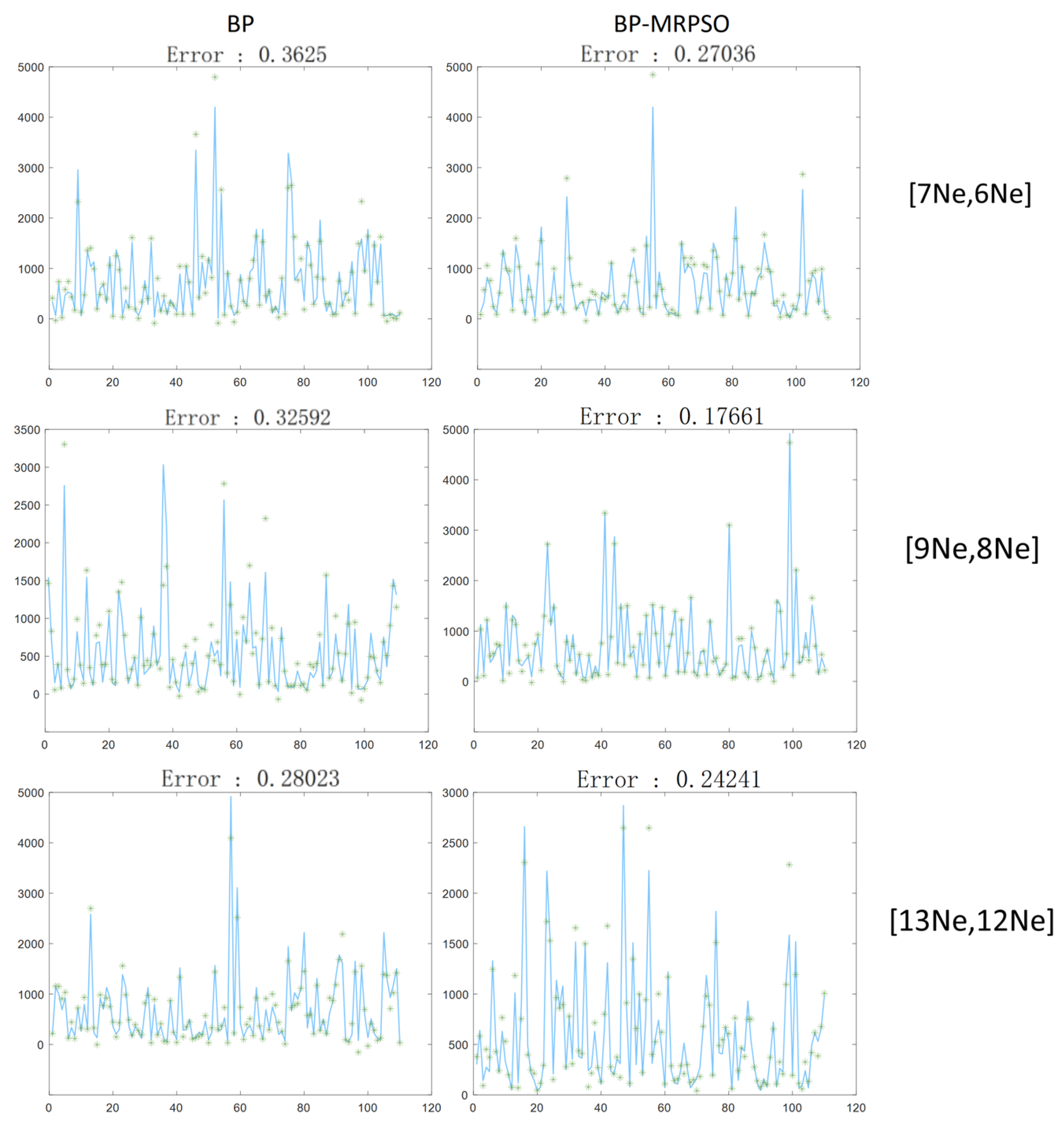
4.1. Comparison of BP-Based and BP-MRPSO Neural Networks
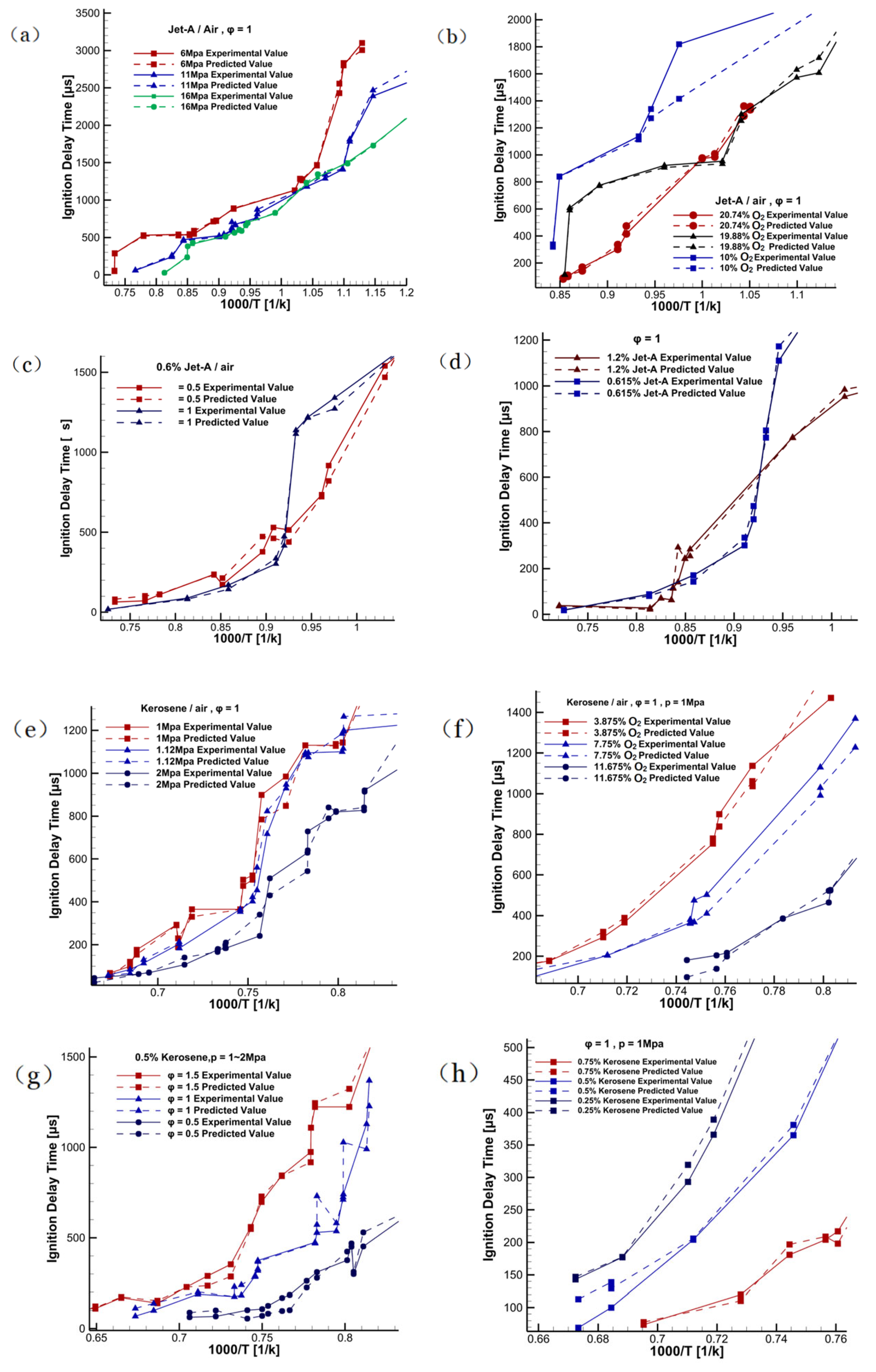
4.2. Analysis of Experimental and Prediction Results of BP-MRPOS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation/Term | Full Name/Explanation |
| AI | Artificial intelligence |
| BP | Back propagation |
| BP-MRPSO | Back propagation-MapReduce particle swarm optimization |
| IDT | Ignition delay time |
| PSO | Particle swarm optimization |
| MapReduce | A programming model for processing and generating large data sets |
| CO | Carbon monoxide |
| UHC | Unburned hydrocarbons |
| ANN | Artificial neural network |
| ϕ | Equivalence ratio |
| p | Pressure, MPa |
| T | Temperature, K |
| O2 | Oxygen concentration, % |
| N2 | Nitrogen concentration, % |
| Ar | Argon concentration, % |
| IDT | Ignition delay time, μs |
References
- Xu, X.; Liu, E.; Zhu, N.; Liu, F.; Qian, F. Current Status of Performance Research on Ammonia Mixed Fuel Systems. Chem. Ind. Prog. 2022, 41, 2332–2339. [Google Scholar]
- Liu, J.; Hu, E.; Huang, Z.; Zeng, W. Ignition Delay Characteristics of RP-3 Aviation Kerosene Simulated Alternative Fuel. Propuls. Technol. 2021, 42, 467–473. [Google Scholar]
- Wei, S.; Wu, L.; Yu, Z.; Sun, L.; Zhang, Z. Analysis of Fuel Chemical Reaction Kinetics Characterization for RP-3 Jet Fuel in the Negative Temperature Coefficient Region. Acta Pet. Sin. 2024, 40, 16. [Google Scholar]
- Bui, T.T.; Luu, H.Q.; Hoang, A.T.; Konur, O.; Huu, T.; Pham, M.T. A review on ignition delay times of 2,5-Dimethylfuran. Energy Sources Part A Recover. Util. Environ. Eff. 2022, 44, 7160–7175. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, W.; Hu, B.; Yin, G.; Zhang, Y.; Ma, H. Experimental Study on Oxidation and Ignition Characteristics of RP-3 Aviation Kerosene/O2. J. Aerosp. Power 2024, 39, 20220381. [Google Scholar]
- Ma, H.; Xie, M.; Zeng, W.; Chen, B. Analysis of Influencing Factors on the Ignition Characteristics of RP-3 Aviation Kerosene. Propuls. Technol. 2015, 36, 306–313. [Google Scholar]
- Wang, M.; Chen, L.; Zeng, W. Analysis of the Mechanism of the Influence of Reactive Particles on the Ignition Characteristics of Aviation Kerosene. Propuls. Technol. 2022, 43, 375–381. [Google Scholar]
- Zhukov, V.P.; Sechenov, V.A.; Starikovskiy, Y.A. Autoignition of kerosene (Jet-A)/air mixtures behind reflected shock waves. Fuel 2014, 126, 169–176. [Google Scholar] [CrossRef]
- Li, B. Deep Network Inversion Analysis and Its Application in Abrasive Waterjet Etching. Master’s Thesis, Dalian University of Technology, Dalian, China, 2022; pp. 1–93. Available online: https://link.cnki.net/doi/10.26991/d.cnki.gdllu.2022.000764 (accessed on 23 April 2024).
- Samanta, B.; Al-Balushi, K.R.; Al-Araimi, S.A. Artificial neural networks and genetic algorithm for bearing fault detection. Soft Comput. 2006, 10, 264–271. [Google Scholar] [CrossRef]
- Wu, G.Q. Fault detection method for ship equipment based on BP neural network. In Proceedings of the 2018 International Conference on Robots & Intelligent System, Changsha, China, 26–27 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 556–559. [Google Scholar]
- Wang, X.M.; Wang, J.; Privault, M. Artificial intelligent fault diagnosis system of complex electronic equipment. J. Intell. Fuzzy Syst. 2018, 35, 4141–4151. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, Q.; Liu, H.; Zheng, Z.; Wang, H.; Yue, Z.; Yao, M. Development of the ignition delay prediction model of n-butane/hydrogen mixtures based on artificial neural network. Energy AI 2020, 2, 100033. [Google Scholar] [CrossRef]
- Huang, Y.; Jiang, C.; Wan, K.; Gao, Z.; Vervisch, L.; Domingo, P.; He, Y.; Wang, Z.; Lee, C.H.; Cai, Q.; et al. Prediction of ignition delay times of Jet A-1/hydrogen fuel mixture using machine learning. Aerosp. Sci. Technol. 2022, 127, 107675. [Google Scholar] [CrossRef]
- Bounaceur, R.; Heymes, R.; Glaude, P.A.; Sirjean, B.; Fournet, R.; Montagne, P.; Auvray, A.; Impellizzeri, E.; Biehler, P.; Picard, A.; et al. Development of an Artificial Intelligence Model to Predict Combustion Properties, With a Focus on Auto-Ignition Delay. J. Eng. Gas Turbines Power 2024, 146, 061011. [Google Scholar] [CrossRef]
- Liang, J.; Wang, S.; Hu, H.; Zhang, S.; Fan, B.; Cui, J. Shock tube study of kerosene ignition delay at high pressures. Sci. China Phys. Mech. Astron. 2012, 55, 947–954. [Google Scholar] [CrossRef]
- Tang, H.C.; Zhang, C.H.; Li, P.; Wang, L.D.; Ye, B.; Li, X.Y. Experimental study on the self ignition characteristics of kerosene. Acta Phys. Chim. Sin. 2012, 28, 787–791. [Google Scholar]
- Vasu, S.S.; Davidson, D.F.; Hanson, R.K. Jet fuel ignition delay times: Shock tube experiments over wide conditions and surrogate model predictions. Combust. Flame 2008, 152, 125–143. [Google Scholar] [CrossRef]
- Li, F.; Ooi, B.C.; Özsu, M.T.; Wu, S. Distributed data management using MapReduce. ACM Comput. Surv. (CSUR) 2014, 46, 1–42. [Google Scholar] [CrossRef]
- Zhai, N.G.; Deng, J.S. Overview of Particle Swarm Optimization Algorithms. Technol. Innov. Guide 2015, 12, 216–217. [Google Scholar]
- dos Santos, C.F.G.; Papa, J.P. Avoiding overfitting: A survey on regularization methods for convolutional neural networks. ACM Comput. Surv. (CSUR) 2022, 54, 1–25. [Google Scholar] [CrossRef]
- Karloff, H.; Suri, S.; Vassilvitskii, S. A model of computation for MapReduce. In Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms, Austin, TX, USA, 17–19 January 2010; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010; pp. 938–948. [Google Scholar]
- Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Houssein, E.H.; Gad, A.G.; Hussain, K.; Suganthan, P.N. Major advances in particle swarm optimization: Theory, analysis, and application. Swarm Evol. Comput. 2021, 63, 100868. [Google Scholar] [CrossRef]
- Wu, Y.T.; Kong, X.D.; Wang, X.H.; Liang, J.H.; Tang, C.L.; Huang, Z.H.; Wang, B.Y.; Zeng, P. Experimental and kinetic studies on self ignition characteristics of aviation kerosene during direct coal liquefaction. Propuls. Technol. 2023, 31, 1–8. [Google Scholar]
- Chaos, M.; Dryer, F.L. Chemical-kinetic modeling of ignition delay: Considerations in interpreting shock tube data. Int. J. Chem. Kinet. 2010, 42, 143–150. [Google Scholar] [CrossRef]
- Pawan, Y.N.; Prakash, K.B.; Chowdhury, S.; Hu, Y.-C. Particle swarm optimization performance improvement using deep learning techniques. Multimed. Tools Appl. 2022, 81, 27949–27968. [Google Scholar] [CrossRef]
| Reference | Ma et al. [6] | Tang et al. [17] | Cui et al. [13] | Liang et al. [16] |
| Systematic Error | 4% | 0.42% | 1.06% | 10% |
| Feature | Range | Division Value |
|---|---|---|
| Equivalent ratio (-) | 0.5–1.5 | 0.1 |
| Pressure (MPa) | 1–18 | 0.01 |
| Temperature (K) | 715.0–1671.0 | 0.1 |
| Fuel concentration (%) | 0.25–1.25 | 0.001 |
| Oxygen concentration (%) | 3.8–23.25 | 0.001 |
| Nitrogen concentration (%) | 0–0.1 | 0.001 |
| Argon concentration (%) | 76.0–95.875 | 0.001 |
| Parameter Type | Parameter Name | Unit |
|---|---|---|
| Input | ϕ | - |
| Input | p | MPa+ |
| Input | T | K |
| Input | O2 | % |
| Input | N2 | % |
| Input | Ar | % |
| Input | Fuel Chemical Composition | Variable |
| Output | IDT | μs |
| Model | Total Parameters | Layer Type | Neuron Number | Activation Function | Mean R-Squared |
|---|---|---|---|---|---|
| Basic BP | 251 | Input | 7 | -- | 83% |
| Dense | 12 | ReLu | |||
| Dense | 11 | ReLu | |||
| Dense (Output) | 1 | ReLu | |||
| BP-MRPSO | 161 | Input | 7 | -- | 92% |
| Dense | 9 | ReLu | |||
| Dense | 8 | ReLu | |||
| Dense (Output) | 1 | ReLu |
| Serial Number | Experimental Value (μs) | Predicted Value (μs) | Absolute Error (μs) | Relative Error |
|---|---|---|---|---|
| 1 | 51.8 | 53.939 | 2.139 | 4.129 |
| 2 | 405 | 410.335 | 5.335 | 1.317 |
| 3 | 45 | 43.391 | 1.608 | 3.575 |
| 4 | 189 | 183.001 | 5.998 | 3.173 |
| 5 | 125 | 121.816 | 3.183 | 2.546 |
| 6 | 237 | 242.848 | 5.848 | 2.467 |
| 7 | 162 | 156.837 | 5.162 | 3.186 |
| 8 | 125 | 121.816 | 3.183 | 2.546 |
| 9 | 175 | 180.410 | 5.410 | 3.091 |
| 10 | 114 | 118.872 | 4.872 | 4.274 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wei, L.; Ma, H.; Liu, Y.; Yue, M.; Shi, J. Study on Hydrocarbon Fuel Ignition Characterization Based on Optimized BP Neural Network. Energies 2024, 17, 2072. https://doi.org/10.3390/en17092072
Chen Z, Wei L, Ma H, Liu Y, Yue M, Shi J. Study on Hydrocarbon Fuel Ignition Characterization Based on Optimized BP Neural Network. Energies. 2024; 17(9):2072. https://doi.org/10.3390/en17092072
Chicago/Turabian StyleChen, Zhihan, Lulin Wei, Hongan Ma, Yang Liu, Meng Yue, and Junrui Shi. 2024. "Study on Hydrocarbon Fuel Ignition Characterization Based on Optimized BP Neural Network" Energies 17, no. 9: 2072. https://doi.org/10.3390/en17092072
APA StyleChen, Z., Wei, L., Ma, H., Liu, Y., Yue, M., & Shi, J. (2024). Study on Hydrocarbon Fuel Ignition Characterization Based on Optimized BP Neural Network. Energies, 17(9), 2072. https://doi.org/10.3390/en17092072







