Optimizing Critical Overloaded Power Transmission Lines with a Novel Unified SVC Deployment Approach Based on FVSI Analysis
Abstract
1. Introduction
1.1. Literature Review
1.2. Organization
2. Methodology
2.1. Power Flow Calculations: Newton–Raphson
2.2. Stability for Transmission Lines: Fast Voltage Stability Index (FVSI)
2.3. Description of the Proposed Methodology
2.3.1. Stage 1: Identification of Weakest Transmission Line
| Algorithm 1: FVSI calculation for all power lines in a system |
|
Step: 1 Load System Data Base electrical parameters from lines, buses, generators, and loads Step: 2 Power Flow Calulations By executing Newton–Raphson method: , , , Step: 3 Reactive power and FVSI calculation for each line for end for Step: 4 Return results |
| Algorithm 2: Identify the weakest power line by FVSI analysis in scenarios |
|
Step: 1 Initialization Step: 2 For each line removal scenario, calculate FVSI for to N do end for Step: 3 Identify the weakest line Step: 4 Output the result return |
2.3.2. Stage 2: Critical Overloading of Bus Bars Associated with the Weakest Transmission Line
| Algorithm 3: Critical load placement for nodes associated with the weakest line |
| Step: 1 Identify Weakest Line () Step: 2 Select Nodes () Step: 3 Stochastic Load Allocation for to M do end for Step: 4 Output Load Scenarios return |
2.3.3. Stage 3: Optimal SVC Sizing and Placement for Scenarios of Critical Overloading in Weakest Buses
| Algorithm 4: Optimal SVC location and sizing based on critical loading scenarios |
| Step: 1 Load M Load Allocation Scenarios from Algorithm 3 Step: 2 Calculate Original FVSI for Each Scenario for each in do end for Step: 3 Apply SVC Optimization Directly for Each Scenario for each in do for to do if is not and is not then for step 5 to do if is minimized then end for end if end for end for Step: 4 Return Optimal SVC Locations and Sizes for Each Scenario return |
2.3.4. Stage 4: Results Validation for Scenarios
2.4. Case Studies
3. Analysis of Results
3.1. Case Study: IEEE 14-Bus Bar System
3.1.1. Weakest Power Line by Analyzing Contingency Scenarios
3.1.2. Overloading of Critical Nodes
3.1.3. Optimal SVC Location and Sizing
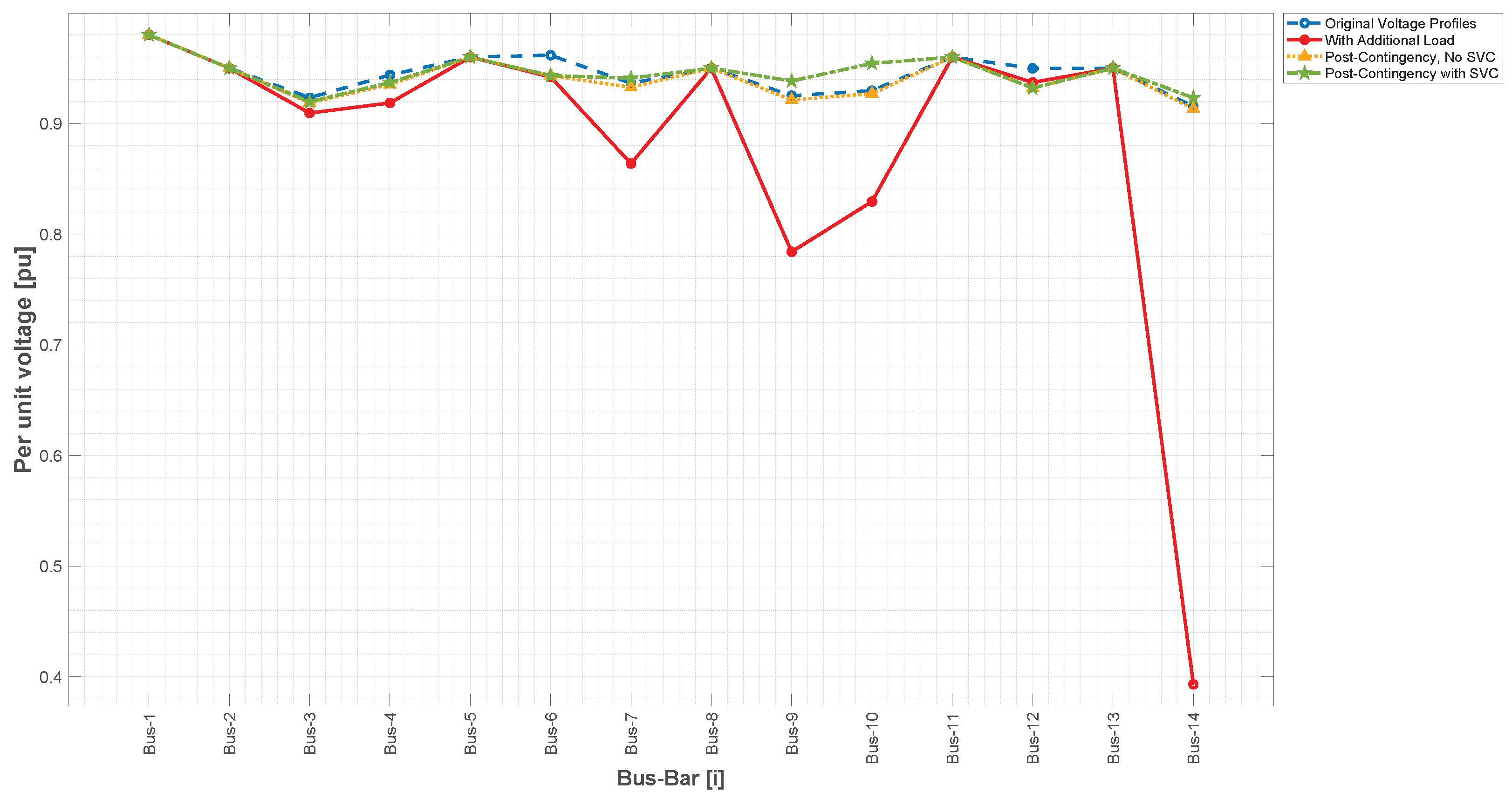
3.1.4. Optimal Solution Validation under Contingency Scenarios
3.2. Case Study: IEEE 30-Bus Bar System
3.2.1. Weakest Power Line by Analyzing Contingency Scenarios
3.2.2. Overloading of Critical Nodes
3.2.3. Optimal SVC Location and Sizing
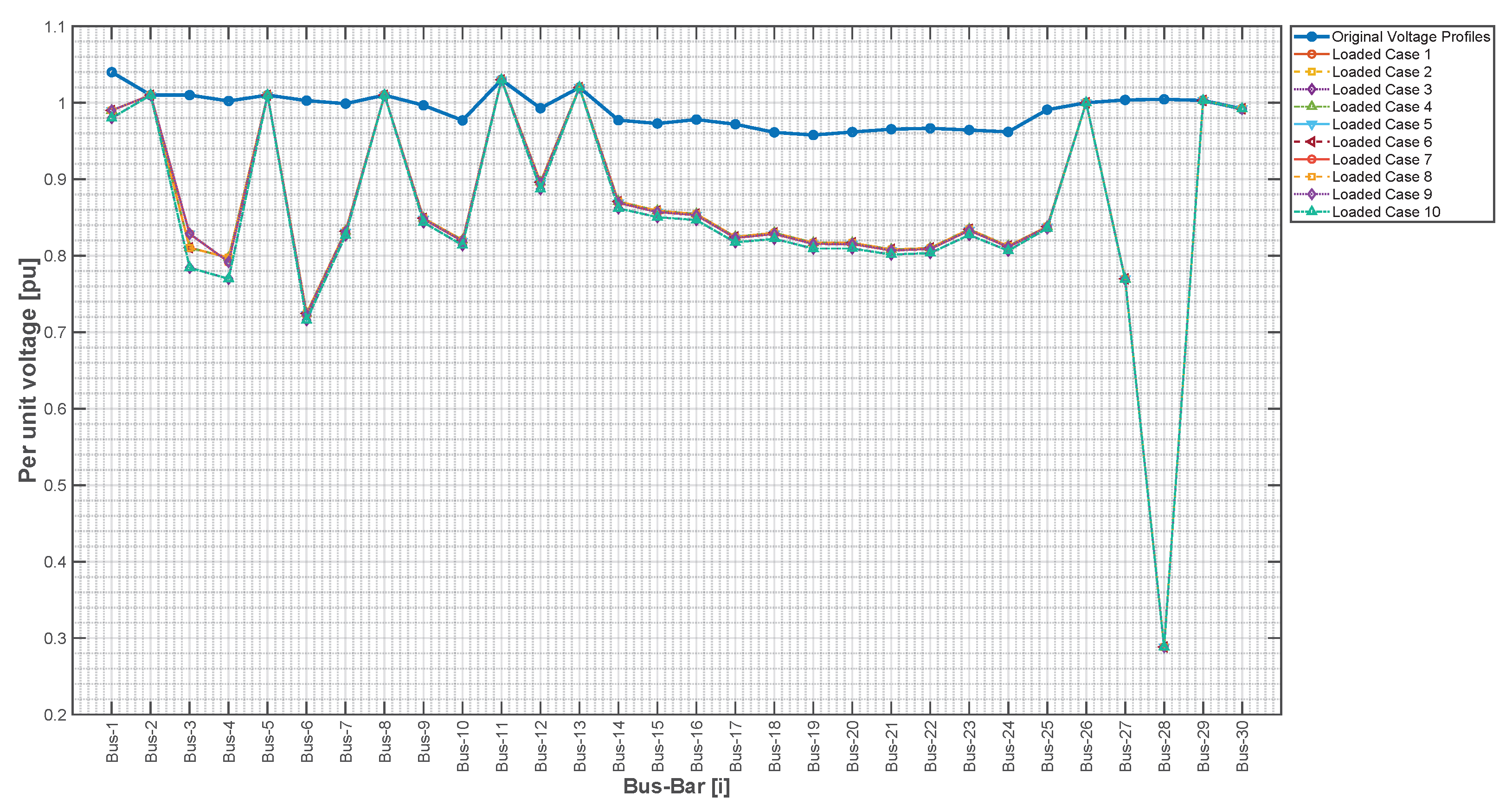
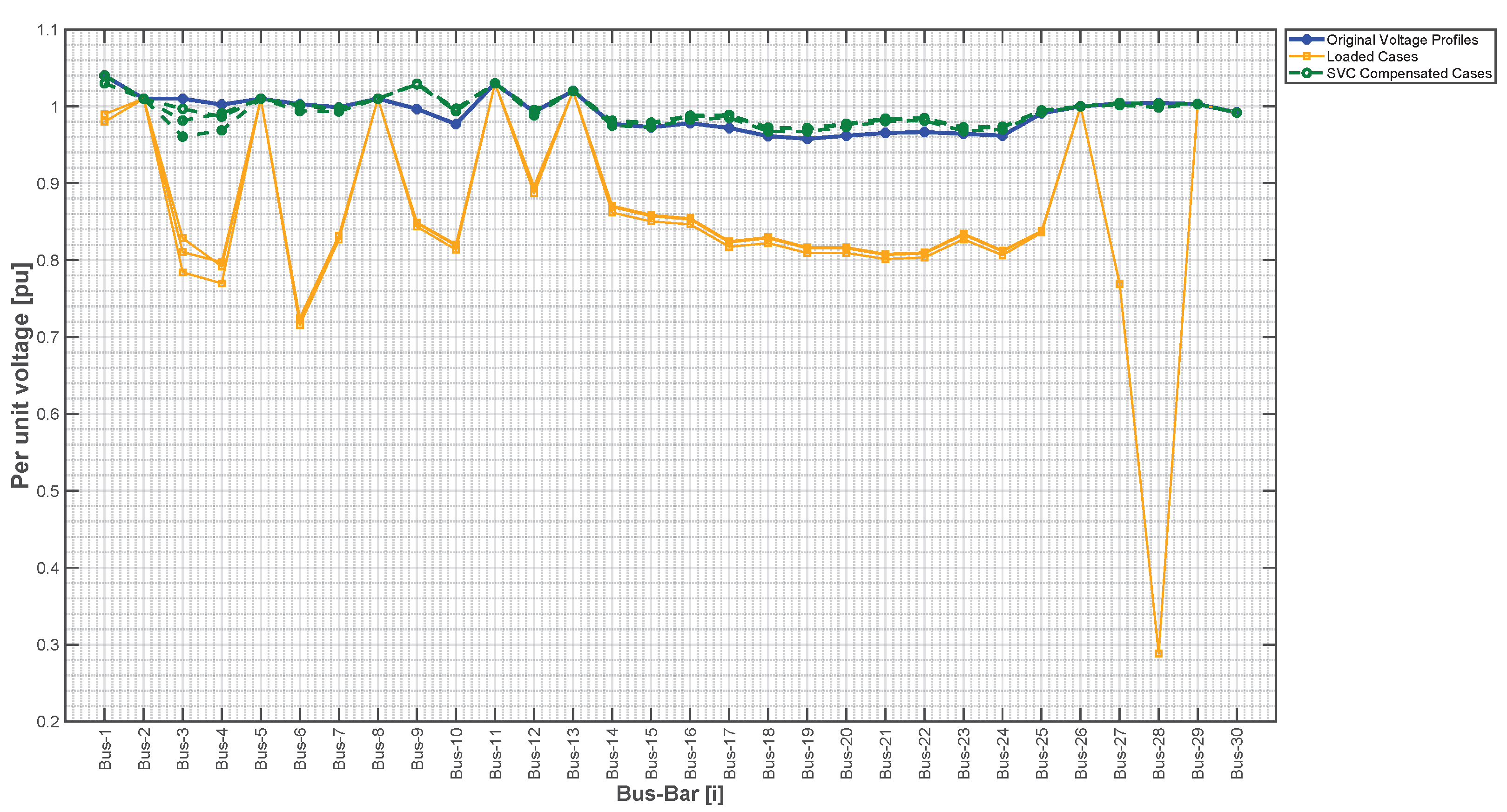
3.2.4. Optimal Solution Validation under Contingency Scenarios
3.3. Case Study: IEEE 118-Bus Bar System
3.3.1. Weakest Power Line by Analyzing Contingency Scenarios
3.3.2. Overloading of Critical Nodes
3.3.3. Optimal SVC Location and Sizing
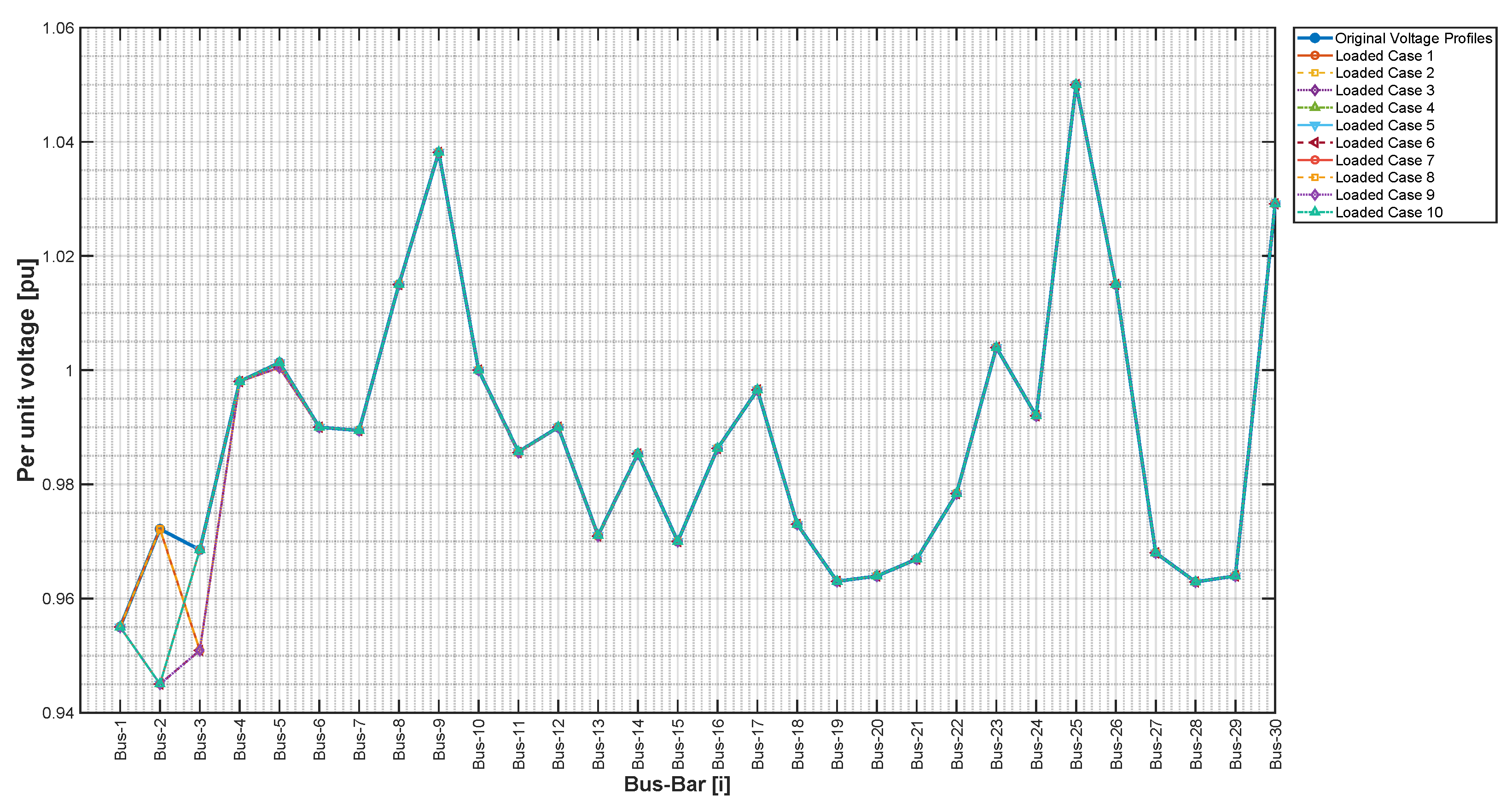
3.3.4. Optimal Solution Validation under Contingency Scenarios
4. Conclusions
5. Future Work and Challenges
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FVSI | Fast voltage stability index |
| SVC | Static VAR compensator |
| Single contingency condition | |
| Active power at node i | |
| Reactive power at node i | |
| Voltage magnitude at bus bar i | |
| Voltage angle at bus bar i | |
| Conductance between bus bars i and j | |
| Susceptance between bus bars i and j | |
| Impedance between bus bars i and j | |
| Reactance between bus bars i and j | |
| Receiving reactive power from node j to node i | |
| Apparent power flow from node j to node i | |
| Electrical parameters of all bus bars in a system | |
| Electrical parameters of lines in a system | |
| Electrical parameters of loads in a system | |
| Electrical parameters of generators in a system | |
| SVC size at a bus bar | |
| Optimal bus bar location for SVC | |
| Optimal sizing of SVC |
References
- Gupta, S.K.; Mallik, S.K. Enhancement in Voltage Stability Using FACTS Devices Under Contingency Conditions. J. Oper. Autom. Power Eng. 2024, 12, 365–378. [Google Scholar] [CrossRef]
- Hosseinzadehtaher, M.; Zare, A.; Khan, A.; Umar, M.F.; D’silva, S.; Shadmand, M.B. AI-Based Technique to Enhance Transient Response and Resiliency of Power Electronic Dominated Grids via Grid-Following Inverters. IEEE Trans. Ind. Electron. 2024, 71, 2614–2625. [Google Scholar] [CrossRef]
- Basha, M.I.; Eldesouky, A.A. Multi-objective-based reactive power planning and voltage stability enhancement using FACTS and capacitor banks. Electr. Eng. 2022, 104, 3173–3196. [Google Scholar] [CrossRef]
- Singh, R.K.; Singh, N.K. Power system transient stability improvement with FACTS controllers using SSSC-based controller. Sustain. Energy Technol. Assess. 2022, 53, 102664. [Google Scholar] [CrossRef]
- Tina, G.M.; Maione, G.; Licciardello, S.; Stefanelli, D. Comparative Technical-Economical Analysis of Transient Stability Improvements in a Power System. Appl. Sci. 2021, 11, 11359. [Google Scholar] [CrossRef]
- Sakipour, R.; Abdi, H. International Journal of Electrical Power and Energy Systems Voltage stability improvement of wind farms by self-correcting static volt-ampere reactive compensator and energy storage. Int. J. Electr. Power Energy Syst. 2022, 140, 108082. [Google Scholar] [CrossRef]
- Ariel, M.; Nwulu, M. Optimal Placement of FACTS Devices Using Filter Feeding Allogenic Engineering Algorithm. Technol. Econ. Smart Grids Sustain. Energy 2022, 7, 2. [Google Scholar] [CrossRef]
- Abdul, A.; Altahir, R.; Marei, M.M. An optimal allocation of UPFC and transient stability improvement of an electrical power system: IEEE-30 buses. Int. J. Electr. Comput. Eng. 2021, 11, 4698–4707. [Google Scholar] [CrossRef]
- Azbe, V.; Mihalic, R. International Journal of Electrical Power and Energy Systems STATCOM control strategies in energy-function-based methods for the globally optimal control of renewable sources during transients. Int. J. Electr. Power Energy Syst. 2022, 141, 108145. [Google Scholar] [CrossRef]
- Balakumar, S.; Getahun, A.; Kefale, S.; Kumar, K.R. Improvement of the Voltage Profile and Loss Reduction in Distribution Network Using Moth Flame Algorithm: Wolaita Sodo, Ethiopia. J. Electr. Comput. Eng. 2021, 2021, 9987304. [Google Scholar] [CrossRef]
- Wartana, I.M.; Agustini, N.P.; Sreedharan, S.; Lbs, M. Improved security and stability of grid connected the wind energy conversion system by unified power flow controller. Indones. J. Electr. Eng. Comput. Sci. 2022, 27, 1151–1161. [Google Scholar] [CrossRef]
- Ghaedi, S.; Abazari, S.; Markadeh, G.A. Transient stability improvement of power system with UPFC control by using transient energy function and sliding mode observer based on locally measurable information. Measurement 2021, 183, 109842. [Google Scholar] [CrossRef]
- Vaidya, P.; Chandrakar, V.K. Exploring the Enhanced Performance of a Static Synchronous Compensator with a Super-Capacitor in Power Networks. Eng. Technol. Appl. Sci. Res. 2022, 12, 9703–9708. [Google Scholar] [CrossRef]
- Rasool, A.A.; Abbas, N.M.; Sheikhyounis, K. Determination of optimal size and location of static synchronous compensator for power system bus voltage improvement and loss reduction using whale optimization algorithm. East.-Eur. J. Enterp. Technol. 2022, 1, 26–34. [Google Scholar] [CrossRef]
- Khan, B.; Redae, K.; Gidey, E.; Prakash, O. Optimal integration of DSTATCOM using improved bacterial search algorithm for distribution network optimization. Alex. Eng. J. 2022, 61, 5539–5555. [Google Scholar] [CrossRef]
- He, P.; Pan, Z.; Fan, J.; Tao, Y.; Wang, M. Coordinated design of PSS and multiple FACTS devices based on the PSO-GA algorithm to improve the stability of wind – PV – thermal-bundled power system. Electr. Eng. 2023, 106, 2143–2157. [Google Scholar] [CrossRef]
- Pattabhi, M.B.; Rangappa, B.; Krishna, L.; Sundar, S. A Novel Method for Contingency Ranking Based On Voltage Stability Criteria in Radial Distribution Systems. Technol. Econ. Smart Grids Sustain. Energy 2022, 7, 9. [Google Scholar] [CrossRef]
- Al-wazni, H.S.M.; Al-kubragyi, S.S.A. A hybrid algorithm for voltage stability enhancement of distribution systems. Int. J. Electr. Comput. Eng. 2022, 12, 50–61. [Google Scholar] [CrossRef]
- Djellad, A.; Belakehal, S.; Chenni, R.; Dekhane, A. Reliability improvement in serial multicellular converters based on statcom control. J. Eur. Des Syst. Autom. 2021, 54, 519–528. [Google Scholar] [CrossRef]
- Jaramillo, M.D.; Carrión, D.F.; Muñoz, J.P. A Novel Methodology for Strengthening Stability in Electrical Power Systems by Considering Fast Voltage Stability Index under N-1 Scenarios. Energies 2023, 16, 3396. [Google Scholar] [CrossRef]
- Musirin, I.; Abdul Rahman, T. Novel fast voltage stability index (FVSI) for voltage stability analysis in power transmission system. In Proceedings of the Student Conference on Research and Development, Shah Alam, Malaysia, 17 July 2002; pp. 265–268. [Google Scholar] [CrossRef]
- Jaramillo, M.; Carrión, D.; Muñoz, J. A Deep Neural Network as a Strategy for Optimal Sizing and Location of Reactive Compensation Considering Power Consumption Uncertainties. Energies 2022, 15, 9367. [Google Scholar] [CrossRef]
- Jaramillo, M.; Tipán, L.; Muñoz, J. A novel methodology for optimal location of reactive compensation through deep neural networks. Heliyon 2022, 8, e11097. [Google Scholar] [CrossRef] [PubMed]







| Author | Methodologies | Test System | Voltage Profile | Power Losses | Stability Indexes | Cost | Variable Loads |
|---|---|---|---|---|---|---|---|
| [1,10] | Analytical Modeling, Simulation, Optimization Techniques | IEEE 14-bus system, NRPG 246-bus system | ✓ | ✓ | - | - | ✓ |
| [2,9,13,16] | Control Strategy Development, Simulation, and Testing | SMIB and IEEE 9-bus systems, 14-bus systems | - | - | ✓ | - | ✓ |
| [3,8,18] | Optimization Algorithms for FACTS Devices | Modified IEEE 30-bus system, South Egypt Electricity network, IEEE 33-bus and Iraqi 65-bus systems | ✓ | ✓ | ✓ | - | ✓ |
| [4,5] | Simulation, SCR Variation Analysis | IEEE 9-bus system | - | - | ✓ | ✓ | - |
| [6,13] | FACTS Devices Integration in Renewable Energy Systems | Wind farms with PMSG, Multi-machine network model | ✓ | - | ✓ | - | ✓ |
| [7,14,15] | Algorithm-Based FACTS Devices Optimization | Kenya’s 87-bus 25-generator Network, Quha feeder, Lachi distribution network | ✓ | ✓ | - | - | ✓ |
| [11,17] | NSGA-II Optimization, Contingency Ranking | Modified IEEE 14-bus system | - | ✓ | ✓ | - | ✓ |
| [19] | Serial Multicellular Converters Integration | MATLAB Simulink model | ✓ | - | ✓ | - | ✓ |
| Transmission Line | FVSI | Transmission Line | FVSI | ||
|---|---|---|---|---|---|
| Sending Node | Receiving Node | Sending Node | Receiving Node | ||
| 2 | 5 | 0.1392 | 9 | 10 | 0.0211 |
| 10 | 11 | 0.1154 | 6 | 12 | 0.0182 |
| 1 | 5 | 0.1108 | 4 | 5 | 0.0181 |
| 13 | 14 | 0.0919 | 3 | 4 | 0.0150 |
| 2 | 3 | 0.0889 | 6 | 13 | 0.0136 |
| 4 | 9 | 0.0682 | 6 | 11 | 0.0130 |
| 7 | 8 | 0.0621 | 1 | 2 | 0.0062 |
| 7 | 9 | 0.0479 | 12 | 13 | 0.0052 |
| 4 | 7 | 0.0261 | 9 | 14 | 0.0030 |
| 5 | 6 | 0.0248 | |||
| Power Line | FVSI AvgValue | Count | Percentage [%] | |
|---|---|---|---|---|
| Node | Node | |||
| 2 | 5 | 0.1392 | 15 | 75 |
| 3 | 4 | 0.1752 | 1 | 5 |
| 10 | 11 | 0.1448 | 4 | 20 |
| Node | Additional Load [MW] | Active Power 80% [MW] | Reactive Power 20% [MVar] |
|---|---|---|---|
| 2 | 40 | 32 | 8 |
| 3 | 50 | 40 | 10 |
| 4 | 20 | 16 | 4 |
| 5 | 25 | 20 | 5 |
| 6 | 15 | 12 | 3 |
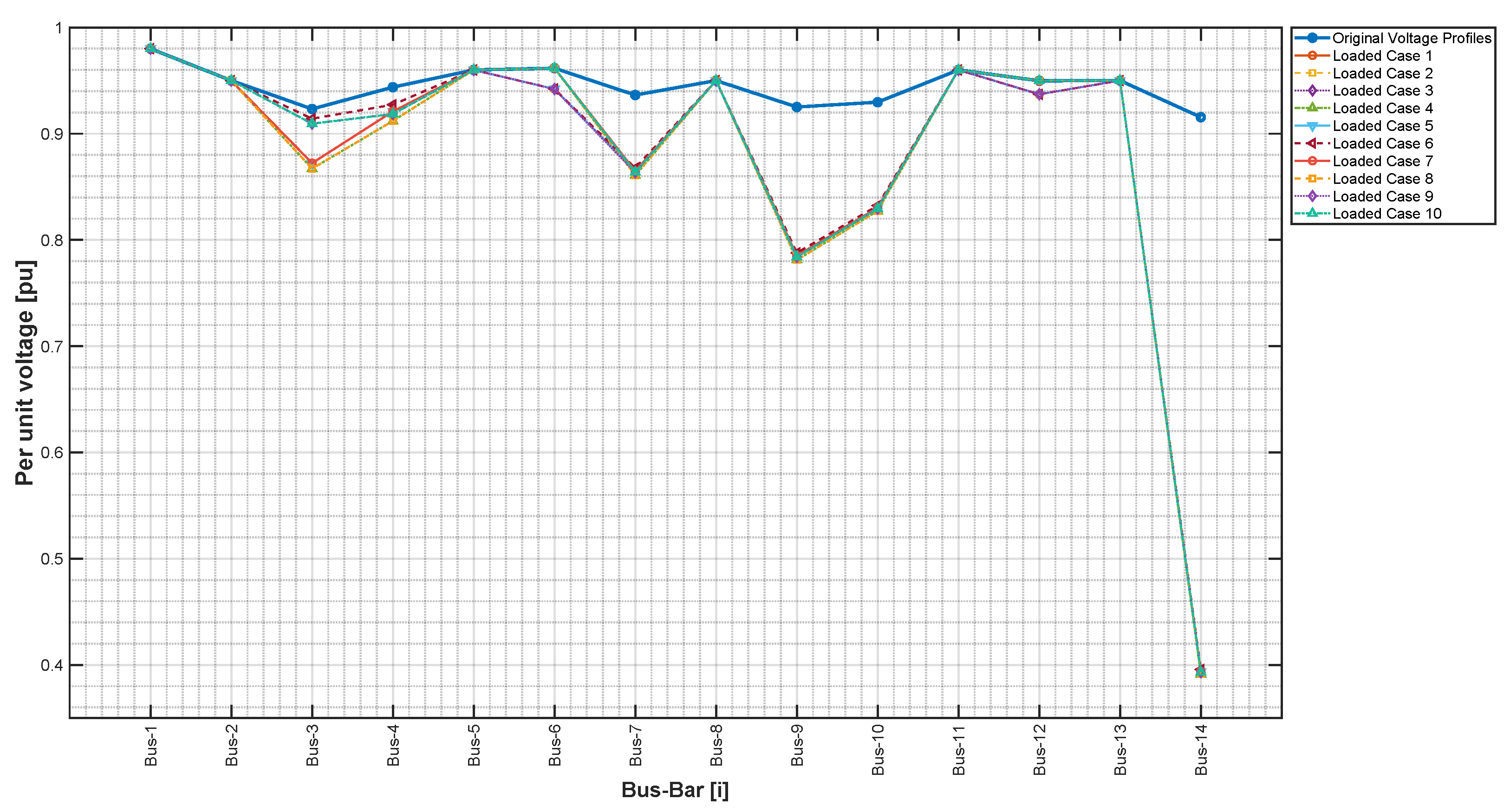
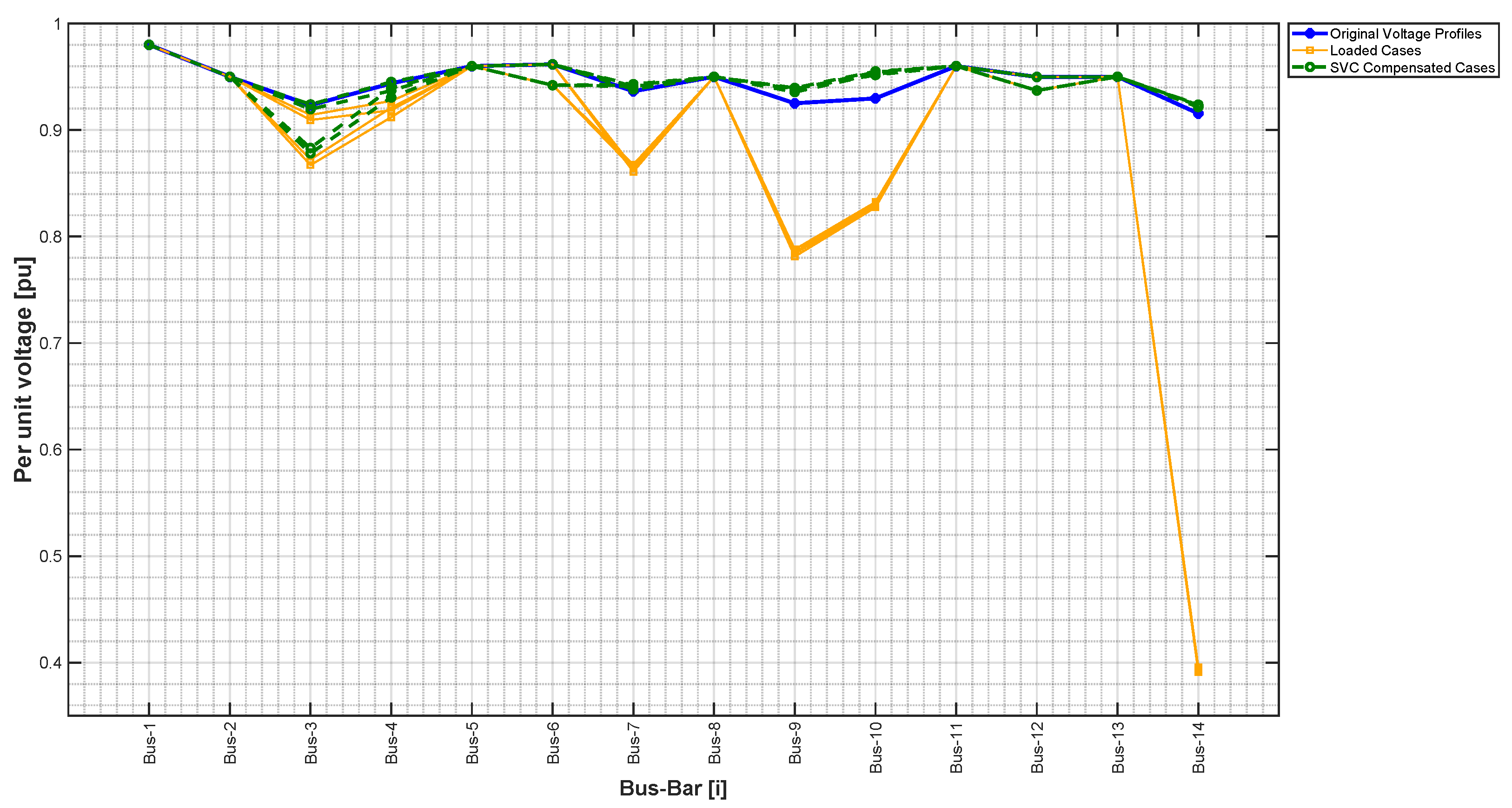
| Parameter | Original System | Loaded Cases | Compensated Cases | % Change (Loaded vs. Original/ Compensated vs. Loaded) |
|---|---|---|---|---|
| Average Voltage [pu] | 0.9453 | 0.8799 | 0.9452 | %/+7.42% |
| Maximum Voltage [pu] | 0.98 | 0.98 | 0.98 | 0%/0% |
| Minimum Voltage [pu] | 0.9155 | 0.3913 | 0.8781 | %/+124.38% |
| Objective Deviation | 0.057243 | 0.188785 | 0.058073 | +229.38%/% |
| Case | Mean | Min | Max | Standard Deviation |
|---|---|---|---|---|
| FVSI original | 0.049877 | 0.00035144 | 0.13917 | 0.044913 |
| Stochastic loaded scenarios | 0.053124 | 0.0031631 | 0.13917 | 0.043307 |
| Contingencies, no SVC scenarios | 0.062323 | 0.0053017 | 0.19473 | 0.052709 |
| Contingencies, with SVC scenarios | 0.05392 | 0.0061847 | 0.1906 | 0.048871 |
| Scenario | Mean Voltage [pu] | Minimum Voltage [pu] | Maximum Voltage [pu] | Standard Deviation |
|---|---|---|---|---|
| Original Profiles | 0.94537 | 0.91553 | 0.98 | 0.017751 |
| Loaded Scenarios | 0.87928 | 0.39318 | 0.98 | 0.15098 |
| Contingencies no SVC | 0.93682 | 0.86778 | 0.98 | 0.027156 |
| Contingencies with SVC | 0.94157 | 0.86926 | 0.98 | 0.025273 |
| Transmission Line | FVSI | Transmission Line | FVSI | ||
|---|---|---|---|---|---|
| Sending Node | Receiving Node | Sending Node | Receiving Node | ||
| 2 | 5 | 0.1952 | 12 | 13 | 0.1170 |
| 9 | 11 | 0.1569 | 24 | 25 | 0.1032 |
| 2 | 6 | 0.1256 | 9 | 10 | 0.0913 |
| 5 | 7 | 0.0768 | 2 | 4 | 0.0716 |
| 1 | 3 | 0.0661 | 25 | 26 | 0.0581 |
| 27 | 29 | 0.0469 | 12 | 16 | 0.0448 |
| 12 | 15 | 0.0442 | 6 | 8 | 0.0437 |
| 4 | 6 | 0.0407 | 27 | 30 | 0.0373 |
| 6 | 9 | 0.0365 | 10 | 21 | 0.0326 |
| 25 | 27 | 0.0324 | 10 | 20 | 0.0302 |
| 12 | 14 | 0.0292 | 1 | 2 | 0.0287 |
| 10 | 22 | 0.0286 | 6 | 7 | 0.0267 |
| 15 | 18 | 0.0257 | 15 | 23 | 0.0253 |
| 8 | 28 | 0.0242 | 16 | 17 | 0.0230 |
| 4 | 12 | 0.0197 | 6 | 28 | 0.0191 |
| 3 | 4 | 0.0144 | 10 | 17 | 0.0131 |
| 14 | 15 | 0.0126 | 23 | 24 | 0.0110 |
| 29 | 30 | 0.0108 | 18 | 19 | 0.0091 |
| 22 | 24 | 0.0090 | 19 | 20 | 0.0080 |
| 21 | 22 | 0.0036 | 28 | 27 | 0.0025 |
| Power Line | FVSI AvgValue | Count | Percentage [%] | |
|---|---|---|---|---|
| Node | Node | |||
| 2 | 5 | 0.195187059 | 38 | 92.68292683 |
| 1 | 3 | 0.72839528 | 1 | 2.43902439 |
| 6 | 10 | 0.244122555 | 1 | 2.43902439 |
| 9 | 11 | 0.138418004 | 1 | 2.43902439 |
| Node | Additional Load [MW] | Active Power 80% [MW] | Reactive Power 20% [MVar] |
|---|---|---|---|
| 4 | 80 | 64 | 16 |
| 2 | 120 | 96 | 24 |
| Parameter | Original System | Loaded Cases | Compensated Cases | % Change (Loaded vs. Original/ Compensated vs. Loaded) |
|---|---|---|---|---|
| Average Voltage [pu] | 0.9911 | 0.8596 | 0.9952 | %/+15.77% |
| Maximum Voltage [pu] | 1.04 | 1.03 | 1.04 | %/+0.97% |
| Minimum Voltage [pu] | 0.9578 | 0.2882 | 0.9607 | %/+233.24% |
| Objective Deviation | 0.02339 | 0.1973 | 0.01874 | +743.82%/% |
| Case | Mean | Min | Max | StdDev |
|---|---|---|---|---|
| FVSI original | 0.044331 | 0.0035763 | 0.19519 | 0.04161 |
| Stochastic loaded scenarios | 0.046021 | 0.0035153 | 0.19519 | 0.043612 |
| Contingencies, no SVC scenarios | 0.054047 | 0.0034813 | 0.19519 | 0.048011 |
| Contingencies, with SVC scenarios | 0.048062 | 0.0011364 | 0.19519 | 0.048058 |
| Scenario | Mean Voltage [pu] | Minimum Voltage [pu] | Maximum Voltage [pu] | StdDev |
|---|---|---|---|---|
| Original Profiles | 0.99111 | 0.95779 | 1.04 | 0.022005 |
| Loaded Scenarios | 0.85958 | 0.28839 | 1.03 | 0.14103 |
| Contingencies No SVC | 0.98321 | 0.94933 | 1.03 | 0.0242 |
| Contingencies with SVC | 0.99265 | 0.96625 | 1.03 | 0.019131 |
| Transmission Line | FVSI | Transmission Line | FVSI | ||
|---|---|---|---|---|---|
| Sending Node | Receiving Node | Sending Node | Receiving Node | ||
| 92 | 100 | 0.2102 | 38 | 65 | 0.0772 |
| 26 | 30 | 0.2015 | 75 | 77 | 0.0761 |
| 65 | 66 | 0.1871 | 54 | 59 | 0.0753 |
| 62 | 66 | 0.1641 | 62 | 67 | 0.0748 |
| 76 | 77 | 0.1558 | 89 | 92 | 0.0745 |
| 32 | 113 | 0.1477 | 49 | 51 | 0.0726 |
| 9 | 10 | 0.1477 | 96 | 97 | 0.0715 |
| 80 | 96 | 0.1451 | 8 | 30 | 0.0710 |
| 26 | 25 | 0.1447 | 42 | 49 | 0.0683 |
| 49 | 54 | 0.1430 | 89 | 90 | 0.0668 |
| 92 | 94 | 0.1293 | 45 | 49 | 0.0658 |
| 49 | 54 | 0.1261 | 93 | 94 | 0.0648 |
| 23 | 25 | 0.1237 | 66 | 67 | 0.0624 |
| 79 | 80 | 0.1135 | 15 | 17 | 0.0622 |
| 94 | 100 | 0.1092 | 1 | 2 | 0.0618 |
| 30 | 17 | 0.1077 | 70 | 75 | 0.0590 |
| 38 | 37 | 0.1043 | 83 | 85 | 0.0580 |
| 100 | 101 | 0.1043 | 103 | 104 | 0.0571 |
| 49 | 69 | 0.1038 | 92 | 93 | 0.0566 |
| 86 | 87 | 0.1030 | 14 | 15 | 0.0564 |
| 110 | 112 | 0.0978 | 33 | 37 | 0.0563 |
| 77 | 80 | 0.0977 | 100 | 104 | 0.0561 |
| 17 | 31 | 0.0943 | 43 | 44 | 0.0541 |
| 19 | 34 | 0.0924 | 2 | 12 | 0.0539 |
| 77 | 82 | 0.0907 | 89 | 92 | 0.0532 |
| Power Line | FVSI AvgValue | Count | Percentage [%] | |
|---|---|---|---|---|
| Node | Node | |||
| 92 | 100 | 0.210239 | 181 | 97.31 |
| 1 | 2 | 0.248576 | 1 | 0.54 |
| 26 | 30 | 0.228579 | 3 | 1.61 |
| 38 | 65 | 0.286559 | 1 | 0.54 |
| Parameter | Original System | Loaded Cases | Compensated Cases | % Change (Loaded vs. Original / Compensated vs. Loaded) |
|---|---|---|---|---|
| Average Voltage [pu] | 0.98795 | 0.98154 | 0.9880 | %/+0.6597% |
| Maximum Voltage [pu] | 1.05 | 1.05 | 1.05 | 0%/0% |
| Minimum Voltage [pu] | 0.95 | 0.4064 | 0.9450 | %/+132.52% |
| Objective Deviation | 0.0255 | 0.0631 | 0.0255 | +147.45%/% |
| Case | Mean | Min | Max | StdDev |
|---|---|---|---|---|
| FVSI original | 0.047368 | 0.00021428 | 0.21024 | 0.041701 |
| Stochastic loaded scenarios | 0.047675 | 0.00021428 | 0.21024 | 0.042505 |
| Contingencies, NO SVC scenarios | 0.047852 | 0.00021428 | 0.21024 | 0.04234 |
| Contingencies, with SVC scenarios | 0.047638 | 0.00021428 | 0.21024 | 0.041679 |
| Scenario | Mean Voltage [pu] | Minimum Voltage [pu] | Maximum Voltage [pu] | StdDev |
|---|---|---|---|---|
| Original Profiles | 0.98796 | 0.95 | 1.05 | 0.022585 |
| Loaded Scenarios | 0.98154 | 0.40641 | 1.05 | 0.060648 |
| Contingencies No SVC | 0.98754 | 0.94104 | 1.05 | 0.023078 |
| Contingencies with SVC | 0.98788 | 0.95 | 1.05 | 0.022688 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaramillo, M.D.; Carrión, D.F. Optimizing Critical Overloaded Power Transmission Lines with a Novel Unified SVC Deployment Approach Based on FVSI Analysis. Energies 2024, 17, 2063. https://doi.org/10.3390/en17092063
Jaramillo MD, Carrión DF. Optimizing Critical Overloaded Power Transmission Lines with a Novel Unified SVC Deployment Approach Based on FVSI Analysis. Energies. 2024; 17(9):2063. https://doi.org/10.3390/en17092063
Chicago/Turabian StyleJaramillo, Manuel Dario, and Diego Francisco Carrión. 2024. "Optimizing Critical Overloaded Power Transmission Lines with a Novel Unified SVC Deployment Approach Based on FVSI Analysis" Energies 17, no. 9: 2063. https://doi.org/10.3390/en17092063
APA StyleJaramillo, M. D., & Carrión, D. F. (2024). Optimizing Critical Overloaded Power Transmission Lines with a Novel Unified SVC Deployment Approach Based on FVSI Analysis. Energies, 17(9), 2063. https://doi.org/10.3390/en17092063







