Passive Super-Twisting Second-Order Sliding Mode Control Strategy for Input Stage of MMC-PET
Abstract
1. Introduction
2. MMC-PET System Structure and Input Stage Mathematical Modeling
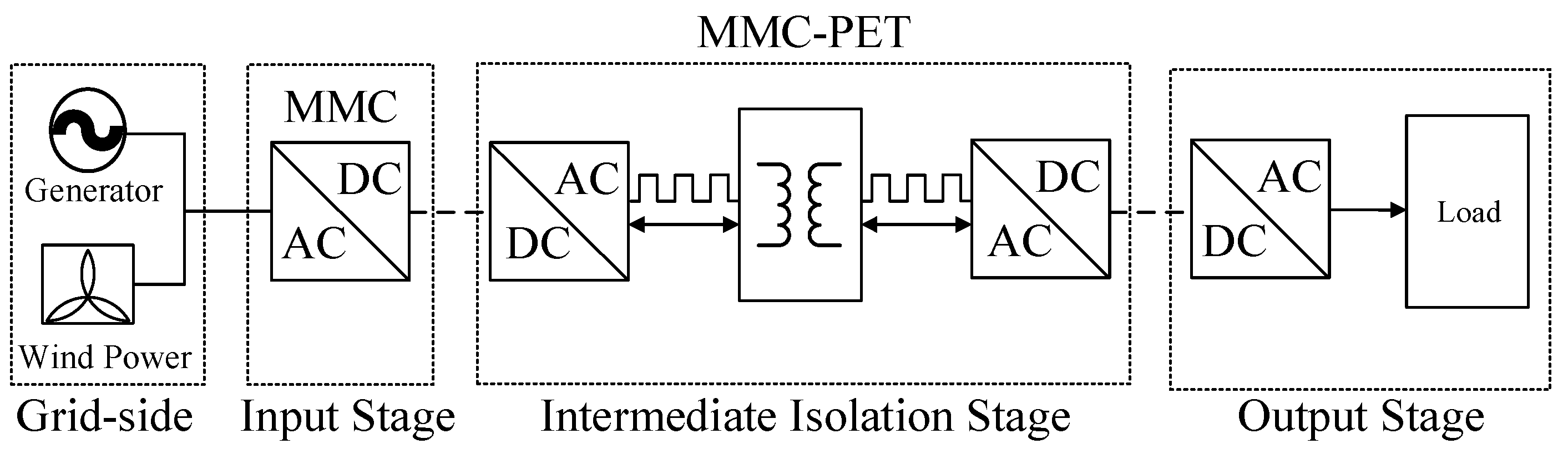
2.1. MMC-PET System Structure
2.2. Mathematical Modeling of the MMC-PET Input Stage
3. Control Strategy for the MMC-PET Input Stage
3.1. Passive Controller Design Based on E-L Modeling
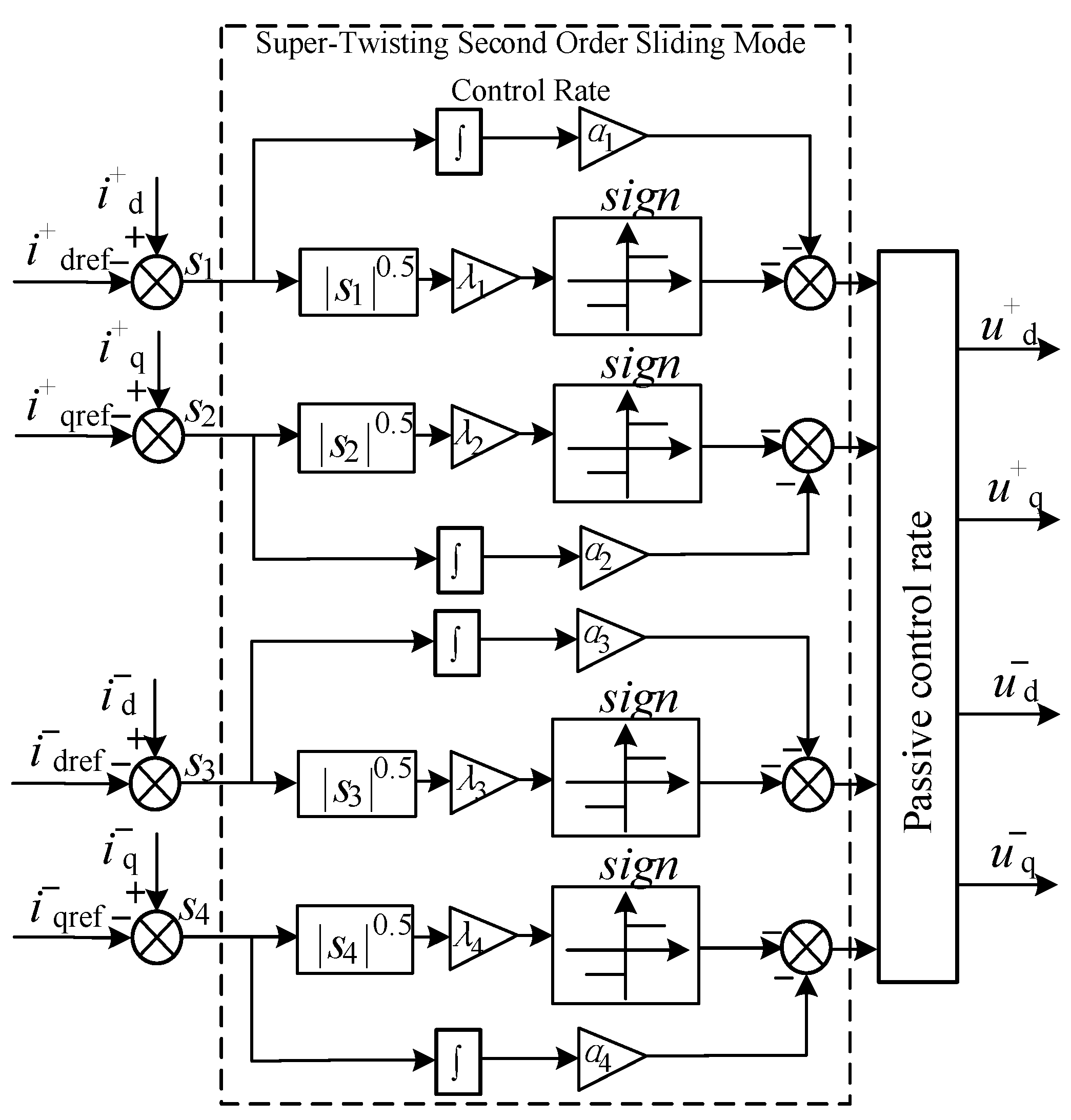
3.2. Passive Super-Twisting Second-Order Sliding Mode Controller Design
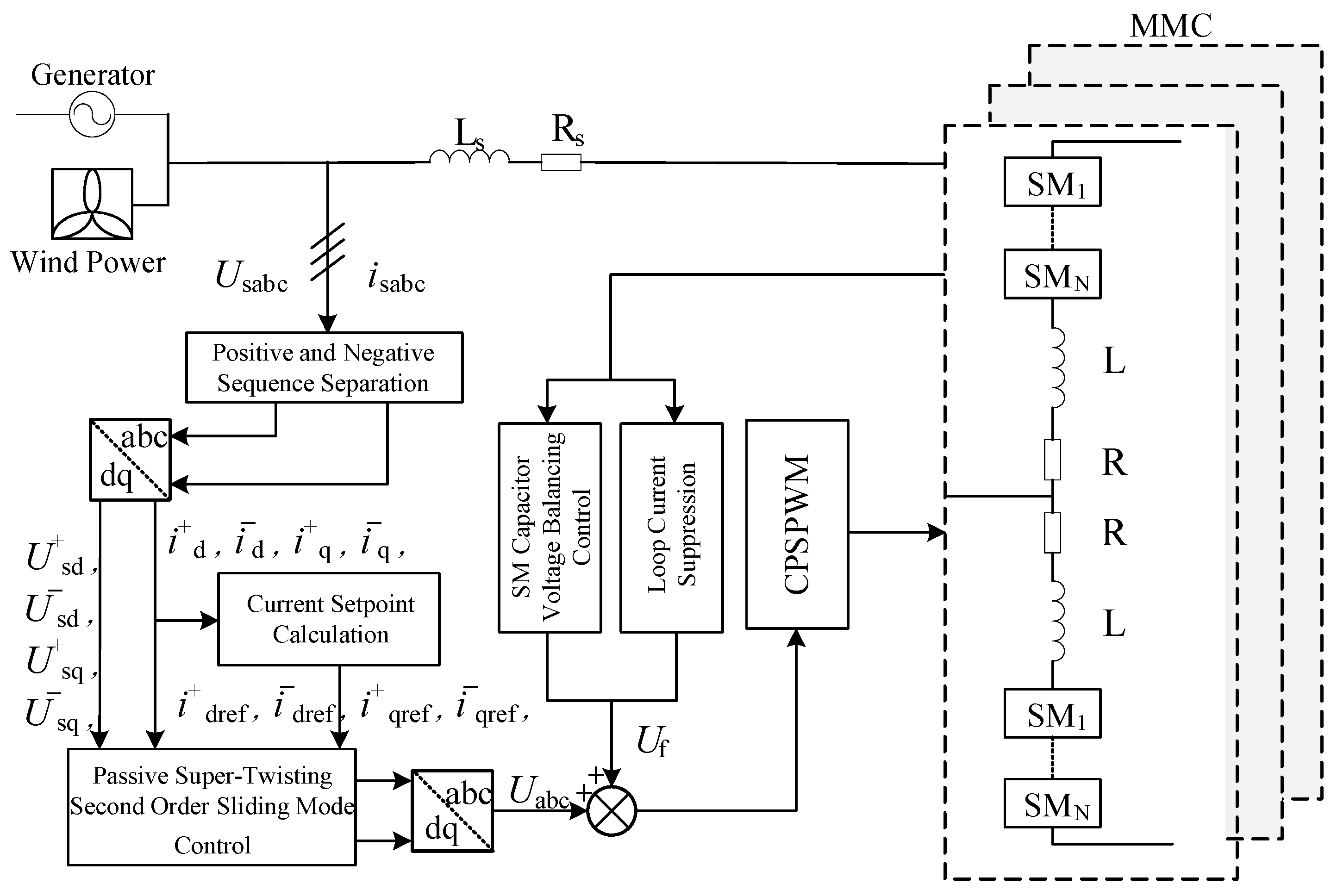
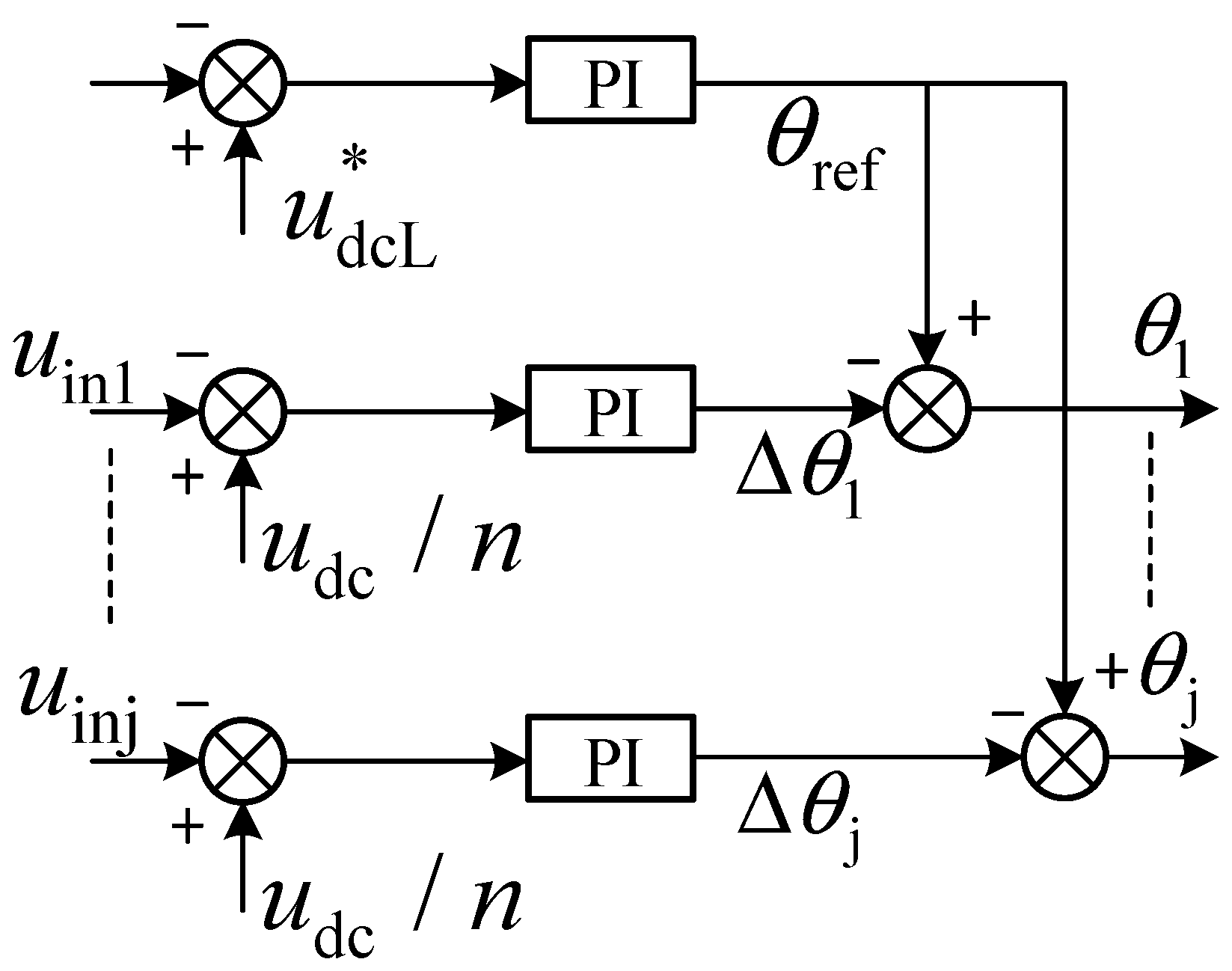
3.3. Overall Control Block Diagram of MMC-PET Input Stage
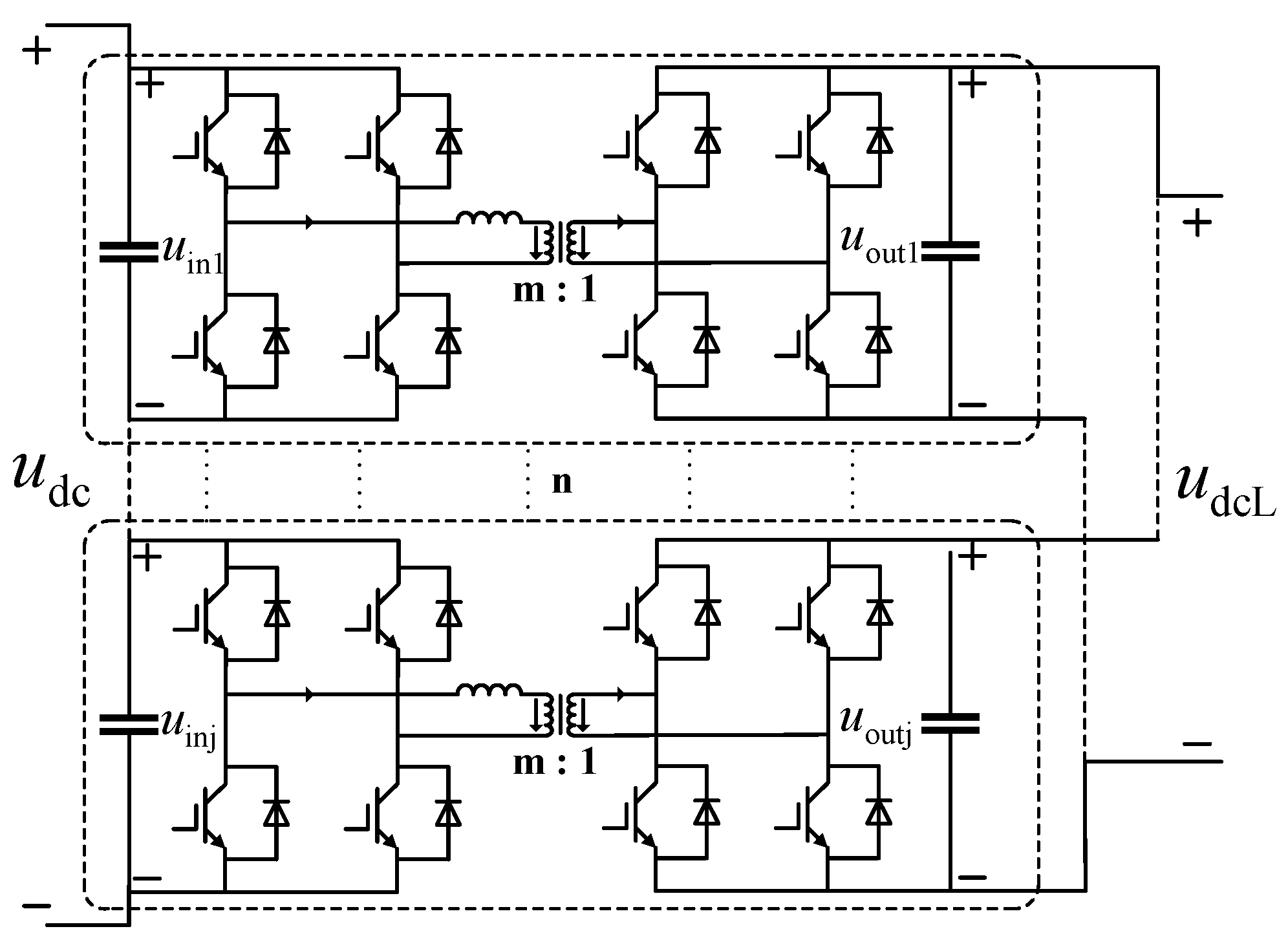
4. Control Strategies for the MMC-PET Intermediate Isolation Stage and Output Stages
5. Simulation Analysis
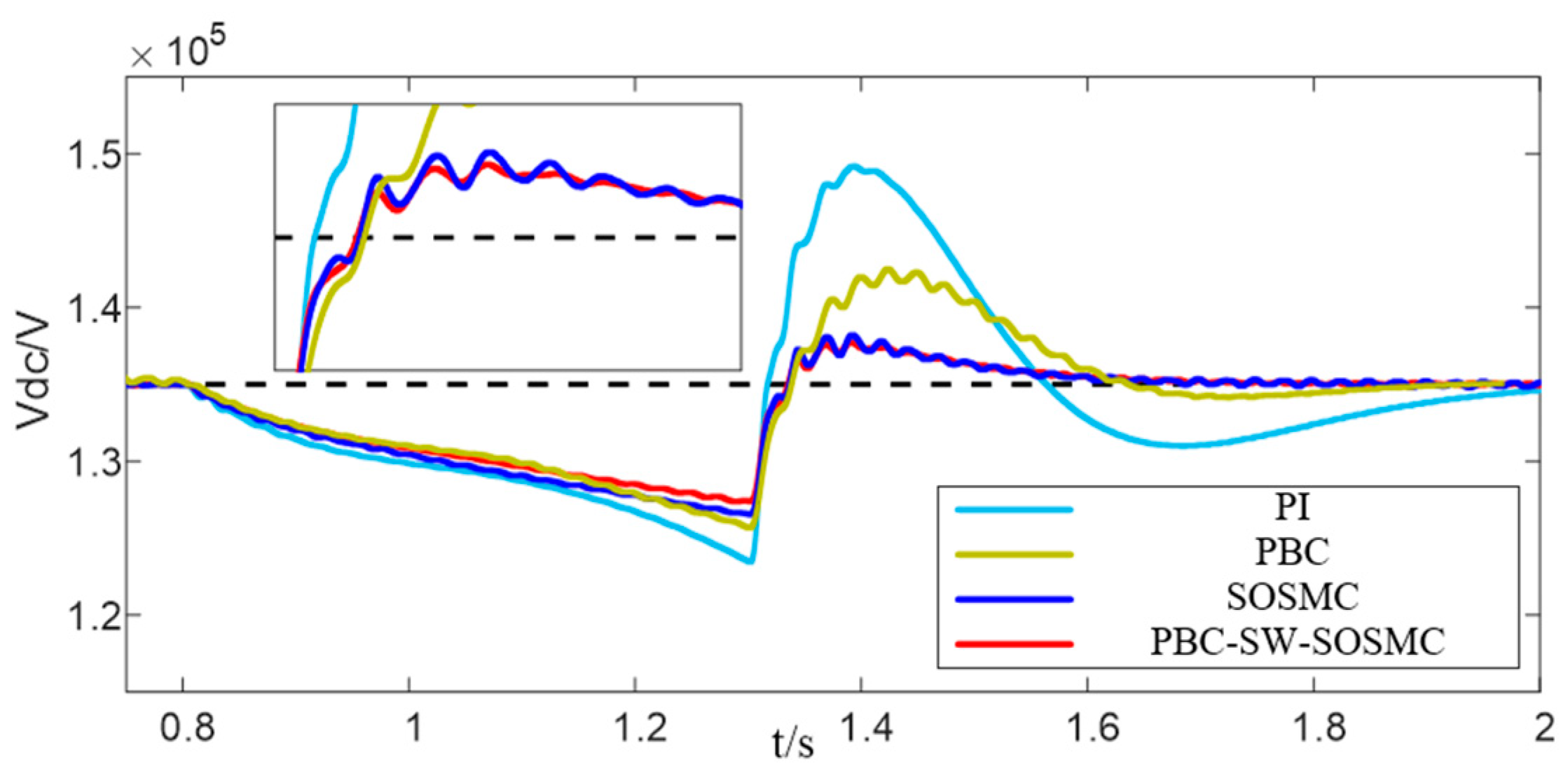
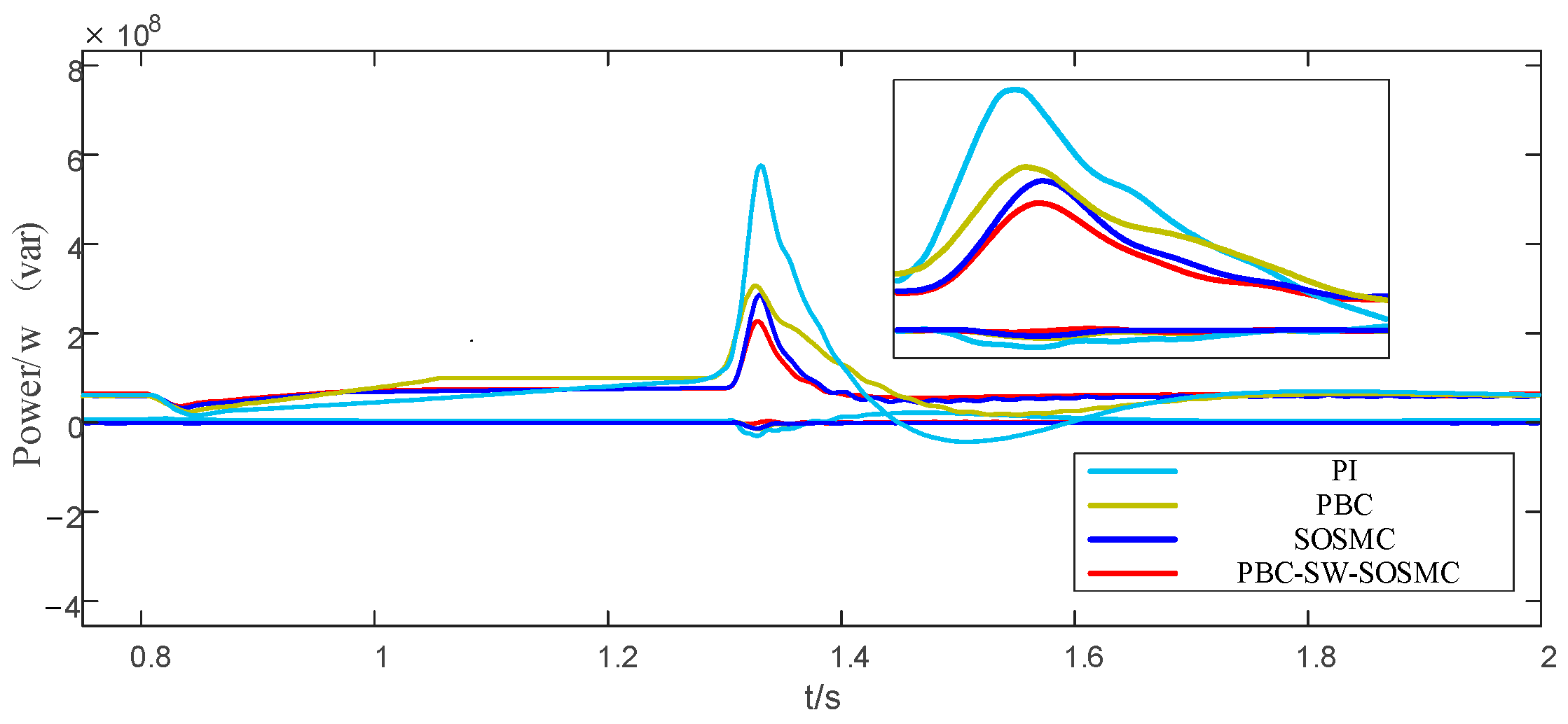
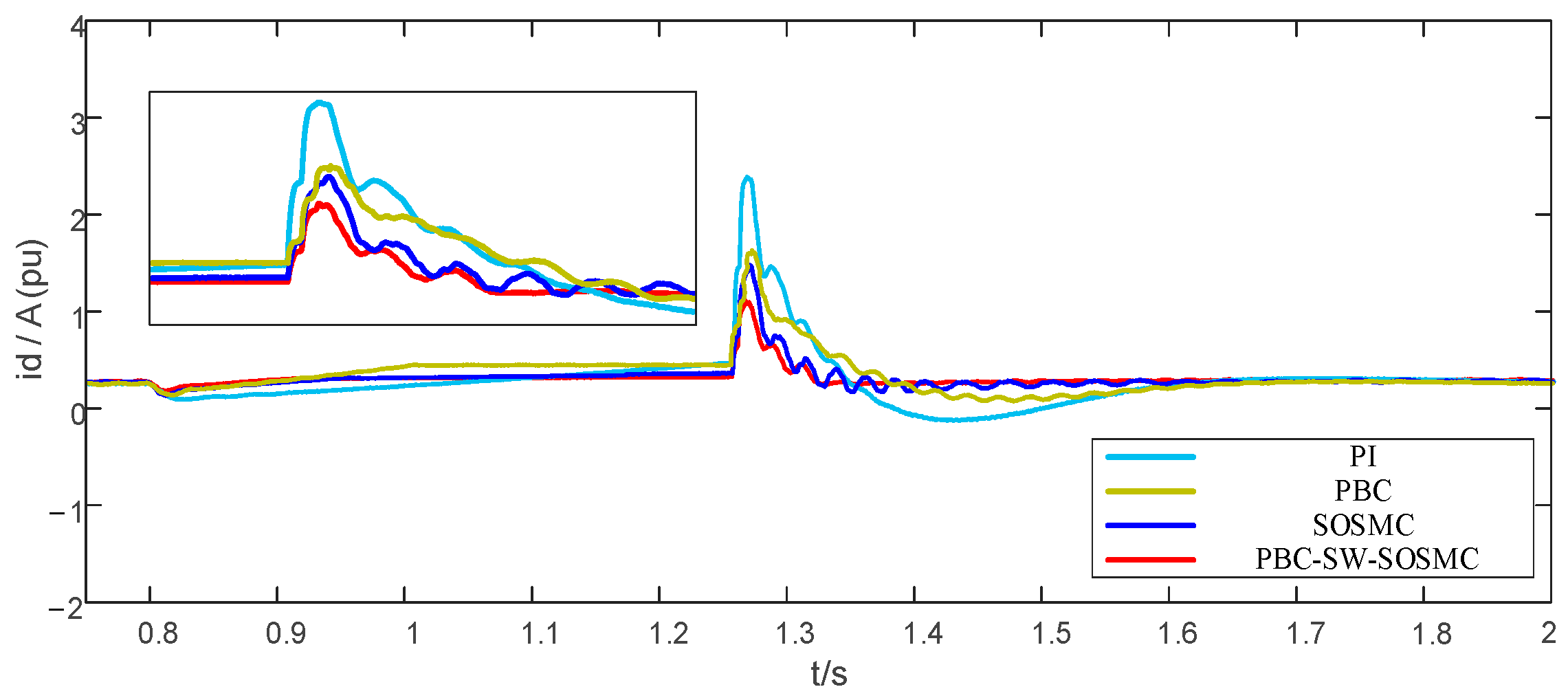
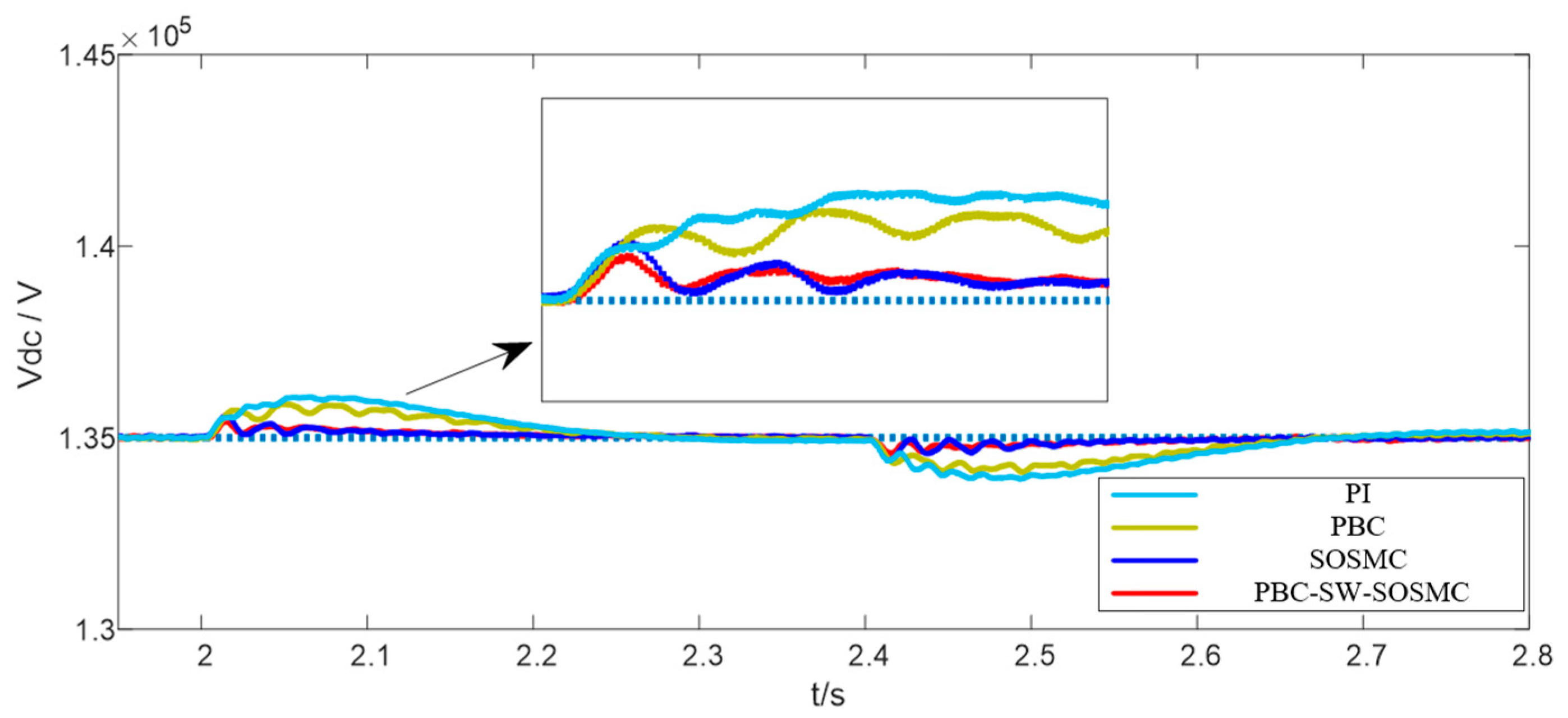
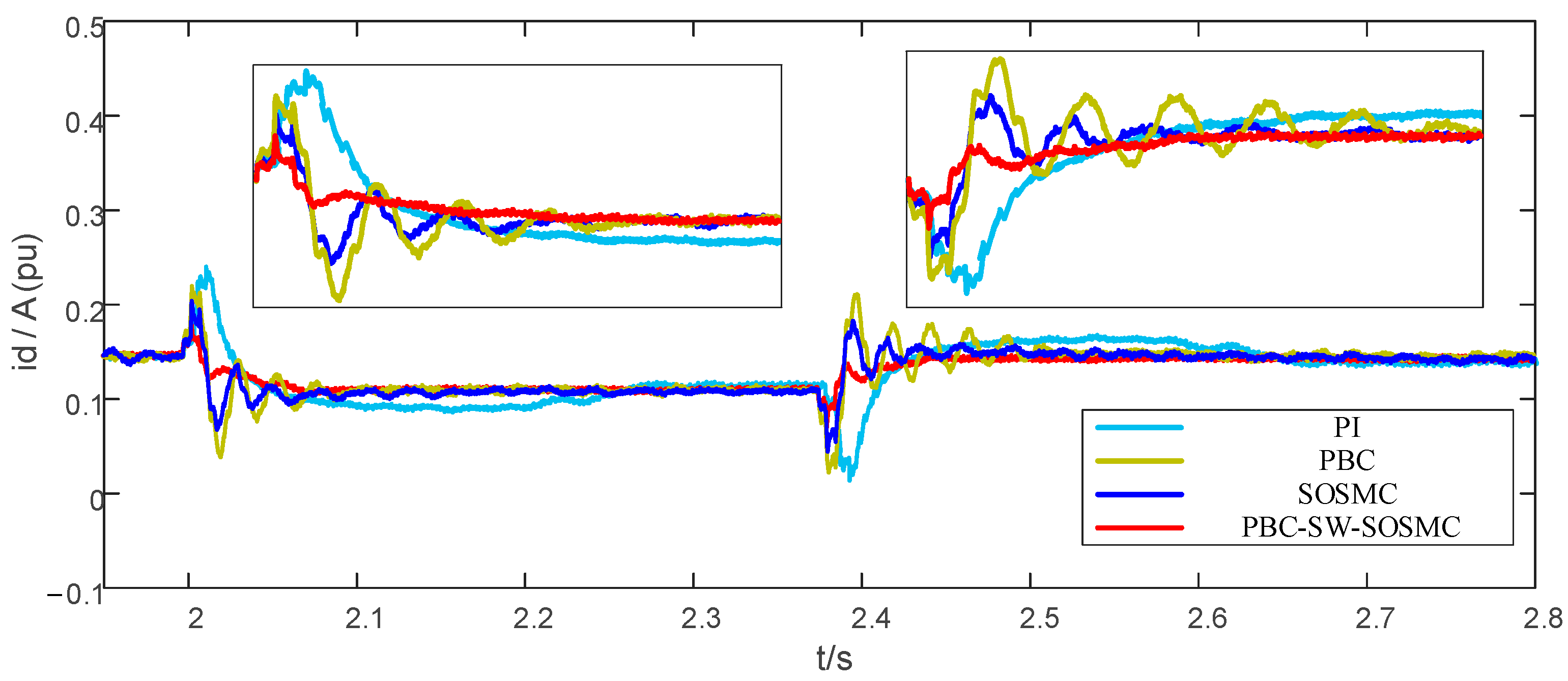
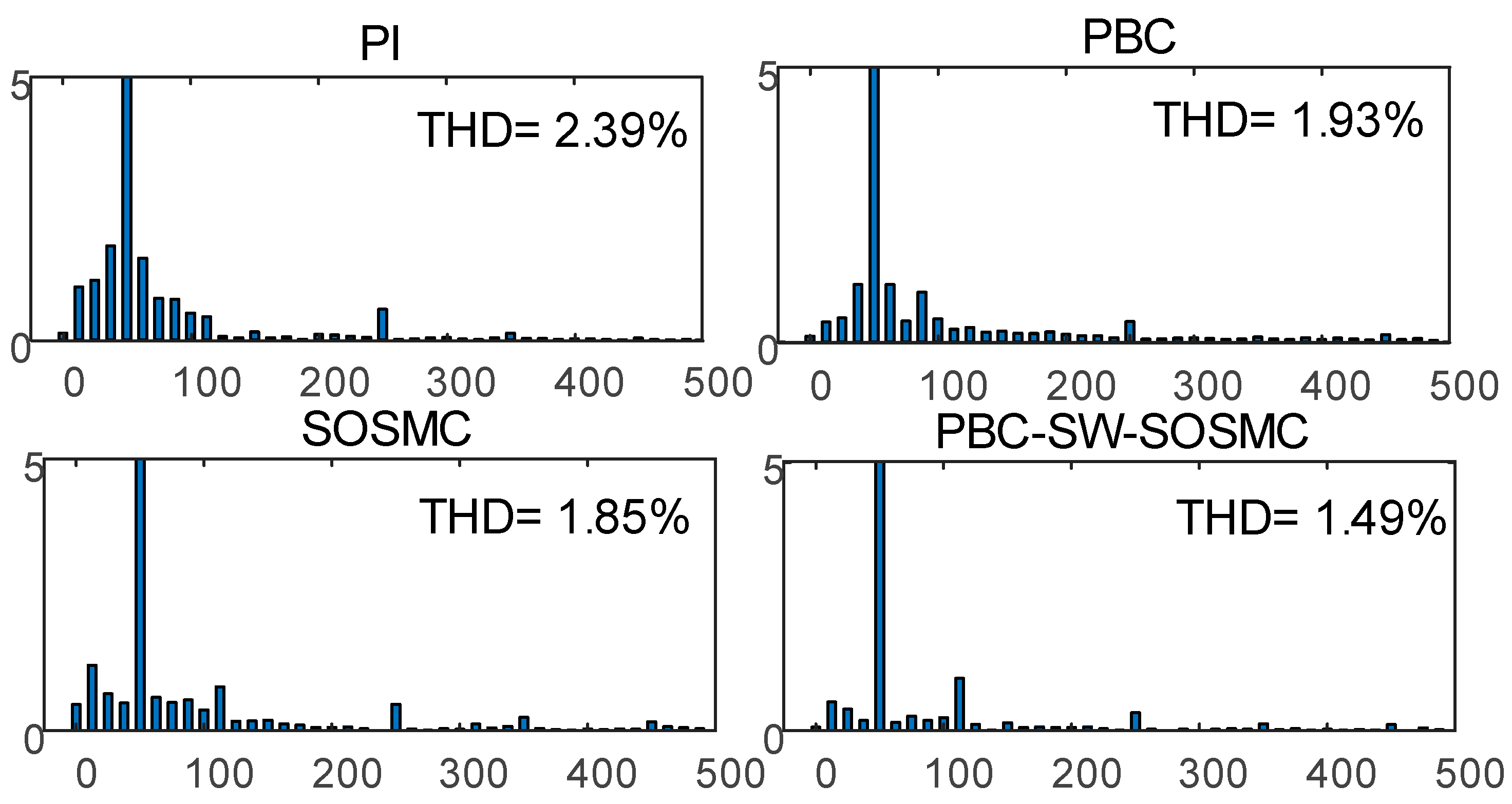
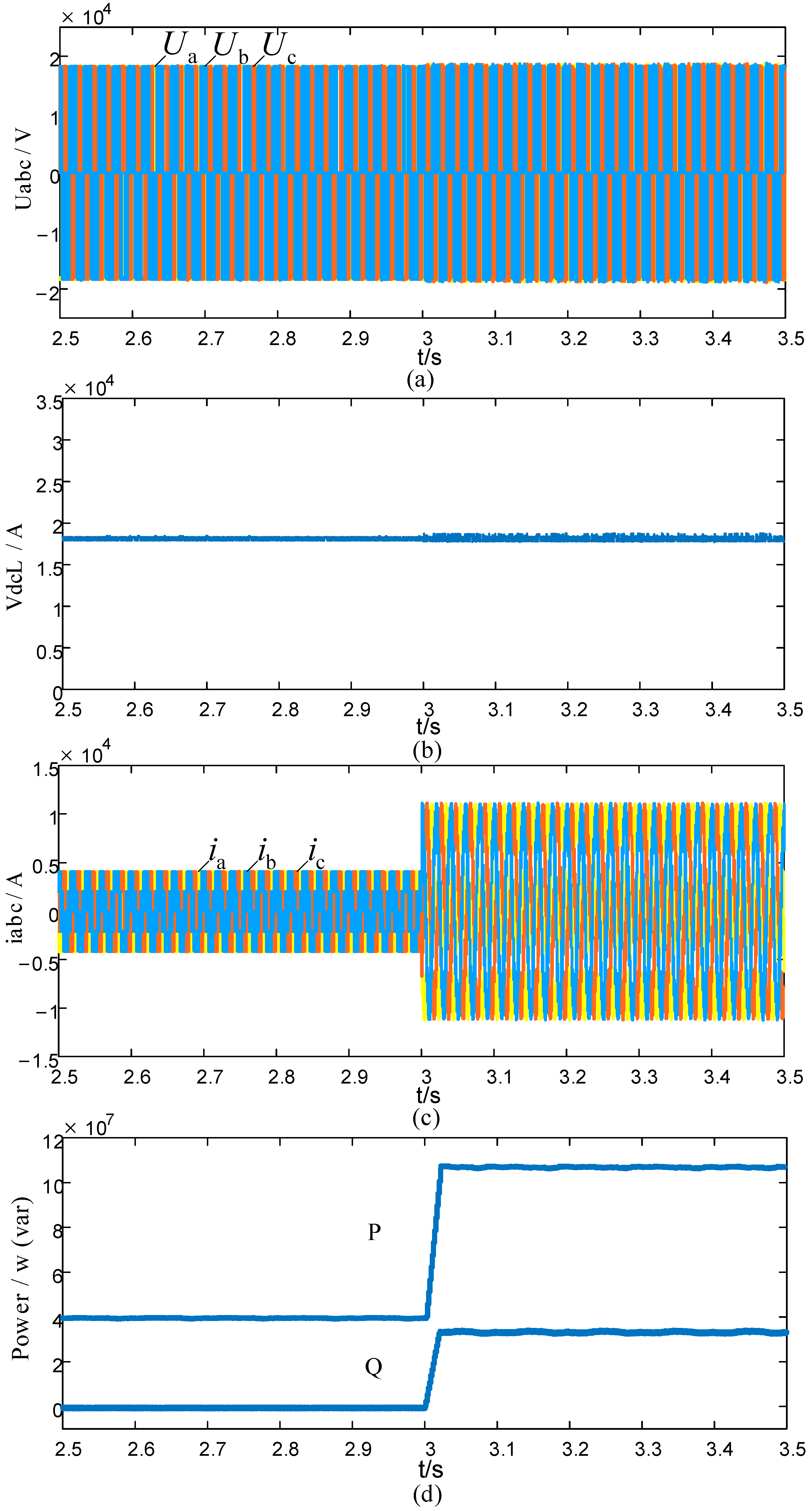
5.1. Grid-Side Load Change
5.2. Temporary Voltage Unbalance
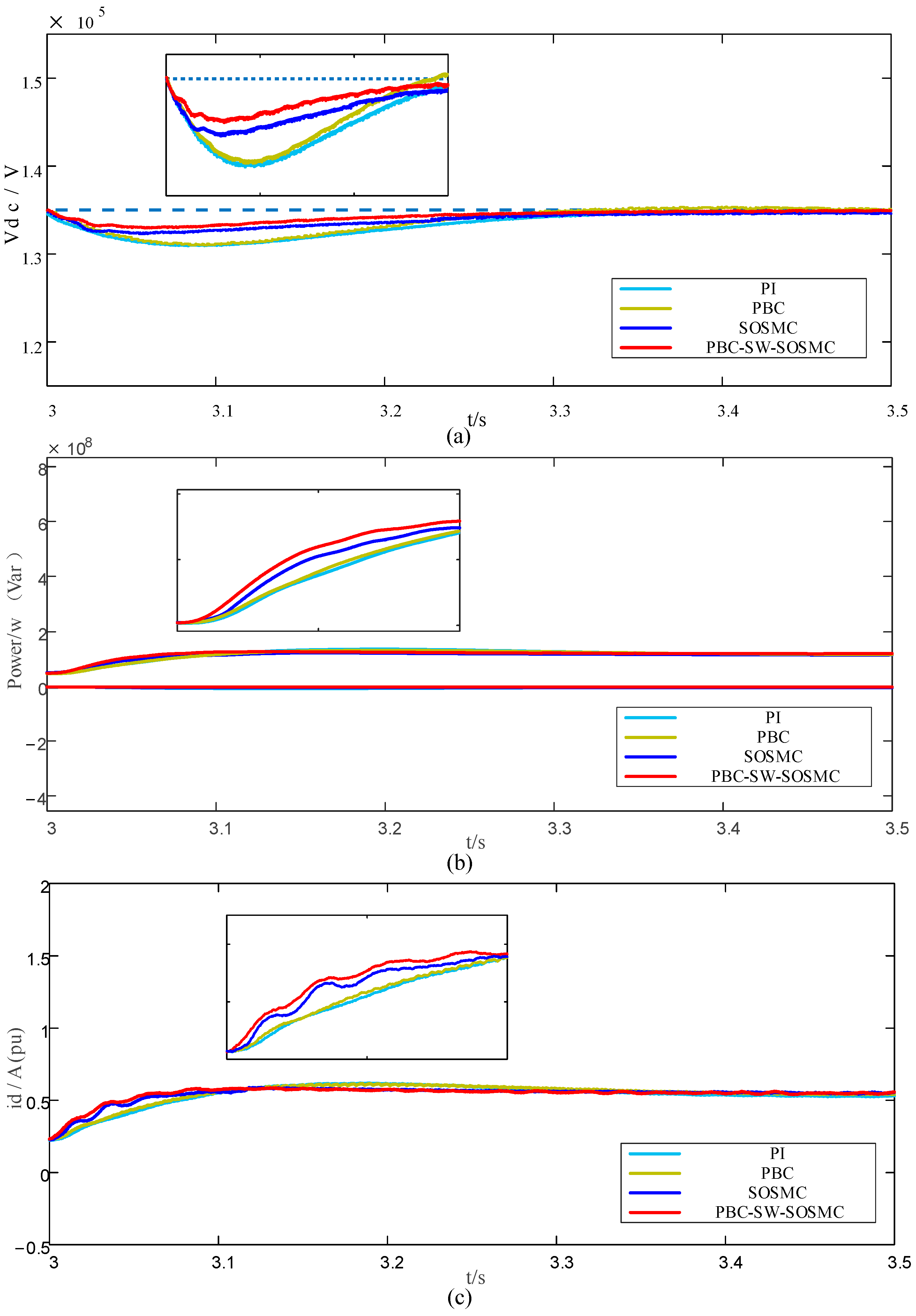
5.3. Output Stage Load Connections
6. Conclusions
- (1)
- The use of passive super-twisting second-order sliding mode control can effectively suppress the DC side voltage, power, and current fluctuations of the MMC-PET under non-ideal operating conditions, thereby improving the reliability of the system operation.
- (2)
- The proposed passive super-twisting second-order sliding mode control strategy has been found to have stronger anti-interference ability, faster response speed, and greater robustness compared to PI control, passivity-based control, and second-order sliding mode control. This makes it more suitable for the transmission and distribution system of MMC-PET.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.X.; Gao, F.Q.; Zhao, C. Research review of power electronic transformer technologies. Proc. CSEE 2018, 38, 1274–1289. [Google Scholar]
- Sun, K.; Lu, S.L.; Yi, Z.Y. A review of high-power high-frequency transformer technology for power electronic transformer applications. Proc. CSEE 2021, 41, 8531–8545. [Google Scholar]
- Ma, D.; Chen, W.; Shu, L. A MMC-Based Multiport Power Electronic Transformer with Shared Medium-frequency Transformer. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 727–731. [Google Scholar] [CrossRef]
- Zhu, L.; Li, C.S.; Lu, Y.P. Fault-tolerant Operation Technology for Three-level Cell Power Electronic Transformer. Autom. Electr. Power Syst. 2023, 47, 144–154. [Google Scholar]
- Xu, W.Y.; Zhen, C.H.; Xu, J.Z.; Zhao, C.Y. Average-value model of cascaded H-bridge type power electronic transformer. Electr. Power Autom. Equip. 2023, 43, 190–196. [Google Scholar]
- Lan, Z.; Tu, C.M.; Xiao, F. The power control of power electronic transformer in hybrid AC-DC microgrid. Trans. China Electrotech. Soc. 2015, 30, 50–57. [Google Scholar]
- Zheng, T.; Wang, K.; Zheng, Z.D.; Pang, J.P.; Li, Y.D. Review of Power Electronic Transformers Based on Modular Multilevel Converters. Proc. CSEE 2022, 42, 5630–5649. [Google Scholar]
- Zhou, Y.D.; Xu, Y.H.; Lv, X.H. Grounding Design and Fault Characteristic Analysis of MMC Based Power Electronic Transformer in Distribution Network. Power Syst. Technol. 2017, 41, 4077–4088. [Google Scholar]
- Zheng, T.; Guo, Y.F.; Lv, W.X.; Piao, Y. Protection for Low-voltage DC Distribution Network Based on Fault Ride-through Strategy of Power Electronic Transformer. Autom. Electr. Power Syst. 2023, 47, 152–161. [Google Scholar]
- Li, Y.X.; Li, Y.; Han, J.Y. A MMC-SST based power quality improvement method for the medium and high voltage distribution network. In Proceedings of the 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2101–2106. [Google Scholar]
- Yuan, Y.S.; Tang, Z. Research on operation of power electronic transformer under voltage drop in intelligent distribution network. Power Autom. Equip. 2019, 39, 44–49. [Google Scholar]
- Khalid, Y.; Nor, Z.B.Y.; Vijanth, S.A. Development of power electronic distribution transformer based on adaptive PI controller. IEEE Access 2018, 6, 44970–44980. [Google Scholar]
- Fang, Y.; Xu, N.; Liu, Y. Hybrid Linear Predictive Control Scheme Based on PIR and MPC for MMC. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 491–495. [Google Scholar]
- Wei, X.; Zhu, X.S.; Ge, J. Improved droop control strategy for parallel operation of cascaded power electronic transformers. High Volt. Technol. 2021, 47, 1274–1282. [Google Scholar]
- Zhang, C.; Jiang, Y.; Xing, X.; Li, X.; Qin, C.; Zhang, B. Passivity-Based Control Method for Three-Level Photovoltaic Inverter to Mitigate Common-Mode Resonant Current. IEEE Trans. Ind. Inform. 2023, 19, 9733–9744. [Google Scholar] [CrossRef]
- Bao, K.Q.; Wu, H.H.; Cheng, Q.M. Passive based control strategy of electric springs based on E-L model. High Volt. Eng. 2021, 1, 1–10. [Google Scholar]
- Xie, Z.K.; Yang, J.M.; Huang, W. Passive control of Archimedes wave swing wave power generation system. Control. Theory Appl. 2019, 36, 383–388. [Google Scholar]
- Cheng, Q.M.; Sun, W.S.; Cheng, Y.M. Passive control strategy of MMC under power grid voltage imbalance. Power Autom. Equip. 2019, 39, 78–85. [Google Scholar]
- Cheng, Q.M.; Fu, W.Q.; Xie, Y.Q.; Zhou, Y.T.; Ye, P.L. Research on Passivity-Based Control Drive System of Permanent Magnet Synchronous Motor Based on MMC-PET. South. Power Syst. Technol. 2022, 16, 83–91. [Google Scholar]
- Liu, Z. Fixed-Time Sliding Mode Control for DC/DC Buck Converters with Mismatched Uncertainties. IEEE Trans. Circuits Syst. 2023, 70, 472–480. [Google Scholar] [CrossRef]
- Shi, S.; Zhang, G.S.; Min, H.F. Prescribed-time SOSM control of nonlinear systems subject to mismatched terms. Control. Decis. 2023, 8, 1–9. [Google Scholar]
- Ma, F.J.; Zhu, Z.; Min, J. Model analysis and sliding mode current controller for multilevel railway power conditioner under the V/v traction system. IEEE Trans. Power Electron. 2019, 34, 1243–1253. [Google Scholar] [CrossRef]
- Guo, J. The Load Frequency Control by Adaptive High Order Sliding Mode Control Strategy. IEEE Access 2022, 10, 25392–25399. [Google Scholar] [CrossRef]
- Swikir, A.; Utkin, V. Chattering analysis of conventional and super twisting sliding mode control algorithm. In Proceedings of the 2016 14th International Workshop on Variable Structure Systems. Nanjing, China, 1–4 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 98–102. [Google Scholar]
- Zhou, J. Decentralized Robust Control for Vehicle Platooning Subject to Uncertain Disturbances via Super-Twisting Second-Order Sliding-Mode Observer Technique. IEEE Trans. Veh. Technol. 2022, 71, 7186–7201. [Google Scholar] [CrossRef]



| Parameter | Value | |
|---|---|---|
| Input stage | Grid-side voltage/kV | 66 |
| Grid-side resistance/ | 0.4 | |
| Grid-side Inductance/mH | 0.002 | |
| Number of bridge arm submodules | 50 | |
| Bridge arm resistors/ | 0.01 | |
| Bridge arm Inductance/mH | 0.15 | |
| Submodule Capacitance/μF | 0.0105 | |
| DC side voltage reference value/kV | 135 | |
| Intermediate isolation stage | High-voltage side capacitor/mF | 1 |
| Low-voltage side capacitor/mF | 8 | |
| Rated Ratio | 7:1 | |
| Rated frequency/Hz | 50 | |
| Output stage | Submodule Capacitance/μF | 0.01 |
| Voltage Frequency/Hz | 50 | |
| Voltage amplitude/kV | 18 | |
| Bridge arm resistors/ | 0.1 |
| Control Strategy | Rising Time/s | Overshoot/% | Adjustment Time/s |
|---|---|---|---|
| PI | 0.453 | 2.32 | 0.441 |
| PBC | 0.335 | 0.96 | 0.322 |
| SOSMC | 0.186 | 0.81 | 0.254 |
| PBC-SW-SOSMC | 0.172 | 0.44 | 0.167 |
| Control Strategy | Rising Time/s | Overshoot/% | Adjustment Time/s |
|---|---|---|---|
| PI | 0.286 | 12.7 | 0.274 |
| PBC | 0.141 | 9.6 | 0.135 |
| SOSMC | 0.083 | 6.4 | 0.075 |
| PBC-SW-SOSMC | 0.045 | 2.1 | 0.041 |
| Control Strategy | Rising Time/s | Overshoot/% | Adjustment Time/s |
|---|---|---|---|
| PI | 0.172 | 11.1 | 0.337 |
| PBC | 0.145 | 10.4 | 0.236 |
| SOSMC | 0.119 | 6.5 | 0.137 |
| PBC-SW-SOSMC | 0.094 | 4.6 | 0.101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Zhou, J.; Yang, H.; Huang, L. Passive Super-Twisting Second-Order Sliding Mode Control Strategy for Input Stage of MMC-PET. Energies 2024, 17, 2036. https://doi.org/10.3390/en17092036
Zhou J, Zhou J, Yang H, Huang L. Passive Super-Twisting Second-Order Sliding Mode Control Strategy for Input Stage of MMC-PET. Energies. 2024; 17(9):2036. https://doi.org/10.3390/en17092036
Chicago/Turabian StyleZhou, Jingtao, Jianping Zhou, Hao Yang, and Liegang Huang. 2024. "Passive Super-Twisting Second-Order Sliding Mode Control Strategy for Input Stage of MMC-PET" Energies 17, no. 9: 2036. https://doi.org/10.3390/en17092036
APA StyleZhou, J., Zhou, J., Yang, H., & Huang, L. (2024). Passive Super-Twisting Second-Order Sliding Mode Control Strategy for Input Stage of MMC-PET. Energies, 17(9), 2036. https://doi.org/10.3390/en17092036






