Optimizing the Building Refurbishment Process Using Improved Evolutionary Algorithms
Abstract
1. Introduction
- In the simplified model, a Genetic Algorithm (GA) was used, while the current approach proposes a Non-dominated Sorting Genetic Algorithm (NSGA-II).
- The simplified model did not use the Pymoo (Multi-Objective Optimization in Python) library.
- The simplified model had fewer variables and input data than the improved model; thus, the windows’ overall heat transfer coefficients and total solar energy transmittance and the doors’ thermal proprieties were not initially simulated and predetermined thermal proprieties were used. The search space was represented by only thickness–thermal conductivity pairs. In addition, the exterior walls and the floor were insulated with expanded polystyrene and extruded polystyrene, but the roof-ceiling was not insulated.
- In the simplified model, the computational outdoor temperature was considered −15 °C, according to the SR1907-1 Standard [14]. The average value of the solar radiation intensity was considered to be 77.03 W/m2 [15]. The current model uses the monthly average solar radiation intensity and the monthly average outdoor temperature.
- In the simplified model, the average ground temperature was considered to be θground = 10 °C at a depth of 2 m (δp) according to [16].
- The simplified model did not include the heat pump-choosing algorithm.
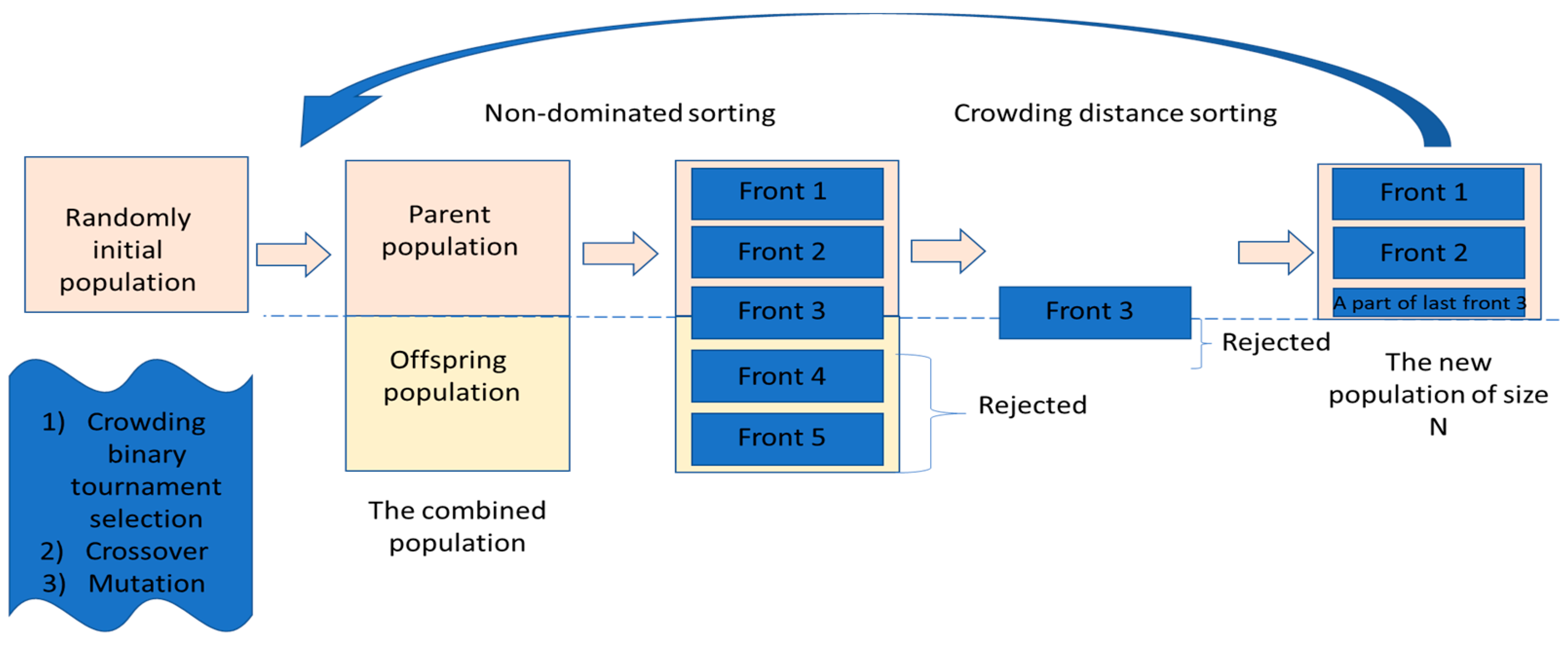
2. The Steps of the Non-Dominated Sorting Genetic Algorithm II
- Establishing the input parameters: the population size, the number of generations, crossover probability, and mutation probability [18]. A random initial population is generated. The objective functions are evaluated. The parents are selected using crowding binary tournament selection.
- Creating the offsprings from the initial parents using the standard operators of the GA (crossover and mutation); thus, a combined population consisting of parents and offspring is created [19].
- Sorting the combined population based on the non-dominated ranks and crowding-distance. Several non-dominated fronts (Pareto fronts) are produced. Each member in each front has assigned a fitness value or rank [20].
- 4.
- Application of crossover and mutation to the new population of size N to produce a new combined population consisting of parents and offspring. The algorithm keeps running from step 2 until the maximum number of generations is achieved [25].
3. Case Study
3.1. Optimization Problem Development
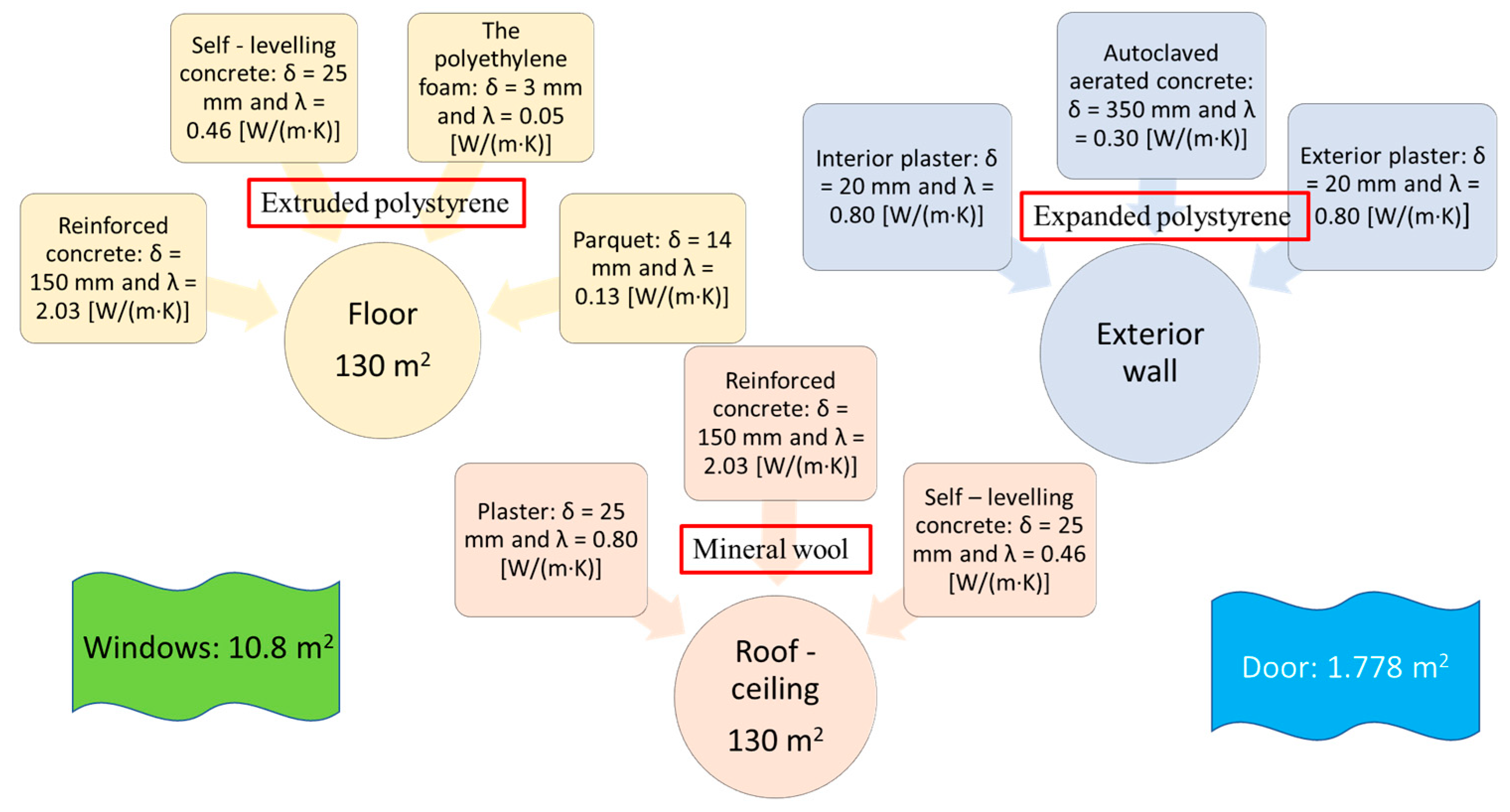
- Thermal conductivities and thicknesses of expanded polystyrene, extruded polystyrene and mineral wool in case of the walls, floor and roof–ceiling.
- Overall heat transfer coefficient and total solar energy transmittance for the windows.
- Overall heat transfer coefficient in case of the door.
3.2. Initialize the NSGA-II
3.3. Results
4. Heat Pump Model Optimization
4.1. The Energy Consumption for Domestic Hot Water Preparation
4.2. Heat Pump Simulation
- 1.
- Simulation 1: A maximum cost that can be allocated to heat pumps is set and the heat pumps falling within this cost limit are compared according to the coefficient of performance (COP), thermal load of the capacitor and number of pumps needed to ensure the energy requirements for heating and hot water preparation:
- Criterion 1: Cost pumps ≤ RON 34,600.where RON 34,600 represents the maximum cost that can be allocated to heat pumps. This cost was obtained through a specific market survey. The heat pumps chosen from among 345 heat pumps models after applying the financial criterion are presented in Table 3.
- Criterion 2: 1 ≤ Npumps < 3;
- Criterion 3: COP ≥ 3;
- Criterion 4: 14.52 ≤ Qctotal ≤ 15.
- 2.
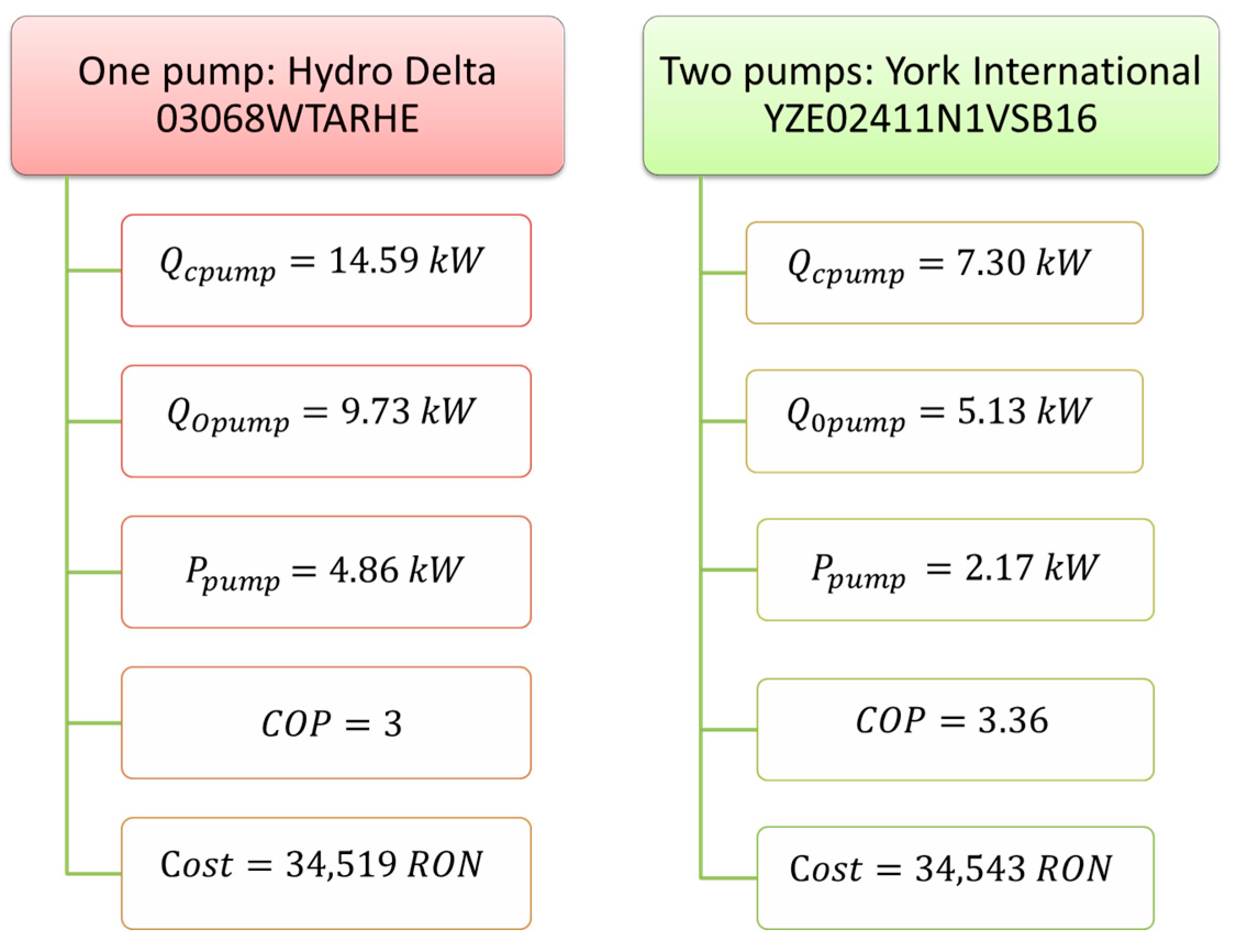
- Simulation 2: the heat pumps were compared based on their technical characteristics, as presented at simulation 1 (COP, Qctotal, Npumps), and then it was verified that the selected pumps respect the maximum cost limit. The simulation result shows that two heat pumps with the specifications presented in Figure 5a or one heat pump with the specifications presented in Figure 5b must be installed to guarantee the 14.52 kW thermal load needed for heating and hot water preparation, according to the technical criteria.
5. Conclusions
- expanded polystyrene with δins1 = 100 mm and λins1 = 0.038 W/(m·K);
- extruded polystyrene with δins2 = 100 mm and λins2 = 0.031 W/(m·K);
- mineral wool δins3 = 200 mm and λins3 = 0.038 W/(m·K);
- triple-glazed IGUs with two 4S glasses and one float glass, separated by argon with Uw = 0.6 W/(m2·K) and g = 0.4;
- one door made of oak covered with stainless steel, with U2 = 0.7 W/(m2·K).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | The specific demand for domestic hot water at 60 °C [m3] |
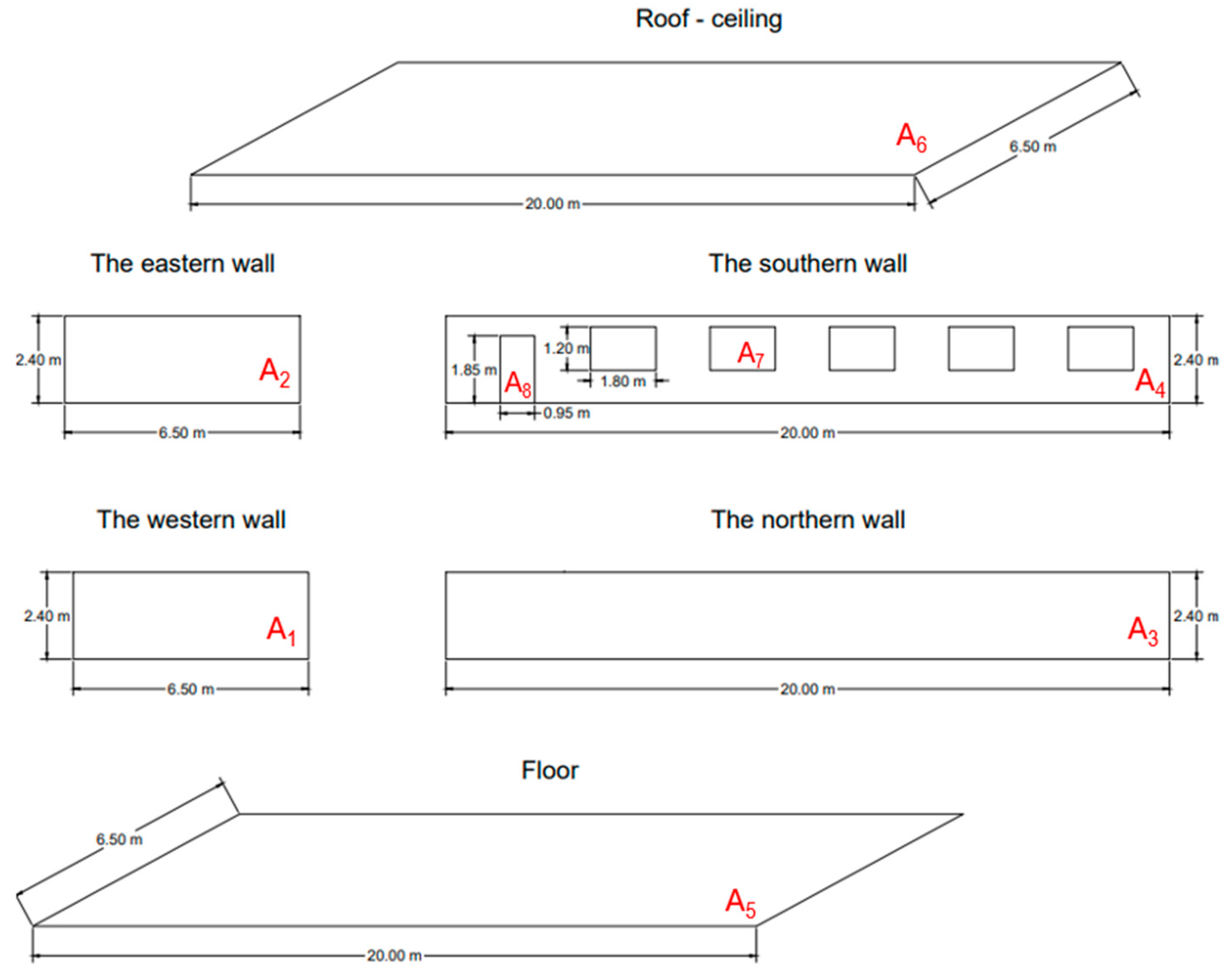
| A1 | The area of the western wall [m2] |
| A2 | The area of the eastern wall [m2] |
| A3 | The area of the northern wall [m2] |
| A4 | The area of unglazed surface of the southern wall [m2] |
| A5 | The area of the floor [m2] |
| A6 | The area of the roof–ceiling [m2] |
| A7 | The area of the windows [m2] |
| A8 | The area of the door [m2] |
| BO-XGBoost | Bayesian optimization with extreme gradient-boosting trees |
| c | Offspring |
| ca | Specific heat of air [kJ/(kg·K)] |
| COP | Coefficient of performance [-] |
| Cost pumps | Maximum cost that can be allocated to heat pumps [RON] |
| cw | Specific heat capacity of liquid water [kJ/(kg·K)] |
| EU | European Union |
| f1 | Coefficient that depends on the type of installation to which the consumption point is connected [-] |
| f2 | Coefficient that depends on the technical condition of the armatures where hot water is consumed [-] |
| g | Total solar energy transmittance [-] |
| GA | Genetic Algorithm |
| GBDT | Gradient-Boosting Decision Tree |
| Gk | Monthly average solar radiation intensity [W/m2] |
| hk | The heating period [h] |
| hpumps | The operating hours of the pump [h/year] |
| HV | The heat loss coefficient of the building through ventilation [W/K] |
| i | The calculation index for consumer categories [-] |
| k | Months in the heating period |
| MLPANN | Multilayer Perception Artificial Neural Network |
| N | The size of the population [-] |
| na | The average number of air changes [h−1] |
| n_constr | The number of constraints [-] |
| n_obj | The number of objectives [-] |
| Npumps | The number of pumps selected to cover most of the energy requirements for heating and hot water preparation [-] |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| Nu | The number of people using hot water [-] |
| n_var | The number of variables [-] |
| p | Parent |
| P1 (δins1, λins1) | The prices of the expanded polystyrene [RON] |
| P2 (δins2, λins2) | The prices of the extruded polystyrene [RON] |
| P3 (δins3, λins3) | The prices of the mineral wool [RON] |
| P4 (g, Uw) | The prices of windows [RON] |
| P5 (U2) | The prices of door [RON] |
| Ppump | The power consumed by the compressor for every studied pump [kW] |
| Ptotal | The total power consumed by compressors [kW] |
| Pymoo | Multi-Objective Optimization in Python |
| Qac | The energy required for domestic hot water preparation [kWh/year] |
| Qac,c | The heat losses related to the waste of domestic hot water [kWh/year] |
| Qam | The energy consumption for domestic hot water preparation [kWh/year] |
| Qcpump | The thermal load of the capacitor for every studied pump [kW] |
| Qctotal | The thermal load for heating and hot water preparation [kW] |
| Qheating | The energy requirement for heating [kWh/year] |
| q1k (δisns1, λins1) | The heat flux through the insulated wall [W/m2] |
| q2k (δins2, λins2) | The heat flux through the insulated floor [W/m2] |
| q3k (δins3, λins3) | The heat flux through the insulated roof–ceiling [W/m2] |
| q4k (g, Uw) | The heat flux through the windows [W/m2] |
| q5k (U2) | The heat flux through the door [W/m2] |
| Qopump | The refrigerating power of the evaporator for every studied pump [kW] |
| Qototal | The total refrigerating power of evaporators [kW] |
| SBX | Simulated Binary Crossover |
| u | Random number between 0 and 1 |
| U2 | The overall heat transfer coefficient of the door [W/(m2·K)] |
| Uw | The overall heat transfer coefficient of the windows [W/(m2·K)] |
| V | The heated volume [m3] |
| Vac | The required volume of domestic hot water [m3] |
| Vac,c | The volume corresponding to losses and waste of hot water [m3] |
| WWR | The window-to-wall ratio |
| Greek symbols | |
| α1in, α1out, α2, α3in, α3out | The convection heat transfer coefficient [W/(m2·K)] |
| βq | The spreading factor [-] |
| ΔTk | The temperature difference [°C] |
| δ1, δ2, δ3, δ4 | The thickness of the construction materials in case of exterior walls, floor, or roof–ceiling [mm] |
| δizol1 | The thickness of the expanded polystyrene [mm] |
| δizol2 | The thickness of the extruded polystyrene [mm] |
| δizol3 | The thickness of the mineral wool [mm] |
| δ1p, δ2p | The depth in the ground [mm] |
| η | The distribution index [-] |
| θac | The hot water preparation temperature [°C] |
| θac,c | The temperature of supply/use of hot water at the point of consumption [°C] |
| θar | The temperature of cold water entering the hot water preparation system [°C] |
| θground k | The ground temperature [°C] |
| θin | The computational indoor temperature [°C] |
| θout k | The monthly average outdoor temperature [°C] |
| λ1, λ2, λ3, λ4 | thermal conductivities of the construction materials in case of exterior walls, floor, or roof–ceiling [W/(m·K)] |
| λins1 | The thermal conductivity of the expanded polystyrene [W/(m·K)] |
| λins2 | The thermal conductivity of the extruded polystyrene [W/(m·K)] |
| λins3 | The thermal conductivity of the mineral wool [W/(m·K)] |
| λ1p , λ2p | The ground thermal conductivity [W/(m·K)] |
| ρ | The density of domestic water [kg/m3] |
| ρa | The air density [kg/m3] |
References
- European Environment Agency (EEA). Resource Efficiency and Low Carbon Economy—Energy Efficiency. 2019. Available online: https://www.eea.europa.eu/airs/2018/resource-efficiency-and-low-carbon-economy/energy-efficiency (accessed on 7 January 2024).
- Ministry of Regional Development and Public Administration. NZEB Romania: Plan to Increase the Number of Nearly Zero-Energy Buildings. 2014. Available online: https://www.mdlpa.ro/userfiles/metodologie_calcul_performanta_energetica_iulie2014.pdf (accessed on 7 January 2024).
- Building Performance Institute Europe (BPIE). Europe’s Buildings under the Microscope: A Country-by-Country Review of the Energy Performance of Buildings. 2011. Available online: https://bpie.eu/wp-content/uploads/2015/10/HR_EU_B_under_microscope_study.pdf (accessed on 14 January 2024).
- Delgarm, N.; Sajadi, B.; Delgarm, S.; Kowsary. A novel approach for the simulation-based optimization of the buildings energy consumption using NSGA-II: Case study in Iran. Energy Build. 2016, 127, 552–560. [Google Scholar] [CrossRef]
- Niemelä, T.; Kosonen, R.; Jokisalo, J. Cost-effectiveness of energy performance renovation measures in Finnish brick apartment buildings. Energy Build. 2017, 137, 60–75. [Google Scholar] [CrossRef]
- Bingham, R.D.; Agelin-Chaab, M.; Rosen, M.A. Whole building optimization of a residential home with PV and battery storage in The Bahamas. Renew. Energy 2019, 132, 1088–1103. [Google Scholar] [CrossRef]
- Acar, U.; Kaska, O.; Tokgoz, N. Multi-objective optimization of building envelope components at the preliminary design stage for residential buildings in Turkey. J. Build. Eng. 2021, 42, 102499. [Google Scholar] [CrossRef]
- Lapisa, R.; Bozonnet, E.; Salagnac, P.; Abadie, M.O. Optimized design of low-rise commercial buildings under various climates—Energy performance and passive cooling strategies. Build. Environ. 2018, 132, 83–95. [Google Scholar] [CrossRef]
- Kahsay, M.T.; Bitsuamlak, G.T.; Tariku, F. Thermal zoning and window optimization framework for high-rise buildings. Appl. Energy 2021, 292, 116894. [Google Scholar] [CrossRef]
- Wang, R.; Lu, S.; Feng, W. A three-stage optimization methodology for envelope design of passive house considering energy demand, thermal comfort and cost. Energy 2020, 192, 116723. [Google Scholar] [CrossRef]
- Yue, N.; Li, L.; Morandi, A.; Zhao, Y. A metamodel-based multi-objective optimization method to balance thermal comfort and energy efficiency in a campus gymnasium. Energy Build. 2021, 253, 111513. [Google Scholar] [CrossRef]
- Wu, C.; Pan, H.; Luo, Z.; Liu, C.; Huang, H. Multi-objective optimization of residential building energy consumption, daylighting, and thermal comfort based on BO-XGBoost-NSGA-II. Build. Environ. 2024, 254, 111386. [Google Scholar] [CrossRef]
- Nicolae, A.E.; Necula, H.; Carutasiu, B.M. Optimization of energy rehabilitation processes of existing buildings. U.P.B. Sci. Bull. 2023, 85. Available online: https://www.scribd.com/document/404094429/337436568-SR-1907-1-2014-pdf (accessed on 7 January 2024).
- Standard SR1907-1; Heating Installations: Calculation Method. Romanian Standards Association: Bucharest, Romania, 2014.
- Methodology for Calculating the Energy Performance of Buildings, MC001, Part IV—Breviary for Calculating the Energy Performance of Buildings and Apartments. The Official Gazette of Romania. 2010; pp. 00062–00064, Number 243. Available online: https://www.mdlpa.ro/userfiles/reglementari/Domeniul_XXVII/27_11_MC_001_4_5_2009.pdf (accessed on 7 January 2024).
- Normative Regarding the Thermotechnical Calculation of Construction Elements in Contact with the Ground, Indicative C107/5; MTCT: Bucharest, Romania, 2005.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Khan, A.; Baig, A.R. Multi-Objective Feature Subset Selection using Non-dominated Sorting Genetic Algorithm. J. Appl. Res. Technol. 2015, 13, 145–159. [Google Scholar] [CrossRef]
- Mkaouer, M.W.; Kessentini, M. Model Transformation Using Multiobjective Optimization. In Advances in Computers; Hurson, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 92, pp. 161–202. ISBN 978-0-12-420232-0. [Google Scholar]
- Halim, I.; Adhitya, A.; Srinivasan, R. Multi-objective Optimization for Integrated Water Network Synthesis. In Computer Aided Chemical Engineering: Proceedings of the 11th International Symposium on Process Systems Engineering, Singapore, 15–19 July 2012; Karimi, A.I., Srinivasan, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; Volume 31, pp. 1432–1436. ISBN 978-0-444-59505-8. [Google Scholar]
- Manne, J.R. Multiobjective Optimization in Water and Environmental Systems Management- MODE Approach. In Handbook of Research on Advanced Computational Techniques for Simulation-Based Engineering; Samui, P., Ed.; Engineering Science Reference: Hershey, PA, USA, 2016; pp. 120–136. ISBN 9781466694798. [Google Scholar]
- Yang, X.-S. Multi-Objective Optimization. In Nature-Inspired Optimization Algorithms; Elsevier: London, UK, 2014; pp. 197–211. ISBN 978-0-12-416743-8. [Google Scholar]
- De Buck, V.; López, C.A.M.; Nimmegeers, P.; Hashem, I.; Van Impe, J. Multi-objective optimisation of chemical processes via improved genetic algorithms: A novel trade-off and termination criterion. In Computer Aided Chemical Engineering, Proceedings of the 29th European Symposium on Computer Aided Process Engineering, Eindhoven, The Netherlands, 16–19 June 2019; Kiss, A.A., Zondervan, E., Lakerveld, R., Özkan, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 46, pp. 613–618. ISBN 978-0-12-818634-3. [Google Scholar]
- Gad, A.F. Practical Computer Vision Applications Using Deep Learning with CNNs; Apress: Berkeley, CA, USA, 2018; ISBN 978-1-4842-4166-0. [Google Scholar]
- Mohanty, R.; Suman, S.; Das, S.K. Modeling the Axial Capacity of Bored Piles Using Multi-Objective Feature Selection, Functional Network and Multivariate Adaptive Regression Spline. In Handbook of Neural Computation; Samui, P., Sekhar, S., Balas, V.E., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 295–309. ISBN 978-0-12-811318-9. [Google Scholar]
- Methodology for Calculating the Energy Performance of Buildings, Indicative MC001-2022; MTCT: Bucharest, Romania, 2023.
- Standard SR4839; Heating Installations: Annual Number of Degrees-Days. Romanian Standards Association: Bucharest, Romania, 2014.
- Standard SR1907-2; Heating Installations: Calculation Heat Demand. Conventional Indoor Computing Temperatures. Romanian Standards Association: Bucharest, Romania, 2014.
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Bailey, E.T.; Caldas, L. Operative generative design using non-dominated sorting genetic algorithm II (NSGA-II). Autom. Constr. 2023, 155, 105026. [Google Scholar] [CrossRef]
- Normative Regarding the Thermotechnical Calculation of Building Construction Elements, Indicative C107/3; MTCT: Bucharest, Romania, 2005.
- Pramanik, S.; Setua, S.K. A steady state Genetic Algorithm for Multiple Sequence Alignment. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics (ICACCI), Delhi, India, 24–27 September 2014. [Google Scholar]
- Lozano, M.; Herrera, F.; Cano, J. Replacement strategies to preserve useful diversity in steady-state genetic algorithms. Inf. Sci. 2008, 178, 4421–4433. [Google Scholar] [CrossRef]
- Zeng, F.; Low, M.Y.H.; Decraene, J.; Zhou, S.; Cai, W. Self-Adaptive Mechanism for Multi-objective Evolutionary Algorithms. In Proceeding of the International Multi Conference of Engineers and Computer Scientists, Hong Kong, China, 17–19 March 2010. [Google Scholar]
- Deb, K.; Agrawal, S. A Niched-Penalty Approach for Constraint Handling in Genetic Algorithms. In Artificial Neural Nets and Genetic Algorithms: Proceedings of the International Conference in Slovenia, Portorož, Slovenia, 6–9 April 1999; Springer: Vienna, Austria, 1999. [Google Scholar]
- Fanggidae, A.; Prasetyo, M.I.C.; Polly, Y.T.; Boru, M. New Approach of Self-Adaptive Simulated Binary Crossover-Elitism in Genetic Algorithms for Numerical Function Optimization. Int. J. Intell. Syst. Appl. Eng. 2024, 12, 174–183. [Google Scholar]
- Deb, K.; Sindhya, K.; Okabe, T. Self-adaptive simulated binary crossover for real-parameter optimization. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, London, UK, 7–11 July 2007. [Google Scholar]


| Month | The Monthly Average Solar Radiation Intensity [W/m2] | The Monthly Average Outdoor Temperature [°C] | Ground Temperature [°C] |
|---|---|---|---|
| January | 59.3 | −1.4 | −2.2 |
| February | 87.3 | 0.1 | 0.0 |
| March | 91.4 | 5.1 | 5.5 |
| April | 91.6 | 11.1 | 12.0 |
| May | 86.0 | 16.8 | 18.3 |
| June | 92.8 | 20.7 | 23.1 |
| July | 89.9 | 22.6 | 26.0 |
| August | 123.8 | 21.8 | 25.6 |
| September | 119.1 | 16.5 | 19.5 |
| October | 104.1 | 10.5 | 12.2 |
| November | 57.4 | 4.5 | 5.2 |
| December | 53.0 | −0.3 | −0.7 |
| Element | Thickness [mm] | Thermal Conductivity [W/(m·K)] | R-Values, Non-Insulated Building [(m2·K)/W] | * U-Values, Non-Insulated Building [W/(m2·K)/] | R-Values, Insulated Building [(m2·K)/W] | * U-Values Insulated Building [W/(m2·K)/] | |
|---|---|---|---|---|---|---|---|
| Exterior wall | Interior plaster | 20 | 0.80 | 0.025 | 0.723 | 0.025 | 0.249 |
| Autoclaved aerated concrete | 350 | 0.30 | 1.166 | 1.166 | |||
| Exterior plaster | 20 | 0.80 | 0.025 | 0.025 | |||
| Expanded polystyrene | 100 | 0.038 | - | 2.632 | |||
| Floor | Reinforced concrete | 150 | 2.03 | 0.074 | 0.485 | 0.074 | 0.189 |
| Self-levelling concrete | 25 | 0.46 | 0.054 | 0.054 | |||
| The polyethylene foam | 3 | 0.05 | 0.06 | 0.06 | |||
| Parquet | 14 | 0.13 | 0.107 | 0.107 | |||
| Extruded polystyrene | 100 | 0.031 | - | 3.226 | |||
| The roof–ceiling | Plater | 25 | 0.80 | 0.031 | 2.718 | 0.031 | 0.178 |
| Reinforced concrete | 150 | 2.03 | 0.074 | 0.074 | |||
| Self-leveling concrete | 25 | 0.46 | 0.054 | 0.054 | |||
| Mineral wool | 200 | 0.038 | - | 5.263 | |||
| Manufacturer | Model | Npumps [-] | Qcpump [kW] | Qopump [kW] | Ppump [kW] | COP [-] | Qc total [kW] | Q0 total [kW] | Ptotal [kW] | Cost [RON] |
|---|---|---|---|---|---|---|---|---|---|---|
| Carrier | 38YZA01832 | 3 | 4.92 | 2.52 | 2.40 | 2.05 | 14.76 | 7.56 | 7.20 | 34,922 |
| Econar | GC180 | 3 | 4.84 | 3.42 | 1.42 | 3.40 | 14.52 | 10.25 | 4.27 | 34,354 |
| FHP | EMO0241CS | 3 | 4.84 | 3.42 | 1.42 | 3.40 | 14.52 | 10.25 | 4.27 | 34,354 |
| Hydro Delta | 03068WTARHE | 1 | 14.59 | 9.73 | 4.86 | 3.00 | 14.59 | 9.73 | 4.86 | 34,519 |
| Trane | GSUF024ICM | 3 | 4.87 | 3.19 | 1.68 | 2.90 | 14.61 | 9.57 | 5.04 | 34,567 |
| York International | YZE02411N1VSB16 | 2 | 7.30 | 5.13 | 2.17 | 3.36 | 14.60 | 10.25 | 4.35 | 34,543 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicolae, A.E.; Necula, H.; Căruțașiu, B.M. Optimizing the Building Refurbishment Process Using Improved Evolutionary Algorithms. Energies 2024, 17, 2022. https://doi.org/10.3390/en17092022
Nicolae AE, Necula H, Căruțașiu BM. Optimizing the Building Refurbishment Process Using Improved Evolutionary Algorithms. Energies. 2024; 17(9):2022. https://doi.org/10.3390/en17092022
Chicago/Turabian StyleNicolae, Adriana Elena, Horia Necula, and Bogdan Mihail Căruțașiu. 2024. "Optimizing the Building Refurbishment Process Using Improved Evolutionary Algorithms" Energies 17, no. 9: 2022. https://doi.org/10.3390/en17092022
APA StyleNicolae, A. E., Necula, H., & Căruțașiu, B. M. (2024). Optimizing the Building Refurbishment Process Using Improved Evolutionary Algorithms. Energies, 17(9), 2022. https://doi.org/10.3390/en17092022






