Harnessing Geothermal Energy Potential from High-Level Nuclear Waste Repositories
Abstract
1. Introduction
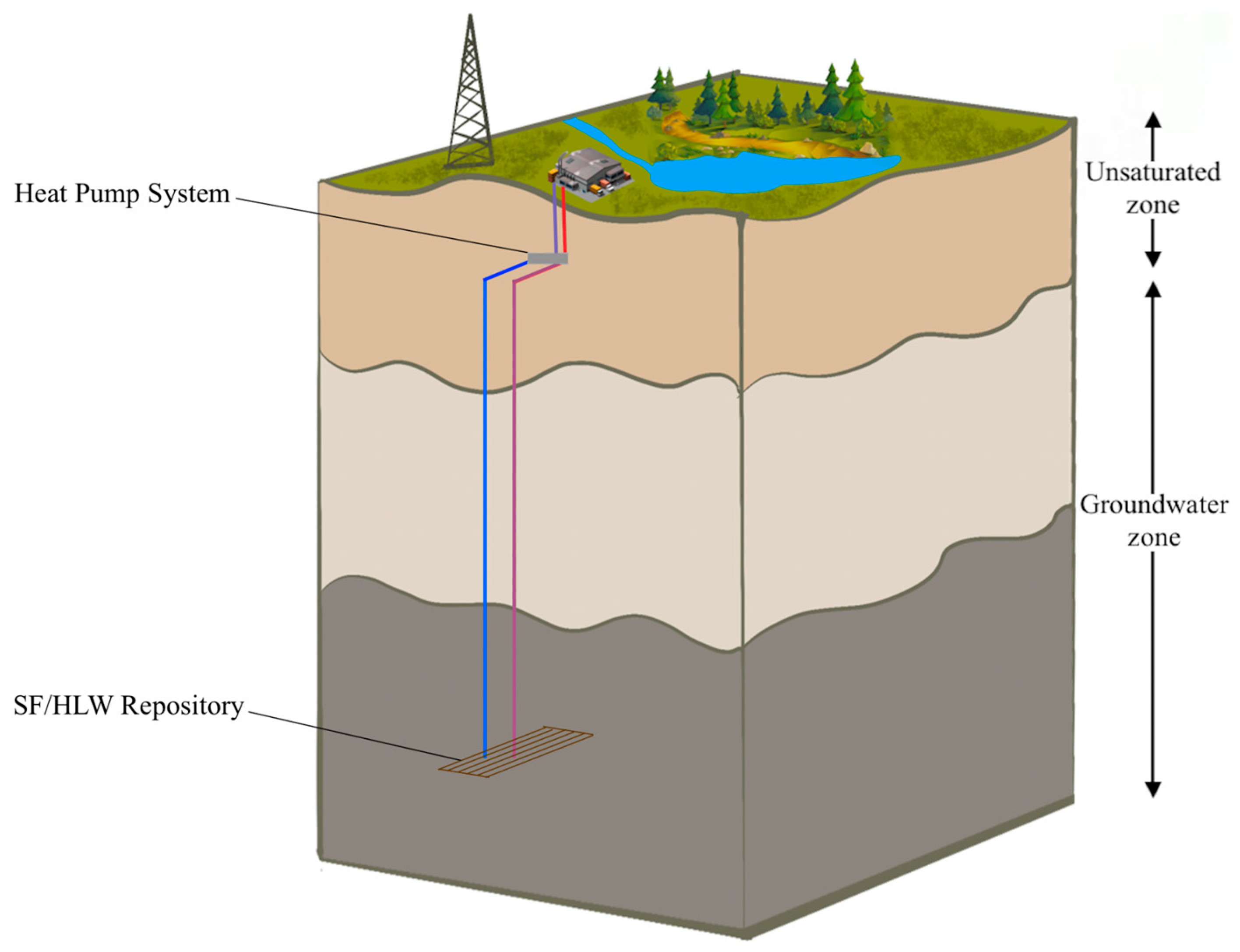
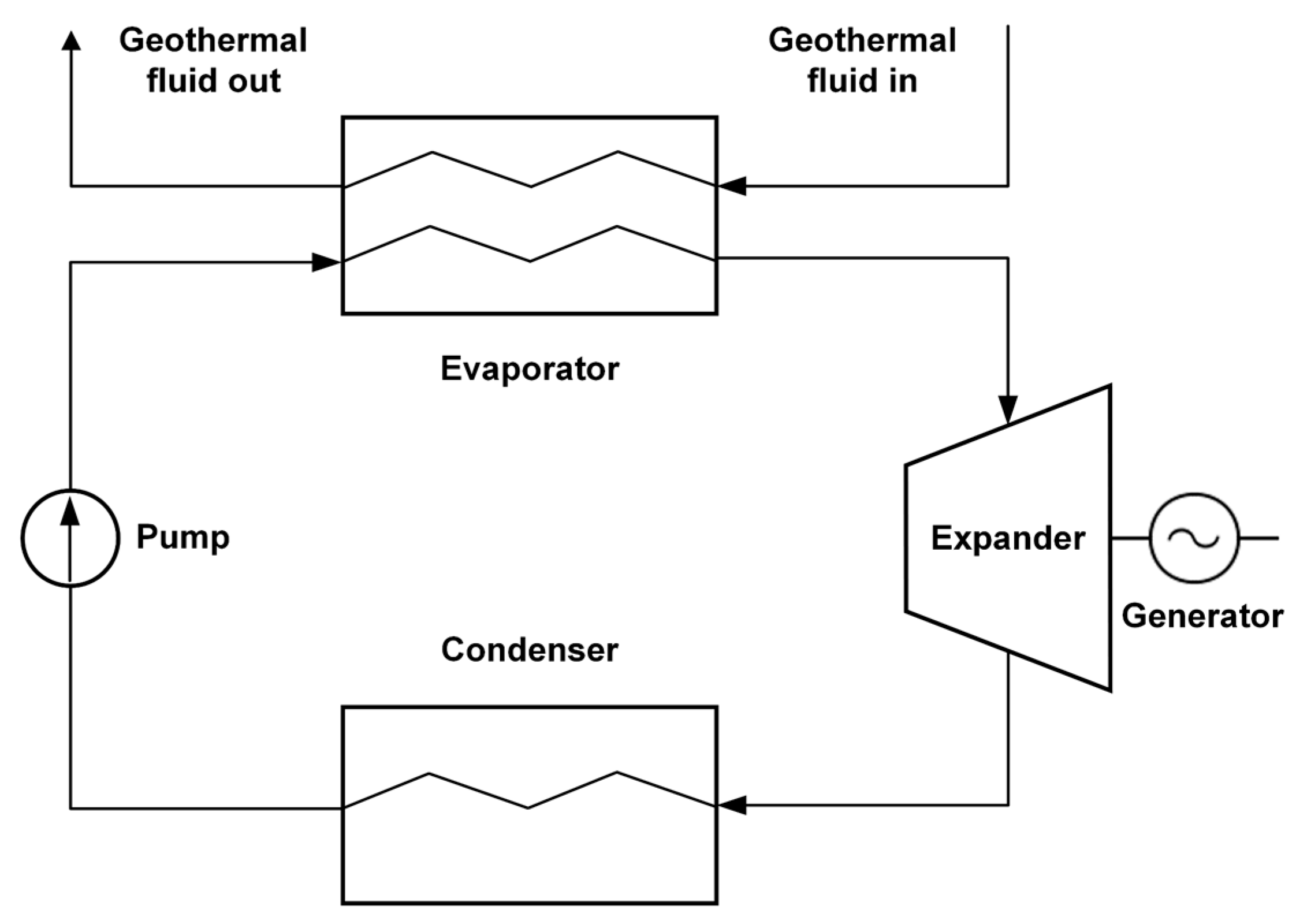
2. System Description
3. Materials and Methods
3.1. Heat Generation
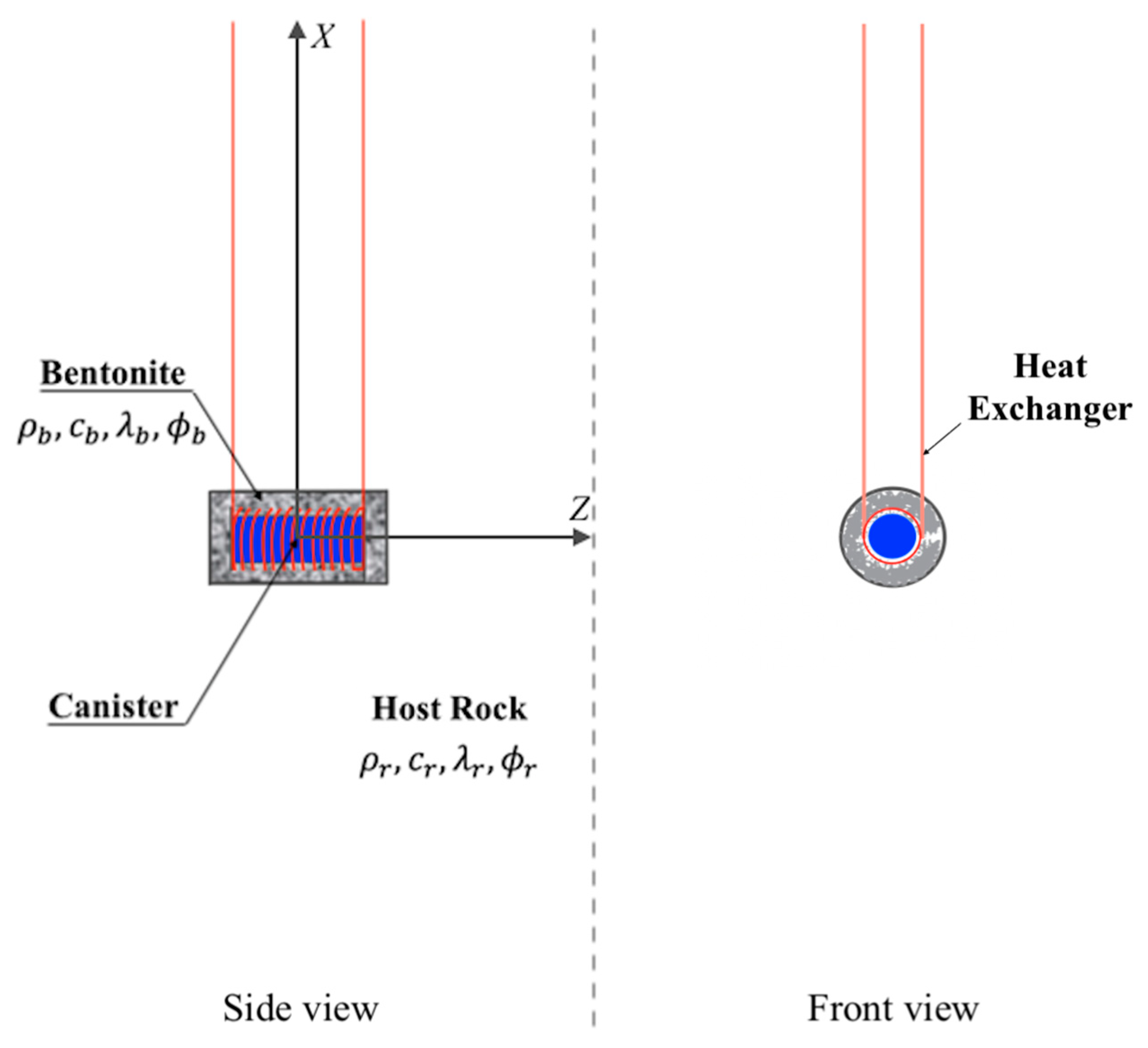
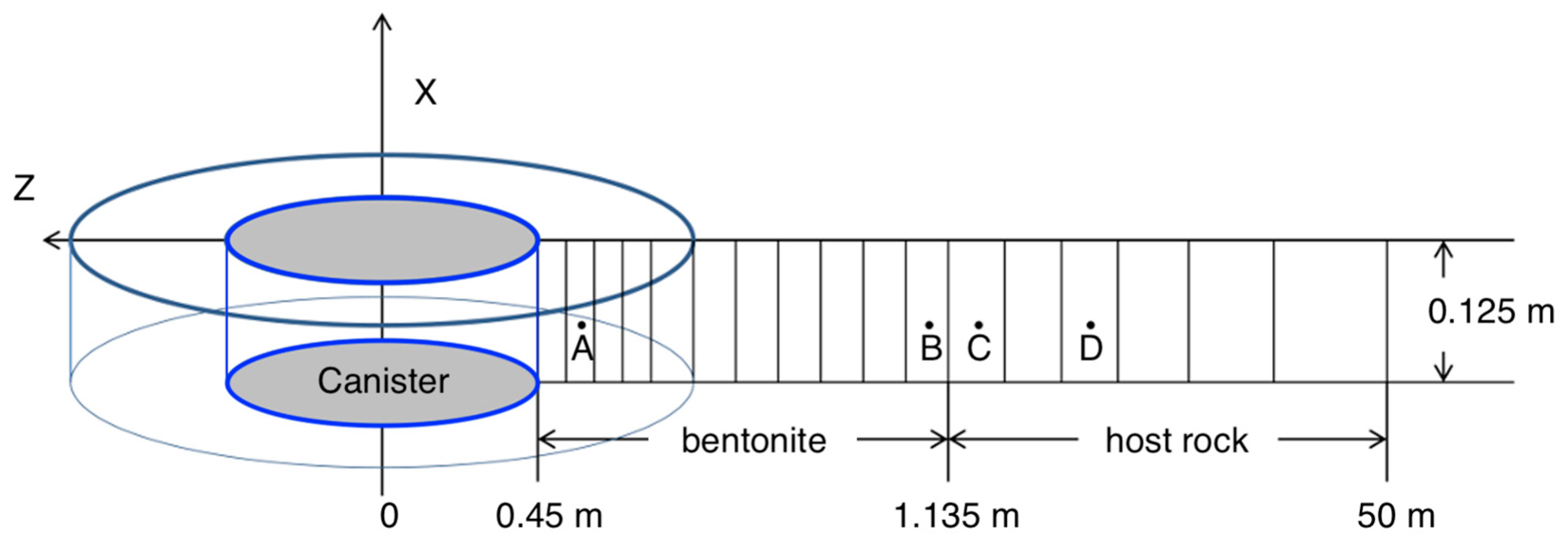
3.2. Thermal–Hydrological (TH) Model
3.3. TH Model Implementation in Numerical Models
3.4. Heat Extraction Cycle Modeling
3.4.1. Heat Exchange between the EBS and VGHE
3.4.2. Heat Exchange between the VGHE and HPS/ORC
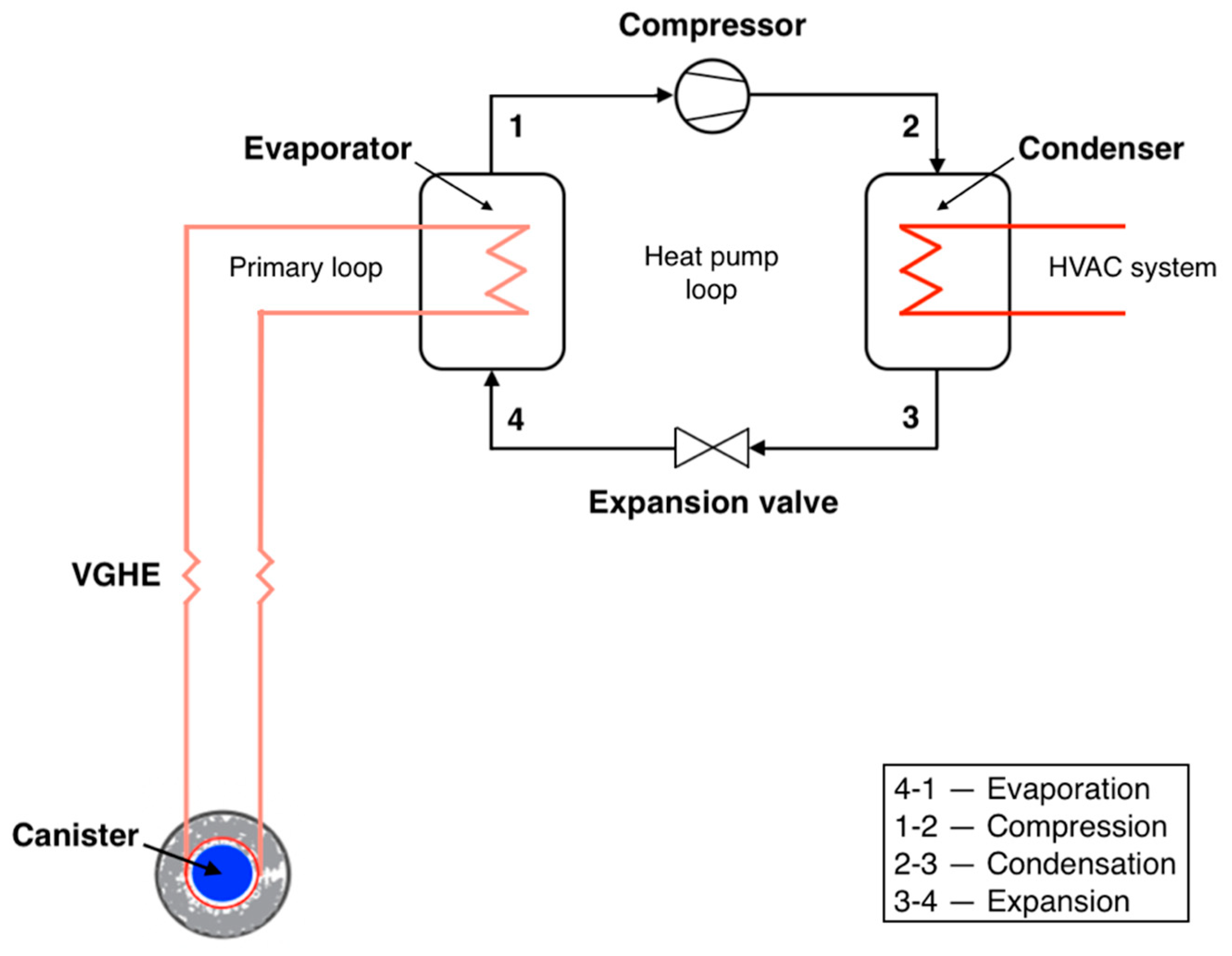
3.4.3. Vapor Compression Heat Pump Cycle
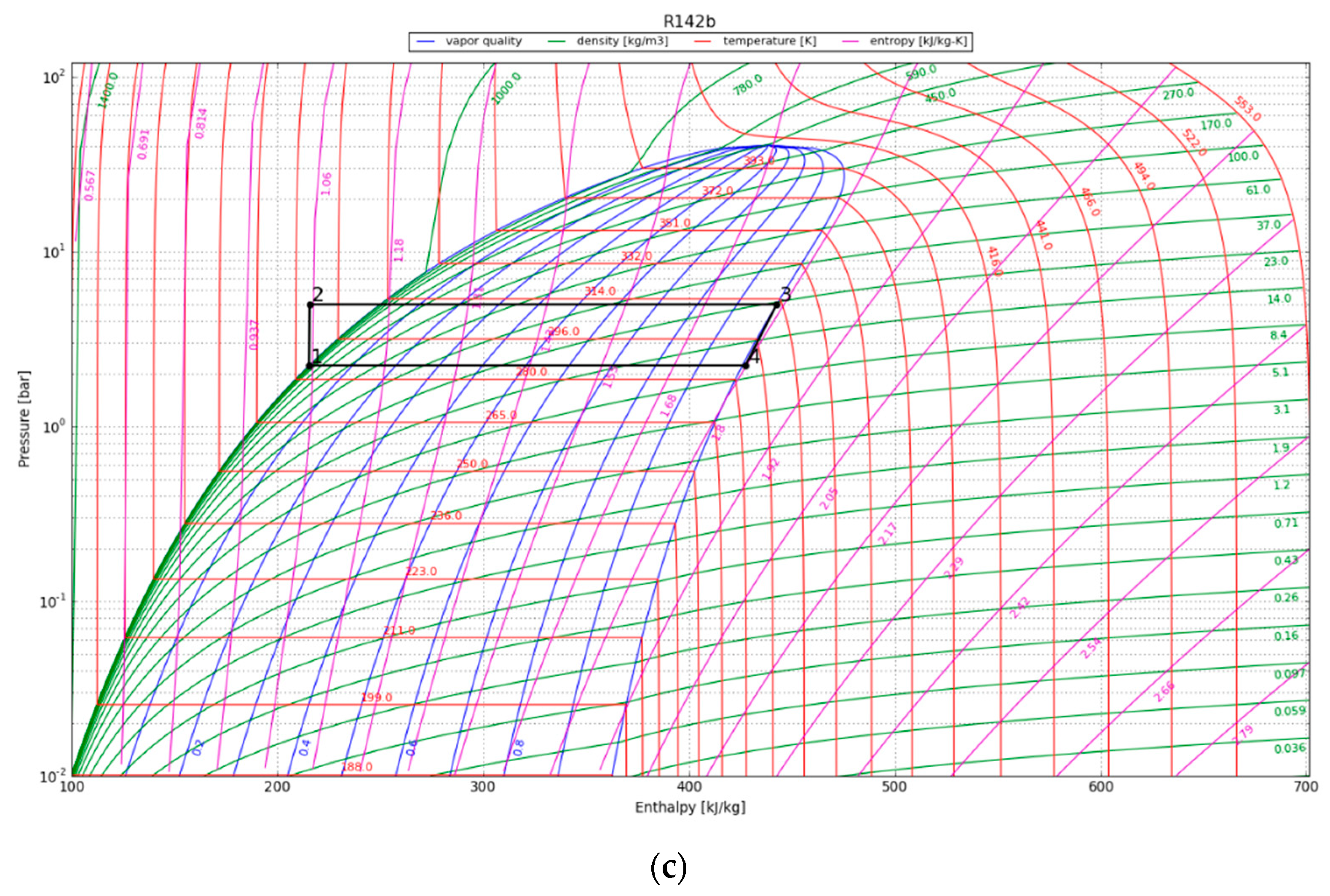
3.4.4. Organic Rankine Cycle
4. Results
4.1. Heat Transfer
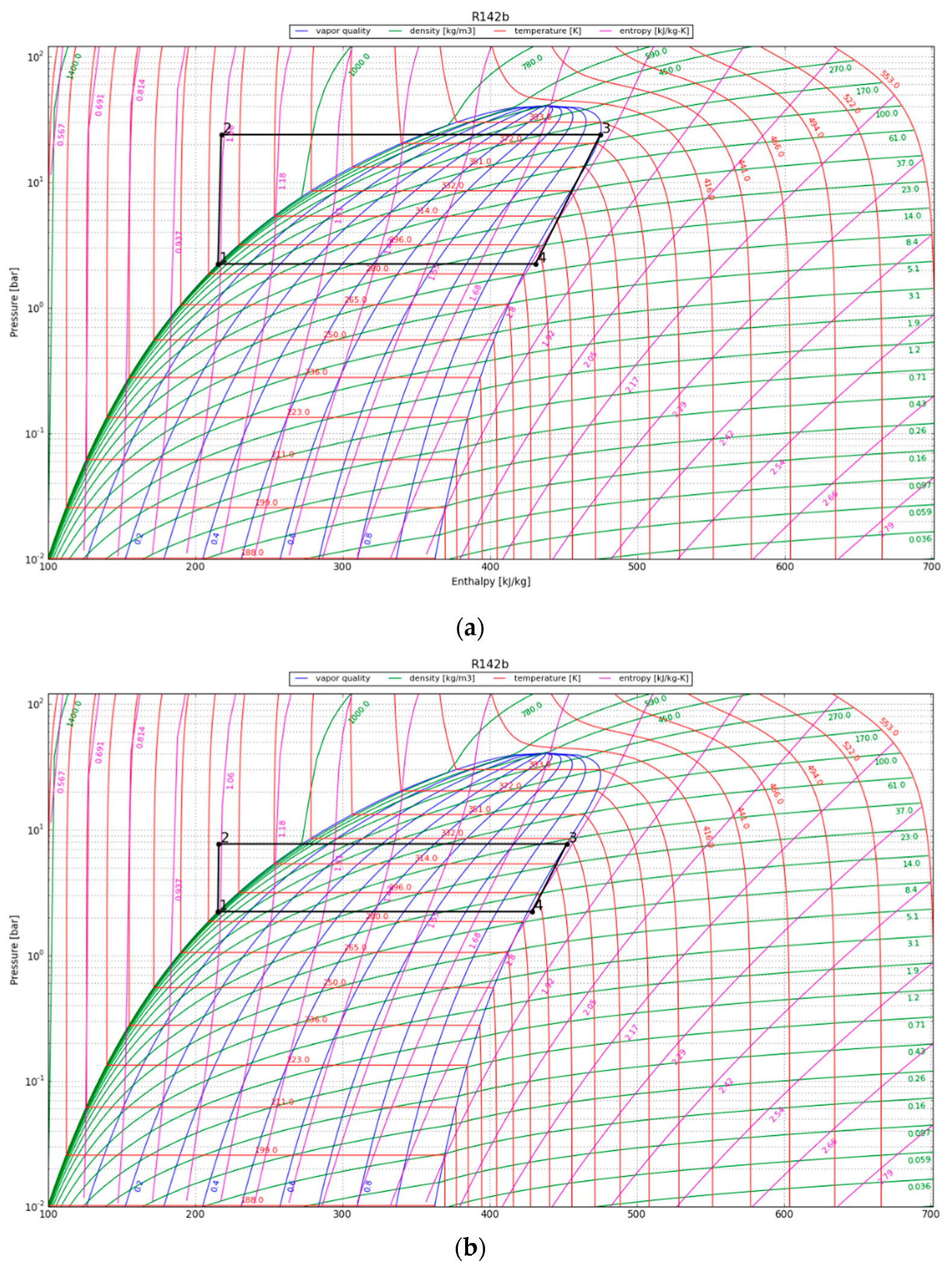
4.2. Vapor Compression Heat Pump Cycle
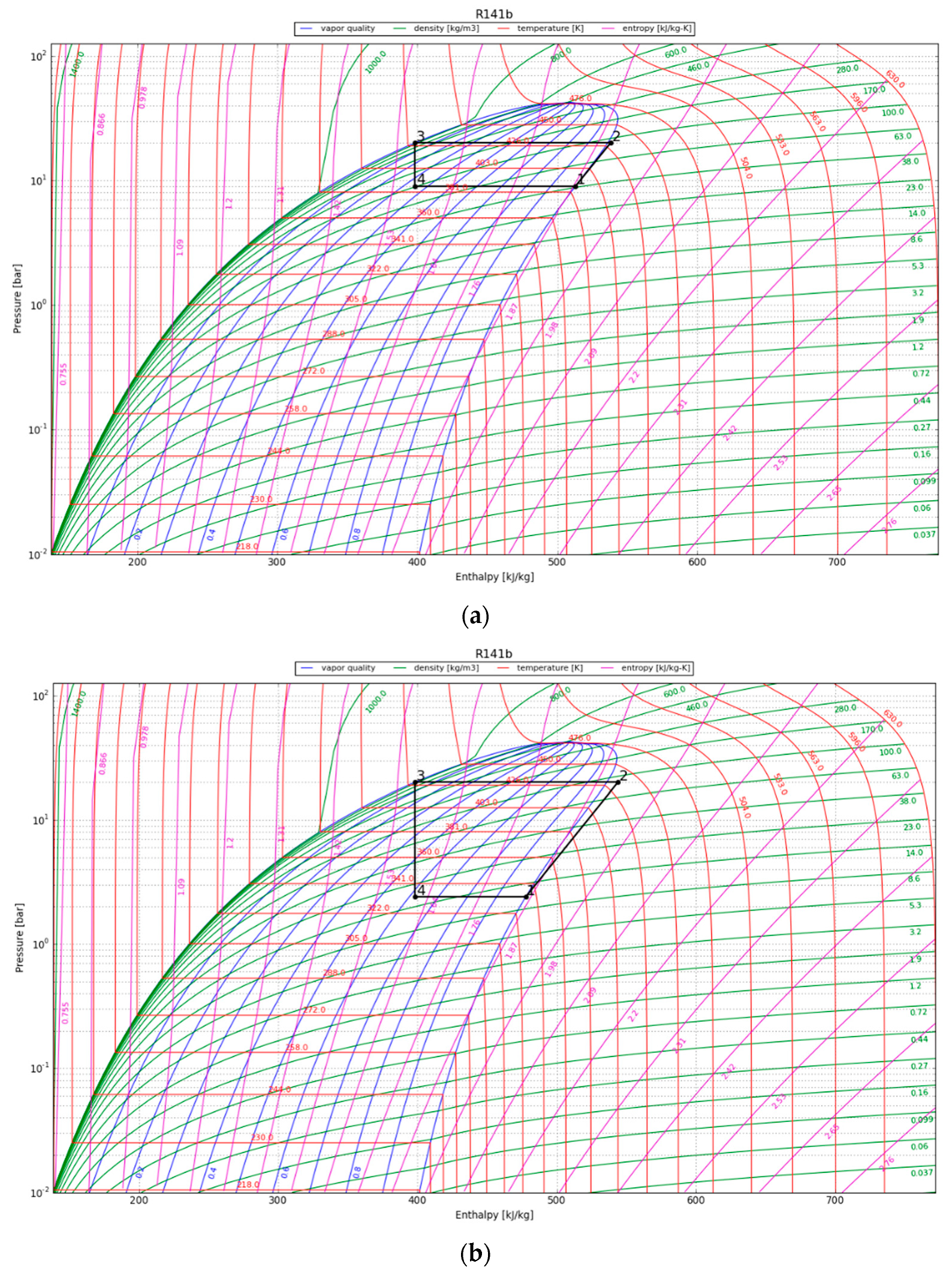
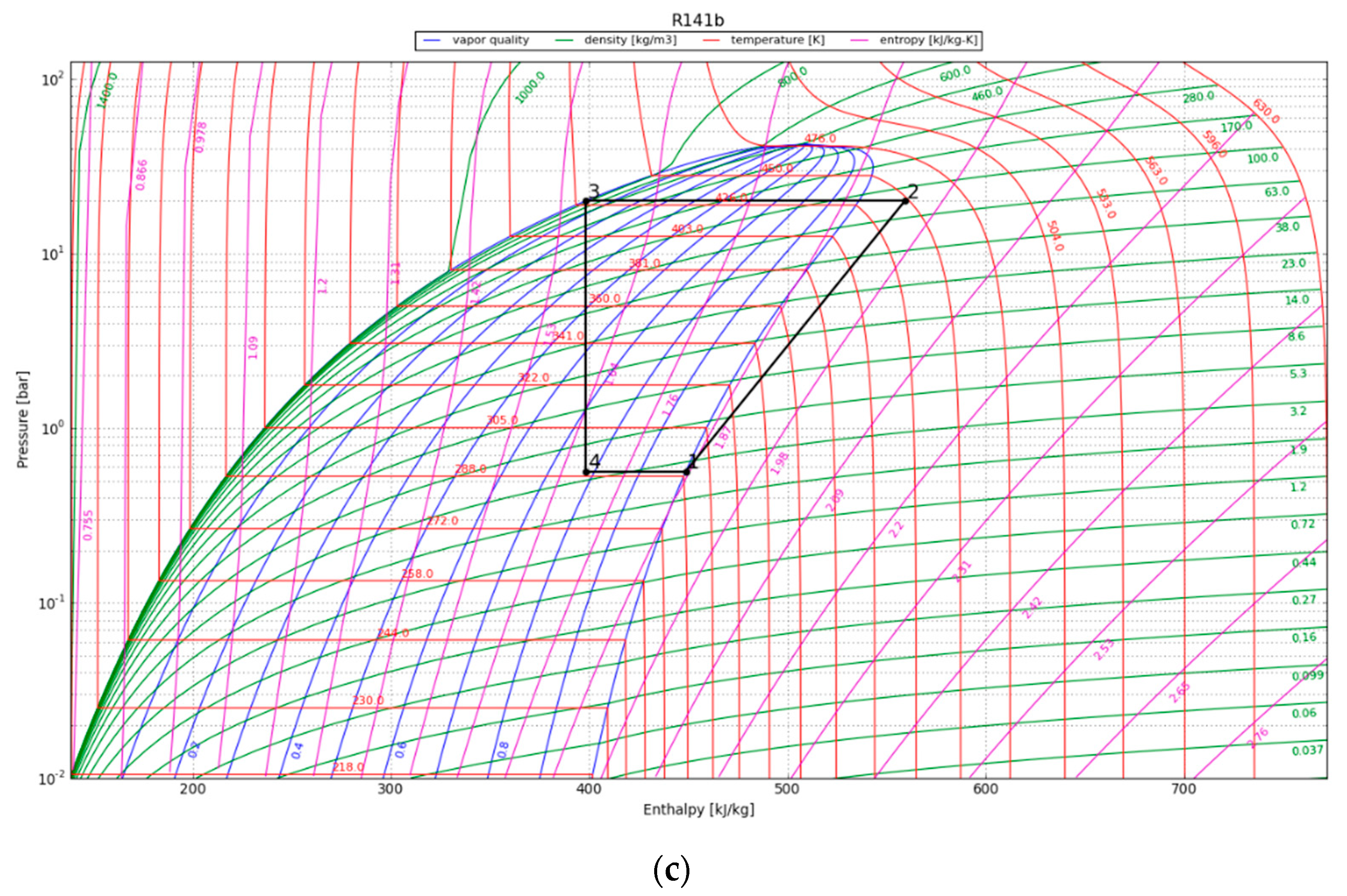
4.3. Organic Rankine Cycle
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Atomic Energy Agency. Status and Trends in Spent Fuel and Radioactive Waste Management; IAEA Nuclear Energy Series NW-T-1.14 (Rev. 1); International Atomic Energy Agency: Vienna, Austria, 2022. [Google Scholar]
- Zheng, L.; Xu, H.; Rutqvist, J.; Birkholzer, J. Predicting the long-term evolution of bentonite buffer based on THMC models calibrated against the FEBEX in situ heater test. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2022. [Google Scholar]
- Johnson, L.; King, F. The effect of the evolution of environmental conditions on the corrosion evolutionary path in a repository for spent fuel and high-level waste in Opalinus clay. Nucl. Mater. 2008, 379, 9–15. [Google Scholar] [CrossRef]
- Hornus, E.C.; Giordano, C.M.; Rodriguez, M.A.; Carranza, R.M. Effect of temperature on the crevice corrosion resistance of Ni-Cr-Mo alloys as engineered barriers in nuclear waste repositories. In Proceedings of the XXXVIII Annual meeting of the Argentine Association of Nuclear Technology, Buenos Aires, Argentina, 14–18 November 2011; Volume 38, pp. 1–8. [Google Scholar]
- Kamei, G.; Mitsui, M.S.; Futakuchi, K.; Hashimoto, S.; Sakuramoto, Y. Kinetics of long-term illitization of montmorillonite—A natural analogue of thermal alteration of bentonite in the radioactive waste disposal system. Phys. Chem. 2005, 66, 612–614. [Google Scholar] [CrossRef]
- Horseman, S.T.; McEwen, T.J. Thermal constraints on disposal of heat-emitting waste in argillaceous rocks. Eng. Geo. 1996, 41, 5–16. [Google Scholar] [CrossRef]
- Nandhini, R.; Sivaprakash, B.; Rajamohan, N. Waste heat recovery from heat pumps, power cycles and integrated systems at low temperature. Review on system performance and environmental perspectives. Sustain. Energy Technol. Assess. 2022, 52, 102214. [Google Scholar] [CrossRef]
- DiPippo, R. Geothermal power plants: Evolution and performance assessments. Geothermics 2015, 53, 291–307. [Google Scholar] [CrossRef]
- Barbier, E. Geothermal Energy Technology and Current Status: An Overview. Renew. Sustain. Energy Rev. 2002, 6, 3–65. [Google Scholar] [CrossRef]
- Tatli, E.; Belechak, J.G.; Lu, B.; Stansbury, C.A.; Guler, C.; Ostrosky, M.J. Power Generation from Decay Heat for Spent Nuclear Fuel Pool Cooling and Monitoring. WO Patent WO2013019589, 7 February 2013. [Google Scholar]
- DiPippo, R. Geothermal Power Plants: Principles, Applications, Case Studies and Environmental Impact; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- Anderson, A.; Rezaie, B. Geothermal technology: Trends and potential role in a sustainable future. Appl. Energy 2019, 248, 18–34. [Google Scholar] [CrossRef]
- Limberger, J.; Boxem, T.; Pluymaekers, M.; Bruhn, D.; Manzella, A.; Calcagno, P.; Beekman, F.; Cloetingh, S.; van Wees, J.D. Geothermal energy in deep aquifers: A global assessment of the resource base for direct heat utilization. Renew. Sustain. Energy Rev. 2018, 82, 961–975. [Google Scholar] [CrossRef]
- Birgersson, M.; Hedström, M.; Karnland, O.; Sjöland, A. Bentonite buffer: Macroscopic performance from nanoscale properties. In Geological Repository Systems for Safe Disposal of Spent Nuclear Fuels and Radioactive Waste, 2nd ed.; Woodhead Publishing: Sawston, UK, 2017; pp. 319–364. [Google Scholar]
- Sellin, P.; Leupin, O.X. The use of clay as an engineered barrier in radioactive–waste management. Clay Clay Miner. 2013, 61, 477–498. [Google Scholar] [CrossRef]
- Breeze, P. Nuclear Power. Power Generation Technologies, 2nd ed.; Elsevier Science: Newnes, Australia, 2014; pp. 353–378. [Google Scholar]
- Pramuditya, S.; Takahashi, M. Core design study for power uprating of integral primary system PWR. Ann. Nucl. Energy 2013, 59, 16–24. [Google Scholar] [CrossRef]
- Favalli, A.; Vo, D.; Grogan, B.; Jansson, P.; Liljenfeldt, H.; Mozin, V.; Schwalbach, P.; Sjöland, A.; Tobin, S.J.; Trellue, H.; et al. Determining initial enrichment, burnup, and cooling time of pressurized-water-reactor spent fuel assemblies by analyzing passive gamma spectra measured at the Clab interim-fuel storage facility in Sweden. Nucl. Instrum. Methods Phys. Res. Sect. A 2016, 820, 102–111. [Google Scholar] [CrossRef]
- Fukaya, Y.; Nishihara, T. Reduction on high level radioactive waste volume and geological repository footprint with high burn-up and high thermal efficiency of HTGR. Nucl. Eng. Des. 2016, 307, 188–196. [Google Scholar] [CrossRef]
- ANSI/ANS-5.1; Decay Heat Power in Light Water Reactors. American National Standards Institute: Washington, DC, USA, 1979.
- Cao, X.; Zheng, L.; Hou, D.; Hu, L. On the Long-Term Migration of Uranyl in Bentonite Barrier for High-Level Radioactive Waste Repositories: The Effect of Different Host Rocks. Chem. Geol. 2019, 525, 46–57. [Google Scholar] [CrossRef]
- Xu, T.F.; Spycher, N.; Sonnenthal, E.; Zhang, G.; Zheng, L.; Pruess, K. TOUGHREACT Version 2.0: A simulator for subsurface reactive transport under non-isothermal multiphase flow conditions. Comput. Geosci. 2011, 37, 763–774. [Google Scholar] [CrossRef]
- Ermakova, D.; Wainwright, H.; Zheng, L.; Shirley, I.; Lu, H. Global Sensitivity Analysis for U(VI) Transport for Integrating Coupled Thermal–Hydrological–Chemical Processes Models Into Performance Assessment Model. ASME J. Nucl. Rad. Sci. 2021, 7, 041902. [Google Scholar] [CrossRef]
- Lu, H.; Ermakova, D.; Wainwright, H.; Zheng, L.; Tartakovsky, D. Data-Informed Emulators for Multi-Physics Simulations. J. Mach. Learn. Model. Comput. 2021, 2, 33–54. [Google Scholar] [CrossRef]
- Zheng, L.; Lammers, L.N.; Fox, P.M.; Chang, C.; Xu, H.; Borglin, S.; Whittaker, M.L.; Chou, C.; Tournassat, C.; Subramanian, N.; et al. Engineered Barrier System Research Activities at LBNL: FY20 Progress Report; Report #: LBNL-2001331; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2020. [Google Scholar]
- SmoWeb. SysMo, Ltd. Bulgaria. Available online: http://platform.sysmoltd.com (accessed on 2 May 2023).
- Gut, J.A.W.; Pinto, J.M. Modeling of plate heat exchangers with generalized configurations. Int. J. Heat Mass Transf. 2003, 46, 2571–2585. [Google Scholar] [CrossRef]
- Bejan, A. Second-Law Analysis in Heat Transfer and Thermal Design. Adv. Heat Transf. 1982, 15, 1–58. [Google Scholar]
- Jordan, C.; Belding, S.; Campos, G.; Lowder, T. High Temperature Heat Pump Model Documentation and Case Studies; NREL/TP-7A40-84560; National Renewable Energy Laboratory: Golden, CO, USA, 2023. [Google Scholar]
- Chen, Y.; Lundqvist, P.; Johansson, A.; Platell, P. A comparative study of the carbon dioxide transcritical power cycle compared with an organic Rankine cycle with R123 as working fluid in waste heat recovery. Appl. Therm. Eng. 2006, 26, 2142–2147. [Google Scholar] [CrossRef]
- Lindeman, L. Thermodynamic Analysis of a High Temperature Heat Pump Coupled with an Organic Rankine Cycle for Energy Storage; Universitat Politècnica de València: Valencia, Spain, 2018; Available online: http://hdl.handle.net/10251/108965 (accessed on 27 March 2024).
- Badr, O.; Probert, S.D.; O’Callaghan, P.W. Selecting a working fluid for a Rankine-cycle engine. Appl. Energy 1985, 21, 1–42. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Fazio, E.; Chen, S.H.; Cupane, A. Specific Heat and Transport Functions of Water. Int. J. Mol. Sci. 2020, 21, 622. [Google Scholar] [CrossRef] [PubMed]
- Tarrad Ali, H. What Every Engineer Should Know about the Organic Rankine Cycle and Waste Energy Recovery; Cambridge Scholars Publishing: Cambridge, UK, 2022. [Google Scholar]
- Wang, D.; Ling, X.; Peng, H.; Liu, L.; Tao, L. Efficiency and optimal performance evaluation of organic Rankine cycle for low grade waste heat power generation. Energy 2013, 50, 343–352. [Google Scholar] [CrossRef]
- Uusitalo, A.; Uusitalo, V.; Grönman, A.; Luoranen, M.; Jaatinen-Värri, A. Greenhouse gas reduction potential by producing electricity from biogas engine waste heat using organic Rankine cycle. J. Clean. Prod. 2016, 127, 399–405. [Google Scholar] [CrossRef]
- Ahmadi, A.; El Haj Assad, M.; Jamali, D.H.; Kumar, R.; Li, Z.X.; Salameh, T.; Al-Shabi, M.; Ehyaei, M.A. Applications of geothermal organic Rankine Cycle for electricity production. J. Clean. Prod. 2020, 274, 122950. [Google Scholar] [CrossRef]
- Shao, P. Eco-Friendly Hydro-Power: Turbulent. In Proceedings of the 6th International Conference on Economic Management and Green Development, Online, 6–12 August 2022; Springer Nature: Singapore, 2023. [Google Scholar]
- Holdmann, G. The Chena Hot Springs 400kW Geothermal Power Plant: Experience Gained During the First Year of Operation. Trans. Geotherm. Resour. Counc. 2008, 31, 515–519. [Google Scholar]
- Bassam, N.; Maegaard, P.; Schlichting, M.L. Distributed Renewable Energies for Off-Grid Communities; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Energy Technology Perspectives; International Energy Agency (IEA): Vienna, Austria, 2008. [Google Scholar]
- Quoilin, S.; Van Den Broek, M.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of Organic Rankine Cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef]
- Lemmens, S. Cost Engineering Techniques & Their Applicability for Cost Estimation of Organic Rankine Cycle Systems. Energies 2016, 9, 485. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Modifications and Optimization of the Organic Rankine Cycle. Improving Recovery of Waste Heat in Industrial Processes. 2017. Available online: www.osti.gov/scitech (accessed on 27 March 2024).
- Cheshire, M.C.; Caporuscio, F.A.; Rearick, M.S.; Jové-Colón, C.; McCarney, M.K. Bentonite Evolution at Elevated Pressures and Temperatures: An Experimental Study for Generic Nuclear Repository Designs. Am. Mineral. 2014, 99, 1662–1675. [Google Scholar] [CrossRef]
- Cheshire, M.; Caporuscio, F.; Jove Colón, C.; Norskog, K.E. Fe-Saponite Growth on Low-Carbon and Stainless Steel in Hydrothermal-Bentonite Experiments. J. Nucl. Mater. 2018, 511, 353–366. [Google Scholar] [CrossRef]
- Zheng, L.; Rutqvist, J.; Xu, H.; Birkholzer, J. Coupled THMC models for bentonite in an argillite repository for nuclear waste: Illitization and its effect on swelling stress under high temperature. Eng. Geol. 2017, 230, 118–129. [Google Scholar] [CrossRef]
- Chang, C.; Borglin, S.; Chou, C.; Zheng, L.; Wu, Y.; Kneafsey, T.; Nakagawa, S.; Voltolini, M.; Birkholzer, J. Hydro-mechanical behavior of heated bentonite buffer for geologic disposal of high-level radioactive waste: A bench-scale X-ray computed tomography investigation. Appl. Clay Sci. 2023, 232, 106792. [Google Scholar] [CrossRef]
- Zhang, Y.; Jung, Y.; Freifeld, B.; Finsterle, S. Using distributed temperature sensing to detect CO2 leakage along the injection well casing. Int. J. Greenh. Gas Control 2018, 74, 9–18. [Google Scholar] [CrossRef]
- Nelson, R.; Patterson, R.; VanLuik, A. The February 2014 Accidents at WIPP-15024 (What Happened and What We Know About Why). In Proceedings of the WM2015 Conference, Phoenix, AZ, USA, 15–19 March 2015. [Google Scholar]
- Gholami, R.; Raza, A.; Iglauer, S. Leakage risk assessment of a CO2 storage site: A review. Earth-Sci. Rev. 2021, 223, 103849. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Grain density | 2780 [kg/m3] |
| Porosity | 0.41 |
| Saturated permeability | 2.15 × 10−21 [m2] |
| Van Genuchten α | 1.10 × 10−8 [1/Pa] |
| Van Genuchten m | 0.60 [m] |
| Compressibility | 6 [1/Pa] |
| Thermal expansion coefficient | 1.0 × 10−4 [1/°C] |
| Dry specific heat | 1091 [J/(kg × °C)] |
| Thermal conductivity dry/wet | 0.47/1.15 [J/(kg × °C)] |
| Effective vapor diffusion coefficient | 2.03 × 10−4 [m2/s] |
| Parameter | Value |
|---|---|
| Molecular weight | 116.95 [g/mol] |
| Boiling point | 32.05 [°C] |
| Freezing point | −107.00 [°C] |
| Critical temperature | 204.50 [°C] |
| Critical pressure | 4.25 [MPa] |
| GWP | 630.00 |
| ODP | 0.11 |
| Parameter | Value |
|---|---|
| Working fluid | R141b |
| Fluid flow rate | 0.5 [kg/s] |
| Pressure (at the condenser) | 2.0 [MPa] |
| Ambient temperature | 12.0 [°C] |
| Compressor type | centrifugal |
| Isentropic efficiency of the compressor | 0.7 |
| Parameter | Value |
|---|---|
| Working fluid | R142b |
| Fluid flow rate | 2 [kg/s] |
| Cooling water temperature | 12 [°C] |
| Pump type | centrifugal |
| Isentropic efficiency of the pump | 0.90 |
| Heat exchange efficiency | 0.80 |
| Heat losses from the turbine, pipeline, and pump | - |
| Generator efficiency | 0.95 |
| Temporal Point after Canister Emplacement [Years] | Bentonite Temperature [°C] | Refrigerant Temperature [°C] | Compressor Power [kW] | Condenser Heat out [kW] | Evaporator Heat in [kW] | COP |
|---|---|---|---|---|---|---|
| 1 | 226.0 | 113.2 | 12.5 | 69.9 | 57.4 | 5.6 |
| 10 | 192.0 | 59.2 | 33.1 | 72.8 | 39.8 | 2.2 |
| 30 | 124.0 | 16.5 | 55.2 | 80.5 | 25.2 | 1.5 |
| Temporal Point after Canister Emplacement [Years] | Bentonite Temperature [°C] | Heat Input [kW] | Refrigerant Temperature [°C] | Pump Power [kW] | Turbine Power [kWe] | Cycle Efficiency [%] |
|---|---|---|---|---|---|---|
| 1 | 226.0 | 1802.8 | 107.4 | 14.7 | 309.7 | 16.4 |
| 10 | 192.0 | 1656.6 | 54.7 | 3.7 | 165.9 | 9.8 |
| 30 | 124.0 | 1590.2 | 38.4 | 1.8 | 107.7 | 6.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarsenbayev, D.; Zheng, L.; Ermakova, D.; Sharipov, R.; Wainwright, H.M. Harnessing Geothermal Energy Potential from High-Level Nuclear Waste Repositories. Energies 2024, 17, 2002. https://doi.org/10.3390/en17092002
Sarsenbayev D, Zheng L, Ermakova D, Sharipov R, Wainwright HM. Harnessing Geothermal Energy Potential from High-Level Nuclear Waste Repositories. Energies. 2024; 17(9):2002. https://doi.org/10.3390/en17092002
Chicago/Turabian StyleSarsenbayev, Dauren, Liange Zheng, Dinara Ermakova, Rashid Sharipov, and Haruko M. Wainwright. 2024. "Harnessing Geothermal Energy Potential from High-Level Nuclear Waste Repositories" Energies 17, no. 9: 2002. https://doi.org/10.3390/en17092002
APA StyleSarsenbayev, D., Zheng, L., Ermakova, D., Sharipov, R., & Wainwright, H. M. (2024). Harnessing Geothermal Energy Potential from High-Level Nuclear Waste Repositories. Energies, 17(9), 2002. https://doi.org/10.3390/en17092002






