Automatic Generation Control of a Multi-Area Hybrid Renewable Energy System Using a Proposed Novel GA-Fuzzy Logic Self-Tuning PID Controller
Abstract
1. Introduction
When a researcher builds a simulation model, they have created a world in which they have access to all of the laws and components of that world, and the relationships among those components. Not only do researchers have access to these things, but they can also manipulate them. To the extent that researchers can match their simulated world to the real world, they should be able to read things off the simulated world that will tell them something about the real world.
2. PID Controller and the Proposed Hybrid Energy System
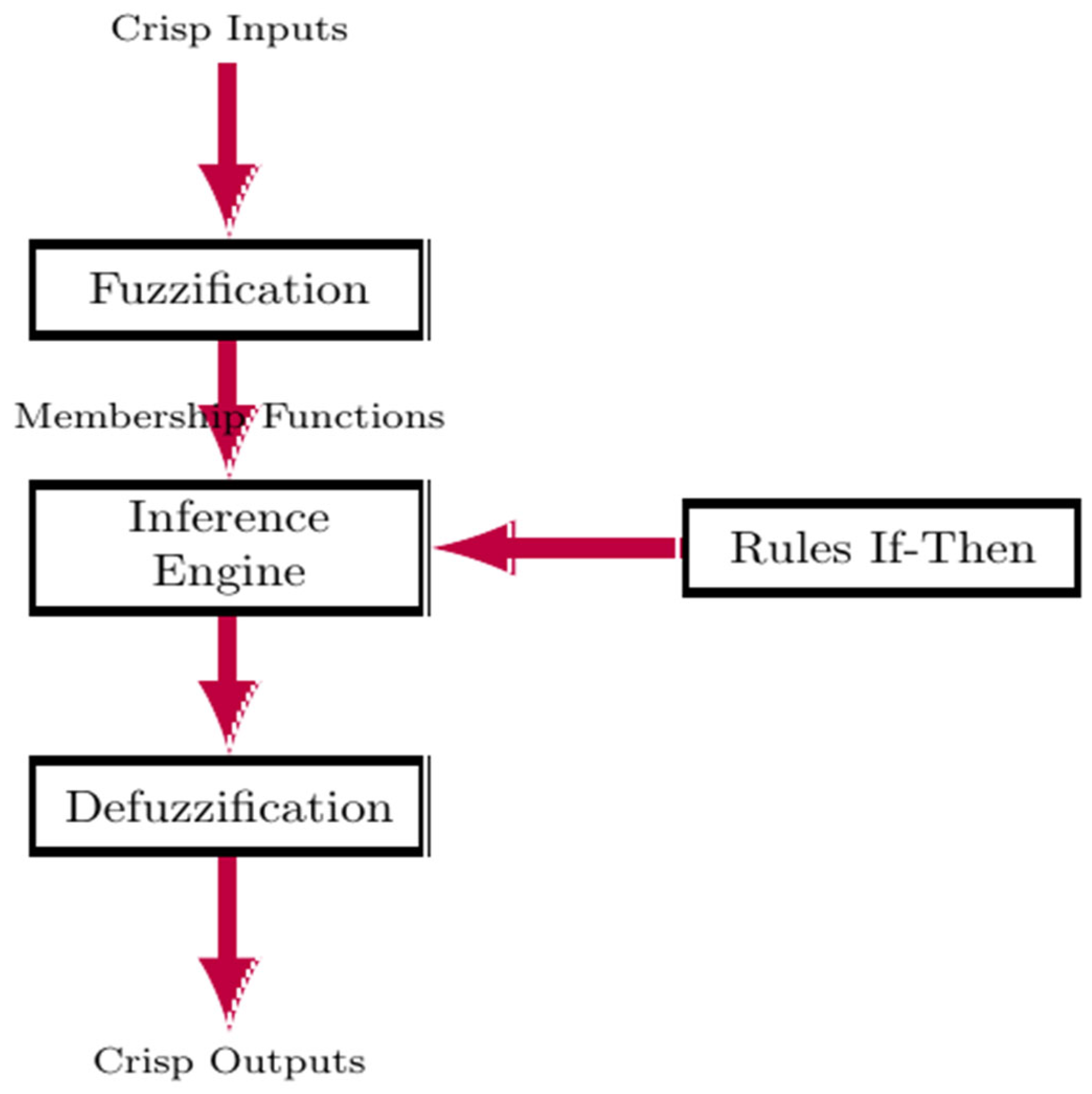
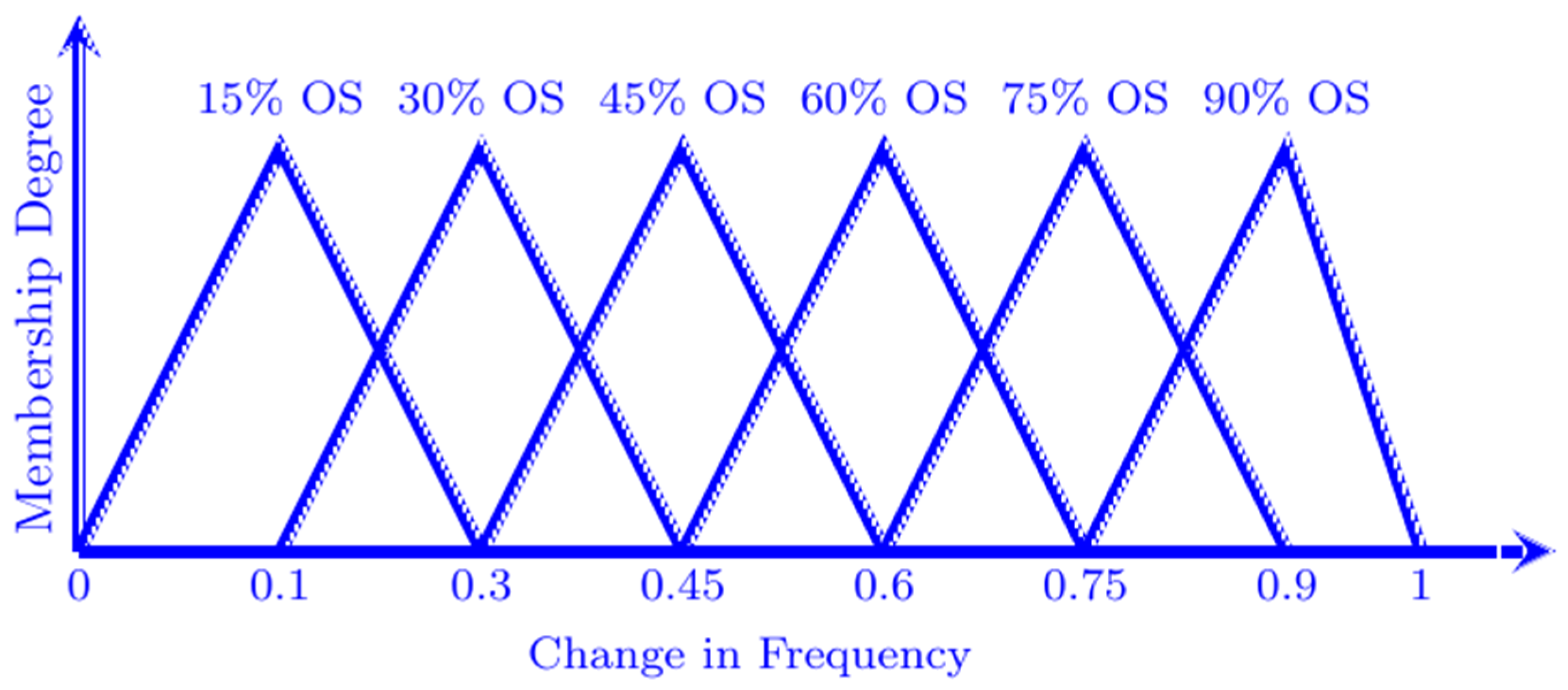
3. Fuzzy Logic Control
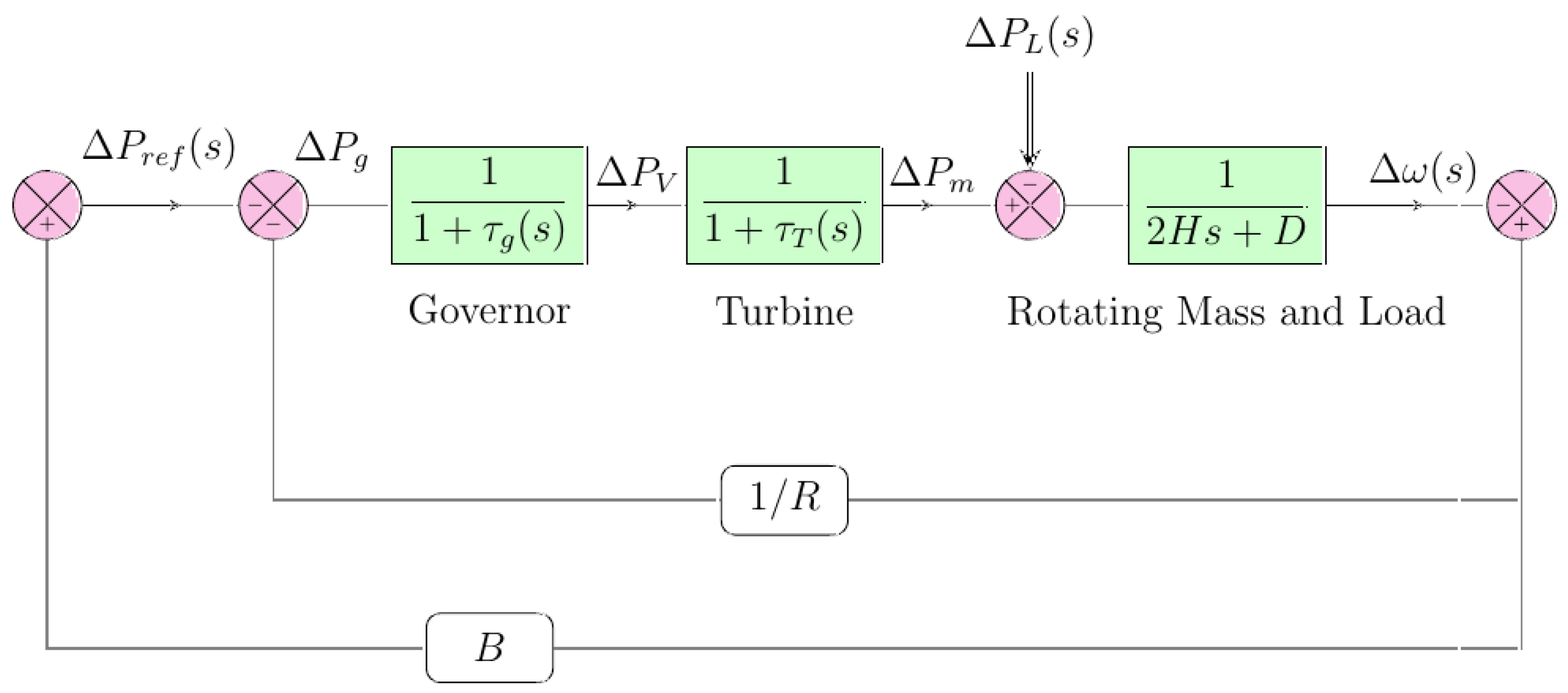
4. System Configuration
5. Mathematical Modeling of the Components
5.1. Mathematical Modeling of the Wind Energy System
5.2. Mathematical Modeling of the Photovoltaic System
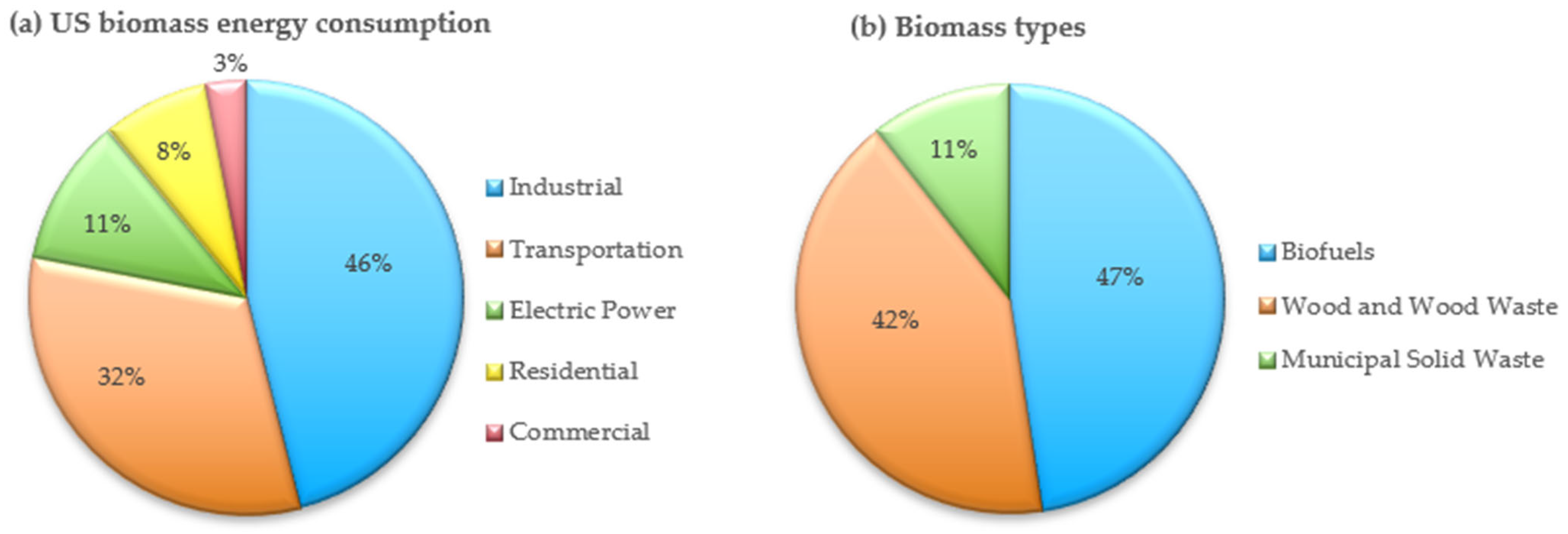
5.3. Mathematical Modeling of the Biomass Gasifier System
5.4. Mathematical Modeling of the Battery Bank Storage System
6. Problem Formulation
6.1. Constraints
6.1.1. Power Reliability Constraints
6.1.2. Battery Bank Storage Limits
6.1.3. Lower and Upper Bounds
6.1.4. Excess Electricity
6.2. Optimization
6.2.1. Meta-Heuristic Classes
- Single-solution based: in Simulated Annealing (SA) [36], for example, the search process starts with one candidate solution and then improves over the course of iterations.
- Population based: They execute the optimization using a set of solutions (population). The search process starts with a random initial population (multiple solutions), which is enhanced over the course of iterations. Swarm Intelligence (SI) is one of the most popular branches of the population-based meta-heuristics. The most popular SI techniques are ACO, Artificial Bee Colony (ABC) [37], and PSO.
6.2.2. Meta-Heuristics Categories
- Evolutionary algorithms (EAs): these algorithms are often inspired by natural concepts of evolution, such as GA and differential evolution (DE) [38].
- SI algorithms: They often mimic the social behavior of swarms, herds, and flocks in nature. Some of the algorithms are PSO, ACO, the ABC and the Bat-inspired Algorithm (BA) [43], and Grey Wolf Optimization (GWO) [44]. According to the No Free Lunch (NFL) theorem, no meta-heuristic can solve all optimization problems. Some algorithms may show promising results on a set of issues, but the same optimization technique may show poor performance on a different set of problems.
6.3. Algorithms Applied for AGC:
- (1)
- Set the values of ω and .
- (2)
- Obtain the values of ω and , then calculate and .
- (3)
- Once the values of and are determines, decide the control action to be made.
- (4)
- Send the control actions to all three plants and calculate ITAE using the GA-fuzzy algorithm.
- (5)
- Use a fixed-length chromosome to represent the problem variable domain. Select the size of the chromosomal population N, the crossover probability , and the mutation probability .
- (6)
- Establish a fitness function to gauge each chromosome’s effectiveness within the issue domain. The fitness function establishes the basis for choosing which chromosomes to mate with during reproduction.
- (7)
- Generate a starting population of size N chromosomes randomly .
- (8)
- Determine the fitness value of every single chromosome: .
- (9)
- Choose a pair of chromosomes from the existing population to mate with. Parent chromosomes are chosen based on fitness-related probability. Fitter chromosomes are more likely to be selected for mating than less suitable ones.
- (10)
- Apply the crossover and mutation genetic operators to produce a pair of offspring chromosomes.
- (11)
- Insert the progeny chromosomes into the newly formed population.
- (12)
- Step 9 should be repeated until the size of the new chromosomal population equals that of the original population, N.
- (13)
- Use the new (offspring) chromosomal population in place of the original (parent) population.
- (14)
- Repeat from step 8 until the termination creation is fulfilled. Examine whether the solution that satisfies the equality constraint is feasible.
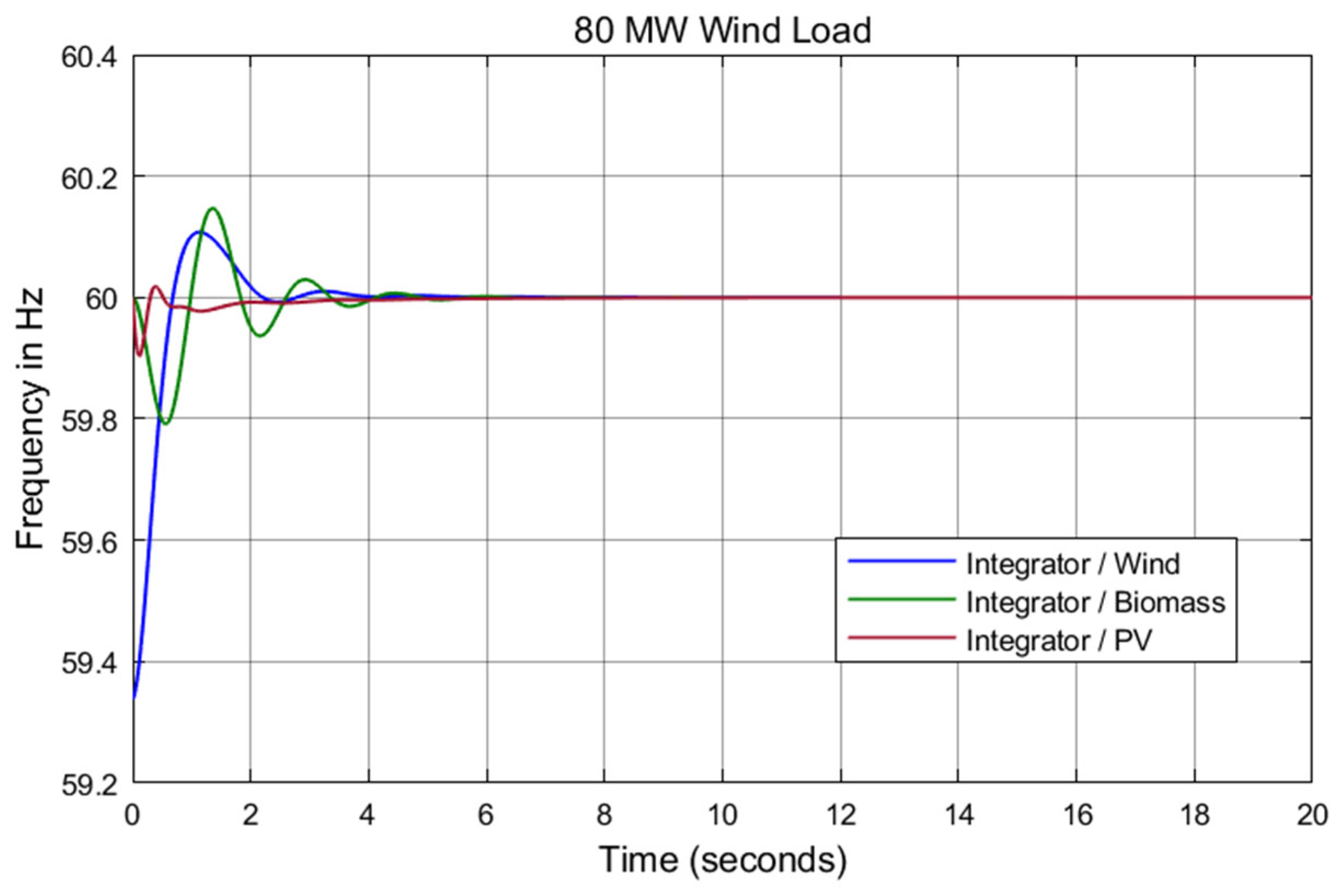
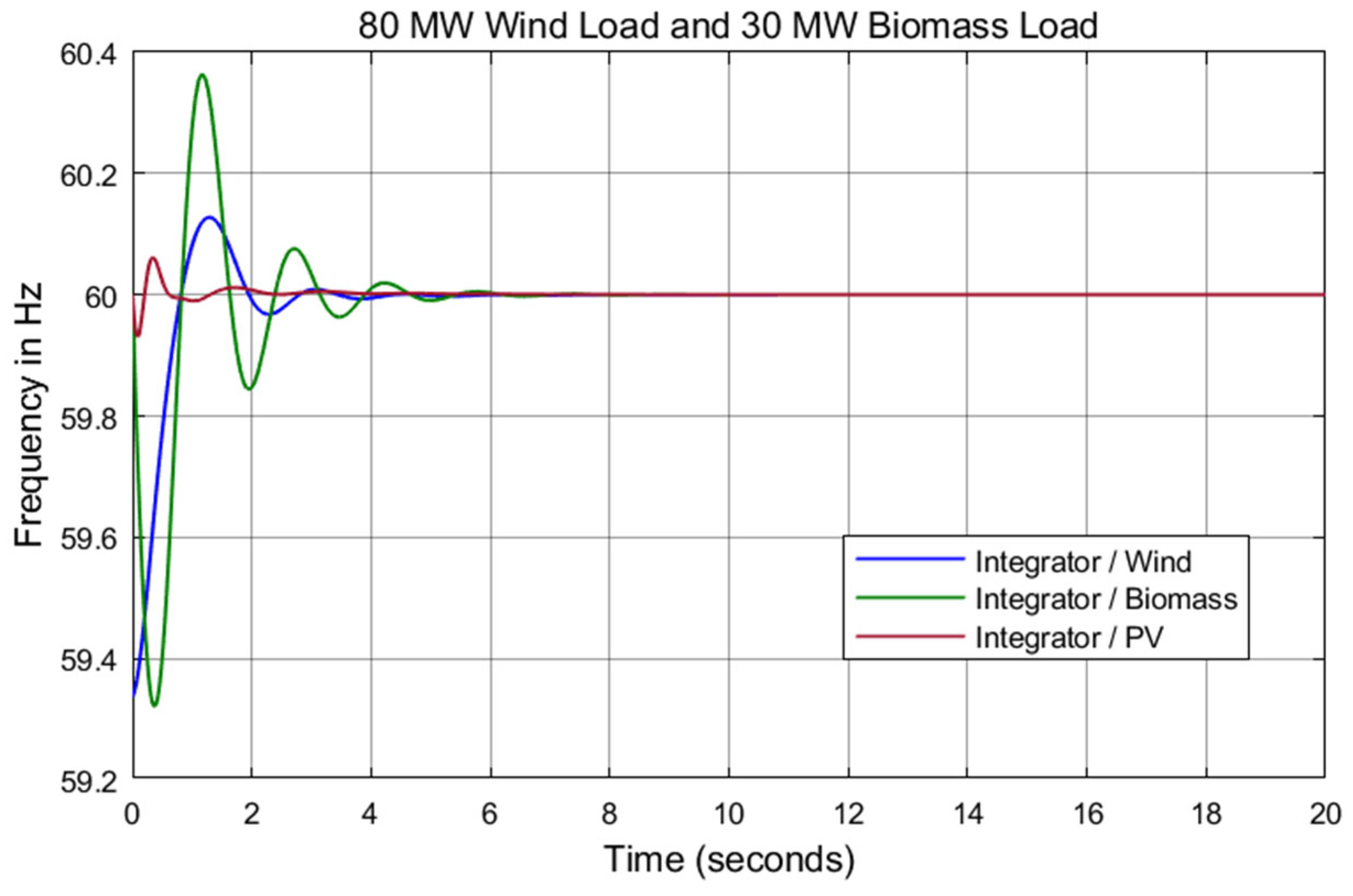
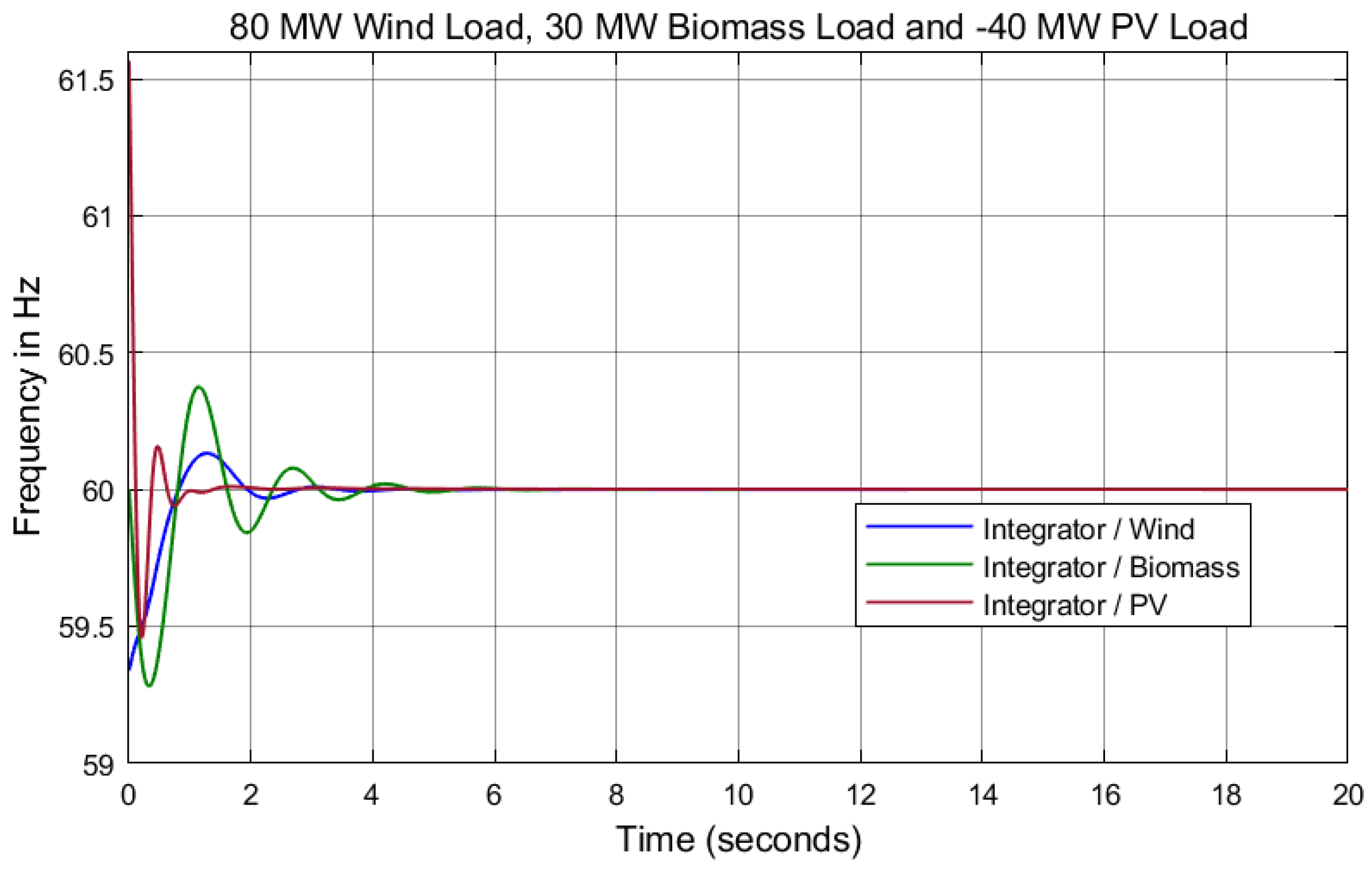
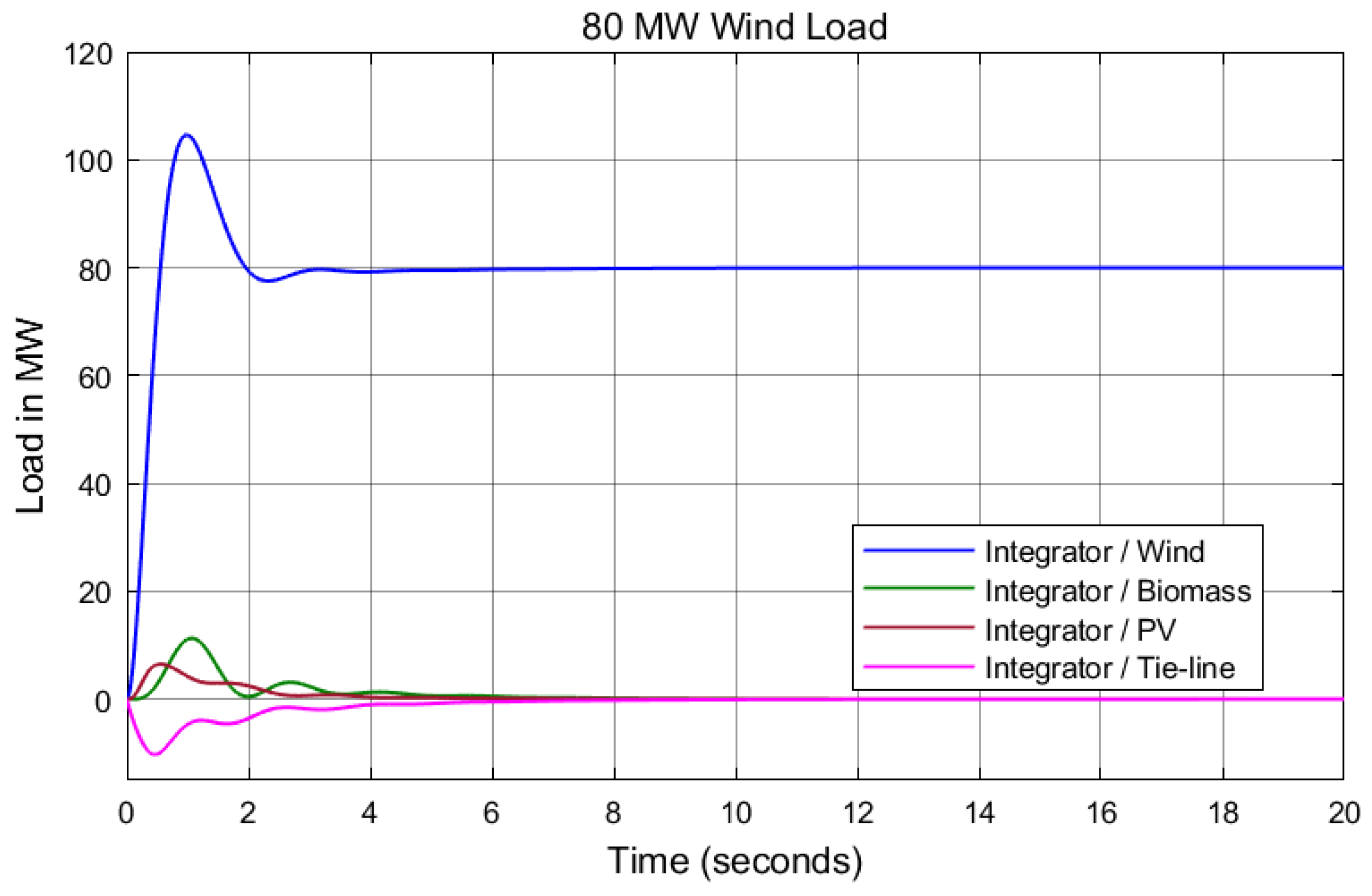
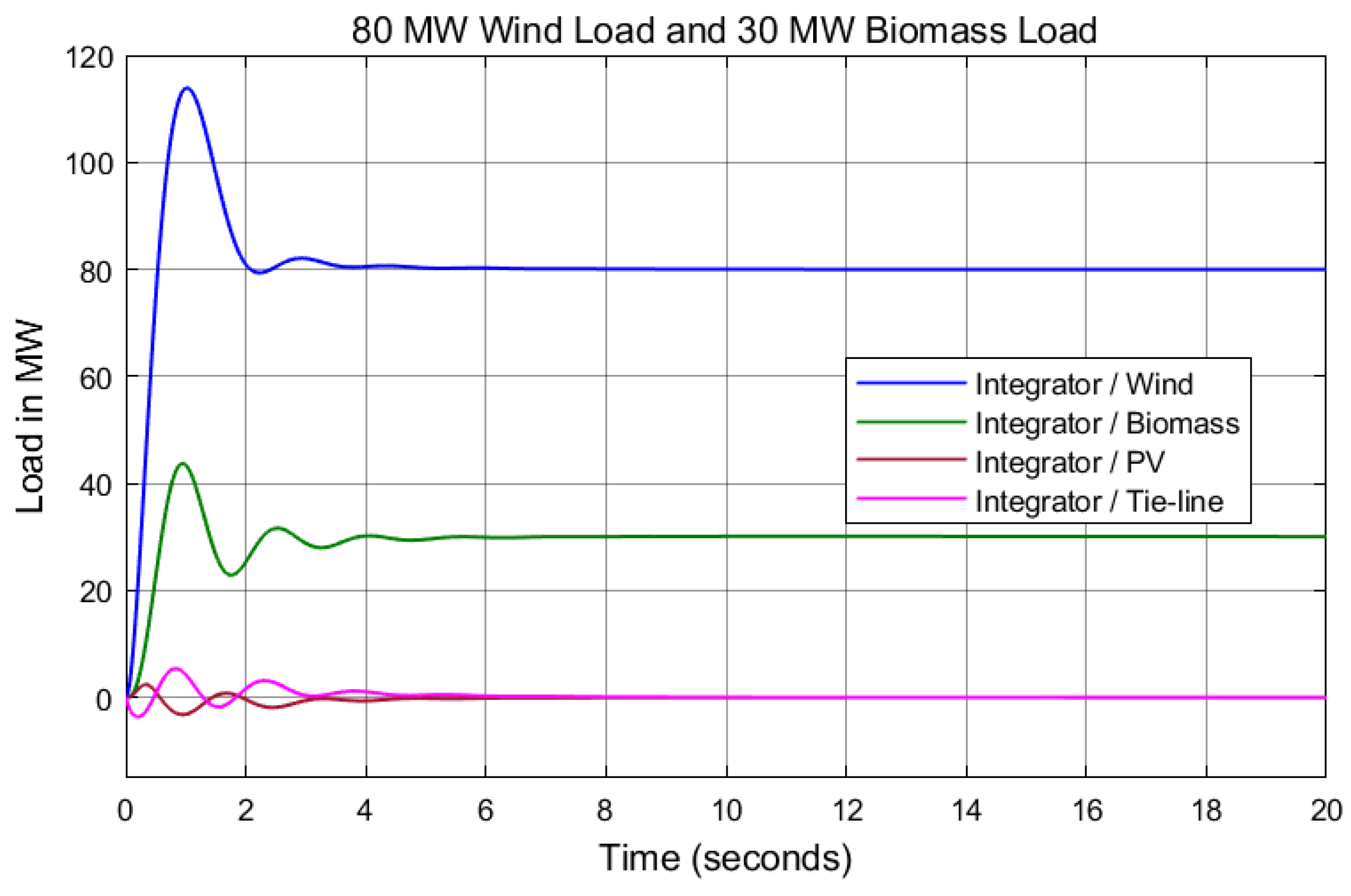
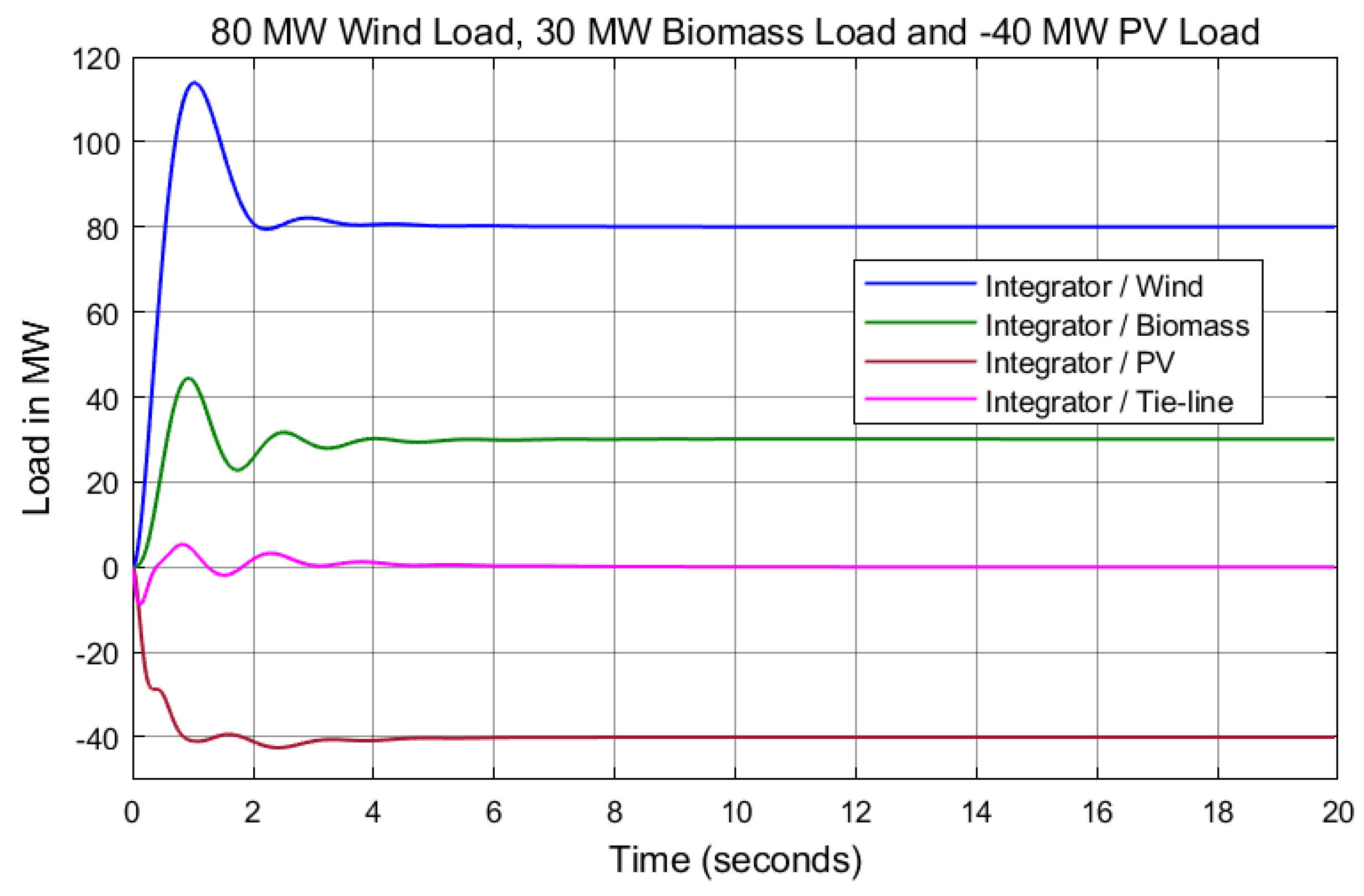
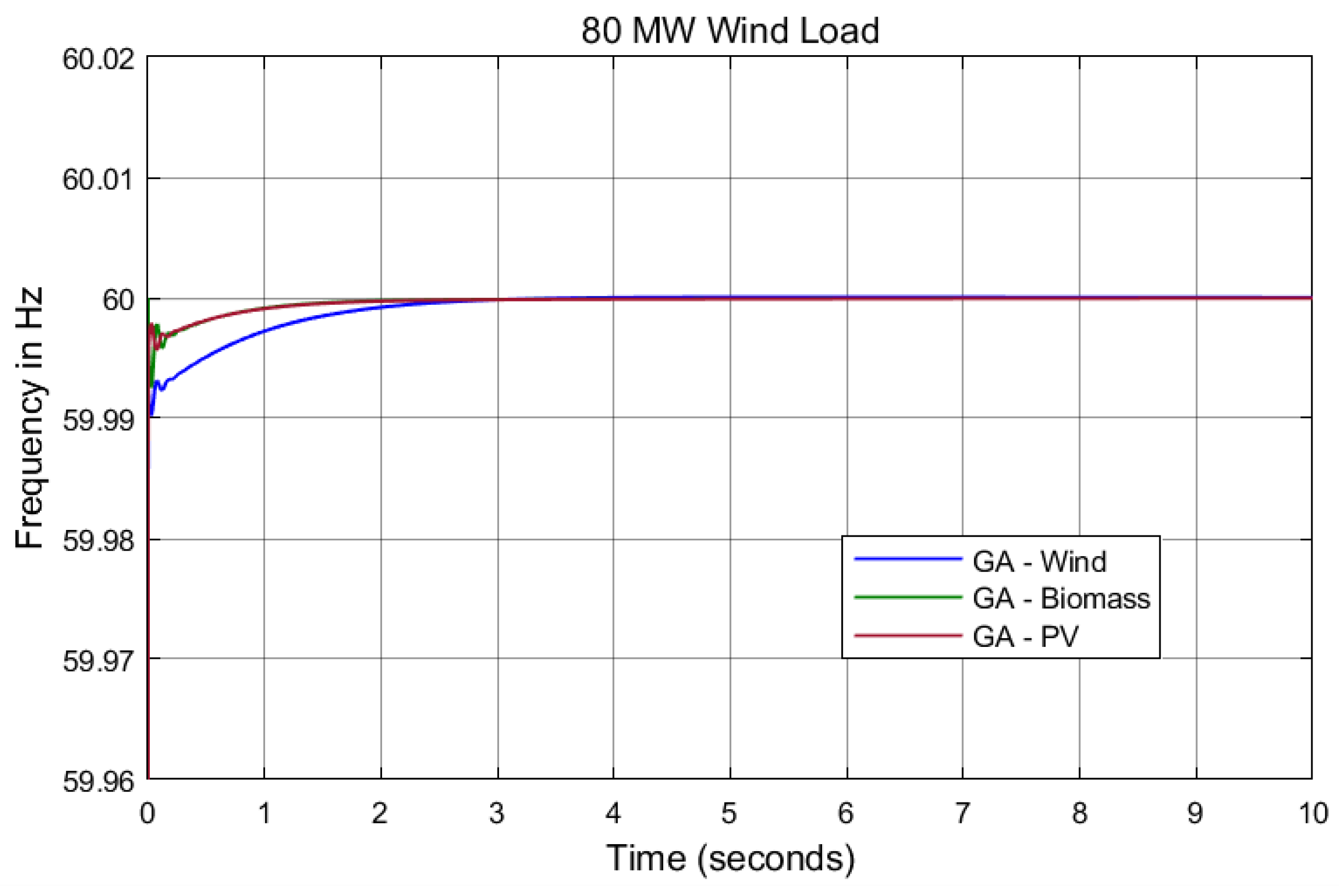
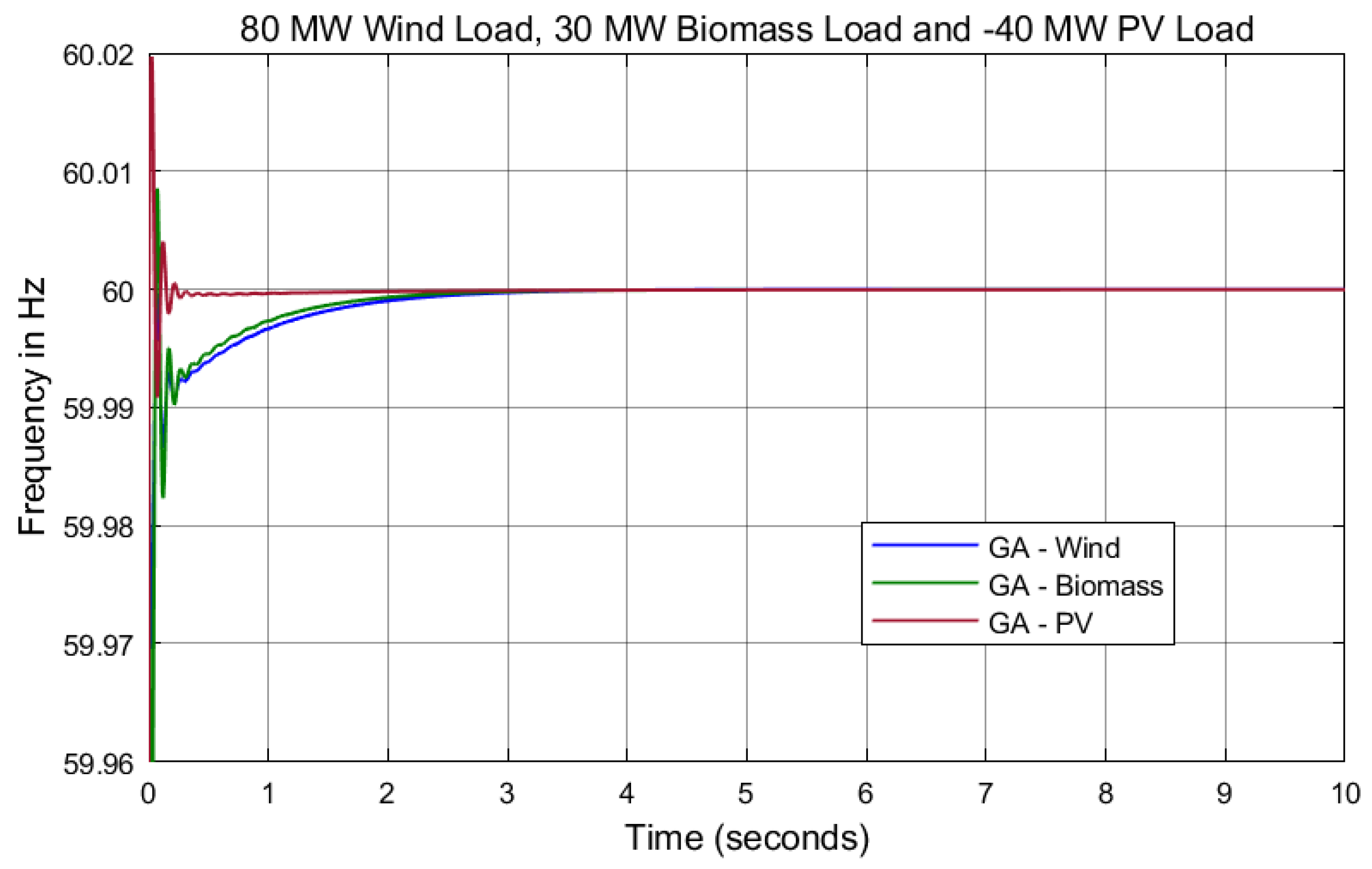
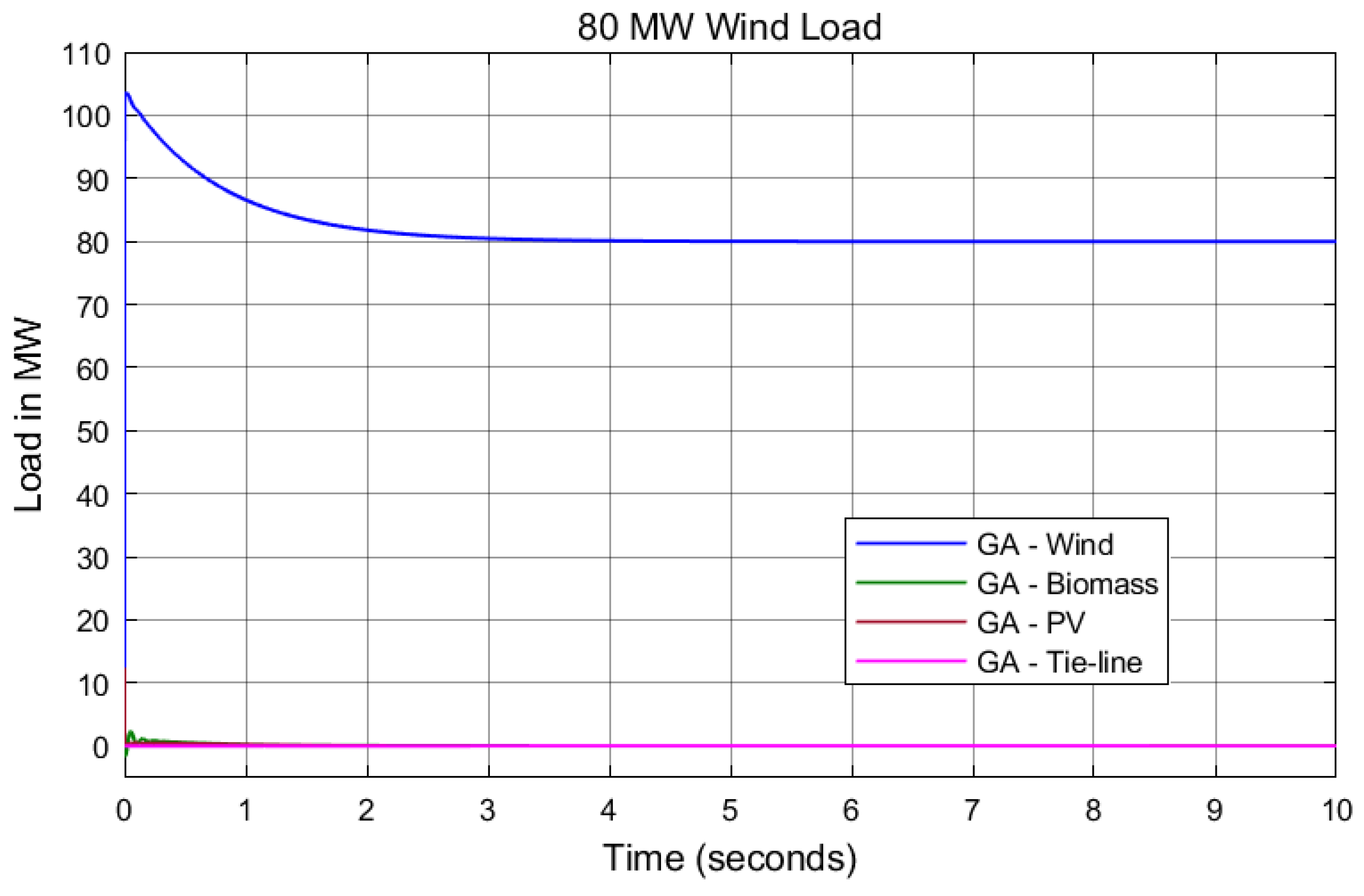
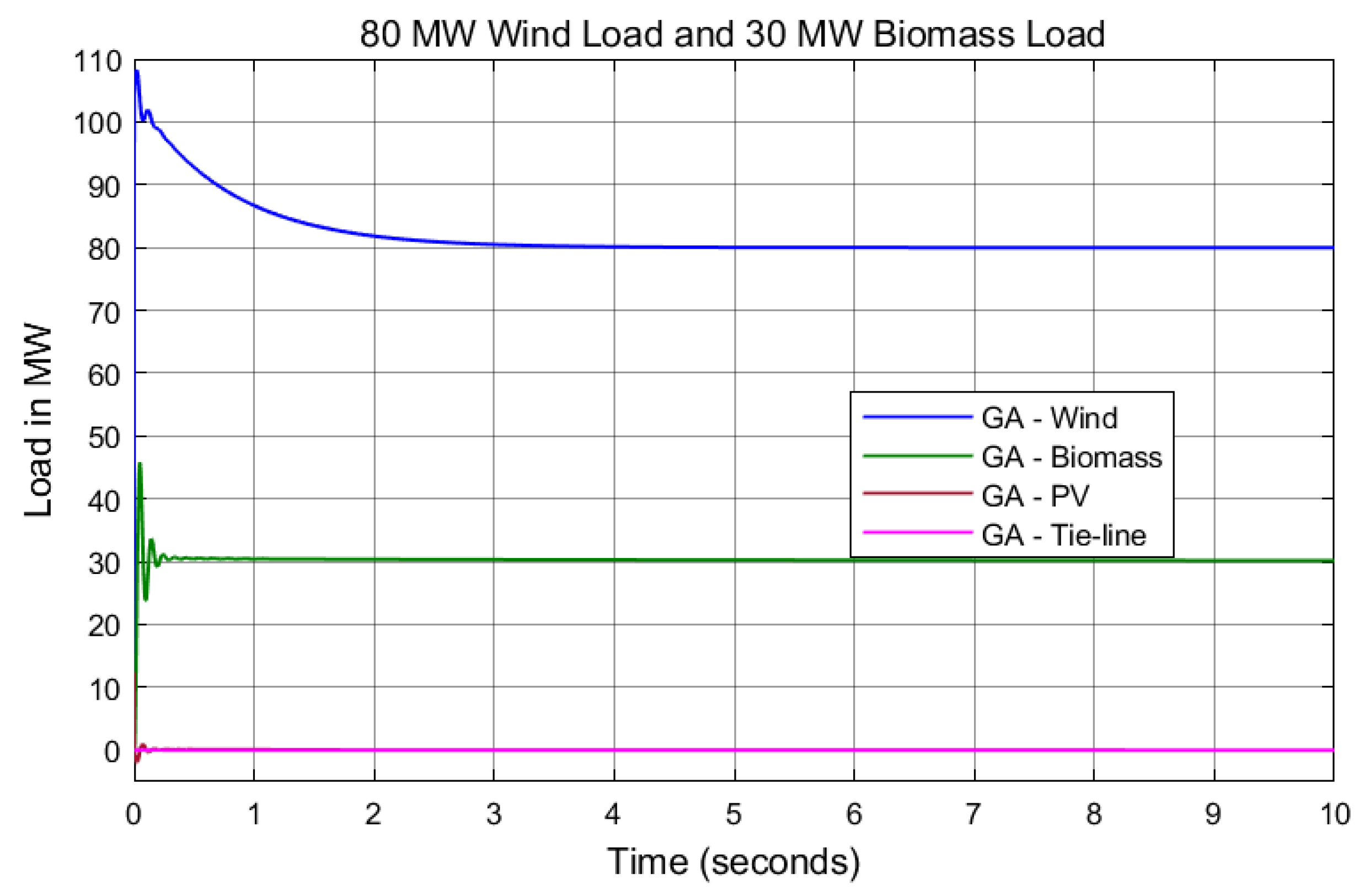
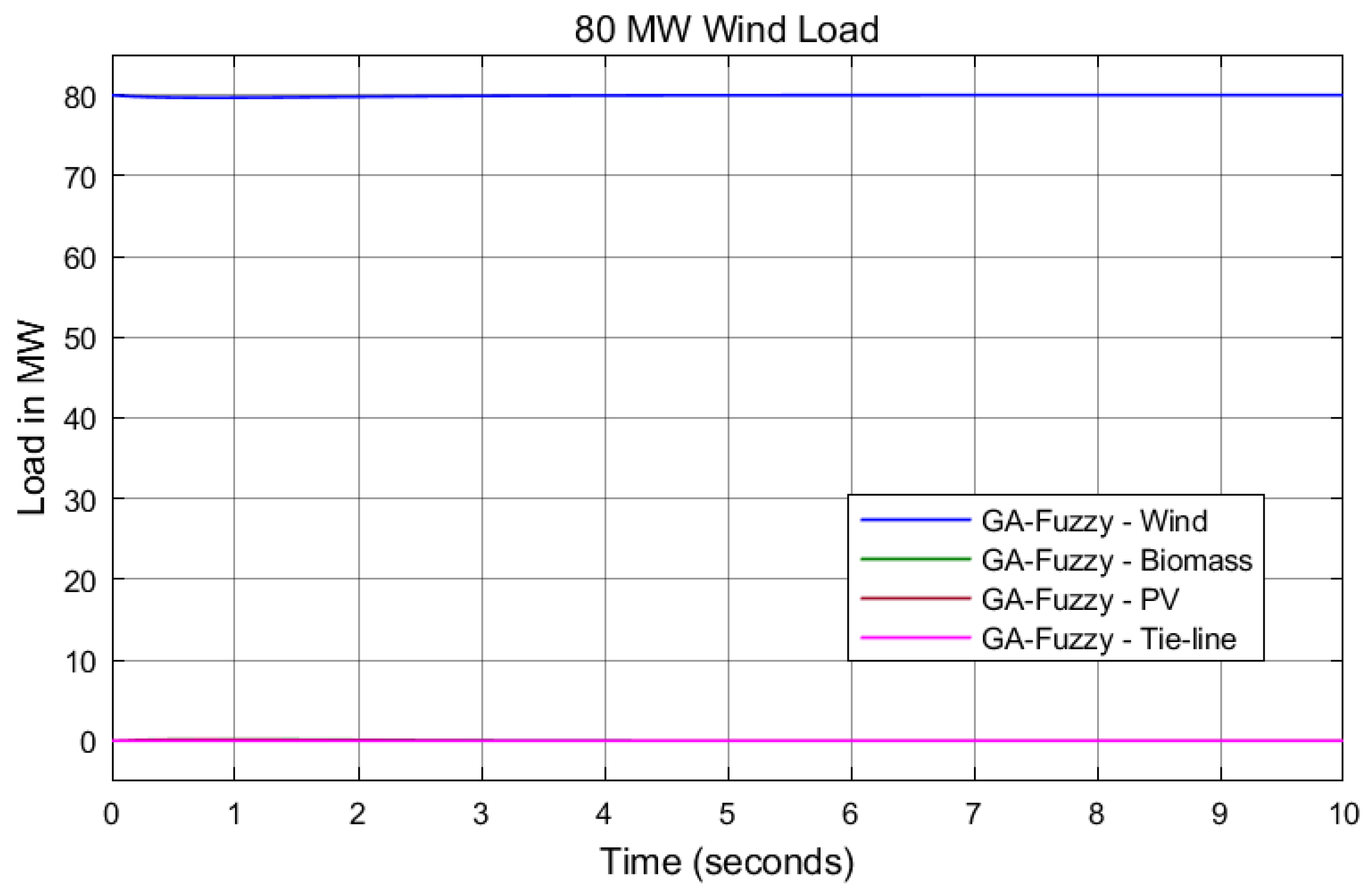
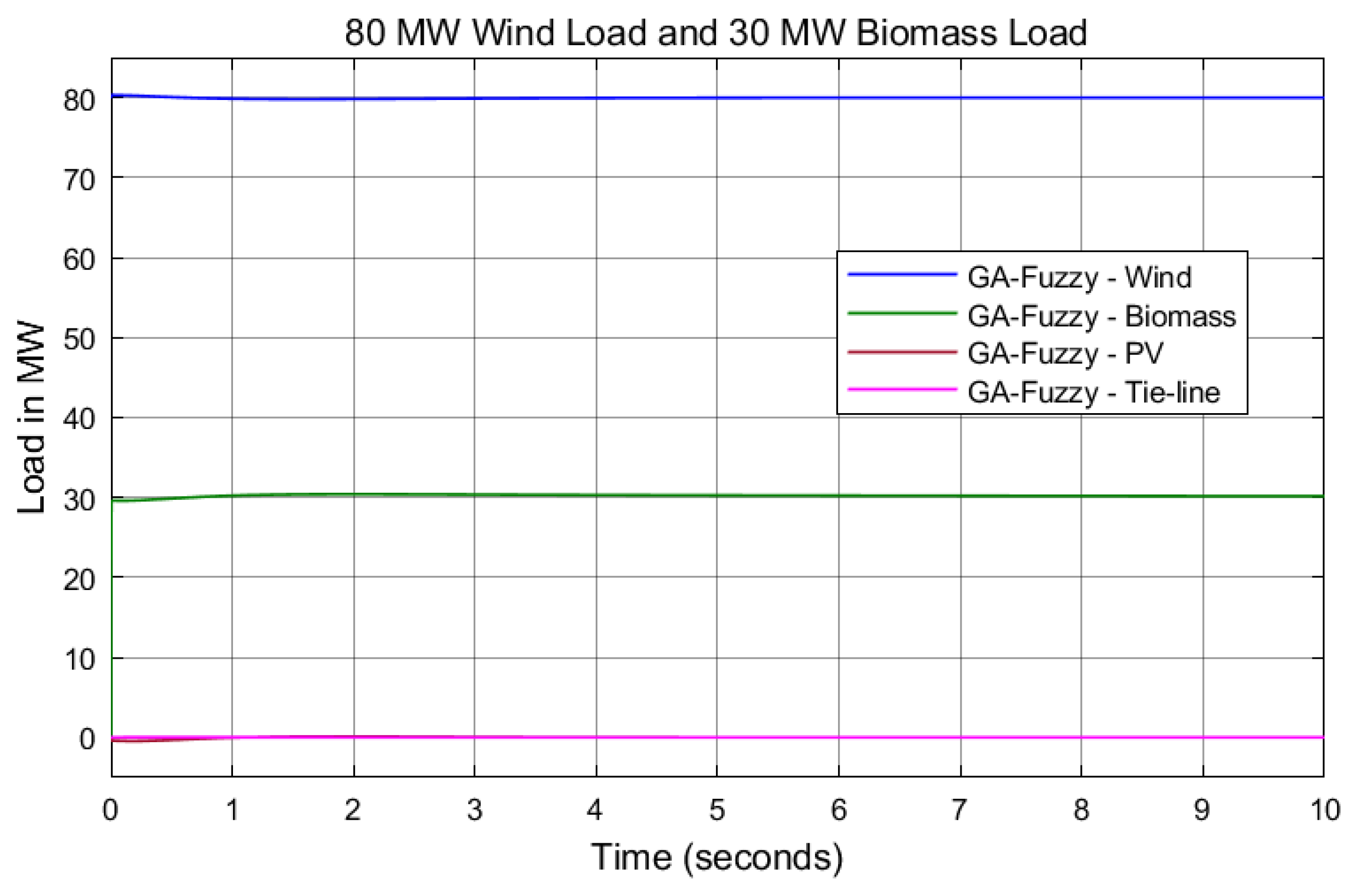
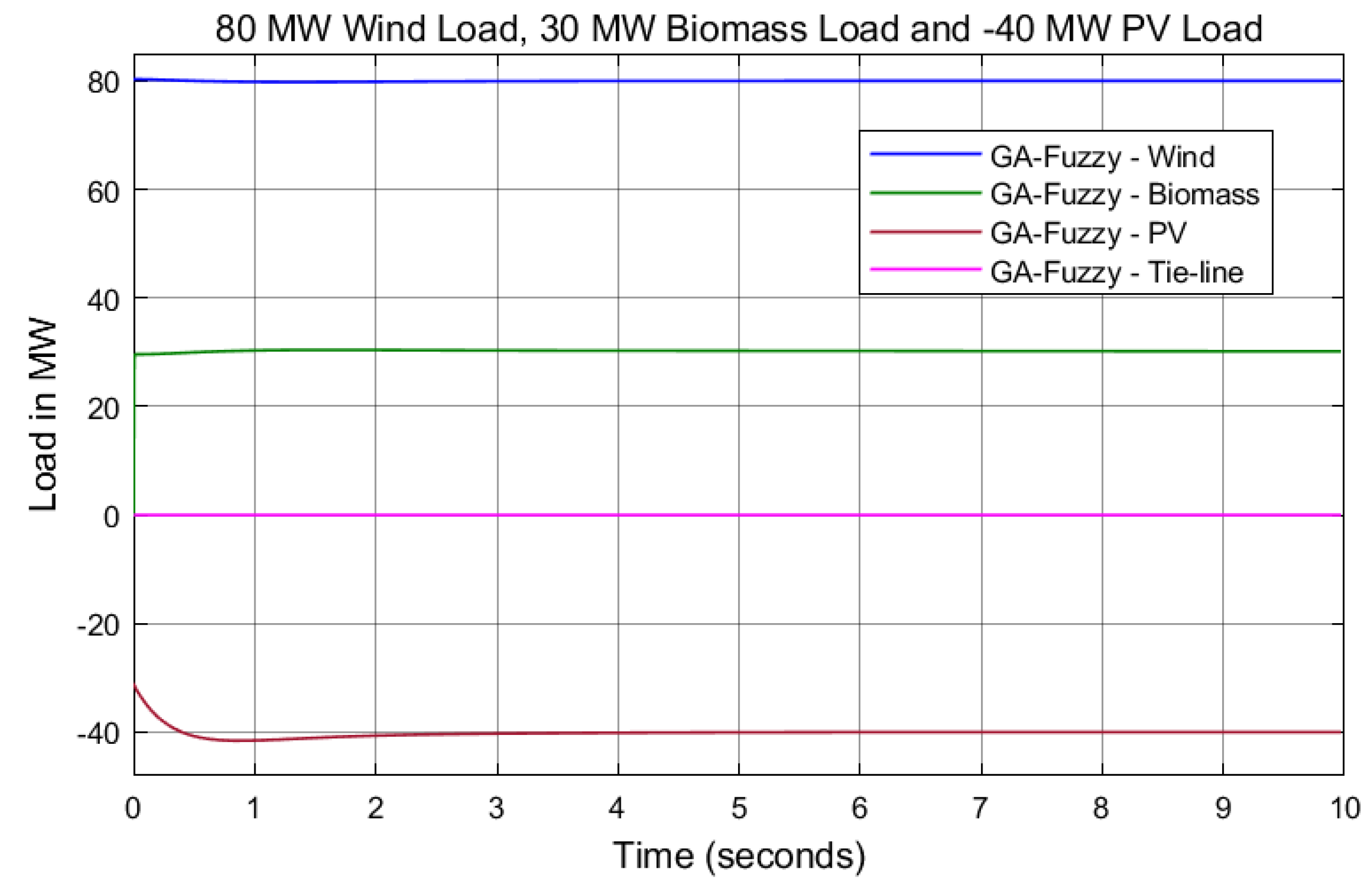
7. Results and Discussion
8. Conclusions and Future Work
8.1. Conclusions
8.2. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- The data for the wind power plant: B1 = 18, R1 = 2.5, α = 0.041, β = 0.2, and γ = 0.75, δ = 1.3.
- The data for the biomass power plant: B2 = 18, R2 = 2.5, ϵ = 0.08, ζ = 0.7, η = 10.06, κ = 10.2, and λ = 0.3.
- The data for the photovoltaic power plant: B3 = 18, R3 = 2.5, μ = 0.05, ν = 0.02, σ = 0.6, ξ = 0.23, and ψ = 0.2.
References
- Saadat, H. Power System Analysis; WCB/McGraw-Hill: Boston, MA, USA, 1999; Volume 2, pp. 567–576. [Google Scholar]
- US Energy Information Administration. Biomass Explained. Eia.gov. EIA. 2023. 30 June 2023. Available online: https://www.eia.gov/energyexplained/biomass/ (accessed on 15 January 2024).
- Ali, G.; El-Hawary, M. Generating Heat and Power from Biomass—An Overview. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019. [Google Scholar] [CrossRef]
- Ali, G.; Aly, H.H.; Little, T. A Modified Ant Lion Optimization Technique for Economic Emission Dispatch Including Biomass. In Proceedings of the 2021 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Kuala Lumpur, Malaysia, 12–13 June 2021. [Google Scholar] [CrossRef]
- Aly, H.H. Dynamic modeling and control of the tidal current turbine using DFIG and DDPMSG for power system stability analysis. Int. J. Electr. Power Energy Syst. 2016, 83, 525–540. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Anand, B.; Samanta, S.; Dey, N.; Ashour, A.S.; Balas, V.E. Design of a proportional-integral-derivative controller for an automatic generation control of multi-area power thermal systems using firefly algorithm. IEEE/CAA J. Autom. Sin. 2019, 6, 503–515. [Google Scholar] [CrossRef]
- Gupta, D.K.; Jha, A.V.; Appasani, B.; Srinivasulu, A.; Bizon, N.; Thounthong, P. Load Frequency Control Using Hybrid Intelligent Optimization Technique for Multi-Source Power Systems. Energies 2021, 14, 1581. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Padhan, S. A hybrid firefly algorithm and pattern search technique for automatic generation control of multi area power systems. Int. J. Electr. Power Energy Syst. 2015, 64, 9–23. [Google Scholar] [CrossRef]
- Ghosh, A.; Ray, A.K.; Nurujjaman; Jamshidi, M. Voltage and frequency control in conventional and PV integrated power systems by a particle swarm optimized Ziegler–Nichols based PID controller. SN Appl. Sci. 2021, 3, 314. [Google Scholar] [CrossRef]
- Barisal, A.; Mishra, S. Improved PSO based automatic generation control of multi-source nonlinear power systems interconnected by AC/DC links. Cogent Eng. 2018, 5, 1422228. [Google Scholar] [CrossRef]
- Bhagat, S.K.; Saikia, L.C.; Raju, D.K.; Babu, N.R.; Ramoji, S.K.; Dekaraja, B.; Behra, M.K. Maiden Application of Hybrid Particle Swarm Optimization with Genetic Algorithm in AGC Studies Considering Optimized TIDN Controller; Springer: Singapore, 2021; Volume 206. [Google Scholar]
- Alhelou, H.H.; Golshan, M.E.H.; Fini, M.H. Wind Driven Optimization Algorithm Application to Load Frequency Control in Interconnected Power Systems Considering GRC and GDB Nonlinearities. Electr. Power Compon. Syst. 2018, 46, 1223–1238. [Google Scholar] [CrossRef]
- Huang, C.; Li, J.; Mu, S.; Yan, H. Linear active disturbance rejection control approach for load frequency control of two-area interconnected power system. Trans. Inst. Meas. Control 2017, 41, 1562–1570. [Google Scholar] [CrossRef]
- Changmai, H.; Buragohain, M. Optimal Controller Design for LFC in Power System, Smart Innovation, Systems and Technologies; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Nivolianiti, E. Harris hawks optimization algorithm for load frequency control of isolated multi-source power generating systems. Int. J. Emerg. Electr. Power Syst. 2023, 1–17. [Google Scholar] [CrossRef]
- Shankar, R.; Chatterjee, K.; Bhushan, R. Impact of energy storage system on load frequency control for diverse sources of interconnected power system in deregulated power environment. Int. J. Electr. Power Energy Syst. 2016, 79, 11–26. [Google Scholar] [CrossRef]
- Çelik, E.; Öztürk, N.; Arya, Y.; Ocak, C. (1 + PD)-PID cascade controller design for performance betterment of load frequency control in diverse electric power systems. Neural Comput. Appl. 2021, 33, 15433–15456. [Google Scholar] [CrossRef]
- Babu, N.R.; Saikia, L.C.; Bhagat, S.K.; Ramoji, S.K.; Dekaraja, B.; Behra, M.K. LFC of a solar thermal integrated thermal system considering CSO optimized TI-DN controller. In Modeling, Simulation and Optimization: Proceedings of CoMSO 2020; Springer: Singapore, 2021; pp. 323–334. [Google Scholar]
- Kumar, R.R.; Yadav, A.K.; Ramesh, M. Hybrid PID plus LQR based frequency regulation approach for the renewable sources based standalone microgrid. Int. J. Inf. Technol. 2022, 14, 2567–2574. [Google Scholar] [CrossRef]
- Pinazo, M.A.; Arias, R.A.; Tarrillo, J.M. Comparison of primary frequency control methods for wind turbines based on the doubly fed induction generator. Wind. Eng. 2022, 46, 1923–1947. [Google Scholar] [CrossRef]
- Patel, V.; Guha, D.; Purwar, S. Fractional-order Adaptive Sliding Mode Approach for Frequency Regulation in Power System. In Proceedings of the 2021 9th IEEE International Conference on Power Systems (ICPS), Kharagpur, India, 16–18 December 2021. [Google Scholar] [CrossRef]
- Saxena, P.; Singh, N.; Pandey, A.K. Investigating the frequency fault ride through capability of solar photovoltaic system: Replacing battery via virtual inertia reserve. Int. Trans. Electr. Energy Syst. 2021, 31, e12791. [Google Scholar] [CrossRef]
- Guo, W.; Yang, J. Stability performance for primary frequency regulation of hydro-turbine governing system with surge tank. Appl. Math. Model. 2018, 54, 446–466. [Google Scholar] [CrossRef]
- Dash, P.; Saikia, L.C.; Sinha, N. Flower Pollination Algorithm Optimized PI-PD Cascade Controller in Automatic Generation Control of a Multi-area Power System. Int. J. Electr. Power Energy Syst. 2016, 82, 19–28. [Google Scholar] [CrossRef]
- El-Sehiemy, R.; Shaheen, A.; Ginidi, A.; Al-Gahtani, S.F. Proportional-Integral-Derivative Controller Based-Artificial Rabbits Algorithm for Load Frequency Control in Multi-Area Power Systems. Fractal Fract. 2023, 7, 97. [Google Scholar] [CrossRef]
- Zadeh, L.A. Is there a need for fuzzy logic? Inf. Sci. 2008, 178, 2751–2779. [Google Scholar] [CrossRef]
- Shafei, M.A.R.; Ibrahim, D.K.; Bahaa, M. Application of PSO tuned fuzzy logic controller for LFC of two-area power system with redox flow battery and PV solar park. Ain Shams Eng. J. 2022, 13, 101710. [Google Scholar] [CrossRef]
- Hussein, T.; Shamekh, A. Design of PI Fuzzy Logic Gain Scheduling Load Frequency Control in Two-Area Power Systems. Designs 2019, 3, 26. [Google Scholar] [CrossRef]
- Khokhar, B.; Dahiya, S.; Parmar, K.P.S. A Novel Hybrid Fuzzy PD-TID Controller for Load Frequency Control of a Standalone Microgrid. Arab. J. Sci. Eng. 2020, 46, 1053–1065. [Google Scholar] [CrossRef]
- Ghafouri, A.; Milimonfared, J.; Gharehpetian, G.B. Fuzzy-Adaptive Frequency Control of Power System Including Microgrids, Wind Farms, and Conventional Power Plants. IEEE Syst. J. 2018, 12, 2772–2781. [Google Scholar] [CrossRef]
- Ben Meziane, K.; Naoual, R.; Boumhidi, I. Type-2 Fuzzy Logic based on PID controller for AGC of Two-Area with Three Source Power System including Advanced TCSC. Procedia Comput. Sci. 2019, 148, 455–464. [Google Scholar] [CrossRef]
- Bloul, A.; Sharaf, A.; El-Hawary, M. An Energy Saving Green Plug Device for Nonlinear Loads. IOP Conf. Ser. Earth Environ. Sci. 2018, 127, 012016. [Google Scholar] [CrossRef]
- Dorigo, M. Ant colony optimization. Scholarpedia 2007, 2, 1461. [Google Scholar] [CrossRef]
- John, H. Holland genetic algorithms. Sci. Am. 1992, 267, 44–50. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Kirkpatrick, S. Optimization by simulated annealing. Science 1984, 220, 4598. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Webster, B.; Bernhard, P.J. A Local Search Optimization Algorithm Based on Natural Principles of Gravitation; Florida Institute of Technology: Melbourne, FL, USA, 2003. [Google Scholar]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Formato, R.A. Central force optimization: A new nature inspired computational framework for multidimensional search and optimization. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2007); Springer: Berlin/Heidelberg, Germany, 2008; pp. 221–238. [Google Scholar]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- González, J.R.; Sancho-Royo, A.; Pelta, D.A.; Cruz, C. Nature-Inspired Cooperative Strategies for Optimization. In Encyclopedia of Networked and Virtual Organizations; IGI Global: Hershey, PA, USA, 2008; pp. 982–989. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]

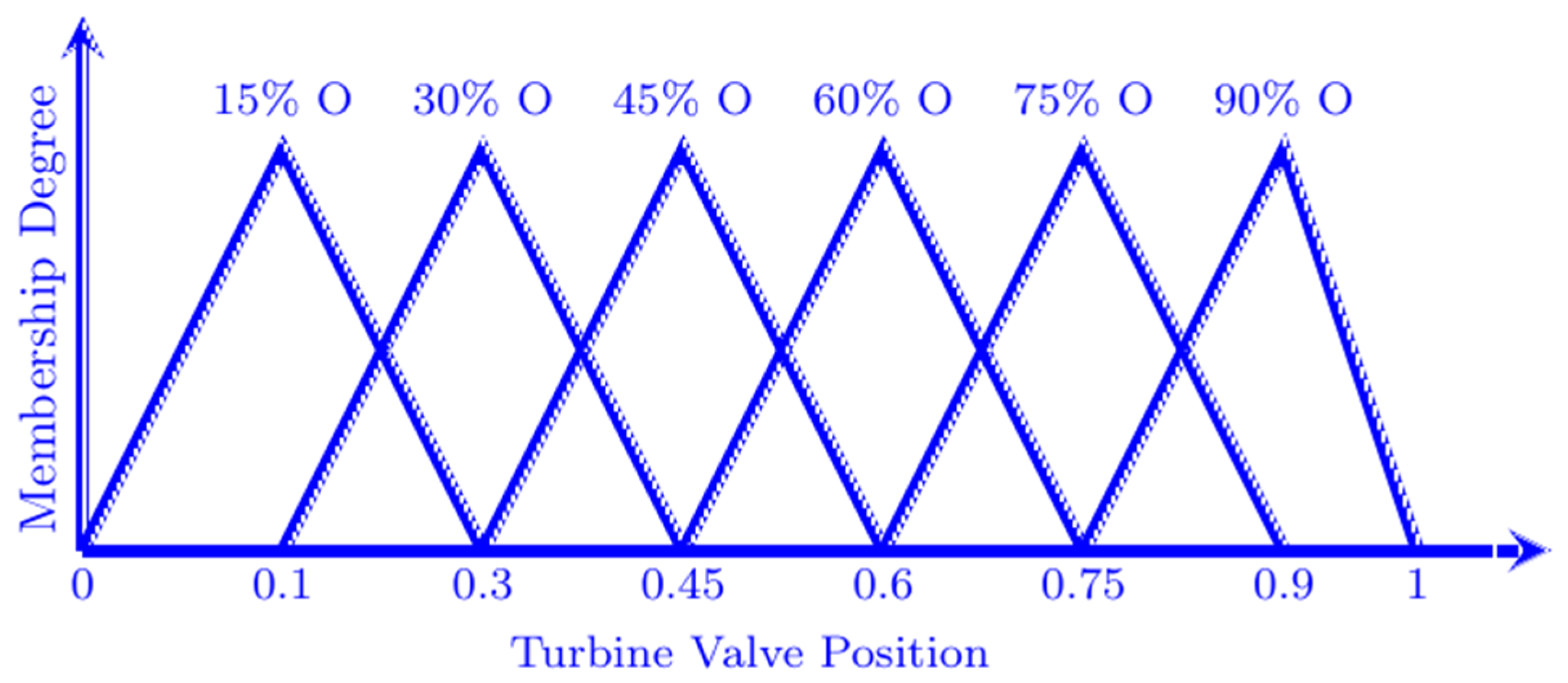

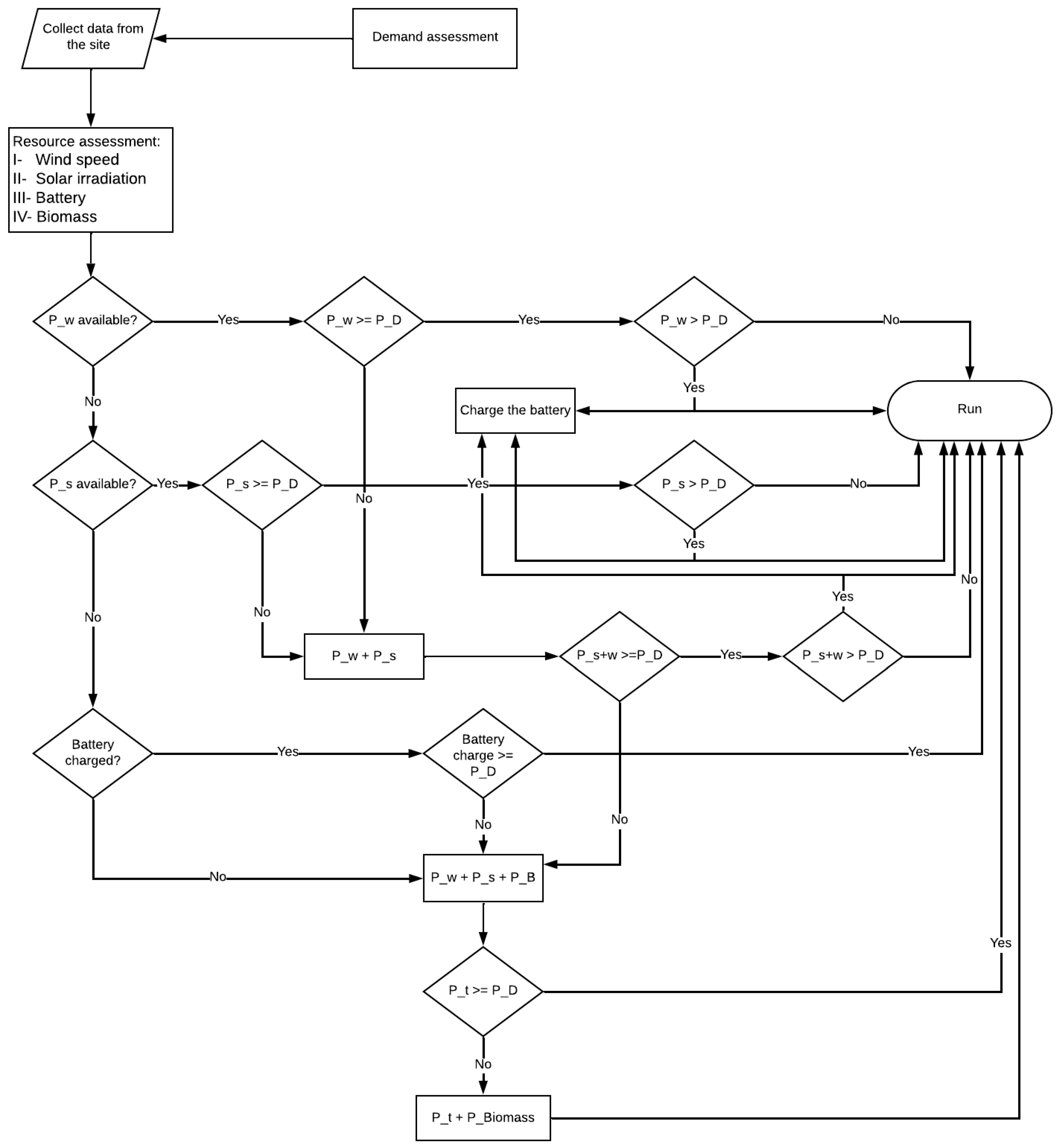


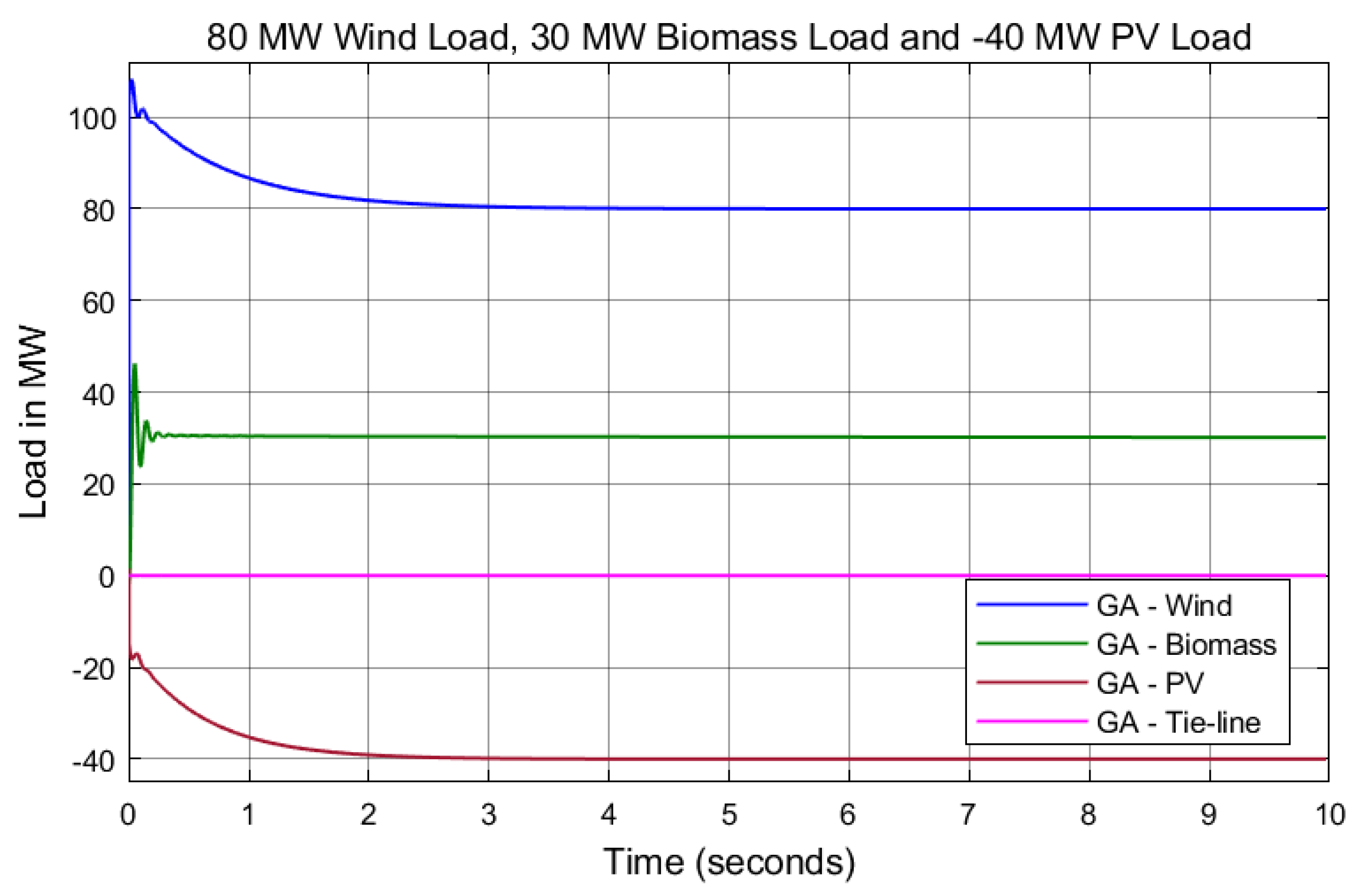
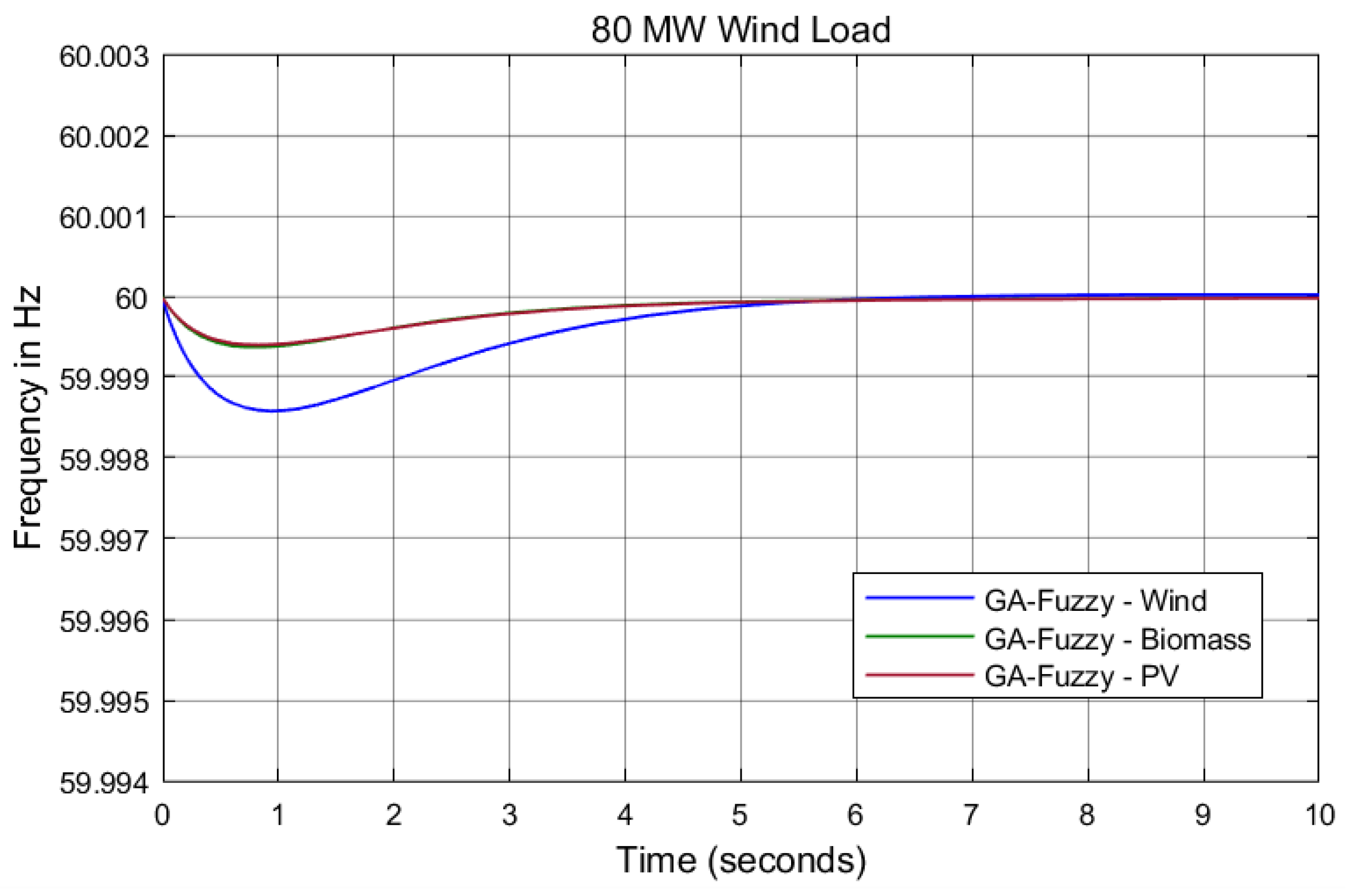
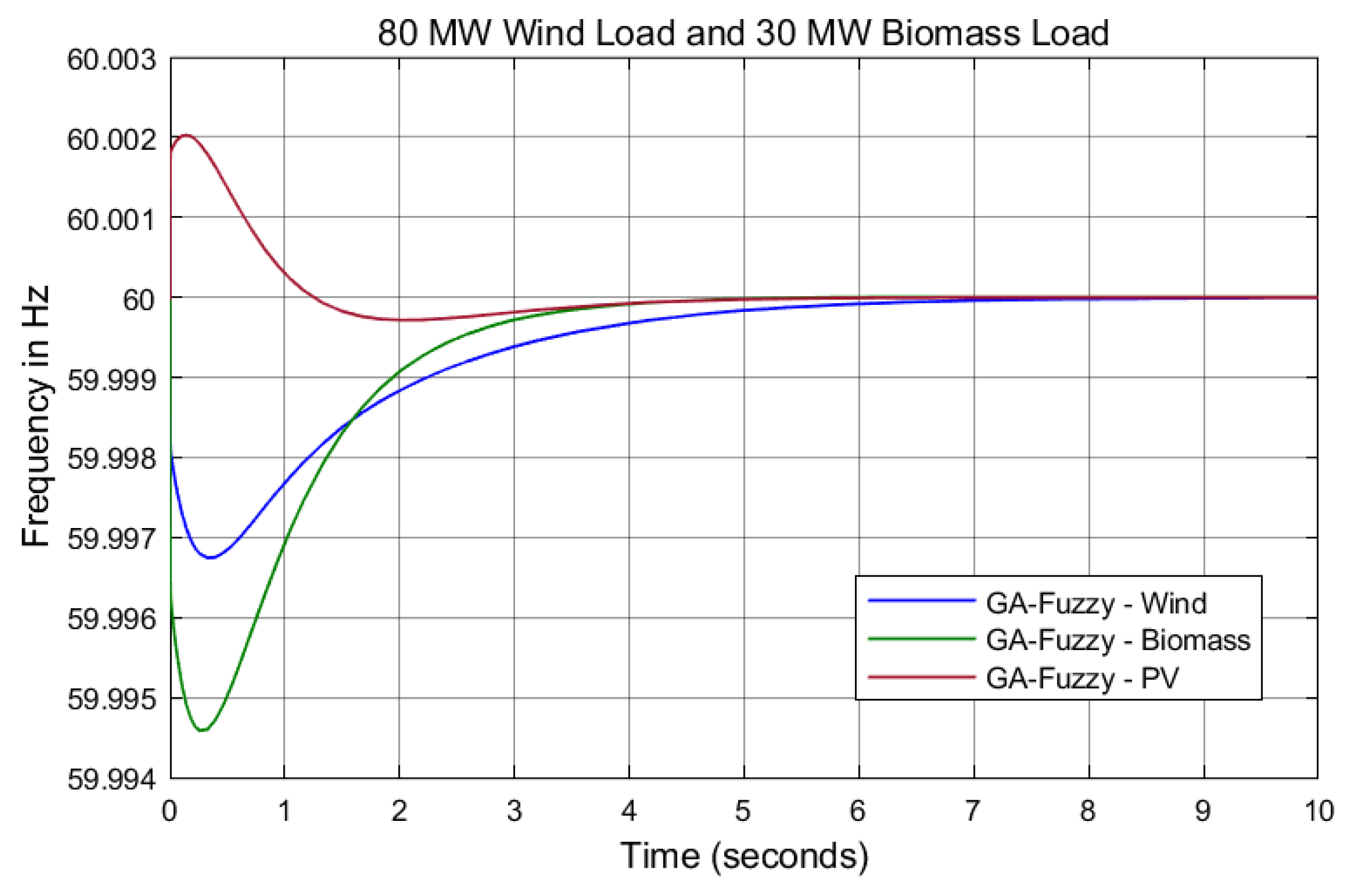
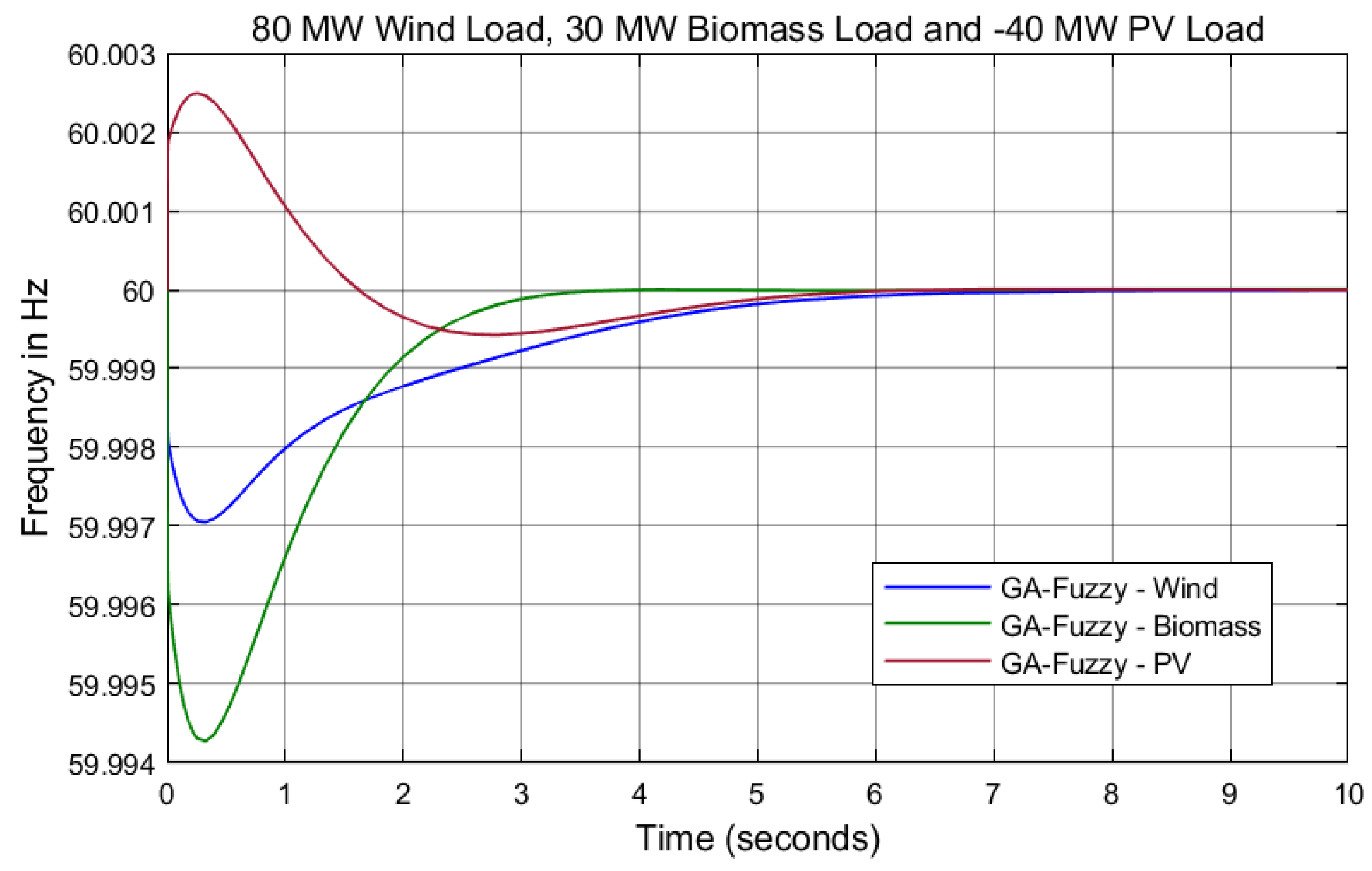
| Turbine Operation in Boolean Algebra | Turbine Operation in Fuzzy Logic |
|---|---|
| If (valve == 0) { // Turbine is off } Else { Turbine is on } | If ((valve >= 0) && (valve < 0.25)) { // Turbine is quarter opened } Else if ((valve >= 0.25) && (valve < 0.5)) { //Turbine is half-opened } Else if ((valve >= 0.5) && (valve < 0.75)) { //Turbine is three-quarters opened } Else if ((valve >= 0.75) && (valve < 1.0)) { //Turbine is fully opened } |
| Parameters | GA | PS | SA | PSO | GA-Fuzzy | |
|---|---|---|---|---|---|---|
| Controller I | P | 21.5457 | 20 | 19.99679 | 20 | 30 |
| I | 17.30914 | 20 | 13.25205 | 15.43407 | 24.08826 | |
| D | 3.633331 | 14.93847 | 3.751003 | 3.970836 | 4.72576 | |
| Controller II | P | 21.71193 | 20 | 6.856002 | 18.72205 | 15.95172 |
| I | 29.9966 | 20 | 19.9941 | 17.68945 | 30 | |
| D | 0.029296 | 0.228512 | 0.005082 | 0 | 0 | |
| Controller II | P | 27.93593 | 20 | 6.517656 | 20 | 29.99936 |
| I | 22.96649 | 20 | 19.99775 | 20 | 27.68385 | |
| D | 3.053391 | 20 | 1.268777 | 8.207062 | 17.06332 | |
| Controller IV | P | 21.17271 | 10.18554 | 19.71834 | 17.08208 | 26.20549 |
| I | 5.398859 | 0.268551 | 5.126602 | 4.375707 | 5.24566 | |
| D | 14.78407 | 0.251951 | 12.20899 | 16.78958 | 27.84191 |
| Rise Time | ||||||
|---|---|---|---|---|---|---|
| Integrator | GA | PS | SA | PSO | GA-Fuzzy | |
| 0.6383 | 5.94 × 10−4 | 1.64 × 10−4 | 2.57 × 10−4 | 6.32 × 10−4 | 3.75 × 100 | |
| 1.21 × 10−5 | 4.97 × 10−7 | 0.0069 | 6.56 × 10−7 | 4.94 × 10−8 | 4.14 × 10−2 | |
| 0.0801 | 5.21 × 10−4 | 1.37 × 10−4 | 2.44 × 10−4 | 5.69 × 10−4 | 8.37 × 10−6 | |
| 2.80 × 10−5 | 1.40 × 10−3 | 1.91 × 10−4 | 1.90 × 10−3 | 9.71 × 10−4 | 2.00 × 10−3 | |
| 0.3718 | 3.91 × 10−4 | 8.59 × 10−5 | 4.14 × 10−4 | 3.43 × 10−4 | 5.48 × 10−5 | |
| 3.39 × 10−1 | 1.63 × 10−2 | 1.65 × 10−2 | 3.58 × 10−2 | 1.89 × 10−2 | 2.50 × 10−3 | |
| 0.768 | 1.11 × 100 | 1.11 × 100 | 1.12 × 100 | 1.11 × 100 | 3.01 × 10−1 | |
| Settling Time | ||||||
|---|---|---|---|---|---|---|
| Integrator | GA | PS | SA | PSO | GA-Fuzzy | |
| 2.6067 | 0.5813 | 0.7642 | 0.7443 | 0.7738 | 6.3051 | |
| 4.389 | 1.6777 | 2.4703 | 1.165 | 2.3389 | 3.0165 | |
| 0.7863 | 0.0863 | 0.0429 | 0.0937 | 0.0951 | 5.5882 | |
| 7.45 | 5.1307 | 0.1585 | 8.9649 | 4.2436 | 10.846 | |
| 3.1814 | 2.1047 | 2.0722 | 2.048 | 2.1251 | 6.2576 | |
| 4.906 | 0.2603 | 0.1037 | 0.489 | 0.2915 | 0.0056 | |
| 2.8787 | 2.0544 | 2.0973 | 2.1189 | 2.015 | 3.5384 | |
| Peak Overshoot | ||||||
|---|---|---|---|---|---|---|
| Integrator | GA | PS | SA | PSO | GA-Fuzzy | |
| 9.29 × 10−6 | 1.35 × 107 | 2.30 × 10−5 | 6.04 × 10−7 | 0.00 × 100 | 0 | |
| 0.0142 | 1.22 × 10−4 | 3.81 × 10−4 | 0.0152 | 8.65 × 10−6 | 0 | |
| 0.0341 | 0.0222 | 0.0589 | 0.0357 | 0.0042 | 0 | |
| 2.16 × 103 | 1.19 × 106 | 6.79 × 106 | 1.93 × 106 | 1.04 × 104 | 1.05 × 101 | |
| 35.2413 | 3.57 × 101 | 3.78 × 101 | 35.9763 | 3.85 × 10−1 | 0 | |
| 53.2843 | 3.07 × 101 | 3.06 × 101 | 51.2822 | 1.18 × 100 | 0 | |
| 0 | 9.36 × 10−2 | 0.00 × 100 | 0.0048 | 3.94 × 100 | 0 | |
| Peak Undershoot | ||||||
|---|---|---|---|---|---|---|
| Integrator | GA | PS | SA | PSO | GA-Fuzzy | |
| 0 | 2.54 × 104 | 0 | 0 | 0 | 9.29 × 10−6 | |
| 0 | 0 | 0 | 0 | 0 | 0.0142 | |
| 0 | 0 | 0 | 0 | 0 | 0.0341 | |
| 7.71 × 103 | 1.90 × 105 | 7.53 × 106 | 5.2 × 106 | 4.41 × 104 | 2.16 × 101 | |
| 0 | 0 | 0 | 0 | 0 | 0.0241 | |
| 6.2888 | 2.2179 | 2.3081 | 4.0984 | 1.0004 | 0.2843 | |
| 3.7812 | 1.542 | 1.9664 | 5.8355 | 0 | 0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, G.; Aly, H.; Little, T. Automatic Generation Control of a Multi-Area Hybrid Renewable Energy System Using a Proposed Novel GA-Fuzzy Logic Self-Tuning PID Controller. Energies 2024, 17, 2000. https://doi.org/10.3390/en17092000
Ali G, Aly H, Little T. Automatic Generation Control of a Multi-Area Hybrid Renewable Energy System Using a Proposed Novel GA-Fuzzy Logic Self-Tuning PID Controller. Energies. 2024; 17(9):2000. https://doi.org/10.3390/en17092000
Chicago/Turabian StyleAli, Gama, Hamed Aly, and Timothy Little. 2024. "Automatic Generation Control of a Multi-Area Hybrid Renewable Energy System Using a Proposed Novel GA-Fuzzy Logic Self-Tuning PID Controller" Energies 17, no. 9: 2000. https://doi.org/10.3390/en17092000
APA StyleAli, G., Aly, H., & Little, T. (2024). Automatic Generation Control of a Multi-Area Hybrid Renewable Energy System Using a Proposed Novel GA-Fuzzy Logic Self-Tuning PID Controller. Energies, 17(9), 2000. https://doi.org/10.3390/en17092000







