Two-Stage Solar–NaOH Thermochemical Heat Pump Heating System for Building Heating: Operations Strategies and Theoretical Performance
Abstract
1. Introduction
2. Materials and Methods
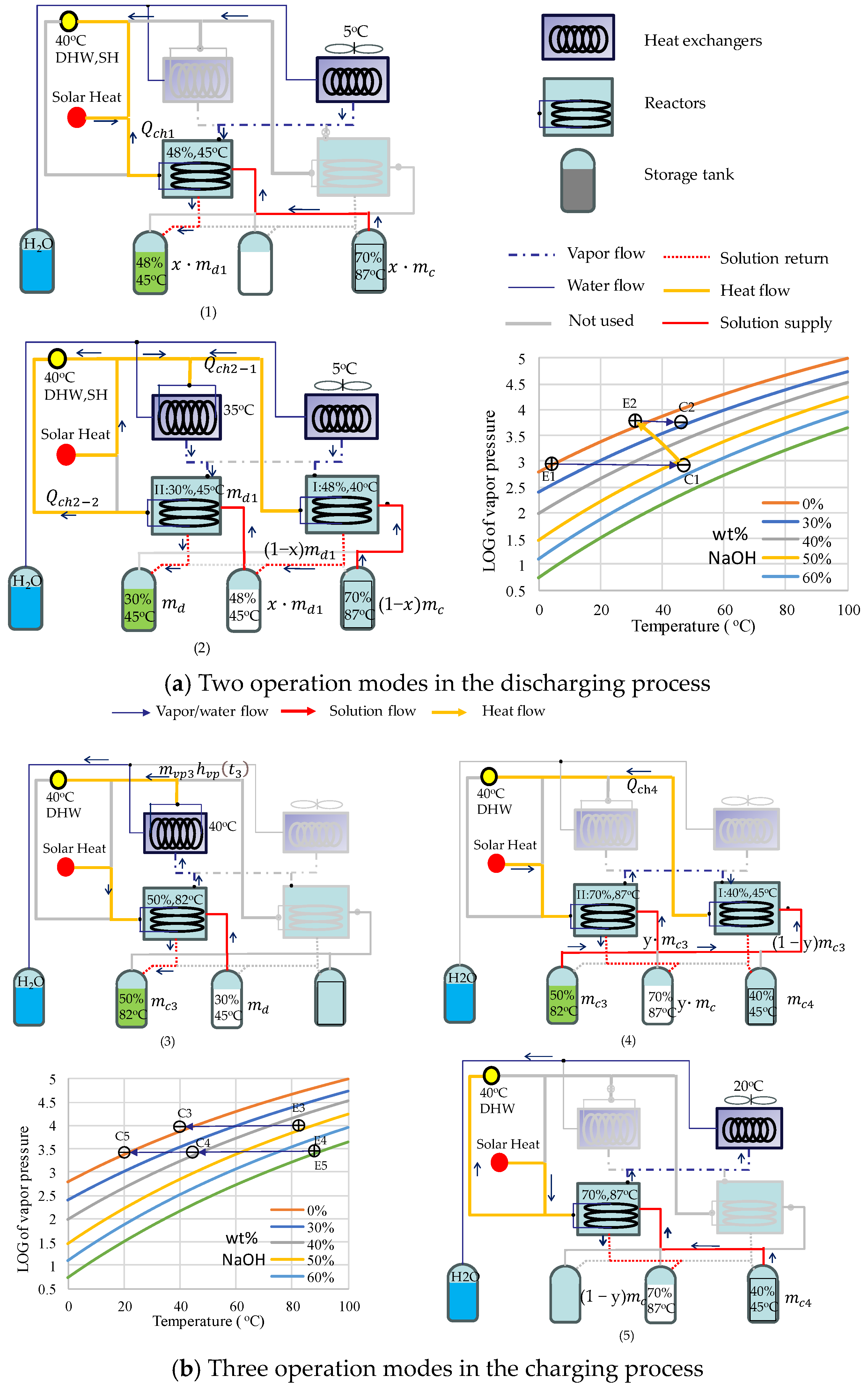
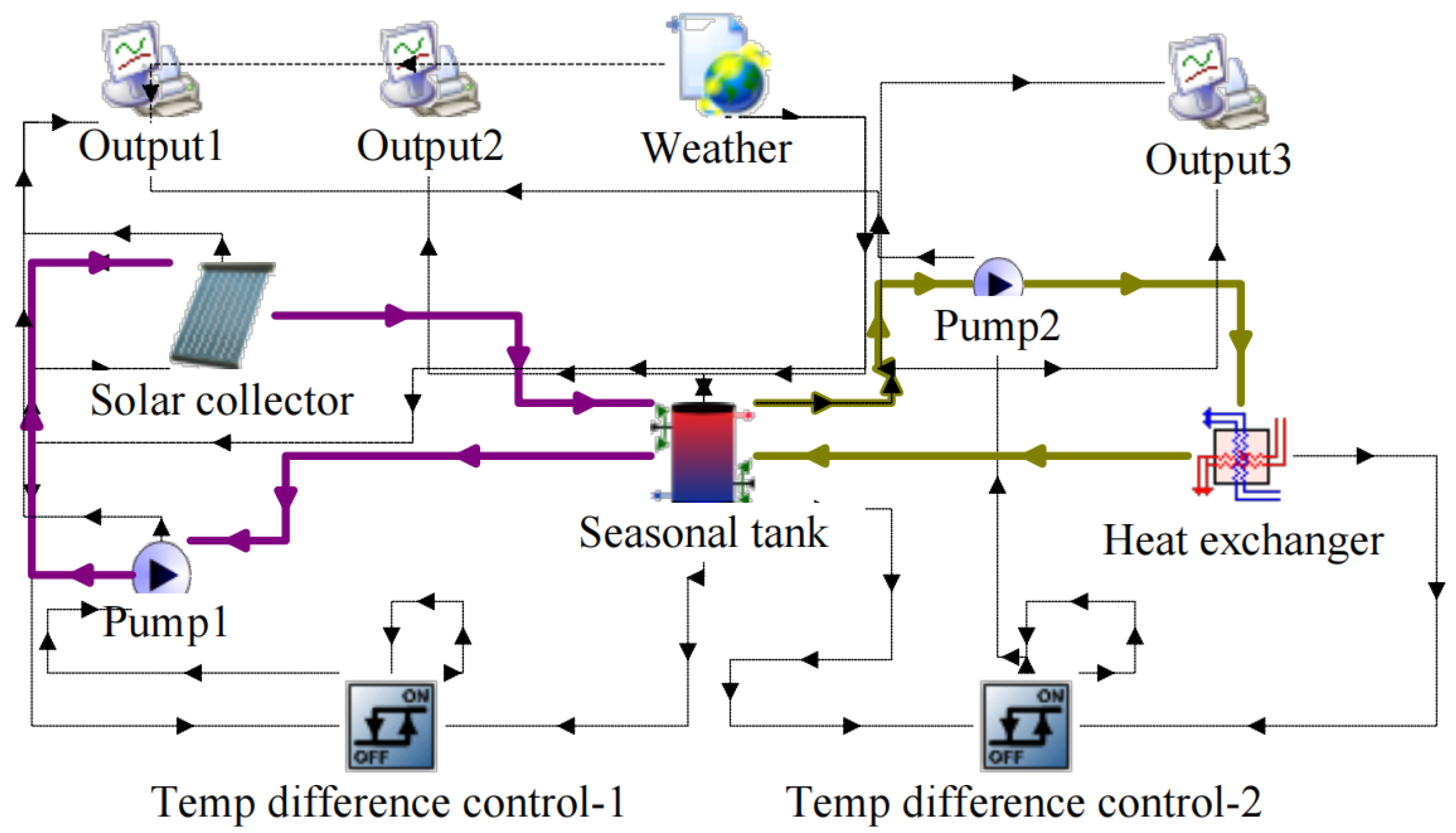
2.1. System Configuration
2.2. Case Study
2.3. Mass and Energy Conservation Equations
- (1)
- The water temperature for both space heating and DHW is 40 °C.
- (2)
- Ideal heat exchangers are assumed.
- (3)
- All thermal losses are neglected.
2.3.1. Discharge Period 1: E1→C1
2.3.2. Discharge Period 2: E1→C1, E2→C2
2.3.3. Charge Period 3: E3→C3
2.3.4. Charge Period 4: E4→C4
2.3.5. Charge Period 5: E5→C5
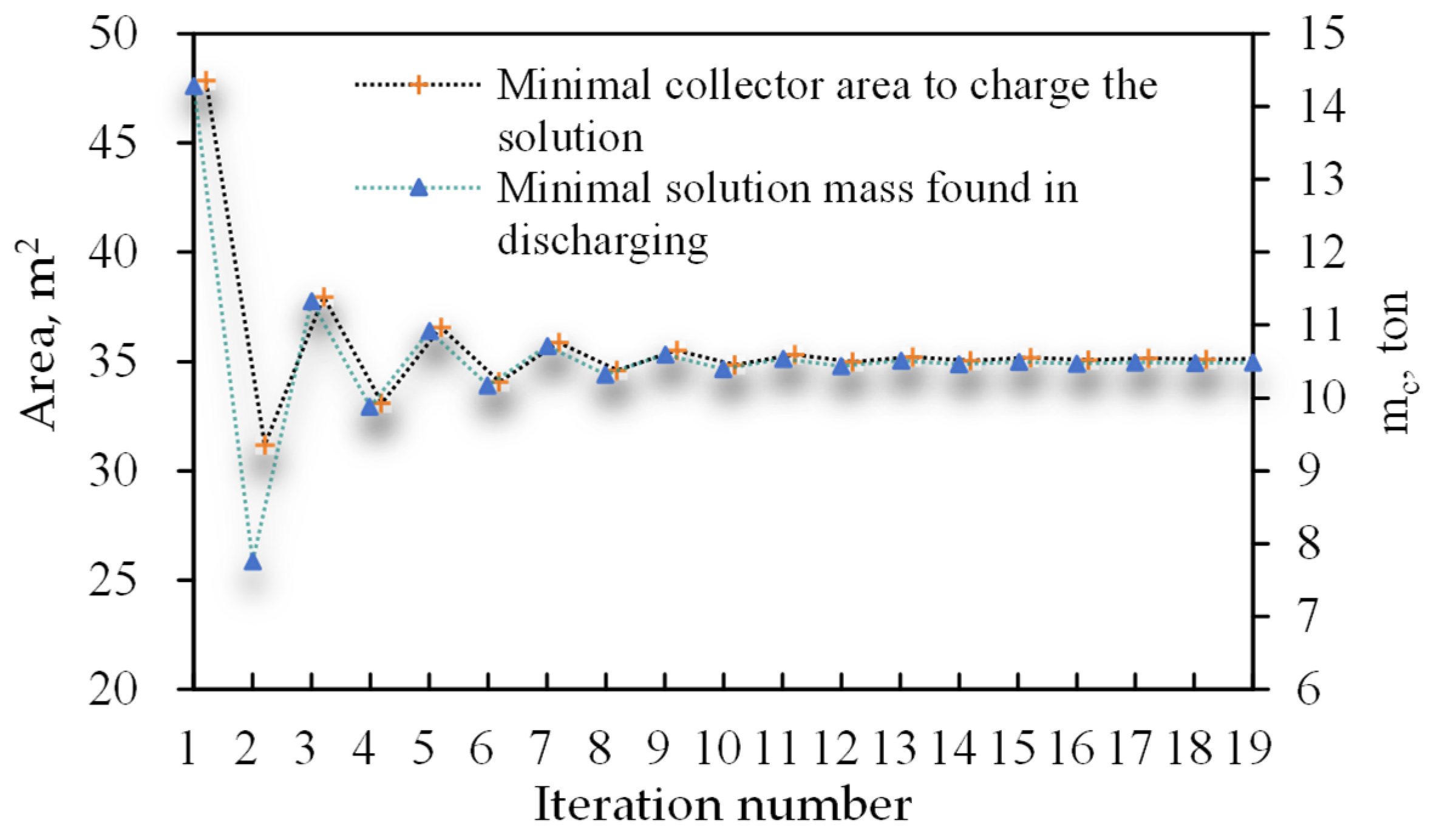
2.3.6. Solving Method
- Assume .
- Solve Equations (1)–(8) for the minimal values of solution mass and collector area in the discharging process.
- Solve Equations (9)–(22) for the minimal collector area required to regenerate the solution.
- Solve Equations (1)–(6), (23) and (24) for the new minimal value of with collector area fixed at the value from the last step. With additional collectors (−) to cover part of the heating demand, this step should produce a smaller value of the solution mass.
- Repeat (C) to update , corresponding to the new value of .
- Repeat (D, E) until the correction of the solution mass is negligible.
2.4. Performance Indices
3. Results and Discussion
3.1. Solution Convergence
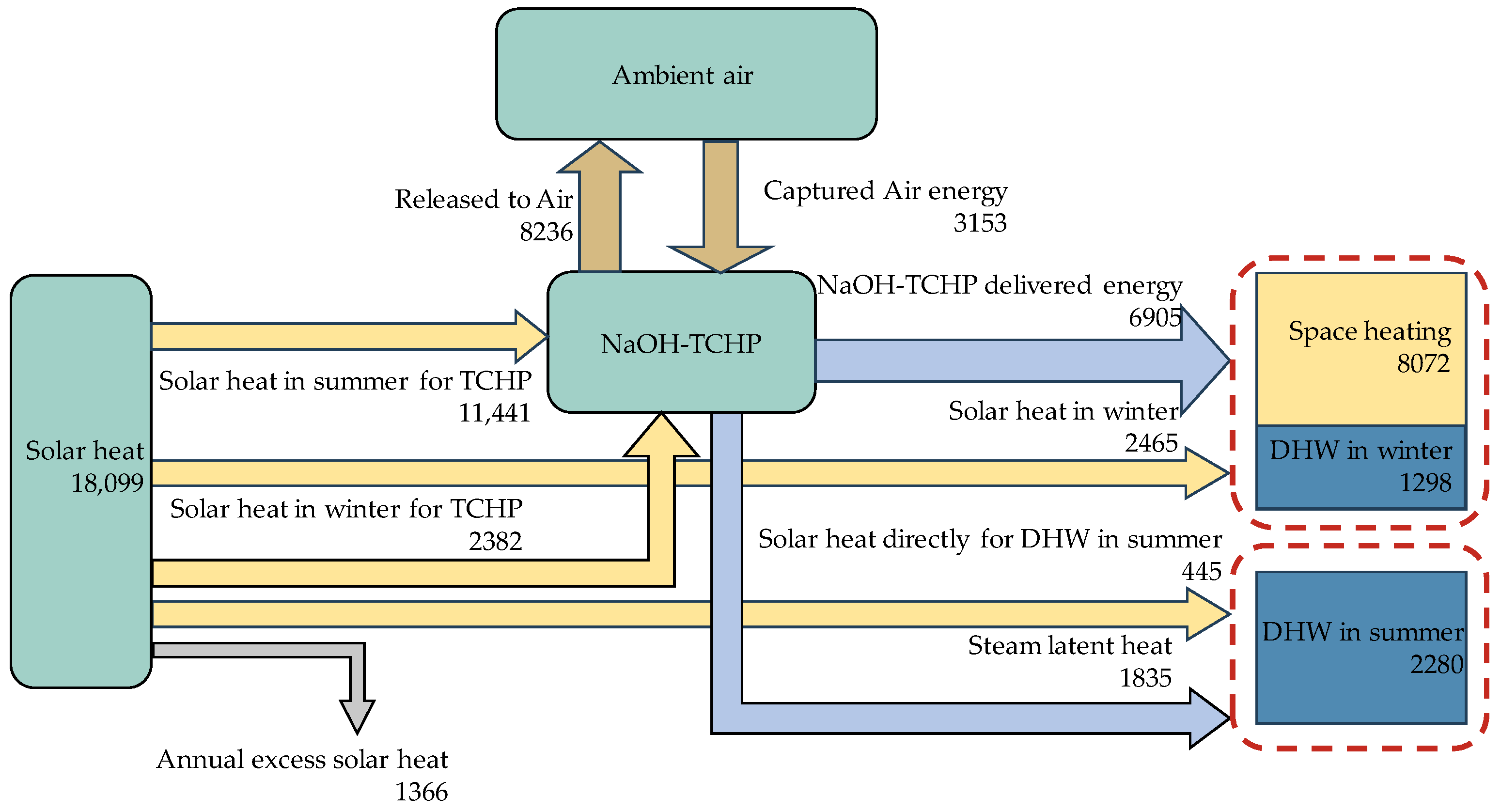
3.2. Thermal Performance
3.3. Space Performance
4. Limitations and Future Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Subscript | Meaning | Terminology | Meaning |
| a | Ambient air | A | Collector area |
| c | Concentrated solution | ESD | Energy storage density |
| ch | Thermochemical energy | h | Specific enthalpy, kJ/kg |
| charging | Charging | m | Mass flow |
| d | Dilute solution | Q | Heat flux, kW |
| DHW | Domestic hot water | q | Heat flux, kW/kg |
| dis | Desorption, discharge | T | Temperature |
| load | Heating load | Storage efficiency | |
| solar | Solar heat need | Collector efficiency | |
| sp | Space heating | ||
| stc | Collected solar heat | ||
| vp | Vapor | ||
| w | Water | ||
| 1, …, 5 | Period no. |
References
- IEA. Final Energy Consumption in the Buildings Sector. 2021. Available online: https://www.iea.org/data-and-statistics/charts/final-energy-consumption-in-the-buildings-sector-2021 (accessed on 12 January 2024).
- Mehari, A.; Xu, Z.Y.; Wang, R.Z. Thermodynamic evaluation of three-phase absorption thermal storage in humid air with energy storage density over 600 kWh/m3. Energy Convers. Manag. 2022, 258, 115476. [Google Scholar] [CrossRef]
- Li, Q.; Liu, J.; Wang, S.; Guo, Y.; Han, X.; Li, Q.; Cheng, Y.; Dong, Z.; Li, X.; Zhang, X. Numerical insights into factors affecting collapse behavior of horizontal wellbore in clayey silt hydrate-bearing sediments and the accompanying control strategy. Ocean Eng. 2024, 297, 117029. [Google Scholar] [CrossRef]
- Li, Q.; Wang, F.; Wang, Y.; Bai, B.; Zhang, J.; Lili, C.; Sun, Q.; Wang, Y.; Forson, K. Adsorption behavior and mechanism analysis of siloxane thickener for CO2 fracturing fluid on shallow shale soil. J. Mol. Liq. 2023, 376, 121394. [Google Scholar] [CrossRef]
- Bundschuh, J.; Kaczmarczyk, M.; Ghaffour, N.; Tomaszewska, B. State-of-the-art of renewable energy sources used in water desalination: Present and future prospects. Desalination 2021, 508, 115035. [Google Scholar] [CrossRef]
- Perez-Mora, N.; Bava, F.; Andersen, M.; Bales, C.; Lennermo, G.; Nielsen, C.; Furbo, S.; Martínez-Moll, V. Solar district heating and cooling: A review. Int. J. Energy Res. 2018, 42, 1419–1441. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; He, B.J.; Xu, W.; Jin, G.; Zhang, X. Application and suitability analysis of the key technologies in nearly zero energy buildings in China. Renew. Sustain. Energy Rev. 2019, 101, 329–345. [Google Scholar] [CrossRef]
- IEA. Technology and Innovation Pathways for Zero-Carbon-Ready Buildings by 2030. Paris. 2022. Available online: https://www.iea.org/reports/technology-and-innovation-pathways-for-zero-carbon-ready-buildings-by-2030 (accessed on 12 January 2024).
- Ucar, A.; Inalli, M. Thermal and economic comparisons of solar heating systems with seasonal storage used in building heating. Renew. Energy 2008, 33, 2532–2539. [Google Scholar] [CrossRef]
- Hongois, S.; Kuznik, F.; Stevens, P.; Roux, J.J. Development and characterisation of a new MgSO4-zeolite composite for long-term thermal energy storage. Sol. Energy Mater. Sol. Cells 2011, 95, 1831–1837. [Google Scholar] [CrossRef]
- Palomba, V.; Frazzica, A. Application of numerical methods for the design of thermocline thermal energy storage: Literature review and critical analysis. J. Energy Storage 2022, 46, 103875. [Google Scholar] [CrossRef]
- Quinnell, J.A.; Davidson, J.H.; Burch, J. Liquid calcium chloride solar storage: Concept and analysis. In Proceedings of the ASME 2010 4th International Conference on Energy Sustainability, Phoenix, AZ, USA, 17–22 May 2010; Volume 2, pp. 715–724. [Google Scholar] [CrossRef]
- Sunku Prasad, J.; Muthukumar, P.; Desai, F.; Basu, D.N.; Rahman, M.M. A critical review of high-temperature reversible thermochemical energy storage systems. Appl. Energy 2019, 254, 113733. [Google Scholar] [CrossRef]
- Guanghui, L.; Hui, C.; Hao, P.; Chun, C.; Yaxuan, X.; Zhu, J.; Lin, C.; Yanqi, Z.; Gan, Z.; Geng, Q.; et al. The new research progress of thermal energy storage materials. Energy Storage Sci. Technol. 2017, 6, 1058. [Google Scholar] [CrossRef]
- Pardo, P.; Anxionnaz-Minvielle, Z.; Rougé, S.; Cognet, P.; Cabassud, M. Ca(OH)2/CaO reversible reaction in a fluidized bed reactor for thermochemical heat storage. Sol. Energy 2014, 107, 605–616. [Google Scholar] [CrossRef]
- Hao, M.; Liu, H.; Wang, W. Research progress of hydrated salt thermochemical heat storage materials. Energy Storage Sci. Technol. 2020, 9, 791–796. [Google Scholar]
- Ding, Y.; Riffat, S.B. Thermochemical energy storage technologies for building applications: A state-of-the-art review. Int. J. Low-Carbon Technol. 2013, 8, 106–116. [Google Scholar] [CrossRef]
- Lahmidi, H.; Mauran, S.; Goetz, V. Definition, test and simulation of a thermochemical storage process adapted to solar thermal systems. Sol. Energy 2006, 80, 883–893. [Google Scholar] [CrossRef]
- Stitou, D.; Mazet, N.; Mauran, S. Experimental investigation of a solid/gas thermochemical storage process for solar air-conditioning. Energy 2012, 41, 261–270. [Google Scholar] [CrossRef]
- Zondag, H.A. Sorption Heat Storage. In Solar Energy Storage; Elsevier Inc.: Amsterdam, The Netherlands, 2015; pp. 135–154. [Google Scholar] [CrossRef]
- Yu, N.; Wang, R.Z.; Wang, L.W. Sorption thermal storage for solar energy. Prog. Energy Combust. Sci. 2013, 39, 489–514. [Google Scholar] [CrossRef]
- N’Tsoukpoe, K.E.; Le Pierrès, N.; Luo, L. Experimentation of a LiBr-H2O absorption process for long-term solar thermal storage: Prototype design and first results. Energy 2013, 53, 179–198. [Google Scholar] [CrossRef]
- Li, T.X.; Wu, S.; Yan, T.; Wang, R.Z.; Zhu, J. Experimental investigation on a dual-mode thermochemical sorption energy storage system. Energy 2017, 140, 383–394. [Google Scholar] [CrossRef]
- Palomba, V.; Sapienza, A.; Aristov, Y. Dynamics and useful heat of the discharge stage of adsorptive cycles for long term thermal storage. Appl. Energy 2019, 248, 299–309. [Google Scholar] [CrossRef]
- Xu, S.Z.; Wang, R.Z.; Wang, L.W.; Zhu, J. Performance characterizations and thermodynamic analysis of magnesium sulfate-impregnated zeolite 13X and activated alumina composite sorbents for thermal energy storage. Energy 2019, 167, 889–901. [Google Scholar] [CrossRef]
- Xu, J.X.; Li, T.X.; Chao, J.W.; Yan, T.S.; Wang, R.Z. High energy-density multi-form thermochemical energy storage based on multi-step sorption processes. Energy 2019, 185, 1131–1142. [Google Scholar] [CrossRef]
- Scapino, L.; Zondag, H.A.; Van Bael, J.; Diriken, J.; Rindt, C.C.M. Sorption heat storage for long-term low-temperature applications: A review on the advancements at material and prototype scale. Appl. Energy 2017, 190, 920–948. [Google Scholar] [CrossRef]
- Mehari, A.; Xu, Z.Y.; Wang, R.Z. Thermal energy storage using absorption cycle and system: A comprehensive review. Energy Convers. Manag. 2020, 206, 112482. [Google Scholar] [CrossRef]
- Kant, K.; Pitchumani, R. Advances and opportunities in thermochemical heat storage systems for buildings applications. Appl. Energy 2022, 321, 119299. [Google Scholar] [CrossRef]
- Ji, L.; Shukla, S.K.; Zuo, Z.; Lu, X.; Ji, X.; Wang, C. An overview of the progress of new working pairs in absorption heat pumps. Energy Rep. 2023, 9, 703–729. [Google Scholar] [CrossRef]
- Frazzica, A.; Freni, A. Adsorbent working pairs for solar thermal energy storage in buildings. Renew. Energy 2017, 110, 87–94. [Google Scholar] [CrossRef]
- Donkers, P.A.J.; Sögütoglu, L.C.; Huinink, H.P.; Fischer, H.R.; Adan, O.C.G. A review of salt hydrates for seasonal heat storage in domestic applications. Appl. Energy 2017, 199, 45–68. [Google Scholar] [CrossRef]
- Li, Z.; Xu, M.; Huai, X.; Huang, C.; Wang, K. Simulation and analysis of thermochemical seasonal solar energy storage for district heating applications in China. Int. J. Energy Res. 2021, 45, 7093–7107. [Google Scholar] [CrossRef]
- Gao, P.; Wang, L. Investigation on the air-source chemisorption heat pump for the severely cold regions. Appl. Therm. Eng. 2020, 179, 115694. [Google Scholar] [CrossRef]
- Gao, J.T.T.; Xu, Z.Y.Y.; Wang, R.Z.Z. Experimental study on a double-stage absorption solar thermal storage system with enhanced energy storage density. Appl. Energy 2020, 262, 114476. [Google Scholar] [CrossRef]
- Tzinnis, E.; Baldini, L. Combining sorption storage and electric heat pumps to foster integration of solar in buildings. Appl. Energy 2021, 301, 117455. [Google Scholar] [CrossRef]
- Weber, R.; Dorer, V. Long-term heat storage with NaOH. Vacuum 2008, 82, 708–716. [Google Scholar] [CrossRef]
- Fumey, B.; Baldini, L.; Borgschulte, A. Water Transport in Aqueous Sodium Hydroxide Films for Liquid Sorption Heat Storage. Energy Technol. 2020, 8, 2000187. [Google Scholar] [CrossRef]
- Fumey, B.; Weber, R.; Baldini, L. Liquid sorption heat storage—A proof of concept based on lab measurements with a novel spiral fined heat and mass exchanger design. Appl. Energy 2017, 200, 215–225. [Google Scholar] [CrossRef]
- Fumey, B.; Weber, R.; Gantenbein, P.; Daguenet-Frick, X.; Stoller, S.; Fricker, R.; Dorer, V. Operation results of a closed sorption heat storage prototype. Energy Procedia 2015, 73, 324–330. [Google Scholar] [CrossRef]
- Fumey, B.; Baldini, L. Static temperature guideline for comparative testing of sorption heat storage systems for building application. Energies 2021, 14, 3754. [Google Scholar] [CrossRef]
- Liu, R.; He, G.; Su, Y.; Yang, Y.; Ding, D. Solar energy for low carbon buildings: Choice of systems for minimal installation area, cost, and environmental impact. City Built Environ. 2023, 1, 16. [Google Scholar] [CrossRef]
- Zhou, L. Experimental Study on Performance of Solar Collector in Solar Membrane Distillation System. Master’s Thesis, Inner Mongolia University of Technology, Hohhot, China, 2009. [Google Scholar]
- Wagner, W.; Cooper, J.R.; Dittmann, A. The IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Zaytsev, I.D.; Aseyev, G.G. Properties of aqueous solutions of electrolytes. Choice Rev. Online 1993, 30, 30–4415. [Google Scholar] [CrossRef][Green Version]
- Chen, H. A correlation of sodium hydroxide enthalpy. Chem. Eng. 1991, 19, 79. [Google Scholar]
- Zhang, X.; Li, M.; Shi, W.; Wang, B.; Li, X. Experimental investigation on charging and discharging performance of absorption thermal energy storage system. Energy Convers. Manag. 2014, 85, 425–434. [Google Scholar] [CrossRef]
- Yu, N.; Wang, R.Z.; Lu, Z.S.; Wang, L.W.; Ishugah, T.F. Evaluation of a three-phase sorption cycle for thermal energy storage. Energy 2014, 67, 468–478. [Google Scholar] [CrossRef]
- Yu, N.; Wang, R.Z.; Lu, Z.S.; Wang, L.W. Study on consolidated composite sorbents impregnated with LiCl for thermal energy storage. Int. J. Heat Mass Transf. 2015, 84, 660–670. [Google Scholar] [CrossRef]
- Köll, R.; van Helden, W.; Engel, G.; Wagner, W.; Dang, B.; Jänchen, J.; Kerskes, H.; Badenhop, T.; Herzog, T. An experimental investigation of a realistic-scale seasonal solar adsorption storage system for buildings. Sol. Energy 2017, 155, 388–397. [Google Scholar] [CrossRef]

| Period No. | Dates | Ambient Temp, , °C | Collector Production Rate, qstc (kWh/m2) | Heating Load , kWh |
|---|---|---|---|---|
| 1 | 15 November–27 November | 11.4 | 14.3 | = 218.20 |
| 2 | 28 November–15 March | 6.7 | 137.1 | = 9151.95 |
| 3 | 15 March–31 July | 22.7 | 225.3 | = 1368.77 |
| 4 | 1 August–30 September | 27.0 | 101.0 | = 466.20 |
| 5 | 1 October–11 November | 18.0 | 44.8 | = 445.06 |
| Working Pair | Reaction Condition | Energy Storage Density, kWh/m3 | Sources |
|---|---|---|---|
| NaOH/H2O | 30 wt% to 70 wt% | 363 | 1. This study |
| NaOH/H2O | 45 wt% to 70 wt% | 257 | 2. [37] |
| NaOH/H2O | 25 wt% to 50 wt% | 435 | 3. [39] |
| CaCl2/H2O | 91~93 (*) | 4. [12] | |
| LiBr/H2O | 226~252 | 5. [22] | |
| LiBr/H2O | 110 (**) | 6. [47] | |
| LiCl/H2O | Crystallization is allowed | 668 | 7. [48,49] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Yang, Y.; He, G.; Liu, R.; Ding, D. Two-Stage Solar–NaOH Thermochemical Heat Pump Heating System for Building Heating: Operations Strategies and Theoretical Performance. Energies 2024, 17, 1976. https://doi.org/10.3390/en17081976
Su Y, Yang Y, He G, Liu R, Ding D. Two-Stage Solar–NaOH Thermochemical Heat Pump Heating System for Building Heating: Operations Strategies and Theoretical Performance. Energies. 2024; 17(8):1976. https://doi.org/10.3390/en17081976
Chicago/Turabian StyleSu, Yujie, Yi Yang, Guoqing He, Renhua Liu, and De Ding. 2024. "Two-Stage Solar–NaOH Thermochemical Heat Pump Heating System for Building Heating: Operations Strategies and Theoretical Performance" Energies 17, no. 8: 1976. https://doi.org/10.3390/en17081976
APA StyleSu, Y., Yang, Y., He, G., Liu, R., & Ding, D. (2024). Two-Stage Solar–NaOH Thermochemical Heat Pump Heating System for Building Heating: Operations Strategies and Theoretical Performance. Energies, 17(8), 1976. https://doi.org/10.3390/en17081976







