Distribution Network Reconfiguration Based on an Improved Arithmetic Optimization Algorithm
Abstract
1. Introduction
2. Mathematical Modeling of Distribution Network Reconfiguration
2.1. Objective Function
2.2. Constraints
2.2.1. Network Topology Constraints
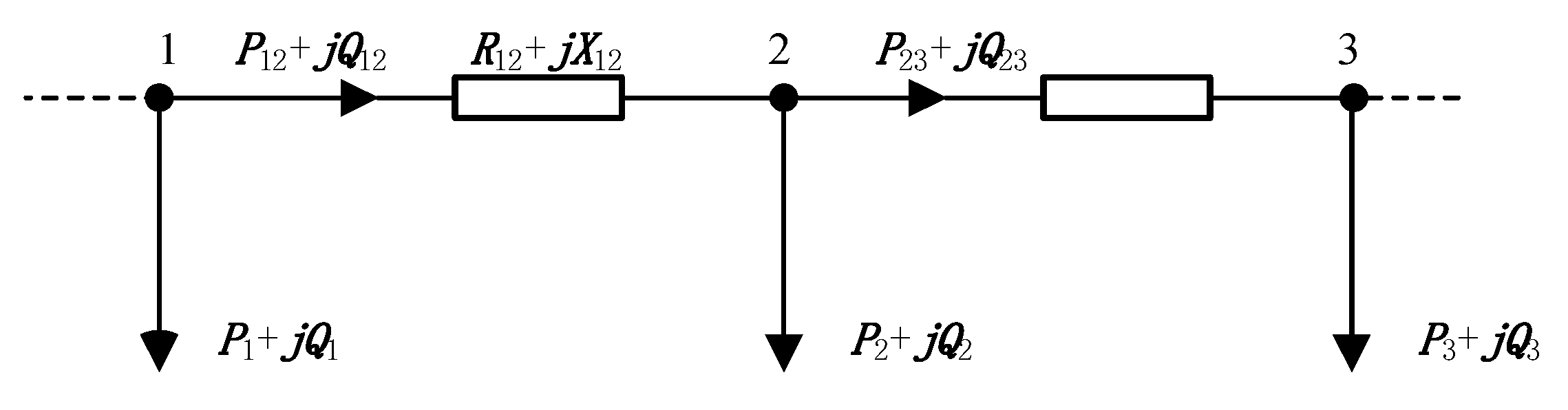
2.2.2. Trend Equation Constraints
2.2.3. Nodal Voltage Constraints
2.2.4. Branch Circuit Capacity Constraints
3. Arithmetic Optimization Algorithms
3.1. Initialization Phase
3.2. Exploration Phase
3.3. Exploitation Phase
4. Improved Arithmetic Optimization Algorithm
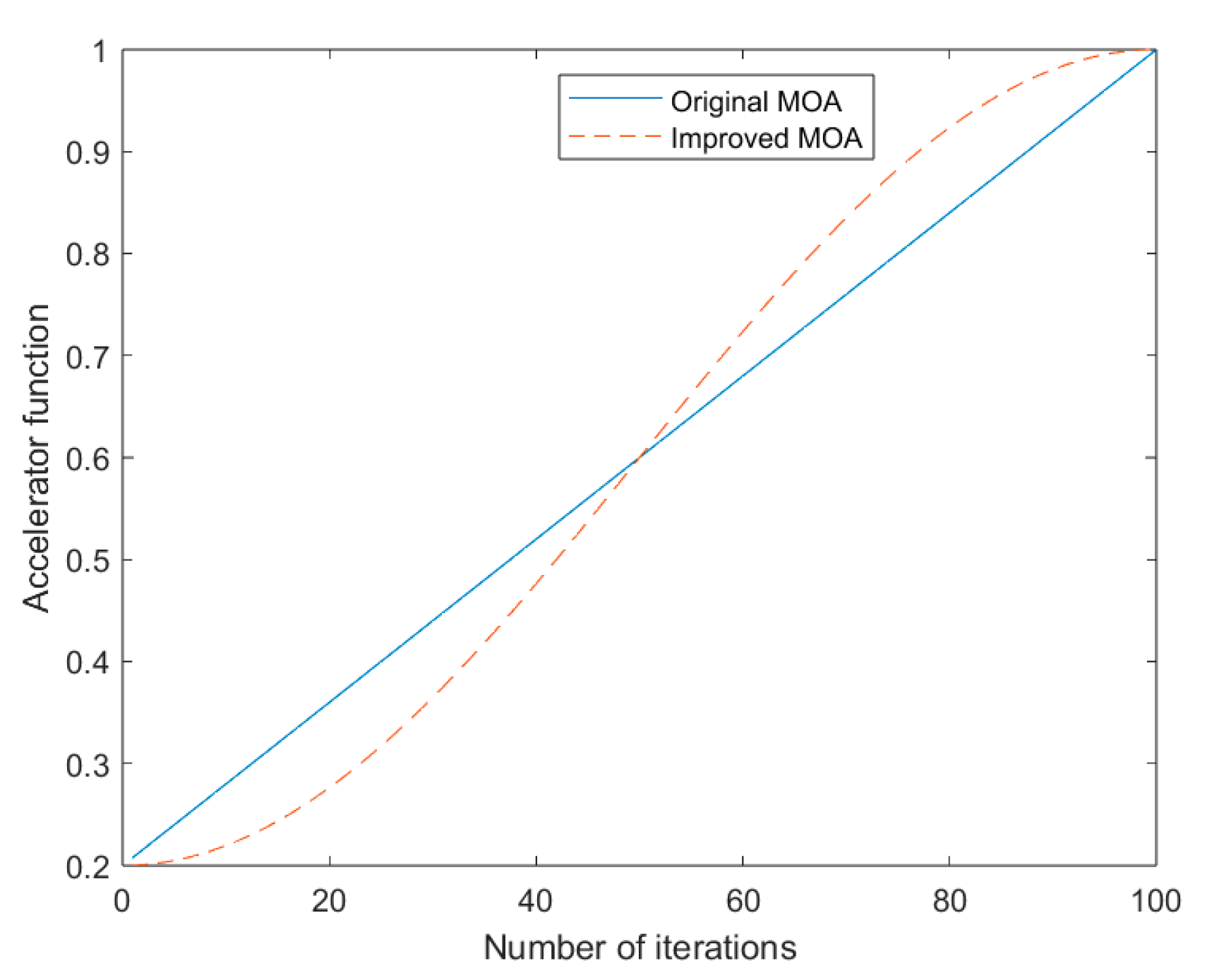
4.1. Reconstruction of MOA by Introducing Cosine Control Factor
4.2. Reverse Difference Evolution Strategy
4.2.1. Variation
4.2.2. Cross
4.2.3. Selection
4.3. Mechanisms of Variation in the Weibull Distribution
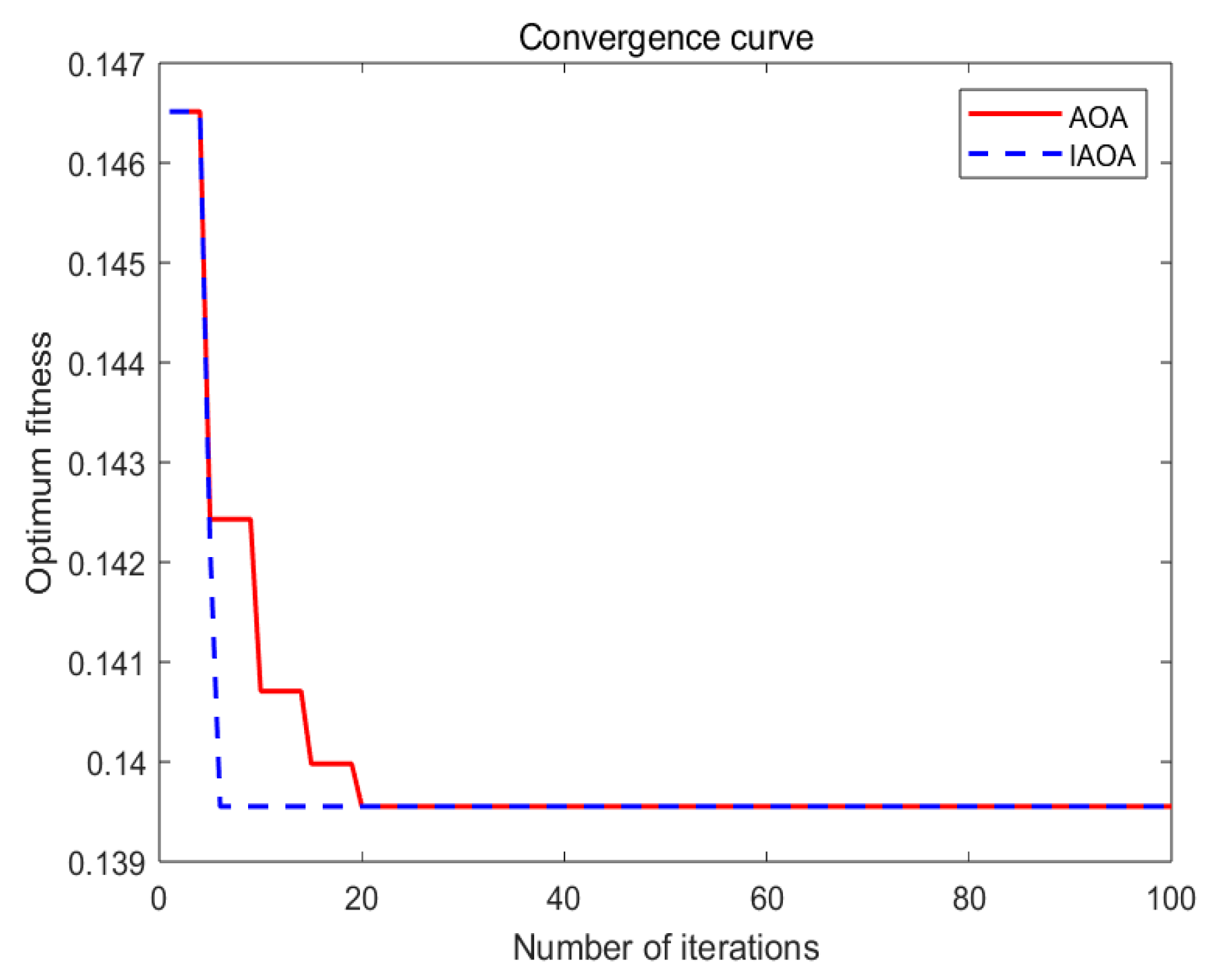
4.4. Algorithm Performance Testing
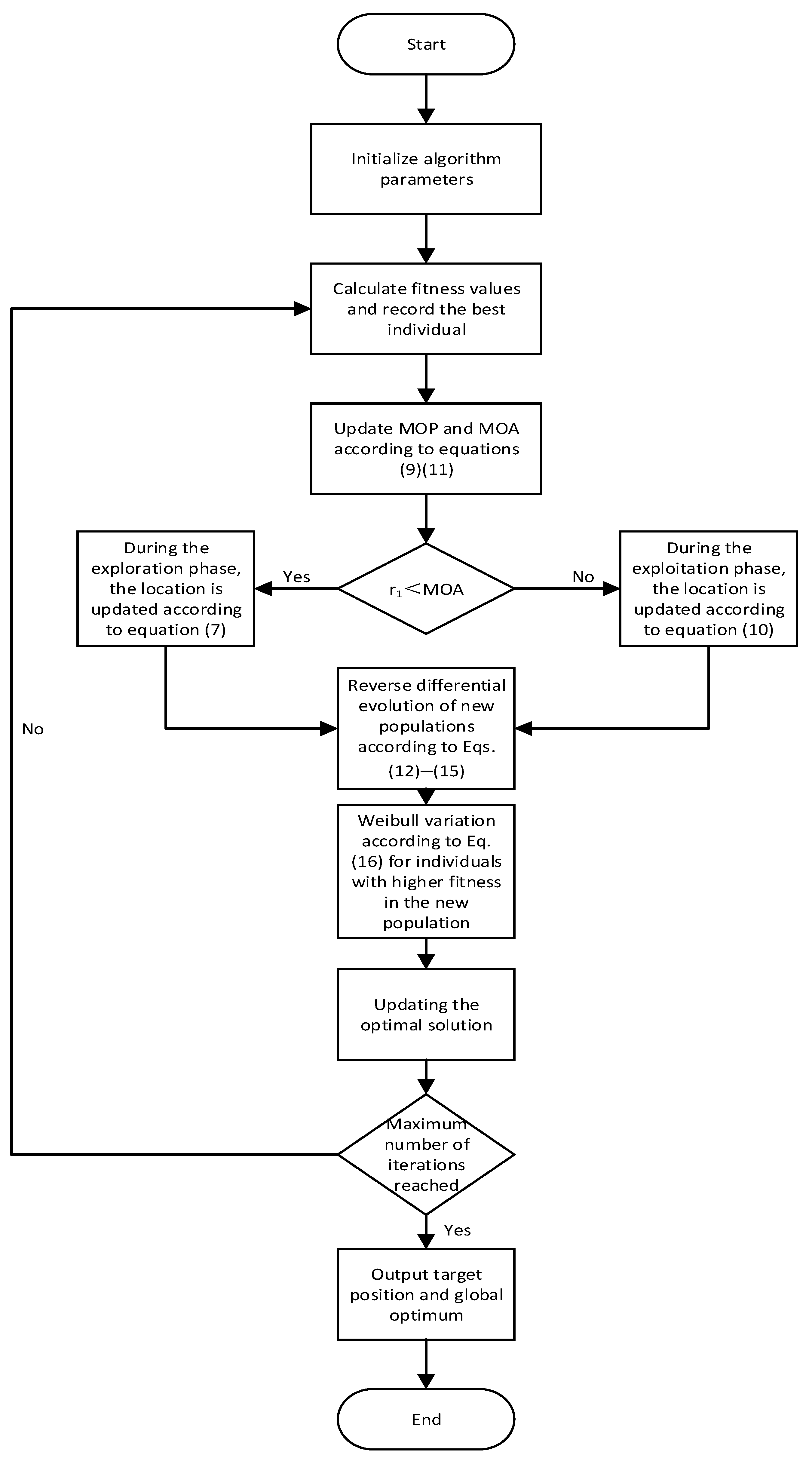
4.5. Flow of the Improved Algorithm
5. Distribution Network Reconfiguration Study
5.1. Tidal Current Calculation Method
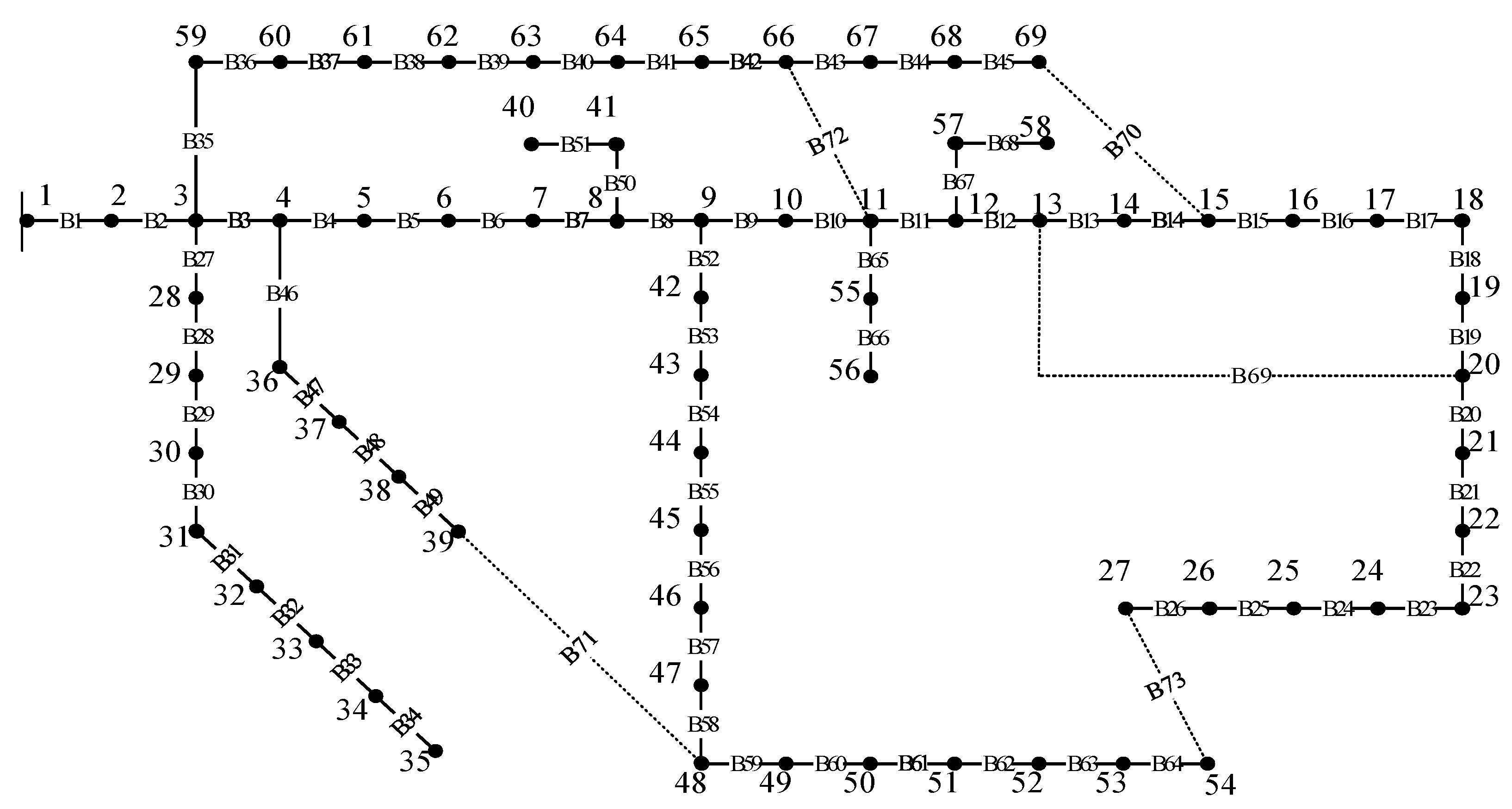
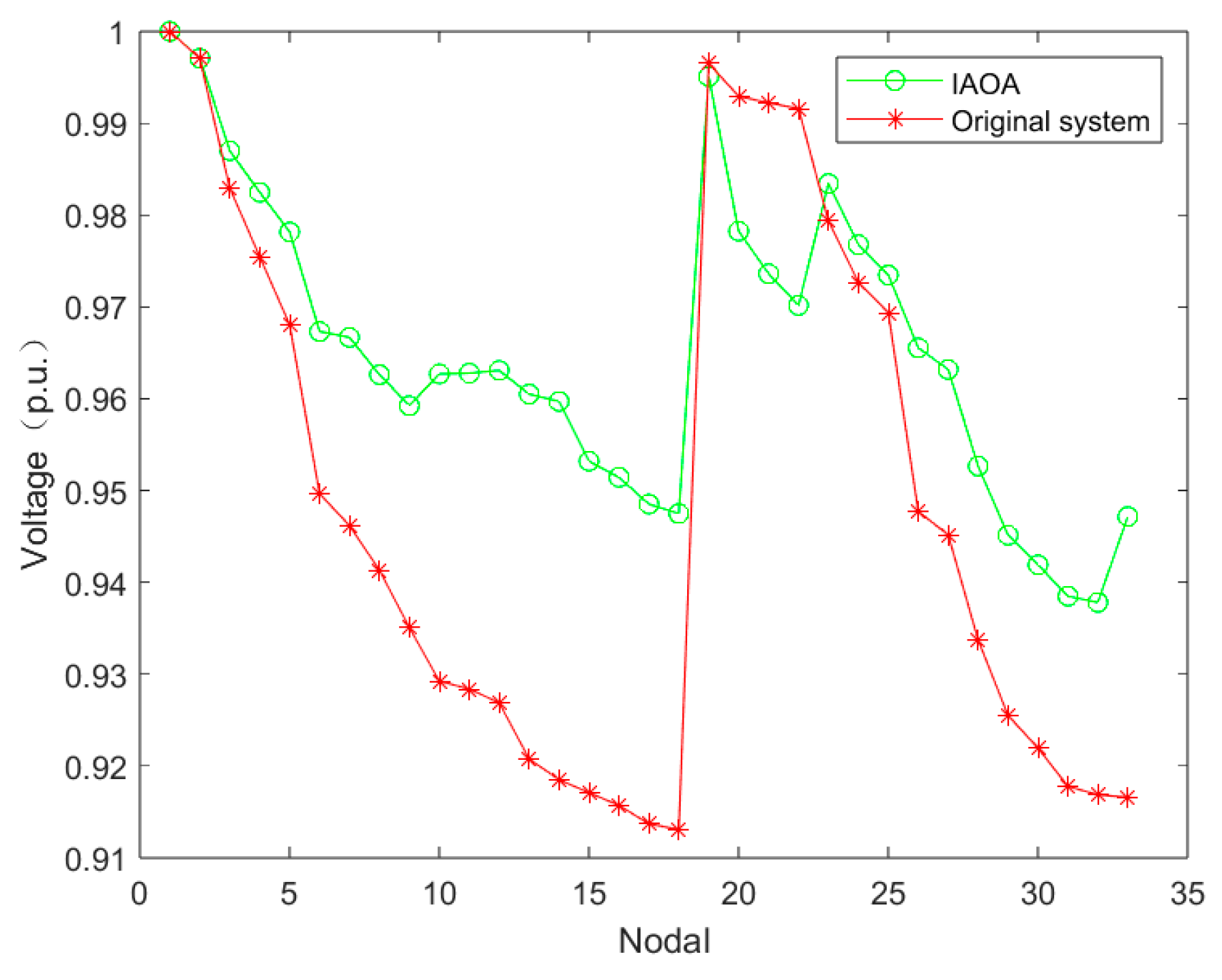
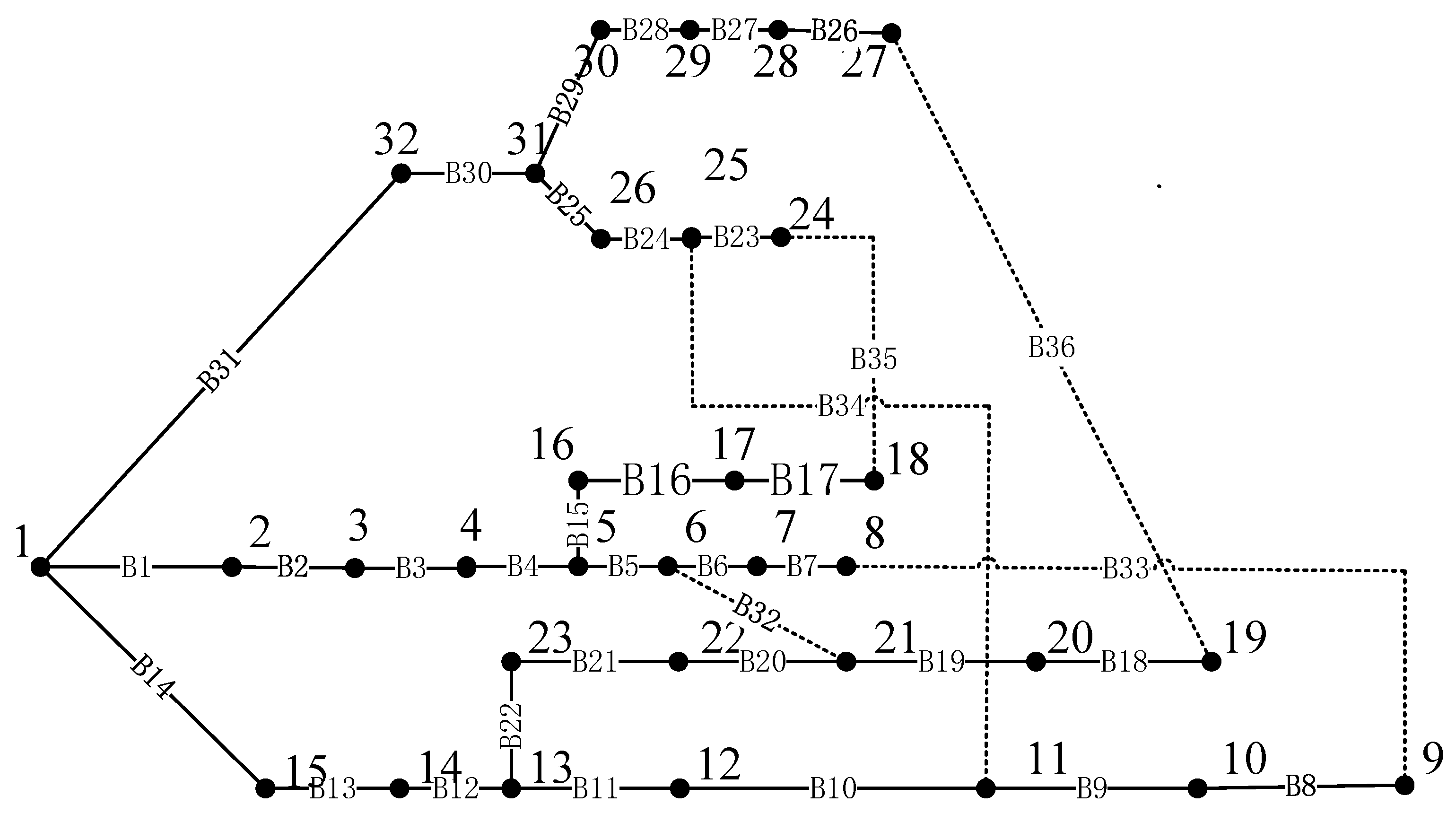
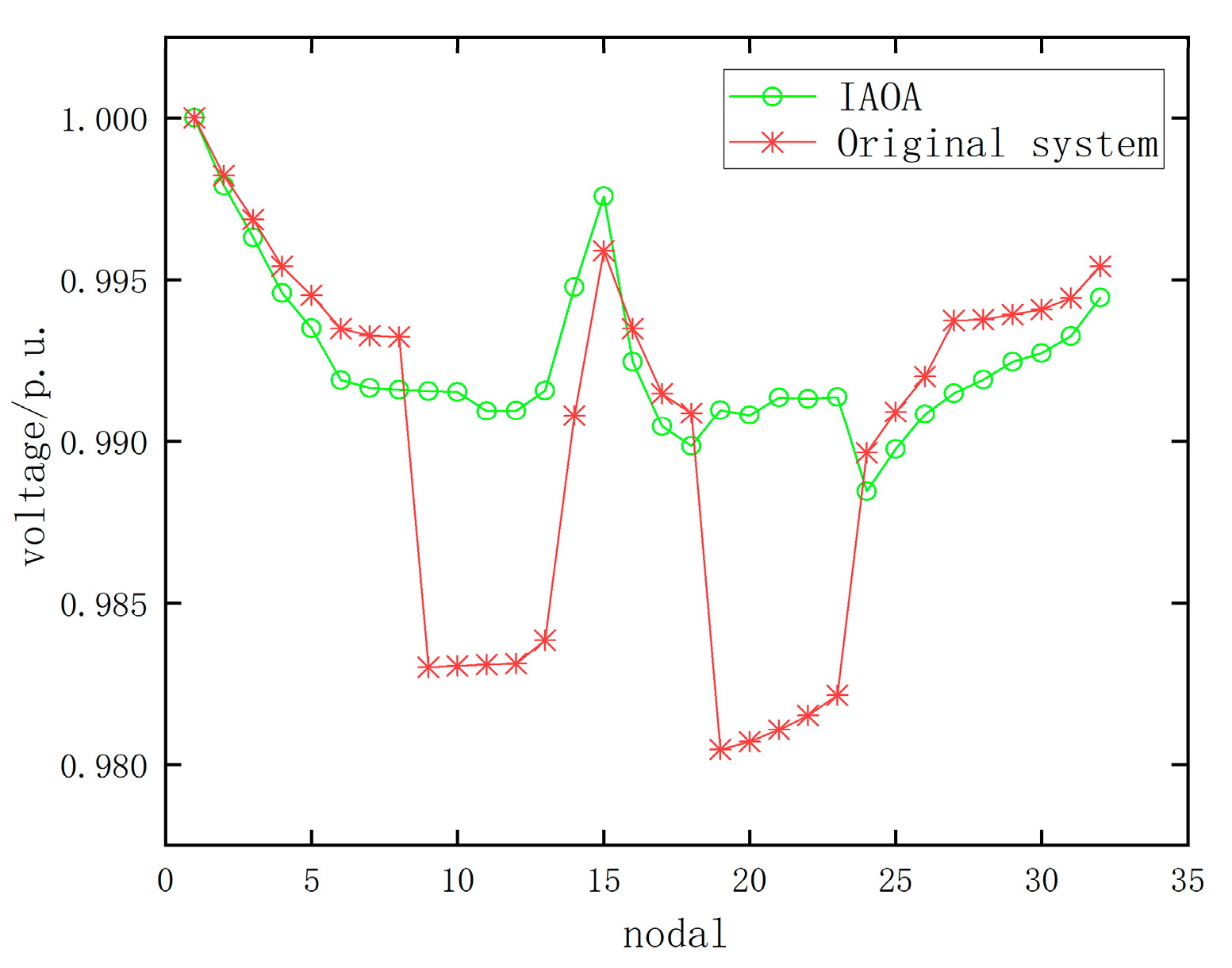
5.2. Example Analysis
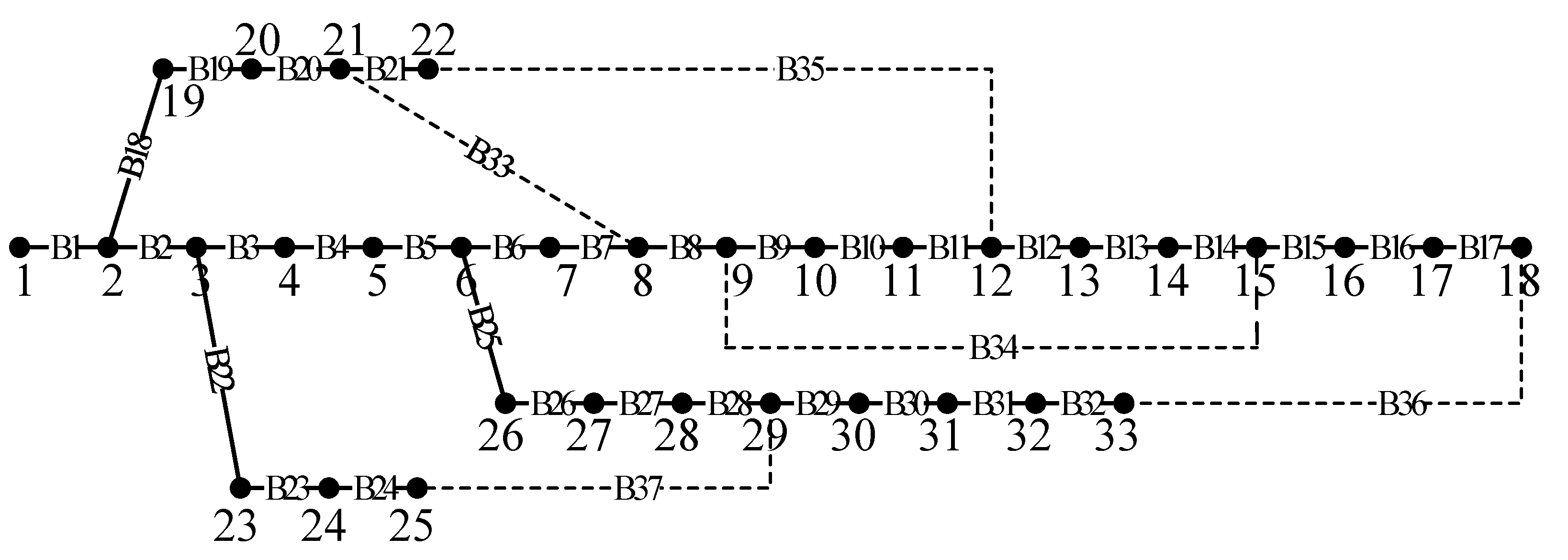
5.2.1. Simulation Analysis of Example 1
5.2.2. Simulation Analysis of Example 2
5.2.3. Simulation Analysis of Example 3
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, C.-Y.; Xue, Y.-K.; Tseng, Y.-C. A review of distribution network reconfiguration research. Electr. Switchg. 2021, 59, 3–8. [Google Scholar]
- Alqahtani, M.; Marimuthu, P.; Moorthy, V.; Pangedaiah, B.; Reddy, C.R.; Kiran Kumar, M.; Khalid, M. Investigation and Minimization of Power Loss in Radial Distribution Network Using Gray Wolf Optimization. Energies 2023, 16, 4571. [Google Scholar] [CrossRef]
- Liao, F.; Chen, J.; Qu, W.; Wang, Y.; Hu, Y.; Wu, N. Active distribution network reconfiguration based on improved social spider algorithm. J. Power Syst. Autom. 2023, 35, 125–133. [Google Scholar]
- Wu, J.; Yu, Y. Multi-objective distribution network reconfiguration optimisation based on improved sum search algorithm. Power Syst. Prot. Control 2021, 49, 78–86. [Google Scholar]
- Merzoug, Y.; Abdelkrim, B.; Larbi, B. Distribution network recon-figuration for loss reduction using PSO method. Int. J. Electr. Comput. Eng. 2020, 10, 5009. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J.; Wang, L.; An, Y.; Zhang, X. Distribution Network Reconfiguration Using Chaotic Particle Swarm Chicken Swarm Fusion Optimization Algorithm. Energies 2023, 16, 7185. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, T.; Fan, L.; Li, X. Reconfiguration of distribution networks containing distributed power sources based on immunogenetic algorithm. J. Power Syst. Autom. 2014, 26, 15–19. [Google Scholar]
- Jin, Y.; Zhang, L.; Wu, P.; Niu, Q.; Shen, Y. Application of improved genetic algorithm in reconfiguration of distribution network containing DG. Sens. Microsyst. 2020, 39, 153–156. [Google Scholar]
- Yang, M.; Liu, J. Distribution network reconfiguration based on genetic ant colony algorithm. Mod. Electron. Technol. 2020, 43, 128–132. [Google Scholar]
- Li, Z.; Zhang, Y.; Aqeel Ashraf, M. Optimization design of reconfiguration algorithm for high voltage power distribution network based on ant colony algorithm. Open Phys. 2018, 16, 1094–1106. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Zhang, W.; Li, S.; Qi, M.; Zhou, X.; Song, Y. Introduced a transitional phase and improvement of the gauss mutation arithmetic optimization algorithm. Small Microcomput. Syst. 2023, 1–12. Available online: http://kns.cnki.net/kcms/detail/21.1106.TP.20230413.1731.019.html (accessed on 3 February 2024).
- Zheng, T.; Liu, S.; Ye, X. Improved arithmetic optimization algorithm with adaptive t-distribution and dynamic boundary strategy. Comput. Appl. Res. 2022, 39, 1410–1414. [Google Scholar]
- Lan, Z.; He, Q. Multi-strategy fusion arithmetic optimization algorithm and its engineering optimization. Comput. Appl. Res. 2022, 39, 758–763. [Google Scholar]
- Abualigah, L.; Diabat, A.; Sumari, P.; Gandomi, A.H. A novel evolutionary arithmetic optimization algorithm for multilevel thresholding segmentation of COVID-19 CT images. Processes 2021, 9, 1155. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Wei, Y. Fault section location Method of Low Voltage Distribution Network based on Arithmetic Optimization Algorithm. Electron. Sci. Technol. 2023, 36, 25–31. [Google Scholar]
- Ding, B.; Kuang, Z.; Lu, L. Three-dimensional trajectory planning for UAVs based on Q-learning arithmetic optimization algorithm. Electro-Opt. Control 2024, 31, 61–69. [Google Scholar]
- Zheng, H.; Yu, J.; Yang, J.; Wei, S. Bat optimization algorithm based on cosine control factor and iterative local search. Comput. Sci. 2020, 47, 68–72. [Google Scholar]
- Zou, Y.; Wu, R.; Tian, X.; Li, H. Realizing the Improvement of the Reliability and Efficiency of Intelligent Electricity Inspection: IAOA-BP Algorithm for Anomaly Detection. Energies 2023, 16, 3021. [Google Scholar] [CrossRef]
- Kuang, X.; Yang, B.; Ma, H.; Tang, W.; Xiao, H.; Chen, L. Multiple strategy to improve dung beetle optimization algorithm. Comput. Eng. 2024, 1–20. Available online: http://kns.cnki.net/kcms/detail/31.1289.TP.20240301.1635.007.html (accessed on 28 March 2024).
- Huang, Y.; Qian, X.; Song, W. An improved differential evolutionary algorithm based on the dual-archive population size adaptive method. Comput. Appl. 2024, 1–14. Available online: http://kns.cnki.net/kcms/detail/51.1307.TP.20240305.0850.002.html (accessed on 7 April 2024).
- Wei, J.; Chen, Y.; Yu, Y.; Chen, Y. Optimal Randomness in Swarm-Based Search. Mathematics 2019, 7, 828. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Yang, Y.; Zhou, H. Multiple strategy fusion algorithm improved Marine predators and its engineering application. Comput. Integr. Manuf. Syst. 2023, 1–21. Available online: http://kns.cnki.net/kcms/detail/11.5946.TP.20230515.1111.008.html (accessed on 5 February 2024).
- Hashim, F.A.; Hussien, A.G. Snake optimizer: A novel meta-heuristic optimization algorithm. Knowl. Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Lee, J.O.; Kim, Y.S.; Jeon, J.H. Generic power flow algorithm for bipolar DC microgrids based on Newton–Raphson method. Int. J. Electr. Power Energy Syst. 2022, 142, 108357. [Google Scholar] [CrossRef]
- Wang, S.; Shao, Z. Complex affine Ybus Gaussian iterative interval tidal current algorithm considering DG operation uncertainty. Power Autom. Equip. 2017, 37, 38–44. [Google Scholar]
- Dong, Z.; Zhang, B.; Liu, K.; Ma, Y. New forward pushback generation trend calculation method for active distribution networks. J. Power Syst. Autom. 2019, 31, 101–107. [Google Scholar]


| Function Name | Dimensionality | Realm | Theoretical Optimum | |
|---|---|---|---|---|
| Sphere | 30 | [−100, 100] | 0 | |
| Schwefel’s problem 2.22 | 30 | [−10, 10] | 0 | |
| Schwefel’s problem 1.2 | 30 | [−100, 100] | 0 | |
| Schwefel’s generalized problem 2.21 | 30 | [−100, 100] | 0 | |
| Rosenbrock’s function | 30 | [−30, 30] | 0 | |
| Quartic | 30 | [−1.28, 1.28] | 0 | |
| Rastrigin’s generalized function | 30 | [−5.12, 5.12] | 0 | |
| Ackley’s function | 30 | [−32, 32] | 0 |
| Function | SO | PSO | AOA | IAOA | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| 4.39 × 10−44 | 2.18 × 10−33 | 19.24 | 2.87 | 1.30 × 10−46 | 2.18 × 10−33 | 7.75 × 10−92 | 7.75 × 10−92 | |
| 3.53 × 10−12 | 2.38 × 10−12 | 15.17 | 3.99 | 8.07 × 10−139 | 2.55 × 10−138 | 0 | 0 | |
| 2.15 × 10−20 | 6.01 × 10−20 | 6.51 × 102 | 2.98 × 102 | 0.012 | 0.015 | 1.59 × 10−139 | 5.04 × 10−139 | |
| 2.98 × 10−13 | 3.09 × 10−13 | 3.13 | 0.57 | 0.034 | 0.017 | 9.56 × 10−61 | 2.88 × 10−60 | |
| 23.74 | 11.04 | 3.81 × 103 | 1.21 × 103 | 28.70 | 0.19 | 28.90 | 0.041 | |
| 5.47 × 10−4 | 6.31 × 10−4 | 41.31 | 17.95 | 2.08 × 10−4 | 1.74 × 10−4 | 1.18 × 10−4 | 7.91 × 10−5 | |
| 22.85 | 18.81 | 2.47 × 102 | 29.59 | 0 | 0 | 0 | 0 | |
| 3.16 × 10−12 | 2.88 × 10−12 | 4.22 | 0.54 | 9.12 × 10−16 | 0 | 8.88 × 10−16 | 0 | |
| Title 1 | Before Refactoring | After Reconfiguration |
|---|---|---|
| Disconnected branch | B33, B34, B35, B36, B37 | B7, B14, B9, B32, B37 |
| System net loss/kW | 202.68 | 139.55 |
| Nodal voltage minimum/p.u. | 0.91309 | 0.93787 |
| Title 1 | Before Refactoring | After Reconfiguration |
|---|---|---|
| Disconnected branch | B69, B70, B71, B72, B73 | B69, B70, B14, B50, B46 |
| System net loss/kW | 226.48 | 100.97 |
| Nodal voltage minimum/p.u. | 0.90893 | 0.94252 |
| Before Refactoring | After Reconfiguration | |
|---|---|---|
| Disconnected branch | B32, B33, B34, B35, B36 | B9, B19, B20, B34, B35 |
| System net loss/kW | 91.37 | 78.88 |
| Nodal voltage minimum/p.u. | 0.98265 | 0.98903 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, H.; Zhu, X.; Cao, W. Distribution Network Reconfiguration Based on an Improved Arithmetic Optimization Algorithm. Energies 2024, 17, 1969. https://doi.org/10.3390/en17081969
Jia H, Zhu X, Cao W. Distribution Network Reconfiguration Based on an Improved Arithmetic Optimization Algorithm. Energies. 2024; 17(8):1969. https://doi.org/10.3390/en17081969
Chicago/Turabian StyleJia, Hui, Xueling Zhu, and Wensi Cao. 2024. "Distribution Network Reconfiguration Based on an Improved Arithmetic Optimization Algorithm" Energies 17, no. 8: 1969. https://doi.org/10.3390/en17081969
APA StyleJia, H., Zhu, X., & Cao, W. (2024). Distribution Network Reconfiguration Based on an Improved Arithmetic Optimization Algorithm. Energies, 17(8), 1969. https://doi.org/10.3390/en17081969






