Short-Term Load Forecasting Based on Optimized Random Forest and Optimal Feature Selection
Abstract
1. Introduction
1.1. Literature Review: Forecasting Models
1.2. Contributions
1.3. Paper Structure
2. Proposed Forecast Model
2.1. Input Data Selection
2.2. Forecasting Model: Random Forest (RF)
| Algorithm 1: Pseudocode of the Random Forest algorithm. |
| Input: Training data. . . . Procedure: Select a bootstrap sample randomly of the same size as the training data. is reached: Step 1: Select n features randomly from all features. Step 2: From these randomly selected n features, choose the best feature that splits the data to compose the current node. Step 3: Split the node into two other nodes. Output: . Calculate the forecast of point : |
3. Simulation Study
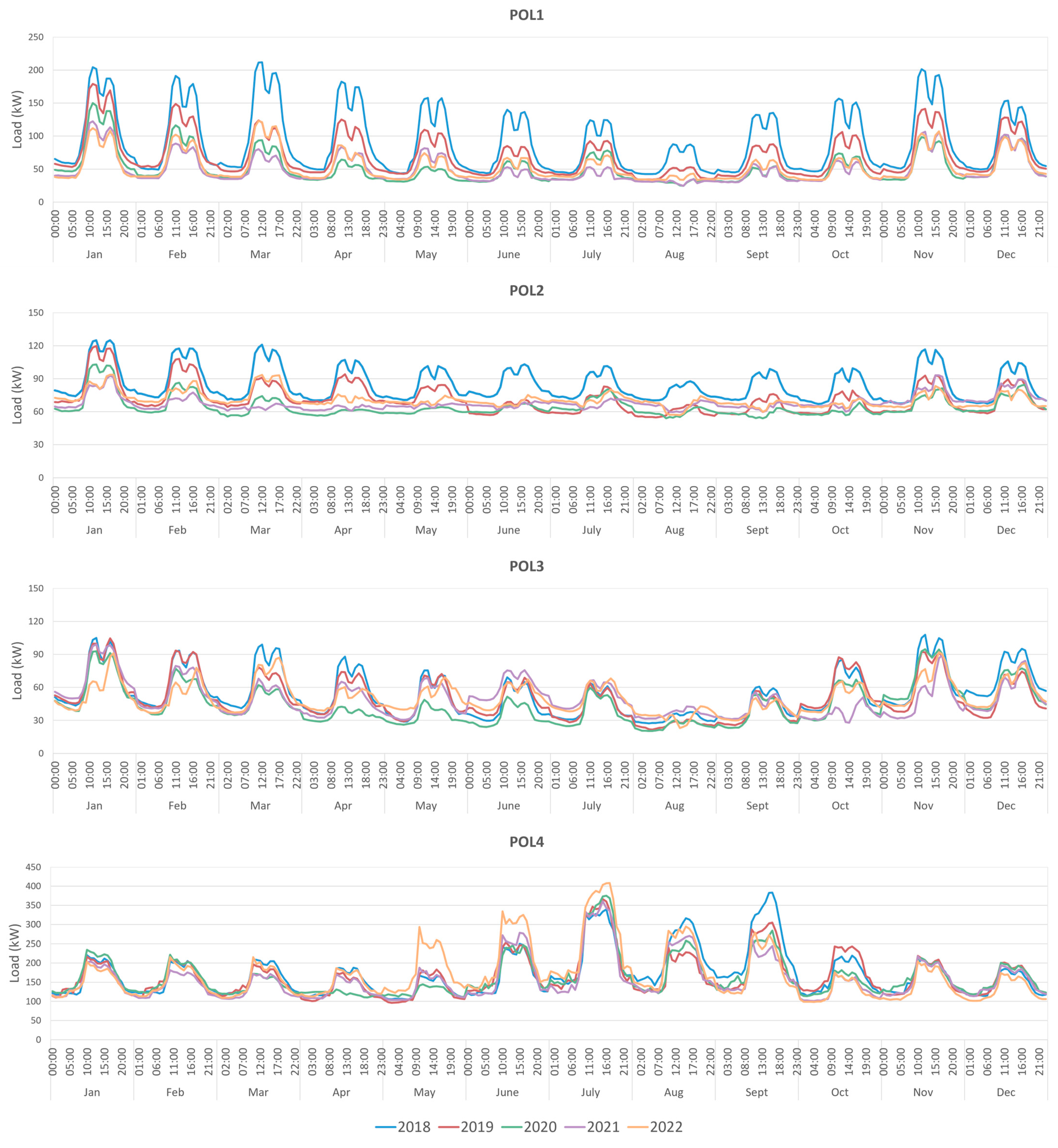
3.1. Statistical Analysis of Data
3.2. Results for All Configurations of Input Patterns and Training Modes
3.3. Results for Best Configuration: Similar Weekday
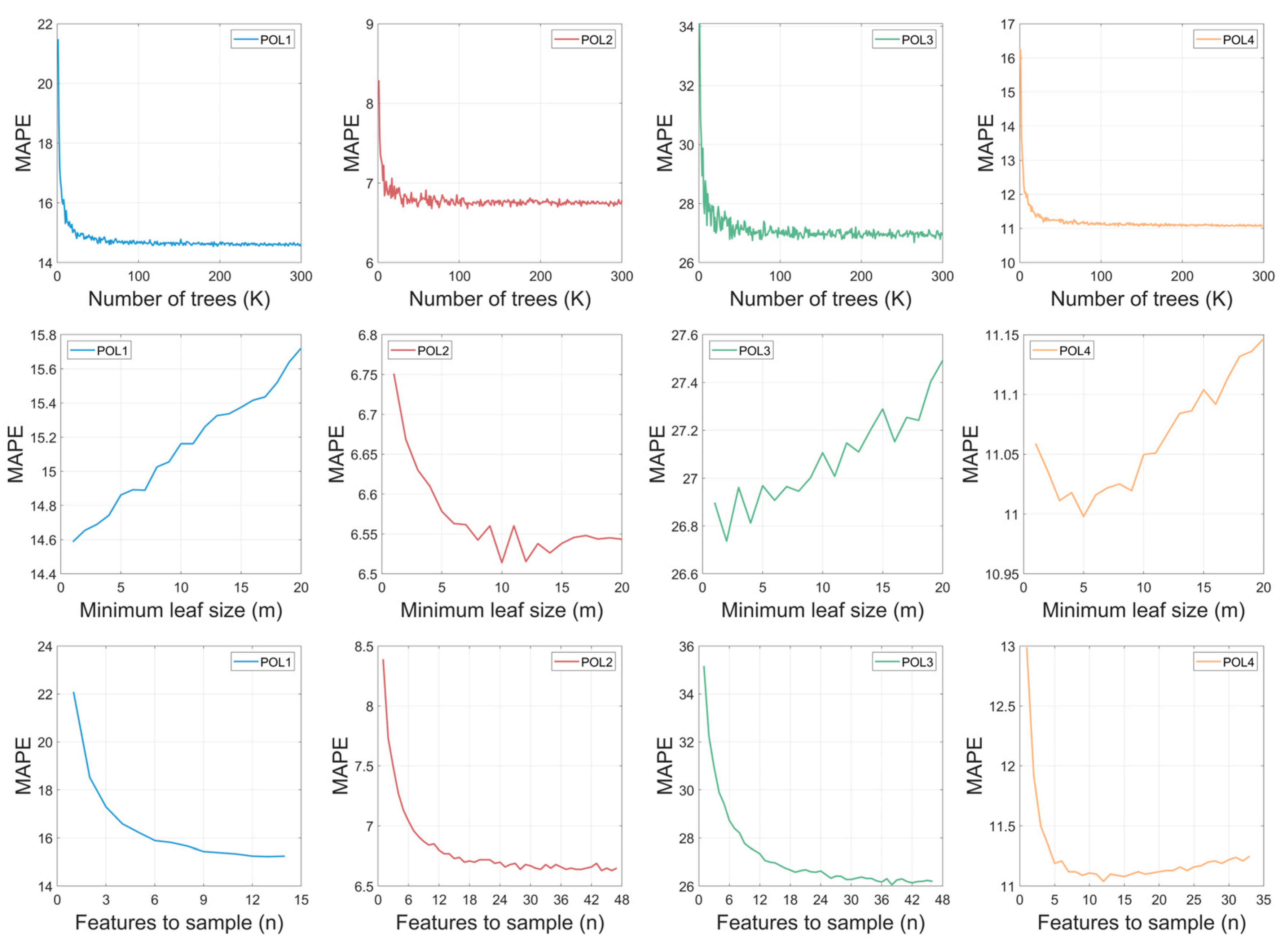
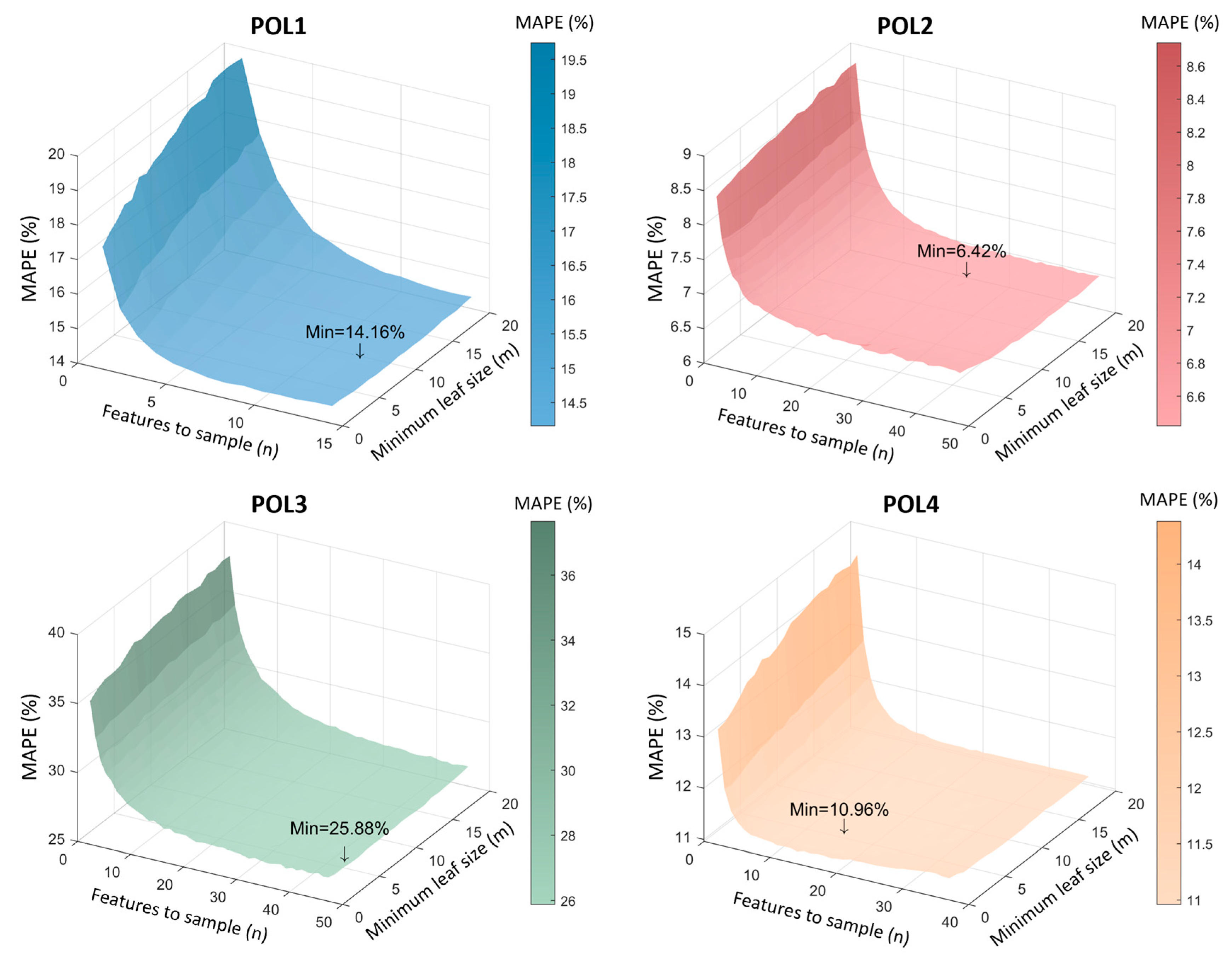
3.4. Tuning the Hyperparameters
- The number of trees (): This parameter defines the number of trees in the forest. It is an essential parameter that significantly influences the model’s performance. Increasing the number of trees offers several advantages, including reducing the variability of the model, leading to more consistent prediction errors and improving prediction accuracy. This increased robustness allows the model to better capture complex patterns in the data and generalize well to unseen instances, improving its overall forecasting capabilities. However, setting too low can result in underfitting, where the model fails to adequately capture essential patterns in the data, leading to sub-optimal prediction performance. On the other hand, setting too high can lead to longer training times without significant improvements in prediction accuracy, potentially wasting computational resources. It is therefore crucial to find the optimal value for , striking a balance between model complexity, computational efficiency and prediction performance.
- The minimum sample leaf size (): This parameter controls the minimum size of the leaves in the tree. It is a fundamental parameter in the construction of decision trees. Adjusting the minimum size of the leaves in the tree appropriately is essential in reducing uncertainty in decision-making. A significant advantage of setting this parameter is the ability to avoid forming excessively deep trees, which, although they may have small biases, also tend to have high variability. However, this setting can result in models with a larger bias and a loss of fine detail in the data. It is therefore essential to find a balance when adjusting this parameter, in order to mitigate uncertainty without compromising the model’s ability to capture the complexity of the data and avoid overfitting.
- The maximum number of features selected randomly for each split (): This parameter is crucial in random forest algorithms. It determines the maximum number of features to be considered when splitting a node during the construction of each tree in the forest. Adjusting this parameter has significant implications for the performance and robustness of the model. One of the main advantages of adjusting this parameter is the introduction of randomness in the process of building the trees. Limiting the number of features considered at each split reduces the correlation between the trees, making the model more robust and less prone to overfitting the training data. This is especially important to ensure that the model generalizes well to new data. Furthermore, adjusting this parameter allows for a customized adjustment of the model according to the specific characteristics of the dataset and the demands of the problem at hand. This provides flexibility in model tuning, allowing for a more precise adaptation to the problem’s needs. However, an improper choice of the value of n can lead to bias in the model. If n is too small, underfitting may occur, as the model may not be able to capture the complexity of the data. On the other hand, if n is too large, the model may become excessively complex, leading to overfitting. Therefore, it is essential to adjust this parameter carefully, seeking a balance between reducing overfitting and maintaining the model’s bias. Experimentation and careful adjustment are necessary to find the ideal value of n that optimizes the model’s performance and ensures good generalization to new data.
3.4.1. Tuning the Hyperparameters: Individually
3.4.2. Tuning the Hyperparameters: Simultaneously
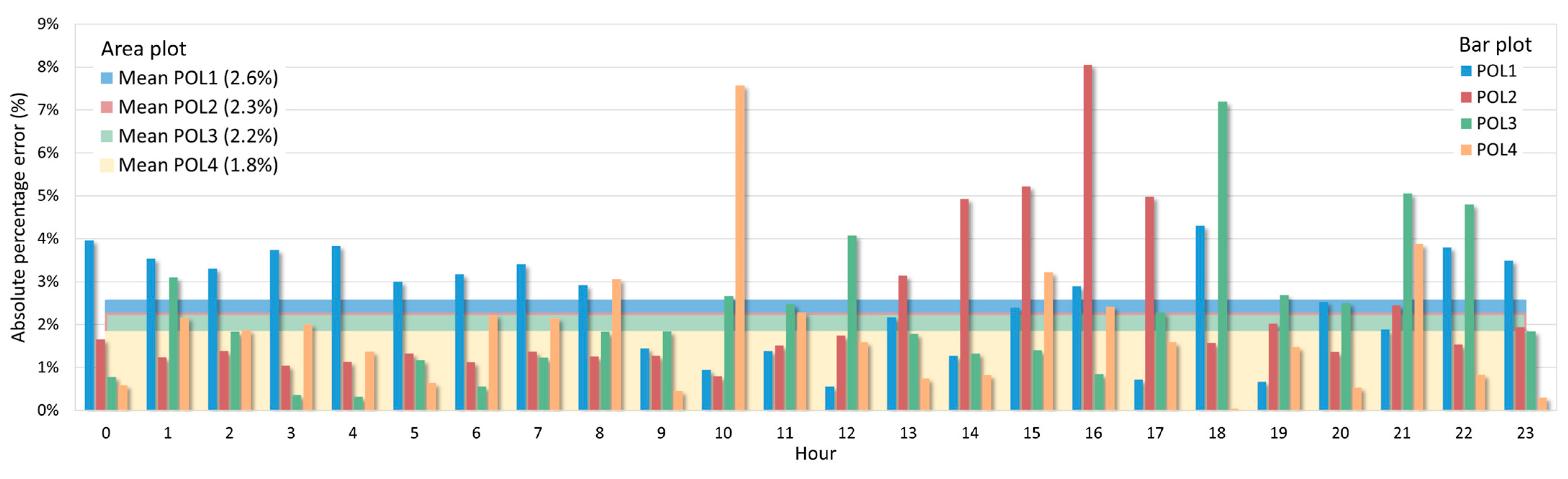
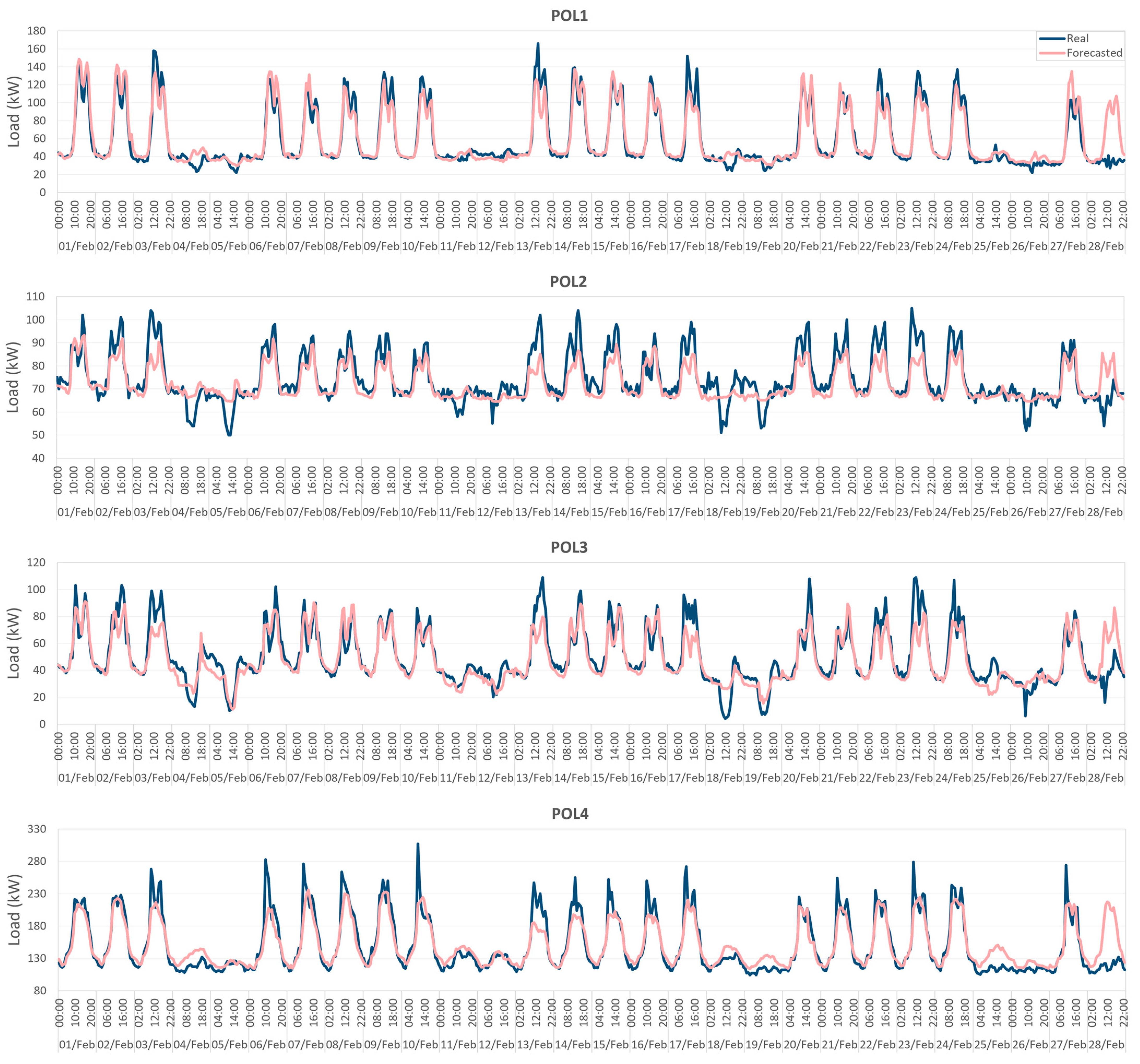
3.5. Results of Training Using Monthly Rolling
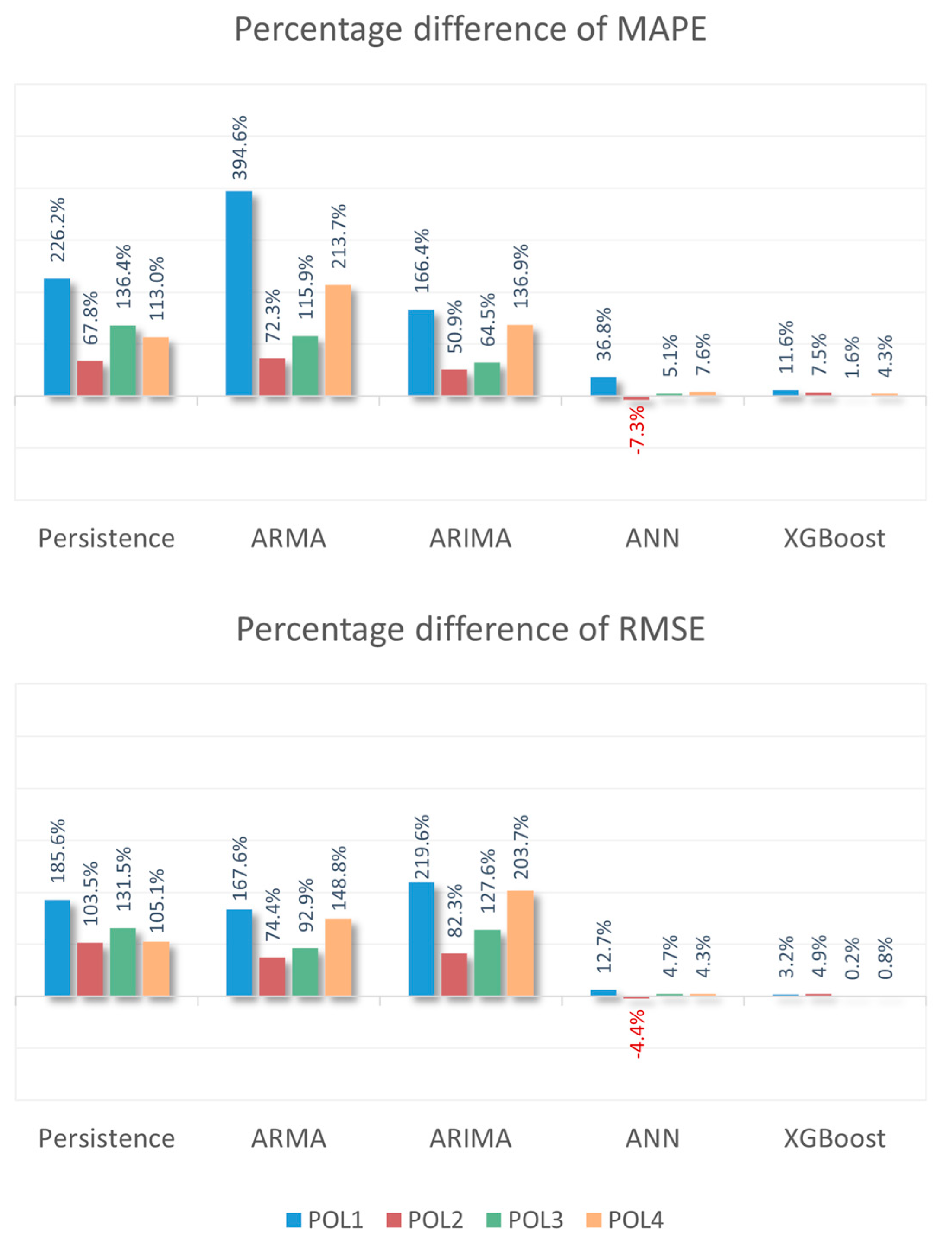
3.6. Baseline Models Comparison
4. Conclusions
5. Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Veeramsetty, V.; Reddy, K.R.; Santhosh, M.; Mohnot, A.; Singal, G. Short-Term Electric Power Load Forecasting Using Random Forest and Gated Recurrent Unit. Electr. Eng. 2022, 104, 307–329. [Google Scholar] [CrossRef]
- Holderbaum, W.; Alasali, F.; Sinha, A. Short Term Load Forecasting (STLF). Lect. Notes Energy 2023, 85, 13–56. [Google Scholar] [CrossRef]
- Pinheiro, M.G.; Madeira, S.C.; Francisco, A.P. Short-Term Electricity Load Forecasting—A Systematic Approach from System Level to Secondary Substations. Appl. Energy 2023, 332, 120493. [Google Scholar] [CrossRef]
- Akhtar, S.; Shahzad, S.; Zaheer, A.; Ullah, H.S.; Kilic, H.; Gono, R.; Jasí Nski, M.; Leonowicz, Z. Short-Term Load Forecasting Models: A Review of Challenges, Progress, and the Road Ahead. Energies 2023, 16, 4060. [Google Scholar] [CrossRef]
- Yang, D.; Guo, J.; Li, Y.; Sun, S.; Wang, S. Short-Term Load Forecasting with an Improved Dynamic Decomposition-Reconstruction-Ensemble Approach. Energy 2023, 263, 125609. [Google Scholar] [CrossRef]
- Leal, P.; Castro, R.; Lopes, F. Influence of Increasing Renewable Power Penetration on the Long-Term Iberian Electricity Market Prices. Energies 2023, 16, 1054. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, J.; Wei, D.; Zhang, Z. Combined Framework Based on Data Preprocessing and Multi-Objective Optimizer for Electricity Load Forecasting. Eng. Appl. Artif. Intell. 2023, 119, 105776. [Google Scholar] [CrossRef]
- Dewangan, F.; Abdelaziz, A.Y.; Biswal, M. Load Forecasting Models in Smart Grid Using Smart Meter Information: A Review. Energies 2023, 16, 1404. [Google Scholar] [CrossRef]
- Alquthami, T.; Zulfiqar, M.; Kamran, M.; Milyani, A.H.; Rasheed, M.B. A Performance Comparison of Machine Learning Algorithms for Load Forecasting in Smart Grid. IEEE Access 2022, 10, 48419–48433. [Google Scholar] [CrossRef]
- Groß, A.; Lenders, A.; Schwenker, F.; Braun, D.A.; Fischer, D. Comparison of Short-Term Electrical Load Forecasting Methods for Different Building Types. Energy Inform. 2021, 4, 13. [Google Scholar] [CrossRef]
- Wang, F.; Li, K.; Zhou, L.; Ren, H.; Contreras, J.; Shafie-khah, M.; Catalão, J.P.S. Daily Pattern Prediction Based Classification Modeling Approach for Day-Ahead Electricity Price Forecasting. Int. J. Electr. Power Energy Syst. 2019, 105, 529–540. [Google Scholar] [CrossRef]
- Pourdaryaei, A.; Mohammadi, M.; Karimi, M.; Mokhlis, H.; Illias, H.A.; Kaboli, S.H.A.; Ahmad, S. Recent Development in Electricity Price Forecasting Based on Computational Intelligence Techniques in Deregulated Power Market. Energies 2021, 14, 6104. [Google Scholar] [CrossRef]
- Bento, P.M.R.; Pombo, J.A.N.; Calado, M.R.A.; Mariano, S.J.P.S.; Rodrigues, F.; Calado, J.M.F. Stacking Ensemble Methodology Using Deep Learning and ARIMA Models for Short-Term Load Forecasting. Energies 2021, 14, 7378. [Google Scholar] [CrossRef]
- Shi, J.; Li, C.; Yan, X. Artificial Intelligence for Load Forecasting: A Stacking Learning Approach Based on Ensemble Diversity Regularization. Energy 2023, 262, 125295. [Google Scholar] [CrossRef]
- Du, J.; Cao, H.; Li, Y.; Yang, Z.; Eslamimanesh, A.; Fakhroleslam, M.; Mansouri, S.S.; Shen, W. Development of hybrid surrogate model structures for design and optimization of CO2 capture processes: Part I. Vacuum pressure swing adsorption in a confined space. Chem. Eng. Sci. 2024, 283, 119379. [Google Scholar] [CrossRef]
- Rao, C.; Zhang, Y.; Wen, J.; Xiao, X.; Goh, M. Energy Demand Forecasting in China: A Support Vector Regression-Compositional Data Second Exponential Smoothing Model. Energy 2023, 263, 125955. [Google Scholar] [CrossRef]
- Luo, J.; Hong, T.; Gao, Z.; Fang, S.C. A Robust Support Vector Regression Model for Electric Load Forecasting. Int. J. Forecast. 2023, 39, 1005–1020. [Google Scholar] [CrossRef]
- Vardhan, B.V.S.; Khedkar, M.; Srivastava, I.; Thakre, P.; Bokde, N.D. A Comparative Analysis of Hyperparameter Tuned Stochastic Short Term Load Forecasting for Power System Operator. Energies 2023, 16, 1243. [Google Scholar] [CrossRef]
- Tran, N.T.; Giang Tran, T.T.; Nguyen, T.A.; Lam, M.B.; City, C.M.; Minh, H.C. A New Grid Search Algorithm Based on XGBoost Model for Load Forecasting. Bull. Electr. Eng. Inform. 2023, 12, 1857–1866. [Google Scholar] [CrossRef]
- Tarmanini, C.; Sarma, N.; Gezegin, C.; Ozgonenel, O. Short Term Load Forecasting Based on ARIMA and ANN Approaches. Energy Rep. 2023, 9, 550–557. [Google Scholar] [CrossRef]
- Donnelly, J.; Daneshkhah, A.; Abolfathi, S. Physics-informed neural networks as surrogate models of hydrodynamic simulators. Sci. Total Environ. 2024, 912, 168814. [Google Scholar] [CrossRef]
- Jiang, L.; Hu, G. A Review on Short-Term Electricity Price Forecasting Techniques for Energy Markets. In Proceedings of the 2018 15th International Conference on Control, Automation, Robotics and Vision, ICARCV 2018, Singapore, 18–21 November 2018; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2018; pp. 937–944. [Google Scholar]
- Li, S.; Kong, X.; Yue, L.; Liu, C.; Khan, M.A.; Yang, Z.; Zhang, H. Short-Term Electrical Load Forecasting Using Hybrid Model of Manta Ray Foraging Optimization and Support Vector Regression. J. Clean. Prod. 2023, 388, 135856. [Google Scholar] [CrossRef]
- Yin, C.; Mao, S. Fractional Multivariate Grey Bernoulli Model Combined with Improved Grey Wolf Algorithm: Application in Short-Term Power Load Forecasting. Energy 2023, 269, 126844. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, S.; Liang, Y.; Du, Z. A Novel Combined Model for Probabilistic Load Forecasting Based on Deep Learning and Improved Optimizer. Energy 2023, 264, 126172. [Google Scholar] [CrossRef]
- Ran, P.; Dong, K.; Liu, X.; Wang, J. Short-Term Load Forecasting Based on CEEMDAN and Transformer. Electr. Power Syst. Res. 2023, 214, 108885. [Google Scholar] [CrossRef]
- Imani, M.H.; Bompard, E.; Colella, P.; Huang, T. Forecasting Electricity Price in Different Time Horizons: An Application to the Italian Electricity Market. IEEE Trans. Ind. Appl. 2021, 57, 5726–5736. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fan, G.F.; Zhang, L.Z.; Yu, M.; Hong, W.C.; Dong, S.Q. Applications of Random Forest in Multivariable Response Surface for Short-Term Load Forecasting. Int. J. Electr. Power Energy Syst. 2022, 139, 108073. [Google Scholar] [CrossRef]
- Matrenin, P.; Safaraliev, M.; Dmitriev, S.; Kokin, S.; Ghulomzoda, A.; Mitrofanov, S. Medium-Term Load Forecasting in Isolated Power Systems Based on Ensemble Machine Learning Models. Energy Rep. 2022, 8, 612–618. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Pandey, A.S.; Houran, M.A.; Kumar, V.; Kumar, D.; Tripathi, S.M.; Gangatharan, S.; Elavarasan, R.M. A Day-Ahead Short-Term Load Forecasting Using M5P Machine Learning Algorithm along with Elitist Genetic Algorithm (EGA) and Random Forest-Based Hybrid Feature Selection. Energies 2023, 16, 867. [Google Scholar] [CrossRef]
- Fang, Z.; Yang, Z.; Peng, H.; Chen, G. Prediction of Ultra-Short-Term Power System Based on LSTM-Random Forest Combination Model. J. Phys. Conf. Ser. 2022, 2387, 012033. [Google Scholar] [CrossRef]
- Kalhori, M.R.N.; Emami, I.T.; Fallahi, F.; Tabarzadi, M. A Data-Driven Knowledge-Based System with Reasoning under Uncertain Evidence for Regional Long-Term Hourly Load Forecasting. Appl. Energy 2022, 314, 118975. [Google Scholar] [CrossRef]
- Kabeyi, M.J.B.; Olanrewaju, O.A. Smart grid technologies and application in the sustainable energy transition: A review. Int. J. Sustain. Energy 2023, 42, 685–758. [Google Scholar] [CrossRef]
- Dudek, G. A Comprehensive Study of Random Forest for Short-Term Load Forecasting. Energies 2022, 15, 7547. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Taylor & Francis: Abingdon, UK, 2017; pp. 1–358. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Ho, K. The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Nurullah, C.; Güneş, F.; Koziel, S.; Pietrenko-Dabrowska, A.; Belen, M.A.; Mahouti, P. Deep-learning-based precise characterization of microwave transistors using fully-automated regression surrogates. Sci. Rep. 2023, 13, 1445. [Google Scholar] [CrossRef]
- Ghayekhloo, M.; Azimi, R.; Ghofrani, M.; Menhaj, M.B.; Shekari, E. A Combination Approach Based on a Novel Data Clustering Method and Bayesian Recurrent Neural Network for Day-Ahead Price Forecasting of Electricity Markets. Electr. Power Syst. Res. 2019, 168, 184–199. [Google Scholar] [CrossRef]
- Mishra, S.; Prasad, K.; Tigga, A.M. Electrical Price Prediction Using Machine Learning Algorithms. In Machine Learning Algorithms and Applications in Engineering; CRC Press: Boca Raton, FL, USA, 2023; pp. 255–270. ISBN 9781003104858. [Google Scholar]
- Nascimento, J.; Pinto, T.; Vale, Z. Electricity Price Forecast for Futures Contracts with Artificial Neural Network and Spearman Data Correlation. Adv. Intell. Syst. Comput. 2019, 801, 12–20. [Google Scholar] [CrossRef]
- Bitirgen, K.; Filik, Ü.B. Electricity Price Forecasting Based on XGBooST and ARIMA Algorithms. BSEU J. Eng. Res. Technol. 2020, 1, 7–13. [Google Scholar]
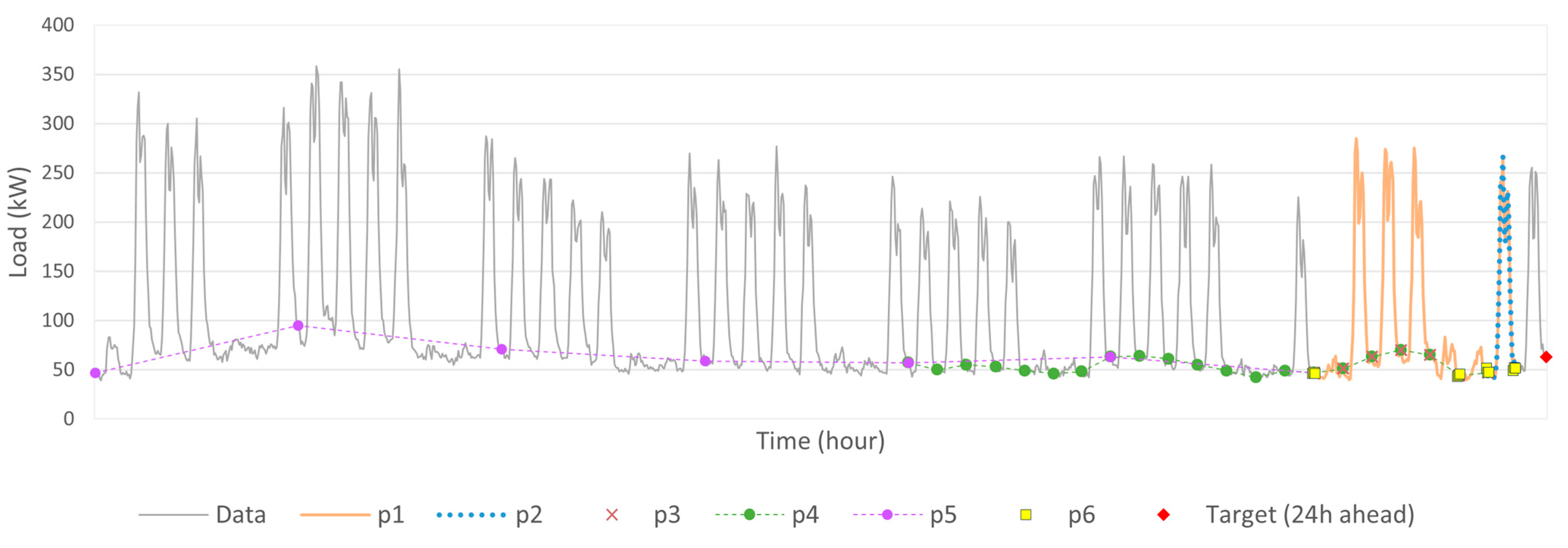

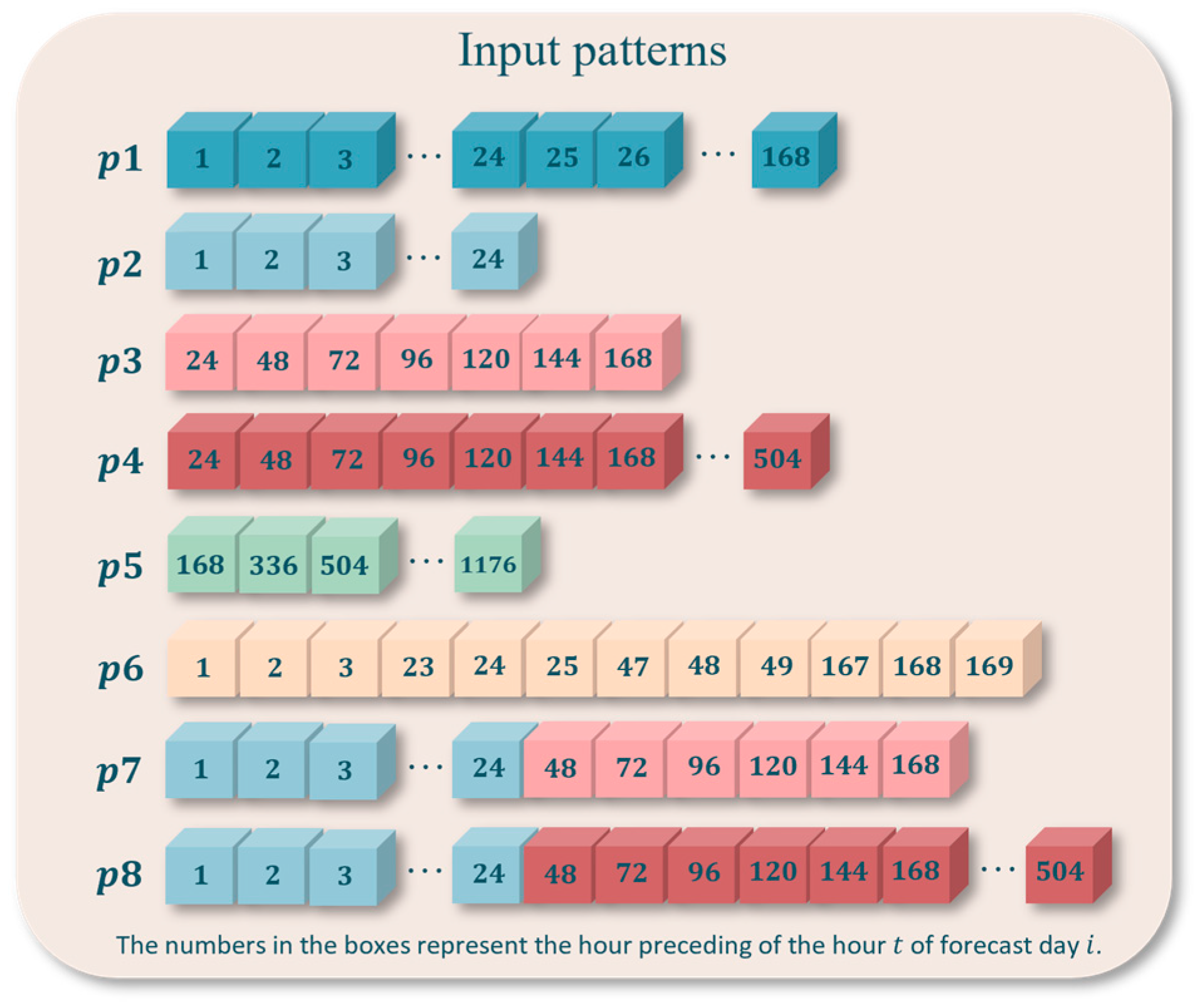
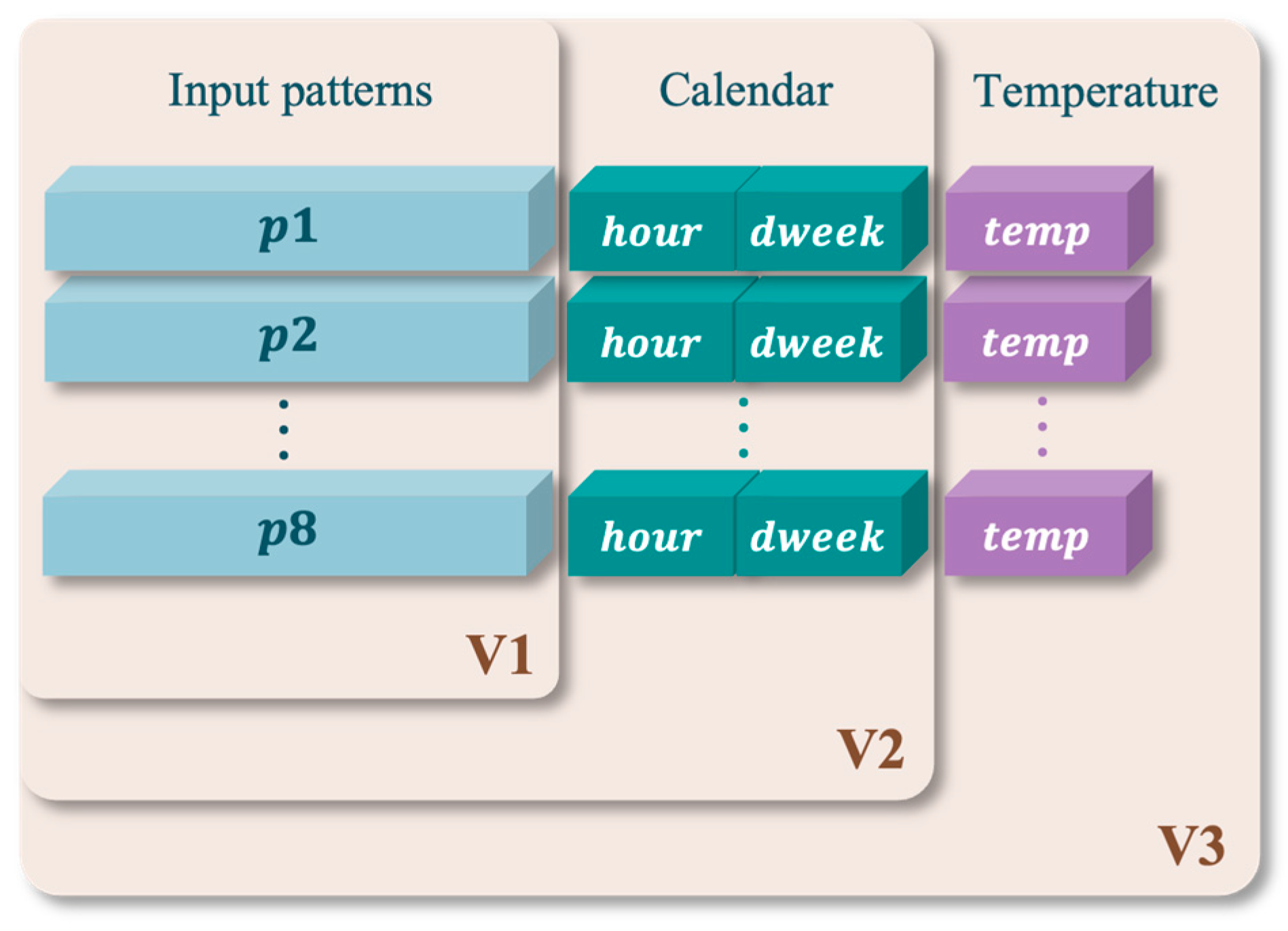
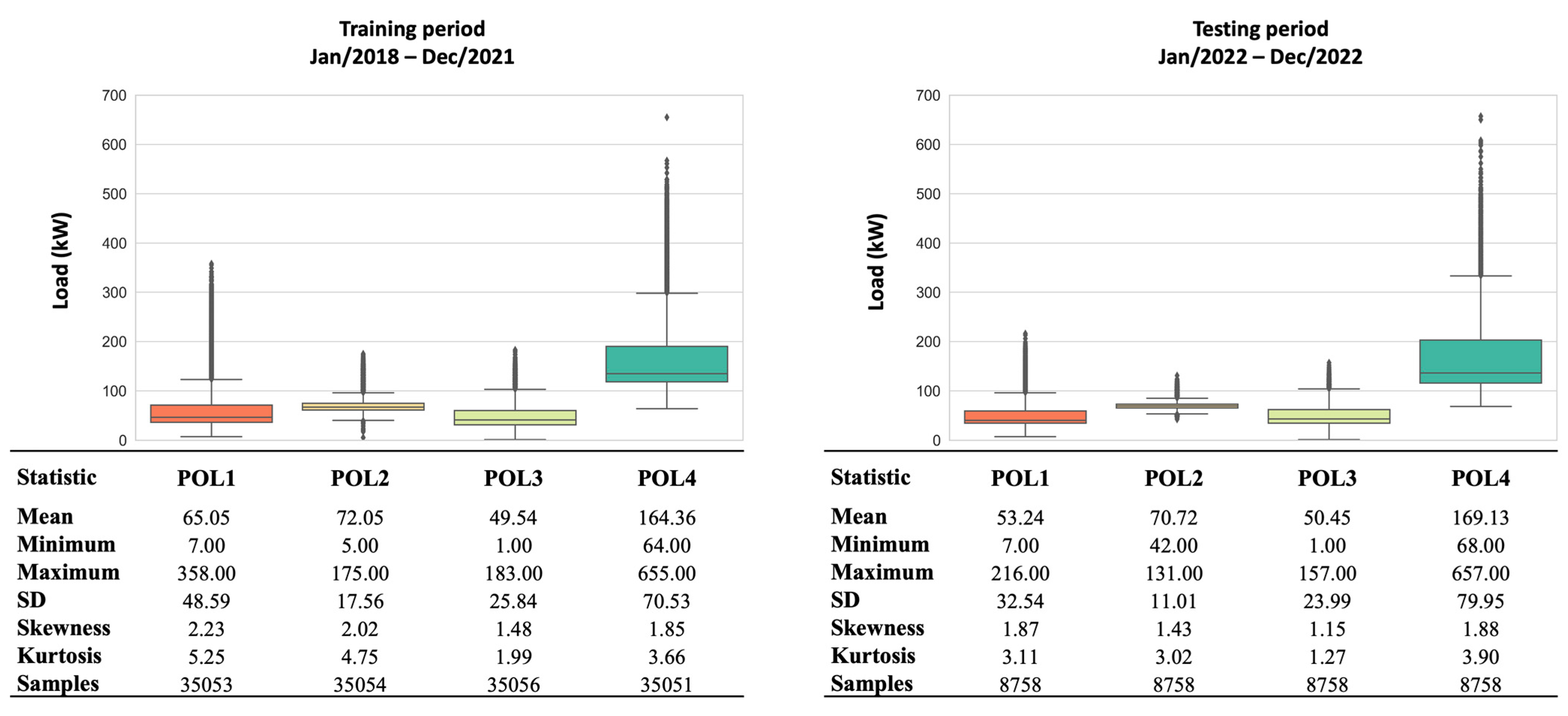
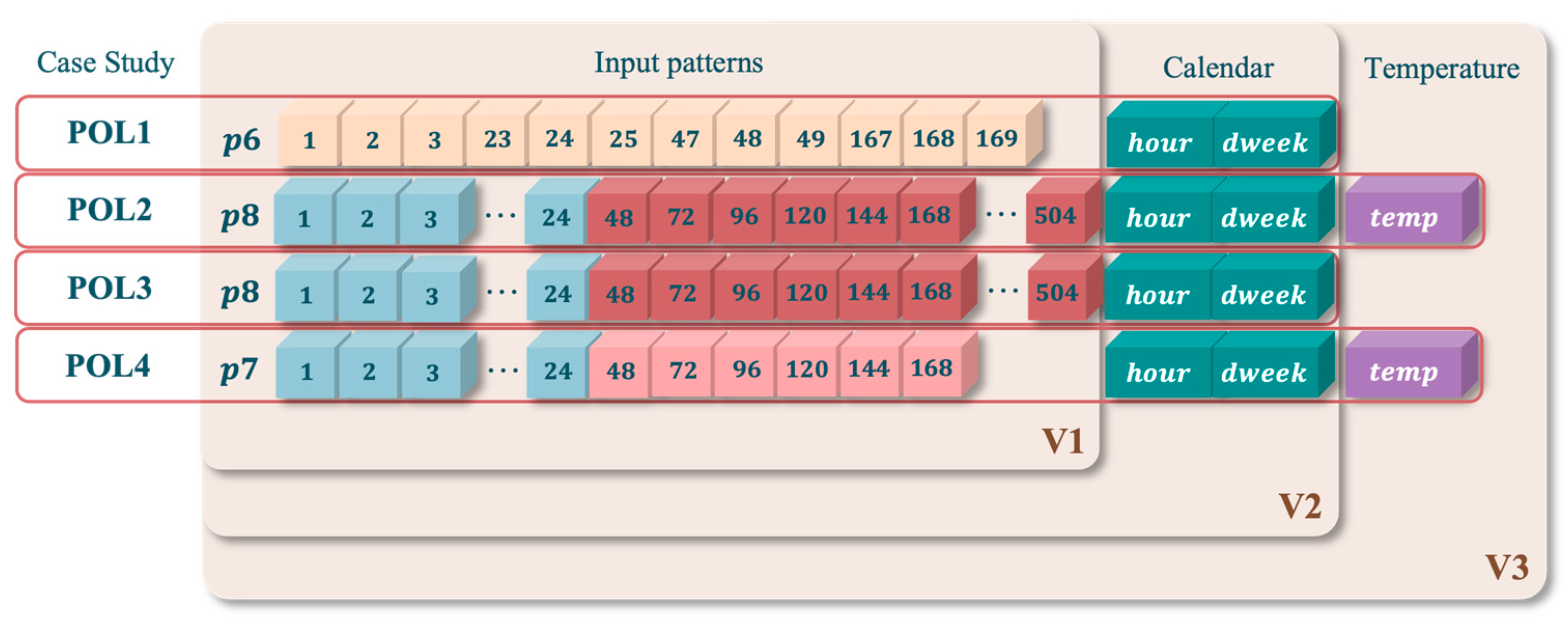
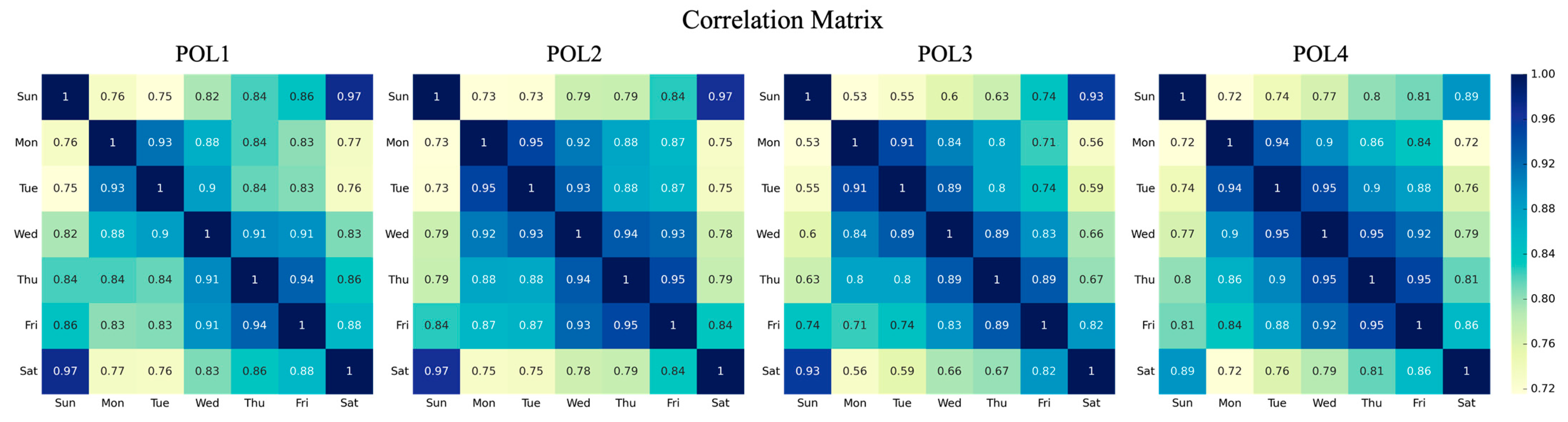
| Input Patterns | Description of Input Patterns | Sequence of Relevant Lags | Set Size |
|---|---|---|---|
| p1 | The sequence is composed of demands from 168 h preceding hour t of day i. | Seq1 = [1,…, 168] | 168 |
| p2 | The sequence is composed of demands from 24 h preceding hour t of day i. | Seq2 = [1,…, 24] | 24 |
| p3 | The sequence is composed of demands at hour t of 7 consecutive days preceding the forecast day i. | Seq3 = [24, 48, 72, 96, 120, 144, 168] | 7 |
| p4 | The sequence is composed of demands at hour t of 21 consecutive days preceding the forecast day i. | Seq4 = [24, 48, 72, 96, 120, 144, 168, …, 504] | 21 |
| p5 | The sequence is composed of demands at hour t of 7 consecutive same weekdays preceding the forecast day i. | Seq5 = [168, 336, 504, …, 1176] | 7 |
| p6 | The sequence is composed of demands of some specific hours preceding the forecast day i. | Seq6 = [1, 2, 3, 23, 24, 25, 47, 48, 49, 167, 168, 169] | 12 |
| p7 | The sequence is a cross-pattern combining p2 and p3. | Seq7 = [1, …, 24, 48, 72, 96, 120, 144, 168] | 30 |
| p8 | The sequence is a cross-pattern combining p2 and p4. | Seq8 = [1, …, 24, 48, 72, 96, 120, 144, 168, …, 504] | 44 |
| Case Study | Variant | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| POL1 | V1 | 16.61 | 40.46 | 17.23 | 15.90 | 34.83 | 23.15 | 17.14 | 15.57 |
| V2 | 15.84 | 20.17 | 15.47 | 15.58 | 20.35 | 14.54 | 15.40 | 15.20 | |
| V3 | 15.83 | 19.20 | 15.65 | 15.44 | 20.60 | 14.89 | 15.39 | 15.12 | |
| POL2 | V1 | 7.35 | 9.75 | 7.61 | 7.29 | 12.07 | 8.69 | 7.34 | 6.88 |
| V2 | 7.10 | 7.88 | 7.25 | 7.27 | 9.03 | 7.50 | 6.95 | 6.75 | |
| V3 | 7.07 | 7.80 | 7.19 | 7.20 | 9.00 | 7.61 | 6.89 | 6.64 | |
| POL3 | V1 | 30.29 | 44.52 | 35.66 | 30.36 | 48.50 | 37.74 | 31.31 | 28.03 |
| V2 | 28.12 | 28.19 | 30.59 | 29.63 | 34.00 | 27.84 | 27.63 | 26.89 | |
| V3 | 28.27 | 27.19 | 30.58 | 29.36 | 32.80 | 27.51 | 27.54 | 26.93 | |
| POL4 | V1 | 12.10 | 16.77 | 13.78 | 13.17 | 22.77 | 14.90 | 12.03 | 11.78 |
| V2 | 11.68 | 11.60 | 12.60 | 12.75 | 16.78 | 11.64 | 11.22 | 11.38 | |
| V3 | 11.49 | 11.42 | 12.09 | 12.14 | 14.43 | 11.40 | 11.08 | 11.16 |
| Case Study | Variant | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| POL1 | V1 | 13.45 | 26.67 | 15.27 | 14.50 | 26.70 | 18.51 | 13.48 | 13.21 |
| V2 | 13.02 | 15.16 | 14.57 | 14.29 | 18.21 | 12.70 | 13.18 | 13.07 | |
| V3 | 12.95 | 14.56 | 14.39 | 14.32 | 18.01 | 12.72 | 13.20 | 13.04 | |
| POL2 | V1 | 7.03 | 9.56 | 7.39 | 7.04 | 10.92 | 8.61 | 7.12 | 6.68 |
| V2 | 6.78 | 7.93 | 6.97 | 7.00 | 8.76 | 7.30 | 6.76 | 6.57 | |
| V3 | 6.76 | 7.85 | 6.88 | 6.93 | 8.51 | 7.28 | 6.70 | 6.48 | |
| POL3 | V1 | 13.73 | 19.17 | 14.76 | 13.61 | 20.91 | 16.62 | 13.55 | 12.78 |
| V2 | 13.12 | 13.61 | 13.83 | 13.45 | 16.25 | 13.04 | 12.68 | 12.55 | |
| V3 | 13.10 | 13.29 | 13.80 | 13.43 | 15.66 | 12.95 | 12.64 | 12.65 | |
| POL4 | V1 | 35.04 | 47.44 | 39.03 | 37.52 | 57.18 | 42.67 | 34.95 | 34.39 |
| V2 | 33.91 | 34.40 | 36.41 | 36.56 | 46.63 | 34.07 | 32.67 | 33.21 | |
| V3 | 33.43 | 33.87 | 34.41 | 34.32 | 40.32 | 33.44 | 32.28 | 32.58 |
| Case Study | Best Combination | MAPE | RMSE | ||
|---|---|---|---|---|---|
| Initial | Initial | ||||
| POL1 | V2— | 14.54 | 17.18 | 12.70 | 13.45 |
| POL2 | V3— | 6.64 | 6.71 | 6.48 | 6.55 |
| POL3 | V2— | 26.89 | 27.97 | 12.55 | 12.82 |
| POL4 | V3— | 11.08 | 11.82 | 32.28 | 34.58 |
| Case Study | MAPE | MAPE | MAPE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| POL1 | 192 | 1 | 5 | 14.54 | 300 | 1 | 5 | 14.59 | 300 | 1 | 13 | 15.23 |
| POL2 | 66 | 1 | 16 | 6.68 | 300 | 10 | 16 | 6.51 | 300 | 1 | 46 | 6.63 |
| POL3 | 265 | 1 | 15 | 26.68 | 300 | 2 | 15 | 26.74 | 300 | 1 | 38 | 26.06 |
| POL4 | 171 | 1 | 11 | 11.05 | 300 | 5 | 11 | 11.00 | 300 | 1 | 12 | 11.04 |
| Case Study | MAPE | MAPE | ||||||
|---|---|---|---|---|---|---|---|---|
| POL1 | 192 | 1 | 13 | 14.32 | 300 | 1 | 13 | 14.30 |
| POL2 | 66 | 10 | 46 | 6.45 | 300 | 10 | 46 | 6.45 |
| POL3 | 265 | 2 | 38 | 26.16 | 300 | 2 | 38 | 26.14 |
| POL4 | 171 | 5 | 12 | 11.01 | 300 | 5 | 12 | 11.01 |
| Case Study | Initial | Tuned | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAPE | RMSE | MAPE | RMSE | |||||||
| POL1 | 300 | 1 | 5 | 14.54 | 12.70 | 300 | 9 | 12 | 14.16 | 12.89 |
| POL2 | 300 | 1 | 16 | 6.64 | 6.48 | 300 | 15 | 28 | 6.42 | 6.34 |
| POL3 | 300 | 1 | 15 | 26.89 | 12.55 | 300 | 4 | 44 | 25.88 | 12.45 |
| POL4 | 300 | 1 | 11 | 11.08 | 32.28 | 300 | 5 | 15 | 10.96 | 32.20 |
| Case Study | Error Metrics | Jan | Feb | Mar | Apr | May | June | July | Aug | Sept | Oct | Nov | Dec | Mean | Annual |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| POL1 | MAPE | 15.51 | 12.99 | 14.21 | 29.16 | 15.35 | 17.37 | 14.81 | 18.88 | 11.36 | 15.29 | 15.10 | 22.55 | 16.88 | 14.16 |
| RMSE | 13.99 | 12.06 | 16.06 | 21.36 | 9.52 | 13.50 | 9.54 | 7.85 | 7.11 | 11.76 | 13.63 | 21.42 | 13.15 | 12.89 | |
| POL2 | MAPE | 5.46 | 5.87 | 7.45 | 7.93 | 4.55 | 6.36 | 5.65 | 5.82 | 4.60 | 5.76 | 6.07 | 8.32 | 6.15 | 6.42 |
| RMSE | 6.20 | 6.27 | 7.82 | 7.86 | 4.45 | 5.74 | 5.55 | 4.68 | 4.07 | 5.06 | 6.04 | 8.46 | 6.02 | 6.34 | |
| POL3 | MAPE | 15.47 | 17.08 | 17.31 | 98.38 | 31.41 | 19.68 | 25.37 | 27.37 | 15.61 | 14.96 | 31.28 | 26.90 | 28.40 | 25.88 |
| RMSE | 10.40 | 9.92 | 12.13 | 17.88 | 14.82 | 13.07 | 15.07 | 8.77 | 7.12 | 11.05 | 16.07 | 18.29 | 12.88 | 12.45 | |
| POL4 | MAPE | 7.60 | 8.06 | 8.28 | 8.56 | 16.40 | 18.26 | 16.75 | 16.82 | 19.18 | 10.49 | 10.24 | 11.89 | 12.71 | 10.96 |
| RMSE | 19.58 | 19.76 | 20.41 | 22.70 | 47.57 | 54.85 | 54.59 | 41.52 | 43.69 | 22.60 | 21.69 | 24.02 | 32.75 | 32.20 |
| Methods | Main Parameters |
|---|---|
| Persistence | The forecast value was defined as the load of the previous 24 h. |
| ARMA | For this model, and . Based on the augmented Dickey–Fuller (ADF) test, ARIMA was used without non-seasonal difference (). |
| ARIMA | For this model, , and , where is the order of the autoregressive (AR) term, is the order of non-seasonal difference and is the order of the moving average (MA) term. These parameters were set according to the autocorrelation function (ACF), the partial autocorrelation function (PACF) and the augmented Dickey–Fuller (ADF) test to verify the series stationarity. |
| ANN | The first layer size was set to 29, the activation function was set to use rectified linear units, the last layer of size one was set to sigmoid activation function, and the solver was set to use Adam. The threshold for training data used to validate was set at 33%. The ANN was trained 20 times, and the results showed are the mean of all evaluations. |
| XGBoost | Number of estimators = 800, learning rate = 0.01, subsample = 0.7, and colsample bytree = 0.7. |
| Methods | POL1 | POL2 | POL3 | POL4 | ||||
|---|---|---|---|---|---|---|---|---|
| MAPE | RMSE | MAPE | RMSE | MAPE | RMSE | MAPE | RMSE | |
| RF (proposed) | 14.16 | 12.89 | 6.42 | 6.34 | 25.88 | 12.45 | 10.96 | 32.20 |
| Persistence | 46.19 | 36.81 | 10.77 | 12.90 | 61.17 | 28.83 | 23.35 | 66.04 |
| ARMA | 70.03 | 34.49 | 11.06 | 11.06 | 55.87 | 24.02 | 34.38 | 80.12 |
| ARIMA | 37.72 | 41.19 | 9.69 | 11.56 | 42.57 | 28.33 | 25.96 | 97.78 |
| ANN | 19.37 | 14.53 | 5.95 | 6.06 | 27.20 | 13.03 | 11.80 | 33.58 |
| XGBoost | 15.80 | 13.30 | 6.90 | 6.65 | 26.30 | 12.47 | 11.43 | 32.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magalhães, B.; Bento, P.; Pombo, J.; Calado, M.d.R.; Mariano, S. Short-Term Load Forecasting Based on Optimized Random Forest and Optimal Feature Selection. Energies 2024, 17, 1926. https://doi.org/10.3390/en17081926
Magalhães B, Bento P, Pombo J, Calado MdR, Mariano S. Short-Term Load Forecasting Based on Optimized Random Forest and Optimal Feature Selection. Energies. 2024; 17(8):1926. https://doi.org/10.3390/en17081926
Chicago/Turabian StyleMagalhães, Bianca, Pedro Bento, José Pombo, Maria do Rosário Calado, and Sílvio Mariano. 2024. "Short-Term Load Forecasting Based on Optimized Random Forest and Optimal Feature Selection" Energies 17, no. 8: 1926. https://doi.org/10.3390/en17081926
APA StyleMagalhães, B., Bento, P., Pombo, J., Calado, M. d. R., & Mariano, S. (2024). Short-Term Load Forecasting Based on Optimized Random Forest and Optimal Feature Selection. Energies, 17(8), 1926. https://doi.org/10.3390/en17081926






