Abstract
Low-enthalpy geothermal energy can make a major contribution towards reducing CO2 emissions. However, the development of geothermal reservoirs is costly and time intensive. In particular, high capital expenditures, data acquisition costs, and long periods of time from identifying a geothermal resource to geothermal heat extraction make geothermal field developments challenging. Conventional geothermal field development planning follows a linear approach starting with numerical model calibrations of the existing subsurface data, simulations of forecasts for geothermal heat production, and cost estimations. Next, data acquisition actions are evaluated and performed, and then the models are changed by integrating the new data before being finally used for forecasting and economics. There are several challenges when using this approach and the duration of model rebuilding with the availability of new data is time consuming. Furthermore, the approach does not address sequential decision making under uncertainty as it focuses on individual data acquisition actions. An artificial intelligence (AI)-centric approach to field development planning substantially improves cycle times and the expected rewards from geothermal projects. The reason for this is that various methods such as machine learning in data conditioning and distance-based generalized sensitivity analysis assess the uncertainty and quantify its potential impact on the final value. The use of AI for sequential decision making under uncertainty results in an optimized data acquisition strategy, a recommendation of a specific development scenario, or advice against further investment. This approach is illustrated by applying AI-centric geothermal field development planning to an Austrian low-enthalpy geothermal case. The results show an increase in the expected value of over 27% and a reduction in data acquisition costs by more than 35% when compared with conventional field development planning strategies. Furthermore, the results are used in systematic trade-off assessments of various key performance indicators.
1. Introduction
Geothermal energy provides a continuous source of sustainable energy in addition to fluctuating renewable energy such as photovoltaics or wind. The worldwide technical potential for geothermal energy is estimated to be at around 200 GW electric and 5000 GW thermal [1]. Geothermal energy can be used to decarbonize heating and cooling, and in particular district heating [2]. Acksel et al. [3] identified Germany’s vast potential for low-enthalpy geothermal energy, exceeding 220 TWh/a and proposing a target of 300 TWh/a by 2040. In Austria, district heating currently relies on 0.2 TWh/a of geothermal energy, with projections anticipating a surge to 6.4 TWh/a by 2050 [4]. Challenges such as prolonged geothermal resource appraisal and high development costs need to be addressed to realize these ambitious targets [5,6]. The objective is to reduce project appraisal and development duration by 30–50% [5].
To achieve this target, geothermal field development planning (FDP) needs to be improved. Instead of planning singular injector–producer doublets, large-scale geothermal heat extraction requires the drilling of a multitude of wells and the installation of large-scale facilities. The historical focus on injector–producer doublets is reflected in early models by the use of simplified subsurface descriptions. Then, the planning evolved to consider vertical [7] and lateral reservoir heterogeneities in the subsurface [8,9,10]. As the demand for low-enthalpy geothermal energy grew, well planning expanded to encompass multiple doublets and their interactions in heterogeneous subsurface settings [11,12,13,14], and to address multiple objectives [15]. Economic assessments play a vital role in evaluating well spacing [16], conducting value of information (VOI) calculations [17], and assessing various development options [18]. Geothermal resource classification challenges, recoverable heat determination, and field development planning similar to hydrocarbon fields were also explored [19,20,21]. However, similar challenges, as in hydrocarbon field development, are observed in geothermal field development planning. Some major issues are biases in production forecasts [22,23] and the VOI of sequential data acquisition [24,25] in particular if data gathering costs of the various actions are different [26]. Despite these efforts, the required time from geothermal field appraisal to heat extraction is 3–7 years [5] and the economics of such projects are challenging [27]; in particular, if value erosion occurs owing to the acquisition of too much data, wrong data, or high costs. Decision making under uncertainty using AI has been comprehensively introduced by Russel and Norvig [28] and was applied to various fields such as aircraft collision avoidance [29], breast cancer screening [30], and energy management [31]. Recently, some aspects of AI were introduced in field development planning for hydrocarbon reservoirs such as reinforcement learning for well planning [32,33], but a systematic methodology including data acquisition and the application to decision making in geothermal field development is missing.
In this paper, we integrate AI into field development planning to address the long duration as well as improving the value of geothermal field developments. We show that using AI outperforms humans in geothermal field development planning and substantially decreases cycle times and costs. Our study not only outlines the systematic introduction of AI-centric methodologies, but also provides a case study to illustrate the practical implications. The case study covers a field case in Austria in which low-enthalpy geothermal heat will be used to decarbonize district heating.
This paper is organized as follows: First, we describe conventional field development planning. Then, we introduce AI-centric field development planning. Finally, we cover a case study of an Austrian geothermal project that illustrate the benefits of low-enthalpy geothermal heat.
2. Conventional Field Development Planning
Identifying, assessing, and developing geothermal energy is a capital-intensive endeavour [34]. There is substantial uncertainty and risk involved in the development of such resources [35]. Geothermal projects were separated by Gehringer and Loksha [34] into eight phases: preliminary survey, exploration, test drilling, project review and planning, field development, power plant construction, commissioning, and operation. The duration from initial resource identification to the initiation of geothermal heat extraction spans five to ten years [36]. In this article, we focus on the post-identification phases. In these phases, methodologies similar to the ones applied in hydrocarbon development projects are applied, where front-end loading is used to avoid costly missteps [37].
Because of historical tendencies toward overestimating hydrocarbon production by project teams [38,39], a stage-gate process has been integrated into hydrocarbon development projects. For multi-well geothermal projects, such a process is suggested as well [40]. Originating from new product development practices [41], a stage-gate process dissects product evolution into distinct stages, with control gates ensuring quality assurance [41]. Adapted by the hydrocarbon industry for field development purposes [42,43], the process involves sequential phases (identify and assess, select, define, and execute) [44], as delineated in Figure 1.

Figure 1.
Example of stage-gate process in the oil and gas industry. SG—stage gate; PR—project review.
The process (Figure 1) is a chronological series of events, with peer reviews for value assurance, denoted by project reviews (PRs) at the conclusion of each phase [42,45]. The conventional methodology involves sequentially calculating P10, P50, and P90 production forecasts [46], followed by determining the associated costs and revenues [47,48].
Using the stage-gate process, as illustrated in Figure 1, presents some challenges. Companies employing simplified subsurface models that inadequately account for all uncertainties face the issue of frequent model updates with the acquisition of new data [49]. This iterative process introduces prolonged intervals between data acquisition and the subsequent appraisal activities. The rigorous PRs conducted prior to decision gates contribute to project execution delays, as these reviews often scrutinize fundamental assumptions, hindering swift progress instead of solely ensuring decision quality at decision gates [50]. Furthermore, the traditional sequential workflow encompassing production modelling, cost and revenue calculations, and subsequent revisions is identified as another bottleneck in project timelines [51].
The next sections describe how we re-evaluate the methodologies to mitigate delays and enhance the overall effectiveness of the stage-gate process.
3. Artificial Intelligence-Centric Field Development Planning
Various machine learning methods were used to address the uncertainty in geothermal energy production [52,53,54]. However, AI-centric approaches for sequential decision making under uncertainty have not been covered. Geothermal field development planning requires development teams to make a sequence of decisions amid inherent uncertainties. These decisions include the choice of data acquisition, as well as which field development they want to pursue and whether they want to walk away from the geothermal opportunity. These challenges can be addressed by the deployment of intelligent decision-making support systems that can be implemented into the software [55]. In the context of field development planning, it is important to integrate these agents into the established processes and workflows of companies, enabling them to efficiently assess and execute field developments.
Conventional decision-making processes, characterized by the utilization of only a fraction of the available information and heuristics, are susceptible to biases and errors [56,57]. To overcome these limitations, Figure 2 illustrates how AI can be integrated into the FDP process. The FDP process is characterised by the interaction of a project team and a decision board. A structured decision dialogue, as proposed by SPE [58] and Spetzler et al. [50], ensures alignment between project objectives and corporate goals. Additionally, portfolio considerations, such as evaluating the impact of the project on overall company risk [59,60,61], play a crucial role. The FDP process is dissected into three phases: frame, evaluate, and commit. Each phase is described in more detail in the subsequent sections.
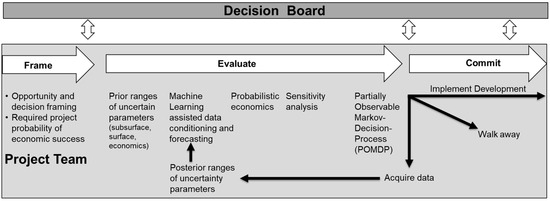
Figure 2.
An artificial intelligence approach to field development planning.
3.1. Framing
The framing phase is the first step in project development, aiming to establish comprehensive high-level boundaries that define the project’s scope and delivery parameters. This includes business needs and objectives, aligning them with the specific goals of the project and ensuring harmonization with broader company objectives [62,63]. Within the framing phase, special attention is dedicated to addressing the probability of economic success (PES) for the project. PES, denoting the likelihood of achieving a net present value (NPV) greater than zero at the selected discount rate, is a critical factor in shaping the project’s trajectory. Determining the required PES involves considering of the company’s risk attitude and the project’s scale relative to the overall wealth of the company.
The impact of the required PES extends significantly to the data acquisition strategy. A higher required PES corresponds to escalated acquisition costs and longer durations of the evaluation phase, as a larger volume of data becomes necessary to mitigate the risk of achieving negative NPVs. Importantly, a higher PES hurdle increases the probability of invoking the walk-away option from a project.
3.2. Evaluation
The evaluation phase is dedicated to identifying the optimal development option, while also considering the possibility of non-development (i.e., walking away from the opportunity). At the core of this phase is the integration of AI, addressing key components of effective decision making: logical reasoning, informed information gathering, consideration of alternatives, and assessment of trade-offs [50,58].
In this phase, critical parameters of subsurface, surface, and economics must be defined. Then, the ranges of these parameters need to be described. Dynamic and economic parameter ranges have to avoid confidence bias and quality assurance has to be addressed. Subsequently, the parameter ranges need to be conditioned to observed data using valid statistical methods including recent machine learning methods. For new geothermal fields, which are characterized by limited data availability (e.g., well tests, production data), posterior parameter ranges reflect larger uncertainties when compared to fields already in production.
Various development options are then assessed across the model ensemble, using the posterior parameter distributions after data conditioning. Probabilistic economics are integrated, resulting in economic forecasts used to calculate NPVs.
The next step is to formulate a data acquisition strategy. To focus on value-adding data acquisition, first, a distance-based generalized sensitivity analysis of the parameters on NPV is conducted. This analysis guides the definition of data acquisition actions, aimed at reducing uncertainty for parameters with the highest sensitivity to decision making.
Results are further evaluated using partially observable Markov decision process (POMDP) agents. The POMDP agent recommends the optimal field development policy, including executing a specific development option, acquiring more data, or walking away. If data acquisition is suggested as the first action of the optimum policy, the corresponding activities are implemented, leading to updated posterior parameter distributions. Then, sensitivity analyses are conducted again to improve the understanding of the impact of the updated parameter distributions on project value. Next, the updates are used by the POMDP agent to suggest the next optimal action in field development. Ultimately, a development option is chosen if the PES hurdle is met and further data acquisition is not expected to increase the project’s expected value. Conversely, the walk-away option is executed if the PES hurdle cannot be achieved, and residual risks remain prohibitively high for project execution (an overview is shown in Figure A1 in Appendix A).
3.3. Commit
The commit phase ensues after the evaluation phase when no data acquisition action can enhance the project’s expected value. In this phase, the decision is made to either walk away from the opportunity or proceed with the selected development option.
3.4. General Aspects
The AI-centric evaluation phase introduces a dynamic approach to quantifying and continually monitoring key performance indicators (KPIs) throughout the project lifecycle. These indicators include metrics such as expected monetary value (EMV), expected appraisal costs, expected loss, the probability of maturation (POM), and the array of potential development scenarios under consideration. By leveraging AI, this phase facilitates the real-time assessment of project progress and crucial decision-making factors.
The subsequent section provides an in-depth exploration of the AI-centric evaluation phase within the context of a geothermal field development project.
4. Case Study
This section provides a demonstration of the application of AI-centric field development planning during the evaluation phase, using an Austrian low-enthalpy geothermal project as an example. An overview of the evaluation phase workflow is given in Appendix A. The following paragraphs detail the specific steps of the evaluation phase, as shown in Figure 2. Sections “Project Set-Up” and “Geothermal Reservoir Setting” offer insights into the overarching project settings, while the subsequent sections systematically delineate the workflow, guiding the reader through each step of the process. Afterwards, the results of the human-based data acquisition strategies are discussed and compared with the AI-centric field development planning results.
4.1. Project Set-Up
To reduce CO2 emissions in Austria, the heat generation could be changed to sustainable energy sources. Büchele et al. [64] summarized the Austrian potential of district heating while Könighofer et al. [65] describes the potential of geothermal energy for district heating and electricity generation in Austria. In this article, an Austrian project is described, aiming at replacing district heating fuelled by fossil energy with sustainable low-enthalpy geothermal energy. Substantial heat in place in a deep saline aquifer was identified as a potential source for low-enthalpy geothermal energy production. Data of several wells are available, confirming the presence of a potentially sufficient permeable conglomerate layer. The scale of the replacement project requires the drilling of 24 to 79 wells, which is dependent on the chosen development option. In addition, surface facilities need to be constructed and flowlines need to be built to connect the wells to the facilities.
4.2. Geothermal Reservoir Setting
The reservoir setting is described by Bayerl et al. [14]: The geothermal reservoir described here is a saline aquifer that is part of the Neogene succession of the Vienna Basin [66]. It has been intensively studied and drilled for hydrocarbon exploration and production [67,68]. The Vienna Basin formed in two discrete stages in the early Miocene (~20 Ma) with the earliest sediments being incorporated in the alpine orogen in a piggy-back position by N–NW-directed thrusting, which ceased in the Karpatian (~17 Ma) and a main depositional phase (~6000 m sediment fill) in the mid Miocene (Badenian ~16 Ma) during the pull-apart basin formation along N–NE-trending normal faults [67,68]. The reservoir unit consists of moderately cemented to loose, massive, clast-supported conglomerates composed of poorly to moderately rounded, medium to coarse gravel with frequent cobbles (limestone, dolostone, and various crystalline components). Intercalations of fine sand and silty marly clay are subordinate [66]. Weissenbäck [69] describes these conglomerates as braided river deposits with numerous amalgamating channels and bars. These fluvial deposits show limited marine influence only reported in distal parts.
4.3. Geological Reservoir Parameterisation
The numerical models consist of approximately 0.82 million cells and cover an area of 8 km from south to north and 6 km from east to west. The average reservoir thickness is approximately 200 m, with the uppermost layer of the reservoir at a depth of 1500 m in the northern region, gradually deepening to 3800 m in the south [70]. The porosity model is governed by well log interpretations, whereas the porosity and permeability distribution is given by geostatistical methods in areas away from the wells. The generation of the subsurface models is based on uniform distributions of the various parameters given in Table A1 in Appendix A. Latin hypercube sampling (LHS) was used to sample from the various parameters. Examples of the resulting porosity distributions are shown in Figure 3. The diagrams show that there is a large variety of possible porosity distributions. In addition, the faults could be sealing or not. The diagram shows a five-spot well pattern, more development scenarios are covered in the Section 4.5.
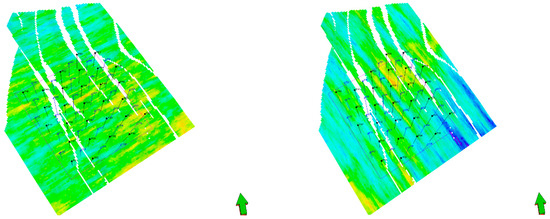
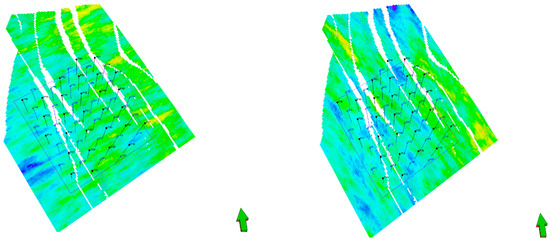
Figure 3.
Examples of the porosity distribution of the reservoir model based on the distributions given in Appendix A.
4.4. Dynamic Reservoir Parameterisation
Concerning the dynamic reservoir parameter ranges, the initial pressures and temperatures were derived from well measurements. Rock compressibility, thermal conductivity, and heat capacity were taken from analogue data. The parameter ranges are given in Table A2. Applying LHS from the geological (Table A1 in Appendix A) and reservoir dynamic parameters (Table A2 in Appendix A), 250 subsurface models were generated. No dynamic data such as pressure, production, or temperature observed data were available for this case. Therefore, the data conditioning step shown in Figure 2 was not required.
4.5. Field Development Scenarios
Many different field development scenarios are possible for geothermal reservoirs. Frequently, five-spot or line drive is used in field developments for which fluid injection and production is required. The reason is that such patterns allow for the economically efficient recovery of fluids or heat from the subsurface [71,72]. The field development scenarios used here are given in Table 1. The wells were completed from top to bottom except for development option 4, in which the wells were completed for the injectors in the bottom half and the producers in the top half of the reservoir.

Table 1.
Field development scenarios. LD—line drive; EW—east-west; NS—north-south.
Without additional information about the reservoir, all these development scenarios might lead to an economically attractive project. In this phase of field development planning, many different development scenarios need to be considered and subsequently applied to the simulation of forecasts using the ensemble of reservoir models.
4.6. Production Forecasts
For the development scenarios given in Table 1, the forecasts of liquid and energy production as well as water and energy injection were performed for all of the 250 subsurface models. Figure 4 shows energy production forecast for four of the development scenarios.
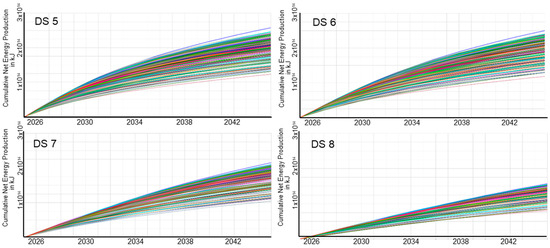
Figure 4.
Examples of cumulative net energy production of four different development scenarios with time. DS—field development scenario.
The cumulative net energy recovery of the various development scenarios is different. For all of the development scenarios, a significant spread of the energy recovery can be observed in Figure 4. The spread is the result of the various different parameter configurations that were sampled using LHS from Table A1 and Table A2 given in Appendix A.
The next step is to include the economic parameters and their ranges in the evaluation.
4.7. Economic Parameters and Economic Analysis
The EMV of the geothermal field development depends on the net energy production but also on operating expenditures (OPEXs), capital expenditure (CAPEXs), and the energy price. Table A3 in Appendix A gives the ranges of the various expenditures and the energy prices used here. For each of the 250 forecasts generated from the 250 geomodels, 50 economic evaluations were performed using LHS from the economic parameters (Table A3 and Table A4 in Appendix A). The workflow ensured the allocation of OPEX to only active wells and the CAPEX costs dependent on the specified surface facilities. In total, 12,500 NPVs were calculated for each development scenario as a combination of the 250 subsurface realisation and 50 economic parameter configurations. A discount factor of 10% was used. The results of the economic calculations are given in Table 2.

Table 2.
Results of the economic analyses for the various field development scenarios.
The results reveal that the highest EMV is associated with development scenario 7, closely followed by development scenario 10, with development scenarios 11 and 6 also demonstrating substantial EMVs. However, the P10 NPV underscores a risk of negative NPVs during project execution. None of the PES values exceed 0.65, indicating a 35% or greater risk of unfavourable outcomes. In the context of our case study, a PES of 65% was deemed insufficient given the company’s risk profile and the substantial expected investment.
To address this, the next phase of evaluation delves into exploring various data acquisition methods. In instances like the one illustrated in this case study, data acquisition becomes imperative to either meet the risk (PES) hurdle [73,74], select the optimal development option [75], or walk away. The challenge lies in identifying sequential data acquisition actions capable of elevating PES and selecting the development option with the highest expected reward. The data acquisition activities should not be too costly to avoid value erosion.
For our case study, development option 10 employs a north-south line drive, development option 11 adopts an east-west line drive, and development option 7 follows a 5-spot pattern. The following question emerges: which sequence of data acquisition actions will yield the highest expected reward and will inform us about which of the development scenario to choose at the final investment decision (FID) or to walk away? With ten geological uncertain parameters, six dynamic uncertain parameters, 13 economic uncertain parameters, and 11 development scenarios, the subsequent section elaborates on performing a sensitivity analysis and delineates the process for defining optimal data acquisition actions.
4.8. Sensitivity Analysis and Data Acquisition Actions
To increase the expected reward, data acquisition needs to be observable, relevant, material, and economic [76]. The distance-based generalized sensitivity analysis, as proposed by Fenwick et al. [77], proves instrumental in showing the sensitivity of parameters, including their interdependencies, on NPV.
Figure 5 visually represents the distance-based generalized sensitivity analysis outcomes for development scenario 7 with respect to NPV.
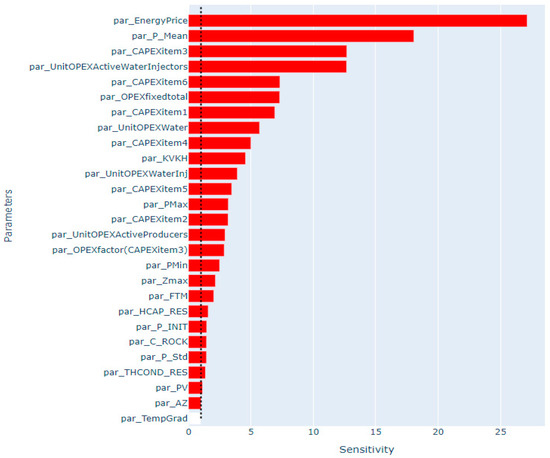
Figure 5.
Distance-based generalized sensitivity analysis on NPV for development scenario 7.
The energy price has the strongest impact on the NPV. However, for the case study, we treat the energy price as residual uncertainty, i.e., an uncertainty that cannot be reduced. The other parameters exerting substantial impact on NPV are economic factors followed by geological parameters.
To address these parameters, they need to be observable, meaning a measurement or study needs to be performed which allows for a decrease in the uncertainty range of one or more parameters. In this case study, the data acquisition actions detailed in Table 3 were identified. Table 3 gives the data acquisition actions as well as the durations, the observed variables, the costs, and the observation uncertainties for which uniform distributions were applied. Note that the drilling of three wells informs several observed variables.

Table 3.
Data acquisitions actions. The first eight actions are measurements, and the last eleven (the economic data acquisition actions) are studies.
The table illustrates the difficulty of selecting a data acquisition program. While the activity must yield informative results to enhance the PES and aid in the choice of a field development option or to walk away, it is imperative that it remains cost-effective and does not introduce delays to the project timeline. Preserving the efficiency of the data acquisition process is crucial to prevent erosion of the time value of money. In the following section, the use of agents is introduced to optimize field developments under uncertainty.
4.9. Partially Observable Markov Decision Process (POMDP)
In this section, first, we introduce the POMDP formulation and the agent. Then, we describe the results of the POMDP agent and compare the results with conventional field development planning.
4.9.1. Introduction of POMDP and Agent
Corso et al. [70] introduced a POMDP agent designed to address challenges in data acquisition. Below, the POMDP and agent as developed by Corso et al. [70] is briefly described.
The study employs a partially observable Markov decision process (POMDP) characterized by the tuple (S, A, T, R, O, Z, γ), where S represents the set of states, A denotes the set of actions, T defines the transition model between states, R signifies the reward function, O represents the observation space, Z stands for the observation model, and γ indicates the discount factor. A POMDP agent comprises two components: a belief updater and a policy (refer to Figure 6). In each time step, the POMDP agent, situated in an environment with state s, selects an action a, leading to a transition to a new state s′ with probability T(s′|s, a), thereby yielding a reward r. Given that states are not directly observable, the agent infers information about the state through a history of observations and actions. Beliefs, denoted as b, are recursively computed by a belief updater using Bayes’ rule, incorporating the action a taken and the observation o received. The policy π of a POMDP agent maps the belief space B to the action set A. The optimal policy π* is one that maximizes the expected discounted sum of future rewards.
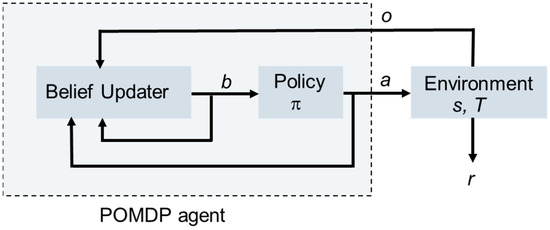
Figure 6.
POMDP agent [70].
Corso et al. [70] used various methods to determine the near optimal policy. Here, we cover the offline solver successive approximations of the reachable space under optimal policies (SARSOP) [78] and the “Acquire all” approach used by Corso et al. [70]. The SARSOP solver is a computationally efficient solver for a variety of POMDP tasks whereas “Acquire all” assumes that all available data acquisition actions are performed before choosing a development option.
The components of the POMDP for the geothermal data acquisition case are as follows [70]:
States: the states consist of a fixed, discrete set of geological and economical models randomly sampled for the distributions given in Table A1, Table A2, Table A3 and Table A4 in Appendix A.
Actions: there are 20 different data acquisition actions (Table 3), 11 development options, and the walk away option, hence the total 32 possible actions.
Reward model: The reward (here negative reward, i.e., cost) of each data acquisition action is shown in Table 3. The reward for walking away is EUR 0, the reward for each development option is the EMV of the respective development option.
Observations: observations are made based on the data acquisition action selected (Table 3).
Observation model: the observation model defines the likelihood for the respective observation after executing an action.
Transition model: here, the state does not change, hence T(s|s, a) = 1.
We use the NativeSARSOP.jl (https://github.com/JuliaPOMDP/NativeSARSOP.jl/tree/main, 10 January 2024) implementation of the SARSOP algorithm [70].
The solver underwent a single adjustment, allowing actions to have variable durations in computing the discount factor. Details of the solver parameters utilized can be found in Table 4 [70].

Table 4.
SARSOP solver parameters.
The POMDP agent was used to determine the approximately optimal data acquisition strategy. The results are given in the next section.
4.9.2. Results of the POMDP Agent
Applying the POMDP agent, one of the following three outcomes shown in Figure 2 is suggested in the decision dialogue of the project team and decision board: to execute a development option, to walk away, or to perform a data acquisition activity. Which of the three activities should be performed depends on the risk attitude of the company as well as the availability of funds for data acquisition. Figure 7 shows the POM as function of PES. SARSOP refers to using the SARSOP policy whereas “Acquire all” assumes that all data is gathered. Option 7 and option 10 show the cases in which no further data acquisition is performed and the respective development option is executed; more results and details of how the results were obtained are given in Corso et al. [70].
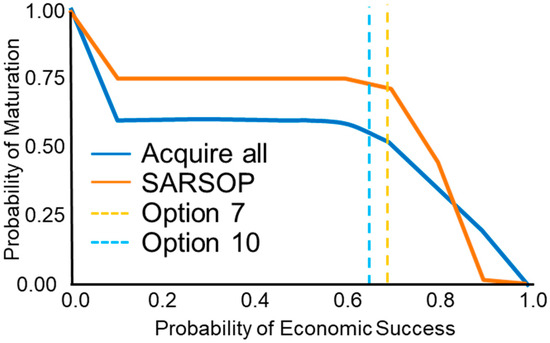
Figure 7.
Probability of maturation versus probability of economic success for different data acquisition strategies. Option 7 and option 10 refer to executing the respective development options without further data acquisition [70].
Figure 7 illustrates the importance of defining the risk attitude in the framing part of field development planning. A company requiring a PES of 61.6% or less could either execute development option 7, option 10, perform the data acquisition strategy “Acquire all”, or the suggested data acquisition of the SARSOP policy. For this case, the POM of a project is larger for the SARSOP than for the “Acquire all” policy. For a PES requirement 61.6% < PES ≤ 66%, option 10 or data acquisition policy “Acquire all” or SARSOP could be followed. For 66% < PES ≤ 82%, SARSOP has a higher POM than “Acquire all” whereas for a PES hurdle of 82% or larger, “Acquire all” has a higher POM. The diagram (Figure 7) shows that the higher the required PES, the lower the POM. This has an implication for selecting projects in the decision dialogue. Dependent on the project portfolio and company strategy, projects with a larger POM might be required to achieve overarching production or value targets. The POM derived by the agent is a quantitative measure of the chance of executing a project. This is solving ambiguities in the concept of chance of development which in current industry practice is based on expert judgement [79,80].
In addition to Figure 7, other KPIs need to be considered in the decision dialogue. Table 5 gives several KPIs of the various policies.

Table 5.
Comparison of KPIs of several policies.
Correct go/no-go in Table 4 refers to the fraction of outcomes for which the correct decision of executing a development scenario was taken. For scenario 7 and scenario 10, this fraction equals the PES. Correct development scenario in Table 4 refers to the fraction of outcomes that result in the correct development scenario. For example, scenario 7 should have only chosen for 18% without data acquisition.
The selection of scenario 7, which has the highest EMV without data acquisition, does not require any budget for data acquisition. However, the PES is 66%, i.e., in 34% of the cases a negative NPV would be the result of the project. Also, this development scenario is the correct development scenario for only 18% of the cases. The expected loss for this case is EUR 51 M (Figure 8).
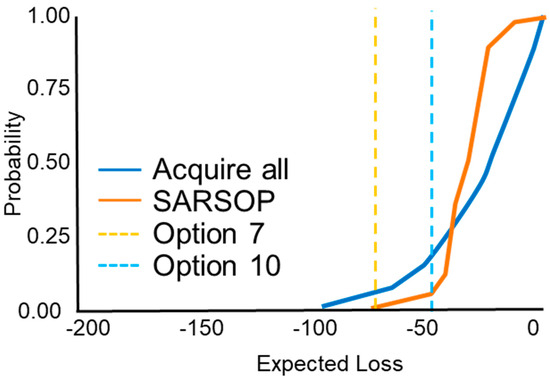
Figure 8.
Cumulative distribution function of expected loss for various development scenarios [70].
Deciding on the next action in the decision dialogue (Figure 2) requires the consideration of the trade-offs. While executing scenario 7 does not incur additional data acquisition costs, it will lead to the wrong development option in 82% of the cases. Choosing the “Acquire all” policy reduces the chance of choosing the wrong development option to 51%; however, it requires expected data acquisition costs of EUR 32 M and reduces the EMV from EUR 106 M for scenario 7 to EUR 77 M. “Acquire all” results in higher maximum expected losses (Figure 8) but reduces the P50 of the expected loss from EUR 51 M for option 7 to EUR 25 M.
The SARSOP policy increases the EMV from EUR 106 M for scenario 7 to EUR 136 M, reduces the data acquisition costs from EUR 32 M for “Acquire all” to EUR 1.4 M, has the highest probability of choosing the correct go/no-go decision with 74%, and has a very similar chance of choosing the correct development scenario as the “Acquire all” policy: 48% versus 49%. The expected loss cumulative distribution function (CDF) indicates a lower maximum expected loss than the “Acquire all” policy; however, it has a higher P50 expected loss of EUR 33 M than the “Acquire all” policy (EUR 25 M).
In the case study, the company required a PES hurdle of 75%. For this case, considering the EUR 1.4 M expected data acquisition costs, the SARSOP policy was chosen as it yields the highest EMV, has the highest chance of resulting in the correct go/no-go decision and has the highest chance to choose the correct development option. The most frequently chosen first action in the SARSOP policy for this case is “Assess OPEX Active Water Injectors”. This action will be executed first.
After performing the data acquisition action, the parameter distributions will be updated, the sensitivity analysis will be performed, and the POMDP evaluation will be performed. Dependent on the result, a development scenario will be chosen and the walk away option or data acquisition step will be executed, as shown in Figure 2.
In the following section, we describe data acquisition strategies suggested by humans for the case study.
4.10. Human Suggested Data Acquisitions Strategies
In addition to using k-fold cross validation to ensure that the POMDP solution is not overestimated (for details see [70]), we compared the effectiveness of AI-centric geothermal field development planning to traditional methods. We sought input from nine professionals with 6–28 years of experience in various field development projects. The results are detailed in Table A5 in Appendix A and described in more detail in Corso et al. [70]. The variations among experts, both in the number and prioritization of suggested data acquisition actions, highlight the complexity of the decision space that exceeds human cognitive capacities.
The human experts differed substantially in the number of data acquisition actions as well as which data acquisition to perform first. As the first data acquisition action, six different actions were suggested by the nine experts. The number of data acquisition actions ranged from 3 to 16. Comparing with the expert achieving the highest EMV, the SARSOP algorithm increased the EMV by 27%, the correct go/no-go decision by 1.2%, and reduced acquisition costs by 35%. The differences with the “average human” are even larger (Table 6). It should also be noted the “best human” decision for EMV and data acquisition costs was from human expert 6, whereas it was human expert 1 for the correct go/no-go and correct development options. Human expert 6 chose data acquisition actions with lower acquisition costs but the result was that the expert would have chosen the correct development option only in 32% of cases (Table A5 in Appendix A). The “best human” expert, human expert 1, achieved a slightly higher percentage for the correct development option; however, it was at much higher acquisition costs and lower EMV than SARSOP (Table A5 in Appendix A). Also, SARSOP suggests action 20 as the first data acquisition (Table 3) which was not picked by any human expert as their first data acquisition action.

Table 6.
Comparison of the SARSOP policy with humans. The percentages refer to the difference in percentage of SARSOP and the “best human” and the average of the outcomes of humans.
4.11. Discussion of the Results of AI-Centric Evaluation Phase
Field development planning for low-enthalpy geothermal fields presents a challenge due to the substantial CAPEX and OPEX involved. The inherent risk of negative NPVs of the project and the necessity for numerous sequential decisions under uncertainty further compound the complexity. Specifically, determining the optimal sequence for data acquisition poses a significant challenge.
In hydrocarbon field developments, VOI was suggested as the evaluation method [81,82]. It was seen that determining the probabilities at the decision notes [83] and incorporating the risk attitude of the decision makers (e.g., [84]), risk hurdles [85] and performing sequential appraisals [86] are particularly difficult. Geothermal field development planning has thus far employed VOI mainly for individual costly data acquisition activities [87] or to compare a limited number of scenarios [88]. These approaches fall short in comprehensively comparing all potential data acquisition actions and addressing the sequential and cascading impact of data acquisition on the initial action.
With no established methodology for sequential decision making, current field development planning adheres to the stage-gate process (Figure 1), relying heavily on human interactions within the project team. The results of comparing the human-suggested data acquisition strategies with AI-centric selection indicate that quality decision making in field development planning is substantially improved by using AI-centric approaches. The reason is that even if group biases are avoided (e.g., [89,90]) the complexity of the decision problem is too high to allow for finding the optimum data acquisition policy. It is impossible for humans to incorporate information from future additional information gains, use constraints such as PES, and capture the multitude of different parameters influencing a decision in field development planning. None of the humans identified action 20 (Table 3) as their first action, which was suggested by SARSOP.
Furthermore, the absence of a quantitative evaluation method in conventional field development planning such as POMDP agents suggests potential shifts in outcomes during team discussions in conventional field development planning. Also, trade-offs cannot be quantified in conventional field development planning and are based on human experiences and heuristics. This emphasizes the substantial impact and efficiency gains achievable through AI-centric strategies in field development planning.
5. Conclusions and Recommendations
Geothermal field development planning is aimed at finding the best development scenario (or walk-away), maximizing the expected reward under uncertainty. To identify the best development scenario, additional data can be acquired if the data acquisition increases the expected reward of the field development.
The conventional geothermal field development is starting with modelling, then cost estimation, calculation of economics, and then focussing on an individual data acquisition action.
AI-centric geothermal field development planning utilizes various methods such as machine learning-supported conditioning of model ensembles to data which are then used for forecasting uncertainty, distance-based generalized sensitivity analyses to assess the impact of parameters on final values, and POMDP agents to determine the optimum policy for data acquisition to select the highest value development scenario under uncertainty (or walk away).
Applying AI-centric geothermal field development planning to an example low-enthalpy case in Austria shows the strengths of the approach. The results show that the AI-centric approach is outperforming conventional approaches by increasing the expected reward by 27% and reducing acquisition costs by 35%. In addition, the approach provides auditable KPIs which can be used to quantify trade-offs. Geothermal field developments will be accelerated as only value-adding data will be acquired. Costs will be reduced and trade-offs will be quantified using AI-centric geothermal field development planning.
This article covers the use of AI for a case of 32 actions including data acquisition, various field developments, and executing the walk-away option. Future work should address the optimization of field development under uncertainty. This will require researchers to forecast thousands of development options. In order to forecast so many cases, surrogate models will need to be developed.
Author Contributions
T.C.: conceptualization, methodology, resources, data curation, and writing (original draft, review, and editing). M.-M.C.: conceptualization, methodology, resources, data curation, writing (review and editing), and visualization. A.C.: conceptualization, methodology, software, validation, formal analysis, and writing (review and editing). M.Z.: conceptualization, methodology, writing (review and editing), and funding acquisition. M.J.K.: conceptualization, methodology, writing (review and editing), and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
OMV Energy provided funding to Stanford University, Agreement Number: 3279987.
Data Availability Statement
Data and code are publicly available on github (as noted in the paper).
Acknowledgments
Thanks to OMV Energy for the permission to publish the paper.
Conflicts of Interest
The authors declare the following financial interests/personal relationships: Torsten Clemens reports a relationship with OMV Exploration and Production GmbH that includes: employment Maria Chiotoroiu reports a relationship with OMV Exploration and Production GmbH that includes: employment. Anthony Corso reports financial support was provided by OMV Exploration and Production GmbH. Markus Zechner reports a relationship with OMV Exploration and Production GmbH that includes: employment. Mykel J. Kochenderfer reports financial support was provided by OMV Exploration and Production GmbH.
Acronyms and Abbreviations
| AI | artificial intelligence |
| CAPEX | capital expenditures |
| CDF | cumulative distribution function |
| EMV | expected monetary value |
| FDP | field development plan |
| FID | final investment decision |
| KPI | key performance indicator |
| LHS | Latin hypercube sampling |
| NPV | net present value |
| OPEX | operating expenditures |
| P10, P50, P90 | 10%, 50%, 90% percentile |
| PES | probability of economic success |
| POM | probability of maturation |
| POMDP | partially observable Markov decision process |
| PR | project review |
| VOI | value of information |
Appendix A
Figure A1 provides an overview of the suggested workflow within the “Evaluate” phase. More details are given in Section 4.4, Section 4.5, Section 4.6, Section 4.7 and Section 4.8.
The first step is to determine prior ranges of geological, dynamic, and economic parameters. From these parameters, a model ensemble (in the case study 250 subsurface models) is created. Field development options are defined and used to forecast production from this model ensemble. Then, the economic parameters are sampled and economic calculations are performed to determine KPIs. Afterwards, a sensitivity analysis is conducted to understand which of the parameters have a high impact on the NPV. Guided by the sensitivity analysis, data acquisition actions are suggested. All the information is then fed to POMDP agents. The results of the POMDP agents lead to the POM versus PES.
Applying the selected PES (risk) hurdles, possible data acquisition strategies (including walk away or executing a field development scenario) are selected. Then, the results of the POMDP agents are used to understand trade-offs of the various KPIs. Finally, an action is suggested, either to execute a specific field development option, to walk away or to perform a data acquisition action. If a data acquisition action is performed, then posterior distributions of the parameters are evaluated, this could be either geological, dynamic, or economic parameters.
The posterior parameter ranges are then used to update the sensitivity analysis and the KPIs. Again, the PES hurdle is applied, trade-offs evaluated, and an action selected (field development, walk away, data acquisition). The process ends if either a field development is selected or the walk-away option is executed if further data acquisition does not increase the expected reward.

Figure A1.
Workflow within the “Evaluate” phase of AI-centric field development planning.
The ranges of the parameters that were used to generate the geological models are given in Table A1.

Table A1.
Ranges of the geological parameters that were used to generate the geological models.
Table A1.
Ranges of the geological parameters that were used to generate the geological models.
| Name | Minimum | Maximum | Unit |
|---|---|---|---|
| Porosity standard deviation | 0.01 | 0.02 | fraction |
| Porosity mean of the normal distribution | 0.065 | 0.135 | fraction |
| Azimuth of the variogram | 0 | 359 | degree |
| Variogram anisotropy—major direction | 200 | 5000 | m |
| Variogram anisotropy—minor direction | 200 | 1000 | m |
| Variogram anisotropy range—vertical direction | 10 | 100 | m |
| Fault transmissibility multiplier | 0 | 1 | - |
| Permeability ratio vertical/horizontal | 0.01 | 0.5 | - |
| Surface trend Z value maximum | 0.085 | 0.195 | - |
| Surface trend Z value minimum | 0.045 | 0.085 | - |
The ranges of the parameters that were used for the reservoir dynamics are given in Table A2. Uniform distributions were applied.

Table A2.
Ranges of the dynamic parameters that were used to generate the geological models.
Table A2.
Ranges of the dynamic parameters that were used to generate the geological models.
| Name | Minimum | Maximum | Unit |
|---|---|---|---|
| Water compressibility | 4.70 × 10−5 | 4.80 × 10−5 | 1/bar |
| Initial reservoir pressure | 240 | 250 | bar |
| Rock compressibility | 3.0 × 10−5 | 8.0 × 10−5 | 1/bar |
| Rock thermal conductivity | 238.7 | 292 | KJ/(mx dx K) |
| Rock heat capacity | 2303.5 | 3116.5 | KJ/(m3x K) |
| Temperature gradient | 0.025 | 0.035 |
Table A3 shows the ranges of the economic parameters used in the evaluation. Uniform distributions were applied. Table A4 gives the details of the costs dependent on the size of the surface facilities and development option.

Table A3.
Ranges of the economic parameters.
Table A3.
Ranges of the economic parameters.
| Name | Minimum | Maximum | Unit |
|---|---|---|---|
| Energy (heat) price | 1.1 10−5 | 1.67 10−5 | EUR/kJ |
| CAPEX injection well | 4 | 8 | EUR M |
| CAPEX production well | 4 | 8 | EUR M |
| CAPEX surface facilities | See Table A4 | See Table A4 | |
| CAPEX flowlines | See Table A4 | See Table A4 | |
| CAPEX production pump | 0.25 | 0.4 | EUR M |
| CAPEX injection pump | 0.15 | 0.25 | EUR M |
| OPEX fixed total | See Table A4 | See Table A4 | |
| OPEX surface facilities | 4.5 | 6 | % of Surface Facility CAPEX |
| OPEX water | 0.17 | 0.22 | EUR/(m3 year) |
| OPEX water injectors | 0.17 | 0.22 | EUR/(m3 year) |
| OPEX active producers | 0.09 | 0.15 | EUR/(well year) |
| OPEX active water injectors | 0.09 | 0.15 | EUR/(well year) |

Table A4.
Cost ranges dependent on the development option and surface facility size.
Table A4.
Cost ranges dependent on the development option and surface facility size.
| Option Number | Facility Type | CAPEX Surface Facilities | CAPEX Flowlines | OPEX Fixed Total |
|---|---|---|---|---|
| 1 | Large | EUR 300–500 M | EUR 100–140 M | EUR 27–39 M |
| 2 | Large | EUR 300–500 M | EUR 100–140 M | EUR 29–42 M |
| 3 | Large | EUR 300–500 M | EUR 100–140 M | EUR 26–38 M |
| 4 | Large | EUR 300–500 M | EUR 100–140 M | EUR 27–39 M |
| 5 | Medium | EUR 270–450 M | EUR 90–126 M | EUR 20–29 M |
| 6 | Medium | EUR 270–450 M | EUR 90–126 M | EUR 17–25 M |
| 7 | Small | EUR 255–425 M | EUR 85–119 M | EUR 12–18 M |
| 8 | Small | EUR 255–425 M | EUR 79–105 M | EUR 8–12 M |
| 9 | Medium | EUR 270–450 M | EUR 90–126 M | EUR 20–29 M |
| 10 | Medium | EUR 270–450 M | EUR 90–126 M | EUR 20–29 M |
| 11 | Medium | EUR 270–450 M | EUR 90–126 M | EUR 19–28 M |
Table A5 gives the results of human experts with 6–28 years of experience in field development planning for suggestions of the data acquisition strategy.

Table A5.
Results of the data acquisition strategies suggested by human experts.
Table A5.
Results of the data acquisition strategies suggested by human experts.
| Human Expert Policy | EMV in EUR M | Number of Acquisition Actions | Data Acquisitions Costs in EUR M |
|---|---|---|---|
| 1 | 75 | 16 | −34 |
| 2 | 76 | 6 | −25 |
| 3 | 92 | 3 | −12 |
| 4 | 84 | 9 | −25 |
| 5 | 99 | 8 | −14 |
| 6 | 107 | 5 | −2 |
| 7 | 71 | 13 | −37 |
| 8 | 71 | 10 | −37 |
| 9 | 68 | 8 | −37 |
References
- IRENA; IGA. Global Geothermal Market and Technology Assessment; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates; International Geothermal Association: The Hague, The Netherlands, 2023. [Google Scholar]
- Fraunhofer IWES/IBP (2017): Wärmewende 2030. Schlüsseltechnologien zur Erreichung der Mittel und Langfristigen Klimaschutzziele im Gebäudesektor. Studie im Auftrag von Agora Energiewende. Agora Energiewende, Berlin, Germany; Studie 107/01-S-2017/DE. Available online: https://www.agora-energiewende.de/ (accessed on 10 January 2024).
- Acksel, D.; Amann, F.; Bremer, J.; Bruhn, D.; Budt, M.; Bussmann, G.; Görke, J.-U.; Grün, G.; Hahn, F.; Hanßke, A.; et al. Roadmap Tiefe Geothermie für Deutschland—Handlungsempfehlungen für Politik, Wirtschaft und Wissenschaft für Eine Erfolgreiche Wärmewende. Strategiepapier von sechs Einrichtungen der Frauenhofer Gesellschaft und der Helmholtz-Gemeinschaft; Fraunhofer Einrichtung für Energieinfrastrukturen und Geothermie, Achen, Germany Helmholtz-Zentrum Potsdam Deutsches GeoForschungsZentrum: Potsdam, Germany, 2022. [Google Scholar] [CrossRef]
- Baumann, M.; Pauritsch, G.; Rohre, M. Roadmap zur Dekarbonisierung der Fernwärme in Österreich; Endbericht Austrian Energy Agency: Wien, Austria, 2020. [Google Scholar]
- BMK. FTI-Roadmap Geothermie—Vision und FTI-Politische Fragestellungen; Bericht, BMK Bundesministerium für Klimaschutz, Umwelt, Energie, Mobilität, Innovation und Technologie: Wien, Austria, 2022. [Google Scholar]
- Ciucci, M. Innovative Technologies in the Development of Geothermal Energy in Europe; Briefing Requested by the ITRE Committee; PE754.200; European Parliament: Luxembourg, 2023. [Google Scholar]
- Poulsen, S.E.; Balling, N.; Nielsen, S.B. A parametric study of the thermal recharge of low enthalpy geothermal reservoirs. Geothermics 2015, 53, 464–478. [Google Scholar] [CrossRef]
- Crooijmans, R.A.; Willems, C.J.L.; Nick, H.M.; Bruhn, D.F. The influence of facies heterogeneity on the doublet performance in low-enthalpy geothermal sedimentary reservoirs. Geothermics 2016, 64, 209–219. [Google Scholar] [CrossRef]
- Shetty, S.; Voskov, D.; Bruhn, D. Numerical Strategy for Uncertainty Quantification in Low Enthalpy Geothermal Projects. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, CA, USA, 12–14 February 2018. Paper SGP-TR-213. [Google Scholar]
- Ganguly, S.; Tan, L.; Date, A.; Kumar, M. Numerical investigation of temperature distribution in a confined heterogeneous geothermal reservoir due to injection-production. Energy Procedia 2017, 110, 143–148. [Google Scholar] [CrossRef]
- Rioseco, E.M.; Ziesch, J.; Wawerzinek, B.; Von Hartmann, H.; Thomas, R.; Buness, H. 3-D Geothermal Reservoir Modeling of the Upper Jurassic Carbonate Aquifer in the City of Munich (Germany) under the Thermal-Hydraulic Influence of Optimized Geothermal Multi-Well Patterns—Project GeoParaMoL. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, CA, USA, 12–14 February 2018. Paper SGP-TR-213. [Google Scholar]
- Babaei, M.; Nick, H.M. Performance of low-enthalpy geothermal systems: Interplay of spatially correlated heterogeneity and well-doublet spacings. Appl. Energy 2019, 253, 113569. [Google Scholar] [CrossRef]
- Willems, C.J.L.; Nick, H.M. Towards optimization of geothermal heat recovery: An example from the West Netherlands Basin. Appl. Energy 2019, 247, 582–593. [Google Scholar] [CrossRef]
- Bayerl, M.; Ebner, M.; Clemens, T. Forecasting Low Enthalpy Geothermal Heat Extraction from Saline Aquifers Under Uncertainty. In Proceedings of the SPE Europe Energy Conference Featured at the 84th EAGE Annual Conference and Exhibition, Vienna, Austria, 5–8 June 2023. Paper SPE-214413. [Google Scholar]
- Schulte, D.O.; Arnold, D.; Geiger, S.; Demyanov, V.; Sass, I. Multi-objective optimization under uncertainty of geothermal reservoirs using experimental design-based proxy models. Geothermics 2020, 86, 101792. [Google Scholar] [CrossRef]
- Juliusson, E.; Bjornsson, S. Optimizing production strategies for geothermal resources. Geothermics 2021, 94, 102091. [Google Scholar] [CrossRef]
- Trainor-Guitton, W.J.; Hoversten, G.M.; Nordquist, G.; Intani, R.G. Value of Information Analysis Using Geothermal Field Data: Accounting for Multiple Interpretations & Determining New Drilling Locations; SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2015. [Google Scholar]
- Porlles, J.W.; Jabbari, H. Simulation-Based Patterns Optimization of Enhanced Geothermal Systems. In Proceedings of the 56th US Rock Mechanics/Geomechanics Symposium, Santa Fe, CA, USA, 26–29 June 2022. Paper ARMA 22-2321. [Google Scholar]
- Williams, C.F. Development of Revised Techniques for Assessing Geothermal Resources. In Proceedings of the Twenty-Ninth Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, CA, USA, 26–28 January 2004. Paper SGP-TR-175. [Google Scholar]
- Falcone, G.; Gnoni, A.; Harrison, B.; Alimonti, C. Classification and Reporting Requirements for Geothermal Resources. In Proceedings of the European Geothermal Congress, Pisa, Italy, 3–7 June 2013. [Google Scholar]
- Dewi, M.P.; Setiawan, A.D.; Latief, Y.; Purwanto, W.W. Investment decisions under uncertainties in geothermal power generation. AIMS Energy 2022, 10, 844–857. [Google Scholar] [CrossRef]
- Nandurdikar, N.; Wallace, L. Failure to Produce: An Investigation of Deficiencies in Production Attainment. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. Paper SPE 145437. [Google Scholar]
- Nesvold, E.; Bratvold, R.B. Field Features Do Not Explain Greenfield Production Forecasting Bias. SPE J. 2022, 28, 1290–1307. [Google Scholar] [CrossRef]
- Wang, L.; Oliver, D.S. Efficient Optimization of Well-Drilling Sequence with Learned Heuristics. SPE J. 2019, 24, 2111–2134. [Google Scholar] [CrossRef]
- Bailey, W.; Prange, M. Flow Control Valve Valuation and Value of Information under Uncertainty. SPE J. 2023, 28, 2036–2051. [Google Scholar] [CrossRef]
- Steineder, D.; Clemens, T. Hydrocarbon Field Re-Development in a Bayesian Framework. In Proceedings of the SPE Europec Featured at 82nd EAGE Conference and Exhibition, Amsterdam, The Netherlands, 18–21 October 2021. Paper SPE 205227. [Google Scholar]
- Soltani, M.; Kashkooli, F.M.; Souri, M.; Rafiei, B.; Jabarifar, M.; Gharali, K.; Nathwani, J.S. Envirnomental, economic and social impacts of geothermal energy systems. Renew. Sustain. Energy 2021, 140, 110750. [Google Scholar] [CrossRef]
- Russel, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 4th ed.; Pearson: London, UK, 2021. [Google Scholar]
- Kochenderfer, M.J. Decision Making Under Uncertainty: Theory and Application; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Ayer, O.A.; Stout, N.K. A POMDP Approach to Personalize Mammography Screening Decisions. Oper. Res. 2012, 60, 1019–1034. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, W.; Yang, Q. Multi-stage optimal energy management of multi-energy microgrid in deregulated electricity markets. Appl. Energy 2022, 310, 118528. [Google Scholar] [CrossRef]
- De Paola, G.; Ibanez-Llano, C.; Rios, J.; Kollias, G. Reinforcement Learning for Field Development Policy Optimization. In Proceedings of the SPE Annual Technical Conference & Exhibition, Denver, CO, USA, 5–7 October 2020. Paper SPE 201254. [Google Scholar]
- He, J.; Tang, M.; Hu, C.; Tanaka, S.; Wang, K.; Wen, X.-H.; Nasir, Y. Deep Reinforcement Learning for Generalizable Field Development Optimization. SPE J. 2021, 27, 226–245. [Google Scholar] [CrossRef]
- Gehringer, M.; Loksha, V. Geothermal Handbook: Planning and Financing Power Generation; ESMAP Technical Report 002/12; The International Bank for Reconstruction and Development: Washington, DC, USA, 2012. [Google Scholar]
- IGA. Best Practices Guide for Geothermal Exploration; Report IGA Service GmbH; IGA: Bochum, Germany, 2014. [Google Scholar]
- Gudmundsson, Y. Geothermal Project Timelines. In Proceedings of the 6th African Rift Geothermal Conference, Addis Ababa, Ethiopia, 2–4 November 2016. [Google Scholar]
- Walkup, G.W.; Ligon, J.R. The Good, the Bad, and the Ugly of the Stage-Gate Project Management Process in the Oil and Gas Industry. In Proceedings of the 2006 SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. Paper SPE 102926. [Google Scholar]
- Merrow, E.W. Oil and Gas Industry Megaprojects: Our Recent Track Record. Oil Gas Facil. 2012, 1, 38–42. [Google Scholar] [CrossRef]
- Bratvold, R.B.; Bickel, J.E.; Lohne, H.P. Value of Information in the Oil and Gas Industry: Past, Present, and Future. SPE Reserv. Eval. Eng. 2009, 12, 630–6384. [Google Scholar] [CrossRef]
- Aragon, A.; Izquiedo-Montalvo, G.; Aragon-Gaspar, D.O.; Barreto-Rivera, D.N. Stages of as Integrated Geothermal Project. In Book Renewable Geothermal Energy Explorations; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Cooper, R.G. Stage-gate systems: A new tool for managing new products. Bus. Horizons 1990, 33, 44–54. [Google Scholar] [CrossRef]
- Mishar, S.N. Improving Major Project Development through a Front End Loading Management System: Medco’s way for Oil & Gas Development Project. In Proceedings of the SPE 162254 presented at the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 11–14 November 2012. [Google Scholar]
- Ambrose, J.; Monette, S.A.; Malani, S. Make Better Decisions. In Proceedings of the SPE Hydrocarbon Economics and Evaluation Symposium, Houston, TX, USA, 19–20 May 2014. SPE Paper 169846. [Google Scholar]
- Khalil, T.; Balsubramanian, N.; Lugon, P. ADNOC Journey in Developing an Unified Value Assurance Process for Capital Investment Projects. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 13–16 November 2017. Paper SPE 188485. [Google Scholar]
- Safra, E.B.; Antelo, S.B. Integrated Project Management Applied in World-Class Gas-Field Development Projects: From Theory to Practice. In Proceedings of the SPE Latin American & Caribbean Petroleum Engineering Conference, Lima, Peru, 1–3 December 2010. Paper SPE 139369. [Google Scholar]
- Gao, G.; Lu, H.; Wang, K.; Jost, S.; Shaikh, S.; Vink, J.; Blom, C.; Wells, T.; Saaf, F. A Practical Approach to Select Representative Deterministic Models Using Multiobjective Optimization from an Integrated Uncertainty Workstream. SPE J. 2023, 28, 2186–2206. [Google Scholar] [CrossRef]
- Balasubramanian, S.; Wang, B.; Li, Y.; Ginger, E.P.; Liang, B.; McKay, D.M.; Brinkman, J.J.; Ogden, K.A.; Kennedy, D.D.; Wilcox, W.T.; et al. Subsurface Appraisal and Field Development Planning of the Gas Condensate Field GVLA. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2013. Paper OTC 24108. [Google Scholar]
- Alkhatib, M.; Ali, A.A.A.; Mukhtar, M.; Park, S.; Ghorayeb, K.; Nasiri, A.; Sha, A.R.; Ojha, A. A Novel Holistic Workflow for Field Development Planning in Green Field Envirnoment: A Case Study. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 12–15 November 2018. Paper SPE 193140. [Google Scholar]
- Ibrahimov, T. History of History Match in Azeri Field. In Proceedings of the SPE Annual Caspian Technical Conference & Exhibition, Baku, Azerbaijan, 4–6 November 2015. Paper SPE 177395. [Google Scholar]
- Spetzler, C.; Winter, H.; Meyer, J. Decision Quality: Value Creation from Better Business Decisions; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Sauve, R.; Lindvig, T.; Stenhaug, M.; Holyfield, S. Integrated Field Development: Process and Productivity. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019. Paper OTC-29631. [Google Scholar]
- Siler, D.L.; Pepin, J.D.; Vessilinov, V.V.; Mudunuru, M.K.; Ahmmed, B. Machine learning to identify geological factors associated with production in geothermal fields: A case-study using 3D geologic data, Brady geothermal field, Nevada. Geotherm. Energy 2021, 9, 17. [Google Scholar] [CrossRef]
- Suzuki, A.; Fukui, K.-I.; Onodera, S.; Ishizaki, J.; Hashida, T. Data-Driven Geothermal Reservoir Modeling: Estimating Permeability Distributions by Machine Learning. Geosciences 2022, 12, 130. [Google Scholar] [CrossRef]
- Major, M.; Daniilidis, A.; Hansen, T.M.; Khait, M.; Voskov, D. Influence of process-based, stochastic and deterministic methods for representing heterogeneity in fluvial geothermal systems. Geothermics 2023, 109, 102651. [Google Scholar] [CrossRef]
- Kochenderfer, M.J.; Tim, A.; Wheeler, T.A.; Wray, K.A. Algorithms for Decision Making; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Tversky, A.; Kahneman, D. Judgment under Uncertainty: Heuristics and Biases. Science 1974, 185, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Kim, N.; Kim, J.; Kang, H. How Does AI Improve Human Decision-Making? Evidence from the AI-Powered Go Program. USC Marshall School of Business Research Paper Sponsored by iORB, No. Forthcoming. 2023. Available online: https://ssrn.com/abstract=3893835 (accessed on 14 January 2024).
- SPE. Guidance for Decision Quality for Multicompany Upstream Projects; Technical Report SPE 181246; Society of Petroleum Engineers: Dallas, TX, USA, 2016. [Google Scholar]
- Schuyler, J. Portfolio Management: What is the Contribution to Shareholder Value? In Proceedings of the SPE Hydrocarbon Economics and Evaluation Symposium, Dallas, TX, USA, 5–8 April 2003. Paper SPE 82031. [Google Scholar]
- Holden, C.W. Maximizing Portfolio Value with Specified Assurance. In Proceedings of the 2005 SPE Hydrocarbon Economics and Evaluation Symposium, Dallas, TX, USA, 3–5 April 2005. Paper SPE 94438. [Google Scholar]
- Allen, D.P.B. Handling Risk and Uncertainty in Portfolio Production Forecasting. SPE Econ. Manag. 2017, 9, 37–42. [Google Scholar] [CrossRef]
- Luan, P. How To Avoid Project Train Wrecks. Oil Gas Facil. 2016, 5, 24–28. [Google Scholar] [CrossRef]
- Paribelli, L.; Guarino, M. Project Strategic Framing Approach—The Strategy Table. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 15–18 November 2021. Paper SPE 207323. [Google Scholar]
- Harzhauser, M.; Kranner, M.; Mandic, O.; Strauss, P.; Siedl, W.; Piller, W.E. Miocene lithostratigraphy of the northern and central Vienna Basin (Austria). Austrian J. Earth Sci. 2020, 113, 169–199. [Google Scholar] [CrossRef]
- Büchele, R.; Haas, R.; Hartner, M.; Hirner, R.; Hummel, M.; Kranzl, L.; Müller, A.; Ponweiser, K.; Bons, M.; Grave, K.; et al. Bewertung des Potenzials für den Hocheffizienten KWK und Effizienter Fernwärme- und Fernkälteversorgung; Technical Report TU Wien and Ecofys; Technical UniversityWien and Ecofys: Wien, Austria, 2015. [Google Scholar]
- Königshofer, K.; Domberger, G.; Gunczy, S.; Hingsamer, M.; Pucker, J.; Schreilechner, M.; Amtmann, J.; Goldbrunner, J.; Heiss, H.P.; Füreder, J.; et al. Potenzial der Tiefengeothermie für die Fernwärme- und Stromproduktion in Österreich; Joanneum Research Forschungsgesellschaft mbH: Graz, Austria, 2014. [Google Scholar]
- Wessely, G. Structure and development of the Vienna basin in Austria. Am. Assoc. Petrol. Geol. Mem. 1988, 45, 333–346. [Google Scholar]
- Arzmüller, G.; Buchta, S.B.; Ralbovsky, E.; Wessely, G. The Vienna Basin. In The Carpathians and Their Foreland: Geology and Hydrocarbon Resources, AAPG Memoir 84; Golonka, J., Picha, F.J., Eds.; American Association of Petroleum Geologists: Tulsa, OK, USA, 2006; pp. 191–204. [Google Scholar] [CrossRef]
- Weissenbäck, M. Lower to Middle Miocene sedimentation model of the central Vienna Basin. In Oil and Gas in Alpidic Thrustbelts and Basins of Central and Eastern Europe; Special Publications 5; European Association of Geoscientists and Engineers EAGE: Utrecht, The Netherlands, 1996; pp. 355–363. [Google Scholar]
- Corso, A.; Chiotoroiu, M.; Clemens, T.; Zechner, M.; Kochenderfer, M.J. Sequentially optimized data acquisition for a geothermal reservoir. Geothermics 2024, 120, 102983. [Google Scholar] [CrossRef]
- Sieberer, M.; Clemens, T.; Peisker, J.; Ofori, S. Polymer-Flood Field Implementation: Pattern Configuration and Horizontal vs. Vertical Wells. SPE Reserv. Eval. Eng. 2019, 22, 577–596. [Google Scholar] [CrossRef]
- Blank, L.; Rioseco, E.M.; Caiazzo, A.; Wilbrandt, U. Modeling, simulation, and optimization of geothermal energy production from hot sedimentary aquifers. Comput. Geosci. 2020, 25, 67–104. [Google Scholar] [CrossRef]
- Steineder, D.; Clemens, T. Including Oil Price Uncertainty in Development Option Selection Taking the Project Portfolio into Account. In Proceedings of the SPE Europec Featured at 81st EAGE Conference and Exhibition, London, UK, 3–6 June 2019. Paper SPE 195440. [Google Scholar]
- Narayanan, M.; Abdulazeez, M.; Bukhamsin, K.; Alshehri, N. Stochastic Economic Ranking—A Prudent Way to Address Risk and Uncertainty for Decision Makers. In Proceedings of the Middle East Oil, Gas and Geosciences Show, Manama, Bahrain, 19–21 February 2023. Paper SPE 213385. [Google Scholar]
- Demirmen, F. Use of “Value of Information” Concept in Justification and Ranking of Subsurface Appraisal. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 6–9 October 1996. Paper SPE 36631. [Google Scholar]
- Bratvold, R.B.; Mohus, E.; Petutschnig, D.; Bickel, E. Production Forecasting: Optimistic and Overconfident—Over and Over Again. SPE Reserv. Eval. Eng. 2020, 23, 0799–0810. [Google Scholar] [CrossRef]
- Fenwick, D.; Scheidt, C.; Caers, J. Quantifying Asymmetric Parameter Interactions in Sensitivity Analysis: Application to Reservoir Modeling. Math. Geosci. 2014, 46, 493–511. [Google Scholar] [CrossRef]
- Kurniawati, H.; Hsu, D.; Lee, W.S. SARSOP: Efficient point-based POMDP planning by approximating optimally reachable belief spaces. In Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Leeftink, T.; Velez, D.A.; Godderij, R. Overestimation in Operators Budgets and Long-Term Forecasting; A Non-Operator Perspective. In Proceedings of the SPE Europec featured at the 81st EAGE Conference and Exhibition, London, UK, 23–26 June 2019. Paper SPE 195519. [Google Scholar]
- Van der Haar, K. The Contingent Resources Class: Non-Differentiation of Contingent Resources and Its Implications. In Proceedings of the SPE/IATMI Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 10–12 October 2023. Paper SPE 215462. [Google Scholar]
- Koninx, J.P.M. Value of Information: From Cost Cutting to Value Creation. J. Pet. Technol. 2001, 53, SPE 69836. [Google Scholar] [CrossRef]
- Coopersmith, E.M.; Cunningham, P.C. A Practical Approach to Evaluating the Value of Information and Real Option Decisions in the Upstream Petroleum Industry. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. Paper SPE 77582. [Google Scholar]
- Wills, H.A.; Graves, R.M.; Miskimins, J. Don’t Be Fooled by Bayes. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004. Paper SPE 90717. [Google Scholar]
- Santos, S.M.G.; Schiozer, D.J. Assessing the Value of Information According to Attitudes Towards Downside Risk and Upside Potential. In Proceedings of the SPE Europec Featured at 79th EAGE Annual Conference and Exhibition, Paris, France, 12–15 June 2017. Paper SPE 185841. [Google Scholar]
- Steineder, D.; Clemens, T.; Osivandi, K.; Thiele, M.R. Maximizing the Value of Information of a Horizontal Polymer Pilot Under Uncertainty Incorporating the Risk Attitude of the Decision Maker. SPE Reserv. Eval. Eng. 2018, 22, 756–774. [Google Scholar] [CrossRef]
- El Souki, O.A.; Saad, G.A. A Stochastic Approach for Optimal Sequencing of Appraisal Wells. SPE Reserv. Eval. Eng. 2016, 20, 334–341. [Google Scholar] [CrossRef]
- Trainor-Guitton, W. The value of geophysical data for geothermal exploration: Examples from empirical, field, and synthetic data. Geophysics 2020, 39, 864–872. [Google Scholar] [CrossRef]
- Akar, S.; Young, K.R. Assessment of New Approaches in Geothermal Exploration Decision Making. In Proceedings of the 40th Workshop on Geothermal Reservoir Engineering, Sanford, FL, USA, 26–28 January 2015. [Google Scholar]
- Bang, D.; Frith, C.D. Making better decisions in groups. R. Soc. Open Sci. 2017, 4, 170193. [Google Scholar] [CrossRef]
- Felfernig, A.; Müslum, A.; Martin Stettinger, M.; Tran, T.N.T.; Leitner, G. Biases in Group Decisions. In Group Recommender Systems—An Introduction; Felfernig, A., Boratto, L., Stettinger, M., Tkalcic, M., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).