A Bi-Level Optimal Scheduling Strategy for Microgrids for Temperature-Controlled Capacity and Time-Shifted Capacity, Considering Customer Satisfaction
Abstract
1. Introduction
2. Temperature-Controlled Capacity and Time-Shifted Capacity Modeling
2.1. Temperature-Controlled Load ETP Model
2.2. Temperature-Controlled Capacity
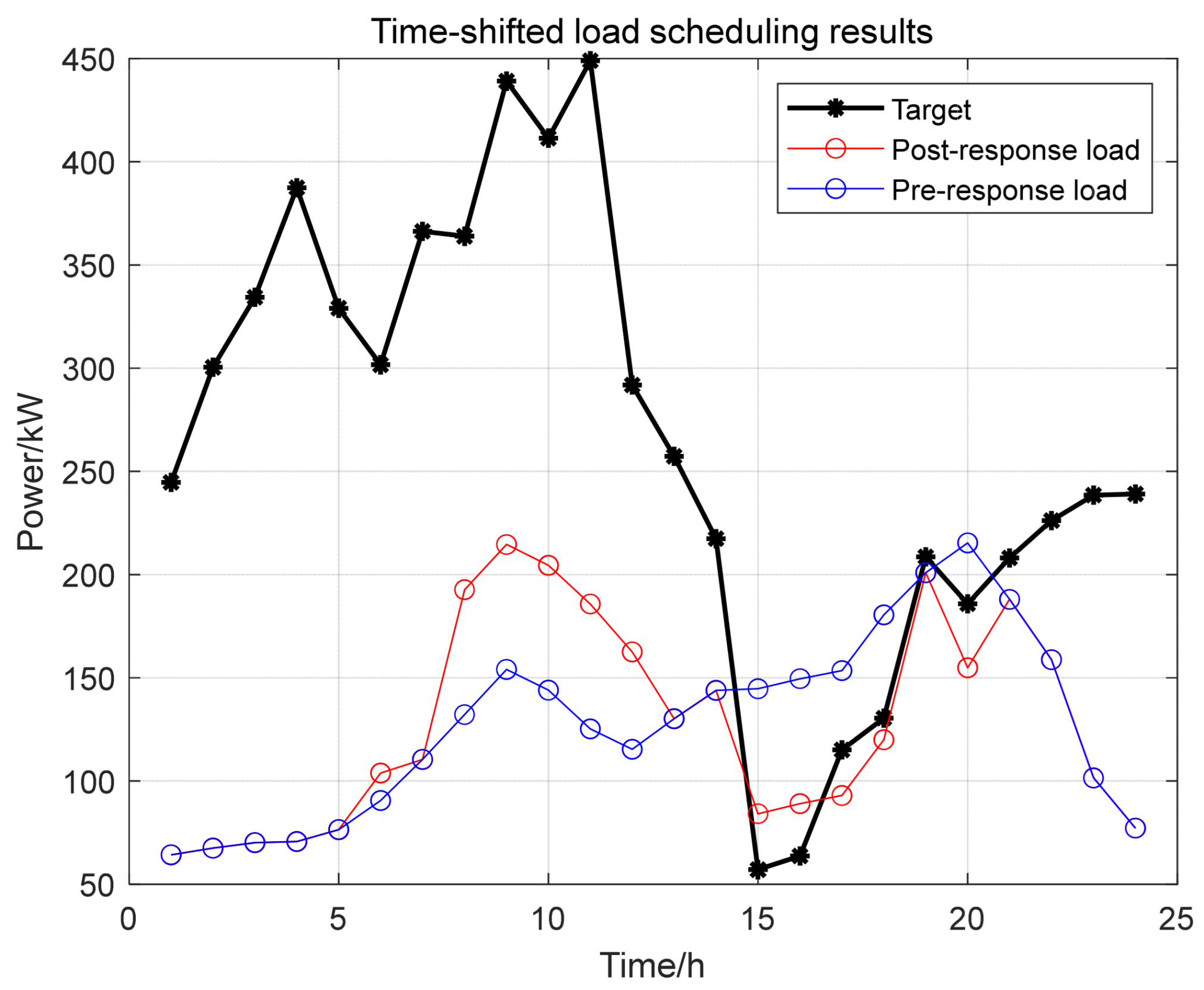
2.3. Time-Shiftable Capacity
3. A Bi-Level Scheduling Model for Microgrids with Satisfaction Consideration
3.1. Overall Composition of the Microgrid
3.2. Objective Function
3.2.1. Upper-Level Optimization Model
3.2.2. Lower-Level Optimization Model
3.2.3. Total Social Benefit Functions
3.3. Constraints
3.3.1. Power Equilibrium Constraint
3.3.2. Upper and Lower Temperature Constraints
3.3.3. Transfer Time and Volume Constraints
3.3.4. Renewable Energy Output Constraints
3.3.5. Micro-Power Output Constraints
3.3.6. Storage Battery Operating Constraints
3.4. Solving Methods
4. Simulation Analysis
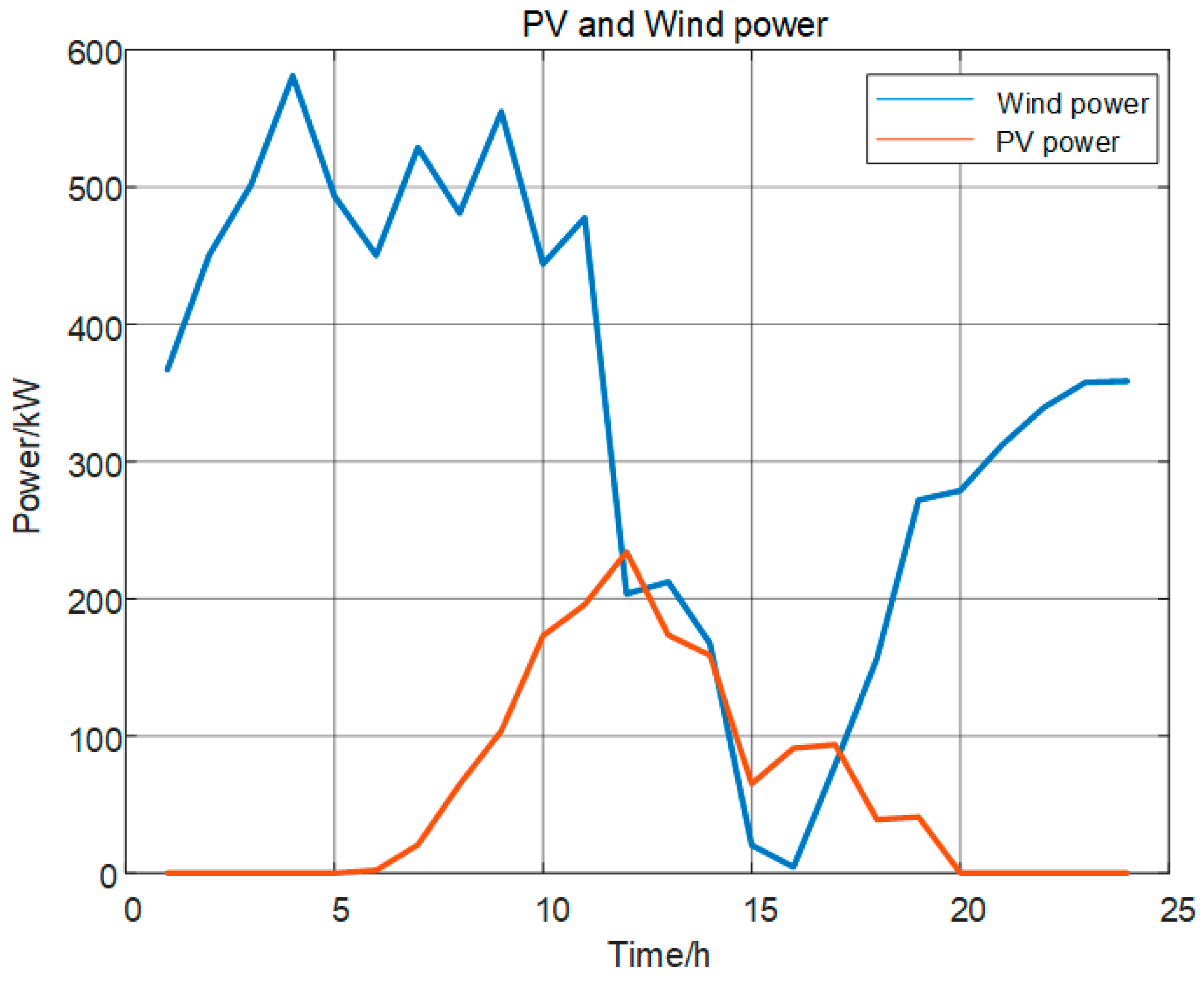
4.1. Experimental Settings
- (1)
- No temperature-controlled capacity and no time-shifted capacity in the microgrid;
- (2)
- Time-shifted capacity but no temperature-controlled capacity in the microgrid;
- (3)
- Temperature-controlled capacity but no time-shifted capacity in the microgrid;
- (4)
- Temperature-controlled capacity and time-shifted capacity in the microgrid.
4.2. Effectiveness Analysis of the Proposed Method
4.3. Scheduling Results
4.3.1. Scenario 1 Scheduling Results
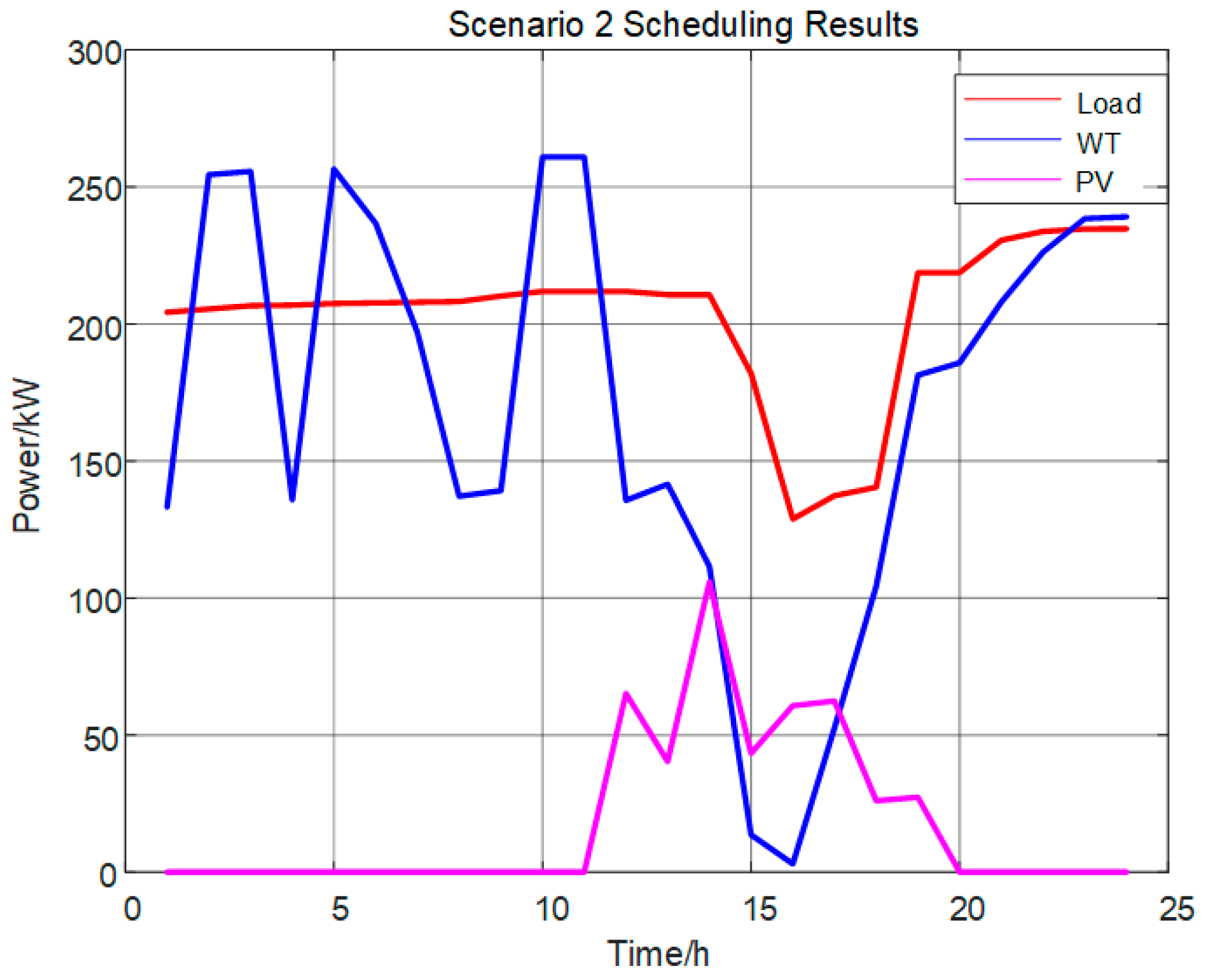
4.3.2. Scenario 2 Scheduling Results
4.3.3. Scenario 3 Scheduling Results
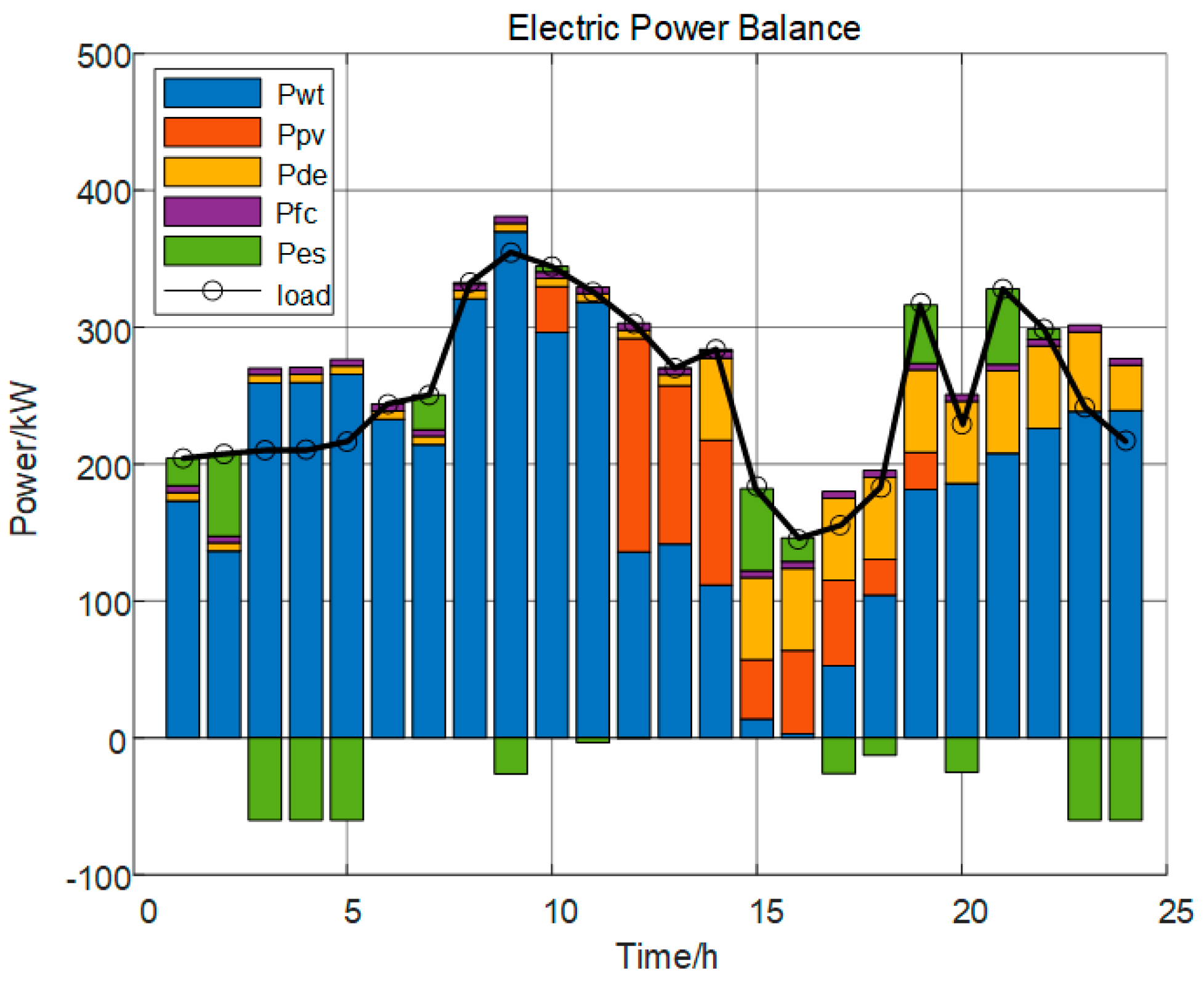
4.3.4. Scenario 4 Scheduling Results
4.4. Temperature-Controlled Capacity and Time-Shifted Capacity Analysis
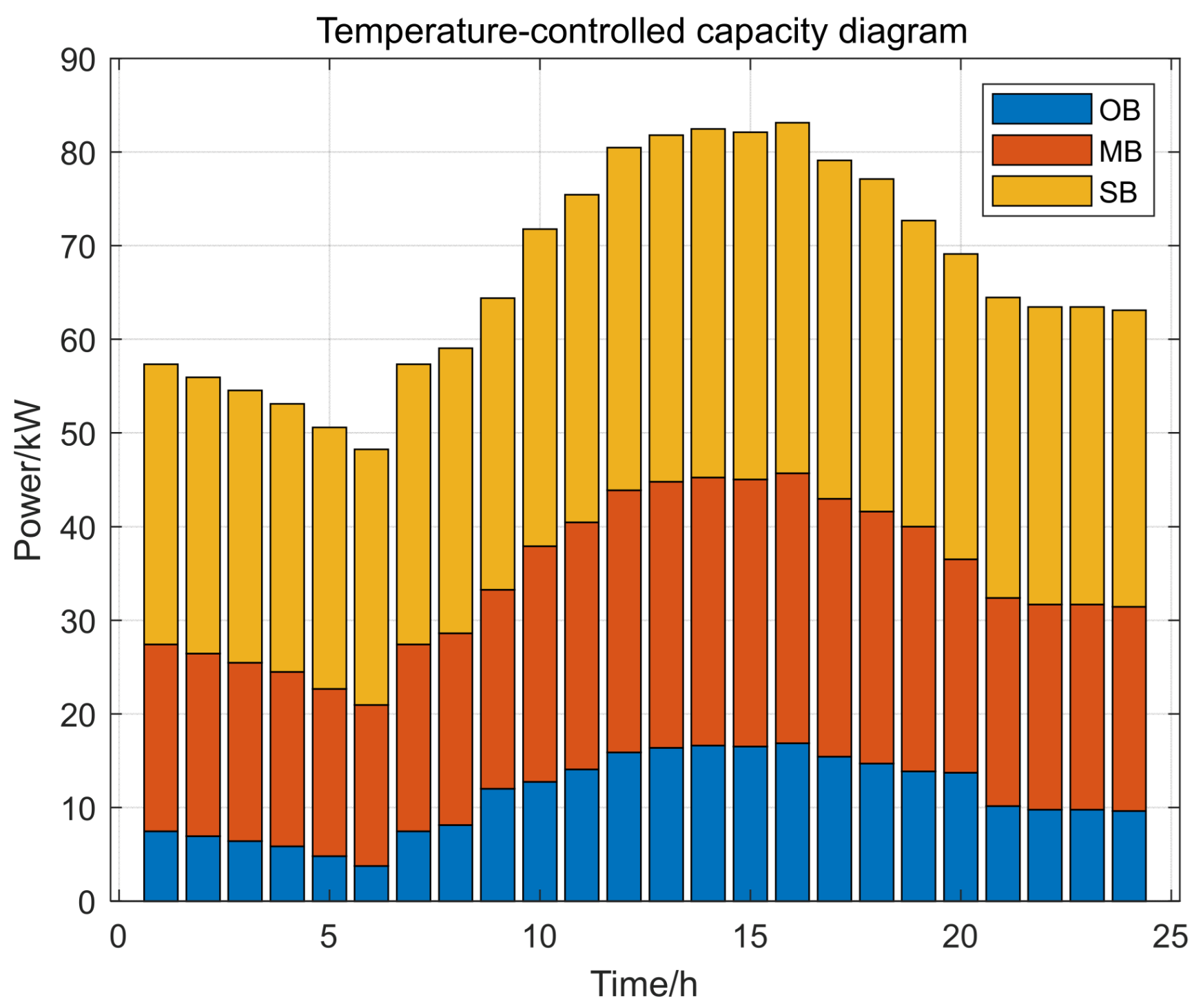
4.4.1. Temperature-Controlled Capacity Analysis
4.4.2. Time-Shifted Capacity Analysis
4.5. Impact of Different Levels of Satisfaction
5. Conclusions
- (1)
- Synthesizing the respective characteristics of the population, the decentralized temperature-controlled loads of different types of residences are aggregated to form a considerable scale of temperature-controlled capacity through the rotation control strategy, which makes the results more reasonable and realistic; the regulation potential of a large number of commonly used time-sharing loads on the user side is utilized through the time-sharing scheduling strategy, which creates time-sharing capacity to participate in the scheduling.
- (2)
- After clustering the two types of loads to form a significant demand response resource, the effectiveness of the model was tested by the measured data in the Xinjiang Uygur Autonomous Region. The results show that the model improves the overall economy of microgrid operation, reduces the peak-to-valley gap of the microgrid system, and greatly improves the new energy consumption rate and the total social benefits.
- (3)
- A comprehensive electricity satisfaction model is used to represent the consumption preferences of residents and also to analyze their impact on the economic efficiency of the microgrid. Favoring comprehensive satisfaction will result in the loss of social benefits, and on the contrary, favoring social benefits will sacrifice users’ electricity consumption habits. The method provides a reference for future microgrids to achieve a better balance between supply and demand, and at the same time can improve the operational efficiency of microgrids.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Time | High-Income Youth | General-Income Youth | High-Income Elderly | General-Income Elderly |
|---|---|---|---|---|
| 00:00–07:00 | [16, 25] | [14, 22] | [18, 26] | [16, 24] |
| 07:00–12:00 | [14, 22] | [14, 19] | [15, 23] | [15, 22] |
| 12:00–16:00 | [14, 22] | [14, 19] | [15, 24] | [14, 23] |
| 16:00–19:00 | [14, 22] | [14, 19] | [15, 23] | [15, 22] |
| 19:00–22:00 | [12, 23] | [14, 20] | [15, 24] | [15, 23] |
| 22:00–24:00 | [16, 25] | [14, 22] | [18, 26] | [16, 24] |
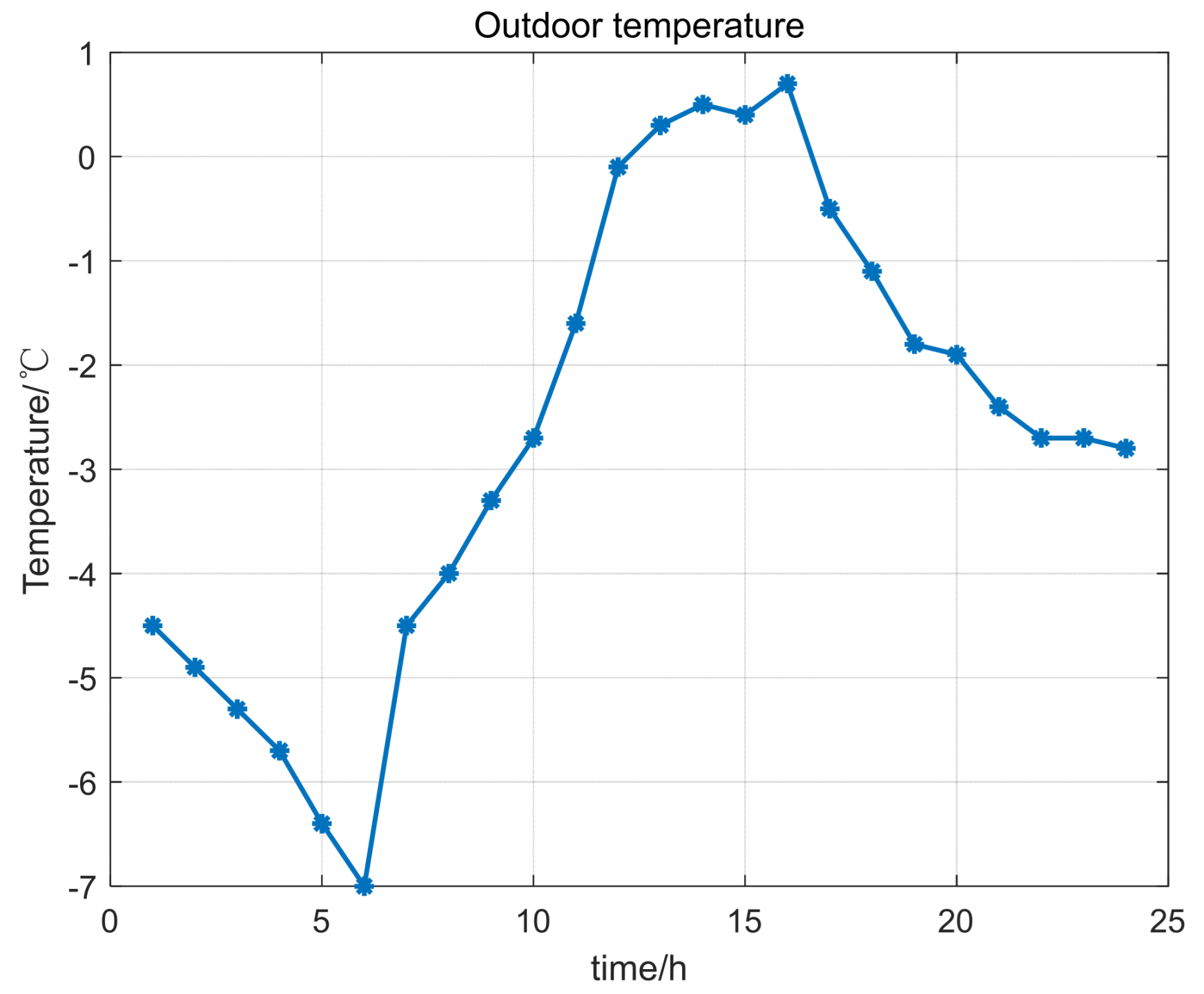
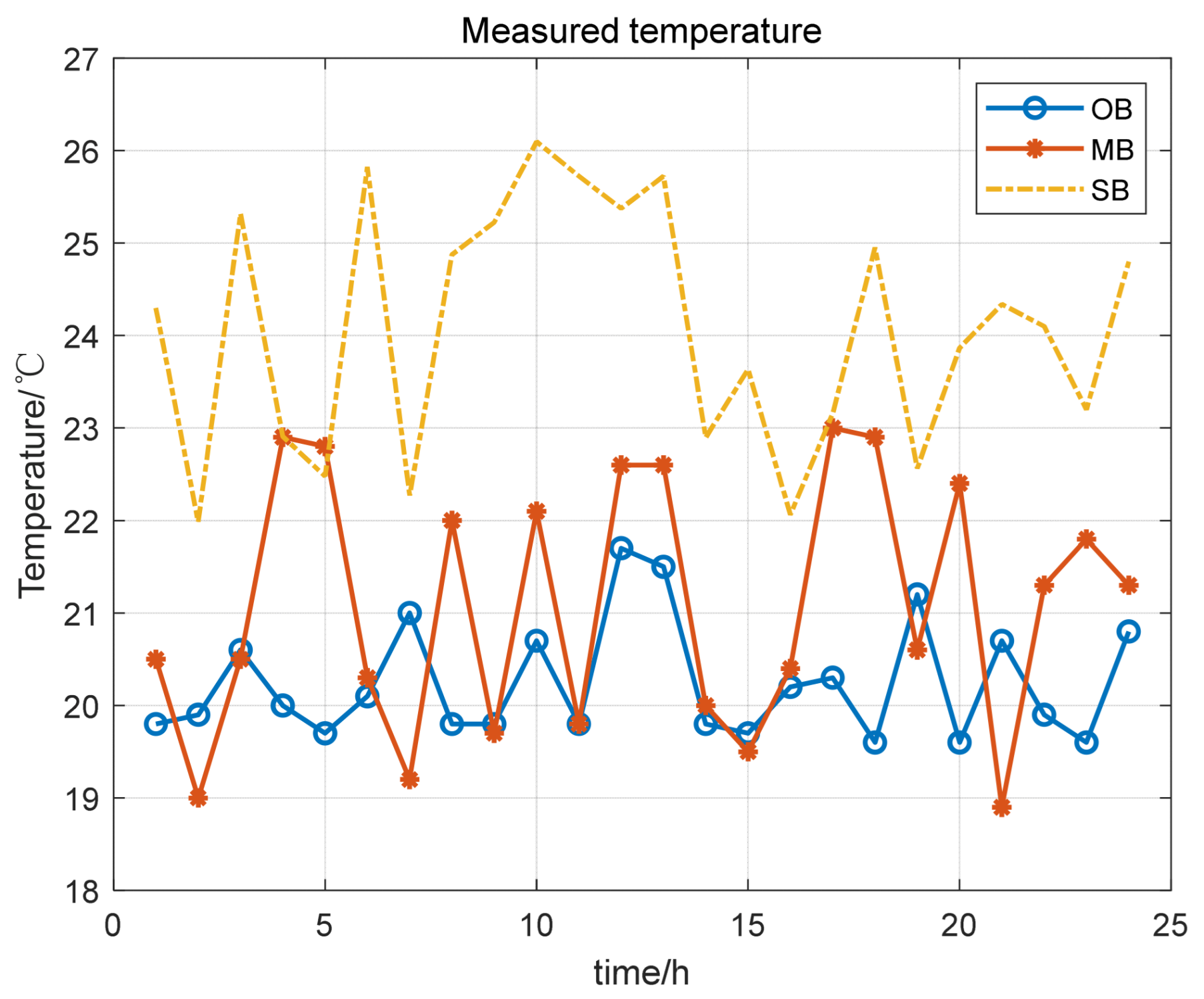
| Type | Thermal Resistance | Thermal Resistance | TL Power/kW |
|---|---|---|---|
| Superior buildings | [5.30, 5.51] | [0.10, 0.14] | 5 |
| Medium buildings | [5.81, 5.92] | [0.14, 0.18] | 6 |
| Ordinary buildings | [6.08, 6.23] | [0.17, 0.23] | 7.2 |
| Power Type | Power Range | Quantity | O and M Cost /(CNY∙kWh−1) | Penalty Cost /(CNY∙kWh−1) |
|---|---|---|---|---|
| WT | [0, 100] | 5 | 0.15 | 0.6 |
| PV | [0, 40] | 5 | 0.25 | 0.6 |
| DE | [5, 60] | 1 | 0.088 | 0 |
| FC | [5, 40] | 1 | 0.0293 | 0 |
| Power Type | CO2/(g∙kWh−1) | SO2/(g∙kWh−1) | NOX/(g∙kWh−1) |
|---|---|---|---|
| WT | 0 | 0 | 0 |
| PV | 0 | 0 | 0 |
| DE | 649 | 0.206 | 9.89 |
| FC | 489 | 0.003 | 0.01 |
| Parameters | CO2/(g∙kWh−1) | SO2/(g∙kWh−1) | NOX/(g∙kWh−1) |
|---|---|---|---|
| Management costs/(CNY∙kg−1) | 0.21 | 14.842 | 62.964 |
References
- Ju, Y.; Li, H.; Yu, Z.; Yan, Y.; Zheng, L. Bi-level Robust Capacity Planning of Micro-grid Considering Multivariate Uncertainties and Reserve Demand. Power Syst. Technol. 2023, 47, 3343–3354. [Google Scholar]
- Liu, S.; Li, Z.; Wang, Y.; Ma, R.; Lu, D.; Liu, H. Optimal capacity allocation of energy storage in micro-grid with distributed generation. Power Syst. Prot. Control 2016, 44, 78–84. [Google Scholar]
- Li, J.; Zheng, X.; Ai, X.; Wen, J.; Sun, S.; Li, G. Optimal design of capacity of distributed generation in island standalone microgrid. Trans. China Electrotech. Soc. 2016, 31, 176–184. [Google Scholar]
- Wang, L.; Liu, J.; Tian, C. Capacity optimization of hybrid energy storage in microgrid based on statistic method. Power Syst. Technol. 2018, 42, 187–194. [Google Scholar]
- Han, L.; Li, F.; Zhou, E. The distributed energy optimization configuration of micro-grid based on cost-benefit. Trans. China Electrotech. Soc. 2015, 30, 388–396. [Google Scholar]
- Ding, M.; Liu, X.; Xie, J.; Pan, H. Optimal planning model of grid-connected micro grid considering comprehensive performance. Power Syst. Prot. Control 2017, 45, 18–26. [Google Scholar]
- Li, Y.; Yao, J.; Yong, T.; Ju, P.; Yang, S.; Shi, X. Estimation approach to aggregated power and response potential of residential thermostatically controlled loads. Proc. CSEE 2017, 37, 5519–5528. [Google Scholar]
- Jiang, A.; Wei, H. A dynamic optimized model and the on-line control strategy response to uncertainty PTR for the CPS of smart air conditioning. Proc. CSEE 2016, 36, 1536–1543. [Google Scholar]
- Yang, Y.L.; Wang, T.; Mu, G.; Yan, Q.; Liu, J.; Han, Y.; Liu, R.; Fan, W. Evaluation of peak-shaving capability of distributed electric heating load group based on measured data. Electr. Power Constr. 2018, 39, 95–101. [Google Scholar]
- Tan, Y.; Guo, L.; Chen, J.; Zhang, H. Carbon crystal electric heating panel heating system test simulation and temperature control adjustment. J. Harbin Inst. Technol. 2012, 44, 70–73. [Google Scholar]
- Vanouni, M.; Lu, N. Improving the centralized control of thermostatically controlled appliances by obtaining the right information. IEEE Trans. Smart Grid 2015, 6, 946–948. [Google Scholar] [CrossRef]
- He, S.; Zheng, Y.; Ca, X. Receding-Horizon Optimization for Microgrid Energy Management. Power Syst. Technol. 2014, 38, 2349–2355. [Google Scholar]
- Chen, Y.; Tian, L.T.; Qi, N.; Zhang, F.; Cheng, L. Optimization method of resource combination for virtual power plant based on modern portfolio theory. Autom. Electr. Power Syst. 2022, 46, 146–154. [Google Scholar]
- Huang, X. Capacity Optimization of Distributed Generation for Stand-alone Microgrid Considering Controllable Load. Proc. CSEE 2018, 38, 1962–1974. [Google Scholar]
- Liu, W.; Wang, Z.; Xiao, T.; Lu, C. AMI data-driven state evaluation method for measurement operation error of electric vehicle charging facilities. Electr. Power Autom. Equip. 2022, 42, 70–76. [Google Scholar]
- Li, Q.; Zhang, Y.; Chen, J.; Yi, Y.; He, F. Development patterns and challenges of ubiquitous power Internet of Things. Autom. Electr. Power Syst. 2020, 44, 13–22. [Google Scholar]
- Fan, K.; Xu, B.; Dong, J. Identification method for feeder topology based on successive polling of smart terminal unit. Autom. Electr. Power Syst. 2015, 39, 180–186. [Google Scholar]
- Zhang, Q.; Wang, X.; Wang, J.; Feng, C.; Liu, L. Survey of demand response research in deregulated electricity markets. Autom. Electr. Power Syst. 2008, 32, 97–106. [Google Scholar]
- Zou, Y.; Yang, L.; Feng, L.; Xu, Z.; Fu, X.; Ye, C. Coordinated heat and power dispatch of microgrid considering two-dimensional controllability of heat loads. Autom. Electr. Power Syst. 2017, 41, 13–19. [Google Scholar]
- Qi, Y.; Wang, D.; Jia, H.; Wang, R.; Chen, N.; Wei, W.; Fan, M. Study on demand response method of temperature control equipment based on normalized temperature extension margin control strategy. Proc. CSEE 2015, 35, 5455–5464. [Google Scholar]
- Nan, M.; Liang, C.; Jian, H. Adaptive behavior and different thermal experiences of real people: A Bayesian neural network approach to thermal preference prediction and classification. Build. Environ. 2021, 198, 107875. [Google Scholar]
- Buratti, C.; Ricciardi, P.; Vergoni, M. A simplified model to predict thermal comfort conditions in moderate environments. Appl. Energy 2013, 104, 117–127. [Google Scholar] [CrossRef]
- Liang, Z.; Zhang, J.; Wang, X.; Zhang, H. Statistical analysis of household controllable load based on questionnaire survey. Power Demand Side Manag. 2023, 25, 102–109. [Google Scholar]
- Zhang, H.; Wang, M.; Yin, S.; Bai, Y.; Zhang, Q.; Zhang, Y. Master-slave game optimization of decentralized electric heating system considering user’s consumption preference. Power Syst. Technol. 2023, 47, 2262–2272. [Google Scholar]
- Le, L. Study of Economic Operation in Microgrid; North China Electric Power University: Beijing, China, 2011; pp. 18–20. [Google Scholar]
- Yi, L. Optimal Configuration of Distributed Generations and Economic Dispatch for Microgrid; Shanghai Electric Power University: Shanghai, China, 2014; pp. 34–36. [Google Scholar]

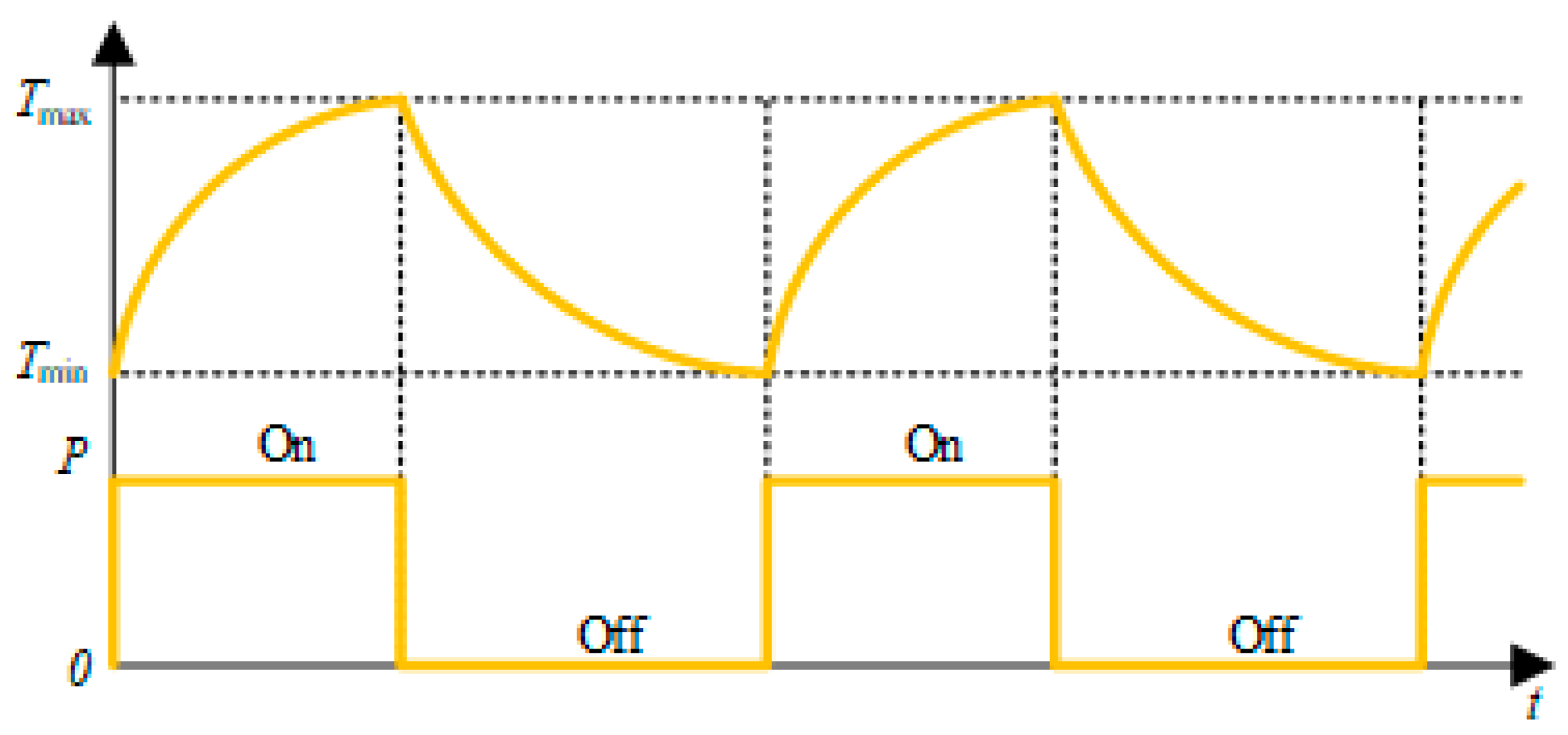

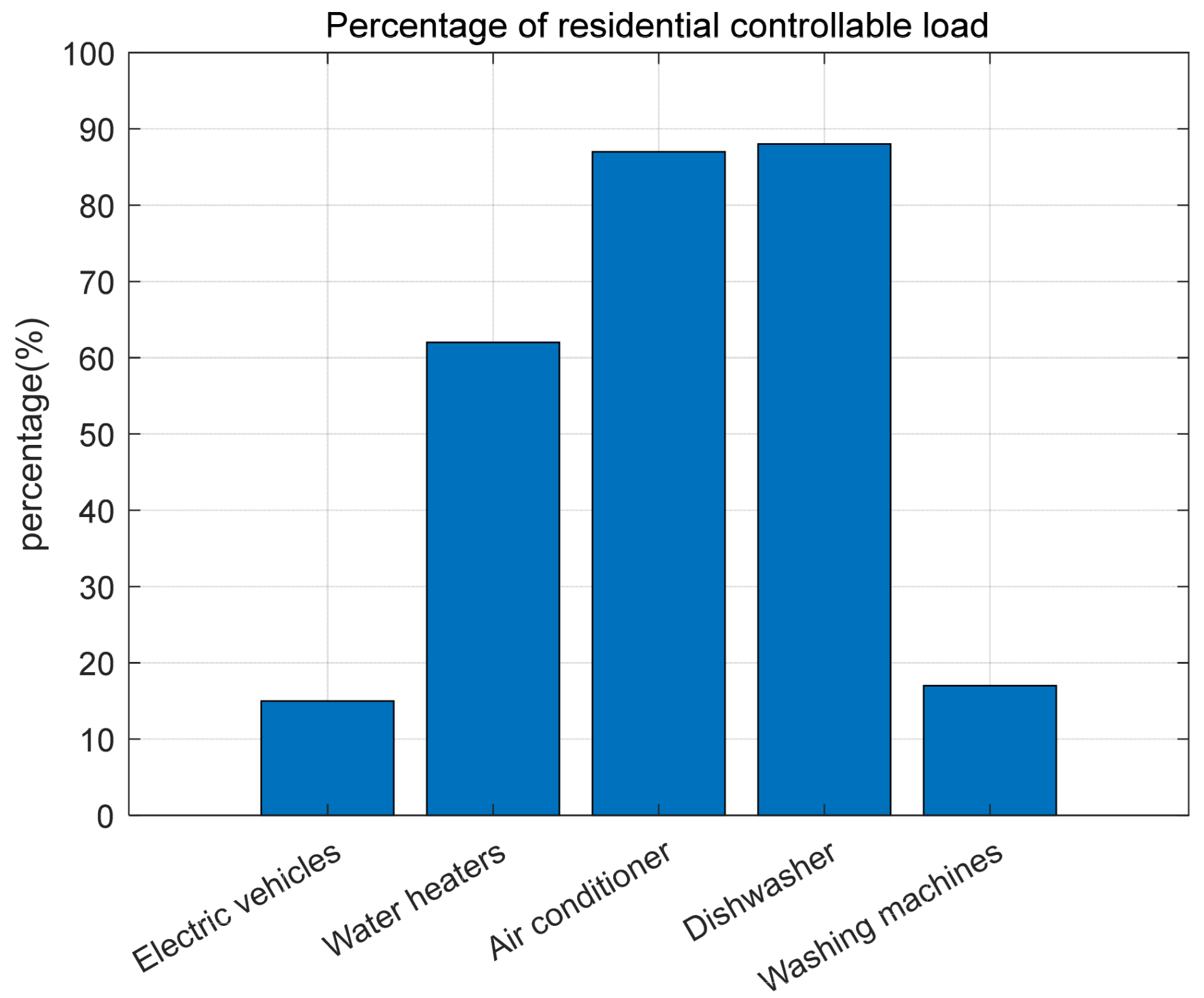





| Type | TR | a | b | c | Optimal Temperature |
|---|---|---|---|---|---|
| The young | 0.5 | 0.272 | 0.248 | 7.245 | 24 |
| 1.0 | 0.242 | 0.614 | 5.587 | 24 | |
| The elderly | 1.0 | 0.149 | −0.107 | 2.640 | 26 |
| 1.5 | 0.148 | −0.137 | 2.524 | 24 |
| Time/min | Temperature-Controlled Load | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 6 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 7 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 8 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 9 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 10 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 11 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 12 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 13 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 14 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 15 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 16 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 17 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 18 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 19 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 20 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Type | Water Heater | Dishwasher | Washing Machine |
|---|---|---|---|
| Power value/kW | [2, 1.6, 1.2] | 0.8 | [0.5, 0.2] |
| Duration/h | [1, 1, 1] | 1 | [1, 1] |
| Period | Tariff | |
|---|---|---|
| Peak | 11:00–14:00 18:00–21:00 | 0.3 |
| Flat | 07:00–11:00 14:00–18:00 21:00–23:00 | 0.2 |
| Valley | 00:00–07:00 23:00–24:00 | 0.1 |
| Scenario Type | TL | SL | Microgrid Benefits/CNY | Consumption |
|---|---|---|---|---|
| 1 | / | / | 178.15 | 53.02% |
| 2 | / | √ | 252.00 | 69.69% |
| 3 | √ | / | 259.24 | 71.32% |
| 4 | √ | √ | 327.43 | 83.55% |
| Microgrid Benefits | Satisfaction | Social Benefits/CNY |
|---|---|---|
| 0.3 | 0.7 | 194.78 |
| 0.5 | 0.5 | 347.41 |
| 0.7 | 0.3 | 499.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhang, Z. A Bi-Level Optimal Scheduling Strategy for Microgrids for Temperature-Controlled Capacity and Time-Shifted Capacity, Considering Customer Satisfaction. Energies 2024, 17, 1803. https://doi.org/10.3390/en17081803
Yang Y, Zhang Z. A Bi-Level Optimal Scheduling Strategy for Microgrids for Temperature-Controlled Capacity and Time-Shifted Capacity, Considering Customer Satisfaction. Energies. 2024; 17(8):1803. https://doi.org/10.3390/en17081803
Chicago/Turabian StyleYang, Yulong, and Zhiwei Zhang. 2024. "A Bi-Level Optimal Scheduling Strategy for Microgrids for Temperature-Controlled Capacity and Time-Shifted Capacity, Considering Customer Satisfaction" Energies 17, no. 8: 1803. https://doi.org/10.3390/en17081803
APA StyleYang, Y., & Zhang, Z. (2024). A Bi-Level Optimal Scheduling Strategy for Microgrids for Temperature-Controlled Capacity and Time-Shifted Capacity, Considering Customer Satisfaction. Energies, 17(8), 1803. https://doi.org/10.3390/en17081803






